Next Article in Journal
Federation in Digital Twins and Knowledge Transfer: Modeling Limitations and Enhancement
Previous Article in Journal
Finite-Time Adaptive Control for Electro-Hydraulic Braking Gear Transmission Mechanism with Unilateral Dead Zone Nonlinearity
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Machines
Volume 12
Issue 10
10.3390/machines12100700
machines-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Impact of Drawing Machine Parameters on Force and Energy Consumption in Borosilicate Glass Tube Production

by
Peng Liu
1,2,
Limin Cang
1,
Zhigang Wan
1,
Ke Yang
1,
Ming Chen
1,
Rangling Li
2 and
Tie Geng
2,*
1
Henan Ancai Hi-Tech Limited Liability Company, Anyang 455000, China
2
School of Mechanical and Electrical Engineering, Henan University of Technology, Zhengzhou 450001, China
*
Author to whom correspondence should be addressed.
Machines 2024, 12(10), 700; https://doi.org/10.3390/machines12100700
Submission received: 15 September 2024 / Revised: 29 September 2024 / Accepted: 1 October 2024 / Published: 3 October 2024
Browse Figures
Versions Notes

Abstract

:
Middle borosilicate glass tubes are critical materials for medical packaging, with the drawing machine playing a pivotal role in their production process. However, the effects of the drawing wheel’s motion parameters on the glass tube remain underexplored. Therefore, based on the finite element method simulation and validation experiment, the effects of experimental factors (angle of upper and lower drawing wheel, AUD; friction factor of glass and rubber, FFGR; and distance of upper and lower drawing wheel, DUD) on experimental indexes (maximum effective stress of glass tube, MES; rotational speed of glass tube, RSG; maximum and average forward driving force, MFDF and AFDF; maximum and average rotational driving force, MRDF and ARDF; total energy consumption and power, TEC and TPD; maximum and average forward driving power, MFDP and AFDP; and maximum and average rotational driving power, MRDP and ARDP) were analyzed. The results indicated that compared to FFGR and AUD, the influence of DUD on experimental indexes was the highest. The positive influence of AUD on RSG, ARDP, and MRDP, the positive influence of FFGR and the negative influence of DUD on MRDF, ARDF, TEC, TPD, ARDP, and MRDP were found, respectively. These findings will provide a theoretical reference for the optimization of drawing machines.

1. Introduction

Pharmaceutical packaging is an important part of the transportation and storage process of drugs, directly affecting the quality of drugs and human health [1,2]. Medium borosilicate glass (MBG) has many advantages, such as excellent chemical stability, heat resistance stability, air tightness, and transparency, which can effectively ensure the safety of drugs and is widely used in storage containers such as vaccines and biological products, blood products, and lyophilized preparations [3,4,5,6,7].
The presented research mainly focused on the forming process of glass plate and the mechanical properties and simulation models of glass, etc. For example, Zhuo et al. (2023) found that the temperature of molten glass, the drawing velocity of the glass tube, the pressure of inflowed air, and the rotational velocity of the cylinder significantly affected the forming of glass tube [8]. Zhou et al. (2009) obtained the elastic modulus and viscosity of glass based on the Burgers model and the Maxwell model [9]. Yan et al. (2024) found that the combination of parameters (initial molding temperature of 60 °C, molding pressure of 2 MPa, and curing temperature of 120 °C for 2 hours) obtained the best mechanical properties of glass fibers [10]. Chen et al. (2023) indicated the effects of the diffractive structure filling and the maximum stress on the surface precision of the lens and found that under the optimum process parameters (temperature of 230 °C and press velocity of 0.1 mm/s), the surface precision deviation and surface roughness were 0.3053 μm and 2.95 nm, respectively [11]. Li et al. (2024), based on the peridynamics method, found that increasing the low initial impact velocity led to a complex crack network gradually [12]. Geng et al. (2022), based on the numerical simulation method, examined the effects of the rotation speed, diameter, and temperature of the press roller on the temperature field of glass in the calendering process of photovoltaic glass [13]. Timothy and Gordon (2011) provided a computational constitutive model for glass subjected to large strains, high strain rates, and high pressures [14]. Yin et al. (2010) found that the optimal parameters of press velocity and operational temperature are based on the equivalent stress distribution of glass [15]. Sheng et al. (2018) found that the temperature of glass liquid and the rotational speed of the calendering roll were the key factors affecting the quality of glass calendaring [16]. Mansour et al. (2021) analyzed the effect of process parameters on the surface roughness of glass fiber-reinforced polymer composite pipes manufactured [17]. In total, the present research is based on simulation experiments and actual experiments to obtain the best combination of parameters, such as press velocity and pressure, the temperature of the glass, and the press roller to provide a reference for improving the productive quality of glass.
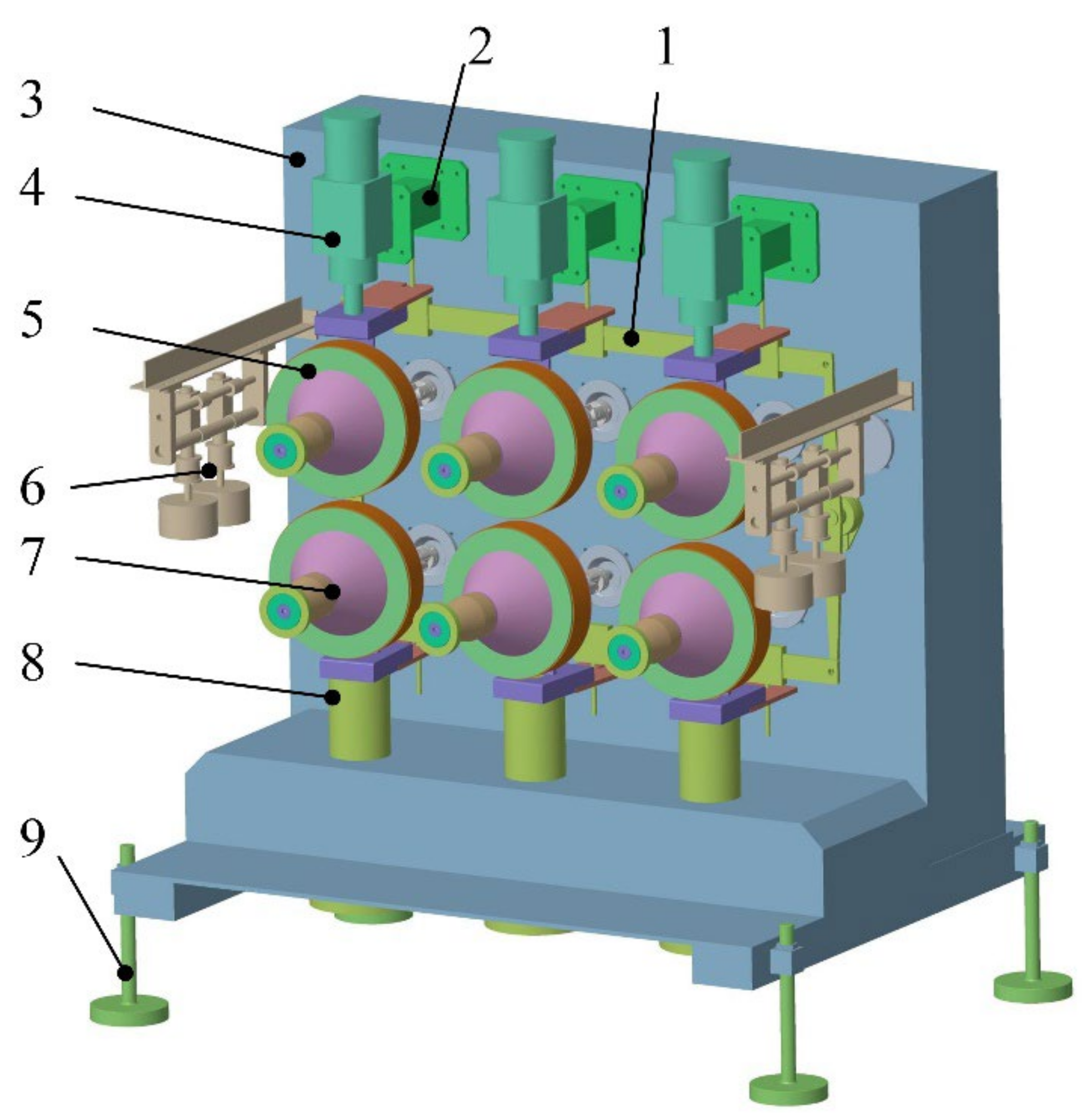
For the medium borosilicate glass tubes, the main productive methods were the Vello and Danner methods, both of which require horizontal drawing of glass tubes [18,19,20]. In these methods, molten glass is continuously formed into tubes by stretching the glass along a horizontal axis. The Vello method utilizes a nozzle to control the diameter of the tube, while the Danner method forms the glass tube by drawing it over a rotating mandrel, allowing for precise control over the wall thickness and dimensions of the glass tube. The drawing machine is the main equipment for realizing the horizontal drawing of glass tubes, and the rotating rubber wheel drives the glass tube forward through friction during the drawing process of the glass tube [21,22,23,24]. Although extensive research has been conducted on the glass-forming process, most studies have focused primarily on the changes that occur in the material properties, such as temperature, velocity, pressure, and viscosity, after the molten glass exits the furnace [8,20,25,26]. These studies often emphasize how these parameters influence the cooling and shaping stages, where the glass solidifies into its final form. However, despite these advancements, there has been limited attention given to the operational parameters of the drawing machine itself. Factors such as the rotational speed of the rubber wheel, the radius of the wheel, and the pressure it applies to the glass tube are crucial, yet often underexplored. These parameters have a direct impact on the surface quality, dimensional accuracy, and overall mechanical integrity of the glass tube. Specifically, the kinematic effects resulting from the structural and operational characteristics of the drawing machine on the formation process of the glass tube remain largely under-researched. This gap in understanding has limited the ability to optimize the drawing process for higher-quality production. As a result, the fine-tuning of operational parameters, such as adjusting the rotational speed or modifying the pressure exerted by the wheel, relies heavily on manual intervention by skilled operators. These directly increased the productive cost and quality.
With the development of computer and simulation software, the finite element method (FEM) simulation was employed to solve the complex engineering problems [27,28,29]. In the analysis of the change process of force, motion, and temperature of glass, Li et al. (2022), using a FEM simulation, found the heat transfer performance of vacuum glazing [30]. Peng et al. (2013), using LS-DYNA software, identified the mechanical behavior of windshield laminated glass through impact experiments [31]. Naumenko, Pander, and Würkner (2022) predicted the damage of float glass using a FEM simulation based on the peridynamics [32]. Therefore, in this study, a FEM simulation was conducted to determine the principles governing the changes in force and motion of the glass tube under various conditions, including different deflection angles of the driving wheel, friction factors between the glass tube and the driving wheel, and the distance between the upper and lower drawing wheels. These findings are expected to offer theoretical insights and technological guidance for the design and optimization of glass tube drawing machines.

2. Materials and Methods

2.1. Structure of the Glass Tube Drawing Machine

The glass tube drawing machine primarily consisted of a driving device, upper and lower glass tube drawing devices, a deflection angle adjustment device for the lower glass tube drawing device, an upper adjusting air cylinder, a glass tube guiding device, a lower adjusting air cylinder, and a level adjustment device (Figure 1). Both upper and lower glass tube drawing devices mainly included a drawing wheel and a rubber ring, and the rotational velocities of both upper and lower drawing wheels were the same, but their rotational directions differed. The distance between the upper and lower drawing wheels was adjusted by the upper and lower adjusting air cylinder to change the drawing force and pressure of the glass tube. The deflection angle of the lower glass tube drawing device was changed by the deflection angle adjustment device to change the rotational velocity of the glass tube. The glass tube guiding device was used to prevent the glass tube from deviating from its path.

2.2. Finite Element Method Simulation

Finite element method simulation is widely used to solve complex problems, such as location of deformation, maximum stress, and optimization of structure [33,34].

2.2.1. Simplification of the Finite Element Model

The precision and efficiency of simulation are the main considerations. With the guarantee of the accuracy of simulation, some reliable simplification of the FEM must be applied to reduce the time cost of simulation. Therefore, the simplifications of the glass tube drawing machine were applied as follows:
a.
The temperature change of the glass tube was ignored in the drawing process because the temperature of the glass tube was 315 ± 7 °C;
b.
The wear of the rubber ring was assumed to be ignored;
c.
Abrasion and deformation of the drawing wheel were ignored;
d.
Static and dynamic friction coefficients between the glass tube and rubber ring were not changed in the drawing process;
e.
Some parts of the drawing machine that did not directly contact the glass tube, such as the level-adjusting device, machine shell, and air cylinder, were ignored.
In the FEM model, the diameter and length of the glass tube were 16 and 2000 mm, respectively, and the thickness of the glass tube was 1 mm. In the drawing process of the glass tube, only three pairs of drawing devices were used to force the glass tube. Therefore, the glass tube drawing machine was simplified, and its structural model was constructed using Creo software (Version 4.0, PTC Corporation, Boston, MA, USA; Figure 2).

2.2.2. Finite Element Method Simulation of Glass Tube Drawing Process

The three-dimensional model of the glass tube drawing device was saved in STEP format in Creo software and then imported into Hypermesh software (Version 2022, Altair Corporation, Troy, MI, USA) for mesh generations. To avoid mesh distortion, ensure stability and accuracy of simulation, and reduce time to convergence, a small cell size for the glass tube was necessary. The length and width of the cell of the glass tube were respectively set as 5.3 and 0.5 mm, and in the areas of a glass tube with force under upper and lower drawing wheels, the cell was densified, and the length of the cell in the densified areas was 3 mm. Both the length and width of the cell of the rubber ring were set as 5 mm. The length and width of the cell of the drawing wheel were set as 15.7 and 6 mm, respectively. The elements and nodes of the glass tube, rubber ring, and drawing wheel were 2.4 × 103 and 5.2 × 103, 6.8 × 104 and 1.02 × 105, and 600 and 1320, respectively. In total, 8.6 × 104 elements and 1.4 × 105 nodes were generated.

2.2.3. Material Properties of Finite Element Method Simulation

In this FEM simulation, *MAT_JOHNSON_HOLMQUIST_CERAMICS was applied for the glass tube (No. 110 material model in the LS-DYNA), *MAT_ELASTIC was used for rubber ring (No. 1 material model in the LS-DYNA), and *MAT_RIGID was used for drawing wheel (No. 20 material model in the LS-DYNA) because of negligible deformation in the drawing process of glass tube to reduce simulated time [35,36]. The properties of these above materials are shown in Table 1.

2.2.4. Boundary and Contact Conditions of FEM

The surfaces of the glass tube and rubber ring served as the slave and master segments, respectively. The contact type of the slave and master segment was defined as *CONTACT_AUTOMATIC_SURFACE_TO_SURFACE. The drawing wheel was constrained to the rubber ring using the keyword *CONSTRAINED_EXTRA_NODES. The rotational speed of all six rubber rings was set as 150 r/min. The calculation timestep was set as 1 × 10−6 s. Finally, a .K file was generated and imported into LS-DYNA (Version R11, Canonsburg, PA, USA) software to solve. The results of the simulation were obtained by LS-Prepost (Version 4.10, Canonsburg, PA, USA).

2.3. Test Parameters of the FEM Simulation

In this study, a full factors test was executed to investigate the principles of change of the glass tube in the drawing process. The angle of upper and lower drawing wheel (AUD: 0–4°, interval: 1°), the friction coefficient between the glass tube and the rubber (FFGR: 0.1–0.4, interval: 0.1), and the distance of upper and lower drawing wheel (DUD, 332.5–334.5 mm, interval: 0.5 mm) were set as the experimental factors (Table 2), and the maximum effective stress (MES), the rotational speed (RSG), the maximum forward driving force (MFDF), the average forward driving force (AFDF), the maximum rotational driving force (MRDF), the average rotational driving force (ARDF), the total energy consumption of drawing process (TEC), the total power of drawing process (TPD), the average forward driving power (AFDP), the maximum forward driving power (MFDP), the maximum rotational driving power (MRDP), and the average rotational driving power (ARDP) were selected as experimental indexes in the drawing process of glass tube.

2.4. Validation Experiment

In the FEM simulation, the driving forces, effective stress, rotational speed, and driving power of the glass tube were obtained in the drawing process. However, because of the high temperature and horizontal motional speed of the glass tube in the drawing process, the driving forces, effective stress, and driving power of the glass tube were measured differently. Therefore, RSG and horizontal drawing speed of the glass tube were set as the validation indexes to obtain the accuracy of the FEM simulation results. In the validation experiment, the parameters of a FFGR of 0.3 and a DUD of 333 mm with different AUDs were selected (Figure 3).
During the experiment, a gauge point was set on the glass tube, and its trajectory was recorded using a high-speed camera (Pco Dimax HD, sampling frequency: 1100 Hz, Excelitas Technologies Corp, Pittsburgh, PA, USA). Based on this trajectory, the radial motion of the gauge point was determined. Finally, the rotational speed of the glass tube was calculated using the recorded motion time from the high-speed camera. The validation experiment was repeated three times.

2.5. Statistical Analyses

Analysis of variance and regression analysis (95% confidence interval) were performed using SPSS software (Version 2017, IBM, Endicott, NY, USA) to illustrate the effects of experimental factors on the experimental indexes. The resulting figures were plotted using OriginPro software (Version 2020, OriginLab, Northampton, MA, USA).

3. Results

3.1. Validation Experiment

To assess the accuracy of the FEM simulations, a FFGR of 0.3 and a DUD of 333 mm with various AUDs were used (Figure 3). The results difference between the FEM simulation and validation experiment were 19.4% (AUD = 1°), 12.3% (AUD = 2°), 2.2% (AUD = 3°), and 7.5% (AUD = 4°), respectively. Furthermore, similar changes in RSG were observed in both the validation and simulated experiments (Figure 4). The difference in RSG between the validation and simulated experiments was less than 20%. In conclusion, the FEM results were accepted. The change principle of RSG, based on both the validation and simulated experiments, was illustrated in the section on the effects on the MES and RSG.

3.2. Analysis of Variance

The analysis of variance was used to identify significant differences between the independent variables (AUD, FFGR, and DUD) and the dependent variables (MES, RSG, MFDF, AFDF, MRDF, ARDF, TEC, TPD, AFDP, MFDP, ARDP, and MRDP; Table 3). The results indicated that AUD had a highly significant influence on RSG, MRDF, ARDF, and ARDP, as well as a very significant influence on MRDP, but a nonsignificant effect on the other experimental indexes. FFGR had a significant influence on TEC, a very significant influence on MRDF, ARDP, and MRDP, and a highly significant influence on MFDF, AFDF, ARDF, TPD, AFDP, and MFDP, but no significant effect on the other experimental indexes. DUD had a highly significant influence on all parameters except RSG. According to the F value, the influence levels of the experimental factors on the dependent variables were determined. Except for RSG, DUD had the highest influence on the dependent variables, while for MES, RSG, MRDF, ARDF, ARDP, and MRDP, the influence ranking was AUD greater than FFGR, and for other dependent variables, FFGR had a greater influence than AUD.

3.3. Effects on the MES and RSG

According to the ANOVA results, due to the nonsignificant effects of AUD and FFGR on MES, only the effects of DUD on MES and AUD on RSG were analyzed. As shown in Figure 5a, a negative quadratic relationship between DUD and MES was identified (R2 = 0.995, p = 0.07). Compared to MES at a DUD of 334 mm, the MES increased by 1.25, 3.79, and 6.12 times at DUD values of 333.5, 333, and 332.5 mm, respectively. Although the variances of MES were considerable, the coefficient of variation for MES across different DUD values was less than 15%, which demonstrated the reliability of the results. In Figure 5b, a positive linear relationship between AUD and RSG was observed through linear fitting (R2 = 0.999, p < 0.001). Compared to RSG at an AUD of 1°, RSG increased by 1.36, 2.84, and 4.18 times at AUD values of 2°, 3°, and 4°, respectively.

3.4. Effects on the MFDF and AFDF

The MFDF increased steadily as FFGR increased from 0.1 to 0.4 and decreased as DUD increased from 332.5 to 334.0 mm (Figure 6). Negative linear slopes of −72.71 (R2 = 0.985, p = 0.0072), −143.28 (R2 = 0.986, p = 0.0069), −213.24 (R2 = 0.981, p = 0.0069), and −289.70 (R2 = 0.987, p = 0.00647) were observed for MFDF under FFGR values of 0.1, 0.2, 0.3, and 0.4, respectively, as DUD increased from 332.5 to 334 mm. Furthermore, MFDF increased by 3.48, 3.19, 3.51, and 2.93 times under DUD values of 334, 333.5, 333, and 332.5 mm, respectively, as FFGR increased from 0.1 to 0.4. The effects of FFGR and DUD on AFDF were more complex (Figure 6b). AFDF showed a positive relationship with FFGR under a DUD of 334 mm, and compared to AFDF at a DUD of 334 mm, AFDF increased by 55.82%, 58.38%, and 26.93% under DUD values of 333.5, 333, and 332.5 mm, respectively. Moreover, compared to AFDF under a FFGR of 0.1, AFDF increased by 10.77%, 7.72%, and 20.29% under FFGR values of 0.2, 0.3, and 0.4, respectively. The maximum AFDF occurred at a DUD of 333 mm and a FFGR of 0.3.

3.5. Effects on the MRDF and ARDF

The FEM simulation results showed that the rotational driving force of the glass tube (MRDF) was positively correlated with FFGR and AUD and negatively correlated with DUD (Figure 7 and Table 4). The MRDF increased from 0.14 N to 7.98 N, 0.32 N to 16.10 N, 0.56 N to 24.56 N, and 0.68 N to 33.40 N as the AUD increased from 1° to 4°. Compared to MRDF at an AUD of 1°, MRDF increased by approximately 1.03, 2.07, and 3.14 times at an AUD of 2°, 3°, and 4°, respectively. The maximum MRDF was observed under a DUD of 332.5 mm, a FFGR of 0.4, and an AUD of 4°. MRDF growth rates increased as the AUD increased from 1° to 4°. Linear regression analysis indicated that DUD had the greatest influence on MRDF compared to other parameters, while the effects of FFGR and AUD on MRDF were similar, based on the t-values (Table 4).
According to Figure 8 and the linear regression analysis (Table 4), a positive relationship was found between ARDF and AUD and ARDF and FFGR, and a negative relationship was found between ARDF and DUD (R2 = 0.73, p < 0.0001). The maximum ARDF values occurred under a FFGR of 0.4 and a DUD of 332.5 mm. Compared to the maximum ARDF value at a FFGR of 0.1, ARDF increased by 93.81%, 140.54%, and 125.63% under a FFGR of 0.2, 0.3, and 0.4, respectively. Additionally, the change rate of ARDF with FFGR was higher than that with DUD and AUD.

3.6. Effects on TEC and TPD

The effects of FFGR and DUD on TEC are illustrated in Figure 9 due to the nonsignificant impact of AUD on TEC. The results demonstrated that the range of TEC values varied from 155 to 170 J. Linear regression analysis results revealed a positive relationship between FFGR and TEC, while a negative impact of DUD on TEC was observed (Table 5). The rate of TEC increase under FFGR was higher compared to DUD; however, the impact of DUD on TEC was greater than that of FFGR, as indicated by the t value. Compared to TEC under a FFGR of 0.1, TEC increased by 1.21%, 1.50%, and 1.72% under a FFGR of 0.2, a FFGR of 0.3, and a FFGR of 0.4, respectively. Conversely, relative to TEC under a DUD of 332.5 mm, TEC decreased by 1.74%, 3.19%, and 5.39%, respectively.
According to Figure 10 and the linear regression in Table 5, a positive effect of FFGR on TPD and a negative effect of DUD were observed, with the range of TPD varying from 47 to 2726 W. Compared to TPD under a FFGR of 0.1, TPD increased by 1.36, 2.58, and 3.89 times under a FFGR of 0.2, 0.3, and 0.4, respectively. The maximum TPD values were 563.59 W under a FFGR of 0.1, 1308.18 W under a FFGR of 0.2, 1970.87 W under a FFGR of 0.3, and 2725.18 W under a FFGR of 0.4, respectively, when DUD was 332.5. Furthermore, relative to TPD under a DUD of 332.5, the decrease rates were −40.84%, −71.42%, and −91.53% for TPD under a DUD of 333, 333.5, and 334, respectively.

3.7. Effects on AFDP and MFDP

Opposite effects of FFGR on AFDP and MFDP (positive) and of DUD on AFDP and MFDP (negative) were observed (Figure 11, Table 6). Compared to AFDP under a DUD of 334 mm, AFDP increased by more than 2.0, 5.5, and 11 times under a DUD of 333.5, 333, and 332.5 mm, respectively. Similarly, compared to AFDP under a FFGR of 0.1, AFDP increased by more than 1.0, 2.0, and 3.0 times under a FFGR of 0.2, 0.3, and 0.4, respectively, regardless of the DUD value. The maximum values of AFDP and MFDP both occurred under a DUD of 332.5 mm and a FFGR of 0.4. In addition, as FFGR increased, the negative change rates of AFDP and MFDP with DUD also increased.

3.8. Effects on the ARDP and MRDP

Both FFGR and AUD positively affected ARDP and MRDP, whereas DUD negatively influenced ARDP and MRDP (Figure 12 and Figure 13, Table 7). The maximum values of MRDP occurred when AUD, FFGR, and DUD were 4°, 0.4, and 332.5 mm, respectively, and the maximum values of ARDP occurred when AUD, FFGR, and DUD were 4°, 0.3, and 332.5 mm, respectively. The ranges of ARDP and MRDP were 0.00018 to 0.021 and 0.0066 to 0.83 W under an AUD of 1°, 0.00043 to 0.03952 and 0.014 to 0.021 W under an AUD of 2°, 0.00075 to 0.04904 and 0.091 to 2.53 W under an AUD of 3°, and 0.00096 to 0.044 and 0.028 to 3.45 W under an AUD of 4°, respectively. Compared to ARDP under an AUD of 1°, ARDP, and MRDP increased by 91.45% and 101.50% under an AUD of 2°, 147.74% and 207.74% under an AUD of 3°, and 125.12% and 319.09% under an AUD of 4°, respectively. Based on the results of linear regression, the rate of change in ARDP and MRDP under FFGR was higher than that under DUD and AUD (Table 7).

4. Discussion

4.1. Accuracy Analysis of FEM Simulation Results

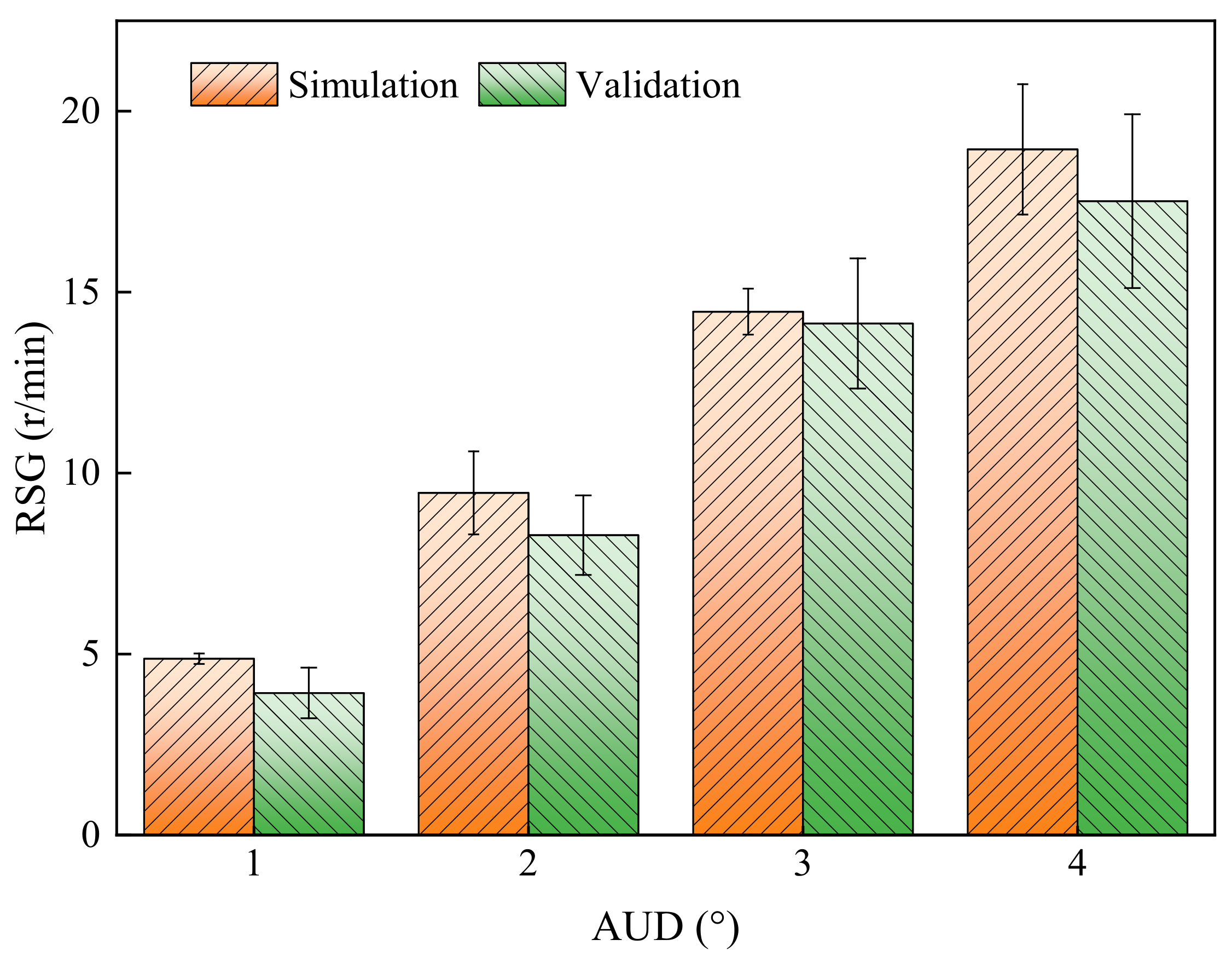
Compared with the FEM simulation and validation experiment results, a similar trend in RSG was observed; however, the RSG from the validation experiment was lower than that from the FEM simulation. The reasons may include the following: (1) during the actual drawing process of the glass tube, the length of the glass tube was greater, and the Danner machine also exerted a force to prevent the rotation of the glass tube; (2) in the validation experiment, the friction factor between the drawing wheel and the glass was lower compared to the FEM simulation experiment due to the wear of rubber wheel; (3) the downward drawing wheel oscillated, and the graphite wheel guide was uneven, causing the glass tube to run out, introducing additional non-stabilizing factors into the RSG measurement; and (4) due to the AUD, the driving force exerted by the pressed drawing wheel not only contributed to the rotation of the glass tube but also generated a sliding force that caused horizontal movement of the glass tube, leading to discrepancies between the FEM simulation and validation experiment results. In summary, the FEM simulation results were consistent with the validation experiment results and indicated that the FEM results could serve as references for elucidating the effects of key drawing machine parameters on the force and energy consumption of the glass tube during the drawing process.

4.2. Effects of AUD

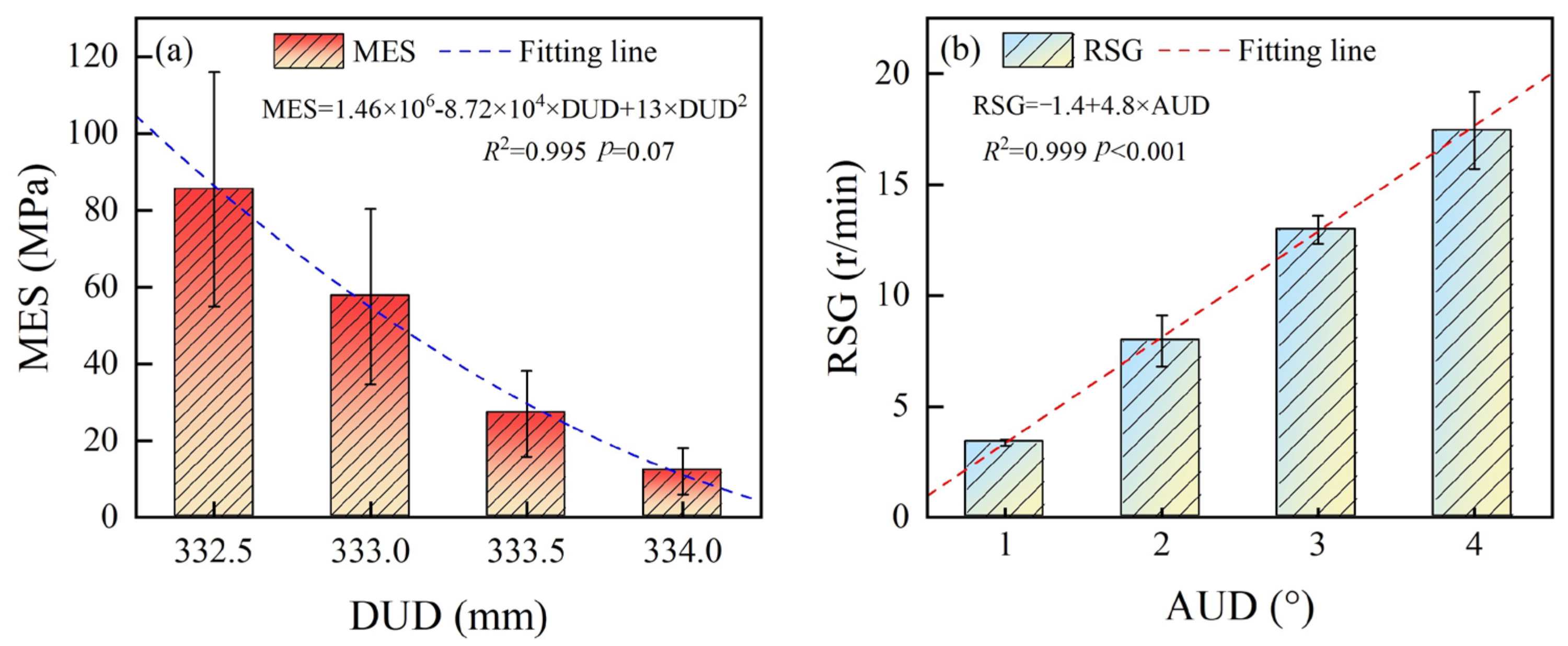
In this study, AUD had a highly significant influence on RSG, MRDF, ARDF, and ARDP (p < 0.01), and a very significant influence on MRDP (p < 0.05), but no significant influence on other experimental indexes. Simultaneously, a positive effect of AUD on RSG, MRDF, ARDF, ARDP, and MRDP was also found. The reason may be that (1) during the drawing process of the glass tube, three upper drawing wheels and three lower drawing wheels pressed the glass tube and provided the driving force. The axial driving force along the axis of the glass tube propelled its forward movement, while the tangential driving force caused its self-rotation; and (2) due to the constant rotational speed of the drawing wheels, RSG reached a constant value, but the acceleration of the glass tube was determined by the friction between the drawing wheels and the tube. However, AUD had nonsignificant effects on MES, MFDF, AFDF, TEC, TPD, AFDP, and MFDP. The reasons may be that (1) AUD only affected the tangential driving force component of the glass tube, while MES was influenced by the pressing force from the drawing wheels, leading to the nonsignificant influence on MES; (2) during the drawing process, the forward driving force, which equals the total driving force multiplied by the cosine of AUD, varied minimally (cosine of AUD ranging from 0.9962 to 1) since the AUD range was between 0° and 5°, resulting in the nonsignificant influence of AUD on MFDF, AFDF, MFDP, and AFDP; and (3) the main energy consumption arose from overcoming the friction between the glass tube and the six drawing wheels, and from the wheels driving the tube along the axial direction. The energy consumed by driving the rotation of the glass tube was relatively low compared to driving its forward movement. Therefore, the nonsignificant influence of AUD on TEC and TPD was observed. Importantly, AUD is a key factor in the drawing process, as the rotational forces on the glass tube from the Danner machine are regulated by adjusting the AUD of the drawing wheel. Additionally, an excessively large AUD increases the rotational torque of the drawing wheels, leading to an increased risk of deviation of the glass tube from its original position. This deviation raises the pressure between the glass tube and the guiding device, increasing the risk of tube breakage.

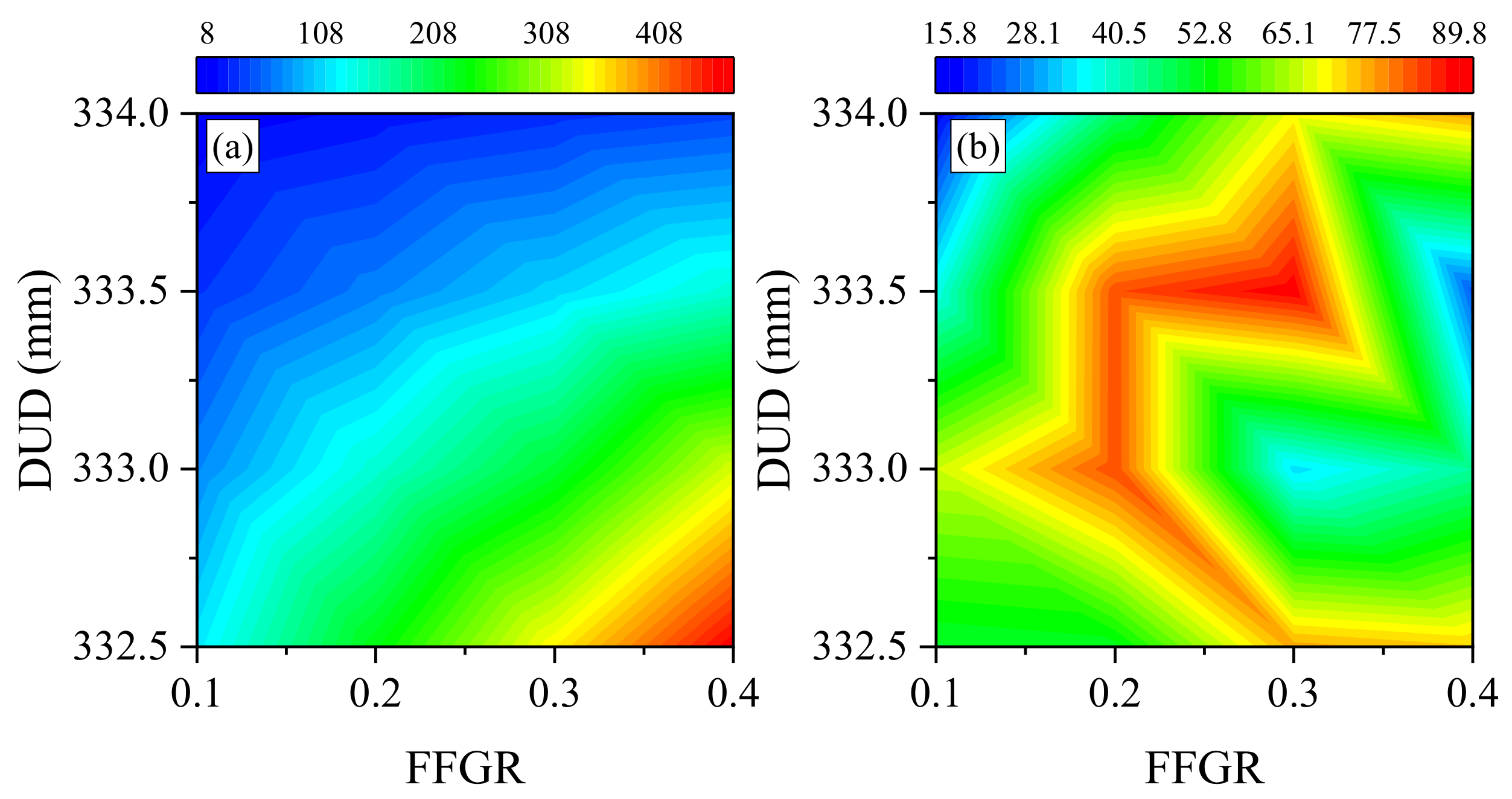
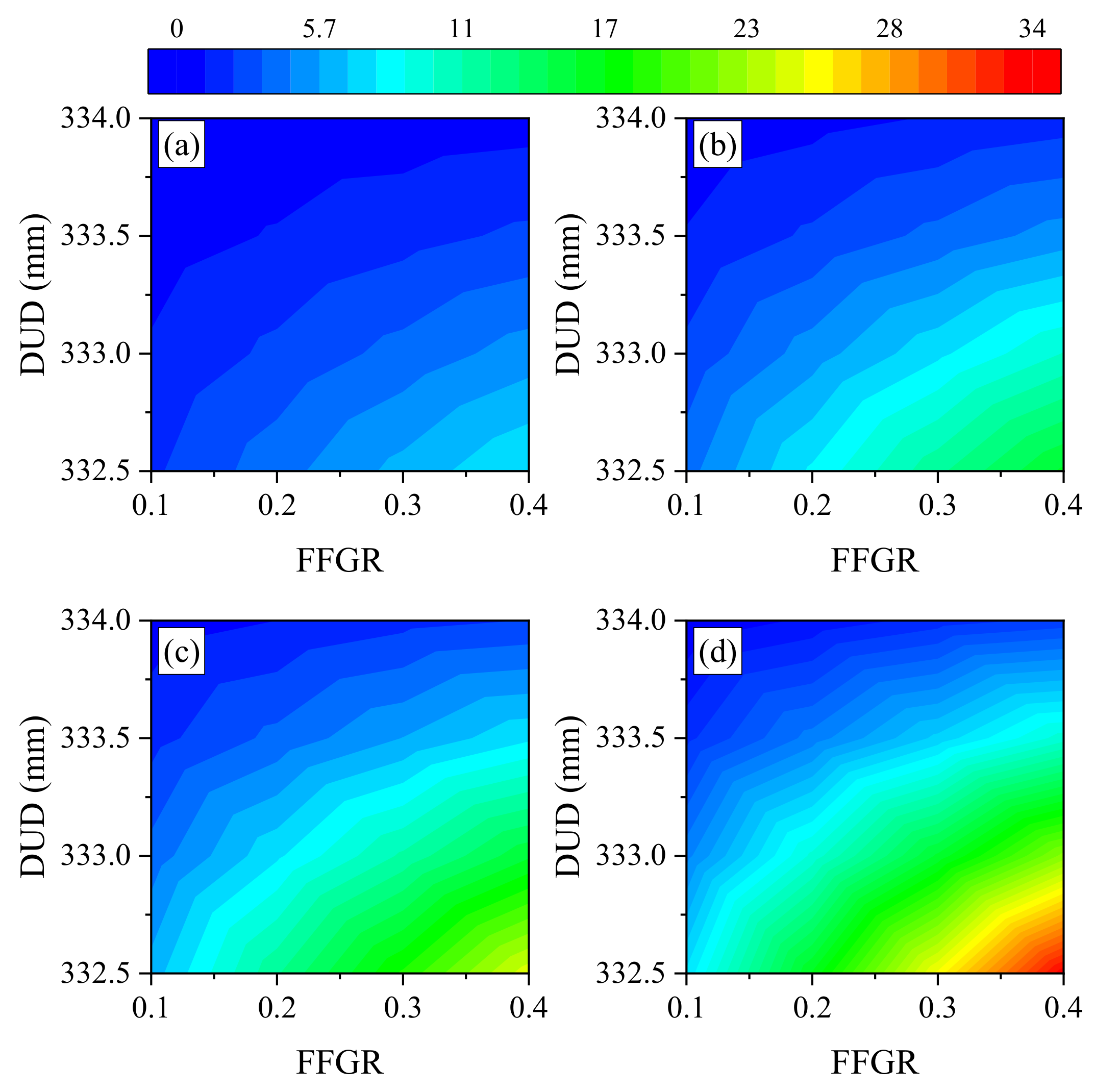
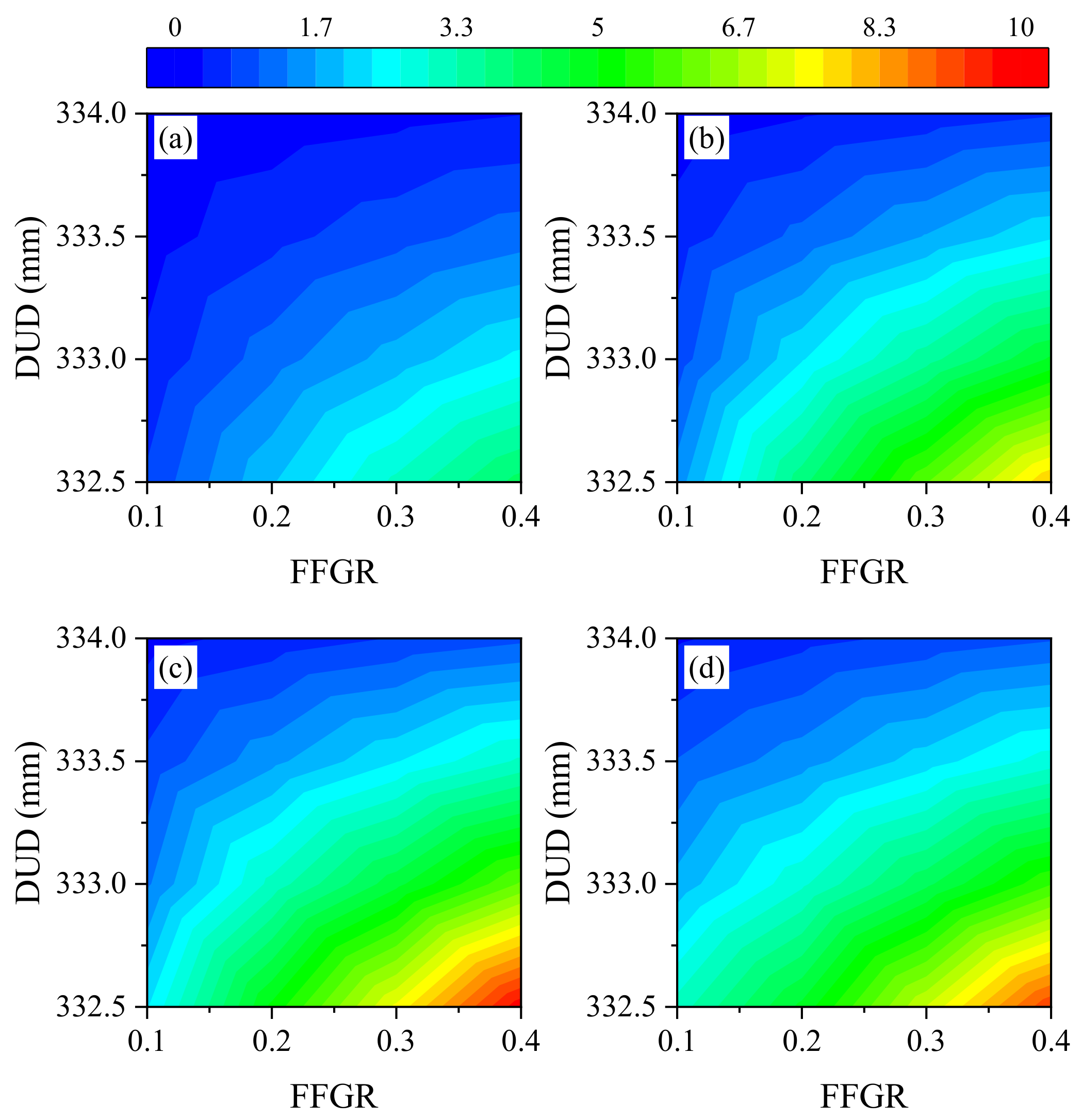
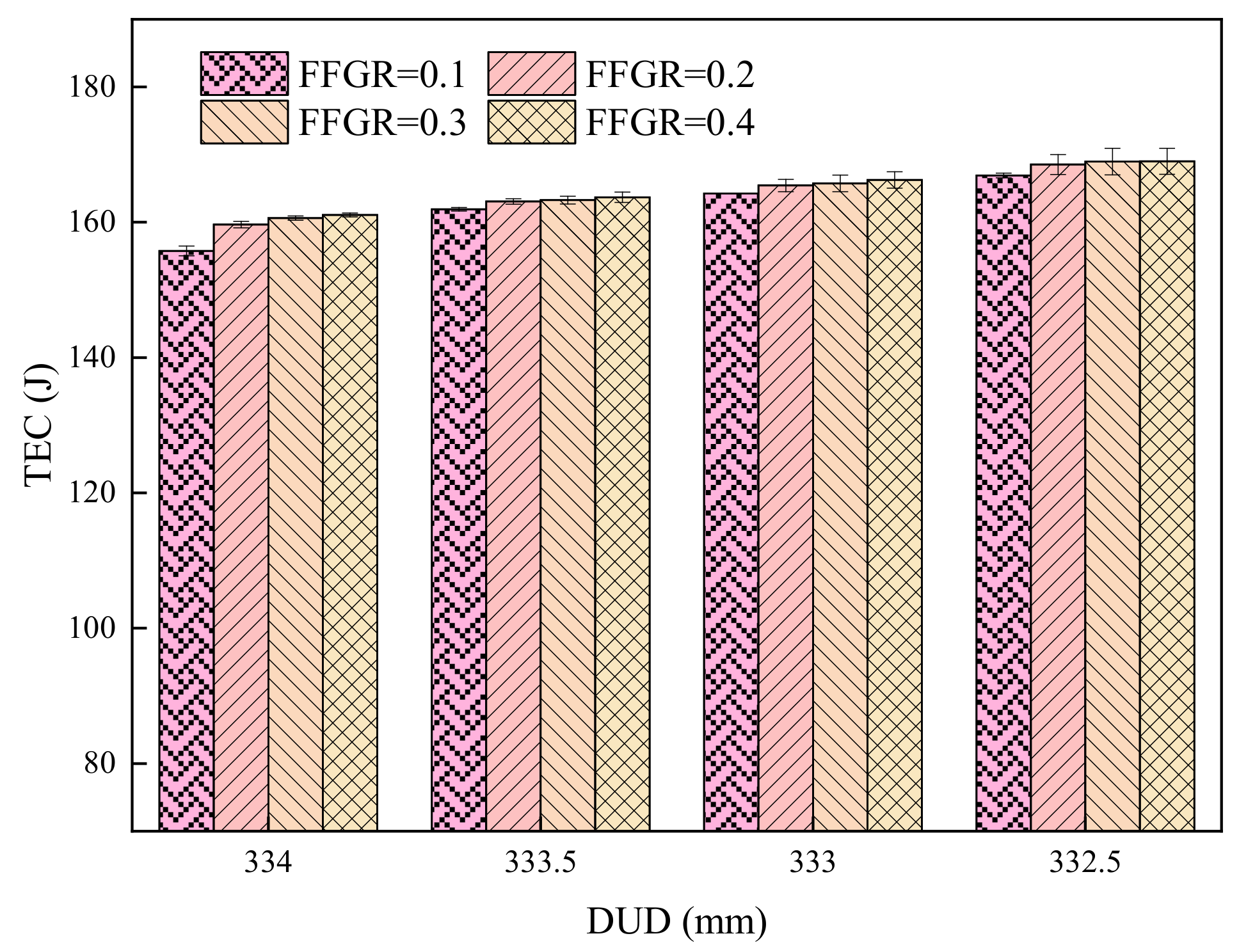
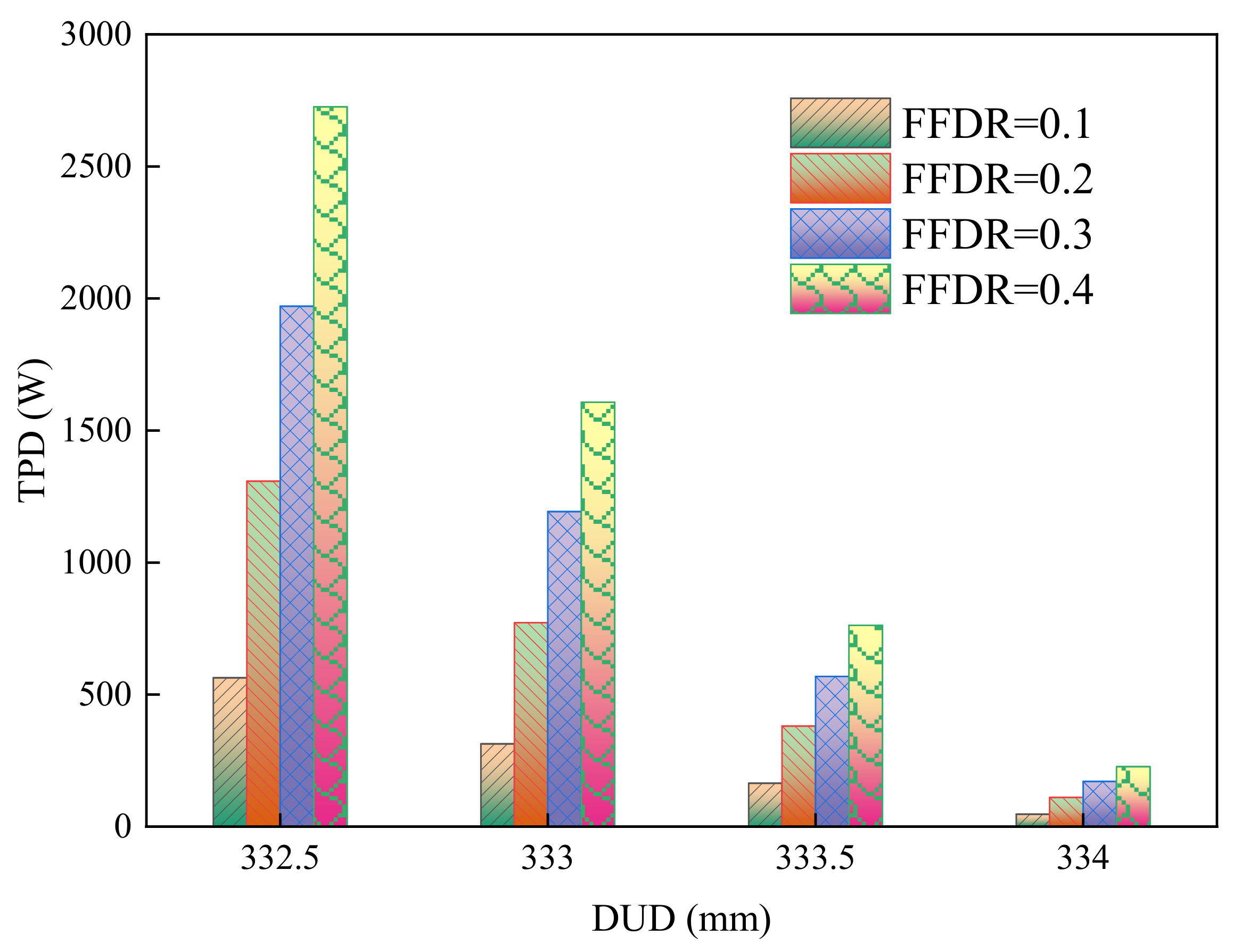
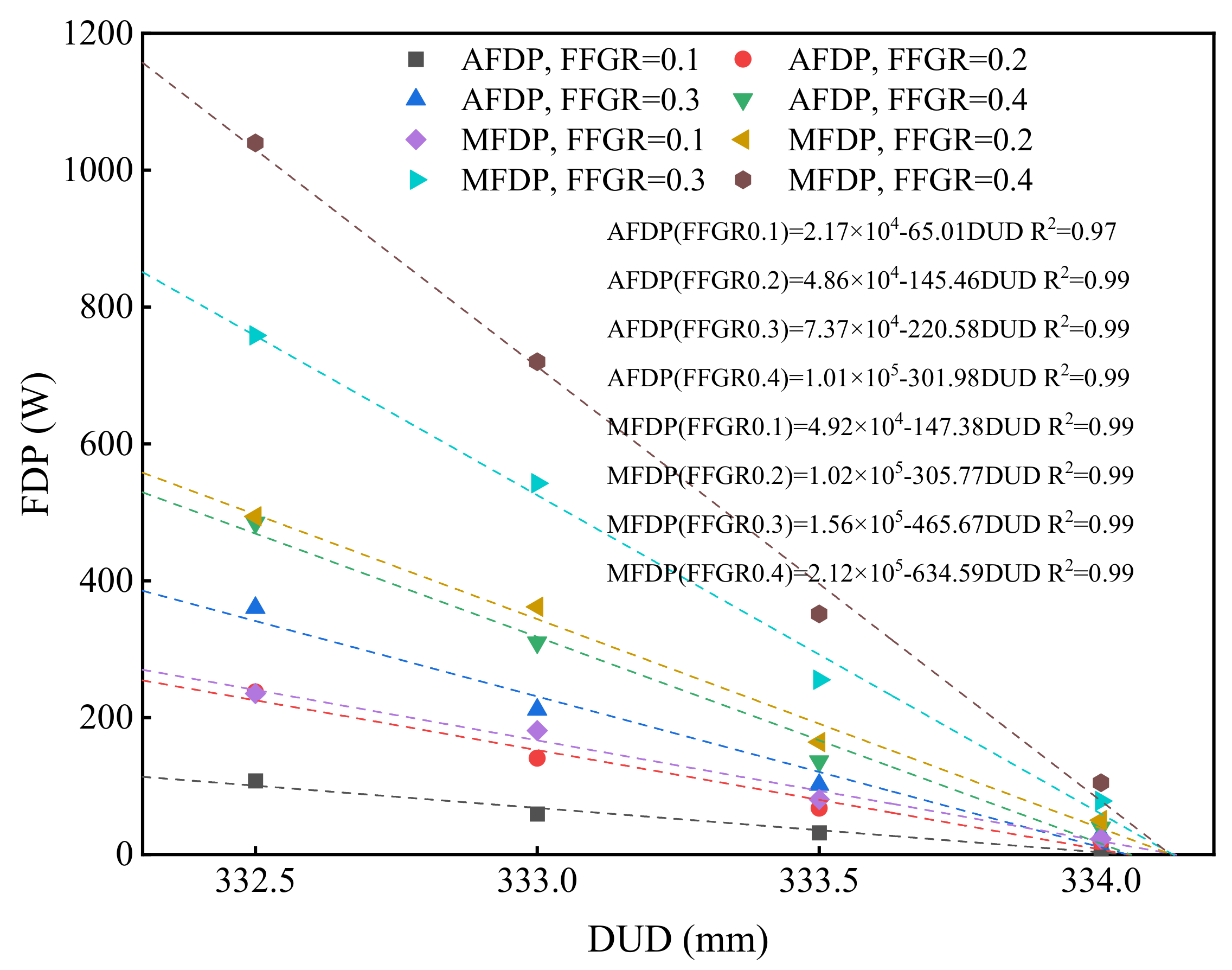
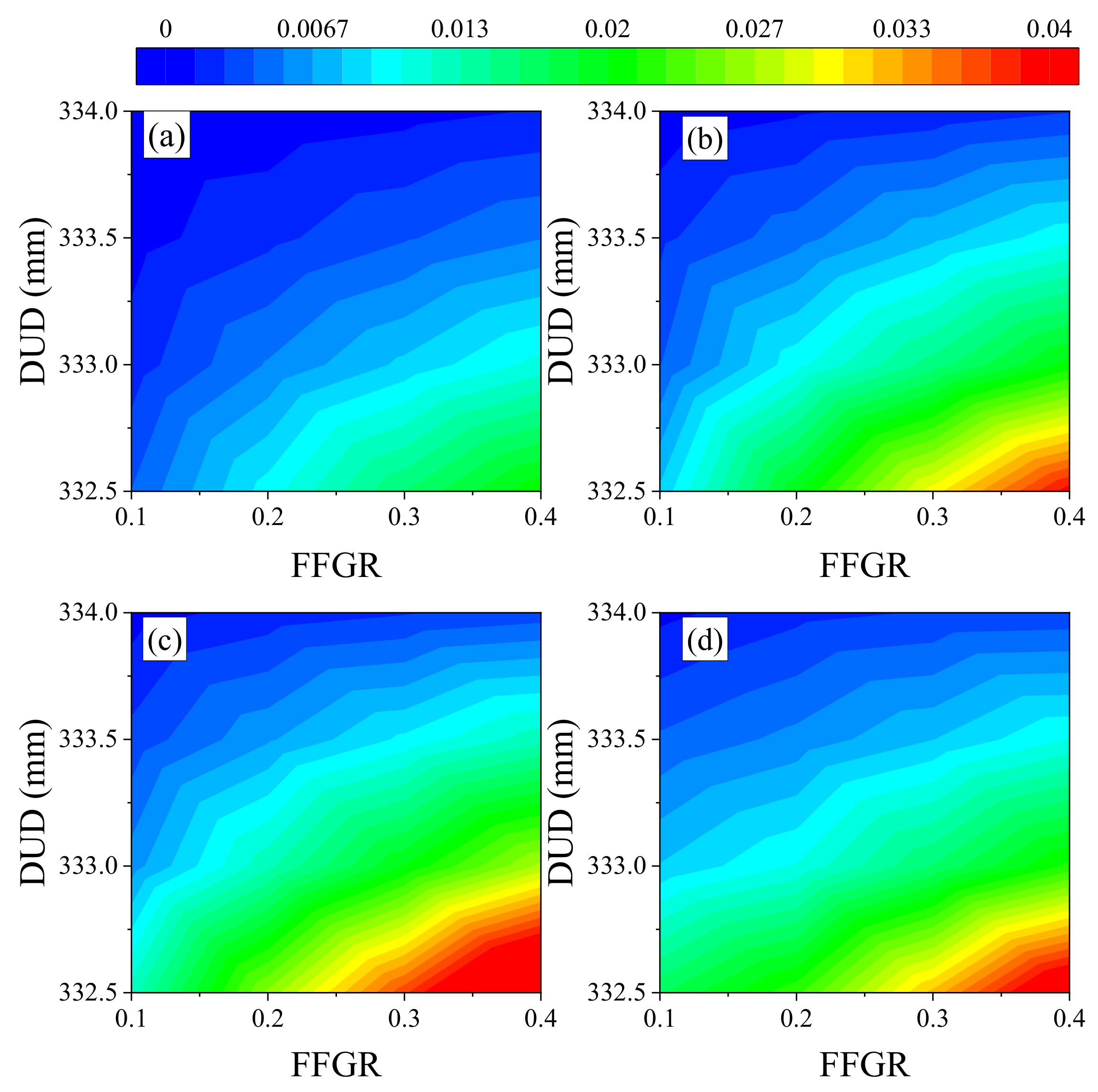
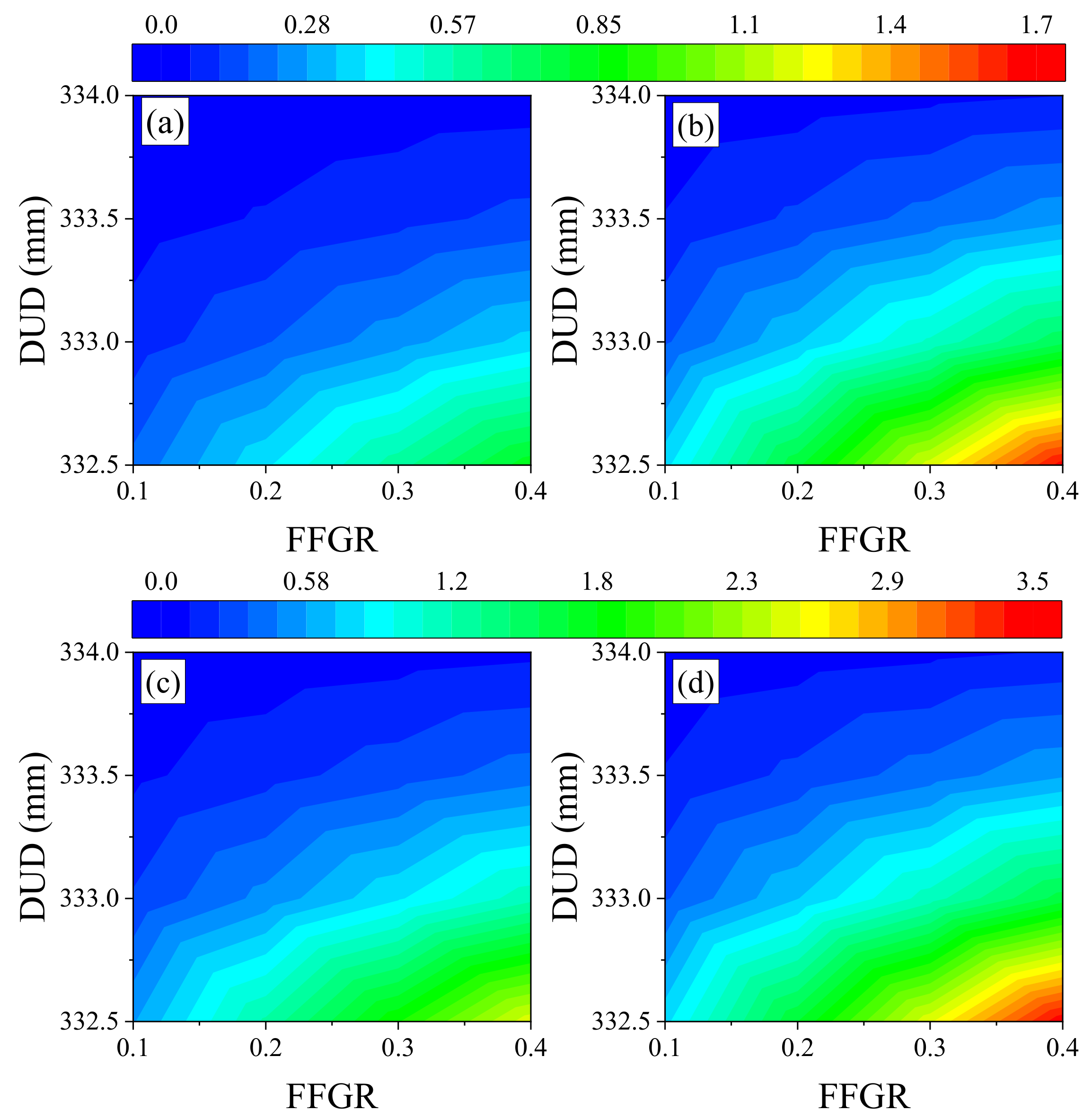
4.3. Effects of FFGR and DUD

This indicated that in the drawing process of the glass tube, adjusting the DUD was the primary step if the quality of the glass tube changed. The positive effects of FFGR on MFDF, AFDF, MRDF, ARDF, TEC, TPD, AFDP, and MFDP, and the negative effects of DUD on MES, MRDF, ARDF, TEC, TPD, AFDP, and MFDP were found. This indicated that in the drawing process, under the premise of ensuring the quality of the operation, reduction of DUD required increasing of FFGR, but it was noted that the impact of DUD is significantly greater than that of FFGR. Therefore, further research is needed to ensure parameter balance in the actual production process. In addition, although reduction of DUD and increase of FFGR improved the pressure on the glass tube from the drawing wheels to improve the stability of drawing, the abrasion of rubber in drawing wheels also increased [37,38]. Therefore, a suitable value of DUD and FFGR in the drawing process needs to be further researched in the future to obtain a balance of operational and economic performance.
In this study, FFGR and DUD significantly affected almost all indexes, except for the insignificant effect of FFGR on MES and RSG, and of DUD on RSG. This indicates that FFGR and DUD are key factors affecting the force and energy consumption in the glass tube drawing process. The insignificant effect of FFGR on MES and RSG may be due to the following reasons: (1) FFGR influences the driving force of the glass tube, while the maximum effective stress is determined by the pressure from the drawing wheels; (2) before the glass tube reaches its specified motional and rotational speed, an increased coefficient of friction reduces the time required for the tube to reach the designated speed. However, once the speed is reached, increasing FFGR reduces the pressure on the glass tube, thereby decreasing the risk of breakage; and (3) due to the angle between the upper and lower drawing wheels, increasing FFGR also increases the lateral force on the glass tube, which raises the risk of the tube shifting to one side of the drawing wheel. According to the F-values, the magnitude of DUD’s influence on the dependent variables surpasses that of FFGR, possibly because DUD primarily affects the pressure on the glass tube, a fundamental parameter in the drawing process. Positive effects of FFGR were observed on MFDF, AFDF, MRDF, ARDF, TEC, TPD, AFDP, and MFDP, while DUD had negative effects on MES, MRDF, ARDF, TEC, TPD, AFDP, and MFDP. This indicates that in the drawing process, to maintain operational quality, reducing DUD requires an increase in FFGR. However, it is important to note that the impact of DUD is significantly greater than that of FFGR. Therefore, further research is necessary to balance these parameters during actual production. Additionally, although reducing DUD and increasing FFGR improved the pressure applied by the drawing wheels on the glass tube, it also led to increased abrasion of the rubber in the wheels. Thus, finding a suitable balance of DUD and FFGR in the drawing process requires further study to optimize operational and economic performance.

5. Conclusions

This study evaluated the influence of experimental factors (DUD, AUD, and FFGR) on experimental indexes (MES, RSG, FDF, RDF, TEC, TPD, FDP, and RDP) during the glass tube drawing process based on the FEM simulation and validation experiments. The main conclusions are as follows:
(1)
AUD had significant effects on RSG, MRDF, ARDF, MRDP, and ARDP, while both FFGR and DUD significantly influenced MRDF, ARDF, TEC, TPD, ARDP, and MRDP.
(2)
DUD had the greatest influence on the experimental indexes compared to the other two factors, and FFGR’s influence was greater than that of AUD, except for MRDP and ARDP.
(3)
AUD showed positive influences on RSG, ARDP, and MRDP, while FFGR had positive effects and DUD had negative effects on MRDF, ARDF, TEC, TPD, ARDP, and MRDP, respectively.
These findings provide reference and support for the design and optimization of glass tube drawing machines. However, this study focused solely on the changes in the glass tube during the drawing process. Future studies should explore multiple processes (e.g., transportation and formation of the glass tube) to further enhance its operational quality.

Author Contributions

Conceptualization, P.L., L.C. and T.G.; methodology, P.L., Z.W. and K.Y.; software, P.L., Z.W. and R.L.; validation, P.L. and M.C.; writing—original draft preparation, P.L.; writing—review and editing, P.L., L.C., Z.W., K.Y., M.C., R.L. and T.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of Henan Province, grant number 242300421560; the Science and Technology Research Project of Henan, grant number 232102110273, 212102210345; and the Scientific Research Foundation for Advanced Talents of Henan University of Technology grant number 2022BS077.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

Authors Peng Liu, Limin Cang, Zhigang Wan, Ke Yang and Ming Chen are employed by Henan Ancai Hi-Tech Limited Liability Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Abbreviations

AbbreviationMeanAbbreviationMean
AUDAngle of upper and lower drawing wheel, °FFGRFriction coefficient of glass and rubber, constant
DUDDistance of upper and lower drawing wheel, mmMESMaximum effective stress of glass tube, MPa
RSGRotational speed of glass tube, r/minMFDFMaximum forward driving force, N
AFDFAverage forward driving force, NMRDFMaximum rotational driving force, N
ARDFAverage rotational driving force, NTECTotal energy consumption, J
TPDTotal power in the drawing process, WMFDPMaximum forward driving power, W
AFDPAverage forward driving power, WMRDPMaximum rotational driving power, W
ARDPAverage rotational driving power, WFEMFinite element method

References

  1. Kumar, G. Pharmaceutical Drug Packaging and Traceability: A Comprehensive Review. Univers. J. Pharm. Pharmacol. 2023, 2, 19–25. [Google Scholar] [CrossRef]
  2. Guadagnino, E.; Guglielmi, M.; Nicoletti, F. Glass: The best material for pharmaceutical packaging. Int. J. Appl. Glass Sci. 2022, 13, 281–291. [Google Scholar] [CrossRef]
  3. Zuccato, D.; Guadagnino, E. Glass for Pharmaceutical Use. In Encyclopedia of Glass Science, Technology, History, and Culture; Wiley-American Ceramic Society: New York, NY, USA, 2021; pp. 879–889. [Google Scholar]
  4. Du, L.S.; Stebbins, J.F. Stebbins Network connectivity in aluminoborosilicate glasses: A high-resolution 11B, 27Al and 17O NMR study. J. Non Cryst. Solids 2005, 351, 3508–3520. [Google Scholar] [CrossRef]
  5. Wang, J.; Wu, M.; Tang, H.; Han, J.; Liu, C.; Cao, X.; Kang, J. Correlation between viscosity, electrical resistivity and network connectivity of alkali-free boroalumiosilicate glasses. J. Non Cryst. Solids 2019, 509, 88–94. [Google Scholar] [CrossRef]
  6. Lin, X.; Wang, Z.; Jiang, X.; Ning, T.; Jiang, Y.; Lu, A. Effect of Al2O3/SiO2 mass ratio on the structure and properties of medical neutral boroaluminosilicate glass based on XPS and infrared analysis. Ceram. Int. 2023, 49, 38499–38508. [Google Scholar] [CrossRef]
  7. Guadagnino, E.; Zuccato, D. Delamination propensity of pharmaceutical glass containers by accelerated testing with different extraction media. PDA J. Pharm. Sci. Technol. 2012, 66, 116–125. [Google Scholar] [CrossRef]
  8. Zhuo, Y.; Lyu, B.; Song, X.; Yang, C.; Ye, X.; Chen, X. Numerical simulation of horizontal drawing forming process of glass tube. Bull. Chin. Ceram. Soc. 2023, 42, 1096–1105. [Google Scholar]
  9. Zhou, T.; Yan, J.; Masuda, J.; Kuriyagawa, T. Investigation on the viscoelasticity of optical glass in ultraprecision lens molding process. J. Mater. Process. Technol. 2009, 209, 4484–4489. [Google Scholar] [CrossRef]
  10. Yan, Z.; Jia, M.; Wang, J.; Xue, P. Effect of process parameters on mechanical properties of glass fibers reinforced TPU by reaction wet compression molding. Chin. Plast. Ind. 2023, 51, 117–121. [Google Scholar]
  11. Chen, J.; Liu, Y.; Li, C.; Song, P.; Xue, C. Simulation analysis and experimental study on compression molding of chalcogenide-glass diffractive surface. Acta Optica Sinica 2023, 43, 0822024. [Google Scholar]
  12. Li, S.B.; Wang, Z.L.; Shen, L.F.; Hua, T.; Li, Z. Numerical simulation of glass panel impact damage based on peridynamics. J. Vib. Shock. 2024, 43, 294–302. [Google Scholar]
  13. Geng, T.; Liu, Y.H.; Hu, J.Z.; Sheng, J.; Yan, L.Q.; Ren, Q.H. Research on the influence of forming parameters on the temperature field during the calendering process of photovoltaic glass. Plat. Finish. 2022, 44, 53–58. [Google Scholar]
  14. Timothy, J.H.; Gordon, R.J. A computational constitutive model for glass subjected to large strains, high strain rates and high pressures. J. Appl. Mech. 2011, 78, 051003. [Google Scholar]
  15. Yin, S.H.; Wang, Y.F.; Zhu, K.J.; Huo, J.J.; Chen, F.J.; Yu, J.W.; Wang, Y. Numerical simulation of ultraprecision glass molding for micro aspherical glass lens. Acta Opt. Sin. 2010, 39, 5. [Google Scholar]
  16. Sheng, J.; Geng, T.; Hu, J.Z.; Wang, S.Q.; Yuan, Y.T. Factors influencing the quality of photovoltaic glass calendaring. Bull. Chin. Ceram. Soc. 2018, 37, 2830–2840. [Google Scholar]
  17. Mansour, G.; Kyratsis, P.; Korlos, A.; Tzetzis, D. Investigation into the Effect of Cutting Conditions in Turning on the Surface Properties of Filament Winding GFRP Pipe Rings. Machines 2021, 9, 16. [Google Scholar] [CrossRef]
  18. Fitt, A.D.; Furusawa, K.; Monro, T.M.; Please, C.P.; Richardson, D.J. The mathematical modelling of capillary drawing for holey fiber manufacture. J. Eng. Math. 2002, 43, 201–227. [Google Scholar] [CrossRef]
  19. Butt, A.I.K.; Pinnau, R. Optimal control of a non-isothermal tube drawing process. J Eng. Math. 2012, 76, 1–17. [Google Scholar] [CrossRef]
  20. Butt, A.I.K.; Abbas, M.; Ahmad, W. A mathematical analysis of an isothermal tube drawing process. Alex. Eng. J. 2020, 59, 3419–3429. [Google Scholar] [CrossRef]
  21. De Vitis, G.A.; Di Tecco, A.; Foglia, P.; Prete, C.A. Fast Blob and Air Line Defects Detection for High Speed Glass Tube Production Lines. J. Imaging. 2021, 7, 223. [Google Scholar] [CrossRef]
  22. Foglia, P.; Prete, C.; Zanda, M. An inspection system for pharmaceutical glass tubes. WSEAS Trans. Syst. 2015, 14, 123–136. [Google Scholar]
  23. Schaut, R.A.; Weeks, W.P. Historical review of glasses used for parenteral packaging. PDA J. Pharm. Sci. Technol. 2017, 71, 279–296. [Google Scholar] [CrossRef]
  24. Sacha, G.A.; Saffell-Clemmer, W.; Abram, K.; Akers, M.J. Practical fundamentals of glass, rubber, and plastic sterile packaging systems. Pharm. Dev. Technol. 2010, 15, 6–34. [Google Scholar] [CrossRef] [PubMed]
  25. Butt, A.I.K.; Shah, N.A.; Ahmad, W.; Botmart, T.; Ahmad, N. On implementation of a semi-analytic strategy to develop an analytical solution of a steady-state isothermal tube drawing model. Sci. Rep. 2022, 12, 7636. [Google Scholar] [CrossRef] [PubMed]
  26. Griffiths, I.M.; Howell, P.D. Mathematical modeling of non-axisymmetric capillary tube drawing. J. Fluid. Mech. 2008, 605, 181–206. [Google Scholar] [CrossRef]
  27. Gonzalez-Delgado, D.; Jaen-Sola, P.; Oterkus, E. A New Zero Waste Design for a Manufacturing Approach for Direct-Drive Wind Turbine Electrical Generator Structural Components. Machines 2024, 12, 643. [Google Scholar] [CrossRef]
  28. Huo, Z.; Li, G.; Tan, L.; Yang, T.; Tian, D.; Li, J. Optimal Design of High-Precision Focusing Mechanism Based on Flexible Hinge. Machines 2024, 12, 627. [Google Scholar] [CrossRef]
  29. Song, Y.; Shi, G.; Gu, C.; Cao, Z.; Ba, K.; Hao, Y.; Kong, X. An Improved Method for Calculating the Power Consumption of Electromagnet Coil. Machines 2024, 12, 602. [Google Scholar] [CrossRef]
  30. Li, H.; Li, J.W.; Chen, P.; Yu, H.T.; Xiong, D.H. Numerical simulation of heat transfer performance of vacuum glazing based on finite element analysis. Bull. Chin. Ceram. Soc. 2022, 41, 1148–1176. [Google Scholar]
  31. Peng, Y.; Yang, J.; Deck, C.; Willinger, R. Finite element modeling of crash test behavior for windshield laminated glass. Int. J. Impact Eng. 2013, 57, 27–35. [Google Scholar] [CrossRef]
  32. Naumenko, K.; Pander, M.; Würkner, M. Damage patterns in float glass plates: Experiments and peridynamics analysis. Theor. Appl. Fract. Mech. 2022, 118, 103264. [Google Scholar] [CrossRef]
  33. David, M.S.; Bonhin, E.P.; Guimaraes, N.M.; Guidi, E.S. Application of the Finite Element Method in the Analysis of Composite Materials: A Review. Polymers 2020, 12, 818. [Google Scholar] [CrossRef] [PubMed]
  34. Mohamad, A.; Qasim, Z.; Qin, Z.; Babak, S.; Mohammed, A. Finite element analysis of natural fibers composites: A review. Nanotechnol. Rev. 2020, 9, 853–875. [Google Scholar]
  35. Tan, S.; Long, S.; Yao, X.; Zhang, X. An improved material model for loading-path and strain-rate dependent strength of impacted soda-lime glass plate. J. Mater. Res. Technol. 2021, 15, 1905–1919. [Google Scholar] [CrossRef]
  36. Wang, Z.; Ren, T.; Suo, T.; Manes, A. Quasi-static and low-velocity impact biaxial flexural fracture of aluminosilicate glass—An experimental and numerical study. Thin-Walled Struct. 2021, 165, 107939. [Google Scholar] [CrossRef]
  37. Zhang, X.; Liang, W.; Jiang, F.; Wang, Z.; Zhao, J.; Zhou, C.; Wu, J. Effects of air-abrasion pressure on mechanical and bonding properties of translucent zirconia. Clinical Oral Investig. 2021, 25, 1979–1988. [Google Scholar] [CrossRef]
  38. He, Z.; Li, J.; Liu, Y.; Nie, M.; Fan, W. Investigating the effects of contact pressure on rail material abrasive belt grinding performance. Int. J. Adv. Manuf. Technol. 2017, 93, 779–786. [Google Scholar]
Machines 12 00700 g001
Figure 1. Structure of glass tube drawing machine. 1. Deflection angle adjustment device. 2. Air cylinder supporting device. 3. Machine shell. 4. Upper adjusting air cylinder. 5. Upper glass tube drawing device. 6. Glass tube guiding device. 7. Lower glass tube drawing device. 8. Lower adjusting air cylinder. 9. Level-adjusting device.
Figure 1. Structure of glass tube drawing machine. 1. Deflection angle adjustment device. 2. Air cylinder supporting device. 3. Machine shell. 4. Upper adjusting air cylinder. 5. Upper glass tube drawing device. 6. Glass tube guiding device. 7. Lower glass tube drawing device. 8. Lower adjusting air cylinder. 9. Level-adjusting device.
Machines 12 00700 g001
Machines 12 00700 g002
Figure 2. Simplified structure of the glass tube drawing machine. 1. Glass tube. 2. Rubber ring. 3. Drawing wheel.
Figure 2. Simplified structure of the glass tube drawing machine. 1. Glass tube. 2. Rubber ring. 3. Drawing wheel.
Machines 12 00700 g002
Machines 12 00700 g003
Figure 3. Validation experiment.
Figure 3. Validation experiment.
Machines 12 00700 g003
Machines 12 00700 g004
Figure 4. Results comparison of simulation and validation experiment. The bar represents the variance.
Figure 4. Results comparison of simulation and validation experiment. The bar represents the variance.
Machines 12 00700 g004
Machines 12 00700 g005
Figure 5. Change of MES and RSG. Error bars represent the variance. (a) represented the relationship between DUD and MES; (b) represented the relationship between AUD and RSG.
Figure 5. Change of MES and RSG. Error bars represent the variance. (a) represented the relationship between DUD and MES; (b) represented the relationship between AUD and RSG.
Machines 12 00700 g005
Machines 12 00700 g006
Figure 6. Effects of FFGR and DUD on MFDF and AFDF. (a,b) represent the change principle of MFDF and AFDF, respectively.
Figure 6. Effects of FFGR and DUD on MFDF and AFDF. (a,b) represent the change principle of MFDF and AFDF, respectively.
Machines 12 00700 g006
Machines 12 00700 g007
Figure 7. Effects of FFGR, DUD, and AUD on the MRDF. (a–d) represent the change of RDF under AUDs of 1°, 2°, 3°, and 4°, respectively.
Figure 7. Effects of FFGR, DUD, and AUD on the MRDF. (a–d) represent the change of RDF under AUDs of 1°, 2°, 3°, and 4°, respectively.
Machines 12 00700 g007
Machines 12 00700 g008
Figure 8. Effects of FFGR, DUD, and AUD on the ARDF. (a–d) represent the change of RDF under AUDs of 1°, 2°, 3°, and 4°, respectively.
Figure 8. Effects of FFGR, DUD, and AUD on the ARDF. (a–d) represent the change of RDF under AUDs of 1°, 2°, 3°, and 4°, respectively.
Machines 12 00700 g008
Machines 12 00700 g009
Figure 9. Effects of DUD and FFGR on TEC. Error bar represents the standard variance.
Figure 9. Effects of DUD and FFGR on TEC. Error bar represents the standard variance.
Machines 12 00700 g009
Machines 12 00700 g010
Figure 10. Effects of DUD and FFGR on TPD.
Figure 10. Effects of DUD and FFGR on TPD.
Machines 12 00700 g010
Machines 12 00700 g011
Figure 11. Effects of DUD and FFGR on ADFP and MFDP. The dotted line was the fitting line with DUD as an independent value under different FFGR with linear regression.
Figure 11. Effects of DUD and FFGR on ADFP and MFDP. The dotted line was the fitting line with DUD as an independent value under different FFGR with linear regression.
Machines 12 00700 g011
Machines 12 00700 g012
Figure 12. Effects of AUD, DUD, and FFGR on ARDP. Figure (a–d) represent the change of RDF under AUDs of 1°, 2°, 3°, and 4°, respectively.
Figure 12. Effects of AUD, DUD, and FFGR on ARDP. Figure (a–d) represent the change of RDF under AUDs of 1°, 2°, 3°, and 4°, respectively.
Machines 12 00700 g012
Machines 12 00700 g013
Figure 13. Effects of AUD, DUD, and FFGR on MRDP. Figure (a–d) represent the change of RDF under AUDs of 1°, 2°, 3°, and 4°, respectively.
Figure 13. Effects of AUD, DUD, and FFGR on MRDP. Figure (a–d) represent the change of RDF under AUDs of 1°, 2°, 3°, and 4°, respectively.
Machines 12 00700 g013
Table 1. Material model in the FEM simulation.
Table 1. Material model in the FEM simulation.
MaterialRubber Ring (*MAT_ELASTIC)Drawing Wheel (*MAT_RIGID)
ParameterDensity (kg/m3)Elastic Modulus (MPa)Poisson RatioDensity (kg/m3)Elastic Modulus (MPa)Poisson Ratio
Value1.2 × 103100.497.83 × 1032.07 × 1050.29
MaterialGlass tube (*MAT_JOHNSON_HOLMQUIST_CERAMICS)
ParameterDensity (kg/m3)Shear Modulus (MPa)Intact normalized strength parameterFractured strength parameterFractured normalized strength parameter,Intact strength parameter
Value2.5 × 1033.04 × 1030.930.0880.350.77
ParameterD1D2K1 (MPa)K2 (MPa)K3 (MPa)BETA
Value0.0530.854.54 × 104−1.38 × 1052.9 × 1051
Table 2. The experimental factors and values.
Table 2. The experimental factors and values.
Experimental FactorValue
Angle of upper and lower drawing wheel (AUD)0°, 1°, 2°, 3°, 4°
Friction coefficient between the glass tube and the rubber (FFGR, constant)0.1, 0.2, 0.3, 0.4
Distance of upper and lower drawing wheel (DUD, mm)332.5, 333, 333.5, 334, 334.5
Table 3. Results of analysis of variance.
Table 3. Results of analysis of variance.
ParametersAUDFFGRDUD
F Valuep ValueF Valuep ValueF Valuep Value
MES1.65NA0.55NA50.32***
RSG470.75***0.12NA0.09NA
MFDF0.04NA9.64***35.73***
AFDF0.65NA8.20***31.46***
MRDF8.16***3.72**8.42***
ARDF6.71***4.26***12.58***
TEC0.64NA2.38*112.07***
TPD0.64NA9.74***30.25***
AFDP0.53NA8.68***30.69***
MFDP0.41NA11.18***31.40***
ARDP5.65***3.92**13.52***
MRDP5.2**3.01**10.09***
Notes: * represents the significant influence (p < 0.1); ** represents the very significant influence (p < 0.05); *** represents the highly significant influence (p < 0.01); NA represents no significance. F value represents the ratio of the variance between the group means to the variance within the groups.
Table 4. Linear regression of the RDF.
Table 4. Linear regression of the RDF.
ModelAt Valuep
MRDF (R2 = 0.73, p < 0.0001)
Constant2647.118.95***
AUD2.896.51***
FFGR28.636.45***
DUD−7.97−8.98***
ARDF (R2 = 0.80, p < 0.0001)
Constant984.8580.73***
AUD0.630.12***
FFGR9.851.21***
DUD−2.960.24***
Notes: t value refers to the t-statistic, which is used to test the null hypothesis that the coefficient of a predictor variable is equal to zero; *** represents the highly significant influence (p < 0.01).
Table 5. Linear regression of the TEC and TPD.
Table 5. Linear regression of the TEC and TPD.
ModelAt Valuep
TEC (R2 = 0.95, p < 0.0001)
Constant2137.8016.49***
FFGR8.864.56***
DUD−5.93−15.25***
TPD (R2 = 0.85, p < 0.0001)
Constant333,908.346.95***
FFGR3507.824.87***
DUD−1002.19−6.95***
Notes: t value refers to the t-statistic, which is used to test the null hypothesis that the coefficient of a predictor variable is equal to zero; *** represents the highly significant influence (p < 0.01).
Table 6. Linear regression of AFDP and MFDP with FFGR and DUD.
Table 6. Linear regression of AFDP and MFDP with FFGR and DUD.
ModelAt Valuep
AFDP (R2 = 0.85, p < 0.0001)
Constant61,059.797.15***
FFGR631.354.93***
DUD−183.267.15***
MFDP (R2 = 0.87, p < 0.0001)
Constant129,405.577.57***
FFGR1413.515.51***
DUD−388.35−7.58***
Notes: t value refers to the t-statistic, which is used to test the null hypothesis that the coefficient of a predictor variable is equal to zero; *** represents the highly significant influence (p < 0.01).
Table 7. Linear regression of ARDP and MRDP with FFGR and DUD.
Table 7. Linear regression of ARDP and MRDP with FFGR and DUD.
ModelAt Valuep
ARDP (R2 = 0.62, p < 0.0001)
Constant216.667.93***
AUD0.216.58***
FFGR1.804.40***
DUD−0.65−7.94***
MRDP (R2 = 0.68, p < 0.0001)
Constant3.969.23***
AUD0.00356.85***
FFGR0.035.40***
DUD−0.01−9.24***
Notes: t value refers to the t-statistic, which is used to test the null hypothesis that the coefficient of a predictor variable is equal to zero; *** represents the highly significant influence (p < 0.01).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Liu, P.; Cang, L.; Wan, Z.; Yang, K.; Chen, M.; Li, R.; Geng, T. Impact of Drawing Machine Parameters on Force and Energy Consumption in Borosilicate Glass Tube Production. Machines 2024, 12, 700. https://doi.org/10.3390/machines12100700

AMA Style

Liu P, Cang L, Wan Z, Yang K, Chen M, Li R, Geng T. Impact of Drawing Machine Parameters on Force and Energy Consumption in Borosilicate Glass Tube Production. Machines. 2024; 12(10):700. https://doi.org/10.3390/machines12100700

Chicago/Turabian Style

Liu, Peng, Limin Cang, Zhigang Wan, Ke Yang, Ming Chen, Rangling Li, and Tie Geng. 2024. "Impact of Drawing Machine Parameters on Force and Energy Consumption in Borosilicate Glass Tube Production" Machines 12, no. 10: 700. https://doi.org/10.3390/machines12100700

APA Style

Liu, P., Cang, L., Wan, Z., Yang, K., Chen, M., Li, R., & Geng, T. (2024). Impact of Drawing Machine Parameters on Force and Energy Consumption in Borosilicate Glass Tube Production. Machines, 12(10), 700. https://doi.org/10.3390/machines12100700

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop