Abstract
Positive displacement pumps are widely employed for their characteristics, but the pulsating flow they produce is a major and well-known drawback. To reduce the flow ripple produced by the pump, which in turn generates a pressure ripple, many methods have been investigated, from optimising the pump geometrical features to the introduction of active and passive systems to the delivery side. A passive system that has demonstrated to be particularly effective is the in-line bladder-type hydraulic pulsation suppressor. This device, consisting of a bladder gas-charged accumulator with a singular geometry, has been the subject of several studies. This paper describes a model based on the lumped parameter method for simulating and predicting the reduction effect on the pressure ripple achieved by the hydraulic suppressor. To validate the model, an experimental study was conducted, which confirmed the good potential of the model proposed thanks to the good agreement between the modelling results and empirical data.
1. Introduction
Positive displacement pumps are well-known and widely employed in industrial and mobile machinery fields due to their high efficiency and reliability. One major drawback in the use of these machines is the fluctuation in the delivery flow they provide. This fluctuation, known as the flow ripple, is in turn the cause of a pressure ripple that can generate noise and vibrations in the pipelines, leading to the early wearing of and damage to system components [1,2].
To reduce the flow ripple caused by positive displacement pumps, different methods have been studied and some of them have been successfully applied. The first way to reduce flow fluctuations is to act on the pump itself, by refining geometric features in the design phase. In [3,4], the geometrical optimisation of axial piston pumps is discussed, while the focus is on external gear pumps in [5,6].
Another way to reduce flow ripple is to employ an external system in the pump delivery line. These flow ripple reduction systems can be divided into two main families: active and passive systems. Active methods involve the use of devices controlled and powered by an external input. An active method presented in [7,8] is based on the high-frequency actuation of the swash plate angle in an axial piston pump by means of a switching valve to reduce the flow ripple produced by the machine. Different studies have investigated the use of piezo-stack actuators to actuate pistons in order to cancel the flow ripple of positive displacement machines by generating a flow signal in phase opposition [9,10]. Active methods have the advantage of being effective regardless of pressure and frequency operating conditions. On the other hand, they are usually complex and expensive. Passive methods are cheaper due to the simpler construction and because they do not require external control or powering. However, the drawback of these kinds of systems is that they are usually optimised to guarantee great performance in a certain range of working conditions, outside of which they lose effectiveness. Passive systems with which to reduce flow ripple are mainly based on the use of elastic components that allow damping flow and pressure fluctuation. An example of this case is represented in the work of Shang [11], who used a spring-type accumulator to attenuate the first harmonic of the flow ripple produced by an axial piston pump; the suggested device is based on discharge and suction self-oscillation taking advantage of the pump’s discharge and suction pressure ripple. A different solution is proposed in [12] where a section of a flexible rubber tube is introduced into the delivery line in order to achieve pressure ripple attenuation.
In this paper, the focus is on the use of a gas-charged bladder-type hydraulic accumulator as a passive flow ripple- and pressure ripple-reducing device. The use of such components to attenuate fluid-borne noise and flow irregularities in hydraulic systems is well-known [13,14]. In a fluid-filled line, in fact, an accumulator serves as a low-pass filter, compensating for sudden peaks, positive and negative, that may occur in the flow, by storing or providing the excess or lack of fluid, respectively. One gas accumulator typology, which represents the main subject of this work, is that of the in-line bladder-type noise suppressor. On this specific device, different studies have been performed and various modelling approaches have been proposed to predict bandwidth and acoustic attenuation performance. In [15,16], linear multimodal models are proposed and validated through experimental procedures. In [17], a method based on the acoustic FEM (finite element method) and plane wave theory is proposed and results are discussed and compared with experimental data. In [18], a similar damper is modelled with a 1D modelling approach with a particular evaluation of the sound speed for the simulation of the wave effects.
The aim of this study is to develop a model based on the lumped parameter method in order to investigate the influence of the main characteristic parameters of the in-line bladder accumulator on its performance. The main features of the device can be supplied as external parameters to the model and simulations at different working conditions can be executed. An experimental campaign has been performed with the aim of obtaining data that are useful for analysing and validating the lumped parameter model.
2. In-Line Bladder Suppressor Description
The in-line bladder noise suppressor has an arrangement that allows it to reduce as much as possible the size of the device and to maximize the pressure ripple reduction effect. A schematic of an in-line bladder suppressor from Wilkes and McLean is reported in Figure 1.
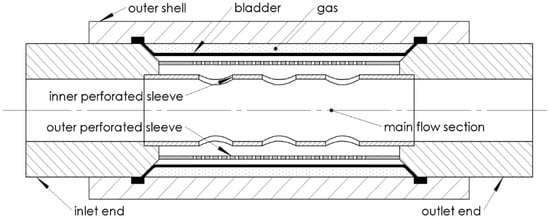
Figure 1.
Schematic of an in-line bladder hydraulic noise suppressor.
The gas charge is contained in an outer shell where it is disposed of circumferentially and surrounds the fluid flowing into the suppressor. The gas, which in most of the cases is nitrogen, is separated from the working fluid by means of a thin rubber bladder. To precharge the device, a pneumatic check valve is fitted onto the outer shell.
Two perforated sleeves are interposed between the main flow section and the gas-charged bladder. The purpose of the outer perforated sleeve is to allow high-pressure gas precharging without damaging the bladder. In fact, the holes are small enough to prevent the bladder from extruding through them when it leans on the sleeve under the pressure of the precharged gas. The inner perforated sleeve has larger holes, and its aim is to maintain the coaxial outer sleeve in its position thanks to a thin metal sheet spirally wound between the two sleeves. The internal assembly is packed thanks to the inlet and outlet end caps that are screwed directly onto the outer shell. The two end caps also have the purpose of ensuring the sealing of the gas inside the bladder by pressing its borders against the outer shell. Both ends are threaded on the inside, so that the device can be easily mounted along the delivery line.
3. Model Description
3.1. Hydraulic Suppressor Model
The mathematical model used to simulate the suppressor is based on the lumped parameter method and it was developed in a Simcenter Amesim© environment. A simplified schematic of the suppressor as modelled is shown in Figure 2.
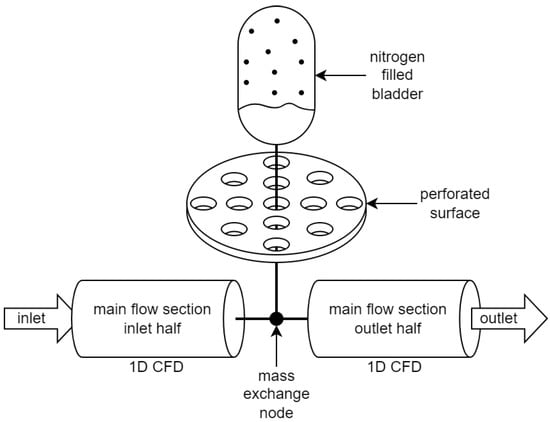
Figure 2.
Simplified schematic of the suppressor.
The main flow section of the suppressor is split into two halves, each modelled as a pipe section with the 1D CFD method, with the aim of accounting for propagation effects; in these sections, continuity and momentum equations are solved.
The fluid mass exchange between the main flow section and the outer volume of the suppressor, where the gas-filled bladder is housed, is considered to be concentrated in a single node located between the two halves in which the inner volume is split. In this node, mass and momentum conservation between the three connected lines are imposed.
The volume outside the outer perforated sleeve is partly occupied by the nitrogen contained in the bladder and that for the remaining part is occupied by the working fluid. These two volumes are, respectively, called Vg and Vf and are not fixed, since the gas volume depends on the pressure of the hydraulic line. The sum of these two volumes is the total accumulator volume, V0. The nitrogen contained in the bladder is modelled as an ideal gas.
As soon as the working fluid static pressure, pf, in the hydraulic line builds up and exceeds that of the gas, the gas in the bladder is compressed and its pressure, pg, equals that of the fluid. Due to the high frequency of the pressure and flow oscillations investigated in this work, the compression and expansion of the gas due to the flow ripple are modelled as adiabatic transformations. For this reason,
where γ is the coefficient for adiabatic transformation set equal to 1.4.
By deriving Equation (1) it is possible to obtain
which evidences the gas bulk modulus.
The outer perforated sleeve separating the main flow section and the external volume is modelled as a concentrated pressure drop. The pressure drop is supposed to be produced only by the outer perforated sleeve. In fact, the inner perforated sleeve has considerably larger holes than the does outer perforated sleeve and therefore its effect is considered negligible. To obtain the outer perforated sleeve pressure drop coefficient, the equations from [19] for the discharge through a thin grid are used. The pressure drop coefficient, ζ, is calculated as
in the case that , or
in the case of where:
- is the Reynolds number calculated for the fluid flowing through the perforated surface holes; is the fluid velocity in the perforated surface holes; is the perforated surface hole diameter; is the ratio between the open area of the holes, , and the total area of the perforated surface F as shown in Figure 3; ,, and , are the parameters determined from different curves reported in [11], where:
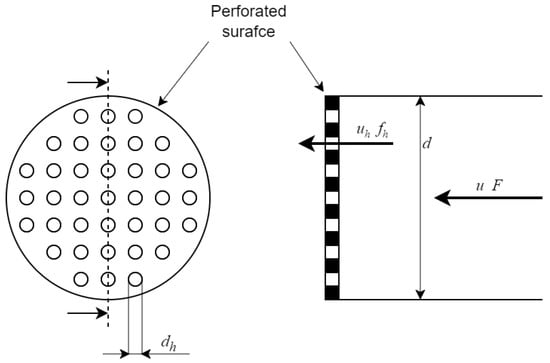 Figure 3. Schematic of flow through a thin perforated surface.
Figure 3. Schematic of flow through a thin perforated surface. - , , .
In Figure 3, a schematic is reported showing the case of flow through a perforated surface used to model the pressure drop caused by the suppressor’s outer perforated sleeve.
The flow, Qh, through the holes of the perforated surface is then obtained according to the orifice law:
3.2. Hydraulic Circuit Model
The Amesim model used to perform simulations, in addition to the suppressor, includes a wider system with the aim of simulating the entire experimental hydraulic circuit illustrated in Figure 4.
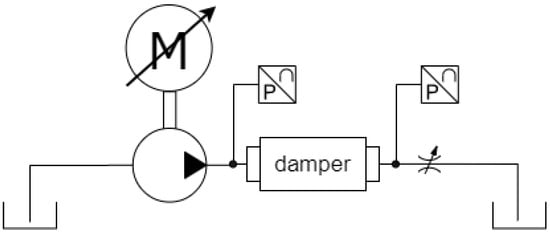
Figure 4.
ISO schematic of hydraulic circuit used for experimental activity.
Two rigid straight pipe sections of 150 mm in length were simulated at the inlet and the outlet of the suppressor, representing the fittings in which, in the experimental apparatus, pressure transducers were placed. The upstream and downstream pressure ripple data obtained by the model were recorded precisely in these sections, in order to make the comparison between model and experimental data as correct as possible. Furthermore, to simplify the model, the piston pump was modelled as an ideal flow source, reproducing the flow rate curves obtained by a previously developed and validated model [20,21]. The main purpose of this work, in fact, is not to investigate pump functioning but to focus on the suppressor effect on the flow and pressure ripple. Finally, a restrictor was modelled as an ideal pressure loss at the outlet of the suppressor to set a static pressure in the simulated line.
3.3. Simulation Parameters
The hydraulic suppressor modelling parameters, which refer to the schematics in Figure 2 and Figure 3, are reported in Table 1. The parameters regarding suppressor’s geometrical features were obtained through direct measurements on the available device. The precharge pressure was checked thanks to a pressure gauge during the precharge procedure.

Table 1.
In-line bladder hydraulic suppressor modelling parameters.
4. Experimental Activity
An experiment was performed in order to investigate suppressor performance and to validate the mathematical model.
The suppressor was fitted into a hydraulic line, the schematic of which is shown in Figure 4. The working fluid is a mineral oil, the characteristics of which are reported in Table 2.

Table 2.
Characteristics of oil used for experimental activity.
The suppressor was mounted on the delivery side of a 9-piston axial piston pump driven by a variable-speed electric motor. On the outlet side of the suppressor, a manual operated variable orifice was used to set the static pressure in the delivery line. On the two sides of the suppressor, two high-frequency piezo-electric pressure transducers (Kistler 6005, 0–1000 bar; 140 kHz bandwidth) were used to measure the upstream and downstream pressure ripple. The two pressure transducers were plugged into two hydraulic fittings, each with a diameter of 19 mm and each 150 mm long. This is an important detail because the two fittings were also replicated in the model.
The suppressor was tested at different pump working conditions, varying the rotation speed and delivery pressure as shown in Table 3. To better understand the influence of the gas precharge pressure on suppressor effectiveness, tests were performed for two different precharge pressure values of 150 and 100 bar.

Table 3.
Pump working conditions.
The oil temperature during the tests was maintained at 50 °C. The temperature of the nitrogen contained in the suppressor was difficult to measure, but was assumed to be equal to the temperature of the oil a within few minutes of starting the flow into the suppressor.
The signal samples from upstream and downstream transducers were collected at a rate of 20 kHz, and every recording lasted for 3 s, for a total of 60,000 samples. For every recording, the amplitude spectrum of the pressure ripple was then obtained. To reduce the leakage effect due to asynchronous data sampling, the flat-top window was applied to each record before performing the frequency analysis and then the amplitude spectrum was corrected by multiplying by a correction factor [20,21].
5. Results
5.1. Experimental and Simulated Data Comparison
The comparison between the numerical results and the experimental data was performed through the analysis of the amplitude spectra of the upstream and downstream pressure signals registered during the experimental tests and obtained from the simulations performed using the described model. In particular, the first- and second-order harmonics of the pressure ripple, which carry most of the pressure oscillation power, were analysed.
The pressure ripple at the downstream side of the hydraulic suppressor is the main factor that has to be taken into account to evaluate the effectiveness of the device. In fact, the hydraulic suppressor has to be fitted as near as possible to the pump delivery in the circuit. Therefore, it is the downstream pressure ripple that propagates along pipes and hydraulic lines producing most of the undesired noise and vibration effects. Focusing on the downstream section results, reported in Figure 5 and Figure 6, it is possible to appreciate the great reduction in the pressure ripple amplitude obtained thanks to the hydraulic suppressor.
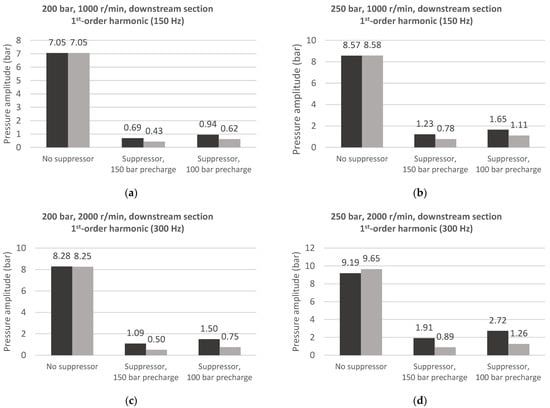
Figure 5.
Pressure ripple 1st-order harmonic amplitude on downstream section with and without hydraulic suppressor. ● Experimental data, ● model results at (a) 1000 r/min, 200 bar; (b) 1000 r/min, 250 bar; (c) 2000 r/min, 200 bar; (d) 2000 r/min, 250 bar.
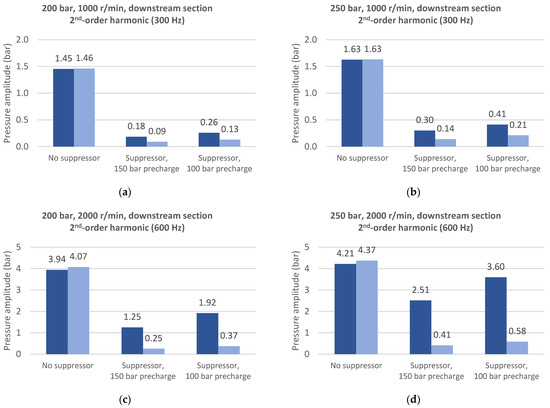
Figure 6.
Pressure ripple 2nd-order harmonic amplitude on downstream section with and without hydraulic suppressor. ● Experimental data, ● model results at (a) 1000 r/min, 200 bar; (b) 1000 r/min, 250 bar; (c) 2000 r/min, 200 bar; (d) 2000 r/min, 250 bar.
Looking at the effect on the first-order pressure ripple harmonic amplitude in Figure 5, it is possible to see how the hydraulic suppressor can produce an 80 to 90% reduction for all the different pump working conditions tested. It is interesting to note that the suppressor precharged at 150 bar always shows better performance compared to the case precharged at 100 bar in terms of pressure ripple reduction. This trend is justified by the fact that the nitrogen contained in the bladder behaves like a spring with different stiffnesses depending on its actual volume. With a 150 bar precharge, the gas volume at a fixed liquid pressure is greater than that with a 100 bar precharge, so the gas behaves like a more flexible spring. From Equation (2) the following can be derived:
which evidences how the pressure variation, dpg, generated in the gas in order to obtain a volume variation, dVg, decreases with the increase in the actual volume, Vg, of the gas.
The model results show good agreement with the experimental values. In fact, the model is able to correctly replicate the dependence of suppressor effectiveness on the precharge pressure. The model also provides a good prediction of the pressure ripple reduction in absolute terms, even if a slight overestimation of the suppressor effectiveness is registered for all tested working conditions. This overestimation in pressure ripple reduction was probably caused by the assumptions made to develop the model. In fact, bladder physics, such as elasticity effects and inertial effects due to the membrane mass, are not modelled in this work and this may have an impact on the simulation results.
Similar considerations are warranted regarding the second-order downstream pressure ripple harmonic as shown in Figure 6. It is possible to see that, as for the first-order harmonic, both experimental data and modelling results show a slight decrease in hydraulic suppressor effectiveness passing from a 150 to 100 bar precharge. The simulations show less accurate agreement for the 2000 r/min pump runs, at a frequency of 600 Hz, where the suppressor seems to lose part of its effectiveness according to the experimental data. This behaviour is not well-replicated by the model that, in this case, heavily overestimates the suppressor damping effect. This is probably due to the fact that, with increasing frequency, inertial effects due to the membrane mass that are not implemented in the model become more relevant.
With the aim of focusing on the lumped parameter model’s ability to replicate the hydraulic suppressor effects, it is interesting to shift the focus onto the upstream section of the device to investigate how it influences the pressure ripple in this portion of the hydraulic system, although this section of the circuit is not the most important for evaluating the suppressor’s effectiveness. For this reason, the focus is only on the first-order harmonic of the upstream pressure ripple, the values of which are reported in Figure 7. Here, it is possible to see that, at 1000 r/min, the amplitude reduction from experimental measurements lies between 90 and 95%. Additionally, in this case, the model’s predicted values are very close to those of the experimental data. Regarding the 2000 r/min results, it is interesting to note that the configuration with a 100 bar precharged suppressor produces a higher amplitude reduction than does the configuration with a 150 bar precharge for both a 200 and 250 bar delivery pressure. This trend is opposite to that registered for the downstream section and it is possible to see that the model is able to predict it, even if there is a slight difference in the absolute values of the amplitude. As seen before, in fact, the lumped parameter model shows a small overestimation of ripple amplitude reduction.
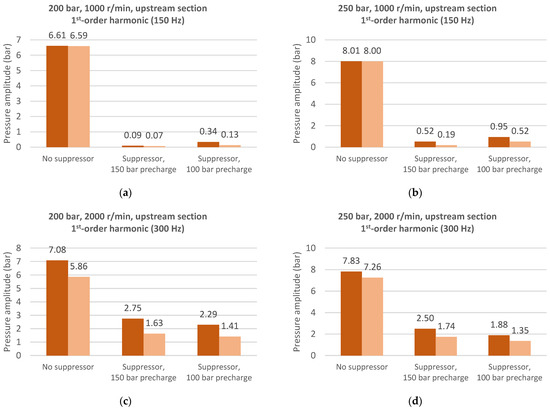
Figure 7.
Pressure ripple 1st-order harmonic amplitude on upstream section with and without hydraulic suppressor. ● Experimental data, ● model results at (a) 1000 r/min, 200 bar; (b) 1000 r/min, 250 bar; (c) 2000 r/min, 200 bar; (d) 2000 r/min, 250 bar.
5.2. Model Results with Reduced Maximum Gas Volume
Having demonstrated that the lumped parameter model is sufficiently accurate in predicting the pressure ripple reduction produced by the hydraulic suppressor, especially regarding downstream side, further simulations were performed in order to evaluate the effects of a reduction in the suppressor size. Under the hypothesis of reducing the length of the gas chamber to ¼ of the original length, simulations were repeated by decreasing the gas volume, V0, to ¼ of the initial value.
Bar graphs in Figure 8 show the comparison of the modelling results of the downstream section, for the cases of the hydraulic suppressor with a full (90 cm3) and reduced (22.5 cm3) gas volume. As the graphs show, the pressure ripple reduction produced by the hydraulic suppressor heavily decreases with the gas volume reduction. On average, the first-order harmonic in the case of a ¼ volume suppressor is about three times the amplitude of that with the full volume. It is clear how reducing the gas volume of the hydraulic suppressor in order to limit its dimensions does not completely prevent the device from abating the pressure ripple but definitely compromises its effectiveness.
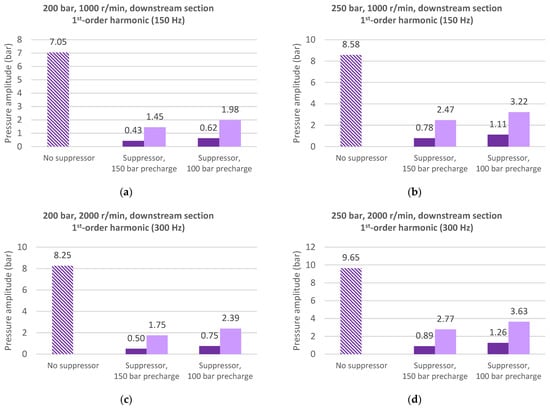
Figure 8.
Pressure ripple 1st-order harmonic amplitude on downstream section, comparison between ○ no suppressor, ● 90 cm3 suppressor, and ● 22.5 cm3 suppressor at (a) 1000 r/min, 200 bar; (b) 1000 r/min, 250 bar; (c) 2000 r/min, 200 bar; (d) 2000 r/min, 250 bar.
6. Conclusions
In this paper, a model based on the lumped parameter method of an in-line bladder-type hydraulic noise suppressor is presented. The model takes into account important features of the device in that he geometrical dimensions of the device are replicated thanks to the one-dimensional modelling of the main flow section; the gas-filled bladder, with his volume and precharge pressure, is modelled as an ideal gas accumulator; a concentrated pressure loss is used to model the passage of fluid through the perforated sleeve using equations for discharge flow through thin grids.
An experimental apparatus was set up in order to measure the upstream and downstream pressure ripple in a circuit with and without the hydraulic suppressor and to compare the modelling results with experimental data, with the aim of validating the lumped parameter model. The experimental apparatus consists of a circuit composed by an axial piston pump, which is fitted onto the delivery side of hydraulic suppressor, and a variable orifice is used to set static delivery pressure. The pressure ripple is measured upstream and downstream the suppressor using wide-bandwidth piezo-electric pressure transducers and sampling the signal at a frequency of 20 kHz.
Both in experimental tests and simulations performed using the described model, different working conditions were investigated, with the delivery pressure set at 200 and 250 bar and the pump speed set at 1000 and 2000 r/min.
To determine the effectiveness of the hydraulic suppressor, the amplitude of the first- and second-order pressure ripple harmonic obtained with FFT were used.
According to the experimental measurements, the hydraulic suppressor has been proven to be highly effective in the whole range of investigated conditions. In fact, the device is able to suppress most of the pressure ripple at the downstream section, which is the most important in terms of vibrations and noise propagation. In particular, the first-order pressure ripple harmonic is reduced by 80–90% for each of the working conditions tested, while the second-order harmonic undergoes lower reduction, especially for the 2000 r/min condition where the frequency is higher (600 Hz).
The lumped parameter model proposed showed results with good agreements with the experimental data. A slight overestimation of the device effectiveness was found in the simulations results, the probable cause of which is to be found in the fact that the physics of the membrane was neglected in the model. This assumption is corroborated by the increasing overestimation of effectiveness with increasing frequency. At higher frequencies, in fact, the inertial effects due to the mass of the membrane take on greater significance.
Apart from that, in most of the simulations performed, the model was able to replicate well the pressure ripple reduction and to predict the dependence of suppressor effectiveness on the precharge pressure. In particular, the model can predict how a higher precharge pressure is desirable to maximize suppressor performance in terms of the reduction in the downstream pressure ripple. On the other hand, since the suppressor does not produce any positive effect as long as the working pressure remains below the precharge pressure, a higher precharge pressure is recommended only in the cases where the working pressure is known to be constant within a certain range. For the cases where the pressure varies frequently, a lower precharge pressure can be used, because the loss of effectiveness at a higher pressure is small enough to justify a wider pressure working range.
Finally, with the aim of investigating the possibility of reducing the suppressor dimensions, a simulation was performed with the gas volume being reduced to ¼ of the original value. The results show how the dimension reduction is possible only at the cost of effectiveness, with this undergoing a significant loss.
Future steps in the development of the lumped parameter model of the hydraulic suppressor will involve the implementation of membrane physics as well as the conduction of more experimental tests in order to investigate a wider range of working conditions and the effects of different positive displacement pump typologies.
Author Contributions
Conceptualisation, P.C. and C.M.V.; methodology, P.C. and C.M.V.; software, C.M.V.; validation, P.C., C.M.V. and M.R.; writing—original draft preparation, P.C. and C.M.V.; writing—review and editing, P.C., C.M.V. and M.R.; supervision, P.C.; project administration, P.C.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to acknowledge the active support of this research provided by Casappa S.p.A., Parma, Italy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Heron, R.A.; Hansford, I. Airborne noise due to structure borne vibrations transmitted through pump mountings and along circuits. In Proceedings of the IMechE Seminar on Quiet Oil Hydraulic Systems; Mechanical Engineering Publication Limited: London, UK, 1977; pp. 41–50. [Google Scholar]
- Johnston, D.N.; Edge, K.A. A Test Method for Measurement of Pump Fluid-Borne Noise Characteristics. Int. Off-Highw. Powerpl. Congr. Expo. 1991, 100, 148–157. [Google Scholar]
- Harrison, A.M.; Edge, K. Reduction of axial piston pump pressure ripple. Proc. Inst. Mech. Eng. 2000, 214, 53–64. [Google Scholar] [CrossRef]
- Zhao, X.; Vacca, A. Theoretical investigation into the ripple source of external gear pumps. Energies 2019, 12, 535. [Google Scholar] [CrossRef]
- Zhao, X.; Vacca, A. Numerical analysis of theoretical flow in external gear machines. Mech. Mach. Theory 2017, 108, 41–56. [Google Scholar] [CrossRef]
- Manring, N. The Discharge Flow Ripple of an Axial-Piston Swash-Plate Type Hydrostatic Pump. J. Dyn. Syst. Meas. Control JUNE 2000, 122, 263–268. [Google Scholar] [CrossRef]
- Casoli, P.; Pastori, M.; Scolari, F.; Rundo, M. Active pressure ripple control in axial piston pumps through high-frequency swash plate oscillations—A theoretical analysis. Energies 2019, 12, 1377. [Google Scholar] [CrossRef]
- Hagstrom, N.; Harens, M.; Chatterjee, A.; Creswick, M. Piezoelectric actuation to reduce pump flow ripple. In Proceedings of the ASME/BATH Symposium on Fluid Power and Motion Control, Sarasota, FL, USA, 7–9 October 2019. [Google Scholar]
- Casoli, P.; Vescovini, C.M.; Scolari, F.; Rundo, M. Theoretical Analysis of Active Flow Ripple Control in Positive Displacement Pumps. Energies 2022, 15, 4703. [Google Scholar] [CrossRef]
- Pan, M.; Ding, B.; Yuan, C.; Zou, J.; Yang, H. Novel Integrated Control of Fluid-Borne Noise in Hydraulic Systems. In Proceedings of the BATH/ASME Symposium on Fluid Power and Motion Control, Bath, UK, 12–14 September 2018. [Google Scholar]
- Shang, Y.; Tang, H.; Sun, H.; Guan, C.; Wu, S.; Xu, Y.; Jiao, Z. A novel hydraulic pulsation reduction component based on discharge and suction self-oscillation: Principle, design and experiment. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 234, 433–445. [Google Scholar] [CrossRef]
- Du, T.; Xu, W.W.; Wu, D.Z.; Wang, L.Q. Experimental study on noise reduction effect of a muffler inserted in liquid transporting pipeline. Mater. Sci. Eng. 2013, 52, 022043. [Google Scholar] [CrossRef]
- Rabie, M.G. On the application of oleopneumatic accumulators for the protection of hydraulic transmission lines against water hammer—A theoretical study. Int. J. Fluid Power 2007, 8, 39–49. [Google Scholar] [CrossRef]
- Yokota, S.; Somada, H.; Yamaguchi, H. Study on an active accumulator. JSME Int. J. 1996, 39, 119–124. [Google Scholar] [CrossRef]
- Marek, A.K.; Gruber, E.R.; Cunefare, K.A. Linear multimodal model for a pressurized gas bladder style hydraulic noise suppressor. Int. J. Fluid Power 2013, 14, 5–16. [Google Scholar] [CrossRef]
- Gruber, E.R.; Cunefare, K.A.; Danzl, P.W.; Marek, K.A.; Beyer, M.A. Optimization of Single and Dual Suppressors Under Varying Load and Pressure Conditions. Int. J. Fluid Power 2013, 14, 27–34. [Google Scholar] [CrossRef]
- Xi, Y.; Li, B.R.; Gao, L.L.; Tang, T.F.; Liao, H.L. Acoustic attenuation performance prediction and analysis of bladder style hydraulic noise suppressors. Appl. Acoust. 2018, 134, 131–137. [Google Scholar] [CrossRef]
- Casoli, P.; Vescovini, C.M.; Rundo, M. One-Dimensional fluid dynamic modelling of a gas bladder hydraulic damper for pump flow pulsation. Energies 2023, 16, 3368. [Google Scholar] [CrossRef]
- Idel’chik, I.E. Handbook of Hydraulic Resistance, 3rd ed.; Begell House: Danbury, CT, USA, 1996. [Google Scholar]
- Casoli, P.; Pastori, M.; Scolari, F. Swash plate design for pressure ripple reduction—A theoretical analysis. In AIP Conference Proceedings, Proceedings of the 74th ATI NATIONAL CONGRESS: Energy Conversion: Research, Innovation and Development for Industry and Territories, Modena, Italy, 11–13 September 2019; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2191, p. 020038. [Google Scholar] [CrossRef]
- Brandt, A. Noise and Vibration Analysis; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).