Research on the Coupled Phase-Tuning Vibration Characteristics of a Two-Stage Planetary Transmission System

Abstract

Mesh phasing has a dramatic impact on the static and dynamic behaviours of planetary gear systems. This research investigates the coupled phase-tuning mechanism of two-stage planetary gear systems and the corresponding relationship with the coupled vibration of the system. Due to the inherent meshing symmetry of the system, the phase-coupled tuning mechanism of the two-stage planetary system is derived based on meshing force relationships and coupling characteristics between different stages. The excitation and suppression relationships associated with the teeth number, harmonic order, and coupling vibration of the coupled system are clearly described. To study the effect of coupled phase tuning on the vibration response of a two-stage planetary gear system, a nonlinear dynamic model was established. The vibration responses under different tuning modes were calculated, and a coupled phase-tuning law for two-stage planetary systems was verified. Model 3 was used as a research tool to build a two-stage planetary transmission experimental platform, and the transverse vibration and torsional vibration of the first stage sun gear were analysed to further verify the correctness of the phase-coupling tuning law.

1. Introduction

In both high-speed transmission and low-to-medium-speed transmission, the industrial trend is aimed at increasing the transmission power to weight ratio in mechanical systems. A multistage planetary gear system has the advantages of a compact structure, high efficiency, and a high power-to-weight ratio; such systems are widely used in aero-engines, industrial transmissions, military vehicles, and other fields, especially in electromechanical coupled power transmission systems, as shown in Figure 1. Stage planetary transmission can promote structural fusion and functional coupling between the motor and the engine so that the system can meet the requirements of continuously variable speed and torque. Compared with single-stage planetary systems, multistage planetary transmission systems have more complex nonlinear coupling characteristics. In the predesign phase, in-depth studies of the relationship between system design parameters and coupling characteristics can potentially identify important mechanisms, reduce system vibration and noise, and ensure that the system is capable of delivering smooth operation across all working conditions.

With nonlinear characteristics such as multiple degrees of freedom and parameter coupling, planetary gears are complex and dynamic. Initially, various degrees of freedom and influential factors were considered when studying the dynamic behaviour of a single meshing pair. Cardona [1] presented a 3-D flexible model for a gear pair to analyse the related meshing characteristics considering the flexible deformation of the tooth surface, backlash, and mesh stiffness fluctuations. Kahraman [2,3] obtained the natural modes and the forced vibration response by studying the dynamic behaviour of a planetary gear pair while considering static transmission errors. Spitas [4] established an accurate 3-D multi-coupled model to predict tooth contact loss and interactions under different variable-torque excitations by considering the backlash, torsional, and lateral displacements, and contact geometry. Lin et al. [5,6] studied the modal characteristics of the planetary gear and the instability of the system parameters, and the key characteristics of the natural frequency and mode were determined. A torsional dynamic model of multistage planetary gear trains was established by Xiang et al. [7] considering the time-varying meshing stiffness, comprehensive gear error and backlash, and the dynamic responses of systems. Liu et al. [8,9] established a nonlinear dynamic model of a planetary gear system; load change, contact loss, and tooth profile modification were considered in the model. Liu [10] established a centralised parameter model that included centrifugal force, inertial force, and Coriolis force of the planetary wheel, thereby closely reflecting actual high-speed operating conditions. This research and model improvements led to dynamic analyses of stable- and variable-speed processes. Xun et al. [11] studied the statistical properties of planetary gear systems by using a stochastic method based on the multiple-scales method. Wei et al. [12] improved the interval harmonic balance method (IHBM) to solve the dynamic problems of gear systems with backlash nonlinearity and time-varying mesh stiffness under uncertainties. Liu et al. [13] studied the influence of clearance configurations on gear system dynamics using the oscillating component of the dynamic transmission error as the dynamic response. Yan [14] calculated the thermal time-varying mesh stiffness and established a nonlinear dynamic model to study the influence of gear temperature on a planetary gear system.

Based on planetary gear system modelling and the inherent characteristics of such systems, scholars began studying the relationships between system parameters and vibration characteristics. Due to the symmetry of planetary gears, the differing mesh phases between the sun–planet and ring–planet meshes have a powerful impact on the dynamic response and can have significant benefits in reducing vibration and noise [15]. R. G. Parker [16] introduced a method for calculating the phase difference between sun–planet meshing, ring–planet meshing, and internal/external meshing in planetary gear systems. Based on the symmetry and meshing periodicity of planetary gears, Ambarisha [17] analytically derived design rules to suppress certain harmonics of the planet mode response in planetary gear dynamics through mesh phasing. Wang [18] investigated steady deformations and measured the spectra of spinning planetary gears with a deformable ring and equally spaced planets; the results verified that planet mesh phasing significantly affects the measured spectral content. Zhang [19] studied the system dynamics of compound planetary gears and calculated the mesh phase. Parker [20] systematically studied the phase relations involving composite planetary wheels and proposed a numbering method to accurately define and calculate the gear phases. Wang [21] studied the relationship between ring gear vibration and the meshing phase and showed that the vibration of a ring gear with meshing phase is mainly influenced by the number of teeth, the number of planetary wheels, the harmonic order, and the vibration mode. Fatourehchi [22] studied the influence of the meshing phase difference on a planetary transmission system based on the dynamic transmission error, and further studied the relationship between the system transmission efficiency and gear meshing phase difference. Sanchez Espiga [23] studied the influence of gear errors and geometry on the load distribution and transmission efficiency of planetary transmission systems. The meshing phase difference of the system will increase the influence of errors on the load distribution of the system.

Past research has shown that differing mesh phases between the sun–planet and, consequently, ring–planet meshes of a single-stage planetary system can have a powerful impact on the dynamic response and significant benefits in reducing vibration and noise. In essence, designers have a variety of options and objectives in choosing the mesh phasing for a given application, and a clear understanding of the relations governing the mesh phasing is essential.

For high-speed and heavy-load hybrid vehicles, multistage planetary transmission systems are widely used, but the coupled phase-tuning law of multistage planetary transmission systems has not been studied in detail. In this research, a two-stage planetary gear transmission system is used as a case study to study the multistage coupled phase-tuning relations in a planetary transmission system. Using the Fourier expansion method, meshing force coupling is further used to explore coupled phase tuning in a system, establish a lumped mass model, and identify the multistage coupled phase-tuning rules for planetary transmission systems.

In this paper, a coupled relationship for phase tuning in a multistage planetary train is proposed. The Fourier expansion method is used to analyse the relationship between the fluctuating meshing forces of the central component and the phase-tuning mode in detail. The coupled tuning principle between planetary stages at different levels is investigated. A nonlinear dynamics model of the two-stage planetary transmission system is established, and the coupled phase-tuning law is verified based on the system amplitude-frequency characteristics.

The rest of the paper is structured as follows. In Section 2, the coupled phase-tuning mechanism of a two-stage planetary transmission system is explored. In Section 3, a two-stage planetary gear system model considering time-varying stiffness, backlash, and other factors is established. Additionally, the coupled phase-tuning law is further studied. In Section 4, the vibration response of the system is simulated and analysed, and the accuracy of coupled phase tuning is verified via frequency analysis and the experiment test. Finally, Section 5 gives some suggestions and conclusions regarding design optimisation based on the research. The relationship of each chapter in the paper is shown in Figure 2.

2. Coupled Phase-Tuning Analysis of a Two-Stage Planetary System

For a single-stage planetary system, the phase-tuning relationship is manifested in four ways: the translational response suppression (TS), translational response excitation (TE), rotational response suppression (RS), and rotational response excitation (RE) of the central component. However, in a two-stage planetary system, the phase-tuning effect of the system is coupled. A schematic diagram of the coupling effect is shown in Figure 3, where one and two correspond to the first and second planetary stages, respectively. ${\mathrm{T}}_{1-2}$, ${\mathrm{F}}_{\mathrm{x}1-2}$, and ${\mathrm{F}}_{\mathrm{y}1-2}$ represent the torque and the bending force in the X and Y directions, respectively, through the connecting shaft between the two stages.

2.1. Relationship between Phase Tuning and the Meshing Force

Parker [16,18] derived a phase calculation method for single-stage planetary systems and analysed the excitation and suppression relationships between the phase-tuning factor k and vibration mode of the system. For a two-stage planetary transmission system with strong coupling, the phase-tuning relationship is also highly coupled. This section derives the coupled phase-tuning relationship for a two-stage planetary system. The initial phase relationship involving the two-stage planetary gears is shown in Figure 4, and the red dotted area in the middle represents the connecting shaft. The central parts of the two planetary stages are concentric circles, and the sun gear centres in the two-stage system are collinear; therefore, the two-stage planetary gears have a common oxy coordinate system, and $e_{dn}^i$ and $e_{dn}^j$ (d = 1, 2) are unit vectors that define planet n, which is in stage d in local coordinates. In the planetary gear coordinate system, i and j are the direction vectors, and n is the planetary gear number.

Taking the first stage as the research object, due to coupling effects, the force of the central component of the second stage is transmitted to the first stage, and the force of the sun gear in the first stage is:

$$\left[\begin{array}{c}{F}_{1nx}\\ F_{1ny}\end{array}\right]=\left[\begin{array}{cc}\cos {\psi }_{1n}& \sin {\psi }_{1n}\\ -\sin {\psi }_{1n}& \cos {\psi }_{1n}\end{array}\right]\left[\begin{array}{c}{F}_{1ni}\\ F_{1nj}\end{array}\right]+\left[\begin{array}{cc}\cos {\psi }_{2n}& \sin {\psi }_{2n}\\ -\sin {\psi }_{2n}& \cos {\psi }_{2n}\end{array}\right]\left[\begin{array}{c}{F}_{2ni}\\ F_{2nj}\end{array}\right]$$

(1)

where $F_{1nx}$ and $F_{1ny}$ are the meshing force components in the X and Y directions of the sun gear in the first stage, respectively. $F_{1ni}$ and $F_{1nj}$ are the meshing force components of each planetary gear. Additionally, ${\psi }_n=z{\phi }_n$, where ${\phi }_n$ is the initial positioning angle of the nth planet.

The Fourier components $F_{{}_{1nx}}^l$ of the sun gear force in the X direction are as follows:

$$\begin{array}{cc}{F}_{1nx}^l=\sum _{l=0}^{\infty }[\hfill & a_{1n}^{l}cos{\phi }_{1n}sin(l{\omega }_{1m}t+l{z}_{1s}{\phi }_{1n})+b_{1n}^{l}cos{\phi }_{1n}cos(l{\omega }_{1m}t+l{z}_{1s}{\phi }_{1n})+\hfill \\ & c_{1n}^{l}sin{\phi }_{1n}sin(l{\omega }_{1m}t+l{z}_{1s}{\phi }_{1n})+d_{1n}^{l}sin{\phi }_{1n}cos(l{\omega }_{1m}t+l{z}_{1s}{\phi }_{1n})+\hfill \\ & a_{2n}^{l}cos{\phi }_{2n}sin(l{\omega }_{2m}t+l{z}_{2s}{\phi }_{2n})+b_{2n}^{l}cos{\phi }_{2n}cos(l{\omega }_{2m}t+l{z}_{2s}{\phi }_{2n})+\hfill \\ & c_{2n}^{l}sin{\phi }_{2n}sin(l{\omega }_{2m}t+l{z}_{2s}{\phi }_{2n})+d_{2n}^{l}sin{\phi }_{2n}cos(l{\omega }_{2m}t+l{z}_{2s}{\phi }_{2n})]\hfill \end{array}$$

(2)

where $l_n$ represents the number of harmonic components for the nth planet; $a_{in}^{l_i}$, $b_{in}^{l_i}$, $c_{in}^{l_i}$, and $d_{in}^{l_i}$ are Fourier coefficients, and they are the same for each planet mesh; that is, $a_{in}^{l_i}=a_i^{l_i}$, with similar expressions for others, and ${\omega }_{im}$(i = 1, 2) is the mesh frequency in the ith planetary stage. The first term, I, in $F_{{}_{1nx}}^l$ in Equation (2) takes the form

$$I={\displaystyle \sum _{l=0}^{\infty }\left\{[a_{1n}^l\cos {\phi }_{1n}\sin (l{\omega }_{1m}t+l{z}_{1s}{\phi }_{1n})]+[a_{2n}^l\cos {\phi }_{2n}\sin (l{\omega }_{2m}t+l{z}_{2s}{\phi }_{2n})]\right\}}$$

(3)

It is assumed that the relation between the amplitude and the initial phase in each stage is as follows:

$$a_{2n}^l=a_{1n}^l-\Delta a$$

$${\phi }_{2n}={\phi }_{1n}+\Delta \phi$$

$\Delta a$ and $\Delta \phi$ are the harmonic amplitude difference and time-varying phase difference, respectively, and $\Delta \phi =({\omega }_1-{\omega }_2)t+({\phi }_1-{\phi }_2)$, where ${\omega }_{1,2}$ represents the rotation speeds in the two-stage system.

$$\begin{array}{ll}I=& {\displaystyle \sum _{n=0}^N[a_{1n}^l\cos {\phi }_{1n}\sin (l{\omega }_{1m}t+l{z}_{1s}{\phi }_{1n})+a_{1n}^l\cos ({\phi }_{1n}+\Delta \phi )\sin (l{\omega }_{2m}t+l{z}_{2s}{\phi }_{2n})+}\\ & \Delta a\cos ({\phi }_{1n}+\Delta \phi )\sin (l{\omega }_{2m}t+l{z}_{2s}{\phi }_{2n})]\end{array}$$

(4)

$$\begin{array}{ll}I=& {\displaystyle \sum _{n=0}^N\{\frac{a_{1n}^l\sin (l{\omega }_{1m}t)}{2}{A}_1+\frac{a_{1n}^l\cos (l{\omega }_{1m}t)}{2}{B}_1+}\frac{A_2\sin (l{\omega }_{2m}t)}{2}[a_{1n}^l({\cos }^2(\Delta \phi )-{\sin }^2(\Delta \phi ))+\Delta a]+\\ & \frac{B_2}{4}[2a_{1n}^l\cos (l{\omega }_{2m}t)({\cos }^2(\Delta \phi )-{\sin }^2(\Delta \phi ))+a_{1n}^l\sin (2\Delta \phi )\sin (l{\omega }_{2m}t)+2\Delta a\cos (l{\omega }_{2m}t)]+\\ & \frac{C_2}{4}{a}_{1n}^l\sin (2\Delta \phi )[\cos (l{\omega }_{2m}t)+\sin (l{\omega }_{2m}t)]+\frac{D_2}{4}\sin (l{\omega }_{2m}t)a_{1n}^l\sin (2\Delta \phi )\}\end{array}$$

(5)

where

$$A_1=\cos (\frac{2\pi (n-1)(k_1-1)}{N_1})+\cos (\frac{2\pi (n-1)(k_1+1)}{N_1})$$

$$B_1=\sin (\frac{2\pi (n-1)(k_1-1)}{N_1})+\sin (\frac{2\pi (n-1)(k_1+1)}{N_1})$$

$$A_2=\cos (\frac{2\pi (n-1)(k_2-1)}{N_2})+\cos (\frac{2\pi (n-1)(k_2+1)}{N_2})$$

$$B_2=\sin (\frac{2\pi (n-1)(k_2-1)}{N_2})+\sin (\frac{2\pi (n-1)(k_2+1)}{N_2})$$

$$C_2=\cos (\frac{2\pi (n-1)(k_2-1)}{N_2})-\cos (\frac{2\pi (n-1)(k_2+1)}{N_2})$$

$$D_2=\sin (\frac{2\pi (n-1)(k_2-1)}{N_2})-\sin (\frac{2\pi (n-1)(k_2+1)}{N_2})$$

where $k_i=\mathrm{mod}(\frac{l{Z}_{is}}{N})$, and the following identities hold for integer values of m:

$$\begin{array}{l}{\displaystyle \sum _{n=1}^N\cos \frac{2\pi (n-1)m}{N}}=\left\{\begin{array}{l}0\hspace{1em}m/N\ne \mathrm{int}eger\hfill \\ N\hspace{1em}m/N=\mathrm{int}eger\end{array}\right.\\ {\displaystyle \sum _{n=1}^N\sin \frac{2\pi (n-1)m}{N}}=0\hfill \end{array}$$

(6)

Equations (5) and (6) show that in the two-stage planetary transmission system, the transverse vibration tuning law of the sun gear in the first stage involves coupled two-stage phase tuning, and the tuning coefficients $k_1$ and $k_2$ are used to adjust the vibration mode of the sun gear. When $k_1\ne 1,N-1$, $A_1$ and $B_1$ in Equation (5) are both zero. Thus, the lth harmonic component of the resultant force acting on the sun gear through planet gears in the first stage disappears. In this case, the tuning result of the second stage has the greatest influence on transverse vibration in the first stage. When $k_2=1,N-1$, neither $A_2$ nor $C_2$ is zero, the transverse force in the second stage is coupled with that in the first stage, and the vibration in the first stage is mainly associated with the lth harmonic of the meshing frequency in the second stage.

2.2. Relation between Phase Tuning and Torque

The torsion moment is generated by the tangential component of the meshing force, so only the force in the j direction needs to be calculated. For a uniform distribution of planetary gears, the following conditions are met:

$$c_n^l=c^l{d}_n^l=d^l$$

The torque acting on the sun gear through the N sun–planet mesh is:

$$\begin{array}{ll}{T}_{sun}/r_{sun}=& {\displaystyle \sum _{n=1}^N{\displaystyle \sum _{l=1}^{\infty }[c_1^l\sin (l{\omega }_{1m}t+l{z}_{s1}{\phi }_{1n})+d_1^l\cos (l{\omega }_{1m}t+l{z}_{s1}{\phi }_{1n})}}\\ & +c_2^l\sin (l{\omega }_{2m}t+l{z}_{s2}{\phi }_{2n})+d_2^l\cos (l{\omega }_{2m}t+l{z}_{s2}{\phi }_{2n})]\end{array}$$

(7)

$$\begin{array}{cc}{T}_{sun}/r_{sun}=\hfill & [c_1^l\sum _{n=1}^{N}cos\frac{2\pi (n-1)k_1}{N}-d_1^l\sum _{n=1}^{N}sin\frac{2\pi (n-1)k_1}{N}]sinl{\omega }_{1m}t\hfill \\ & +[c_1^l\sum _{n=1}^{N}sin\frac{2\pi (n-1)k_1}{N}+d_1^l\sum _{n=1}^{N}cos\frac{2\pi (n-1)k_1}{N}]cosl{\omega }_{1m}t\hfill \\ & +\{[c_2^{l}sin\left(l{\omega }_{2m}t\right)+d_2^{l}cos\left(l{\omega }_{2m}t\right)]cos(\frac{2\pi (n-1)k_2}{N})\hfill \\ & +[c_2^{l}cos\left(l{\omega }_{2m}t\right)-d_2^{l}sin\left(l{\omega }_{2m}t\right)]sin(\frac{2\pi (n-1)k_2}{N})\}cos(\Delta \phi )\hfill \\ & -\{[c_2^{l}sin\left(l{\omega }_{2m}t\right)+d_2^{l}cos\left(l{\omega }_{2m}t\right)]sin(\frac{2\pi (n-1)k_2}{N})\hfill \\ & -[c_2^{l}cos\left(l{\omega }_{2m}t\right)-d_2^{l}sin\left(l{\omega }_{2m}t\right)]cos(\frac{2\pi (n-1)k_2}{N})\}sin(\Delta \phi )\hfill \end{array}$$

(8)

Equation (8) shows that in a two-stage planetary transmission system, the torsional vibration tuning law for the sun gear in the first stage involves coupled phase tuning in two stages.

Taking the tuning law of the central components in the first stage as an example, the coupled tuning law of the two-stage planetary transmission system is shown in

Table 1. Coupled phase-tuning law of a two-stage planetary system.

k1 = mod(lZs1/N1)	k2 = mod(lZs2/N2)	Influences Dynamic Response
0	0	TSl1TSl2REl1REl2
	1, N − 1	TSl1TEl2REl1RSl2
	k ≠ 0, 1, N − 1	TSl1TSl2REl1RSl2
1, N − 1	0	TEl1TSl2RSl1REl2
	1, N − 1	TEl1TEl2RSl1RSl2
	k ≠ 0, 1, N − 1	TEl1TSl2RSl1RSl2
k ≠ 0, 1, N − 1	0	TSl1TSl2RSl1REl2
	1, N − 1	TSl1TEl2RSl1RSl2
	k ≠ 0, 1, N − 1	TSl1TSl2RSl1RSl2

. TS_li indicates that the lth harmonic translational response of the mesh frequency in the ith stage is suppressed, and TE_li, RS_li, and RE_li can be similarly defined.

3. Analysis of the Coupling and Tuning Mechanisms of a Two-Stage Planetary System

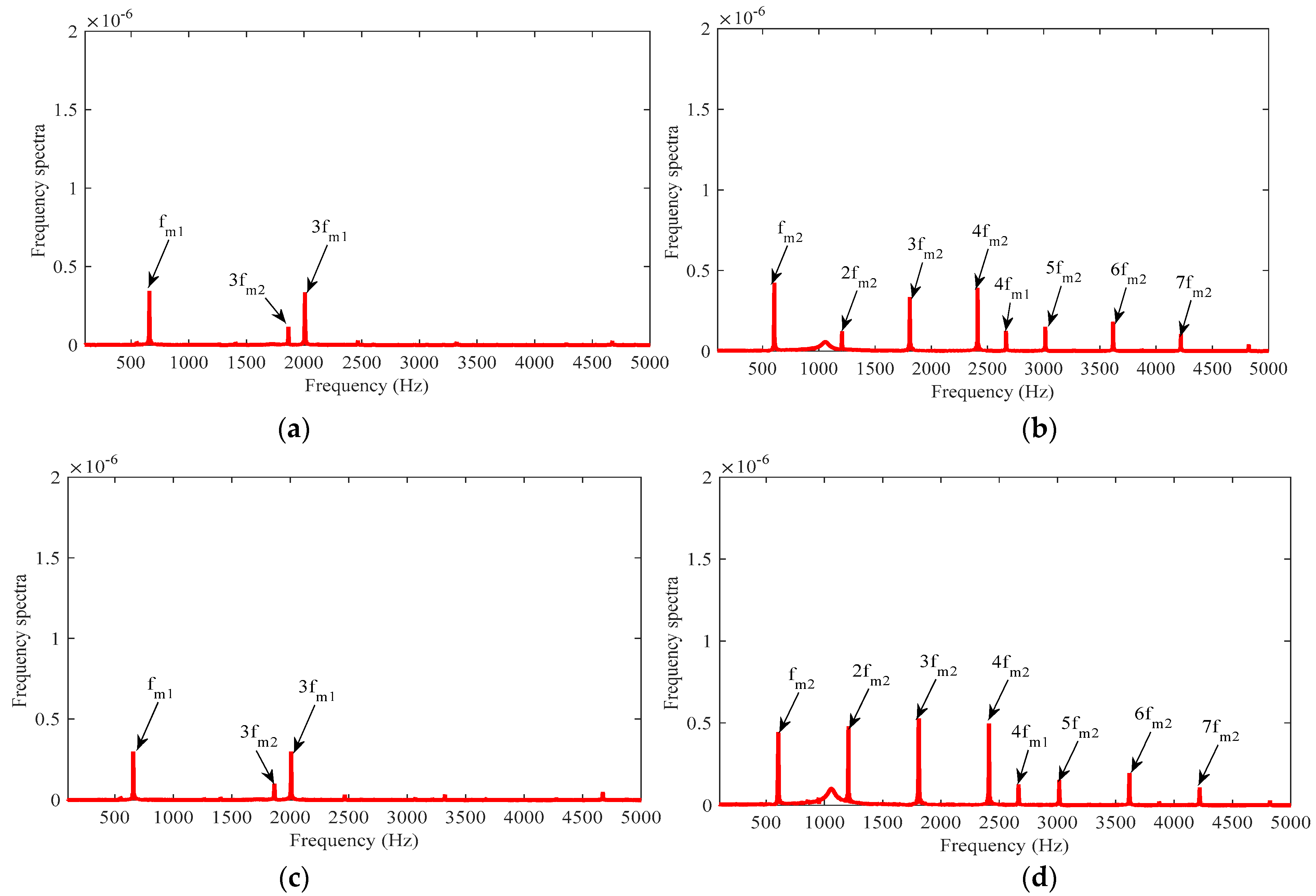
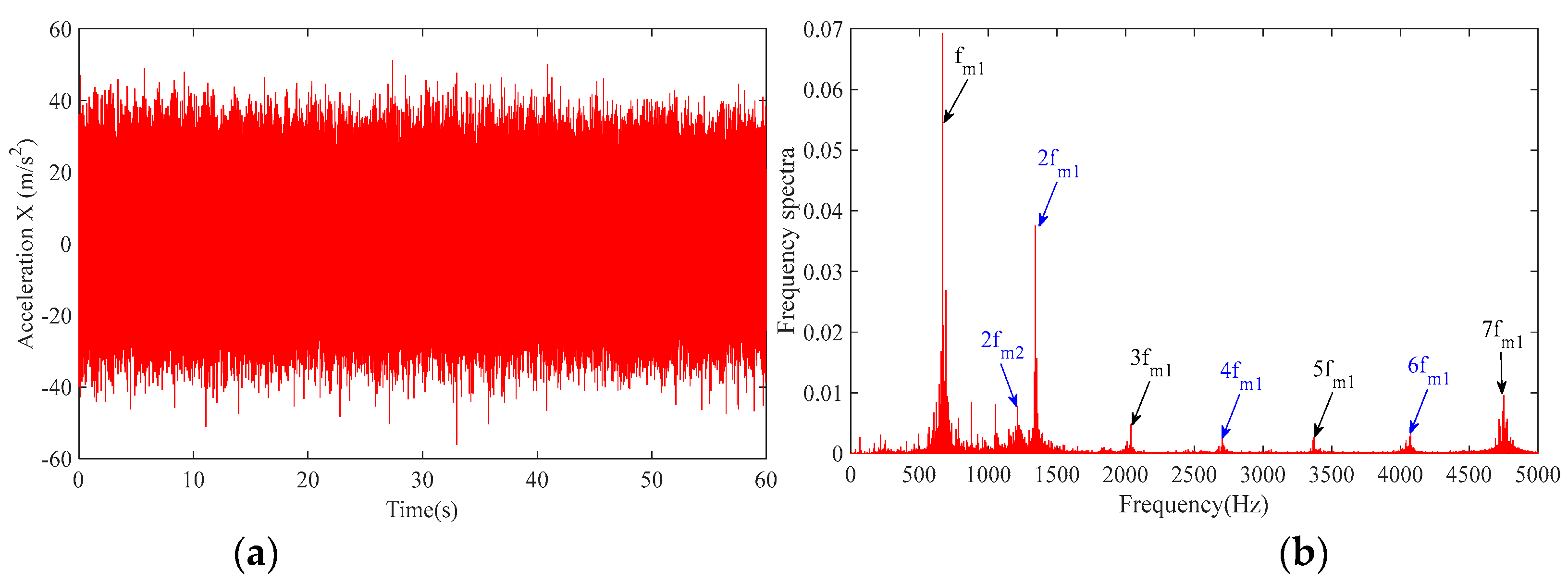
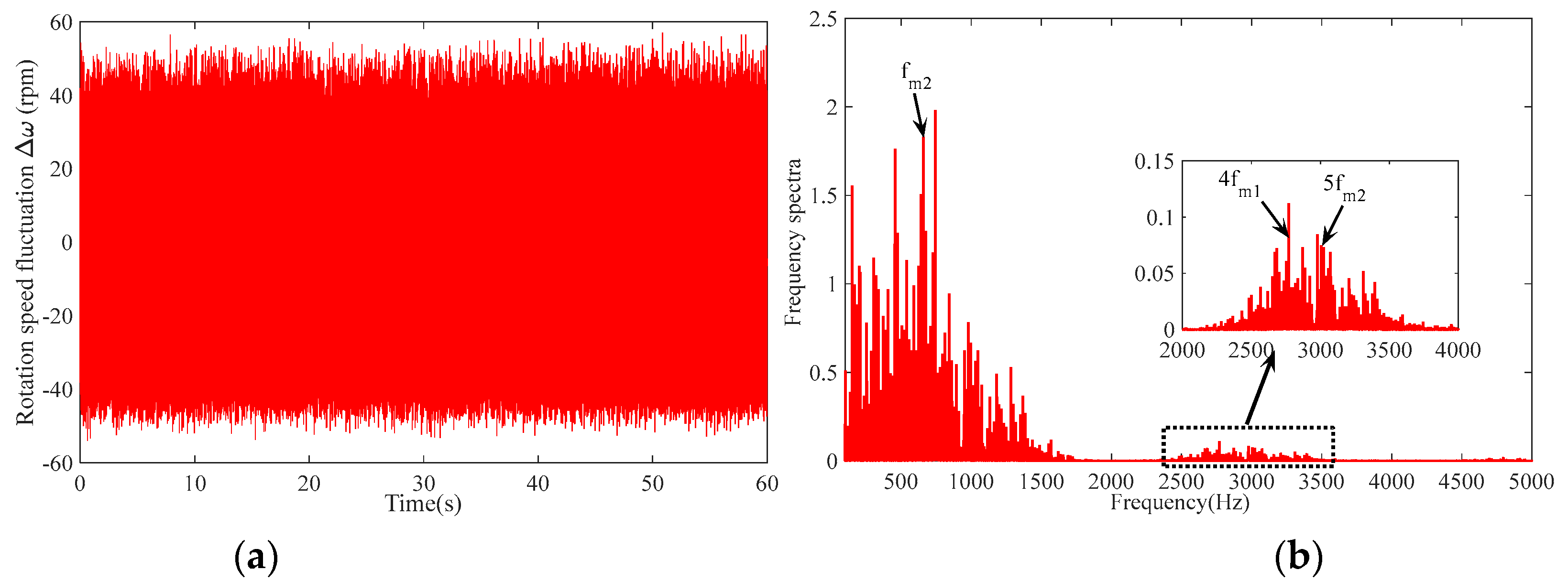
Based on a theoretical analysis of the coupled tuning of a two-stage planetary transmission system in the previous chapter, a nonlinear dynamic model of the system is established, and a numerical analysis method is used to determine and verify the coupling and tuning laws of the two-stage planetary transmission system.

3.1. Nonlinear Dynamic Model of Multistage Planetary Gear Systems

A planetary gear transmission system is a multi-clearance, multi-parameter, coupled, multi-degree-of-freedom system. In order to more clearly study the phase relationship of the system, we ignored the influence of mass eccentricity and gear installation error in the research process.

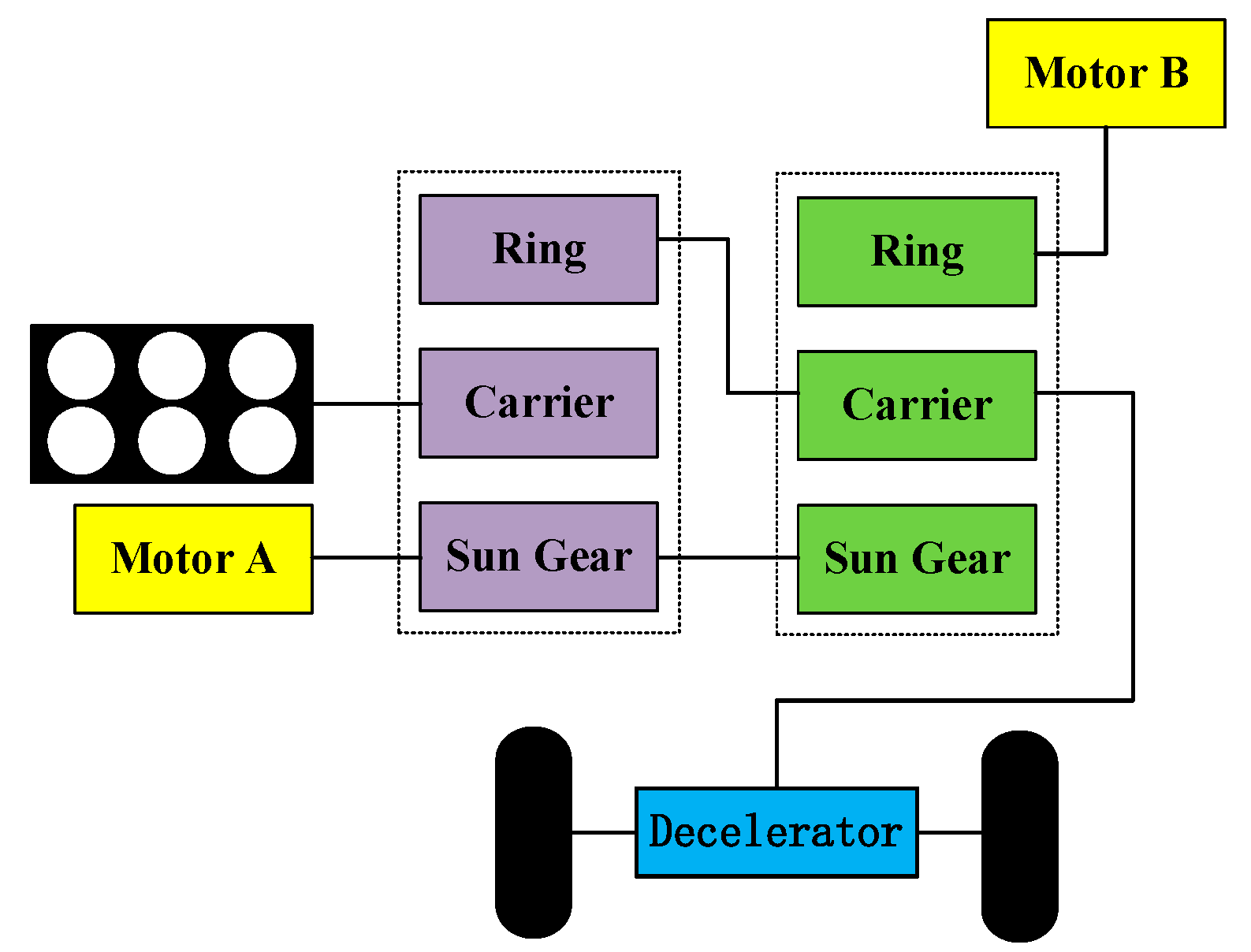
This research focuses on a two-stage planetary transmission system commonly used in automatic transmissions in vehicles. The physical system is shown in Figure 5. Each planetary line contains a sun gear, a ring gear, a planet carrier, and four planetary gears. The sun gear in the first stage is connected to the sun gear in the second stage, and the carrier in the first stage is connected to the ring gear in the second stage. The power is input from the first stage sun gear shaft and output from the second stage ring gear. Torque is applied to the input terminal and the output terminal as the driving force and load, respectively.

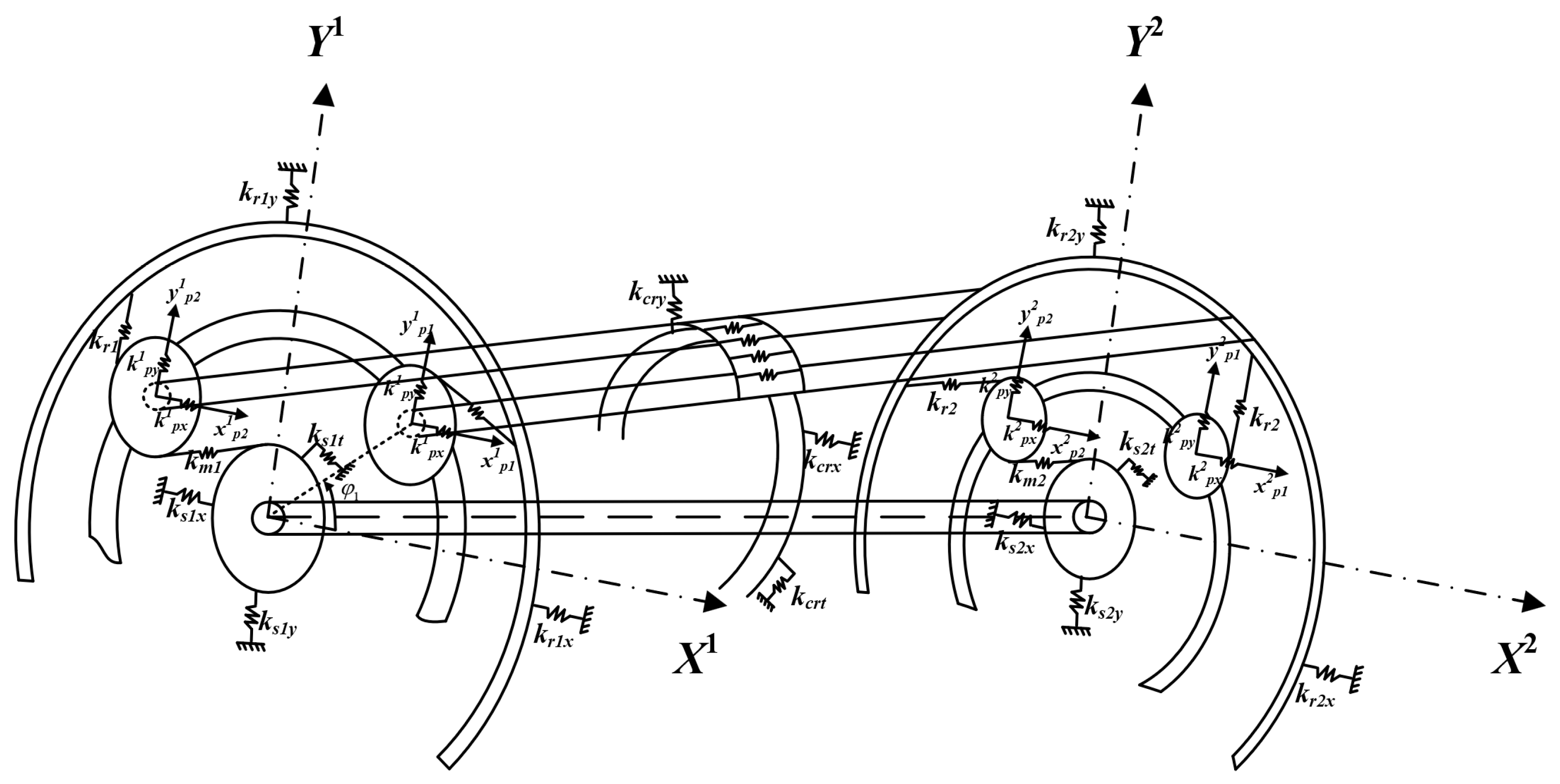
A lumped parameter model for spur planetary gears is shown in Figure 6. The subscripts $s_i$, $c_i$, $r_i$, and $p_{ij}$ (i = 1, 2; j = 1, 2, 3, 4) represent the i_th stage sun gear, carrier gear, and ring gear and j_th planet gear in the i_th stage, respectively. $x_a$, $y_a$, and ${\theta }_a$ are the small translational displacement and small angular displacement of component a (a = $s_i$, $c_i$, $r_i$, $p_{ij}$). k_sipij, c_sipij, and b_sipij are the time-varying meshing stiffness, meshing damping, and backlash for sun–planet gear pairs in the i_th stage, respectively, and the means of k_ripij, c_ripij, and b_ripij are similarly defined. k_xa and k_ya are the support stiffnesses along the horizontal and vertical axes.

Backlash must be assessed in advance to ensure that a gear pair can work normally. Notably, backlash is a main nonlinear factor in a gear system, and the backlash function of a gear pair can be written as shown in Equation (9); the same function is relevant for a ring gear and planet gear pair.

$$f(L_{sipij},b_{sipij})=\left\{\begin{array}{cc}{L}_{sipij}-b_{sipij}& L_{sipij}>b_{sipij}\\ 0& \left|L_{sipij}\right|\le b_{sipij}\\ L_{sipij}+b_{sipij}& L_{sipij}<-b_{sipij}\end{array}\right.$$

(9)

$L_{\mathrm{s}i\mathrm{p}ij}$ is the meshing line deformation between the sun gear and planet gear, and $b_{\mathrm{s}i\mathrm{p}ij}$ is the backlash. Due to gear installation error, manufacturing error, and displacement, the meshing line length will change. The meshing line deformation variables $L_{\mathrm{s}i\mathrm{p}ij}$ and $L_{ri\mathrm{p}ij}$ are included in the mathematical model and can be expressed as

$$\left\{\begin{array}{l}{L}_{sipij}=L_{sipij}^u+L_{sipij}^{xy}\\ L_{ripij}=L_{ripij}^u+L_{ripij}^{xy}\end{array}\right.$$

(10)

$L_{ni\mathrm{p}ij}^{\mathrm{u}}$ is the variation in the meshing line caused by small torsional displacement, $L_{ni\mathrm{p}ij}^{\mathrm{xy}}$ is the variation in meshing line caused by small translational displacement, n = s or r for the sun or ring gear, i = 1 or 2 is the stage of the planet gear system, and j = 1, 2, 3, or 4 for the planet gears.

The meshing line deformation caused by small torsional displacement can be expressed as:

$$\left\{\begin{array}{l}{L}_{sipij}^u={\theta }_{si}{R}_{si}-{\theta }_{ci}{R}_{si}-{\theta }_{pij}{R}_{pij} \\ L_{ripij}^u={\theta }_{pij}{R}_{pij}-{\theta }_{ci}{R}_{ri}-{\theta }_{ri}{R}_{ri}\end{array}\right.$$

(11)

The variation in the meshing line caused by minor displacement $L_{ni\mathrm{p}ij}^{\mathrm{xy}}$ can be expressed as

$$\left\{\begin{array}{l}{L}_{\mathrm{s}i\mathrm{p}ij}^{\mathrm{xy}}=x_{\mathrm{s}i}\sin \left({\psi }_{ij}+\alpha \right)-y_{\mathrm{s}i}\cos \left({\psi }_{ij}+\alpha \right)-x_{\mathrm{c}i}\sin \left({\psi }_{ij}+\alpha \right)+y_{\mathrm{c}i}\cos \left({\psi }_{ij}+\alpha \right)\\ \hspace{1em}\hspace{1em}-x_{\mathrm{p}ij}\sin \alpha +y_{\mathrm{p}ij}\cos \alpha \\ L_{\mathrm{r}i\mathrm{p}ij}^{\mathrm{xy}}=-x_{\mathrm{r}i}\sin \left({\psi }_{ij}-\alpha \right)+y_{\mathrm{r}i}\cos \left({\psi }_{ij}-\alpha \right)+x_{\mathrm{c}i}\sin \left({\psi }_{ij}-\alpha \right)-y_{\mathrm{c}i}\cos \left({\psi }_{ij}-\alpha \right)\\ \hspace{1em}\hspace{1em}-x_{\mathrm{p}ij}\sin \alpha -y_{\mathrm{p}ij}\cos \alpha \end{array}\right.$$

(12)

The nonlinear meshing force can be written as shown in Equation (13).

$$\left\{\begin{array}{c}{F}_{sipij}=k_{sipij}f(L_{sipij},b_{sipij})+c_{sipij}{\dot{L}}_{sipij}\\ F_{ripij}=k_{ripij}f(L_{ripij},b_{ripij})+c_{ripij}{\dot{L}}_{ripij}\end{array}\right.$$

(13)

In Equation (13), $k_{sipij}$ and $k_{ripij}$ are the time-varying meshing stiffness of the sun–planet gear pair and ring–planet gear pair, respectively.

Then, the equations of motion for the two-stage planet gear system can be written as shown in Equations (14)–(23) according to the Lagrange equations. In these equations, $m_a$ and $J_a$ (a = $s_i$$c_i$$r_i$$p_{ij}$) are the mass and inertia of component a.

The differential equation of vibration for the first stage sun gear is

$$\left\{\begin{array}{c}{m}_{\mathrm{s}1}{\ddot{x}}_{\mathrm{s}1}+{\displaystyle \sum _{j=1}^4\sin \left({\psi }_{\mathrm{p}1j}+\alpha \right)F_{\mathrm{s}1\mathrm{p}1j}}+k_{\mathrm{xs}1}{x}_{\mathrm{s}1}+c_{\mathrm{xs}1}{\dot{x}}_{\mathrm{s}1}+F_{\mathrm{bys}1\mathrm{s}2}=0\\ m_{\mathrm{s}1}{\ddot{y}}_{\mathrm{s}1}-{\displaystyle \sum _{j=1}^4\cos \left({\psi }_{\mathrm{p}1j}+\alpha \right)F_{\mathrm{s}1\mathrm{p}1j}+k_{\mathrm{ys}1}{y}_{\mathrm{s}1}+c_{\mathrm{ys}1}{\dot{y}}_{\mathrm{s}1}+F_{\mathrm{bxs}1\mathrm{s}2}=0 }\\ J_{\mathrm{s}1}{\ddot{\theta }}_{\mathrm{s}1}+{\displaystyle \sum _{j=1}^4{F}_{\mathrm{s}1\mathrm{p}1j}{R}_{\mathrm{s}1}}+T_{\mathrm{s}1\mathrm{s}2}=T_{\mathrm{in}}\end{array}\right.$$

(14)

The differential equation of vibration for the first stage ring gear is

$$\left\{\begin{array}{c}{m}_{\mathrm{r}1}{\ddot{x}}_{\mathrm{r}1}-{\displaystyle \sum _{j=1}^4\sin \left({\psi }_{\mathrm{p}1j}-\alpha \right)F_{\mathrm{r}1\mathrm{p}1j}+k_{\mathrm{xr}1}{x}_{\mathrm{r}1}+c_{\mathrm{xr}1}{\dot{x}}_{\mathrm{r}1}=0}\\ m_{\mathrm{r}1}{\ddot{y}}_{\mathrm{r}1}+{\displaystyle \sum _{j=1}^4\cos \left({\psi }_{\mathrm{p}1j}-\alpha \right)F_{\mathrm{r}1\mathrm{p}1j}+k_{\mathrm{yr}1}{y}_{\mathrm{r}1}+c_{\mathrm{yr}1}{\dot{y}}_{\mathrm{r}1}=0}\\ J_{\mathrm{r}1}{\ddot{\theta }}_{\mathrm{r}1}-{\displaystyle \sum _{j=1}^4{F}_{\mathrm{r}1\mathrm{p}1j}{R}_{\mathrm{r}1}}=-T_{brake}\end{array}\right.$$

(15)

The differential equation of vibration for the first stage carrier is

$$\begin{array}{cc}\hfill & m_{\mathrm{c}1}{\ddot{x}}_{\mathrm{c}1}+{\ddot{x}}_{\mathrm{c}1}\sum _{j=1}^4{m}_{\mathrm{p}1j}+\sum _{j=1}^4{m}_{\mathrm{p}1j}{\ddot{x}}_{\mathrm{p}1j}cos{\psi }_{\mathrm{p}1j}-\sum _{j=1}^4{m}_{\mathrm{p}1j}{\ddot{y}}_{\mathrm{p}1j}sin{\psi }_{\mathrm{p}1j}-{\omega }_{\mathrm{c}1}^2\sum _{j=1}^4{m}_{\mathrm{p}1j}{x}_{\mathrm{p}1j}cos{\psi }_{\mathrm{p}2j}\hfill \\ \hfill & +{\omega }_{\mathrm{c}1}^2\sum _{j=1}^4{m}_{\mathrm{p}1j}{y}_{\mathrm{p}1j}sin{\psi }_{\mathrm{p}1j}-2{\omega }_{\mathrm{c}1}\sum _{j=1}^4{m}_{\mathrm{p}1j}{\dot{x}}_{\mathrm{p}1j}sin{\psi }_{\mathrm{p}1j}-2{\omega }_{\mathrm{c}1}\sum _{j=1}^4{m}_{\mathrm{p}1j}{\dot{y}}_{\mathrm{p}1j}cos{\psi }_{\mathrm{p}1j}\hfill \\ \hfill & -\sum _{j=1}^{4}sin\left({\psi }_{\mathrm{p}1j}+\alpha \right)F_{\mathrm{s}1\mathrm{p}1j}+\sum _{j=1}^{4}sin\left({\psi }_{\mathrm{p}1j}-\alpha \right)F_{\mathrm{r}1\mathrm{p}1j}+k_{\mathrm{xc}1}{x}_{\mathrm{c}1}+c_{\mathrm{xc}1}{\dot{x}}_{\mathrm{c}1}+F_{\mathrm{bxc}1\mathrm{r}2}=0\hfill \end{array}$$

$$\begin{array}{cc}\hfill & m_{\mathrm{c}1}{\ddot{y}}_{\mathrm{c}1}+{\ddot{y}}_{\mathrm{c}1}\sum _{j=1}^4{m}_{\mathrm{p}1j}+\sum _{j=1}^4{m}_{\mathrm{p}1j}{\ddot{x}}_{\mathrm{p}1j}sin{\psi }_{\mathrm{p}1j}+\sum _{j=1}^4{m}_{\mathrm{p}1j}{\ddot{y}}_{\mathrm{p}1j}cos{\psi }_{\mathrm{p}1j}-{\omega }_{\mathrm{c}1}^2\sum _{j=1}^4{m}_{\mathrm{p}1j}{x}_{\mathrm{p}1j}sin{\psi }_{\mathrm{p}1j}\hfill \\ \hfill & -{\omega }_{\mathrm{c}1}^2\sum _{j=1}^4{m}_{\mathrm{p}1j}{y}_{\mathrm{p}1j}cos{\psi }_{\mathrm{p}1j}+2{\omega }_{\mathrm{c}1}\sum _{j=1}^4{m}_{\mathrm{p}1j}{\dot{x}}_{\mathrm{p}1j}cos{\psi }_{\mathrm{p}1j}-2{\omega }_{\mathrm{c}1}\sum _{j=1}^4{m}_{\mathrm{p}1j}{\dot{y}}_{\mathrm{p}1j}sin{\psi }_{\mathrm{p}1j}\hfill \\ \hfill & +\sum _{j=1}^{4}cos\left({\psi }_{\mathrm{p}1j}+\alpha \right)F_{\mathrm{s}1\mathrm{p}1j}-\sum _{j=1}^{4}cos\left({\psi }_{\mathrm{p}1j}-\alpha \right)F_{\mathrm{r}1\mathrm{p}1j}+k_{\mathrm{yc}1}{y}_{\mathrm{c}1}+c_{\mathrm{yc}1}{\dot{y}}_{\mathrm{c}1}+F_{\mathrm{byc}1\mathrm{r}2}=0\hfill \end{array}$$

$$\begin{array}{l}{J}_{\mathrm{c}1}{\ddot{\theta }}_{\mathrm{c}1}-{\displaystyle \sum _{j=1}^4{J}_{\mathrm{p}1j}{\ddot{\theta }}_{\mathrm{c}1}}+{\displaystyle \sum _{j=1}^4{J}_{\mathrm{p}1j}{\ddot{\theta }}_{\mathrm{p}1j}}+{\displaystyle \sum _{j=1}^4{m}_{\mathrm{p}1j}{R}_{\mathrm{bc}1}^2{\ddot{\theta }}_{\mathrm{c}1}}-{\displaystyle \sum _{j=1}^4{F}_{\mathrm{s}1\mathrm{p}1j}{R}_{\mathrm{bs}1}}\\ -{\displaystyle \sum _{j=1}^4{F}_{\mathrm{r}1\mathrm{p}1j}{R}_{\mathrm{br}1}}+T_{\mathrm{c}1\mathrm{r}2}=0\end{array}$$

(16)

The differential equation of vibration for the first stage planet gear is

$$\left\{\begin{array}{c}{m}_{p1j}{\ddot{x}}_{c1}cos{\psi }_{p1j}+m_{p1j}{\ddot{y}}_{c1}sin{\psi }_{p1j}+m_{p1j}{\ddot{x}}_{p1j}-2m_{p1j}{\omega }_{c1}{\dot{y}}_{p1j}\hfill \\ -m_{p1j}{\omega }_{c1}^2{x}_{p1j}-sin\alpha F_{s1p1j}-sin\alpha F_{r1p1j}+k_{xp1j}{x}_{p1j}+c_{xp1j}{\dot{x}}_{p1j}=0\hfill \\ -m_{p1j}{\ddot{x}}_{c1}sin{\psi }_{p1j}+m_{p1j}{\ddot{y}}_{c1}cos{\psi }_{p1j}+m_{p1j}{\ddot{y}}_{p1j}+2m_{p1j}{\omega }_{c1}{\dot{x}}_{p1j}\hfill \\ -m_{p1j}{\omega }_{c1}^2{y}_{p1j}+cos\alpha F_{s1p1j}-cos\alpha F_{r1p1j}+k_{yp1j}{y}_{p1j}+c_{yp1j}{\dot{y}}_{p1j}=0\hfill \\ -J_{p1j}{\ddot{\theta }}_{c1}+J_{p1j}{\ddot{\theta }}_{p1j}-F_{s1p1j}{R}_{p1j}+F_{r1p1j}{R}_{p1j}=0\hfill \end{array}\right.$$

(17)

The differential equation of vibration for the second stage sun gear is

$$\left\{\begin{array}{c}{m}_{\mathrm{s}2}{\ddot{x}}_{\mathrm{s}2}+{\displaystyle \sum _{j=1}^4\sin \left({\psi }_{\mathrm{p}2j}+\alpha \right)F_{\mathrm{s}2\mathrm{p}2j}+k_{\mathrm{xs}2}{x}_{\mathrm{s}2}+c_{\mathrm{xs}2}{\dot{x}}_{\mathrm{s}2}-F_{\mathrm{bxs}1\mathrm{s}2}=0}\\ m_{\mathrm{s}2}{\ddot{y}}_{\mathrm{s}2}-{\displaystyle \sum _{j=1}^4\cos \left({\psi }_{\mathrm{p}2j}+\alpha \right)F_{\mathrm{s}2\mathrm{p}2j}+k_{\mathrm{ys}2}{y}_{\mathrm{s}2}+c_{\mathrm{ys}2}{\dot{y}}_{\mathrm{s}2}-F_{\mathrm{bys}1\mathrm{s}2}=0}\\ J_{\mathrm{s}2}{\ddot{\theta }}_{\mathrm{s}2}+{\displaystyle \sum _{j=1}^4{F}_{\mathrm{s}2\mathrm{p}2j}{R}_{\mathrm{s}2}}-T_{\mathrm{s}1\mathrm{s}2}=0 \end{array}\right.$$

(18)

The differential equation of vibration for the second stage ring gear is

$$\left\{\begin{array}{c}{m}_{\mathrm{r}2}{\ddot{x}}_{\mathrm{r}2}-{\displaystyle \sum _{j=1}^4\sin \left({\psi }_{\mathrm{p}2j}-\alpha \right)F_{\mathrm{r}2\mathrm{p}2j}+k_{\mathrm{xr}2}{x}_{\mathrm{r}2}+c_{\mathrm{xr}2}{\dot{x}}_{\mathrm{r}2}-F_{\mathrm{bxc}1\mathrm{r}2}=0}\\ m_{\mathrm{r}2}{\ddot{y}}_{\mathrm{r}2}+{\displaystyle \sum _{j=1}^4\cos \left({\psi }_{\mathrm{p}2j}-\alpha \right)F_{\mathrm{r}2\mathrm{p}2j}+k_{\mathrm{yr}2}{y}_{\mathrm{r}2}+c_{\mathrm{yr}2}{\dot{y}}_{\mathrm{r}2}-F_{\mathrm{byc}1\mathrm{r}2}=0 }\\ J_{\mathrm{r}2}{\ddot{\theta }}_{\mathrm{r}2}+{\displaystyle \sum _{j=1}^4{F}_{\mathrm{r}2\mathrm{p}2j}{R}_{\mathrm{r}2}}-T_{\mathrm{c}1\mathrm{r}2}= 0 \end{array}\right.$$

(19)

The differential equation of vibration for the second stage carrier is

$$\begin{array}{c}{m}_{\mathrm{c}2}{\ddot{x}}_{\mathrm{c}2}+{\ddot{x}}_{\mathrm{c}2}\sum _{j=1}^4{m}_{\mathrm{p}2j}+\sum _{j=1}^4{m}_{\mathrm{p}2j}{\ddot{x}}_{\mathrm{p}2j}cos{\psi }_{\mathrm{p}2j}-\sum _{j=1}^4{m}_{\mathrm{p}2j}{\ddot{y}}_{\mathrm{p}2j}sin{\psi }_{\mathrm{p}2j}-{\omega }_{\mathrm{c}2}^2\sum _{j=1}^4{m}_{\mathrm{p}2j}{x}_{\mathrm{p}2j}cos{\psi }_{\mathrm{p}2j}\hfill \\ +{\omega }_{\mathrm{c}2}^2\sum _{j=1}^4{m}_{\mathrm{p}2j}{y}_{\mathrm{p}2j}sin{\psi }_{\mathrm{p}2j}-2{\omega }_{\mathrm{c}2}\sum _{j=1}^4{m}_{\mathrm{p}2j}{\dot{x}}_{\mathrm{p}2j}sin{\psi }_{\mathrm{p}2j}-2{\omega }_{\mathrm{c}2}\sum _{j=1}^4{m}_{\mathrm{p}2j}{\dot{y}}_{\mathrm{p}2j}cos{\psi }_{\mathrm{p}2j}\hfill \\ -\sum _{j=1}^{4}sin\left({\psi }_{\mathrm{p}2j}+\alpha \right)F_{\mathrm{s}2\mathrm{p}2j}+\sum _{j=1}^{4}sin\left({\psi }_{\mathrm{p}2j}-\alpha \right)F_{\mathrm{r}2\mathrm{p}2j}+k_{\mathrm{xc}2}{x}_{\mathrm{c}2}+c_{\mathrm{xc}2}{\dot{x}}_{\mathrm{c}2}=0\hfill \end{array}$$

$$\begin{array}{c}{m}_{\mathrm{c}2}{\ddot{y}}_{\mathrm{c}2}+{\ddot{y}}_{\mathrm{c}2}\sum _{j=1}^4{m}_{\mathrm{p}2j}+\sum _{j=1}^4{m}_{\mathrm{p}2j}{\ddot{x}}_{\mathrm{p}2j}sin{\psi }_{\mathrm{p}2j}+\sum _{j=1}^4{m}_{\mathrm{p}2j}{\ddot{y}}_{\mathrm{p}2j}cos{\psi }_{\mathrm{p}2j}-{\omega }_{\mathrm{c}2}^2\sum _{j=1}^4{m}_{\mathrm{p}2j}{x}_{\mathrm{p}2j}sin{\psi }_{\mathrm{p}2j}\hfill \\ -{\omega }_{\mathrm{c}2}^2\sum _{j=1}^4{m}_{\mathrm{p}2j}{y}_{\mathrm{p}2j}cos{\psi }_{\mathrm{p}2j}+2{\omega }_{\mathrm{c}2}\sum _{j=1}^4{m}_{\mathrm{p}2j}{\dot{x}}_{\mathrm{p}2j}cos{\psi }_{\mathrm{p}2j}-2{\omega }_{\mathrm{c}2}\sum _{j=1}^4{m}_{\mathrm{p}2j}{\dot{y}}_{\mathrm{p}2j}sin{\psi }_{\mathrm{p}2j}\hfill \\ +\sum _{j=1}^{4}cos\left({\psi }_{\mathrm{p}2j}+\alpha \right)F_{\mathrm{s}2\mathrm{p}2j}-\sum _{j=1}^{4}cos\left({\psi }_{\mathrm{p}2j}-\alpha \right)F_{\mathrm{r}2\mathrm{p}2j}+k_{\mathrm{yc}2}{y}_{\mathrm{c}2}+c_{\mathrm{yc}2}{\dot{y}}_{\mathrm{c}2}=0\hfill \end{array}$$

(20)

$$\begin{array}{l}{J}_{\mathrm{c}2}{\ddot{\theta }}_{\mathrm{c}2}-{\displaystyle \sum _{j=1}^4{J}_{\mathrm{p}2j}{\ddot{\theta }}_{\mathrm{c}2}}+{\displaystyle \sum _{j=1}^4{J}_{\mathrm{p}2j}{\ddot{\theta }}_{\mathrm{p}2j}}+{\displaystyle \sum _{j=1}^4{m}_{\mathrm{p}2j}{R}_{\mathrm{bc}2}^2{\ddot{\theta }}_{\mathrm{c}2}}-{\displaystyle \sum _{j=1}^4{F}_{\mathrm{s}2\mathrm{p}2j}{R}_{\mathrm{bs}2}}\\ -{\displaystyle \sum _{j=1}^4{F}_{\mathrm{r}2\mathrm{p}2j}{R}_{\mathrm{br}2}}=-T_{\mathrm{out}}\end{array}$$

The differential equation of vibration for the second stage planet gear is

$$\left\{\begin{array}{c}{m}_{\mathrm{p}2j}{\ddot{x}}_{\mathrm{c}2}cos{\psi }_{\mathrm{p}2j}+m_{\mathrm{p}2j}{\ddot{y}}_{\mathrm{c}2}sin{\psi }_{\mathrm{p}2j}+m_{\mathrm{p}2j}{\ddot{x}}_{\mathrm{p}2j}-2m_{\mathrm{p}2j}{\omega }_{\mathrm{c}2}{\dot{y}}_{\mathrm{p}2j}\hfill \\ -m_{\mathrm{p}2j}{\omega }_{\mathrm{c}2}^2{x}_{\mathrm{p}2j}-sin\alpha F_{\mathrm{s}2\mathrm{p}2j}-sin\alpha F_{\mathrm{r}2\mathrm{p}2j}+k_{\mathrm{xp}2j}{x}_{\mathrm{p}2j}+c_{\mathrm{xp}2j}{\dot{x}}_{\mathrm{p}2j}=0\hfill \\ -m_{\mathrm{p}2j}{\ddot{x}}_{\mathrm{c}2}sin{\psi }_{\mathrm{p}2j}+m_{\mathrm{p}2j}{\ddot{y}}_{\mathrm{c}2}cos{\psi }_{\mathrm{p}2j}+m_{\mathrm{p}2j}{\ddot{y}}_{\mathrm{p}2j}+2m_{\mathrm{p}2j}{\omega }_{\mathrm{c}2}{\dot{x}}_{\mathrm{p}2j}\hfill \\ -m_{\mathrm{p}2j}{\omega }_{\mathrm{c}2}^2{y}_{\mathrm{p}2j}+cos\alpha F_{\mathrm{s}2\mathrm{p}2j}-cos\alpha F_{\mathrm{r}2\mathrm{p}2j}+k_{\mathrm{yp}2j}{y}_{\mathrm{p}2j}+c_{\mathrm{yp}2j}{\dot{y}}_{\mathrm{p}2j}=0\hfill \\ -J_{\mathrm{p}2j}{\ddot{\theta }}_{\mathrm{c}2}+J_{\mathrm{p}2j}{\ddot{\theta }}_{\mathrm{p}2j}-R_{\mathrm{p}2j}{F}_{\mathrm{s}2\mathrm{p}2j}+R_{\mathrm{p}2j}{F}_{\mathrm{r}2\mathrm{p}2j}=0\hfill \end{array}\right.$$

(21)

where

$$\left\{\begin{array}{l}{T}_{\mathrm{s}1\mathrm{s}2}=k_{\mathrm{s}1\mathrm{s}2}\left({\theta }_{\mathrm{s}1}-{\theta }_{\mathrm{s}2}\right)+c_{\mathrm{s}1\mathrm{s}2}\left({\dot{\theta }}_{\mathrm{s}1}-{\dot{\theta }}_{\mathrm{s}2}\right)\\ F_{\mathrm{bxs}1\mathrm{s}2}=k_{\mathrm{bs}1\mathrm{s}2}\left(x_{\mathrm{s}1}-x_{\mathrm{s}2}\right)+c_{\mathrm{bs}1\mathrm{s}2}\left({\dot{x}}_{\mathrm{s}1}-{\dot{x}}_{\mathrm{s}2}\right)\\ F_{\mathrm{bys}1\mathrm{s}2}=k_{\mathrm{bs}1\mathrm{s}2}\left(y_{\mathrm{s}1}-y_{\mathrm{s}2}\right)+c_{\mathrm{bs}1\mathrm{s}2}\left({\dot{y}}_{\mathrm{s}1}-{\dot{y}}_{\mathrm{s}2}\right)\end{array}\right.$$

(22)

k_bs1s2, k_s1s2, c_s1s2, and c_bs1s2 are the bending stiffness, torsional stiffness, bending damping, and torsional damping of the shaft between the sun gears, respectively.

The torsional torque and transverse force of the shaft between the first stage ring gear and the second stage carrier can be expressed by Equation (23).

$$\left\{\begin{array}{l}{T}_{\mathrm{c}1\mathrm{r}2}=k_{\mathrm{c}1\mathrm{r}2}\left({\theta }_{\mathrm{c}1}-{\theta }_{\mathrm{r}2}\right)+c_{\mathrm{c}1\mathrm{r}2}\left({\dot{\theta }}_{\mathrm{c}1}-{\dot{\theta }}_{\mathrm{r}2}\right)\\ F_{\mathrm{bxc}1\mathrm{r}2}=k_{\mathrm{bc}1\mathrm{r}2}\left(x_{\mathrm{c}1}-x_{\mathrm{r}2}\right)+c_{\mathrm{bc}1\mathrm{r}2}\left({\dot{x}}_{\mathrm{c}1}-{\dot{x}}_{\mathrm{r}2}\right)\\ F_{\mathrm{byc}1\mathrm{r}2}=k_{\mathrm{bc}1\mathrm{r}2}\left(y_{\mathrm{c}1}-y_{\mathrm{r}2}\right)+c_{\mathrm{bc}1\mathrm{r}2}\left({\dot{y}}_{\mathrm{c}1}-{\dot{y}}_{\mathrm{r}2}\right)\end{array}\right.$$

(23)

k_bc1r2, k_c1r2, c_bc1r2, and c_c1r2 are the bending stiffness, torsional stiffness, bending damping, and torsional damping of the connecting shaft between the first stage carrier and second stage ring gear, respectively.

3.2. Analysis of the Tuning Mechanisms of Different Models

The symmetrical arrangement of the planetary transmission system makes the meshing positions symmetrical, and this relation is the source of phase tuning. The meshing force itself is a complex nonlinear periodic function. To study the coupled phase-tuning relationships in the two-stage planetary transmission system, starting from the meshing force, the characteristics of excitation forces acting on central components at all levels were analysed, and the component locations were assessed. The characteristics of the resultant force or the resultant moment were obtained to determine the coupled vibration mode and law for the central part of the two-stage planetary transmission system. In the following description, positive direction refers to the clockwise direction, and negative direction refers to the counter-clockwise direction. Three tuning models are established, and the specific tuning parameters are shown in

Table 2. System parameters.

	Item	Sun Gear	Ring Gear	Carrier	Planet Gear
Model 1	Number of teeth	27/39	77/77	—	25/29
Model 2	Number of teeth	28/36	76/76	—	24/20
Model 3	Number of teeth	28/39	76/77	—	24/29
General parameters	Number of planets	4
	Half backlash/mm	bs1p1j = 0.18 br1p1j = 0.2 bs2p2j = 0.2 br2p2j = 0.2
	Module	4
	Pressure angle/°	20

.

3.2.1. Model 1: Coupled Tuning Mechanism Analysis

The two-stage planetary transmission system in model 1 displays meshing phase differences, and these differences are listed in

Table 3. Meshing phase difference of model 1.

	Meshing Phase Difference
Stage number	${\gamma }_{sp1}$	${\gamma }_{sp2}$	${\gamma }_{sp3}$	${\gamma }_{sp4}$
1st stage	0	0.75	0.5	0.25
2nd stage	0	0.75	0.5	0.25
Stage number	${\gamma }_{rp1}$	${\gamma }_{rp2}$	${\gamma }_{rp3}$	${\gamma }_{rp4}$
1st stage	0	0.25	0.5	0.75
2nd stage	0	0.25	0.5	0.75

; ${\gamma }_{spj}$ and ${\gamma }_{rpj}$ represent the meshing phase difference of S–P and R–P, respectively.

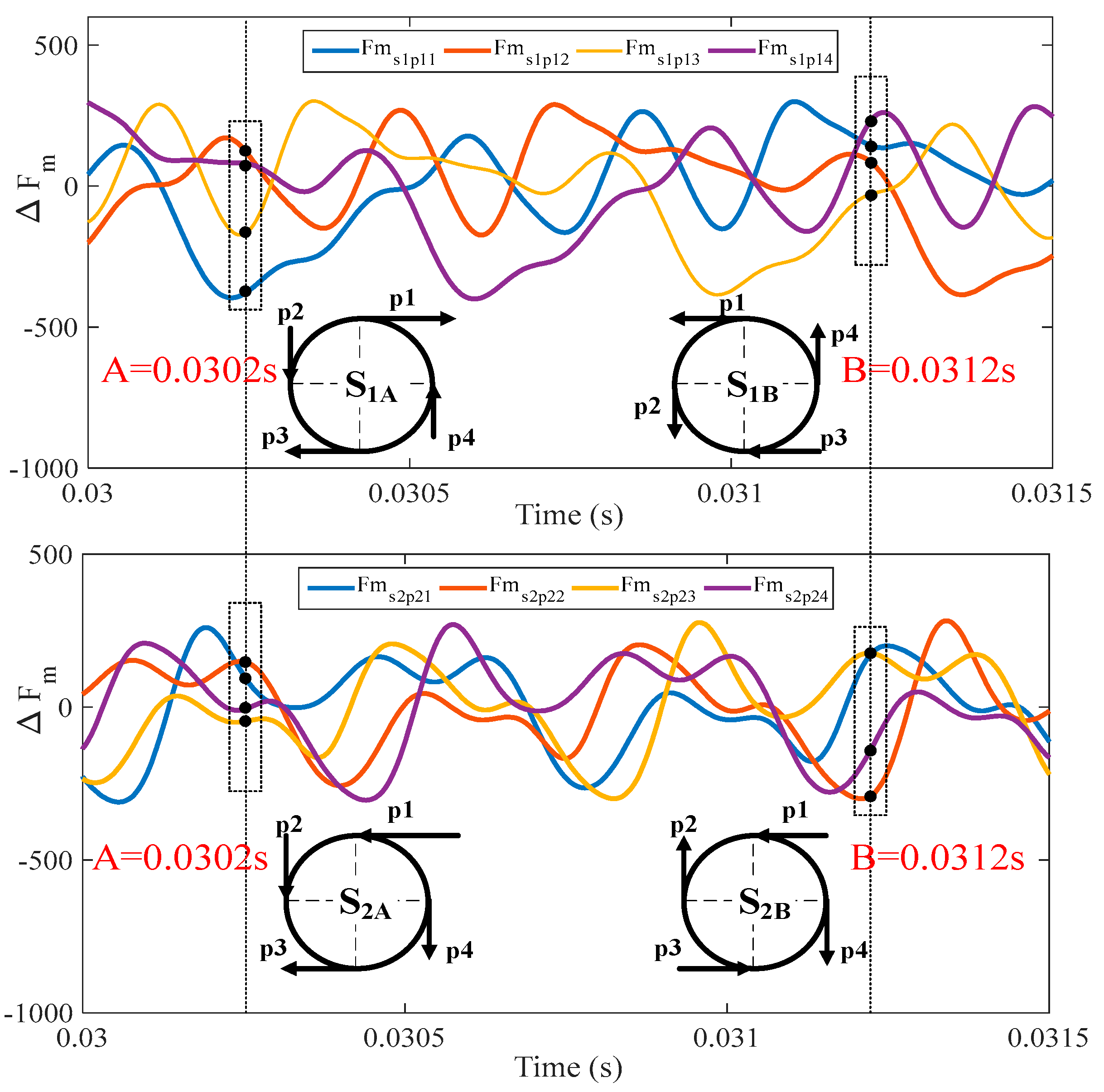
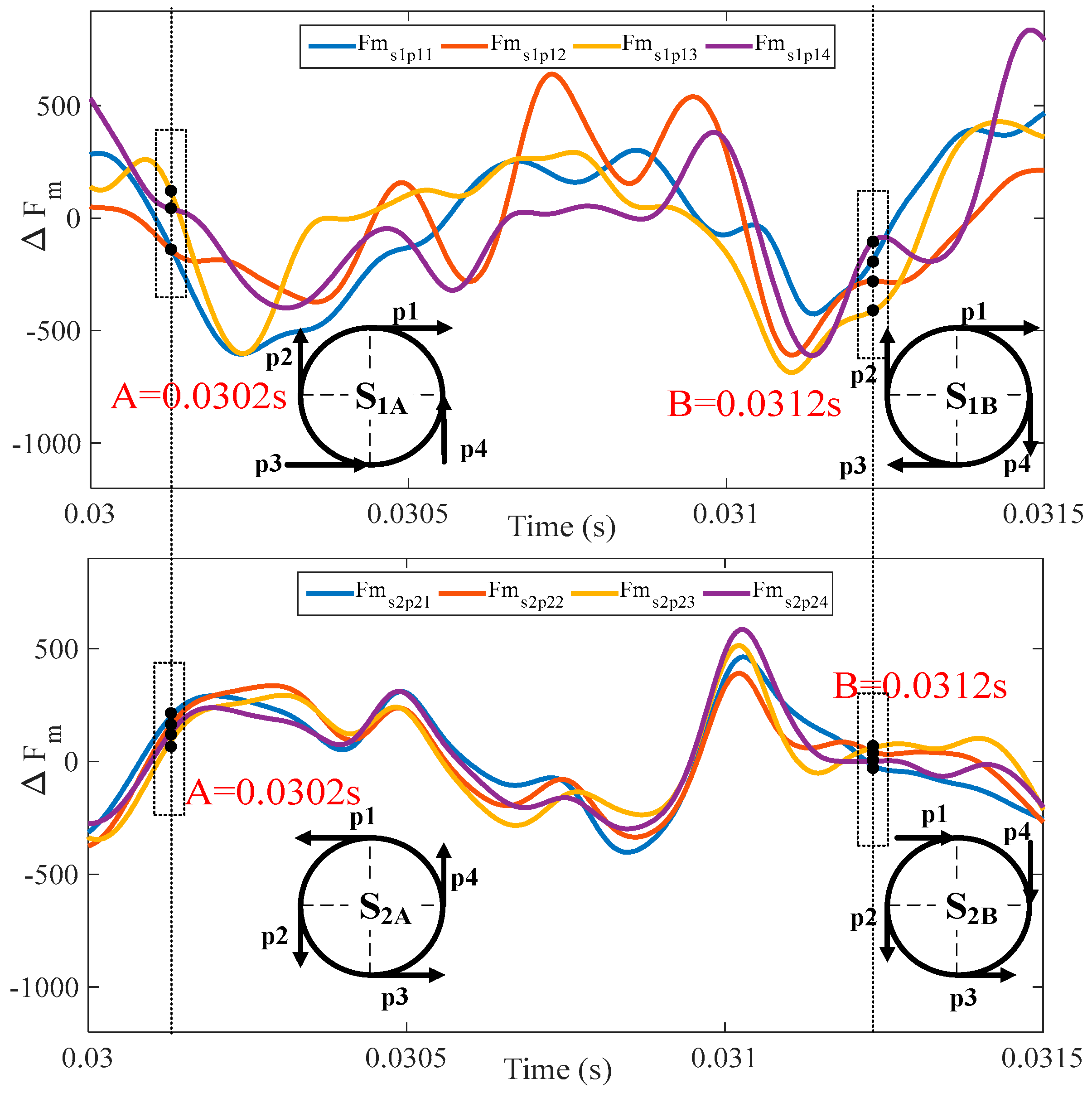
Figure 7 shows the time-domain curve of the fluctuating meshing force of the sun gears in each stage in mode 1 and the instantaneous force diagram at time points A and B. The time-domain curve shows that the direction and magnitude of the meshing force between each planetary gear and the sun gear change over time. Consequently, the resultant force acting on the sun gear is converted from a lateral force to a torsional moment, resulting in the transient vibration of the sun gear.

To further analyse the fluctuating meshing force of sun gears at different times, the time points A = 0.0302 s and B = 0.0312 s were selected, and the corresponding force diagrams were obtained. In Figure 7, $F{m}_{{}_{sipin}}$ indicates the fluctuating meshing force for S–P gear pairs, where i = 1, 2 and n = 1, 2, 3, 4 indicate the stage number and the number of planet gears, respectively; the two black dotted lines correspond to A = 0.0302 s and B = 0.0312 s. The instantaneous meshing force diagrams between four planetary gears and the sun gear are shown below the dotted frame, where S_1A represents the force diagram of the sun gear in the first stage at time point A, with similar expressions for others.

S_1A and S_2A are taken as examples to illustrate the relationship between the force on the sun gear and the vibration mode in mode 1. For S_1A, the meshing forces of the four planetary gears are represented by p1, p2, p3, and p4. If $\left|\mathrm{p}1\right|\approx \left|\mathrm{p}2\right|\approx \left|\mathrm{p}3\right|\approx \left|\mathrm{p}4\right|$, then these four forces will cancel each other, and the sun gear will maintain the TS and TE vibration modes; if $(\left|\mathrm{p}1\right|\approx \left|\mathrm{p}3\right|)>(\left|\mathrm{p}2\right|\approx \left|\mathrm{p}4\right|)$, then the RE mode will be triggered. For S_2A, the force directions of p1 and p3 are the same, as are those of p2 and p4; therefore, the TE mode of translational vibration for the sun gear is directly excited.

The above analysis indicates that when the two-stage planetary transmission system exhibits a phase difference, the vibration mode of the central part of the system switches between translational vibration, torsional vibration, and equilibrium based on the relevant forces. Due to the periodicity of the meshing force, the vibration mode of the central part of the system also periodically varies.

3.2.2. Model 2: Coupled Tuning Mechanism Analysis

In model 2, the meshing phase differences in the first stage and second stage are zero, and these differences are listed in

Table 4. Meshing phase differences for model 2.

	Meshing Phase Difference
Stage number	${\gamma }_{sp1}$	${\gamma }_{sp2}$	${\gamma }_{sp3}$	${\gamma }_{sp4}$
1st stage	0	0	0	0
2nd stage	0	0	0	0
Stage number	${\gamma }_{rp1}$	${\gamma }_{rp2}$	${\gamma }_{rp3}$	${\gamma }_{rp4}$
1st stage	0	0	0	0
2nd stage	0	0	0	0

; ${\gamma }_{spj}$ and ${\gamma }_{rpj}$ represent the meshing phase differences of S–P and R–P, respectively.

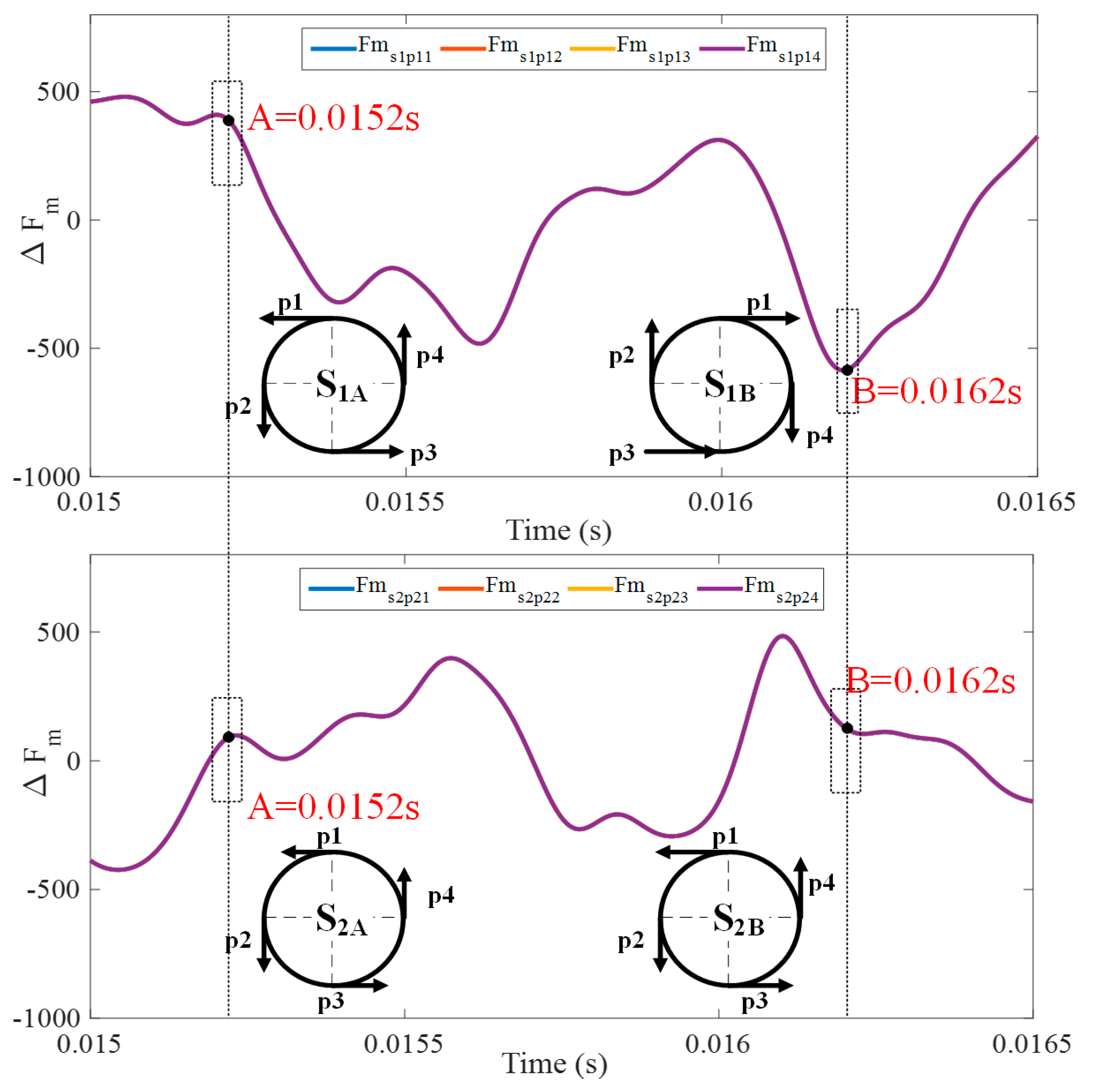
Figure 8 shows the time-domain curve of the fluctuating meshing force in each stage for sun gears in mode 2 and the instantaneous force diagram at time points A and B. The time-domain curve shows that the direction and magnitude of the meshing force between each planetary gear and the sun gear are the same; therefore, the force acting on the sun gear always includes a torsional torque component, leading to the torsional vibration of the sun gear.

To further analyse the fluctuating meshing force acting on the sun gear at different times, the time points A = 0.0152 s and B = 0.0162 s were selected, and the corresponding force diagrams were obtained. S1A is taken as an example to illustrate the relationship between the force on the sun gear and the vibration mode in mode 2. For S1A, the meshing forces of the four planetary gears are represented by p1, p2, p3, and p4, and their direction and magnitude are the same (i.e., $\left|\mathrm{p}1\right|=\left|\mathrm{p}2\right|=\left|\mathrm{p}3\right|=\left|\mathrm{p}4\right|$); then, these four forces form a torsional torque, which directly excites the RE mode of torsional vibration for the sun gear. According to the above analysis, when the phase difference between the two planetary transmission systems is 0, the vibration mode of the centre part of the system is dominated by torsional vibration.

3.2.3. Model 3: Coupled Tuning Mechanism Analysis

In model 3, the meshing phase differences in the first stage and second stage are listed in

Table 5. Meshing phase differences for model 3.

	Meshing Phase Differences
Stage number	${\gamma }_{snp1}$	${\gamma }_{snp2}$	${\gamma }_{snp3}$	${\gamma }_{snp4}$
1st stage	0	0.75	0.5	0.25
2nd stage	0	0	0	0
Stage number	${\gamma }_{rnp1}$	${\gamma }_{rnp2}$	${\gamma }_{rnp3}$	${\gamma }_{rnp4}$
1st stage	0	0.25	0.5	0.75
2nd stage	0	0	0	0

; ${\gamma }_{spj}$ and ${\gamma }_{rpj}$ represent the meshing phase differences of S–P and R–P, respectively.

Figure 9 shows the time-domain curve of the fluctuating meshing force for each stage of the sun gears in mode 3 and the instantaneous force diagram at time points A and B. The time-domain curve shows that the direction and magnitude of the meshing force between each planetary gear and the sun gear change over time, resulting in the force acting on the sun gear being converted between a lateral force and torsional moment; consequently, the vibration mode of the sun gear is a couple mode.

To further analyse the fluctuating meshing force on the sun gear at different times, the time points A = 0.0302 s and B = 0.0312 s were selected, and the corresponding force diagrams were obtained. The two black dotted lines correspond to A = 0.0302 s and B = 0.0312 s.

S_1B and S_2B are taken as examples to illustrate the relationship between the force on the sun gear and the vibration mode in mode 3. For S_1B, the meshing forces of the four planetary gears are represented by p1, p2, p3, and p4, and their directions are the same (counter clockwise). Regardless of whether the magnitude is the same, these four forces will form a torsional torque, which directly excites the RE mode of torsional vibration for the sun gear. For S_2B, the force directions of p1 and p3 are the same, as are those of p2 and p4; therefore, the TE mode of translational vibration for the sun gear is directly excited.

Based on the above analytical comparison to a single-stage planetary system, the phase tuning of the two-stage planetary transmission system has strong coupling characteristics, and due to this coupling, the vibration characteristics of the two-stage planetary transmission system can significantly vary. In mode 1, the magnitude and direction of the fluctuating meshing forces on the sun gear change with time, and because the direction of the force is inconsistent, the torsional moment cannot be directly formed, so translational vibration is dominant. In mode 2, the magnitude and direction of the fluctuating meshing forces on the sun gear are always consistent, directly leading to torsional torque and stimulating the torsional vibration mode of the system. In mode 3, when the tuning modes in the first and second stages are different, the tuning of the sun gear differs from that in a single-stage system, and a coupled tuning phenomenon appears. Theoretically, the force characteristics of the sun gear in the first stage should be the same as those in mode 1. However, under the coupled effect of secondstage tuning, the directions of the fluctuating meshing forces on the sun gear in the first stage gradually become the same, resulting in torque action, which directly excites torsional vibration. Similarly, the second stage sun gear is theoretically influenced by torsional vibration only. Additionally, under the coupled tuning effect in the first stage, the direction of the fluctuating meshing forces on the sun gear gradually changes and can even reverse the forces, thus producing a lateral resultant force and exciting the lateral vibration.

4. Analysis of Coupled Tuning Vibration in a Two-Stage Planetary Transmission System

4.1. Analysis of Coupled Tuning Vibration in Model 1

Due to the meshing phase differences, each harmonic of the meshing frequency has a corresponding tuning vibration mode. The phase-tuning relationships in the two-stage planetary system in model 1 are shown in

Table 6. The coupled tuning law for model 1.

Stage Number	Order Number
	1	2	3	4	5
1st stage	TE	TS	TE	TS	TE
	RS	RS	RS	RE	RS
2nd stage	TE	TS	TE	TS	TE
	RS	RS	RS	RE	RS

.

Figure 10 is the vibration frequency spectral for the two stages of the sun gears, where Figure 10a,b are the X-direction and $\theta$-direction vibration frequency domain diagrams of the first stage sun gear and Figure 10c,d are the X-direction and $\theta$-direction vibration frequency domain diagrams of the second stage sun gear. Notably, the vibration form of the planetary gear transmission system recurs periodically as harmonic order increases. The abscissa in the figure is the frequency, and the ordinate is the amplitude of the corresponding component frequency.

Based on Figure 10 and Table 6, the main vibration modes of the two-stage planetary transmission system are consistent with the phase-tuning law; the first, third, and fifth order harmonics of the two-stage planetary system meshing frequency excitation are the translational vibration, and the fourth-order harmonic excitation is the torsional vibration. Taking the first and fourth harmonics of the meshing frequency as examples, Figure 9 shows that the amplitude of the translational vibration line is non-zero at the first-order meshing frequency of the two rows of sun gears, whereas the torsional vibration line has an amplitude of zero; therefore, this component stimulates excitation of translational vibration but suppresses torsional vibration. At the fourth-order meshing frequency, the amplitude of the translational vibration line is zero, and the amplitude of the torsional vibration line is not zero; therefore, this component stimulates torsional vibration excitation and the suppression of translational vibration. Due to the coupling effect between the two planetary stages, the meshing frequency component of each planet includes meshing frequencies from both stages, and each order of the vibration frequency is determined by the corresponding order of the planetary stages. Transverse vibration is dominated by the meshing frequency in the first stage, and torsional vibration is dominated by the meshing frequency in the second stage.

4.2. Analysis of Coupled Tuning Vibration for Model 2

Since there is no meshing phase difference for model 2, the tuning mode of each planetary stage involves excited torsional vibration and the suppression of translational vibration. The phase-tuning relationships in the two-stage planetary system in model 2 are shown in

Table 7. The coupled tuning law for model 2.

Stage Number	Order Number
	1	2	3	4	5
1st stage	TS
	RE
2nd stage	TS
	RE

.

Figure 11 illustrates the vibration frequency domain diagrams for the two stages of sun gears, where Figure 11a and Figure 11b, respectively, are the X-direction and $\theta$-direction vibration frequency spectral diagrams of the first stage sun gear and c) and d) are the X-direction and $\theta$-direction vibration frequency domain diagrams of the second stage sun gear, respectively. The abscissa in the figure is the frequency, and the ordinate is the amplitude of the corresponding component frequency.

Figure 11 shows that the amplitude of the translational vibration spectrum for each order of meshing frequency harmonics related to lateral vibration of the sun gear in the first and second stages is zero. However, the amplitude of the torsional vibration spectrum is not zero, and this situation leads to stimulated torsional vibration and suppressed translational vibration. Through the tuning effect, only the torque vibration is transmitted between the two stages, and the lateral excitation is suppressed. This finding is consistent with the force analysis conclusion in Section 2, and the frequency-domain diagram of directional vibration includes the meshing frequencies of the two stages.

4.3. Analysis of Coupled Tuning Vibration for Model 3

The phase-tuning relationships for the two-stage planetary system in model 3 are shown in

Table 8. The coupled tuning law for model 3.

Stage Number	Order Number
	1	2	3	4	5
1st stage	TE	TS	TE	TS	TE
	RS	RS	RS	RE	RS
2nd stage	TS
	RE

.

Figure 12 shows the vibration frequency spectral diagram of sun gears in two stages, where Figure 12a,b are the X-direction and $\theta$-direction vibration frequency domain diagrams of the first stage sun gear and Figure 12c,d are the X-direction and $\theta$-direction vibration frequency domain diagrams of the second stage sun gear, respectively. The abscissa in the figure is the frequency, and the ordinate is the amplitude of the corresponding component frequency.

The first-order and fourth-order harmonics of the meshing frequency are used as examples. Figure 12 shows that the amplitude of the translational vibration line is not zero at the first-order meshing frequency of the sun gear in the first stage. However, the amplitude of the torsional vibration line is zero. In this case, translational vibration is stimulated, and torsional vibration is suppressed. At the fourth-order meshing frequency, the amplitude of the translational vibration spectrum is zero, but the amplitude of the torsional vibration spectrum is not zero. Therefore, in this case, torsional vibration is stimulated, and translational vibration is suppressed. There is no phase difference in the second stage, and all harmonics are excited torsional vibrations. Lateral vibration is mainly caused by bending forces from the first stage transmitted by the connecting shaft. Therefore, the lateral vibration of the second stage is the same as that of the first stage, as suggested by the tuning law. At this time, in addition to the fourth-order harmonics in the first stage, the torsional vibration of the entire system is mainly excited in the second stage. Therefore, the frequency-domain diagram of the torsional vibration of the central parts of the system in all two stages are the meshing frequency and the corresponding frequency components of the second stage.

4.4. Experimental Verification

To verify the effectiveness of the coupled tuning law, a vibration response test involving a two-stage planetary gear system was performed. The vibration characteristic test is a dynamic simulation performed in the laboratory, as shown in Figure 13.

For the coupled tuning test, model 3, containing two different tuning modes, is investigated, and the design parameters are shown in

Table 9. Parameters of the two-stage planetary transmission system.

Item	Sun Gear	Ring Gear	Carrier	Planet Gear
Number of teeth	27/36	77/76	—	25/20
Mass/kg	4.600/3.973	6.145/15.055	39.051/25.939	1.322/0.823
Mass moment/kg·m2	0.0094/0.0122	0.1654/0.4995	0.4762/0.3283	0.0021/0.0009
Module		3
Pressure angle/°		20
Tooth width/mm		25

. In this test, a motor is used to drive and rotate the gearbox, and a dynamometer is used to apply load torque. An acceleration sensor is installed on the bearing seat to measure the lateral vibration acceleration of the two sun gears. The test conditions were as follows: the drive motor input speed was approximately 2000 r/min, and the load torque of the load dynamometer was 400 Nm. The first stage mesh frequency was 667 Hz, and the second stage mesh frequency was 604 Hz.

We installed a vibration acceleration sensor on the bearing outer-ring closest to the input sun gear and output carrier gear, as shown in Figure 14.

In the process of studying the coupled phase-tuning law, other sources of excitation, such as gear error, were excluded from the corresponding model. However, in actual tests, gear errors, including installation error, mass eccentricity, and manufacturing error, are inevitable, and these errors will influence the vibration response of the system. Figure 15 shows the vibration acceleration spectrum of the first stage sun gear in mode 3 in the X direction, where Figure 15a is the vibration spectrum without considering the gear error and Figure 15b is the vibration spectrum with gear error. Through comparison, the gear error increases the vibration amplitude of the meshing frequency, especially for the first-order vibration and even-order vibrations.

Figure 16 shows the vibration acceleration spectrum of the sun gear in the X direction obtained during the test. The actual transmission system model contains errors and various nonlinear factors, which significantly impact the system response and influence the phase-tuning phenomenon. Figure 16a,b is the spectrum of time-domain vibration acceleration and frequency-domain vibration, respectively. By comparison with that in Figure 14, the amplitude marked in blue in Figure 16b is excited by nonlinear error factors, and the amplitude marked in black in Figure 16 is excited by phase-tuning relations. As shown in Figure 16b, the vibration of the central part of the first planetary gear is dominated by the odd-order first stage meshing frequencies, and the amplitude corresponding to the first-order frequency is the largest. At this time, the transverse vibration of the second stage is in a state of suppression, and the vibration associated with the second stage meshing frequency and its components is not obvious.

Figure 17 shows the torsional vibration spectrum of the first sun gear in the $\theta$ direction obtained during the test. The actual transmission system model contains errors and various nonlinear factors, which produce more tuned frequencies, reduce the resolution of frequency spectrum, and greatly disturb the phase-tuning phenomenon. According to the tuning law shown in Table 8 and Figure 13, the torsional vibration of the first stage sun gear in model 3 is mainly excited by the fourth-order meshing frequency and coupled with each order meshing frequency of the second stage. In Figure 17b, the torsional vibration of the first stage sun gear is mainly distributed at the rotational frequency, the first-order meshing frequency of the second stage, and its side frequency band. Only the meshing frequency is marked in the figure. At the same time, it can be seen that the fourth-order meshing frequency 2700 Hz of the first stage also plays a significant role in stimulating torsional vibration, and this matches the tuning law of model 3.

Combined with simulation analysis and experimental verification, it can be concluded that the tuning law of planetary transmission systems also has coupling characteristics. This characteristic can clearly show the relationship between the tooth number of gears in the planetary stage and the coupling vibration response of the system, which provides a method and theoretical basis for the further study of coupling vibration for the system.

5. Conclusions

A coupled phase-tuning theory for a multistage planetary transmission system was proposed, and the corresponding mathematical relations were deduced. A nonlinear coupled vibration model of a two-stage planetary transmission system was established, and the coupled phase-tuning law was verified and described. The main results are as follows.

• A coupled phase-tuning theory for a multistage planetary transmission system is proposed. In a multi-stage planetary gear drive system, the phase-tuning law of each stage will affect the vibration characteristics of each component of the system, so that the component presents a variety of excitation characteristics. Additionally, the mathematical expression of coupled phase tuning in this system is obtained according to the basic force relations of the central components. The relationship between the change in the meshing phase of each planetary stage and the coupled vibration of the system is theoretically described.
• The symmetry of the meshing forces is the fundamental driver of the phase-tuning relationship, and there is a strong coupling relationship between the meshing forces of each stage of the planetary system. The number of tooth and planetary gears in the single-stage system can make the resultant force of the central component present three tuning characteristics of torsional moment, lateral impact force, and mutual cancellation, and in the multi-stage planetary system, the coupling transmission characteristics of the central component force leads to the coupling of the phase-tuning law. Therefore, the change of phase-tuning parameters in one stage will change the coupling vibration response of the whole system through the coupling characteristics of the meshing forces.
• Due to the highly coupled characteristics of the system, the tuning coefficients k₁ and k₂ not only dominate the respective planetary stages, but also generate excitation and suppression related to the corresponding harmonic order of the frequency in other planetary stages. Combined with the simulation and experimental results, the error has a disturbing effect on the phase-tuning law, which will strengthen the vibration amplitude of the system phase-tuning excitation and excite the vibration mode of phase-tuning suppression. Finally, the correctness of the phase-coupling tuning law of the two-stage planetary gear transmission system is further verified by experiments.

By studying the coupled phase-tuning law for a two-stage planetary transmission system, the nonlinear coupling relationship between the design parameters and vibration response of the system is further understood. Thus, this study lays a foundation for research on the coupled characteristics of multistage planetary transmission systems and provides an effective guide for resonance analyses of systems in the predesign stage.