Characterization of Dimensional Variations in Turning Process for Multistep Rotary Shaft of High-Speed Motorized Spindle
Abstract
1. Introduction
1.1. Literature Review
1.1.1. The Impact of Various Errors on Surface Quality
1.1.2. Error-Compensation Method for Workpiece Features
1.2. Paper Research Content
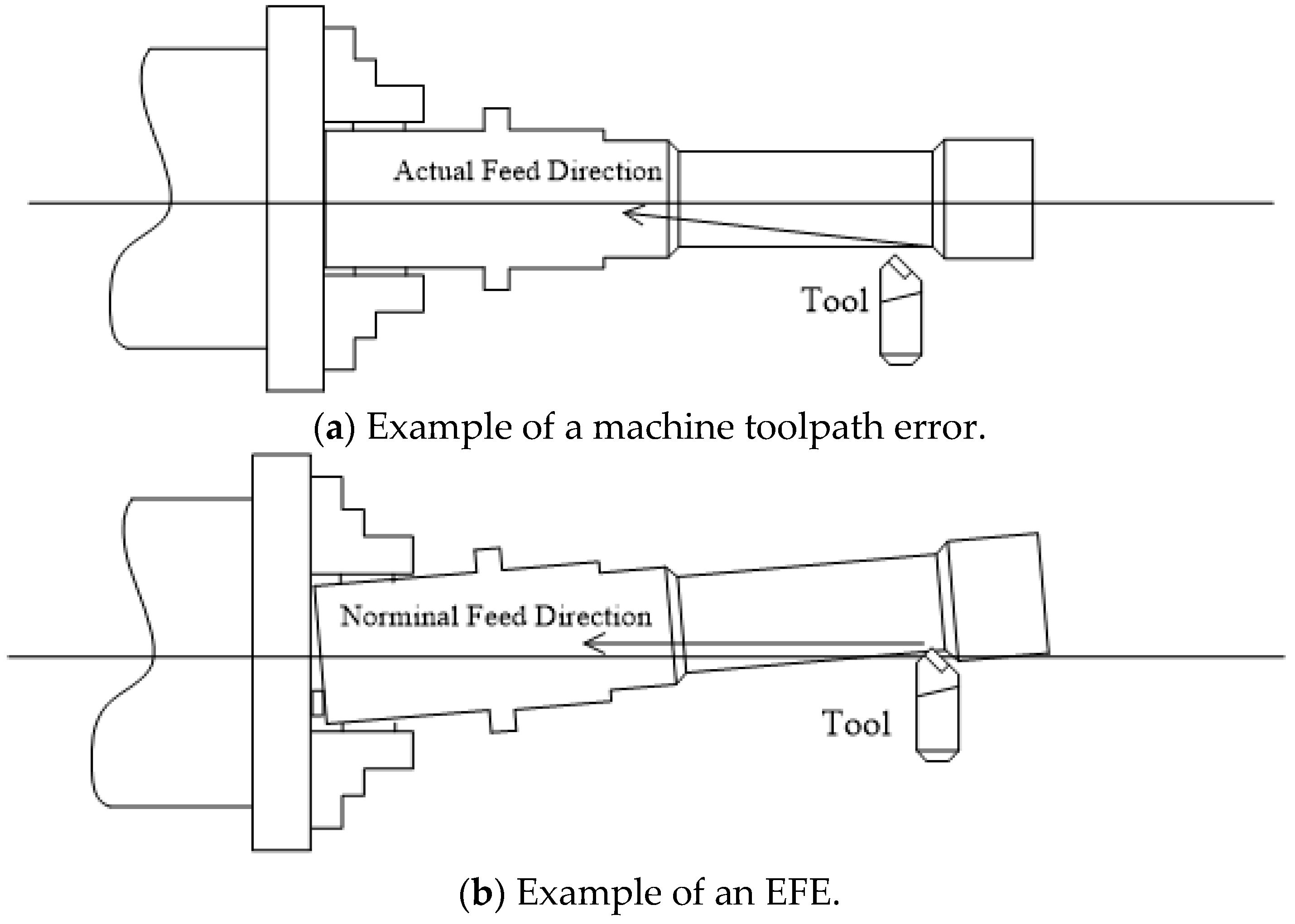
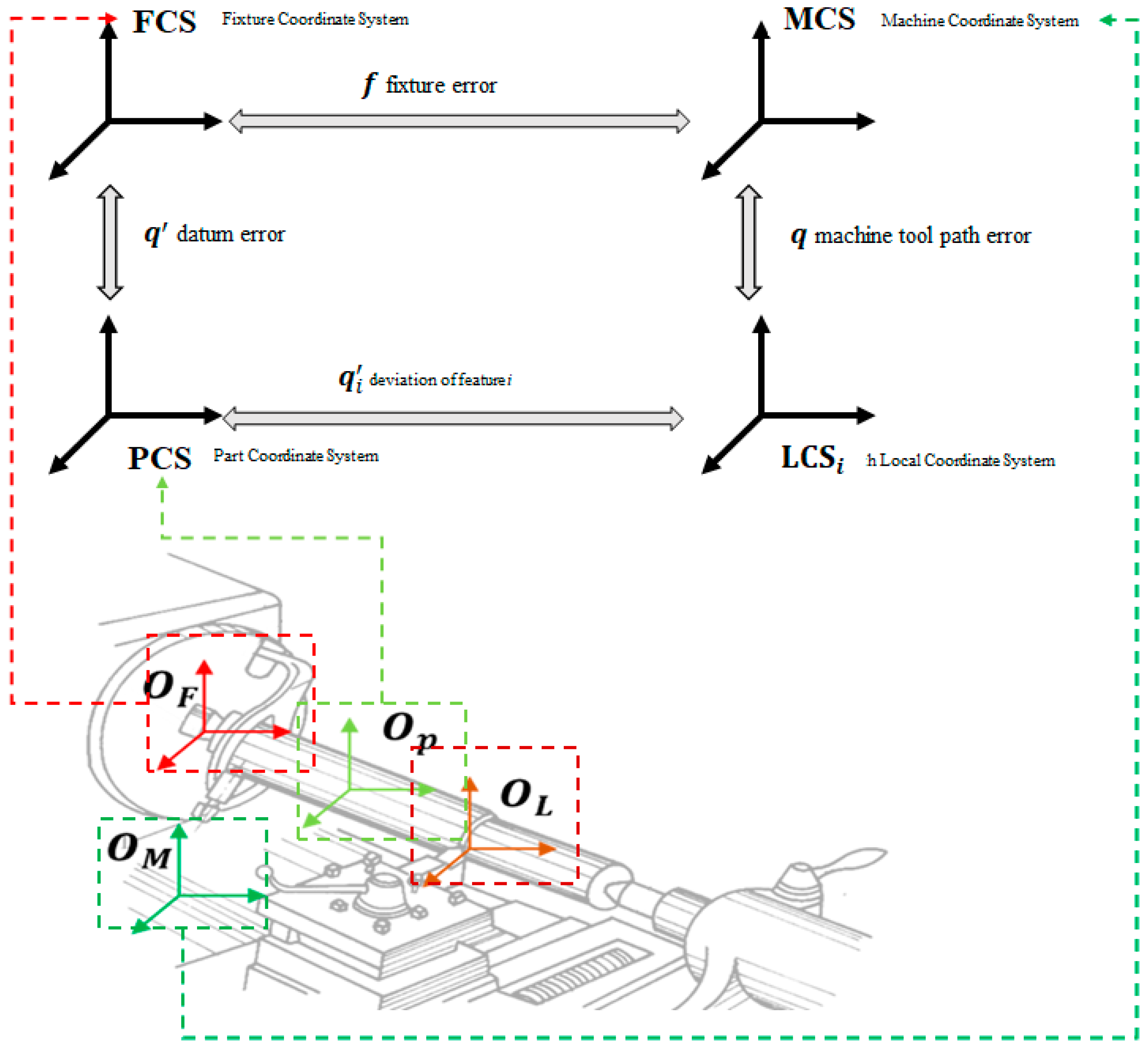
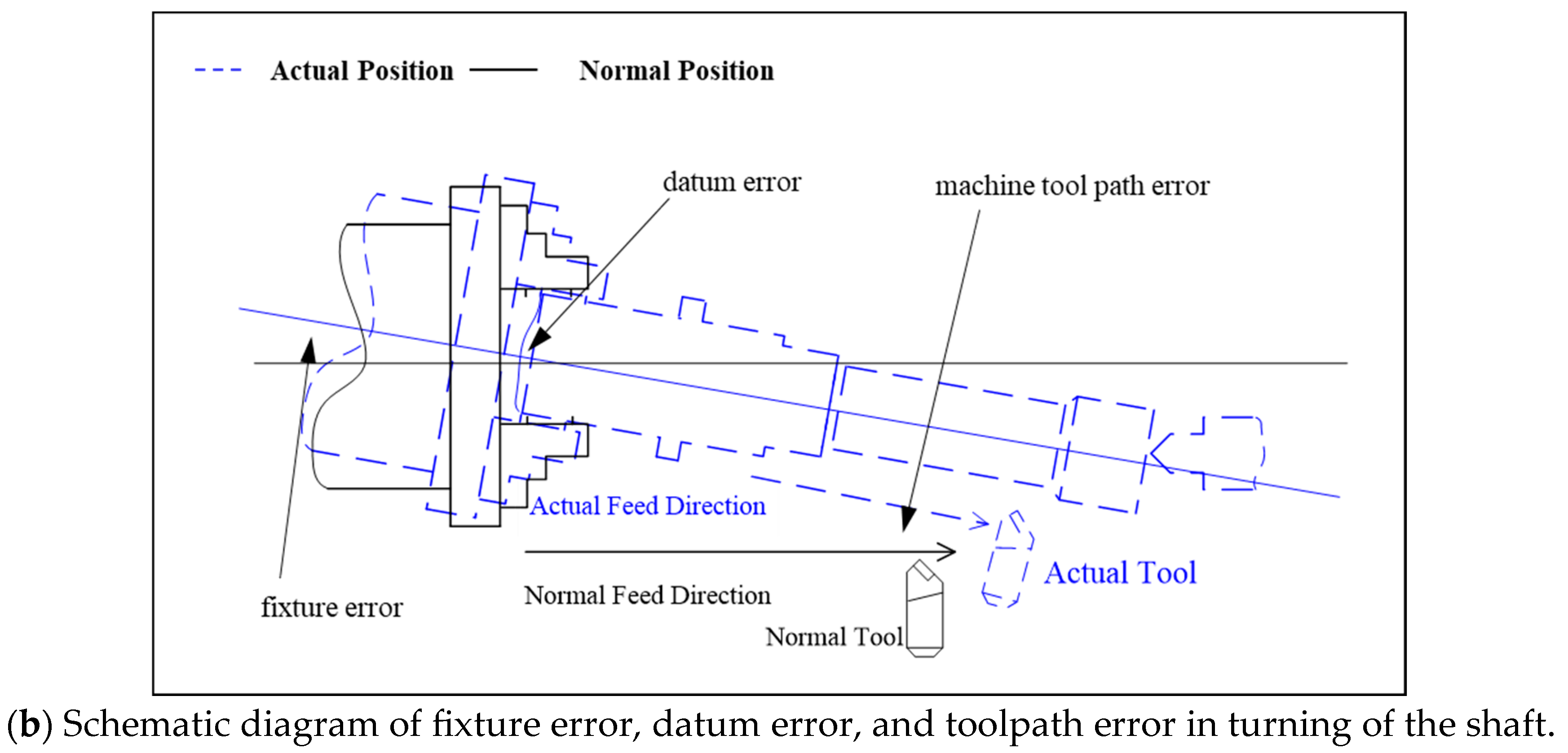
2. Description of Locating Errors in Multistage Turning Processes
2.1. Model for Equivalent Error
2.2. Model Derivation for Multistage Turning Processes
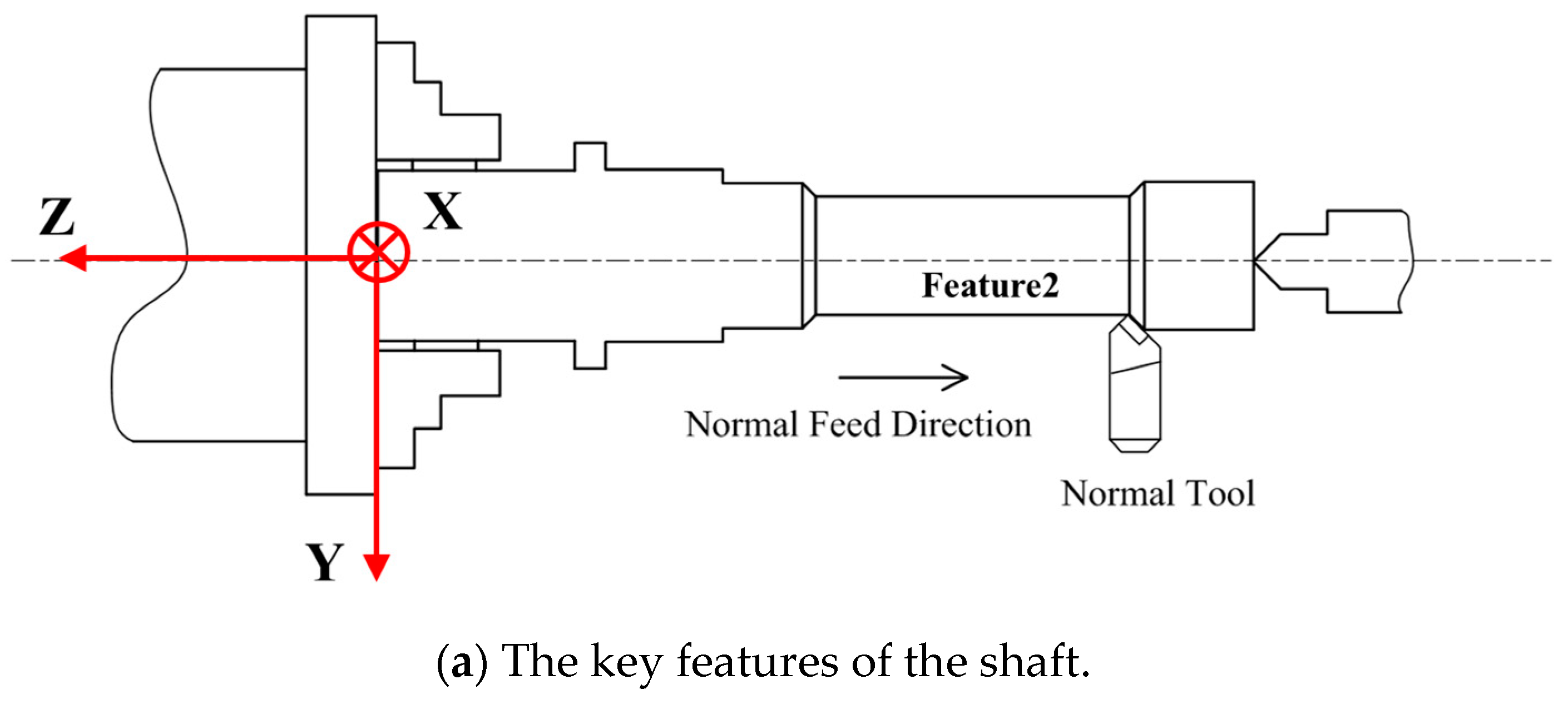
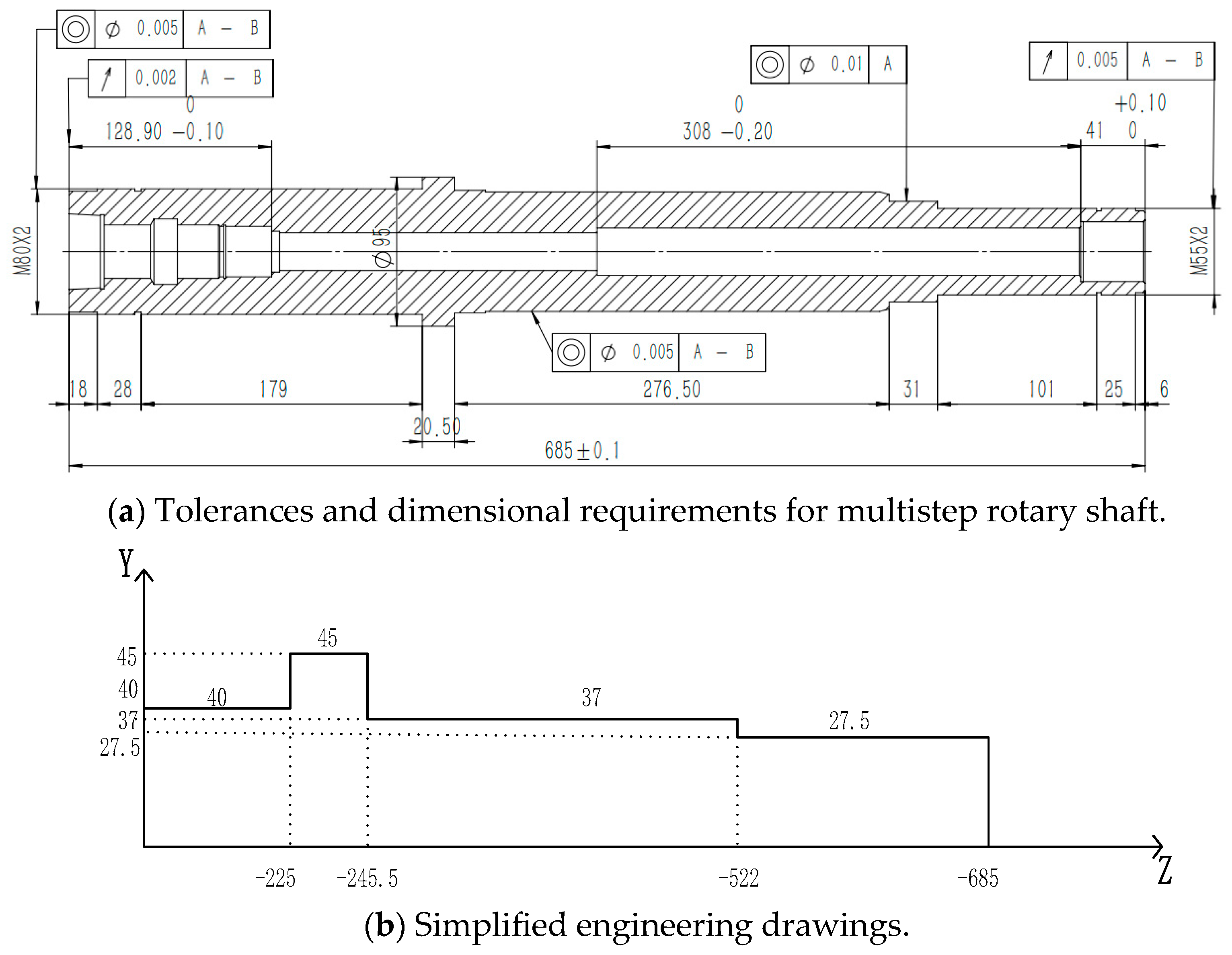
3. Case Study
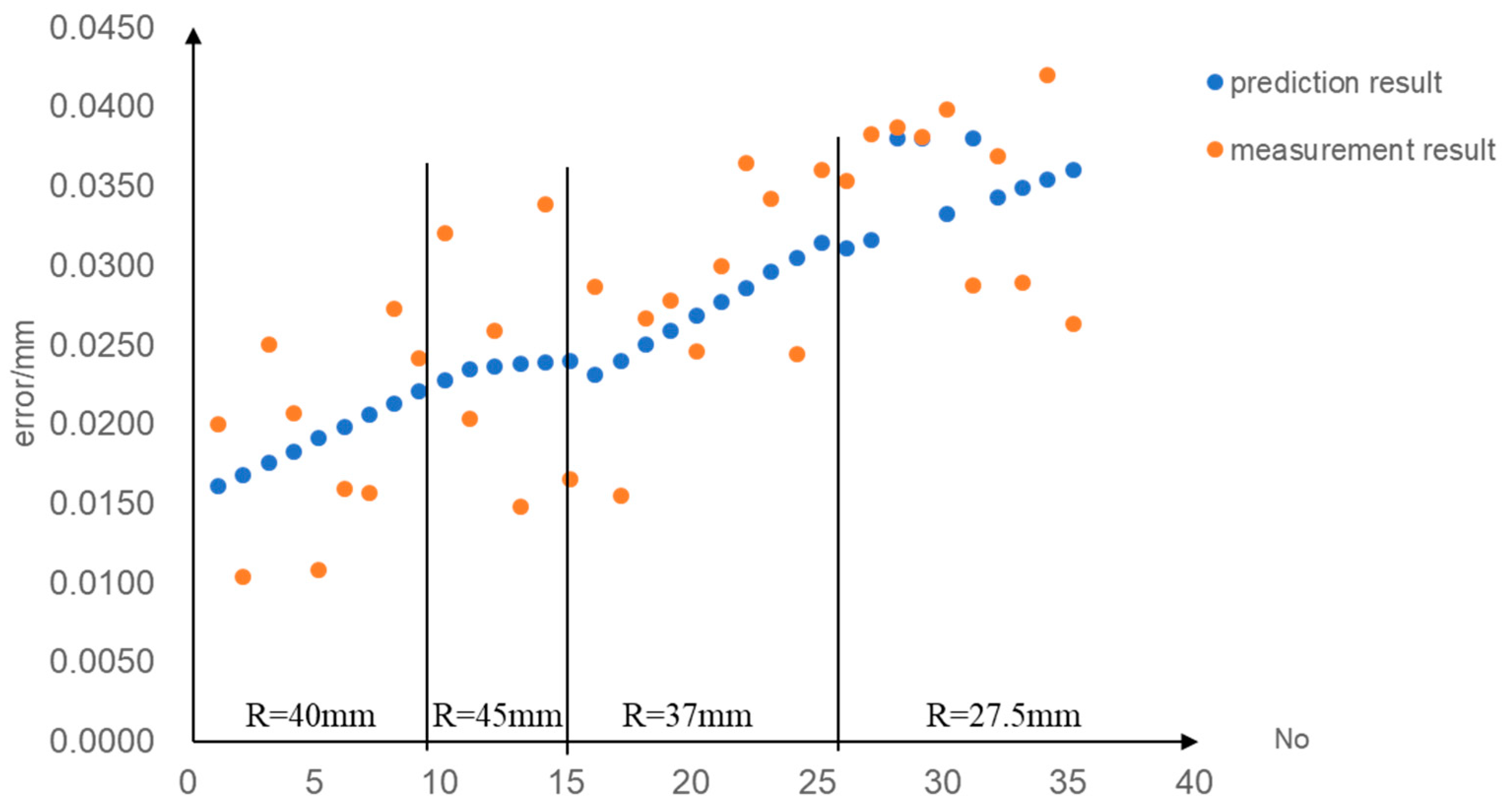
3.1. Error Prediction Simulation
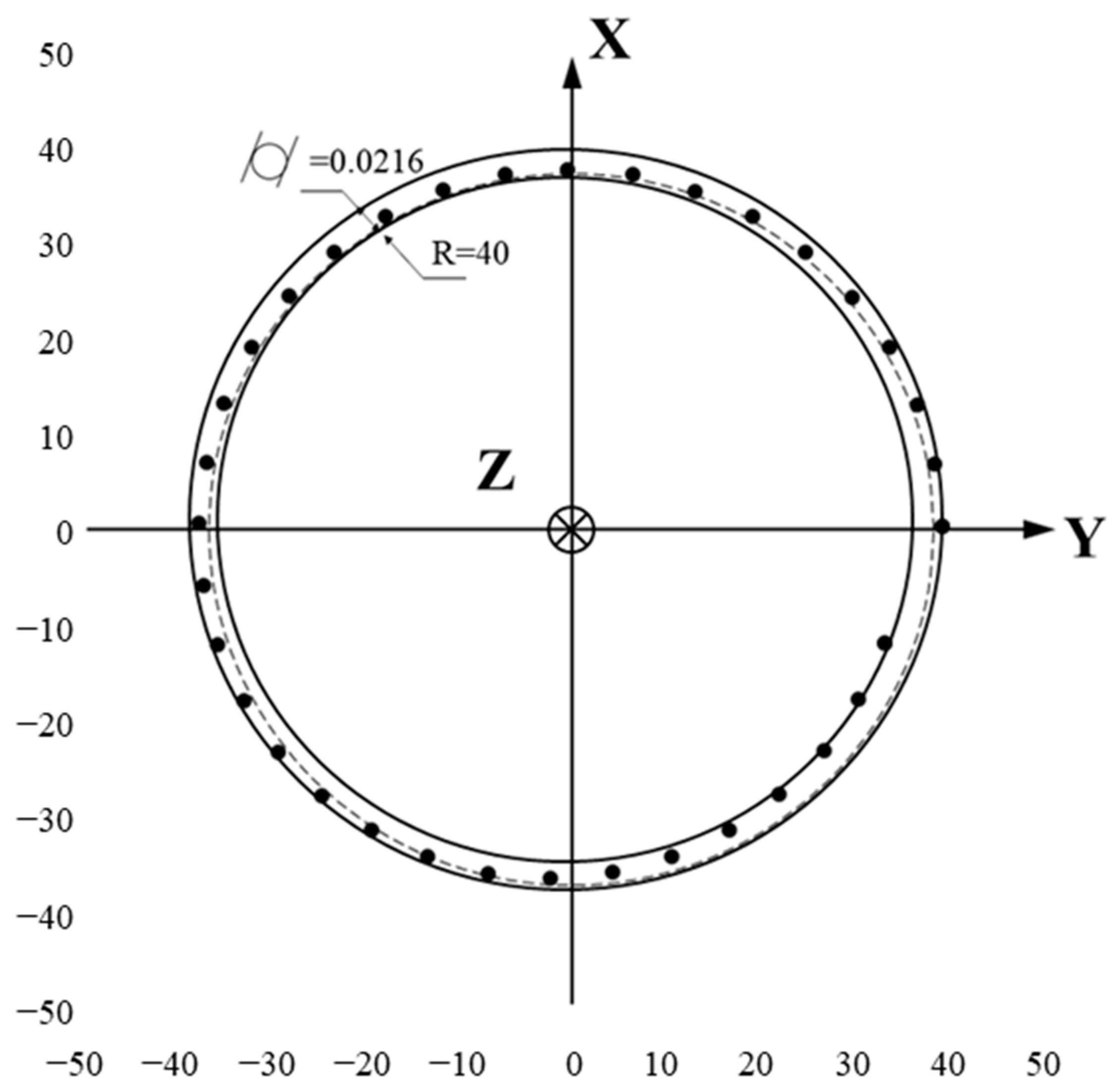
3.2. Experimental Validation of Compensation
3.3. Discussion
3.3.1. Model Accuracy
3.3.2. Model Application
4. Conclusions
- For the multistep rotary shaft, the final dimensional accuracy is mainly affected by datum errors, fixture errors, and machine toolpath errors. In this paper, an EFE method is proposed to solve the problem of equating the error sources of fixture error, datum error, and toolpath error in the rotary machining of multistep axes by combining them with the theory of equivalent error. By equating each error source to the toolpath error, the toolpath can be adjusted in real time to compensate for the multi-attitude of the workpiece during machining.
- This article demonstrates the accuracy of the prediction model and the effectiveness of the compensation model through experiments. The accuracy of the model was demonstrated by comparing the predicted values with the actual measured values for multistage stepped axis turning, and the proposed compensation method was demonstrated to be effective in reducing errors in workpiece features during machining. By extending the prediction model from single-point prediction to multi-point prediction, it is possible to make predictions for form tolerance parameters, such as cylindricity of shaft parts.
- The model presented in this article provides a framework for the prediction and compensation of machining errors for rotary-type parts. To increase the generalizability of the model, flexible deformations, such as holding deformation, tool letting deformation, cutting forces, thermal deformation, and residual stress deformation, can be introduced into the framework for error compensation of annular thin-walled parts, such as aero-engine magazines and flame cartridges. These potential works using EFE models will be continued and reported in the future.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramesh, R.; Mannan, M.A.; Poo, A.N. Error compensation in machine tools—A review: Part I: Geometric, cutting-force induced and fixture-dependent errors. Int. J. Mach. Tools Manuf. 2000, 40, 1235–1256. [Google Scholar] [CrossRef]
- Cai, W.; Hu, S.J.; Yuan, J.X. A Variational Method of Robust Fixture Configuration Design for 3-D Workpieces. J. Manuf. Sci. Eng. 1997, 119, 593–602. [Google Scholar] [CrossRef]
- Yu Wang, M. Tolerance analysis for fixture layout design. Assem. Autom. 2002, 22, 153–162. [Google Scholar] [CrossRef]
- Jin, S.; Liu, S.; Zhang, X.; Chen, K. A unified prediction model of 3D surface topography in face milling considering multi-error sources. Int. J. Adv. Manuf. Technol. 2019, 102, 705–717. [Google Scholar] [CrossRef]
- Chen, K.; Liu, S.; Tian, A.; Mo, W.; Jin, S. Interaction analysis of geometric tolerance of multi-axis machine tools based on kinematic Jacobian-Torsor model. Proc. Inst. Mech. Eng. Part B-J. Eng. Manuf. 2023, 237, 240–249. [Google Scholar] [CrossRef]
- Qing, G.H.; Wang, M.M.; Lin, F. Fixturing Layout Optimal Method Based on TOPSIS and MOEA/D. Comput. Integr. Manuf. Syst. 2022, 1–24. Available online: http://kns.cnki.net/kcms/detail/11.5946.TP.20220613.0842.004.html (accessed on 1 April 2023).
- Zmarzły, P. Analysis of Technological Heredity in the Production of Rolling Bearing Rings Made of AISI 52100 Steel Based on Waviness Measurements. Materials 2022, 15, 3959. [Google Scholar] [CrossRef]
- Zheng, A.Q.; Ji, F.F.; Sun, Q.; Liu, Z.Q. Experimental study on optimization of cutting parameters for fixed pitch propelle. Manuf. Technol. Mach. Tool 2019, 689, 168–172. [Google Scholar]
- Huang, Q.; Zhou, N.; Shi, J. Stream of Variation Modeling and Diagnosis of Multi-Station Machining Processes. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–10 November 2000; Volume 11, pp. 81–88. [Google Scholar]
- Djurdjanovic, D.; Ni, J. Linear state space modeling of dimensional machining errors. Trans. NAMRI/SME 2001, 29, 541–548. [Google Scholar]
- Zhou, S.; Huang, Q.; Shi, J. State space modeling of dimensional variation propagation in multistage machining process using differential motion vectors. IEEE Trans. Robot. Autom. 2003, 19, 296–309. [Google Scholar] [CrossRef]
- Loose, J.P.; Zhou, S.; Ceglarek, D. Kinematic analysis of dimensional variation propagation for multistage machining processes with general fixture layouts. IEEE Trans. Autom. Sci. Eng. 2007, 4, 141–152. [Google Scholar] [CrossRef]
- Abellan-Nebot, J.V.; Liu, J.; Romero, F. State space modeling of variation propagation in multistation machining processes considering machining-induced variations. J. Manuf. Sci. Eng.-Trans. ASME 2012, 134, 021002. [Google Scholar] [CrossRef]
- Abellan-Nebot, J.V.; Liu, J. Variation propagation modeling for multi-station machining processes with fixtures based on locating surfaces. Int. J. Prod. Res. 2013, 51, 4667–4681. [Google Scholar] [CrossRef]
- Jia, F.; Jiang, P.Y.; Liu, D.Y.; Zheng, M. Error propagation control method for multistage batches machining processes of blades. Comput. Integr. Manuf. Syst. 2012, 18, 76–86. [Google Scholar]
- Zeng, W.; Fang, F.; Ma, X. On-position measurement method for position-error compensation in machining. Int. J. Precis. Eng. Manuf. 2021, 22, 1179–1189. [Google Scholar] [CrossRef]
- Du, Z.C.; Ge, G.Y.; Xiao, Y.K.; Feng, X.B.; Yang, J.G. Modeling and Compensation of Comprehensive Errors for Thin-walled Parts Machining Based on On-machine Measurement. Int. J. Adv. Manuf. Technol. 2021, 115, 11–12. [Google Scholar] [CrossRef]
- Deng, M.; Li, H.; Xiang, S.; Liu, P.; Feng, X.; Du, Z.; Yang, J. Geometric errors identification considering rigid-body motion constraint for rotary axis of multi-axis machine tool using a tracking interferometer. Int. J. Mach. Tools Manuf. 2020, 158, 103625. [Google Scholar] [CrossRef]
- Pan, S.L.; Zhao, G.B. A real-time compensation method for thermal deformation of high speed machine spindle based on SINUMERIK CNC system. Manuf. Technol. Mach. Tool 2021, 707, 119–123. [Google Scholar]
- Ravichandra, R.; Manjunath, P.G.C.; Chate, G.R.; Deepak, L.; Avinash, L.; Khaled, G.; Pimenov, D.Y. Coaxiality error analysis and optimization of cylindrical parts of CNC turning process. Int. J. Adv. Manuf. Technol. 2022, 120, 6617–6634. [Google Scholar]
- Zhu, M.; Ge, G.; Feng, X.; Du, Z.; Yang, J. A novel error compensation method for multistage machining processes based on differential motion vector sets of multiple contour points. J. Manuf. Sci. Eng. 2021, 143, 061010. [Google Scholar] [CrossRef]
- Liu, C.; Jin, S.; Wang, D.; Luo, Z.; Yu, J.; Zhou, B.; Yang, C. Constrained oversampling: An oversampling approach to reduce noise generation in imbalanced datasets with class overlapping. IEEE Access 2020, 10, 91452–91465. [Google Scholar] [CrossRef]
- Wei, X.Y.; Chen, Y.C.; Miao, E.M.; Feng, X.G.; Pan, Q.S. Application of principal component algorithm in spindle thermal error modeling of CNC machine tools. Opt. Precis. Eng. 2021, 29, 2649–2660. [Google Scholar] [CrossRef]
- Okafor, A.C.; Ertekin, Y.M. Derivation of machine tool error models and error compensation procedure for three axes vertical machining center using rigid body kinematics. Int. J. Mach. Tools Manuf. 2000, 40, 1199–1213. [Google Scholar] [CrossRef]
- Yang, J.; Yuan, J.; Ni, J. Thermal error mode analysis and robust modeling for error compensation on a CNC turning center. Int. J. Mach. Tools Manuf. 1999, 39, 1367–1381. [Google Scholar] [CrossRef]
- Wu, H.; Turyagyenda, G.; Yang, J.G. Modeling and Real-time Compensation of Cutting Force-induced Errors on NC Turning Center. In Key Engineering Marterials; Advances in Machining & Manufacturing Technology VIII; Trans Tech Publications Ltd.: Zurich, Switzerland, 2006; Volume 315–316. [Google Scholar]
- Wang, H.; Huang, Q.; Katz, R. Multi-operational machining processes modeling for sequential root cause identification and measurement reduction. Trans. ASME J. Manuf. Sci. Eng. 2005, 127, 512–521. [Google Scholar] [CrossRef]
- Wang, H.; Huang, Q. Error cancellation modeling and its application to machining process control. IIE Trans. 2006, 38, 355–364. [Google Scholar] [CrossRef]
- Yang, F.; Xing, Y.; Li, X. A comprehensive error compensation strategy for machining process with general fixture layouts. Int. J. Adv. Manuf. Technol. 2020, 107, 2707–2717. [Google Scholar] [CrossRef]
- Du, S.C.; Yao, X.F.; Huang, D.L.; Wang, M. Three-dimensional variation propagation modeling for multistage turning process of rotary workpieces. Comput. Ind. Eng. 2015, 82, 41–53. [Google Scholar] [CrossRef]
- Du, S.; Yao, X.; Huang, D. Engineering model-based Bayesian monitoring of ramp-up phase of multistage manufacturing process. Int. J. Prod. Res. 2015, 53, 4594–4613. [Google Scholar] [CrossRef]
- Wang, K.; Du, S.; Xi, L. Three-Dimensional Tolerance Analysis Modelling of Variation Propagation in Multi-stage Machining Processes for General Shape Workpieces. Int. J. Precis. Eng. Manuf. 2020, 21, 31–44. [Google Scholar] [CrossRef]

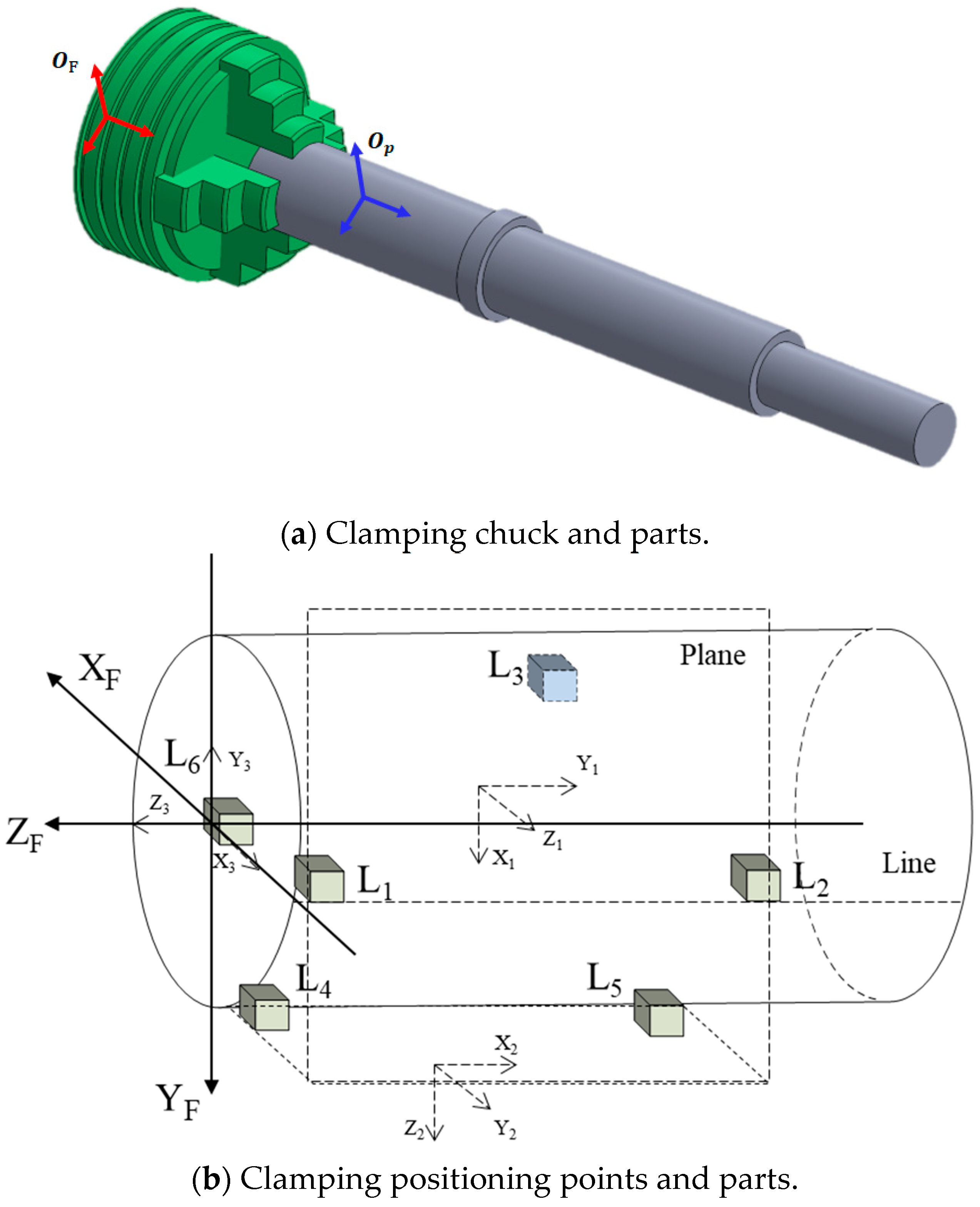

| Name of Feature | Positions | Orientations | |
|---|---|---|---|
| [−45,0,0] | [−1,0,0] | [−π/2,−π/2,0] | |
| [−45,0,−60] | [−1,0,0] | [−π/2,−π/2,0] | |
| [−45,−45,−30] | [−1,0,0] | [−π/2,−π/2,0] | |
| [0,45,0] | [0,1,0] | [−π/2,0,π/2] | |
| [0,45,−60] | [0,1,0] | [−π/2,0,π/2] | |
| [0,0,0] | [0,0,1] | [0,0,π] | |
| Machined Feature | [0,44.85,−685] | [1,0,0] | [π/2,0,π] |
| No. | Normal Position (x, y, z) (mm, mm, mm) | Feature-Point Predicted Error (Δx, Δy, Δz) (mm, mm, mm) | CMM Measurement (Δx, Δy, Δz) (mm, mm, mm) |
|---|---|---|---|
| (0, 40, −22.5) | (0.0309, 0.0161, 0.001) | (0.0314, 0.018, −0.0003) | |
| 2 | (0, 40, −45) | (0.0259, 0.0168, 0.001) | (0.0264, 0.0153, 0.0007) |
| 3 | (0, 40, −67.5) | (0.0208, 0.0176, 0.001) | (0.0205, 0.02, 0.0027) |
| 4 | (0, 40, −90) | (0.0158, 0.0183, 0.001) | (0.0161, 0.0196, −0.0004) |
| 5 | (0, 40, −112.5) | (0.0107, 0.0191, 0.001) | (0.0101, 0.0167, 0.0024) |
| 6 | (0, 40, −135) | (0.0056, 0.0198, 0.001) | (0.0035, 0.0208, 0.0008) |
| 7 | (0, 40, −157.5) | (0.0006, 0.0206, 0.001) | (0.0009, 0.0204, −0.0002) |
| 8 | (0, 40, −180) | (−0.0045, 0.0213, 0.001) | (−0.0049, 0.0229, 0.0023) |
| 9 | (0, 40, −202.5) | (−0.0096, 0.0221, 0.001) | (−0.0092, 0.0207, 0.0014) |
| 10 | (0, 40, −225) | (−0.0146, 0.0228, 0.001) | (−0.0154, 0.0239, 0.003) |
| 11 | (0, 45, −229.1) | (−0.0146, 0.0235, −0.0001) | (−0.0133, 0.0249, 0.0001) |
| 12 | (0, 45, −233.2) | (−0.0155, 0.0236, −0.0001) | (−0.013, 0.0244, −0.0006) |
| 13 | (0, 45, −237.3) | (−0.0165, 0.0238, −0.0001) | (−0.015, 0.0234, 0.0007) |
| 14 | (0, 45, −241.4) | (−0.0174, 0.0239, −0.0001) | (−0.0177, 0.0241, −0.0008) |
| 15 | (0, 45, −245.5) | (−0.0183, 0.024, −0.0001) | (−0.016, 0.025, −0.0012) |
| 16 | (0, 37, −273.15) | (−0.0192, 0.0231, 0.0017) | (−0.0186, 0.0219, 0.0025) |
| 17 | (0, 37, −300.8) | (−0.0255, 0.024, 0.0017) | (−0.0275, 0.0249, 0.0002) |
| 18 | (0, 37, −328.45) | (−0.0317, 0.025, 0.0017) | (−0.0304, 0.0227, 0.0013) |
| 19 | (0, 37, −356.1) | (−0.0379, 0.0259, 0.0017) | (−0.0377, 0.0238, 0.002) |
| 20 | (0, 37, −383.75) | (−0.0441, 0.0268, 0.0017) | (−0.0462, 0.0271, 0.0035) |
| 21 | (0, 37, −411.4) | (−0.0503, 0.0277, 0.0017) | (−0.0526, 0.026, 0.0029) |
| 22 | (0, 37, −439.05) | (−0.0566, 0.0286, 0.0017) | (−0.0555, 0.0267, 0.0024) |
| 23 | (0, 37, −466.7) | (−0.0628, 0.0296, 0.0017) | (−0.0641, 0.0286, 0.0028) |
| 24 | (0, 37, −494.35) | (−0.069, 0.0305, 0.0017) | (−0.0681, 0.03, 0.0019) |
| 25 | (0, 37, −522) | (−0.0752, 0.0314, 0.0017) | (−0.0734, 0.0301, 0.0024) |
| 26 | (0, 27.5, −538.3) | (−0.0814, 0.0311, 0.0038) | (−0.0797, 0.0332, 0.003) |
| 27 | (0, 27.5, −554.6) | (−0.0851, 0.0316, 0.0038) | (−0.0866, 0.0307, 0.006) |
| 28 | (0, 27.5, −570.9) | (−0.0888, 0.0322, 0.0038,0) | (−0.0864, 0.0018, 0.0013) |
| 29 | (0, 27.5, −587.2) | (−0.0925, 0.0327, 0.0038,0) | (−0.09, 0.0052, −0.0018) |
| 30 | (0, 27.5, −603.5) | (−0.0961, 0.0332, 0.0038) | (−0.0962, 0.0319, 0.0035) |
| 31 | (0, 27.5, −619.8) | (−0.0998, 0.0338, 0.0038,0) | (−0.1007, 0.0018, 0.0007) |
| 32 | (0, 27.5, −636.1) | (−0.1035, 0.0343, 0.0038) | (−0.1054, 0.0343, 0.0045) |
| 33 | (0, 27.5, −652.4) | (−0.1071, 0.0349, 0.0038) | (−0.1054, 0.0325, 0.0039) |
| 34 | (0, 27.5, −668.7) | (−0.1108, 0.0354, 0.0038) | (−0.1121, 0.0332, 0.0017) |
| 35 | (0, 27.5, −685) | (−0.1145, 0.036, 0.0038) | (−0.1169, 0.037, 0.0032) |
| No. | Datum Error | EFE |
|---|---|---|
| No. | Fixture Error | EFE Error |
|---|---|---|
| L5 |
| No. | R/mm | MRE |
|---|---|---|
| 1 | 40 | 2.78% |
| 2 | 45 | 2.85% |
| 3 | 37 | 12.12% |
| 4 | 27.5 | 6.53% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, A.; Du, X.; Liu, S.; Jin, S. Characterization of Dimensional Variations in Turning Process for Multistep Rotary Shaft of High-Speed Motorized Spindle. Machines 2023, 11, 561. https://doi.org/10.3390/machines11050561
Tian A, Du X, Liu S, Jin S. Characterization of Dimensional Variations in Turning Process for Multistep Rotary Shaft of High-Speed Motorized Spindle. Machines. 2023; 11(5):561. https://doi.org/10.3390/machines11050561
Chicago/Turabian StyleTian, Ang, Xueming Du, Shun Liu, and Sun Jin. 2023. "Characterization of Dimensional Variations in Turning Process for Multistep Rotary Shaft of High-Speed Motorized Spindle" Machines 11, no. 5: 561. https://doi.org/10.3390/machines11050561
APA StyleTian, A., Du, X., Liu, S., & Jin, S. (2023). Characterization of Dimensional Variations in Turning Process for Multistep Rotary Shaft of High-Speed Motorized Spindle. Machines, 11(5), 561. https://doi.org/10.3390/machines11050561






