Path Planning for 5-Axis CMM Inspection Considering Path Reuse
Abstract
1. Introduction
1.1. Literature Review
1.1.1. Path Planning Considering Inspection Time
1.1.2. Path Planning Considering Dynamic Tasks
1.1.3. Path Planning Considering Inspection Accuracy
1.1.4. Contribution of This Paper
- (1)
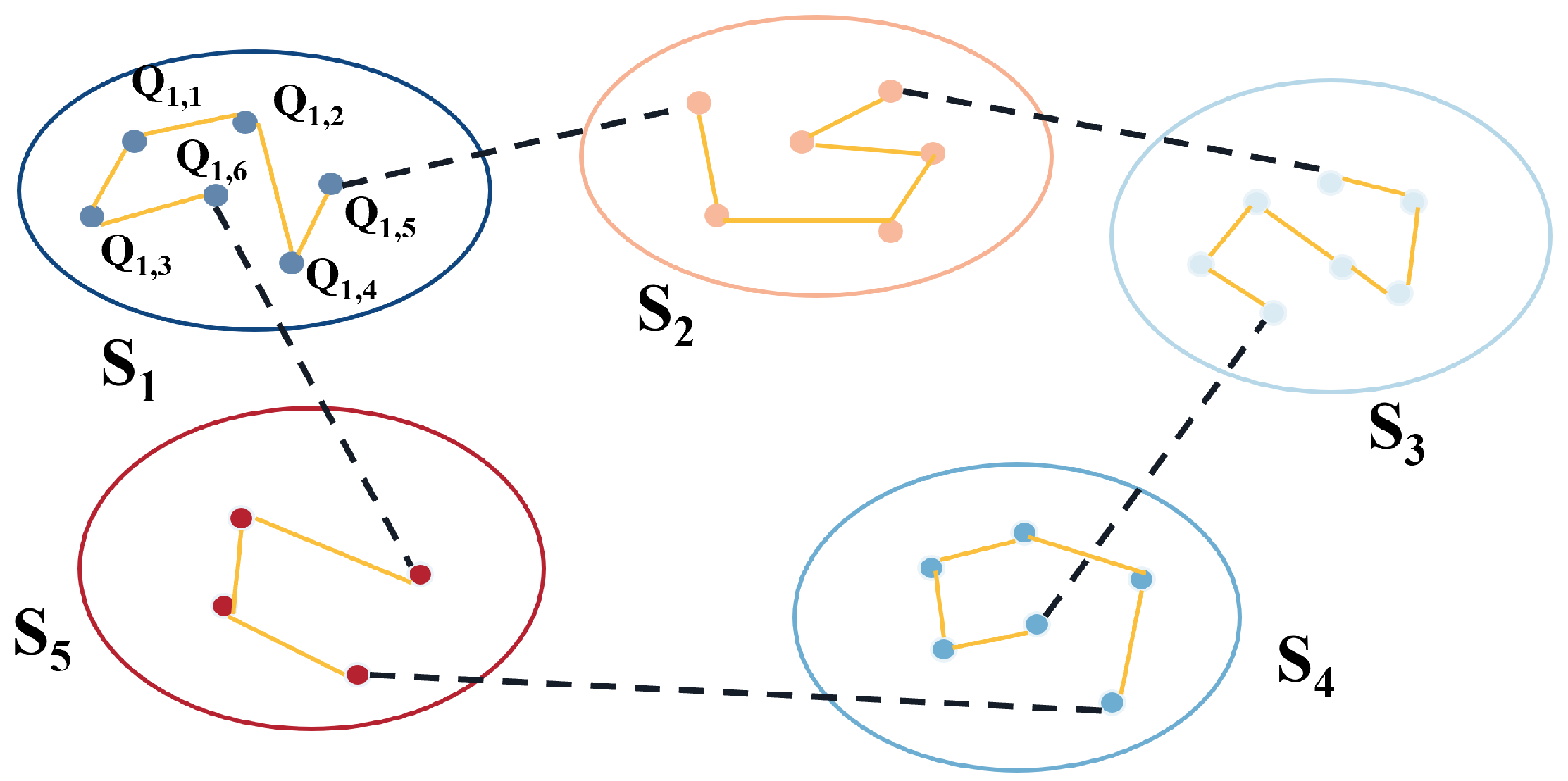
- Based on the feasible measurement orientation cone and accessibility, the set covering problem model for MPs classification is established, and the minimum coverage cluster is solved based on greedy algorithm.
- (2)
- The rapidly exploring random trees with multi-root node competition algorithm is proposed to implement inspection path planning considering inspection path reuse.
- (3)
- The global path planning problem with multiple measuring points clusters is transformed into a Generalized Traveling Salesman Problem (GTSP) model and solved based on an enhanced Genetic Algorithm (GA) algorithm.
2. Problem Statement
2.1. Problem Description
- (1)
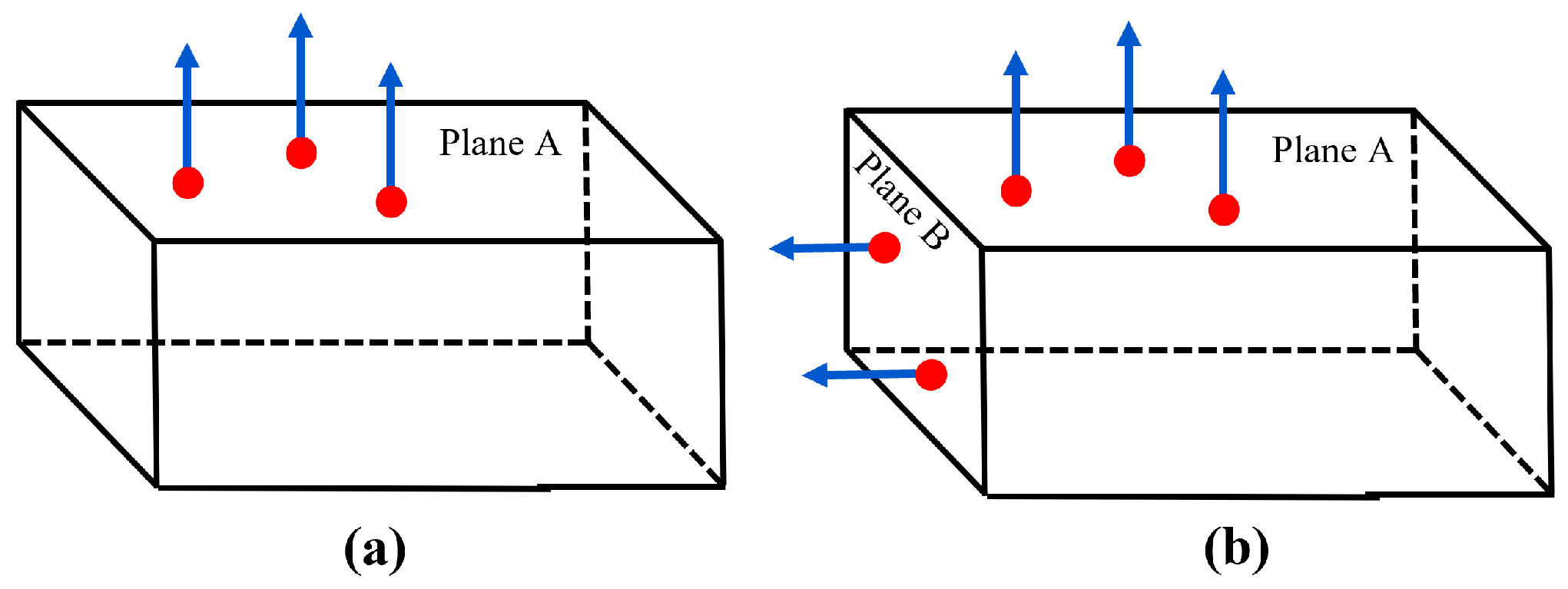
- Probe tolerability: The frequent probe rotations not only increase the inspection time, but also increase the inspection error. Therefore, the number of probe rotations need to be used as the optimization objective to classify the MPs.
- (2)
- Path reusability: For the initial planned collision-free path, the planned path result is still a collision-free path after deleting some of MPs and obstacle avoidance points.
- (3)
- Inspection efficiency: For the classified MPs, the inspection time of in-group and inter-group MPs need to be optimized.
2.2. Path Reuse Planning Optimization Modeling
- (1)
- The 5-axis CMM consists of a rotating 2-axis probe and a traditional moving 3-axis. During the inspection process, only movement or rotation is executed at one time.
- (2)
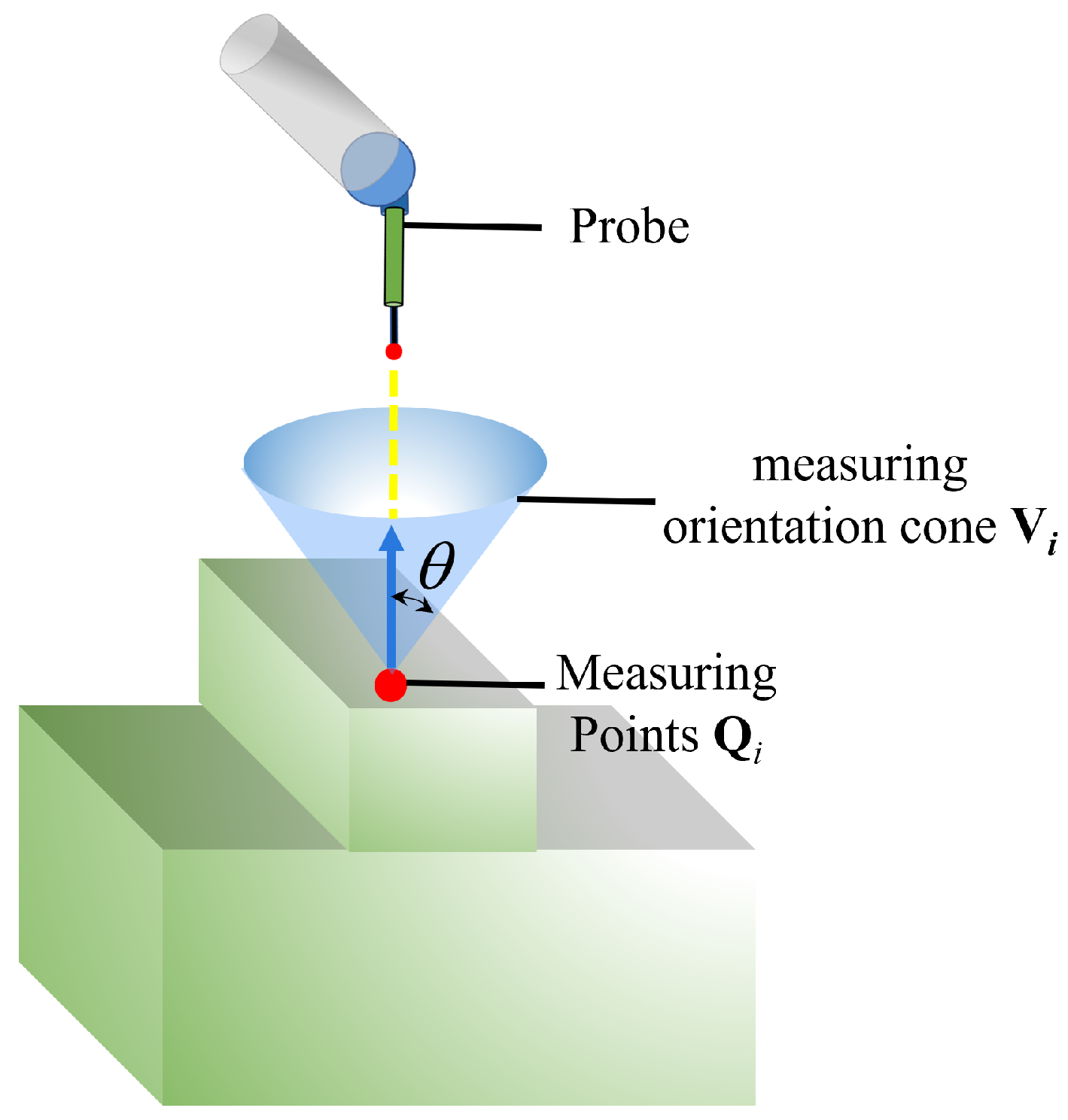
- During the measurement process, the angle between the vector direction of the probe and the normal direction of the feature should meet the constraints of the measurement specification to ensure measurement accuracy.
- (3)
- The velocity and acceleration of the CMM are assumed to be constant throughout the inspection process.
3. Path Planning Considering Path Reuse
3.1. Measuring Points Classification and Probe Matching
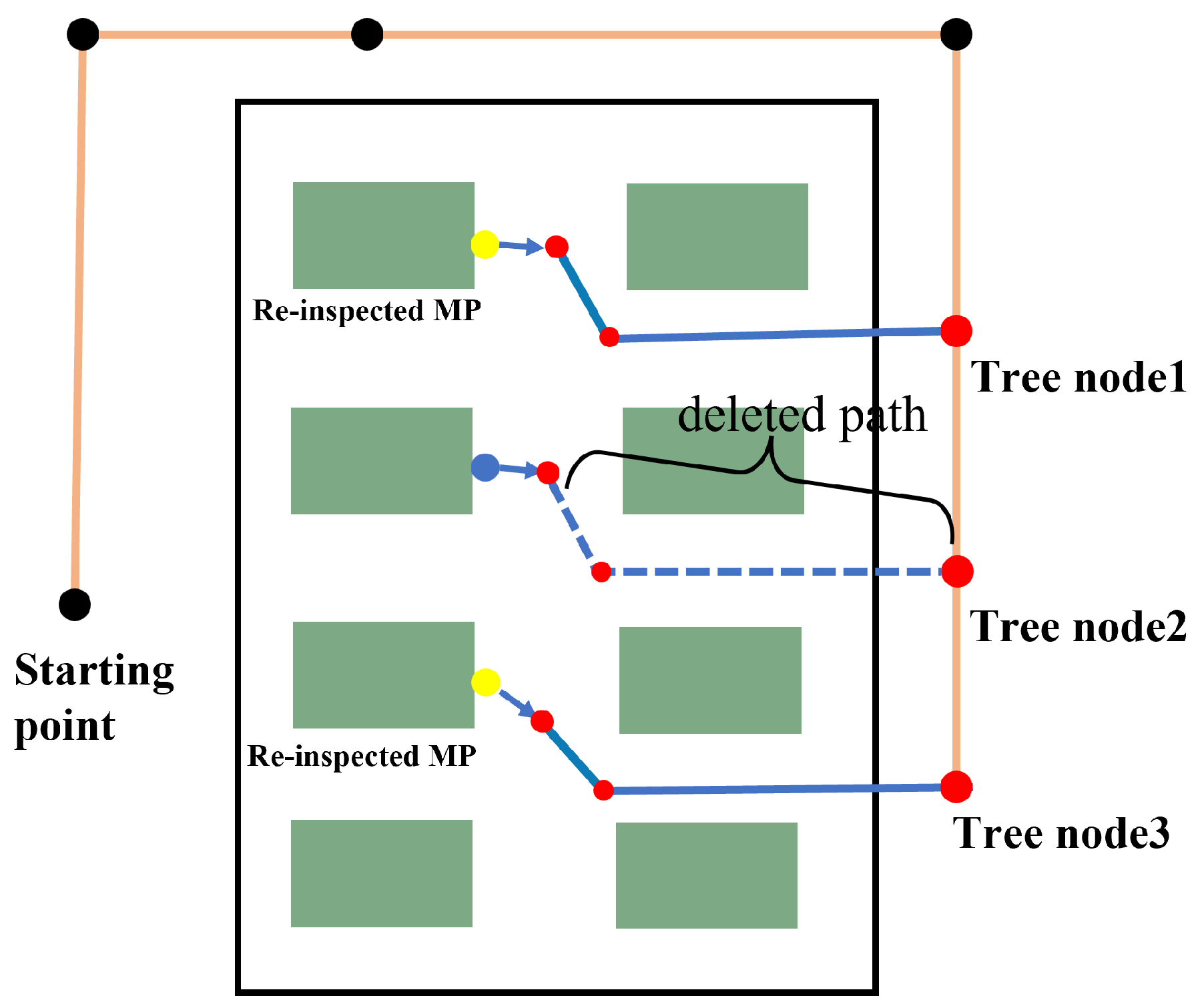
3.2. Inspection Path Reuse Based on RRT-MRNC
| Algorithm 1 Local path planning based on RRT-MRNC algorithm |
|
- (1)
- Without adding avoidance points, all paths between root nodes and from root nodes to the start are collision-free.
- (2)
- The determined root node must be within the safe space.
- (3)
- Ignore collision between root nodes and MP path.
| Algorithm 2 Candidate tree nodes determination |
|
| Algorithm 3 Searching for candidate tree nodes |
|
| Algorithm 4 Determining the optimal tree nodes |
|
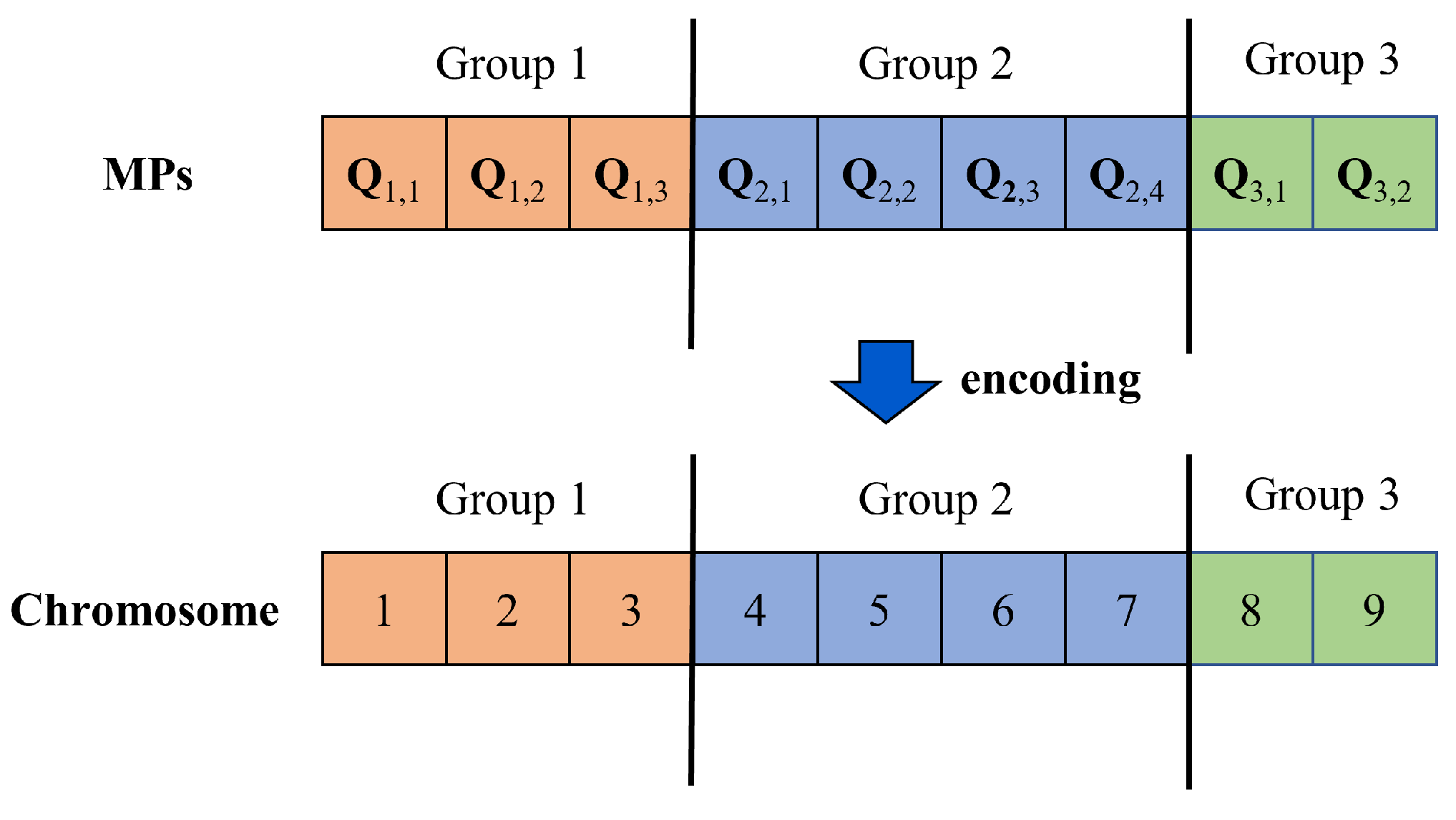
3.3. Global Path Planning Based on Enhanced Genetic Algorithm
| Algorithm 5 Optimize global path via enhanced GA |
|
- (1)
- A new individual can be determined by randomly selecting X positions of encoding from the individuals and arbitrarily swapping the positions with each other.
- (2)
- Calculate the fitness function of new individuals and select the individual with the smallest fitness as the new individual.
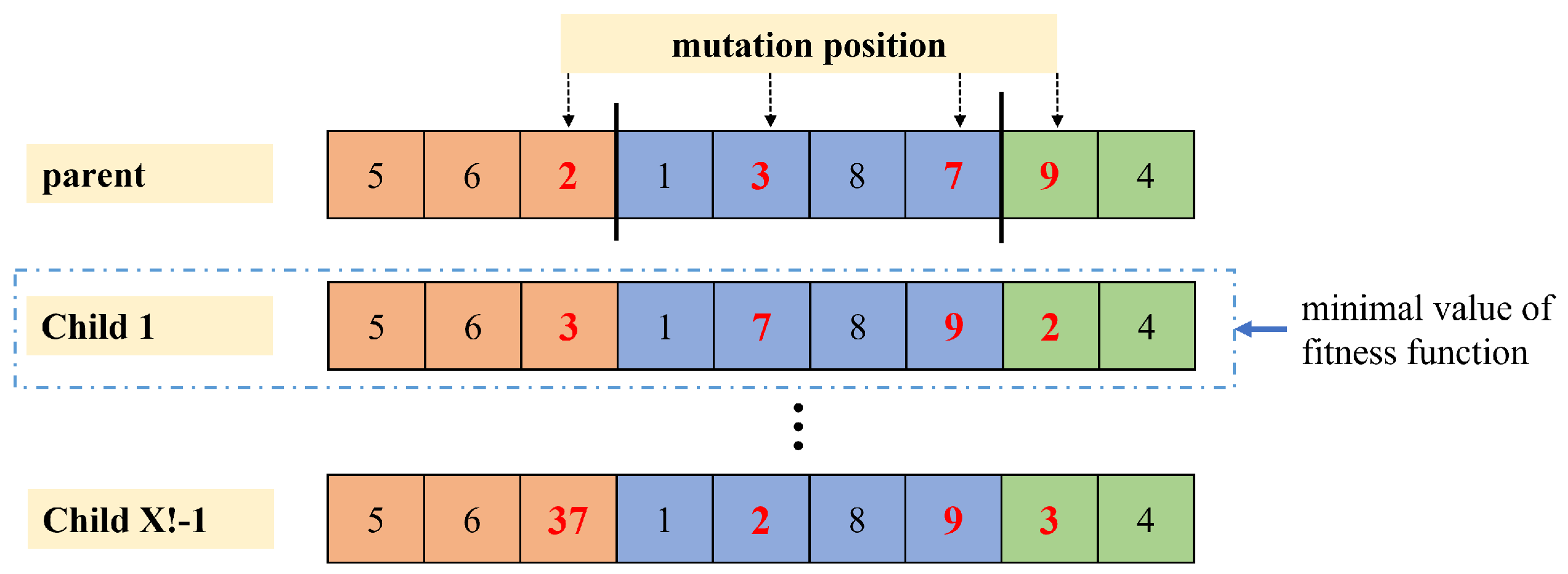
- (1)
- The genes with the maximum and minimum values in any sub-segment of the chromosome are randomly selected, and the positions are exchanged between each other to determine the new individual.
- (2)
- If the fitness function of the newly generated individual is smaller than the previous one, then use the newly generated individual as a new individual. Otherwise, go to step1.
4. Experiment and Discussion
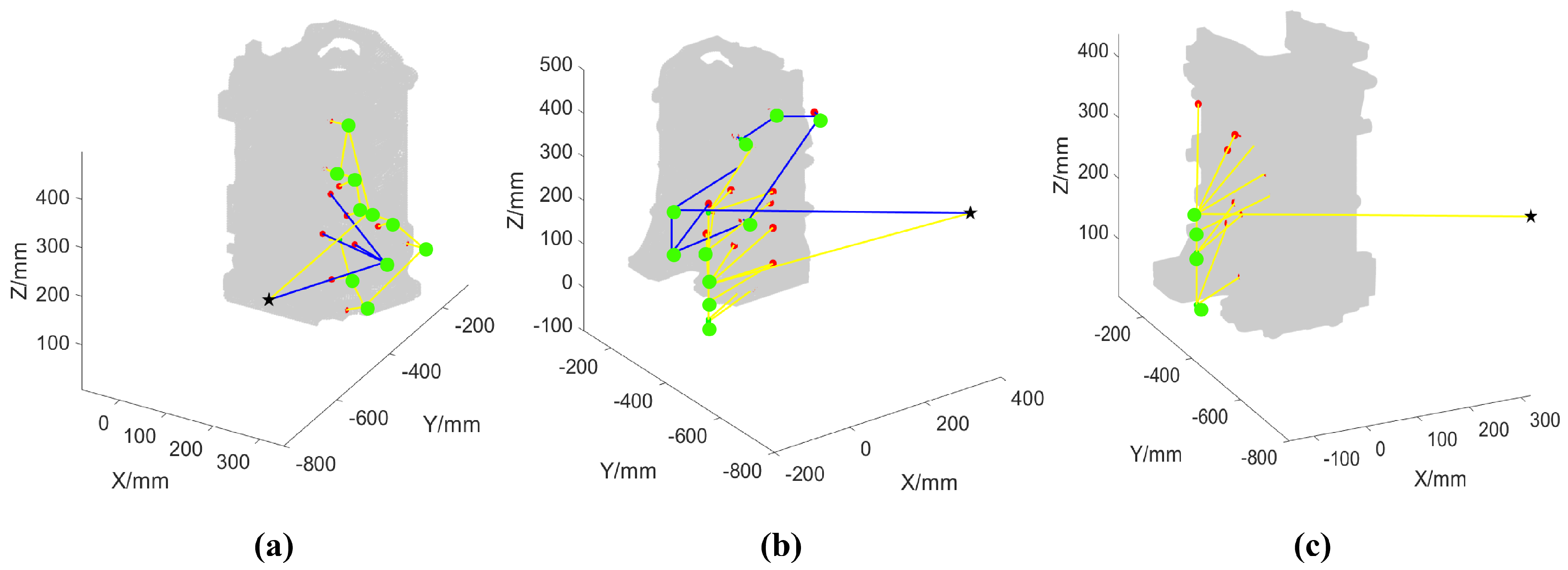
4.1. Comparative Analysis and Verification
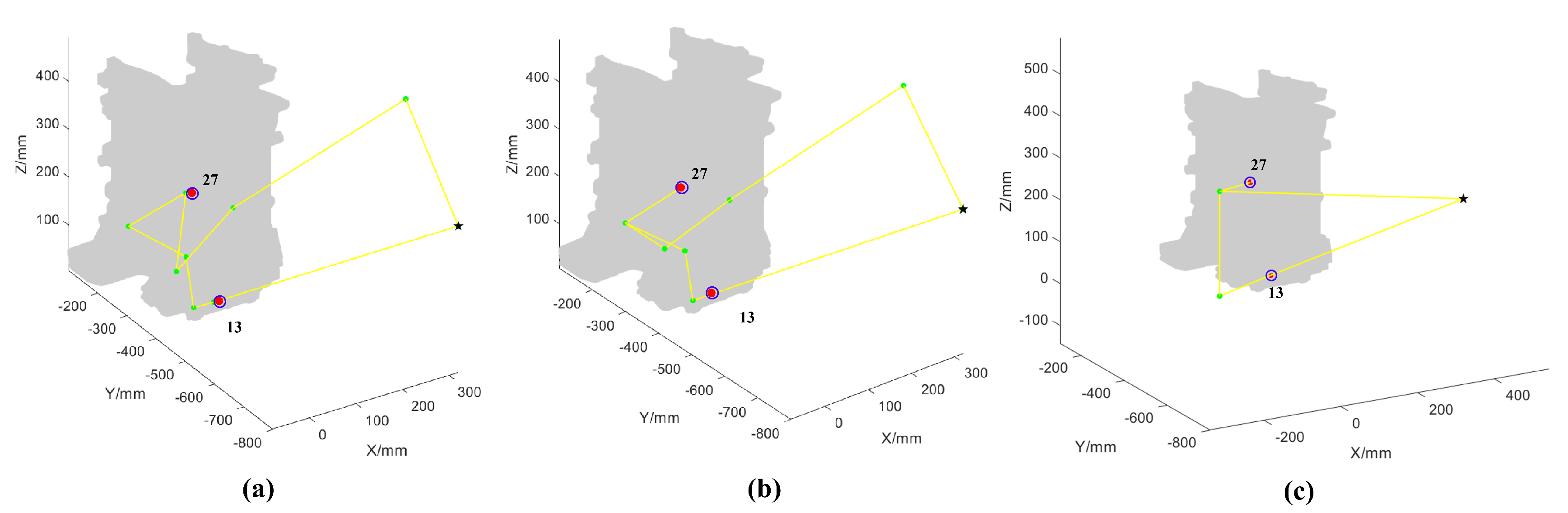
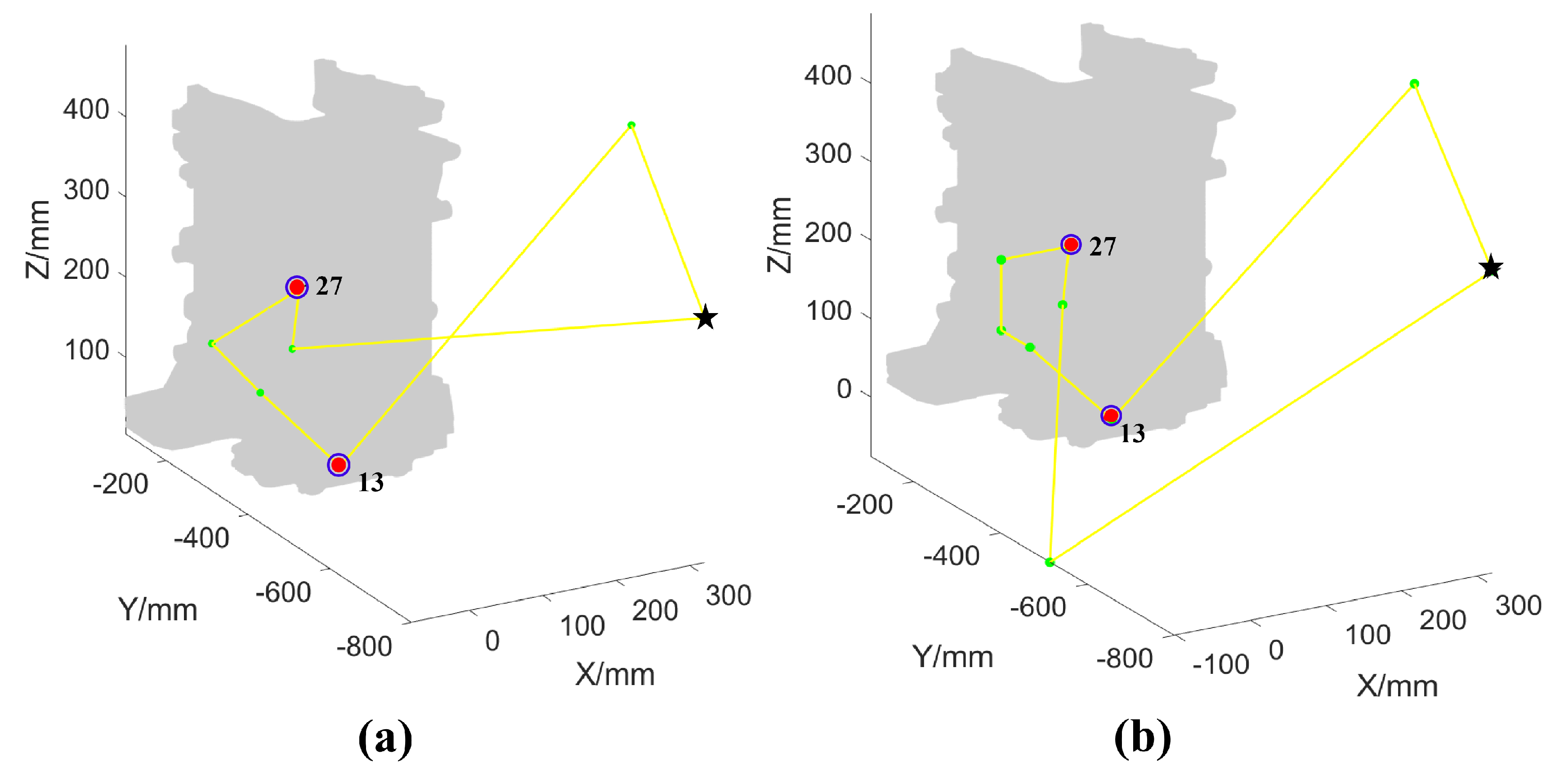
4.2. Path Reusability Analysis
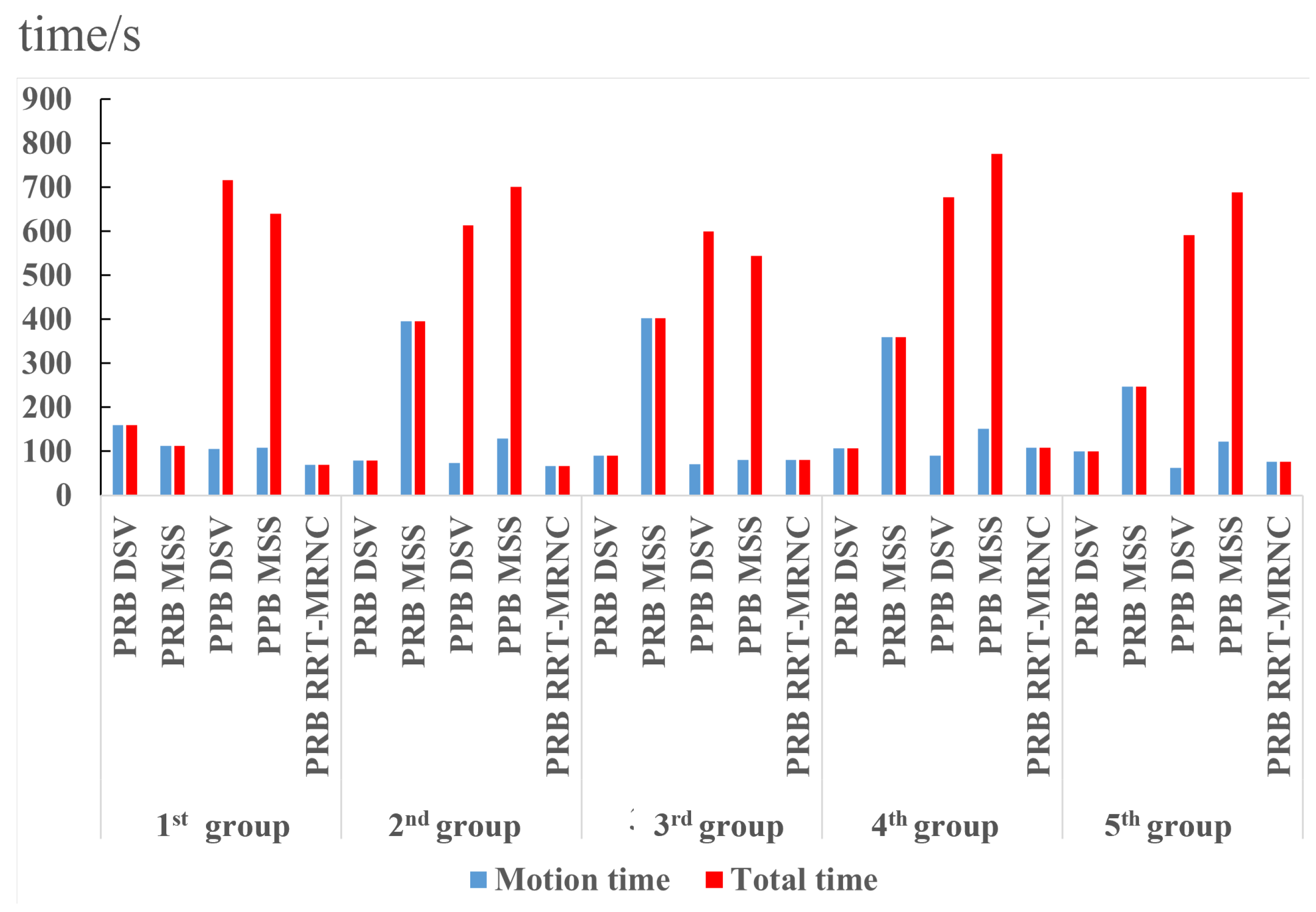
4.3. Numerical Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anagnostakis, D.; Ritchie, J.; Lim, T.; Sivanathan, A.; Dewar, R.; Sung, R.; Bosché, F.; Carozza, L. Knowledge capture in CMM measurement planning: Barriers and challenges. Procedia CIRP 2016, 52, 216–221. [Google Scholar] [CrossRef]
- Li, W.L.; Wang, G.; Zhang, G.; Li, Q.D.; Yin, Z.P.; Tang, K.; Xie, C. Interference-free measurement path generation for impeller blades using an on-machine probe. IEEE/ASME Trans. Mechatron. 2017, 22, 1218–1226. [Google Scholar] [CrossRef]
- Liu, Y.H.; Zhao, W.Z.; Sun, R.; Yue, X.W. Optimal path planning for automated dimensional measurement of free-form surfaces. J. Manuf. Syst. 2020, 56, 84–92. [Google Scholar] [CrossRef]
- Stojadinovic, S.M.; Majstorovic, V.D.; Gąska, A.; Sładek, J.; Durakbasa, N.M. Development of a coordinate measuring machine—Based inspection planning system for industry 4.0. Appl. Sci. 2021, 11, 8411. [Google Scholar] [CrossRef]
- Slavenko, M.S.; Vidosav, D.M.; Numan, M.D.; Tatjana, V.S. Ants colony optimisation of a measuring path of prismatic parts on a CMM. Metrol. Meas. Syst. 2016, 23, 119–132. [Google Scholar]
- Liu, Y.H.; An, C.; Duan, Z.X. A Safety-Space-Based approach to inspection path planning for the sheet metal assemblies. In Proceedings of the ASME 2021 International Mechanical Engineering Congress and Exposition, Virtual, 1–5 November 2021. [Google Scholar]
- Ren, M.J.; Kong, L.B.; Sun, L.J.; Cheung, C.F. A curve network sampling strategy for measurement of freeform surfaces on Coordinate Measuring Machines. IEEE Trans. Instrum. Meas. 2017, 66, 3032–3043. [Google Scholar] [CrossRef]
- Chen, X.; You, X.; Jiang, J.; Ye, J.; Wu, H. Trajectory planning of dual-Robot cooperative assembly. Machines 2022, 10, 689. [Google Scholar] [CrossRef]
- Bai, Y.; Ding, X.; Hu, D.; Jiang, Y. Research on dynamic path planning of multi-AGVs based on reinforcement learning. Appl. Sci. 2022, 12, 8166. [Google Scholar] [CrossRef]
- Han, Z.H.; Liu, S.G.; Yu, F.; Zhang, X.D.; Zhang, G.X. A 3D measuring path planning strategy for intelligent CMMs based on an improved ant colony algorithm. Int. J. Adv. Manuf. Technol. 2017, 93, 1487–1497. [Google Scholar] [CrossRef]
- Li, B.; Feng, P.F.; Zeng, L.; Xu, C.; Zhang, J.F. Path planning method for on-machine measurement of aerospace structures based on adjacent feature graph. Robot. Comput.-Integr. Manuf. 2018, 54, 17–34. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, Y.; Tang, K. Sweep scan path planning for efficient free-form surface measurement on five-axis CMM. Comput.-Aided Des. 2016, 77, 1–17. [Google Scholar] [CrossRef]
- Devaurs, D.; Siméon, T.; Cortés, J. Optimal path planning in complex cost spaces with sampling-based algorithms. IEEE Trans. Autom. Sci. Eng. 2016, 13, 415–424. [Google Scholar] [CrossRef]
- Slavenko, M.S.; Vidosav, D.M.; Numan, M.D.; Tatjana, V.S. Towards an intelligent approach for CMM measurement planning of prismatic parts. Measurement 2016, 92, 326–339. [Google Scholar]
- Zhao, H.B.; Jean, P.K.; Nick, V.G.; Bart, B.; Philip, B. Automated dimensional measurement planning using the combination of laser scanner and tactile probe. Measurement 2012, 45, 1–17. [Google Scholar] [CrossRef]
- Suh, J.; Gong, J.; Songhwai, O. Fast sampling-based cost-aware path planning With nonmyopic extensions using cross entropy. IEEE Trans. Robot. 2017, 13, 1313–1326. [Google Scholar] [CrossRef]
- Lai, T.; Morere, P.; Ramos, F.; Francis, G. Bayesian local sampling-based planning. IEEE Trans. Ind. Electron. 2020, 5, 1954–1961. [Google Scholar] [CrossRef]
- Qi, J.; Yang, H.; Sun, H.X. MOD-RRT*: A sampling-based algorithm for robot path planning in dynamic environment. IEEE Robot. Autom. Lett. 2021, 68, 7244–7251. [Google Scholar] [CrossRef]
- Yang, L.; Fu, L.; Li, P.; Mao, J.; Guo, N. An effective dynamic Path Planning Approach for Mobile Robots Based on Ant Colony Fusion Dynamic Windows. Machines 2022, 10, 50. [Google Scholar] [CrossRef]
- Li, D.C.; Yin, W.P.; Wong, W.E.J.; Chau, M.Y.M. Quality-oriented hybrid path planning based on A* and Q-Learning for unmanned aerial vehicle. IEEE Access 2022, 10, 7664–7674. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Z.; Li, Q.B.; Prorok, A. Mobile Robot Path Planning in Dynamic Environments Through Globally Guided Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 6932–6939. [Google Scholar] [CrossRef]
- Li, X.; Liu, H.; Dong, M.; Prorok, A. A General Framework of Motion Planning for Redundant Robot Manipulator Based on Deep Reinforcement Learning. IEEE Trans. Ind. Inform. 2021, 18, 5253–5263. [Google Scholar] [CrossRef]
- Mussa, M.; David, J.; Michaël, R.; Ahmed, I.; Jean, F. 3D part measurement path planning of a laser scanner with control on the uncertainty. Comput.-Aided Des. 2011, 43, 345–355. [Google Scholar]
- Yi, B.W.; Qiao, F.; Li, H.; Wang, X.S.; Wu, S.J.; Huang, N. Touch trigger probe-based interference-free measurement path planning for free-form surfaces by optimizing the probe posture. IEEE Trans. Instrum. Meas. 2022, 71, 1–8. [Google Scholar]
- Zhang, S.G.; Ajmal, A.; Wootton, J.; Chisholm, A. A feature-based measurement process planning system for co-ordinate measuring machine (CMM). J. Mater. Process. Technol. 2000, 107, 111–118. [Google Scholar] [CrossRef]
- Li, Y.M.; Zeng, L.; Tang, K.; Xie, C. Orientation-point relation based measurement path planning method for 5-axis OMI system. Robot. Comput.-Integr. Manuf. 2020, 61, 101827. [Google Scholar] [CrossRef]
- Anagnostakis, D.; Ritchie, J.; Lim, T.; Sung, R.; Dewar, R. A Virtual CMM measurement Tool for Capturing Planning Strategies. In Proceedings of the ASME 2017 International Mechanical Engineering Congress and Exposition, Cleveland, OH, USA, 6–9 August 2017. [Google Scholar]
- Martínez-Pelliter, S.; Barreiro, J.; Cuesta, E.; Fernández-Abia, A.I. Knowledge base model for automatic probe orientation and configuration planning with CMMs. Robot. Comput.-Integr. Manuf. 2018, 49, 285–300. [Google Scholar] [CrossRef]
- Wang, S.Q. Research on randomized greedy algorithm for k-median problem. In Proceedings of the 2011 International Conference on Uncertainty Reasoning and Knowledge Engineering, Bali, Indonesia, 4–7 August 2011; pp. 98–101. [Google Scholar]
- Liu, Y.H.; Zhao, W.Z.; Liu, H.P.; Wang, Y.N.; Yue, X.W. Coverage Path Planning for Robotic Quality Inspection With Control on Measurement Uncertainty. IEEE/ASME Trans. Mechatron. 2022. [Google Scholar] [CrossRef]
- Chen, L.; Yang, H.; Shan, Y.X.; Tian, W.; Li, B.J.; Cao, D.P. A Fast and Efficient Double-Tree RRT*-Like Sampling-Based Planner Applying on Mobile Robotic Systems. IEEE/ASME Trans. Mechatron. 2018, 23, 2568–2578. [Google Scholar] [CrossRef]
- Gohar, V.; Mehdi, Y.; Mahdieh, P.; Naghibi, S. A New Approach to Solve Traveling Salesman Problem Using Genetic Algorithm Based on Heuristic Crossover and Mutation Operator. In Proceedings of the International Conference of Soft Computing and Pattern Recognition, Malacca, Malaysia, 4–7 December 2009; pp. 112–116. [Google Scholar]
- Li, Z.; Janardhanan, M.N.; Ponnambalam, S.G. Cost-oriented robotic assembly line balancing problem with setup times: Multi-objective algorithms. J. Intell. Manuf. 2021, 32, 989–1007. [Google Scholar] [CrossRef]






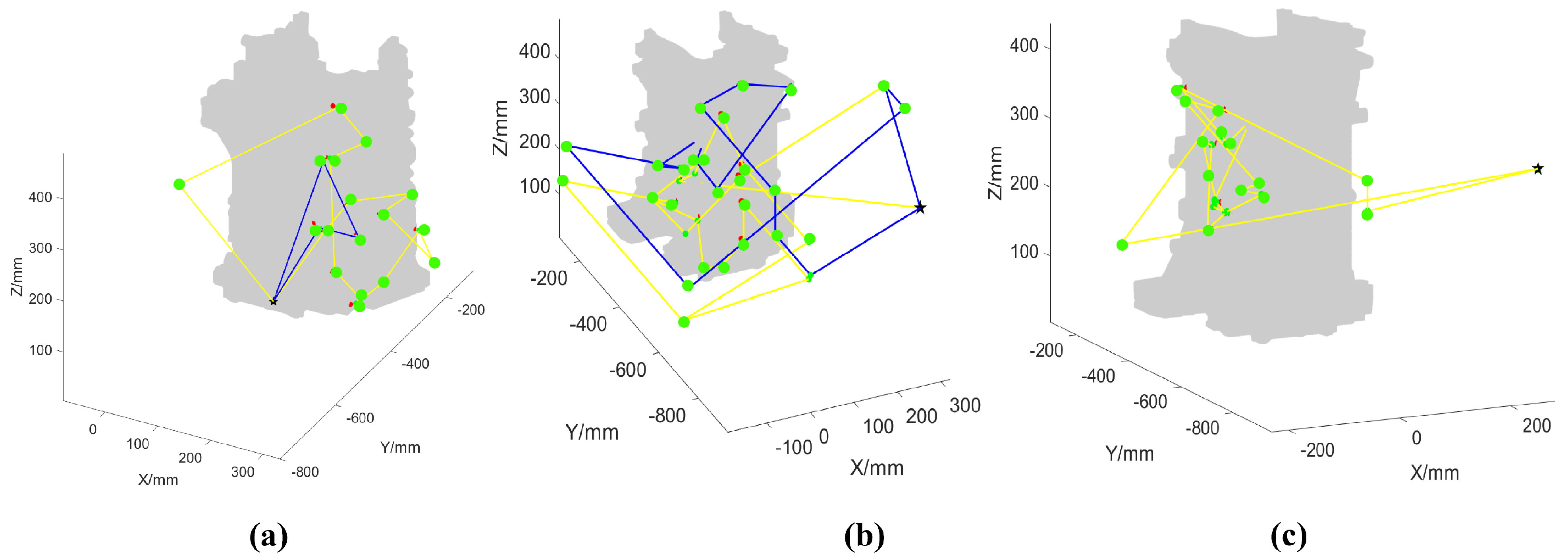
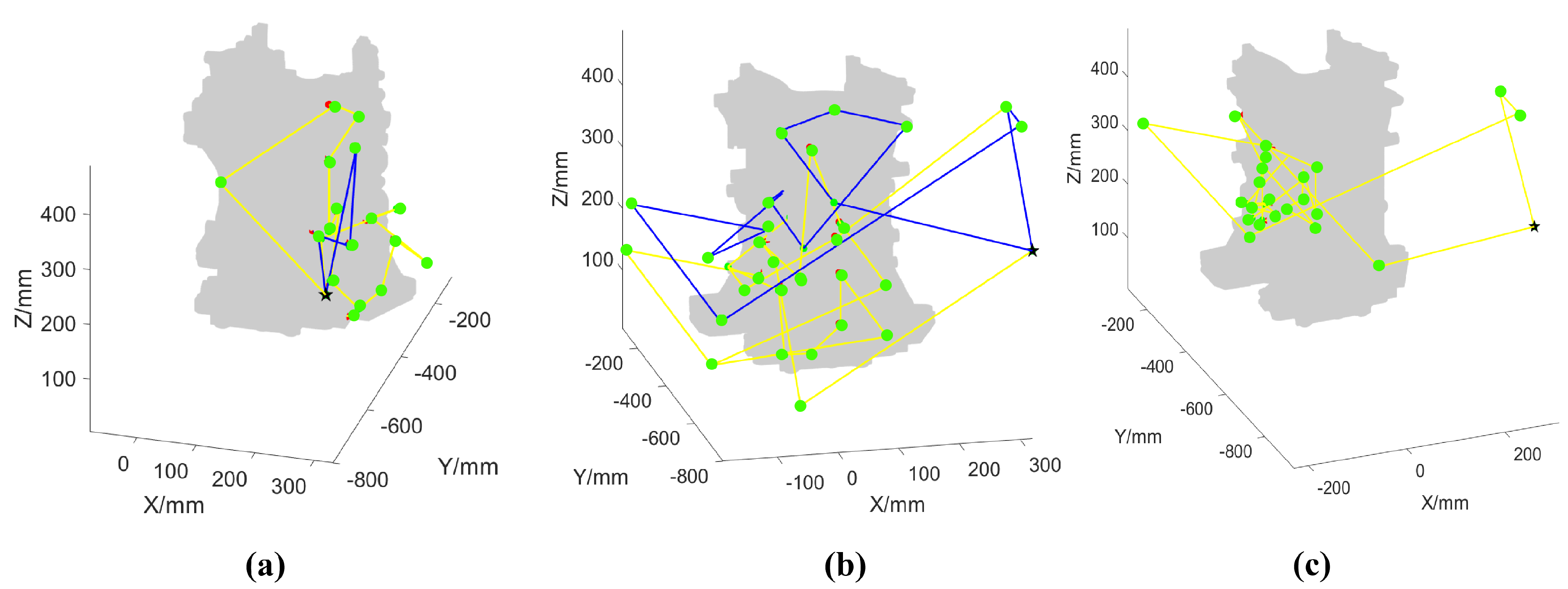
| Parameters | L1 (mm) | L2 (mm) | D0 (mm) | D1 (mm) | D2 (mm) | Rotation Speed (mm/s) | Movement Speed (mm/s) | MP Inspection Time (s) |
|---|---|---|---|---|---|---|---|---|
| Value | 50 | 150 | 3 | 3 | 11 | 1 | 85 | 1 |
| Subgroup | |||||
|---|---|---|---|---|---|
| MP No. | {1, 2, 3, 30, 32, 33, 34, 36, 38} | {7,31,35} | {18,27,29,39,8,9,10,11,12,13,14} | {4,5,6,26,28,27} | {15,16,17,19,20,21,23,24,25,37} |
| Computation Time (s) | Probe Movement Time (s) | Probe Rotation Time (s) | Inspection Time (s) | Motion Time (s) | Teaching Time (s) | Total Time (s) | |
|---|---|---|---|---|---|---|---|
| DSV | 935.7 | 122.0 | 117.0 | 39.0 | 278.0 | 546.9 | 1760.5 |
| MSS | 864.1 | 203.7 | 197.0 | 39.0 | 439.7 | 890.5 | 2194.3 |
| RRT-MRNC | 213.2 | 177.4 | 96.0 | 39.0 | 312.4 | 759.3 | 1285.0 |
| Computation Time (s) | Motion Time (s) | Teaching Time (s) | Total Time (s) | |
|---|---|---|---|---|
| Path reuse based on DSV | 0.0 | 86.0 | 0.0 | 86.0 |
| Path reuse based on MSS | 0.0 | 85.4 | 0.0 | 85.4 |
| Path re-planning based on DSV | 337.5 | 61.1 | 129.8 | 528.3 |
| Path re-planning based on MSS | 277.5 | 69.4 | 147.5 | 494.5 |
| Path reuse based on RRT-MRNC | 0.0 | 38.5 | 0.0 | 38.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Wang, X.; Liu, Y. Path Planning for 5-Axis CMM Inspection Considering Path Reuse. Machines 2022, 10, 973. https://doi.org/10.3390/machines10110973
Zhao W, Wang X, Liu Y. Path Planning for 5-Axis CMM Inspection Considering Path Reuse. Machines. 2022; 10(11):973. https://doi.org/10.3390/machines10110973
Chicago/Turabian StyleZhao, Wenzheng, Xueqi Wang, and Yinhua Liu. 2022. "Path Planning for 5-Axis CMM Inspection Considering Path Reuse" Machines 10, no. 11: 973. https://doi.org/10.3390/machines10110973
APA StyleZhao, W., Wang, X., & Liu, Y. (2022). Path Planning for 5-Axis CMM Inspection Considering Path Reuse. Machines, 10(11), 973. https://doi.org/10.3390/machines10110973





