Abstract
In this paper, the problem of distributed adaptive consensus tracking control for second-order nonlinear heterogeneous multi-agent systems (MASs) with input quantization is considered. A distributed output feedback control scheme based on a K-filter is developed to suppress the influences of unknown disturbances and input quantization. In contrast to existing approaches, an additional design parameter is introduced into the controller design to ensure that the subsystem tracking error converges to an arbitrarily small residual set. Through Lyapunov stability analysis, it can be proved that the proposed control scheme can achieve distributed consensus tracking control of second-order nonlinear heterogeneous MASs. In addition, all signals in the closed-loop system are shown to be globally uniformly bounded. Finally, a practical example demonstrates the effectiveness of the proposed control method.
1. Introduction
In recent years, cooperative control of multi-agent systems (MASs) has attracted a lot of attention, such as for unmanned aerial vehicle formation [1], wireless sensor networks [2], and multi-robot manipulator collaboration [3]. Compared with a single agent, MASs can accomplish complex control tasks through division of labor and cooperation among agents. Researchers have developed many effective cooperative control schemes for MASs.
The consensus problem of MASs has been a hot research topic in the field of cooperative control, and many outstanding research results have been presented, such as the mean square consensus problem [4], the consensus optimization problem [5], the robust consensus problem [6], and the adaptive consensus problem [7]. Different from the general consensus control problem, consensus tracking control requires each agent to track a dynamic desired trajectory and, thus, has broader application prospects. In [8], a consensus tracking control scheme was developed for linear leader-follower networks by designing a class of distributed reference observers. In [9], an extra estimator was designed for each agent to solve the consensus tracking control for nonlinear high-order MASs with unknown parameters. In [10], an event-triggered consensus control scheme was proposed for switched stochastic nonlinear systems to reduce the communication traffic. The above research results assume that all agents have the same dynamical model. In some practical applications, different agents need to be equipped with different devices to accomplish complex control tasks—the corresponding systems are called heterogeneous MASs. In [11,12], the consensus problem and the mean-square consensus problem of heterogeneous MASs were studied, and the conditions for the system to achieve consensus were given. In [13], consensus protocols were proposed for second-order heterogeneous dynamic agents, and the sufficient conditions for all agents to reach consensus were given. However, in the above literature, it is assumed that the states of agents can be observed, which may not be satisfied in practical applications.
In the past decade, distributed control schemes for MASs using only system outputs have been widely studied. For example, in [14], a distributed cyclic small gain output feedback control scheme was developed for nonlinear MASs. In [15], a distributed observer was designed to solve the output regulation problem when the follower cannot directly obtain the external system state. In [16], the bipartite consensus problem for continuous-time MASs was studied, and a dynamic output feedback method was proposed to design bipartite consensus controllers. In [17], considering switched directed networks, a formation tracking control scheme using the output information of agents was designed. However, the dynamics of all agents considered in the above literature are the same. According to the above analysis, it is more practical to study the distributed output feedback consensus tracking control of heterogeneous MASs, which is the first motivation for this paper.
Quantitative control has been widely used in industrial fields, such as power systems and network control systems. For example, in order to save limited bandwidth resources in wireless communication networks, quantization techniques are needed to reduce the communication rate during information transmission. Information transmission between agents in MASs generally needs to be quantified due to network bandwidth limitations, and information quantization will affect the performance and stability of the system. Therefore, it is necessary to study the influence of signal quantization on the cooperative control of MASs. In order to avoid chattering, hysteresis quantizers have been intensively studied. In [18], the consensus tracking control of nonlinear MASs with quantized input was solved using a new quantizer decomposition method and command filtering neural control. In [19], based on a prescribed performance function, an adaptive fuzzy event-triggered control strategy was designed for MASs with input quantization. In [20], a consensus tracking control strategy was designed for MASs with more general nonlinearities, in which some online estimators were introduced to reduce the effect of input quantization. The existing approaches have studied the distributed input quantization consensus tracking control problem of MASs with the same dynamic model of agents. However, the research on distributed control of heterogeneous MASs with input quantization is still limited, which is the second motivation for this paper.
In this paper, a distributed consensus tracking control scheme is designed for second-order nonlinear heterogeneous MASs. The novelty of the proposed control scheme is highlighted as follows:
- Compared with the existing results for distributed consensus tracking control of MASs with input quantization, the MASs considered in this paper use a more general dynamic model.
- Different from the general K-filters in [21,22,23], an additional design parameter is introduced into the proposed K-filter, and this design parameter can improve the estimation performance of the filter.
- In this paper, the consensus tracking errors of MASs can converge to an arbitrarily small set by adjusting only one controller parameter. Compared with the results in [24], the proposed method has a wider range of parameter selections.
This paper is organized as follows. In Section 2, some basic knowledge and preliminary descriptions are given. In Section 3, a distributed output feedback consensus tracking control scheme is designed. In Section 4, the effectiveness of the developed scheme is verified. Finally, Section 5 concludes the paper.
2. Preliminaries and Problem Statement
In this section, some basic information is presented. Then, the distributed consensus tracking control problem for nonlinear MASs with input quantization is formulated.
2.1. Notations and Algebraic Graph Basics
For matrices X and Y, represents their Kronecker product. and represent the minimum eigenvalue and maximum eigenvalue of a matrix M, respectively. denotes the Euclidean norm of a vector or the induced 2-norm of a matrix.
Consider a MAS with N agents. If each agent is regarded as a vertex, the communication topology among agents can be described by a directed graph , where represents the set of vertices, and represents the set of edges. For each agent, the neighbor set is defined as : agent i can receive information from agent . A weight is assigned to each edge , if and otherwise. Then, the Laplacian matrix associated with is given as , where and . The digraph contains a directed spanning tree if at least one node has a directed path to all the other nodes, and this node is called the root node. In addition, the adjacency matrix is defined as , and if the desired trajectory can be obtained directly by agent i and otherwise.
2.2. Problem Formulation
Consider a second-order nonlinear heterogeneous MAS, the dynamics of each agent are as follows:
where , and are the system states, quantified control input, and output of the ith agent, respectively; is an unknown constant parameter vector; and with are smooth nonlinear functions; and are unknown time-varying disturbances.
Remark 1.
Note that system (1) can be used to describe many practical application systems, such as single-link robot manipulator systems [25] and ship formation [26]. In addition, the model parameters in system (1) can be unknown. Compared with the results in [27,28,29], the MAS considered in this paper is more general.
Assumption 1.
The communication topology among agents contains a directed spanning tree. In addition, the root node has direct access to the desired trajectory.
Assumption 2.
The desired trajectory is piecewise continuous and bounded.
Assumption 3.
The unknown disturbances are bounded, and there exists an unknown positive constant such that .
Remark 2.
Assumptions 1–3 are standard requirements in dealing with the distributed consensus tracking control problem of MASs. Assumption 2 is more relaxed than the existing ones in [30,31,32], in which the desired trajectory needs to be linearly parameterized.
This paper considers the hysteresis quantizer, which is modeled as
where , , and . The parameters and determine the quantization density of the hysteresis quantizer (2). represents the status prior to , and is in the set . The map of the hysteresis quantizer (2) is plotted in Figure 1.
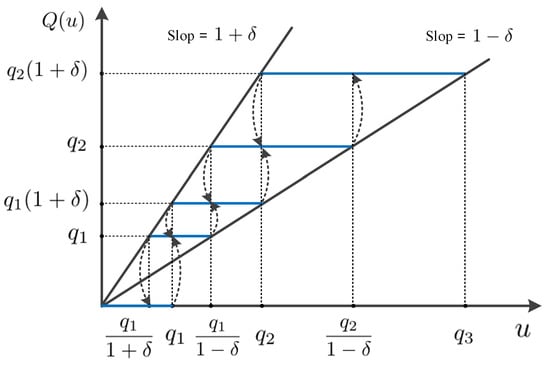
Figure 1.
Hysteretic quantizer.
Remark 3.
In contrast to the general quantizer, the hysteresis quantizer (2) can enhance the ability to reduce chattering. In addition, can be rewritten as , and
In view of Figure 1, one has
where .
The control objective is to design a distributed consensus tracking control scheme for the second-order nonlinear heterogeneous MAS (1) such that: (i) all signals of the considered MAS are globally uniformly bounded; (ii) the output of each agent can track the desired trajectory.
3. Distributed Adaptive Controller Design and Stability Analysis
In this section, a distributed output feedback control scheme is presented for second-order nonlinear heterogeneous MASs, and it is proved that the proposed distributed control scheme can ensure the stability of second-order nonlinear MASs.
3.1. State Estimation
For the ith agent, a K-filter is designed to estimate the unmeasured states
where , , and are the filter states; , , and ; and is a design parameter; and are chosen such that the polynomial is Hurwitz; and .
Then, the state estimation can be expressed as
From (1) and (4), the estimation error satisfies
Further, by applying the transformation
Then, the following error system can be obtained
where is Hurwitz.
Consider the following Lyapunov function
where the matrix is the solution of .
From Assumption 3 and , the derivative of is obtained as
Remark 4.
Different from the K-filters in [21,22,23], an additional design parameter is introduced into the proposed K-filter (3). This design parameter can improve the estimation performance of the filter in the face of unknown disturbances and quantization errors. After the error transformation, appears in the negative term of (9), which will be useful for the tracking performance analysis in the next section.
3.2. Backstepping Design Procedure
Now, the distributed backstepping controller is designed. From (1) and (6), the derivative of satisfies
For each agent, some positive scalars , , , , , , , and are introduced as design parameters and define:
where is a virtual control function. Next, consider the following design steps:
Step 1: From (11), the derivative of satisfies
where , , and .
Consider the following function
where and . Moreover, and are the estimations of and , respectively; and are positive definite matrices.
In view of (13) and (14), the derivative of satisfies
According to Assumption 3, the following inequalities can be obtained
Choose the first virtual control function
Define the following tuning functions
Substituting (16)–(20) into (15), and noting , it follows that
Step 2: Define . The derivative of satisfies
where , and , .
Consider the second Lyapunov function
where , and is the estimation of .
From Remark 2, the control input of each agent can be rewritten as
where and , are quantizer parameters.
According to Assumption 3 and (24), the following inequalities can be obtained
Choose the second virtual control function
Define the following tuning functions
In addition, the adaptive laws and are designed as
From (23)–(30), one has
The control law is designed as
where the adaptive law is updated by
By considering the inequality , it can be obtained that
Substituting (33) and (34) into (31) and noting , it follows that
Remark 5.
Note that the designed control scheme is fully distributed. To reduce the information interaction between agents, an adaptive law is introduced for each agent to estimate the uncertain parameter vector of its neighbors. In addition, an adaptive law is introduced in the controller to compensate for the influence of the hysteresis quantizer.
3.3. Stability Analysis
The main results are summarized as follows.
Theorem 1.
Consider the second-order nonlinear heterogeneous MAS (1), the hysteresis quantizer (2), the K-filter (3), the adaptive laws (30), (33), and the control law (32). All signals of the second-order nonlinear heterogeneous MAS are globally bounded, and the tracking error of each agent can converge to an arbitrary small set.
Proof.
Considering , , , and
Then, the inequality (35) can be rewritten as
where
It follows from (37) that
As a result
It follows that are bounded. From (3) and (11), together with the boundedness of , it is known that , and are bounded. Then, , , , and are bounded. Thus, all signals are globally bounded. In addition, it can be seen from (38) that the tracking errors can converge to an arbitrary small set by increasing . Since increases monotonically with increase in , by adjusting , the tracking errors can converge to an arbitrary small set. This completes the proof. □
Remark 6.
By adjusting the parameter , the tracking errors of MASs can converge to an arbitrary small set without further adjusting other parameters as required in [24]. Therefore, the proposed method can be more convenient for adjusting the consensus tracking control performance of MASs in practical applications. Although the consensus tracking performance of MASs can be improved by increasing , it can be seen from the distributed control law (32) that too large may cause the high gain problem of the controller. Therefore, in practical applications, the selection of should not be too large.
4. An Illustrative Example
Consider an MAS containing four agents, where the dynamics of each agent are as follows:
where is the course angular velocity; is the control input; , M and l are unknown constant parameters.
By defining , , , , = , and . Then, the system (40) can be rewritten as follows
In the simulation, the communication topology of the MAS is shown in Figure 2. The parameters of the MAS are selected as , , , and the desired trajectory is generated by . The time-varying disturbances are set as .
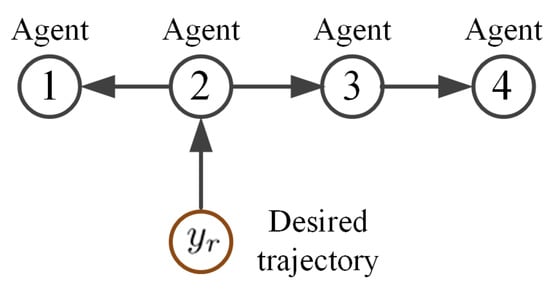
Figure 2.
Communication topology graph .
The initial state of each agent is set to , and all other initial conditions are zero. The parameters of the hysteresis quantizer (2) are chosen as and . The design parameters are chosen as , , , , , , , , , , , and .
Applying the proposed distributed control method, the output and tracking errors of each agent are shown in Figure 3. The quantized control inputs of the MAS are shown in Figure 4. It can be seen that the distributed consensus control of second-order nonlinear heterogeneous MASs with input quantization has been implemented. In addition, the proposed distributed control method is robust to unknown disturbances.
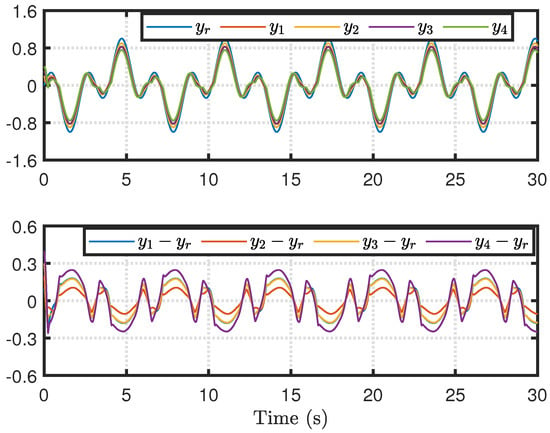
Figure 3.
Agent outputs and tracking errors.
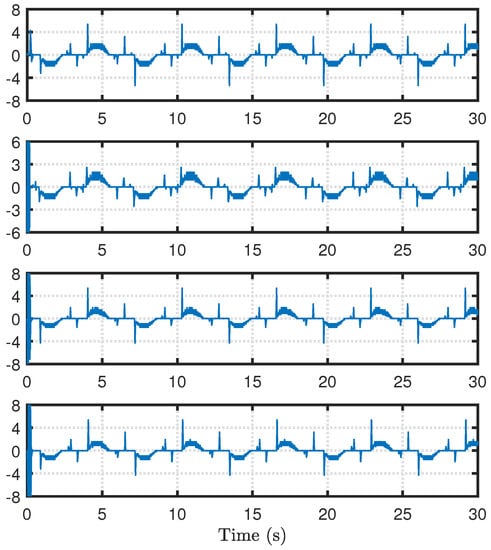
Figure 4.
Quantified control inputs.
Next, we demonstrate through simulation that the tracking error can be reduced by adjusting . In the simulation, is adjusted to 10, while other parameters remain unchanged. Then, the output and tracking errors of each agent are shown in Figure 5. By comparing Figure 3 and Figure 5, the conclusions in Remark 6 are verified. In addition, the quantized control inputs of the MAS are shown in Figure 6. As can be seen from Figure 6, increasing will not have a significant impact on the quantization control input, but may cause the gain of the controller to become larger at the initial moment.
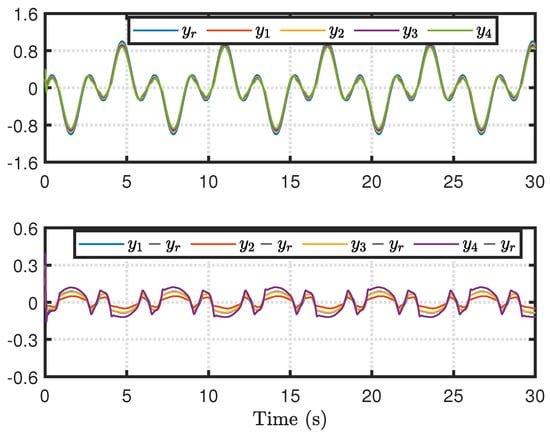
Figure 5.
Agent outputs and tracking errors.
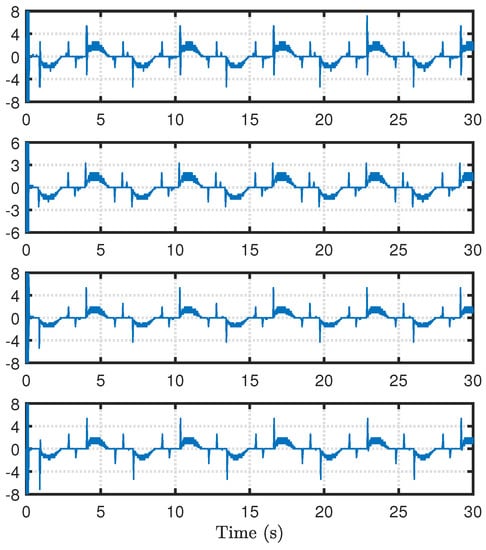
Figure 6.
Quantified control inputs ().
5. Conclusions
In this paper, the distributed consensus tracking control problem has been addressed for second-order nonlinear heterogeneous MASs with input quantization. A distributed output feedback control scheme based on a K-filter has been proposed. Different from the results in the existing literature, an additional design parameter is introduced into the proposed controller design. By adjusting this parameter, the tracking errors of MASs can converge to an arbitrarily small residual set. A practical example verifies the effectiveness of the proposed scheme.
Author Contributions
Conceptualization, L.X. and Y.L.; methodology, L.X.; software, L.X.; validation, L.X. and Y.L.; formal analysis, L.X.; investigation, L.X.; resources, L.X.; data curation, L.X.; writing—original draft preparation, L.X.; writing—review and editing, L.X.; visualization, L.X.; supervision, L.X.; project administration, L.X.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation of China (Grant No. 62103251) and the China Postdoctoral Science Foundation (Grant No. 2021M702075).
Data Availability Statement
The data presented in this study are available on request from the corresponding author after obtaining permission of an authorized person.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dong, X.; Zhou, Y.; Ren, Z.; Zhong, Y. Time-varying formation tracking for second-order multi-agent systems subjected to switching topologies with application to quadrotor formation flying. IEEE Trans. Ind. Electron. 2016, 64, 5014–5024. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, J.; Yu, X.; Hill, D.J. Multi-agent systems with dynamical topologies: Consensus and applications. IEEE Circ. Syst. Mag. 2013, 13, 21–34. [Google Scholar] [CrossRef]
- Yao, D.; Li, H.; Lu, R.; Shi, Y. Event-based distributed sliding mode formation control of multi-agent systems and its applications to robot manipulators. Inform. Sci. 2022, 614, 87–103. [Google Scholar] [CrossRef]
- Li, T.; Zhang, J.F. Mean square average-consensus under measurement noises and fixed topologies: Necessary and sufficient conditions. Automatica 2009, 45, 1929–1936. [Google Scholar] [CrossRef]
- Lin, P.; Ren, W.; Yang, C.; Gui, W. Distributed optimization with nonconvex velocity constraints, nonuniform position constraints. IEEE Trans. Autom. Control 2018, 64, 2575–2582. [Google Scholar] [CrossRef]
- Zhang, B.; Jia, Y.; Matsuno, F.; Endo, T. Task-space synchronization of networked mechanical systems with uncertain parameters and communication delays. IEEE Trans. Cybern. 2016, 47, 2288–2298. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, J.; Lin, C.; Yu, H. Distributed adaptive fixed-time consensus tracking for second-order multi-agent systems using modified terminal sliding mode. Appl. Math. Comput. 2017, 312, 23–35. [Google Scholar] [CrossRef]
- Wang, X.; Yang, G.H. Fault-tolerant consensus tracking control for linear multiagent systems under switching directed network. IEEE Trans. Cybern. 2019, 50, 1921–1930. [Google Scholar] [CrossRef]
- Wang, W.; Wen, C.; Huang, J. Distributed adaptive asymptotically consensus tracking control of nonlinear multi-agent systems with unknown parameters and uncertain disturbances. Automatica 2017, 77, 133–142. [Google Scholar] [CrossRef]
- Zou, W.; Shi, P.; Xiang, Z.; Shi, Y. Consensus tracking control of switched stochastic nonlinear multiagent systems via event-triggered strategy. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 1036–1045. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhu, Y.; Wang, L. Consensus of heterogeneous multi-agent systems. IET Control Theory Appl. 2011, 5, 1881–1888. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, L. Distributed consensus of heterogeneous multi-agent systems with fixed and switching topologies. Int. J. Control 2012, 85, 1967–1976. [Google Scholar] [CrossRef]
- Feng, Y.; Xu, S.; Lewis, F.L.; Zhang, B. Consensus of heterogeneous first-and second-order multi-agent systems with directed communication topologies. Int. J. Robust Nonlinear Control 2015, 25, 362–375. [Google Scholar] [CrossRef]
- Liu, T.; Jiang, Z.P. Distributed output-feedback control of nonlinear multi-agent systems. IEEE Trans. Autom. Control 2013, 58, 2912–2917. [Google Scholar] [CrossRef]
- Su, Y.; Huang, J. Cooperative output regulation of linear multi-agent systems. IEEE Trans. Autom. Control 2011, 57, 1062–1066. [Google Scholar]
- Zhang, H.; Chen, J. Bipartite consensus of multi-agent systems over signed graphs: State feedback and output feedback control approaches. Int. J. Robust Nonlinear Control 2017, 27, 3–14. [Google Scholar] [CrossRef]
- Wang, R. Adaptive output-feedback time-varying formation tracking control for multi-agent systems with switching directed networks. J. Frankl. Inst. 2020, 357, 551–568. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, Z.; Zhang, Y.; Chen, C.P. Command filtered neural control of multi-agent systems with input quantization and unknown control direction. Neurocomputing 2021, 430, 47–57. [Google Scholar] [CrossRef]
- Wang, W.; Ma, H.; Basin, M.V.; Liang, H. Adaptive event-triggered consensus control of multi-agent systems with prescribed performance and input quantization. Int. J. Adapt. Control 2021, 35, 1454–1477. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, Z.; Zhang, Y.; Chen, C.P. Distributed adaptive cooperative control for uncertain nonlinear multi-agent systems with hysteretic quantized input. J. Frankl. Inst. 2020, 357, 4645–4663. [Google Scholar] [CrossRef]
- Tang, X.; Tao, G. An adaptive nonlinear output feedback controller using dynamic bounding with an aircraft control application. Int. J. Adapt. Control 2009, 23, 609–639. [Google Scholar]
- Zhang, Z.; Chen, W. Adaptive output feedback control of nonlinear systems with actuator failures. Inf. Sci. 2009, 179, 4249–4260. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, S.; Guo, Y.; Chu, Y. Robust adaptive output-feedback control for a class of nonlinear systems with time-varying actuator faults. Int. J. Adapt. Control 2010, 24, 743–759. [Google Scholar] [CrossRef]
- Wang, C.; Wen, C.; Guo, L. Adaptive consensus control for nonlinear multiagent systems with unknown control directions and time-varying actuator faults. IEEE Trans. Autom. Control 2020, 66, 4222–4229. [Google Scholar] [CrossRef]
- Yang, T.; Dong, J. Predefined-time adaptive fault-tolerant control for switched odd-rational-power multi-agent systems. IEEE Trans. Autom. Sci. Eng. 2022. [Google Scholar] [CrossRef]
- Xu, L.X.; Ma, H.J. Distributed output-feedback cooperative tracking control of non-linear multi-agent systems with unknown actuator failures. IET Control Theory Appl. 2019, 13, 2465–2475. [Google Scholar] [CrossRef]
- Du, H.; He, Y.; Cheng, Y. Finite-time synchronization of a class of second-order nonlinear multi-agent systems using output feedback control. IEEE Trans. Circuits Syst. I Reg. Pap. 2014, 61, 1778–1788. [Google Scholar]
- Su, Y. Cooperative global output regulation of second-order nonlinear multi-agent systems with unknown control direction. IEEE Trans. Autom. Control 2015, 60, 3275–3280. [Google Scholar] [CrossRef]
- Song, Q.; Cao, J.; Yu, W. Second-order leader-following consensus of nonlinear multi-agent systems via pinning control. Syst. Control Lett. 2010, 59, 553–562. [Google Scholar] [CrossRef]
- Deng, C.; Wen, C.; Wang, W.; Li, X.; Yue, D. Distributed adaptive tracking control for high-order nonlinear multi-agent systems over event-triggered communication. IEEE Trans. Autom. Control 2023, 66, 4222–4229. [Google Scholar]
- Hu, J.; Zheng, W.X. Adaptive tracking control of leader–follower systems with unknown dynamics and partial measurements. Automatica 2014, 50, 1416–1423. [Google Scholar] [CrossRef]
- Wang, W.; Huang, J.; Wen, C.; Fan, H. Distributed adaptive control for consensus tracking with application to formation control of nonholonomic mobile robots. Automatica 2014, 50, 1254–1263. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).