Industrial Process Monitoring Based on Parallel Global-Local Preserving Projection with Mutual Information
Abstract
:1. Introduction
- Block modeling. Each block is modeled by related methods, i.e., PLS, PCA, ICA, etc.
- Statistics fusion. For an online dataset, several groups of statistics are generated by a well-trained monitoring model. In order to obtain consistent monitoring results, a flexible fusion strategy is required to generate the final statistic pair. According to the literature review, Bayesian inference and voting methods are the common strategies for plant-wide process monitoring.
- MI-PGLPP utilizes mutual information of the variables and divides data blocks automatically, which does not require prior knowledge of the process.
- MI-PGLPP naturally meets the independent condition of Bayesian inference since variables in each block are divided by the independence of mutual information.
- MI-DGLPP utilizes GLPP to obtain the latent matrix and transformation matrix of each data block. The intrinsic features of global and local structures are well preserved during the projection.
2. Preliminaries
2.1. Global-Local Preserving Projection
2.2. Mutual Information
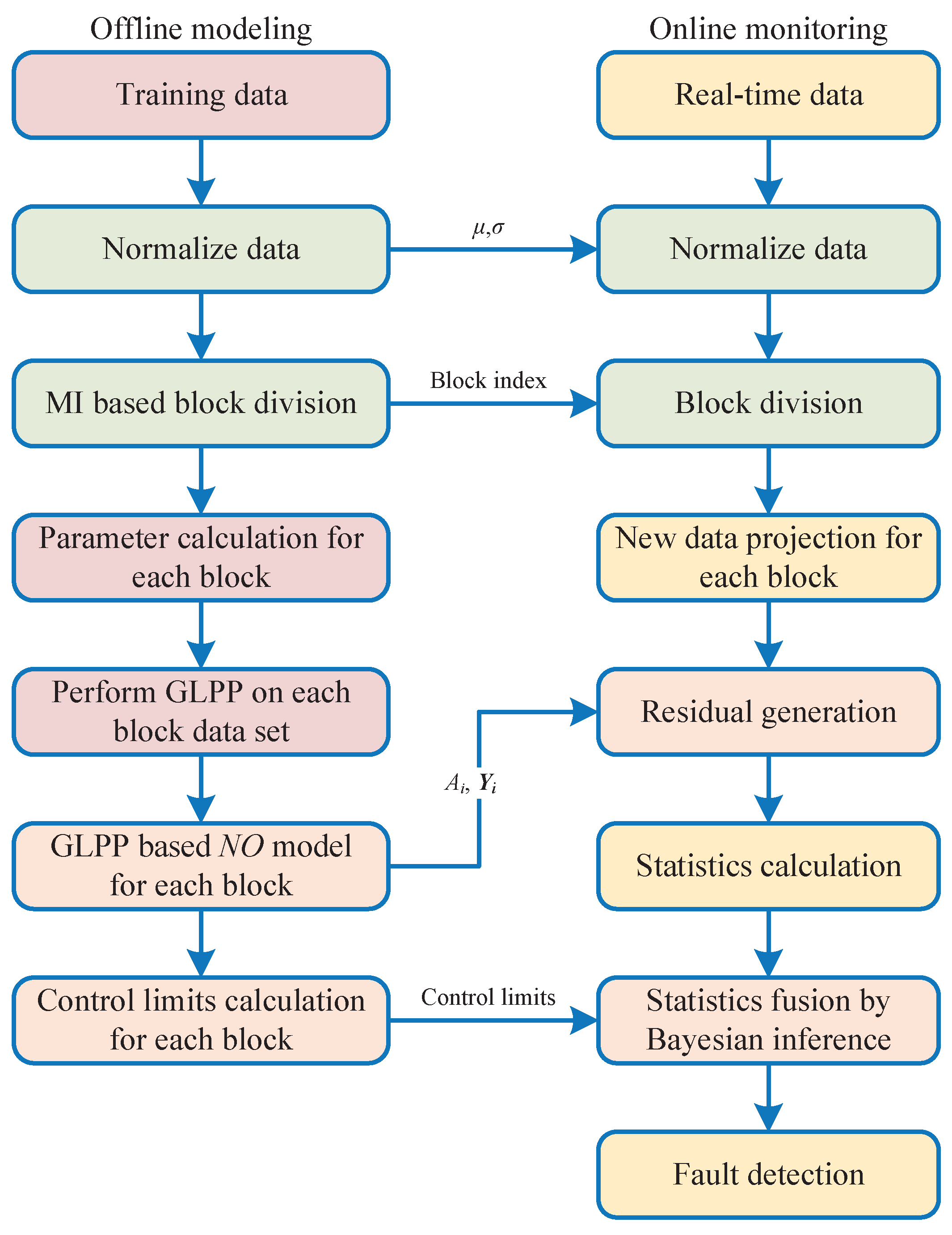
3. Fault Diagnosis Based on MI-PGLPP
- Step 1: Block selection. The original dataset is divided into several subblocks.
- Step 2: Offline model training. The block model is obtained by the subblocks of the dataset.
- Step 3: Online monitoring. The statistics of each subblock is generated by the online data and the final statistics pair is calculated by fusion strategies.
3.1. Mutual Information-Based Variable Block Division
3.2. GLPP-Based Block Data Modeling
3.3. Bayesian Inference-Based Monitoring Result Fusion
3.4. Monitoring Procedure
- Normalize each data block by Z-score standardization and generate data mean and variance.
- Analyze the variable dependence of training dataset by Equation (10), and then generate the data blocks and block index.
- Construct adjacent weighting matrix and nonadjacent weighting matrix by Equation (4).
- Calculate the tradeoff parameter by Equation (17) for each data block.
- Perform GLPP on each data block by Equation (7) and generate transformation matrices , latent matrices and model.
- Define significance level and calculate control limits for each data block by Equation (16).
- Acquire the new sample data and perform normalization with the mean and variance of training samples.
- Divide new data into N blocks with the variable index generated by the training data.
- Project each block data point on the model and generate residual of each block by Equation (18).
- Calculate the statistics of each block by Equation (19).
- Perform statistics fusion with Bayesian inference by Equation (24).
- Monitor the process by Equation (25).
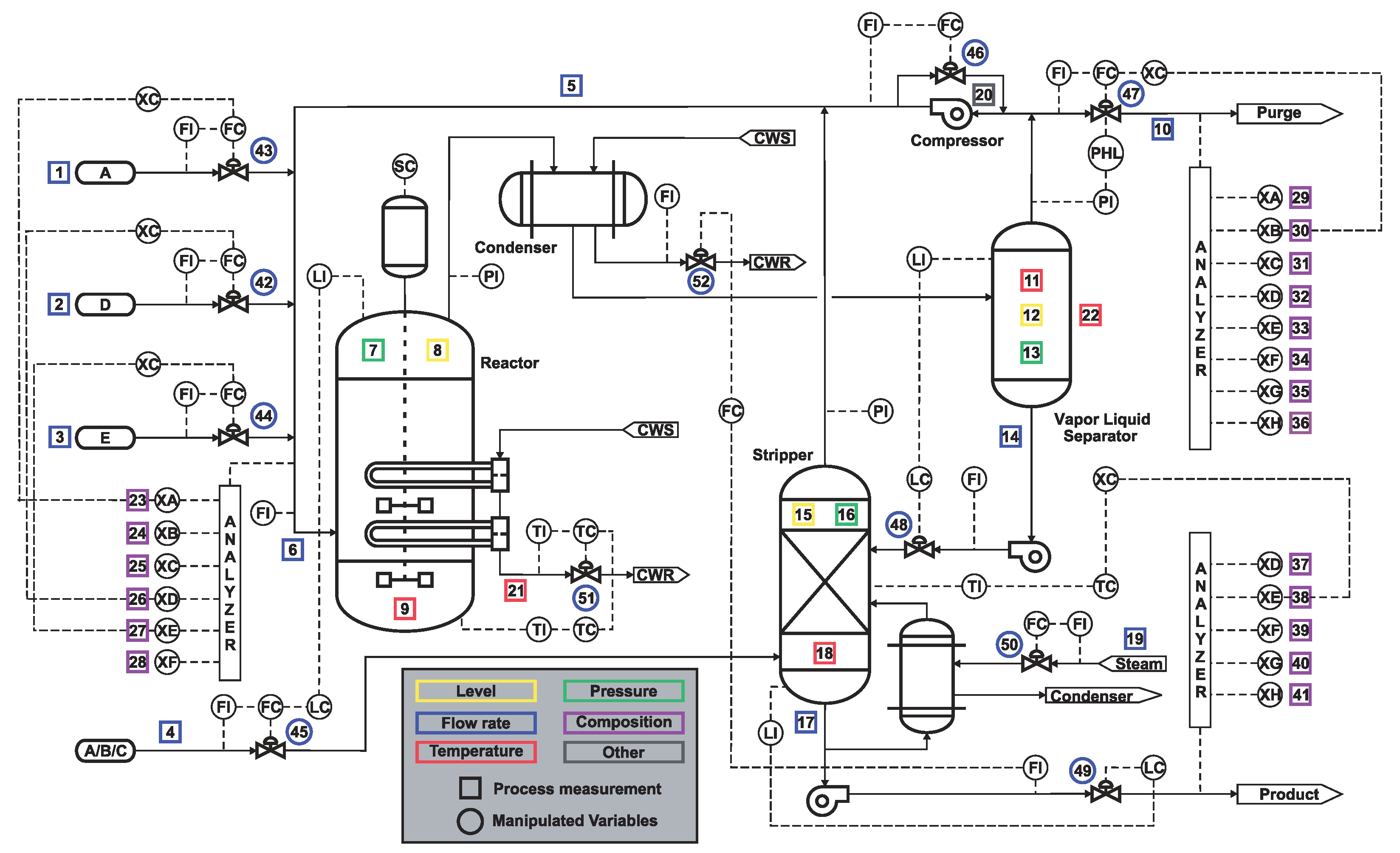
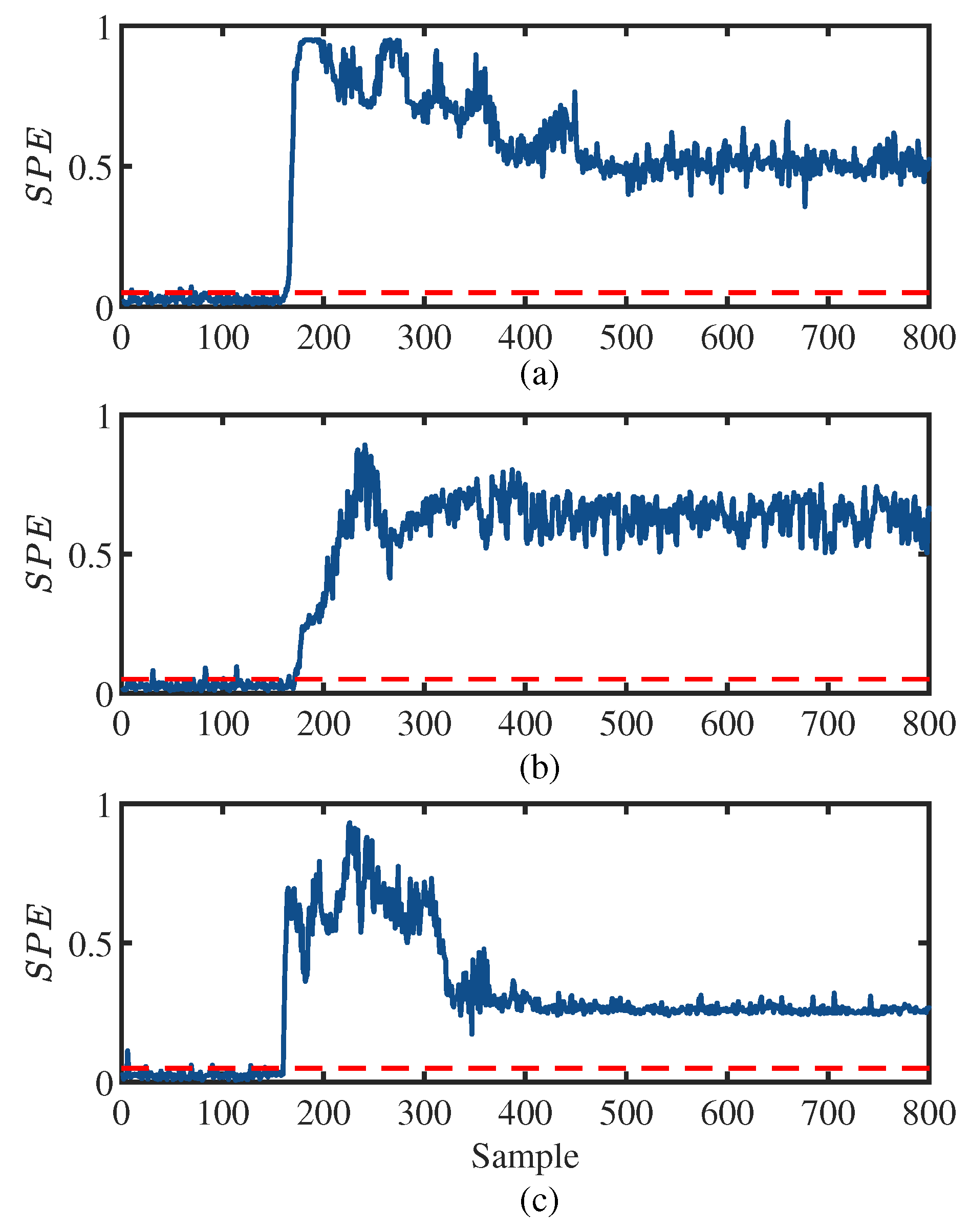
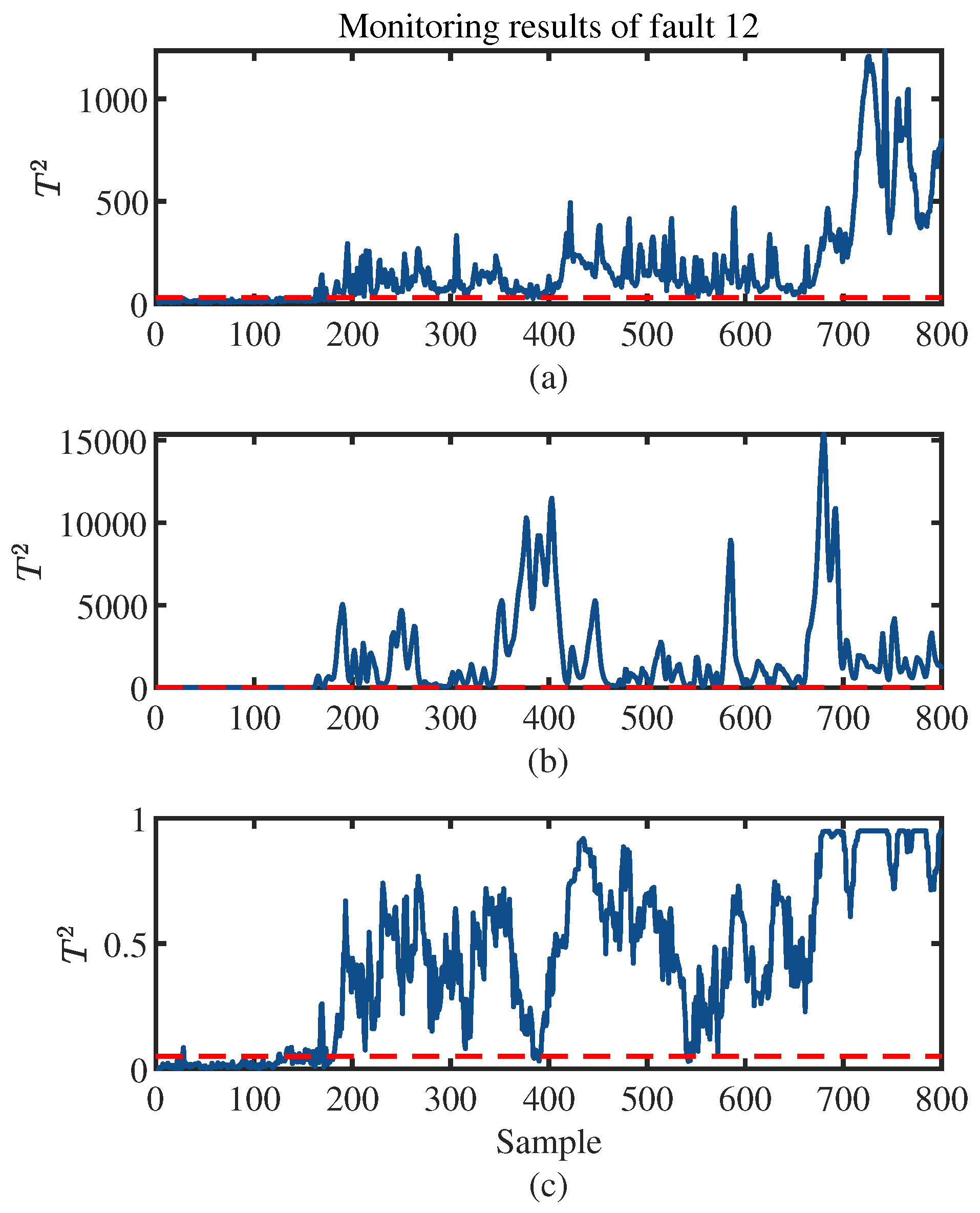
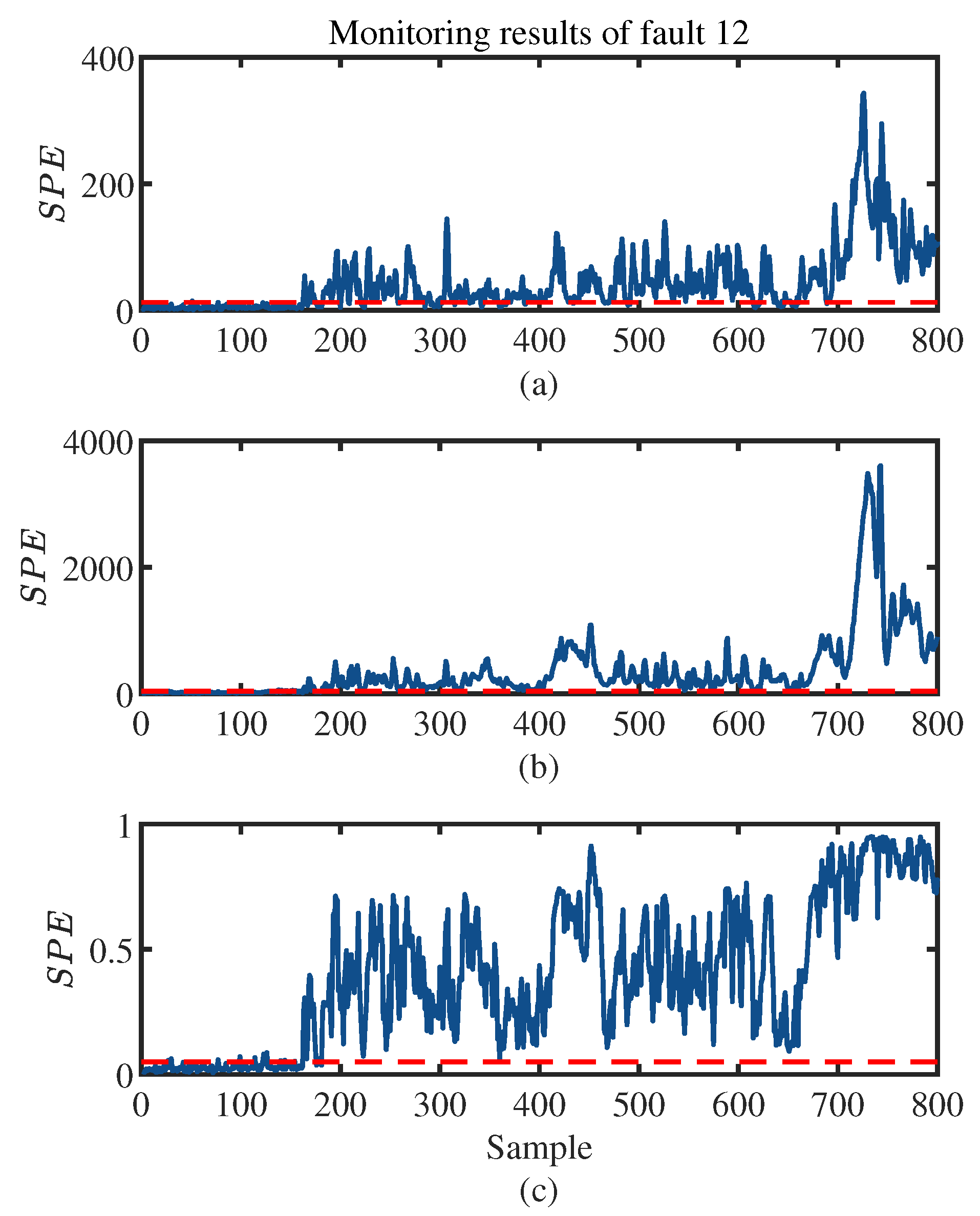
4. Experiments and Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, W.; Zhao, C.; Huang, B.; Wu, M. A Robust Dissimilarity Distribution Analytics with Laplace Distribution for Incipient Fault Detection. IEEE Trans. Ind. Electron. 2023; early access. [Google Scholar] [CrossRef]
- Cai, L.; Yin, H.; Lin, J.; Zhou, H.; Zhao, D. A Relevant Variable Selection and SVDD-Based Fault Detection Method for Process Monitoring. IEEE Trans. Autom. Sci. Eng. 2022; early access. [Google Scholar] [CrossRef]
- Tang, Q.; Chai, Y.; Qu, J.; Fang, X. Industrial process monitoring based on Fisher discriminant global-local preserving projection. J. Process Control 2019, 81, 76–86. [Google Scholar] [CrossRef]
- Luo, L. Process monitoring with global-local preserving projections. Ind. Eng. Chem. Res. 2014, 53, 7696–7705. [Google Scholar] [CrossRef]
- Choi, S.W.; Lee, I.B. Multiblock PLS-based localized process diagnosis. J. Process Control 2005, 15, 295–306. [Google Scholar] [CrossRef]
- Zhou, B.; Ye, H.; Zhang, H.; Li, M. Process monitoring of iron-making process in a blast furnace with PCA-based methods. Control Eng. Pract. 2016, 47, 1–14. [Google Scholar] [CrossRef]
- Chen, Z.; Ding, S.X.; Zhang, K.; Li, Z.; Hu, Z. Canonical correlation analysis-based fault detection methods with application to alumina evaporation process. Control Eng. Pract. 2016, 46, 51–58. [Google Scholar] [CrossRef]
- He, X.B.; Wang, W.; Yang, Y.P.; Yang, Y.H. Variable-weighted Fisher discriminant analysis for process fault diagnosis. J. Process Control 2009, 19, 923–931. [Google Scholar] [CrossRef]
- Lee, J.M.; Yoo, C.; Lee, I.B. Statistical process monitoring with independent component analysis. J. Process Control 2004, 14, 467–485. [Google Scholar] [CrossRef]
- Ge, Z.; Zhang, M.; Song, Z. Nonlinear process monitoring based on linear subspace and Bayesian inference. J. Process Control 2010, 20, 676–688. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Haghani, A.; Hao, H.; Zhang, P. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. J. Process Control 2012, 22, 1567–1581. [Google Scholar] [CrossRef]
- Huang, J.; Yan, X. Related and independent variable fault detection based on KPCA and SVDD. J. Process Control 2016, 39, 88–99. [Google Scholar] [CrossRef]
- Zhang, M.; Ge, Z.; Song, Z.; Fu, R. Global–Local Structure Analysis Model and Its Application for Fault Detection and Identification. Ind. Eng. Chem. Res. 2011, 50, 6837–6848. [Google Scholar] [CrossRef]
- Luo, L.; Bao, S.; Mao, J.; Tang, D. Nonlinear process monitoring based on kernel global-local preserving projections. J. Process Control 2016, 38, 11–21. [Google Scholar] [CrossRef]
- Huang, C.; Chai, Y.; Liu, B.; Tang, Q.; Qi, F. Industrial process fault detection based on KGLPP model with Cam weighted distance. J. Process Control 2021, 106, 110–121. [Google Scholar] [CrossRef]
- Tang, Q.; Liu, Y.; Chai, Y.; Huang, C.; Liu, B. Dynamic process monitoring based on canonical global and local preserving projection analysis. J. Process Control 2021, 106, 221–232. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X. Plant-wide process monitoring based on mutual information-multiblock principal component analysis. ISA Trans. 2014, 53, 1516–1527. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Yuan, X.; Wang, Y.; Gui, W. Hierarchical hybrid distributed PCA for plant-wide monitoring of chemical processes. Control Eng. Pract. 2021, vol. 111, 104784. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z. Distributed PCA Model for Plant-Wide Process Monitoring. Ind. Eng. Chem. Res. 2013, 52, 1947–1957. [Google Scholar] [CrossRef]
- Ge, Z.; Chen, J. Plant-Wide Industrial Process Monitoring: A Distributed Modeling Framework. IEEE Trans. Ind. Inform. 2016, 12, 310–321. [Google Scholar] [CrossRef]
- Zhu, J.; Ge, Z.; Song, Z. Distributed Parallel PCA for Modeling and Monitoring of Large-Scale Plant-Wide Processes With Big Data. IEEE Trans. Ind. Inform. 2017, 13, 1877–1885. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, B.; Yan, X. Multiblock independent component analysis integrated with hellinger distance and bayesian inference for non-gaussian plant-wide process monitoring. Ind. Eng. Chem. Res. 2015, 54, 2497–2508. [Google Scholar] [CrossRef]
- Huang, J.; Yan, X. Dynamic process fault detection and diagnosis based on dynamic principal component analysis, dynamic independent component analysis and Bayesian inference. Chemom. Intell. Lab. Syst. 2015, 148, 115–127. [Google Scholar] [CrossRef]
- Jiang, Q.; Huang, B.; Yan, X. GMM and optimal principal components-based Bayesian method for multimode fault diagnosis. Comput. Chem. Eng. 2016, 84, 338–349. [Google Scholar] [CrossRef]
- Zou, X.; Zhao, C.; Gao, F. Linearity Decomposition-Based Cointegration Analysis for Nonlinear and Nonstationary Process Performance Assessment. Ind. Eng. Chem. Res. 2020, 59, 3052–3063. [Google Scholar] [CrossRef]
- Yu, H.; Khan, F.; Garaniya, V. Modified Independent Component Analysis and Bayesian Network-Based Two-Stage Fault Diagnosis of Process Operations. Ind. Eng. Chem. Res. 2015, 54, 2724–2742. [Google Scholar] [CrossRef]
- Gharahbagheri, H.; Imtiaz, S.A.; Khan, F. Root Cause Diagnosis of Process Fault Using KPCA and Bayesian Network. Ind. Eng. Chem. Res. 2017, 56, 2054–2070. [Google Scholar] [CrossRef]
- Tang, Q.; Li, B.; Chai, Y.; Qu, J.; Ren, H. Improved sparse representation based on local preserving projection for the fault diagnosis of multivariable system. Sci. China Inf. Sci. 2021, 64, 254–256. [Google Scholar] [CrossRef]
- Zeng, J.; Huang, W.; Wang, Z.; Liang, J. Mutual information-based sparse multiblock dissimilarity method for incipient fault detection and diagnosis in plant-wide process. J. Process Control 2019, 83, 63–76. [Google Scholar] [CrossRef]
- Jia, Q.; Li, S. Process Monitoring Based on the Multiblock Rolling Pin Vine Copula. Ind. Eng. Chem. Res. 2020, 59, 18050–18060. [Google Scholar] [CrossRef]
- Huang, J.; Yan, X. Quality Relevant and Independent Two Block Monitoring Based on Mutual Information and KPCA. IEEE Trans. Ind. Electron. 2017, 64, 6518–6527. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Kano, M. Quality Prediction in Complex Batch Processes with Just-in-Time Learning Model Based on Non-Gaussian Dissimilarity Measure. Ind. Eng. Chem. Res. 2015, 54, 7694–7705. [Google Scholar] [CrossRef]
- Qin, Y.; Arunan, A.; Yuen, C. Digital twin for real-time Li-ion battery state of health estimation with partially discharged cycling data. IEEE Trans. Ind. Inform. 2023; early access. [Google Scholar] [CrossRef]
- Qin, Y.; Adams, S.; Yuen, C. Transfer learning-based state of charge estimation for Lithium-ion battery at varying ambient temperatures. IEEE Trans. Ind. Inform. 2021, 17, 7304–7315. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z. Bayesian inference and joint probability analysis for batch process monitoring. AIChE J. 2013, 59, 3702–3713. [Google Scholar] [CrossRef]
- Tong, C.; Palazoglu, A.; Yan, X. Improved ICA for process monitoring based on ensemble learning and Bayesian inference. Chemom. Intell. Lab. Syst. 2014, 135, 141–149. [Google Scholar] [CrossRef]
- Downs, J.; Vogel, E. A plant-wide industrial process control problem. Comput. Chem. Eng. 1993, 17, 245–255. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X. Nonlinear plant-wide process monitoring using MI-spectral clustering and Bayesian inference-based multiblock KPCA. J. Process Control 2015, 32, 38–50. [Google Scholar] [CrossRef]
- Zhan, C.; Li, S.; Yang, Y. Enhanced Fault Detection Based on Ensemble Global–Local Preserving Projections with Quantitative Global–Local Structure Analysis. Ind. Eng. Chem. Res. 2017, 56, 10743–10755. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, J.; Yao, Y. Online Monitoring of Multivariate Processes Using Higher-Order Cumulants Analysis. Ind. Eng. Chem. Res. 2014, 53, 4328–4338. [Google Scholar] [CrossRef]
- Zhao, C.; Gao, F. A sparse dissimilarity analysis algorithm for incipient fault isolation with no priori fault information. Control Eng. Pract. 2017, 65, 70–82. [Google Scholar] [CrossRef]





| Block Number | Variables | Block Number | Variables |
|---|---|---|---|
| 1 | , , , , , ,
, , , , , , , , | 5 | , |
| 2 | , , , , | 6 | , |
| 3 | , , , | 7 | , |
| 4 | , , |
| Fault No. | PCA | GLPP | MI-MBPCA | GDISSIM | MI-PGLPP |
|---|---|---|---|---|---|
| 1 | 97.88 | 99.25 | 65 | 99.15 | 99.75 |
| 2 | 96.5 | 98.25 | 29.74 | 98.43 | 98.75 |
| 3 | 2.63 | 7.64 | 4.28 | 5.75 | 11.88 |
| 4 | 20.88 | 81.75 | 39.33 | 20.94 | 7.88 |
| 5 | 24.13 | 43.23 | 44.83 | 24.15 | 31 |
| 6 | 99.13 | 100 | 93.45 | 99.19 | 100 |
| 7 | 99.75 | 99.37 | 58.45 | 100 | 100 |
| 8 | 96.88 | 96.63 | 92.83 | 96.97 | 98.25 |
| 9 | 1.75 | 7.5 | 7.95 | 3.25 | 11 |
| 10 | 29.63 | 44.88 | 82.75 | 29.64 | 53.13 |
| 11 | 74.88 | 67.25 | 94.13 | 40.67 | 52.88 |
| 12 | 96.38 | 98.63 | 98.83 | 98.45 | 99.50 |
| 13 | 93.63 | 94.5 | 90 | 93.62 | 95.13 |
| 14 | 99.25 | 99.62 | 57.75 | 99.38 | 100 |
| 15 | 3 | 12.25 | 13.75 | 10.64 | 14.38 |
| 16 | 27.38 | 27 | 96.32 | 13.58 | 40 |
| 17 | 76.25 | 90.5 | 93.35 | 76.37 | 95.38 |
| 18 | 90.13 | 88.75 | 86.33 | 89.35 | 91 |
| 19 | 12.5 | 25.5 | 37.6 | 11 | 42 |
| 20 | 49.75 | 50.5 | 84.45 | 31.83 | 55.75 |
| 21 | 47.25 | 51.63 | 42.32 | 39.35 | 50.75 |
| Average | 59.03 | 61.22 | 62.30 | 56.27 | 64.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, T.; Yin, H.; Yang, Z.; Yao, J.; Qin, Y.; Wu, P. Industrial Process Monitoring Based on Parallel Global-Local Preserving Projection with Mutual Information. Machines 2023, 11, 602. https://doi.org/10.3390/machines11060602
Wu T, Yin H, Yang Z, Yao J, Qin Y, Wu P. Industrial Process Monitoring Based on Parallel Global-Local Preserving Projection with Mutual Information. Machines. 2023; 11(6):602. https://doi.org/10.3390/machines11060602
Chicago/Turabian StyleWu, Tianshu, Hongpeng Yin, Zhimin Yang, Jie Yao, Yan Qin, and Peng Wu. 2023. "Industrial Process Monitoring Based on Parallel Global-Local Preserving Projection with Mutual Information" Machines 11, no. 6: 602. https://doi.org/10.3390/machines11060602
APA StyleWu, T., Yin, H., Yang, Z., Yao, J., Qin, Y., & Wu, P. (2023). Industrial Process Monitoring Based on Parallel Global-Local Preserving Projection with Mutual Information. Machines, 11(6), 602. https://doi.org/10.3390/machines11060602









