Deep PCA-Based Incipient Fault Diagnosis and Diagnosability Analysis of High-Speed Railway Traction System via FNR Enhancement
Abstract
1. Introduction
- (1)
- An intelligent decomposition levels selection scheme is proposed by quantifying the similarity of detail components, and the selection of noise threshold is determined and optimized to further improve the accuracy of noise reduction.
- (2)
- A continuous wavelet transform-based fault information enhancement approach is proposed from the perspective of fault energy.
- (3)
- A Deep-PCA based diagnosability analysis is provided, including detectability and isolatability analyses using geometric descriptions.
2. FNR Enhancement of Fault Data
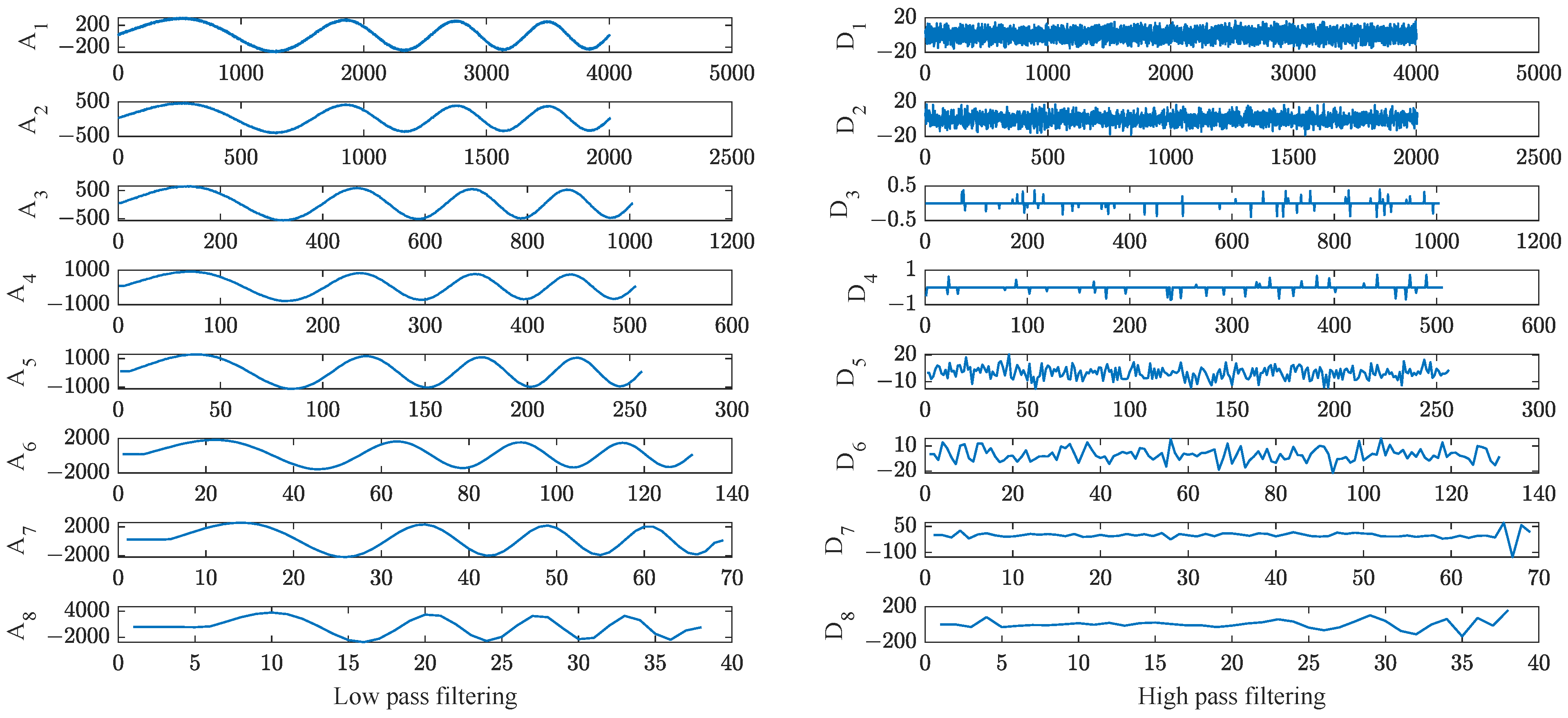
2.1. Noise Reduction Method Based on Discrete Wavelet Transform
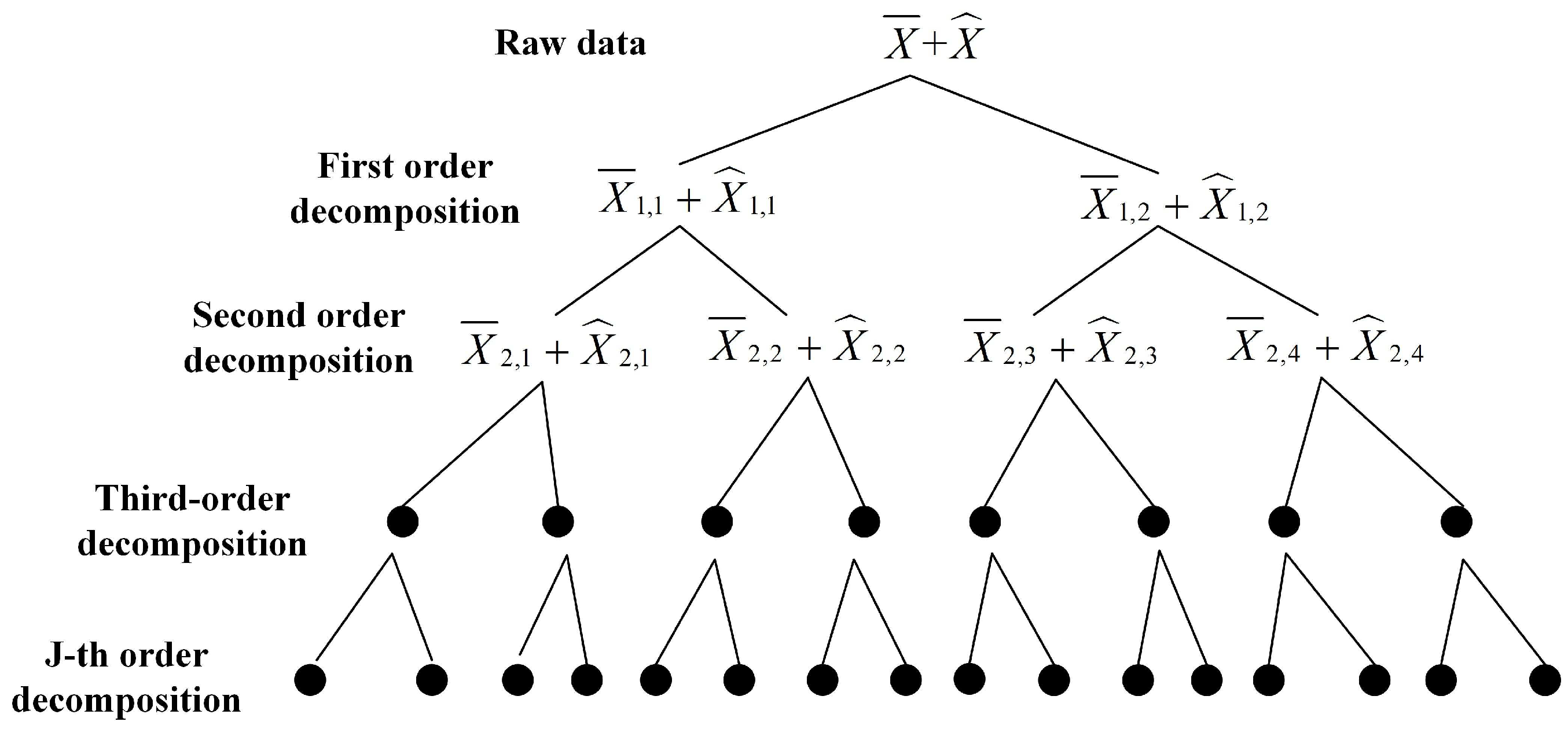
2.1.1. An Intelligent Decomposition Levels Selection Scheme
- (1)
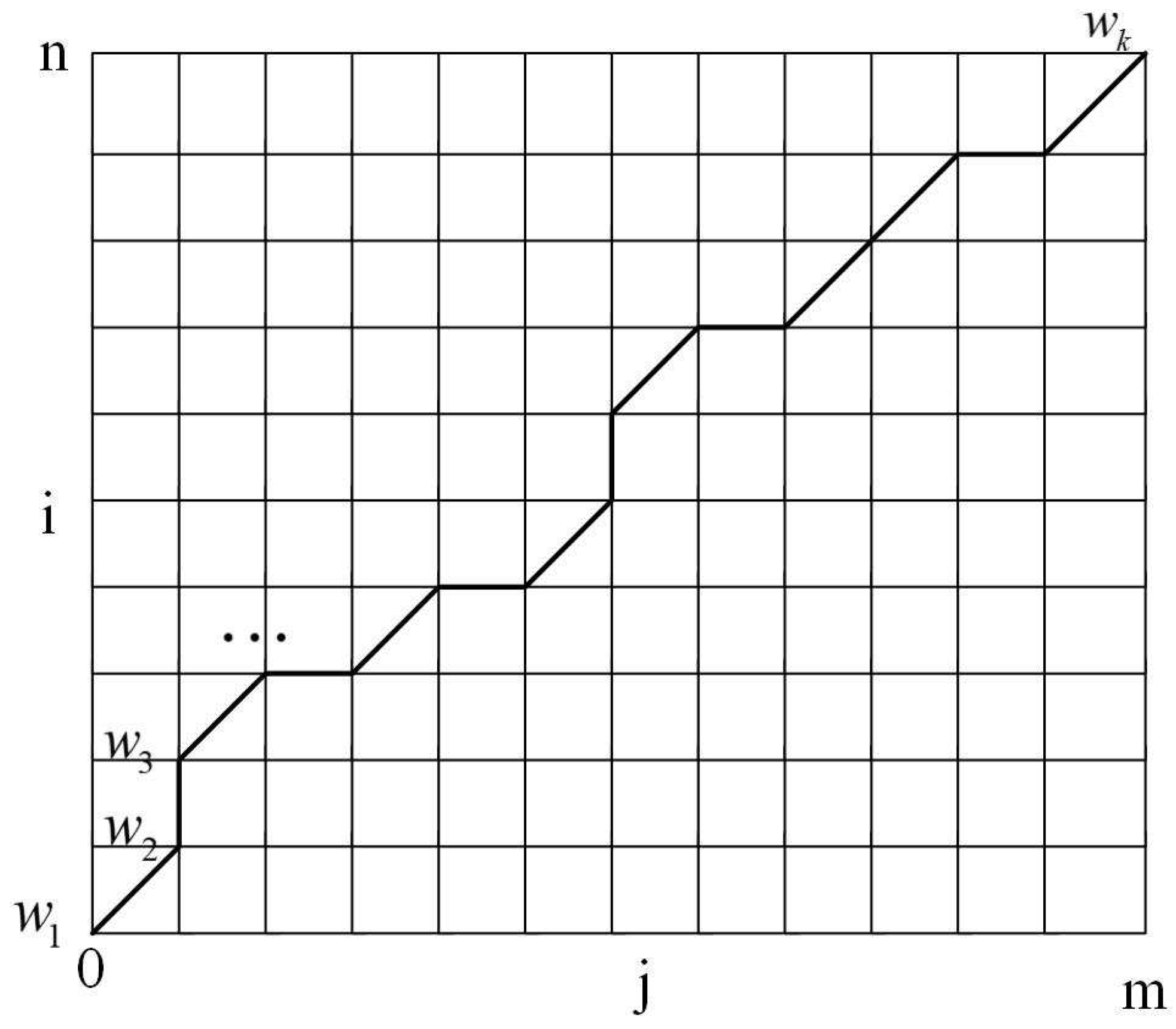
- Boundary conditions: and , indicating that the warping path should start at one corner and end at the other corner in a diagonal direction;
- (2)
- Continuity condition: each actual warping path should be continuous, that is, if and , then and .
- (3)
- Monotonicity condition: neither warping path of two time series should intersects the other, that is, if and , then and .
2.1.2. Noise Threshold Selection
- (1)
- .
- (2)
- and .
- (3)
- and .
2.2. Fault Information Enhancement Technology Based on Continuous Wavelet Transform
3. Deep-PCA Based Diagnosability Analysis
3.1. Detectability Analysis
- (1)
- Fault detectability analysis based on statistic
- (2)
- Fault detectability analysis based on statistic
3.2. Isolatability Analysis
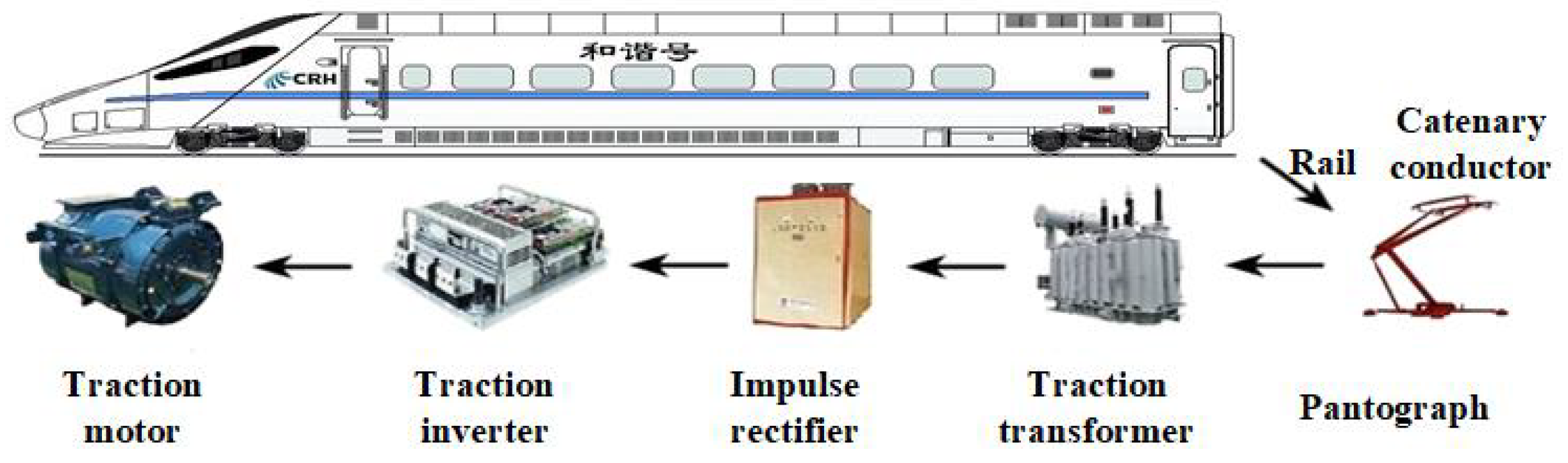
4. Experimental Verification
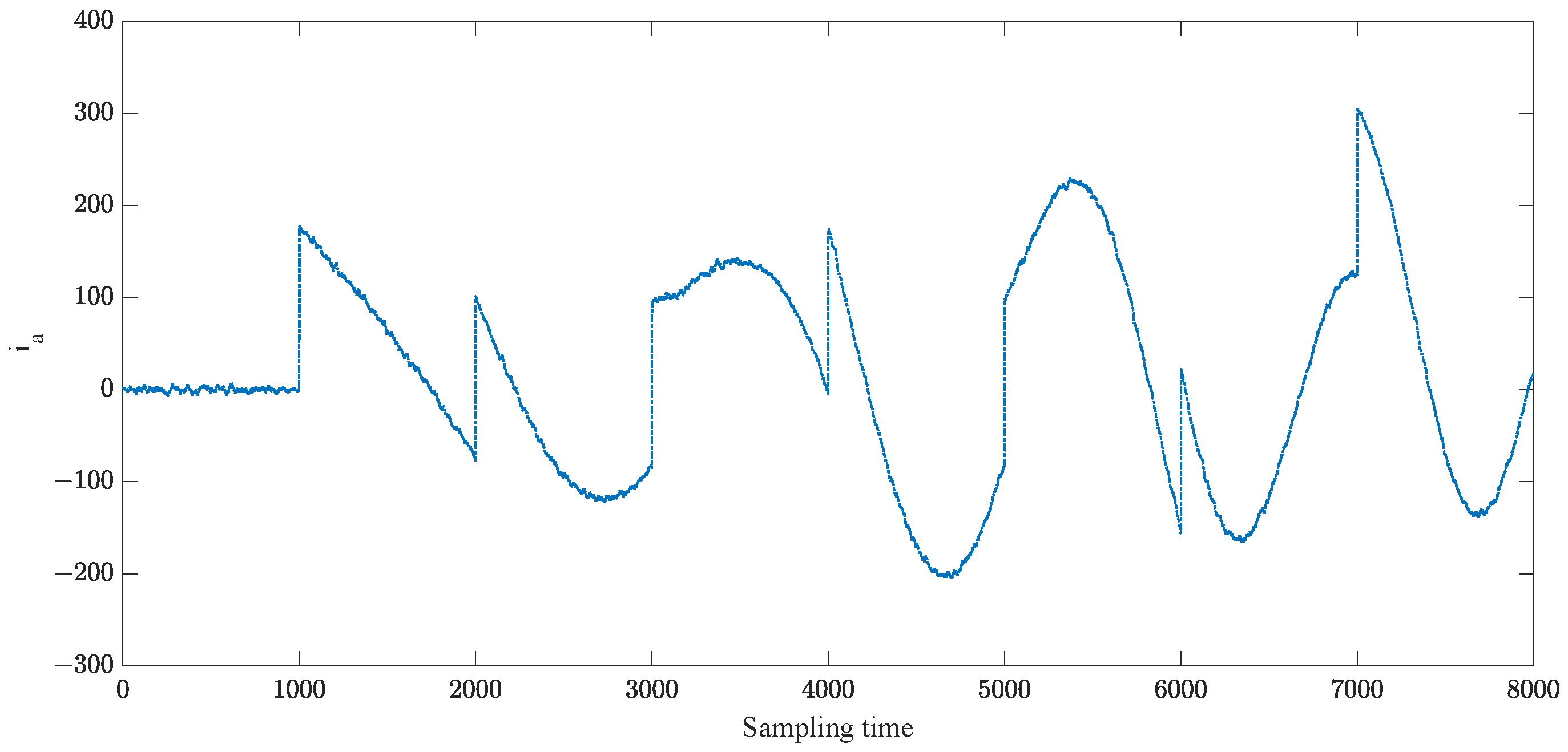
4.1. Experimental Results for FNR Enhancement-Based Data Preprocessing
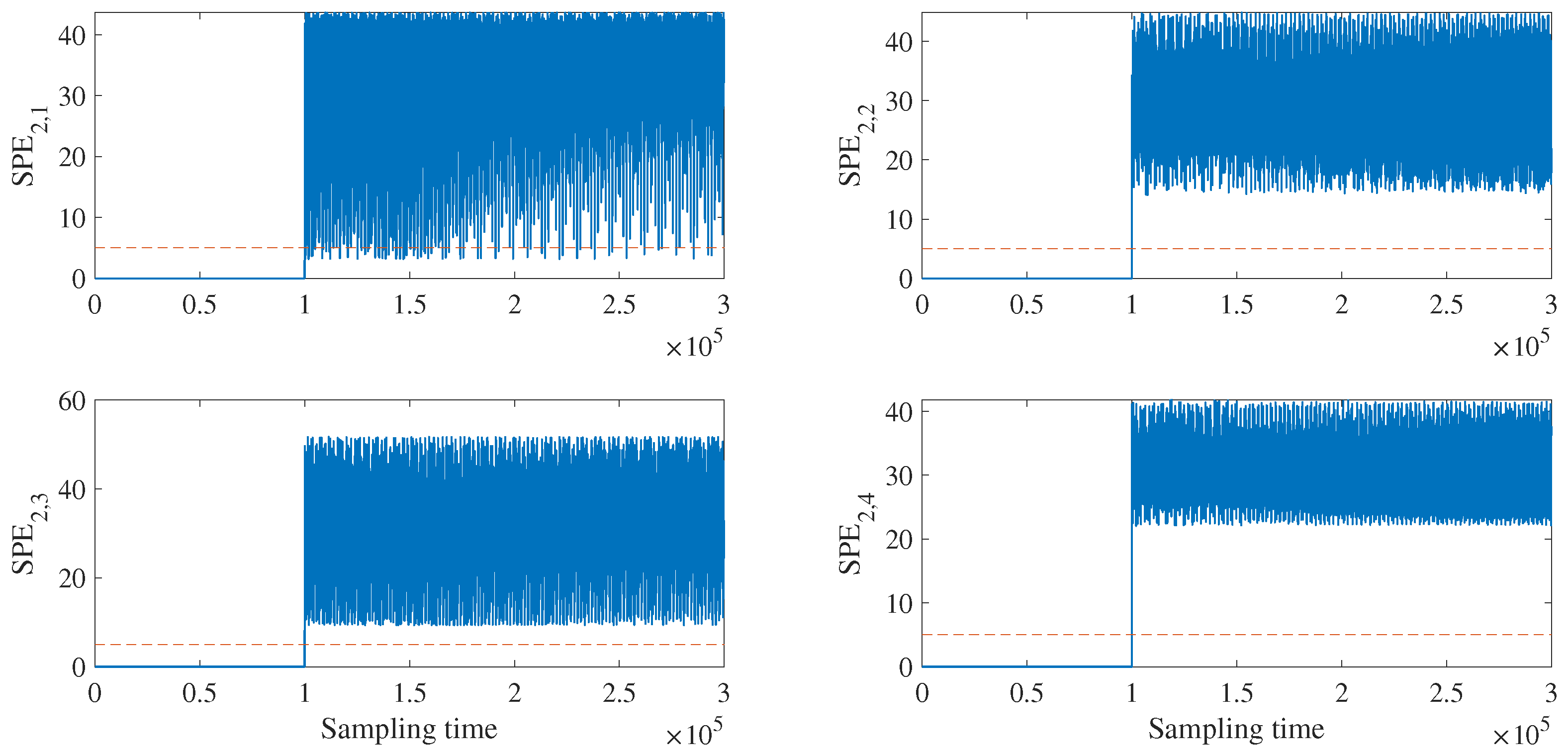
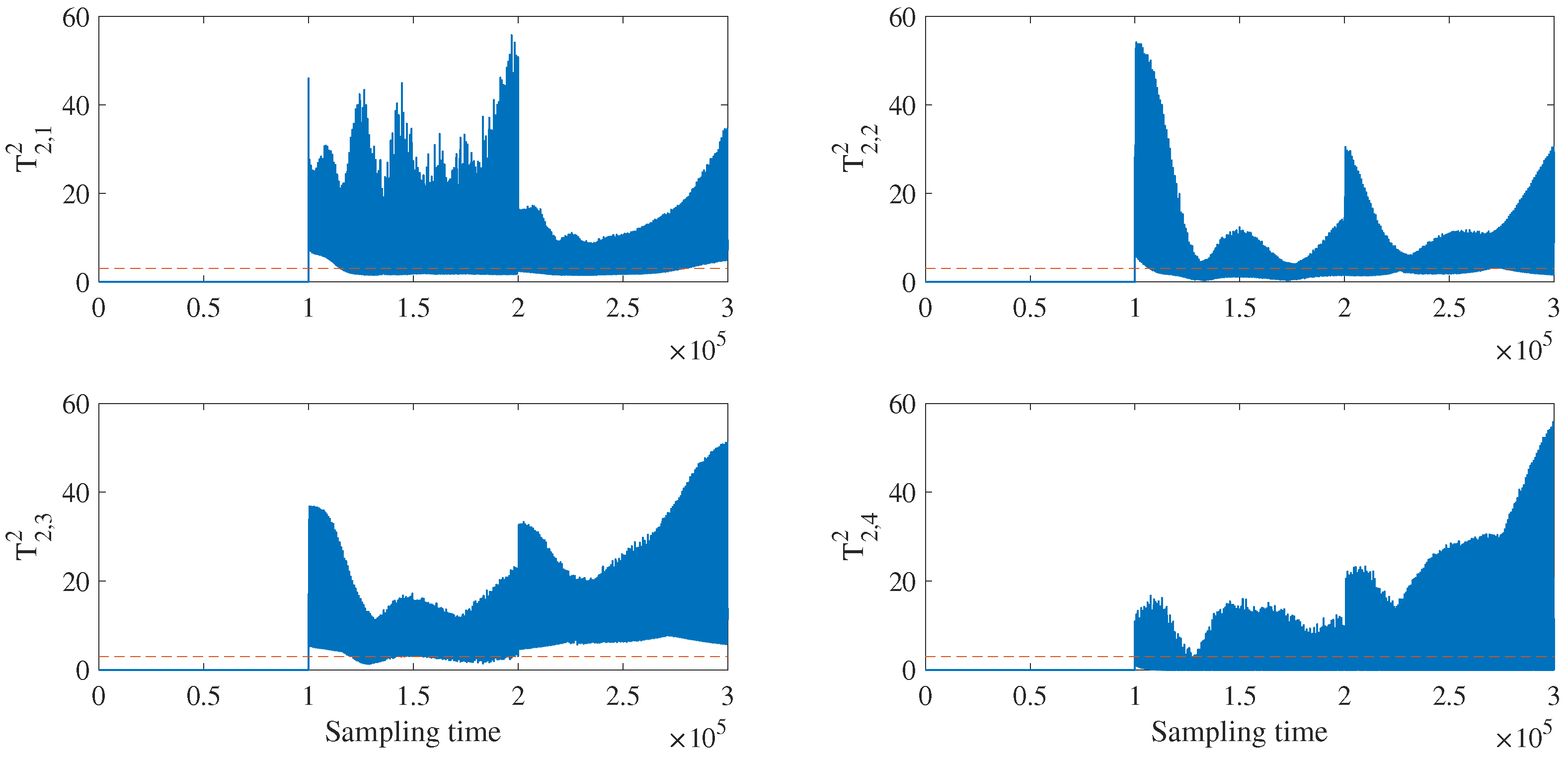
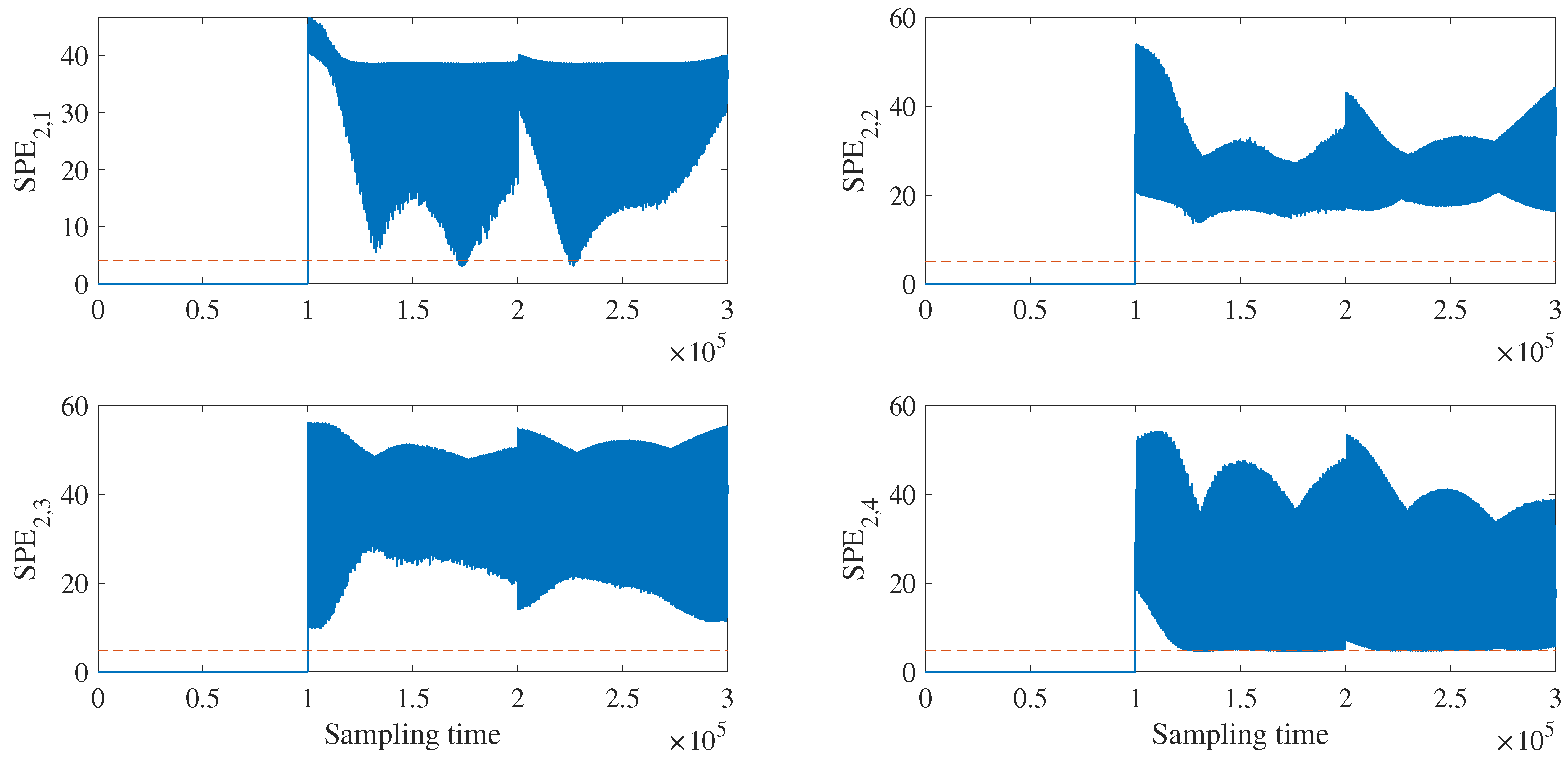
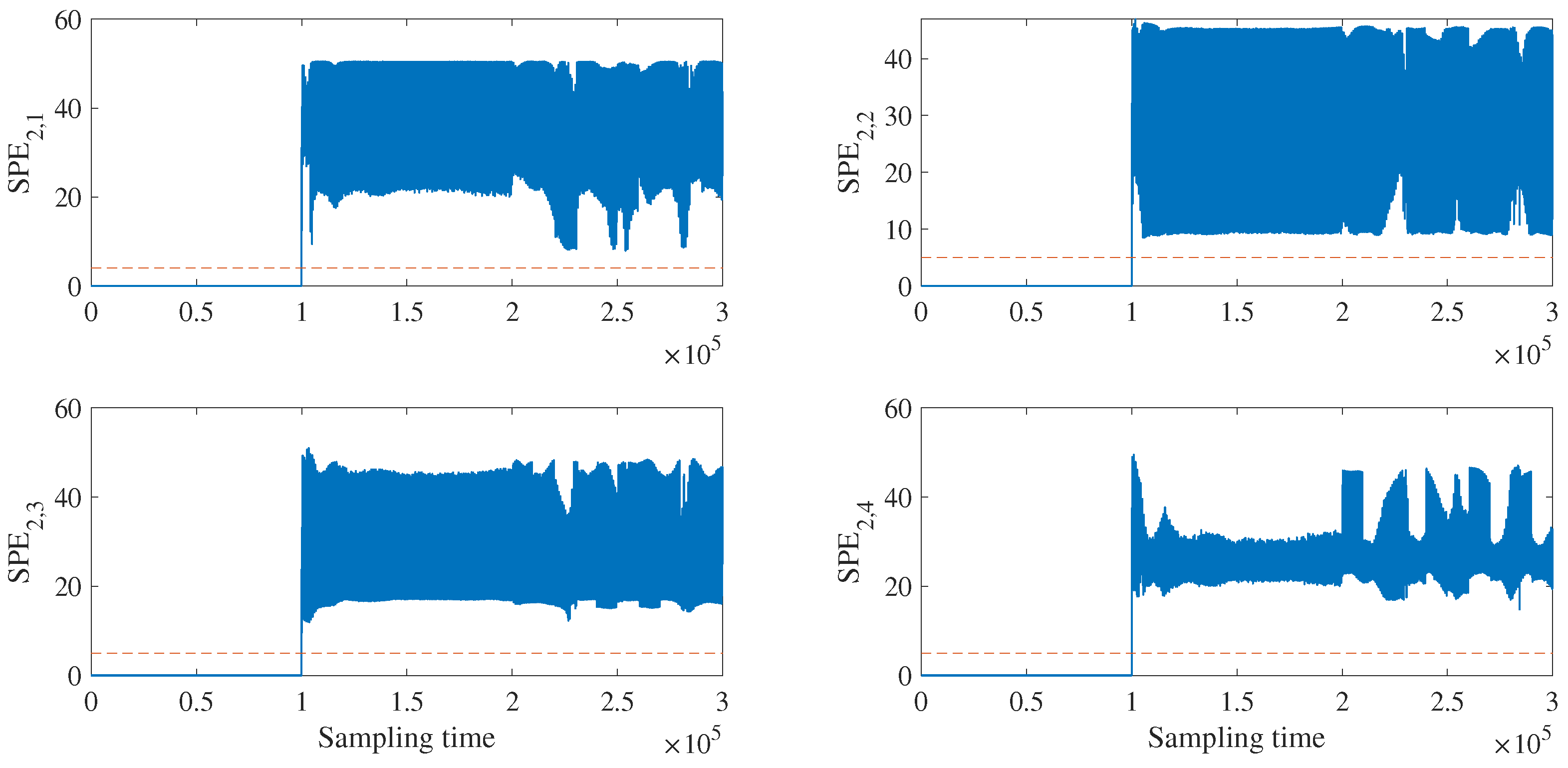
4.2. Fault Detection and Isolation
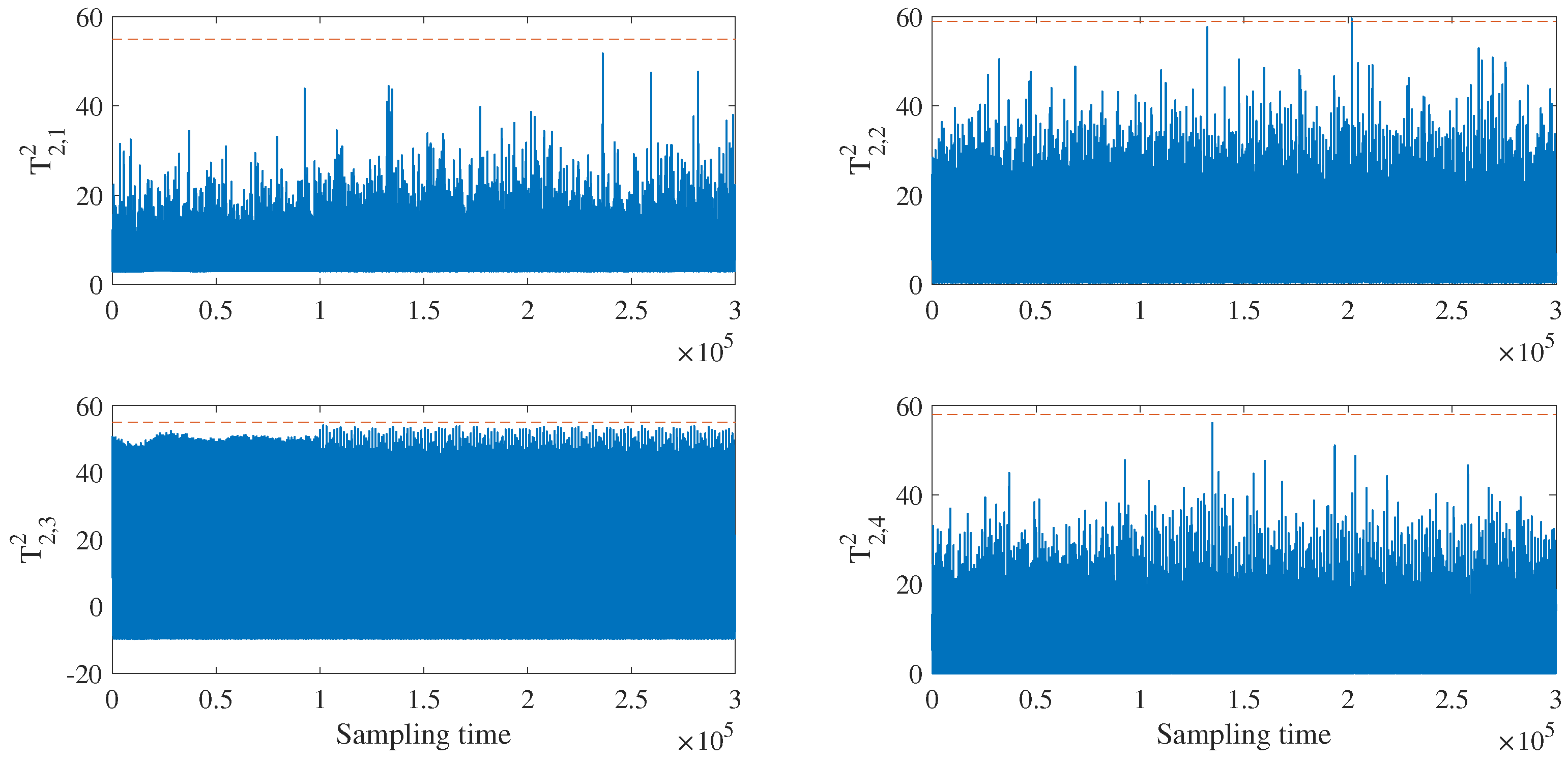
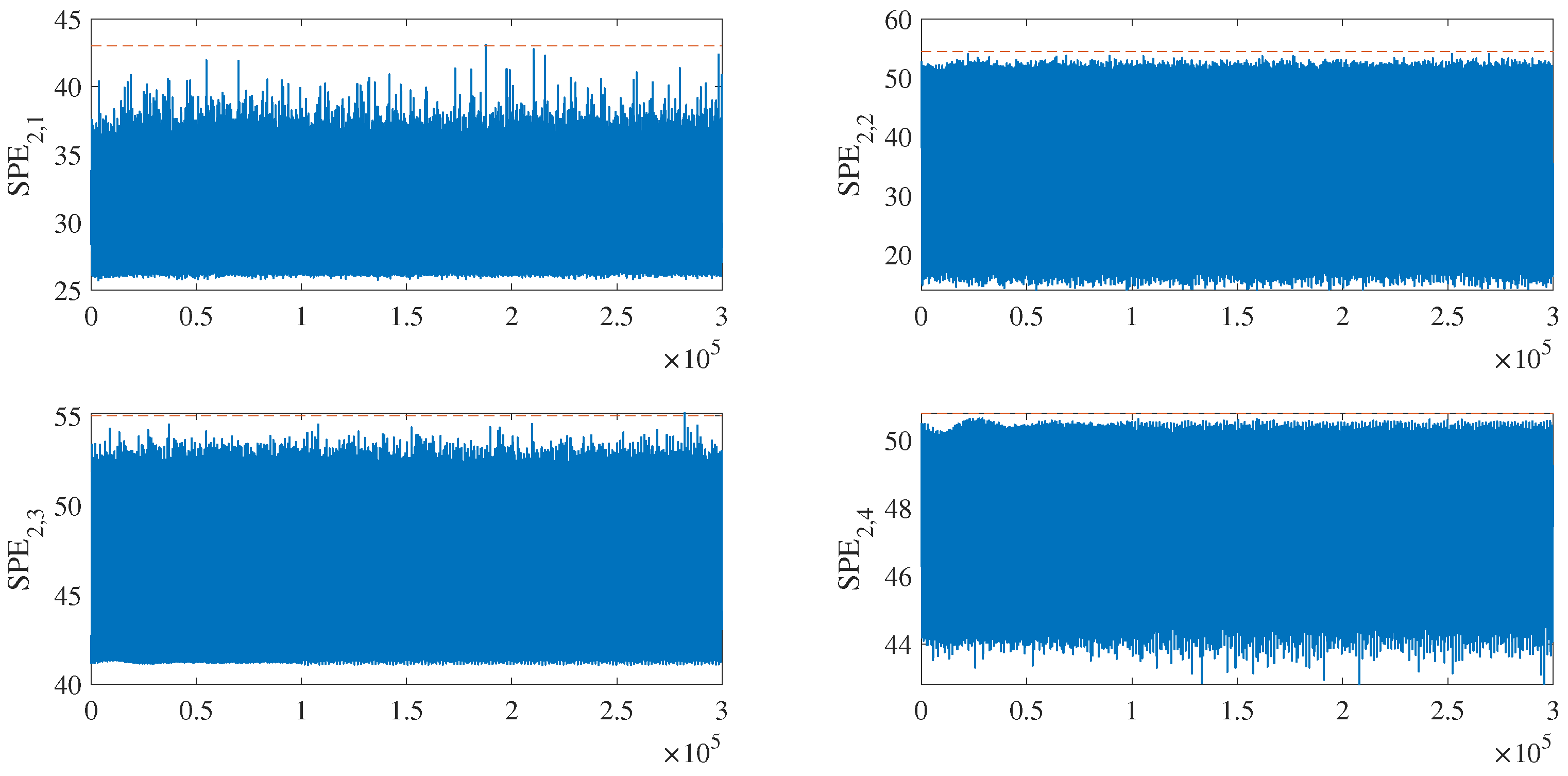
4.2.1. Fault Detection and Isolation of Raw Data
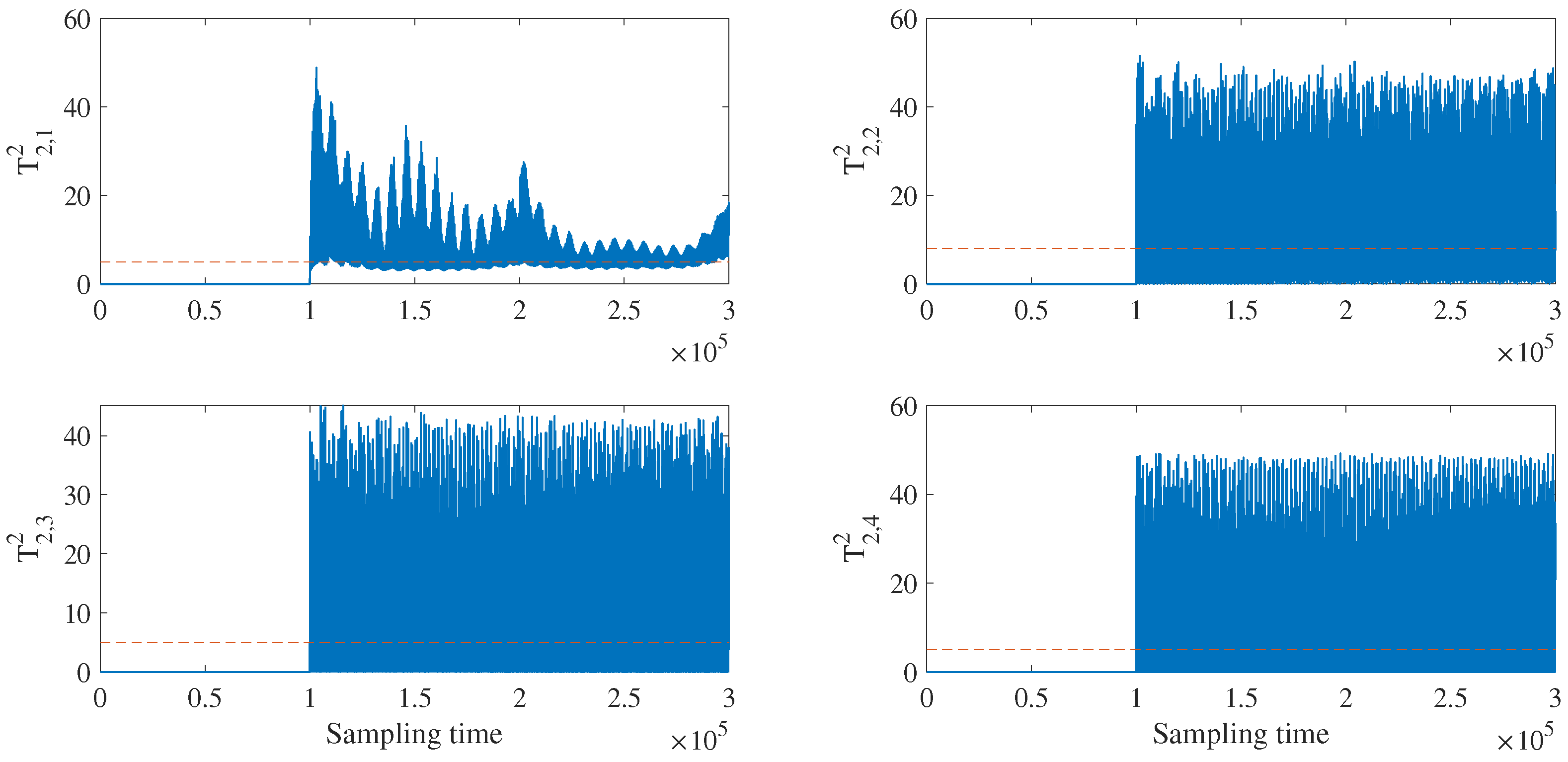
4.2.2. Fault Detection and Isolation for Data with FNR Enhancement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FDD | Fault Detection and Diagnosis |
| PCA | Principal Component Analysis |
| KPCA | Kernel Principal Component Analysis |
| DTW | Dynamic Time Warping |
| KLD | Kullback–Leibler Divergence |
References
- Chen, H.T.; Jiang, B. A review of fault detection and diagnosis for the traction system in high-speed trains. IEEE Trans. Intell. Transp. Syst. 2020, 21, 450–465. [Google Scholar] [CrossRef]
- Chen, H.T.; Jiang, B.; Ding, S.X.; Huang, B. Data-driven fault diagnosis for traction systems in high-speed trains: A survey, challenges, and perspectives. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1700–1716. [Google Scholar] [CrossRef]
- Yu, W.K.; Zhao, C.H.; Huang, B. MoniNet with concurrent analytics of temporal and spatial information for fault detection in industrial processes. IEEE Trans. Cybern. 2021, 52, 8340–8351. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.K.; Zhao, C.H.; Huang, B. Recursive cointegration analytics for adaptive monitoring of nonstationary industrial processes with both static and dynamic variations. J. Process. Control. 2020, 92, 319–332. [Google Scholar] [CrossRef]
- Cai, T.; Silverman, B.W. Incorporating information on neighbouring coefficients into wavelet estimation. Sankhy. Indian. J. Statist. B 2001, 63, 127–148. [Google Scholar]
- Messer, S.R.; Agzarian, J.; Abbott, D. Optimal wavelet denoising for phonocar diograms. Microelectron. J. 2001, 32, 931–941. [Google Scholar] [CrossRef]
- Ali, M.N.; Dahshan, E.l.; Yahia, E.A. Denoising of Heart Sound Signals Using Discrete Wavelet Transform. Circuits Syst. Signal. Process. 2017, 36, 4482–4497. [Google Scholar] [CrossRef]
- Dawid, G.; Grzegorz, R.L. Wavelet-based denoising method for real phonocardiography signal recorded by mobile devices in noisy environment. Comput. Biol. Med. 2014, 52, 119–129. [Google Scholar]
- Jiang, J.; Guo, J.; Fan, W.; Chen, Q. An improved adaptive wavelet denoising method based on neighboring coefficients. In Proceedings of the 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010; Volume 10, pp. 2894–2898. [Google Scholar]
- Patil, P.B.; Chavan, M.S. A wavelet based method for denoising of biomedical signal. In Proceedings of the International Conference on Pattern Recognition, Informatics and Medical Engineering (PRIME-2012), Salem, India, 21–23 March 2012; Volume 10, pp. 278–283. [Google Scholar]
- Rao, B.C.; Latha, M.M. Selective neighbouring wavelet coefficients approach for image denoising. Int. J. Commun. Syst. 2011, 2, 73–77. [Google Scholar]
- Qin, X.W.; Yue, Y.; Dong, X.G. An improved method of image denoising based on wavelet transform. In Proceedings of the 2010 International Conference on Computer, Mechatronics, Control and Electronic Engineering, Changchun, China, 24–26 August 2010; Volume 10, pp. 167–170. [Google Scholar]
- Golroudbari, M.A. Signal denoising based on wavelet transform using a multi-level threshold function. In Proceedings of the 2013 7th International Conference on Application of Information and Communication Technologies, Baku, Azerbaijan, 23–25 October 2013; Volume 7, pp. 1–5. [Google Scholar]
- Chen, G.Y.; Bui, T.D. Multiwavelets denoising using neighboring coefficients. IEEE Signal. Process. Lett 2003, 10, 211–214. [Google Scholar] [CrossRef]
- Om, H.; Biswas, M. A generalized image denoising method using neighbouring wavelet coefficients. Signal Image Video Process. 2015, 9, 191–200. [Google Scholar] [CrossRef]
- Yang, G.R.G.; Ren, M.W. RETRACTED: Wavelet denoising using principal component analysis. Exp. Sys. App. 2011, 38, 1073–1076. [Google Scholar] [CrossRef]
- Chen, G.Y.; Kegl, B. Image denoising with complex ridgelets. Artif. Neural Netw. Pattern. Recognit. 2007, 40, 578–585. [Google Scholar] [CrossRef]
- Om, H.; Biswas, M.T. An Improved Image Denoising Method Based on Wavelet Thresholding. J. Signal Inf. Process. 2012, 1, 8–28. [Google Scholar] [CrossRef]
- Zhou, D.; Cheng, W. Image denoising with an optimal threshold and neighbouring window. Pattern Recognit. Lett. 2008, 29, 1694–1697. [Google Scholar]
- Cetin, A.E.; Tofighi, M. Projection-based wavelet denoising. IEEE Signal. Process. Mag. 2015, 32, 120–124. [Google Scholar] [CrossRef]
- Zhao, R.M.; Cui, H.M. Improved threshold denoising method based on wavelet transform. In Proceedings of the 2015 7th International Conference on Modelling, Identification and Control (ICMIC), Sousse, Tunisia, 18–20 December 2015; Volume 10, pp. 1–4. [Google Scholar]
- Biswas, M.; Om, H. An image denoising threshold estimation method. Choice 2013, 1000, 2l. [Google Scholar]
- Madhu, S.; Bhavani, H.B.; Sumathi, S.; Vidya, H.A. A novel algorithm for denoising of simulated partial discharge signals using adaptive wavelet thresholding methods. In Proceedings of the 2015 2nd International Conference on Electronics and Communication Systems (ICECS), Coimbatore, India, 26–27 February 2015; Volume 10, pp. 1596–1602. [Google Scholar]
- Madadi, Z.; Anand, G.V.; Premkumar, A.B. Signal detection in generalized Gaussian noise by nonlinear wavelet denoising. IEEE Trans. Circuits Syst. I Reg. Papers 2013, 11, 2973–2986. [Google Scholar] [CrossRef]
- Madhu, S.; Bhavani, H.B.; Umathi, S.S. Performance analysis of thresholding techniques for denoising of simulated partial discharge signals corrupted by Gaussian white noise. In Proceedings of the 2015 International Conference on Power and Advanced Control Engineering (ICPACE), Bangalore, India, 12–14 August 2015; Volume 10, pp. 399–404. [Google Scholar]
- Tyagi, B.; Vidya, H.A. Application of Wavelet Shrinkage Denoising Method Based on Genetic Algorithm to Partial Discharge Signals. In Proceedings of the International Conference on VLSI, Communication, Advanced Devices, Signals & Systems and Networking (VCASAN-2013), Bangalore, India, 17–19 July 2013; Springer: New Delhi, India, 2013; Volume 258, pp. 142–149. [Google Scholar]
- Hamadi, S.H.K.; Isa, M.; Ishak, L.M.; Rohani, M.N.K.H.; Yii, C.C.; Ismail, B.; Shafiq, M. Evaluation of denoising performance indices for noisy partial discharge signal based on DWT technique. In Proceedings of the 2017 IEEE 15th Student Conference on Research and Development (SCOReD), Wilayah Persekutuan Putrajaya, Malaysia, 13–14 December 2017; Volume 5, pp. 392–397. [Google Scholar]
- Hussein, R.; Shaban, K.B.; El-Hag, A.H. Histogram-based thresholding in discrete wavelet transform for partial discharge signal denoising. In Proceedings of the 2015 International Conference on Communications, Signal Processing, and their Applications (ICCSPA’15), Sharjah, United Arab Emirates, 17–19 February 2015; Volume 10, pp. 1–5. [Google Scholar]
- Guo, S.; Wu, F.; Wei, W.; Guo, J.; Ji, Y.; Wang, Y. A novel wavelet denoising method used for droplet volume detection in the microfluidic system. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013; Volume 10, pp. 1732–1737. [Google Scholar]
- Weil, W.; Guo, S.; Wu, F.; Ji, Y.; Wang, Y. Image processing-based measurement of volume for droplets in the microfluidic system. In Proceedings of the 2013 ICME International Conference on Complex Medical Engineering, Beijing, China, 25–28 May 2013; Volume 10, pp. 518–522. [Google Scholar]
- Xie, X.Y.; Liu, Y.; Lin, X.M.; Wang, H. The application of adaptive step threshold method in fluorescence signal detection. In Proceedings of the 2017 2nd IEEE International Conference on Computational Intelligence and Applications (ICCIA), Beijing, China, 8–11 September 2017; Volume 10, pp. 411–416. [Google Scholar]
- Huang, C.; Xia, G.; Jin, S.; Hu, M.; Wu, S.J. Denoising analysis of compact CCD-based spectrometer. Optik 2018, 157, 693–703. [Google Scholar] [CrossRef]
- Srivastava, M.; Anderson, S.C.L.; Freed, J.H. A New Wavelet Denoising Method for Selecting Decomposition Levels and Noise Thresholds. IEEE Access. 2016, 4, 3862–3877. [Google Scholar] [CrossRef] [PubMed]
- Albert, C.T.; Jeffrey, R.M. Wavelet denoising techniques with applications to experimental geophysical data. Signal Process. 2009, 2, 144–160. [Google Scholar]
- Alexander, M.E.; Baumgartner, R.; Summers, A.R. A wavelet-based method for improving signal-to-noise ratio and contrast in MR images. Magn. Reson. Imaging. 2000, 2, 169–180. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.Y.; Hsu, C.C.; Chen, M.C. Adaptive Kernel Principal Component Analysis (KPCA) for Monitoring Small Disturbances of Nonlinear Processes. Ind. Eng. Chem. Res. 2010, 49, 2254–2262. [Google Scholar] [CrossRef]
- Puspita, V. Time series forecasting for electricity consumption using kernel principal component analysis (kPCA) and support vector machine (SVM). J. Phys. Conf. Ser. 2001, 1196, 012073. [Google Scholar] [CrossRef]
- Chen, H.T.; Jiang, B.; Lu, N.Y.; Mao, Z.H. Deep PCA based real-time incipient fault detection and diagnosis methodology for electrical drive in high-speed trains. IEEE Trans. Veh. Technol. 2018, 67, 4819–4830. [Google Scholar] [CrossRef]


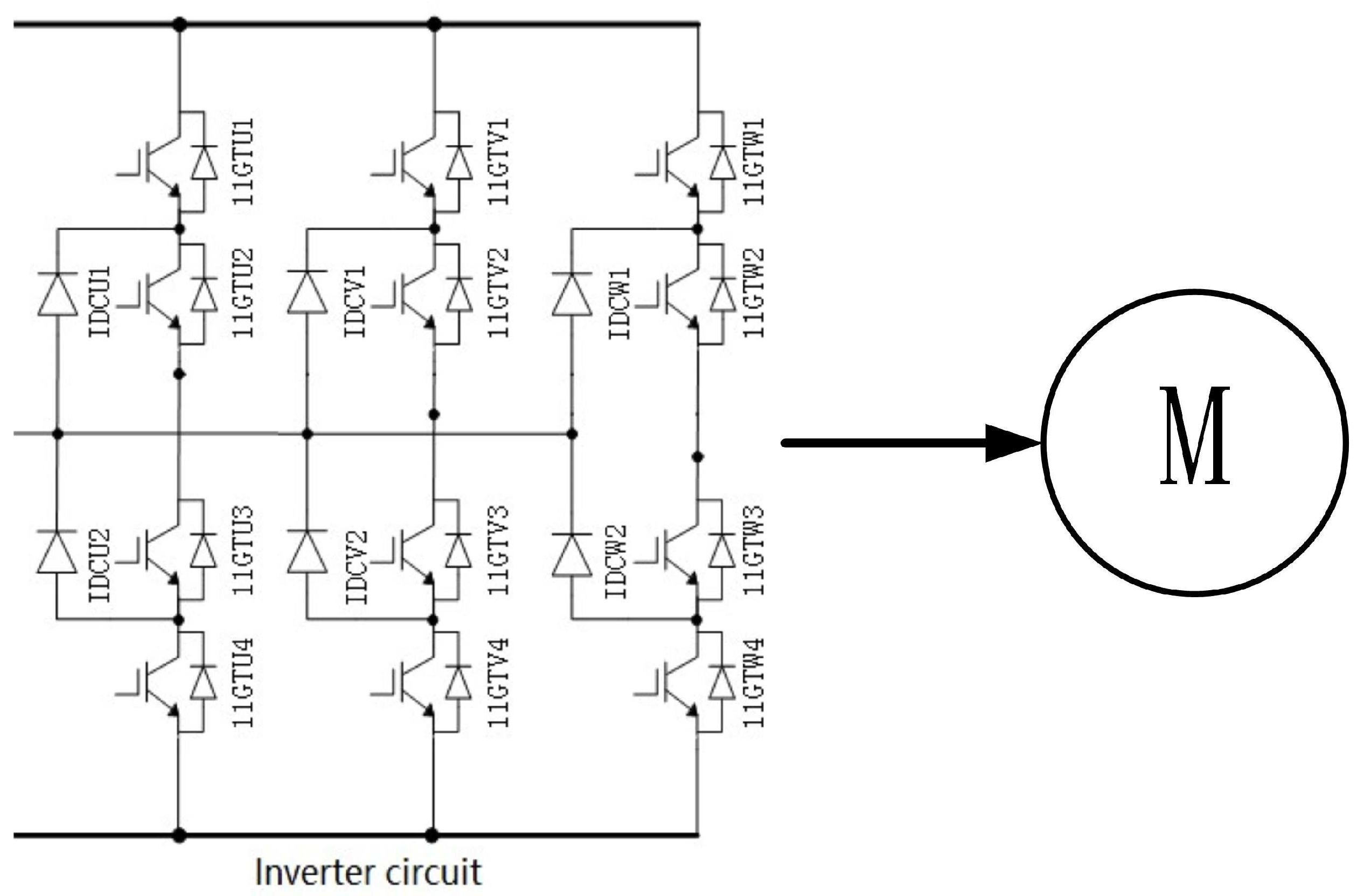
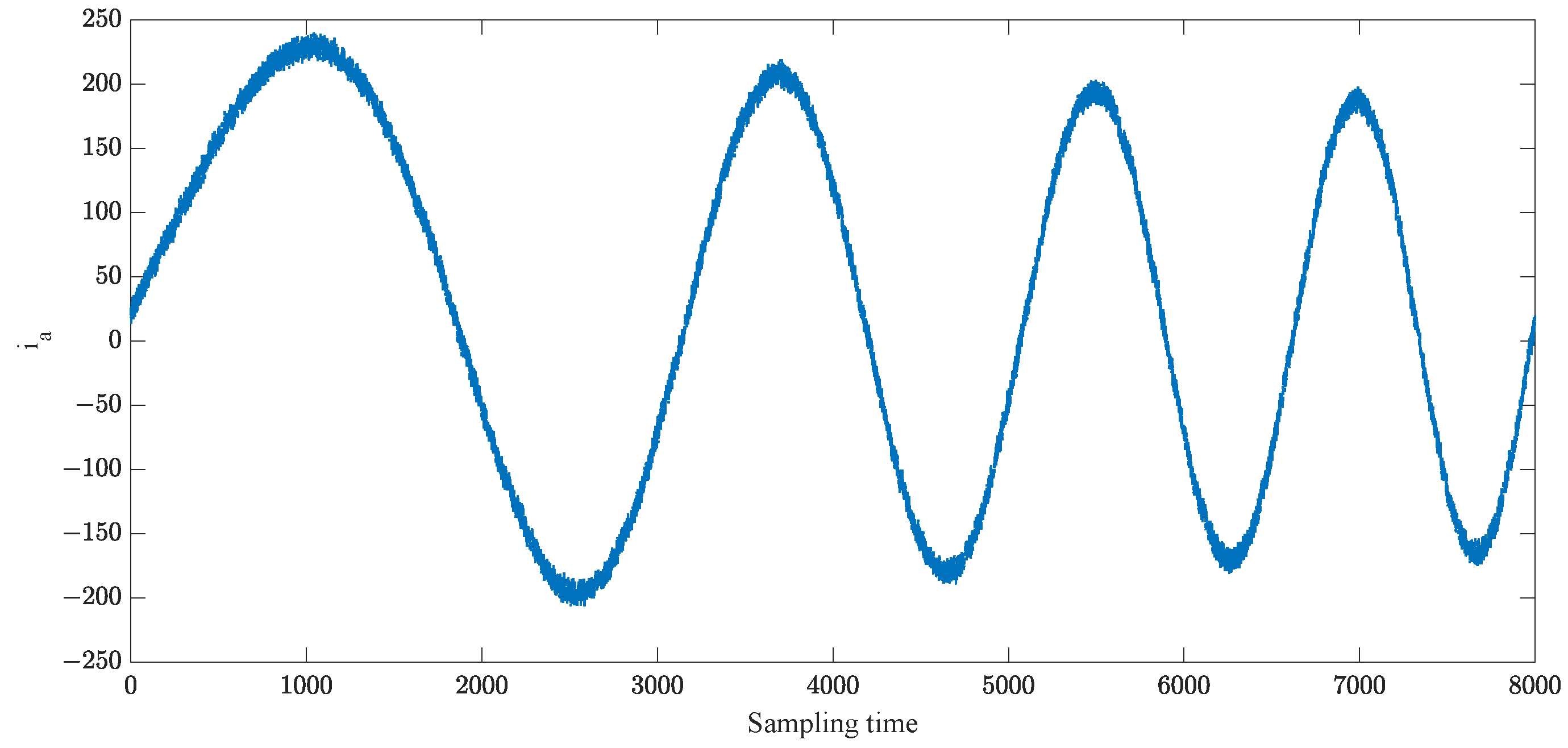
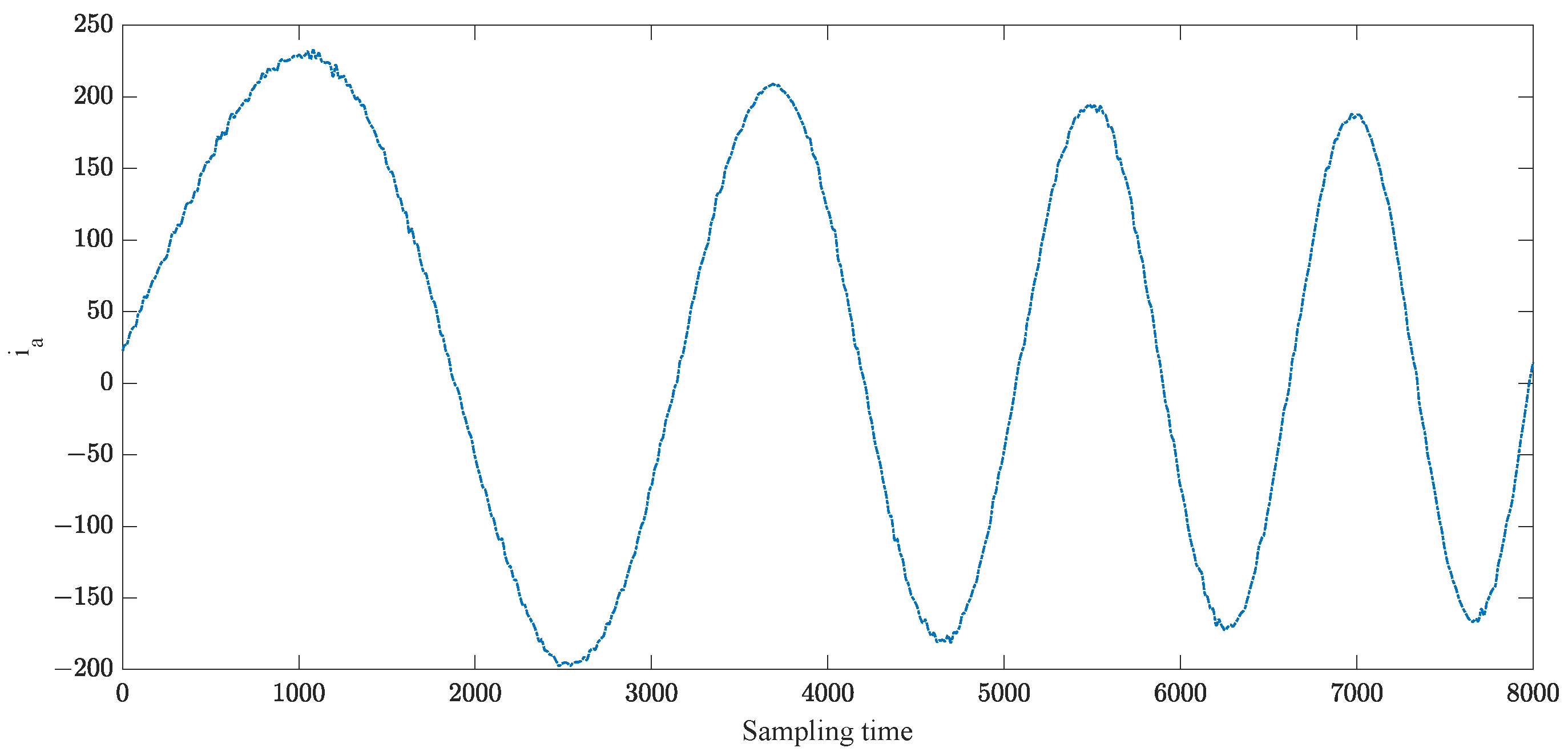

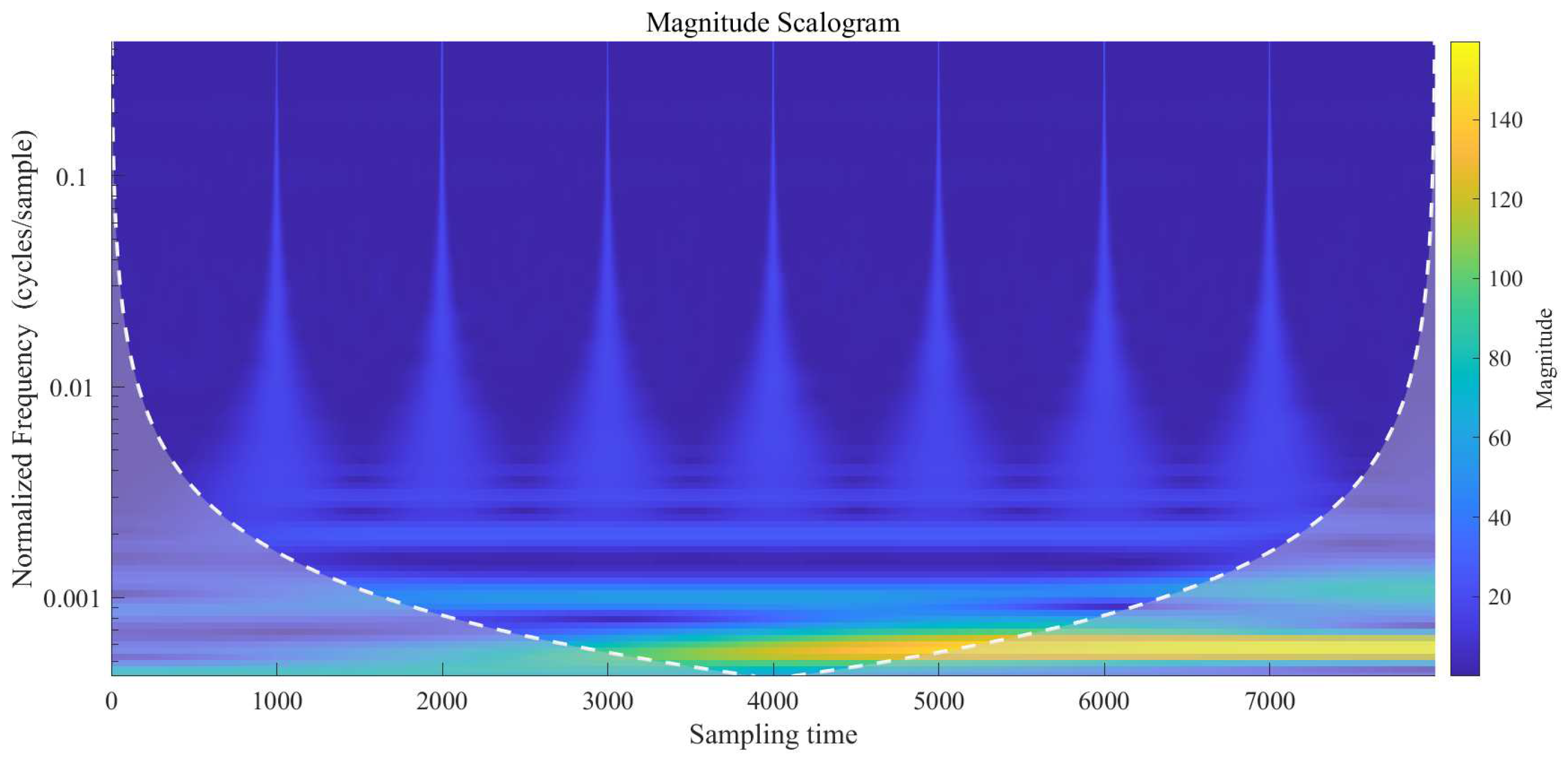

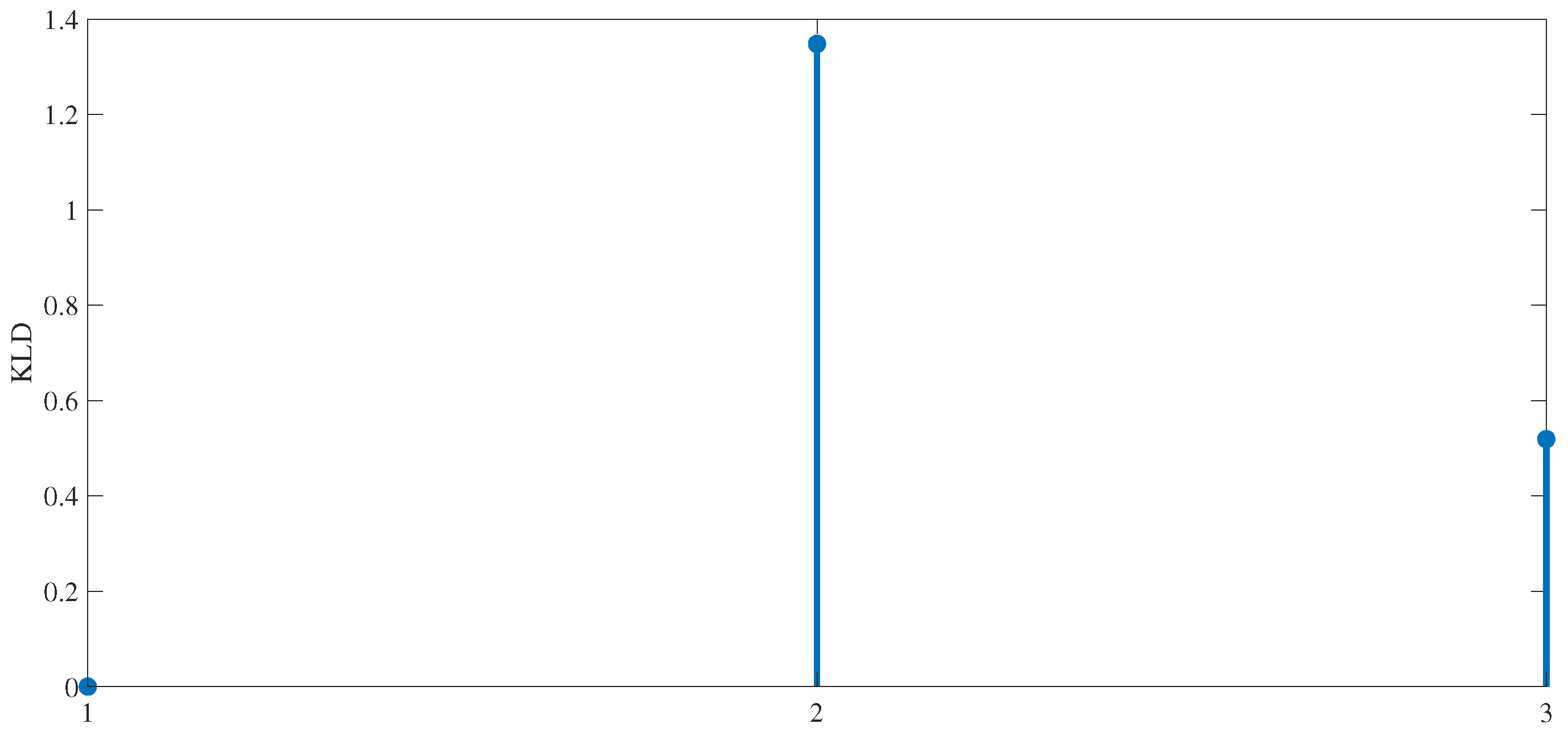


| Number | Type | Time |
|---|---|---|
| Incipient bearing fault on induction motor | sampling time | |
| Incipient drift fault on inverter sensors | sampling time | |
| Incipient periodic fault on inverter circuit | sampling time |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Liu, X.; Zhou, Y. Deep PCA-Based Incipient Fault Diagnosis and Diagnosability Analysis of High-Speed Railway Traction System via FNR Enhancement. Machines 2023, 11, 475. https://doi.org/10.3390/machines11040475
Wu Y, Liu X, Zhou Y. Deep PCA-Based Incipient Fault Diagnosis and Diagnosability Analysis of High-Speed Railway Traction System via FNR Enhancement. Machines. 2023; 11(4):475. https://doi.org/10.3390/machines11040475
Chicago/Turabian StyleWu, Yunkai, Xiangqian Liu, and Yang Zhou. 2023. "Deep PCA-Based Incipient Fault Diagnosis and Diagnosability Analysis of High-Speed Railway Traction System via FNR Enhancement" Machines 11, no. 4: 475. https://doi.org/10.3390/machines11040475
APA StyleWu, Y., Liu, X., & Zhou, Y. (2023). Deep PCA-Based Incipient Fault Diagnosis and Diagnosability Analysis of High-Speed Railway Traction System via FNR Enhancement. Machines, 11(4), 475. https://doi.org/10.3390/machines11040475








