Characteristics of Surface Wave on the Unstable Interface in Gas Jet Forming
Abstract
1. Introduction
2. Mechanism of the Gas–Liquid Interface Instability in Gas Jet Forming
2.1. The Interface Instability
2.2. Mechanism of the Instability
3. The Gas Jet-Forming Experiment
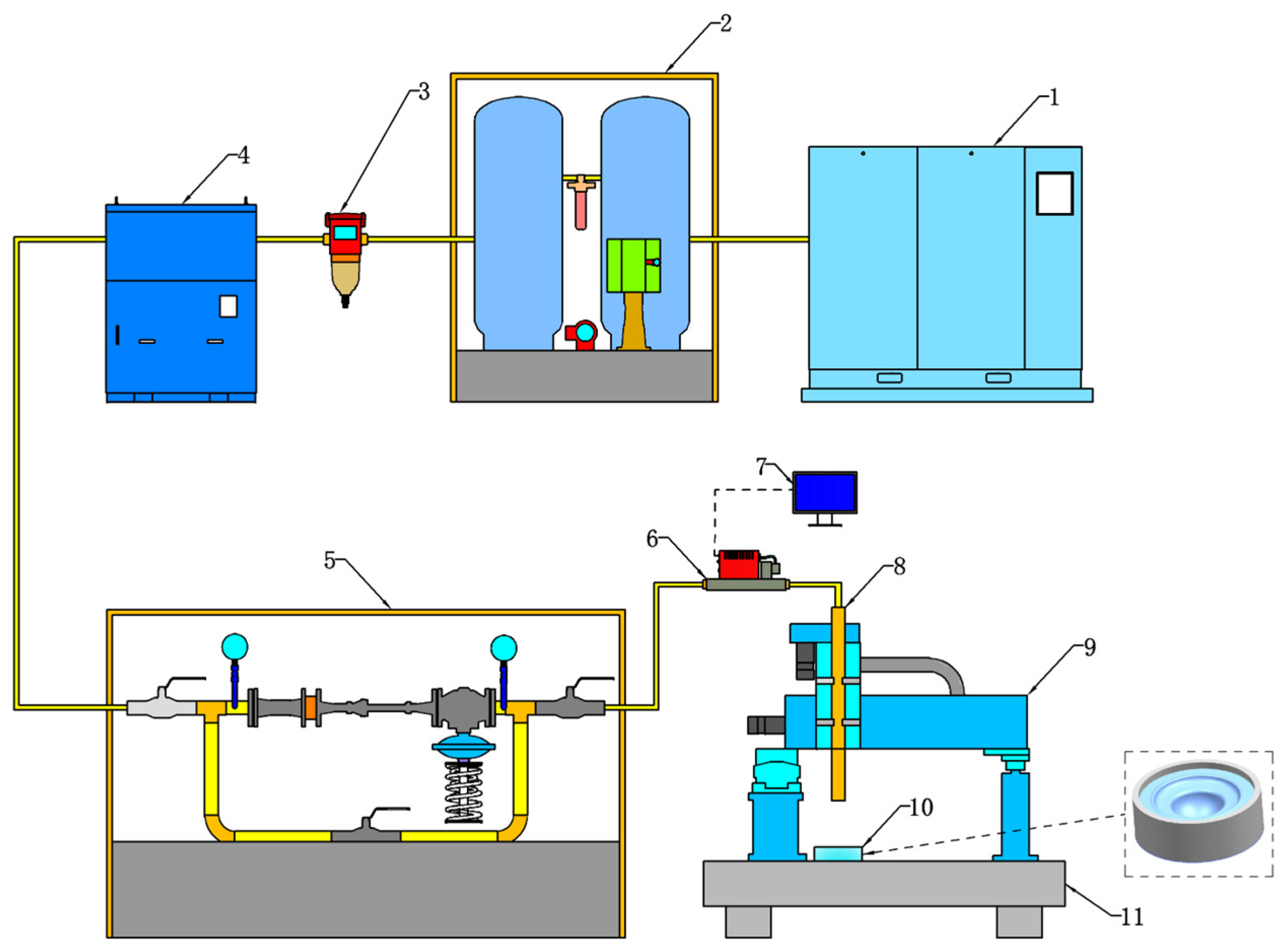
3.1. Experimental Device
3.2. Experimental Process
3.3. Experiment Parameters
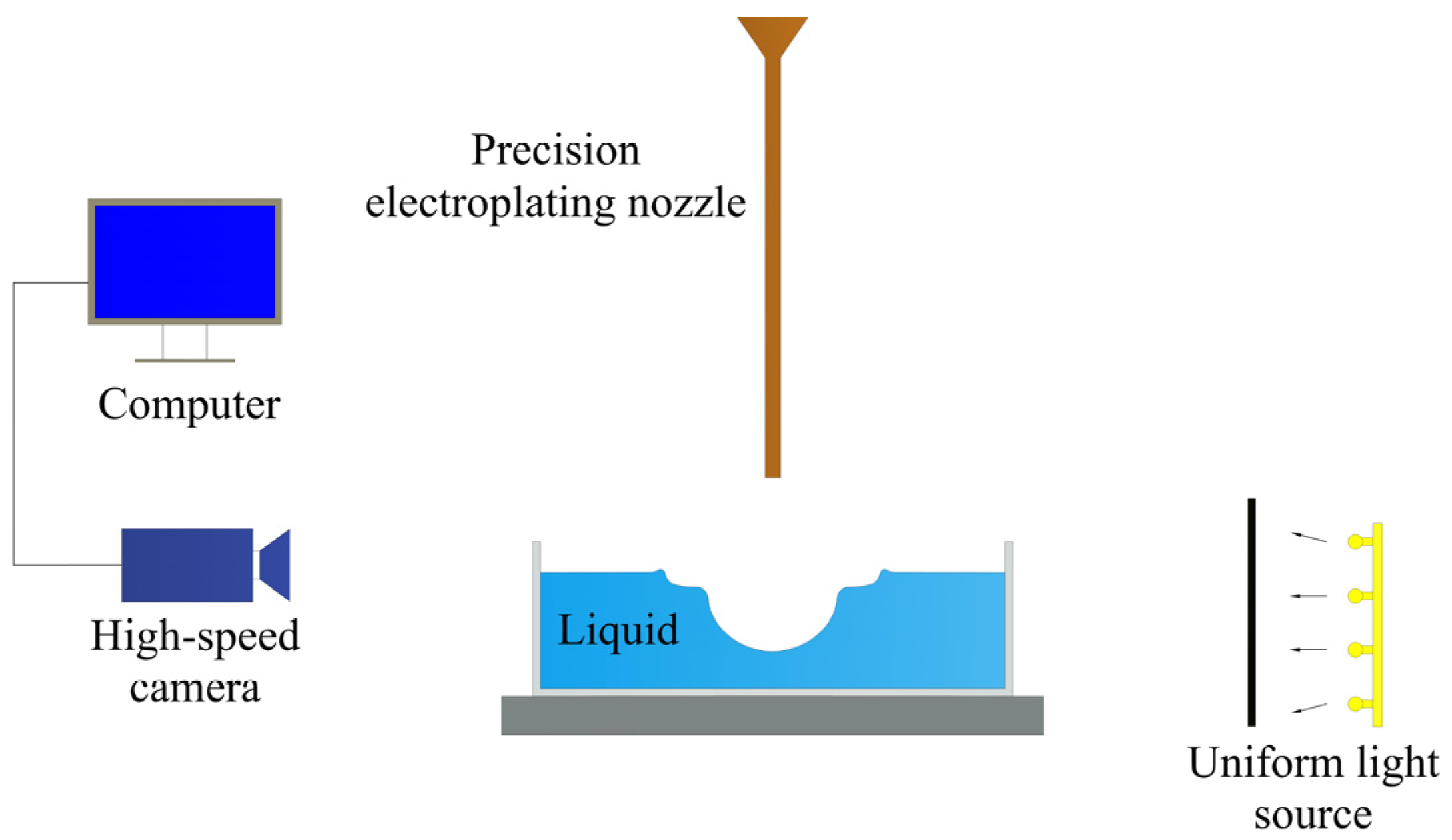
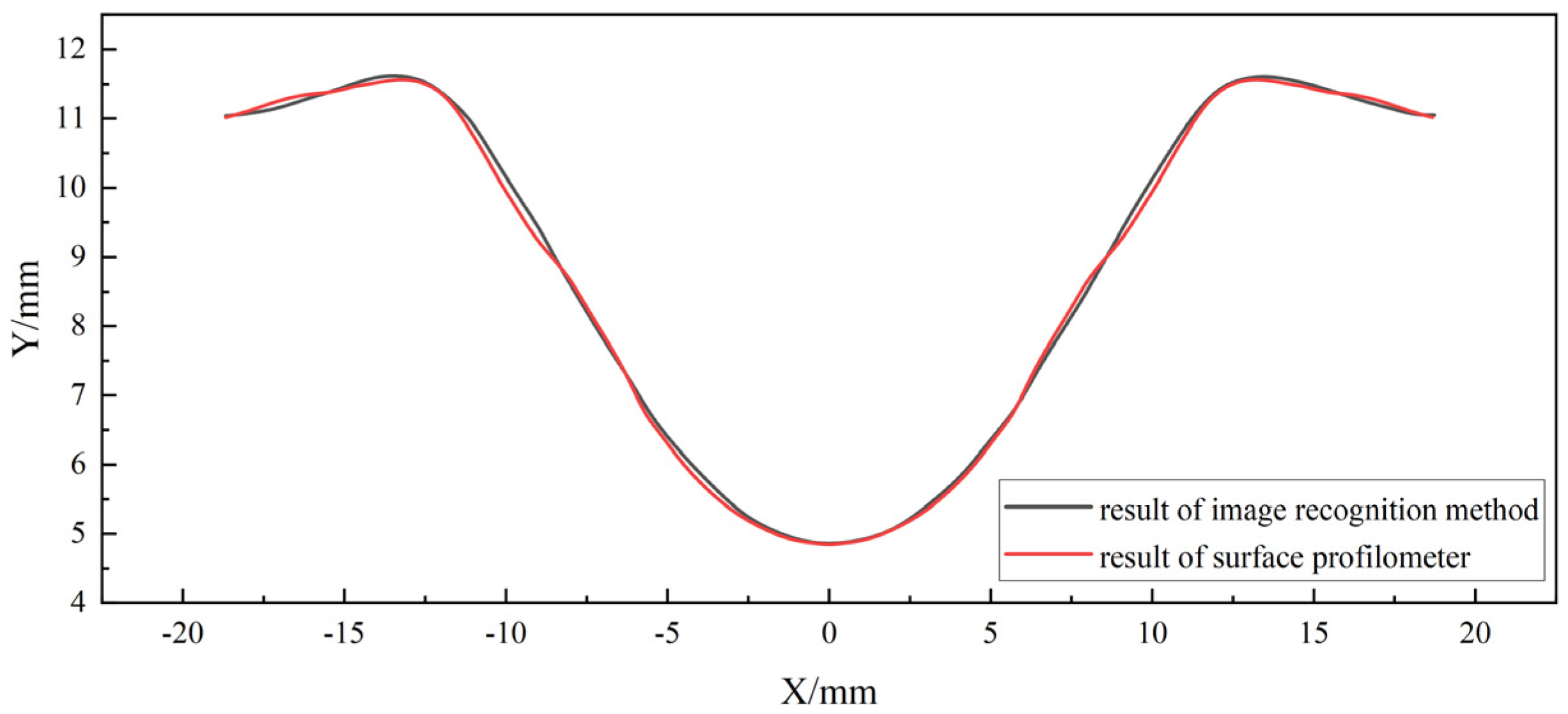
3.4. Measuring Method
4. Analysis of Experiment Results
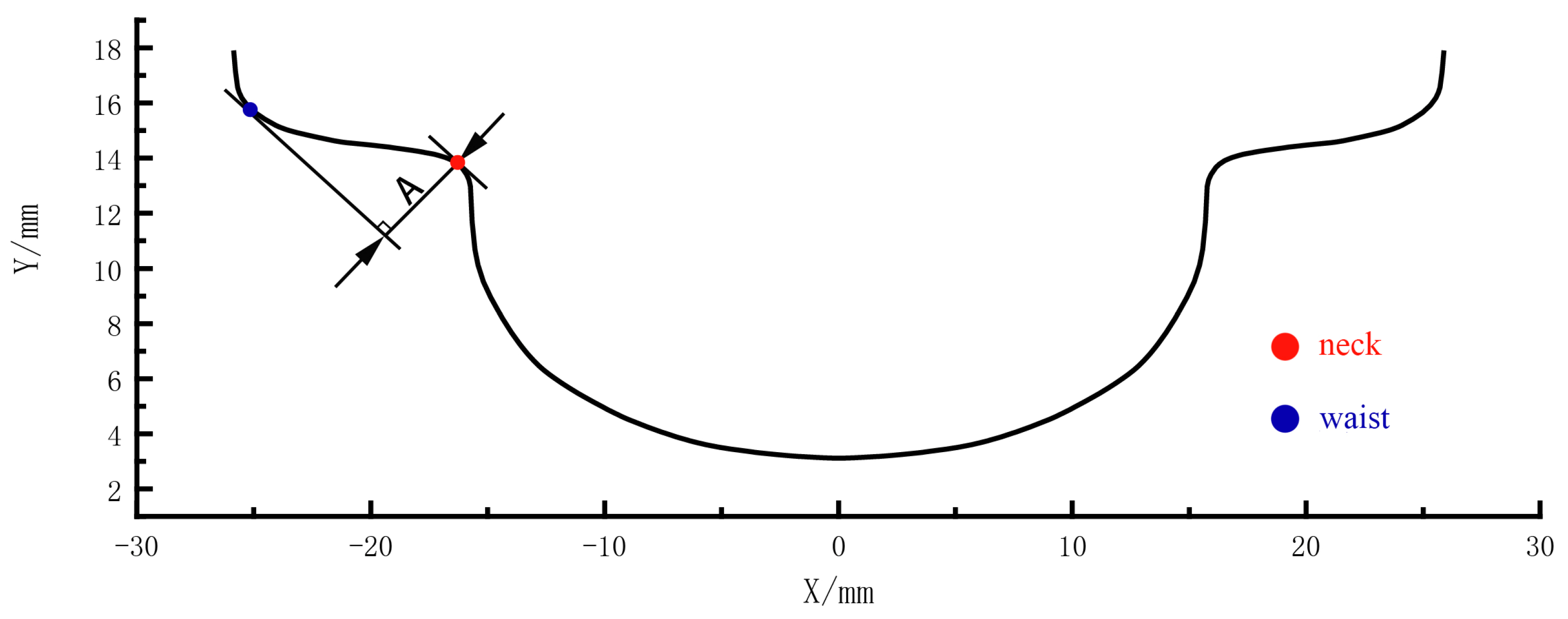
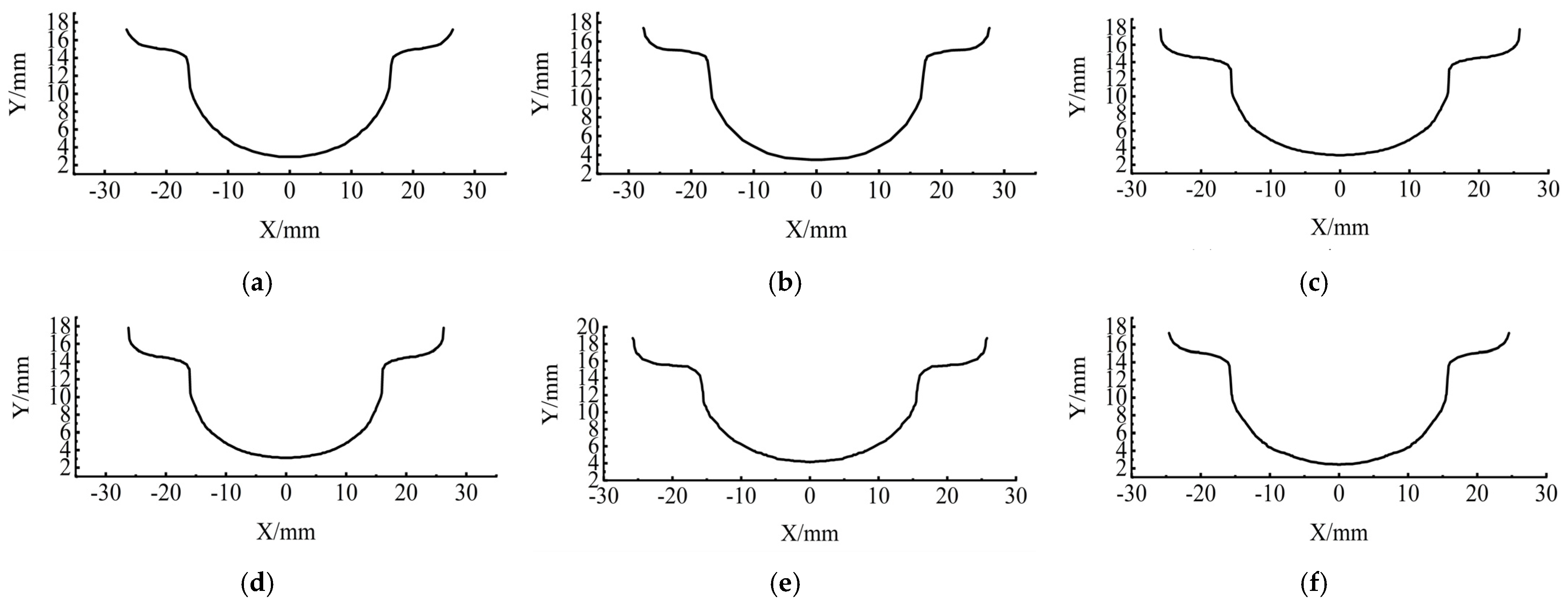
4.1. Experiment Results
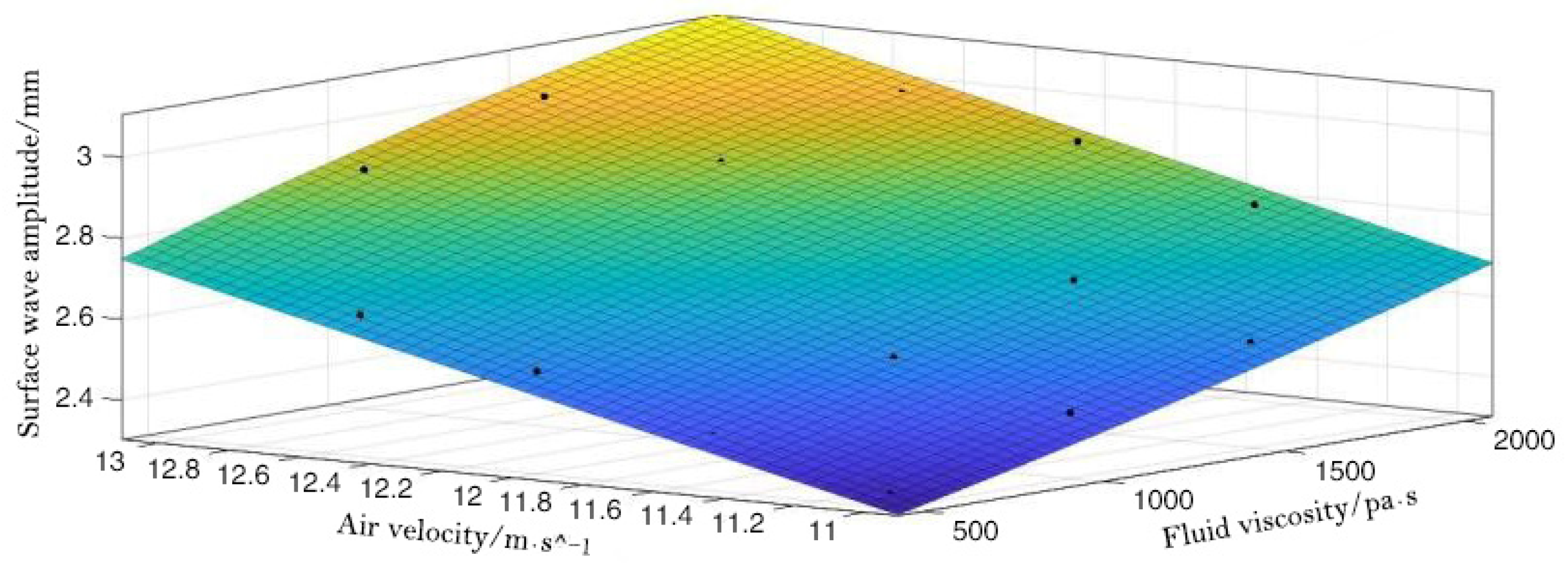
4.2. Influence of the Gas Jet Velocity and the Dimethyl Silicone Oil Viscosity on the Amplitude
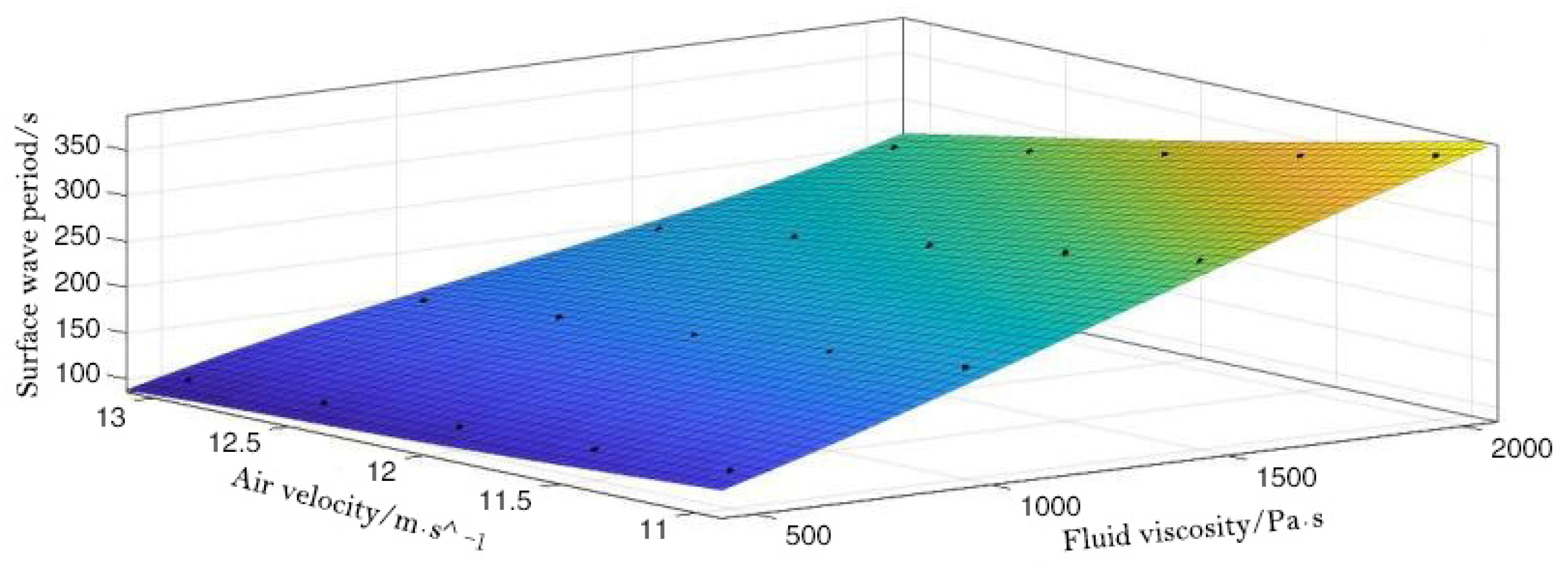
4.3. Influence of the Gas Jet Velocity and the Dimethyl Silicone Oil Viscosity on the Transfer Period
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jedamzik, R.; Werner, T.; Westerhoff, T. Production of the 4.26 m ZERODUR mirror blank for the Advanced Technology Solar telescope (ATST). Proc. SPIE 2014, 9151, 311–319. [Google Scholar]
- Westerhoff, T.; Schäfer, M.; Thomas, A.; Weissenburger, M.; Werner, T.; Werz, A. Manufacturing of the ZERODUR 1.5-m primary mirror for the solar telescope GREGOR as preparation of light weighting of blanks up to 4-m diameter. Proc. Spie 2010, 7739, 206–214. [Google Scholar]
- Yan, G.P.; Zhang, Y.; You, K.; Li, Z.X.; Yuan, Y.K.; Fang, F.Z. Off-spindle-axis spiral grinding of aspheric microlens array mold inserts. Opt. Express 2019, 27, 10873–10889. [Google Scholar] [CrossRef] [PubMed]
- Chkhalo, N.I.; Churin, S.A.; Pestov, A.E.; Salashchenko, N.N.; Vainer, Y.A.; Zorina, M.V. Roughness measurement and ion-beam polishing of super-smooth optical surfaces of fused quartz and optical ceramics. Opt. Express 2014, 22, 20094–20106. [Google Scholar] [CrossRef] [PubMed]
- Han, J.Y.; Kim, S.W.; Han, I.; Kim, G.H. Evolutionary grinding model for nanometric control of surface roughness for aspheric optical surfaces. Opt. Express 2008, 16, 3786–3797. [Google Scholar] [CrossRef] [PubMed]
- Yi, L.Q.; Zhang, X.J.; Hu, H.F.; Zhang, Z.Y.; Zeng, X.F.; Luo, X.; Xue, D.L.; Zhang, G. Equivalent thin-plate method for stressed mirror polishing of an off-axis aspheric silicon carbide lightweight mirror. Opt. Express 2020, 28, 36413–36431. [Google Scholar] [CrossRef] [PubMed]
- Yi, A.; Jain, A. Compression molding of aspherical glass lenses-a combined experimental and numerical analysis. J. Am. Ceram. Soc. 2005, 88, 579–586. [Google Scholar] [CrossRef]
- Ristok, S.; Roeder, M.; Thiele, S.; Hentschel, M.; Guenther, T.; Zimmermann, A.; Herkommer, A.M.; Giessen, H. Mass-producible micro-optical elements by injection compression molding and focused ion beam structured titanium molding tools. Opt. Lett. 2020, 45, 1184–1187. [Google Scholar] [CrossRef] [PubMed]
- Moon, S.D.; Lee, N.; Kang, S. Fabrication of a microlens array using micro-compression molding with an electroformed mold insert. J. Micromech. Microeng. 2002, 13, 98–103. [Google Scholar] [CrossRef]
- Yi, A.Y.; Huang, C.; Klocke, F.; Brecher, C.; Pongs, G.; Winterschladen, M.; Demmer, A.; Lange, S.; Bergs, T.; Merz, M. Development of a compression molding process for three-dimensional tailored free-form glass optics. Appl. Opt. 2006, 45, 6511–6518. [Google Scholar] [CrossRef] [PubMed]
- Kang, C.G.; Rohatgi, P.K. Transient thermal analysis of solidification in a centrifugal casting for composite materials containing particle segregation. Metall. Mater. Trans. B 1996, 27, 277–285. [Google Scholar] [CrossRef]
- Mueller, R.W.; Hoeness, H.W.; Marx, T. Spin-cast Zerodur mirror substrates of the 8-m class and lightweighted substrates for secondary mirrors. Int. Soc. Opt. Photonics 1990, 1236, 723–734. [Google Scholar]
- Borra, E.; Ferrari, M.; Girard, L.; Moretto, B.; Tremblay, G. Liquid mirrors. Can. J. Phys. 1995, 73, 109–125. [Google Scholar] [CrossRef]
- Fu, W.J.; Zhang, X.M. Experimental and numerical simulation study on gas jet forming of optical mirror blank. Optik 2020, 207, 164451. [Google Scholar] [CrossRef]
- Fu, W.J.; Zhang, X.M. Experimental and simulation research on the interface instability in gas jet forming. Optik 2020, 216, 164911. [Google Scholar] [CrossRef]
- Kravchenko, I.V.; Sultanov, V.G.; Patlazhan, S.A. Mechanism of stability of the shear flow of a two-layer system of viscous liquids. Dokl. Phys. Chem. 2011, 440, 171–173. [Google Scholar] [CrossRef]
- Forbes, L.K.; Chen, M.J.; Trenham, C.E. Computing unstable periodic waves at the interface of two inviscid fluids in uniform vertical flow. J. Comput. Phys. 2007, 221, 269–287. [Google Scholar] [CrossRef]
- Evrensel, C.A.; Zhou, L.; Khan, M.R.U. Response of a two-layer compliant slab to inviscid incompressible fluid flow. J. Acoust. Soc. Am. 1985, 101, 2070–2074. [Google Scholar] [CrossRef]
- Ohkitani, K. Motion of an interface between two uniform-vorticity regions in two-dimensional inviscid fluids. Tokyo Sugaku Kaisya Zasshi 2007, 58, 121–128. [Google Scholar] [CrossRef]
- Liu, Q.; Lin, Z.; Chen, X.P.; Zhu, Z.C.; Cui, B.L. Surface wave generation via a gas-jet penetration into a liquid sheet. Exp. Therm. Fluid Sci. 2018, 97, 1–11. [Google Scholar] [CrossRef]
- Miles, J.W. On the generation of surface waves by shear flows. J. Fluid Mech. Digit. Arch. 1957, 3, 185–204. [Google Scholar] [CrossRef]
- Young, W.R.; Wolfe, C.L. Generation of surface waves by shear-flow instability. J. Fluid Mech. 2014, 739, 276–307. [Google Scholar] [CrossRef]
- Dogan, N.; Brooks, G.A.; Rhamdhani, M.A. Comprehensive model of oxygen steelmaking Part 1: Model development and validation. ISIJ Int. 2011, 51, 1086–1092. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, M.; Fu, W. The Variation of Surface Shape in the Gas Jet Forming. Appl. Sci. 2023, 13, 504. [Google Scholar] [CrossRef]
- Kim, T.; Song, J. Effects of turbulence enhancement on combustion process using a double injection strategy in direct-injection spark-ignition gasoline engines. Int. J. Heart Fluid Flow 2015, 56, 124–136. [Google Scholar] [CrossRef]







| Epoxy Resin | Dimethyl Silicone Oil | |
|---|---|---|
| Density (kg/m3) | 980 | 978 |
| Viscosity (Pa·s) | 500~2000 | 500~2000 |
| Surface tension (N/m) | 0.0216 | 0.0216 |
| Number | Viscosity (Pa·s) |
|---|---|
| 1 | 500 |
| 2 | 1000 |
| 3 | 1500 |
| 4 | 2000 |
| Parameter | Value |
|---|---|
| the nozzle diameter (mm) | 500 |
| the inner diameter of glass mould (mm) | 1000 |
| the height between nozzle and the liquid surface (mm) | 1500 |
| Numbers | The Viscosity of Dimethyl Silicone Oil (Pa·s) | The Jet Velocity (m/s) | Numbers | The Viscosity of Dimethyl Silicone Oil (Pa·s) | The Jet Velocity (m/s) |
|---|---|---|---|---|---|
| 1 | 500 | 11.00 | 11 | 1500 | 11.00 |
| 2 | 500 | 11.50 | 12 | 1500 | 11.50 |
| 3 | 500 | 12.00 | 13 | 1500 | 12.00 |
| 4 | 500 | 12.50 | 14 | 1500 | 12.50 |
| 5 | 500 | 13.00 | 15 | 1500 | 13.00 |
| 6 | 1000 | 11.00 | 16 | 2000 | 11.00 |
| 7 | 1000 | 11.50 | 17 | 2000 | 11.50 |
| 8 | 1000 | 12.00 | 18 | 2000 | 12.00 |
| 9 | 1000 | 12.50 | 19 | 2000 | 12.50 |
| 10 | 1000 | 13.00 | 20 | 2000 | 13.00 |
| η = 500 Pa·s | η = 1000 Pa·s | η = 1500 Pa·s | η = 2000 Pa·s | |
|---|---|---|---|---|
| v = 11 m/s | 2.338 | 2.463 | 2.562 | 2.672 |
| v = 11.5 m/s | 2.437 | 2.556 | 2.674 | 2.785 |
| v = 12 m/s | 2.555 | 2.645 | 2.761 | 2.898 |
| v = 12.5 m/s | 2.651 | 2.759 | 2.879 | 2.976 |
| v = 13 m/s | 2.743 | 2.892 | 2.998 | 3.069 |
| a0 | a1 | a2 | a3 | a4 | a5 |
|---|---|---|---|---|---|
| 0.2586 | −4.707 × 10−4 | 0.1802 | 2.976 × 10−7 | 6.046 × 10−5 | −2.58 × 10−8 |
| Number | Parameters | Results of the Prediction Model Calculations (mm) | Results of Experimental Measurements (mm) |
|---|---|---|---|
| 1 | v = 11.3 m/s η = 500 Pa·s | 2.4026 | 2.390 |
| 2 | v = 11.3 m/s η = 600 Pa·s | 2.4245 | 2.413 |
| 3 | v = 11.3 m/s η = 700 Pa·s | 2.4465 | 2.436 |
| 4 | v = 11.3 m/s η = 800 Pa·s | 2.4686 | 2.458 |
| 5 | v = 11.7 m/s η = 900 Pa·s | 2.5763 | 2.563 |
| 6 | v = 11.7 m/s η = 1000 Pa·s | 2.5991 | 2.586 |
| 7 | v = 11.7 m/s η = 1100 Pa·s | 2.6218 | 2.610 |
| 8 | v = 11.7 m/s η = 1200 Pa·s | 2.6444 | 2.630 |
| 9 | v = 12.3 m/s η = 1300 Pa·s | 2.7959 | 2.784 |
| 10 | v = 12.3 m/s η = 1400 Pa·s | 2.8178 | 2.804 |
| 11 | v = 12.3 m/s η = 1500 Pa·s | 2.8392 | 2.828 |
| 12 | v = 12.3 m/s η = 1600 Pa·s | 2.8602 | 2.850 |
| 13 | v = 12.7 m/s η = 1700 Pa·s | 2.9939 | 2.980 |
| 14 | v = 12.7 m/s η = 1800 Pa·s | 3.0165 | 3.005 |
| 15 | v = 12.7 m/s η = 1900 Pa·s | 3.0386 | 3.026 |
| 16 | v = 12.7 m/s η = 2000 Pa·s | 3.0603 | 3.049 |
| η = 500 Pa·s | η = 1000 Pa·s | η = 1500 Pa·s | η = 2000 Pa·s | |
|---|---|---|---|---|
| v = 11 m/s | 126 | 207 | 291 | 374 |
| v = 11.5 m/s | 118 | 192 | 269 | 342 |
| v = 12 m/s | 111 | 179 | 245 | 312 |
| v = 12.5 m/s | 105 | 167 | 223 | 284 |
| v = 13 m/s | 99 | 154 | 200 | 257 |
| a0 | a1 | a2 | a3 | a4 | a5 | a6 |
| −3.105 × 104 | −2.367 | 1.077 × 104 | 1.261 × 10−3 | 0.4563 | −1385 | −2.051 × 10−7 |
| a7 | a8 | a9 | a10 | a11 | a12 | a13 |
| −1.483 × 10−4 | −0.02686 | 78.67 | 1.76 × 10−8 | 3.429 × 10−6 | 5.333 × 10−4 | −1.667 |
| Number | Parameters | Results of the Prediction Model Calculations (s) | Results of Experimental Measurements (s) |
|---|---|---|---|
| 1 | v = 11.3 m/s η = 500 Pa·s | 202.5 | 202.3 |
| 2 | v = 11.3 m/s η = 600 Pa·s | 217.4 | 217.5 |
| 3 | v = 11.3 m/s η = 700 Pa·s | 232.5 | 232.8 |
| 4 | v = 11.3 m/s η = 800 Pa·s | 247.8 | 247.6 |
| 5 | v = 11.7 m/s η = 900 Pa·s | 258.4 | 258.2 |
| 6 | v = 11.7 m/s η = 1000 Pa·s | 272.6 | 272.9 |
| 7 | v = 11.7 m/s η = 1100 Pa·s | 286.8 | 286.5 |
| 8 | v = 11.7 m/s η = 1200 Pa·s | 300.9 | 301.0 |
| 9 | v = 12.3 m/s η = 1300 Pa·s | 300.0 | 299.9 |
| 10 | v = 12.3 m/s η = 1400 Pa·s | 311.7 | 311.5 |
| 11 | v = 12.3 m/s η = 1500 Pa·s | 323.4 | 323.3 |
| 12 | v = 12.3 m/s η = 1600 Pa·s | 335.3 | 335.1 |
| 13 | v = 12.7 m/s η = 1700 Pa·s | 332.5 | 332.8 |
| 14 | v = 12.7 m/s η = 1800 Pa·s | 344.0 | 343.9 |
| 15 | v = 12.7 m/s η = 1900 Pa·s | 356.0 | 356.2 |
| 16 | v = 12.7 m/s η = 2000 Pa·s | 368.8 | 368.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, W.; Zhang, X.; Wang, M.; Zhang, X. Characteristics of Surface Wave on the Unstable Interface in Gas Jet Forming. Machines 2023, 11, 285. https://doi.org/10.3390/machines11020285
Fu W, Zhang X, Wang M, Zhang X. Characteristics of Surface Wave on the Unstable Interface in Gas Jet Forming. Machines. 2023; 11(2):285. https://doi.org/10.3390/machines11020285
Chicago/Turabian StyleFu, Weijie, Xu Zhang, Mingwei Wang, and Xinming Zhang. 2023. "Characteristics of Surface Wave on the Unstable Interface in Gas Jet Forming" Machines 11, no. 2: 285. https://doi.org/10.3390/machines11020285
APA StyleFu, W., Zhang, X., Wang, M., & Zhang, X. (2023). Characteristics of Surface Wave on the Unstable Interface in Gas Jet Forming. Machines, 11(2), 285. https://doi.org/10.3390/machines11020285






