A Rolling Bearing Fault Diagnosis Method Based on Switchable Normalization and a Deep Convolutional Neural Network
Abstract
1. Introduction
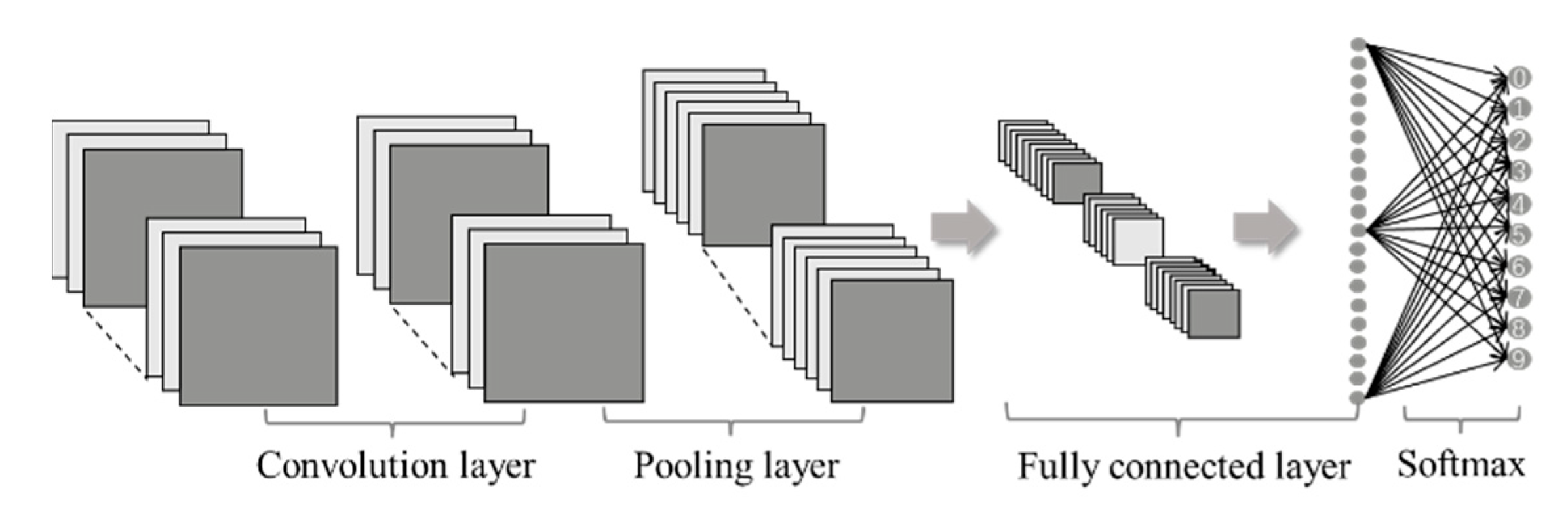
2. Convolutional Neural Network
2.1. Convolution Layer
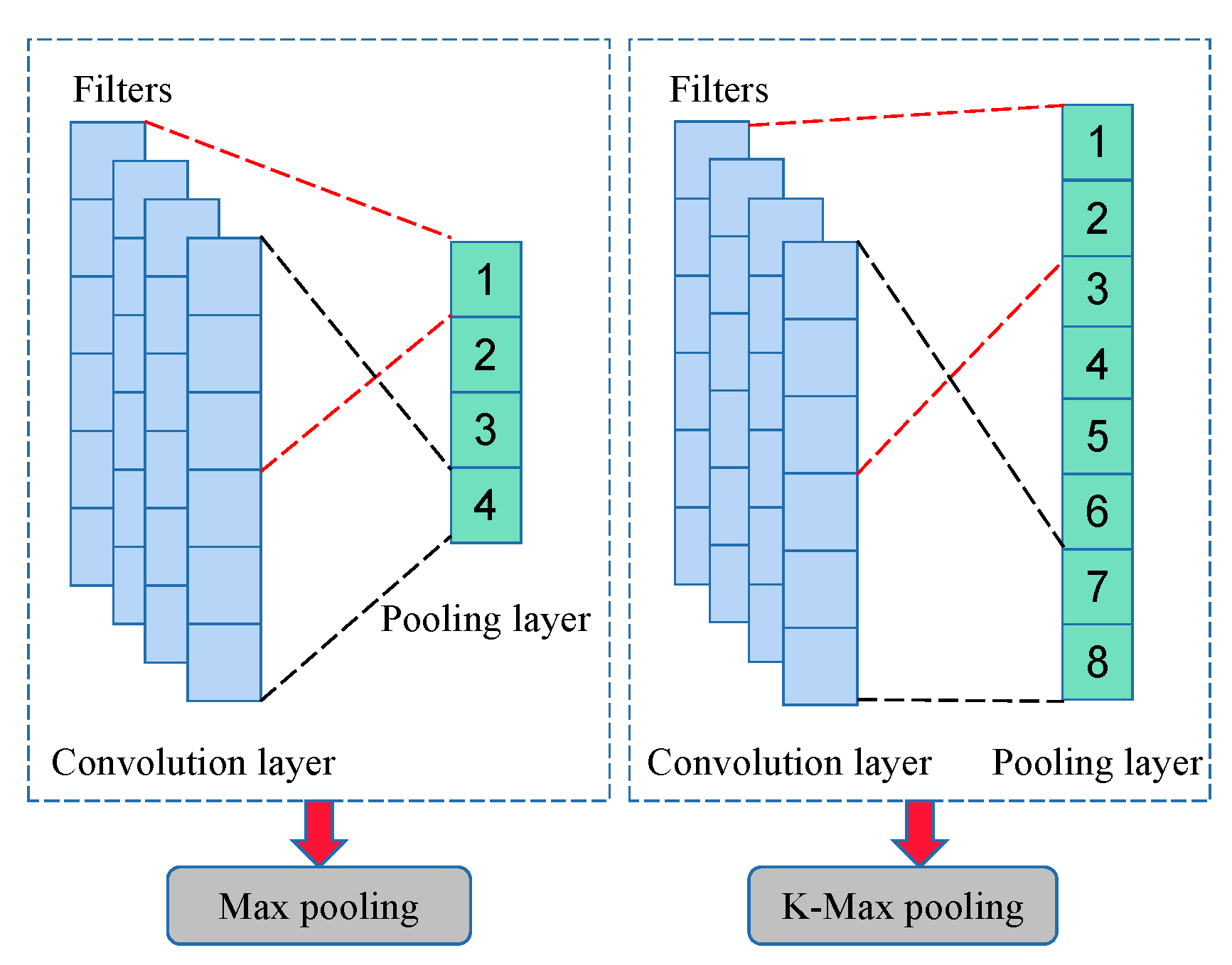
2.2. Pooling Layer
2.3. Fully Connected Layer
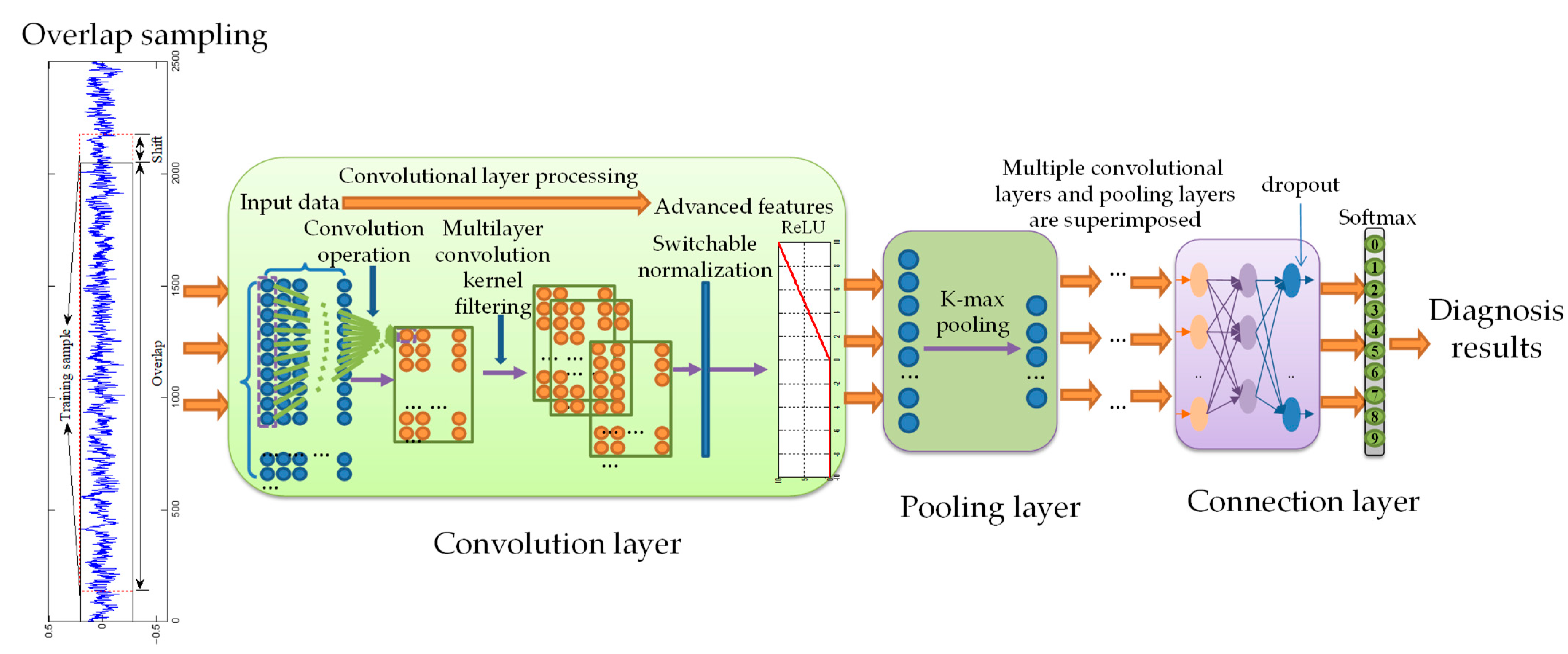
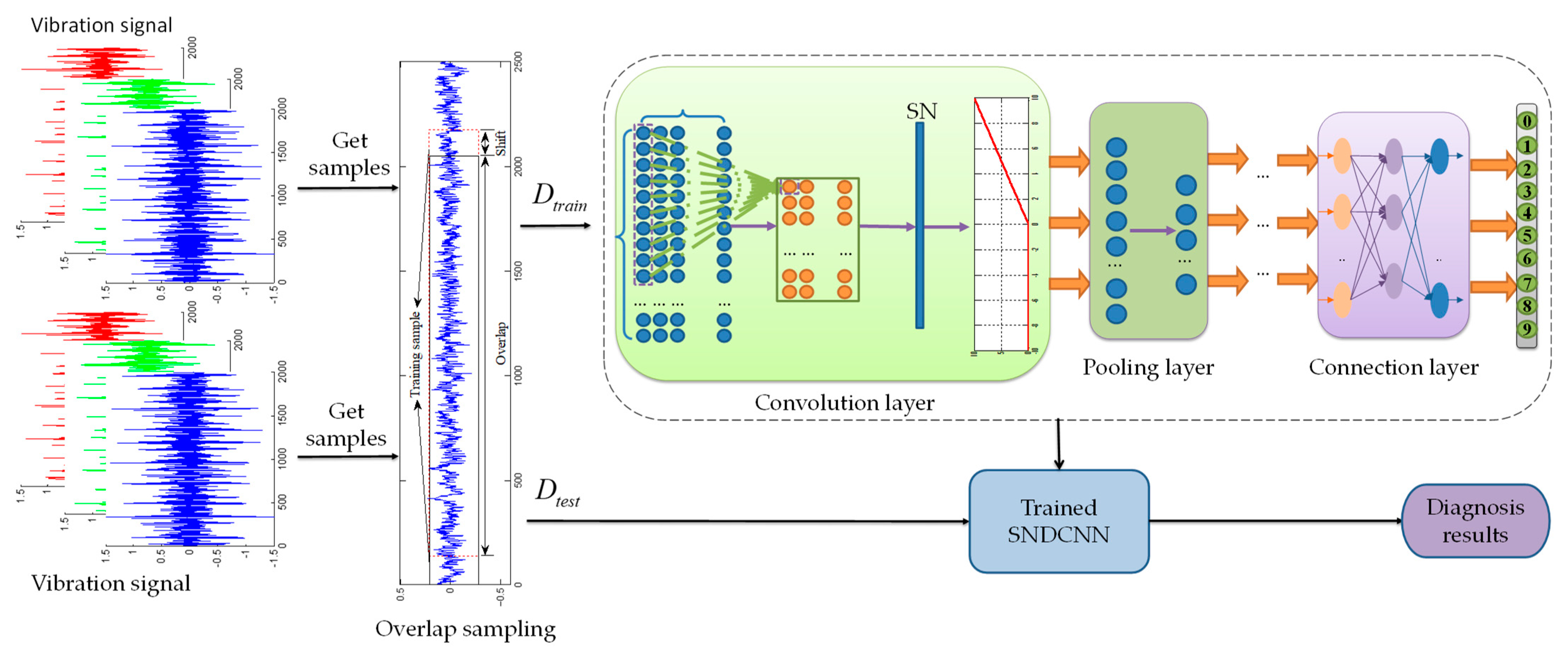
3. Rolling Bearing Fault Diagnosis Method Based on SNDCNN
3.1. Structural Parameters of the SNDCNN
3.2. Switchable Normalization
3.3. Adaptive Momentum Algorithm
3.4. Fault Diagnostic Process
- (1)
- Training Stage:
- (2)
- Testing Stage:
4. Experimental Verification
4.1. Case 1—Western Reserve University Rolling Bearing Data Analysis
4.1.1. Dataset Division
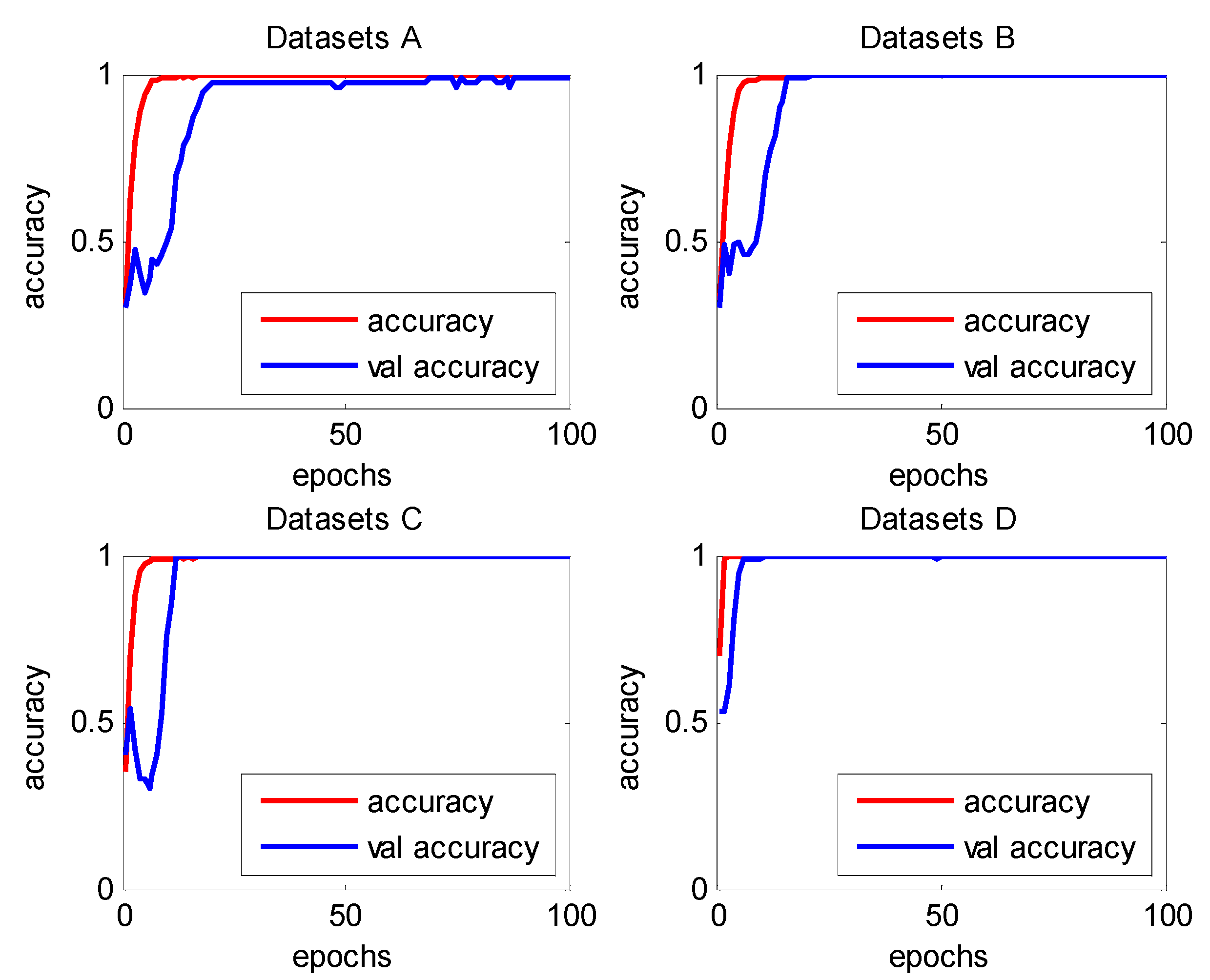
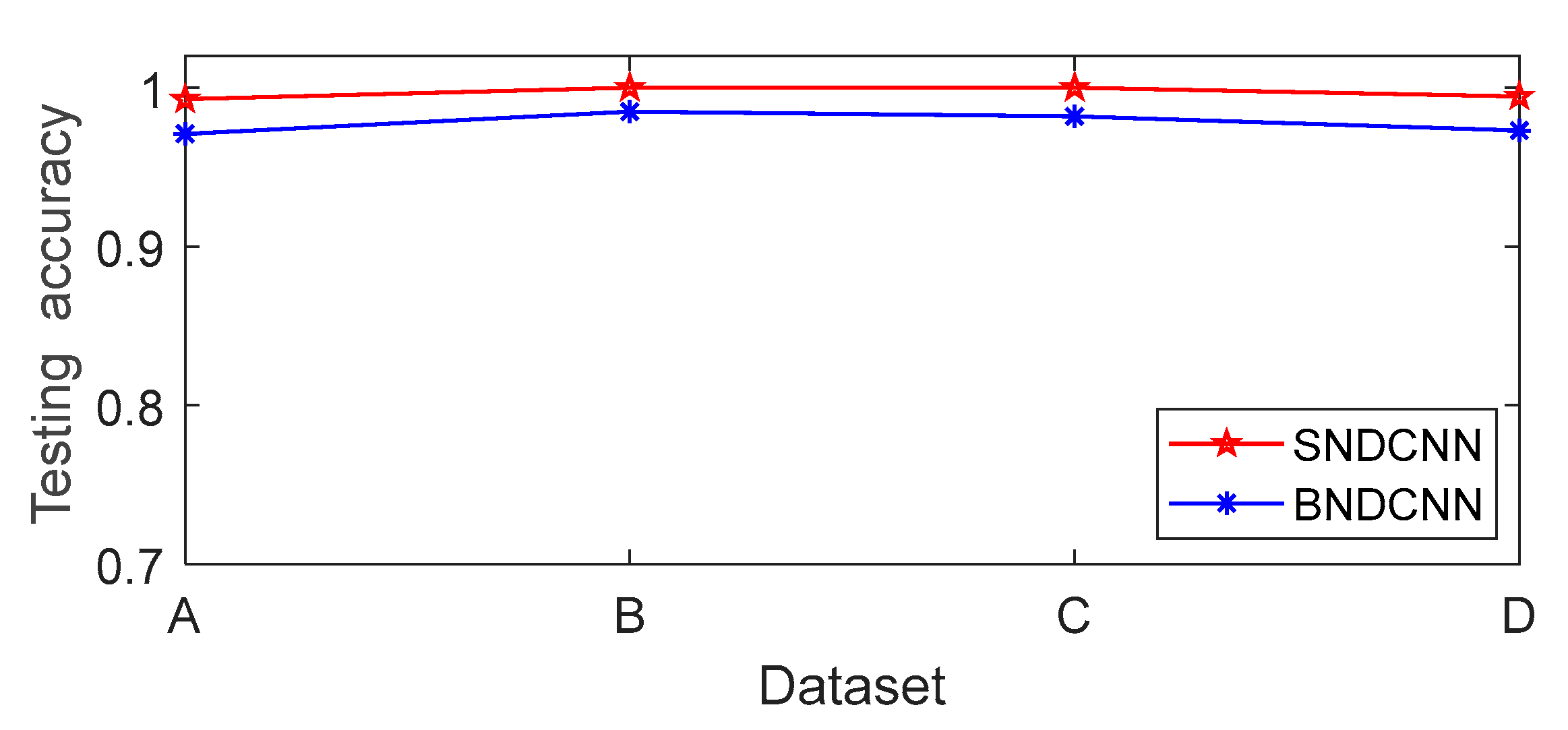
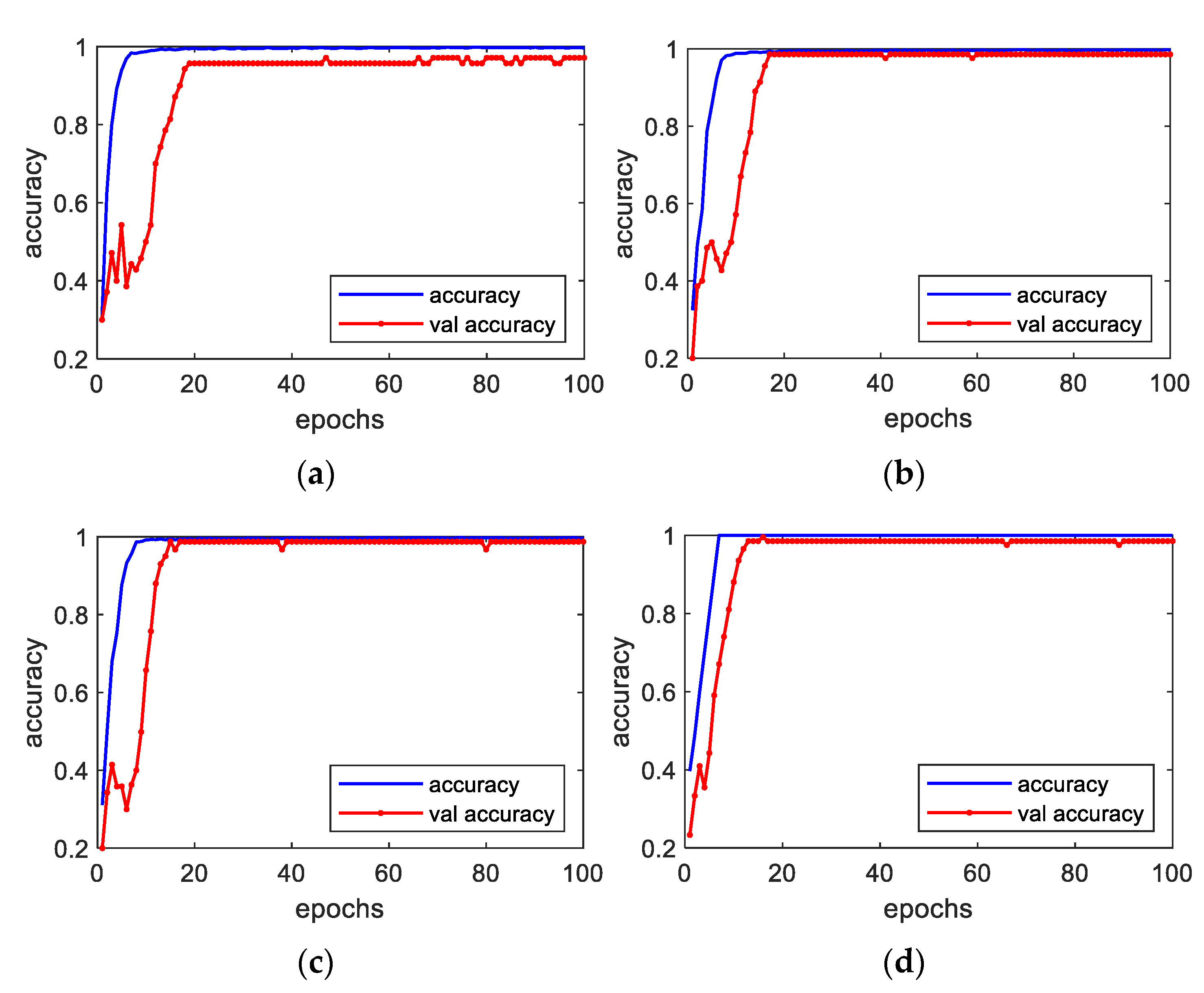
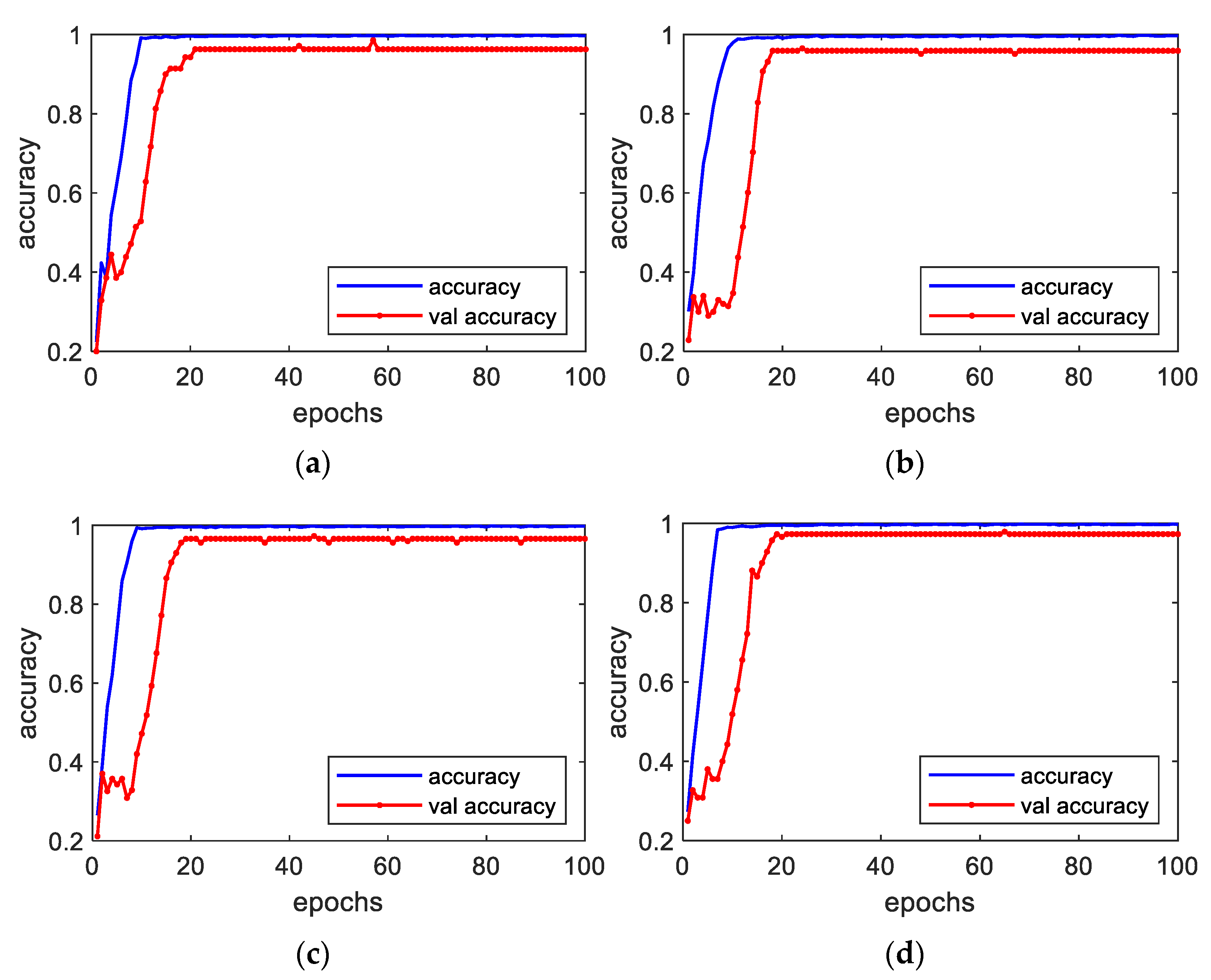
4.1.2. Diagnostic Results under Steady Conditions
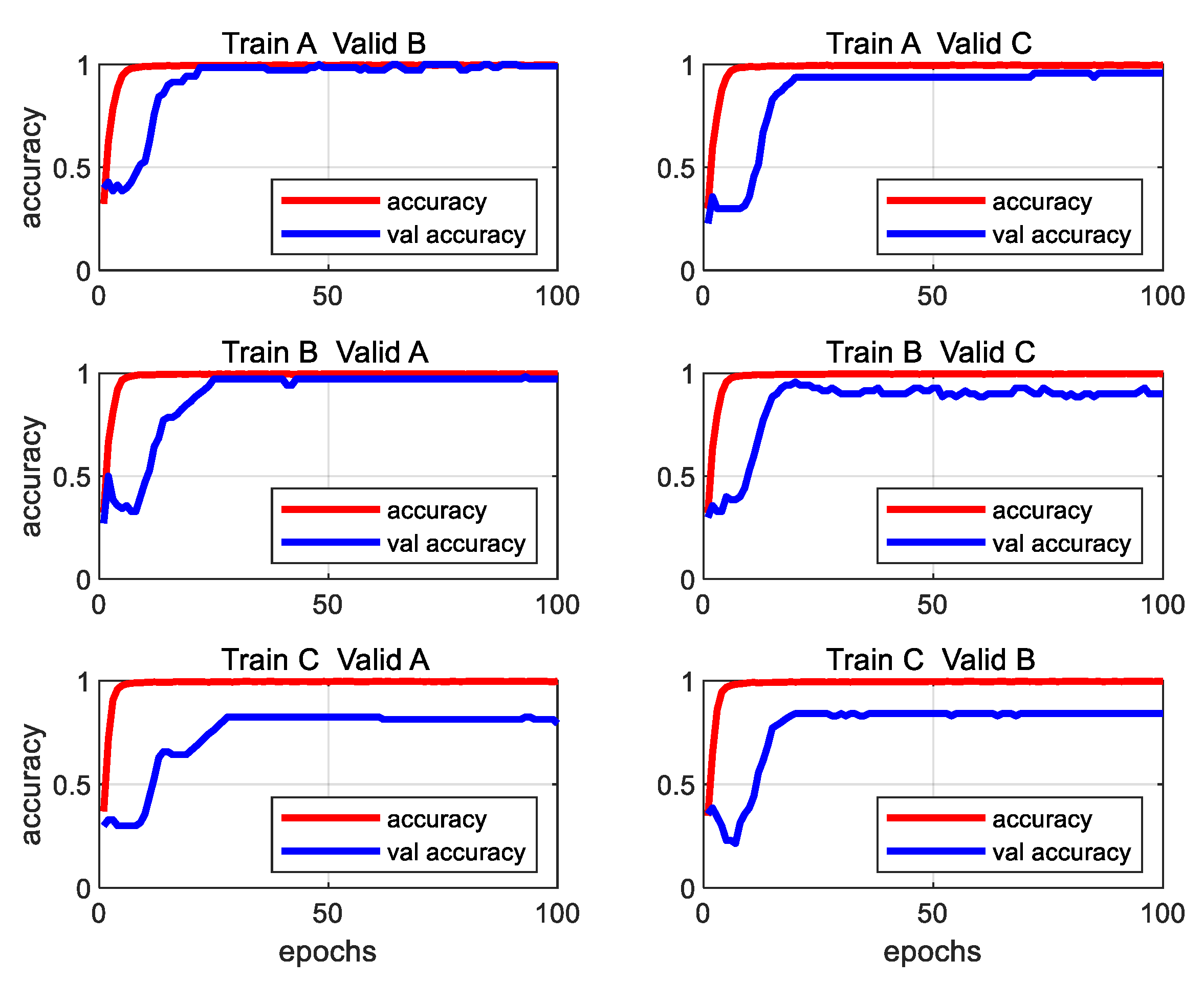
4.1.3. Diagnostic Results under Variable Load Conditions
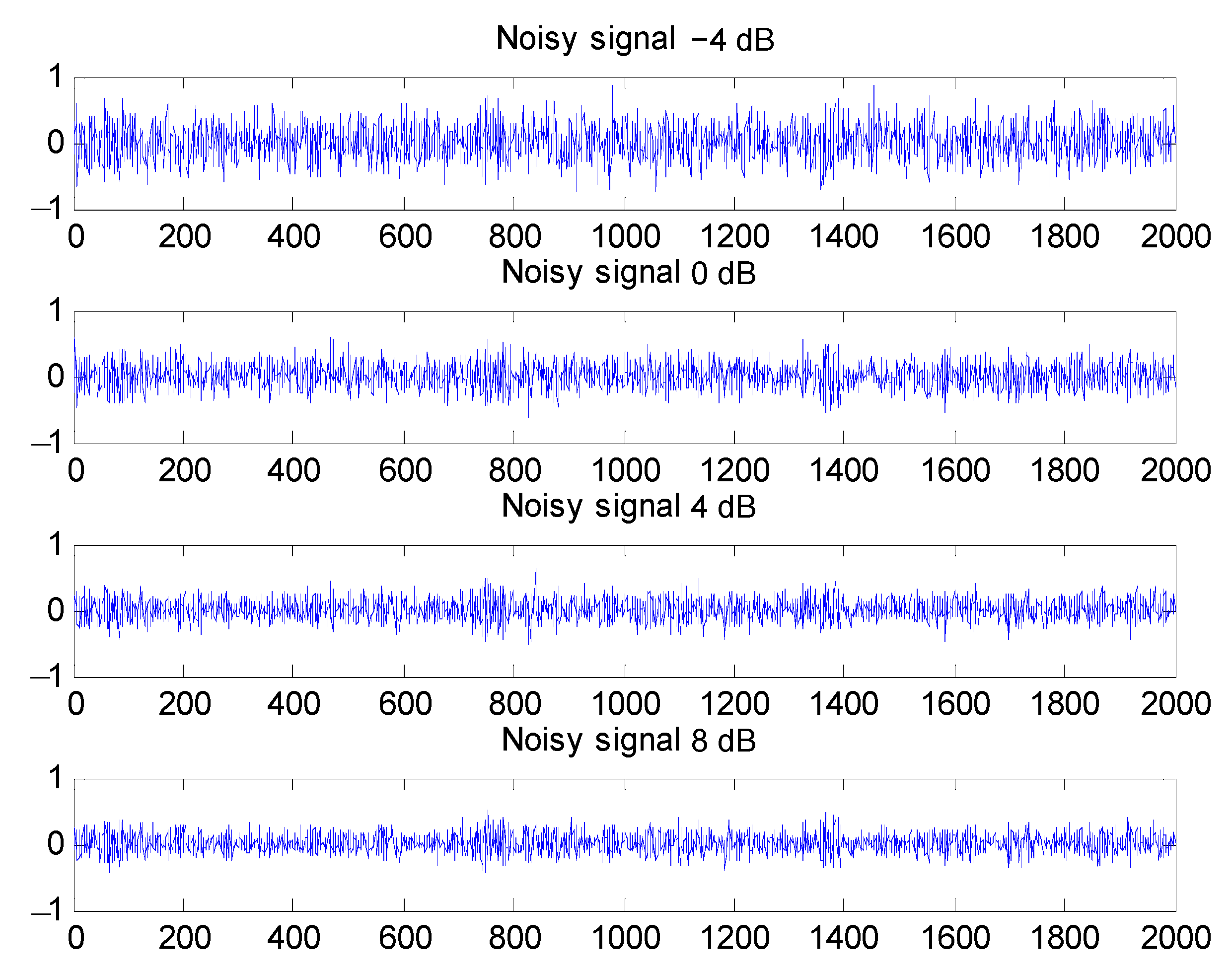
4.1.4. Diagnostic Results under Different Noise Conditions
4.2. Case 2—Rolling Bearing Test Platform Data Analysis
4.2.1. Test Bench Description
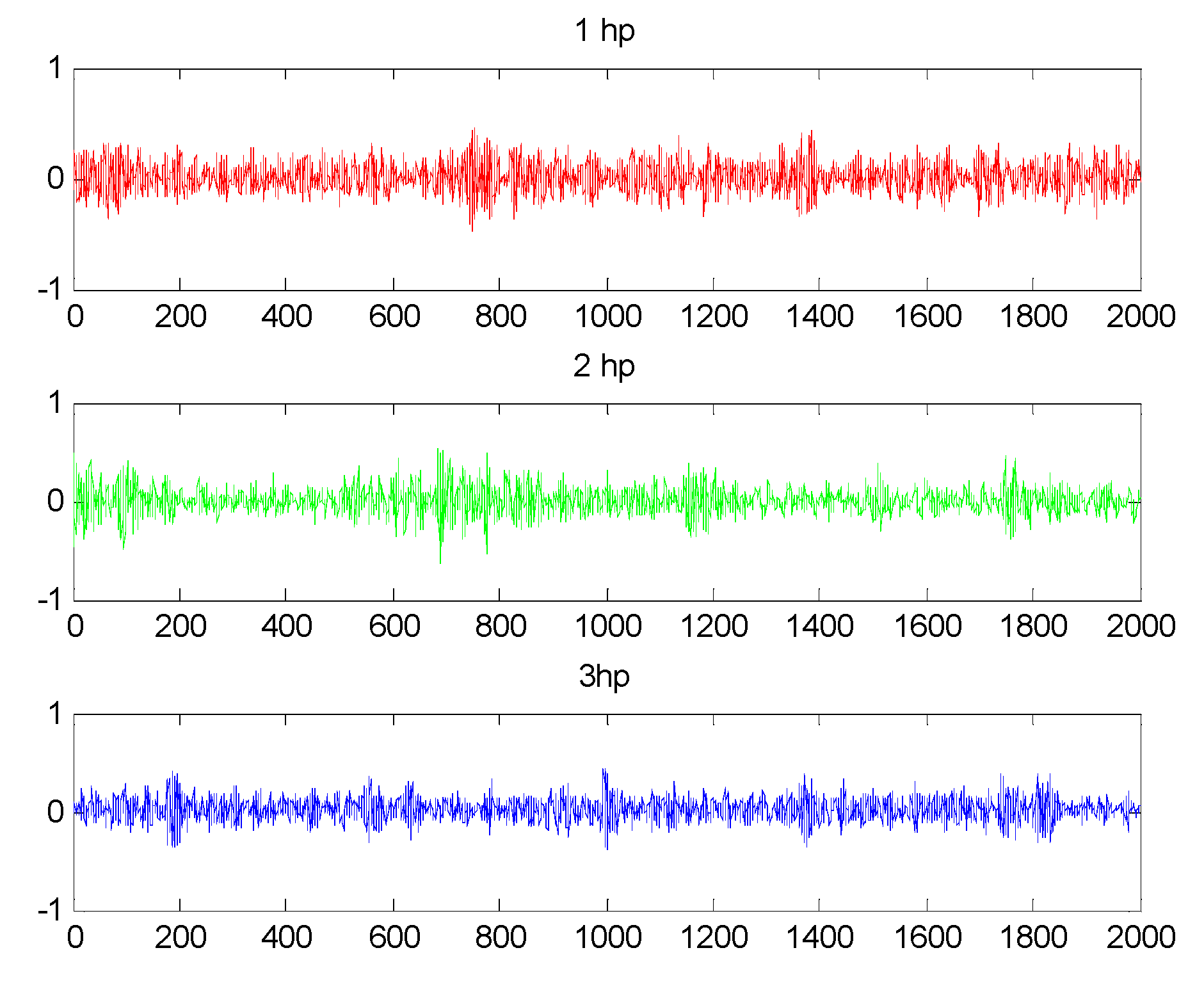
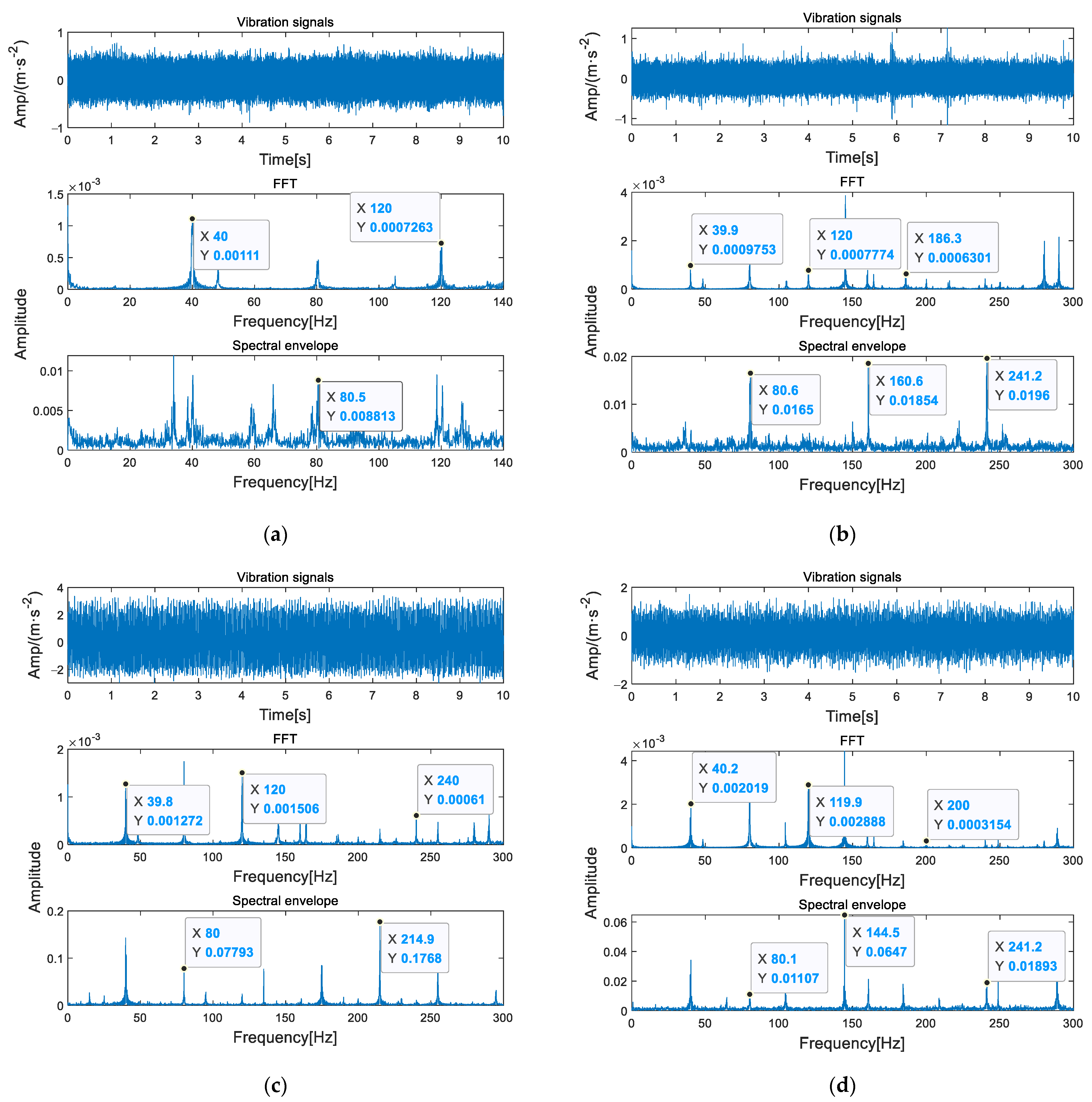
4.2.2. Bearing Fault Forms and Vibration Signal Analysis
4.2.3. Diagnostic Results under Steady Conditions
4.2.4. Diagnosis Results under Variable Speed Conditions
5. Conclusions
- The SNDCNN model, applicable to complex operating conditions, could directly input the raw vibration signal, and the fault detection rate reached 99.45% under multiple operating conditions.
- The method of increasing the convolution kernel width of the first layer and multi-layer convolution kernel stacking could effectively extract fault features and suppress high-frequency noise.
- The pooling operation of K-max pooling was used in the pooling layer, which could effectively retain the strong feature information.
- Each convolutional layer and fully connected layer adopted a switchable normalization method, which could effectively suppress overfitting and improve the model’s generalization performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description |
| SN | switchable normalization |
| DCNN | deep convolutional neural network |
| SVM | support vector machine |
| CNN | convolutional neural network |
| DTS | dislocated time series |
| IN | instance normalization |
| LN | layer normalization |
| BN | batch normalization |
| GN | group normalization |
| Adam | adaptive momentum |
| CWRU | Case Western Reserve University |
| EEMD | ensemble empirical mode decomposition |
| STFT | short-time Fourier transform |
| SNR | signal–noise ratio |
| MLP | multi-layer perceptron |
References
- Ambrozkiewicz, B.; Syta, A.; Gassner, A.; Georgiadis, A.; Litak, G.; Meier, N. The influence of the radial internal clearance on the dynamic response of self-aligning ball bearings. Mech. Syst. Signal Process. 2022, 171, 108954–108964. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Enrico, Z.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Huang, W.; Gao, G.; Li, N.; Jiang, X.; Zhu, Z. Time-Frequency Squeezing and Generalized Demodulation Combined for Variable Speed Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2018, 8, 2819–2829. [Google Scholar] [CrossRef]
- Li, J.; Wang, H.; Wang, X.; Zhang, Y. Rolling bearing fault diagnosis based on improved adaptive parameterless empirical wavelet transform and sparse denoising. Measurement 2020, 152, 107392. [Google Scholar] [CrossRef]
- Guo, J.; Zhen, D.; Li, H.; Shi, Z.; Gu, F.; Andrew, D.B. Fault feature extraction for rolling element bearing diagnosis based on a multi-stage noise reduction method. Measurement 2019, 139, 226–235. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.; Cao, H.; Zhang, X. Subband averaging kurtogram with dual-tree complex wavelet packet transform for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2020, 142, 106755. [Google Scholar] [CrossRef]
- Yu, K.; Lin, T.; Tan, J.; Ma, H. An adaptive sensitive frequency band selection method for empirical wavelet transform and its application in bearing fault diagnosis. Measurement 2019, 134, 375–384. [Google Scholar] [CrossRef]
- Cao, H.; Fan, F.; Zhou, K.; He, Z. Wheel-bearing fault diagnosis of trains using empirical wavelet transform. Measurement 2016, 82, 439–449. [Google Scholar] [CrossRef]
- Jiang, F.; Zhu, Z.; Li, W. An Improved VMD With Empirical Mode Decomposition and Its Application in Incipient Fault Detection of Rolling Bearin. IEEE Access 2018, 6, 44483–44493. [Google Scholar] [CrossRef]
- Yang, J.; Huang, D.; Zhou, D.; Liu, H. Optimal IMF selection and unknown fault feature extraction for rolling bearings with different defect modes. Measurement 2020, 157, 107660. [Google Scholar] [CrossRef]
- Li, J.; Yao, X.; Wang, H.; Zhang, J. Periodic impulses extraction based on improved adaptive VMD and sparse code shrinkage denoising and its application in rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2019, 126, 568–589. [Google Scholar] [CrossRef]
- Li, J.; Meng, Z.; Yin, N.; Pan, Z.; Cao, L.; Fan, F. Multi-source feature extraction of rolling bearing compression measurement signal based on independent component analysis. Measurement 2020, 172, 108908. [Google Scholar] [CrossRef]
- Hu, Y.; Bao, W.; Tu, X.; Li, F.; Li, K. An Adaptive Spectral Kurtosis Method and Its Application to Fault Detection of Rolling Element Bearings. IEEE Trans. Instrum. Meas. 2019, 69, 739–750. [Google Scholar] [CrossRef]
- Udmale, S.S.; Singh, S.K. Application of Spectral Kurtosis and Improved Extreme Learning Machine for Bearing Fault Classification. IEEE Trans. Instrum. Meas. 2019, 68, 4222–4233. [Google Scholar] [CrossRef]
- Sohaib, M.; Kim, J. Fault Diagnosis of Rotary Machine Bearings Under Inconsistent Working Conditions. IEEE Trans. Instrum. Meas. 2019, 69, 3334–3347. [Google Scholar] [CrossRef]
- Jin, G.; Zhu, T.; Akram, M.W.; Jin, Y.; Zhu, C. An Adaptive Anti-Noise Neural Network for Bearing Fault Diagnosis Under Noise and Varying Load Conditions. IEEE Access 2020, 8, 74793–74807. [Google Scholar] [CrossRef]
- Qin, M.; Yan, S.; Tang, X.; Xu, C. Deep Convolutional and LSTM Recurrent Neural Networks for Rolling Bearing Fault Diagnosis Under Strong Noises and Variable Loads. IEEE Access 2020, 8, 66257–66269. [Google Scholar]
- Wang, Z.; Yao, L.; Cai, Y. Rolling bearing fault diagnosis using generalized refined composite multiscale sample entropy and optimized support vector machine. Measurement 2020, 156, 107574. [Google Scholar] [CrossRef]
- He, C.; Wu, T.; Liu, C.; Chen, T. A novel method of composite multiscale weighted permutation entropy and machine learning for fault complex system fault diagnosis. Measurement 2020, 158, 107748. [Google Scholar] [CrossRef]
- Yuan, H.; Wu, N.; Chen, X.; Wang, Y. Fault diagnosis of rolling bearing based on shift invariant sparse feature and optimized support vector machine. Machines 2021, 9, 98. [Google Scholar] [CrossRef]
- Wan, L.; Gong, K.; Zhang, G.; Yuan, X.; Li, C.; Deng, X. An Efficient Rolling Bearing Fault Diagnosis Method Based on Spark and Improved Random Forest Algorithm. IEEE Access 2021, 9, 37866–37882. [Google Scholar] [CrossRef]
- Chen, F.; Cheng, M.; Tang, B.; Chen, B.; Xiao, W. Pattern recognition of a sensitive feature set based on the orthogonal neighborhood preserving embedding and adaboost_SVM algorithm for rolling bearing early fault diagnosis. Meas. Sci. Technol. 2020, 31, 105007. [Google Scholar] [CrossRef]
- Li, J.; Yao, X.; Wang, X.; Yu, Q.; Zhang, Y. Multiscale local features learning based on BP neural network for rolling bearing intelligent fault diagnosis. Measurement 2020, 153, 107419. [Google Scholar] [CrossRef]
- Wang, G.; Luo, Z.; Qin, X.; Leng, Y.; Wang, T. Fault identification and classification of rolling element bearing based on time-varying autoregressive spectrum. Mech. Syst. Signal Process. 2008, 22, 934–947. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Hauptmann, A.G. Simultaneous Bearing Fault Recognition and Remaining Useful Life Prediction Using Joint-Loss Convolutional Neural Network. IEEE Trans. Ind. Inform. 2020, 16, 87–96. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, J.; Zheng, Y.; Jiang, W.; Zhang, Y. Fault diagnosis of rolling bearings with recurrent neural network-based autoencoders. ISA Trans. 2018, 77, 167–178. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Z.; Zhang, X.; Zhang, W.; Xia, X. Fault diagnosis of rolling bearing under fluctuating speed and variable load based on TCO Spectrum and Stacking Auto-encoder. Measurement 2019, 138, 162–174. [Google Scholar] [CrossRef]
- Meng, Z.; Zhan, X.; Li, J.; Pan, Z. An enhancement denoising autoencoder for rolling bearing fault diagnosis. Measurement 2018, 130, 448–454. [Google Scholar] [CrossRef]
- Kong, X.; Mao, G.; Wang, Q.; Ma, H.; Yang, W. A multi-ensemble method based on deep auto-encoders for fault diagnosis of rolling bearings. Measurement 2020, 151, 107132. [Google Scholar] [CrossRef]
- Xiao, Y.; Shao, H.; Han, S.; Huo, Z.; Wan, J. Novel Joint Transfer Network for Unsupervised Bearing Fault Diagnosis From Simulation Domain to Experimental Domain. IEEE-ASME Trans. Mechatron. 2022, 27, 5254–5263. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587–106626. [Google Scholar] [CrossRef]
- Chen, X.; Wang, S.; Qiao, B.; Chen, Q. Basic research on machinery fault diagnostics: Past, present, and future trends. Front. Mech. Eng. 2018, 13, 264–291. [Google Scholar] [CrossRef]
- Guo, J.; Liu, X.; Li, S.; Wang, Z. Bearing Intelligent Fault Diagnosis Based on Wavelet Transform and Convolutional Neural Network. Shock Vib. 2020, 2020, 6380486. [Google Scholar] [CrossRef]
- He, F.; Ye, Q. A Bearing Fault Diagnosis Method Based on Wavelet Packet Transform and Convolutional Neural Network Optimized by Simulated Annealing Algorithm. Sensors 2022, 22, 1410. [Google Scholar] [CrossRef] [PubMed]
- Xiong, S.; Zhou, H.; He, S.; Zhang, L.; Xia, Q.; Xuan, J.; Shi, T. A Novel End-To-End Fault Diagnosis Approach for Rolling Bearings by Integrating Wavelet Packet Transform into Convolutional Neural Network Structures. Sensors 2020, 20, 17. [Google Scholar] [CrossRef]
- Guo, S.; Yang, T.; Gao, W.; Zhang, C. A novel fault diagnosis method for rotating machinery based on a convolutional neural network. Sensors 2018, 18, 1429. [Google Scholar] [CrossRef]
- Guo, S.; Yang, T.; Gao, W.; Zhang, C.; Zhang, Y. An intelligent fault diagnosis method for bearings with variable rotating speed based on pythagorean spatial pyramid pooling CNN. Sensors 2018, 18, 3857. [Google Scholar] [CrossRef]
- Sun, W.; Yao, B.; Zeng, N.; Chen, B.; He, Y.; Cao, X.; He, W. An intelligent gear fault diagnosis methodology using a complex wavelet enhanced convolutional neural network. Materials 2017, 10, 790. [Google Scholar] [CrossRef]
- Cao, X.; Chen, B.; Yao, B.; He, W. Combining translation-invariant wavelet frames and convolutional neural network for intelligent tool wear state identification. Comput. Ind. 2019, 106, 71–84. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, T.; Yang, W.; Fu, H.; Wu, W. A Robust Fault Diagnosis Method for Rolling Bearings Based on Deep Convolutional Neural Network. In Proceedings of the 2019 Prognostics and System Health Management Conference, Qingdao, China, 25–27 October 2019; pp. 1–6. [Google Scholar]
- Han, T.; Liu, C.; Wu, L.; Sumik, S.; Jiang, D. An adaptive spatiotemporal feature learning approach for fault diagnosis in complex systems. Mech. Syst. Signal Process. 2018, 117, 170–187. [Google Scholar] [CrossRef]
- Zhang, Y.; Xing, K.; Bai, R.; Sun, D.; Meng, Z. An enhanced convolutional neural network for bearing fault diagnosis based on time–frequency image. Measurement 2020, 157, 107667. [Google Scholar] [CrossRef]
- Liu, R.; Meng, G.; Yang, B.; Sun, C.; Chen, X. Dislocated time series convolutional neural architecture: An intelligent fault diagnosis approach for electric machine. IEEE Trans. Ind. Inform. 2017, 13, 1310–1320. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A new convolutional neural network-based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Zhou, P.; Zhou, G.; Zhu, Z.; Tang, C.; He, Z.; Li, W.; Jiang, F. Health monitoring for balancing tail ropes of a hoisting system using a convolutional neural network. Appl. Sci. 2018, 8, 1346. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Yan, R.; Gao, R. A New Intelligent Bearing Fault Diagnosis Method Using SDP Representation and SE-CNN. IEEE Trans. Instrum. Meas. 2020, 69, 2377–2389. [Google Scholar] [CrossRef]
- Shao, H.; Xia, M.; Han, G.; Zhang, Y.; Wang, J. Intelligent Fault Diagnosis of Rotor-Bearing System Under Varying Working Conditions With Modified Transfer Convolutional Neural Network and Thermal Images. IEEE Trans. Instrum. Meas. Info. 2021, 17, 3488–3496. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Z.; Yang, G.; Wu, C.; Ye, Q. An Improved Fault Diagnosis Using 1D-Convolutional Neural Network Model. Electronics 2020, 10, 59. [Google Scholar] [CrossRef]
- Xue, Y.; Dou, D.; Yang, J. Multi-fault diagnosis of rotating machinery based on deep convolution neural network and support vector machine. Measurement 2020, 156, 107571. [Google Scholar] [CrossRef]
- Luo, P.; Zhang, R.; Ren, J.; Peng, Z.; Li, J. Switchable Normalization for Learning-to-Normalize Deep Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 712–728. [Google Scholar] [CrossRef] [PubMed]
- Yao, D.; Yang, J.; Cheng, X.; Wang, X. Railway rolling bearing fault diagnosis based on muti-scale IMF permutation entropy and SA-SVM classifier. J. Mech. Eng. 2018, 54, 168–176. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, X.; Zhang, X.; He, Z. A novel intelligent gear fault diagnosis model based on EMD and multi-class TSVM. Measurement 2012, 45, 30–40. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, S. Fault diagnosis of roller bearing based on relative wavelet energy. J. Electron. Meas. Instrum. 2011, 25, 44–49. [Google Scholar] [CrossRef]
- Zhang, C.; Feng, J.; Hu, C.; Liu, Z.; Cheng, L.; Zhou, Y. An Intelligent Fault Diagnosis Method of Rolling Bearing Under Variable Working Loads Using 1-D Stacked Dilated Convolutional Neural Network. IEEE Access 2020, 8, 63027–63042. [Google Scholar] [CrossRef]



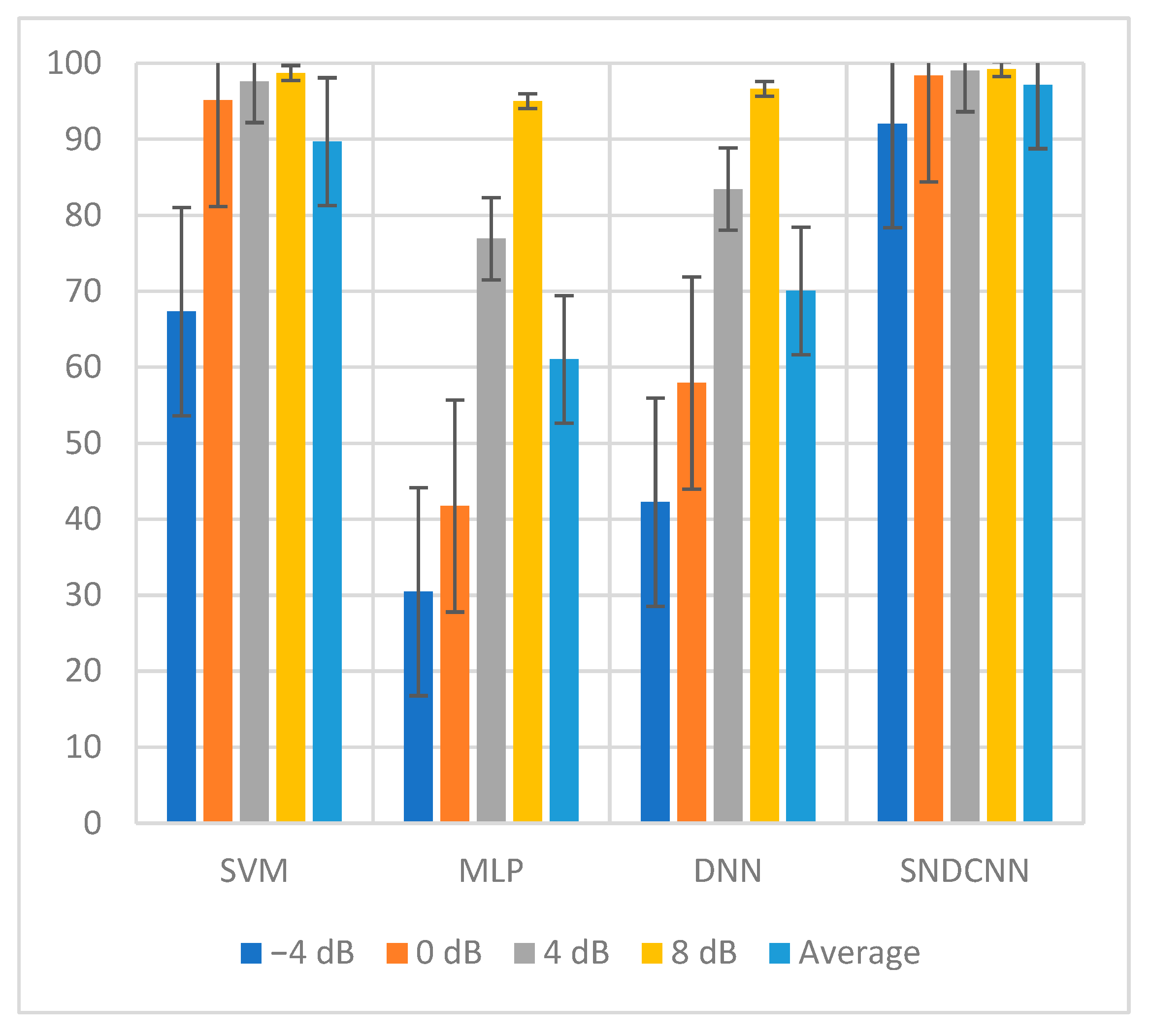


| No. | Layer Type | Size | Stride | Kernel Number | Padding (Yes or No) |
|---|---|---|---|---|---|
| 1 | C1 | 80 × 1 | 8*1 | 8 | Y |
| 2 | P1 | 4 × 1 | 2*1 | 16 | N |
| 3 | C2 | 5 × 1 | 1*1 | 32 | Y |
| 4 | P2 | 2 × 1 | 2*1 | 32 | N |
| 5 | C3 | 3 × 1 | 1*1 | 64 | Y |
| 6 | P3 | 2 × 1 | 2*1 | 64 | N |
| 7 | C4 | 3 × 1 | 1*1 | 64 | Y |
| 8 | P4 | 2 × 1 | 2*1 | 64 | N |
| 9 | C5 | 3 × 1 | 1*1 | 64 | Y |
| 10 | P5 | 2 × 1 | 2*1 | 64 | N |
| 11 | C6 | 3 × 1 | 1*1 | 64 | Y |
| 12 | P6 | 2 × 1 | 2*1 | 64 | N |
| 13 | F1 | 100 | 100 | 1 | N |
| 14 | Softmax | 10 | 10 | 1 | N |
| Fault Location | None | Ball | Inner Race | Outer Race | Load (hp) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Labels | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Fault Diameter (inches) | 0 | 0.007 | 0.014 | 0.021 | 0.007 | 0.014 | 0.021 | 0.007 | 0.014 | 0.021 | ||
| A | Training | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 1 |
| Testing | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | ||
| Validation | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | ||
| B | Training | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 2 |
| Testing | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | ||
| Validation | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | ||
| C | Training | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 3 |
| Testing | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | ||
| Validation | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | ||
| D | Training | 2400 | 2400 | 2400 | 2400 | 2400 | 2400 | 2400 | 2400 | 2400 | 2400 | 1,2,3 |
| Testing | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | ||
| Validation | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | ||
| Detection Rate | Loss Function | Time (ms/step) | Iterations | |
|---|---|---|---|---|
| Dataset A | 99.27% | 0.061 | 0.653 | 100 |
| Dataset B | 100.00% | 0.054 | 0.749 | 100 |
| Dataset C | 100.00% | 0.011 | 0.671 | 100 |
| Dataset D | 99.45% | 0.063 | 0.687 | 100 |
| Diagnosis Method | Accuracy (%) | |||
|---|---|---|---|---|
| Dataset A | Dataset B | Dataset C | Dataset D | |
| EEMD + SVM [51] | 92.25 | 93.16 | 92.56 | 87.25 |
| STFT + SVM [52] | 94.76 | 93.55 | 95.05 | 86.39 |
| WT + BP [53] | 93.65 | 92.14 | 94.85 | 84.27 |
| BPNN [54] | 62.11 | — | — | — |
| MSCNN [54] | 98.46 | — | — | — |
| DTS-CNN [54] | 99.14 | — | — | — |
| 1D-DCNN [54] | 98.43 | — | — | — |
| SNDCNN | 99.27 | 100.00 | 100.00 | 99.45 |
| Detection Rate | Loss Function | Time (ms/step) | Iterations | |
|---|---|---|---|---|
| A→B | 99.18% | 0.101 | 0.674 | 100 |
| A→C | 95.72% | 0.431 | 0.703 | 100 |
| B→A | 97.14% | 0.372 | 0.689 | 100 |
| B→C | 90.00% | 0.624 | 0.683 | 100 |
| C→A | 79.40% | 3.195 | 0.714 | 100 |
| C→B | 84.15% | 0.961 | 0.692 | 100 |
| Average | 90.93% | 0.947 | 0.693 | 100 |
| SVM | MLP | DNN | SNDCNN | |
|---|---|---|---|---|
| −4 dB | 67.35 | 30.48 | 42.24 | 92.05 |
| 0 dB | 95.15 | 41.75 | 57.93 | 98.37 |
| 4 dB | 97.62 | 76.93 | 83.45 | 99.03 |
| 8 dB | 98.73 | 95.02 | 96.64 | 99.25 |
| Average | 89.7125 | 61.045 | 70.065 | 97.175 |
| Type | Diameter of the Ball | Pitch Diameter | Ball Number | Contact Angle |
|---|---|---|---|---|
| TPI6205 | 0.3126 inches | 1.537 inches | 9 | 0 |
| Filename | Load | Rotational Speed (rpm) | Filename | Load | Rotational Speed (rpm) | Comment |
|---|---|---|---|---|---|---|
| Test_001 | 0 | 800 | Test_013 | 3 | 800 | |
| Test_002 | 0 | 1600 | Test_014 | 3 | 1600 | |
| Test_003 | 0 | 2400 | Test_015 | 3 | 2400 | |
| Test_004 | 0 | 3200 | Test_016 | 3 | 3200 | |
| Test_005 | 1 | 800 | Test_017 | 0 | raising speed 40 rpm/s | 800 to 3200 rpm |
| Test_006 | 1 | 1600 | Test_018 | 0 | raising speed 80 rpm/s | 800 to 3200 rpm |
| Test_007 | 1 | 2400 | Test_019 | 1 | raising speed 40 rpm/s | 800 to 3200 rpm |
| Test_008 | 1 | 3200 | Test_020 | 1 | raising speed 80 rpm/s | 800 to 3200 rpm |
| Test_009 | 2 | 800 | Test_021 | 2 | raising speed 40 rpm/s | 800 to 3200 rpm |
| Test_010 | 2 | 1600 | Test_022 | 2 | raising speed 80 rpm/s | 800 to 3200 rpm |
| Test_011 | 2 | 2400 | Test_023 | 3 | raising speed 40 rpm/s | 800 to 3200 rpm |
| Test_012 | 2 | 3200 | Test_024 | 3 | raising speed 80 rpm/s | 800 to 3200 rpm |
| Fault Location | None | Ball | Inner Race | Outer Race | Load | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Labels | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Fault Degree | None | Mild | Moderate | Severe | Mild | Moderate | Severe | Mild | Moderate | Severe | ||
| A | Training | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 0 |
| Testing | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | ||
| B | Training | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 1 |
| Testing | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | ||
| C | Training | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 2 |
| Testing | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | ||
| D | Training | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 800 | 3 |
| Testing | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | ||
| Detection Rate | Loss Function | Time (ms/step) | Iterations | |
|---|---|---|---|---|
| Dataset A | 97.14% | 0.083 | 0.638 | 100 |
| Dataset B | 98.57% | 0.069 | 0.726 | 100 |
| Dataset C | 98.71% | 0.067 | 0.645 | 100 |
| Dataset D | 99.52% | 0.069 | 0.633 | 100 |
| Fault Location | None | Ball | Inner Race | Outer Race | Load | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Labels | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Fault Degree | None | Mild | Moderate | Severe | Mild | Moderate | Severe | Mild | Moderate | Severe | ||
| A | Training | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 |
| Testing | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | ||
| B | Training | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 1 |
| Testing | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | ||
| C | Training | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 2 |
| Testing | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | ||
| D | Training | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 3 |
| Testing | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 | ||
| Detection Rate | Loss Function | Time (ms/step) | Iterations | |
|---|---|---|---|---|
| Dataset A | 95.79% | 0.089 | 0.652 | 100 |
| Dataset B | 95.33% | 0.092 | 0.701 | 100 |
| Dataset C | 97.69% | 0.081 | 0.633 | 100 |
| Dataset D | 98.52% | 0.079 | 0.655 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Cao, Y.; Luan, J.; Ao, R.; Feng, W.; Li, S. A Rolling Bearing Fault Diagnosis Method Based on Switchable Normalization and a Deep Convolutional Neural Network. Machines 2023, 11, 185. https://doi.org/10.3390/machines11020185
Han X, Cao Y, Luan J, Ao R, Feng W, Li S. A Rolling Bearing Fault Diagnosis Method Based on Switchable Normalization and a Deep Convolutional Neural Network. Machines. 2023; 11(2):185. https://doi.org/10.3390/machines11020185
Chicago/Turabian StyleHan, Xiaoyu, Yunpeng Cao, Junqi Luan, Ran Ao, Weixing Feng, and Shuying Li. 2023. "A Rolling Bearing Fault Diagnosis Method Based on Switchable Normalization and a Deep Convolutional Neural Network" Machines 11, no. 2: 185. https://doi.org/10.3390/machines11020185
APA StyleHan, X., Cao, Y., Luan, J., Ao, R., Feng, W., & Li, S. (2023). A Rolling Bearing Fault Diagnosis Method Based on Switchable Normalization and a Deep Convolutional Neural Network. Machines, 11(2), 185. https://doi.org/10.3390/machines11020185






