On Constraints and Parasitic Motions of a Tripod Parallel Continuum Manipulator

Abstract

A parallel continuum manipulator (PCM) is a mechanism of closed-loop morphology with flexible elements such that their deformation contributes to its mobility. Flexible hexapods are six-degrees-of-freedom (DoF) fully parallel continuum mechanisms already presented in the literature. Devices of reduced mobility, i.e., lower mobility than six DoF, have not been studied so far. An essential characteristic of lower mobility mechanisms is that reduced mobility is due to kinematic constraints generated by mechanical arrangements and passive joints. In rigid-link parallel manipulators, those constraints are expressed as a set of equations relating to the parameters representing the end effector’s pose. As a consequence, independent output pose variables are controllable with the position equations, while dependent output variables undergo parasitic motions. In this paper, the performance of a tripod-type parallel continuum manipulator, $3P\underline{F}S$, is compared with the operation of its rigid counterpart $3\underline{P}RS$. We will show that in PCMs there are no such geometric constraints expressible with algebraic equations, but it is difficult to perform some types of motion in the end effector with the input torques. Another goal of this paper is to evaluate such limitation of motion in a tripod-like PCM and compare it with the constraints of the rigid $3\underline{P}RS$. Finally, the paper shows that there are strong similarities in the reduced mobility of both mechanisms.

1. Introduction

Parallel kinematic mechanisms (PKMs) are closed-loop mechanisms with rigid links and kinematic joints that connect an end effector to a fixed frame via several kinematic chains with actuators distributed on them to achieve better stiffness and accuracy [1]. The hexapod is a typical mechanism of this type with full mobility (six DoFs). Lower mobility PKMs are those that have less than six DoFs. Such mechanisms are subjected to a set of permanent geometrical constraints that condition some output motions. In some cases, those geometric constraints impose a certain constant value on several of the output parameters, as in a Delta robot with translational three-DoF motion. In other cases, the geometric constraints generate a set of equations that relate some output parameters to others, as in tripod parallel kinematic machines of the type $3\underline{P}RS$ chosen in this paper to illustrate the subject, where two translational output coordinates and one orientation angle are dependent on the other two orientation angles and the other one translational coordinate. The type of motion resultant is a $2R1T$ mixed-freedom motion [2].

The constraint analysis is a key task of the kinematic analysis of a mechanism because it determines the type of motion allowed at the end effector, and then, it shows the suitability of the morphology chosen to accomplish the objective motions of the machine. However, it is also fundamental in order to define the inverse kinematic (IK) position problem. This is because we need to know which are the independent output pose variables to be used to control the IK problem and which are the functions that generate the values of the dependent output variables. With that information, the output pose is completely defined and the IK problem can be solved using the loop-closure equations of each limb. In the case of the tripod chosen for this paper, $3\underline{P}RS$, these are two angles and one coordinate, while the dependent output parameters acquire values along motions that are called parasitic motions [3,4]. The permanent geometrical constraints imposed are due to passive kinematic pairs and rigid links not controlled by the actuator system.

Compliant mechanisms are a group of mechanisms that acquire mobility thanks to the relative flexibility of some of their parts [5,6,7]. A subset of them is the so-called continuum mechanisms, these are slender systems with a flexible backbone actuated using parallel assemblies of tendons. They are motivated by the problem of manipulation in confined, hard-to-reach workspaces [8], and suitable for minimally invasive procedures due to their dexterity and ease of miniaturization [9,10]. An evolution of the aforementioned systems is parallel continuum mechanisms (PCMs). These are flexible mechanical devices with a rigid end effector that is connected to a fixed frame using flexible slender links whose nonlinear deformation is the cause of its mobility [11]. An appropriate model for the nonlinear deformation of the rods used as elements is the Cosserat rod model [12,13]. This model is used extensively, and it can be mathematically expressed in different ways, a nonlinear system of differential equations (ODEs) being the most accurate one. The closed-loop system of flexible rods and rigid elements generates a coupling of large deformation modeling equations and force equilibrium ones to accommodate the deformation’s internal forces and moments to the load. A sustained line of research on hexapod-like flexible devices has been performed, solving a variety of problems such as real-time position control and elastic analysis [14,15,16,17,18,19].

In the case of parallel continuum mechanisms, permanent constraints to reduce the full mobility as in the above-mentioned tripod are not feasible because the flexible links can deform under actuation and load reaching any configuration in the space. However, some mechanical arrangements can introduce a much higher limitation of deformation in some directions, producing a similar constraining effect. Nevertheless, the resultant type of motion can no longer be obtained with an algebraic manipulation of some geometric constraints, and the expected relationships between output parameters cannot be obtained in closed form.

In this paper, we are aiming to show that PCMs of lower mobility exist, they have strong similarities to their rigid-links counterparts, their basic kinematic principles apply equally, and whether numerical procedures have to be devised to perform their kinematic constraint analysis. In rigid lower-mobility parallel manipulators, the kinematic constraints that reduce their mobility are defined by a set of equations. In the case of parallel continuum mechanisms, these geometric constraints expressible with algebraic equations do not exist. In this paper, we will try to propose an analytical expression that related the output independent parameters to the parasitic motion. To better understand this and other aspects of the kinematics of this type of mechanism, we propose the analysis of a flexible $3P\underline{F}S$ parallel continuum tripod model, and introduce some changes to the above-mentioned flexible hexapod already studied in the literature. Then, a numerical analysis will be used to solve the forward kinematics (FK) position problem following the procedure in [14] with some modifications. By introducing any set of inputs in that FK problem, it is possible to obtain the possible output motion, to compare it to the rigid-link tripod $3\underline{P}RS$, and to deduce from those numerical results the type of motion and the parasitic motions.

2. Method

The goal of this research is to verify if tripod PCMs have a type of motion, constraint equations, and parasitic motions that match the results in their rigid-links PKM counterparts, and if the constraint analysis on the latter applies to the former. In order to achieve the goal of this research we will follow the following procedure.

First, we choose a classical lower mobility PKM with mixed freedoms, the rigid-link $3\underline{P}RS$ tripod (see Figure 1), as a way of example to demonstrate the relevance of the problem of constraint analysis in closed-loop spatial mechanisms.

The family of tripod-like parallel mechanisms is a paradigmatic example because it fulfills several conditions: it has a high number of constraints, the constraints are coupled so that output motions are related between them, it has symmetry, it has many different variants, and it has been extensively studied in the literature using many different kinematic methods. This type of spatial mechanism has reduced mobility to 3 degrees of freedom, involving three geometrical constraints; and very often the resultant type of motion on the end effector is a $2R1T$ (2 rotational and 1 translational). This means that the constraint equations impose a set of equations among the output parameters of the end effector such that the other 2 translations and the 1 rotation parameters are dependent on the independent ones, and hence, as motion is produced, we acquire values that are called parasitic motions. For our purpose, we have chosen the symmetric geometric arrangement shown in Figure 1. The three limbs are placed in vertical planes ${\pi }_i$ ${120}^{\circ }$ apart. The linear actuators are vertical and fixed to the base at points $A_i$. The end effector is an equilateral triangle with barycenter at P and circumradius r and spherical joints at its vertices $B_i$ join with rigid links of length L attached to revolute pairs at $C_i$. These are oriented with vectors ${\mathbf{u}}_i$ normal to ${\pi }_i$.

The constraint analysis of this PKM is done using Euler–Rodrigues parameters to express the orientation of the end effector. This redundant parametrization is an alternative to the use of any set of three angles (Euler angles for example). Redundant parametrizations avoid the use of trigonometric functions in the analysis and generate polynomial equations for easier analysis. By using the geometric conditions imposed by passive revolute joints on the feasible output motion of the end effector, it is possible to get a closed-form solution of the equations that relate output parameters between them. That result shows the type of output motion of the mechanism, and the constrained motion of the dependent output parameters, i.e., the parasitic motion. These results serve as reference comparisons for the kinematic analysis of the corresponding flexible mechanism.

Second, we devise a lower mobility PCM with 3 DoF looking for an analogy to the rigid-link tripod. The 6-degrees-of-freedom flexible hexapod shown in Figure 2, where the end effector is connected to 6 flexible rods whose length is controlled by actuators, has been studied in [14]. There, the FK and IK problems are solved using the Cosserat rod model for the nonlinear deformation of flexible rods, and the minimization of a set of geometric and force equilibrium conditions. It requires a known home position configuration so that contiguous configurations are solved with a boundary value problem upon slight changes of either input or output variables.

The hexapod mechanism in Figure 2 can be modified to get the tripod-like PCM shown in Figure 3. The end of the rods $(2j-1)$ and $2j$ ($j=1,2,3$) are joined to the end effector at coincident points $B_{(2j-1)}$ and $B_{2j}$ with a single spherical joint that introduces no restriction of the rod’s self-rotation. The same rods $(2j-1)$ and $2j$ are connected to the base at fixed points $A_{(2j-1)}$ and $A_{\left(2j\right)}$ distributed symmetrically at circumradius $r_A$ and with a fixed vertical orientation, again with no restriction of intrinsic rotation so that torsion effects on the rods are avoided. At the connection to the fixed base, rods are conducted through said guiding holes $A_i$ to the 3 linear actuators j below the base that control the length of the rods $(2j-1)$ and $2j$ together ($j=1,2,3$). Rods are free to undergo deformations between the base and the end effector, being subjected only to bending, not torsion, shear, or axial deformations. Due to the arrangements of the flexible rods, the bending of each pair from $A_{(2j-1)}$ and $A_{\left(2j\right)}$ to $B_{(2j-1)}=B_{\left(2j\right)}$ is easier about an horizontal axis of direction $A_{(2j-1)}{A}_{\left(2j\right)}$, being analogous morphology to the $\underline{P}RS$ kinematic chain used in the above-mentioned tripod PKM. The resultant PCM is denoted $3P\underline{F}S$, where F indicates the bending flexibility of the limb.

The following step is to solve the position problem, i.e., to evaluate the relationship between the location of the end effector platform under some load and the effective length $L_i$ of each pair of flexible rods. By effective length we mean the longitude of the rod that can deform, i.e., the one between the attachments to fixed frame $A_i$ and the join to end effector at $B_i$. The location of the end effector platform is depicted through the combination of the position vector of reference point P in the fixed frame, $\mathbf{p}$, and the orientation of the moving frame with respect to the fixed frame given by the rotation matrix ${\mathbf{R}}_{EE}$. The FK problem determines the pose of the end effector, i.e., the position vector $\mathbf{p}$ and the rotation matrix ${\mathbf{R}}_{EE}$ when each rod i takes a certain value of its effective length $L_i$ and a given load is imposed. Its solution is straightforward using the procedure in [14] because the tripod PCM works, in this case, as a particular type of hexapod morphology actuated with 6 input lengths that are equal two by two $L_{(2j-1)}=L_{\left(2j\right)}$ ($j=1,2,3$).

However, the IK problem cannot be solved straightforwardly because to start the process we need to introduce a desired output pose of the end effector. For that, we need to know which are the independent parameters that can be used and which is the constrained value of the dependent ones. Again, as in classical PKMs we need to solve a constraint analysis first. In this paper, we will check if the constraint analysis performed for the rigid-link PKM is valid for the PCM, and if we can use the same independent output variables and the same constraint equations.

For that purpose, the final step in this study is to introduce a variety of input values in the FK solver of the tripod PCM, obtain the output pose parameters, and verify the degree of accomplishment of the constraint equations obtained for the tripod PKM.

3. Results

In this section we will elaborate on the above-mentioned methodology: first, to deduce the constraint equations applicable and the parasitic motions produced in the rigid-link parallel mechanism $3\underline{P}RS$; second, to perform the kinematic analysis of the analogous flexible parallel continuum mechanism; third, to compare and discuss the fulfillment of $3\underline{P}RS$ constraint equations with the simulated output motions of the $3P\underline{F}S$.

3.1. Constraint Analysis of a $3\underline{P}RS$ Tripod using Euler–Rodrigues Parameters

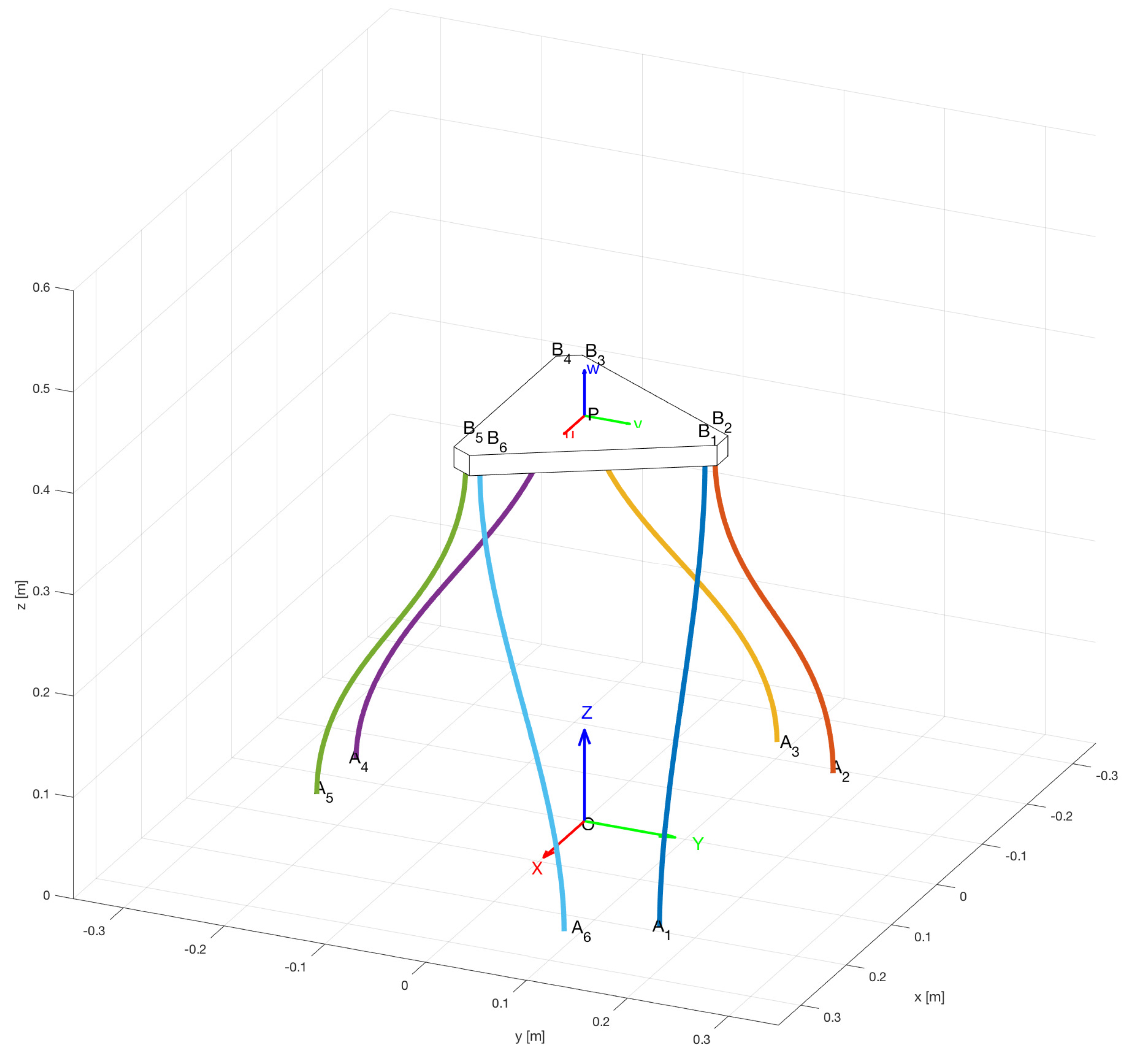
The rigid-link parallel kinematic mechanism chosen for the discussion is a tripod-like mechanism with the $3\underline{P}RS$ morphology, as shown in Figure 1. The mechanism is formed by a rigid end effector joined by spherical joints to rigid links of constant length L, that are joined to vertical linear actuators through revolute joints of horizontal axes. A moving frame is attached to the end effector at reference point P, whose position in a fixed frame is $\mathbf{p}={[x,y,z]}^T$. The orientation of the moving frame with respect to the fixed frame, i.e., orientation of the end effector, is defined either using a rotation matrix ${\mathbf{R}}_{EE}$ or Euler–Rodrigues parameters (a unit quaternion $\tilde{\mathbf{e}}$). The position vector of spherical joints’ attachment points $B_i$ expressed in the end effector’s frame is ${\mathbf{r}}_i$. The position vector of the actuators’ attachment point $A_i$ expressed in the fixed frame attached to the base at origin O is ${\mathbf{a}}_i$. Revolute joints at points $C_i$ have horizontal axis ${\mathbf{u}}_i$.

Three loop-closure equations at $B_i$ can be stated through the three limbs of the parallel kinematic mechanism as:

$$\begin{array}{c}\hfill \mathbf{p}+{\mathbf{R}}_{EE}{\mathbf{r}}_i={\mathbf{a}}_i+({\mathbf{c}}_i-{\mathbf{a}}_i)+({\mathbf{b}}_i-{\mathbf{c}}_i)i=1...3\end{array}$$

(1)

As the passive revolute joint of each limb constrains its corresponding point $B_i$ to be on a vertical plane ${\pi }_i$ perpendicular to ${\mathbf{u}}_i$ through $C_i$, which also contains points O and $A_i$, we get the set of three constraint equations by dot-multiplying Equation (1) by vectors ${\mathbf{u}}_i$, namely:

$$\begin{array}{c}\hfill (\mathbf{p}+{\mathbf{R}}_{EE}{\mathbf{r}}_i)·{\mathbf{u}}_i=0i=1...3\end{array}$$

(2)

Using Euler–Rodrigues parameters $(e_0,e_1,e_2,e_3)$ to express the rotation matrix allows a polynomial representation of output orientation, namely:

$${\mathbf{R}}_{EE}=\left[\begin{array}{ccc}{e}_0^2+e_1^2-e_2^2-e_3^2& 2(e_1{e}_2-e_0{e}_3)& 2(e_1{e}_3+e_0{e}_2)\\ 2(e_1{e}_2+e_0{e}_3)& e_0^2-e_1^2+e_2^2-e_3^2& 2(e_2{e}_3-e_0{e}_1)\\ 2(e_1{e}_3-e_0{e}_2)& 2(e_2{e}_3+e_0{e}_1)& e_0^2-e_1^2-e_2^2+e_3^2\end{array}\right]$$

(3)

subject to:

$$\begin{array}{c}\hfill e_0^2+e_1^2+e_2^2+e_3^2=1\end{array}$$

(4)

where the Euler–Rodrigues parameters are related to the Euler pole $\mathbf{a}$ and the angle rotated $\varphi$ in the following way:

$$\begin{array}{c}\hfill e_0=cos(\varphi /2)\end{array}$$

(5)

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{e}_1\\ e_2\\ e_3\end{array}\right\}=sin(\varphi /2)·\mathbf{a}\end{array}$$

(6)

If the symmetrical arrangement of the system shown in Figure 1 is considered, we have an equilateral triangular end effector with a circumradius r so that in the moving frame we get:

$${\mathbf{r}}_1=\left\{\begin{array}{c}0\\ r\\ 0\end{array}\right\}{\mathbf{r}}_2=\left\{\begin{array}{c}-\sqrt{3}r/2\\ -r/2\\ 0\end{array}\right\}{\mathbf{r}}_3=\left\{\begin{array}{c}\sqrt{3}r/2\\ -r/2\\ 0\end{array}\right\}$$

(7)

and revolute axes oriented in the fixed frame as:

$${\mathbf{u}}_1=\left\{\begin{array}{c}1\\ 0\\ 0\end{array}\right\}{\mathbf{u}}_2=\left\{\begin{array}{c}-1/2\\ \sqrt{3}/2\\ 0\end{array}\right\}{\mathbf{u}}_3=\left\{\begin{array}{c}1/2\\ \sqrt{3}/2\\ 0\end{array}\right\}$$

(8)

Upon substitution of Equations (3), (7), and (8) into Equation (2), and considering Equation (4), we get the following constraint equations:

$$\begin{array}{c}\hfill e_0{e}_3=0\\ \hfill x+2·r·e_1{e}_2=0\\ \hfill y+r·(e_1^2-e_2^2)=0\\ \hfill e_0^2+e_1^2+e_2^2+e_3^2=1\end{array}$$

(9)

As a consequence, for the kinematic analysis of this tripod mechanism we can choose $z,e_1,e_2$ as the three independent output pose parameters, with dependent parameters $x,y,e_0,e_3$ determined from the constraint equations Equation (9). Moreover, as $e_0=cos(\varphi /2)$ is only null when there is no output rotation the constraint equations can be expressed as:

$$\begin{array}{c}\hfill e_3=0\\ \hfill x+2·r·e_1{e}_2=0\\ \hfill y+r·(e_1^2-e_2^2)=0\\ \hfill e_0^2+e_1^2+e_2^2=1\end{array}$$

(10)

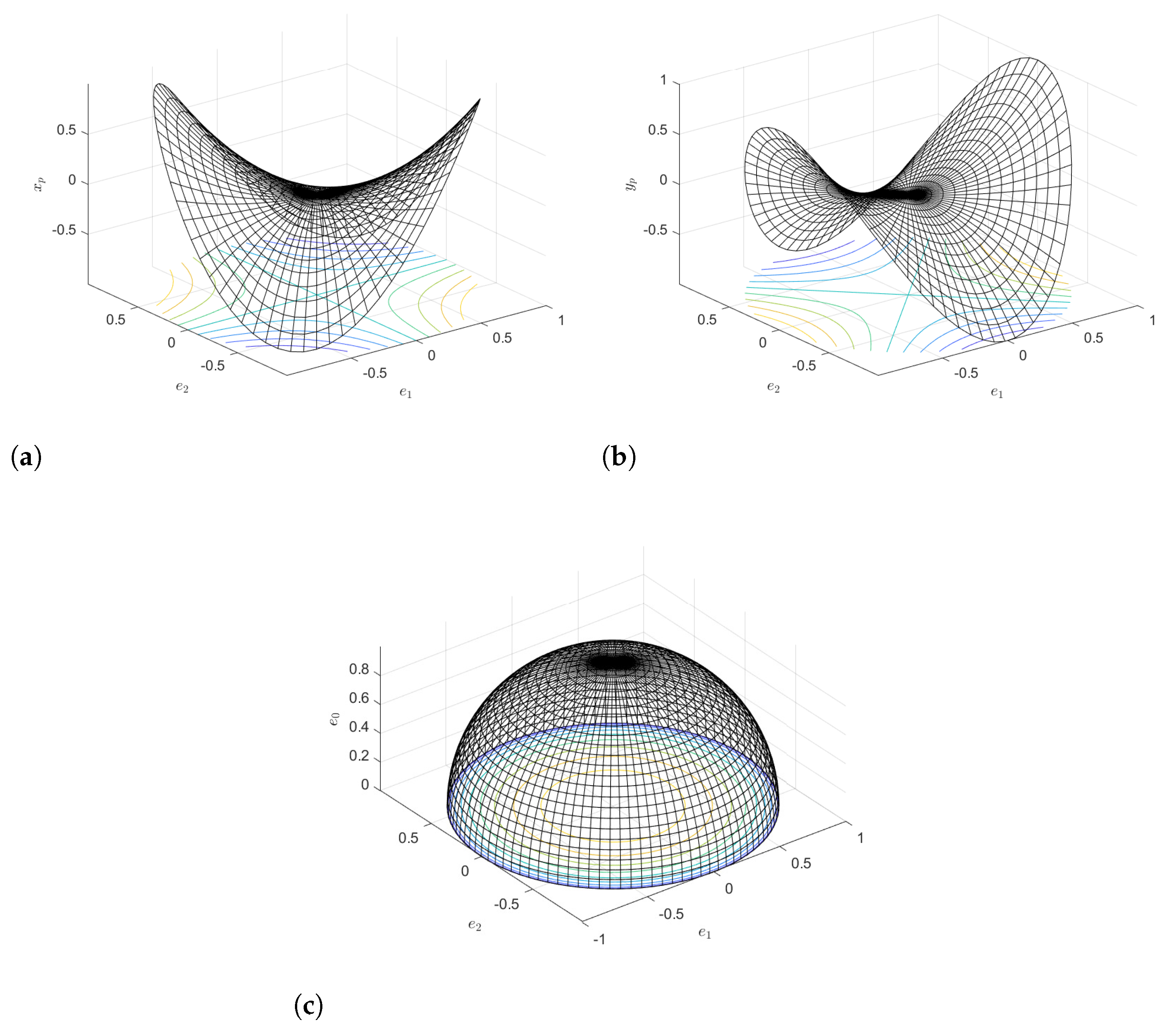
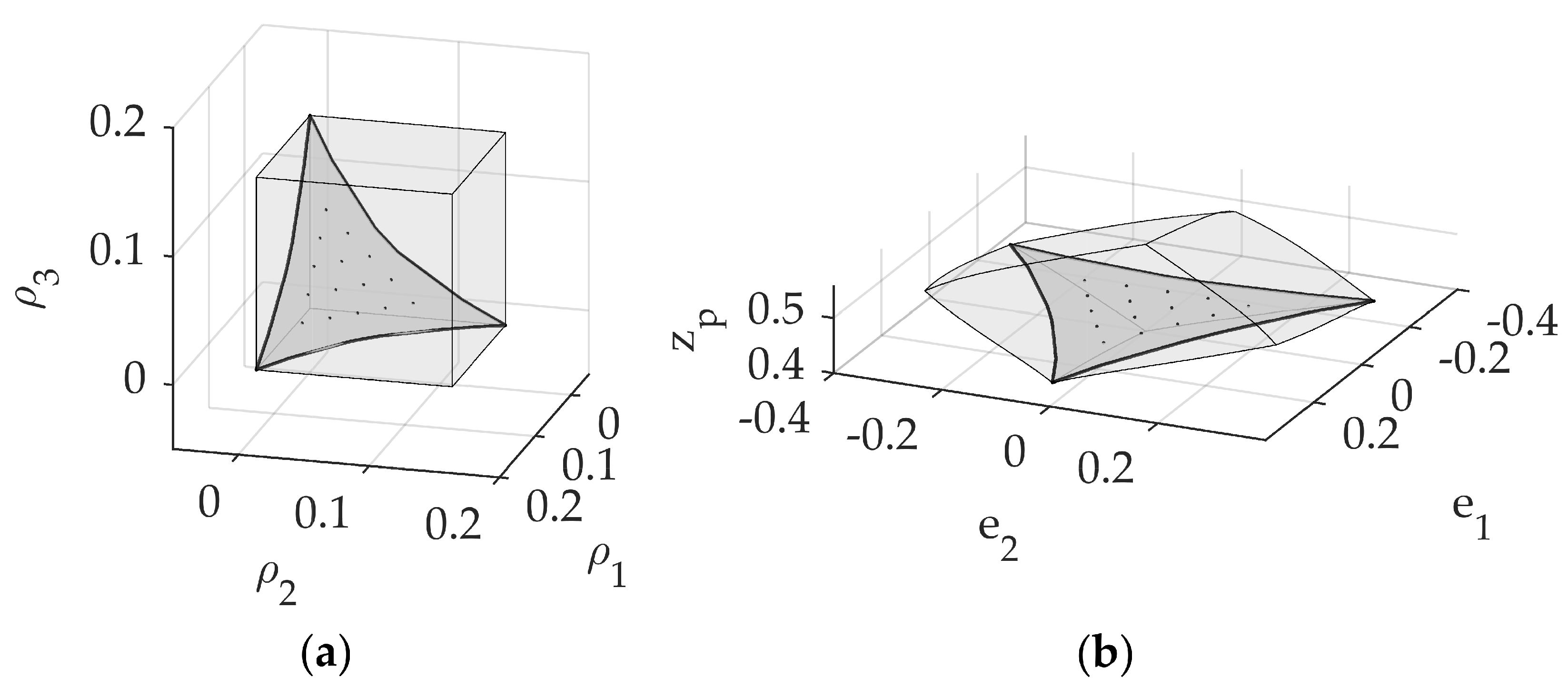
Dependent parameters $x,y,e_0$ acquire non-null values as the end effector moves; these are called parasitic motions. We can plot the workspace of the mechanism in the space $z,e_1,e_2$. Moreover, as dependent parameters are expressed solely in terms of $e_1,e_2$ in constraint equations Equation (10), parasitic motions for any possible motion of the mechanism can be plotted in the space $[e_1,e_2]$ where $e_1^2+e_2^2\le 1$ as shown in Figure 4 for $r=1$. This result of the constraint analysis is proof of its reduced mobility of three degrees of freedom. Moreover, the analysis of the effect of the three geometrical constraints justifies that the type of motion on the end effector is a $2R1T$ (two rotational and one translational).

The kinematic analysis of the relationship between the actuators’ input lengths ${\rho }_i$ and the independent output parameters $z,e_1,e_2$, using the loop-closure equations (Equation (1)), provides the solution to either the forward (FK) or the inverse (IK) position problem. First, we get rid of passive variables by finding the Euclidean norm of $({\mathbf{b}}_i-{\mathbf{c}}_i)$ in Equation (1), namely:

$$\begin{array}{c}\hfill ({\mathbf{b}}_i-{\mathbf{c}}_i)=\mathbf{p}+{\mathbf{R}}_{EE}{\mathbf{r}}_i-{\mathbf{a}}_i-({\mathbf{c}}_i-{\mathbf{a}}_i)i=1...3\\ \hfill L=\parallel \mathbf{p}+{\mathbf{R}}_{EE}{\mathbf{r}}_i-{\mathbf{a}}_i-({\mathbf{c}}_i-{\mathbf{a}}_i)\parallel i=1...3\end{array}$$

(11)

where a symmetrical arrangement of actuators with $A_i$ points at a circumradius $r_A$ defines:

$${\mathbf{a}}_1=\left\{\begin{array}{c}0\\ r_A\\ 0\end{array}\right\}{\mathbf{a}}_2=\left\{\begin{array}{c}-\sqrt{3}{r}_A/2\\ -r_A/2\\ 0\end{array}\right\}{\mathbf{a}}_3=\left\{\begin{array}{c}\sqrt{3}{r}_A/2\\ -r_A/2\\ 0\end{array}\right\}$$

(12)

and actuators’ inputs are given by:

$${\mathbf{c}}_1-{\mathbf{a}}_1=\left\{\begin{array}{c}0\\ 0\\ {\rho }_1\end{array}\right\}{\mathbf{c}}_2-{\mathbf{a}}_2=\left\{\begin{array}{c}0\\ 0\\ {\rho }_2\end{array}\right\}{\mathbf{c}}_3-{\mathbf{a}}_3=\left\{\begin{array}{c}0\\ 0\\ {\rho }_3\end{array}\right\}$$

(13)

Finally, we introduce constraint equations from Equation (10) into Equation (11). The resultant system has three equations in three unknowns: $z,e_1,e_2$ for the FK and ${\rho }_1,{\rho }_2,{\rho }_3$ for the IK.

Velocity analysis is performed on the derivative of the loop-closure equations Equation (1), namely

$$\begin{array}{c}\hfill \dot{\mathbf{p}}+\omega \times {\mathbf{r}}_i={\dot{\rho }}_i\mathbf{k}+{\omega }_i\times ({\mathbf{b}}_i-{\mathbf{c}}_i)i=1\dots 3\end{array}$$

(14)

where $\omega$ is the angular velocity of the end effector, and ${\omega }_i$ is the angular velocity of the rigid connecting link $\left(C_i{B}_i\right)$.

Dot-multiplying Equation (14) by $({\mathbf{b}}_i-{\mathbf{c}}_i)$, we get rid of ${\omega }_i$, obtaining a relationship between velocity inputs and velocity outputs:

$$\begin{array}{c}\hfill ({\mathbf{b}}_i-{\mathbf{c}}_i)·\dot{\mathbf{p}}+({\mathbf{r}}_i\times ({\mathbf{b}}_i-{\mathbf{c}}_i))·\omega ={\dot{\rho }}_i[({\mathbf{b}}_i-{\mathbf{c}}_i)·\mathbf{k}]i=1\dots 3\end{array}$$

(15)

and dot-multiplying Equation (14) by ${\mathbf{u}}_i$, we get the relationship between derivatives of output independent and dependent variables, i.e., the derivative of the constraint equations:

$$\begin{array}{c}\hfill {\mathbf{u}}_i·\dot{\mathbf{p}}+({\mathbf{r}}_i\times {\mathbf{u}}_i)·\mathsf{\omega }=0i=1\dots 3\end{array}$$

(16)

Upon assembly of Equations (15) and (16), we get the Jacobian equation:

$$\left[\begin{array}{cc}({\mathbf{b}}_i-{\mathbf{c}}_i)& {\mathbf{r}}_i\times ({\mathbf{b}}_i-{\mathbf{c}}_i)\\ {\mathbf{u}}_i& {\mathbf{r}}_i\times {\mathbf{u}}_i\end{array}\right]\left\{\begin{array}{c}\dot{\mathbf{p}}\\ \mathsf{\omega }\end{array}\right\}=\left[\begin{array}{ccc}({\mathbf{b}}_1-{\mathbf{c}}_1)·\mathbf{k}& 0& 0\\ 0& ({\mathbf{b}}_2-{\mathbf{c}}_2)·\mathbf{k}& 0\\ 0& 0& ({\mathbf{b}}_3-{\mathbf{c}}_3)·\mathbf{k}\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\left\{\begin{array}{c}{\dot{\rho }}_1\\ {\dot{\rho }}_2\\ {\dot{\rho }}_3\end{array}\right\}$$

(17)

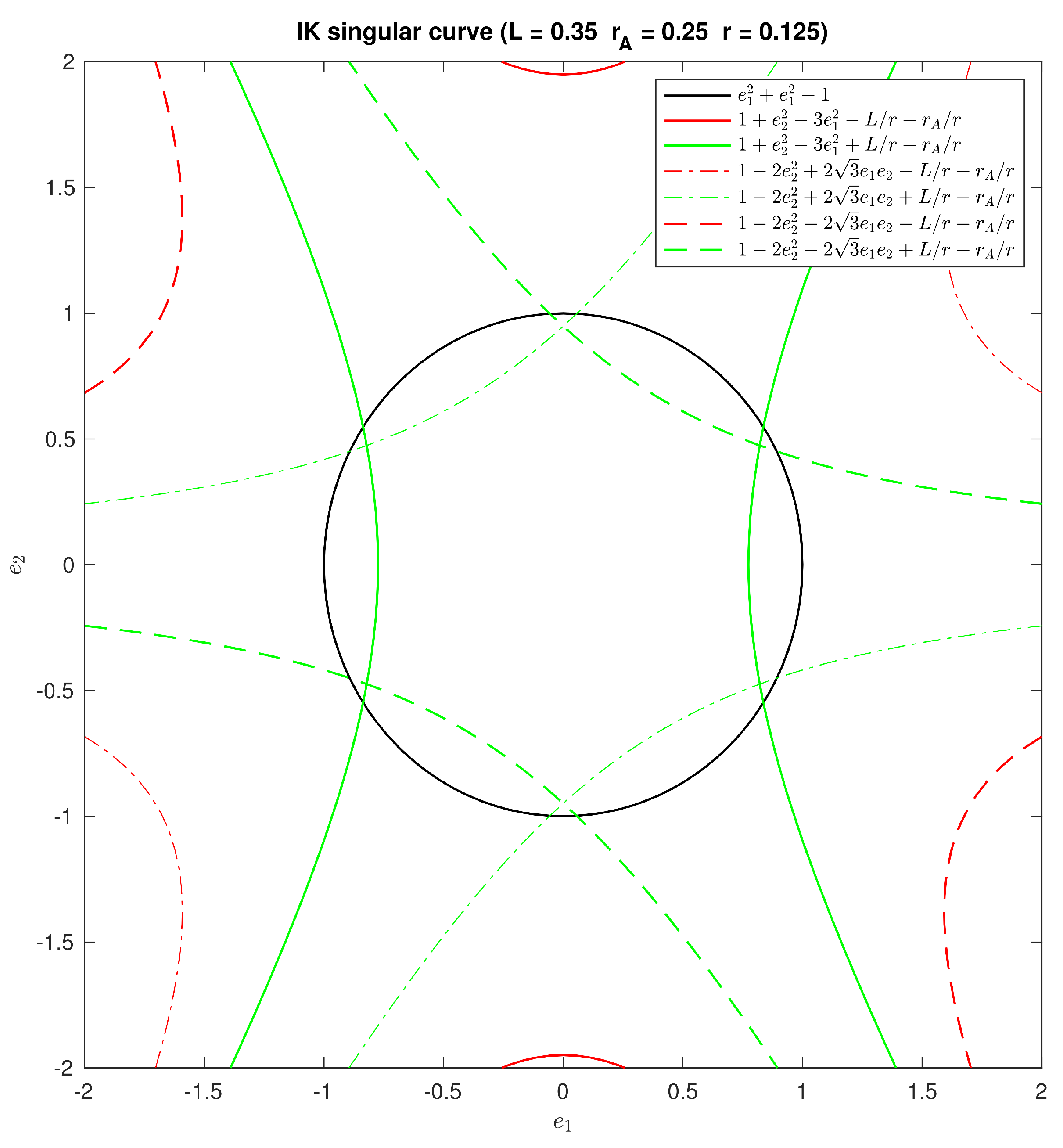
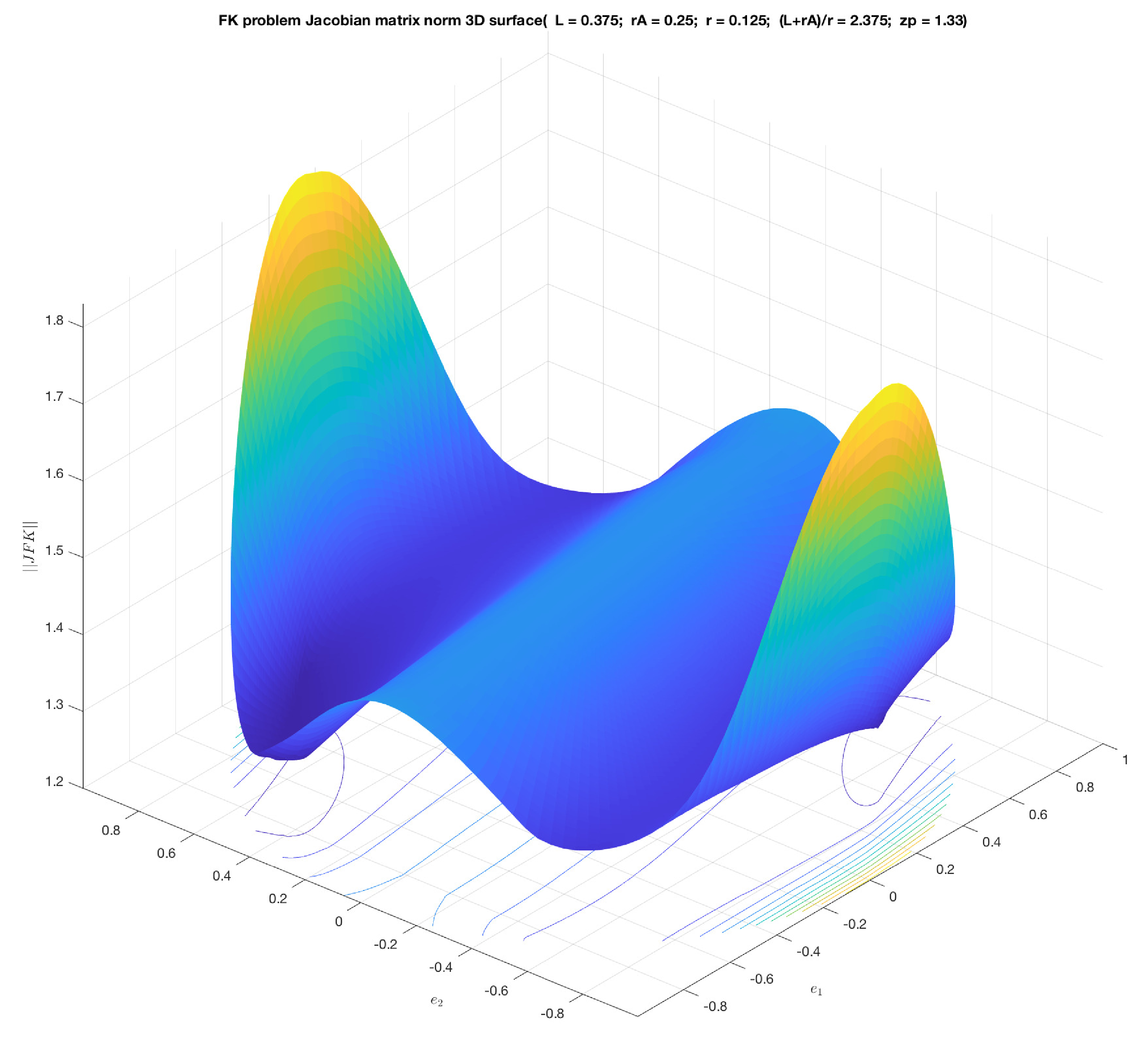
With those Jacobians, we can perform the singularity analysis to determine the limits of the position analysis. IK singularity is determined by the conditions for rank deficiency in:

$$\begin{array}{c}\hfill {\mathbf{J}}_{IK}=\left[\begin{array}{ccc}({\mathbf{b}}_1-{\mathbf{c}}_1)·\mathbf{k}& 0& 0\\ 0& ({\mathbf{b}}_2-{\mathbf{c}}_2)·\mathbf{k}& 0\\ 0& 0& ({\mathbf{b}}_3-{\mathbf{c}}_3)·\mathbf{k}\end{array}\right]\end{array}$$

(18)

which developed in terms of output variables result:

$$\begin{array}{c}\hfill 1-3e_1^2+e_2^2=\frac{{\displaystyle r_A\pm L}}{r}\\ \hfill 1+2\sqrt{3}{e}_1{e}_2-2e_2^2=\frac{{\displaystyle r_A\pm L}}{r}\\ \hfill 1-2\sqrt{3}{e}_1{e}_2-2e_2^2=\frac{{\displaystyle r_A\pm L}}{r}\end{array}$$

(19)

As a result, the space of parasitic motions shown in Figure 4 will be limited by IK singularity loci (see Figure 5 with $r_A=0.25$, $L=0.35$, and $r=0.125$).

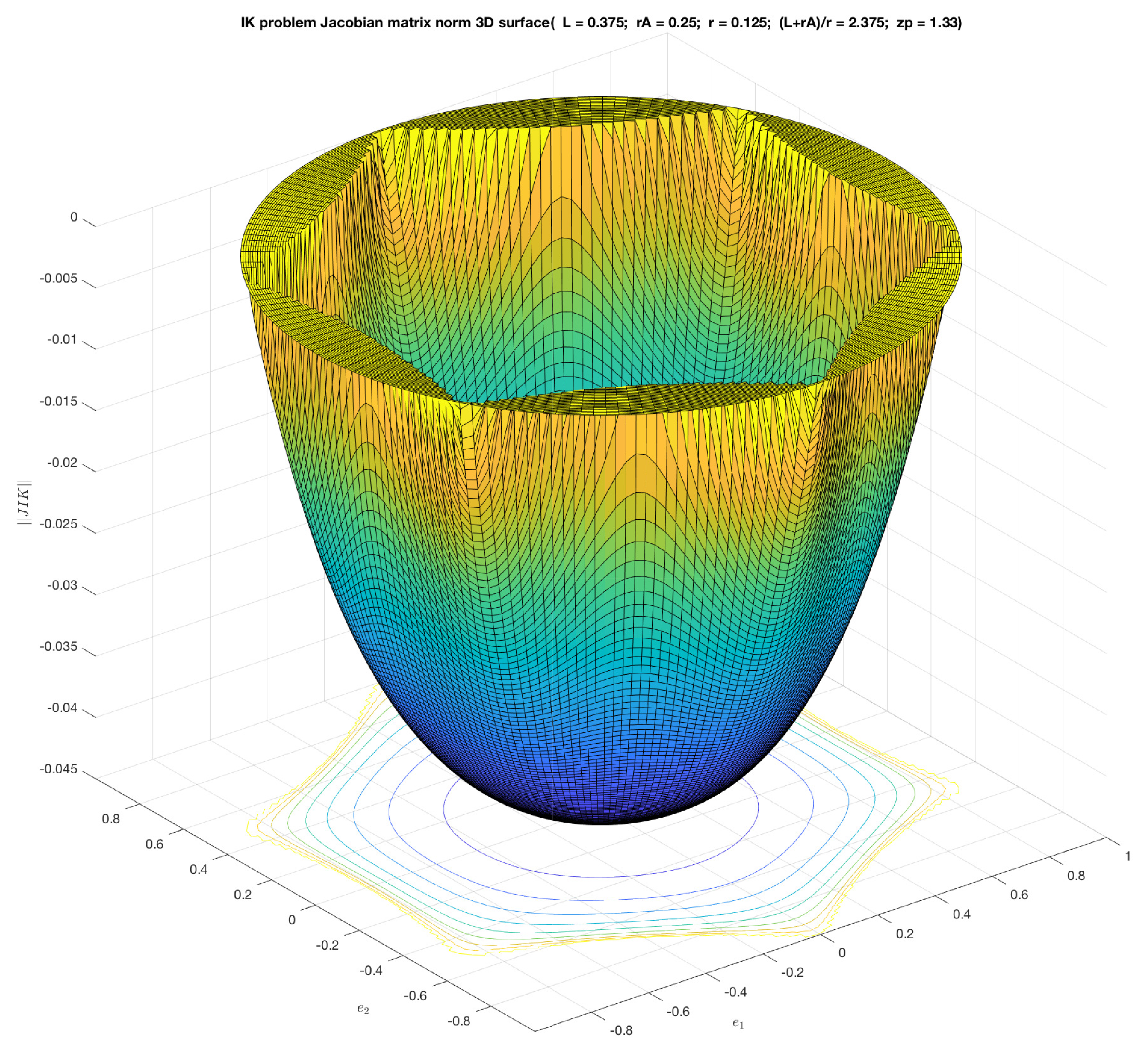
The aforementioned Jacobians can be analyzed on this workspace to obtain dexterity indices, as shown in Figure 6 and Figure 7.

Nevertheless, the parasitic motion functions do not change, and the mobility analysis can be fully defined with the constraint equation (Equation (10)) and the plots in Figure 4. These will be used in the comparison with the motion of the flexible tripod mechanism.

3.2. Forward Kinematic Analysis of a $3P\underline{F}S$ Parallel Continuum Tripod

The second step in the method is to analyze the flexible $3P\underline{F}S$ parallel continuum tripod shown in Figure 3 and to check the type of motion performed as inputs are introduced. As before, a moving frame is attached to the end effector at reference point P, whose position in a fixed frame is $\mathbf{p}$. The orientation of the moving frame with respect to the fixed frame, i.e., the orientation of the end effector, is defined using a rotation matrix ${\mathbf{R}}_{EE}$ in terms of Euler–Rodrigues parameters (i.e., a unit quaternion $\tilde{\mathbf{e}}$). The position vector of rod attachment point $B_i$ expressed in the end effector frame is ${\mathbf{r}}_i$. The position vector of rod attachment point $A_i$ expressed in the fixed frame attached to the base at origin O is ${\mathbf{a}}_i$.

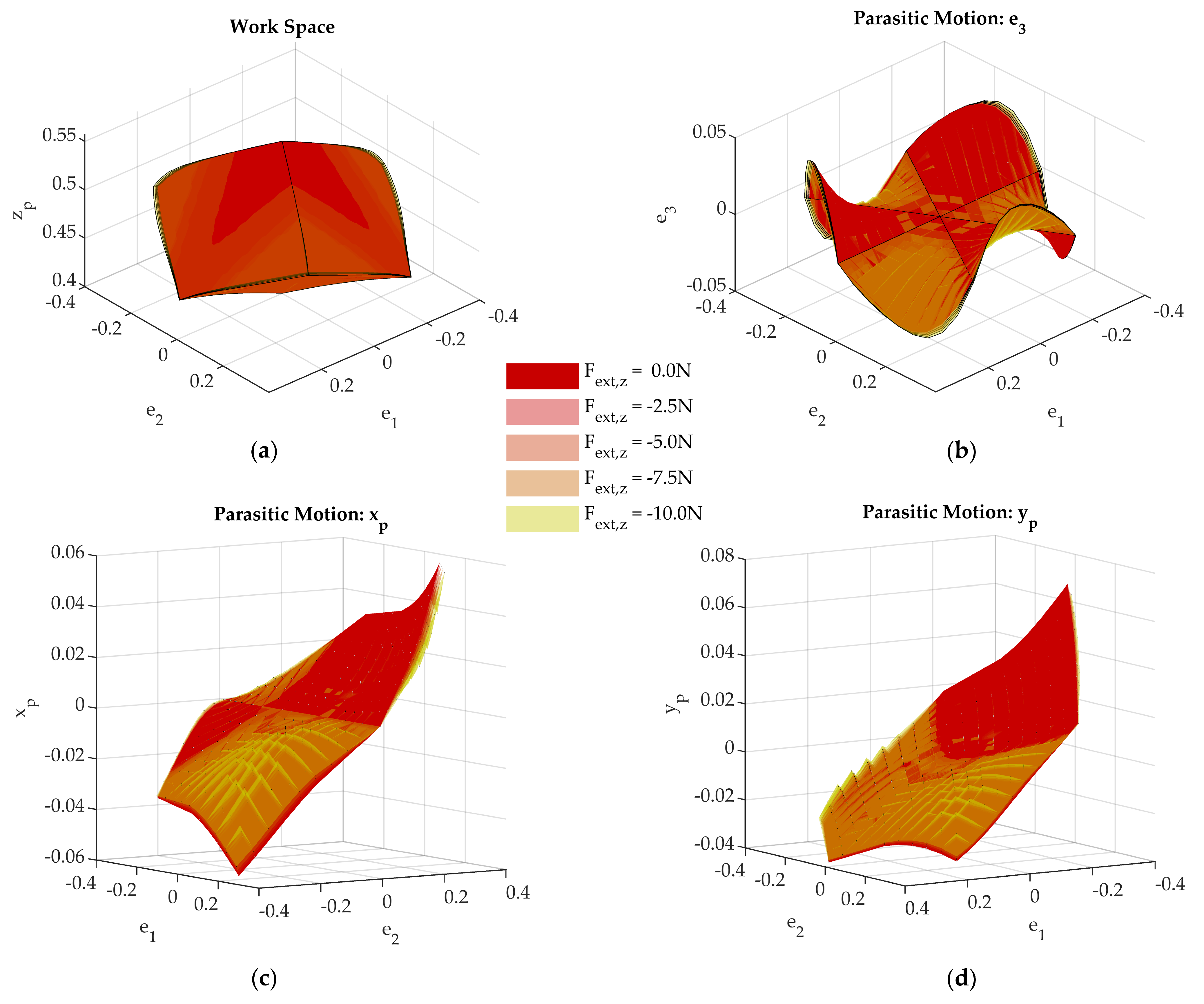
The forward kinematics problem consists of determining the pose of the end effector, i.e., the position vector of reference point P, $\mathbf{p}$, and the orientation given by the rotation matrix ${\mathbf{R}}_{EE}$, when each rod i takes a certain value of its effective length $L_i$ and a given load ${\mathbf{F}}_{ext};{\mathbf{M}}_{ext}$ is imposed.

The nonlinear large deformation of the flexible rods is analyzed with the Kirchhoff model [12]. Each cross-section of the rod i along the arc length s is located with a vector pointing its centroid ${\mathbf{p}}_i\left(s\right)$ and a local frame oriented with a unit quaternion ${\tilde{\mathbf{q}}}_i\left(s\right)$ (see Figure 8). The rods’ internal moments $\mathbf{m}\left(s\right)$ are related to the rods’ curvature $\mathbf{u}\left(s\right)$ along length s, or vice-versa, with the material constitutive law given by $\mathbf{u}={\mathbf{K}}_{BT}^{-1}{\mathbf{R}}^T\mathbf{m}$, where ${\mathbf{K}}_{BT}$ is a stiffness matrix for bending and torsion; no extension–compression or shear effects are considered in this model to affect internal forces $\mathbf{n}\left(s\right)$.

The change of shape of the flexible rod and the equilibrium of internal forces and moments with the load along s are related through a system of differential equations $\frac{d\mathbf{y}}{ds}=\mathbf{f}$ that can be stated with the vector $\mathbf{y}$ of variables

$$\begin{array}{c}\hfill \mathbf{y}=\left\{\begin{array}{c}\mathbf{p}\\ \tilde{\mathbf{q}}\\ \mathbf{n}\\ \mathbf{u}\end{array}\right\}\end{array}$$

(20)

and the vector of functions $\mathbf{f}$:

$$\begin{array}{c}\hfill \mathbf{f}=\left\{\begin{array}{c}\mathbf{R}{\mathbf{e}}_3\\ \frac{1}{2}\tilde{\mathbf{q}}\tilde{\mathbf{u}}\\ \mathbf{0}\\ -{\mathbf{K}}_{BT}^{-1}\left(\left(\widehat{\mathbf{u}}{\mathbf{K}}_{BT}\right)\mathbf{u}+{\widehat{\mathbf{e}}}_3{\mathbf{R}}^T\mathbf{n}\right)\end{array}\right\}\end{array}$$

(21)

Considering the expression of the rotation matrix that defines the orientation of each cross section along the arc length s in terms of a unit quaternion:

$$\begin{array}{c}\hfill \mathbf{R}\left(s\right)=\left[\begin{array}{ccc}{q}_0^2+q_1^2-q_2^2-q_3^2& 2(q_1{q}_2-q_0{q}_3)& 2(q_1{q}_3+q_0{q}_2)\\ 2(q_1{q}_2+q_0{q}_3)& q_0^2-q_1^2+q_2^2-q_3^2& 2(q_2{q}_3-q_0{q}_1)\\ 2(q_1{q}_3-q_0{q}_2)& 2(q_2{q}_3+q_0{q}_1)& q_0^2-q_1^2-q_2^2+q_3^2\end{array}\right]\end{array}$$

(22)

and the change of the quaternion along s with $\mathbf{u}$

$$\frac{d\tilde{\mathbf{q}}}{ds}=\frac{1}{2}\tilde{\mathbf{q}}\tilde{\mathbf{u}}=\frac{1}{2}\left[\begin{array}{cccc}0& -u_x& -u_y& -u_z\\ u_x& 0& u_z& -u_y\\ u_y& -u_z& 0& u_x\\ u_z& u_y& -u_x& 0\end{array}\right]\left\{\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right\}$$

(23)

where $u_z=0$ everywhere because the flexible rods used in the mechanism are free of torsional effects.

We get the following system of differential equations:

$$\frac{d}{ds}\left\{\begin{array}{c}x\\ y\\ z\\ q_0\\ q_1\\ q_2\\ q_3\\ n_x\\ n_y\\ n_z\\ u_x\\ u_y\end{array}\right\}=\left\{\begin{array}{c}2(q_1{q}_3+q_0{q}_2)\\ 2(q_2{q}_3-q_0{q}_1)\\ q_0^2-q_1^2-q_2^2+q_3^2\\ \frac{1}{2}(-u_x{q}_1-u_y{q}_2)\\ \frac{1}{2}(u_x{q}_0-u_y{q}_3)\\ \frac{1}{2}(u_y{q}_0+u_x{q}_3)\\ \frac{1}{2}(u_y{q}_1-u_x{q}_2)\\ 0\\ 0\\ 0\\ \frac{1}{EI}(2n_x(q_1{q}_2-q_0{q}_3)+n_y(q_0^2-q_1^2+q_2^2-q_3^2)+2n_z(q_2{q}_3+q_0{q}_1))\\ \frac{1}{EI}(-n_x(q_0^2+q_1^2-q_2^2-q_3^2)-2n_y(q_1{q}_2+q_0{q}_3)-2n_z(q_1{q}_3-q_0{q}_2))\end{array}\right\}$$

(24)

As it can be observed, with no load applied along the arc length of the rod, the internal force $\mathbf{n}$ is constant along the rod, while the evolution of ${\mathbf{p}}_i\left(s\right)$, ${\tilde{\mathbf{q}}}_i\left(s\right)$, and $u_{xi}\left(s\right)$, $u_{yi}\left(s\right)$ can be obtained upon integration of the system of equations using, for example, the Runge–Kutta method, from $s=0$ to $s=L_i$.

Hence, solving the position problem of the mechanism is started with the integration of each rod numerically by Runge–Kutta from known data values at $s=0$ (the position of the base tip of the rod ${\mathbf{p}}_i(s=0)$ and orientation of the base tip ${\tilde{\mathbf{q}}}_i(s=0)$, and given inputs $L_i$), and guess values of $u_{xi}(s=0)$, $u_{yi}(s=0)$, ${\mathbf{n}}_i\left(0\right)$. To reach convergence with certain security, starting from a known home pose helps to initialize the solving of the problem because those values serve as guess values to find the next solution with the new input values of actuators chosen close enough to secure convergence. The step-by-step solution will lead from that home pose to the required one.

As a result of this iteration, we get for each rod its end tip location ${\mathbf{p}}_i(s=L_i)$ and curvature components $u_{xi}(s=L_i)$, $u_{yi}(s=L_i)$, to verify the conditions imposed by the mechanism assembly and load. This is done by expressing those conditions in terms of residuals that have to be minimized following an iterative procedure ruled by a Newton scheme.

There are two main conditions that must be satisfied so that a pose of the flexible mechanism is achieved with the data introduced: first, that it can be assembled geometrically; and second, that the configuration is in static equilibrium.

Regarding the first condition, we have the coordinates of the distal end $B_i$ as a function of the output pose of the end effector, namely

$$\begin{array}{c}\hfill {\mathbf{b}}_i=\mathbf{p}+{\mathbf{R}}_{EE}{\mathbf{r}}_i\end{array}$$

(25)

to be related to the coordinates of the end tip of the flexible rod ${\mathbf{p}}_i(s=L_i)$ obtained from the deformation model (as explained before) and the known and fixed position ${\mathbf{a}}_i$ of the proximal end $A_i$ of each rod:

$$\begin{array}{c}\hfill {\mathbf{b}}_i={\mathbf{a}}_i+{\mathbf{p}}_i(s=L_i)\end{array}$$

(26)

so the following set of conditions ($i=1\dots 6$) must be fulfilled:

$$\begin{array}{c}\hfill \mathbf{0}={\mathbf{a}}_i+{\mathbf{p}}_i(s=L_i)-\mathbf{p}-{\mathbf{R}}_{EE}{\mathbf{r}}_i\end{array}$$

(27)

Additionally, as distal ends are joined to the end effector through spherical joints, no moment must appear there. Moreover, no torsional effects are present anywhere on the rods due to the type of joint to the base. Bearing in mind that we can easily change from the rods’ internal moments $\mathbf{m}$ to the rods’ curvature $\mathbf{u}$ along length s, or vice-versa, with the material constitutive law given by $\mathbf{u}={\mathbf{K}}_{BT}^{-1}{\mathbf{R}}^T\mathbf{m}$, the null moment conditions at distal ends ($i=1...6$) to be verified are simply expressed in terms of the components of curvature in the cross-section of the distal ends as:

$$\left\{\begin{array}{c}{u}_{xi}(s=L_i)\\ u_{yi}(s=L_i)\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\end{array}\right\}$$

(28)

Static equilibrium conditions, unlike geometric ones, are stated for the whole device at the same time. This means that the end effector and all rods’ values are highly coupled in the set of equations. The end effector may be subjected to external load ${\mathbf{F}}_{ext}$ at P and ${\mathbf{M}}_{ext}$, and to reaction forces and moments at the attachment to rods due to their deformation, namely internal forces ${\mathbf{n}}_i$ and moments ${\mathbf{m}}_i$ at $(s=L_i)$. So, the following static equilibrium can be stated, taking moments about O:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{i=1}^6\left[{\mathbf{n}}_i\left(L_i\right)\right]-{\mathbf{F}}_{ext}& =\mathbf{0}\hfill \\ \hfill \sum _{i=1}^6[\left({\mathbf{a}}_i+{\mathbf{p}}_i\left(L_i\right)\right)\times {\mathbf{n}}_i\left(L_i\right)+{\mathbf{m}}_i\left(L_i\right)]-\mathbf{p}\times {\mathbf{F}}_{ext}-{\mathbf{M}}_{ext}& =\mathbf{0}\hfill \end{array}\end{array}$$

(29)

The problem to be solved is made up of the geometric conditions on the position of distal ends (Equation (27)), i.e., 3 scalar equations at each rod for a total of 18; the geometric conditions on the attachment of distal ends to end effector (Equation (28)), i.e., 2 equations for each rod, 12 in total; and the static equilibrium conditions on the end effector (Equation (29)), i.e., 6 more, to make a total of 36 conditions.

The unknowns are due to the state variables of each rod necessary to integrate the six subsystems of differential equations for each rod, i.e., the unknowns in $\mathbf{n}$ and $\mathbf{m}$ (alternatively $\mathbf{u}$) being five because there is no torsion; plus the six unknowns that define the end effector pose $\mathbf{p}$ and ${\mathbf{R}}_{EE}$, a total of thirty-six unknowns.

As the orientation of the end effector with respect to the fixed frame is more effectively expressed with a unit quaternion $\tilde{\mathbf{e}}=\left[e_0{e}_1{e}_2{e}_3\right]$, the corresponding rotation matrix ${\mathbf{R}}_{EE}$ has four components to be used as unknowns instead of three, making a total of thirty-seven unknowns and another condition has to be added, namely the unity condition of the quaternion:

$$\begin{array}{c}\hfill e_0^2+e_1^2+e_2^2+e_3^2=1\end{array}$$

(30)

Hence resulting in a problem of 37 unknowns in 37 conditions.

Due to the integration involved in each rod, the solution must be approached as a boundary value problem: guess values of unknowns at the lower end $s=0$ for each rod (namely ${\mathbf{u}}_i{|}_{xy}\left(0\right)$, ${\mathbf{n}}_i\left(0\right)$) and the output pose ($\mathbf{p}$ and $\tilde{\mathbf{e}}$) are introduced, and a shooting method iterates until residuals of the boundary conditions are below a tolerance.

The chosen order of those residuals will provide an adequate distribution of terms to lower the computational cost. First, the geometric constraints for the rod $i=1$, i.e., Equations (27) and (28), then the same geometric constraints but for the rod $i=2$, and so on until $i=6$. The last elements of the residue vector are formed by the equations of equilibrium (Equation (29)), and the normalization condition of the end effector quaternion (Equation (30)), namely

$$\begin{array}{c}\hfill {\mathbf{g}}_{res}=\left\{\begin{array}{c}{\mathbf{p}}_1\left(L_1\right)-\mathbf{p}-{\mathbf{R}}_{EE}{\mathbf{r}}_1+{\mathbf{a}}_1\\ u_{x1}\left(L_1\right)\\ u_{y1}\left(L_1\right)\\ ine⋮\\ ine{\mathbf{p}}_6\left(L_6\right)-\mathbf{p}-{\mathbf{R}}_{EE}{\mathbf{r}}_6+{\mathbf{a}}_6\\ u_{x6}\left(L_6\right)\\ u_{y6}\left(L_6\right)\\ ine\sum _{i=1}^6\left[{\mathbf{n}}_i\left(L_i\right)\right]-{\mathbf{F}}_{ext}\\ \sum _{i=1}^6[\left({\mathbf{a}}_i+{\mathbf{p}}_i\left(L_i\right)\right)\times {\mathbf{n}}_i\left(L_i\right)+{\mathbf{m}}_i\left(L_i\right)]-\mathbf{p}\times {\mathbf{F}}_{ext}-{\mathbf{M}}_{ext}\\ ine{e}_0^2+e_1^2+e_2^2+e_3^2-1\end{array}\right\}\end{array}$$

(31)

The Newton method used in the shooting method requires the evaluation of a Jacobian of the residue vector function with respect to the variables of the problem, i.e., the guess values ${\mathbf{u}}_i{|}_{xy}\left(0\right)$, ${\mathbf{n}}_i\left(0\right)$ and output pose $\mathbf{p}$ and $\tilde{\mathbf{e}}=\left[e_0{e}_1{e}_2{e}_3\right]$, in order to update the guess values accordingly. A special order for the guess values is also considered to generate a Jacobian sparse matrix. They are grouped so that the guess values associated with a rod are together:

$$\begin{array}{cc}\hfill {\mathbf{v}}_{guess}& =\left\{\begin{array}{c}\begin{array}{c}{u}_{x1}^{guess}\hfill \\ u_{y1}^{guess}\hfill \\ {\mathbf{n}}_1^{guess}\hfill \\ ine⋮\hfill \\ ine{u}_{x6}^{guess}\hfill \\ u_{y6}^{guess}\hfill \\ {\mathbf{n}}_6^{guess}\hfill \\ ine{\mathbf{p}}^{guess}\hfill \\ {\tilde{\mathbf{e}}}^{guess}\hfill \end{array}\end{array}\right\}\hfill \end{array}$$

(32)

The Jacobian is then obtained as:

$$\begin{array}{cc}\hfill \mathbf{J}\left({\mathbf{v}}_{guess}\right)& =\frac{\partial {\mathbf{g}}_{res}\left({\mathbf{v}}_{guess}\right)}{\partial {\mathbf{v}}_{guess}}\hfill \end{array}$$

(33)

The Jacobian related to the forward kinematic problem is a sparse matrix $\mathbf{J}\in {\mathbb{R}}_{37x37}$ of the form

$$\begin{array}{cc}\hfill \mathbf{J}& =\left[\begin{array}{cccccccc}{\mathbf{A}}_1& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathbf{C}}_1& {\mathbf{D}}_1\\ \mathbf{0}& {\mathbf{A}}_2& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathbf{C}}_2& {\mathbf{D}}_2\\ \mathbf{0}& \mathbf{0}& {\mathbf{A}}_3& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathbf{C}}_3& {\mathbf{D}}_3\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathbf{A}}_4& \mathbf{0}& \mathbf{0}& {\mathbf{C}}_4& {\mathbf{D}}_4\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathbf{A}}_5& \mathbf{0}& {\mathbf{C}}_5& {\mathbf{D}}_5\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathbf{A}}_6& {\mathbf{C}}_6& {\mathbf{D}}_6\\ {\mathbf{B}}_1& {\mathbf{B}}_2& {\mathbf{B}}_3& {\mathbf{B}}_4& {\mathbf{B}}_5& {\mathbf{B}}_6& {\mathbf{C}}_7& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathbf{D}}_7\end{array}\right]\hfill \end{array}$$

(34)

Each sub-matrix ${\mathbf{A}}_i\in {\mathbb{R}}_{5x5}$ is calculated considering the residue associated with the geometric conditions for the rod i and the kinematic variables used as guess values for the rod i. Similarly, matrix ${\mathbf{B}}_i\in {\mathbb{R}}_{6x5}$ is defined considering the residue associated with the static conditions that affect the whole mechanism and the kinematic variables used as guess values for rod i. Matrix ${\mathbf{C}}_i\in {\mathbb{R}}_{5x3}$ is calculated considering the residue associated with the geometric conditions for the rod i and the coordinates of P are used as guess values. Matrix ${\mathbf{D}}_i\in {\mathbb{R}}_{5x4}$ is calculated considering the residue associated with the geometric conditions for the rod i and the kinematic variables used as guess values for the orientation of the end effector. Finally, matrix ${\mathbf{C}}_7\in {\mathbb{R}}_{6x3}$ is defined considering the residue associated with the static conditions and the output position of P of the end effector; while matrix ${\mathbf{D}}_7\in {\mathbb{R}}_{1x4}$ is defined considering the residue associated to the quaternion normalization condition and the orientation of the end effector.

After each iteration j, guess values are updated with:

$$\begin{array}{c}\hfill {\mathbf{v}}_{guess}^{j+1}={\mathbf{v}}_{guess}^j-{\mathbf{J}}^{-1}{\mathbf{g}}_{res}^j\end{array}$$

(35)

and the process starts again until ${\mathbf{g}}_{res}$ is below a given tolerance.

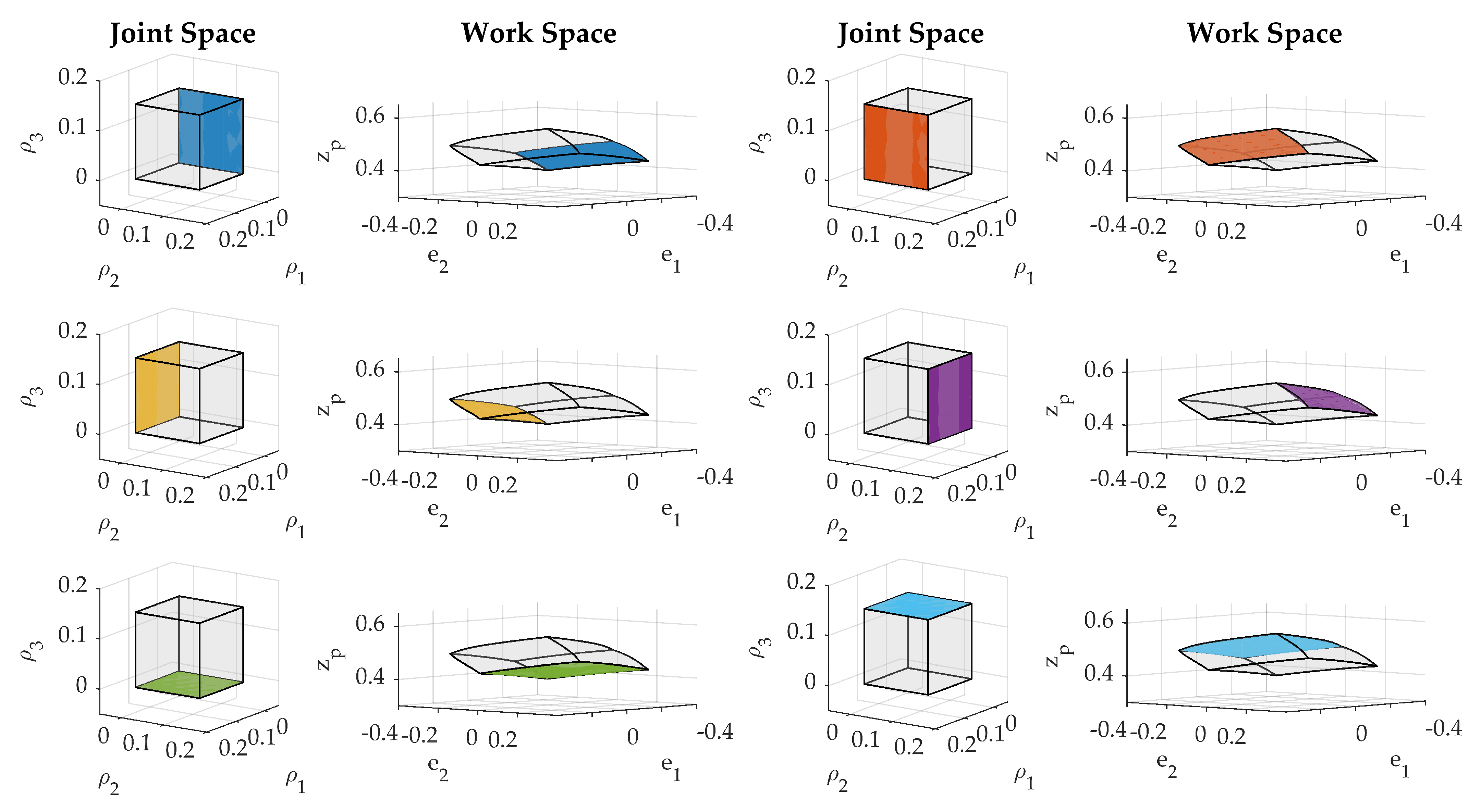
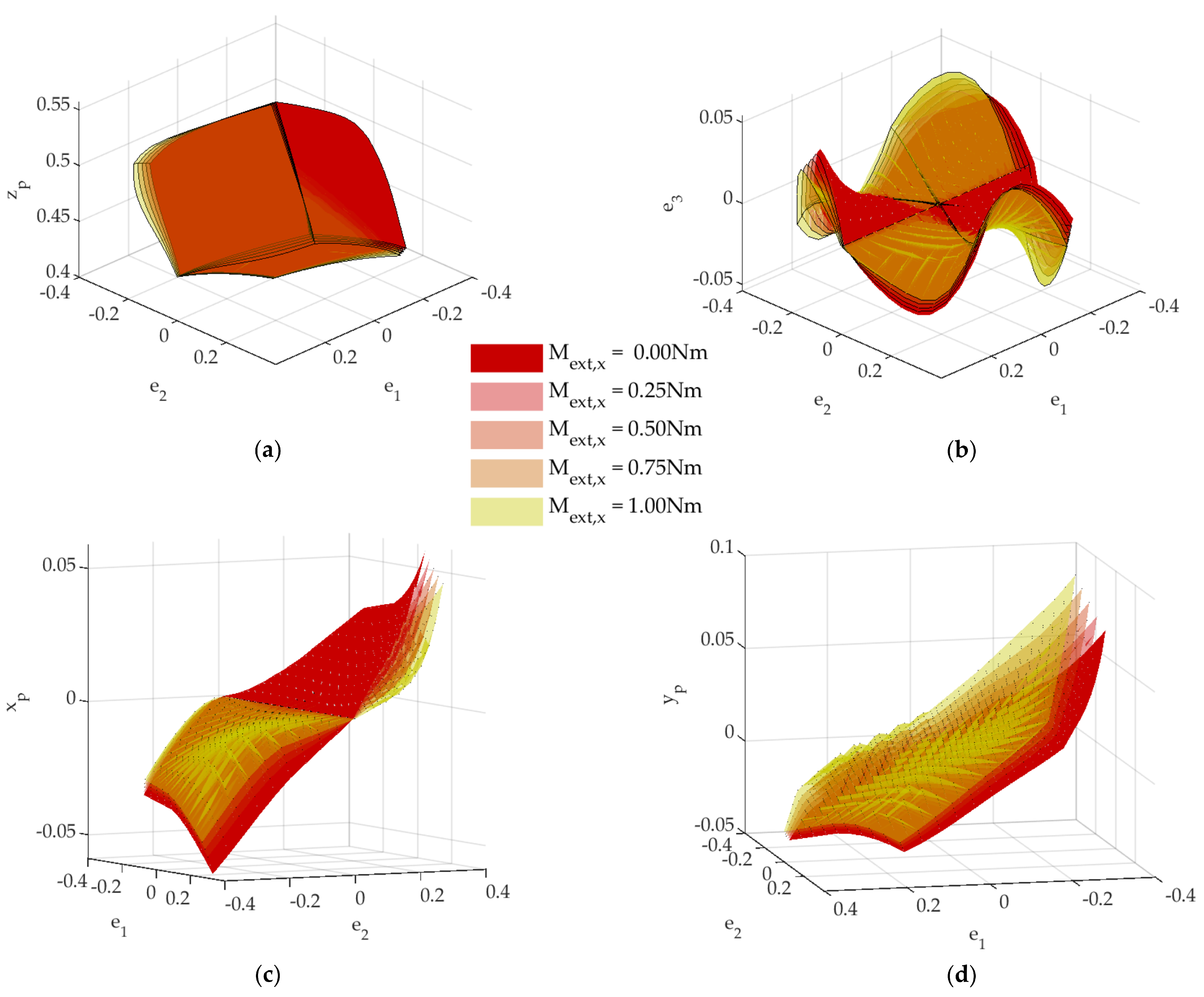
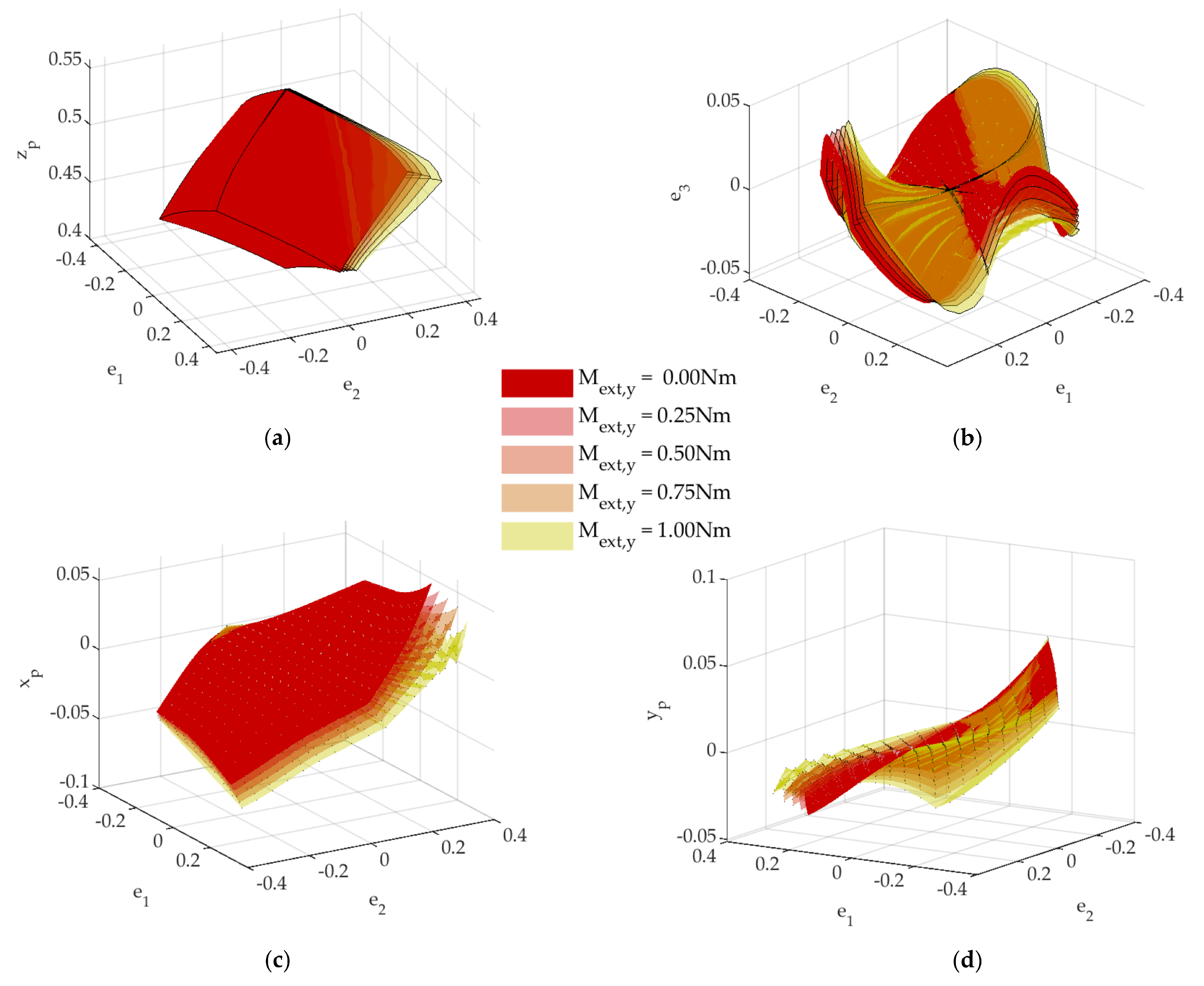
Starting from a home pose where the end effector is placed horizontally at a certain height, introducing a variation in inputs following the distribution on the jointspace, as shown in Figure 9, and solving the FK position problem using the procedure above, we get the set of output poses represented in the workspace $e_1,e_2,z_P$.

As the geometrical arrangement of flexible rods and actuators produces a workspace that is independent of $z_P$ as in the $3\underline{P}RS$, it is convenient to get the jointspace subset that produces the output poses on a horizontal plane, as shown in Figure 10.

From the solutions found in the above-mentioned analysis, it is possible to do a comparison with those obtained for the rigid link parallel mechanism analyzed in the first part of this work. In the next section some of these preliminary results will be discussed.

4. Discussion

In order to compare the motion capabilities of the flexible tripod $3P\underline{F}S$ with the rigid link counterpart $3\underline{P}RS$, we have chosen to plot together the results of parasitic motions of the dependent output variables $e_3,x_P,y_P$ against the independent output parameters $e_1,e_2$, for different $z_P=h$ values of the end effector’s initial position. The same jointspace represented in Figure 10a has been explored in this analysis. For the study presented in this section, the data of the flexible rods used in the $3P\underline{F}S$ manipulator are rod material, $Nitinol$; Young modulus, 83 GPa; rod diameter, 3 mm.

The output-dependent parameter $e_3$ is the one better defining the type of motion of the tripod. Its null value in the rigid-link mechanism implies that only rotations about horizontal axes are possible. The comparison plot corresponding to it is shown in Figure 11. The $e_3$ parameter in the flexible mechanisms has small changes from the null value, so the motion is fairly similar to the rigid tripod. To quantitatively compare the result obtained for the $3P\underline{F}S$ with the $3PRS$ rigid counterpart, the root mean square error ($RMSE$) between the two datasets has been computed for each value h. The results corresponding to the initial heights h = 0.2 m, h = 0.4 m and h = 0.6 m are respectively ${RMSE}_{e_3}=0.0132$, ${RMSE}_{e_3}=0.0095$, and ${RMSE}_{e_3}=0.0065$. Therefore, due to the low value of the error, the motion of the $3P\underline{F}S$ is similar to the rigid tripod. Moreover, for the flexible mechanism there seems to be some dependence of results with h contrary to the rigid case. As expected, the magnitude of the parasitic motions increases as the length of the rods decreases because of the increase in stiffness.

Output dependent parameters $x_{P}and{y}_P$ acquire non-null values for the rigid and flexible tripods with some slight differences, as shown in Figure 12 and Figure 13. Such difference is due to the fact that the mechanical arrangement of flexible rods does not constrain rigidly the spherical joints on the corresponding vertical planes ${\pi }_i$. However, these differences do not compromise the type of motion of the mechanism.

To obtain an analytical expression that relates the output independent parameters $e_1$ and $e_2$ with the parasitic motions $e_3$, $x_p$, and $y_p$, a fitting method based on polynomial approximation has been used. The resulting Equation (36) fits with low error to the blue plots of Figure 11, Figure 12 and Figure 13.

$$\begin{array}{c}\hfill e_3=-3c_0{e}_1^2{e}_2+c_0{e}_2^3\\ \hfill x_p=c_3{e}_1^4{e}_2+2c_2{e}_1^3{e}_2-4c_4{e}_1^2{e}_2^3+c_3{e}_1^2{e}_2+2c_2{e}_1{e}_2-c_4{e}_1{e}_2^3+c_1{e}_2+c_3{e}_2^3-c_5{e}_2^5\\ \hfill y_p=2c_2{e}_1^5+\frac{c_6}{5}{e}_1^4-2c_4{e}_1^3{e}_2^2+c_3{e}_1^3+c_6{e}_1^2{e}_2^2+c_2{e}_1^2+2c_4{e}_1{e}_2^4+c_3{e}_1{e}_2^2-c_1{e}_1-c_5{e}_2^4-c_2{e}_2^2\\ \hfill e_0^2+e_1^2+e_2^2+e_3^2=0\end{array}$$

(36)

where $c_0$ = 1.6; $c_1$ = 0.077 m; $c_2$ = 0.24 m; $c_3$ = 0.64 m; $c_4$ = 0.60 m; $c_5$ = 0.11 m; $c_6$ = 0.80 m

The expression (36) represents for the $3P\underline{F}S$ what Equation (10) does for the $3\underline{P}RS$. These relations will be fundamental to evaluating feasible poses of the end effector to be used as inputs of the inverse kinematic problem that will be investigated in future works.

This study has been done for a null applied load. Figure 14, Figure 15 and Figure 16 show the simulation results in terms of output parameters $e_1$, $e_2$, and $z_p$, and parasitic motions $e_3$, $x_p$, and $y_p$ under three different load configurations, respectively. Figure 14 is related to a constant centred vertical load ${\mathbf{F}}_{ext}={\left[00F_{ext,z}\right]}^T$, Figure 15 to a constant torque around the x axis of the fixed frame ${\mathbf{M}}_{ext}={\left[M_{ext,x}00\right]}^T$, and Figure 16 to a constant torque around the y axis of the fixed frame ${\mathbf{M}}_{ext}={\left[0M_{ext,y}0\right]}^T$.

In the case of a vertical load, a little contraction of the output parameters is shown. Higher differences from the null load results are observed as the end effector rotates. This behavior indicates higher stiffness of the robot when its orientation is parallel to the home configuration. The parasitic motions under vertical loads are characterized by a scaling effect while their shapes over the $e_1$ and $e_2$ workspace remain the same.

Similar considerations can be made in the cases of non-null external torques applied to the end effector. Moreover, in these cases an additional shifting effect is observed. Due to the nonsymmetric arrangement of the robot over the x and y axes of the fixed frame, the effects of torques around these two axes are not equal, as expected.

To quantitatively describe the influence of external load on the end effector’s position, the root mean square error ($RMSE$) between each load configuration and the unloaded one has been computed. To make it easier to read, the RMSE has been normalized over the size of the range of each variable; therefore, the results presented in

Table 1. Relative $RMS$ error of variables $z_p$, $e_3$, $x_p$, and $y_p$ between loaded and unloaded case under three loading configurations: ${\mathbf{F}}_{ext}={\left[00F_{ext,z}\right]}^T$, ${\mathbf{M}}_{ext}={\left[M_{ext,x}00\right]}^T$, and ${\mathbf{M}}_{ext}={\left[0M_{ext,y}0\right]}^T$. Rod diameter 3 mm.

${\mathit{F}}_{\mathbf{ext},\mathit{z}}$, (N)	${\mathit{RMS}}_{{\mathit{z}}_{\mathit{p}}}$, (%)	${\mathit{RMS}}_{{\mathit{e}}_3}$, (%)	${\mathit{RMS}}_{{\mathit{x}}_{\mathit{p}}}$, (%)	${\mathit{RMS}}_{{\mathit{y}}_{\mathit{p}}}$, (%)
−2.50	0.2994	0.3316	0.0587	0.1847
−5.00	0.6567	0.7274	0.1250	0.3962
−7.50	1.0903	1.2076	0.2019	0.6465
−10.00	1.6276	1.8027	0.2950	0.9569
$M_{ext,x}$, (Nm)	$RM{S}_{z_p}$, (%)	$RM{S}_{e_3}$, (%)	$RM{S}_{x_p}$, (%)	$RM{S}_{y_p}$, (%)
0.25	1.0801	2.9173	0.0884	2.1147
0.50	2.1333	6.0013	0.1852	4.2585
0.75	3.1661	9.2941	0.3330	6.5019
1.00	4.1868	12.8431	0.5599	8.9256
$M_{ext,y}$, (Nm)	$RM{S}_{z_p}$, (%)	$RM{S}_{e_3}$, (%)	$RM{S}_{x_p}$, (%)	$RM{S}_{y_p}$, (%)
0.25	2.5773	1.2163	0.1080	2.1356
0.50	5.1938	2.4509	0.2622	4.3486
0.75	7.8955	3.7245	0.5055	6.7339
1.00	10.7512	5.0638	0.9096	9.4405

are relative errors between the loaded and unloaded case.

The same analysis has been performed again with a rod diameter of 4 mm to study the effect of the stiffness on the $3P\underline{F}S$ response to external loads. The results are presented in

Table 2. Relative $RMS$ error of variables $z_p$, $e_3$, $x_p$, and $y_p$ between loaded and unloaded case under three loading configurations: ${\mathbf{F}}_{ext}={\left[00F_{ext,z}\right]}^T$, ${\mathbf{M}}_{ext}={\left[M_{ext,x}00\right]}^T$, and ${\mathbf{M}}_{ext}={\left[0M_{ext,y}0\right]}^T$. Rod diameter 4 mm.

${\mathit{F}}_{\mathbf{ext},\mathit{z}}$, (N)	${\mathit{RMS}}_{{\mathit{z}}_{\mathit{p}}}$, (%)	${\mathit{RMS}}_{{\mathit{e}}_3}$, (%)	${\mathit{RMS}}_{{\mathit{x}}_{\mathit{p}}}$, (%)	${\mathit{RMS}}_{{\mathit{y}}_{\mathit{p}}}$, (%)
−2.50	0.0348	0.0385	0.0070	0.0219
−5.00	0.0702	0.0778	0.0141	0.0441
−7.50	0.1065	0.1179	0.0213	0.0667
−10.00	0.1434	0.1589	0.0286	0.0896
$M_{ext,x}$, (Nm)	$RM{S}_{z_p}$, (%)	$RM{S}_{e_3}$, (%)	$RM{S}_{x_p}$, (%)	$RM{S}_{y_p}$, (%)
0.25	0.1367	0.3571	0.0122	0.2652
0.50	0.2730	0.7162	0.0239	0.5300
0.75	0.4087	1.0775	0.0352	0.7943
1.00	0.5440	1.4410	0.0461	1.0585
$M_{ext,y}$, (Nm)	$RM{S}_{z_p}$, (%)	$RM{S}_{e_3}$, (%)	$RM{S}_{x_p}$, (%)	$RM{S}_{y_p}$, (%)
0.25	0.3215	0.1517	0.0125	0.2655
0.50	0.6431	0.3035	0.0251	0.5312
0.75	0.9649	0.4554	0.0379	0.7972
1.00	1.2868	0.6073	0.0510	1.0636

. As expected, an increase of stiffness in the system results in lower differences between loaded and unloaded configuration.

5. Conclusions

In this paper, the performance of a tripod-type parallel continuum manipulator, $3P\underline{F}S$, is compared with the operation of its rigid counterpart $3\underline{P}RS$. On the one hand, in rigid lower mobility parallel manipulators their reduced mobility is expressed as a set of equations relating the parameters representing the pose of the end effector. On the other hand, in continuum architectures, such geometric constraints expressible with algebraic equations are not feasible because flexible links can deform under actuation and load reaching any configuration in space. However, some mechanical arrangements can introduce a much greater limitation of deformation in some directions, producing a similar constraint effect.

The flexible $3P\underline{F}S$ parallel continuum tripod is modeled by introducing some changes to the flexible hexapod already studied in the literature and the forward kinematics position problem is solved numerically. Introducing a variety of input values in the FK solver of the tripod PCM, we verify the degree of accomplishment of the constraint equations obtained for the tripod PKM. Thus, for the flexible mechanism there seems to be some dependence of the output-dependent parameters on the end effector, contrary to the rigid case. This difference is due to the fact that the mechanical arrangement of the flexible rods does not rigidly constrain the spherical joints in the corresponding vertical planes. However, these differences do not compromise the type of motion of the mechanism. From this analysis, an analytical expression relating the output independent parameters to the parasitic motions is obtained by means of a fitting method. This expression represents for the $3P\underline{F}S$ what the constraint equations do for the $3\underline{P}RS$.

In conclusion, in this paper we show that PCMs of lower mobility exist and that they have strong similarities with their rigid-link counterparts and that their basic kinematic principles are applicable. The obtained analytical expression referred to above will be fundamental to evaluate the feasible end effector poses to be used as inputs for the inverse kinematic problem to be investigated in future work.