4D Printing of Hydrogels Controlled by Hinge Structure and Spatially Gradient Swelling for Soft Robots
Abstract
1. Introduction
2. Concept and Design
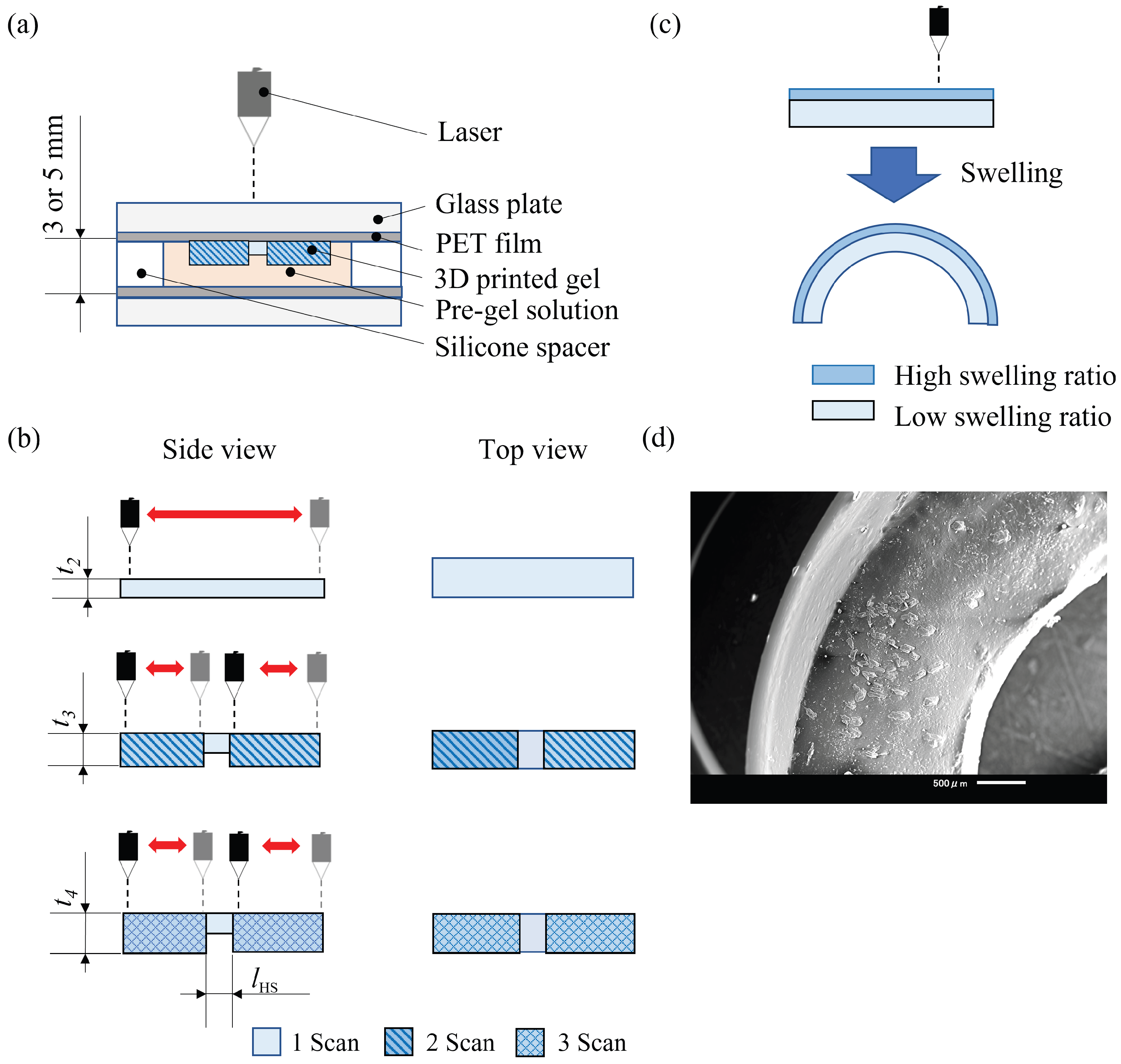
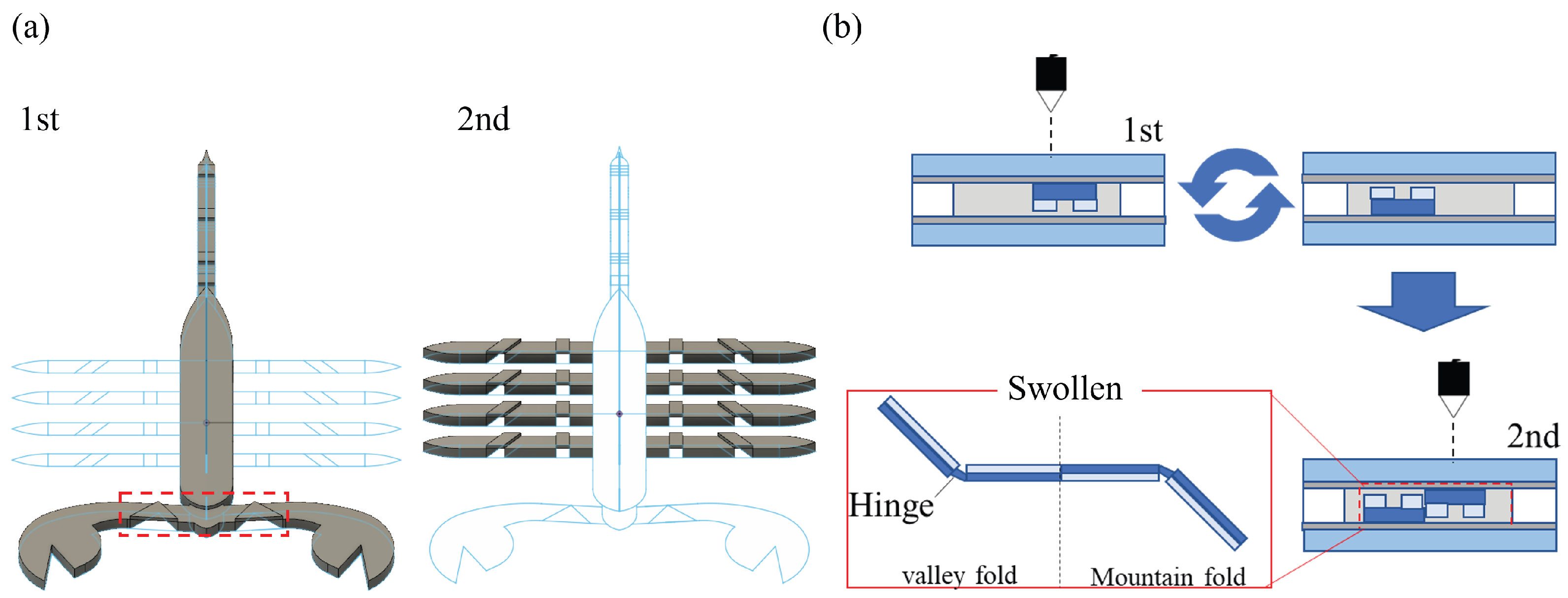
2.1. 4D Printing Concept
2.2. Materials
3. Factors for Actuation
3.1. Materials Composition
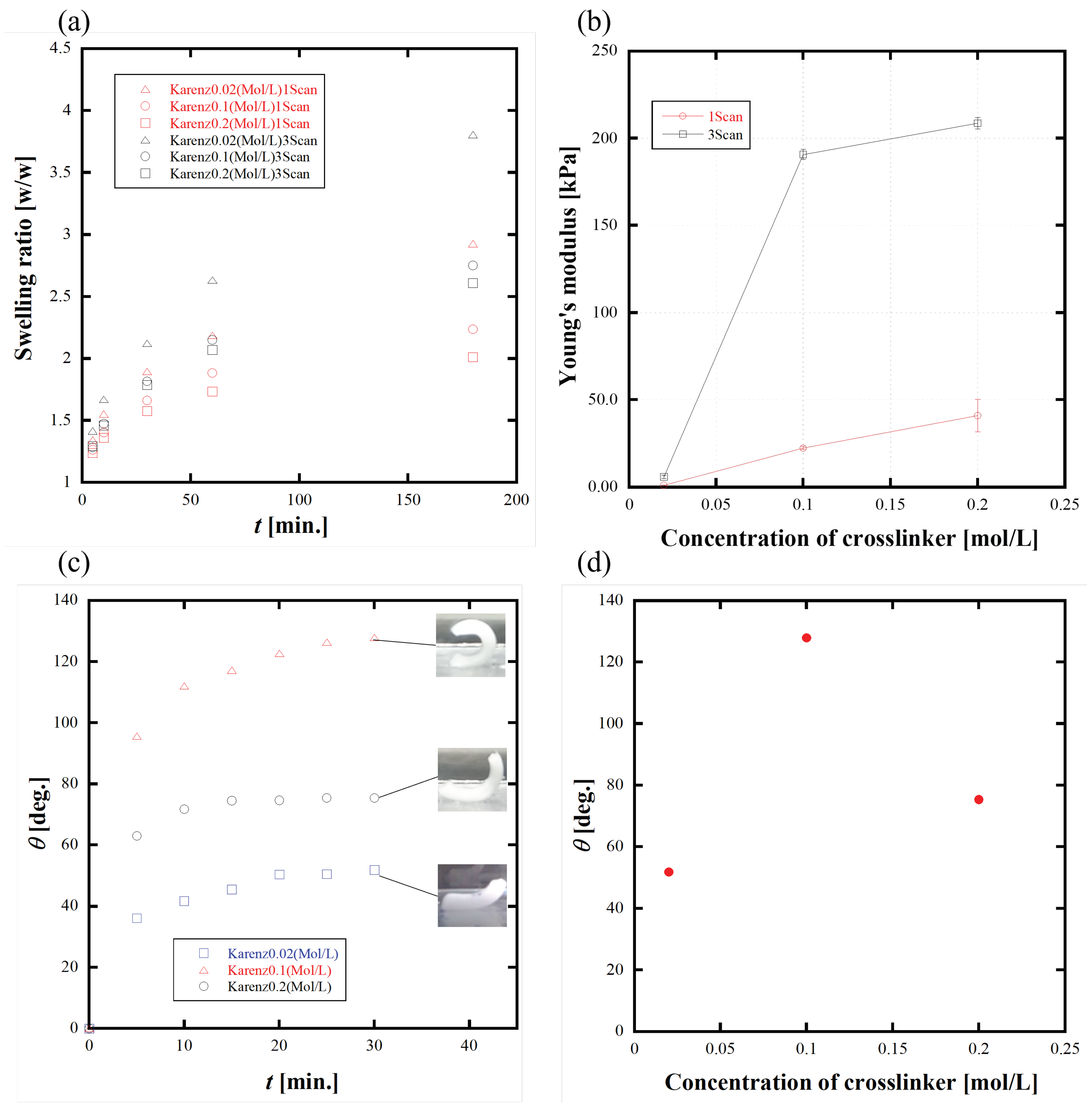
3.1.1. Initiator Concentration
3.1.2. Crosslinker Concentration
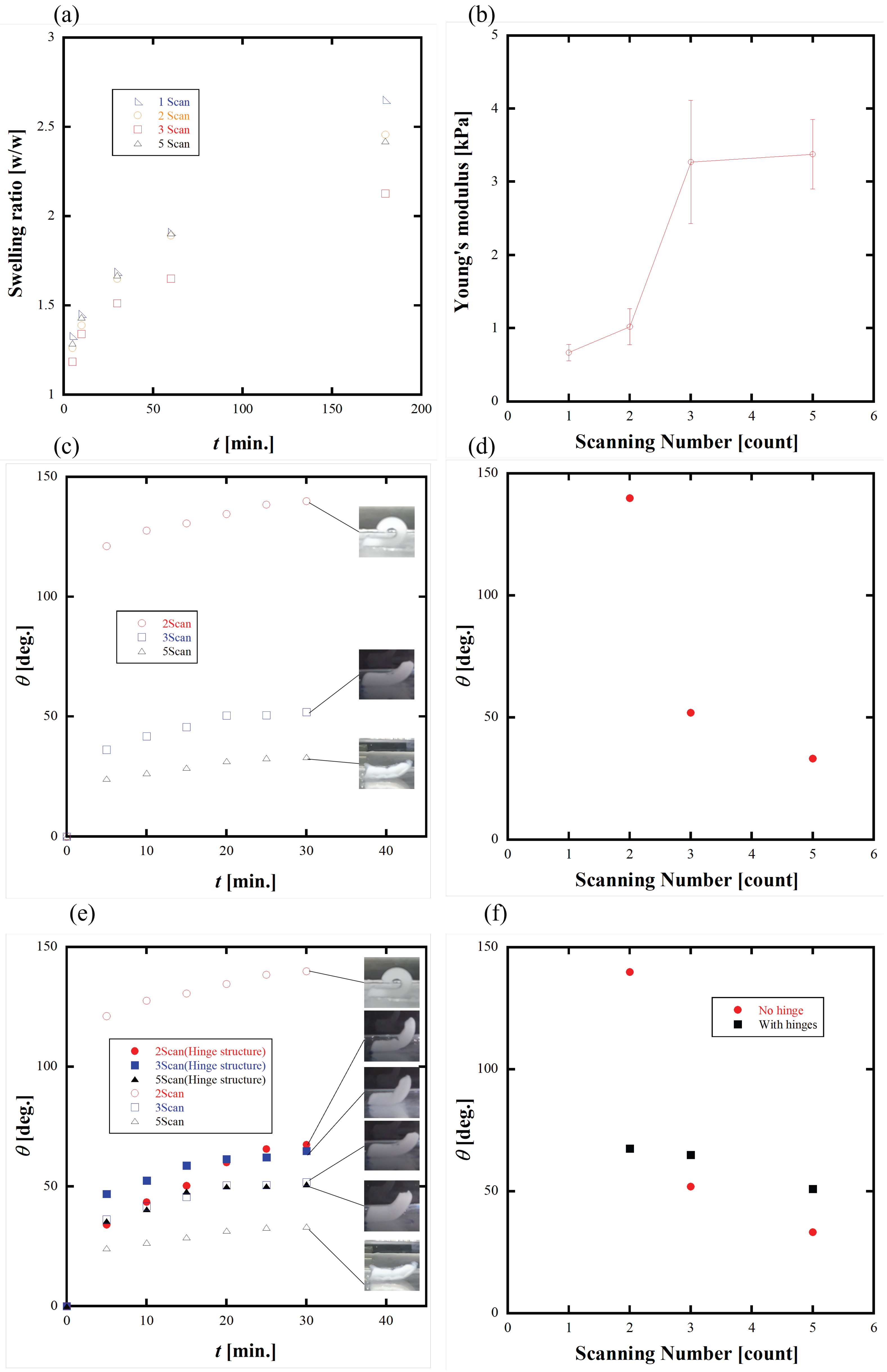
3.2. Structure
Thickness and Hinge Structure
3.3. Important Factors
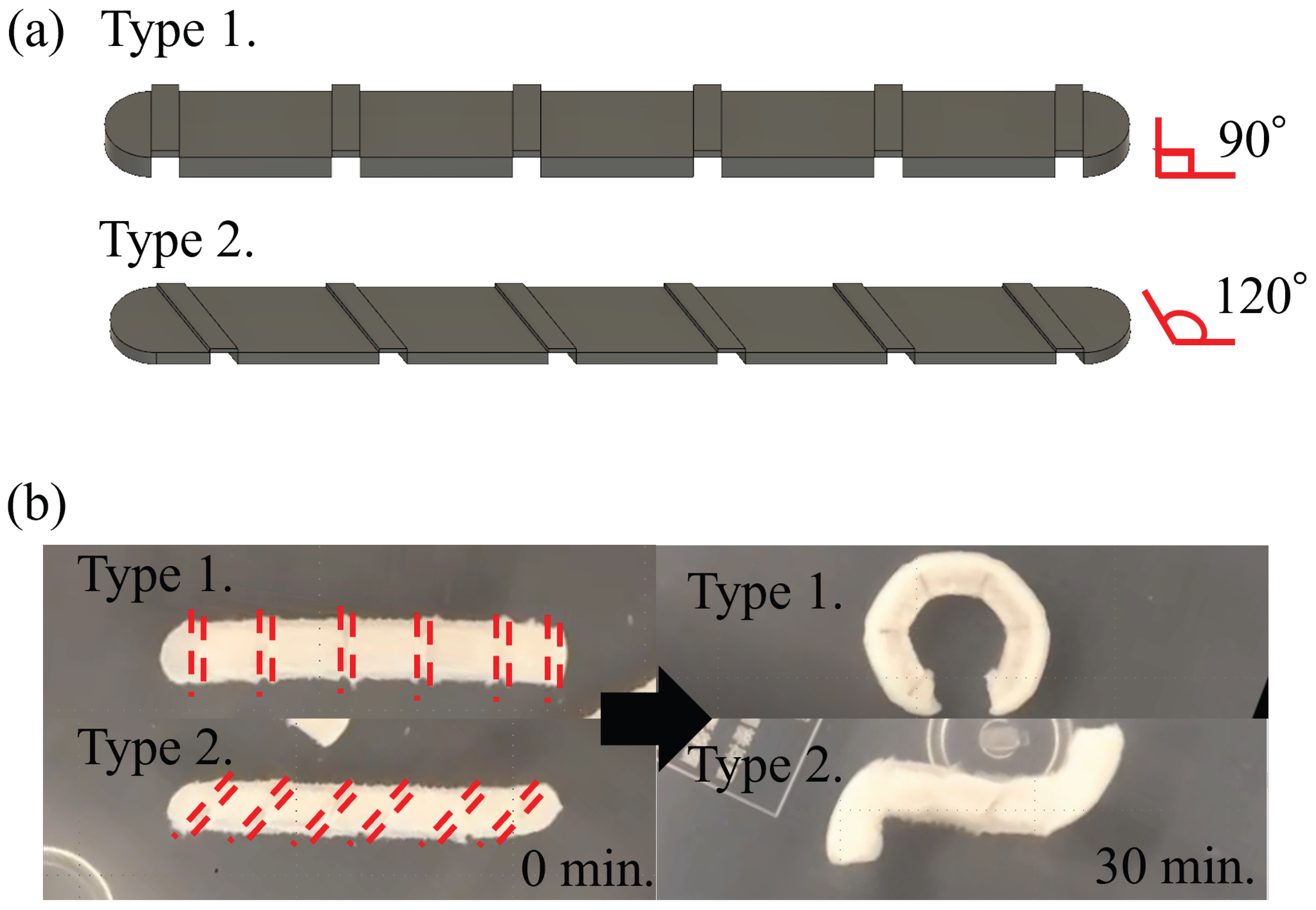
4. Application of Hinge Structure
5. Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tibbits, S. 4D Printing: Multi-Material Shape Change. Archit. Des. 2014, 84, 116–121. [Google Scholar] [CrossRef]
- Tibbits, S.; McKnelly, C.; Olguin, C.; Dikovsky, D.; Hirsch, S. 4D printing and universal transformation. In Proceedings of the 34th Annual Conference of the Association for Computer Aided Design in Architecture (ACADIA 2014 Design Agency), Los Angeles, CA, USA, 23–25 October 2014; pp. 539–548. [Google Scholar]
- More Talent Literacy; Less Talent Management. Clearing the Way for Pivotal 21st-Century Innovation. Gift. Talent. 21st Century 2016, 10, 163–179. [Google Scholar]
- Ge1, Q.; Qi, H.J.; Dunn, M.L. Active materials by four-dimension printing. Appl. Phys. Lett. 2013, 103, 131901. [Google Scholar]
- Huang, L.; Jiang, R.; Wu, J.; Song, J.; Bai, H.; Li, B.; Zhao, Q.; Xie, T. Ultrafast digital printing toward 4D shape changing materials. Adv. Mater. 2017, 29, 1605390. [Google Scholar] [CrossRef]
- Kuang, X.; Roach, D.J.; Wu, J.; Hamel, C.M.; Ding, Z.; Wang, T.; Dunn, M.L.; Qi, H.J. Advances in 4D printing: Materials and applications. Adv. Funct. Mater. 2019, 29, 1805290. [Google Scholar] [CrossRef]
- Pei, E. 4D Printing: Dawn of an emerging technology cycle. Assem. Autom. 2014, 34, 310–314. [Google Scholar] [CrossRef]
- Khoo, Z.X.; Teoh, J.E.M.; Liu, Y.; Chua, C.K.; Yang, S.; An, J.; Leong, K.F.; Yeong, W.Y. 3D printing of smart materials: A review on recent progresses in 4D printing. Virtual Phys. Prototyp. 2015, 10, 103–122. [Google Scholar] [CrossRef]
- Raviv, D.; Zhao, W.; McKnelly, C.; Papadopoulou, A.; Kadambi, A.; Shi, B.; Hirsch, S.; Dikovsky, D.; Zyracki, M.; Olguin, C.; et al. Active printed materials for complex self-evolving deformations. Sci. Rep. 2014, 4, 7422. [Google Scholar] [CrossRef]
- Mao, Y.; Yu, K.; Isakov, M.S.; Wu, J.; Dunn, M.L.; Qi, H.J. Sequential Self-Folding Structures by 3D Printed Digital Shape Memory Polymers. Sci. Rep. 2016, 7, 163–179. [Google Scholar] [CrossRef]
- Kai, Y.; Dunn, M.L.; Qi, H.J. Digital manufacture of shape changing components. Extrem. Mech. Lett. 2015, 4, 9–17. [Google Scholar]
- Wu, J.; Yuan, C.; Ding, Z.; Isakov, M.; Mao, Y.; Wang, T.; Dunn, M.L.; Qi, H.J. Multi-shape active composites by 3D printing of digital shape memory polymers. Sci. Rep. 2016, 6, 24224. [Google Scholar] [CrossRef]
- Kuksenok, O.; Balazs, A.C. Stimuli-responsive behavior of composites integrating thermo-responsive gels with photo-responsive fibers. Mater. Horizons 2016, 3, 53–62. [Google Scholar] [CrossRef]
- Bakarich, S.E.; Gorkin, R., III; Panhuis, M.I.H.; Spinks, G.M. 4D printing with mechanically robust, thermally actuating hydrogels. Macromol. Rapid Commun. 2015, 36, 1211–1217. [Google Scholar] [CrossRef]
- Zhou, J.; Sheiko, S.S. Reversible shape-shifting in polymeric materials. Gift. Talent. 21st Century 2016, 54, 1365–1380. [Google Scholar] [CrossRef]
- Jeong, H.Y.; Woo, B.H.; Kim, N.; Jun, Y.C. Multicolor 4D printing of shape-memory polymers for light-induced selective heating and remote actuation. Sci. Rep. 2020, 10, 6258. [Google Scholar] [CrossRef]
- Lai, J.; Ye, X.; Liu, J.; Wang, C.; Li, J.; Wang, X.; Ma, M.; Wang, M. 4D printing of highly printable and shape morphing hydrogels composed of alginate and methylcellulose. Mater. Des. 2021, 205, 109699. [Google Scholar] [CrossRef]
- Rahmatabadi, D.; Aberoumand, M.; Soltanmohammadi, K.; Soleyman, E.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Bodaghi, M. 4D Printing-Encapsulated Polycaprolactone–Thermoplastic Polyurethane with High Shape Memory Performances. Adv. Eng. Mater. 2022, 2201309. [Google Scholar] [CrossRef]
- Bodaghi, M.; Damanpack, A.R.; Liao, W.H. Adaptive metamaterials by functionally graded 4D printing. Mater. Des. 2017, 135, 26–36. [Google Scholar] [CrossRef]
- Song, Z.; Ren, L.; Zhao, C.; Liu, H.; Yu, Z.; Liu, Q.; Nonuniform, L.R.B. Dual-Stimuli Self-Morphing Enabled by Gradient Four-Dimensional Printing. ACS Appl. Mater. Interfaces 2020, 12, 6351–6361. [Google Scholar] [CrossRef]
- Ge, Q.; Sakhaei, A.H.; Lee, H.; Dunn, C.K.; Fang, N.X.; Dunn, M.L. Multimaterial 4D printing with tailorable shape memory polymers. Sci. Rep. 2016, 6, 31110. [Google Scholar] [CrossRef]
- Shiblee, M.N.I.; Ahmed, K.; Kawakami, M.; Furukawa, H. 4D Printing of Shape-Memory Hydrogels for Soft-Robotic Functions. Adv. Mater. Technol. 2019, 4, 1900071. [Google Scholar] [CrossRef]
- Shiblee, M.N.I.; Ahmed, K.; Khosl, A.; Kawakami, M.; Furukawa, H. 3D printing of shape memory hydrogels with tunable mechanical properties. Soft Matter 2018, 14, 7809–7817. [Google Scholar] [CrossRef]
- Rahmatabadi, D.; Aberoumand, M.; Soltanmohammadi, K.; Soleyman, E.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Zolfagharian, A.; Bodaghi, M.; Baghani, M. A New Strategy for Achieving Shape Memory Effects in 4D Printed Two-Layer Composite Structures. Polymers 2022, 24, 5446. [Google Scholar] [CrossRef] [PubMed]
- Muroi, H.; Hidema, R.; Gong, J.; Furukawa, H. Development of optical 3D gel printer for fabricating free-form soft & wet industrial materials and evaluation of printed double-network gels. J. Solid Mech. Mater. Eng. 2013, 7, 163–168. [Google Scholar]
- Ota, T.; Saito, A.; Tase, T.; Sato, K.; Tanaka, M.; Yoshida, K.; Takamatsu, K.; Kawakami, M.; Furukawa, H. 3D Printing of Tough Gels Having Tunable Elastic Modulus from the Same Pre-Gel Solution. Macromol. Chem. Phys. 2019, 220, 1800498. [Google Scholar] [CrossRef]
- Okumura, Y.; Ito, K. The polyrotaxane gel: A topological gel by figure-of-eight cross-links. Adv. Mater. 2001, 13, 485–487. [Google Scholar] [CrossRef]
- Haraguchi, K.; Takehisa, T. TNanocomposite Hydrogels: A Unique Organic–Inorganic Network Structure with Extraordinary Mechanical, Optical, and Swelling/De-swelling Properties. Adv. Mater. 2002, 14, 1120–1124. [Google Scholar] [CrossRef]
- Gong, J.P.; Katsuyama, Y.; Kurokawa, T.; Osada, Y. Double-Network Hydrogels with Extremely High Mechanical Strength. Adv. Mater. 2003, 15, 1155–1158. [Google Scholar] [CrossRef]
- Yin, J.; Fan, W.; Xu, Z.; Duan, J.; Xia, Y.; Nie, Z.; Sui, K. Precisely defining local gradients of stimuli-responsive hydrogels for complex 2D-to-4D shape evolutions. Small 2022, 18, 2104440. [Google Scholar] [CrossRef]
- Kuksenok, O.; Yashin, V.V.; Kinoshita, M.; Sakai, T.; Yoshidab, R.; Balazs, A.C. Exploiting gradients in cross-link density to control the bending and self-propelled motion of active gels. J. Mater. Chem. 2011, 21, 8360–8371. [Google Scholar] [CrossRef]
- Fan, W.; Shan, C.; Guo, H.; Sang, J.; Wang, R.; Zheng, R.; Sui, K.; Nie, Z. Dual-gradient enabled ultrafast biomimetic snapping of hydrogel materials. Sci. Adv. 2019, 5, eaav7174. [Google Scholar] [CrossRef]
- Ge1, Q.; Dunn, C.K.; Qi, H.J.; Dunn, M.L. Active origami by 4D printing. SMart Mater. Struct. 2014, 23, 094007. [Google Scholar]
- Chalapat, K.; Chekurov, N.; Jiang, H.; Li, J.; Parviz, B.; Paraoanu, G.S. Self-Organized origami structures via Ion-Induced plastic strain. Adv. Mater. 2013, 25, 91–95. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Zhang, F.; Lan, X.; Leng, J.; Liu, S.; Jia, X.; Cotton, C.; Sun, B.; Bohong, G. Shape memory behavior and recovery force of 4D printed laminated Miura-origami structures subjected to compressive loading. Compos. Part Eng. 2018, 153, 233–242. [Google Scholar] [CrossRef]
- Jamal, M.; Kadam, S.S.; Xiao, R.; Jivan, F.; Onn, T.M.; Fernandes, R.; Nguyen, T.D.; Gracias, D.H. Bio-origami hydrogel scaffolds composed of photocrosslinked PEG bilayers. Adv. Healthc. Mater. 2015, 5, 1–12. [Google Scholar] [CrossRef]
- Takada, G.; Hidema, R.; Furukawa, H. Ultrahigh Ductile Gels Having Inter-Crosslinking Network (ICN) Structure. e-J. Surf. Sci. Nanotechnol. 2012, 10, 346–350. [Google Scholar] [CrossRef]
- Takada, G.; Hidema, R.; Furukawa, H. Ultrahigh ductile gels developed by inter cross-linking network (ICN). J. Solid Mech. Mater. Eng. 2012, 6, 169–177. [Google Scholar] [CrossRef]
- Watanabe, Y.; Inoue, S.; Saito, A.; Kawakawami, M.; Furukawa, H. 3D printable inter cross-linking network (ICN) gels for reversible transparency control with water content. Microsyst. Technol. 2022, 28, 167–171. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Saito, A.; Yamazaki, M.; Watanabe, Y.; Shiblee, M.N.I.; Khosla, A.; Ogawa, J.; Kawakami, M.; Nango, J.; Furukawa, H. TheSimultaneous 3D Printing of White and Transparent Gels for Medical Models. ECS Trans. 2020, 98, 47. [Google Scholar] [CrossRef]
- Takishima, Y.; Yoshida, K.; Khosla, A.; Kawakami, M.; Furukawa, H. Fully 3D-printed hydrogel actuator for jellyfish soft robots. ECS J. Solid State Sci. Technol. 2021, 10, 037002. [Google Scholar] [CrossRef]





| TPO 0.005 (Mol/L) | TPO 0.01 (Mol/L) | TPO 0.02 (Mol/L) | |
| 1 Scan |  |  |  |
| 3 Scan |  |  |  |
| Max. Angle | Role for Deformation | |
|---|---|---|
| Initiator concentration | 52° | Must |
| Crosslinker concentration | 128° | Enhancement |
| Thickness (scanning number) | 140° | Enhancement |
| Hinge structure | 67° | Limitation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kameoka, M.; Watanabe, Y.; Shiblee, M.N.I.; Kawakami, M.; Ogawa, J.; Khosla, A.; Furukawa, H.; Zhang, S.; Hirai, S.; Wang, Z. 4D Printing of Hydrogels Controlled by Hinge Structure and Spatially Gradient Swelling for Soft Robots. Machines 2023, 11, 103. https://doi.org/10.3390/machines11010103
Kameoka M, Watanabe Y, Shiblee MNI, Kawakami M, Ogawa J, Khosla A, Furukawa H, Zhang S, Hirai S, Wang Z. 4D Printing of Hydrogels Controlled by Hinge Structure and Spatially Gradient Swelling for Soft Robots. Machines. 2023; 11(1):103. https://doi.org/10.3390/machines11010103
Chicago/Turabian StyleKameoka, Masanari, Yosuke Watanabe, MD Nahin Islam Shiblee, Masaru Kawakami, Jun Ogawa, Ajit Khosla, Hidemitsu Furukawa, Shengyang Zhang, Shinichi Hirai, and Zhongkui Wang. 2023. "4D Printing of Hydrogels Controlled by Hinge Structure and Spatially Gradient Swelling for Soft Robots" Machines 11, no. 1: 103. https://doi.org/10.3390/machines11010103
APA StyleKameoka, M., Watanabe, Y., Shiblee, M. N. I., Kawakami, M., Ogawa, J., Khosla, A., Furukawa, H., Zhang, S., Hirai, S., & Wang, Z. (2023). 4D Printing of Hydrogels Controlled by Hinge Structure and Spatially Gradient Swelling for Soft Robots. Machines, 11(1), 103. https://doi.org/10.3390/machines11010103










