Abstract
Continuum robots are good candidates for shape morphing. However, due to the coupled problem between kinematics and statics, the inverse kinematics of continuum robots is highly nonlinear, posing a challenging problem for real-time applications. This paper presents a simplified approach to solving the inverse kinematics of a flexible panel continuum robot efficiently. Through an experiment, two approximate relationships are discovered. First, the arc length of the middle backbone can be estimated from the arc lengths of the two panels; second, the length difference between the two panels can be related to the tip angle of the end-effector. Based on these two discovered relationships, a simplified inverse kinematics method is proposed based on a constant curvature model. This method has been validated by the experimental data with high accuracy of less than 2% error, thereby demonstrating the effectiveness of the proposed method for real-time applications.
1. Introduction
Continuum robots have become a topic of recent research, mainly owing to their ability to mimic the movement of certain animals such as snakes [1], elephants (trunks) [2] and octopuses (tentacles) [3]. These robots are made up of flexible materials possessing good ability of bending and dexterity to maneuver in congested environments through shape morphing [4]. Specific applications include medical surgery [5], nuclear reactor maintenance [6], disaster relief [7] and other industrial uses [8].
Continuum robots are often kinematically redundant and highly nonlinear, rendering their kinematic analysis more complex than their rigid-link counterparts. Unlike the rigid robots where the pose of any point in the robot workspace can be fully defined by link lengths and joint angles, the kinematics of continuum robots remains challenging to solve due to the under-determined nature of the underlying problem.
Substantial research has been carried out in the past. Jones and Walker [9,10] developed a modified homogenous transformation matrix in terms of Denavit–Hartenberg (D-H) parameters to analyze the kinematics of the continuum robot. Simaan et al. [11] proposed a differential method to divide the continuum robot into several small units and then computed the position of the end-effector by using an integration method. Godage et al. [12] presented a new three-dimensional kinematic model for multisection continuum arms using a shape-function-based approach and incorporating geometrically constrained structures [13]. Another interesting approach was presented in [14], where the authors used torus segments to represent the sections of a continuum robot called a bionic handling assistant (BHA) manipulator. Escande et al. [15] put forward a forward kinematics model for the compact bionic handling assistant (CBHA) based on the constant curvature assumption. The above-mentioned methods share a common problem in that the inverse kinematics cannot be directly derived from the forward kinematics. Usually, numerical methods such as Least Squares [16] and Newton–Raphson methods [17] are adopted, but they are computationally intensive and not applicable for real-time applications. Because of this reason, qualitative methods have also been explored. Giorelli et al. [18] modeled the inverse kinematics (IK) of a flexible manipulator using feed-forward Neural Networks (NN). Rolf and Steil [19] introduced a goal babbling approach to solve the IK of the bionic handling assistant robot. Melingui et al. [20] used the NN through a distal supervised learning scheme to solve the IK of the CBHA robot. Although the accuracy has been improved, these methods are still time-consuming and computationally expensive.
In conclusion, using the existing methods to solve the kinematics of the continuum robot mainly has the following problems: it is impossible or difficult to find the inverse kinematic solution, the calculation is large and the accuracy of the results is low. For these reasons, we are exploring a simple approach to solving the inverse kinematics for real-time applications.
The rest of this paper is arranged as follows. Section 2 describes the forward kinematics based on the long beam theory. In Section 3, the DOFs are analyzed to determine the number of parameters to be controlled. In Section 4, a simplified model is proposed to solve the inverse kinematics of a flexible parallel robot based on the experimental studies. At last, a number of case studies are supplied to show the effectiveness of the method.
2. Kinematic Analysis Based on Large Deformation Beam Theory
2.1. System Description
As shown in Figure 1, the continuum robot under study consists of two flexible panels made of carbon fibers. Each panel is connected to a linear actuator on one end and runs through the gap between two sets of rollers to connect to the moving platform on the other end. Both linear actuators and rollers are mounted on a frame fixed to the ground. The two sets of rollers (top and bottom) form the base of the flexible panels. Since the panels are mainly subject to bending, their deformations are directional, very flexible in the length direction yet very rigid in the width direction.
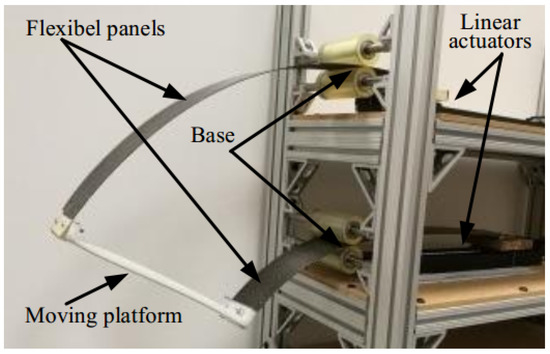
Figure 1.
Structure of the flexible panel continuum robot.
Due to this directionality, they are naturally constrained only to deform along the length direction, i.e., in the X–Z plane, as shown in Figure 2. Thus, the two panels along with the base and the moving platform form a planar flexible panel continuum robot. As the two linear actuators move back and forth, the panel lengths change to cause the robot to curve up or down, depending on the direction of the length difference between the two panels.
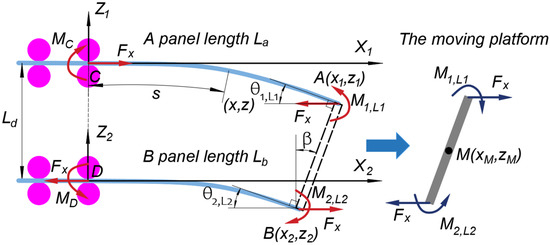
Figure 2.
Analysis model without gravity (Fx is the pushing force constrained along the X1 axis and imposed at point C, and are moments generated by the bending of top panel A and MC and MD are the reaction moments).
Kinematically, this continuum robot is formed by four points: A and B for the moving platform (the moving platform is considered as a rigid body) and C and D for the fixed base. There are two sets of coordinate frames: for top plate A and for the bottom plate B. The distance between the origin of two coordinate frames is along the common Z axis. The top panel length is denoted by and the bottom one by . and are the changing variables controlled by the respective linear actuators; , represent the coordinates of the end point of the top panel (point A) and , the coordinates of the end point of the bottom panel (point B), in their respective coordinate frames.
2.2. Review of Forward Kinematic Modeling
A brief review of our previous work on forward kinematic modeling of this continuum robot [21] is provided to show the coupling between the nonlinear deformation of two flexible plates. As described in [21], the deformation equations were established based on Euler–Bernoulli beam theory at first for the problem of nonlinear deformation of a single flexible plate. The deformation curves of two flexible panels under a certain length were given in the form of differential equations (D.E.) with boundary conditions (B.C.), as shown in Equation (1). In Equations (2) and (3), the elliptic integral was used for calculation. Then, the relationship between the lengths of two panels and the position and orientation of the moving platform was established using a kinematically constrained optimization model, as shown in Equation (4). Finally, the forward kinematics model was obtained as expressed in Equation (5) to Equation (8).
where is the slope at any point , s is the arc distance of that point along the panel curve from its fixed end, is the axial force exerted by the linear actuator, EI is the stiffness of this mechanism, is the end slope of the panel i, and stands for panel A and for panel B. By Equations (2) and (3), we can obtain the lengths of panel a () and panel b (), respectively.
where , is the end moment of the panel, and stands for panel A and for panel B.
The constrained minimization problem in Equation (4) is a nonlinear optimization problem with pure equality constraints. Similarly, they can also be solved by using the SQP method from MATLAB.
where is the distance between points C and D (Figure 2).
From Equation (5) to Equation (8), the positions of the end point A and B can be solved. The position and orientation (also called tip angle) of the moving platform can be calculated from these two points as
To this end, the forward kinematics of the continuous robot is solved. In actual applications, however, a desired tip posture is specified, and the inverse problem becomes essential to determine the actuator lengths that correspond to the desired tip posture. From Equations (1)–(10), for given robot’s posture and β, though x1, x2, z1 and z2 can be determined by Equations (9) and (10), the actuator lengths La and Lb will have to be solved by elliptical integration using Equations (2) and (3), which makes the inverse kinematics a very challenging problem. For this reason, we need to explore a simplified method for real-time applications.
3. Mobility Analysis of the Continuum Robot
For the purpose of understanding the problem at hand, a mobility analysis may be necessary in order to determine the number of parameters involved in the inverse kinematics. This analysis is conducted based on a pseudo-rigid-body model that is usually feasible when the end of a flexible beam is of interest. Previous studies have validated the pseudo-rigid-body models, such as 1R [22,23,24], 2R [25], 3R [26] and PR [27].
By using a 2R pseudo-rigid-body model, a sliding flexible panel can be simplified as a PRR link, with the P joint for sliding, the first R joint for bending deflection (vertical) and the second R joint for bending curvature. As shown in Figure 3, the flexible panel mechanism is modeled by five rigid parts (part 1 to part 5), two planar prismatic pairs (pair a and pair f) and four revolute pairs (pair b to pair e). Among them, pair a and pair f represent the sliding motion of the upper and lower panels driven by their respective linear actuators. Correspondingly, pair b to pair e represent the bending deflections of the two panels and their bending curvatures. With this model, the DOFs of our robot can be calculated as
where is the degrees of freedom (DOFs) of this mechanism, is the number of links, i.e., , and represents the number of low pair joints, i.e., Therefore, the DOFs of this mechanism are . Thus, if three parameters, i.e., the position and orientation of the continuum mechanism X, Z and β, are fully defined, the mechanism can be well controlled. In other words, though there are only two actuators for three pose parameters, which is traditionally considered as under-actuation, the flexibility of the panels adds additional degrees of freedom that are used for full pose control of the robot, a very interesting finding that sets a base for our work on the inverse kinematics.
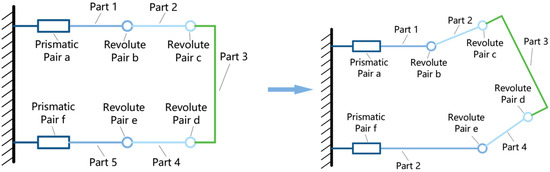
Figure 3.
A simplified model of the flexible panel continuum mechanism.
4. A Quasi-Rigid Model for Inverse Kinematics
Knowing that our continuum robot can realize full pose control, we propose a quasi-rigid model for solving its inverse kinematics for real-time applications. To achieve this goal, first we conducted a series of experiments by inputting the panel lengths and then measuring the end positions of the two panels by an optical coordinated machine measurement (CMM) device from Northern Digital Polaris Vicra. As shown in Figure 4a, by using the two end points A and B , we can calculate the middle point of the moving platform and its orientation as defined before as , and tip angle in Equations (9) and (10).
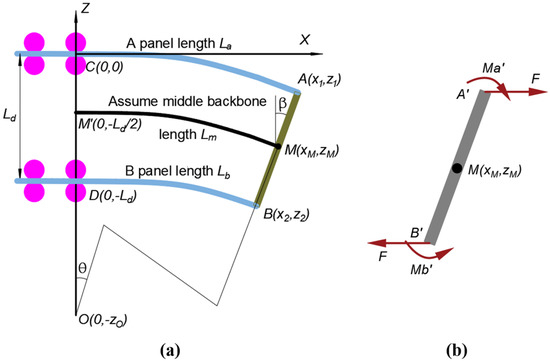
Figure 4.
Planar parallel continuum robot and static analysis of the moving platform: (a) A virtual backbone that runs through the middle axis of the two panels; (b) A pushing force at point A and a pulling force at point B.
Table 1 records the experimental data in terms of panel lengths La and Lb. In the experiment, both panels start from 150 mm and end at 400 mm. In total, there are five series with an increment of 50 mm for Lb, and within each series La changes in an increment of 50 mm. For series 1, Lb is at the initial position of 150 mm and Lb changes from 200 mm to 400 mm in an increment of 50 mm. For series 2, Lb advances to 200 mm and La changes from 250 mm to 400 mm in an increment of 50 mm. Note that this robot is symmetric along the horizontal axis; La does not have to start from the initial position at 150 mm, as this case is already covered by series 1. For series 3, 4 and 5, Lb advances to 250 mm, 300 mm and 350 mm, respectively, while La starts after the respective Lb values for the same reason. As a result, both panels are taken into consideration.

Table 1.
Experimental results unit: mm.
After the experiment, we wanted to delve into if a quasi-rigid model could be established. Upon comparison, one may notice that there is no centric backbone in our robot, as opposed to conventional continuum robots. For this reason, we assume a virtual backbone that runs through the middle axis of the two panels, as shown in Figure 4a. Furthermore, by examining the moving platform in terms of internal forces, there is a pushing force at point A and a pulling force at point B, or vice versa, hence forces are always balanced but only with a moment, as shown in Figure 4b. According to the Bernoulli–Euler beam theory, a beam with a pure-moment load will resemble a circular arc. This loading condition under a pure-moment scenario indicates that the middle backbone would bend into a circular shape. Therefore, we assume the shape of the middle axis (virtual backbone) is of an arc. Since the arc is perpendicular to the Z axis at the start point, the center coordinate of the arc is 0 in X direction and in Z direction. In other words, the middle backbone has the start point at and the end point at . Therefore, a circle equation can be written as
from which zo can be determined for given and as
To this end, we have found the center of the circular arc of the middle axis of the robot. The next step is to determine the radius of the circle. This can be readily obtained by subtracting zo by the half of the distance between the two panels, as shown in Figure 4.
Based on the circle center, we can obtain the following relation
leading to the angle θ as
Based on this angle, the arc length of the middle backbone can be determined as
Now let us look at the experiment data to draw certain useful relationships. Table 2 shows the length of the middle backbone under different panel lengths. In this table, represents the difference between the two panels. The initial lengths of the two panels were both at 0.15 m, and panel A is pushed forward by 0.05 m for each increment. By using the previously mentioned 3D optical device, the end coordinates of the two panels were measured and the position of the moving platform and were calculated by using Equations (9) and (10). We further determined the center of the middle backbone and the radius by Equations (13) and (14), and angle θ and the middle backbone length by Equations (16) and (17). Table 3, Table 4, Table 5 and Table 6 repeated the same experiments but with different start lengths of panel B to cover the entire motion range for our study. According to Equations (13), (14), (16) and (17), the arc length of the middle backbone can be expressed in terms of , β and as

Table 2.
The length of the assumed backbone in difference ∆L (data from experiment, Lb = 0.15 m).

Table 3.
The length of assumed backbone in difference ∆L (data from experiment, Lb = 0.20 m).

Table 4.
The length of assumed backbone in difference ∆L (data from experiment, Lb =0.25 m).

Table 5.
The length of assumed backbone in difference ∆L (data from experiment, Lb = 0.30 m).

Table 6.
The length of assumed backbone in difference ∆L (data from experiment, Lb =0.35 m).
The proposed inverse kinematics is based on the observation from Table 2 to Table 6. It can be found from these tables that and have very close values, from which the first approximate relation is obtained to relate the panel lengths to Lm as
Furthermore, Figure 5 is the experiment data of Table 1 showing that the tip angle β is linearly proportional to the length difference of the two panels [21], from which the second approximate relationship is obtained as
where is the tip angle defined before and k is the constant coefficient depending on the material of the two panels. From Equations (20) and (21), we can now solve the panel lengths as
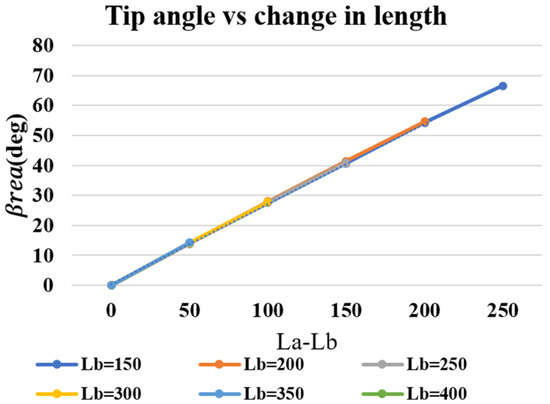
Figure 5.
Tip angle vs. change in length.
To summarize, the inverse kinematic problem at hand can be solved by our proposed simplified approach as follows. For the given pose of the robot’s end-effector (moving platform), i.e., and β, Equation (19) is first used to determine Lm, and then Equation (22) and Equation (23) are used to determine the panel lengths and that will drive the robot to reach the given position and orientation angle β. Apparently, the proposed method provides an approximate closed-form solution that can be readily implemented for real-time applications. The only caveat is that k needs to be calibrated beforehand based on the panel material used.
5. Accuracy Analysis of The Method
Now we have shown that the proposed inverse kinematic solution can be drastically simplified from Equations (2) and (3) involving elliptical integration to simply algebraic closed-form solutions Equations (21) and (22). The remaining part is to test its accuracy. To validate the proposed method, we use the experiment data recorded in Table 2, Table 3, Table 4, Table 5 and Table 6. In this validation, the original lengths of the two panels are taken as the actual lengths. As explained before, the original lengths were used to input to the robot and then the position and orientation of the robot were measured. For comparison, the measured robot position and orientation were used to solve the lengths using the steps described in the proceeding section. The comparison results are given in Figure 6, where the X label is with the length of and the Y label represents the error of panel length A and B. Figure 6 has four small figures covering four cases of different Lb. It can be seen from Figure 6 that the maximum error of the simplified method is less than 2% compared to the actual input values. Therefore, we can claim our inverse kinematic method is valid and effective.
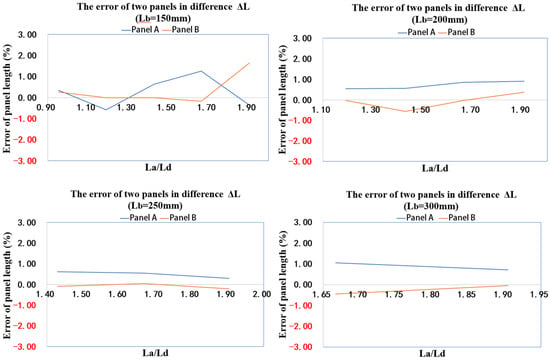
Figure 6.
Error analysis of the method.
6. Conclusions
This paper presented a simplified method for solving the inverse kinematics of a continuum robot driven by flexible panels. It was shown that the planar panel continuum robot under study, though having two actuators, can control fully the position and orientation of the robot. Through experiment, two approximate relationships were obtained. First, the arc length of the middle backbone can be estimated from the arc lengths of the two panels; second, the length difference between the two panels can be related to the tip angle. Based on these two approximate relationships, a closed-form inverse kinematics method was proposed for real-time applications. The proposed method was validated by the experiment data with less than 2% of error, thereby the effectiveness of the proposed method was demonstrated.
Author Contributions
Conceptualization, W.W. and Y.T.; methodology, W.W. and Y.T.; software, X.Y. and Y.Z.; validation, X.Y., Y.Z. and L.L.; formal analysis, Y.L.; investigation, W.W.; resources, Y.T. and F.X.; data curation, W.W.; writing—original draft preparation, W.W.; writing—review and editing, X.Y. and Y.Z.; visualization, Y.L. and L.L.; supervision, F.X.; project administration, Y.T.; funding acquisition, W.W. and Y.T.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the Shenzhen Polytechnic Fund (Grant No. 6019310001K), in part by the Innovation Team Project of Ordinary Colleges and Universities in Guangdong Province (Grant No. 2020KCXTD047), and in part by the Special Projects in Key Fields of Ordinary Colleges and Universities in Guangdong Province (Grant No. 2020ZDZX2070).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hirose, S.; Mori, M. Biologically inspired snake-like robots. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenyang, China, 22–26 August 2004. [Google Scholar]
- Hannan, M.W.; Walker, I.D. Kinematics and the implementation of an elephant’s trunk manipulator and other continuum style robots. J. Robot. Syst. 2003, 20, 45–63. [Google Scholar] [CrossRef] [PubMed]
- Laschi, C.; Mazzolai, B.; Mattoli, V.; Cianchetti, M.; Dario, P. Design of a biomimetic robotic octopus arm. Bioinspiration Biomim. 2009, 4, 015006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Walker, I.D.; Dawson, D.M.; Flash, T.; Grasso, F.W.; Hanlon, R.T.; Hochner, B.; Kier, W.M.; Pagano, C.C.; Rahn, C.D.; Zhang, Q.M. Continuum robot arms inspired by cephalopods. In Proceedings SPIE, Defense and Security; SPIE: Orlando, FL, USA, 2005. [Google Scholar]
- Jabbari, M.; Zakeri, M. Motion planning of a continuum robot in medical surgeries. In Proceedings of the 2nd Al Farabi International Congress on Applied Sciences, Nakhchivan, Azerbaijan, 2–4 May 2021. [Google Scholar]
- Robotics, O.C. Snake-arm robots access the inaccessible. Nucl. Technol. 2008, 1, 92–94. [Google Scholar]
- Walker, I.D. Use of continuum robots for remote inspection operations. In Proceedings of the 2017 Computing Conference, London, UK, 18–20 July 2017.
- Xiang, L.Q.; Feng, J.U.; Fei, Q.; Wang, Y.M.; Hua, D.W.; Chen, B. Kinematics research of continuum robot for in-situ detection of aero-engine. J. Mech. Electr. Eng. 2019, 36, 464–469. [Google Scholar]
- Jones, B.A.; Walker, I.D. Practical kinematics for real time implementation of continuum robots. IEEE Trans. Robot. 2006, 22, 1087–1099. [Google Scholar] [CrossRef] [Green Version]
- Jones, B.A.; Walker, I.D. Kinematics for multi-section continuum robots. IEEE Trans. Robot. 2006, 22, 43–55. [Google Scholar] [CrossRef]
- Simaan, N.; Taylor, R.; Flint, P. A dexterous system for laryngeal surgery. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), New Orleans, LA, USA, 26 April–1 May 2004. [Google Scholar]
- Godage, I.S.; Guglielmino, E.; Branson, D.T.; Medrano-Cerda, G.A.; Caldwell, D.G. Novel modal approach for kinematics of multisection continuum arms. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011. [Google Scholar]
- Godage, I.S.; Branson, D.T.; Guglielmino, E.; Medrano-Cerda, G.A.; Caldwell, D.G. Shape function-based kinematics and dynamics for variable length continuum robotic arms. In Proceedings of the IEEE International Conference on Robotics & Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Rolf, M.; Steil, J.J. Constant curvature continuum kinematics as fast approximate model for the bionic handling assistant. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012. [Google Scholar]
- Escande, C.; Merzouki, R.; Pathak, P.M.; Coelen, V. Geometric modelling of multisection bionic manipulator: Experimental validation on robotinoxt. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, 11–14 December 2012. [Google Scholar]
- Hollerbach, J.M.; Wampler, C.W. The calibration index and taxonomy for robot kinematic calibration methods. Int. J. Robot. Res. 1996, 15, 573–591. [Google Scholar] [CrossRef]
- AGoldenberg; Benhabib, B.; Fenton, R.G. A complete generalized solution to the inverse kinematics of robots. IEEE J. Robot. Autom. 1985, 1, 14–20. [Google Scholar] [CrossRef]
- Giorelli, M.; Renda, F.; Ferri, G.; Laschi, C. A feed-forward neural network learning the inverse kinetics of a flexible cable-driven manipulator moving in three-dimensional space. In Proceedings of the EEE/RSJ International Conference on Intelligent Robots and Systems. IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 23–27 October 2013. [Google Scholar]
- Rolf, M.; Steil, J.J. Efficient exploratory learning of inverse kinematics on a bionic elephant trunk. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1147–1160. [Google Scholar]
- Mahl, T.; Hildebrandt, A.; Sawodny, O. Forward kinematics of a compliant pneumatically actuated redundant manipulator. In Proceedings of the 2012 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 June 2012. [Google Scholar]
- Wang, W.; Xi, F.; Tian, Y.; Zhao, Y. Modeling and Analysis of a planar flexible panel continuum mechanism. ASME J. Mech. Robot. 2020, 12, 044503. [Google Scholar] [CrossRef]
- Howell, L.; Midha, A. Parametric deflection approximations for end loaded large deflection beams in compliant mechanisms. ASME Trans. J. Mech. Des. 1995, 117, 156–165. [Google Scholar] [CrossRef]
- Howell, L.; Midha, A. Evaluation of equivalent spring stiffness for use in a pseudo-rigid-body model of large deflection compliant mechanisms. ASME Trans. J. Mech. Des. 1996, 118, 126–131. [Google Scholar] [CrossRef] [Green Version]
- Midha, A.; Howell, L. A method for the design of compliant mechanism with small-length flexural pivots. ASME Trans. J. Mech. Des. 1994, 116, 280–290. [Google Scholar]
- Zhonglei, F.; Yueqing, Y.; Wenjing, W. 2R Pseudo-rigid-body Model of Compliant Mechanisms with Compliant Links to Simulate Tip Characteristic. J. Mech. Eng. 2011, 47, 37–42. [Google Scholar]
- Su, H.-J. A pseudo-rigid-body 3R model for determining large deflection of cantilever beams subject to tip loads. ASME J. Mech. Robot. 2009, 1, 021008. [Google Scholar] [CrossRef]
- Yu, Y. New PR pseudo-rigid-body model of compliant mechanisms subject to combined loads. J. Mech. Eng. 2013, 49, 9–14. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).