Planet Load-Sharing and Phasing
Abstract
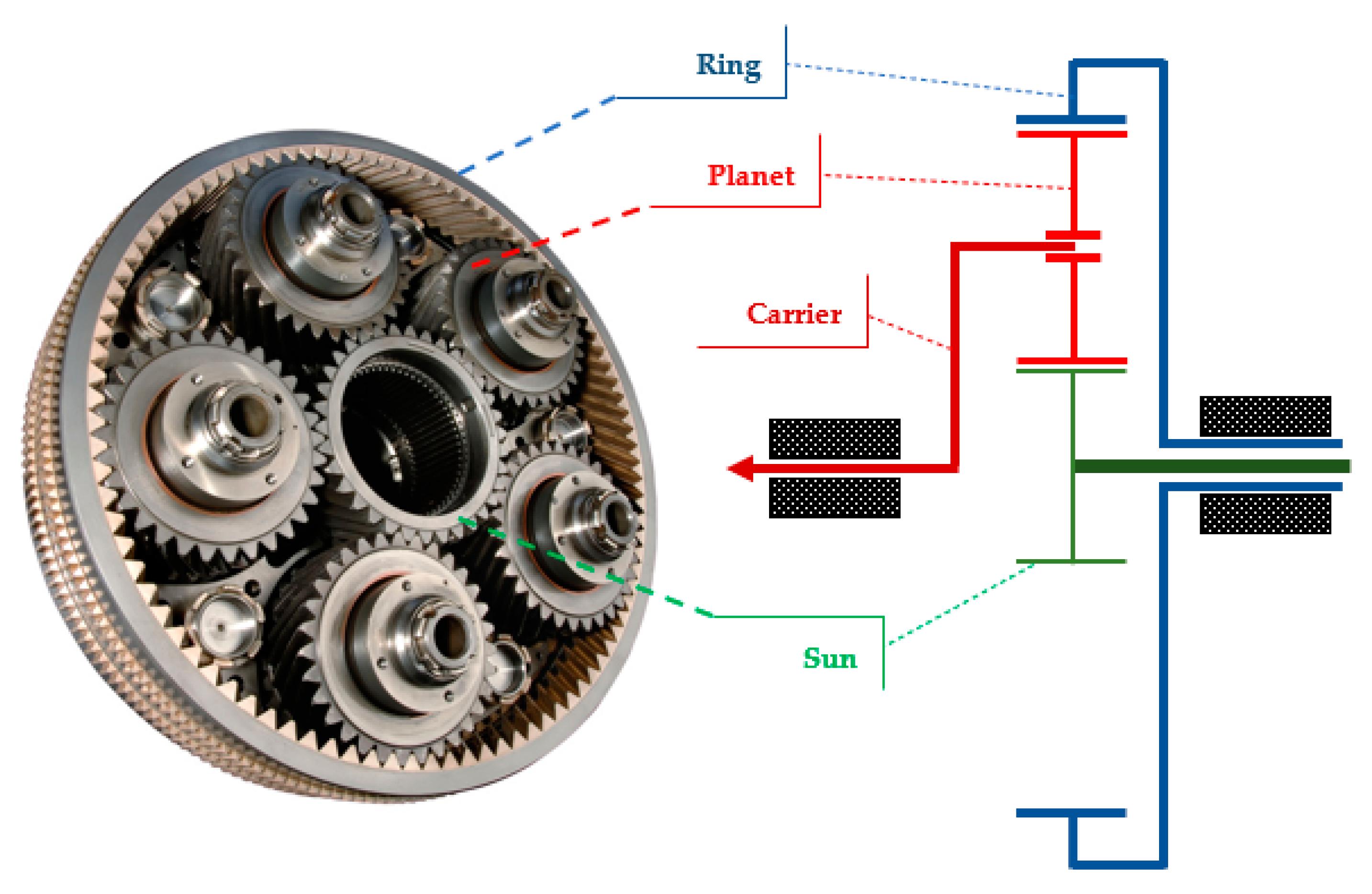
1. Introduction
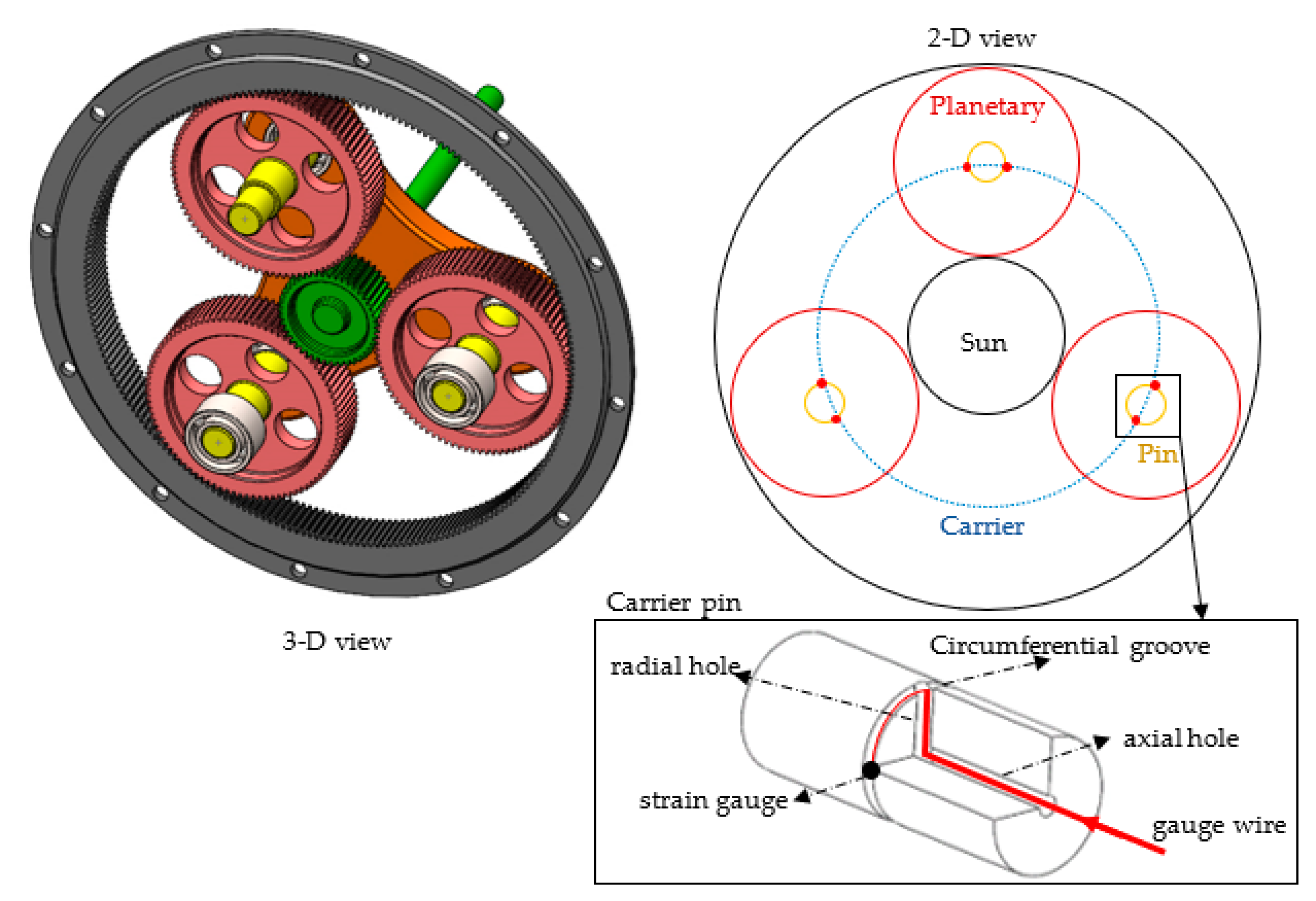
2. Load Sharing Model
- Not applicable to gear sets having a small module
- Require strain gauges with high accuracy and sufficient sampling rate
- Increase the probability of measurement error due to the high dependency on the deviations of actual gauge-mounting locations from the desired nominal location
- Since errors in the planets, e.g., spacing, indexing, and run-out errors or eccentricities, could be time-dependent, the results might not be sufficiently accurate.
3. Effective Parameters on Load-Sharing
- Manufacturing errors
- Elastic deformation
- Bearing effects
- Backlash
3.1. Manufacturing Errors
- Time-invariant and assembly-independent errors: such as carrier and planet pinhole position errors and pinhole diameter errors.
- Time-invariant and assembly-dependent errors: these errors, once the planetary gear set is assembled, maintain their value as the gears rotate, but the gear set can have different load-sharing outcomes depending on how each planet gear and planet pin are assembled in the carrier. Planet tooth thickness errors, planet bore diameter errors, planet bearing needle diameter errors, and planet pin diameter errors are some examples of these errors.
- Time-varying and assembly-dependent errors: they have a time-varying effect on the load taken by each planet due to the way they are placed during the assembly of the gear set, since they are both rotation and assembly dependent, such as pitch line run-outs of the sun gear, planets, and the internal gear.
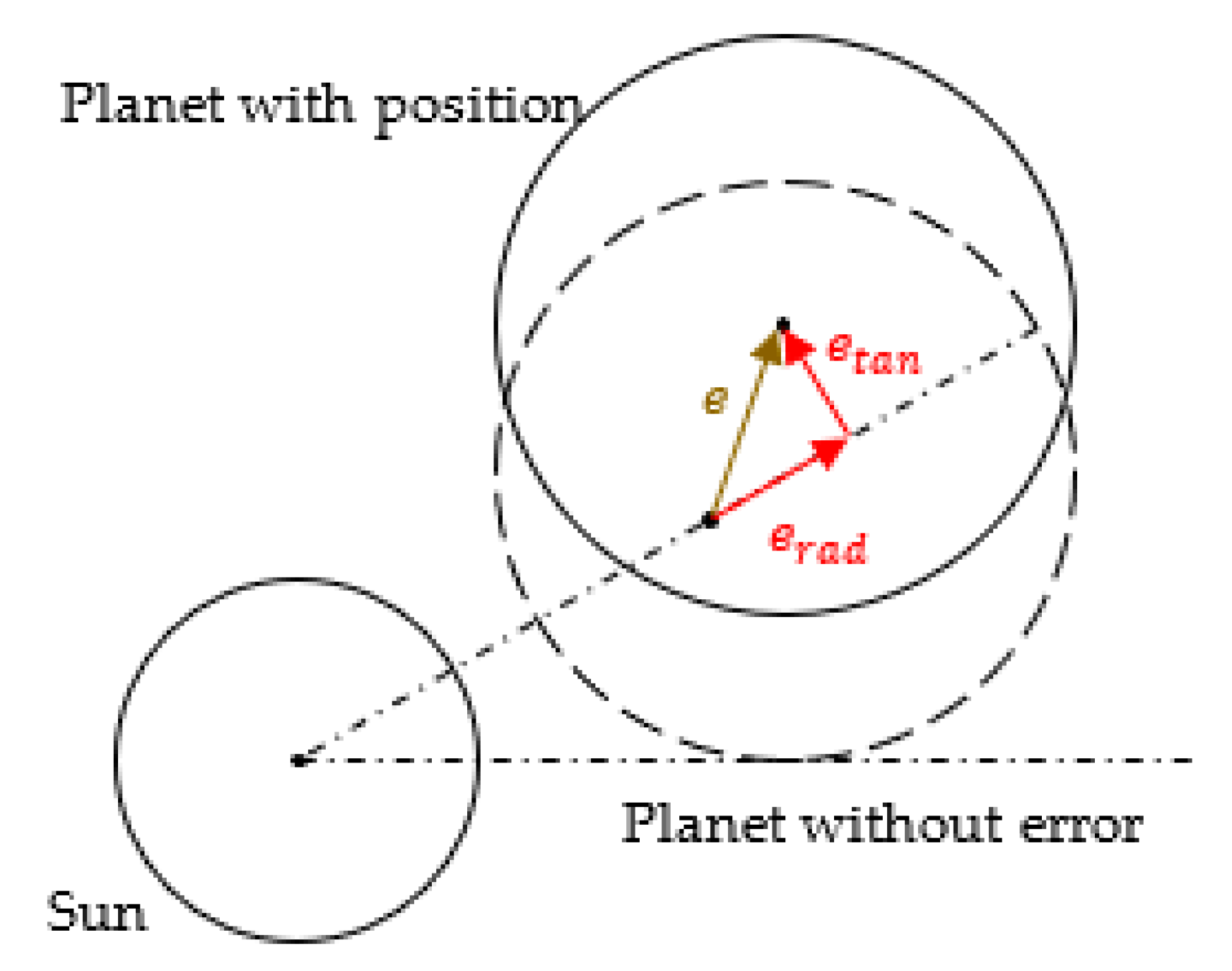
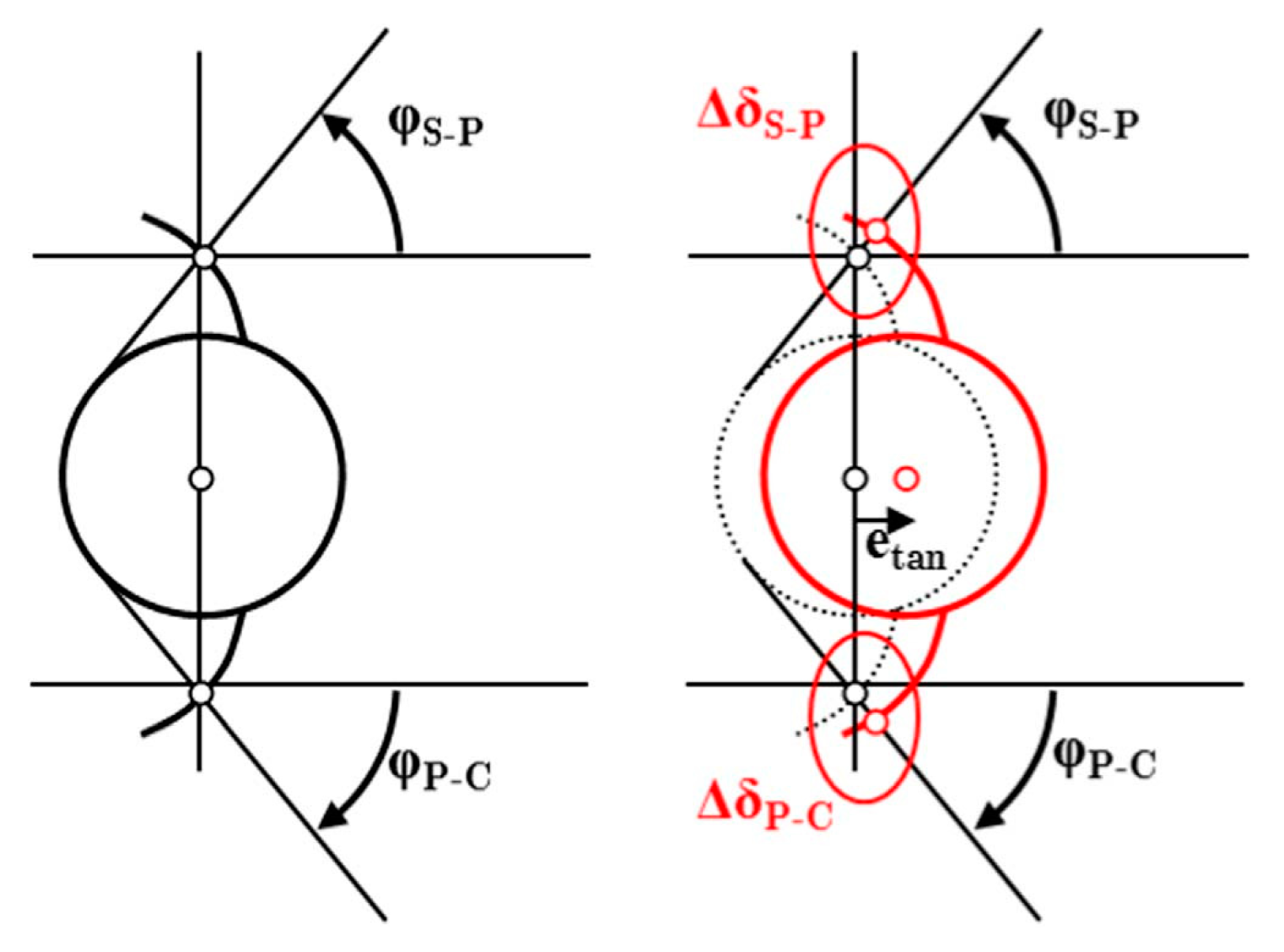
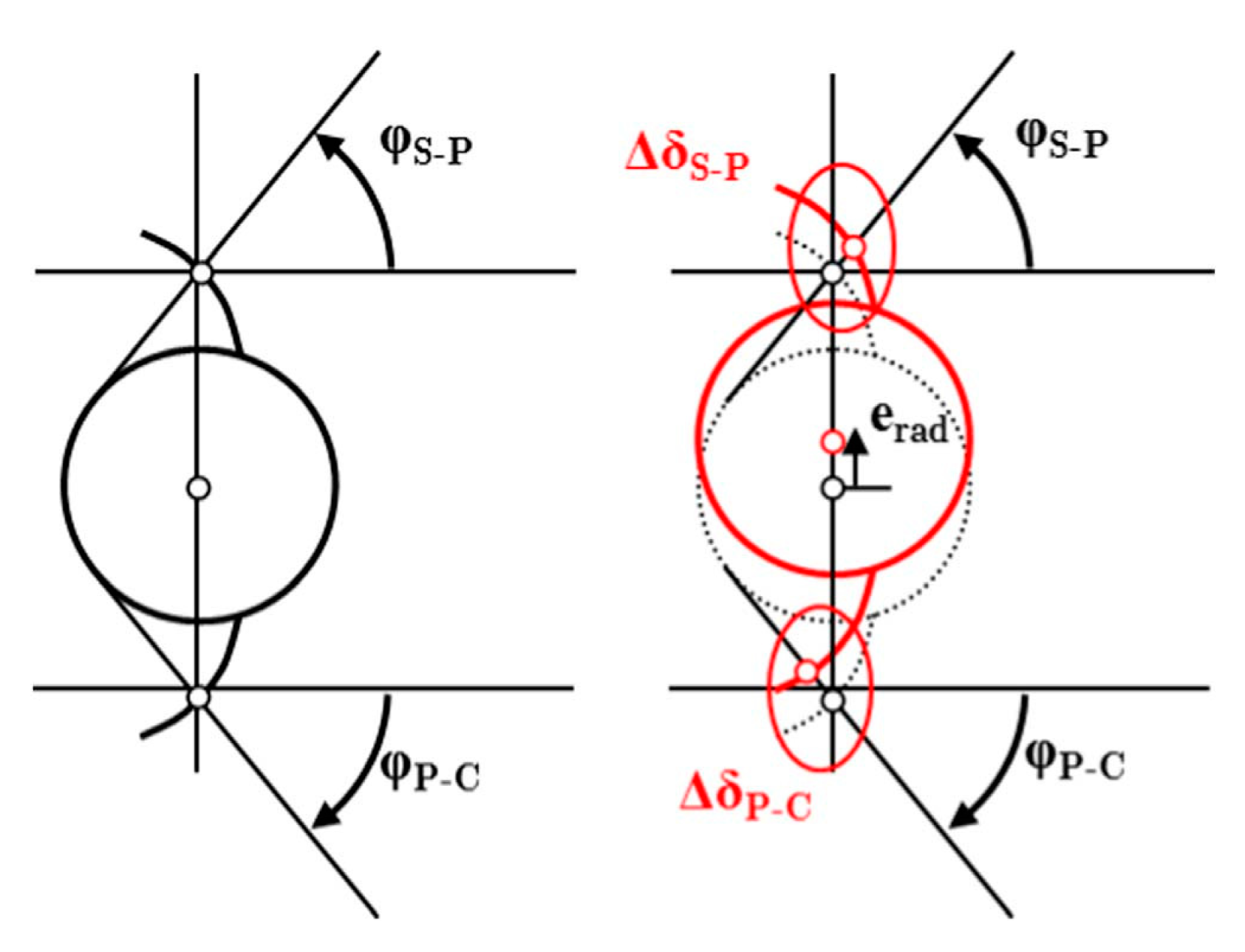
3.2. Position Error
3.3. Run-Out Error
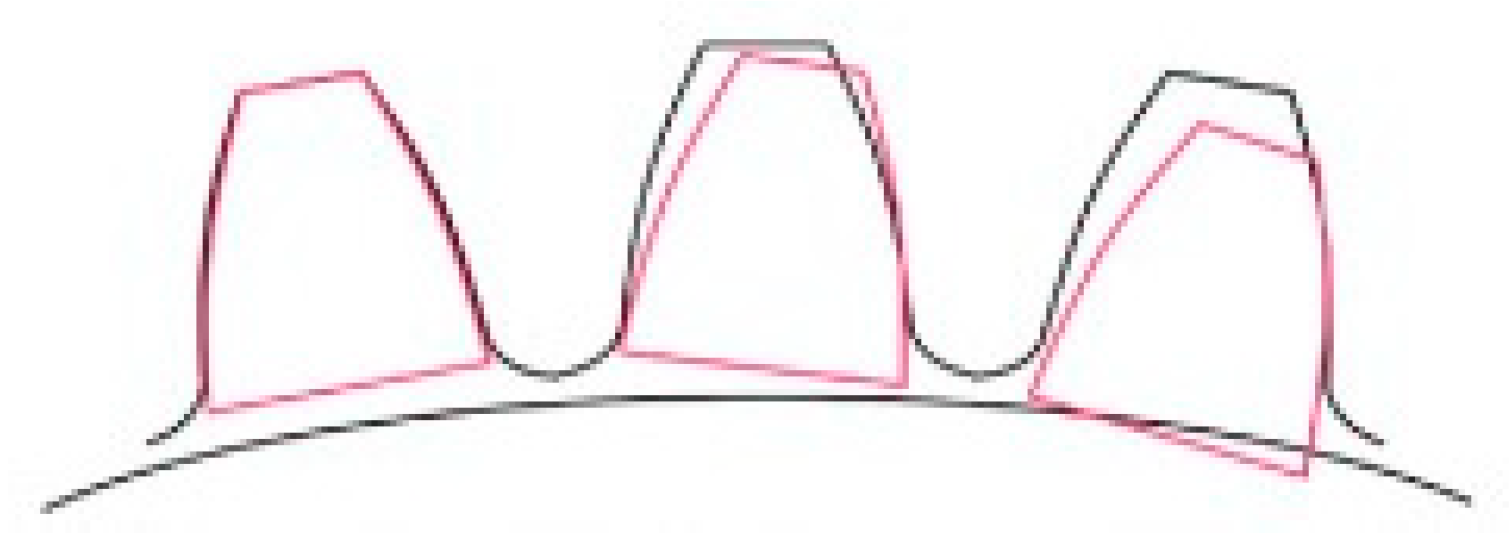
3.4. Influence of Bearing and Backlash
4. Enhance the Load-Sharing
- Flexible ring gears
- Floating sun gear
- Floating planet carrier
- Double helical gear with floating members
- Floating planetary gear
- Flexible pin (flex-pin)
- Higher quality gear members.
- Increased precision of carrier elements that locate planet gears.
- Matching planet gear sets by tooth thickness.
- Improve tooth alignment of compound planets by using matched sets of planets (compound epicyclic only).
- Oil film thickness variation due to changes in oil flow and loads in journal bearings.
- Allowing radial float of one or more elements.
- Elastic deformation of the ring or the sun gear, or both.
- Reducing tooth stiffness.
- Elastic deformation of planet gear shafts.
- Elastic deformation of planet carrier.
- Eccentric planet shafts with load responsive rotation device.
- Load sensitive displacement of journal bearing oil films.
- Load sensitive consumption of planet shaft material when utilized as a journal bearing.
- Improved gear and shaft alignment.
- Reduced shaft run-out.
- Improved bearing quality and alignment (true position of bearing location in carrier).
- Improved assembly (location) of the carrier if the carrier is split axially.
- Improved compliance of components (gears, shafts, bearings, housing).
- Improved dynamics (operating speed versus resonant frequencies).
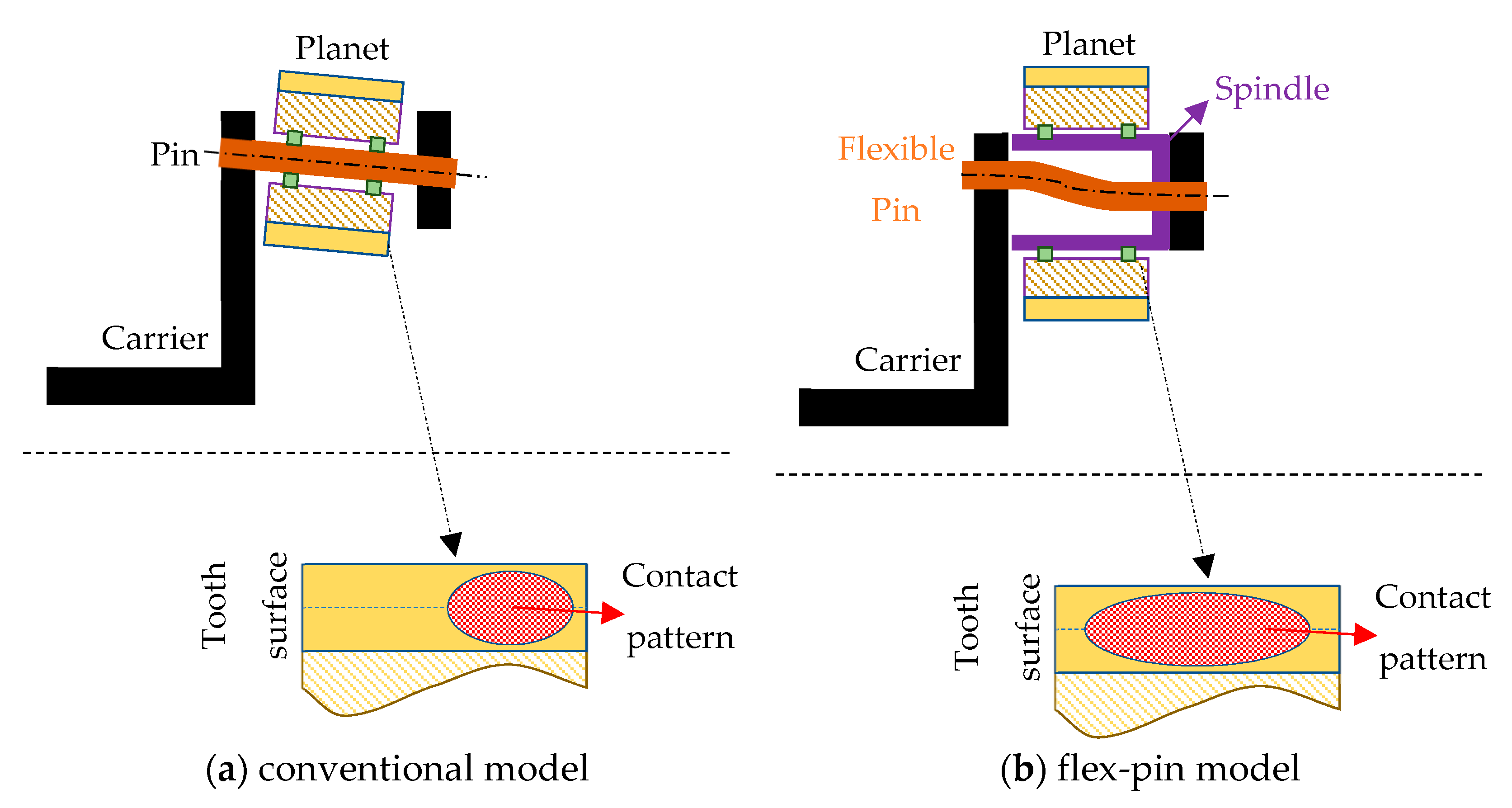
4.1. Floating Systems
4.2. Flexible Pin
5. Planetary Gear Phasing
5.1. Efficiency Effects
5.2. Experimental Investigations
5.3. Frequency Interplay
5.4. Instability
6. Fault Effects on Planet Phasing
7. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols
| N | Number of planets |
| The load on each planet as part of the whole load in the system | |
| The load on each planet | |
| LSR | Load-sharing ratio |
| LSFn(t) | Load sharing factor of the nth planet |
| SGLR | Strain gauge load ratio |
| Total input torque | |
| The meshing torque in the sun due to each of the planet–sun meshes | |
| Each peak-to-peak value obtained from the strain gauge in contact with each planet | |
| Each peak-to-peak value obtained from the strain gauge in contact with each planet as part of the summation of all the peak-to-peak values | |
| Pin bending stresses | |
| Pin bending stresses as part of the whole pin bending stress |
References
- Lanchester, F.; Lanchester, G. Epicyclic gears. Proc. Inst. Mech. Eng. 1924, 107, 605–631. [Google Scholar] [CrossRef]
- Müller, H.W. Epicyclic Drive Trains: Analysis, Synthesis, and Applications; Wayne State University Press: Detroit, MI, USA, 1982. [Google Scholar]
- Gouda, E.; Mezani, S.; Baghli, L.; Rezzoug, A. Comparative study between mechanical and magnetic planetary gears. IEEE Trans. Magn. 2010, 47, 439–450. [Google Scholar] [CrossRef]
- Parker, R.G.; Agashe, V.; Vijayakar, S.M. Dynamic response of a planetary gear system using a finite element/contact mechanics model. J. Mech. Des. 2000, 122, 304–310. [Google Scholar] [CrossRef]
- Iglesias, M.; Del Rincon, A.F.; De-Juan, A.; Garcia, P.; Diez-Ibarbia, A.; Viadero, F. Planetary transmission load sharing: Manufacturing errors and system configuration study. Mech. Mach. Theory 2017, 111, 21–38. [Google Scholar] [CrossRef]
- Zhang, H.; Shen, X. A dynamic tooth wear prediction model for reflecting “two-sides” coupling relation between tooth wear accumulation and load sharing behavior in compound planetary gear set. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2020, 234, 1746–1763. [Google Scholar] [CrossRef]
- Guo, Y.; Parker, R.G. Dynamic modeling and analysis of a spur planetary gear involving tooth wedging and bearing clearance nonlinearity. Eur. J. Mech. A/Solids 2010, 29, 1022–1033. [Google Scholar] [CrossRef]
- Kahraman, A.; Vijayakar, S. Effect of internal gear flexibility on the quasi-static behavior of a planetary gear set. J. Mech. Des. 2001, 123, 408–415. [Google Scholar] [CrossRef]
- Bodas, A.; Kahraman, A. Influence of carrier and gear manufacturing errors on the static load sharing behavior of planetary gear sets. JSME Int. J. Ser. C 2004, 47, 908–915. [Google Scholar] [CrossRef]
- Cheon, G.-J.; Parker, R.G. Influence of manufacturing errors on the dynamic characteristics of planetary gear systems. KSME Int. J. 2004, 18, 606–621. [Google Scholar] [CrossRef]
- Singh, A. Application of a system level model to study the planetary load sharing behavior. J. Mech. Des. 2005, 127, 469–476. [Google Scholar] [CrossRef]
- Singh, A. Influence of planetary needle bearings on the performance of single and double pinion planetary systems. J. Mech. Des. 2007, 129, 85–94. [Google Scholar] [CrossRef]
- Ligata, H.; Kahraman, A.; Singh, A. An experimental study of the influence of manufacturing errors on the planetary gear stresses and planet load sharing. J. Mech. Des. 2008, 130, 041701. [Google Scholar] [CrossRef]
- Hidaka, T.; Terauchi, Y. Dynamic behavior of planetary gear: 1st report load distribution in planetary gear. Bull. JSME 1976, 19, 690–698. [Google Scholar] [CrossRef]
- Cunliffe, F.; Smith, J.; Welbourn, D. Dynamic tooth loads in epicyclic gears. J. Eng. Ind. 1974, 96, 578–584. [Google Scholar] [CrossRef]
- Hidaka, T.; Terauchi, Y.; Nagamura, K. Dynamic behavior of planetary gear: 7th report, influence of the thickness of the ring gear. Bull. JSME 1979, 22, 1142–1149. [Google Scholar] [CrossRef]
- Botman, M. Vibration measurements on planetary gears of aircraft turbine engines. J. Aircr. 1980, 17, 351–357. [Google Scholar] [CrossRef]
- Ma, P.; Botman, M. Load sharing in a planetary gear stage in the presence of gear errors and misalignment. J. Mech. Des. 1985, 107, 4–10. [Google Scholar] [CrossRef]
- Hayashi, T.; Li, X.Y.; Hayashi, I.; Endo, K.; Watanabe, W. Measurement and some discussions on dynamic load sharing in planetary gears. Bull. JSME 1986, 29, 2290–2297. [Google Scholar] [CrossRef][Green Version]
- August, R.; Kasuba, R. Torsional vibrations and dynamic loads in a basic planetary gear system. J. Vib. Acoust. 1986, 108, 348–353. [Google Scholar] [CrossRef]
- Krantz, T.L. Gear tooth stress measurements of two helicopter planetary stages. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Scottsdale, AZ, USA, 13–16 September 1992. [Google Scholar] [CrossRef]
- Kahraman, A. Load sharing characteristics of planetary transmissions. Mech. Mach. Theory 1994, 29, 1151–1165. [Google Scholar] [CrossRef]
- Kahraman, A. Static load sharing characteristics of transmission planetary gear sets: Model and experiment. SAE Trans. 1999, 108, 1954–1963. Available online: https://www.jstor.org/stable/44733845 (accessed on 1 June 2022).
- Li, T.J.; Zhu, R.P.; Bao, H.Y. Study on dynamic load sharing behavior of two-stage planetary gear train based on a nonlinear vibration model. Appl. Mech. Mater. 2011, 86, 611–614. [Google Scholar] [CrossRef]
- Suzuki, A.; Aoyama, T.; Sugiura, N.; Inagaki, M.; Shimizu, T. Influence of bearing clearance on load sharing in planetary gears. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011. [Google Scholar] [CrossRef]
- Fuchun, Y.; Jutao, Z.; Xiaojun, Z.; Hongqing, Z. Axial thrust force of compound planetary spur gear set. J. Mech. Des. 2011, 133, 091004. [Google Scholar] [CrossRef]
- Cooley, C.G.; Parker, R.G. A review of planetary and epicyclic gear dynamics and vibrations research. Appl. Mech. Rev. 2014, 66, 040804. [Google Scholar] [CrossRef]
- Park, Y.-J.; Lee, G.-H.; Oh, J.-S.; Shin, C.-S.; Nam, J.-S. Effects of non-torque loads and carrier pinhole position errors on planet load sharing of wind turbine gearbox. Int. J. Precis. Eng. Manuf. Green Technol. 2019, 6, 281–292. [Google Scholar] [CrossRef]
- Qiu, X.; Han, Q.; Chu, F. Load-sharing characteristics of planetary gear transmission in horizontal axis wind turbines. Mech. Mach. Theory 2015, 92, 391–406. [Google Scholar] [CrossRef]
- Guo, Y.; Keller, J.; Lacava, W. Planetary gear load sharing of wind turbine drivetrains subjected to non-torque loads. Wind Energy 2015, 18, 757–768. [Google Scholar] [CrossRef]
- Guo, Y.; Keller, J.; Parker, R.G. Nonlinear dynamics and stability of wind turbine planetary gear sets under gravity effects. Eur. J. Mech. A/Solids 2014, 47, 45–57. [Google Scholar] [CrossRef]
- Li, Z.; Wen, B.; Peng, Z.; Dong, X.; Qu, Y. Dynamic modeling and analysis of wind turbine drivetrain considering the effects of non-torque loads. Appl. Math. Model. 2020, 83, 146–168. [Google Scholar] [CrossRef]
- Götz, J.; Siglmüller, F.; Fürst, M.; Otto, M.; Stahl, K. Experimental investigation of the dynamic load sharing of planetary gearboxes. Forsch. Im Ing. 2021, 1–8. [Google Scholar] [CrossRef]
- Ryali, L.; Verma, A.; Hong, I.; Talbot, D.; Zhu, F. Experimental and Theoretical Investigation of Quasi-Static System Level Behavior of Planetary Gear Sets. J. Mech. Des. 2021, 143, 103401. [Google Scholar] [CrossRef]
- Xun, C.; Dai, H. Dynamic Load Sharing Behaviours of Planetary Gear Trains and Parameter Study through Perturbation Analysis. Shock Vib. 2021, 2021, 8832908. [Google Scholar] [CrossRef]
- Xu, X.; Luo, T.; Luo, J.; Hua, X.; Langari, R. Dynamical load sharing behaviors of heavy load planetary gear system with multi-floating components. Int. J. Model. Simul. Sci. Comput. 2018, 9, 1850005. [Google Scholar] [CrossRef]
- Kim, J.-G.; Park, Y.-J.; Lee, S.-D.; Oh, J.-Y.; Kim, J.-H.; Lee, G.-H. Influence of the carrier pinhole position errors on the load sharing of a planetary gear train. Int. J. Precis. Eng. Manuf. 2018, 19, 537–543. [Google Scholar] [CrossRef]
- Nejad, A.R.; Xing, Y.; Guo, Y.; Keller, J.; Gao, Z.; Moan, T. Effects of floating sun gear in a wind turbine’s planetary gearbox with geometrical imperfections. Wind Energy 2015, 18, 2105–2120. [Google Scholar] [CrossRef]
- Hu, S.; Fang, Z.; Xu, Y.; Guan, Y.; Shen, R. Meshing impact analysis of planetary transmission system considering the influence of multiple errors and its effect on the load sharing and dynamic load factor characteristics of the system. Proc. Inst. Mech. Eng. K J. Multi-Body Dyn. 2021, 235, 57–74. [Google Scholar] [CrossRef]
- Sanchez-Espiga, J.; Fernandez-Del-Rincon, A.; Iglesias, M.; Viadero, F. Influence of the phase in planetary gears load sharing and transmission error. In Proceedings of the IFToMM World Congress on Mechanism and Machine Science, Krakow, Poland, 15–18 July 2019. [Google Scholar] [CrossRef]
- Masoumi, A.; Pellicano, F.; Samani, F.S.; Barbieri, M. Symmetry breaking and chaos-induced imbalance in planetary gears. Nonlinear Dyn. 2015, 80, 561–582. [Google Scholar] [CrossRef]
- Theling, J.; Brimmers, J.; Brecher, C. Reducing mass while improving the operational behavior: Form optimization of planetary gearbox housings. Forsch. Im Ing. 2021, 85, 543–551. [Google Scholar] [CrossRef]
- Sanchez-Espiga, J.; Fernandez-Del-Rincon, A.; Iglesias, M.; Viadero, F. Influence of errors in planetary transmissions load sharing under different mesh phasing. Mech. Mach. Theory 2020, 153, 104012. [Google Scholar] [CrossRef]
- Seager, D.L. Load sharing among planet gears. SAE Trans. 1970, 79, 651–656. Available online: https://www.jstor.org/stable/44717979 (accessed on 1 June 2022).
- Mo, S.; Zhang, Y.; Wu, Q.; Matsumura, S.; Houjoh, H. Load sharing behavior analysis method of wind turbine gearbox in consideration of multiple-errors. Renew. Energy 2016, 97, 481–491. [Google Scholar] [CrossRef]
- Leque, N.; Kahraman, A. A three-dimensional load sharing model of planetary gear sets having manufacturing errors. J. Mech. Des. 2017, 139, 033302. [Google Scholar] [CrossRef]
- Hu, Y.; Talbot, D.; Kahraman, A. A load distribution model for planetary gear sets. J. Mech. Des. 2018, 140, 053302. [Google Scholar] [CrossRef]
- Hu, Y.; Ryali, L.; Talbot, D.; Kahraman, A. A theoretical study of the overall transmission error in planetary gear sets. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2019, 233, 7200–7211. [Google Scholar] [CrossRef]
- Ryali, L.; Talbot, D. A dynamic load distribution model of planetary gear sets. Mech. Mach. Theory 2021, 158, 104229. [Google Scholar] [CrossRef]
- Pedrero, J.I.; Pleguezuelos, M.; Sánchez, M.B. Influence of meshing stiffness on load distribution between planets of planetary gear drives. Mech. Mach. Theory 2022, 170, 104718. [Google Scholar] [CrossRef]
- Sanchez-Espiga, J.; Fernandez-Del-Rincon, A.; Iglesias, M.; Viadero, F. Numerical evaluation of the accuracy in the load sharing calculation using strain gauges: Sun and ring gear tooth root. Mech. Mach. Theory 2022, 175, 104923. [Google Scholar] [CrossRef]
- Iglesias, M.; Fernandez Del Rincon, A.; De-Juan, A.; Diez-Ibarbia, A.; Garcia, P.; Viadero, F. Advanced model for the calculation of meshing forces in spur gear planetary transmissions. Meccanica 2015, 50, 1869–1894. [Google Scholar] [CrossRef]
- Sanchez-Espiga, J.; Fernandez-Del-Rincon, A.; Iglesias, M.; Viadero, F. Planetary gear transmissions load sharing measurement from tooth root strains: Numerical evaluation of mesh phasing influence. Mech. Mach. Theory 2021, 163, 104370. [Google Scholar] [CrossRef]
- Boguski, B.; Kahraman, A.; Nishino, T. A new method to measure planet load sharing and sun gear radial orbit of planetary gear sets. J. Mech. Des. 2012, 134, 071002. [Google Scholar] [CrossRef]
- Singh, A.; Kahraman, A.; Ligata, H. Internal gear strains and load sharing in planetary transmissions: Model and experiments. J. Mech. Des. 2008, 130, 072602. [Google Scholar] [CrossRef]
- Ge, H.; Shen, Y.; Zhu, Y.; Xiong, Y.; Yuan, B.; Fang, Z. Simulation and experimental test of load-sharing behavior of planetary gear train with flexible ring gear. J. Mech. Sci. Technol. 2021, 35, 4875–4888. [Google Scholar] [CrossRef]
- Kim, J.-G.; Park, Y.-J.; Lee, G.-H.; Kim, J.-H. An experimental study on the effect of carrier pinhole position errors on planet gear load sharing. Int. J. Precis. Eng. Manuf. 2016, 17, 1305–1312. [Google Scholar] [CrossRef]
- Hidaka, T.; Terauchi, Y.; Nohara, M.; Oshita, J.-I. Dynamic behavior of planetary gear: 3rd report, Displacement of ring gear in direction of line of action. Bull. JSME 1977, 20, 1663–1672. [Google Scholar] [CrossRef]
- Montestruc, A.N. A numerical approach to calculation of load sharing in planetary gear drives. J. Mech. Des. 2010, 132, 014503. [Google Scholar] [CrossRef]
- Singh, A. Epicyclic load sharing map—development and validation. Mech. Mach. Theory 2011, 46, 632–646. [Google Scholar] [CrossRef]
- Ligata, H.; Kahraman, A.; Singh, A. A closed-form planet load sharing formulation for planetary gear sets using a translational analogy. J. Mech. Des. 2009, 131, 021007. [Google Scholar] [CrossRef]
- Han, H.; Zhao, Z.; Tian, H.; Ma, H.; Yang, Y.; Li, X. Fault feature analysis of planetary gear set influenced by cracked gear tooth and pass effect of the planet gears. Eng. Fail. Anal. 2021, 121, 105162. [Google Scholar] [CrossRef]
- Singh, A. Load sharing behavior in epicyclic gears: Physical explanation and generalized formulation. Mech. Mach. Theory 2010, 45, 511–530. [Google Scholar] [CrossRef]
- Fan, Z.; Zhu, C.; Song, C. Dynamic analysis of planetary gear transmission system considering the flexibility of internal ring gear. IJST-T Mech. Eng. 2020, 44, 695–706. [Google Scholar] [CrossRef]
- Li, G.; Niu, L.; Ma, L.; Dong, D. Load sharing analysis of compound planetary gear set with cracked sun gear. In Proceedings of the 2019 IEEE International Conference on Prognostics and Health Management (ICPHM), San Francisco, CA, USA, 17–20 June 2019. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Z.; Dong, J. Load sharing characteristics of multi-stage planetary gear train using analytical and finite element model. Int. J. Comput. Appl. Technol. 2016, 53, 107–120. [Google Scholar] [CrossRef]
- Gu, X.Y.; Velex, P. A lumped parameter model to analyse the dynamic load sharing in planetary gears with planet errors. Appl. Mech. Mater. 2011, 86, 374–379. [Google Scholar] [CrossRef]
- Gu, X.; Velex, P. On the dynamic simulation of eccentricity errors in planetary gears. Mech. Mach. Theory 2013, 61, 14–29. [Google Scholar] [CrossRef]
- Liu, W.; Li, J.; Kang, Y.; Liu, Y.; Xu, X.; Dong, P. Load sharing behavior of double-pinion planetary gear sets considering manufacturing errors. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Melbourne, Australia, 12–13 October 2019; IOP Publishing: Bristol, UK. [Google Scholar] [CrossRef]
- Mo, S.; Zhang, T.; Jin, G.; Feng, Z.; Gong, J.; Zhu, S. Influence mechanism of multi-coupling error on the load sharing characteristics of herringbone gear planetary transmission system. Proc. Inst. Mech. Eng. K J. Multi-Body Dyn. 2019, 233, 792–816. [Google Scholar] [CrossRef]
- Cao, Z.; Rao, M. Coupling effects of manufacturing error and flexible ring gear rim on dynamic features of planetary gear. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2021, 235, 5234–5246. [Google Scholar] [CrossRef]
- Gill-Jeong, C.; Parker, R.G. Influence of bearing stiffness on the static properties of a planetary gear system with manufacturing errors. KSME Int. J. 2004, 18, 1978–1988. [Google Scholar] [CrossRef]
- Gupta, K.; Jain, N.K.; Laubscher, R. Chapter 7—Measurement of Gear Accuracy. In Advanced Gear Manufacturing and Finishing: Classical and Modern Processes; Matthew Deans: London, UK, 2017. [Google Scholar]
- Alhadeff, L.; Slatter, T. A straightforward and low-cost pre-inspection measurement method for small gears. Manuf. Lett. 2020, 23, 23–28. [Google Scholar] [CrossRef]
- Sheng, D.-P.; Zhu, R.-P.; Jin, G.-H.; Lu, F.-X.; Bao, H.-Y. Dynamic load sharing behavior of transverse-torsional coupled planetary gear train with multiple clearances. J. Cent. South Univ. 2015, 22, 2521–2532. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, S.; Peng, Z. A nonlinear dynamic model for analysis of the combined influences of nonlinear internal excitations on the load sharing behavior of a compound planetary gear set. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2016, 230, 1048–1068. [Google Scholar] [CrossRef]
- Chen, Y.-F.; Wu, X.-Y. Dynamic load sharing behavior of planetary gear train with backlashes. In Proceedings of the 2009 International Conference on Engineering Computation, Hong Kong, China, 2–3 May 2009. [Google Scholar] [CrossRef]
- Zhang, C.; Wei, J.; Wang, F.; Hou, S.; Zhang, A.; Lim, T.C. Dynamic model and load sharing performance of planetary gear system with journal bearing. Mech. Mach. Theory 2020, 151, 103898. [Google Scholar] [CrossRef]
- Guo, Z.; Li, S.; Wu, W.; Zhang, L. Quasi-Static Load Sharing Characteristics of a Planetary Gear Set with Planet Journal Bearings. Appl. Sci. 2020, 10, 1113. [Google Scholar] [CrossRef]
- Lewicki, D.G.; Ballarini, R. Effect of rim thickness on gear crack propagation path. J. Mech. Des. 1997, 119, 88–95. [Google Scholar] [CrossRef]
- Fox, G.P.; Jallat, E. Use of the Integrated Flexpin Bearing for Improving the Performance of Epicyclical Gear Systems. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 2–6 September 2003. [Google Scholar] [CrossRef]
- Bahk, C.-J.; Parker, R.G. Analytical investigation of tooth profile modification effects on planetary gear dynamics. Mech. Mach. Theory 2013, 70, 298–319. [Google Scholar] [CrossRef]
- Iglesias, M.; Del Rincón, A.F.; De-Juan, A.M.; Garcia, P.; Diez, A.; Viadero, F. Planetary gear profile modification design based on load sharing modelling. Chin. J. Mech. Eng. 2015, 28, 810–820. [Google Scholar] [CrossRef]
- Bonori, G.; Barbieri, M.; Pellicano, F. Optimum profile modifications of spur gears by means of genetic algorithms. J. Sound Vib. 2008, 313, 603–616. [Google Scholar] [CrossRef]
- Faggioni, M.; Samani, F.S.; Bertacchi, G.; Pellicano, F. Dynamic optimization of spur gears. Mech. Mach. Theory 2011, 46, 544–557. [Google Scholar] [CrossRef]
- American Gear Manufacturers Association. Design Manual for Enclosed Epicyclic Gear Drives. 2006. Available online: https://webstore.ansi.org/Standards/AGMA/ansiagma6123b06 (accessed on 1 June 2022).
- Kahraman, A.; Kharazi, A.; Umrani, M. A deformable body dynamic analysis of planetary gears with thin rims. J. Sound Vib. 2003, 262, 752–768. [Google Scholar] [CrossRef]
- James, B.; Harris, O. Predicting unequal planetary load sharing due to manufacturing errors and system deflections, with validation against test data. SAE Trans. 2002, 111, 1056–1064. [Google Scholar]
- Chung, W.-J.; Oh, J.-S.; Han, H.-W.; Kim, J.-T.; Park, Y.-J. Analytical study of floating effects on load sharing characteristics of planetary gearbox for off-road vehicle. Adv. Mech. Eng. 2020, 12, 1–16. [Google Scholar] [CrossRef]
- Montestruc, A.N. Influence of planet pin stiffness on load sharing in planetary gear drives. J. Mech. Des. 2011, 133, 014501. [Google Scholar] [CrossRef]
- Gu, X.; Velex, P. A dynamic model to study the influence of planet position errors in planetary gears. J. Sound Vib. 2012, 331, 4554–4574. [Google Scholar] [CrossRef]
- Hicks, R.J. Load Equalizing Means for Planetary Pinions. Google Patent US3303713A, 14 February 1967. Available online: https://patents.google.com/patent/US3303713A/en (accessed on 1 June 2022).
- Vosátka, J. A Little Flexing and Synthetic Lube May Be Better for Wind-Turbine and Tidal-Water Gearboxes. 2016. Available online: https://www.windpowerengineering.com/a-little-flexing-and-synthetic-lube-may-be-better-for-wind-turbine-and-tidal-water-gearboxes/.cited (accessed on 29 June 2022).
- Fox, G.P. Epicyclic Gear Systems. Google Patents. Google Patent US7297086B2, 20 November 2007. Available online: https://patents.google.com/patent/US7297086B2/en (accessed on 1 June 2022).
- Zhu, C.; Xu, X.; Lim, T.C.; Du, X.; Liu, M. Effect of flexible pin on the dynamic behaviors of wind turbine planetary gear drives. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2013, 227, 74–86. [Google Scholar] [CrossRef]
- Yoo, H.-G.; Chung, W.-J.; Kim, B.-S.; Park, Y.-J.; Kim, S.-C.; Lee, G.-H. Application of flexible pin for planetary gear set of wind turbine gearbox. Sci. Rep. 2022, 12, 1713. [Google Scholar] [CrossRef] [PubMed]
- Hidaka, T.; Terauchi, Y.; Nagamura, K. Dynamic behavior of planetary gear: 6th report, influence of meshing-phase. Bull. JSME 1979, 22, 1026–1033. [Google Scholar] [CrossRef]
- Parker, R.G. A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration. J. Sound Vib. 2000, 236, 561–573. [Google Scholar] [CrossRef]
- Parker, R.G.; Lin, J. Mesh phasing relationships in planetary and epicyclic gears. J. Mech. Des. 2004, 126, 365–370. [Google Scholar] [CrossRef]
- Shweiki, S.; Mundo, D.; Korta, J.; Oranges, P.; Palermo, A. Investigation of mesh phasing in a planetary gear train using combined FE and Multibody simulations. In Proceedings of the International Conference on Noise and Vibration engineering (ISMA2016), Leuven, Belgium, 19–21 September 2016. [Google Scholar]
- Ambarisha, V.K.; Parker, R.G. Nonlinear dynamics of planetary gears using analytical and finite element models. J. Sound Vib. 2007, 302, 577–595. [Google Scholar] [CrossRef]
- Huang, Q.; Tang, W.-C.; Lu, R.-X.; Xie, J.-J.; Wu, K. Influence of system-inherent phase in spur gear multi-state mesh based on nonlinear dynamics. Mech. Syst. Signal. Process. 2022, 172, 108749. [Google Scholar] [CrossRef]
- Wang, C.; Parker, R.G. Nonlinear dynamics of lumped-parameter planetary gears with general mesh phasing. J. Sound Vib. 2022, 523, 116682. [Google Scholar] [CrossRef]
- Mohammadpour, M.; Theodossiades, S.; Rahnejat, H. Dynamics and efficiency of planetary gear sets for hybrid powertrains. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2016, 230, 1359–1368. [Google Scholar] [CrossRef]
- Fatourehchi, E.; Mohammadpour, M.; King, P.D.; Rahnejat, H.; Trimmer, G.; Williams, A.; Womersley, R. Effect of mesh phasing on the transmission efficiency and dynamic performance of wheel hub planetary gear sets. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2018, 232, 3469–3481. [Google Scholar] [CrossRef]
- Gawande, S.; Shaikh, S. Experimental investigations of noise control in planetary gear set by phasing. J. Eng. 2014, 2014, 857462. [Google Scholar] [CrossRef][Green Version]
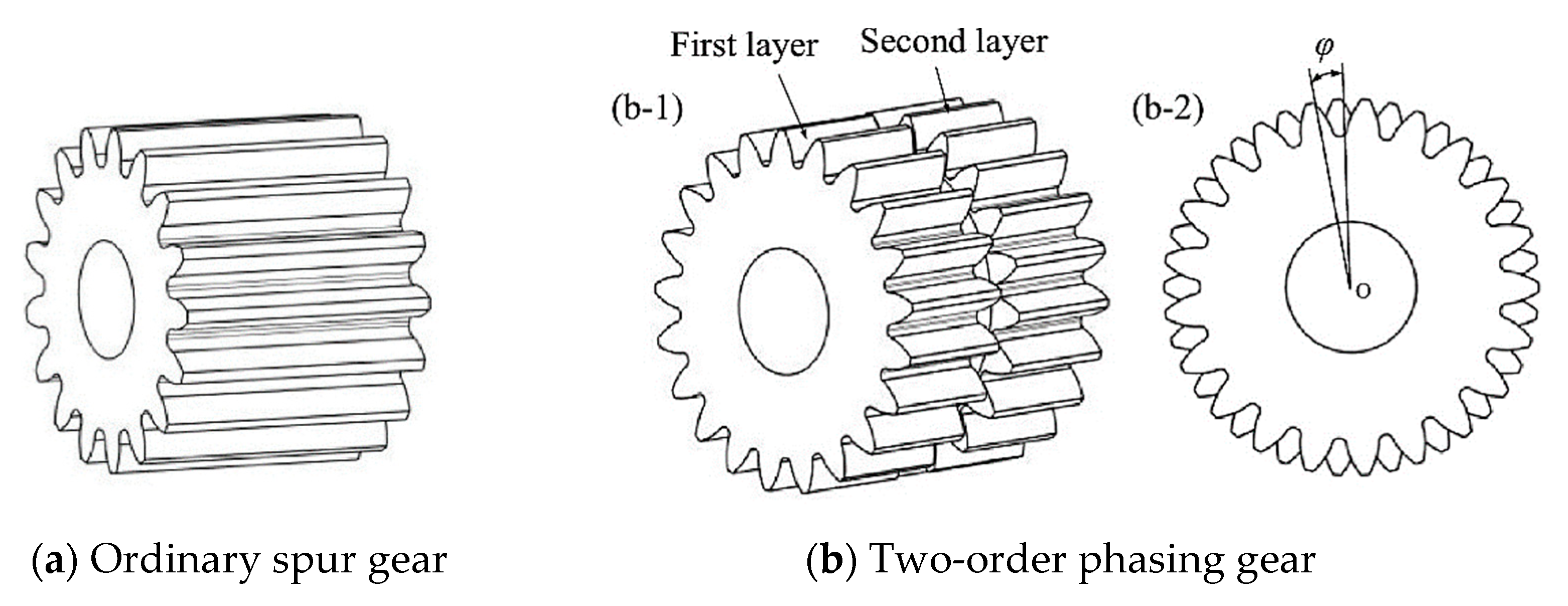
- Chen, X.; Wei, J.; Zhang, J.; Zhang, C.; Wang, C.-L.; Xu, Z.; Gao, H.; Zhang, A.; Yu, G. A Novel Method to Reduce the Fluctuation of Mesh Stiffness by High-order Phasing Gear Sets: Theoretical Analysis and Experiment. J. Sound Vib. 2022, 524, 116752. [Google Scholar] [CrossRef]
- Ambarisha, V.K.; Parker, R.G. Suppression of planet mode response in planetary gear dynamics through mesh phasing. J. Vib. Acoust. 2006, 128, 133–142. [Google Scholar] [CrossRef]
- Guo, J.; Su, Y.; Su, J. Suppression of several different modal responses in split-path transmissions by mesh phasing. Mech. Mach. Theory 2022, 173, 104855. [Google Scholar] [CrossRef]
- Lin, J.; Parker, R. Planetary gear parametric instability caused by mesh stiffness variation. J. Sound Vib. 2002, 249, 129–145. [Google Scholar] [CrossRef]
- Canchi, S.V.; Parker, R.G. Effect of ring-planet mesh phasing and contact ratio on the parametric instabilities of a planetary gear ring. J. Mech. Des. 2008, 130, 014501. [Google Scholar] [CrossRef]
- Parker, R.G.; Wu, X. Parametric instability of planetary gears having elastic continuum ring gears. J. Vib. Acoust. 2012, 134, 041011. [Google Scholar] [CrossRef]
- Wu, X.; Parker, R.G. Modal properties of planetary gears with an elastic continuum ring gear. J. Appl. Mech. 2008, 75, 031014. [Google Scholar] [CrossRef]
- Wang, C.; Parker, R.G. Modal properties and parametrically excited vibrations of spinning epicyclic/planetary gears with a deformable ring. J. Sound Vib. 2021, 494, 115828. [Google Scholar] [CrossRef]
- Ericson, T.M.; Parker, R.G. Experimental measurement and finite element simulation of elastic-body vibration in planetary gears. Mech. Mach. Theory 2021, 160, 104264. [Google Scholar] [CrossRef]
- Feng, K.; Wang, K.; Ni, Q.; Zuo, M.J.; Wei, D. A phase angle based diagnostic scheme to planetary gear faults diagnostics under non-stationary operational conditions. J. Sound Vib. 2017, 408, 190–209. [Google Scholar] [CrossRef]
- Peng, D.; Smith, W.A.; Randall, R.B.; Peng, Z. Use of mesh phasing to locate faulty planet gears. Mech. Syst. Signal. Process. 2019, 116, 12–24. [Google Scholar] [CrossRef]
- Liu, J.; Pang, R.; Ding, S.; Li, X. Vibration analysis of a planetary gear with the flexible ring and planet bearing fault. Measurement 2020, 165, 108100. [Google Scholar] [CrossRef]
- Luo, Y.; Cui, L.; Zhang, J.; Ma, J. Vibration mechanism and improved phenomenological model of planetary gearbox with broken sun gear fault. Measurement 2021, 178, 109356. [Google Scholar] [CrossRef]
- Ha, J.M.; Youn, B.D. Fault diagnosis of a planetary gearbox by D norm-based time synchronous averaging (DTSA) with roughly estimated phase information under an encoder-less operating condition. J. Sound Vib. 2022, 520, 116546. [Google Scholar] [CrossRef]
- Hu, A.; Liu, S.; Xiang, L.; Zhang, Y. Dynamic modeling and analysis of multistage planetary gear system considering tooth crack fault. Eng. Fail. Anal. 2022, 137, 106408. [Google Scholar] [CrossRef]
- Figlus, T.; Kozioł, M.; Kuczyński, Ł. Impact of application of selected composite materials on the weight and vibroactivity of the upper gearbox housing. Materials 2019, 12, 2517. [Google Scholar] [CrossRef] [PubMed]
- Figlus, T.; Kozioł, M.; Kuczyński, Ł. The effect of selected operational factors on the vibroactivity of upper gearbox housings made of composite materials. Sensors 2019, 19, 4240. [Google Scholar] [CrossRef]
- Gil, L.; Przystupa, K.; Pieniak, D.; Kozłowski, E.; Antosz, K.; Gauda, K.; Izdebski, P. Influence of Contamination of Gear Oils in Relation to Time of Operation on Their Lubricity. Appl. Sci. 2021, 11, 11835. [Google Scholar] [CrossRef]


| Section | Main Key Points | Author (Year) [References] | |
|---|---|---|---|
| Load sharing model | Non-torque load | Park et al. (2019) [28]; Qiu et al. (2015) [29]; Guo et al. (2015) [30]; Guo et al. (2014) [31]; Li et al. (2020) [32]; Chung et al. (2020) [89]; | |
| Input load effects | Xun and Dai (2021) [35]; Xu et al. (2018) [36]; Sanchez-Espiga et al. (2020) [43]; Iglesias et al. (2015) [52]; Kim et al. (2016) [57]; Singh (2011) [60]; | ||
| Lifetime | Kim et al. (2018) [37]; Rasekhi Nejad et al. (2015) [38]; | ||
| Load-sharing model | Cunliffe et al. (1974) [15]; Kahraman (1999) [23]; Li et al. (2011) [24]; Suzuki et al. (2011) [25]; Cooley and Parker (2014-Review Paper) [27]; Guo et al. (2015) [30]; Rasekhi Nejad et al. (2015) [38]; Seager (1970) [44]; Leque and Kahraman (2017) [46]; Hu et al. (2018) [47]; Hu et al. (2019) [48]; Ryali and Talbot (2021) [49]; Pedrero et al. (2022) [50]; Singh et al. (2008) [55]; Ge et al. (2021) [56]; Hidaka et al. (1977) [58]; Ligata et al. (2009) [61]; Han et al. (2021) [62]; Lewicki and Ballarini (1997) [80]; AGMA (2006) [86]; | ||
| Experiment test | Ligata et al. (2008) [13]; Hidaka and Terauchi (1976) [14]; Hidaka et al. (1979) [16]; Hayashi et al. (1986) [19]; Krantz (1992) [21]; Kahraman (1999) [23]; Suzuki et al. (2011) [25]; Funchun et al. (2011) [26]; Guo et al. (2015) [30]; Götz et al. (2021) [33]; Ryali et al. (2021) [34]; Rasekhi Nejad et al. (2015) [38]; Mo et al. (2016) [45]; Sanchez-Espiga et al. (2022) [51]; Sanchez-Espiga et al. (2021) [53]; Boguski et al. (2012) [54]; Singh et al. (2008) [55]; Ge et al. (2021) [56]; Kim et al. (2016) [57]; Han et al. (2021) [62]; Guo et al. (2020) [79]; Lewicki and Ballarini (1997) [80]; Fox and Jallat (2003) [81]; | ||
| FEM | Kahraman and Vijayakar (2001) [8]; Bodas and Kahraman (2004) [9]; Cheon and Parker (2004) [10]; Singh (2005) [11]; Botman (1980) [17]; Li et al. (2020) [32]; Iglesias et al. (2015) [52]; Hidaka et al. (1977) [58]; Ligata et al. (2009) [61]; Han et al. (2021) [62]; Li et al. (2016) [66]; Gill-Jeong and Parker (2004) [72]; Bakh and Parker (2013) [82]; Montestruc (2011) [90]; | ||
| Other | Meshing impact: | Hu et al. (2021) [39]; | |
| Geometrical configuration: | Singh (2005) [11]; Ligata et al. (2008) [13]; Sanchez-Espiga et al. (2019) [40]; Sanchez-Espiga et al. (2020) [43]; Hu et al. (2018) [47]; Pedrero et al. (2022) [50]; Sanchez-Espiga et al. (2022) [51]; Singh et al. (2008) [55]; Ligata et al. (2009) [61]; Singh (2010) [63]; Liu et al. (2019) [69]; Kahraman et al. (2003) [87]; Montestruc (2011) [90]; | ||
| Structural optimization: | Theling et al. (2021) [42]; | ||
| Effective parameters on load-sharing | Manufacturing error: | Bodas and Kahraman (2004) [9]; Cheon and Parker (2004) [10]; Xun and Dai (2021) [35]; Sanchez-Espiga et al. (2020) [43]; Leque and Kahraman (2017) [46]; Hu et al. (2018) [47]; Kim et al. (2016) [57]; Li et al. (2016) [66]; Cao and Rao (2021) [71]; James and Harris (2002) [88]; | |
| Position Error | Iglesias et al. (2017) [5]; Bodas and Kahraman (2004) [9]; Cheon and Parker (2004) [10]; Singh (2005) [11]; Ligata et al. (2008) [13]; Kahraman (1994) [22]; Kahraman (1999) [23]; Park et al. (2019) [28]; Ryali et al. (2021) [34]; Xun and Dai (2021) [35]; Xu et al. (2018) [36]; Kim et al. (2018) [37]; Sanchez-Espiga et al. (2020) [43]; Sanchez-Espiga et al. (2020) [43]; Leque and Kahraman (2017) [46]; Hu et al. (2018) [47]; Sanchez-Espiga et al. (2021) [53]; Boguski et al. (2012) [54]; Singh et al. (2008) [55]; Kim et al. (2016) [57]; Singh (2011) [60]; Ligata et al. (2009) [61]; Singh (2010) [63]; Gu and Velex (2011) [67]; Liu et al. (2019) [69]; Fox and Jallat (2003) [81]; Chung et al. (2020) [89]; Gu and Velex (2012) [91]; Zhu et al. (2013) [95]; | ||
| Run-out Error | Kahraman and Vijayakar (2001) [8]; Bodas and Kahraman (2004) [9]; Cheon and Parker (2004) [10]; Kahraman (1994) [22]; Kahraman (1999) [23]; Leque and Kahraman (2017) [46]; Hu et al. (2018) [47]; Hu et al. (2019) [48]; Gupta et al. (2017) [73]; | ||
| Misalignment: | Ma and Botman (1985) [18]; Rasekhi Nejad et al. (2015) [38]; Fan et al. (2020) [64]; Fox and Jallat (2003) [81]; Zhu et al. (2013) [95]; | ||
| Crack: | Han et al. (2021) [62]; Li et al. (2019) [65]; Lewicki and Ballarini (1997) [80]; | ||
| Eccentricity: | Iglesias et al. (2017) [5]; Hidaka et al. (1979) [16]; Kahraman (1994) [22]; Rasekhi Nejad et al. (2015) [38]; Hu et al. (2021) [39]; Mo et al. (2016) [45]; Leque and Kahraman (2017) [46]; Li et al. (2016) [66]; Gu and Velex (2013) [68]; Liu et al. (2019) [69]; Mo et al. (2019) [70]; Sheng et al. (2015) [75]; | ||
| Influence of bearing and backlash | Singh (2007) [12]; Li et al. (2011) [24]; Suzuki et al. (2011) [25]; Funchun et al. (2011) [26]; Guo et al. (2015) [30]; Guo et al. (2014) [31]; Kim et al. (2018) [37]; Mo et al. (2016) [45]; Gill-Jeong and Parker (2004) [72]; Sheng et al. (2015) [75]; Zhang et al. (2016) [76]; Chen et al. (2009) [77]; Zhang et al. (2020) [78]; Guo et al. (2020) [79]; Fox and Jallat (2003) [81]; | ||
| Tooth wedging: | Guo and Parker (2010) [7]; Guo et al. (2014) [31]; | ||
| Tooth wear | Zhang et al. (2020) [6]; | ||
| Enhance the load-sharing | Floating systems | Iglesias et al. (2017) [5]; Kahraman and Vijayakar (2001) [8]; Botman (1980) [17]; August and Kasuba (1986) [20]; Kahraman (1994) [22]; Kahraman (1999) [23]; Ryali et al. (2021) [34]; Xu et al. (2018) [36]; Kim et al. (2018) [37]; Rasekhi Nejad et al. (2015) [38]; Seager (1970) [44]; Mo et al. (2016) [45]; Sanchez-Espiga et al. (2022) [51]; Boguski et al. (2012) [54]; Singh (2010) [63]; Li et al. (2016) [66]; Gu and Velex (2011) [67]; Gu and Velex (2013) [68]; Gill-Jeong and Parker (2004) [72]; Müller (1982) [2]; Chung et al. (2020) [89]; Gu and Velex (2012) [91]; Yoo et al. (2022) [96]. | |
| Flexible pin | Cunliffe et al. (1974) [15]; Xu et al. (2018) [36]; Montestruc (2010) [59]; Zhang et al. (2020) [78]; Fox and Jallat (2003) [81]; Montestruc (2011) [90]; Hicks (1967) [92]; Vosátka (2016) [93]; Fox (2007) [94]; Zhu et al. (2013) [95]; Yoo et al. (2022) [96] | ||
| Profile modification | Xun and Dai (2021) [35]; Rasekhi Nejad et al. (2015) [38]; Hu et al. (2018) [47]; Ryali and Talbot (2021) [49]; Bakh and Parker (2013) [82]; Iglesias et al. (2015) [83]; | ||
| Flexible ring | Kahraman and Vijayakar (2001) [8]; Ma and Botman (1985) [18]; Iglesias et al. (2015) [52]; Ge et al. (2021) [56]; Hidaka et al. (1977) [58]; Fan et al. (2020) [64]; Gu and Velex (2011) [67]; Cao and Rao (2021) [71]; Zhang et al. (2020) [78]; Kahraman et al. (2003) [87]; | ||
| Planetary gear phasing | Phasing | Hidaka et al. (1979) [97]; Parker (2000) [98]; Parker and Lin (2004) [99]; Shweiki et al. (2016) [100]; Ambarisha and Parker (2007) [101]; Huang et al. (2022) [102]; Wang and Parker (2022) [103]; Ryali and Talbot (2021) [49]; Sanchez-Espiga et al. (2021) [53]. Ryali et al. (2021) [34]; Sanchez-Espiga et al. (2019) [40]; Sanchez-Espiga et al. (2020) [43]; Bakh and Parker (2013) [82]; Zhu et al. (2013) [95]; | |
| Efficiency effects | Mohammadpour et al. (2016) [104]; Fatourehchi et al. (2018) [105]. | ||
| Experimental research | Gawande and Shaikh (2014) [106]; Chen et al. (2022) [107]. | ||
| Frequency interplay | Ambarisha and Parker (2006) [108]; Guo et al. (2022) [109]. | ||
| Instability | Lin and Parker (2002) [110]; Canchi et al. (2008) [111]; Parker and Wu (2012) [112]; Wu and Parker (2008) [113]; Wang and Parker (2021) [114]; Ericson and Parker (2021) [115]. | ||
| Fault effects on planet phasing | Fault effects on planet phasing | Feng et al. (2017) [116]; Peng et al. (2019) [117]; Liu et al. (2020) [118]; Sanchez-Espiga et al. (2020) [40]; Luo et al. (2021) [119]; Ha and Youn (2022) [120]; Hu et al. (2022) [121] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molaie, M.; Deylaghian, S.; Iarriccio, G.; Samani, F.S.; Zippo, A.; Pellicano, F. Planet Load-Sharing and Phasing. Machines 2022, 10, 634. https://doi.org/10.3390/machines10080634
Molaie M, Deylaghian S, Iarriccio G, Samani FS, Zippo A, Pellicano F. Planet Load-Sharing and Phasing. Machines. 2022; 10(8):634. https://doi.org/10.3390/machines10080634
Chicago/Turabian StyleMolaie, Moslem, Samira Deylaghian, Giovanni Iarriccio, Farhad S. Samani, Antonio Zippo, and Francesco Pellicano. 2022. "Planet Load-Sharing and Phasing" Machines 10, no. 8: 634. https://doi.org/10.3390/machines10080634
APA StyleMolaie, M., Deylaghian, S., Iarriccio, G., Samani, F. S., Zippo, A., & Pellicano, F. (2022). Planet Load-Sharing and Phasing. Machines, 10(8), 634. https://doi.org/10.3390/machines10080634









