Fractional Order KDHD Impedance Control of the Stewart Platform
Abstract
:1. Introduction
2. Half-Order Derivative: Definition and Digital Implementation Issues
3. The Proposed KDHD Impedance Control
3.1. KD Impedance Control of Six-Degree-of-Freedom Non-Redundant Parallel Robots
3.2. KDHD Impedance Control of Six-Degree-of-Freedom Non-Redundant Parallel Robots
3.3. KDHDc Impedance Control of Six-Degree-of-Freedom Non-Redundant Parallel Robots
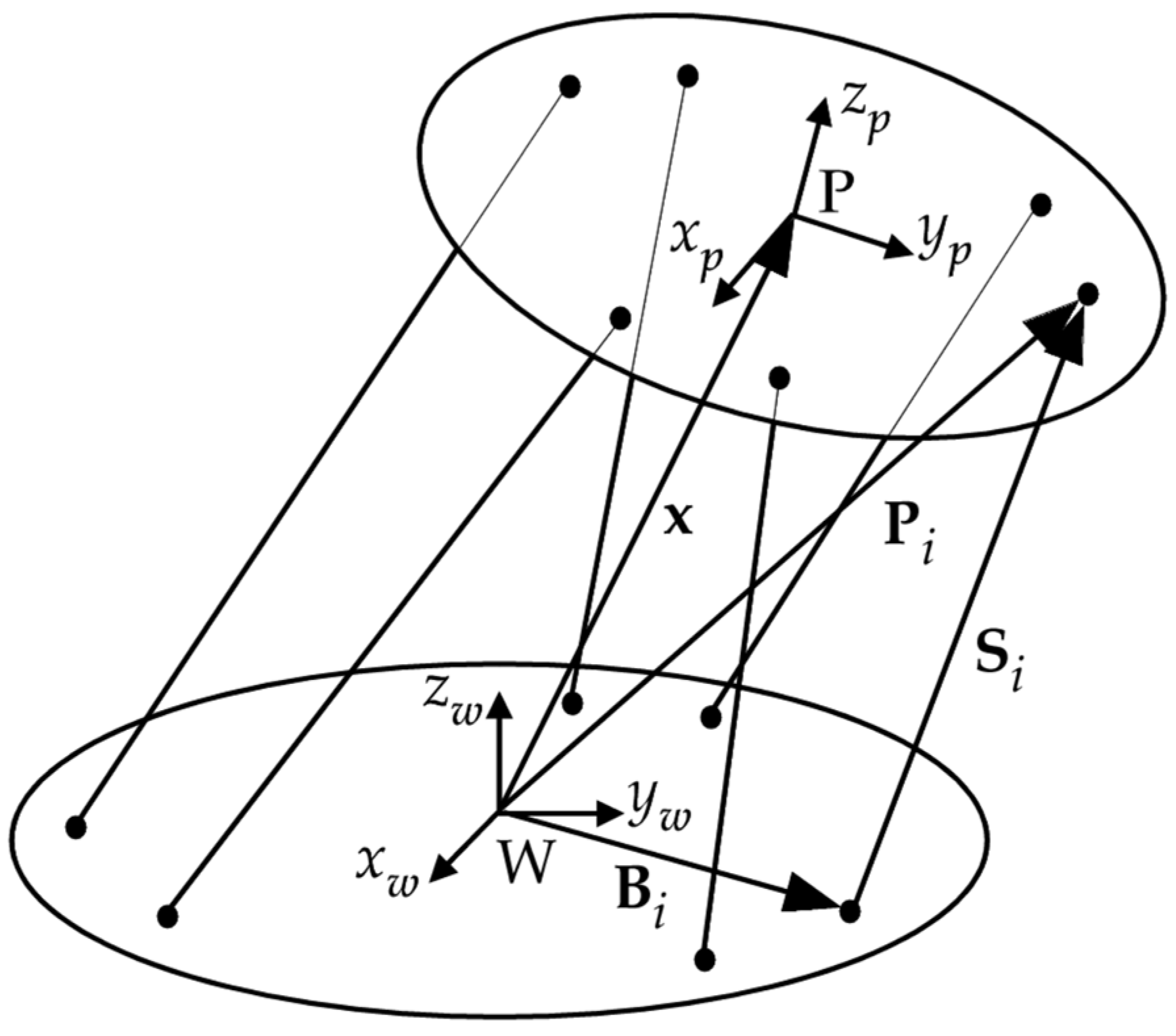
4. Kinematic Model of the Stewart Platform
5. Multibody Model of the Stewart Platform
6. Simulation Results
- (A)
- Approach/depart motion without contact with the environment: the end-effector follows a reference trajectory, defined by time-varying reference values of xd and Ed (external coordinates), without external forces acting on the end-effector; for each external coordinate a trapezoidal speed law is imposed, and the end-effector compliance is isotropic: the stiffness and damping matrices are diagonal, with three equal elements for the translational and rotational submatrices.
- (B)
- Interaction with the environment: the end-effector reference external coordinates are constant, and an external generalized force is applied to the end-effector. The stiffness and damping matrices are diagonal in the world frame W, which coincides with the principal stiffness/damping reference frames PT and PR, but the end-effector behavior is not isotropic, since the three diagonal elements of each submatrix are not equal.
- (C)
- Interaction with the environment: similarly to case B, the end-effector reference external coordinates are constant, and an external generalized force is applied to the end-effector, but differently from case B the principal stiffness/damping frames PT and PR do not coincide with W; therefore, the stiffness and damping matrices are block-diagonal but not diagonal.
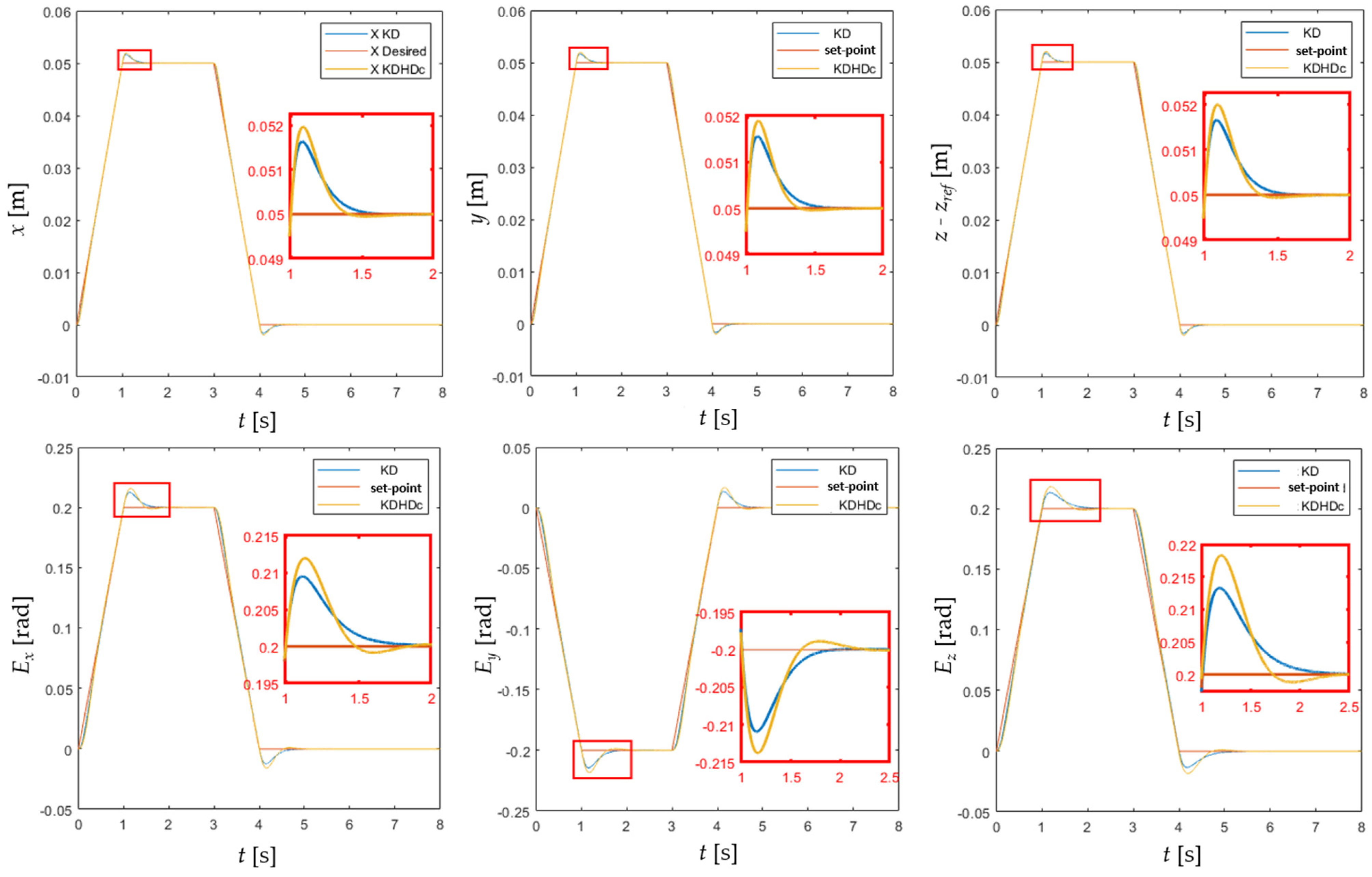
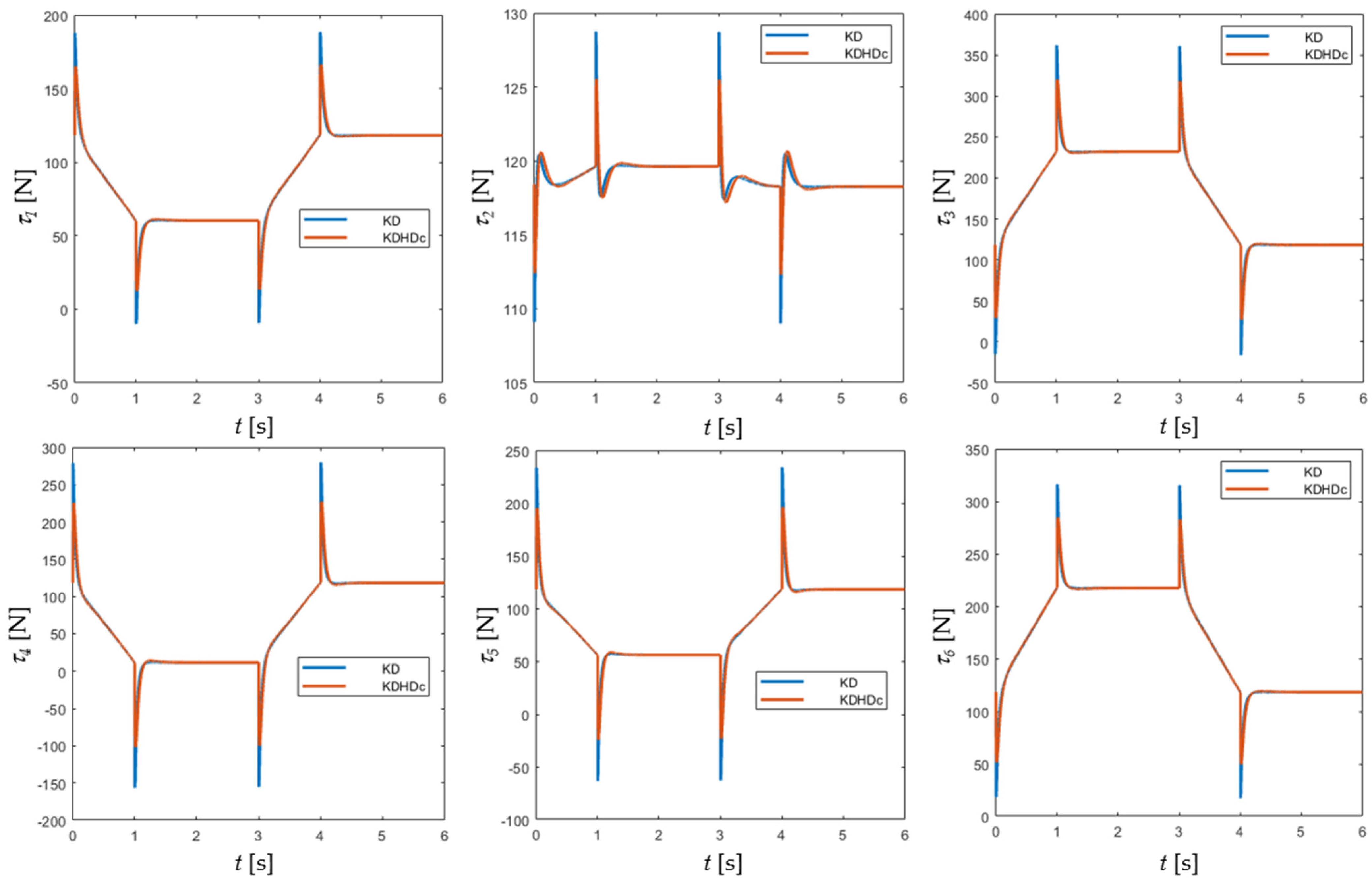
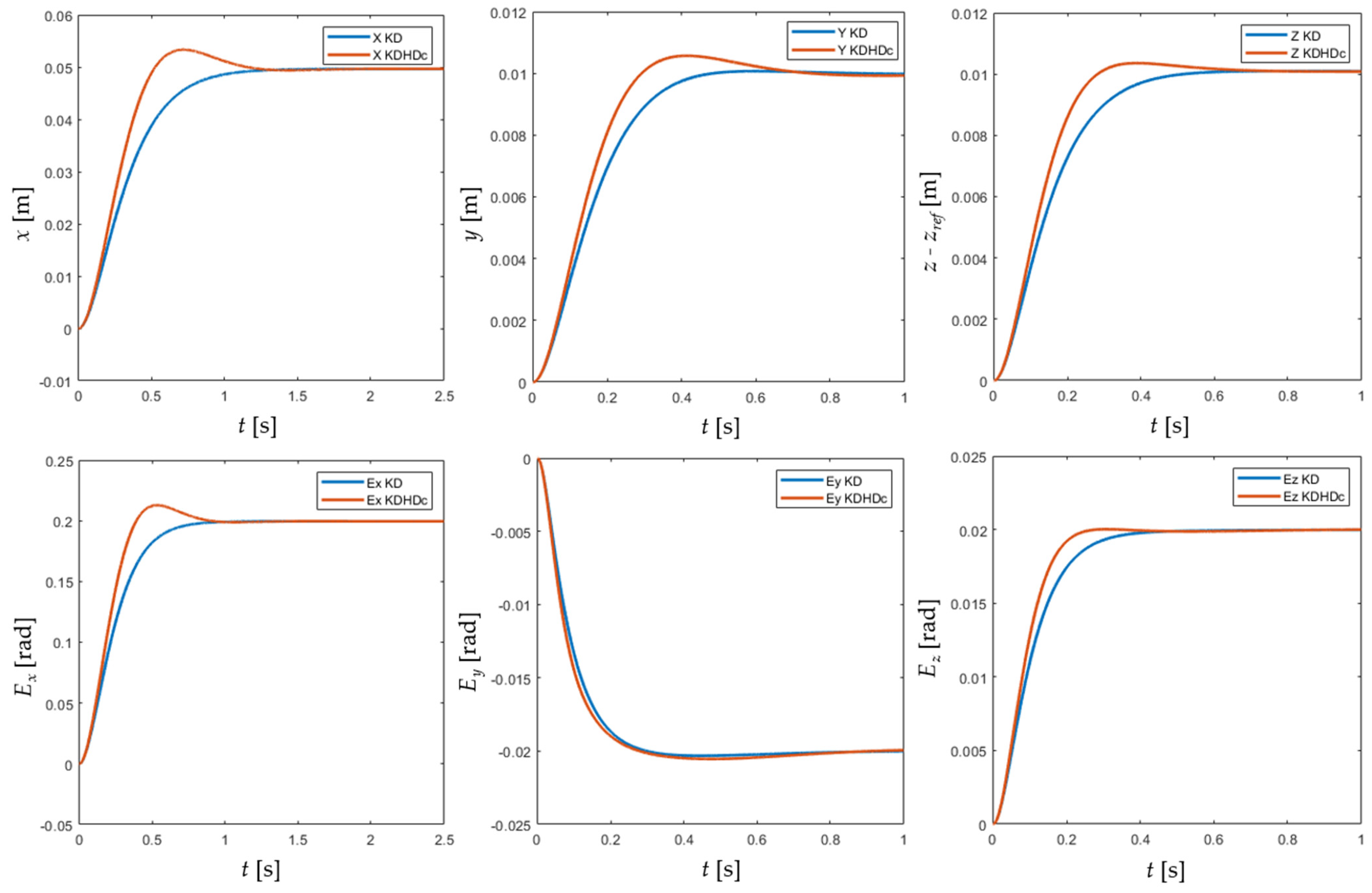
6.1. Case Study A: Approach/Depart Motion without Contact with the Environment
- KKDt is diagonal with diagonal values kKDt,i, i = 1…3;
- KKDr is diagonal with diagonal values kKDr,i, i = 1…3;
- DKDt is diagonal with diagonal values dKDt,i, i = 1…3;
- DKDr is diagonal with diagonal values dKDr,i, i = 1…3.
- KKDHDt is diagonal with diagonal values kKDHDt,i, i = 1…3;
- KKDHDr is diagonal with diagonal values kKDHDr,i, i = 1…3;
- DKDHDt is diagonal with diagonal values dKDHDt,i, i = 1…3;
- DKDHDr is diagonal with diagonal values dKDHDr,i, i = 1…3;
- HDKDHDt is diagonal with diagonal values hdKDHDt,i, i = 1…3;
- HDKDHDr is diagonal with diagonal values hdKDHDr,i, i = 1…3.
- A PD closed-loop control with a given ζ (reference PD) is applied to the position control of G(s), applying a step input, and the settling energy of the step response is calculated.
- There are infinite combinations of ζ and ψ for a PDD1/2 controller with the same proportional gain and the same settling energy of the reference PD; among these, the ζ–ψ combination which minimizes the settling time is selected.
- kKDt,i = kKDHDt,i = 1 × 103 N/m, i = 1…3,
- kKDr,i = kKDHDr,i = 1 × 102 Nm/rad, i = 1…3,
- Phase 1: xd varies with constant velocity from xref to xref + [0.05, 0.05, 0.05]T [m], while Ed varies with constant velocity from 0 to [0.2, −0.2, 0.2]T [rad]. The duration of this phase is tramp = 1 s.
- Phase 2:xd remains constant in xref + [0.05, 0.05, 0.05]T [m] and Ed remains constant in [0.2, −0.2, 0.2]T [rad] for tstop = 2 s.
- Phase 3:xd and Ed return to the initial values (xref and 0) with constant velocity in tramp.
- Phase 4:xd and Ed remain constant in xref and 0 for tstop.
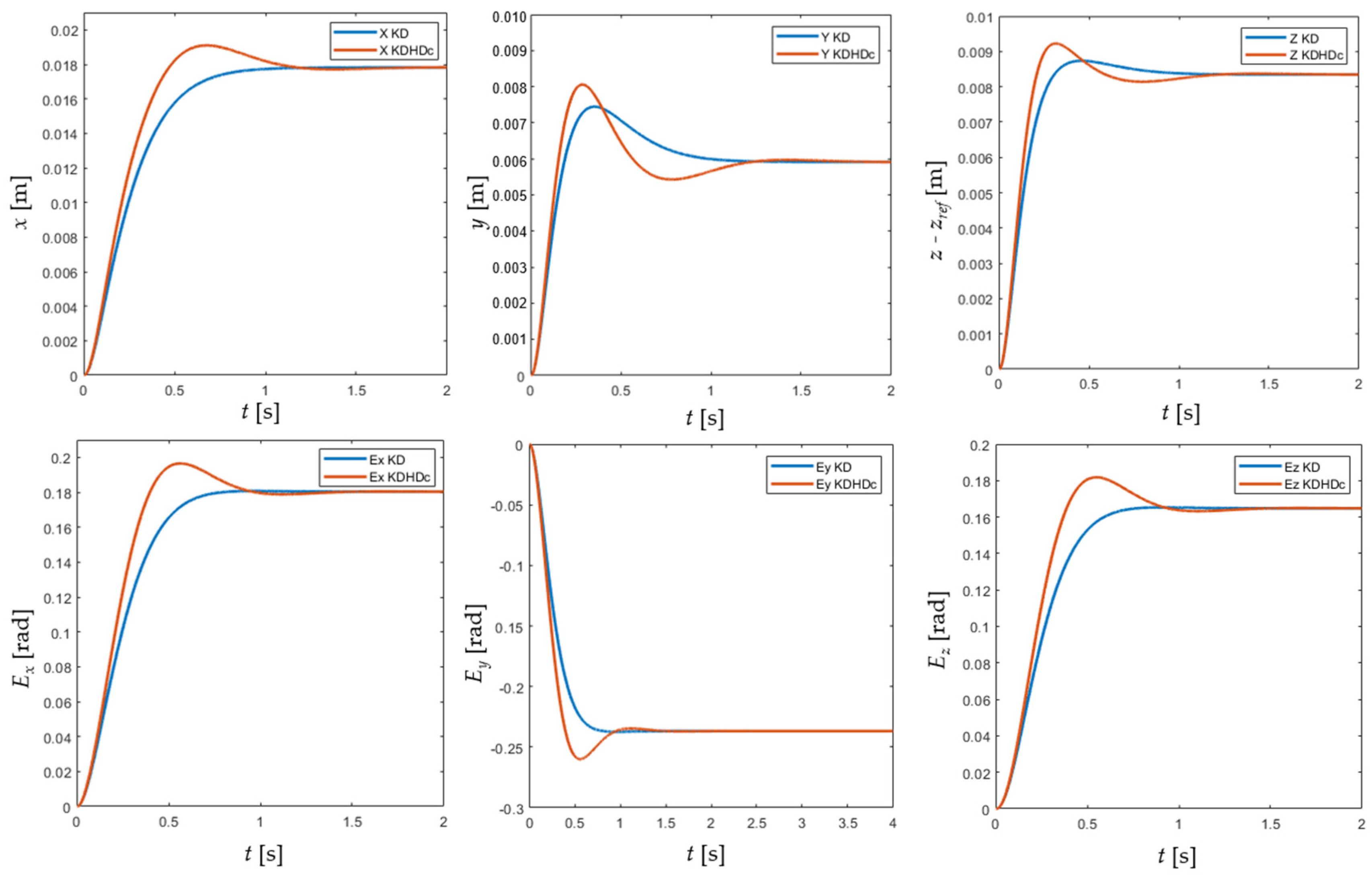
6.2. Case Study B: Interaction with the Environment, Diagonal Stiffness and Damping Matrices
- kKDt,1 = kKDHDt,1 = 2 × 103 N/m; kKDt,2 = kKDHDt,2 = kKDt,3 = kKDHDt,3 = 1 × 104 N/m,
- kKDr,1 = kKDHDr,1 = 1 × 102 Nm/rad; kKDr,2 = kKDHDr,2 = kKDr,3 = kKDHDr,3 = 1 × 103 Nm/rad,
6.3. Case Study C: Interaction with the Environment, Non-Diagonal Stiffness and Damping Matrices
7. Conclusions and Future Research Directions
- The application of the half-derivative damping term allows for tuning of the impedance control with additional degrees of freedom, with potential benefits. For instance, the tuning criterion used in case study A, derived from the one proposed in [20] for a single-degree-of-freedom, an almost linear mechatronic axis, leads in free motion to lower actuation forces, almost equal control effort, lower settling time with slightly higher overshoot. These results are qualitatively similar to what happens for the single mechatronic axis, conforming the validity of the approach of deriving the KDHDc tuning form the PDD1/2 tuning. However, the system can be tuned differently, focusing on other performance indices, exploiting the additional regulation opportunities provided by the half-derivative damping.
- The real-time digital implementation of the half-derivative term introduces a remarkable alteration to the stiffness of the impedance control in steady state, as discussed in Section 2, invalidating the capability of the KDHD impedance control to regulate the contact force between the end-effector and the environment through the measurement of the position error. Nevertheless, the proposed KDHDc compensation, Equation (16), has been proven to be effective also for the rotational behavior (case studies B and C).
- a systematic investigation on possible tuning approaches for the KDHDc impedance control will be carried out, in order to maximize different performance indices; to this aim, both extension of PDD1/2 tuning methods and numerical optimization techniques will be considered;
- the KDHDc impedance control will be applied to different serial and parallel architectures; by now, two kinds of mobilities have been taken into account: three translational degrees of freedom and full mobility, without redundancy (equal numbers of internal and external coordinates); in the following, also the cases of limited-degree-of-freedom robots, mixing translational and rotational motions, will be analyzed, both for serial [29,30] and parallel/hybrid manipulators [31,32];
- impedance control of redundant manipulators, which has interesting theoretical aspects [33], will also be considered;
- the problem of impedance control for manipulators equipped with flexure joints [34], requiring a proper stiffness compensation of the joint elastic return force, should be addressed;
- another possible application of the proposed fractional-order approach is impedance control of cable-driven parallel robots [35];
- as regards the validation methodology, only simulation results are available by now; in the future, besides performing experimental tests of the considered case studies (approach/depart motions without external forces, interactions with the environment with constant force/moment) the effectiveness of the KDHDc impedance control will be assessed in real working conditions, for example peg-in-hole or milling tasks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Craig, J. Introduction to Robotics. Mechanics and Control; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Raibert, M.H.; Craig, J.J. Hybrid Position/Force Control of Manipulators. ASME J. Dyn. Syst. Meas. Control 1981, 103, 126–133. [Google Scholar] [CrossRef]
- Caccavale, F.; Siciliano, B.; Villani, L. Robot Impedance Control with Nondiagonal Stiffness. IEEE Trans. Autom. Control 1999, 44, 1943–1946. [Google Scholar] [CrossRef]
- Valency, T.; Zacksenhouse, M. Accuracy/Robustness Dilemma in Impedance Control. J. Dyn. Syst. Meas. Control 2003, 125, 310–319. [Google Scholar] [CrossRef]
- Bruzzone, L.; Molfino, R.M.; Zoppi, M. An impedance-controlled parallel robot for high-speed assembly of white goods. Ind. Robot Int. J. 2005, 32, 226–233. [Google Scholar] [CrossRef]
- Angeles, J. Rational Kinematics; Springer: New York, NY, USA, 1988. [Google Scholar]
- Bonev, I.A.; Ryu, J. A new approach to orientation workspace analysis of 6-DOF parallel manipulators. Mech. Mach. Theory 2001, 36, 15–28. [Google Scholar] [CrossRef]
- Caccavale, F.; Siciliano, B.; Villani, L. The role of Euler parameters in robot control. Asian J. Control 1999, 1, 25–34. [Google Scholar] [CrossRef]
- Bruzzone, L.; Molfino, R.M. A geometric definition of rotational stiffness and damping applied to impedance control of parallel robots. Int. J. Robot. Autom. 2006, 21, 197–205. [Google Scholar] [CrossRef]
- Ikeura, R.; Inooka, H. Variable impedance control of a robot for cooperation with a human. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; Volume 3, pp. 3097–3102. [Google Scholar]
- Tsumugiwa, T.; Yokogawa, R.; Hara, K. Variable impedance control with virtual stiffness for human-robot cooperative peg-in-hole task. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; Volume 2, pp. 1075–1081. [Google Scholar]
- Shimizu, M. Nonlinear impedance control to maintain robot position within specified ranges. In Proceedings of the 2012 SICE Annual Conference (SICE), Akita, Japan, 20–23 August 2012; pp. 1287–1292. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Kizir, S.; Elşavi, A. Position-Based Fractional-Order Impedance Control of a 2 DOF Serial Manipulator. Robotica 2021, 39, 1560–1574. [Google Scholar] [CrossRef]
- Liu, X.; Wang, S.; Luo, Y. Fractional-order impedance control design for robot manipulator. In Proceedings of the ASME 2021 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, Online, 17–19 August 2021; Volume 7, p. V007T07A028. [Google Scholar]
- Fotuhi, M.J.; Bingul, Z. Novel fractional hybrid impedance control of series elastic muscle-tendon actuator. Ind. Robot Int. J. Robot. Res. Appl. 2021, 48, 532–543. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PIλDμ controllers. IEEE Trans. Autom. Control 1999, 44, 208–213. [Google Scholar] [CrossRef]
- Bruzzone, L.; Fanghella, P.; Basso, D. Application of the Half-Order Derivative to Impedance Control of the 3-PUU Parallel Robot. Actuators 2022, 11, 45. [Google Scholar] [CrossRef]
- Bruzzone, L.; Fanghella, P. Comparison of PDD1/2 and PDμ position controls of a second order linear system. In Proceedings of the IASTED International Conference on Modelling, Identification and Control, Innsbruck, Austria, 17–19 February 2014; pp. 182–188. [Google Scholar]
- Bruzzone, L.; Fanghella, P. Fractional-order control of a micrometric linear axis. J. Control Sci. Eng. 2013, 2013, 947428. [Google Scholar] [CrossRef] [Green Version]
- Bruzzone, L.; Fanghella, P.; Baggetta, M. Experimental assessment of fractional-order PDD1/2 control of a brushless DC motor with inertial load. Actuators 2020, 9, 13. [Google Scholar] [CrossRef] [Green Version]
- Machado, J.T. Fractional-order derivative approximations in discrete-time control systems. J. Syst. Anal. Model. Simul. 1999, 34, 419–434. [Google Scholar]
- Das, S. Functional Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Bruzzone, L.; Callegari, M. Application of the rotation matrix natural invariants to impedance control of rotational parallel robots. Adv. Mech. Eng. 2010, 2010, 284976. [Google Scholar] [CrossRef]
- Stewart, D. A Platform with Six Degrees of Freedom. Proc. Inst. Mech. Eng. 1965, 180, 371–386. [Google Scholar] [CrossRef]
- Fichter, E.F. A Stewart Platform-based Manipulator: General Theory and Practical Construction. Int. J. Robot. Res. 1986, 5, 157–182. [Google Scholar] [CrossRef]
- Ma, O.; Angeles, J. Optimum Architecture Design of Platform Manipulators. In Proceedings of the 5th International Conference on Advanced Robotics, Pisa, Italy, 19–22 June 1991; Volume 2, pp. 1130–1135. [Google Scholar]
- Bruzzone, L.; Bozzini, G. PDD1/2 control of purely inertial systems: Nondimensional analysis of the ramp response. In Proceedings of the IASTED International Conference on Modelling, Identification and Control, Innsbruck, Austria, 14–16 February 2011; pp. 308–315. [Google Scholar]
- Makino, H.; Furuya, N. Selective compliance assembly robot arm. In Proceedings of the First International Conference on Assembly Automation (ICAA), Brighton, UK, 25–27 March 1980; pp. 77–86. [Google Scholar]
- Bruzzone, L.; Bozzini, G. A statically balanced SCARA-like industrial manipulator with high energetic efficiency. Meccanica 2011, 46, 771–784. [Google Scholar] [CrossRef]
- Fang, Y.; Tsai, L.-W. Structure synthesis of a class of 4-DoF and 5-DoF parallel manipulators with identical limb structures. Int. J. Robot. Res. 2002, 21, 799–810. [Google Scholar] [CrossRef]
- Dong, C.; Liu, H.; Xiao, J.; Huang, T. Dynamic Modeling and Design of a 5-DOF Hybrid Robot for Machining. Mech. Mach. Theory 2021, 165, 2021165. [Google Scholar] [CrossRef]
- Xiong, G.; Zhou, Y.; Yao, J. Null-Space Impedance Control of 7-Degree-of-Freedom Redundant Manipulators Based on the Arm Angles. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420925297. [Google Scholar] [CrossRef]
- Bruzzone, L.; Molfino, R.M. A novel parallel robot for current microassembly applications. Assem. Autom. 2006, 26, 299–306. [Google Scholar] [CrossRef]
- Reichert, C.; Müller, K.; Bruckmann, T. Robust Internal Force-Based Impedance Control for Cable-Driven Parallel Robots. Mech. Mach. Sci. 2015, 32, 131–143. [Google Scholar]
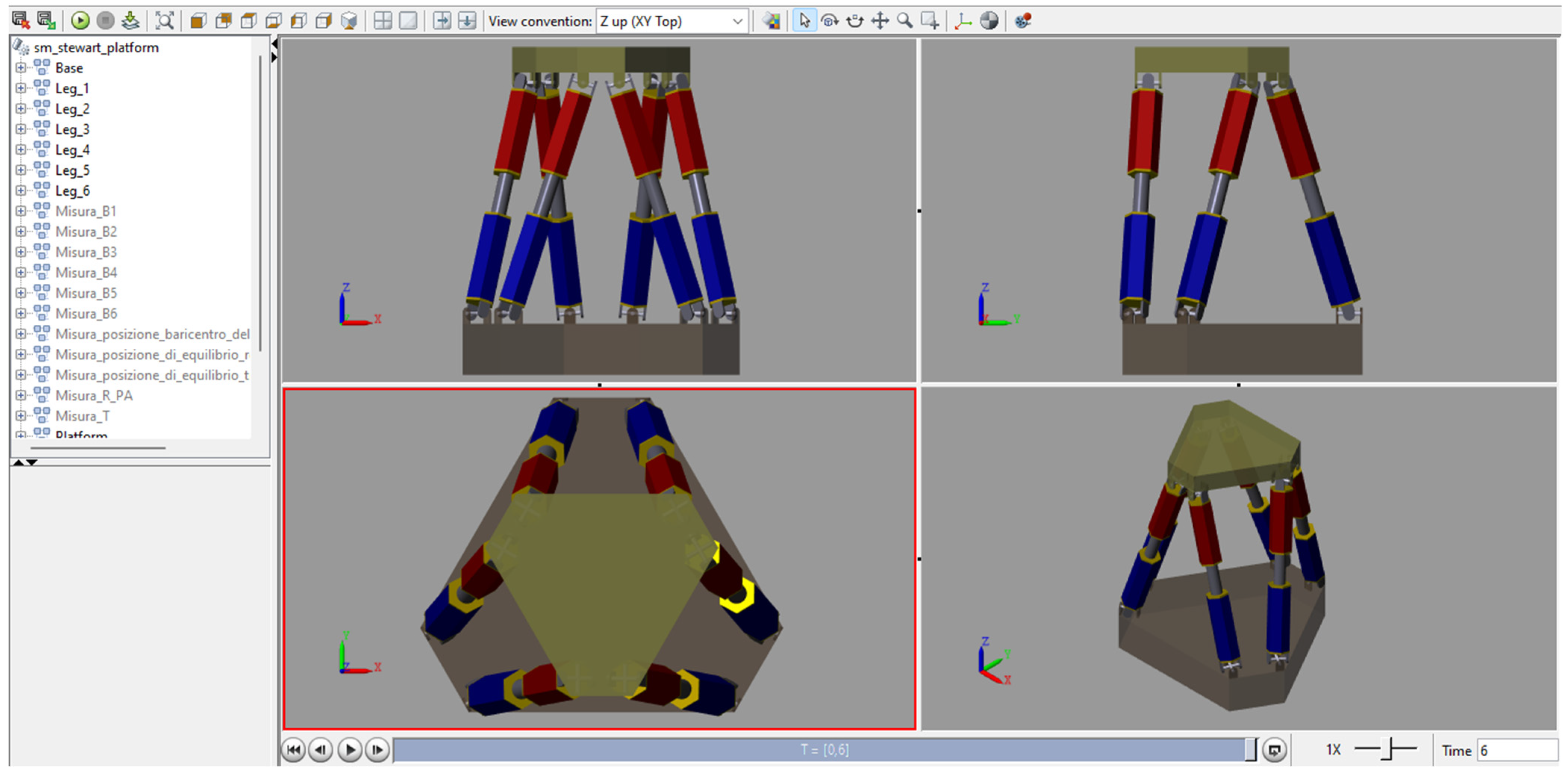
| Symbol | Parameter | Value | Unit |
|---|---|---|---|
| |Bi|, i = 1…6 | base platform radius | 0.28 | m |
| |Pi − x|, i = 1…6 | moving platform radius | 0.3864 | m |
| angular distances of the platform joint centers | 20°/100°/20°/100°/20°/100° | degrees | |
| angular distances of the base joint centers | 100°/20°/100°/20°/100°/20° | degrees | |
| mmp | moving platform mass, with payload | 63 | kg |
| ml | mass of the upper part of one leg | 1 | kg |
| ms | mass of the lower part of one leg | 1.5 | kg |
| [J1, J2, J3] | principal moments of inertia of the moving platform (frame P) | [1.636, 1.636, 3.221] | kg·m2 |
| xref = [0, 0, zref] | reference workspace central position | [0, 0, 0.69] | m |
| KD/KDHD Comparison | PD Control/ KD Impedance Control | PDD1/2 Control/ KDHD Impedance Control | |
|---|---|---|---|
| ζKD | ζKDHD | ψKDHD | |
| I | 0.8 | 0.46 | 0.7990 |
| II | 1 | 0.45 | 1.4266 |
| III | 1.2 | 0.48 | 2.1510 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruzzone, L.; Polloni, A. Fractional Order KDHD Impedance Control of the Stewart Platform. Machines 2022, 10, 604. https://doi.org/10.3390/machines10080604
Bruzzone L, Polloni A. Fractional Order KDHD Impedance Control of the Stewart Platform. Machines. 2022; 10(8):604. https://doi.org/10.3390/machines10080604
Chicago/Turabian StyleBruzzone, Luca, and Alessio Polloni. 2022. "Fractional Order KDHD Impedance Control of the Stewart Platform" Machines 10, no. 8: 604. https://doi.org/10.3390/machines10080604
APA StyleBruzzone, L., & Polloni, A. (2022). Fractional Order KDHD Impedance Control of the Stewart Platform. Machines, 10(8), 604. https://doi.org/10.3390/machines10080604







