Abstract
Additive manufacturing (AM) systems are currently evolving into network-based models, where the distributed manufacturing resources from multiple enterprises are coordinated to complete product orders. The layer-by-layer approach of AM technologies gives manufacturers unprecedented freedom to create complex parts tailored to customer needs, but this comes at slow build rates. Consequently, for AM to become mainstream in the industry, challenges in production planning remain to be addressed to increase AM system productivity. This paper considers two practical problems encountered in AM systems, namely, production planning and part-to-printer assignment, and a series of heuristic algorithms are proposed to solve these problems. In particular, an approach for automatically determining part orientation, part-to-printer allocation, and nesting of multiple parts for a distributed network of fused filament fabrication three-dimensional printers is described to reduce the total production cost and time regarding the context of social manufacturing. The proposed method is implemented through a web application. The case study, using real-world parts and comparative analysis findings, indicated that the proposed method produces high-performance results.
1. Introduction
Additive manufacturing (AM), regularly referred to as three-dimensional (3D) printing, is a set of technologies that manufacture objects from digital 3D models by layering material rather than subtracting it [1]. As a result, it enables the creation of customized and highly complex component geometries that can be difficult to manufacture using conventional processes. While the possibilities from a design perspective are endless, the production throughput speed of AM systems is slow, limiting their use for mass production [2]. In this regard, AM is still considered a niche technology for the rapid prototyping and production of small-batch products. Therefore, today’s AM challenges revolve around enhancing productivity to meet industry demands for mass personalization.
Meanwhile, the latest advancements in AM combined with social networks are opening up a new world of possibilities for the manufacturing industry and fostering the development of new collaborative business models, such as social manufacturing (SocialMfg) [3,4]. A key factor behind the growth of SocialMfg is the ability of AM technologies to enable on-demand production and rapid innovation for small and medium-sized enterprises (SMEs), and even individual entrepreneurs [5,6]. In a nutshell, in SocialMfg, heterogeneous orders from multiple customers are coordinated to be completed by a distributed network of AM machines from several SMEs that interact and collaborate on a peer-to-peer (p2p) basis, as shown in Figure 1. In this setting, it becomes critical to investigate production planning approaches for a network of AM machines in which several 3D printers are shared to allow on-demand production for flexible and geographically distributed production units.

Figure 1.
Concept model for AM production planning in SocialMfg.
In AM, production planning includes selecting part orientation, packing or nesting multiple parts together, setting process parameters, slicing, and assigning parts to machines. Each of these tasks requires a high degree of manual intervention, which affects the overall efficiency of the 3D printing process. Indeed, selecting the build orientation of a part remains a manual operation and relies on the knowledge and experience of the process planner. Furthermore, parts with similar production requirements are usually grouped by batch to meet order due dates [7]. Several parts must be nested in a build plate for each batch and printed simultaneously in a single run to reduce the production time and operating costs [8,9]. Manually arranging the placement of a group of parts with complex geometries is, however, time-consuming and can become a difficult task [10,11]. As a result, the automation of production planning looks highly promising to stimulate the productivity of AM systems, especially for a network-based organization involving shared 3D printers.
This study investigates the feasibility of an automated multi-part production planning system in the context of SocialMfg. The paper addresses, in particular, three research questions: how to optimally orient a part, how to allocate parts to AM machines, and how to optimally place multiple parts in build plates. A further question is whether this automated production planning system can quickly assign parts, using the few possible build plates, while ensuring part quality. Although these questions have been substantially investigated in the literature, no study has yielded an integrated solution. However, it is necessary to consider part orientation selection, part-to-printer assignment, and nesting, as a whole, to increase AM production rates and lower operating costs.
In this work, we focus on a prominent material extrusion technology called fused filament fabrication (FFF), one of the most widely used AM techniques. Initially adopted for rapid prototyping, FFF is gradually used for industrial applications to deliver rapid tooling and spare parts. This paper aims to enhance the FFF process via an industrial-like production logic by providing a realistic solution to production planning and scheduling problems. First, efficient heuristic algorithms are presented for optimizing part build orientation, part-to-printer assignment, and the nesting of parts. In fact, in the field of combinatorial optimization, heuristic algorithms have proven to be effective. Compared to other methods, they allow for satisfactory results with less computational effort. A web application (web app) is also developed in which the parts’ stereolithography (STL) files are entered, and the packing result is returned. Lastly, the effectiveness and operability of the developed system are investigated using a case study with real-world components and comparative analysis.
The contribution of this work is threefold:
- As part of the SocialMfg, this is one of the first works in AM production planning and scheduling that includes part orientation selection, part-to-printer assignment, and two-dimensional nesting;
- Orientation-dependent factors that affect the part quality and printing time are considered, and the two-dimensional (2D) packing is solved using a rasterization technique and quadtree representation. Moreover, the proposed 2D nesting algorithm outperforms the top existing methods in terms of packing density and computational time;
- A real-world case study to evaluate the proposed method confirms the effectiveness of considering part orientation and nesting in AM machine scheduling.
The balance of this paper is arranged as follows: Section 2 summarizes the related work and indicates research gaps. Section 3 describes the scenario considered and details the proposed methodology. The prototype web app and a case study are reported in Section 4. In Section 5, the performance of the proposed method is discussed. Finally, Section 6 provides the conclusion to this investigation.
2. Literature Review
This section summarizes existing studies regarding orientation selection in AM and provides an overview of the most prevalent approaches for AM production planning and scheduling.
2.1. Part Orientation in AM
The problem of part orientation in AM has been thoroughly investigated [12]. Some researchers presented a one-step approach. Notably, they proposed a customized algorithm [13,14,15] or applied an existing optimization algorithm, most commonly an evolutionary algorithm, such as a genetic algorithm [16,17], to directly search an orientation, allowing several considered factors to be optimal from a large number of alternative orientations. The challenge with this one-step approach is to define the suitable rotation angle or step size. A large rotation angle reduces the number of computations and raises the risk of missing the real optimal build orientation. Contrarily, the risk is reduced when the rotation angle is slight, but the number of computations will increase considerably. This situation attracted several researchers to investigate the part orientation problem from other perspectives and propose a two-step approach. The initial phase is to generate some practical alternative orientations among all possible orientations. The second phase consists of identifying the best orientation among the generated options. A multi-criteria decision-making (MCDM) technique is usually used to select the best orientation [13,18,19].
Despite decades of research, automatic determination of optimal build orientation remains an open issue in AM. Compared to the vat photopolymerization (VPP) process, few attempts have been made to identify optimal part build orientation for the FFF process, where the staircase effect affects the surface quality more severely. Selecting the optimal build orientation should improve the print quality, regardless of the intended purpose of the part. Considering this background, this research proposed a two-step strategy and new orientation-dependent factors, inexpensive in computation, to address the optimal build orientation determination problem for the FFF technique.
2.2. Planning and Scheduling of AM Production
In the context of scheduling a set of unrelated parallel machines with non-identical job sizes, Li et al. [20] proposed heuristics based on best-fit and longest processing time (LPT) to reduce the makespan. Similarly, Arroyo and Leung [21] introduced several heuristics that allow the realization of varied-sized jobs with unrelated parallel machines, while minimizing the makespan and grouping jobs into batches. Ransikanbum et al. [22] adjusted the workload balance between FFF 3D printers to lower the parts’ total cost and completion time. Moreover, Li et al. [23] investigated several techniques to manufacture multiple components in an industrial setting. They examined the costs and reaction times of centralized and decentralized manufacturing methods. Zhang et al. [24] addressed the part-to-printer assignment and part placement problems for the VPP process. They also developed a heuristic and genetic algorithm that can be used for the FFF technique. Cadiou et al. [25] recently suggested a framework based on reasoning algorithms to solve the on-demand production planning of non-identical AM parts in Fab labs made up of unrelated parallel FFF 3D printers.
In addition, several studies investigated the 3D nesting problem [8,26] to enhance AM machine utilization by reducing the overall build time and cost per machine. However, the literature review here focuses on prior research that has explored the 2D nesting problem. Indeed, this study focuses on the FFF process, where parts are placed in a single layer rather than stacked [10]. Approaches for nesting can be categorized as parallel or serial [27]. In parallel nesting, all parts are arranged simultaneously in the build plate, and the packing result is evaluated. Such approaches are described in [10,27]. However, in serial nesting, the parts are arranged one at a time, emulating how a human operator can place parts in a print bed. This strategy has been implemented in most earlier works [28,29,30,31] because it can decrease the computational cost while still providing satisfactory results.
A decisive step of the nesting process is the need to develop a geometric tool for handling the complexity of the parts to be packed. The simplest method uses the bounding box [28,29,32] of part projections on the printer bed. Using a bounding box to replace a part’s actual shape can waste the workspaces of an AM machine when packing parts, although such an approach eases the problem of detecting collision between parts. There are several other solutions for part representation using polygons [10,27,30]. However, in the AM nesting process, the input is not polygons, but a set of triangular facets (i.e., STL files). The polygon union of all these facets can be computed using the no-fit-polygon (NFP) algorithm, or direct trigonometric method, to represent the shape of the parts. Nevertheless, as the number of facets in the STL model increases drastically, such an operation becomes computationally complex and time-consuming [30].
Furthermore, a critical problem with NFP is that as the number of parts to place increases, or as pieces rotate, the NFP computation becomes too large to be practical. Another possible solution for dealing with the geometry of parts in 2D nesting problems is the pixel/raster method [31]. This technique can generate a nearly exact part shape, regardless of its geometrical complexity, in a short time. Although the computation cost can increase rapidly with increasing resolutions to obtain a more accurate raster representation of the STL files, high resolution is not usually required [31,33].
Another methodological concern of nesting for AM is the rotation of parts in the print bed to find the best possible position. In many previous works, no rotation of the parts is allowed [26,29,30]. On the other hand, some studies considered the rotation of parts on the XY plane by 90 degrees increment [8,28]. In such an approach, the part is rotated before placement to find an optimal positioning. It should also be emphasized that most current nesting methods rely on genetic algorithms to optimize the part placement strategy. Although this algorithm can achieve reasonably good solutions, it has a high computational burden.
In synthesis, in the past, methods and techniques for planning and scheduling AM production primarily focused on the part-to-printer assignment, or the nesting of several components in a single printing run. Concerning the nesting problem, despite the considerable number of solutions that have been proposed, a closer inspection of the literature reveals several gaps and shortcomings. On the one hand, little attention has been given to 2D nesting for the FFF process. Previous studies have almost exclusively focused on the VPP and laser powder bed fusion (LPBF) processes. Without considering the characteristics and constraints of the FFF technique, generating part layout based on part geometry is ineffective.
On the other hand, approaches based on genetic algorithms used to determine part layout are practical, but they appear to be computationally expensive [31]. Moreover, many studies are simplified using bounding boxes or rectangular shapes in the packing process, resulting in a waste of workspace of AM machines. Consequently, this study proposes a new nesting approach based on pixel/raster representation of the STL models, which considers the FFF constraints.
3. Methods
In SocialMfg, orders from several customers can be allocated to a network of AM machines. Each order can include multiple parts. After receiving the orders, planners compose batches of parts to be assigned to AM machines, according to customer specifications and different planning objectives (e.g., reducing operating cost and processing time). Concerning a particular printer, multiple parts composing a batch need to be optimally placed to use the printer efficiently. However, when placing several parts in a print bed, the space utilization ratio must be maximized to lower the production time and cost, and the quality of the parts must be guaranteed [10,27]. In addition, with the FFF process, producing multiple parts in a single run does not necessarily improve productivity if part orientation is not optimal. Part orientation, nesting, and part-to-printer assignment are all significant considerations in this situation. As a result, the methodology presented here begins with a group of heterogeneous parts assigned to one or more FFF 3D printers. First, the optimal build orientation of each part is identified. Afterward, the optimally oriented parts are taken as an input set and are assigned to the FFF 3D printers. Finally, parts are optimally placed in build plates according to two objectives: to maximize the print bed utilization and ensure the quality of the parts. Figure 2 shows a graphic depiction of this approach.
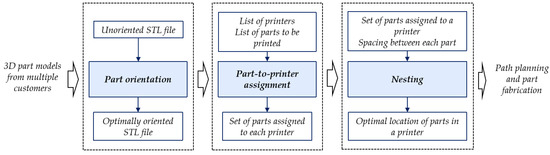
Figure 2.
The framework of the proposed approach.
The following assumptions have been formulated to limit the production planning problems to our research objectives.
- The parts to be oriented and nested are assigned to a FFF 3D printer and have identical manufacturing requirements. In other words, the service provider and service demander agreed on the parts’ materials, production deadline, and characteristics.
- The optimal build orientation of each part is selected before the nesting process. Nevertheless, the rotation of the parts along the vertical axis is allowed because of its relatively small impact on the quality of printed parts [22,30].
It is essential to clarify that AM service providers receive diverse printing tasks from multiple customers. Thus, some parts can be pre-oriented adequately by customers. Accordingly, this paper explores the optimal build orientation determination for a single part instead of orientation optimization for several parts in a build, as in the work of [10,27].
The optimization strategy adopted here can be segmented into three consecutive stages. The first stage involves optimizing each part’s build orientation separately to improve the production quality. Then, the second stage aims to assign the parts to FFF 3D printers to minimize the makespan, ensure load balance among the printers, and efficiently use the manufacturing resources. The last stage involves placing the parts on build plates in the most compact way to achieve higher productivity with the FFF 3D printers. The following paragraphs of this section detail the heuristic algorithms proposed to solve these combinatorial optimization problems.
3.1. Heuristic Algorithm-Based Part Orientation Selection
In theory, a part can be built in many possible orientations. By orienting the part in different directions, there is a significant difference in part quality. Therefore, optimizing part orientation is crucial in AM. For many industrial applications, the surface quality of the part is critical. Good surface quality is more appealing and gives greater dimensional accuracy necessary for the correct functioning of assembly parts. In actual experiments, it is found that the key to achieving good quality printed parts with the FFF process is to prevent overhangs. Indeed, the overhanging surfaces of an STL model are difficult to print; they usually require additional support structures and print poorly.
Nevertheless, there are admissible overhangs. These are typically overhanging surfaces with angles between the normal vector and the build direction lower than 135°. Therefore, it is preferable to differentiate the support contact area [34,35] (i.e., the overhang that requires support structures) from other tolerable overhanging surfaces. Intuitively, minimizing the support contact area would reduce the need for support structures, thus leading to better surface quality and decreasing the post-processing time. As a result, build orientation optimization is the determination of a desirable orientation that minimizes the support contact area. It involves generating a set of alternative build orientations (ABOs) and determining the best build orientation from the ABOs generated.
Another way to enhance the surface quality of the parts is to maximize the area of the non-stepped surfaces [36,37]. It is possible to achieve this by maximizing the bottom surface area (i.e., the area of the part in contact with the build plate). There are at least two reasons to consider optimizing this criterion. First, surfaces horizontal to the build plate do not have a stair-stepping effect, guaranteeing a good surface quality. Second, using a large area as the bottom face can drastically decrease the number of layers and the build time. It is also necessary to consider the perimeter of this bottom face because for STL models with a spherical shape, for example, the bottom face could be a circle without any resulting area. Accordingly, in the present work, three orientation-dependent factors are considered when searching for the optimal build orientation: support contact area, bottom surface area, and bottom surface perimeter. These can be directly computed using geometrical analysis of the STL model [34,35,36]. These factors are weighted and summed to calculate the degree quality for each ABO.
The optimal build orientation determination procedure is formalized with pseudocode, as shown in Algorithm 1. The algorithm requires an STL file as input and produces an STL file optimally oriented as output. The appropriate weights to assign to each orientation-dependent factor must be found because the optimal build orientation depends strongly on the chosen weight values.
| Algorithm 1: Pseudocode for the orientation optimization algorithm |
| Input: Unoriented STL file Output: Optimally oriented STL file 1: Generate the alternative build orientations of the part (Oi) 2: Compute the orientation-dependent factors (Fj) of the i-th alternative orientation 3: for each value of the j-th factor of the i-th alternative orientation () do 4: Convert each orientation-dependent factor value into a number in [0, 1] as follows: 5: Normalize the converted results using 6: end for 7: Assign the weights to the considered factors 8: Compute a summary value of factors for each alternative orientation 9: Determine the optimal build orientation for the part 10: return the optimally oriented STL file |
3.2. Heuristic Algorithm-Based Part-to-Printer Assignment
As stated in Section 1, this paper investigates the production planning of a network of dispersed AM machines to meet the low-quantity needs of multiple customers. The network of AM machines can be made up of unrelated parallel machines that can accomplish the same task but have different capacities. The entire available build volume determines the capacity of an AM machine. The problem is allocating parts from multiple customers to a network of AM machines, with varying operating costs and speed characteristics, while minimizing the total production cost and time.
According to the customer orders, there is a set of parts with various sizes, heights, and geometries. The orders are allocated to AM machines on a part-by-part basis, considering the part sizes and heights, and then divided into batches or printing jobs. In fact, due to the limited build volume of AM machines, some parts may not be able to be manufactured on all available machines. For example, a part higher than the maximum height supported by a machine cannot be assigned to that machine.
When given a set of parts, each with a different build time and several available AM machines, the part-to-printer assignment involves allocating all parts to machines with the goal of optimizing the workloads. As the SocialMfg can receive multiple print jobs from several customers and a network of various AM machines, production scheduling decisions must be relatively quick to effectively schedule these jobs for all the distributed 3D printers. Therefore, this study proposes an optimized LPT algorithm [38] to solve the part-to-printer assignment due to its simplicity and practical effectiveness. Indeed, LPT has good adaptability to a variety of scheduling tasks. This algorithm sorts parts in non-ascending order of their build time and then assigns them to the machine with the earliest end time. In particular, it entails attributing the parts one at a time to the FFF 3D printers to minimize the processing times of the machines. The LPT rule schedules the longest tasks first so that no large task overruns at the end of the schedule, significantly extending the execution time of the last job. The total manufacturing times of all the parts assigned to a machine is its completion time. The printing time is estimated after the parts are oriented in their optimal build direction. The heuristic procedure for part-to-printer assignment is realized through Algorithm 2.
| Algorithm 2: Heuristic procedure for the part-to-printer assignment |
| Input: Set of AM machines M, set of oriented parts to be printed P Output: Batch of parts allocated to each machine 1: Estimate the build time of all the parts 2: Sort the parts in decreasing order of build time 3: while P is not empty do 4: Let Pk be the next part in the sorted order 5: if Pk can be scheduled then 6: Assign the part to the machine which has the minimum total processing time 7: Remove the assigned part from the list of parts 8: end if 9: end while 10: return parts allocated to AM machines |
3.3. Heuristic Algorithm-Based Nesting
The FFF technique allows the printing of multiple parts simultaneously when they fit the build plate. Nesting optimizes the process of laying out parts on the print bed of an AM machine. The gain is the reduction in the total processing time to build and arrange the parts. Manually finding the position of multiple STL files on the print bed can take exponential time. However, the nesting or part packing in AM should be relatively fast because, unlike in subtractive manufacturing, the only gain is production time (i.e., no waste or material). Thus, the time spent nesting parts becomes proportional to the build time.
The proposed nesting method considers the rotation of the parts along the vertical axis (i.e., build direction), in 90° increments, to find a better positioning, which can improve the packing solution in terms of compactness. Figure 3 shows the flowchart of the nesting procedure. First, data are initialized to specify the spacing between each part and the printing space dimensions. Next, a rasterization algorithm transforms the STL models into raster images. The main iteration of the nesting strategy repeats until all parts have been placed. Within the space available in the print bed, parts are sequentially placed as far as feasible to the bottom, then, as far as possible to the left. The available space dimensions must be larger than part dimensions in order to arrange a part within the packing area. It follows that if this requirement is not met, the current packing area is abandoned, and another is tried until all available spaces have been explored. When the placement of the part is feasible, the selected slot is removed from the list of available space, and the part is removed from the part list. The next part is chosen once the previous one has been placed, and the same packing procedure is repeated. When all the parts in the input list are placed, the optimized part layout is generated as an STL file. The rasterization procedure and placement strategy are further discussed in the following subsections.

Figure 3.
Flowchart of the 2D nesting algorithm.
3.3.1. Raster Method
Here, the rasterization is the task of converting the STL file into a 2D bitmap. The simplest form of a bitmap, a black and white image, is used; all white pixels are represented as 0, meaning void space, and all black pixels are represented as 1, which means the presence of a part. Rasterization aims to divide the irregular shapes of STL files into discrete areas, which thus reduces the geometric information. The basic idea is that a blank scene whose size corresponds to the print bed is created at the beginning. The facets of the STL model are projected onto the scene as 2D triangles. Once a part has been placed in the scene, it is updated. In the first step of the rasterization process, each triangular facet in the STL model is transformed from 3D to 2D space using projection matrices. The second step is to fill all the pixels in the region covered by the triangles. These two steps are illustrated in Figure 4. Finding out which pixels are covered by the resulting projected profiles, i.e., which pixel should be 0 or 1, is realized using the D-function [33].
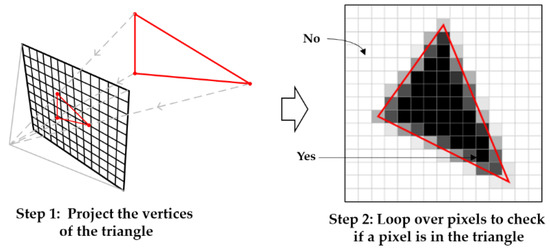
Figure 4.
Two-step procedure of the raster method.
Part projection profiles are represented as region quadtrees [39] to reduce the complexity and computation time. Moreover, 2D pixel dilation is used to handle the part spacing. This is an operation to enlarge the boundaries of the pixels. The raster method provides a simplistic and relatively inexpensive approach for processing the geometric representation of the STL files. In addition, it makes the test of possible placement trivial because we must simply check that all the pixels are located where the part will be placed.
3.3.2. Improved Bottom-Left-Fill Algorithm
In this paper, the proposed placement heuristic, called improved bottom-left-fill (I-BLF), follows the BLF strategy [40], with a slight variation, using the lowest gravity center of the part. The algorithm will prefer the orientation where the center of mass of the part is as close as possible to the lower left of the build plate. For several parts, experiments have shown that placing the center of mass as close as possible to the lower-left leaves a maximum amount of space on the top right. The parts are placed using an exhaustive search, as the algorithm tries every possible orientation (relative to the vertical axis) for the parts. The center of mass of the part is calculated using the average of the coordinates of the pixels covered by the raster image. The placement algorithm is described in Algorithm 3. The sequence order of the parts is significant and can affect the solution obtained because the algorithm is greedy. Sorting parts from the largest to the smallest is the best approach; from the authors’ knowledge, it always leads to better results than sorting the smallest to the largest area.
The packing strategy begins with a print bed of fixed dimensions and a set of STL files. The part is placed according to the I-BLF strategy for each STL file. The packing position of the chosen part will be checked to see if it is viable. The algorithm performs two checks: first, it ensures that the part does not penetrate the boundary of the print bed. Last, it is verified that the part does not overlap with previously packed parts. If part i fits in position j, the part position is set as j, and the void space of the layout is updated by deleting position j. If part i cannot be packed into all j-th positions of the current packing area, the next available packing area is considered. The packing operation ends once all the parts on the list have been placed, and an STL file representing the nesting layout is generated.
| Algorithm 3: Pseudocode for the improved-BLF packing algorithm |
| Input: Set of STL files Output: STL file (s) of the placement layout 1: Initialize print bed size and part spacing 2: repeat 3: for each part (Pi) of the set do 4: Place the part according to the BLF policy 5: Rotate the part to find the lowest gravity center 6: for the j-th position of the part Pi do 7: if the part can be packed into j-th position then 8: Set position j as the packed position of part Pi 9: Delete part Pi from the part list 10: Update the available space in the layout 11: end if 12: end for 13: end for 14: until the part list is empty 15: return placement layout as STL file |
4. Prototype Implementation and Case Study
In this section, the proposed approach is encapsulated into a web app to illustrate its effectiveness in solving the AM production planning and scheduling problems of multiple parts with a network of FFF 3D printers, and a case study is conducted.
4.1. Prototype Implementation
The web app is based on a browser/server architecture and consists of three main modules: a user interface embedded in a web browser, an autorotation module to find the best build orientation of the parts, and a nesting module to find out the optimal part layout. HTML, JavaScript, CSS, and other programming languages are used to build the web app. In particular, the orientation algorithm introduced in our previous work [41] is adopted, as its reasoning capabilities align with the technique described in Section 3.1. The LPT rule presented in Algorithm 2 has been implemented in Python language. Lastly, the 2D nesting algorithm detailed in Figure 3 has been coded in C++. All the algorithms were tested on a computer with a 3 GHz Intel Core i5-9500 processor and 8 GB RAM.
The web app operation is as follows. First, the operator/user imports a set of STL files. The user interface serves as a visualization environment for manipulating STL models and an interface to the production planning and scheduling services. Second, if necessary, the user can invoke the autorotation function to orient the parts in optimal build orientation. The optimally oriented STL model is returned to the user. Then, the STL files can be assigned to the available FFF 3D printers following the LPT rule. Finally, the user can invoke the nesting algorithm to generate an optimal layout from the STL files. For this last step, the user needs to input the quantity of each part and the print bed size. Each build plate generated by the algorithm is returned to the user as an STL file.
4.2. Case Study
The operability and overall workflow of the web app are illustrated through a case study. A set of 19 non-identical parts (named 1 to 19 in Figure 5), whose shapes reflect actual part geometries, are introduced. Table 1 sums up the information of these parts. The aim is to optimize the STL files in terms of print direction before assigning them to FFF 3D printers and to compactly place them in build plates for fabrication. We assume that all the parts have similar manufacturing requirements and priorities.

Figure 5.
Group of parts considered for production planning. The numbers 1 to 19 represent the part IDs.

Table 1.
Sample data related to the parts used for the case study.
Regarding the FFF 3D printers, we used a JG Aurora Z-603S-C and a JG Aurora Z-603S (hereafter Machine 1 and Machine 2, respectively) available in our lab; the first machine has a build volume of 300 mm × 200 mm × 200 mm, while the second has a build area of 280 mm × 180 mm and 180 mm in height. However, in most desktop FFF 3D printers, the parts cannot occupy the entire print bed area. In practice, the extruder cannot travel to the edges of the build plate to precisely deposit a layer. Therefore, to ensure an efficient printing process, we have defined a packing area of 280 mm × 180 mm for Machine 1, and 260 mm × 160 mm for Machine 2, instead of the full print-bed size. Furthermore, the spacing between each part is fixed at 1.5 mm to avoid overlapping due to the accuracy error of the 3D printer and to prevent stringing caused by excess filament oozing from the nozzle.
The web app operation for the case study example is shown in Figure 6. First, the parts are uploaded to the web app user interface. The visualization window allows for the displaying of the selected STL file. Then, the parts are oriented in their optimal build orientation using the autorotation function. The web app provides an estimated build time for each STL file, which is necessary for the part-to-printer assignment step. The dimensions of the parts supplied in Table 1 show that none of the parts is higher than the maximum height capacity of Machine 1 and Machine 2. As a result, all the parts can be assigned to both machines. The parts are selected individually and assigned to AM machines following the LPT rule in Section 3.2. Table 2 lists the results of the part-to-printer assignment.

Figure 6.
A snapshot of the web app operation.

Table 2.
Allocation of the parts.
The packing area of each printer is specified to generate the optimal layout for printing the parts. The batch of parts allocated to Machines 1 and Machine 2 can be produced in a single run, as shown in Figure 7. In particular, the nesting result of Machine 1 (see Figure 7a) exhibits the advantage of the I-BLF strategy, which allows small parts to fill up the void area left by the previously placed large parts. In addition, the large parts are present in the two machines; this helps to balance the workload and reduce the total processing time. As all components have the same priority, printing operations must be completed concurrently to minimize production delays and maintain consistent operating costs.
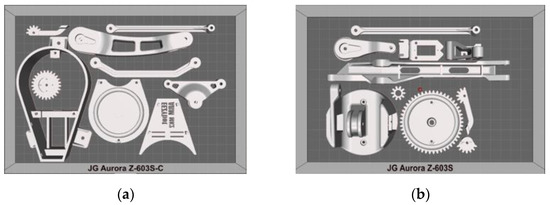
Figure 7.
Results of the part-to-printer assignment with nesting: (a) Machine 1; (b) Machine 2.
4.3. Performance Analysis
The ratio of the total projection area of all nested parts to the area of the print bed, called printing area covered (PAC) [30], must be as great as possible.
Since the parts in AM have irregular shapes and freeform surfaces, it is challenging to guarantee a high PAC value. The defined spacing between the parts also reduces the overall PAC value. Therefore, the performance of the nesting algorithm may vary in different situations and is heavily influenced by the geometry of the parts. As the objective of this paper is to investigate the feasibility of an automated production planning system, the benchmark criteria for evaluating the efficiency of the proposed method are the number of build plates generated and the computation time. The nesting results for the case study example are calculated in tens of seconds, as shown in Table 3, indicating that the proposed method exhibits satisfactory performance. The computation time includes rasterization and part placement.

Table 3.
Computation results of the case study.
5. Discussion
5.1. Comparison of the Proposed Nesting Approach to Existing Methods
A comparative study is conducted to illustrate and validate the efficacy of the proposed nesting method with other existing methods reported by the authors of [30,31], and the results are listed in Table 4 and Table 5, respectively.

Table 4.
Comparison between the LBDB and NFP method in the study in [30] and the proposed approach.

Table 5.
Packing density comparison between the method in the study in [31] and the proposed method.
When the packing results of the approaches detailed in [30,31] and the proposed method are compared, the proposed method outperforms the others in terms of packing efficiency and computing time. Table 4 shows that better nesting results for the test case in [30] are obtained using the method proposed in this paper. All the models to be nested are present in the generated nesting layout (see Figure 8), unlike the layout arrangement obtained using the left-border-down-border (LBDB) heuristic and NFP placement strategy detailed in [30], where a part was not present. Moreover, as shown in Table 5, approximately 97.5% of the first print bed is used compared to 81.2% in the scene-driven method [31], resulting in a 16.3% increase in PAC value. The proposed method packed 25 parts (see Figure 9), while the approach reported in [31] only packed 20 parts in the same printing area. These performances are mainly due to the ability of the I-BLF algorithm to fill the void spaces surrounded by parts already placed, which allows for increased compactness.

Figure 8.
Nesting layouts for the test case data from [30] using the proposed method.

Figure 9.
Nesting layouts for the dataset from [31] using the proposed method: (a) The first batch; (b) the second batch.
Comparing this study with two existing methods has demonstrated that the proposed method can provide viable nesting solutions, with maximum print bed utilization ratio and high compactness, considerably quickly. Thus, the process planner can benefit from the time saved, to a certain extent. In the SocialMfg environment, this advantage makes it possible to process many parts quickly. In addition, with such a system, service providers can quickly and easily adjust production plans when additional parts are introduced into the initial batch.
5.2. Multi-Parts Production in SocialMfg Scenario
Recently, SocialMfg has gained significant interest from researchers and manufacturers. It provides a network-based production approach in which distributed service consumers and providers can interact and share resources. In the SocialMfg environment, several print jobs from multiple customers may need to be assigned to a network of FFF 3D printers. In such a scenario, there is a need for software solutions to allocate parts to printers rapidly. The work presented in this paper corresponds in this direction. Indeed, the proposed approach can improve the production rates of FFF 3D printers by packing multiple parts into a single print bed to ensure the efficient use of AM resources.
Some of the assumptions made in this study must be discussed to provide new prospects. In particular, negotiation, order allocation, and resource sharing techniques between multiple service providers have not been studied. However, investigating these mechanisms will respond to major scientific concerns, which will help advance the SocialMfg paradigm. Indeed, in a network of FFF 3D printers, order splitting, and resource sharing might be considered to be a strategic measure to balance production and meet production deadlines. Transferring some workloads from one service provider to another may reduce the maximum processing time. Nevertheless, it should be noted that decomposing a print job into sub-jobs to balance production in AM may not lead to a considerable advantage. Indeed, splitting a job entails dividing the part into numerous bodies, each of which will require an assembly afterward.
6. Conclusions
This paper introduced a multi-part production planning system for a distributed network of FFF 3D printers. Part orientation selection, part-to-printer assignment, and nesting of the parts are carried out successively to minimize the total production time and cost while ensuring part quality. A comparative study verified the performance of the proposed method, and a real-world case study demonstrated its feasibility and added value. The findings of this study indicate that the proposed nesting algorithm, which is based on a rasterization technique and an I-BLF algorithm, exhibits good performance in most cases. Furthermore, with its robustness and relatively low computation time, the proposed method can be employed in a SocialMfg context where multiple parts must be efficiently assigned to distributed AM machines.
Despite its effectiveness, the proposed approach can still be extended in many ways. For instance, this study only considers 2D nesting because of the FFF process, while many AM technologies allow pieces to be stacked vertically. As a result, future investigations could be conducted to provide effective packing solutions for LPBF processes where parts can be stacked on top of each other. Besides, as heuristic algorithms for scheduling can lack generality, future studies could overcome this issue by training a reinforcement learning model or a neural network capable of generating highly efficient AM machine scheduling solutions.
Author Contributions
Conceptualization, I.L.D.M.; funding acquisition, P.J.; methodology, I.L.D.M.; resources, W.G.; supervision, P.J.; visualization, I.L.D.M. and H.S.; writing—original draft, I.L.D.M. and H.S.; writing—review and editing, M.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The research work was funded by the National Natural Science Foundation of China, grant number 51975464.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to Yuanbin Wang, from the State Key Laboratory of Fluid Power and Mechatronic Systems of Zhejiang University in China, and Vassilios Canellidis, from the Laboratory of Advanced Manufacturing Technologies and Testing of the University of Piraeus in Greece, for providing the STL files.
Conflicts of Interest
The authors declare no conflict of interest.
References
- F2792-12a; Standard Terminology for Additive Manufacturing Technologies. ASTM International: West Conshohocken, PA, USA, 2012.
- Thomas-Seale, L.E.J.; Kirkman-Brown, J.C.; Attallah, M.M.; Espino, D.M.; Shepherd, D.E.T. The barriers to the progression of additive manufacture: Perspectives from UK industry. Int. J. Prod. Econ. 2018, 198, 104–118. [Google Scholar] [CrossRef]
- Jiang, P.; Ding, K.; Leng, J. Towards a cyber-physical-social-connected and service-oriented manufacturing paradigm: Social Manufacturing. Manuf. Lett. 2016, 7, 15–21. [Google Scholar] [CrossRef]
- Guo, W.; Li, P.; Yang, M.; Liu, J.; Jiang, P. Social Manufacturing: What are its key fundamentals? IFAC-Pap. OnLine 2020, 53, 65–70. [Google Scholar] [CrossRef]
- Hamalainen, M.; Karjalainen, J. Social manufacturing: When the maker movement meets interfirm production networks. Bus Horiz. 2017, 60, 795–805. [Google Scholar] [CrossRef]
- Markillie, P. A Third Industrial Revolution: Collaborative Manufacturing. The Economist. 2012. Available online: http://web.mit.edu/pie/news/Economist.pdf (accessed on 19 April 2022).
- Zhang, Y.C.; Bernard, A. Grouping parts for multiple parts production in Additive Manufacturing. Variety Management in Manufacturing. Procedia CIRP 2014, 17, 308–313. [Google Scholar] [CrossRef] [Green Version]
- Gogate, A.S.; Pande, S.S. Intelligent layout planning for rapid prototyping. Int. J. Prod. Res. 2008, 46, 5607–5631. [Google Scholar] [CrossRef]
- Manogharan, G.; Wysk, R.A.; Harrysson, O.L.A. Additive manufacturing-integrated hybrid manufacturing and subtractive processes: Economic model and analysis. Int. J. Comput. Integr. Manuf. 2016, 29, 473–488. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Bernard, A.; Harik, R.; Fadel, G. A new method for single-layer-part nesting in additive manufacturing. Rapid Prototyp. J. 2018, 24, 840–854. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, B.; Zeng, Y.; Gu, P. Model layout optimization for solid ground curing rapid prototyping processes. Robot. Comput.-Integr. Manuf. 2002, 18, 41–51. [Google Scholar] [CrossRef]
- Di Angelo, L.; Di Stefano, P.; Guardiani, E. Search for the Optimal Build Direction in Additive Manufacturing Technologies: A Review. J. Manuf. Mater. Process. 2020, 4, 71. [Google Scholar] [CrossRef]
- Byun, H.-S.; Lee, K.H. Determination of the optimal build direction for different rapid prototyping processes using multi-criterion decision making. Robot. Comput.-Integr. Manuf. 2006, 22, 69–80. [Google Scholar] [CrossRef]
- Lan, P.T.; Chou, S.Y.; Chen, L.L.; Gemmill, D. Determining fabrication orientations for rapid prototyping with stereolithography apparatus. Comput.-Aided Des. 1997, 29, 53–62. [Google Scholar] [CrossRef]
- Cheng, W.; Fuh, J.Y.H.; Nee, A.Y.C.; Wong, Y.S.; Loh, H.T.; Miyazawa, T. Multi-objective optimization of part-building orientation in stereolithography. Rapid Prototyp. J. 1995, 1, 12–23. [Google Scholar] [CrossRef]
- Masood, S.H.; Rattanawong, W.; Iovenitti, P. A generic algorithm for a best part orientation system for complex parts in rapid prototyping. J. Mater. Process. Technol. 2003, 139, 110–116. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y. A unit sphere discretization and search approach to optimize building direction with minimized volumetric error for rapid prototyping. Int. J. Adv. Manuf. Technol. 2013, 67, 733–743. [Google Scholar] [CrossRef]
- Qin, Y.C.; Qi, Q.F.; Shi, P.Z.; Scott, P.J.; Jiang, X.Q. Automatic determination of part build orientation for laser powder bed fusion. Virtual Phys. Prototyp. 2021, 16, 29–49. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Bernard, A.; Gupta, R.K.; Harik, R. Feature based building orientation optimization for additive manufacturing. Rapid Prototyp. J. 2016, 22, 358–376. [Google Scholar] [CrossRef]
- Li, X.L.; Huang, Y.L.; Tan, Q.; Chen, H.P. Scheduling unrelated parallel batch processing machines with non-identical job sizes. Comput. Oper. Res. 2013, 40, 2983–2990. [Google Scholar] [CrossRef]
- Arroyo, J.E.C.; Leung, J.Y.T. Scheduling unrelated parallel batch processing machines with non-identical job sizes and unequal ready times. Comput. Oper. Res. 2017, 78, 117–128. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Ha, S.; Ma, J.; Kim, N. Multi-objective optimization analysis for part-to-Printer assignment in a network of 3D fused deposition modeling. J. Manuf. Syst. 2017, 43, 35–46. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, Y.; Hu, Q.; Zhou, S.H.; Ma, L.; Lim, M.K. The influence of additive manufacturing on the configuration of make-to-order spare parts supply chain under heterogeneous demand. Int. J. Prod. Res. 2019, 57, 3622–3641. [Google Scholar] [CrossRef]
- Zhang, J.M.; Yao, X.F.; Li, Y. Improved evolutionary algorithm for parallel batch processing machine scheduling in additive manufacturing. Int. J. Prod. Res. 2020, 58, 2263–2282. [Google Scholar] [CrossRef]
- Cadiou, T.; Demoly, F.; Gomes, S. A Multi-Part Production Planning Framework for Additive Manufacturing of Unrelated Parallel Fused Filament Fabrication 3D Printers. Designs 2022, 6, 11. [Google Scholar] [CrossRef]
- Wu, S.; Kay, M.G.; King, R.E.; Vila-Parrish, A.R.; Fitts, E.P.; Warsing, D.P. Multi-objective Optimization of 3D Packing Problem in Additive Manufacturing. In Proceedings of the IIE Annual Conference, Montréal, QC, Canada, 31 May–3 June 2014. [Google Scholar]
- Zhang, Y.C.; Gupta, R.K.; Bernard, A. Two-dimensional placement optimization for multi-parts production in additive manufacturing. Robot. Comput.-Integr. Manuf. 2016, 38, 102–117. [Google Scholar] [CrossRef]
- Wodziak, J.R.; Fadel, G.M.; Kirschman, C. A genetic algorithm for optimizing multiple part placement to reduce build time. In Proceedings of the Fifth International Conference on Rapid Prototyping, Dayton, OH, USA, 12–15 June 1994; pp. 201–210. [Google Scholar]
- Canellidis, V.; Dedoussis, V.; Mantzouratos, N.; Sofianopoulou, S. Pre-processing methodology for optimizing stereolithography apparatus build performance. Comput. Ind. 2006, 57, 424–436. [Google Scholar] [CrossRef]
- Canellidis, V.; Giannatsis, J.; Dedoussis, V. Efficient parts nesting schemes for improving stereolithography utilization. Comput.-Aided Des. 2013, 45, 875–886. [Google Scholar] [CrossRef]
- Wang, Y.B.; Pai, Z.; Xun, X.; Yang, H.Y.; Jun, Z. Production planning for cloud-based additive manufacturing-A computer vision-based approach. Robot. Comput.-Integr. Manuf. 2019, 58, 145–157. [Google Scholar] [CrossRef]
- Li, Q.; Kucukkoc, I.; Zhang, D.Z. Production planning in additive manufacturing and 3D printing. Comput. Oper. Res. 2017, 83, 157–172. [Google Scholar] [CrossRef]
- Bennell, J.A.; Oliveira, J.F. The geometry of nesting problems: A tutorial. Eur. J. Oper. Res. 2008, 184, 397–415. [Google Scholar] [CrossRef]
- Allaire, G.; Bihr, M.; Bogosel, B. Support optimization in additive manufacturing for geometric and thermo-mechanical constraints. Struct. Multidiscip. Optim. 2020, 61, 2377–2399. [Google Scholar] [CrossRef] [Green Version]
- Das, P.; Mhapsekar, K.; Chowdhury, S.; Samant, R.; Anand, S. Selection of build orientation for optimal support structures and minimum part errors in additive manufacturing. Comput.-Aided Des. Appl. 2017, 14, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Pande, S.S.; Kumar, S. A generative process planning system for parts produced by rapid prototyping. Int. J. Prod. Res. 2008, 46, 6431–6460. [Google Scholar] [CrossRef]
- Pandey, P.M.; Reddy, N.V.; Dhande, S.G. Part deposition orientation studies in layered manufacturing. J. Mater. Process. Technol. 2007, 185, 125–131. [Google Scholar] [CrossRef]
- Della Croce, F.; Scatamacchia, R. The Longest Processing Time rule for identical parallel machines revisited. J. Sched. 2020, 23, 163–176. [Google Scholar] [CrossRef] [Green Version]
- Samet, H.; Tamminen, M. Computing Geometric-Properties of Images Represented by Linear Quadtrees. IEEE Trans. Pattern Anal. Mach. Intell. 1985, 7, 229–240. [Google Scholar] [CrossRef] [PubMed]
- Chazelle, B. The Bottom-Left Bin-Packing Heuristic—An Efficient Implementation. IEEE Trans. Comput. 1983, 32, 697–707. [Google Scholar] [CrossRef]
- Makanda, I.L.D.; Jiang, P. A Web-based Generative Process Planning System for FDM-based Additive Manufacturing. IFAC-Pap. Online 2020, 53, 83–88. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).