Pick–and–Place Trajectory Planning and Robust Adaptive Fuzzy Tracking Control for Cable–Based Gangue–Sorting Robots with Model Uncertainties and External Disturbances
Abstract
1. Introduction
1.1. Pick–and–Place Trajectory Planning
1.2. Pick–and–Place Trajectory Tracking Control
- Proposing a four-stage trajectory planning scheme for the end–grab of the cable–based gangue–sorting robot while taking account the effect of the synchronous movement of the gangues with the belt conveyor as well as the location of the gangue recovery bin;
- Developing a robust adaptive fuzzy control strategy in the task space to track a given trajectory for the cable–based gangue–sorting robot in the presence of model uncertainties, varying payloads, and external disturbances while guaranteeing closed-loop control system stability;
- Demonstrating the validity of the proposed pick–and–place trajectory planning scheme and the robust adaptive fuzzy tracking control strategy through numerical simulation.
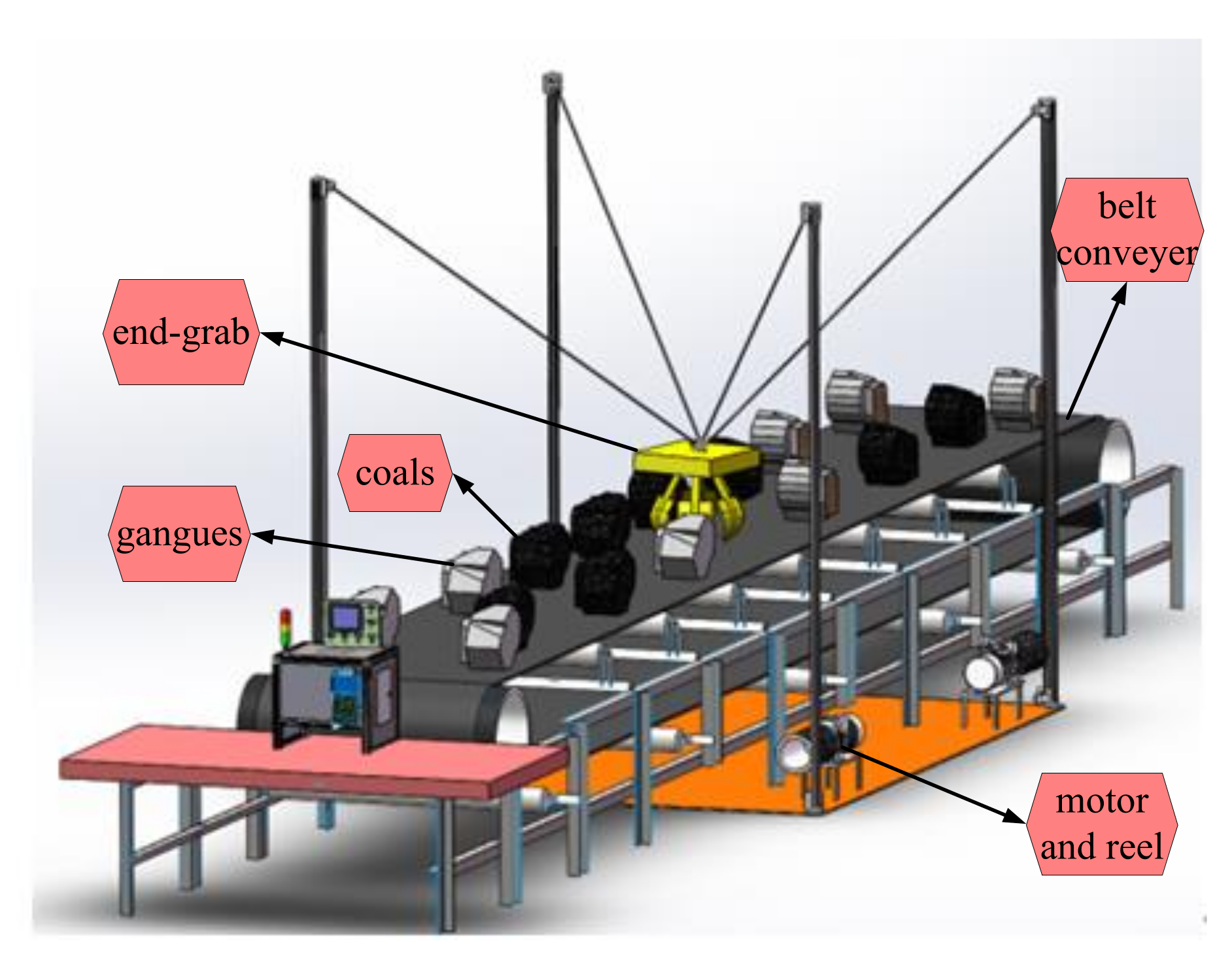
2. Description and Modeling of a Cable-Based Gangue-Sorting Robot
2.1. Description of the Robot
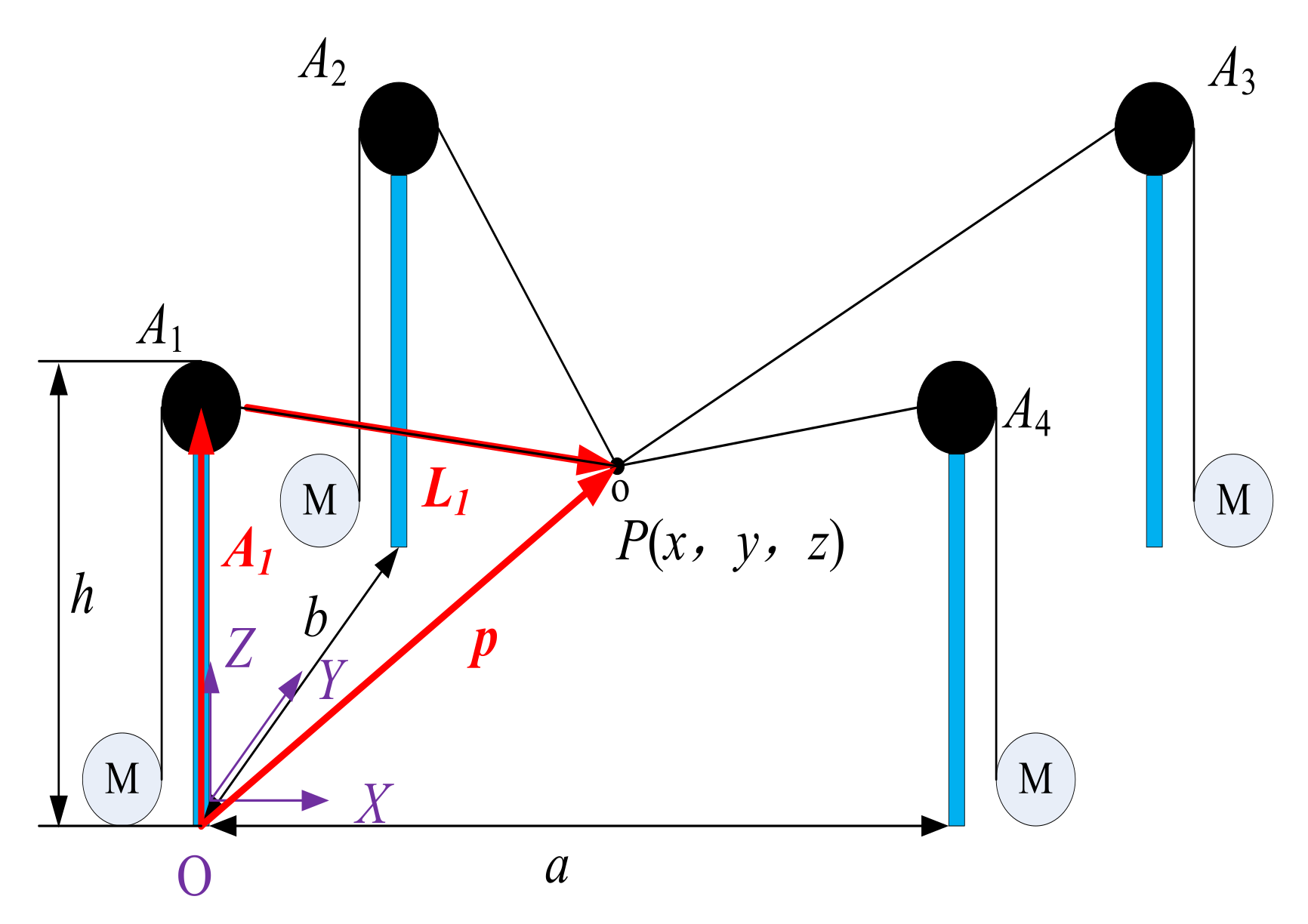
2.2. Modeling of the Robot
3. Control System
3.1. Proposed Trajectory Planner
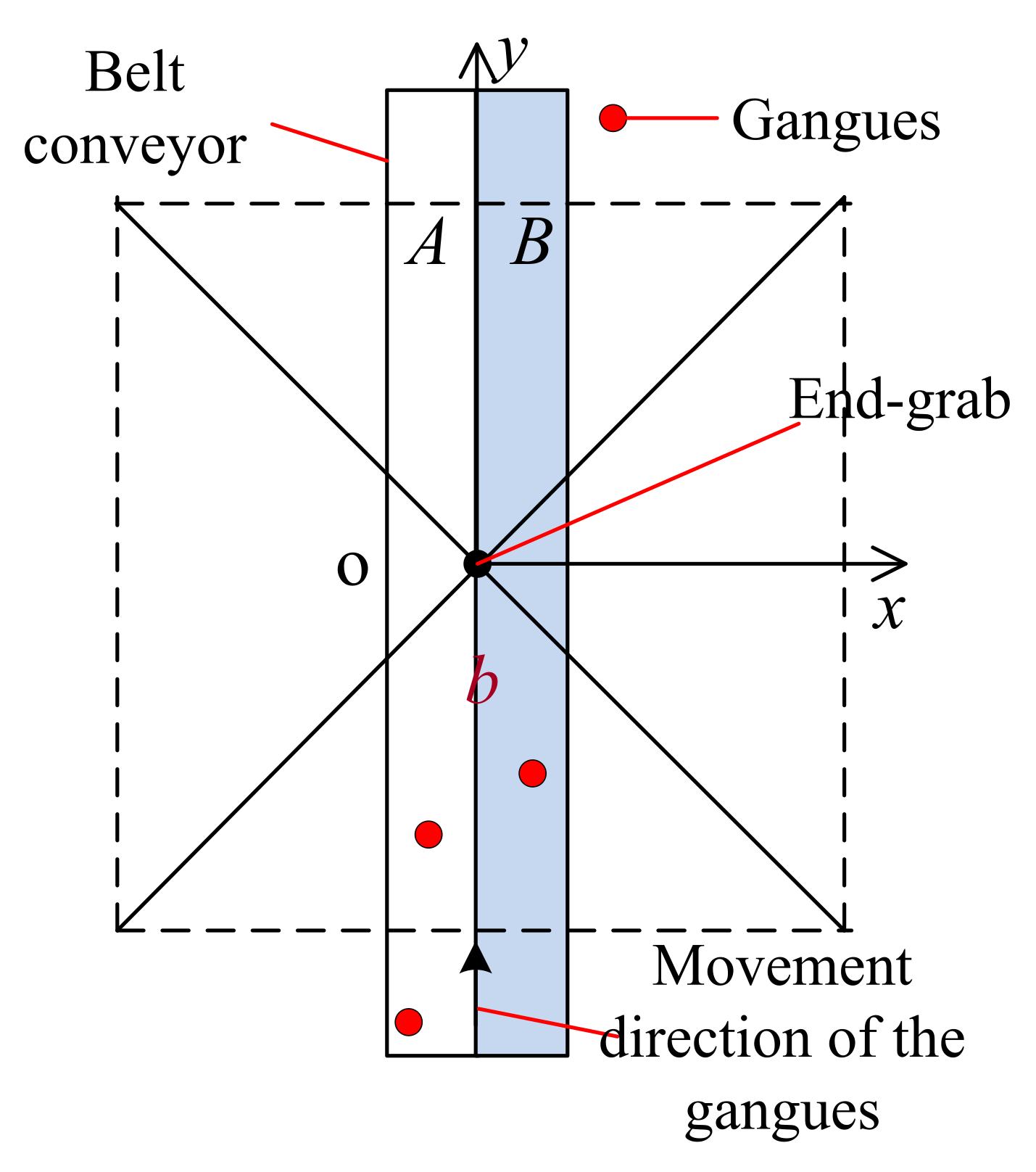
3.1.1. Requirements for Trajectory Planning
- (1)
- Starting period: the movement velocity of the end–grab increases from 0 to a predetermined constant speed while the robot starts for the first time. There inevitably is an acceleration stage for the end–grab, and therefore, the motion state of the end–grab should be continuous and smooth.
- (2)
- Preparation period: in order to avoid impact during the process of picking the target gangue, the end–grab and the target gangue to be grabbed should be in a relatively static state. Therefore, there needs to be a constant linear motion along the movement direction of the target gangue.
- (3)
- Picking period: no impact can occur during the operation of carrying the picked gangue after the target gangue is captured by the end–grab. In addition, in order to ensure that the captured gangue can fall into the gangue bin at a fixed direction and speed, the end–grab should also have a uniform linear motion at this stage.
- (4)
- Placing period: in order to avoid repeated acceleration leading to a discontinuous trajectory for the end–grab, the end–grab directly enters stage (2) to perform the pick–and–place operation of the next target gangue after the current picked gangue is placed in the gangue recovery bin.
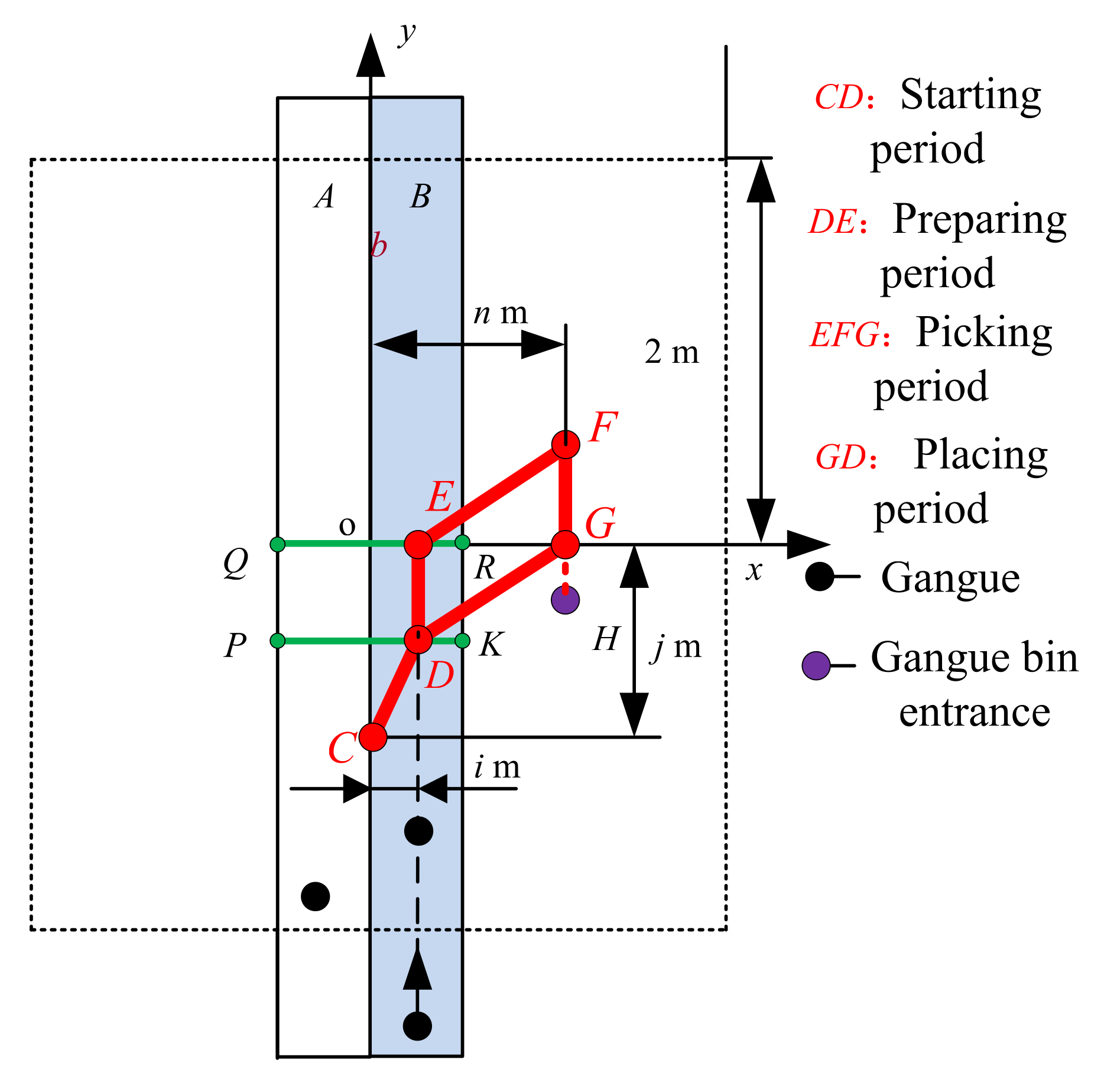
3.1.2. Trajectory Planning Scheme
- (1)
- Determination of the end-grab position and zero position
- (2)
- Determination of the starting period and preparation period
- (3)
- Determination of the picking period
- (4)
- Determination of the placing period
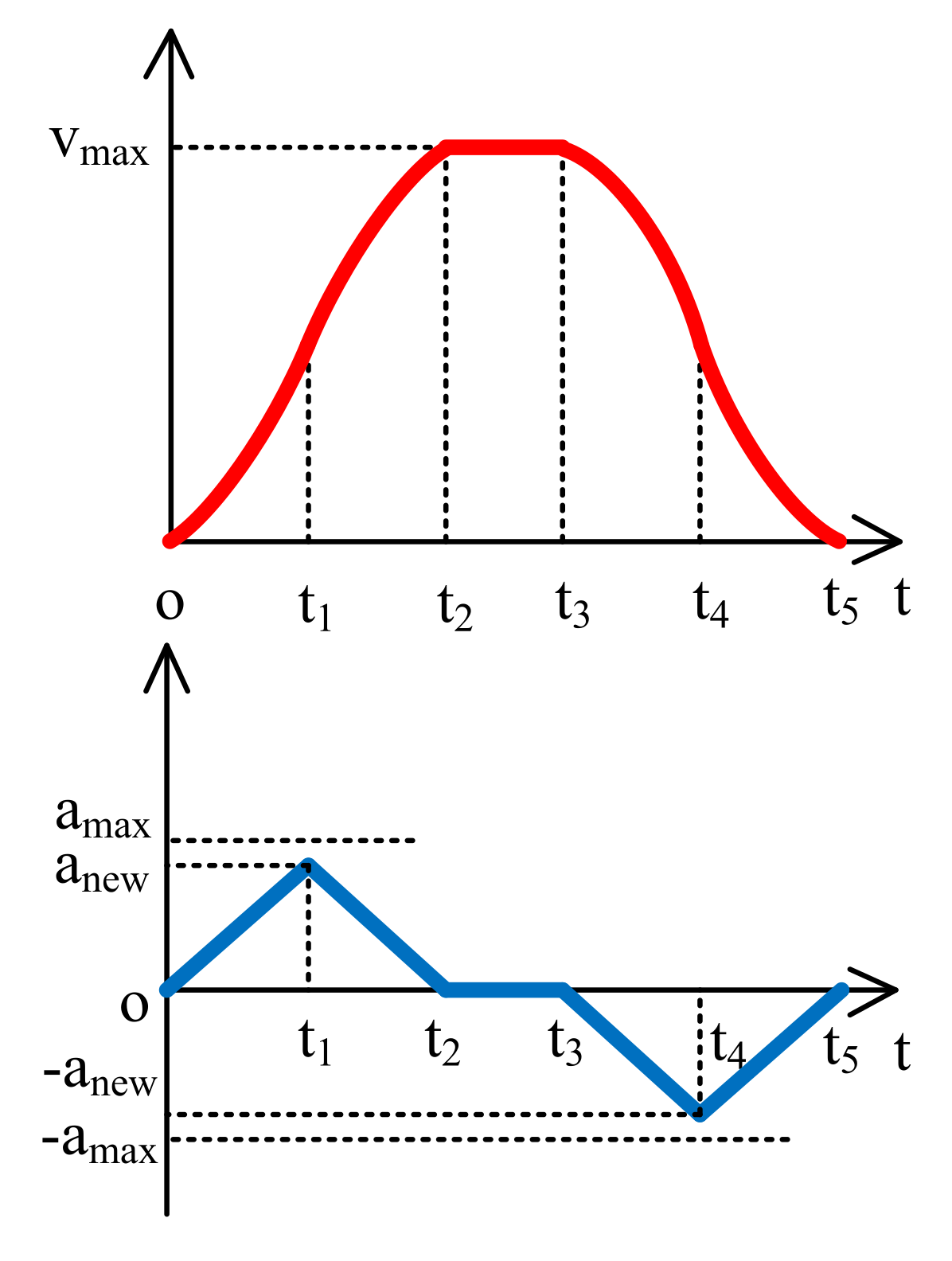
3.1.3. Implementation Methods of Each Trajectory for the Four Periods
- (1)
- S-shaped acceleration/deceleration algorithm
- (2)
- Quintic polynomials
3.2. Proposed Controller
4. Simulation Study
4.1. Generation of the Proposed Pick–and–Place Trajectory
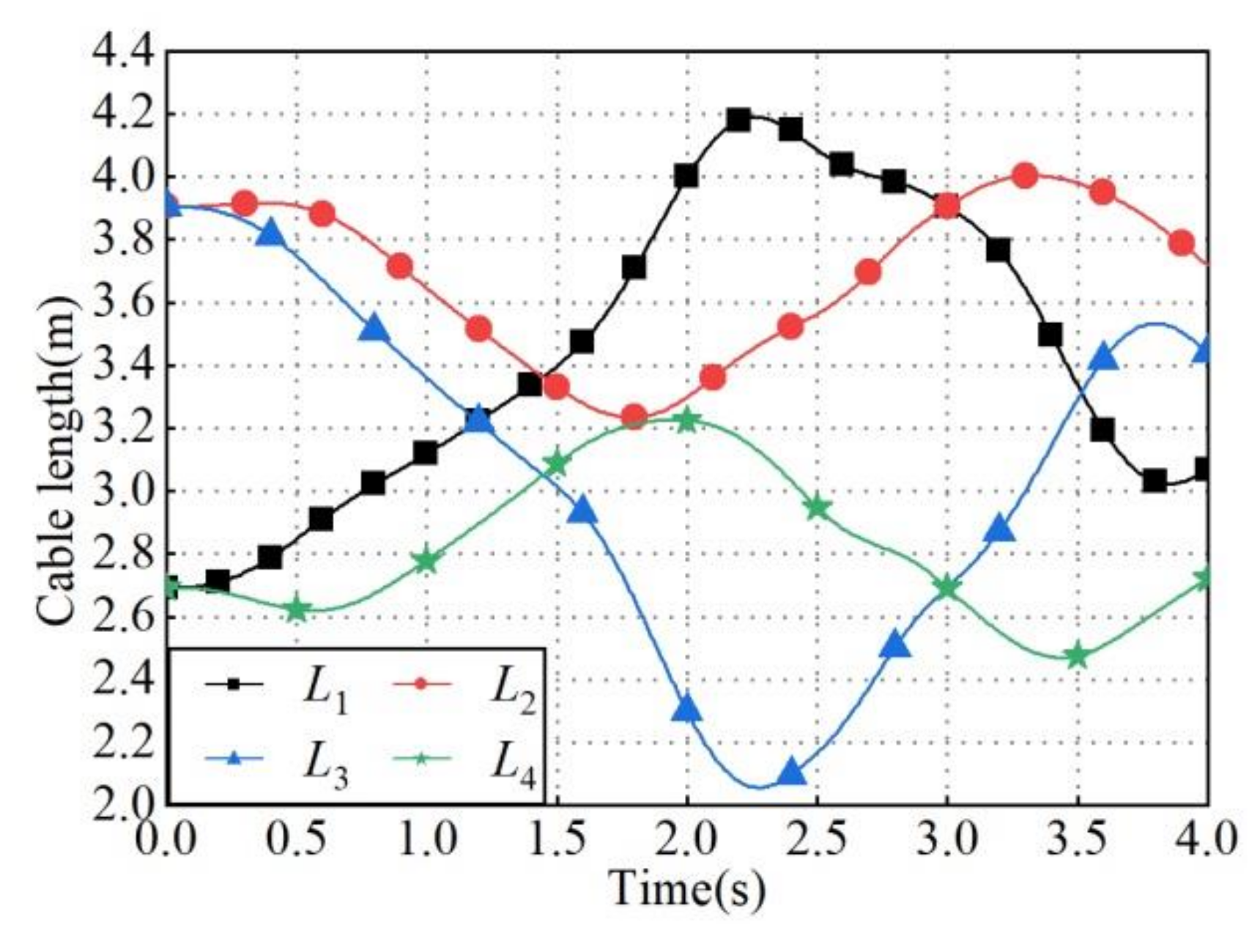
4.2. Control System Validation
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, P.; Qiao, X.Z.; Zhang, X.H. Stability sensitivity for a cable–based coal–gangue picking robot based on grey relational analysis. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211059729. [Google Scholar] [CrossRef]
- Wang, R.; Xie, Y.; Chen, X.; Li, Y. Kinematic and dynamic modeling and workspace analysis of a suspended cable-driven parallel robot for Schönflies motions. Machines 2022, 10, 451. [Google Scholar] [CrossRef]
- Tang, X.Q. An overview of the development for cable-driven parallel manipulator. Adv. Mech. Eng. 2014, 6, 823028. [Google Scholar] [CrossRef]
- Zarebidoki, M.; Dhupia, J.S.; Xu, W. A review of cable-driven parallel robots: Typical configurations, analysis techniques, and control methods. IEEE Robot. Autom. Mag. 2022, 2–19. [Google Scholar] [CrossRef]
- Liu, Z.H.; Tang, X.Q.; Shao, Z. Research on longitudinal vibration characteristic of the six-cable-driven parallel manipulator in FAST. Adv. Mech. Eng. 2013, 2013, 547416. [Google Scholar] [CrossRef]
- Su, Y.; Qiu, Y.; Liu, P.; Tian, J.W.; Wang, Q.; Wang, X.G. Dynamic modeling, workspace analysis and multi-objective structural optimization of the large-span high-speed cable-driven parallel camera robot. Machines 2022, 10, 565. [Google Scholar] [CrossRef]
- Zi, B.; Zhang, L.; Zhang, D.; Qian, S. Modeling, analysis, and co-simulation of cable parallel manipulators for multiple cranes. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 1693–1707. [Google Scholar] [CrossRef]
- Russo, M.; Ceccarelli, M. Analysis of a wearable robotic system for ankle rehabilitation. Machines 2020, 8, 48. [Google Scholar] [CrossRef]
- Tourajizadeh, H.; Yousefzadeh, M.; Khalaji, A.K.; Bamdad, M. Design, modeling and control of a simulator of an aircraft maneuver in the wind tunnel using cable robot. Int. J. Control Autom. Syst. 2022, 20, 1671–1681. [Google Scholar] [CrossRef]
- Bosscher, P.; Riechel, A.T.; Ebert-Uphoff, I. Wrench-feasible workspace generation for cable-driven robots. IEEE Trans. Robot. 2006, 22, 890–902. [Google Scholar] [CrossRef]
- Pham, C.B.; Yeo, S.H.; Yang, G. Workspace analysis of fully restrained cable-driven manipulators. Robot. Auton. Syst. 2009, 57, 901–912. [Google Scholar] [CrossRef]
- Kieu, V.N.D.; Huang, S.C. Dynamic and wrench-feasible workspace analysis of a cable-driven parallel robot considering a nonlinear cable tension model. Appl. Sci. 2022, 12, 244. [Google Scholar] [CrossRef]
- Liu, P.; Qiu, Y.Y.; Su, Y. A new hybrid force-position measure approach on the stability for a camera robot. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 2508–2516. [Google Scholar] [CrossRef]
- Wei, H.L.; Qiu, Y.Y.; Sheng, Y. An approach to evaluate stability for cable-driven parallel camera robots with hybrid tension-stiffness properties. Int. J. Adv. Robot. Syst. 2015, 12, 185. [Google Scholar] [CrossRef]
- Su, Y.; Qiu, Y.Y.; Wei, H.L. Dynamic modeling and tension optimal distribution of cable-driven parallel robots considering cable mass and inertia force effects. Eng. Mech. 2016, 33, 231–239. [Google Scholar] [CrossRef]
- Su, Y.; Qiu, Y.Y.; Sheng, Y. Optimal cable tension distribution of the high-speed redundant driven camera robots considering cable sag and inertia effects. Adv. Mech. Eng. 2014, 2014, 729020. [Google Scholar] [CrossRef]
- Liu, P.; Qiu, Y.Y.; Su, Y.; Chang, J.T. On the minimum cable tensions for the cable–based parallel robots. J. Appl. Math. 2014, 2014, 350492. [Google Scholar] [CrossRef]
- Amine, L.M.; Giuseppe, C.; Said, Z. On the optimal design of cable driven parallel robot with a prescribed workspace for upper limb rehabilitation tasks. J. Bionic Eng. 2019, 16, 503–513. [Google Scholar] [CrossRef]
- Yao, R.; Tang, X.; Wang, J.; Huang, P. Dimensional optimization design of the four-cable-driven parallel manipulator in FAST. IEEE/ASME Trans. Mechatron. 2010, 15, 932–941. [Google Scholar] [CrossRef]
- Zhang, F.; Shang, W.; Zhang, B.; Cong, S. Design optimization of redundantly actuated cable-driven parallel robots for automated warehouse system. IEEE Access 2020, 8, 56867–56879. [Google Scholar] [CrossRef]
- Kawamura, S.; Kino, H.; Won, C. High-speed manipulation by using parallel wire-driven robots. Robotica 2000, 18, 13–21. [Google Scholar] [CrossRef]
- Qian, S.; Bao, K.L.; Zi, B.; Zhu, W.D. Dynamic trajectory planning for a three degrees-of-freedom cable-driven parallel robot using quintic B-splines. J. Mech. Design 2020, 142, 073301. [Google Scholar] [CrossRef]
- Zhao, T.; Zi, B.; Qian, S.; Zhao, J.H. Algebraic method-based point-to-point trajectory planning of an under-constrained cable-suspended parallel robot with variable angle and height cable mast. Chin. J. Mech. Eng. 2020, 33, 073301. [Google Scholar] [CrossRef]
- Xu, J.J.; Park, K.S. Moving obstacle avoidance for cable-driven parallel robots using improved RRT. Microsyst. Technol. 2020, 27, 2281–2292. [Google Scholar] [CrossRef]
- Jiang, X.; Barnett, E.; Gosselin, C. Dynamic point-to-point trajectory planning beyond the static workspace for six-DOF cable-suspended parallel robots. IEEE Trans. Robot. 2018, 34, 781–793. [Google Scholar] [CrossRef]
- Hwang, S.W.; Bak, J.H.; Yoon, J.; Park, J.H.; Park, J.O. Trajectory generation to suppress oscillations in under-constrained cable-driven parallel robots. J. Mech. Sci. Technol. 2016, 30, 5689–5697. [Google Scholar] [CrossRef]
- Jiang, M.; Yang, Z.M.; Li, Y.; Sun, Z.; Zi, B. Smooth Trajectory Planning for a Cable-Driven Waist Rehabilitation Robot Using Quintic NURBS. In Intelligent Robotics and Applications. ICIRA 2021. Lecture Notes in Computer Science; Liu, X.J., Nie, Z., Yu, J., Xie, F., Song, R., Eds.; Springer: Cham, Switzerland, 2021; p. 13013. [Google Scholar] [CrossRef]
- Idá, E.; Briot, S.; Carricato, M. Identification of the inertial parameters of underactuated cable-driven parallel robots. Mech. Mach. Theory 2022, 167, 104504. [Google Scholar] [CrossRef]
- Dion-Gauvin, P.; Gosselin, C. Beyond-the-static-workspace point-to-point trajectory planning of a 6-DoF cable-suspended mechanism using oscillating SLERP. Mech. Mach. Theory 2022, 174, 104894. [Google Scholar] [CrossRef]
- Scalera, L.; Gasparetto, A.; Zanotto, D. Design and experimental validation of a 3-DOF underactuated pendulum-like robot. IEEE/ASME Trans. Mechatron. 2019, 25, 217–228. [Google Scholar] [CrossRef]
- Zi, B.; Sun, H.H.; Zhang, D. Design, analysis and control of a winding hybrid-driven cable parallel manipulator. Robot. Comput. Integr. Manuf. 2017, 48, 196–208. [Google Scholar] [CrossRef]
- Fang, S.Q.; Franitza, D.; Torlo, M.; Bekes, F.; Hiller, M. Motion control of a tendon-based parallel manipulator using optimal tension distribution. IEEE/ASME Trans. Mechatron. 2004, 9, 561–568. [Google Scholar] [CrossRef]
- Ji, H.; Shang, W.W.; Cong, S. Adaptive synchronization control of cable-driven parallel robots with uncertain kinematics and dynamics. IEEE T Ind. Electron. 2021, 68, 8444–8454. [Google Scholar] [CrossRef]
- Khalilpour, S.A.; Khorrambakht, R.; Taghirad, H.D.; Cardou, P. Robust cascade control of a deployable cable-driven robot. Mech. Syst. Signal Processing 2019, 127, 513–530. [Google Scholar] [CrossRef]
- Jia, H.Y.; Shang, W.W.; Xie, F.; Zhang, B.; Cong, S. Second-order sliding-mode-based synchronization control of cable-driven parallel robots. IEEE/ASME Trans. Mechatron. 2020, 25, 383–394. [Google Scholar] [CrossRef]
- Santos, J.C.; Gouttefarde, M.; Chemori, A. A nonlinear model predictive control for the position tracking of cable-driven parallel robots. IEEE Trans. Robot. 2022, 38, 2597–2616. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Liu, L.F.; Yuan, M.X.; Di, Q.X.; Chen, B. Time-delay control using a novel nonlinear adaptive law for accurate trajectory tracking of cable-driven robots. IEEE Trans. Ind. Inform. 2020, 16, 5234–5243. [Google Scholar] [CrossRef]
- Aflakiyan, A.; Bayani, H.; Masouleh, M.T. Computed torque control of a cable suspended parallel robot. In Proceedings of the 2015 3rd RSI International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 7–9 October 2015; pp. 749–754. [Google Scholar] [CrossRef]
- Wang, T.C.; Tong, S.C.; Yi, J.Q.; Li, H.Y. Adaptive inverse control of cable-driven parallel system based on type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 2015, 23, 1803–1816. [Google Scholar] [CrossRef]
- Izadbakhsh, A.; Asl, H.J.; Narikiyo, T. Robust adaptive control of over-constrained actuated cable-driven parallel robots. In Cable-Driven Parallel Robots; Pott, A., Bruckmann, T., Eds.; Springer: Cham, Switzerland, 2019; Volume 74, pp. 209–220. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Liu, L.F.; Yuan, M.X.; Di, Q.X.; Chen, B.; Wu, H.T. A new model-free robust adaptive control of cable-driven robots. Int. J. Control Autom. Syst. 2021, 19, 3209–3222. [Google Scholar] [CrossRef]
- Oh, S.-R.; Agrawal, S.K. Cable suspended planar robots with redundant cables: Controllers with positive tensions. IEEE Trans. Robot. 2005, 21, 457–465. [Google Scholar] [CrossRef]
- Shao, Z.F.; Tang, X.Q.; Wang, L.P.; Chen, X. Dynamic modeling and wind vibration control of the feed support system in FAST. Nonlinear Dyn. 2012, 67, 965–985. [Google Scholar] [CrossRef]
- Duan, X.C.; Mi, J.W.; Zhao, Z. Vibration isolation and trajectory following control of a cable suspended stewart platform. Machines 2016, 4, 20. [Google Scholar] [CrossRef]
- Schenk, C.; Bülthoff, H.H.; Masone, C. Robust adaptive sliding mode control of a redundant cable driven parallel robot. In Proceedings of the 2015 19th International Conference on System Theory, Control and Computing (ICSTCC), Cheile Gradistei, Romania, 14–16 October 2015; pp. 427–434. [Google Scholar] [CrossRef]
- Jafarlou, F.; Peimani, M.; Lotfivand, N. Fractional order adaptive sliding-mode finite time control for cable-suspended parallel robots with unknown dynamics. Int. J. Dynam. Control. 2022, 1–11. [Google Scholar] [CrossRef]
- Hosseini, M.I.; Khalilpour, S.A.; Taghirad, H.D. Practical robust nonlinear PD controller for cable-driven parallel manipulators. Nonlinear Dyn. 2021, 106, 405–424. [Google Scholar] [CrossRef]
- Aghaseyedabdollah, M.; Abedi, M.; Pourgholi, M. Supervisory adaptive fuzzy sliding mode control with optimal Jaya based fuzzy PID sliding surface for a planer cable robot. Soft Comput. 2022, 26, 8441–8458. [Google Scholar] [CrossRef]
- Inel, F.; Medjbouri, A.; Carbone, G. A non-linear continuous-time generalized predictive control for a planar cable-driven parallel robot. Actuators 2021, 10, 97. [Google Scholar] [CrossRef]
- Zi, B. Fuzzy Control System Design and Analysis for Completely Restrained Cable-Driven Manipulators. In Fuzzy Logic: Controls, Concepts, Theories and Applications; Dadios, E., Ed.; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef][Green Version]
- Miermeister, P.; Pott, A. Modelling and real-time dynamic simulation of the cable-driven parallel robot IPAnema. In New Trends in Mechanism Science. Mechanisms and Machine Science; Pisla, D., Ceccarelli, M., Husty, M., Corves, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 5. [Google Scholar] [CrossRef]
- Korayem, M.H.; Yousefzadeh, M.; Beyranvand, B. Dynamics and control of a 6-dof cable-driven parallel robot with visco-elastic cables in presence of measurement noise. J. Intell. Robot. Syst 2017, 88, 73–95. [Google Scholar] [CrossRef]
- Korayem, M.H.; Yousefzadeh, M.; Manteghi, S. Dynamics and input–output feedback linearization control of a wheeled mobile cable-driven parallel robot. Multibody Syst. Dyn. 2017, 40, 55–73. [Google Scholar] [CrossRef]
- Caverly, R.J.; Forbes, J.R. Dynamic modeling and noncollocated control of a flexible planar cable-driven manipulator. IEEE Trans. Robot. 2014, 30, 1386–1397. [Google Scholar] [CrossRef]
- Fang, S.X.; Cao, J.G.; Cheng, W.D. Study on high-speed and smooth transfer of robot motion trajectory based on modified S-shaped acceleration/deceleration algorithm. IEEE Access 2020, 8, 199747–199758. [Google Scholar] [CrossRef]
- Ni, H.P.; Ji, S.; Liu, Y.N.; Ye, Y.X.; Zhang, C.R.; Chen, J.W. Velocity planning method for position–velocity–time control based on a modified S-shaped acceleration/deceleration algorithm. Int. J. Adv. Robot. Syst. 2022, 19, 17298814211072418. [Google Scholar] [CrossRef]
- Lu, S.; Ding, B.X.; Li, Y.M. Minimum-jerk trajectory planning pertaining to a translational 3-degree-of-freedom parallel manipulator through piecewise quintic polynomials interpolation. Adv. Mech. Eng. 2020, 12, 1687814020913667. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, G.Y.; Lin, S.X.; Gao, J. Adaptive fuzzy computed-torque control for robot manipulator with uncertain dynamics. Int. J. Adv. Robot. Syst. 2012, 9, 237. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, L.J.; Wu, C.W.; Li, H.Y.; Du, H.P. Adaptive fuzzy control for nonstrict-feedback systems with input saturation and output constraint. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1–12. [Google Scholar] [CrossRef]
- Babaghasabha, R.; Khosravi, M.A.; Taghirad, H.D. Adaptive robust control of fully constrained cable robots: Singular perturbation approach. Nonlinear Dyn. 2016, 85, 607–620. [Google Scholar] [CrossRef]
- Liu, P.; Qiu, Y.Y. Approach with a hybrid force-position property to assessing the stability for camera robots. J. Xidian Univ. 2016, 43, 87–93. [Google Scholar] [CrossRef]

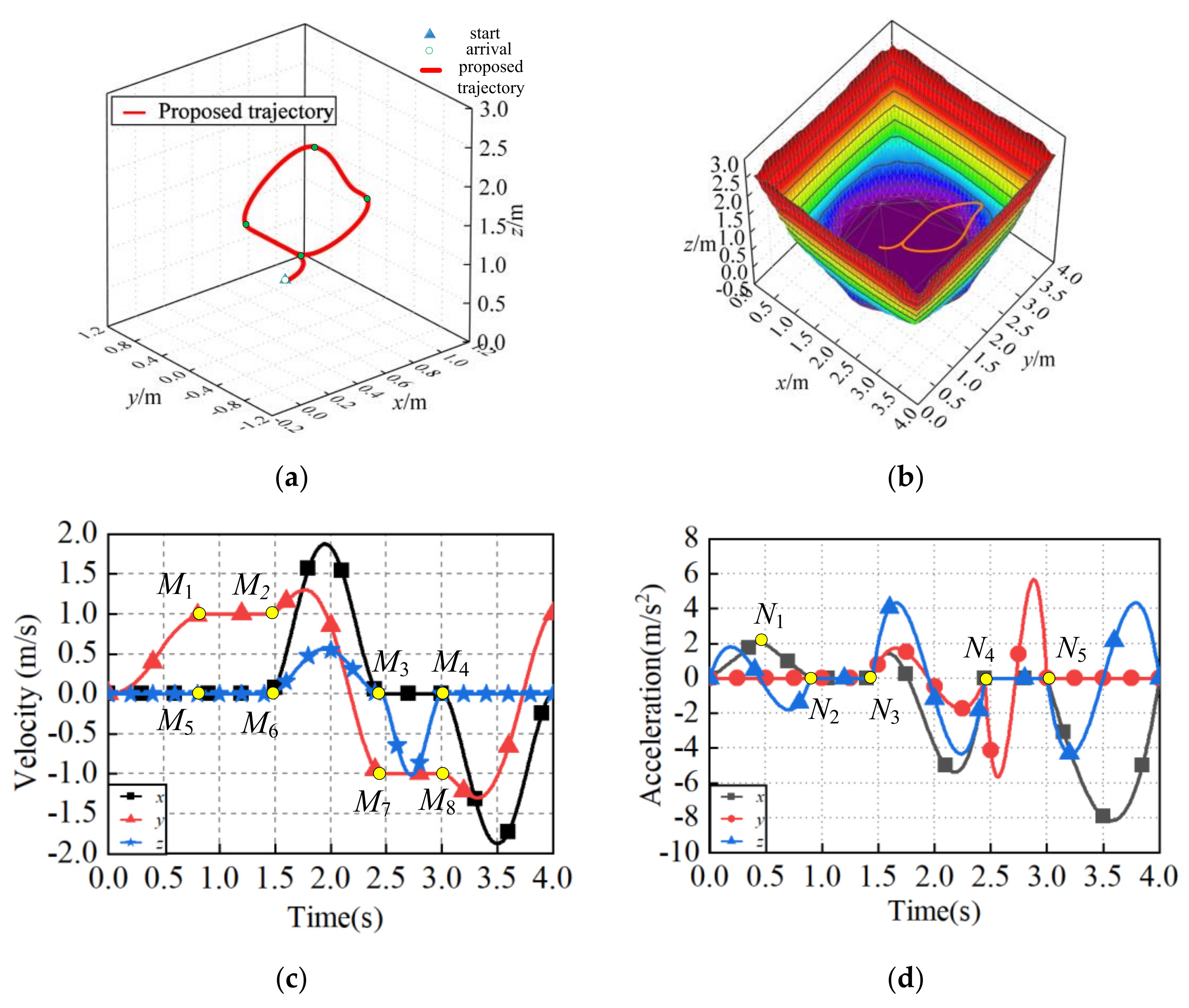
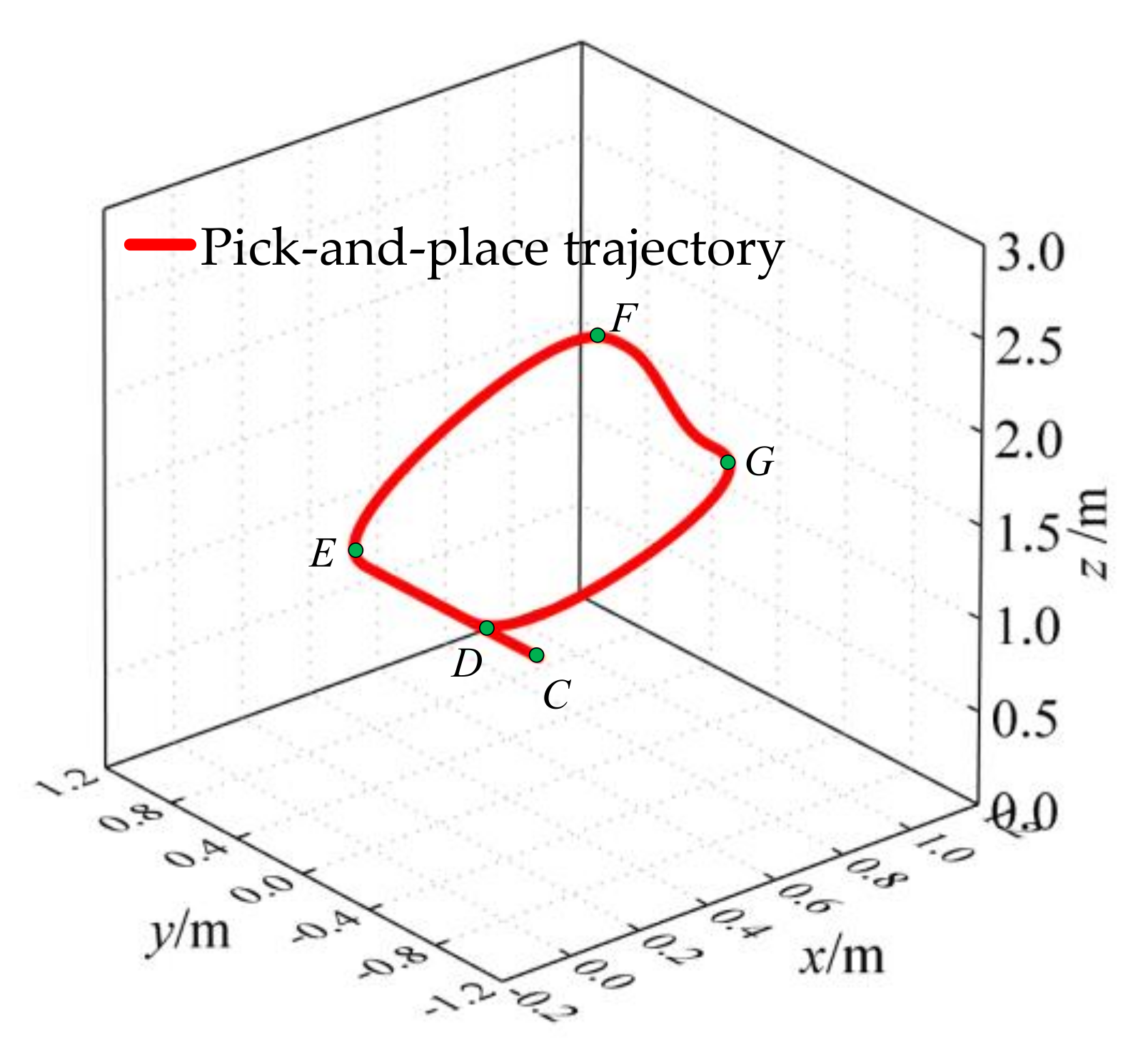
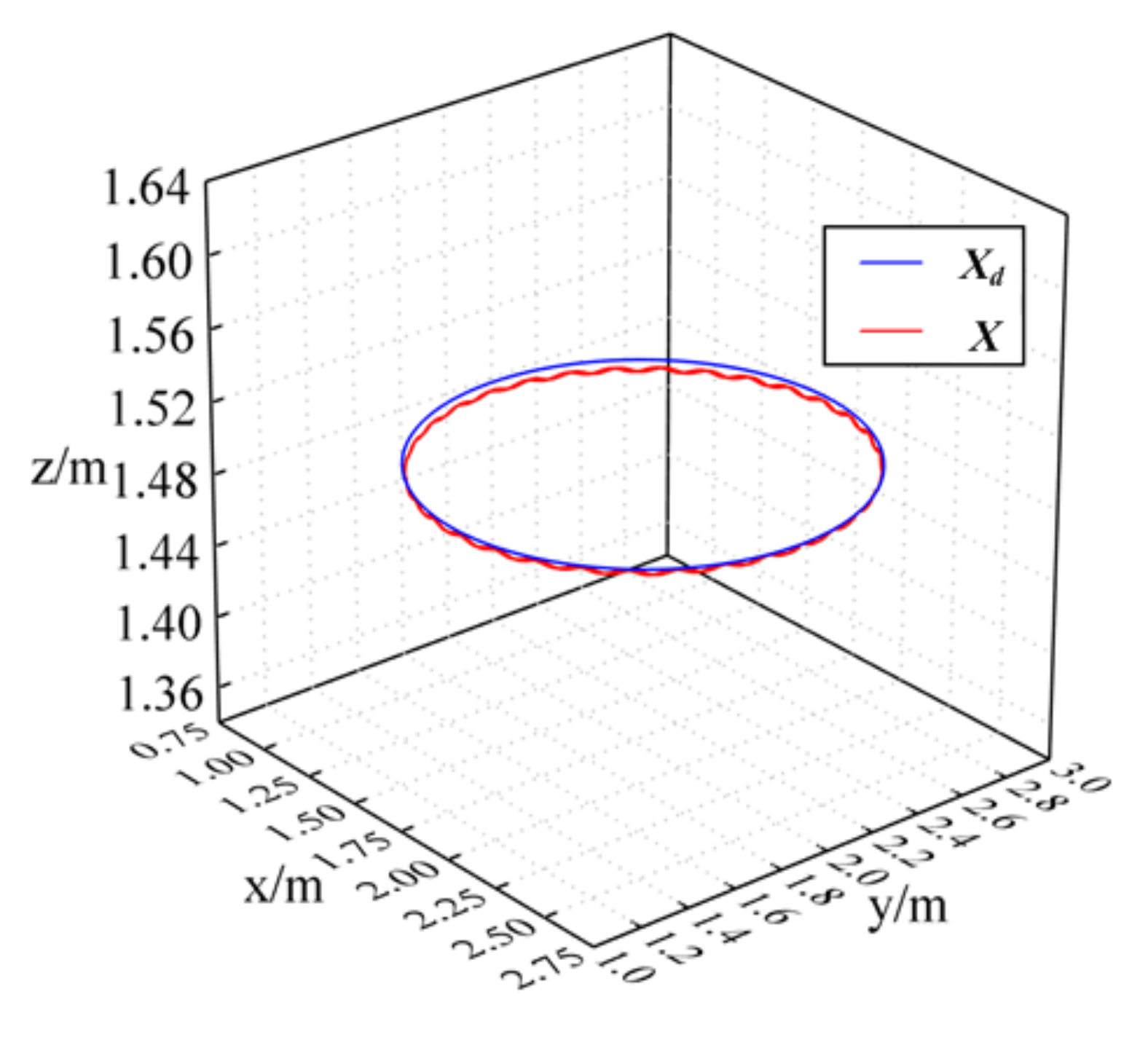
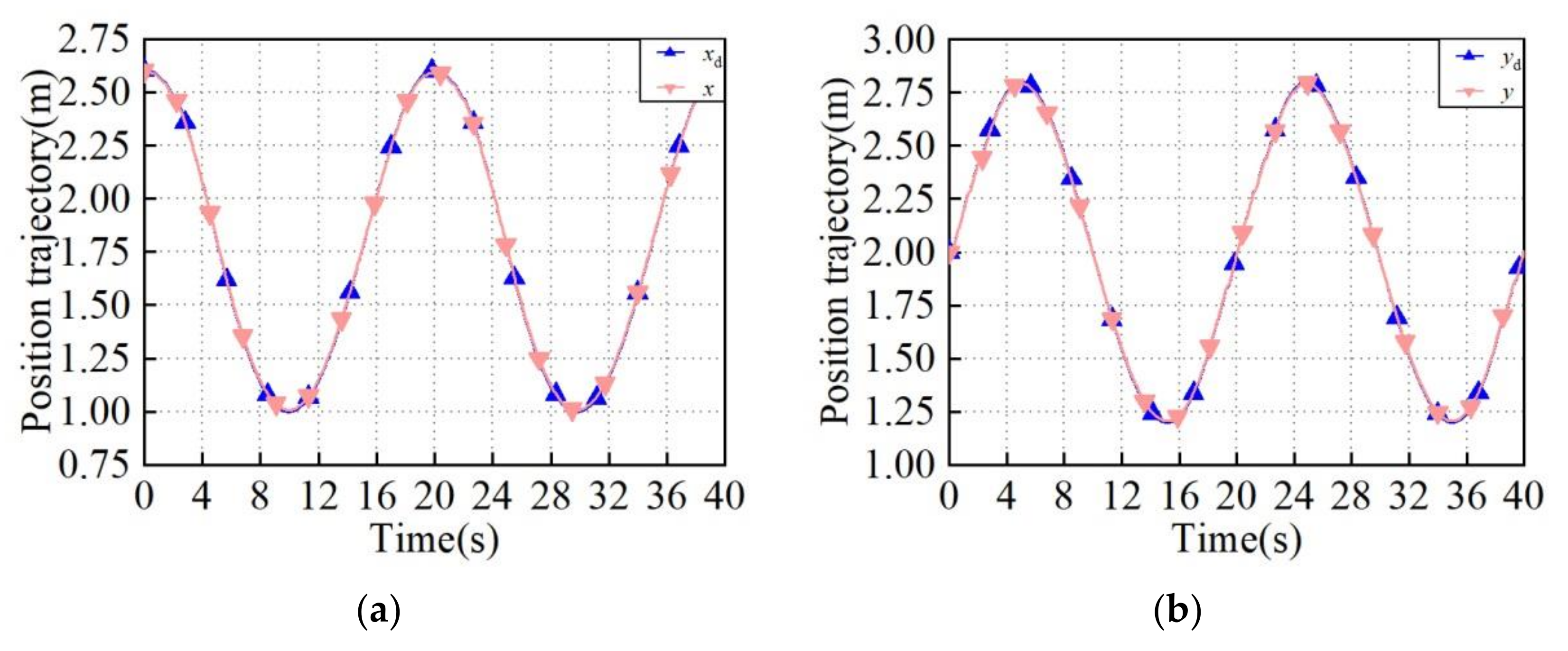
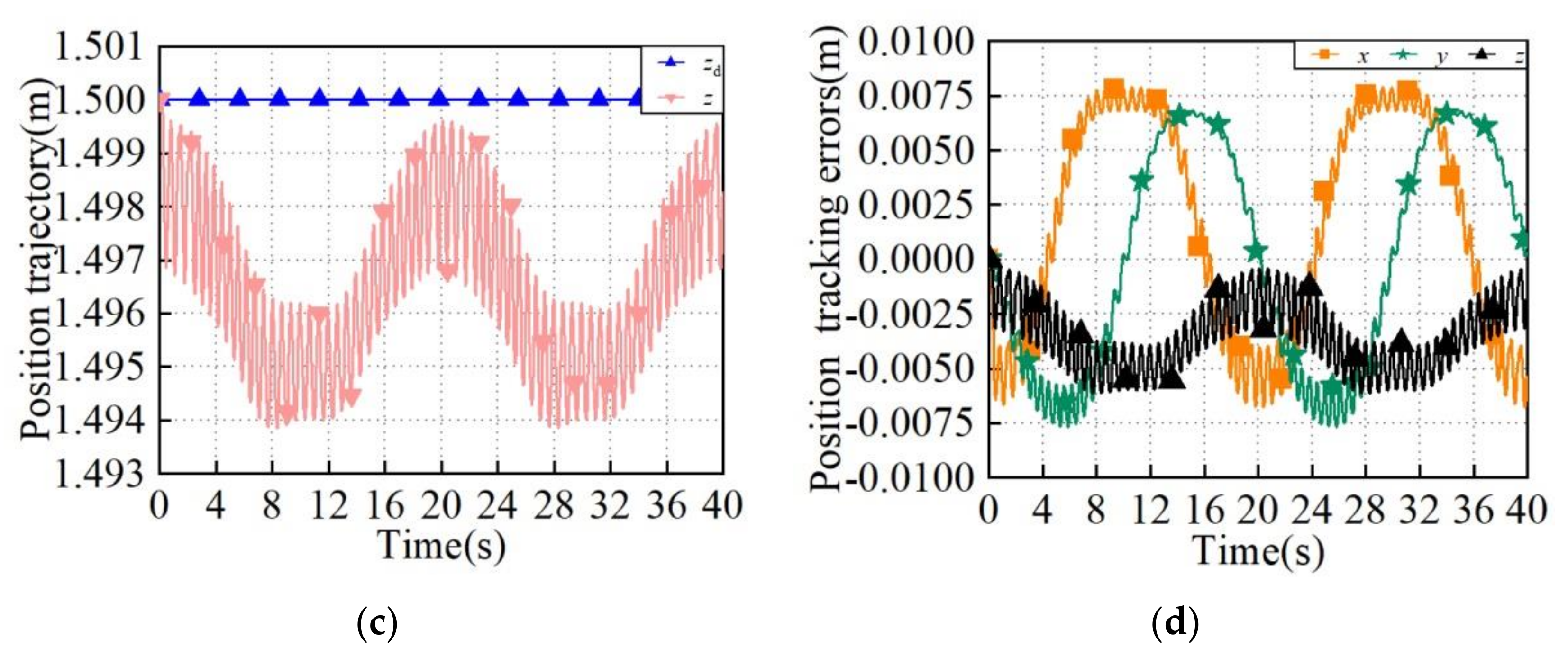
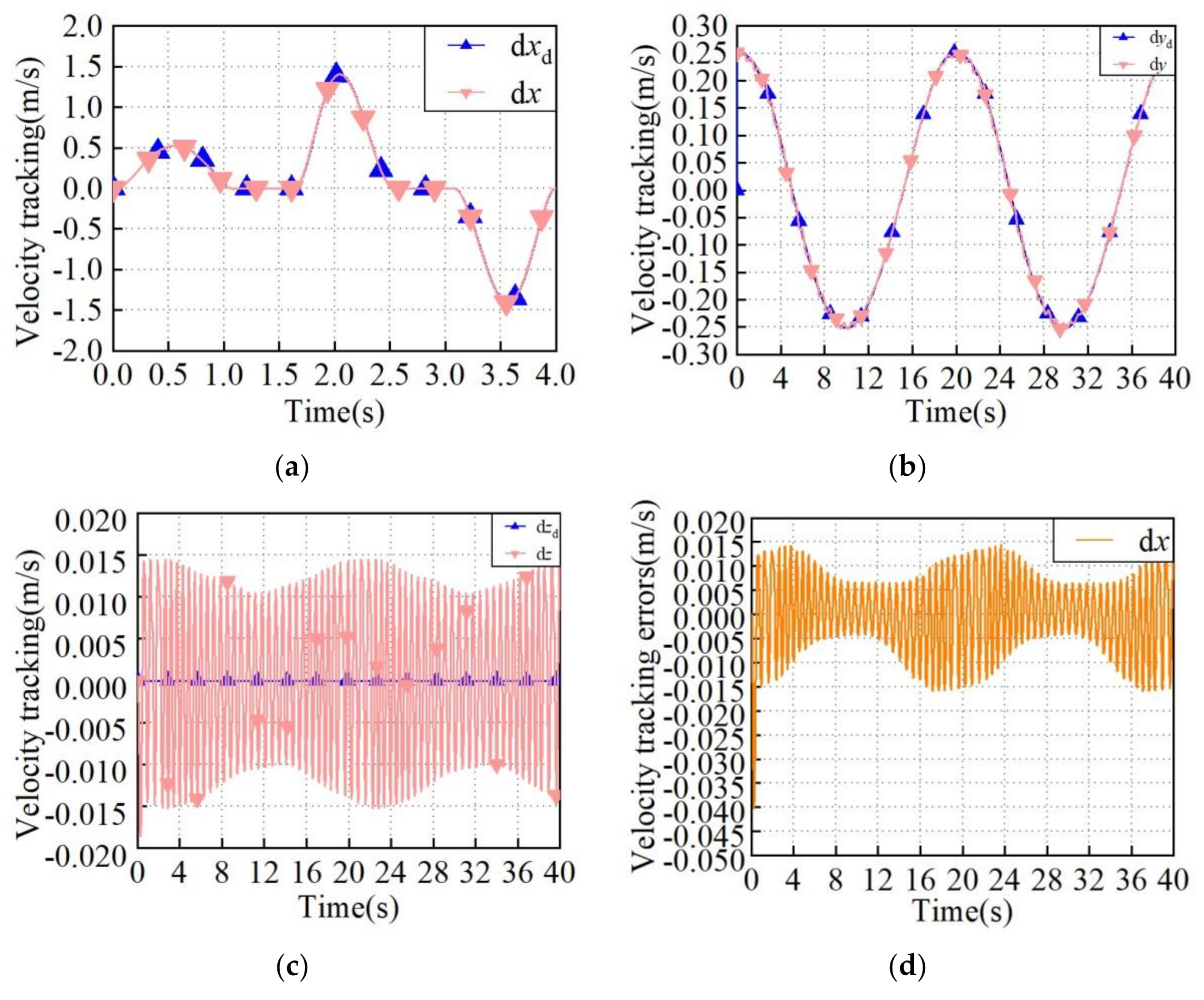



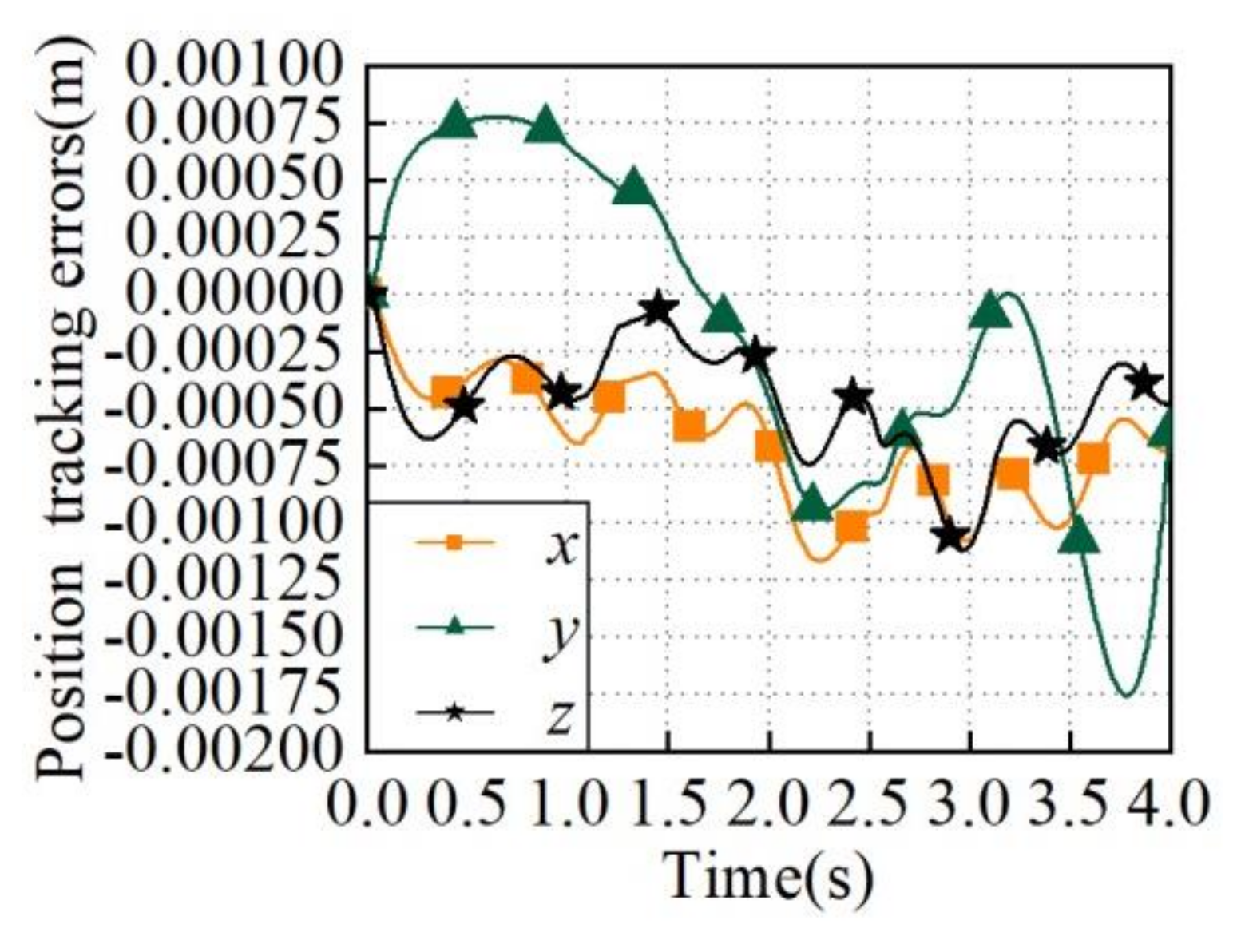
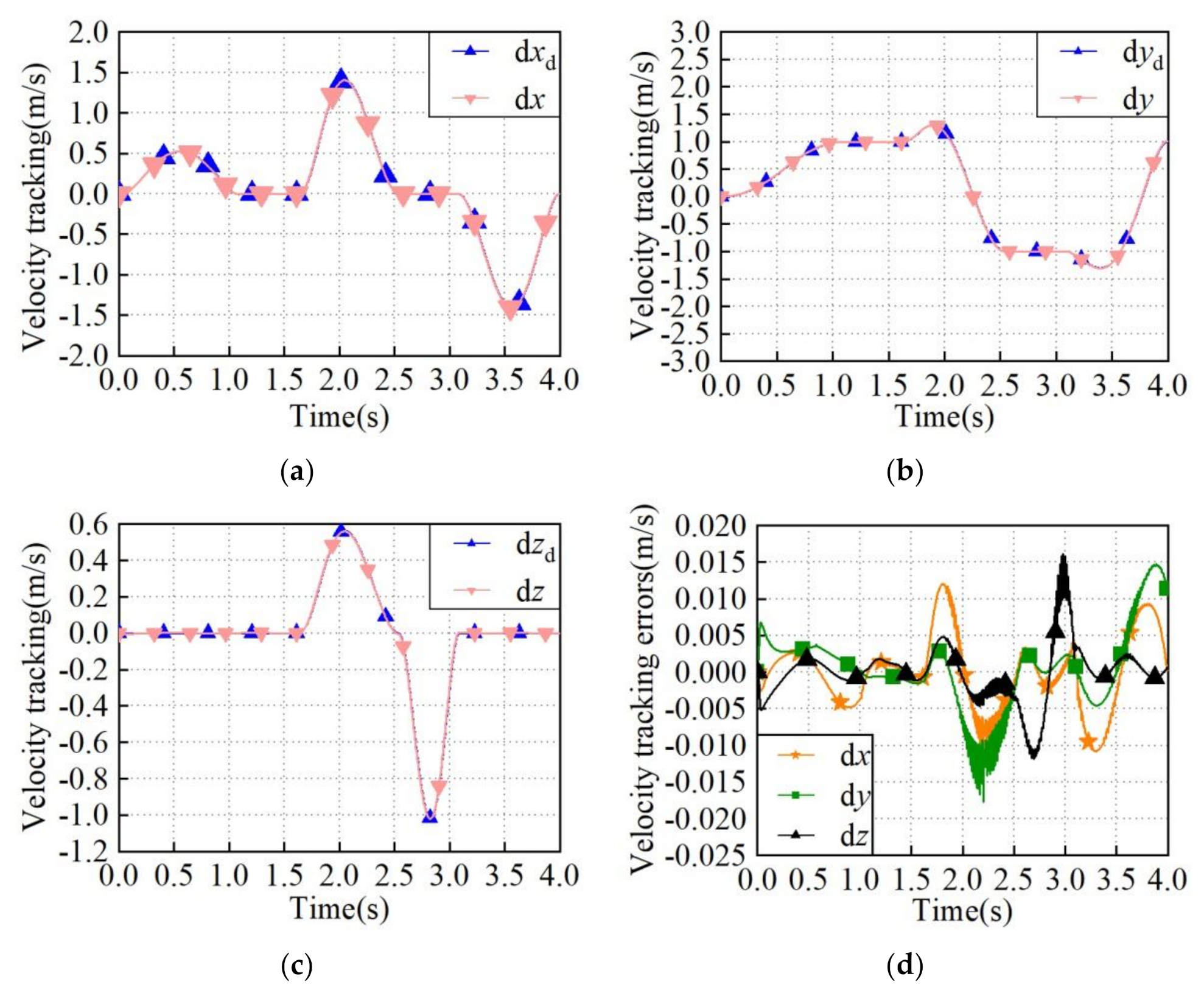
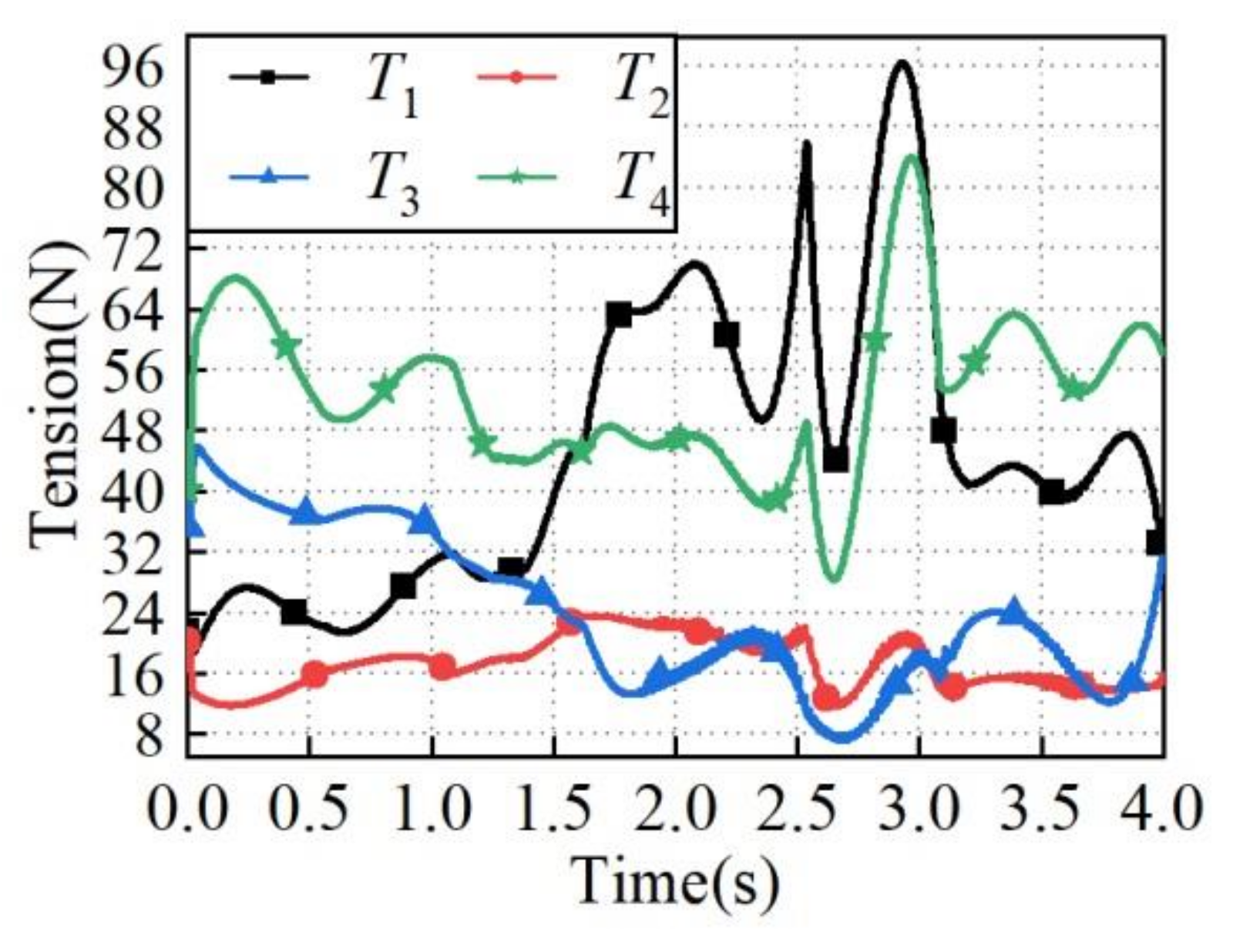
| Periods | Direction | Used Trajectory Planning Method |
|---|---|---|
| Starting period CD | x | Quintic polynomials |
| y | S-shaped acceleration/deceleration algorithm | |
| z | No displacement | |
| Preparation period DE | x | No displacement |
| y | S-shaped acceleration/deceleration | |
| z | No displacement | |
| Picking period EF | x | Quintic polynomials |
| y | Quintic polynomials | |
| z | Quintic polynomials | |
| Picking period FG | x | No displacement |
| y | S-shaped acceleration/deceleration | |
| z | Quintic polynomials | |
| Placing period GD | x | Quintic polynomials |
| y | Quintic polynomials | |
| z | No displacement |
| Parameter | Symbol | Value |
|---|---|---|
| Height of the pillar, Figure 3 | h | 3 m |
| Length of the rectangle formed by Ai | b | 4 m |
| Width of the rectangle | a | 4 m |
| Mass of the end–grab | m | 5 kg |
| Acceleration of gravity | g | 9.8 m/s2 |
| Gain matrix | KD | 250 I4×4 |
| Matrix of the sliding surface | 10 I3×3 | |
| Adaptation law matrix | Diag(10,10,10) × 10−4 | |
| Gain matrix of the robust term | Diag(0.2,0.2,0.2) |
| Controller | RMSE | MAE |
|---|---|---|
| Proposed controller | 8.9867 × 10−4 m | 2 × 10−2 m |
| Fuzzy controller | 9.1872 × 10−4 m | 2 × 10−2 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Tian, H.; Cao, X.; Qiao, X.; Gong, L.; Duan, X.; Qiu, Y.; Su, Y. Pick–and–Place Trajectory Planning and Robust Adaptive Fuzzy Tracking Control for Cable–Based Gangue–Sorting Robots with Model Uncertainties and External Disturbances. Machines 2022, 10, 714. https://doi.org/10.3390/machines10080714
Liu P, Tian H, Cao X, Qiao X, Gong L, Duan X, Qiu Y, Su Y. Pick–and–Place Trajectory Planning and Robust Adaptive Fuzzy Tracking Control for Cable–Based Gangue–Sorting Robots with Model Uncertainties and External Disturbances. Machines. 2022; 10(8):714. https://doi.org/10.3390/machines10080714
Chicago/Turabian StyleLiu, Peng, Haibo Tian, Xiangang Cao, Xinzhou Qiao, Li Gong, Xuechao Duan, Yuanying Qiu, and Yu Su. 2022. "Pick–and–Place Trajectory Planning and Robust Adaptive Fuzzy Tracking Control for Cable–Based Gangue–Sorting Robots with Model Uncertainties and External Disturbances" Machines 10, no. 8: 714. https://doi.org/10.3390/machines10080714
APA StyleLiu, P., Tian, H., Cao, X., Qiao, X., Gong, L., Duan, X., Qiu, Y., & Su, Y. (2022). Pick–and–Place Trajectory Planning and Robust Adaptive Fuzzy Tracking Control for Cable–Based Gangue–Sorting Robots with Model Uncertainties and External Disturbances. Machines, 10(8), 714. https://doi.org/10.3390/machines10080714






