Kinematic Modeling and Motion Planning of the Mobile Manipulator Agri.Q for Precision Agriculture
Abstract
:1. Introduction
- -
- The differential kinematic model of the whole custom system, described by a linear mapping from the velocity input commands to the system velocities. The kinematic model for the planar motion of the base was already completed by the authors in [17], where the base was treated as a mobile rover and the pitch mobility was not considered; so, the work is here significantly extended considering the pitch motion, which translates and rotates the manipulator base, and the manipulator mobility itself.
- -
- The description of a decoupled motion planning algorithm for sampling and pick/place tasks, where the base mobility is used to properly reach the target and also take advantage of the manipulator dexterity.
- -
- Manipulator inverse kinematics formulation with the use of the elbow or swivel angle, which is a closed form analytic solution of the inverse kinematics problem. An open-source algorithm written in Matlab code is provided (https://github.com/giocolucci/Jaco2SwivelIK; https://it.mathworks.com/matlabcentral/fileexchange/108419-jaco2swivelik, accessed in 21 March 2022).
1.1. Agri.Q Mobile Manipulator
2. Kinematic Model
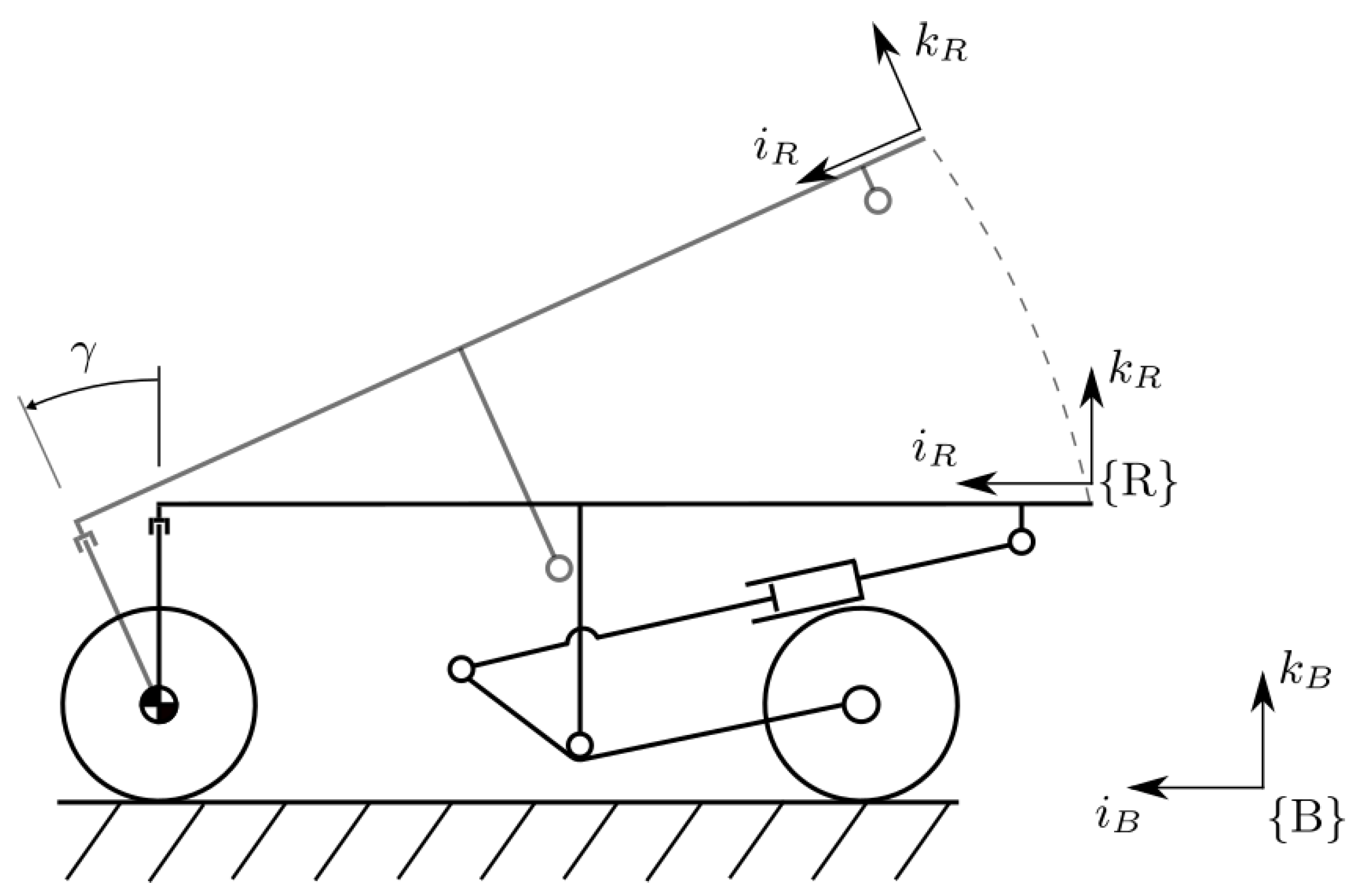
2.1. Hypotheses and Representation of the System
- -
- The traction wheels are subject to pure rolling conditions;
- -
- No lateral slip of the front and back modules is enabled;
- -
- The surface is flat and no out-of-plane motion are considered;
- -
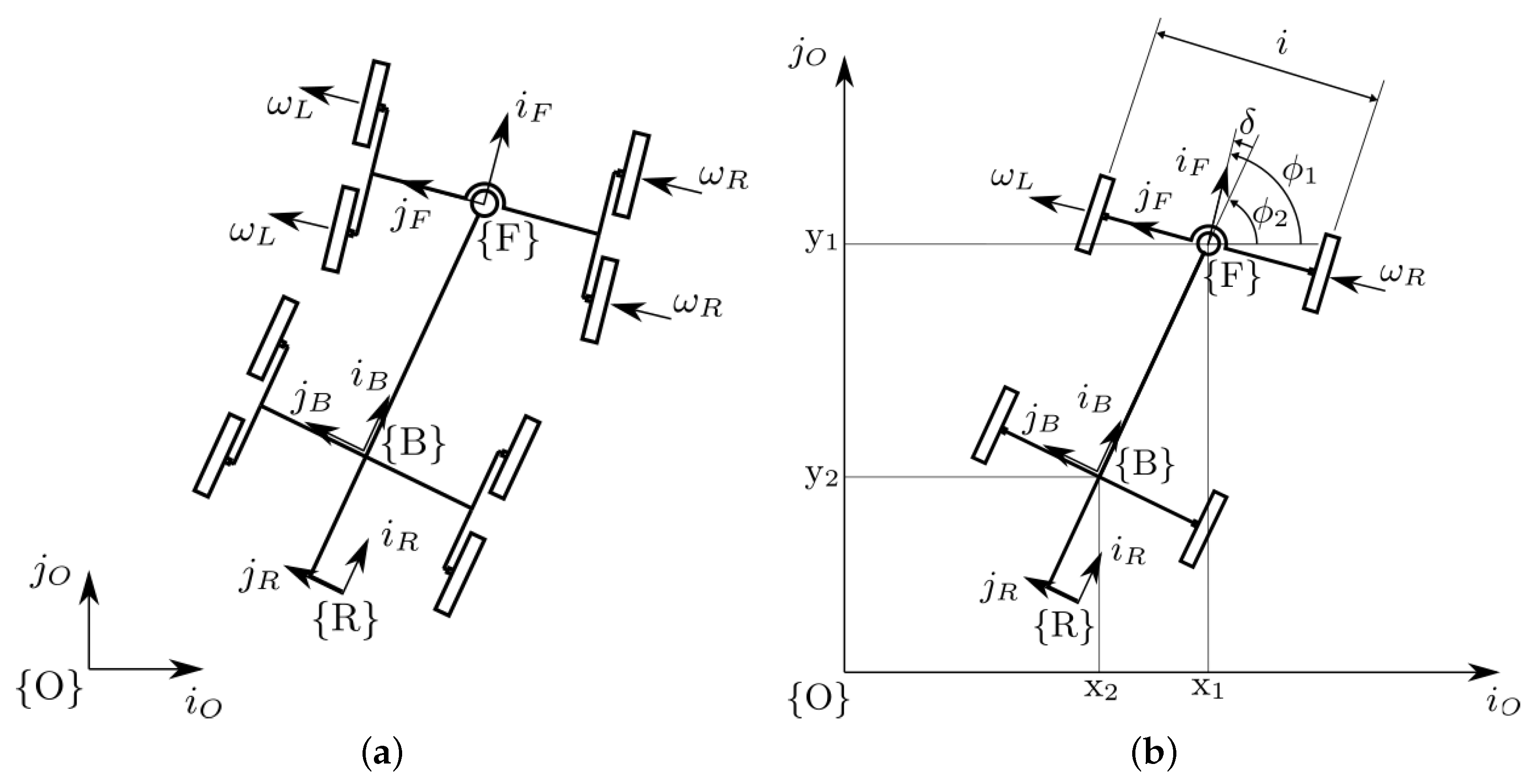
- Each couple of wheels can be reduced to a single virtual wheel with the rotation axis aligned with the module body, as showed in Figure 3b.
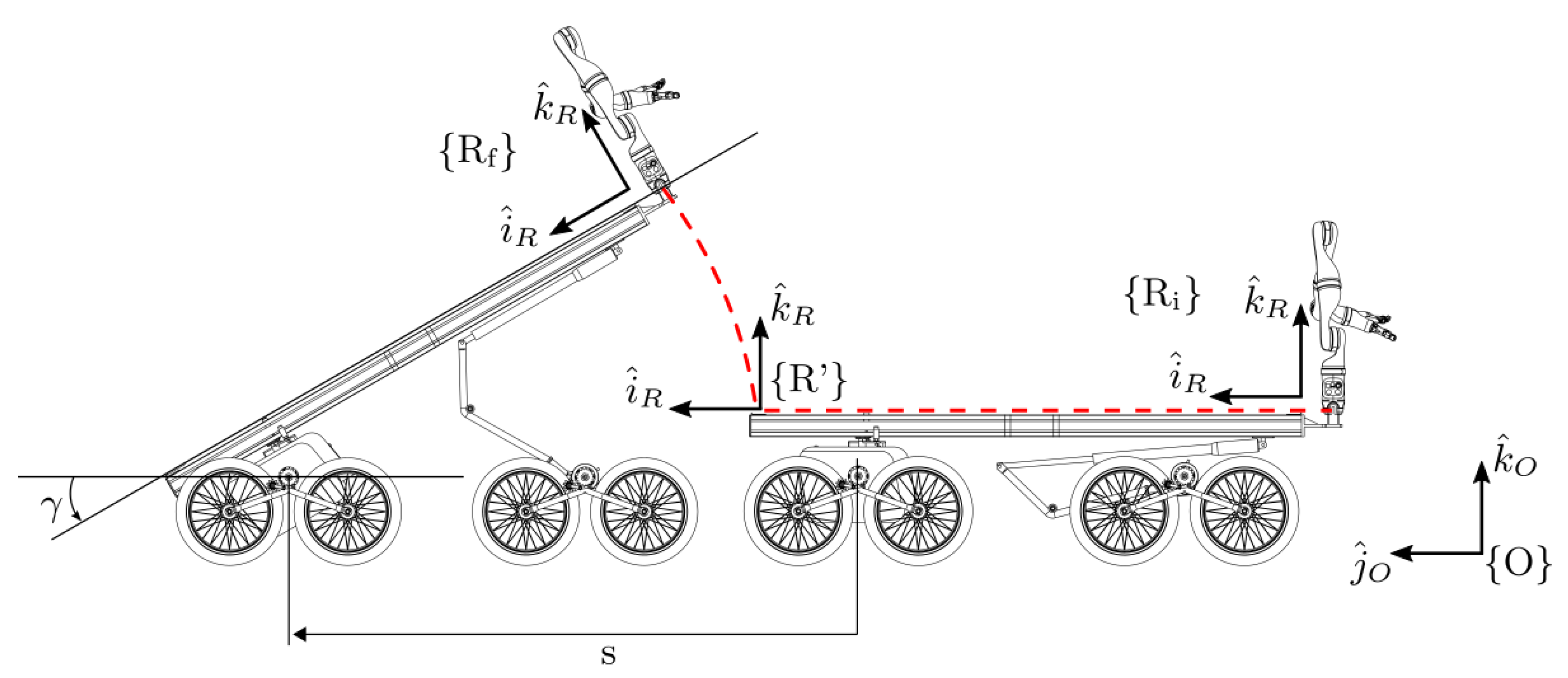
2.2. Kinematic Model of the Mobile Base
2.3. Analytic Jacobian of the System
- -
- represents the transformation matrix from the fixed frame to , fixed to the front module. It depends on the three degrees of freedom of the front module motion in the plane;
- -
- represents the transformation from to , which is the reference frame fixed to the manipulator base, and it depends on the relative yaw angle between the front and back modules and the pitch angle . It also contains information about the mounting parameters , , and ;
- -
- describes the forward kinematics of the serial kinematic chain of the manipulator.
3. Motion Planning Pipeline for Decoupled Motion
- -
- Start phase: a high-level command requires the execution of a given task, such as a pick-and-place execution, which corresponds to a crop sampling task;
- -
- First perception phase: according to the specifications indicated in the start phase, a perception system, e.g., a depth camera, recognizes the target and evaluates its position and orientation with respect to the manipulator base frame ;
- -
- Mobile base motion planning and execution: while the arm is still fixed, the mobile base is moved to enable the arm to reach the target and, moreover, to place the manipulator in a proper way;
- -
- Second perception phase: the perception system recomputes the new position and orientation of the target with respect to the arm base frame;
- -
- Arm motion planning and execution: while the base is now fixed, the arm performs the task taking care to not collide with the mobile base and the rest of the environment.
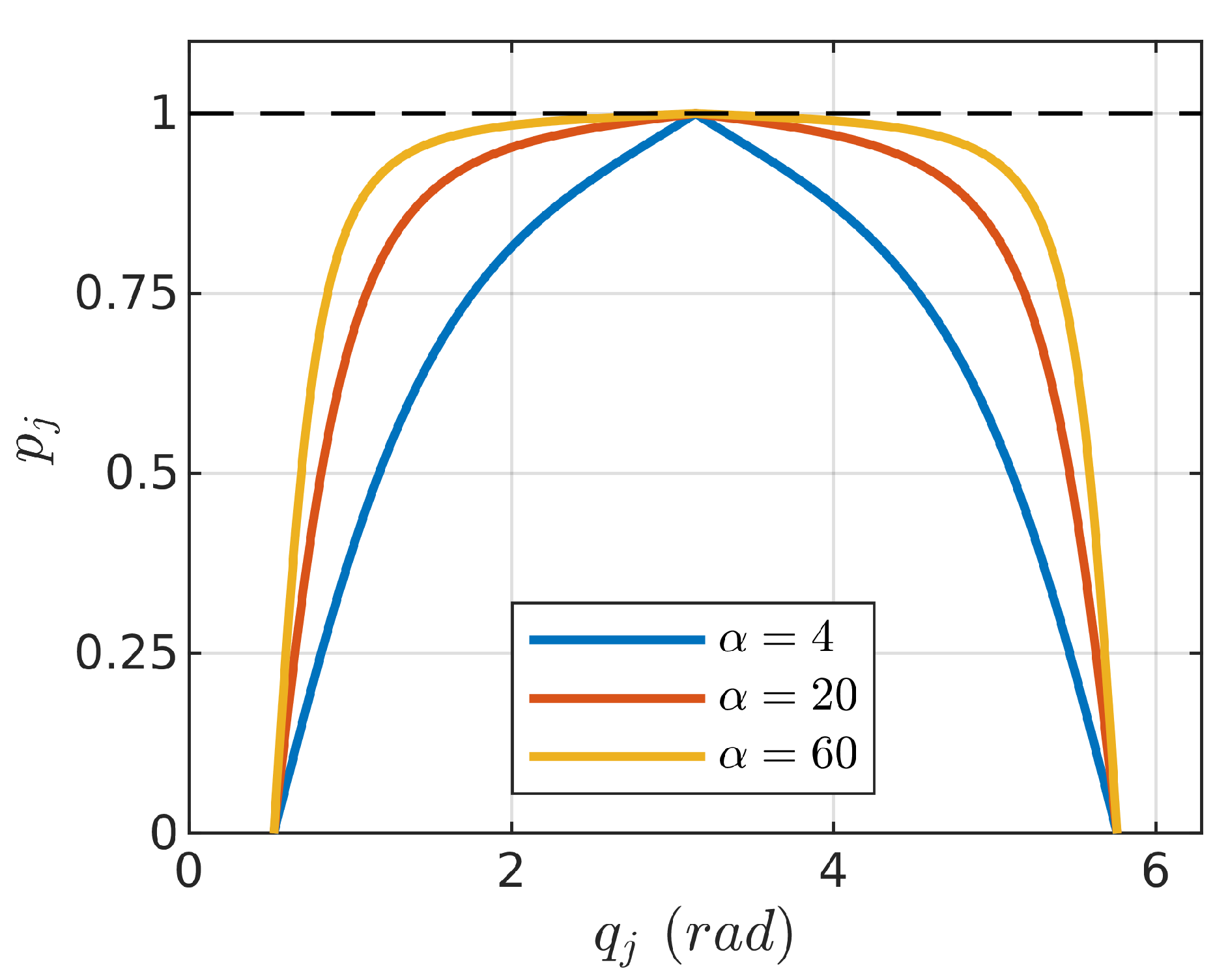
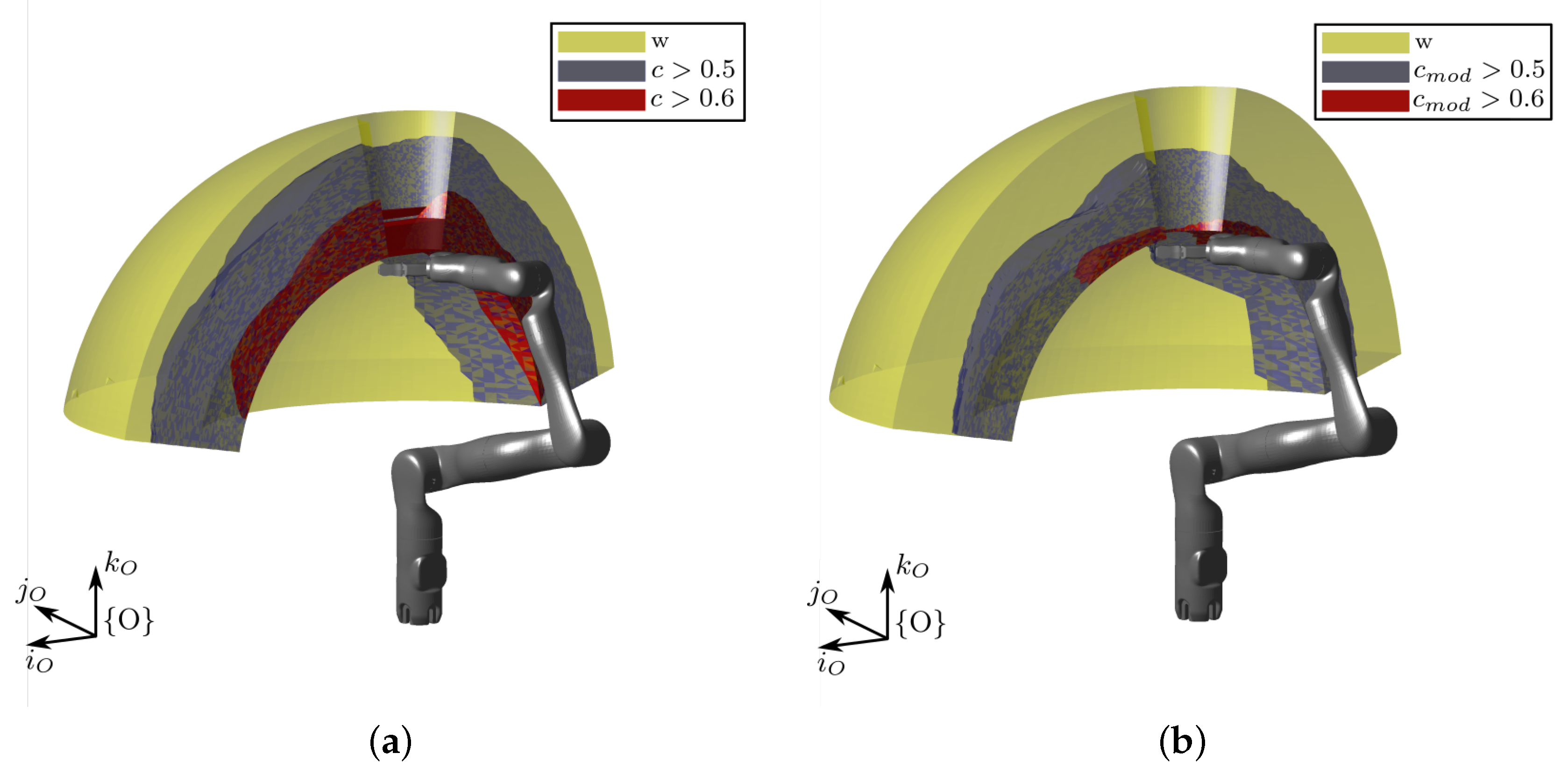
3.1. Modified Manipulability Index of the Manipulator
3.2. Manipulator Manipulability Mapping
3.3. Mobile Base Motion Planning
- -
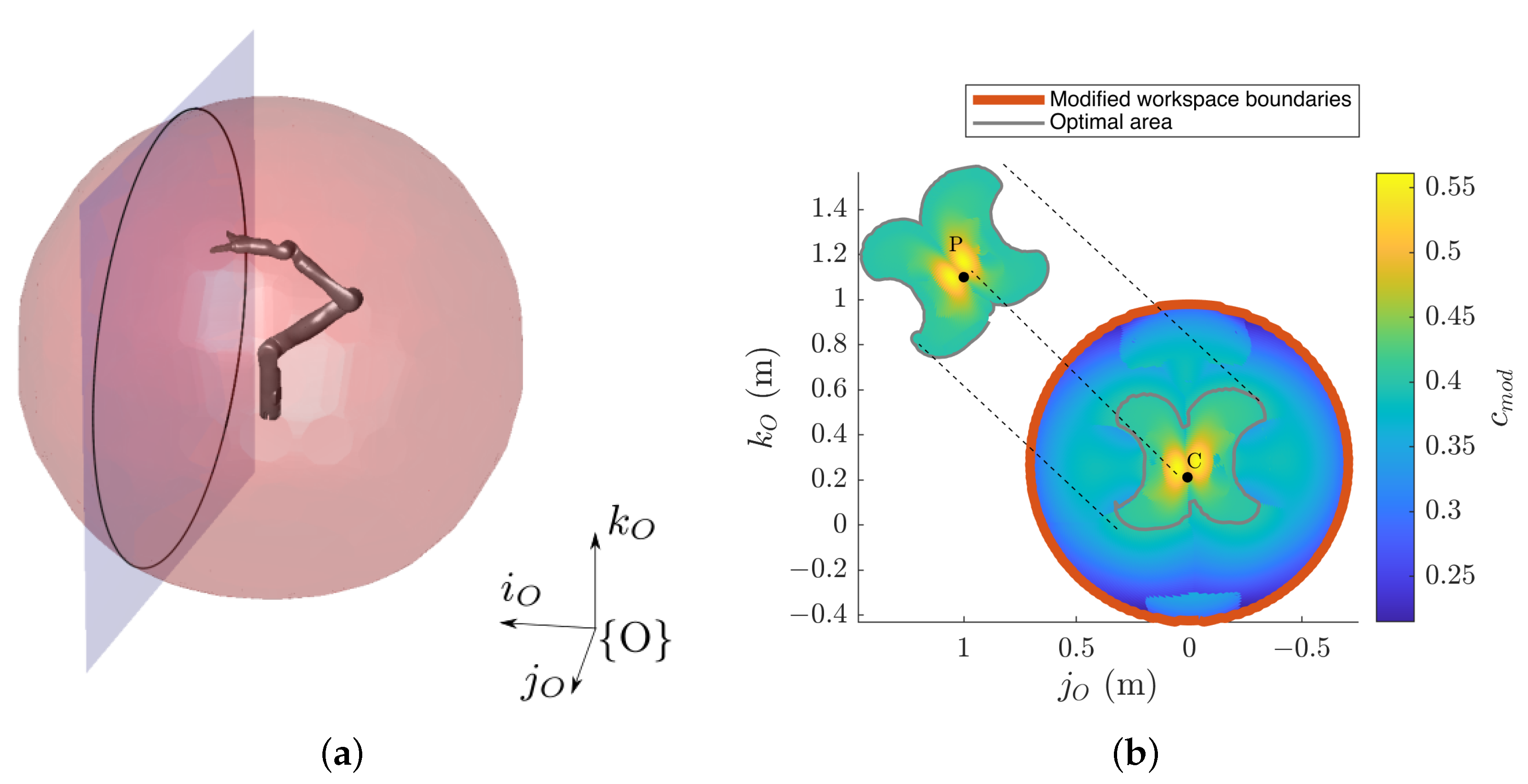
- Starting from a desired goal pose, described by the homogeneous transformation matrix with respect to , a slice of the entire workspace, parallel to the plane and passing through the P target point, is extracted, depicted in Figure 8a as the circle in black.
- -
- Inside the extracted domain, one can evaluate what portion of the workspace can be actually reached with the desired end-effector orientation. It is worth pointing out that, in general, the domain of the reachable points with a desired pose does not coincide with the manipulator workspace, which, instead, considers all the possible reachable points without an orientation specification. The boundaries of the modified workspace are described in Figure 8b with the red line.
- -
- One can evaluate whether the point P lies inside the modified workspace boundaries. If it does, the manipulator can actually reach the target, and no motion of the mobile base is requested. If it does not, the mobile base must move to reach the target point.
- -
- If a mobile base motion is requested, the reduced workspace domain is mapped in terms of the modified manipulability index , defined in Equation (26).
- -
- An optimal area where , represented in the figure inside the gray line, is calculated as a portion of the modified workspace. Its manipulability barycenter coordinates C are calculated with respect to :where is the position vector of the i-th point inside the optimal area, and is its modified manipulability index.In the reported example, .
- -
- are calculated in order to move C to the target point P. In general, the procedure implies the rotation of the optimal area due to .
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| d.o.f. | degree of freedom |
| r.f. | reference frame |
References
- Hvilshøj, M.; Bøgh, S.; Skov Nielsen, O.; Madsen, O. Autonomous industrial mobile manipulation (AIMM): Past, present and future. Ind. Robot. Int. J. 2012, 39, 120–135. [Google Scholar] [CrossRef]
- Outón, J.L.; Villaverde, I.; Herrero, H.; Esnaola, U.; Sierra, B. Innovative Mobile Manipulator Solution for Modern Flexible Manufacturing Processes. Sensors 2019, 19, 5414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- RB Kairos + Mobile Manipulator. Available online: https://robotnik.eu/products/mobile-manipulators/rb-kairos/ (accessed on 17 April 2022).
- KMR Iiwa. Available online: https://www.kuka.com/en-se/products/mobility/mobile-robots/kmr-iiwa (accessed on 17 April 2022).
- Kemp, C.C.; Edsinger, A.; Clever, H.M.; Matulevich, B. The Design of Stretch: A Compact, Lightweight Mobile Manipulator for Indoor Human Environments. arXiv 2021, arXiv:2109.10892. [Google Scholar]
- Hello Robot Website. Available online: https://hello-robot.com/product (accessed on 15 March 2022).
- Toyota Global Site | Frontier Research. Available online: https://www.toyota-global.com/innovation/partner_robot/index.html (accessed on 15 March 2022).
- Yamamoto, T.; Terada, K.; Ochiai, A.; Saito, F.; Asahara, Y.; Murase, K. Development of Human Support Robot as the research platform of a domestic mobile manipulator. ROBOMECH J. 2019, 6, 4. [Google Scholar] [CrossRef]
- Li, Z.; Moran, P.; Dong, Q.; Shaw, R.J.; Hauser, K. Development of a tele-nursing mobile manipulator for remote care-giving in quarantine areas. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3581–3586. [Google Scholar] [CrossRef]
- Intelligent Motion Laboratory at Duke University. Available online: http://motion.pratt.duke.edu/nursing/index.html (accessed on 15 March 2022).
- Oberti, R.; Marchi, M.; Tirelli, P.; Calcante, A.; Iriti, M.; Tona, E.; Hočevar, M.; Baur, J.; Pfaff, J.; Schütz, C.; et al. Selective spraying of grapevines for disease control using a modular agricultural robot. Biosyst. Eng. 2016, 146, 203–215. [Google Scholar] [CrossRef]
- De Preter, A.; Anthonis, J.; De Baerdemaeker, J. Development of a Robot for Harvesting Strawberries. IFAC-PapersOnLine 2018, 51, 14–19. [Google Scholar] [CrossRef]
- Strawberry Picker. Available online: http://www.octinion.com/strawberry-picker (accessed on 15 March 2022).
- Habibian, S.; Dadvar, M.; Peykari, B.; Hosseini, A.; Salehzadeh, M.H.; Hosseini, A.H.M.; Najafi, F. Design and Implementation of a Maxi-Sized Mobile Robot (Karo) for Rescue Missions. ROBOMECH J. 2021, 8, 1. [Google Scholar] [CrossRef]
- Novotny, G.; Emsenhuber, S.; Klammer, P.; Pöschko, C.; Voglsinger, F.; Kubinger, W. A Mobile Robot Platform for Search and Rescue Applications. In Proceedings of the 30th DAAAM International Symposium, Zadar, Croatia, 23–26 October 2019; pp. 0945–0954. [Google Scholar] [CrossRef]
- Silwal, A.; Davidson, J.R.; Karkee, M.; Mo, C.; Zhang, Q.; Lewis, K. Design, integration, and field evaluation of a robotic apple harvester. J. Field Robot. 2017, 34, 1140–1159. [Google Scholar] [CrossRef]
- Botta, A.; Cavallone, P.; Tagliavini, L.; Colucci, G.; Carbonari, L.; Quaglia, G. Modelling and simulation of articulated mobile robots. Int. J. Mech. Control 2021, 22, 15–26. [Google Scholar]
- Quaglia, G.; Visconte, C.; Scimmi, L.S.; Melchiorre, M.; Cavallone, P.; Pastorelli, S. Design of a UGV Powered by Solar Energy for Precision Agriculture. Robotics 2020, 9, 13. [Google Scholar] [CrossRef] [Green Version]
- Quaglia, G.; Visconte, C.; Scimmi, L.S.; Melchiorre, M.; Cavallone, P.; Pastorelli, S. Design of the positioning mechanism of an unmanned ground vehicle for precision agriculture. In Advances in Mechanism and Machine Science; Uhl, T., Ed.; Mechanisms and Machine Science; Springer International Publishing: Cham, Switzerland, 2019; Volume 73, pp. 3531–3540. [Google Scholar] [CrossRef]
- Botta, A.; Cavallone, P. Robotics Applied to Precision Agriculture: The Sustainable Agri.q Rover Case Study. In Proceedings of the I4SDG Workshop 2021, Online, 25–26 November 2021; Quaglia, G., Gasparetto, A., Petuya, V., Carbone, G., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 41–50. [Google Scholar]
- De Luca, A.; Oriolo, G.; Giordano, P. Kinematic modeling and redundancy resolution for nonholonomic mobile manipulators. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation (ICRA 2006), Orlando, FL, USA, 15–19 May 2006; pp. 1867–1873. [Google Scholar] [CrossRef] [Green Version]
- Lynch, K.M.; Park, F.C. Modern Robotics; Cambridge University Press: Cambridge, UK, 2017; pp. 475–476. [Google Scholar]
- Merlet, J.P. Jacobian, Manipulability, Condition Number, and Accuracy of Parallel Robots. J. Mech. Des. 2005, 128, 199–206. [Google Scholar] [CrossRef]
- Chan, T.F.; Dubey, R. A weighted least-norm solution based scheme for avoiding joint limits for redundant joint manipulators. IEEE Trans. Robot. Autom. 1995, 11, 286–292. [Google Scholar] [CrossRef]
- Vahrenkamp, N.; Asfour, T.; Metta, G.; Sandini, G.; Dillmann, R. Manipulability analysis. In Proceedings of the 2012 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012), Osaka, Japan, 29 November–1 December 2012; pp. 568–573. [Google Scholar] [CrossRef]
- Chen, F.; Selvaggio, M.; Caldwell, D.G. Dexterous Grasping by Manipulability Selection for Mobile Manipulator With Visual Guidance. IEEE Trans. Ind. Inform. 2019, 15, 1202–1210. [Google Scholar] [CrossRef]
- Colucci, G.; Baglieri, L.; Botta, A.; Cavallone, P.; Quaglia, G. Optimal Positioning of Mobile Manipulators Using Closed Form Inverse Kinematics. In Advances in Service and Industrial Robotics; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Artemiadis, P. Closed-form Inverse Kinematic Solution for Anthropomorphic Motion in Redundant Robot Arms. In Proceedings of the ICRA 2013, Karlsruhe, Germany, 6–10 May 2013. [Google Scholar] [CrossRef] [Green Version]
- Faria, C.; Ferreira, F.; Erlhagen, W.; Monteiro, S.; Bicho, E. Position-based kinematics for 7-DoF serial manipulators with global configuration control, joint limit and singularity avoidance. Mech. Mach. Theory 2018, 121, 317–334. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colucci, G.; Botta, A.; Tagliavini, L.; Cavallone, P.; Baglieri, L.; Quaglia, G. Kinematic Modeling and Motion Planning of the Mobile Manipulator Agri.Q for Precision Agriculture. Machines 2022, 10, 321. https://doi.org/10.3390/machines10050321
Colucci G, Botta A, Tagliavini L, Cavallone P, Baglieri L, Quaglia G. Kinematic Modeling and Motion Planning of the Mobile Manipulator Agri.Q for Precision Agriculture. Machines. 2022; 10(5):321. https://doi.org/10.3390/machines10050321
Chicago/Turabian StyleColucci, Giovanni, Andrea Botta, Luigi Tagliavini, Paride Cavallone, Lorenzo Baglieri, and Giuseppe Quaglia. 2022. "Kinematic Modeling and Motion Planning of the Mobile Manipulator Agri.Q for Precision Agriculture" Machines 10, no. 5: 321. https://doi.org/10.3390/machines10050321
APA StyleColucci, G., Botta, A., Tagliavini, L., Cavallone, P., Baglieri, L., & Quaglia, G. (2022). Kinematic Modeling and Motion Planning of the Mobile Manipulator Agri.Q for Precision Agriculture. Machines, 10(5), 321. https://doi.org/10.3390/machines10050321






