Fuzzy Sliding Mode Control for Microbial Fuel Cells
Abstract
:1. Introduction
2. Introduction of MFCs
2.1. Mfc Reaction Mechanism
2.2. Mfc Mathematical Model
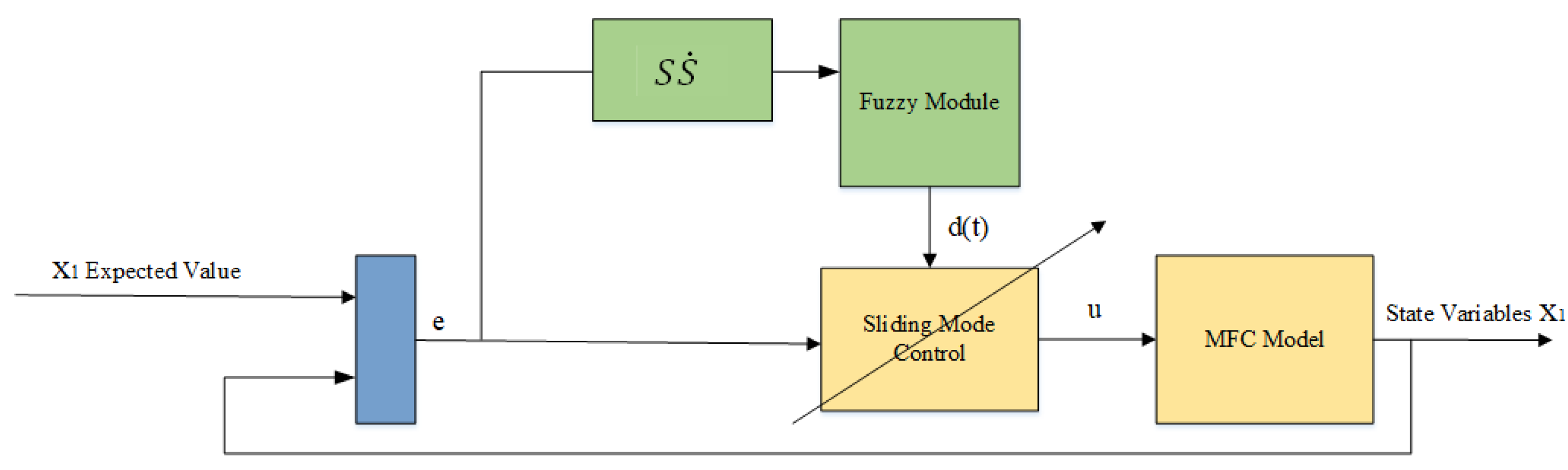
3. Controller Design
3.1. Sm Control
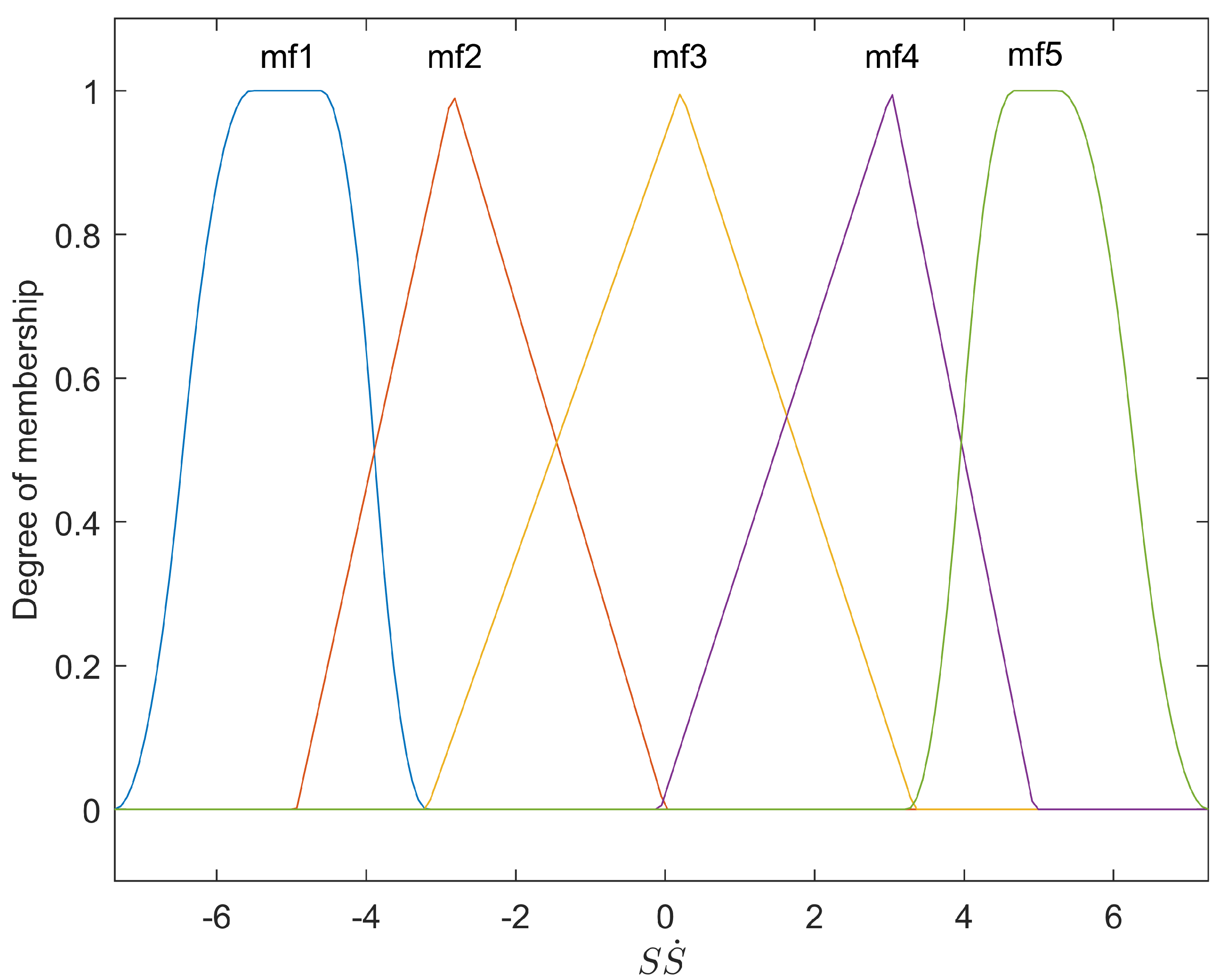
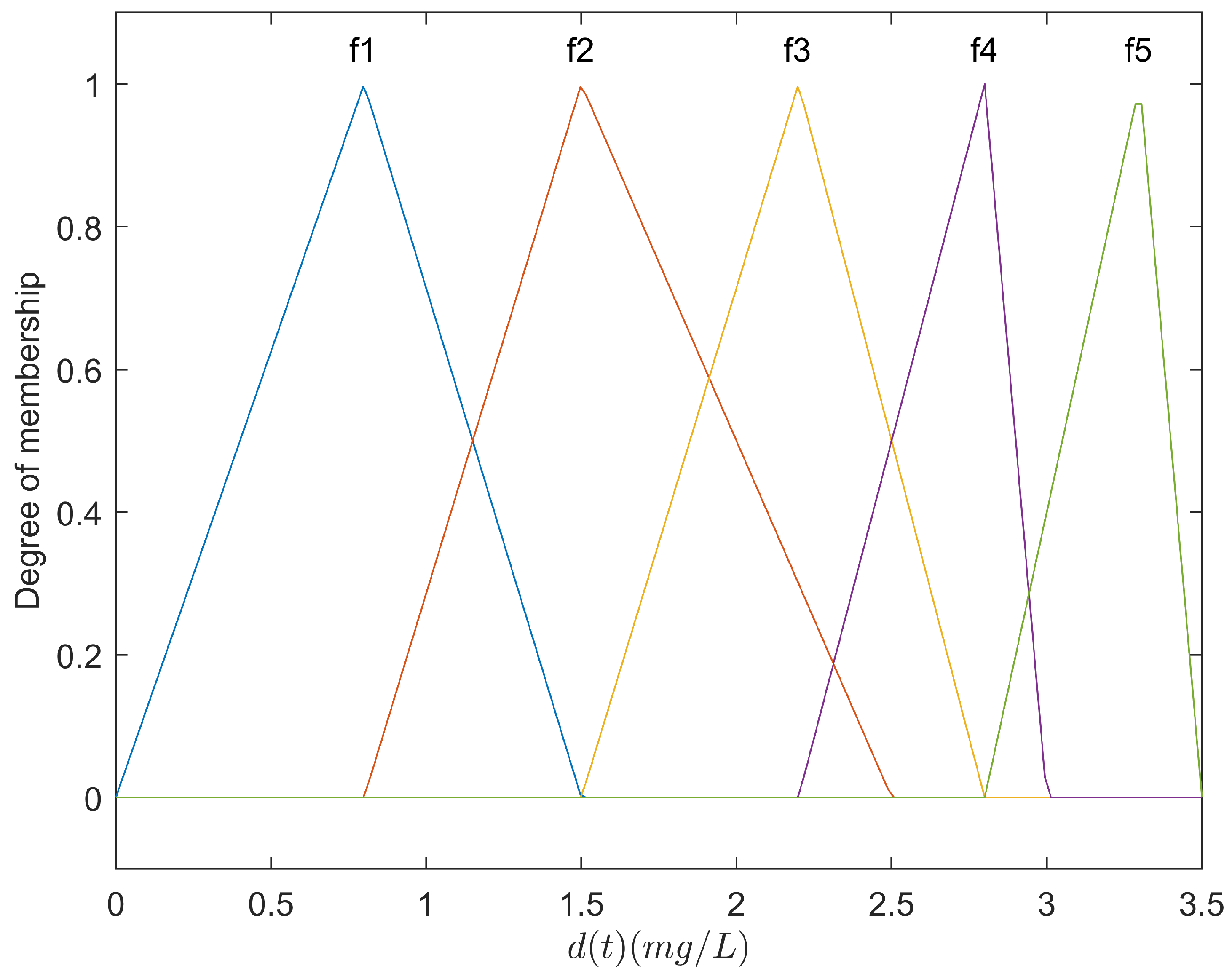
3.2. Fuzzy Rule Design
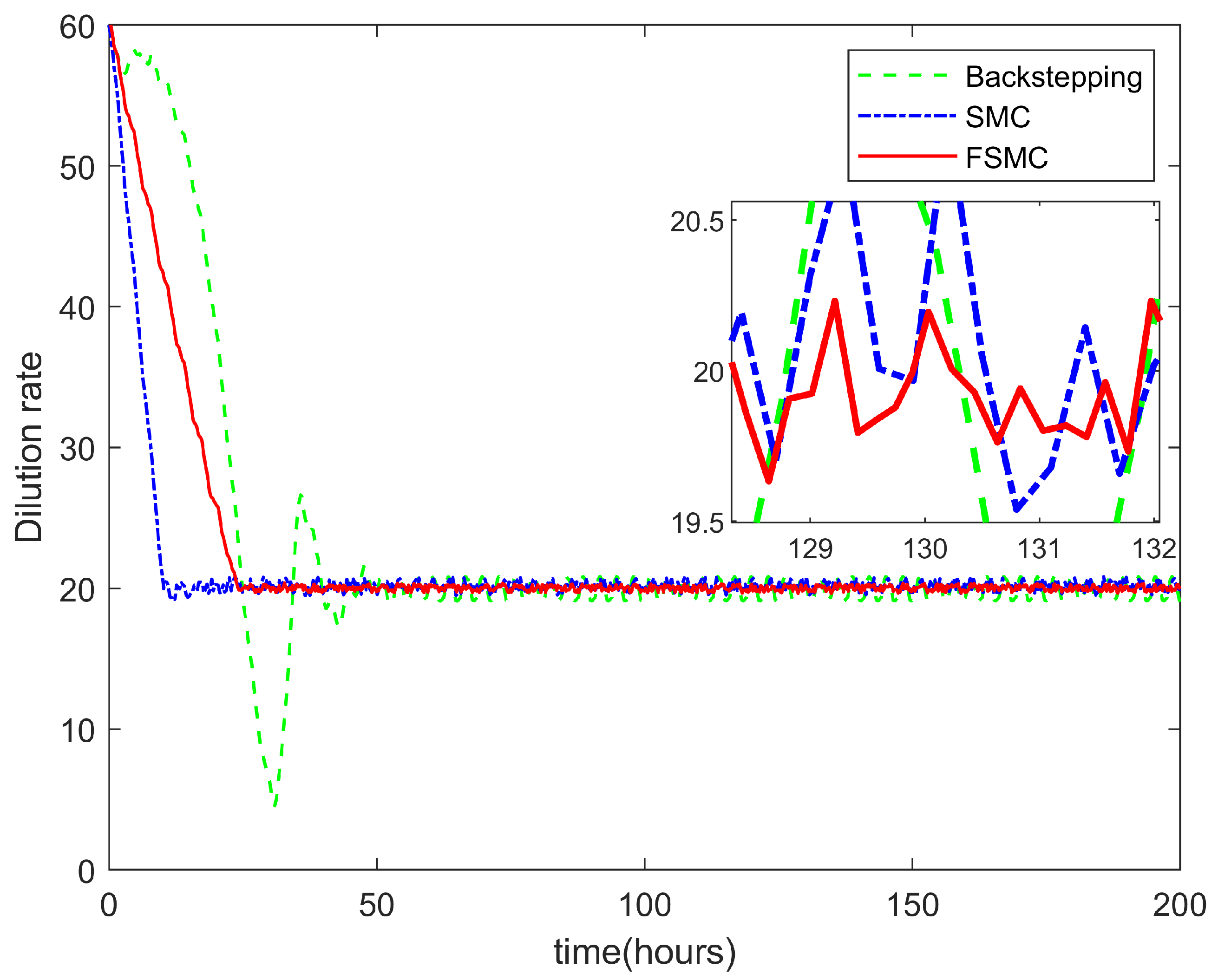
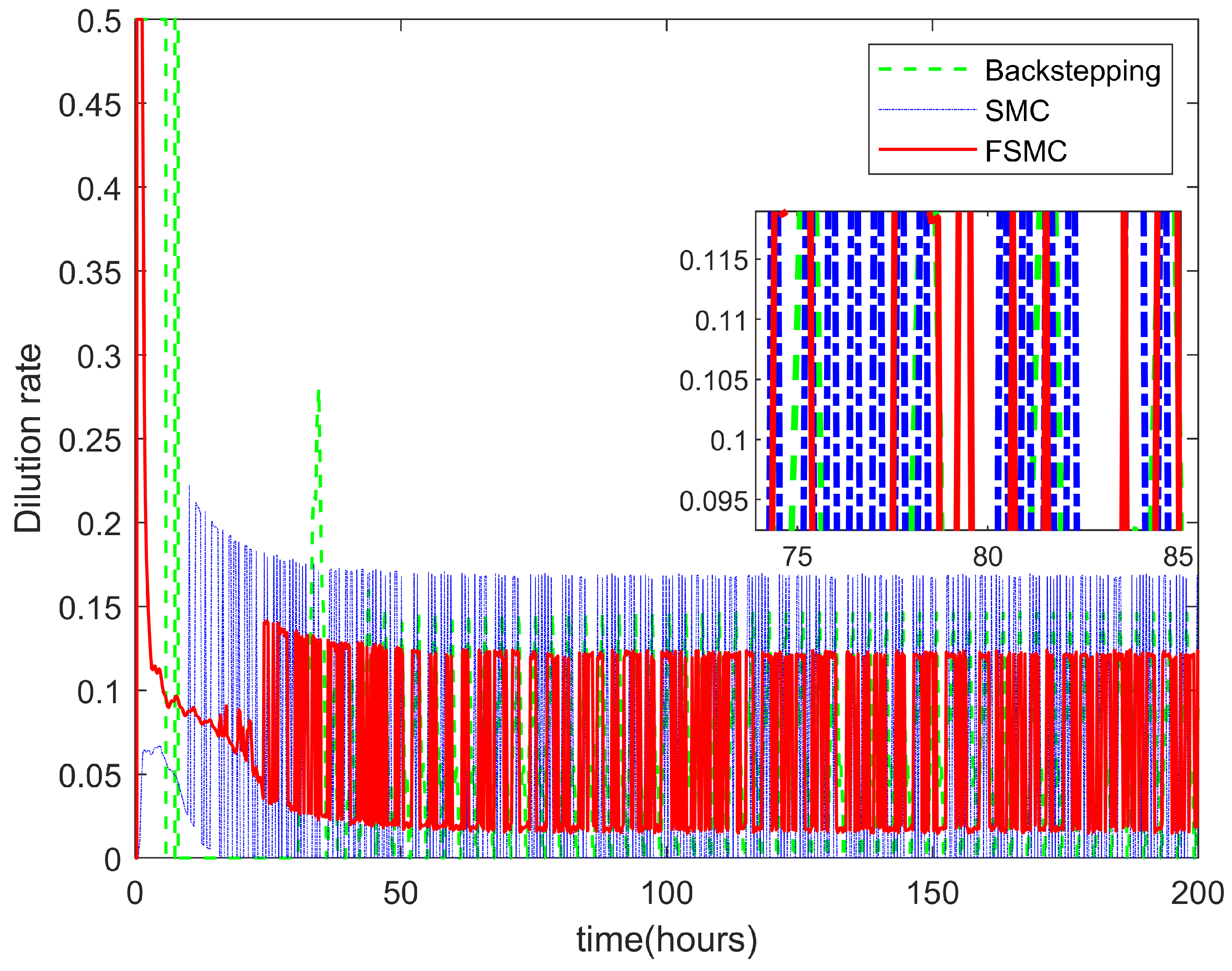
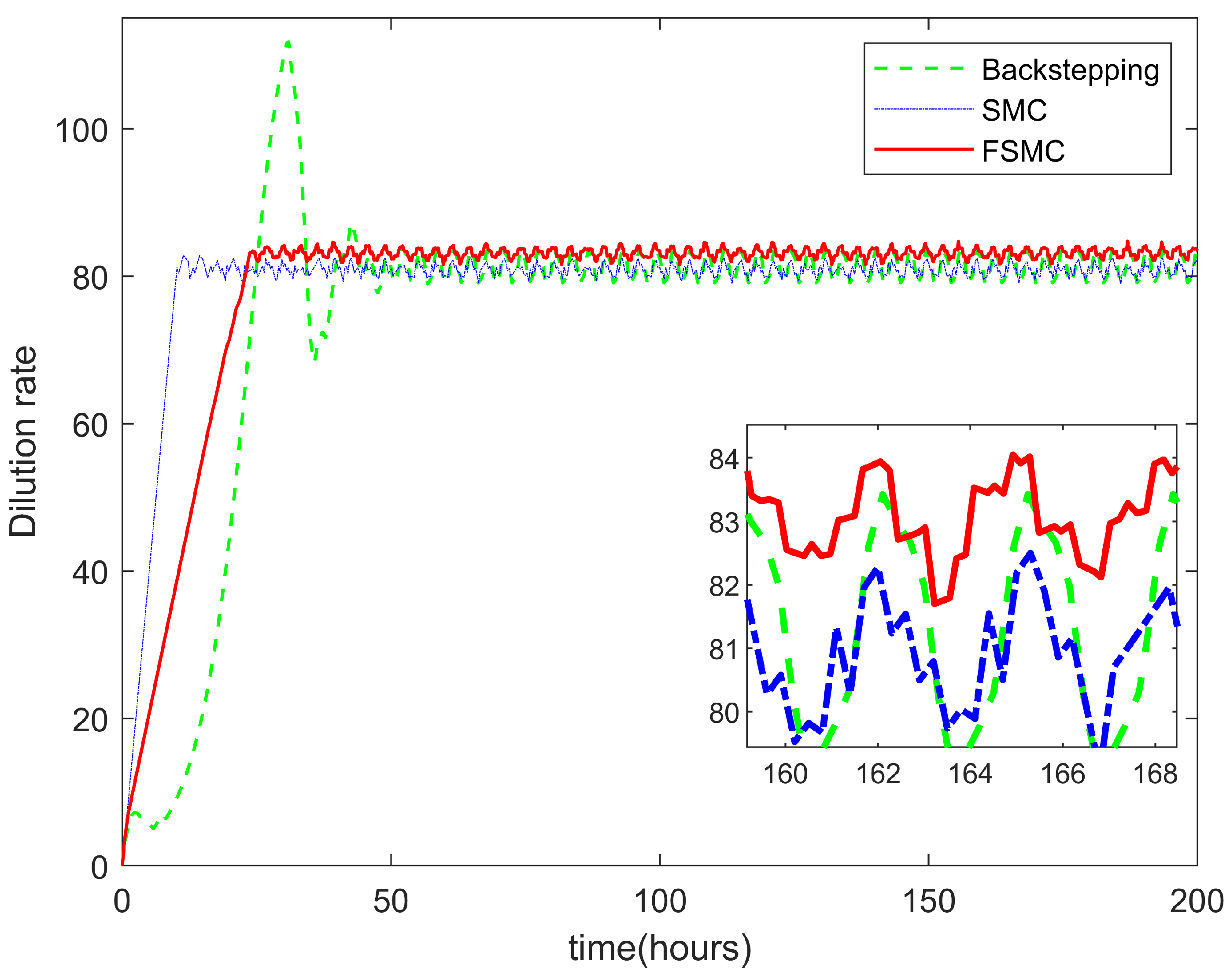
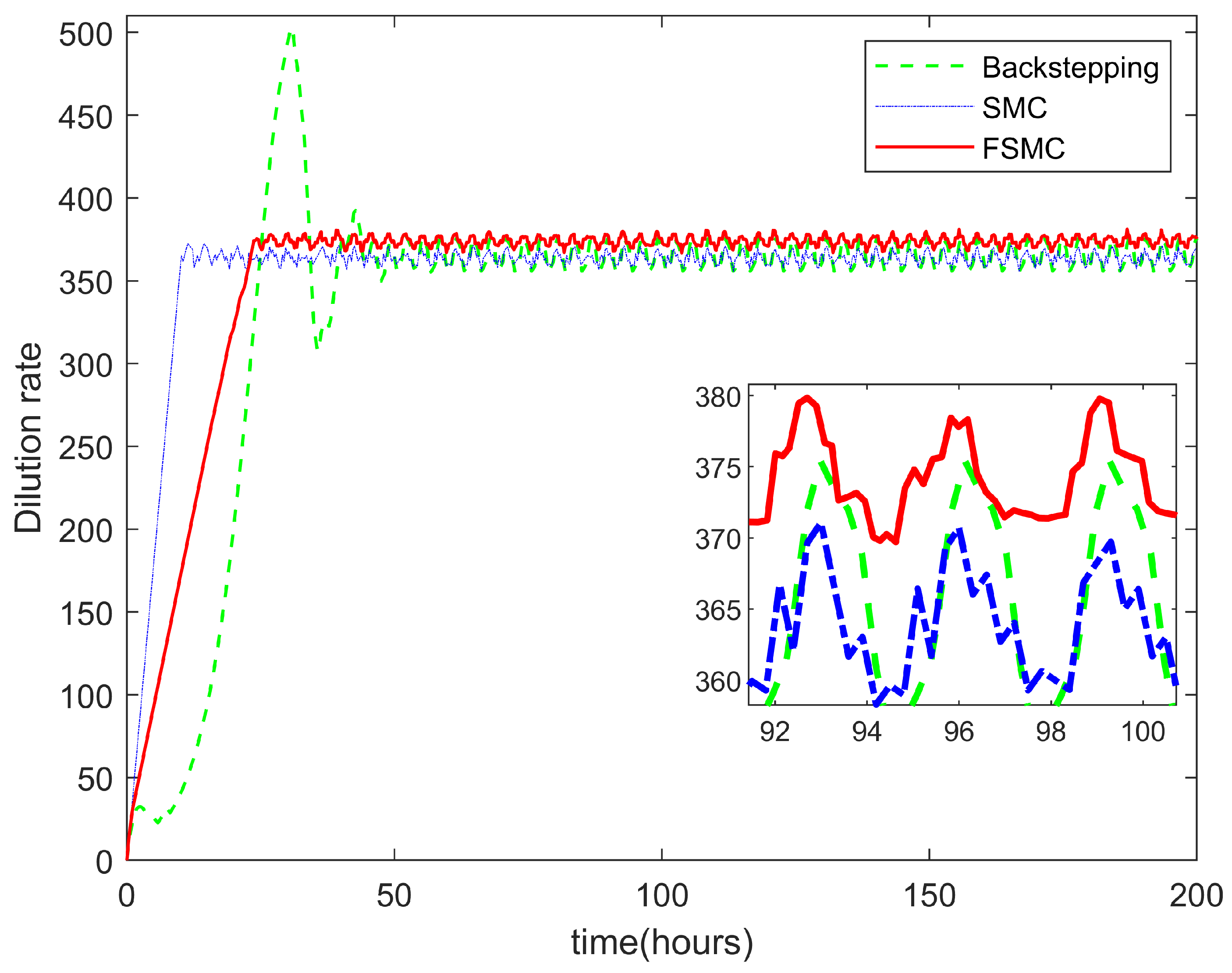
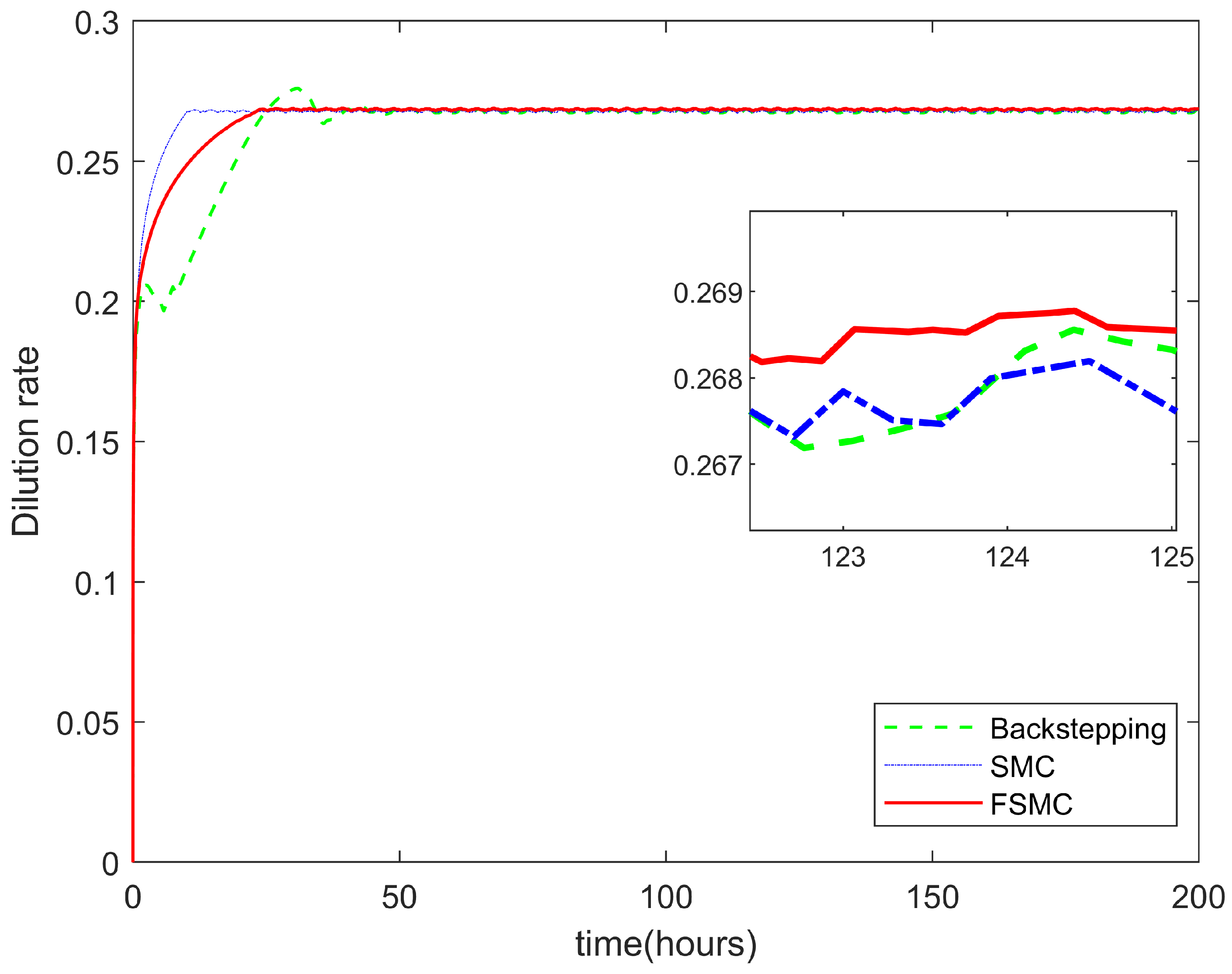
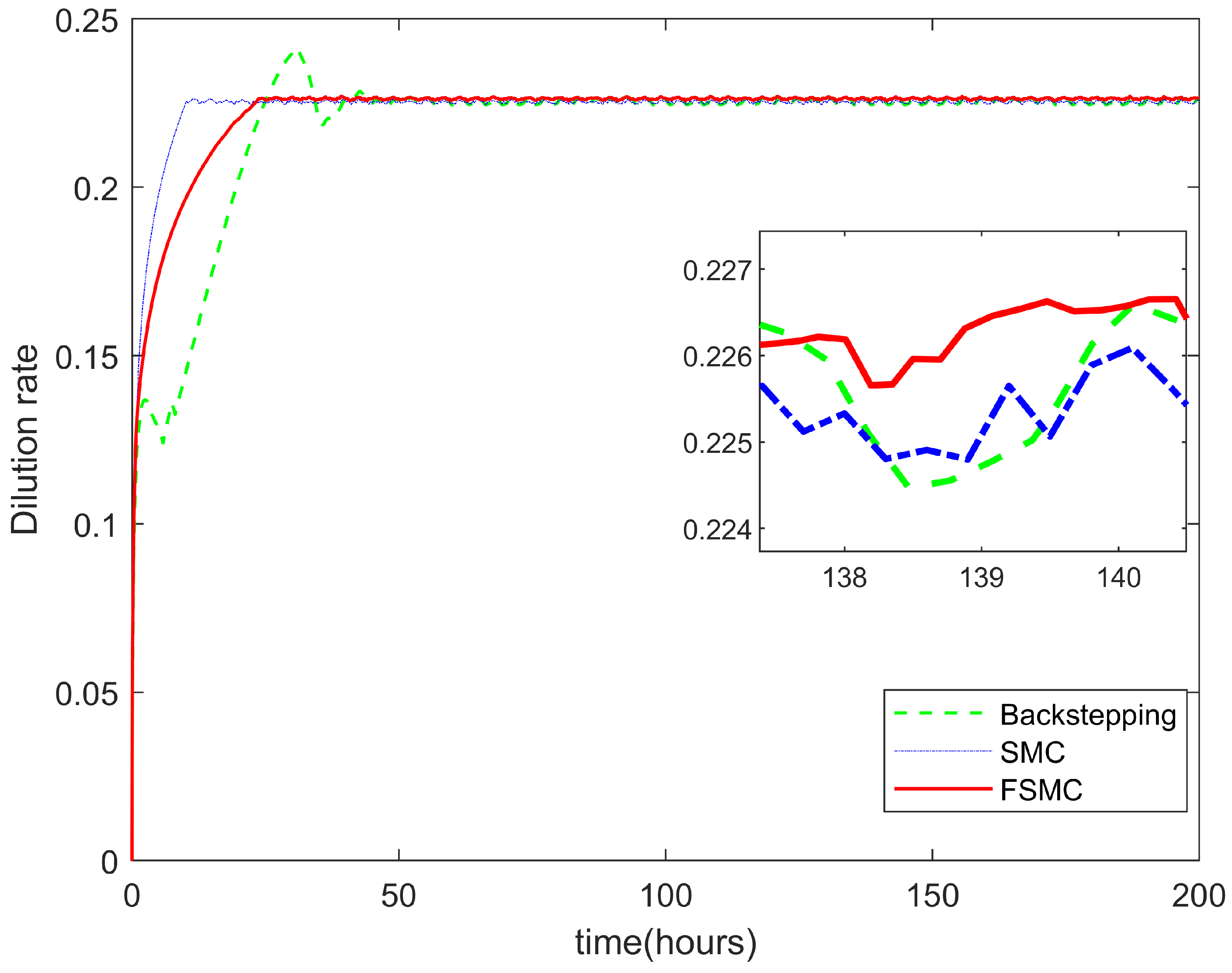
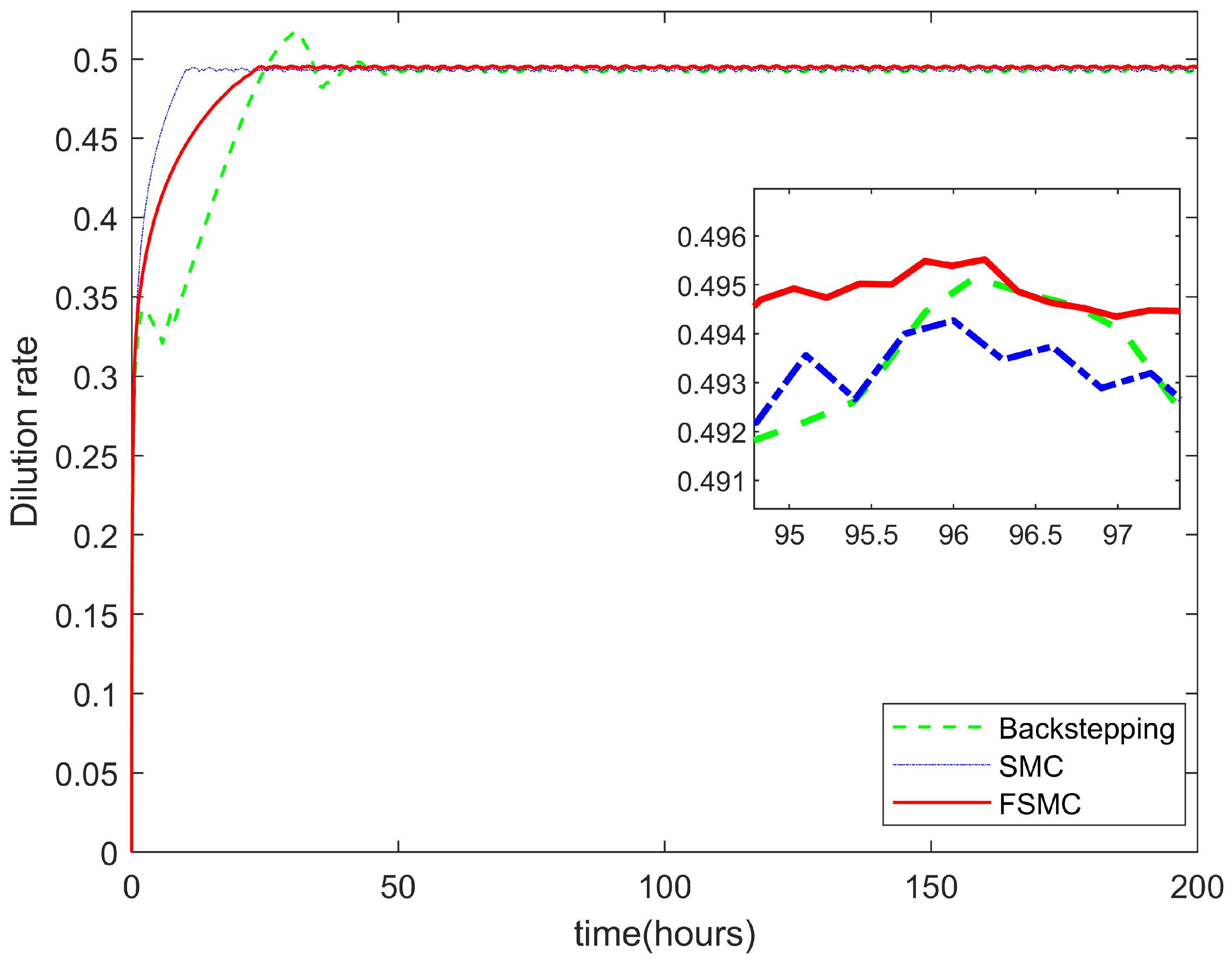
4. Experiments and Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Vakulchuk, R.; Overland, I.; Scholten, D. Renewable energy and geopolitics: A review. Renew. Sustain. Energy Rev. 2020, 122, 109547. [Google Scholar] [CrossRef]
- Burke, M.J.; Stephens, J.C. Political power and renewable energy futures: A critical review. Energy Res. Soc. Sci. 2018, 35, 78–93. [Google Scholar] [CrossRef]
- Boudet, H.S. Public perceptions of and responses to new energy technologies. Nat. Energy 2019, 4, 446–455. [Google Scholar] [CrossRef]
- Palanisamy, G.; Jung, H.Y.; Sadhasivam, T.; Kurkuri, M.D.; Kim, S.C.; Roh, S.H. A comprehensive review on microbial fuel cell technologies: Processes, utilization, and advanced developments in electrodes and membranes. J. Clean. Prod. 2019, 221, 598–621. [Google Scholar] [CrossRef]
- Gajda, I.; Greenman, J.; Ieropoulos, I.A. Recent advancements in real-world microbial fuel cell applications. Curr. Opin. Electrochem. 2018, 11, 78–83. [Google Scholar] [CrossRef]
- Li, M.; Zhou, M.; Tian, X.; Tan, C.; McDaniel, C.T.; Hassett, D.J.; Gu, T. Microbial fuel cell (MFC) power performance improvement through enhanced microbial electrogenicity. Biotechnol. Adv. 2018, 36, 1316–1327. [Google Scholar] [CrossRef]
- Ezziat, L.; Elabed, A.; Ibnsouda, S.; El Abed, S. Challenges of microbial fuel cell architecture on heavy metal recovery and removal from wastewater. Front. Energy Res. 2019, 7, 1. [Google Scholar] [CrossRef]
- Wu, Q.; Jiao, S.; Ma, M.; Peng, S. Microbial fuel cell system: A promising technology for pollutant removal and environmental remediation. Environ. Sci. Pollut. Res. 2020, 27, 6749–6764. [Google Scholar] [CrossRef]
- Patel, R.; Deb, D. Parametrized control-oriented mathematical model and adaptive backstepping control of a single chamber single population microbial fuel cell. J. Power Sources 2018, 396, 599–605. [Google Scholar] [CrossRef]
- Yadav, G.; Sharma, I.; Ghangrekar, M.; Sen, R. A live bio-cathode to enhance power output steered by bacteria-microalgae synergistic metabolism in microbial fuel cell. J. Power Sources 2020, 449, 227560. [Google Scholar] [CrossRef]
- Kim, B.; Mohan, S.V.; Fapyane, D.; Chang, I.S. Controlling voltage reversal in microbial fuel cells. Trends Biotechnol. 2020, 38, 667–678. [Google Scholar] [CrossRef] [PubMed]
- Mian, M.M.; Liu, G.; Fu, B. Conversion of sewage sludge into environmental catalyst and microbial fuel cell electrode material: A review. Sci. Total Environ. 2019, 666, 525–539. [Google Scholar] [CrossRef] [PubMed]
- Haavisto, J.; Dessì, P.; Chatterjee, P.; Honkanen, M.; Noori, M.T.; Kokko, M.; Lakaniemi, A.M.; Lens, P.N.; Puhakka, J.A. Effects of anode materials on electricity production from xylose and treatability of TMP wastewater in an up-flow microbial fuel cell. Chem. Eng. J. 2019, 372, 141–150. [Google Scholar] [CrossRef]
- Yan, M.; Fan, L. Constant voltage output in two-chamber microbial fuel cell under fuzzy PID control. Int. J. Electrochem. Sci. 2013, 8, 3321–3332. [Google Scholar]
- Fan, L.; Zhang, J.; Shi, X. Performance improvement of a microbial fuel cell based on model predictive control. Int. J. Electrochem. Sci 2015, 10, 737–748. [Google Scholar]
- Islam, M.A.; Karim, A.; Mishra, P.; Dubowski, J.J.; Yousuf, A.; Sarmin, S.; Khan, M.M.R. Microbial synergistic interactions enhanced power generation in co-culture driven microbial fuel cell. Sci. Total Environ. 2020, 738, 140138. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, X.; Wang, H.; Long, X.; Li, X. Simultaneous enhancement of heavy metal removal and electricity generation in soil microbial fuel cell. Ecotoxicol. Environ. Saf. 2020, 192, 110314. [Google Scholar] [CrossRef]
- Alipanahi, R.; Rahimnejad, M.; Najafpour, G. Improvement of sediment microbial fuel cell performances by design and application of power management systems. Int. J. Hydrogen Energy 2019, 44, 16965–16975. [Google Scholar] [CrossRef]
- Ma, F.; Fu, C.; Yang, J.; Yang, Q. Control strategy for adaptive active energy harvesting in sediment microbial fuel cells. J. Energy Eng. 2020, 146, 04019034. [Google Scholar] [CrossRef]
- Xiao, N.; Wu, R.; Huang, J.J.; Selvaganapathy, P.R. Development of a xurographically fabricated miniaturized low-cost, high-performance microbial fuel cell and its application for sensing biological oxygen demand. Sens. Actuators B Chem. 2020, 304, 127432. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S. Sliding Mode Control: Theory and Applications; T. J. International Ltd.: Padstow, UK, 1998. [Google Scholar]
- Young, K.D.; Utkin, V.I.; Ozguner, U. A control engineer’s guide to sliding mode control. IEEE Trans. Control Syst. Technol. 1999, 7, 328–342. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Utkin, V.I. Chattering suppression methods in sliding mode control systems. Annu. Rev. Control 2007, 31, 179–188. [Google Scholar] [CrossRef]
- Utkin, V.; Poznyak, A.; Orlov, Y.; Polyakov, A. Conventional and high order sliding mode control. J. Frankl. Inst. 2020, 357, 10244–10261. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, H.; Liu, H.; Yu, X. A survey on sliding mode control for networked control systems. Int. J. Syst. Sci. 2021, 52, 1129–1147. [Google Scholar] [CrossRef]
- Yu, X.; Feng, Y.; Man, Z. Terminal sliding mode control–An overview. IEEE Open J. Ind. Electron. Soc. 2020, 2, 36–52. [Google Scholar] [CrossRef]
- Utkin, V.; Lee, H. Chattering problem in sliding mode control systems. In Proceedings of the International Workshop on Variable Structure Systems, Alghero, Sardinia, 5–7 June 2006; pp. 346–350. [Google Scholar]
- Wu, X.; Jin, P.; Zou, T.; Qi, Z.; Xiao, H.; Lou, P. Backstepping trajectory tracking based on fuzzy sliding mode control for differential mobile robots. J. Intell. Robot. Syst. 2019, 96, 109–121. [Google Scholar] [CrossRef]
- Abul, A.; Zhang, J.; Steidl, R.; Reguera, G.; Tan, X. Microbial fuel cells: Control-oriented modeling and experimental validation. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 412–417. [Google Scholar]


| Parameter | Unit | Value |
|---|---|---|
| day | 3.6 | |
| day | 0.4 | |
| mg/L | 60 | |
| mg L | 32.4 | |
| b | day | 0.084 |
| V | 0.15 | |
| V | 1.019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, T.; Ma, F.; Zhu, B.; Ji, P.; Lian, L. Fuzzy Sliding Mode Control for Microbial Fuel Cells. Machines 2022, 10, 320. https://doi.org/10.3390/machines10050320
Ouyang T, Ma F, Zhu B, Ji P, Lian L. Fuzzy Sliding Mode Control for Microbial Fuel Cells. Machines. 2022; 10(5):320. https://doi.org/10.3390/machines10050320
Chicago/Turabian StyleOuyang, Tianyu, Fengying Ma, Baolong Zhu, Peng Ji, and Lei Lian. 2022. "Fuzzy Sliding Mode Control for Microbial Fuel Cells" Machines 10, no. 5: 320. https://doi.org/10.3390/machines10050320
APA StyleOuyang, T., Ma, F., Zhu, B., Ji, P., & Lian, L. (2022). Fuzzy Sliding Mode Control for Microbial Fuel Cells. Machines, 10(5), 320. https://doi.org/10.3390/machines10050320






