Abstract
As one of the fastest running animals on land, the ostrich’s excellent athletic ability benefits from its unique leg structure. Based on the idea of bionics, this paper intends to obtain a kind of robotic leg structure with a similar buffering capacity to that of the ostrich. For this purpose, the structural characteristics of a seven-link parallel mechanism are analyzed firstly, having some specific features similar to ostrich legs, such as the center of mass (COM) located at the root of the leg, a large folding/unfolding ratio, and so on. Then, the kinematic model of the bionic leg is established, and the energy storage of the flexible parts of the leg is investigated. Finally, an impact experiment of the structure onto the ground is carried out to verify the accuracy of the established kinematic model. This paper systematically reveals the nonlinear law of the elasticity of an ostrich-like leg and provides the buffering performance characteristics of the leg in the process of hitting the ground, based on its elastic properties by the kinematic model and the experiment.
1. Introduction
The flexible locomotion of humans and pods depends on close cooperation between legs. Compared with terrestrial animals without feet, bipeds move faster, adapt to more complex environments, and have stronger anti-interference abilities [1,2]. At present, many researchers have reported the dynamics of robotic bionic legs. For example, He et al. [3] studied the nonlinear mechanical control of a single-legged jumping robot in the flight stage. By transforming the dynamics into chain form, an exponentially stabilizable control method based on the integral backstepping process was proposed. Komarsofla et al. [4] established a single-leg jumping mechanism performing hopping by transferring linear momentum between the reciprocating mass and its main body. Larin et al. [5] considered the inertia characteristics of single-leg jumping and designed the spatial motion model. The reports presented above all focus on driving mechanisms. As for underactuated robots, Zhang et al. [6] proposed a 3-DOF underactuated leg mechanism and built dynamics formulas to calculate the driving force based on the principle of virtue work. He et al. [7] investigated the locomotion control method of an underactuated jumping robot and proposed the corresponding modeling, motion planning, and control method. In these papers, the elastic properties of the mechanism were rarely analyzed from the perspective of the material characteristics of the elastic parts [8]. In this study, the influence factors of the nonlinear elasticity of the underactuated leg are investigated systematically, including the elasticity of the leaf springs, and the buffering performance is concluded by a kinematic model and experiment.
2. Structural Analysis of Ostrich Leg
As the fastest biped running on land, the ostrich has strong and powerful lower limbs and has the ability for steady, lasting, and high-speed running [9] (Figure 1). The ostrich weighs 100 kg, with a continuous running speed of about 60 km/h, a sprint speed of more than 70 km/h, and can last for about 30 min [10]. Ostriches have such obvious advantages in speed and energy saving, partly because of their unique leg and foot structure [11]. The muscle at the root of the ostrich’s thigh accounts for 80% of the weight of the whole lower limb [12], which can reduce the moment of inertia of the ostrich’s leg during movement and facilitate the rapid change of its speed. In addition, the length of the ostrich’s calf bone is similar to that of the thigh bone, and there are few muscles in the knee and calf. Therefore, the leg has a large folding/unfolding ratio. What is more, the distance between the two legs of an ostrich is four-fifths of its body width; this ratio makes it difficult to fall when the upper body swings from side to side.
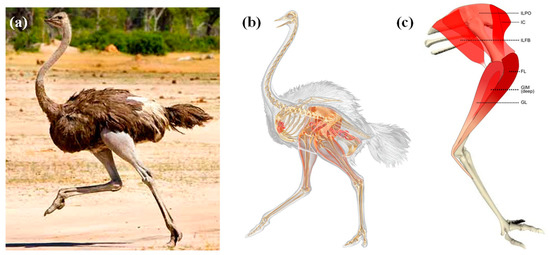
Figure 1.
Ostrich and its leg structure: (a) ostrich running, (b) bone and muscle structure, (c) leg structure.
What is more important, the ostrich’s legs have good buffering performance because the muscles and tendons on the ostrich’s thigh are mixed, and the tendons have good elasticity, which slows down the impact acceleration of the legs when they collide with the ground. This characteristic, in turn, helps the ostrich keep running at a high speed on an uneven road without damaging the legs due to the mild collision with the ground [13].
3. Structural Characteristics of Bionic Legs
The leg is an important part of a robot and plays a very important role in the movement of a legged robot [14]. According to the principle of engineering bionics, the superior performance of the ostrich leg can be applied to the design of a biped robot leg structure. The single leg designed in this experiment is shown in Figure 2. Two motors are set at the hip to simulate the hip and knee joints of an ostrich. The hip motor (M) is mainly used to control the swing of the leg. The knee motor (N) is mainly used to control the expansion and contraction of the leg. In order to imitate the tendon of the thigh, an additional joint is set at point P and constrained with a leaf spring to form the elastic joint, and BQ is also set as a leaf spring to reduce impact acceleration [15]. The center of mass (COM) of the whole leg is located at its root, which is similar to the mass distribution of the ostrich leg. In order to imitate the meniscus buffer structure of the ostrich knee joint, the output link of the driving motor for the toe joint is set as a leaf spring, so that the impact acceleration will be greatly reduced when the leg collides with the ground. In addition, the energy stored in the leaf spring can help the bionic leg take off from the ground during running [16]. In terms of leg length distribution, following the leg size of an ostrich, the length ratio of connecting rod AF to AN is set to 0.75.
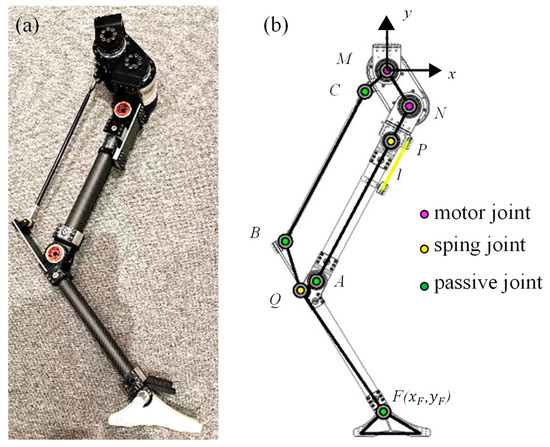
Figure 2.
Schematic diagram of the single-leg structure: (a) prototype, (b) schematic diagram of the structure.
Analyzed in essence, the leg belongs to a seven-link parallel structure. The weight of the connecting rod is much lighter than that of the motor, thus it can be ignored in order to facilitate calculation. If the leg stands on the ground, the corresponding static balance relationships are:
The letters in the above equations correspond to those in Figure 2b.
The leaf springs of elastic joints are equivalent to cantilever beam under loading, and the relationship between its stiffness and elastic modulus is as follows:
where is the bending force, is the elastic modulus, is the inertial moment, and L is the length of the cantilever beam.
where is the moment of the cantilever beam, is the joint angle, in rad, b = 50 mm, h = 3 mm considering the influence of connectors at both ends, L is equal to the 0.57, and is the length of the leaf spring. Therefore,
3.1. Influencing Factors of Equivalent Elastic Modulus of the Ostrich-like Leg
Different from active compliance control [17], this mechanism improves the buffering properties through passive compliance. The material 65 Mn spring-steel is selected for the two leaf springs P and Q, thus the elastic moduli Ep and Eq are both 197 GPa, and the compression force range is from 300 N to 1300 N. This loading range is employed here because the weight of a single bionic leg is 17 kg. Considering the jump gait during rapid movement, the maximum impact force is more than 300 N. As shown in Figure 3, the equivalent elastic modulus () of the leg, i.e., the change rate of the compressive force to compression, decreases during the process of compression. The data fitting of the equivalent elastic modulus is shown in Formula (10), and the fitting error is 2.679, indicating that the ability of the spring leg to store elastic properties is nonlinear and decreases with the increment of compression.
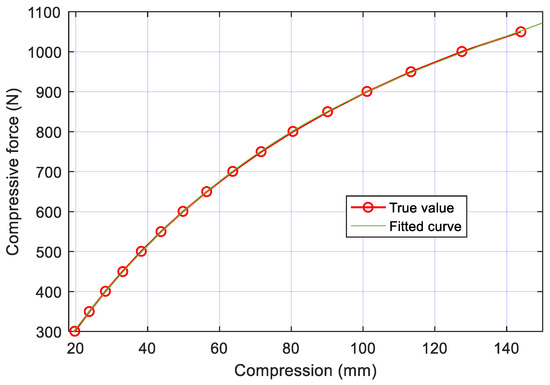
Figure 3.
Leg length change under different compressive forces, Ep = 197 GPa, Eq = 197 GPa, initial length = 800.9 mm.
3.2. Influence of Ep, Eq on the and Fx of the Ostrich-like Leg
The core problem we are concerned about is the influence of the leaf spring as a flexible part on the energy storage and buffering capacity of the structure. Therefore, the effect of the elastic modulus of the P and Q leaf springs on the equivalent elastic modulus () of the structure is analyzed. When Eq = 197 GPa, the initial length equals 800.9 mm and the compressive force F equals 300 N. The change of the equivalent elastic modulus with Ep is shown in Figure 4. The results indicate that the increasing rate of decreases with the increase in Ep. The horizontal swing of the leg first decreases, arriving at 0, and then increases positively, the rate of change decreasing with the increasing Ep.
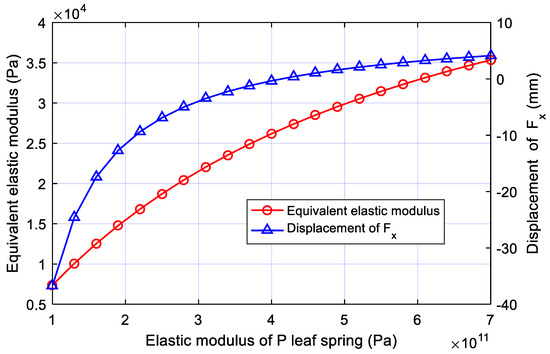
Figure 4.
Variation of equivalent elastic modulus and the x-direction displacement of the bionic leg () with Ep, Eq = 197 GPa, initial length 800.9 mm, and the compressive force is 300 N.
While simplifying the structure as a spring, we find that when the compressive force is applied, the F point of the leg (Figure 2) will move in the x-direction (), which indicates that the robot will move in the horizontal plane when squatting. This may cause the change of the robot’s centroid of mass (COM) on the horizontal plane, and it should be corrected by the control algorithm. In order to reduce the adjusting time, it is feasible that the change on the horizontal plane is small during the squatting process of the robot, so the Ep and Eq that makes the close to 0 should be preferred.
In order to analyze the influence of Eq on the equivalent elastic modulus of the spring leg, we set Ep = 197 GPa and initial length = 800.9 mm (Figure 5). The value range of Eq is 100–700 GPa and the elastic modulus of few materials exceeds 300 GPa. Here, it is extended to 700 GPa to analyze the trend of change. The results show that both the equivalent elastic modulus and the displacement of the F point of the structure increase with Eq, and the rate of change keeps decreasing.
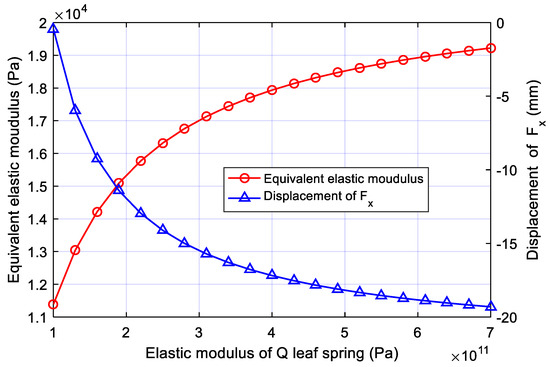
Figure 5.
Variation of equivalent elastic modulus and displacement in the x-direction of the bionic leg with Eq, Ep = 197 GPa, initial length 800.9 mm, and compressive force 300 N.
When Ep is 197 GPa, the initial length is 800.9 mm, and the compressive force is 300 N, from the perspective of control stability, the greater the elastic modulus of the Q leaf spring, the greater the swinging of the fuselage. Generally, the larger the elastic modulus of the leaf spring, the lower the flexibility of the structure; however, the rule breaks here. The cause is the parallel structure characteristics of bionic legs. If the elastic modulus of the P leaf spring is smaller than that of the Q leaf spring, more deformation is concentrated on the P leaf spring, resulting in an increment in the horizontal displacement of the upper end of the fuselage. If the P and Q elastic moduli are configured in an appropriate proportion, the sloshing on the horizontal plane of the fuselage can be close to 0.
For the underactuated parallel mechanism [18], the swing of the fuselage cannot be fully controlled by the driving motors. Because the flexible parts of the leg will lose their static balance in a short time after being loaded, they inevitably have a process of swinging to consume energy and rebalance. The superposition of this swinging and the active rotation of the motors will reduce the locomotion stability of the robot.
The equivalent elastic modulus can be controlled by the thickness of the leaf spring; specifically, the value of the elastic modulus can be increased by adding the number of leaf springs. Therefore, when the elastic modulus of the leaf spring needs to be increased, the material of the spring does not need to be changed. It is also effective to stack and fix two or more original leaf springs to the connection position of the leg.
Moreover, it should be noted that the influence of the Q leaf spring here is limited. The reason is that the elastic modulus of most materials that can be employed as the leaf springs is below 250 GPa, therefore the displacement of in this range is below 15 mm for the bionic leg with an initial length of 800.9 mm, so it has little influence on the control stability.
In order to verify the universality of the above laws, the variation trend of equivalent elastic modulus with Ep under different Eq is investigated. As shown in Figure 6, the blue curves represent the value of and red curves represent the of the single leg. Among the curves with the same colors (red or blue), the lighter colors represent smaller Eq, and the curves with darker colors correspond to the values on the condition of larger Eq. The results show that the value of increases with Eq under the same Ep condition, and so does the increment rate. With the increase in the value of Eq, the displacement of the F point in the x-direction, , increases, and the rate increases too. The laws presented above are the same as the ones illustrated in Figure 5, indicating that the variation trend is universal.
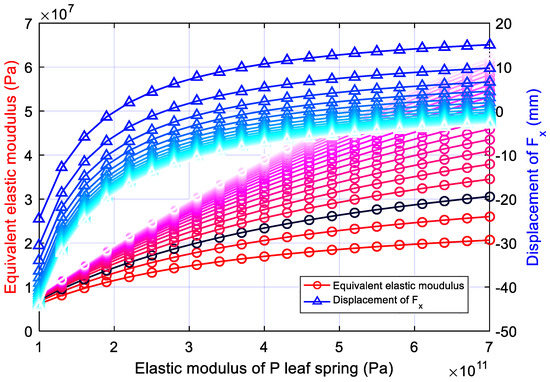
Figure 6.
Effect of different Ep and Eq on the equivalent elastic modulus and x-direction displacement () of the bionic leg.
As can be seen from Figure 6, with appropriate values of Ep and Eq, the horizontal displacement in the x-direction can turn to 0, but this does not mean that the horizontal displacement of the F point of the bionic leg in Figure 2 can remain unchanged in the whole process of locomotion, because the other two influencing factors, namely the initial length and load, will also lead to the change in the displacement of the F point in the x-direction. Therefore the absolute zero horizontal displacement in the process will not be realized, while a deformation range that approximates zero can be selected.
3.3. Influence of Initial Length to of the Ostrich-like Leg
The initial length is adjusted by the angle at points M and N. The effect of the initial length of the spring leg on . increases with the initial length, and the variation rate also increases with the initial length. This rule allows us to adjust the length of the leg on the appropriate premise so that the leg can store more energy during impact.
decreases first and then increases with the increase of the initial length. The lowest extreme point is located at about 840 mm (Figure 7). Therefore, the leg length should be set near this value, at which the shaking of the upper body during locomotion turns out to be the least, in theory.
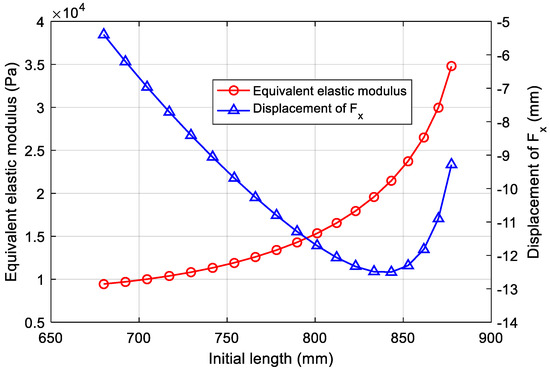
Figure 7.
Effect of different initial lengths on the equivalent elastic moduli and the lateral displacement of the bionic leg.
In order to eliminate the interference of randomly selected compressive force on the above conclusions, The variation law of and is obtained under different initial lengths and loads, as shown in Figure 8. increases with the increment of compressive force in a static equilibrium state at the same initial length, and the increment of the elastic modulus increases monotonously. also increases with the compression force, and the increment is the largest when the initial height is about 840 mm, while first decreases and then increases with compressive force when the initial height is about 680 mm.
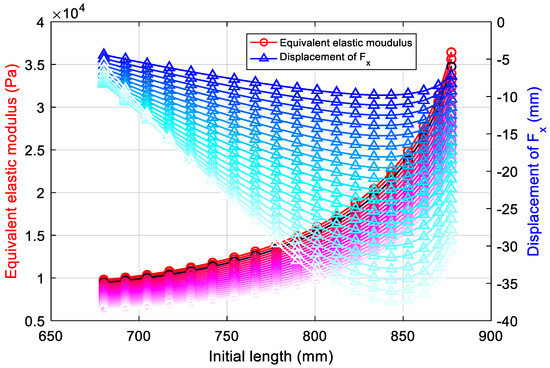
Figure 8.
Effect of the and of the bionic leg under different compression forces and initial lengths.
4. Buffering Characteristics of the Bionic Leg
4.1. The Energy Storage of the Leaf Spring
The influence of Ep and Eq on energy storage is reflected in the rotation angle of the leaf spring under compression. The stored energy increases with the increment of the rotation angle. Therefore, the change of energy stored in the leaf spring with compression force is calculated according to Formula (1):
where, = 15, = −0.082, and = 1.9
where the initial length is 800.9 mm and Ep and Eq are both equal to 197 GPa.
The variation law of compressive force to can be calculated and is shown in Figure 9, by calculating with regard to the change of compressive force.
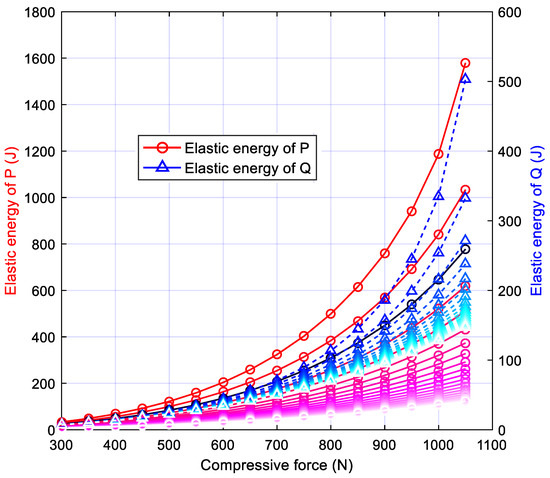
Figure 9.
Energy storage of two leaf springs of the bionic leg under different compression forces and Ep.
As shown in Figure 9, the blue curves represent the elastic energy of Q and the red curves represent the elastic energy of P of the single bionic leg. Among the curves with the same colors (red or blue), the lighter colors represent smaller Ep, and the curves with darker colors correspond to the values on the condition of larger Ep. It can be seen from the trend that the energy stored in the P and Q leaf springs increases with the compression force, and the rate is also increasing. Under the same compression force, the stored energy of P and Q increases with the increment of the elastic modulus of the P leaf spring, The increasing rate of P is larger than that of Q.
4.2. Buffering Model Prediction
The buffering performance of the structure is usually evaluated by impact acceleration during the compression of the bionic leg:
where = + + is the compression when considering the leg as spring. Ep = 197 GPa, Eq = 197 GPa, and the initial length is equal to 800.9 mm:
where = 100 mm, y is obtained through Newton’s iterative calculation, and the value is 90.14 mm:
The maximum impact acceleration, , is equal to 1.57 g.
5. Experimental Process and Analysis
An experiment is designed to test the accuracy of the above kinematic model. The peak value of the acceleration while the leg impacts the ground is measured by the acceleration sensor. The sensor is set at the upper end of the bionic leg, which is buffered by the leaf spring (Figure 10).

Figure 10.
Impact acceleration detection device: (a) the single leg assembled on the test platform, (b) an enlarged view of the single-leg installation, (c) the acceleration sensor, and (d) the power supply and data acquisition system.
Based on the designed model, the single leg was processed and assembled. The maximum torque of the hip and knee driving motor is 60 N·m. The maximum speed is 60 rpm, the rated voltage is 48 V, and Ethernet communication was adopted. The movable end of the bionic leg was mounted on the movable table of the assembled frames. The movable table has one degree of freedom along the vertical direction. The acceleration sensor was fixed on the top surface of a movable table. The impact acceleration measurement system includes a sensor, NI data acquisition system, DC power supply, and a LabVIEW data display terminal. The sensor range is 30 g, the corresponding voltage of 1 g is 0.02 V, and the sampling frequency is set to 10 kHz, which can capture the impact wave.
The motor was powered to maintain its designed behavior after the fixing of the leg. The leg was let down from a height of 10 cm and the impact acceleration was measured at the upper end of the movable table. The data measured by the sensor is illustrated in Figure 11. According to the analysis of the data results, the frequency of the impact wave is about 3 Hz, which is very low due to the buffering of the leaf springs. The measured value of the first wave peak is 0.04 V, indicating that the impact acceleration is about 2 g, which is close to the calculated value. There may be two factors responsible for the prediction error: (1) connection mode, the leaf spring is connected to the fuselage by screws, thus the actual action length of the leaf spring is uncertain; (2) the complex stress state of the leaf spring is simplified as a plane force state in the model, however, it will be subjected to the force along the width direction under actual conditions, which can affect the prediction results of the model to a certain extent.
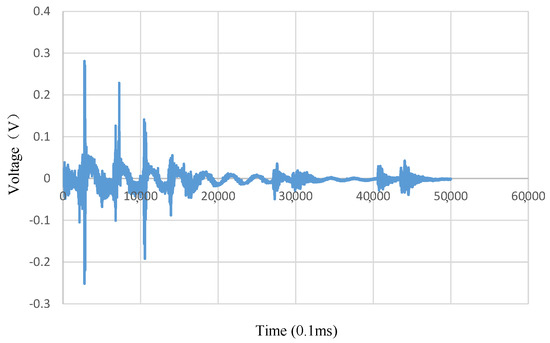
Figure 11.
Signal voltage of bionic leg detected by the acceleration sensor.
The subsequent decaying waveform indicates that there are several damped cyclic movements of the bionic leg after the first impact.
The leaf spring is an important flexible part of the mechanism. If the elastic modulus of the leaf spring is extremely large, it would not have an ideal buffering effect, while a too-small elastic modulus would worsen the control accuracy. The mechanical properties of spring steel are most suitable for the requirements of this experiment, however, its determination is high density. Therefore, several fiber-reinforced composites were tried as illustrated in Figure 12, including high-strength carbon fiber-reinforced thermosetting composites (HSCF + TSM), high-strength carbon fiber-reinforced thermoplastic composites (HSCF + TPM), high-strength glass fiber-reinforced thermosetting (HSGF + TSM) and thermoplastic (HSGF + TPM) matrix materials, and medium-strength glass fiber-reinforced thermosetting (MSGF + TSM) and thermoplastic (MSGF + TPM) matrix materials.

Figure 12.
Failure of leaf springs made of different materials.
Various thicknesses of leaf springs were employed for these materials as required because the stiffness and strength of each plate are different. The results indicate that no matter what material of the matrix of the composite is used, the brittle fracture always occurs in carbon fiber reinforced composite, indicating that the high strength and low elongation of carbon fiber make it unsuitable for leaf spring materials.
The toughness of the glass fiber composite plate is much better than that of carbon fiber. Even if the medium-strength glass fiber-reinforced and thermoplastic polymer-matrixed (MSGF + TPM) plate breaks at the joint, its property can be further improved by optimizing the structure of the joint. The HSGF + TPM plate is proved to be the most suitable material, better than the spring steel after a comprehensive comparison in strength and weight.
In addition, it is found through experiments that the bending strength of the leaf spring is different even for the same material and total thickness, For example, the bending leaf spring shown in Figure 12 is made of five 2 mm thick stacked plates with a 10 mm total thickness, whose material is HSGF + TPM, and the bionic leg cannot stand on the ground completely after the motor is powered on, which results from over-bending at the Q leaf spring. However, two 5 mm stacked plates with a 10 mm total thickness are qualified for jumping even when made of the same material.
6. Prospect
On the basis of the above exploration, further research on the following aspects is planned:
Firstly, the two legs should be assembled to improve the stability in the process of standing up and squatting and the buffering effect of the leaf spring in boosting gait should be analyzed.
Subsequently, as the leaf spring is the core part of the bionic leg, and its performance directly affects the buffering and jumping ability of the bionic leg, the analysis of the optimal value of the mechanical performance of the leaf spring is necessary for updating the bionic leg.
Finally, further improvements to the structure are needed to reduce the movement of the center of mass on the horizontal plane. The center of mass should be specially investigated and adjusted by controlling the rotation angle of the motors.
7. Conclusions
This paper intends to obtain a kind of robotic leg with a similar buffering capacity to that of the ostrich based on the idea of bionics. The structural and functional characteristics of the ostrich-like leg are investigated and the buffering performance of the seven-link parallel mechanism is analyzed from the perspective of the leaf spring. The feasibility of the kinematic model is verified by experiments. Attempts are made to optimize the material of the leaf spring. The following conclusions could be drawn:
- 1.
- For a single leg with an initial length of 800.9 mm and a compressive force of 300 N, the equivalent elastic modulus of the structure () and the displacement of point F in the x-direction (Fx) also increases with the increase of the elastic moduli of the P and Q leaf springs, and the rate of change decreases with the elastic moduli of the leaf springs.
- 2.
- Compared with the ~1000 Hz impact wave frequency of the rigid body, the frequency of this leg is about 3 Hz, indicating that the structure has good buffering performance.
- 3.
- The initial height of the bionic leg has a significant impact on the equivalent elastic modulus of the structure and the movement stability of the robot in the horizontal plane. When the initial height is about 850 mm, the stability of the robot is the best.
- 4.
- The calculation result of impact acceleration by the kinematic model is close to the measured one, and the error is due to the connection mode and the complex stress form of the leaf spring.
- 5.
- Due to the small bending strain of carbon fiber-reinforced leaf spring, it has less ability for energy storage in this structure and is prone to brittle fracture. The material of HSCF + TPM composite has the merits of being lightweight and having good impact resistance. It may be ideal for the spring leaf of a bionic leg.
Author Contributions
D.N.: theme selection and general planning. R.D.: design of the experiment and investigation of research status. J.T.: writing of the paper. P.Z.: implementation and optimization of the experiment. F.S.: formal analysis and check of the paper. J.G.: contact relevant experimental equipment. Y.F.: supervision. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded by the National Natural Science Foundation of the People’s Republic of China, grant number 51905495, and supported by Zhejiang Provincial Natural Science Foundation of China under Grant No. LQ22E050024, and China Postdoctoral Science Foundation (No. 2021M692955).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not Applicable.
Acknowledgments
The authors would like to thank Doudou Chen from Shiyanjia Lab (www.shiyanjia.com, accessed on 22 March 2022) for the tests of mechanical properties of the specimens.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wood, B. Four legs good, two legs better. Nature 1993, 363, 587–588. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Ma, S.; Shen, Y. A Motion Planning Approach for Nonprehensile Manipulation and Locomotion Tasks of a Legged Robot. IEEE Trans. Robot. 2020, 36, 855–874. [Google Scholar] [CrossRef]
- He, G.; Geng, Z. Exponentially stabilizing an one-legged hopping robot with non-SLIP model in flight phase. Mechatronics 2009, 19, 364–374. [Google Scholar] [CrossRef]
- Komarsofla, A.K.; Yazdi, E.A.; Eghtesad, M. Dynamic Modeling and Control of a Novel One-Legged Hopping Robot. Robotica 2021, 39, 1692–1710. [Google Scholar] [CrossRef]
- Larin, V.B. A 3D model of one-legged hopping machine. Int. Appl. Mech. 2004, 40, 583–591. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Jin, Z.L.; Zhao, Y.M. Dynamics analysis of leg mechanism of six-legged firefighting robot. J. Mech. Sci. Technol. 2018, 32, 351–361. [Google Scholar] [CrossRef]
- He, G.-P.; Tan, X.-L.; Zhang, X.-H. Modeling, motion planning, and control of one-legged hopping robot actuated by two arms. Mech. Mach. Theory 2008, 43, 33–49. [Google Scholar] [CrossRef]
- Luo, G.; Du, R.; Zhu, S. Design and Dynamic Analysis of a Compliant Leg Configuration towards the Biped Robot’s Spring-Like Walking. J. Intell. Robot. Syst. 2022, 104, 64. [Google Scholar] [CrossRef]
- Muyshondt, P.G.G.; Claes, R.; Aerts, P. Quasi-static and dynamic motions of the columellar footplate in ostrich (Struthio camelus) measured ex vivo. Hear. Res. 2018, 357, 10–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schaller, N.U.; Herkner, B.; Villa, R. The intertarsal joint of the ostrich (Struthio camelus): Anatomical examination and function of passive structures in locomotion. J. Anat. 2009, 214, 830–847. [Google Scholar] [CrossRef] [PubMed]
- Smith, N.C.; Payne, R.C.; Jespers, K.J. Muscle moment arms of pelvic limb muscles of the ostrich (Struthio camelus). J. Anat. 2007, 211, 313–324. [Google Scholar] [CrossRef] [PubMed]
- Ramesh, P.; Sundaresan, S.S.; Shobana, N. Structural studies of hemoglobin from two flightless birds, ostrich and turkey: Insights into their differing oxygen-binding properties. Acta Crystallogr. D 2021, 77, 690–702. [Google Scholar] [CrossRef] [PubMed]
- Smith, N.C.; Wilson, A.M.; Jespers, K.J. Muscle architecture and functional anatomy of the pelvic limb of the ostrich (Struthio camelus). J. Anat. 2006, 209, 765–779. [Google Scholar] [CrossRef] [PubMed]
- Du, R.; Song, S.; Yuan, H. Discussion on the Stiffness of the Drive Chain in the Legs of Biped Robots. Actuators 2022, 11, 79. [Google Scholar] [CrossRef]
- Rodino, S.; Curcio, E.M.; Di Bella, A. Design, Simulation, and Preliminary Validation of a Four-Legged Robot. Machines 2020, 8, 82. [Google Scholar] [CrossRef]
- Wang, F.T.; Li, C.B.; Niu, S.H. Design and Analysis of a Spherical Robot with Rolling and Jumping Modes for Deep Space Exploration. Machines 2022, 10, 126. [Google Scholar] [CrossRef]
- Fabrègue, D.; Mouawad, B.; Hutchinson, C.R. Enhanced recovery and recrystallization of metals due to an applied current. Scr. Mater. 2014, 92, 3–6. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. Forward and Inverse Dynamics of a Unicycle-Like Mobile Robot. Machines 2019, 7, 5. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).