Design and Control of a Hydraulic Hexapod Robot with a Two-Stage Supply Pressure Hydraulic System
Abstract
1. Introduction
- A SMRC controller is designed to improve the joint trajectory tracking performance;
- The high order sliding mode differentiator (HOSMD) is designed to help get the angular velocity and acceleration of HHR;
- A two-stage supply pressure hydraulic system (TSS) is utilized in HHR to save the energy of legs in the swing phase.
2. HHR System Overview
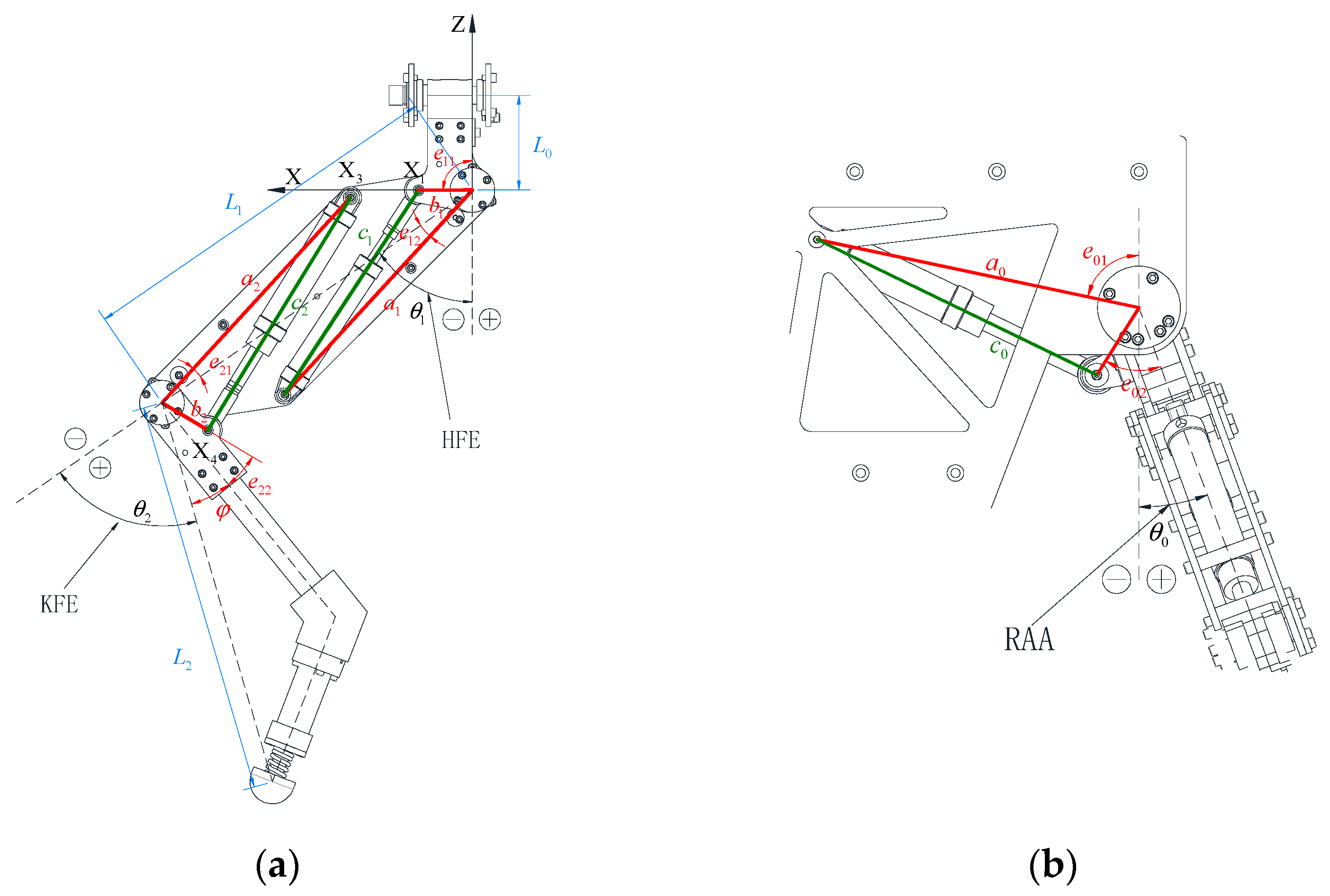
2.1. Mechanical Structure
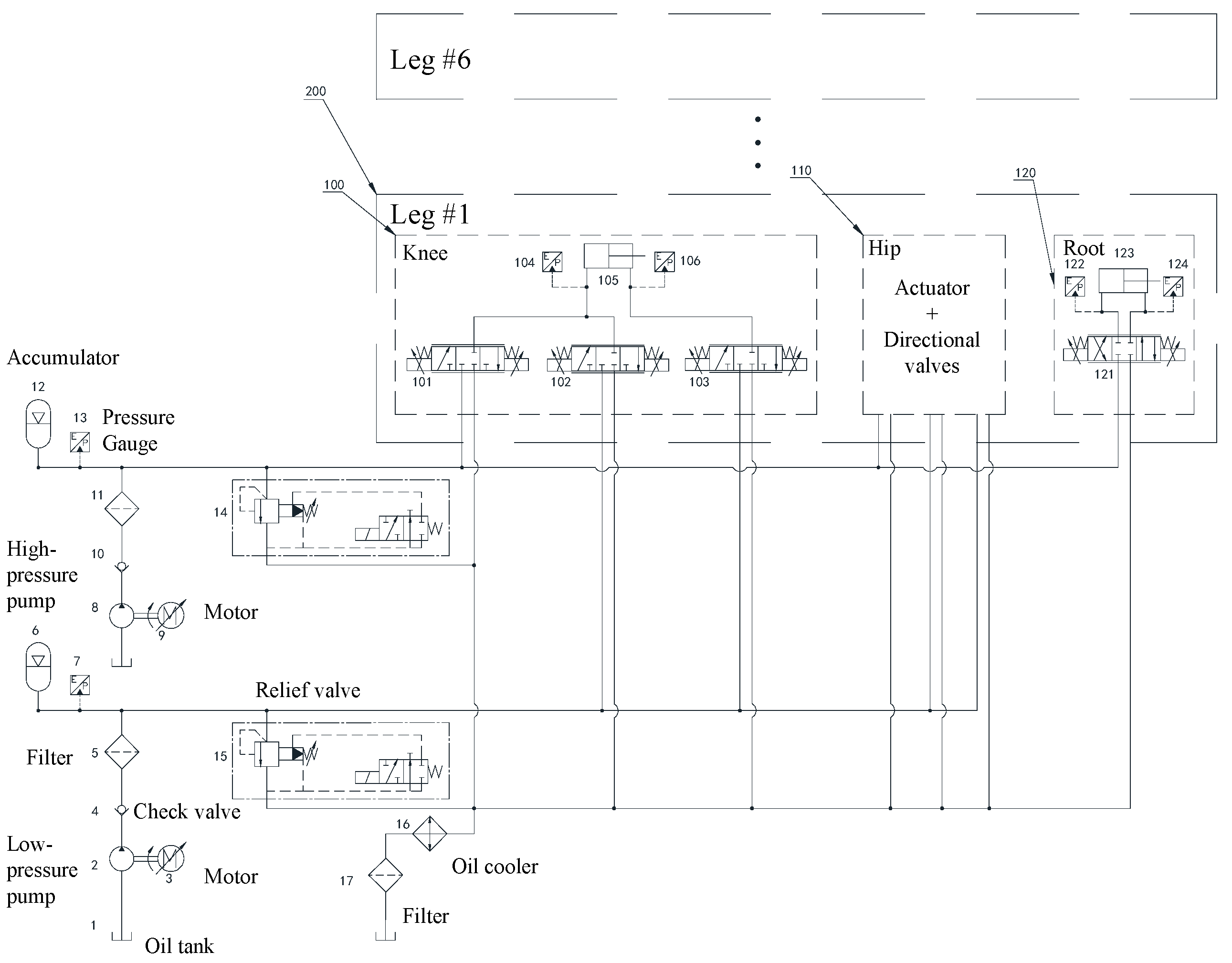
2.2. Onboard Hydraulic System
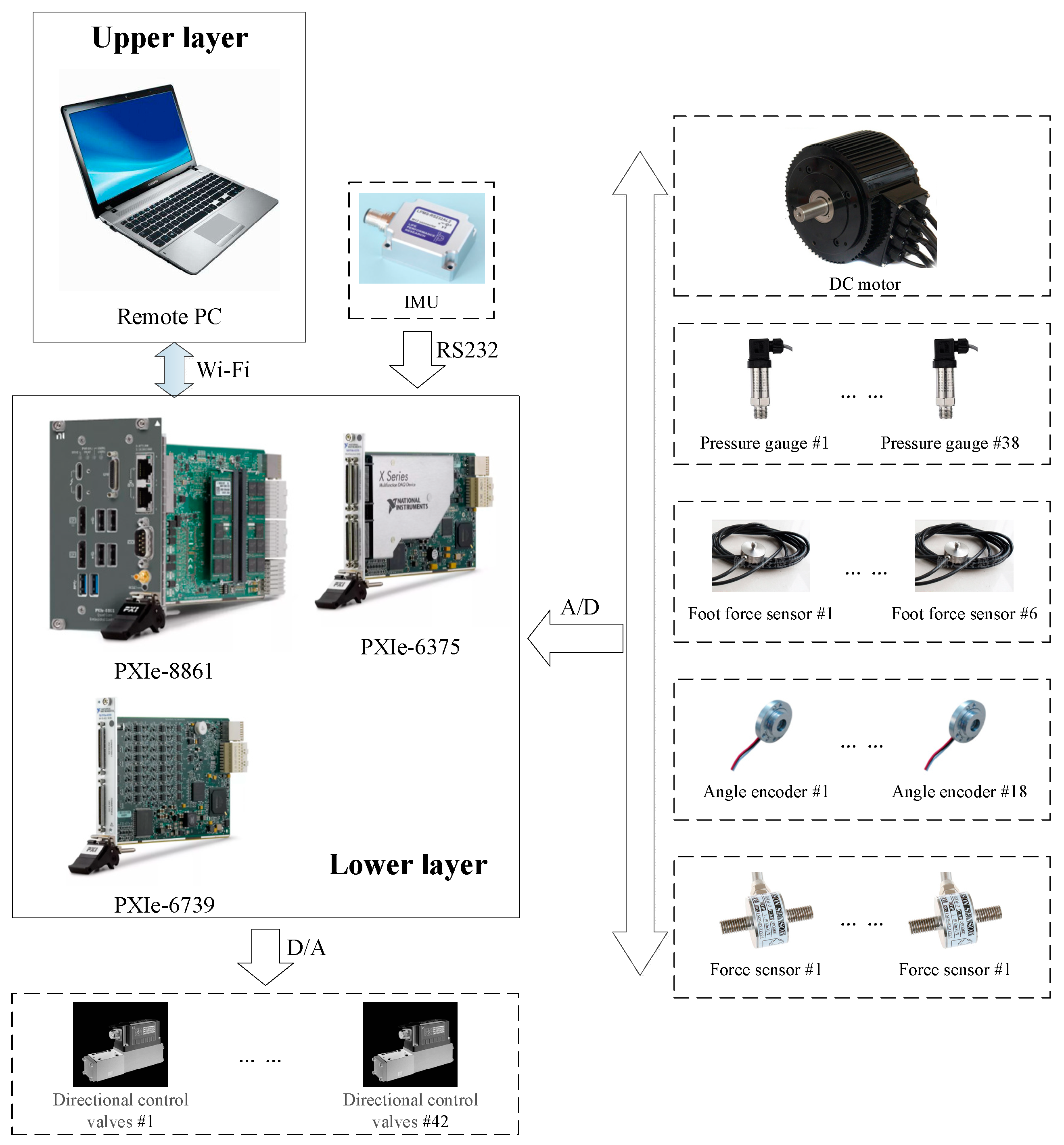
2.3. Control System Architecture
3. System Modelling
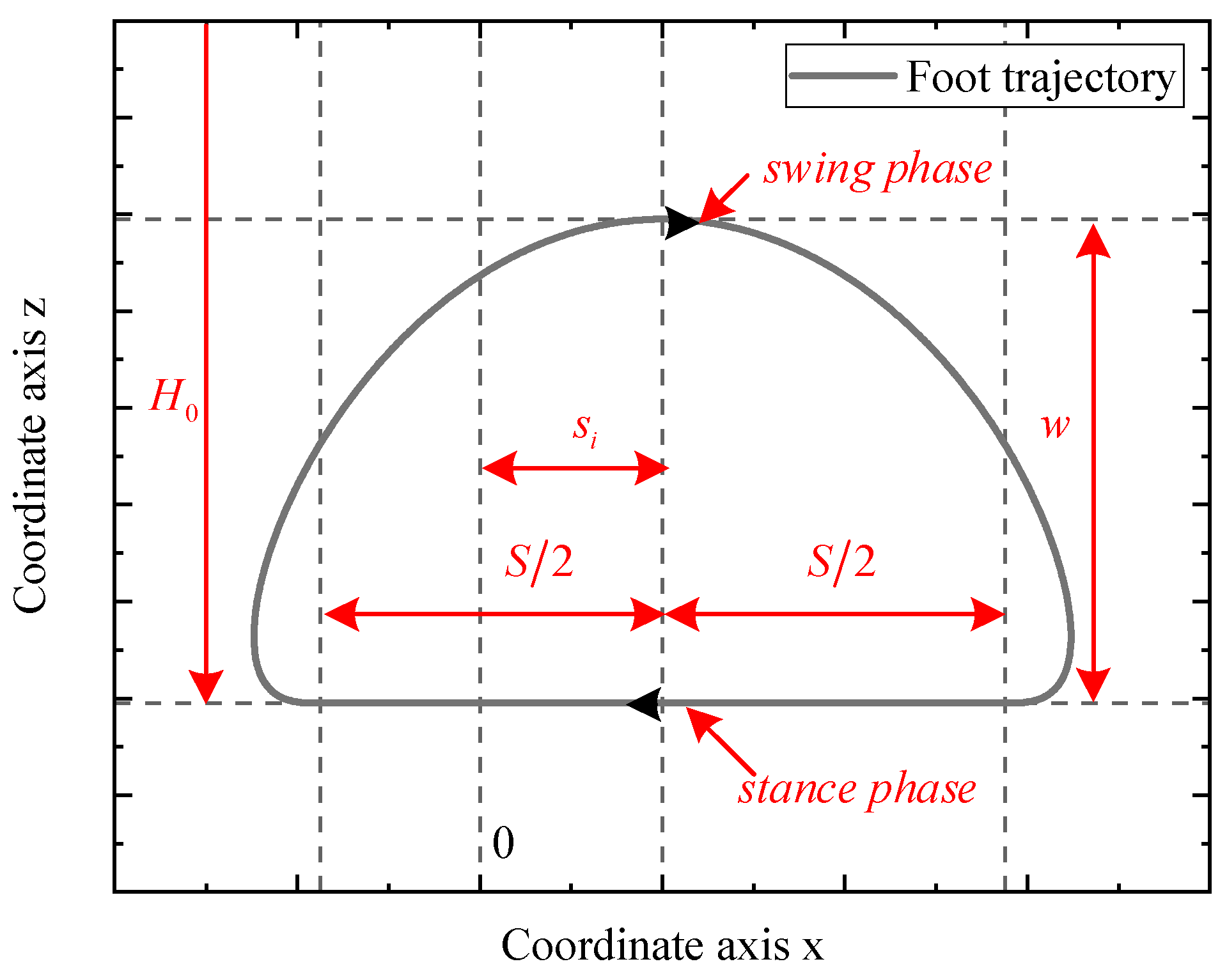
3.1. Kinematics Modelling
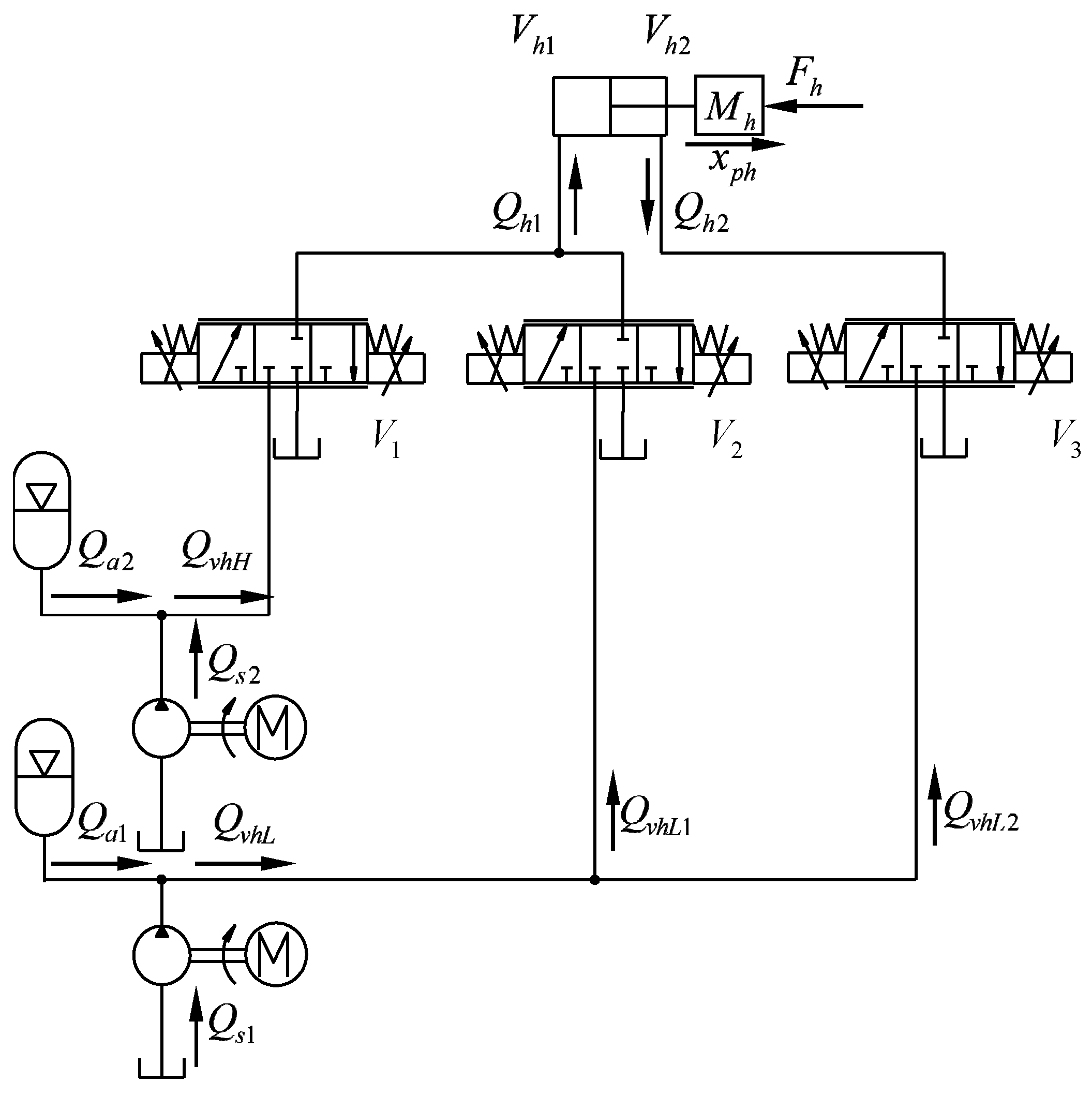
3.2. Hydraulic System Modelling
4. Controller Design
4.1. Valve Configuration in TSS
4.2. Sliding Mode Repetitive Control
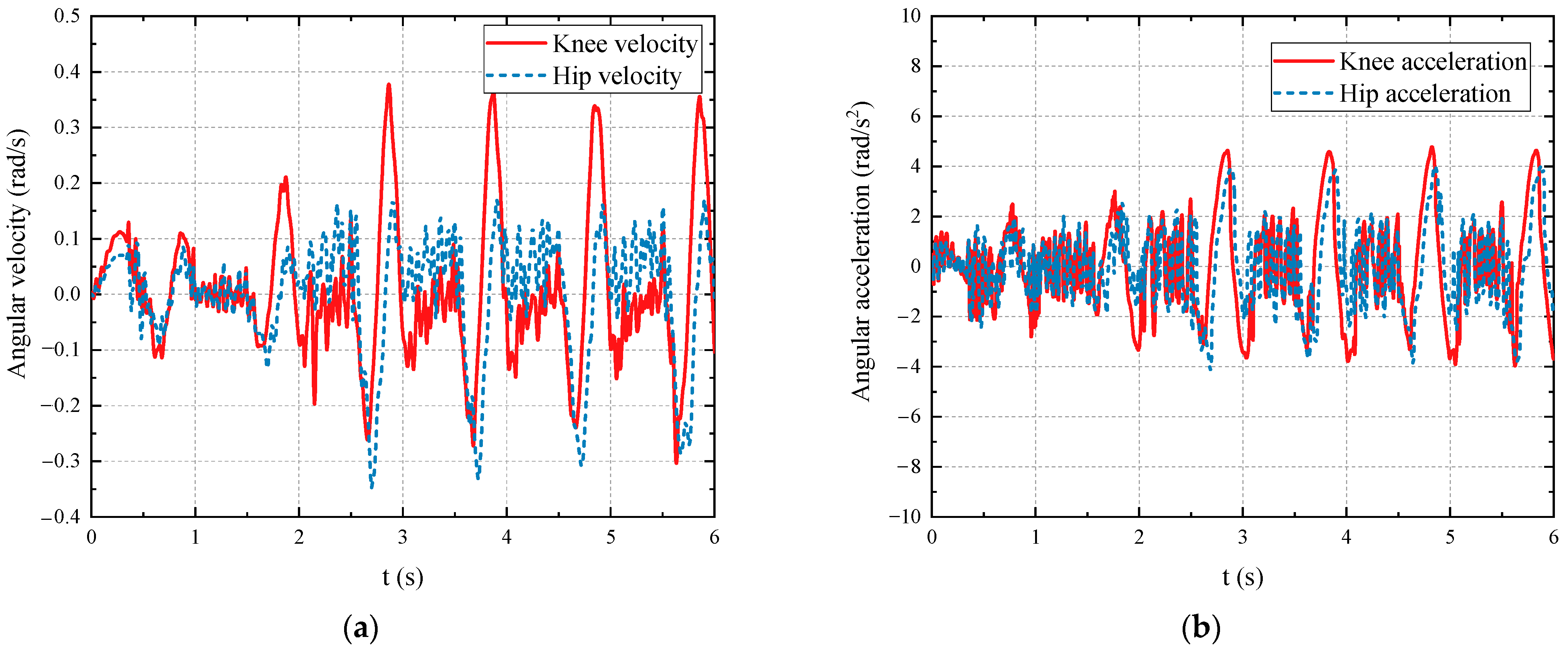
4.3. High-Order Sliding Mode Differentiator
5. Simulation and Analysis
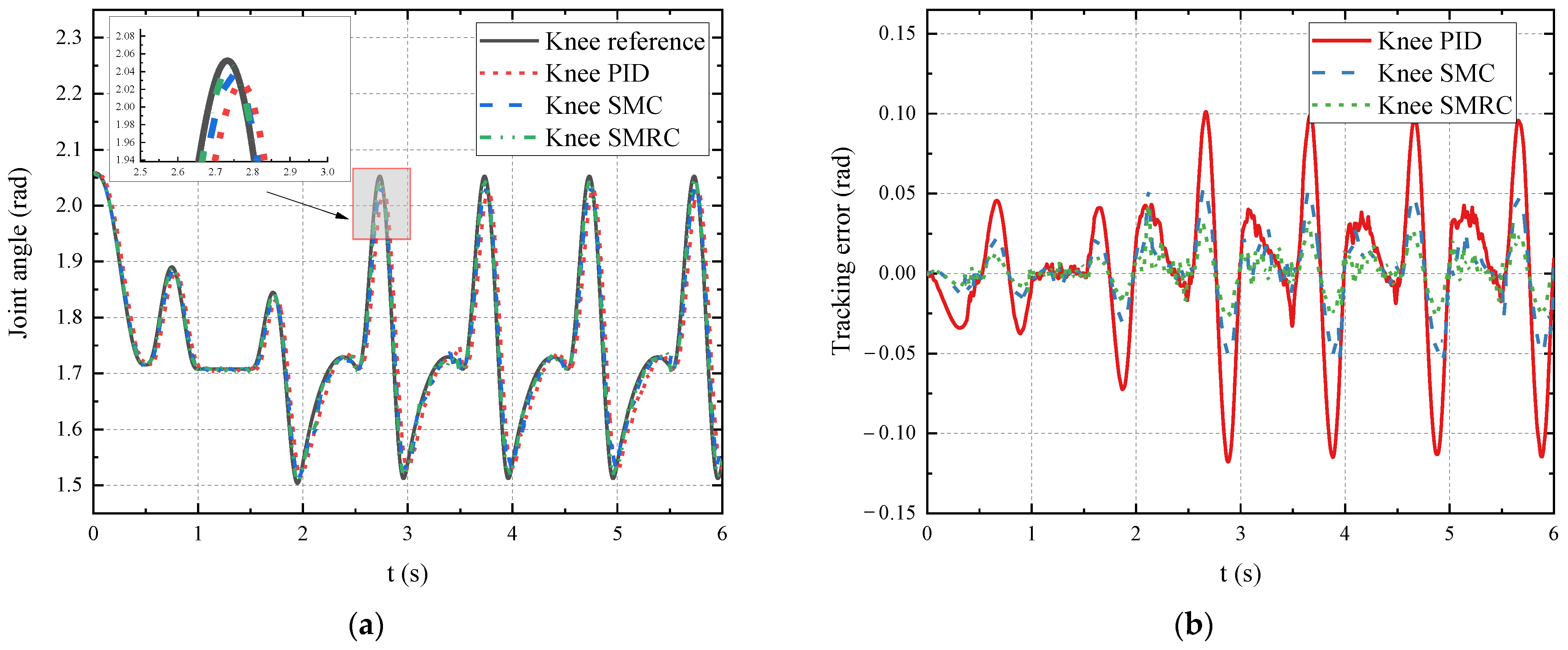
5.1. Joint Trajectory Tracking
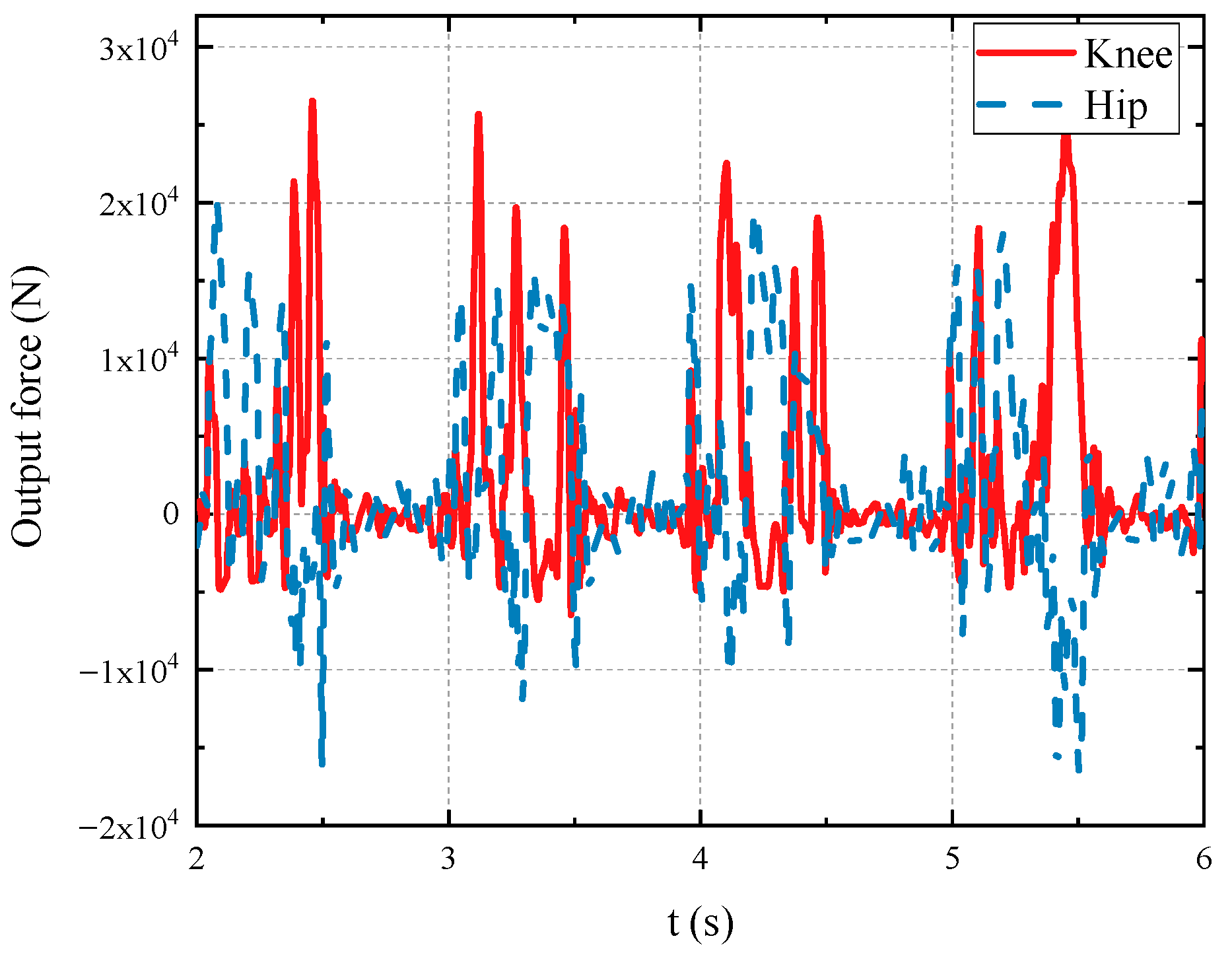
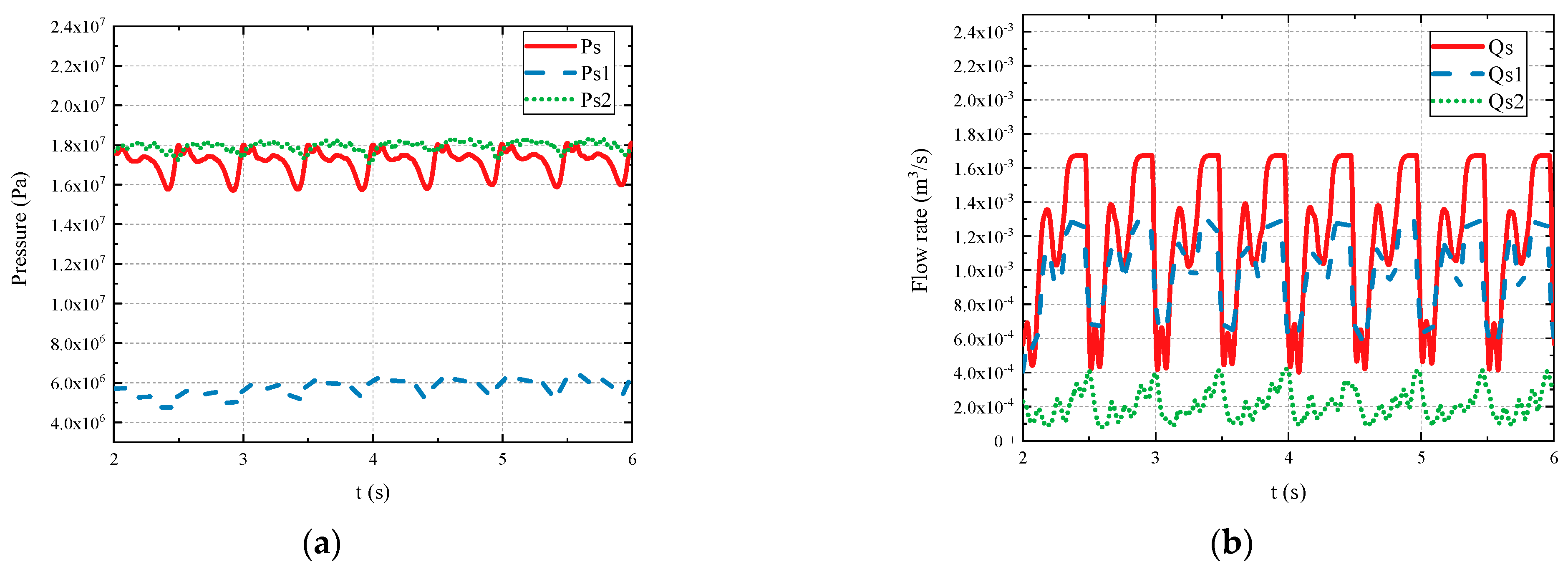
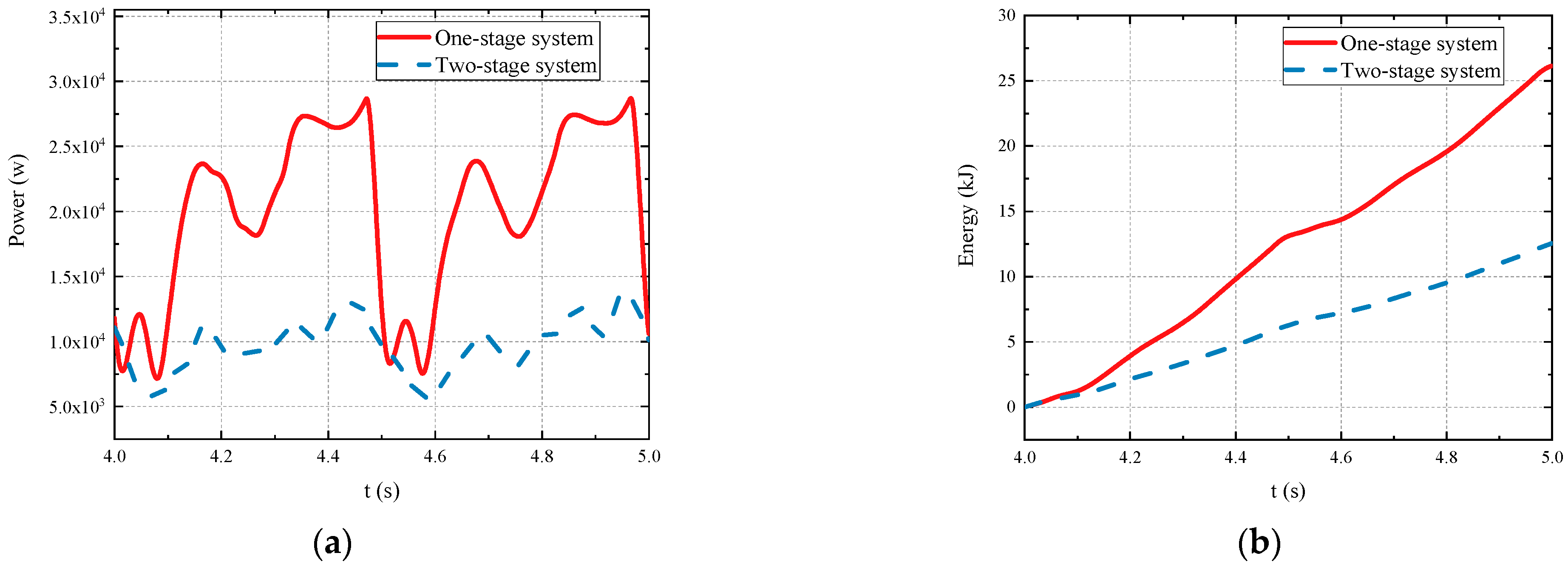
5.2. Energy Consumption Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Suzumori, K.; Faudzi, A.A. Trends in hydraulic actuators and components in legged and tough robots: A review. Adv. Robot. 2018, 32, 458–476. [Google Scholar] [CrossRef]
- He, J.; Gao, F. Mechanism, actuation, perception, and control of highly dynamic multilegged robots: A review. Chin. J. Mech. Eng. 2020, 33, 1–30. [Google Scholar] [CrossRef]
- Tedeschi, F.; Carbone, G. Design issues for hexapod walking robots. Robotics 2014, 3, 181–206. [Google Scholar] [CrossRef]
- Raibert, M.; Blankespoor, K.; Nelson, G.; Playter, R. BigDog, the rough-terrain quadruped robot. IFAC Proc. Vol. 2008, 41, 10822–10825. [Google Scholar] [CrossRef]
- Semini, C.; Tsagarakis, N.G.; Guglielmino, E.; Focchi, M.; Cannella, F.; Caldwell, D.G. Design of HyQ—A hydraulically and electrically actuated quadruped robot. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2011, 225, 831–849. [Google Scholar] [CrossRef]
- Khan, H.; Kitano, S.; Frigerio, M.; Camurri, M.; Barasuol, V.; Featherstone, R.; Caldwell, D.G.; Semini, C. Development of the lightweight hydraulic quadruped robot—Minihyq. In Proceedings of the 2015 IEEE International Conference on Technologies for Practical Robot Applications (TePRA), Boston, MA, USA, 11–12 May 2015. [Google Scholar]
- Semini, C.; Barasuol, V.; Goldsmith, J.; Frigerio, M.; Focchi, M.; Gao, Y.; Caldwell, D.G. Design of the hydraulically actuated, torque-controlled quadruped robot hyq2max. IEEE/ASME Trans. Mechatron. 2017, 22, 635–646. [Google Scholar] [CrossRef]
- Jungsan, C.; Jin Tak, K.; Sangdeok, P.; Youngsoo, L.; Kabil, K. Jinpoong, posture control for the external force. In Proceedings of the IEEE ISR 2013, Seoul, Korea, 24–26 October 2013. [Google Scholar]
- Rong, X.; Li, Y.; Ruan, J.; Li, B. Design and simulation for a hydraulic actuated quadruped robot. J. Mech. Sci. Technol. 2012, 26, 1171–1177. [Google Scholar] [CrossRef]
- Chen, T.; Rong, X.; Li, Y.; Ding, C.; Chai, H.; Zhou, L. A compliant control method for robust trot motion of hydraulic actuated quadruped robot. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418813235. [Google Scholar] [CrossRef]
- Yang, K.; Zhou, L.; Rong, X.; Li, Y. Onboard hydraulic system controller design for quadruped robot driven by gasoline engine. Mechatronics 2018, 52, 36–48. [Google Scholar] [CrossRef]
- Chen, X.; Gao, F.; Qi, C.; Tian, X.; Zhang, J. Spring parameters design for the new hydraulic actuated quadruped robot. J. Mech. Robot. 2014, 6, 021003. [Google Scholar] [CrossRef]
- Li, M.; Jiang, Z.; Wang, P.; Sun, L.; Ge, S.S. Control of a quadruped robot with bionic springy legs in trotting gait. J. Bionic Eng. 2014, 11, 188–198. [Google Scholar] [CrossRef]
- Chen, C.; An, H.; Wang, J.; Ma, H.; Wei, Q. Velocity control for trotting of a nudt quadruped robot. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016. [Google Scholar]
- Junyao, G.; Xingguang, D.; Qiang, H.; Huaxin, L.; Zhe, X.; Yi, L.; Xin, L.; Wentao, S. The research of hydraulic quadruped bionic robot design. In Proceedings of the 2013 ICME International Conference on Complex Medical Engineering, Beijing, China, 25–28 May 2013. [Google Scholar]
- Barai, R.K.; Nonami, K. Robust adaptive fuzzy control law for locomotion control of a hexapod robot actuated by hydraulic actuators with dead zone. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006. [Google Scholar]
- Irawan, A.; Nonami, K. Optimal impedance control based on body inertia for a hydraulically driven hexapod robot walking on uneven and extremely soft terrain. J. Field Robot. 2011, 28, 690–713. [Google Scholar] [CrossRef]
- Davliakos, I.; Roditis, I.; Lika, K.; Breki, C.-M.; Papadopoulos, E. Design, development, and control of a tough electrohydraulic hexapod robot for subsea operations. Adv. Robot. 2018, 32, 477–499. [Google Scholar] [CrossRef]
- Tong, Z.; Ye, Z.; Gao, H.; He, J.; Deng, Z. Electro-hydraulic control system and frequency analysis for a hydraulically driven six-legged robot. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016. [Google Scholar]
- Cunha, T.B.; Semini, C.; Guglielmino, E.; De Negri, V.J.; Yang, Y.; Caldwell, D.G. Gain scheduling control for the hydraulic actuation of the hyq robot leg. In Proceedings of the COBEM, Gramado, Brazil, 15–20 November 2009. [Google Scholar]
- Focchi, M.; Guglielmino, E.; Semini, C.; Boaventura, T.; Yang, Y.; Caldwell, D.G. Control of a hydraulically-actuated quad-ruped robot leg. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010. [Google Scholar]
- Bin, C.; Zhongcai, P.; Zhiyong, T. Self-tuning fuzzy-pid control for hydraulic quadruped robot. J. Harbin Inst. Technol. 2016, 48, 140–144. [Google Scholar]
- Ke, X.; Lin, L.; Qing, W.; Hongxu, M. Design of single leg foot force controller for hydraulic actuated quadruped robot based on adrc. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015. [Google Scholar]
- Barai, R.K.; Nonami, K. Locomotion control of a hydraulically actuated hexapod robot by robust adaptive fuzzy control with self-tuned adaptation gain and dead zone fuzzy pre-compensation. J. Intell. Robot. Syst. 2008, 53, 35–56. [Google Scholar] [CrossRef]
- Wei, S.; Sun, C. Robust adaptive dynamic surface control for hydraulic quadruped robot hip joint. Trans. Beijing Inst. Technol. 2016, 36, 599–604. [Google Scholar]
- Wang, C.; Li, Y.; Ruan, J.; Rong, X. Fuzzy sliding mode control of hydraulic cylinders driving a quadruped robot. In Proceedings of the 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010. [Google Scholar]
- Quan, L.; Wei, Z.; Yu, B.; Liang, H. Decoupling control research on test system of hydraulic drive unit of quadruped robot based on diagonal matrix method. Intell. Control Autom. 2013, 04, 287–292. [Google Scholar] [CrossRef][Green Version]
- Gao, B.; Han, W. Neural network model reference decoupling control for single leg joint of hydraulic quadruped robot. Assem. Autom. 2018, 38, 465–475. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, C.; Jin, B.; Zhai, S.; Dong, J. Design and development of an embedded controller for a hydraulic walking robot WLBOT. Appl. Sci. 2021, 11, 5335. [Google Scholar] [CrossRef]
- Seok, S.; Wang, A.; Meng Yee, C.; Otten, D.; Lang, J.; Kim, S. Design principles for highly efficient quadrupeds and implementation on the mit cheetah robot. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013. [Google Scholar]
- Zhai, S.; Jin, B.; Cheng, Y. Mechanical design and gait optimization of hydraulic hexapod robot based on energy conservation. Appl. Sci. 2020, 10, 3884. [Google Scholar] [CrossRef]
- Barasuol, V.; Villarreal-Magaña, O.A.; Sangiah, D.; Frigerio, M.; Baker, M.; Morgan, R.; Medrano-Cerda, G.A.; Caldwell, D.G.; Semini, C. Highly-integrated hydraulic smart actuators and smart manifolds for high-bandwidth force control. Front. Robot. AI 2018, 5, 51. [Google Scholar] [CrossRef] [PubMed]
- Hua, Z.; Rong, X.; Li, Y.; Chai, H.; Li, B.; Zhang, S. Analysis and verification on energy consumption of the quadruped robot with passive compliant hydraulic servo actuator. Appl. Sci. 2020, 10, 340. [Google Scholar] [CrossRef]
- Dong, J.; Jin, B.; Zhai, S.; Liu, Z.; Cheng, Y. Planning and analysis of centroid fluctuation gait for hydraulic hexapod robot. IEEE Access 2021, 9, 63538–63549. [Google Scholar] [CrossRef]
- Yang, K.; Li, Y.; Zhou, L.; Rong, X. Energy efficient foot trajectory of trot motion for hydraulic quadruped robot. Energies 2019, 12, 2514. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, Y.; Ding, L.; Gao, H.; Yu, H.; Liu, Z. Motion planning and simulation verification of a hydraulic hexapod robot based on reducing energy/flow consumption. J. Mech. Sci. Technol. 2015, 29, 4427–4436. [Google Scholar] [CrossRef]
- Tani, K.; Nabae, H.; Hirota, Y.; Endo, G.; Suzumori, K. Walking trajectory design of hydraulic legged robot with limited powered pump. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Guglielmino, E.; Semini, C.; Yang, Y.; Caldwell, D.; Kogler, H.; Scheidl, R. Energy efficient fluid power in autonomous legged robotics. In Proceedings of the Dynamic Systems and Control Conference, Hollywood, CA, USA, 12–14 October 2009. [Google Scholar]
- Xue, Y.; Yang, J.; Shang, J.; Wang, Z. Energy efficient fluid power in autonomous legged robotics based on bionic multi-stage energy supply. Adv. Robot. 2014, 28, 1445–1457. [Google Scholar] [CrossRef]




| Sensor | Model | Input Range | Output Range | Resolution |
|---|---|---|---|---|
| Angular encoder | R22H | 270° | 0–5 V | 0.0659° |
| Pressure | MIK-P300 | 0–25 MPa | 0–5 V | - |
| Force | BSLM-3 | 0–20 kN | 0–5 V | - |
| Foot force | CHHBM-1 | 0–500 kg | 0–5 V | - |
| IMU | LPMS-RS232AL2 | Roll: ±180°, Pitch: ±90°; Yaw: ±180° | - | - |
| Phase | Flow Rate | |||
|---|---|---|---|---|
| Stance phase | On | Off | On | |
| Swing phase | Off | On | On |
| Parameters | Value | Unit |
|---|---|---|
| Stiffness | ||
| Force exponent | 2.2 | - |
| Damping | ||
| Penetration depth | m | |
| Static coefficient | 0.7 | - |
| Dynamic coefficient | 0.55 | - |
| Stiction transition velocity | 0.1 | |
| Friction transition velocity | 10 |
| Constraints | X Direction | Z Direction |
|---|---|---|
| 0 | ||
| 0 | ||
| 0 | 0 | |
| 0 | 0 |
| Parameters | Value | Unit |
|---|---|---|
| 0.0013 | ||
| 50 | kg | |
| 2000 | ||
| 439.823 | rad/s | |
| 0.707 | - |
| Controller | Gain | Value |
|---|---|---|
| PID | 50 | |
| 1 | ||
| 0.001 | ||
| SMRC | 50 | |
| 0.3 | ||
| 0.001 | ||
| 0.01 | ||
| 0.1 | ||
| 10 | ||
| 0.95 |
| Control Strategy | ||||
|---|---|---|---|---|
| PID | 0.141 | 0.118 | 0.043 | 0.046 |
| SMC | 0.092 | 0.054 | 0.027 | 0.022 |
| SMRC | 0.057 | 0.043 | 0.015 | 0.012 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Jin, B.; Dong, J.; Zhai, S.; Tang, X. Design and Control of a Hydraulic Hexapod Robot with a Two-Stage Supply Pressure Hydraulic System. Machines 2022, 10, 305. https://doi.org/10.3390/machines10050305
Liu Z, Jin B, Dong J, Zhai S, Tang X. Design and Control of a Hydraulic Hexapod Robot with a Two-Stage Supply Pressure Hydraulic System. Machines. 2022; 10(5):305. https://doi.org/10.3390/machines10050305
Chicago/Turabian StyleLiu, Ziqi, Bo Jin, Junkui Dong, Shuo Zhai, and Xuan Tang. 2022. "Design and Control of a Hydraulic Hexapod Robot with a Two-Stage Supply Pressure Hydraulic System" Machines 10, no. 5: 305. https://doi.org/10.3390/machines10050305
APA StyleLiu, Z., Jin, B., Dong, J., Zhai, S., & Tang, X. (2022). Design and Control of a Hydraulic Hexapod Robot with a Two-Stage Supply Pressure Hydraulic System. Machines, 10(5), 305. https://doi.org/10.3390/machines10050305







