Operational Stability Analysis on the Roller-Coating Process for a Roll Coating-Simulation Test Equipment
Abstract
1. Introduction
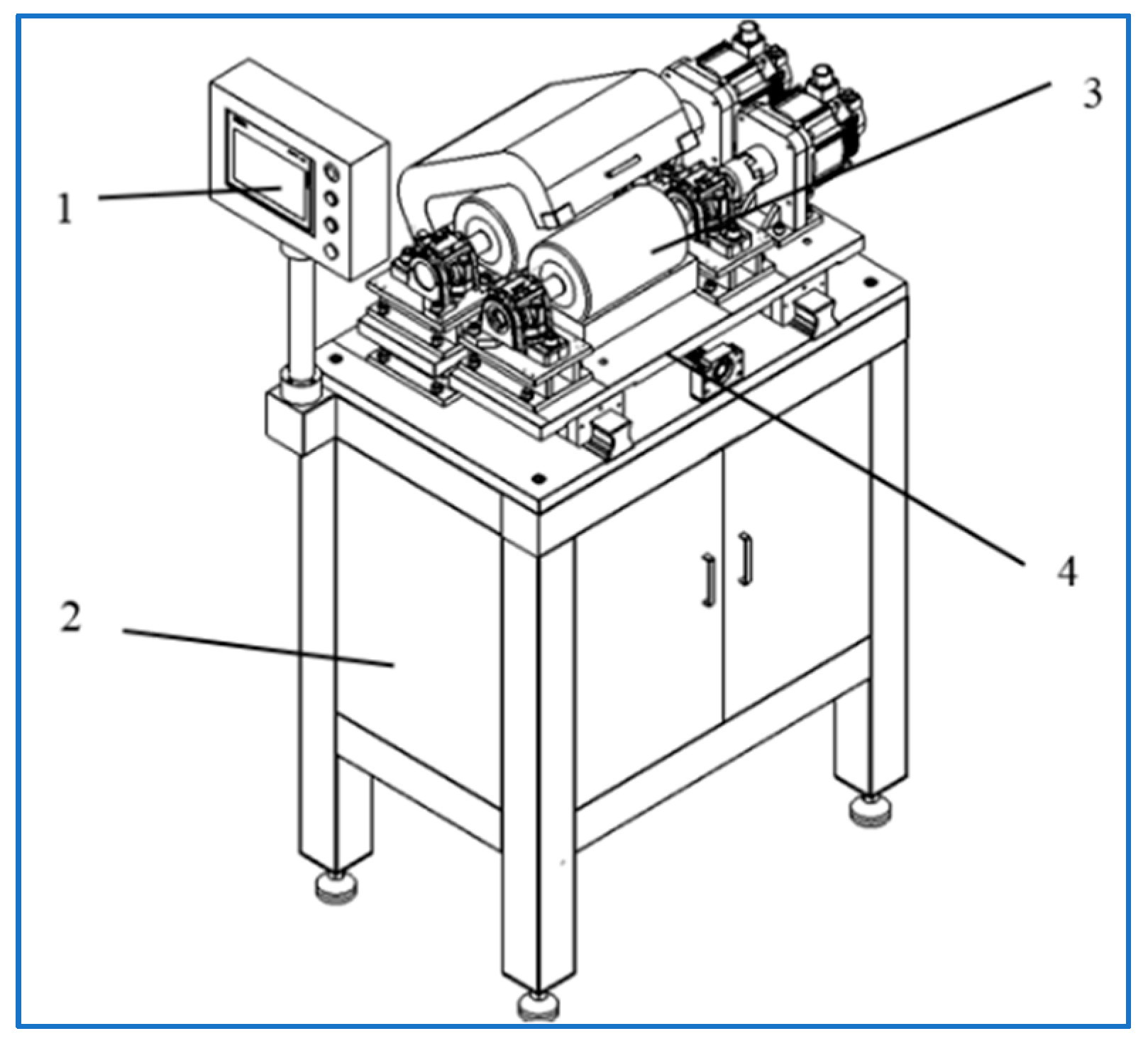
2. Roll Coating Simulation Test Equipment
2.1. Design and Modeling
2.2. Design and Requirements of Rotor Components
3. Dynamics Simulation and Roll Coating Simulation
3.1. Vibration Response Analysis of Rotor Components
3.1.1. Theory of Unbalanced Vibration Analysis
3.1.2. Unbalance Response Analysis of Rotor Components
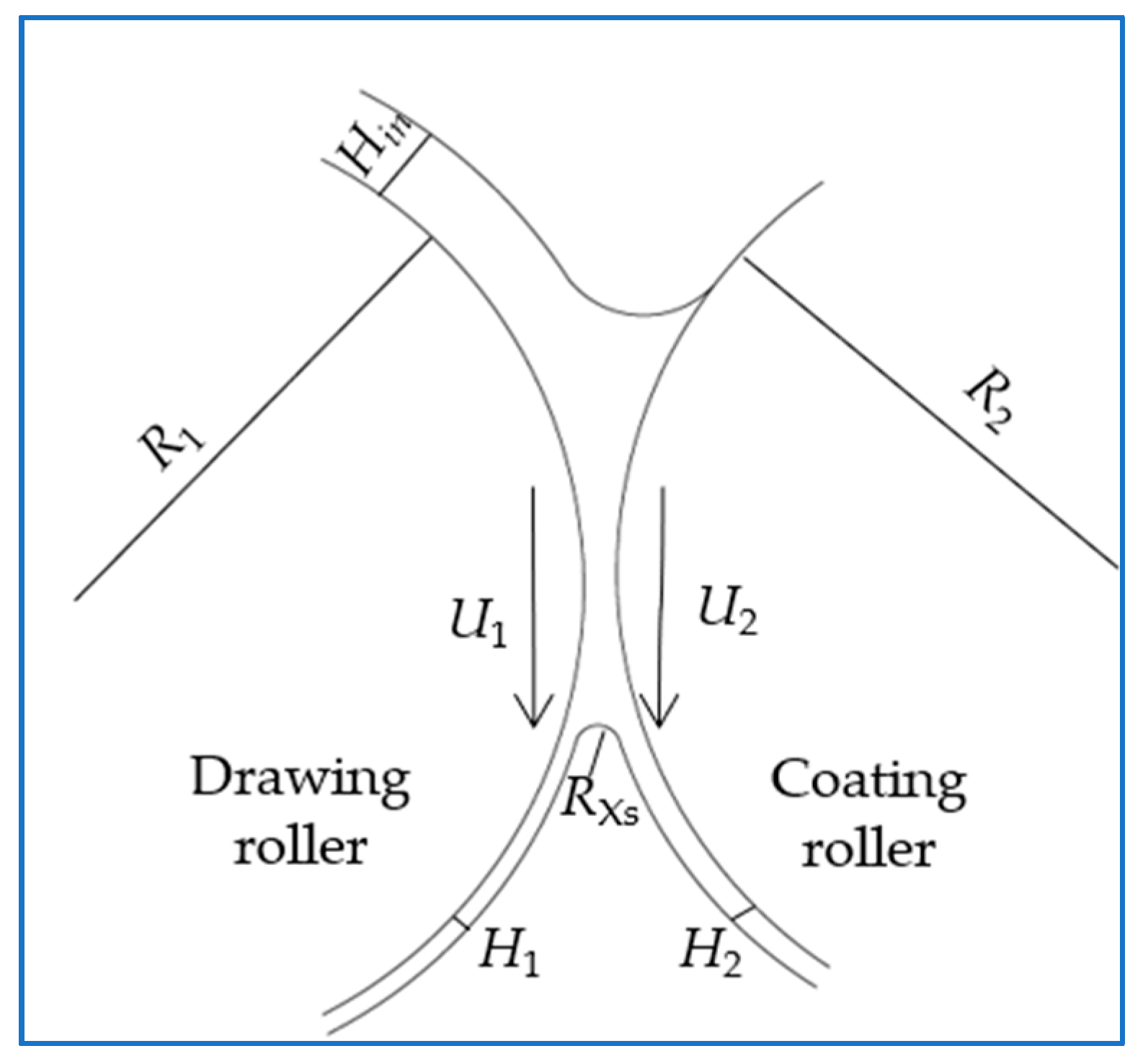
3.2. Stability Analysis of Roll Coating
3.2.1. Theoretical Derivation of Roll Coating Stability
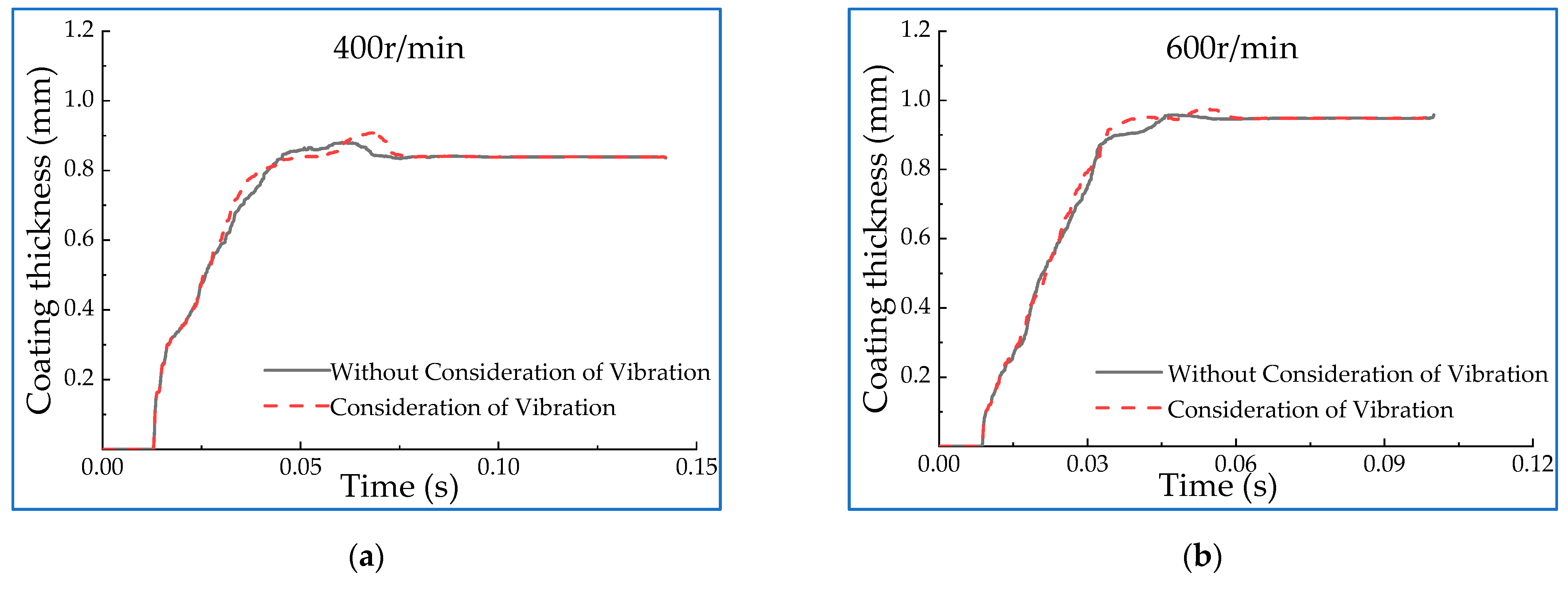
3.2.2. Simulation of the Roller-Coating Process
- (1)
- Influence of roller velocity on roll coating stability under vibration condition
- (2)
- Influence of coating viscosity on roll coating stability under vibration condition
- (3)
- Influence of distance between rollers on roll coating stability under vibration condition
4. Experimental Research and Discussion
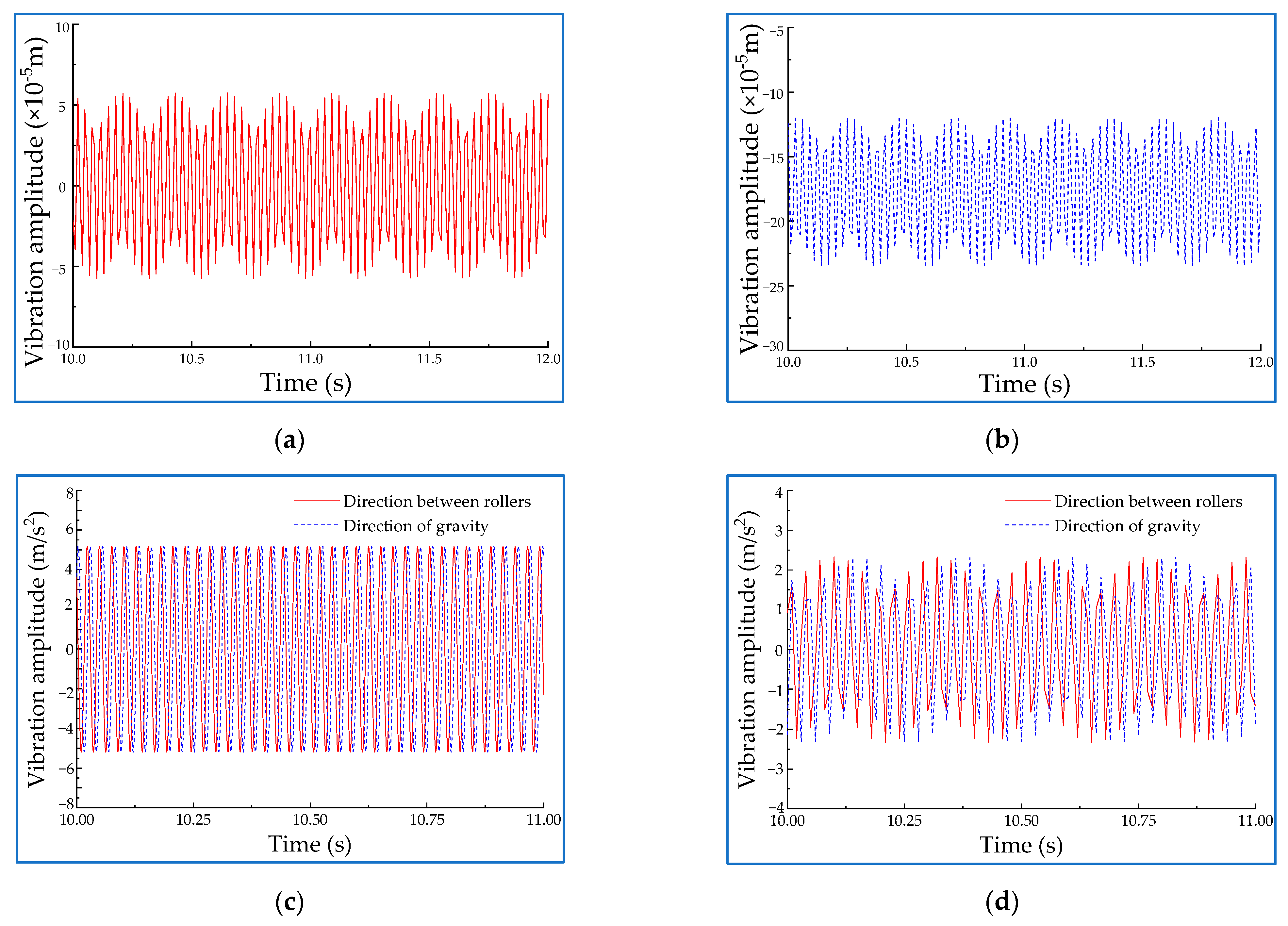
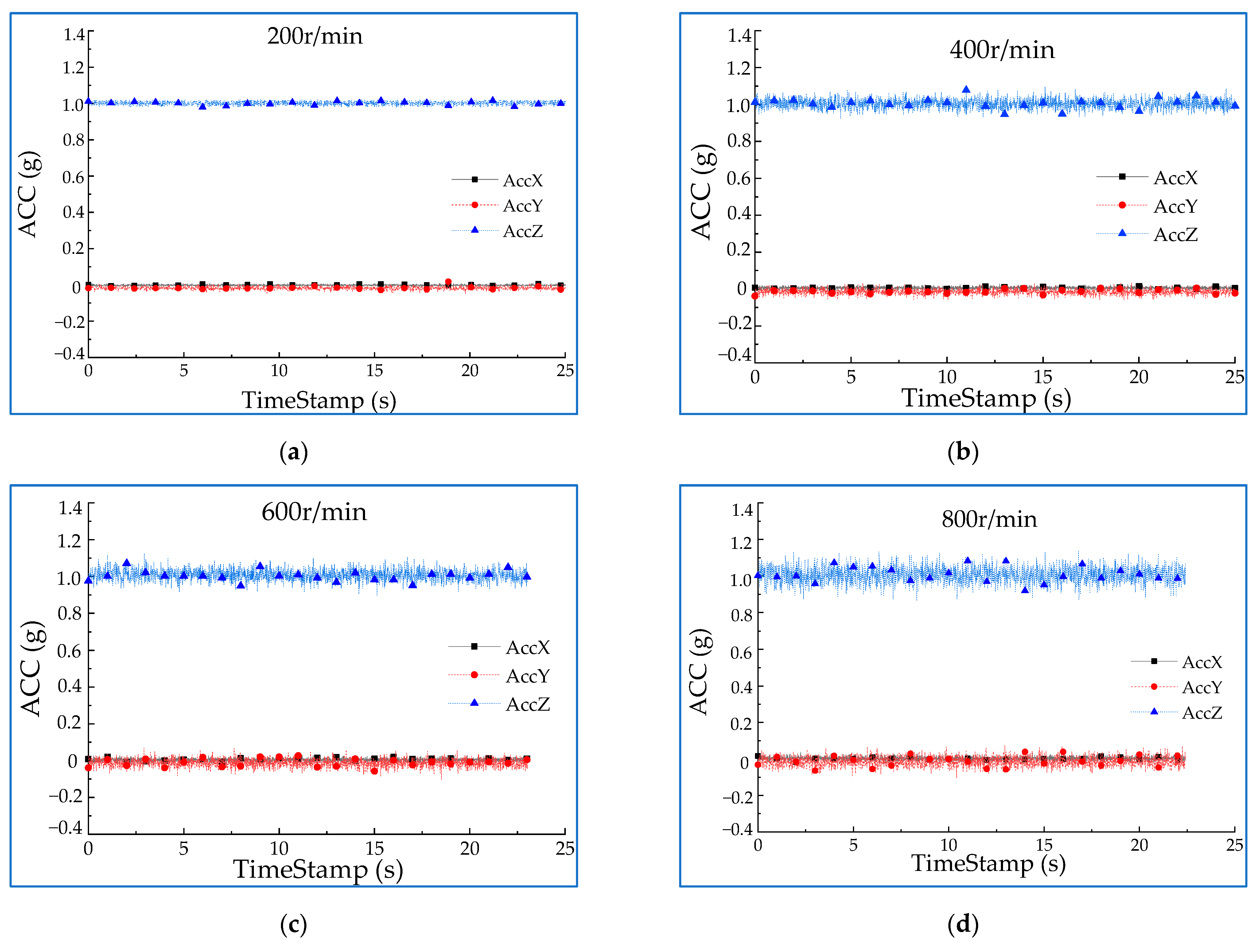
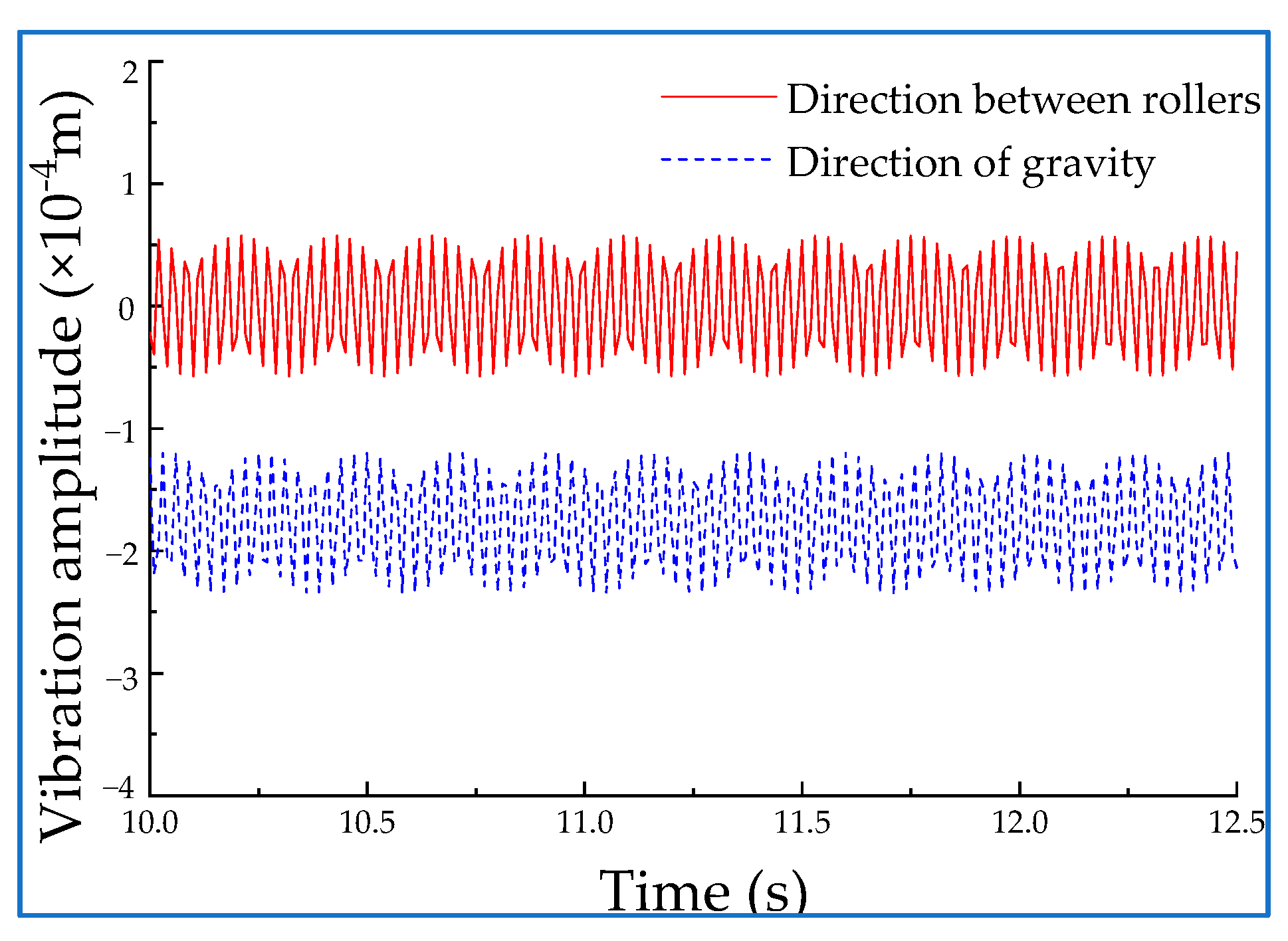
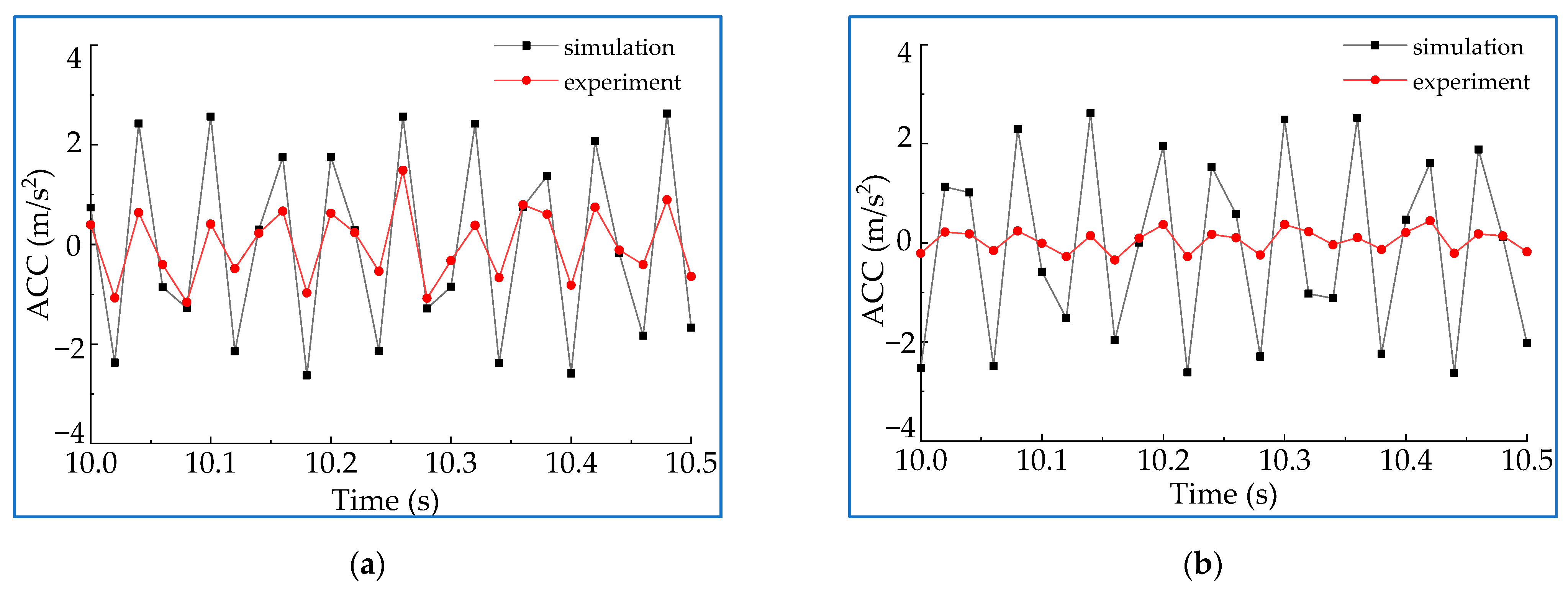
4.1. Stability Test of Roll Coating Rotor Components
4.2. Discussion and Analysis
5. Conclusions
- (1)
- Based on the requirements of the roll coating equipment and the theoretical analysis of vibration, a dynamic model of roll coating rotor components is established. Through numerical simulation and experiment, it is obtained that the vibration amplitude of the equipment does not exceed 0.06 mm, and the vibration acceleration is much less than the critical value, which satisfies the vibration requirements under the specified rotational velocity of the vibration value of rotating machinery standard, and the stability requirements of the test equipment under the maximum limit condition.
- (2)
- In the simulation of the roller-coating process, the correlation coefficients of the curves before and after the introduction of the disturbance amount are calculated, and the results are all above 0.95. The overall equipment can still ensure good stability even when vibration is considered. It can be found from further analysis of the influencing factors that the increase of the rotational velocity and the distance between the two rollers can significantly improve the stability of the roll coating, while the viscosity has little effect on that. The results provide a theoretical and experimental reference for the design of this type of roll coating equipment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen-Yang, Y.W.; Chuang, J.R.; Yang, Y.C.; Li, C.Y.; Chiu, Y.S. New UV—Curable cyclotriphosphazenes as fire—Retardant coating materials for wood. J. Appl. Polym. Sci. 1998, 69, 115–122. [Google Scholar] [CrossRef]
- Ali, F.; Hou, Y.; Zahid, M.; Rana, M.A. Theoretical study of the reverse roll coating of non-isothermal magnetohydrodynamics viscoplastic fluid. Coatings 2020, 10, 940. [Google Scholar] [CrossRef]
- Savage, M. Mathematical models for coating processes. J. Fluid Mech. 1982, 117, 443–455. [Google Scholar] [CrossRef]
- Savage, M. Variable speed coating with purely viscous non-Newtonian fluids. Z. Angew. Math. Phys. ZAMP 1983, 34, 358–369. [Google Scholar] [CrossRef]
- Greener, J.; Sullivan, T.; Turner, B.; Middleman, S. Ribbing instability of a two-roll coater: Newtonian fluids. Chem. Eng. Commun. 1980, 5, 73–83. [Google Scholar] [CrossRef]
- Greener, J.; Middleman, S. Reverse roll coating of viscous and viscoelastic liquids. Ind. Eng. Chem. Fundam. 1981, 20, 63–66. [Google Scholar] [CrossRef]
- Zafar, M.; Rana, M.; Zahid, M.; Malik, M.; Lodhi, M. Mathematical analysis of roll coating process by using couple stress fluid. J. Nanofluids 2019, 8, 1683–1691. [Google Scholar] [CrossRef]
- Zahid, M.; Zafar, M.; Rana, M.A.; Lodhi, M.S.; Awan, A.S.; Ahmad, B. Mathematical analysis of a non-Newtonian polymer in the forward roll coating process. J. Polym. Eng. 2020, 40, 703–712. [Google Scholar] [CrossRef]
- Zahid, M.; Haroon, T.; Rana, M.; Siddiqui, A. Roll coating analysis of a third grade fluid. J. Plast. Film Sheeting 2017, 33, 72–91. [Google Scholar] [CrossRef]
- Benkreira, H.; Shibata, Y.; Ito, K. The fluid mechanics of tensioned web roll coating. Chem. Eng. Sci. 2021, 239, 116612. [Google Scholar] [CrossRef]
- Chien, C.-H.; Jang, J.-Y. Numerical and experimental studies of thin liquid film flow between two forward-rollers. J. Mech. Sci. Technol. 2007, 21, 1892–1900. [Google Scholar] [CrossRef]
- Carvalho, M.; Scriven, L. Three-dimensional stability analysis of free surface flows: Application to forward deformable roll coating. J. Comput. Phys. 1999, 151, 534–562. [Google Scholar] [CrossRef]
- Kapur, N. A parametric study of direct gravure coating. Chem. Eng. Sci. 2003, 58, 2875–2882. [Google Scholar] [CrossRef]
- Ascanio, G.; Carreau, P.; Brito-De La Fuente, E.; Tanguy, P. Forward deformable roll coating at high speed with Newtonian fluids. Chem. Eng. Res. Des. 2004, 82, 390–397. [Google Scholar] [CrossRef]
- Ascanio, G.; Carreau, P.; Tanguy, P. High-speed roll coating with complex rheology fluids. Exp. Fluids 2006, 40, 1–14. [Google Scholar] [CrossRef]
- Roper, J.A., III; Salminen, P.; Urscheler, R.; Bousfield, D.W. Studies of orange peel formation in high-speed film coating. Tappi J. 1999, 82, 231–238. [Google Scholar]
- Pitts, E.; Greiller, J. The flow of thin liquid films between rollers. J. Fluid Mech. 1961, 11, 33–50. [Google Scholar] [CrossRef]
- Sasaki, M.; Miyake, M.; Nakata, N. Visualization study of flow stability in reverse roll coating. ISIJ Int. 2015, 55, 863–869. [Google Scholar] [CrossRef]
- Grashof, B.; Delgado, A. Analysis of influencing parameters in deformable roll coating of counter-rotating rolls. J. Coat. Technol. Res. 2015, 12, 63–73. [Google Scholar] [CrossRef]
- Liu, J.N. Rotordynamic Characteristic Research for the Active Magnetic Bearing—Rotor System of Flywheel Energy Storage System; Harbin Engineering University: Harbin, China, 2014. [Google Scholar]
- Carvalho, M. Effect of thickness and viscoelastic properties of roll cover on deformable roll coating flows. Chem. Eng. Sci. 2003, 58, 4323–4333. [Google Scholar] [CrossRef]
- Wilson, M.; Gaskell, P.; Savage, M. Flow in a double-film-fed fluid bead between contra-rotating rolls Part 1: Equilibrium flow structure. Eur. J. Appl. Math. 2001, 12, 395–411. [Google Scholar] [CrossRef][Green Version]
- Kapur, N.; Gaskell, P.; Bates, A. A parametric study of offset gravure coating. Chem. Eng. Res. Des. 2001, 79, 41–50. [Google Scholar] [CrossRef]
- Greener, J.; Middleman, S. Theoretical and experimental studies of the fluid dynamics of a two-roll coater. Ind. Eng. Chem. Fundam. 1979, 18, 35–41. [Google Scholar] [CrossRef]




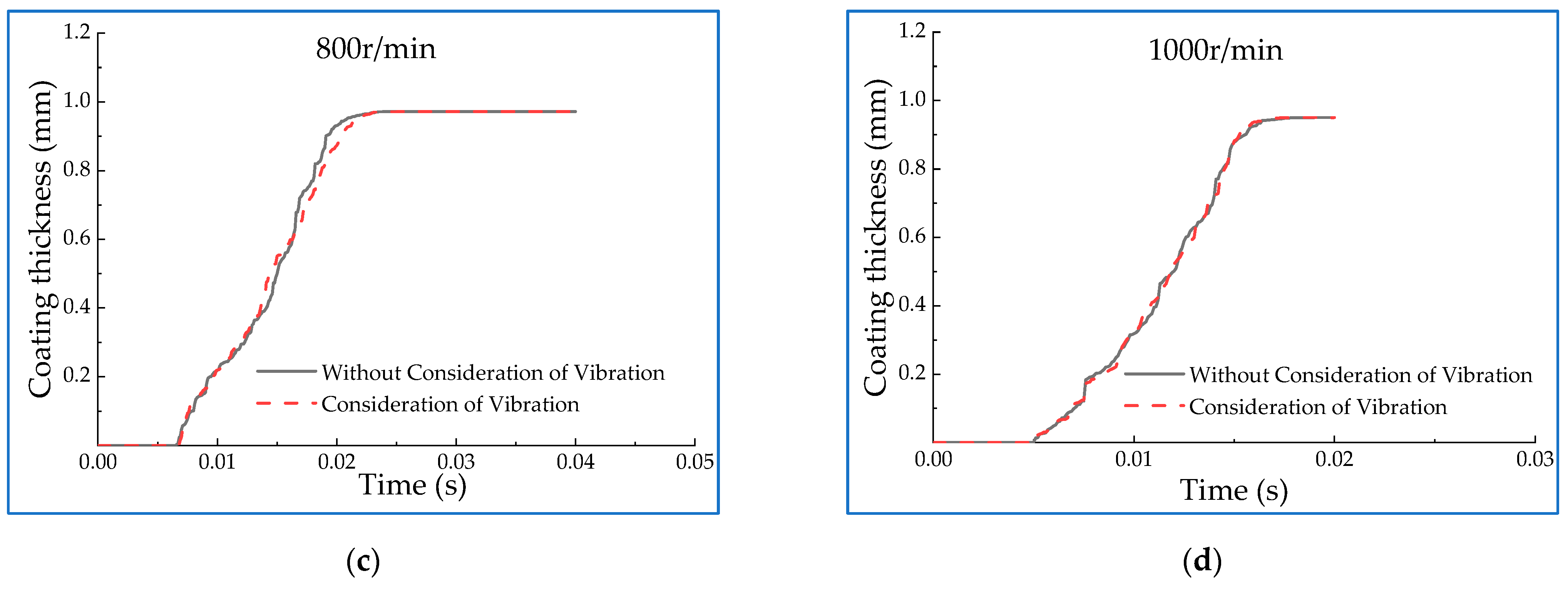
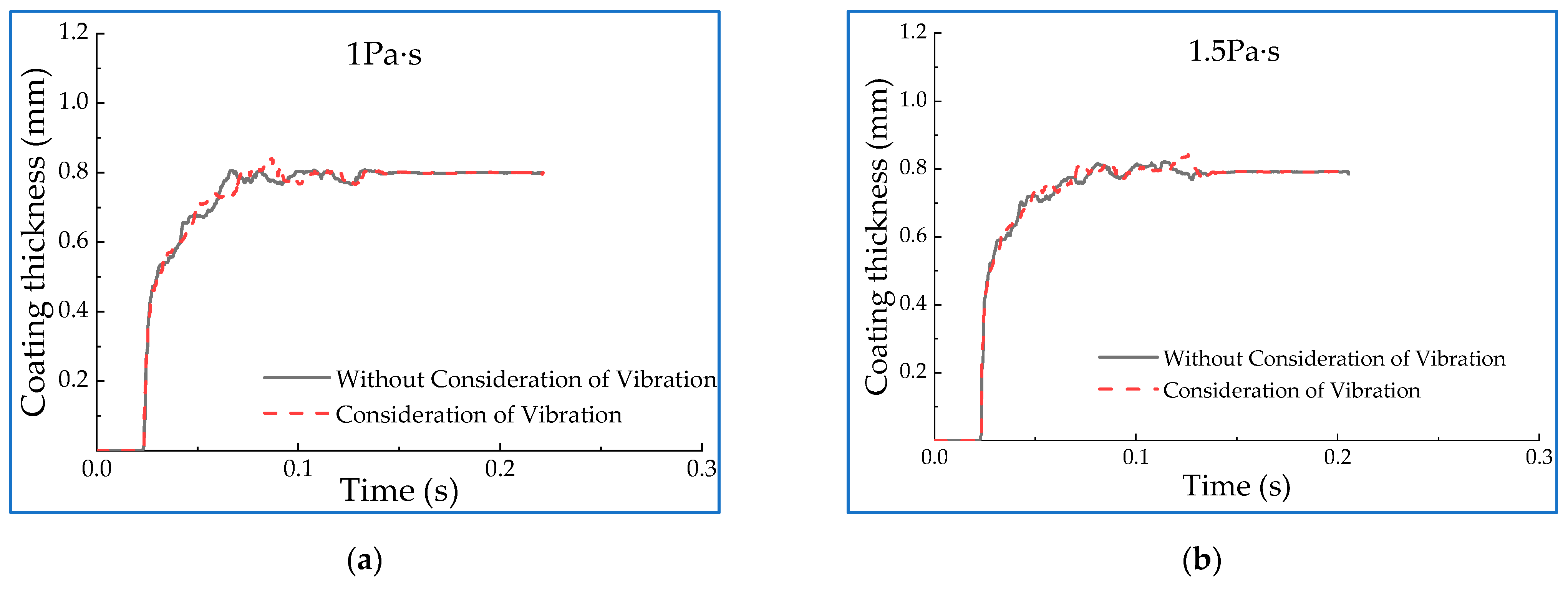
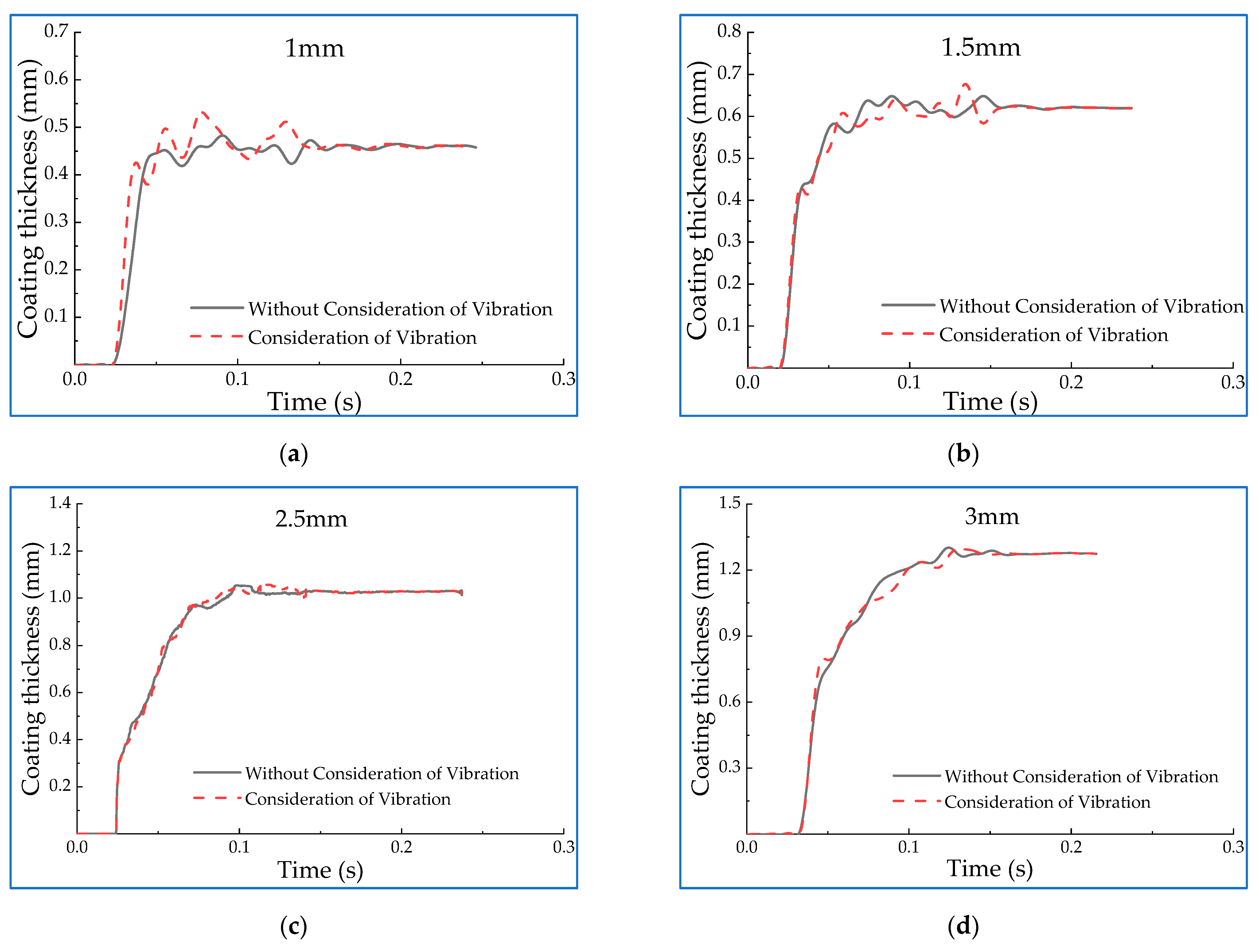


| Rotating Velocity (r/min) | Correlation Coefficient | Viscosity (Pa·s) | Correlation Coefficient | Spacing (mm) | Correlation Coefficient |
|---|---|---|---|---|---|
| 200 | 0.99798 | 0.5 | 0.99798 | 1 | 0.96957 |
| 400 | 0.99854 | 1 | 0.99766 | 1.5 | 0.99323 |
| 600 | 0.99888 | 1.5 | 0.99709 | 2 | 0.99798 |
| 800 | 0.99862 | 2.5 | 0.99818 | ||
| 1000 | 0.99951 | 3 | 0.99895 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, H.; Yang, K.; You, J.; Wang, S. Operational Stability Analysis on the Roller-Coating Process for a Roll Coating-Simulation Test Equipment. Machines 2022, 10, 304. https://doi.org/10.3390/machines10050304
Lv H, Yang K, You J, Wang S. Operational Stability Analysis on the Roller-Coating Process for a Roll Coating-Simulation Test Equipment. Machines. 2022; 10(5):304. https://doi.org/10.3390/machines10050304
Chicago/Turabian StyleLv, Hongzhan, Kehang Yang, Jia You, and Shuyan Wang. 2022. "Operational Stability Analysis on the Roller-Coating Process for a Roll Coating-Simulation Test Equipment" Machines 10, no. 5: 304. https://doi.org/10.3390/machines10050304
APA StyleLv, H., Yang, K., You, J., & Wang, S. (2022). Operational Stability Analysis on the Roller-Coating Process for a Roll Coating-Simulation Test Equipment. Machines, 10(5), 304. https://doi.org/10.3390/machines10050304






