Review with Analytical-Numerical Comparison of Contact Force Models for Slotted Joints in Machines
Abstract
1. Introduction
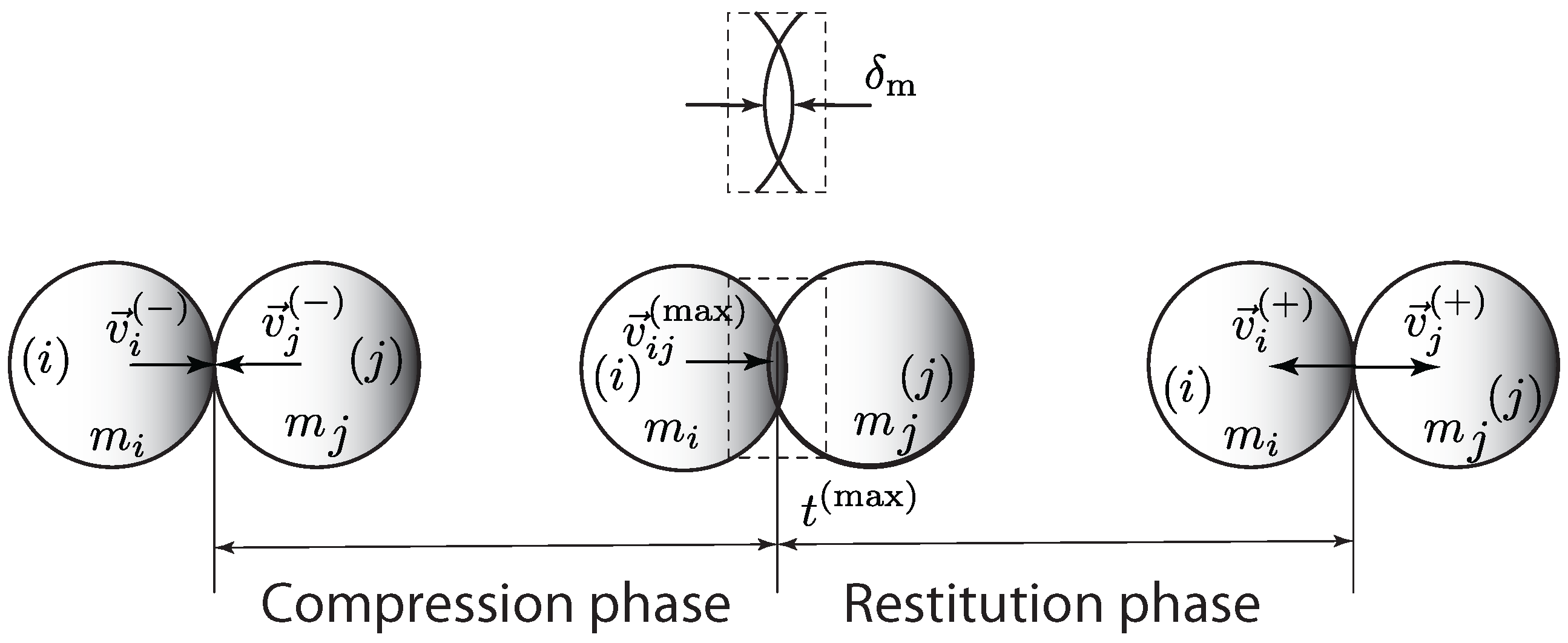
- the damping component force has a discontinuity at the beginning of the contact;
- although at the end of restitution phase there is a null indentation, the contact force is negative due to a nonzero relative contact velocity;
- the damping coefficient is constant for the entire impact time interval.
- (1)
- To propose a novel polynomial fitting of implicit elastic contact force models.
- (2)
- To offer a summary of the analytical derivations leading to some viscous force contact models available in the literature.
- (3)
- To investigate the difference in the different elastic contact force models in a multibody dynamics simulation.
- In Section 2, the cylindrical elastic models have been summarized in their original formulation. Then, polynomial fits that explicitly link force and elastic indentation have been summarized in tables for different compliances.
- In Section 3, for different viscous analytical models, the main analytical steps that brought to their deduction have been reported.
- In Section 4, the multibody dynamics simulations of a scotch–yoke linkage with a curved pin in the slot have been discussed. In particular, for each simulation, a different elastic contact model was assumed and tested.
- Finally, Section 5 contains the conclusions.
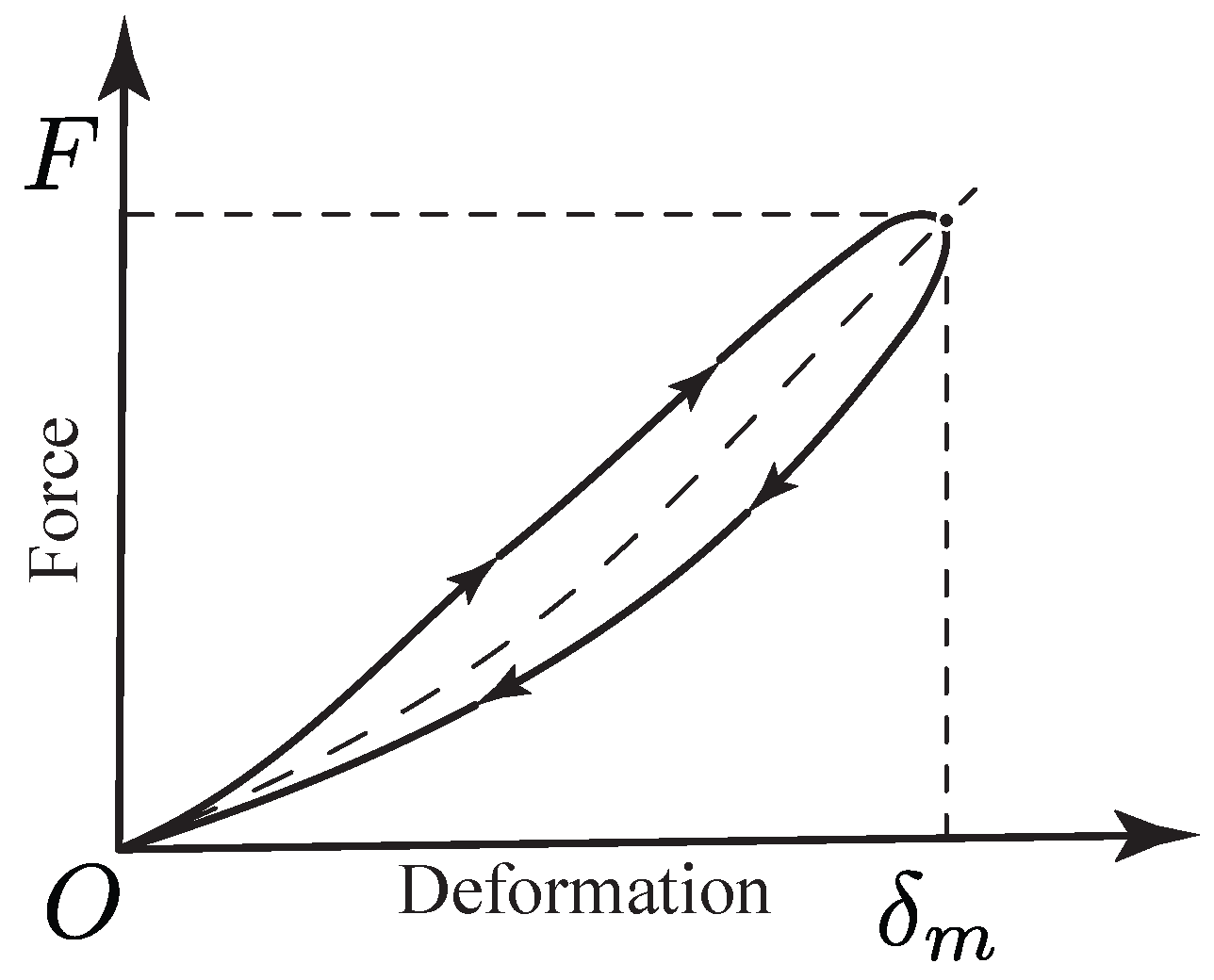
2. Cylindrical Elastic Contact Models
mm | K N/mm | n | Max Error % |
|---|---|---|---|
| 0.50 | 1.04 ⋅ 10 | 1.162 | 6.1 |
| 5.00 | 6.24 ⋅ 10 | 1.118 | 4.1 |
| 10.0 | 5.55 ⋅ 10 | 1.109 | 3.8 |
| 30.0 | 4.72 ⋅ 10 | 1.097 | 3.2 |
| 60.0 | 4.32 ⋅ 10 | 1.091 | 3.0 |
| 80.0 | 4.17 ⋅ 10 | 1.089 | 2.9 |
mm | K N/mm | n | Max Error % |
|---|---|---|---|
| 0.50 | 41.308 ⋅ 10 | 1.195 | 14.6 |
| 5.00 | 22.979 ⋅ 10 | 1.135 | 9.0 |
| 10.0 | 20.228 ⋅ 10 | 1.123 | 8.0 |
| 30.0 | 16.993 ⋅ 10 | 1.108 | 6.7 |
| 60.0 | 15.434 ⋅ 10 | 1.100 | 6.1 |
| 80.0 | 14.867 ⋅ 10 | 1.098 | 5.8 |
mm | K N/mm | n | Max Error % |
|---|---|---|---|
| 0.50 | 1.42 ⋅ 10 | 1.192 | 7.4 |
| 5.00 | 7.53 ⋅ 10 | 1.133 | 4.8 |
| 10.0 | 6.54 ⋅ 10 | 1.122 | 4.3 |
| 30.0 | 5.44 ⋅ 10 | 1.107 | 3.7 |
| 60.0 | 4.91 ⋅ 10 | 1.100 | 3.4 |
| 80.0 | 4.72 ⋅ 10 | 1.097 | 3.2 |
mm | K N/mm | n | Max Error % |
|---|---|---|---|
| 0.50 | 60.628 ⋅ 10 | 1.242 | 18.9 |
| 5.00 | 28.324 ⋅ 10 | 1.155 | 10.9 |
| 10.0 | 24.286 ⋅ 10 | 1.140 | 9.5 |
| 30.0 | 19.782 ⋅ 10 | 1.121 | 7.8 |
| 60.0 | 17.703 ⋅ 10 | 1.111 | 7.0 |
| 80.0 | 16.962 ⋅ 10 | 1.083 | 6.7 |
mm | K N/mm | n | Max Error % |
|---|---|---|---|
| 0.50 | 2.86 ⋅ 10 | 1.066 | 2.0 |
| 5.00 | 2.39 ⋅ 10 | 1.057 | 1.6 |
| 10.0 | 2.27 ⋅ 10 | 1.055 | 1.5 |
| 30.0 | 2.09 ⋅ 10 | 1.051 | 1.4 |
| 60.0 | 1.94 ⋅ 10 | 1.048 | 1.3 |
| 80.0 | 1.84 ⋅ 10 | 1.046 | 1.2 |
mm | K N/mm | n | Max Error % |
|---|---|---|---|
| 0.50 | 10.032 ⋅ 10 | 1.071 | 3.7 |
| 5.00 | 8.354 ⋅ 10 | 1.061 | 2.9 |
| 10.0 | 7.933 ⋅ 10 | 1.058 | 2.8 |
| 30.0 | 7.273 ⋅ 10 | 1.054 | 2.5 |
| 60.0 | 6.752 ⋅ 10 | 1.050 | 2.3 |
| 80.0 | 6.394 ⋅ 10 | 1.048 | 2.1 |
mm | K N/mm | n | Max Error % |
|---|---|---|---|
| 0.50 | 2.84 ⋅ 10 | 1.165 | 12.2 |
| 5.00 | 1.77 ⋅ 10 | 1.119 | 8.0 |
| 10.0 | 1.59 ⋅ 10 | 1.110 | 7.2 |
| 30.0 | 1.36 ⋅ 10 | 1.098 | 6.1 |
| 60.0 | 1.25 ⋅ 10 | 1.092 | 5.6 |
| 80.0 | 1.21 ⋅ 10 | 1.090 | 5.4 |
mm | K N/mm | n | Max Error % |
|---|---|---|---|
| 0.50 | 10.868 ⋅ 10 | 1.165 | 23.6 |
| 5.00 | 6.395 ⋅ 10 | 1.119 | 14.4 |
| 10.0 | 5.691 ⋅ 10 | 1.110 | 12.8 |
| 30.0 | 4.849 ⋅ 10 | 1.098 | 10.7 |
| 60.0 | 4.437 ⋅ 10 | 1.092 | 9.6 |
| 80.0 | 4.286 ⋅ 10 | 1.090 | 9.3 |
3. Viscous Contact Models
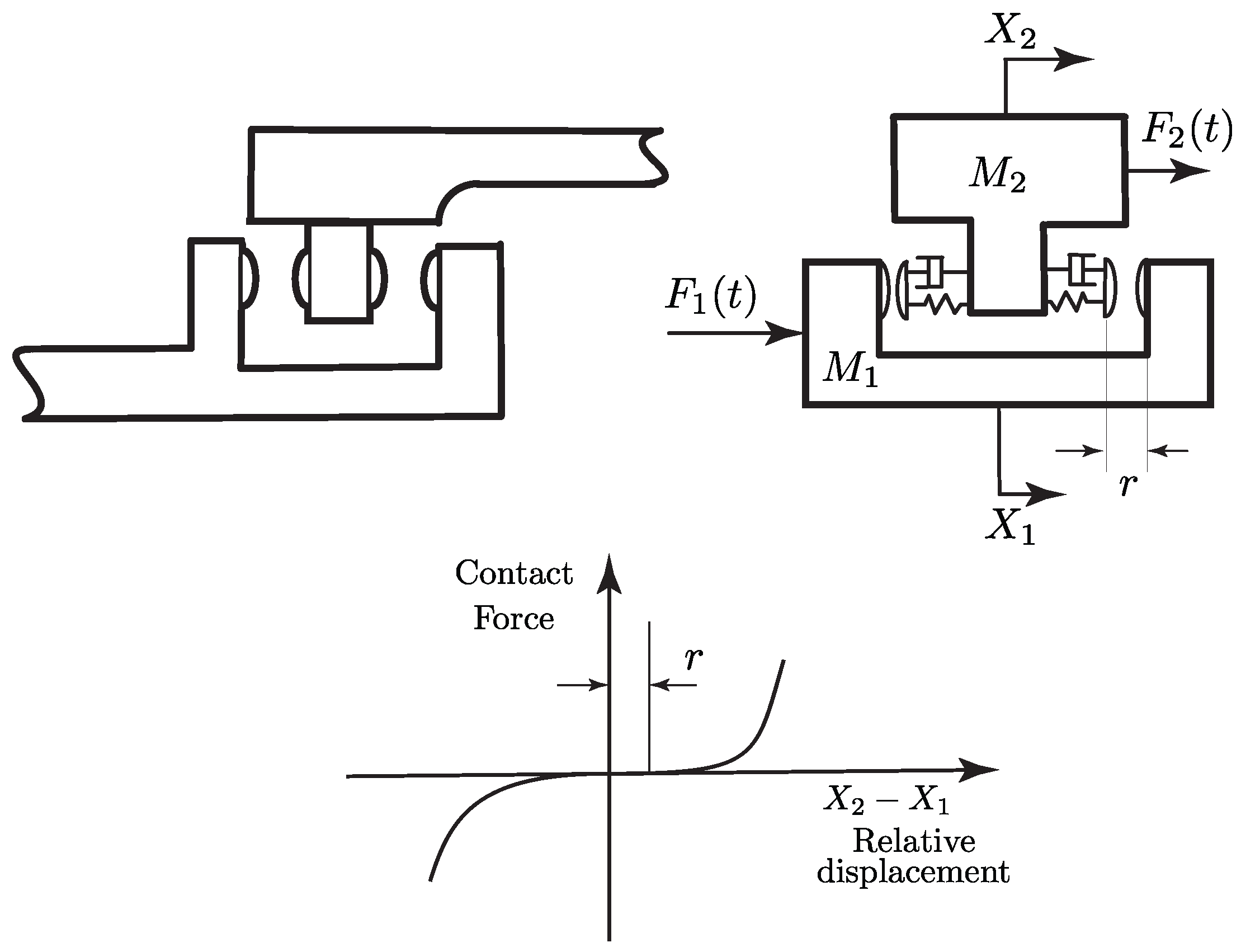
3.1. Dubowsky and Freudenstein (1971)
- Non-contact period
- Contact period
3.2. Hunt and Crossley (1975)
3.3. Herbert and McWhannel (1975)
3.4. Lee and Wang (1983)
3.5. Khulief and Shabana (1985)
- the compression phase, during which the relative velocity is gradually reduced to zero and elastic energy is stored;
- the restitution phase, which begins at the release of the stored elastic energy and finishes when the bodies separate.
3.6. Lankarani and Nikravesh (1988)
- the energy loss computed as a difference between the bodies’ kinetic energies at the beginning and at the end of the impact:
- the conservation of linear momentum:
- the coefficient of restitution:
- the energy balance equation
- the linear momentum conservation equation
3.7. Tsuji et al. (1992)
3.8. Lankarani and Nikravesh (1994)
- the sliding mode, when the pin and journal are in contact;
- free-flight mode, when the pin motion is governed by its own inertia and acting forces;
- impact mode, when the pin and journal begin contact.
3.9. Marhefka and Orin (1999)
3.10. Ghontier et al. (2004)
- , a good initial guess is ;
- the solution must be consistent with (110);
- the solution corresponding to the model of Hunt and Crossley is .
3.11. Flores et al. (2011–2016)
3.12. Gharib and Hurmuzlu (2012)
3.13. Hu and Guo (2015)
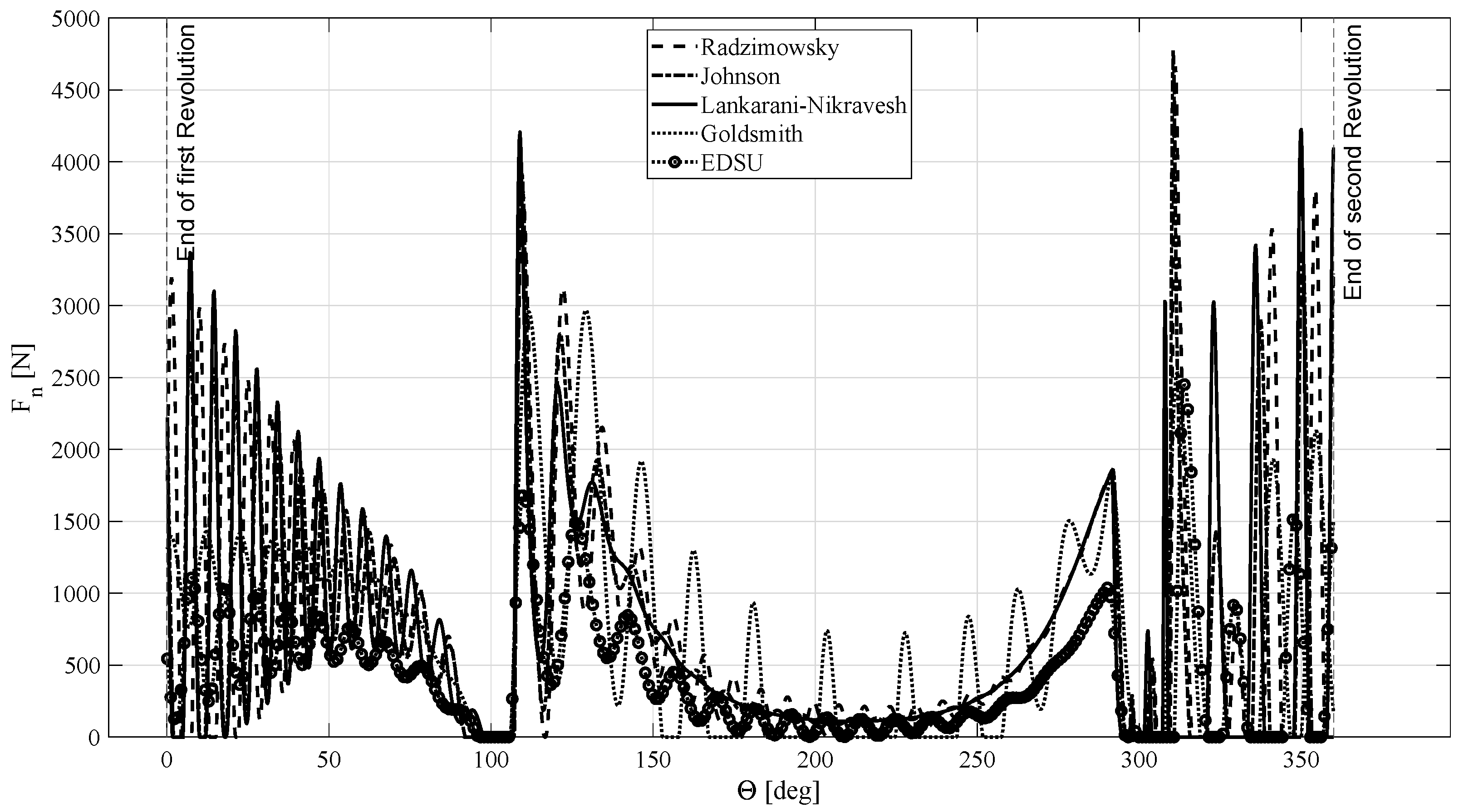
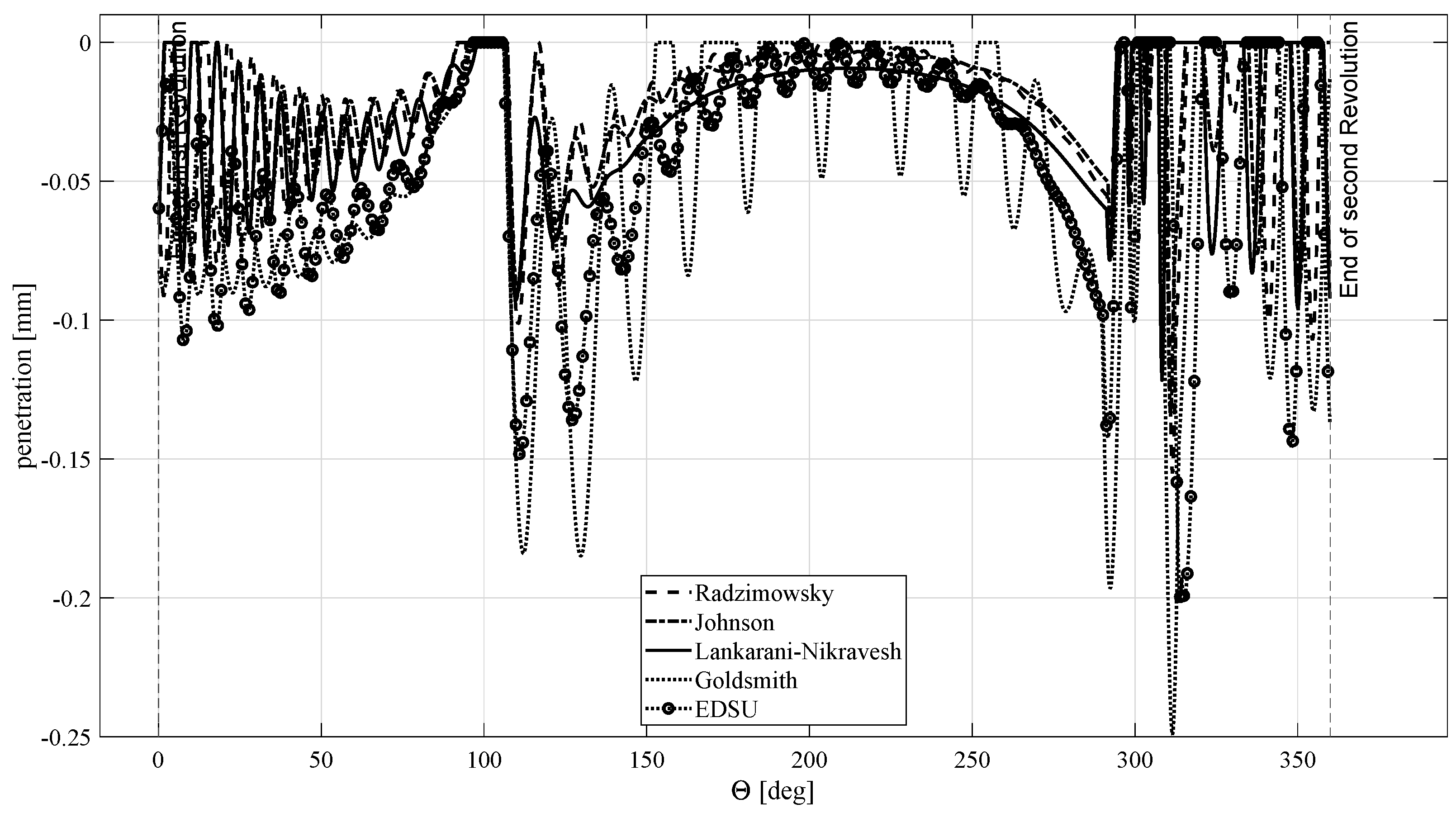
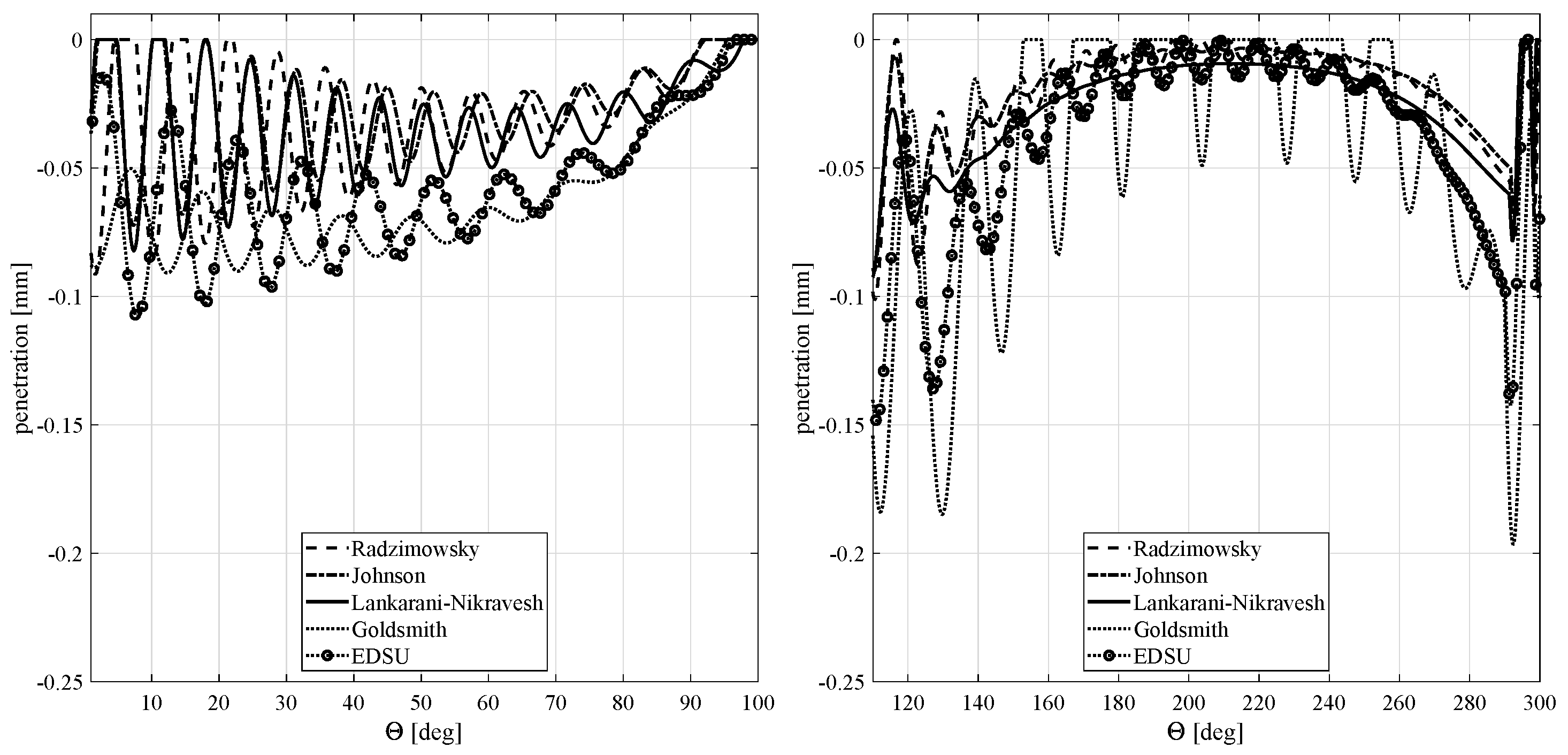
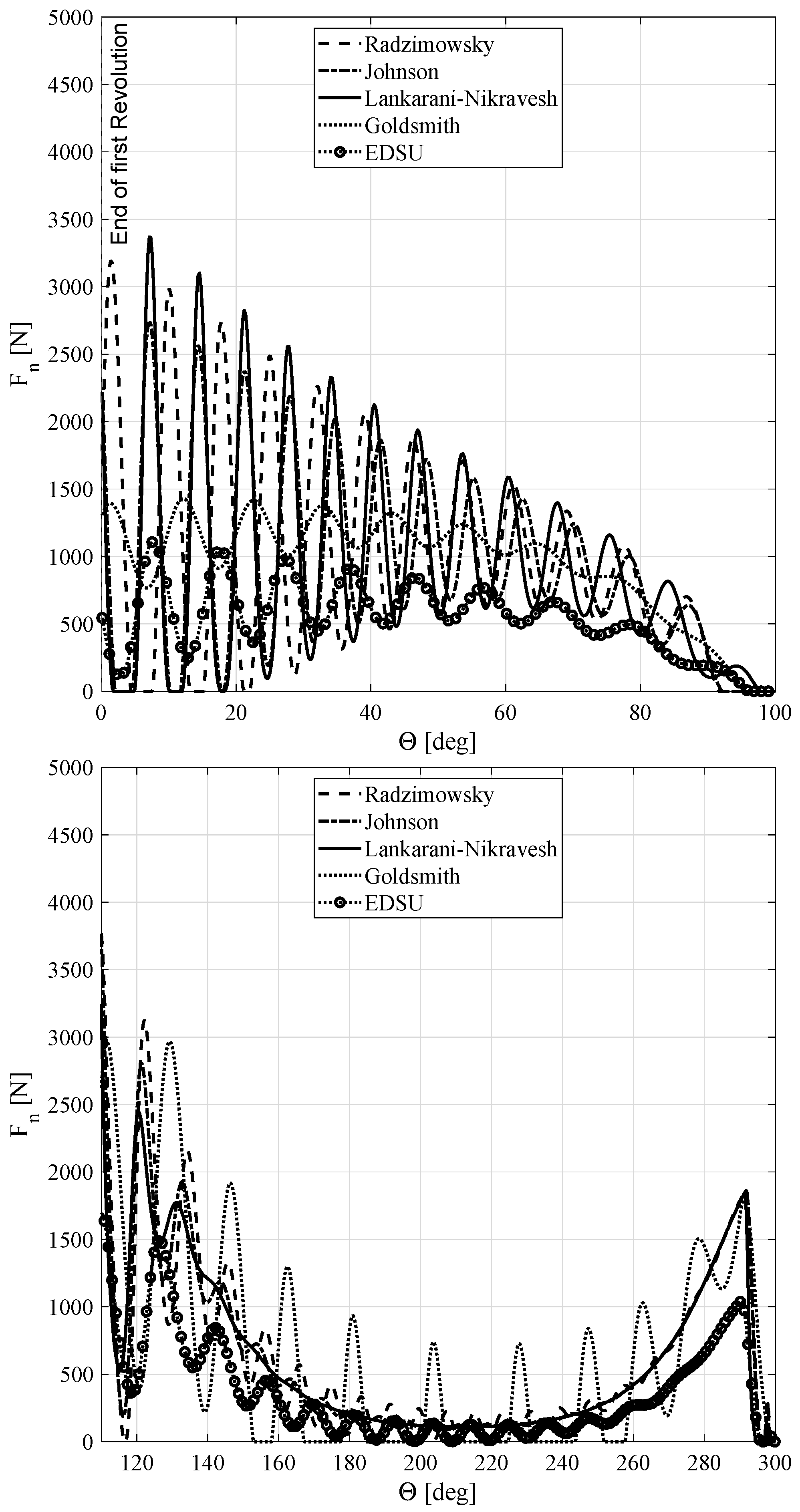
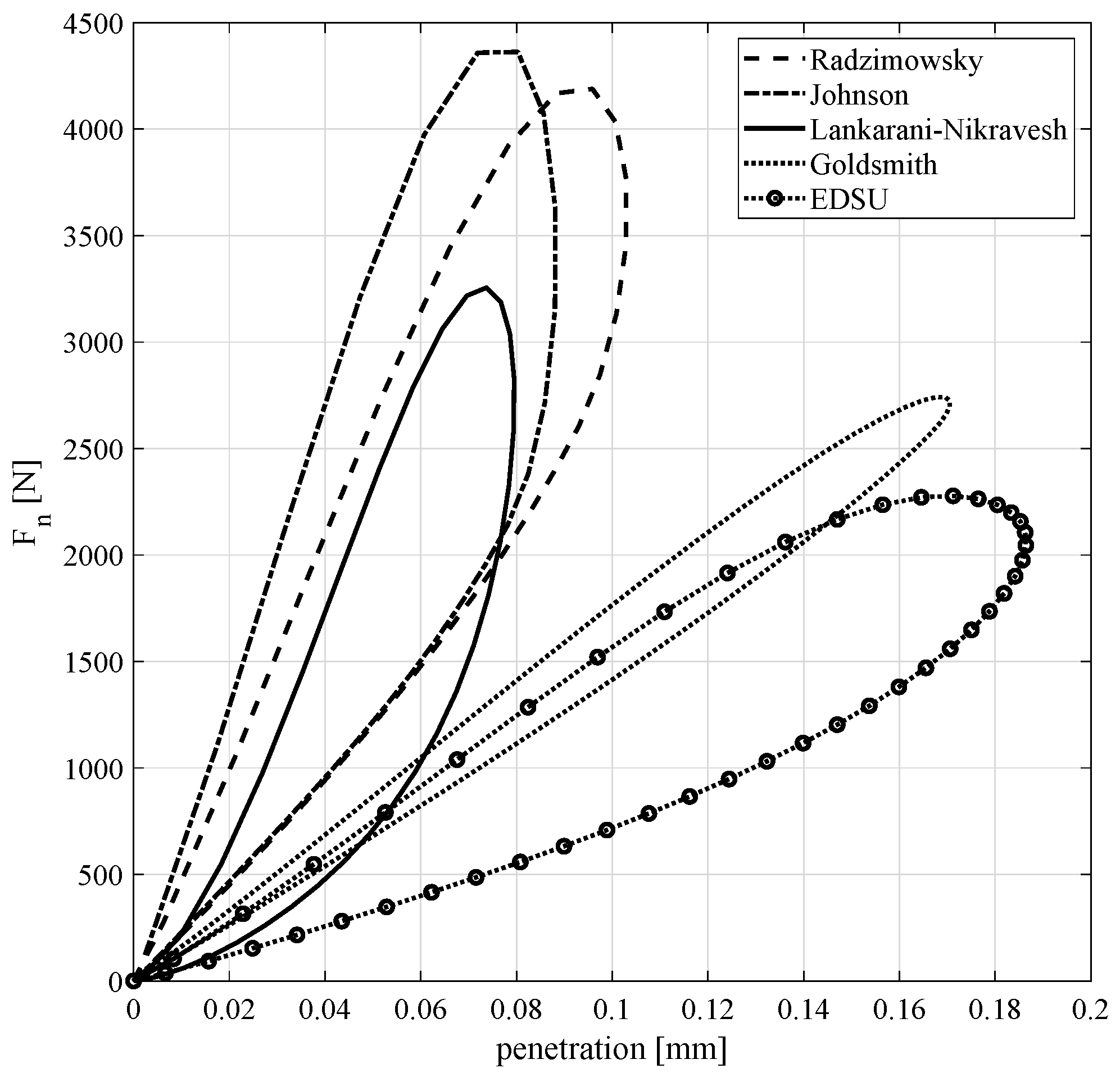
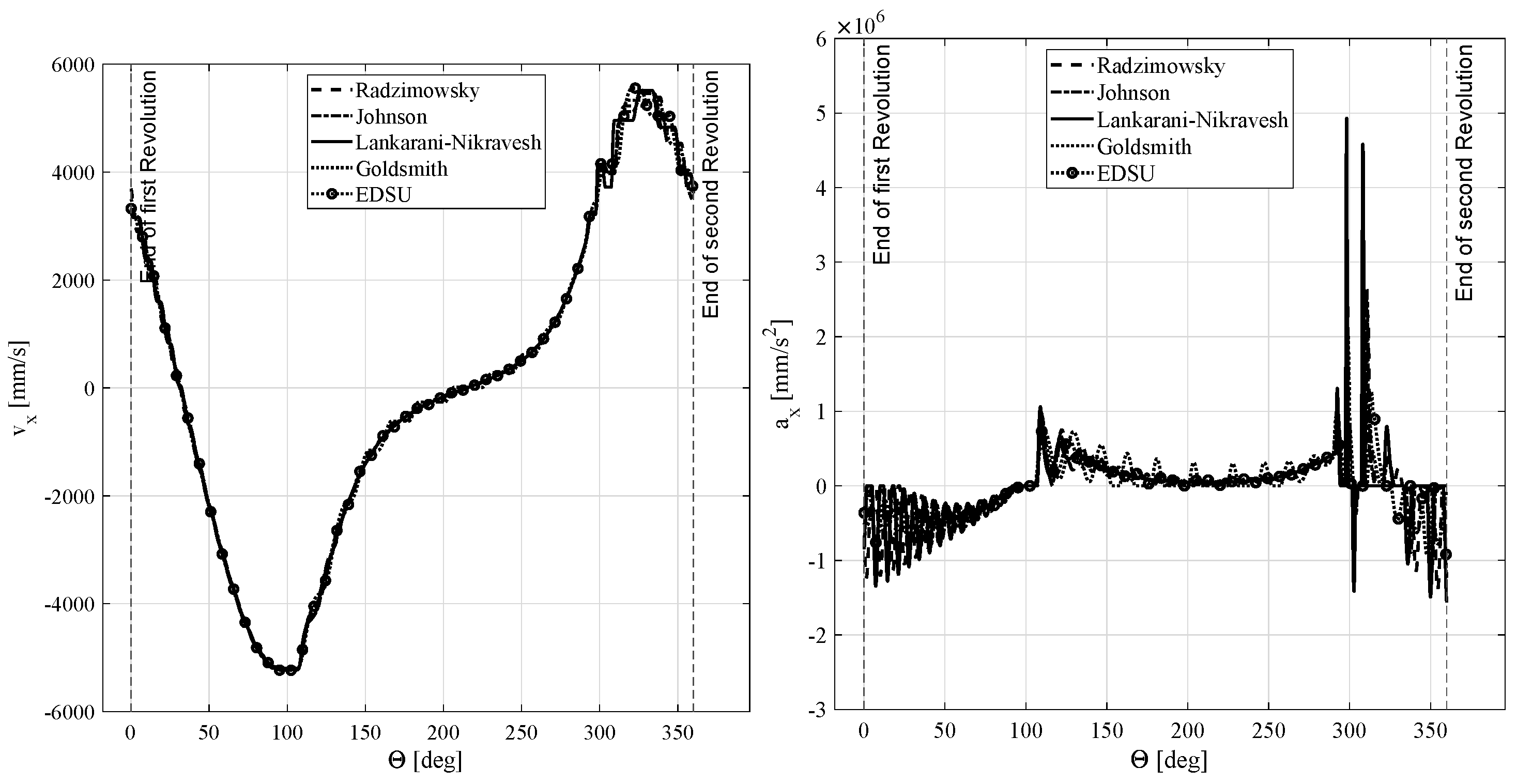
4. Numerical Example
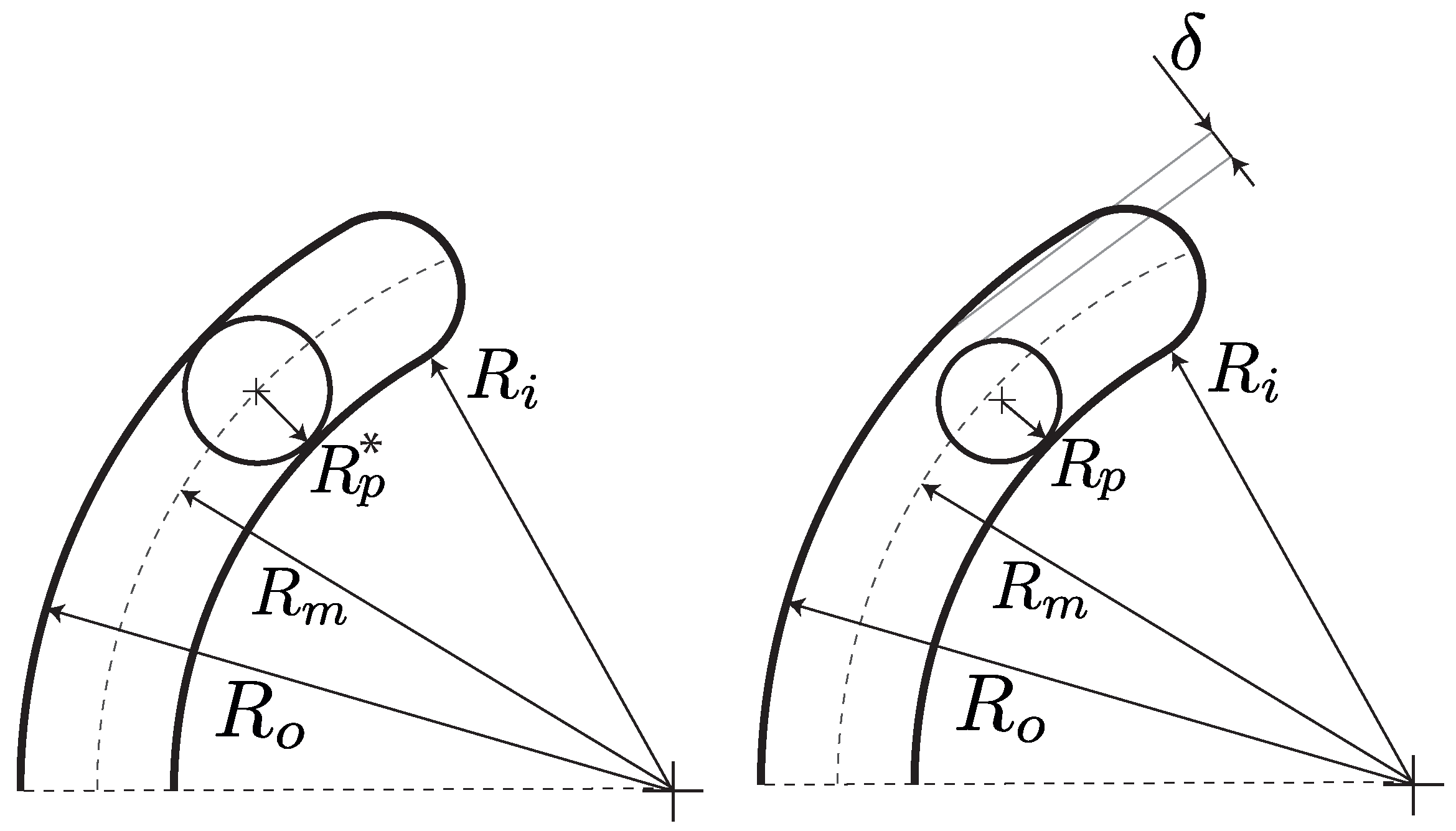
- Pin to inner track: external contact between the pin with radius and the inner track with radius ;
- Pin to outer track: internal contact between the pin with radius and the outer track with radius ;
- Pin to circular track: internal contact between the pin with radius and the circumferential track with radius .
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | damping coefficient |
| D | damping coefficient |
| e | kinematic coefficient of restitution |
| composite Young modulus | |
| Young modulus of body k () | |
| maximum contact force | |
| normal force | |
| , | forces acting on the masses of the Dubowsky and Freudenstein impact pair |
| maximum contact force | |
| contact force as function of relative displacement | |
| () | |
| K | contact stiffness parameter |
| L | length of the contact |
| m | exponent of penetration velocity |
| effective mass | |
| n | Hertz exponent |
| masses | |
| cylinder radius of body k | |
| t | time |
| time at the end of outward contact phase | |
| , | relative speeds before and after collision |
| clearance (+/−: External/Internal contact) | |
| variation of kinetic energy | |
| , and | initial time of compression, the time of maximum indentation and the final |
| time of restitution, respectively | |
| , | system kinetic energies at times and , respectively |
| kinetic energy at the end of impact compression phase | |
| maximum strain energy at the end of impact compression phase | |
| , | body k velocities at times and , respectively () |
| common velocity of the bodies at the end of the contact compression phase | |
| , | relative velocities at the beginning and at the end of contact, respectively |
| elastic wave propagation speed in colliding solids | |
| contact force per unit length | |
| , | masses displacements of the Dubowsky and Freudenstein impact pair |
| a constant based on the slope of the curve | |
| relative indentation between contacting bodies | |
| relative indentation at the end of contact | |
| indentation of sphere k, | |
| maximum relative indentation value | |
| permanent indentation after impact | |
| relative approach velocity (same as ) | |
| relative departing velocity (same as ) | |
| hysteresis damping factor | |
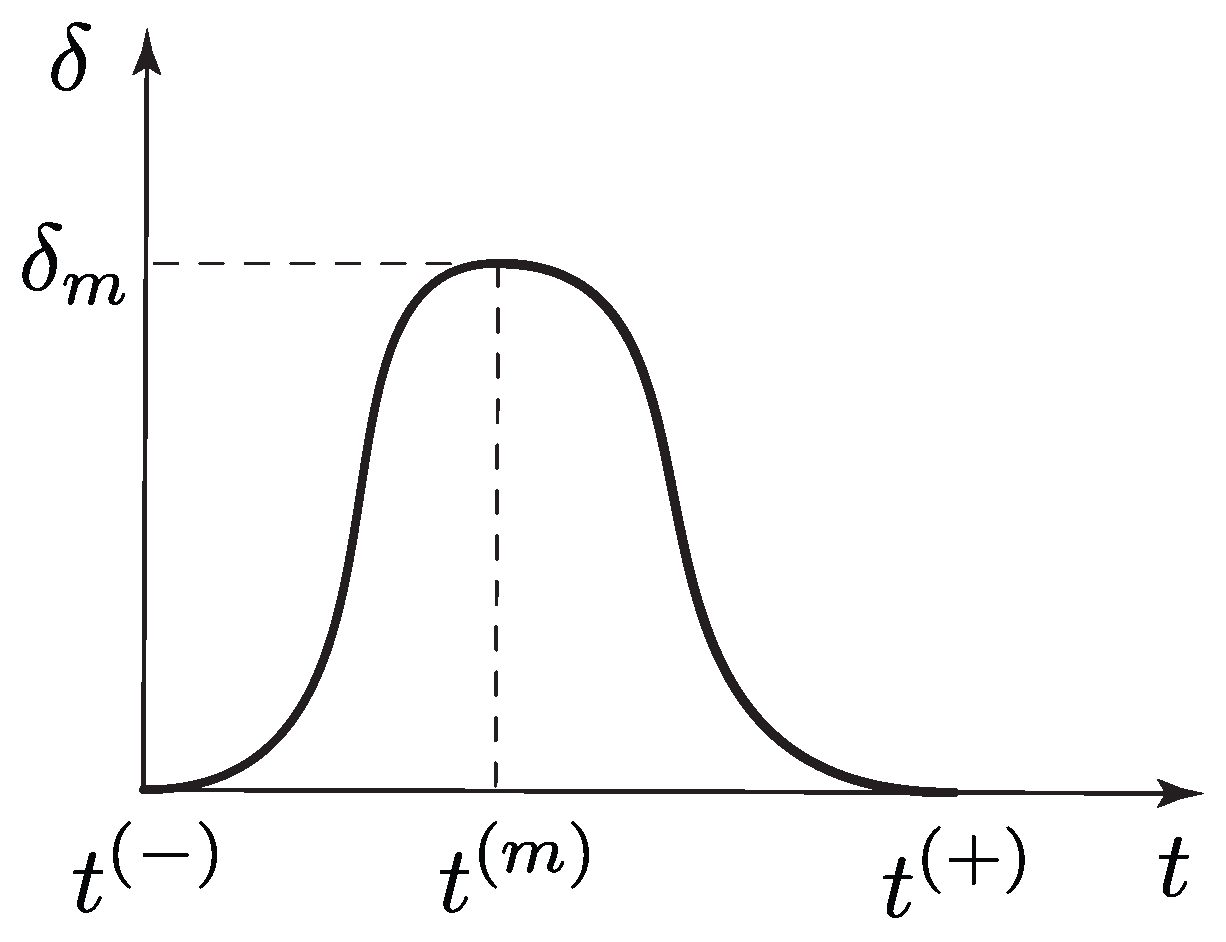
| width of the transition zone (see Figure 3) | |
| Poisson ratio of body k () | |
| system natural frequency |
References
- Pennestri, E.; Stefanelli, R.; Valentini, P.P.; Vita, L. Efficiency and wear in cam actuated robotized gearbox using virtual model. Int. J. Veh. Des. 2008, 46, 347. [Google Scholar] [CrossRef]
- Cera, M.; Cirelli, M.; Pennestrì, E.; Valentini, P. The kinematics of curved profiles mating with a caged idle roller—higher-path curvature analysis. Mech. Mach. Theory 2021, 164, 104414. [Google Scholar] [CrossRef]
- Cera, M.; Cirelli, M.; Pennestrì, E.; Valentini, P.P. Design analysis of torsichrone centrifugal pendulum vibration absorbers. Nonlinear Dyn. 2021, 104, 1023–1041. [Google Scholar] [CrossRef]
- Cirelli, M.; Cera, M.; Pennestrì, E.; Valentini, P.P. Nonlinear design analysis of centrifugal pendulum vibration absorbers: An intrinsic geometry-based framework. Nonlinear Dyn. 2020, 102, 1297–1318. [Google Scholar] [CrossRef]
- Cera, M.; Cirelli, M.; Pennestrì, E.; Valentini, P.P. Nonlinear dynamics of torsichrone CPVA with synchroringed form closure constraint. Nonlinear Dyn. 2021, 105, 2739–2756. [Google Scholar] [CrossRef]
- Cera, M.; Cirelli, M.; Pennestrì, E.; Valentini, P. Design and comparison of centrifugal dampers modern architectures: The influence of roller kinematics on tuning conditions and absorbers nonlinear dynamics. Mech. Mach. Theory 2022, 174, 104876. [Google Scholar] [CrossRef]
- Kobrinsky, A. Mechanisms with Elastic Couplings, NASA Technical Translation TT F-534; Technical Report; NASA: Washington, DC, USA, 1964.
- Lankarani, H.M. Canonical Equations of Motion and Estimation of Parameters in the Analysis of Impact Problems. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 1988. [Google Scholar]
- Lankarani, H.M.; Nikravesh, P.E. A contact force model with hysteresis damping for impact analysis of multibody systems. In Proceedings of the 15th Design Automation Conference: Volume 3—Mechanical Systems Analysis, Design and Simulation. American Society of Mechanical Engineers, Montreal, QC, Canada, 17–21 September 1989; pp. 45–51. [Google Scholar] [CrossRef]
- Flores, P.; Ambrósio, J.A.C.; Pimenta Claro, J.C.; Lankarani, H.M. Kinematics and Dynamics of Multibody Systems with Imperfect Joints: Models and Case Studies; Springer International Publishing: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Li, W.; Wang, C.; Sheng, C.l.; Yang, H.; Lu, E. Pin-slot clearance joints in multibody systems. Int. J. Precis. Eng. Manuf. 2017, 18, 1719–1729. [Google Scholar] [CrossRef]
- Han, I.; Gilmore, B.J. Multi-Body Impact Motion with Friction Analysis, Simulation, and Experimental Validation. J. Mech. Des. 1993, 115, 412–422. [Google Scholar] [CrossRef]
- Zhang, Y.; Sharf, I. Validation of nonlinear viscoelastic contact force models for low speed impact. J. Appl. Mech. 2009, 76, 051002. [Google Scholar] [CrossRef]
- Flores, P.; Machado, M.; Silva, M.T.; Martins, J.M. On the continuous contact force models for soft materials in multibody dynamics. Multibody Syst. Dyn. 2011, 25, 357–375. [Google Scholar] [CrossRef]
- Keller, J.B. Impact With Friction. J. Appl. Mech. 1986, 53, 1–4. [Google Scholar] [CrossRef]
- Schiehlen, W.; Seifried, R. Three approaches for elastodynamic contact in multibody systems. Multibody Syst. Dyn. 2004, 12, 1–16. [Google Scholar] [CrossRef]
- Gilardi, G.; Sharf, I. Literature survey of contact dynamics modelling. Mech. Mach. Theory 2002, 37, 1213–1239. [Google Scholar] [CrossRef]
- Schwab, A.; Meijaard, J.; Meijers, P. A comparison of revolute joint clearance models in the dynamic analysis of rigid and elastic mechanical systems. Mech. Mach. Theory 2002, 37, 895–913. [Google Scholar] [CrossRef]
- Haddadi, A.; Hashtrudi-Zaad, K. A New Method for Online Parameter Estimation of Hunt-Crossley Environment Dynamic Models. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 981–986. [Google Scholar]
- Zhang, Y. Contact Dynamics for Rigid Bodies: Modeling and Experiments. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 2007. [Google Scholar]
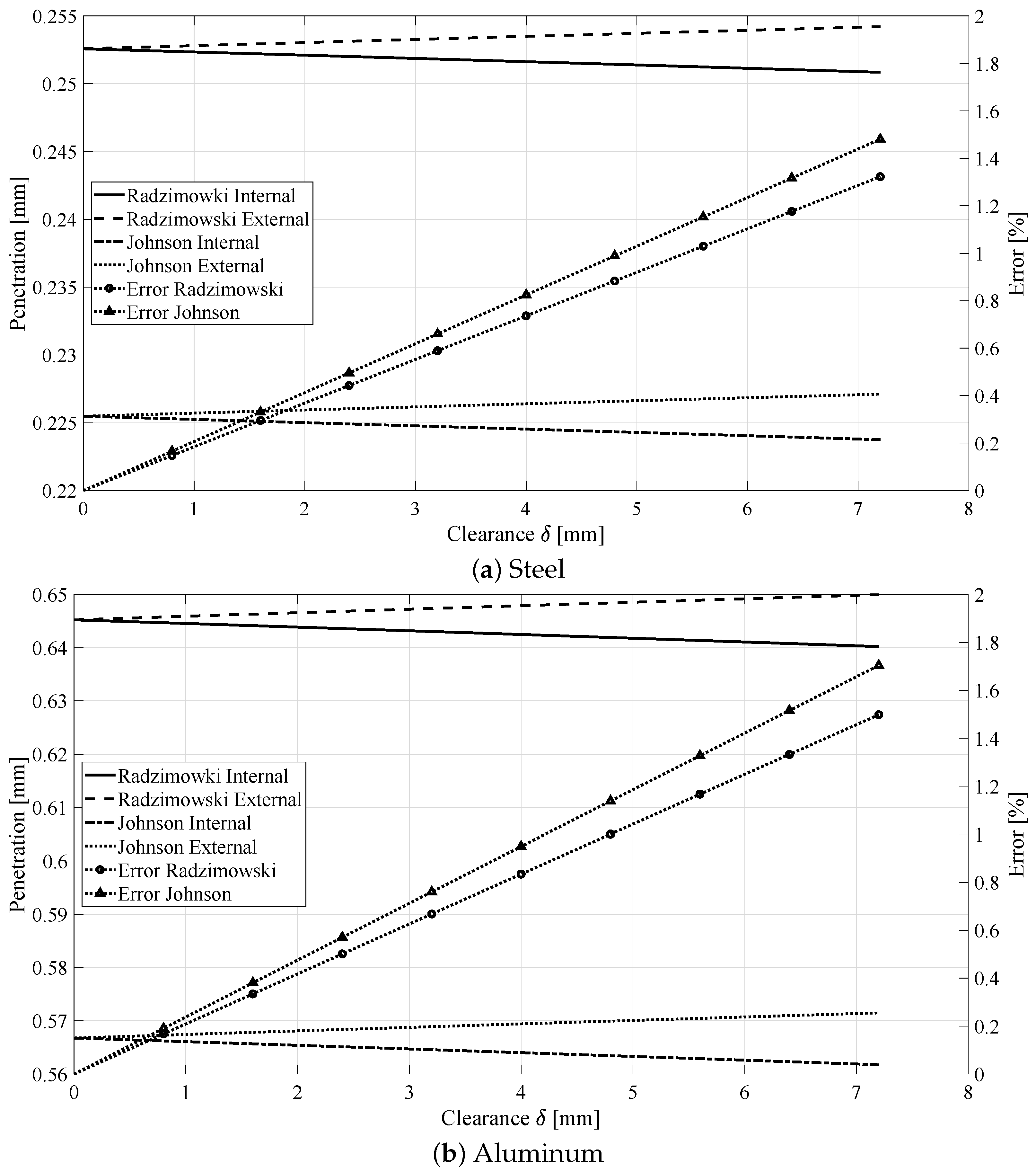
- Pereira, C.M.; Ramalho, A.L.; Ambrósio, J.A.C. A critical overview of internal and external cylinder contact force models. Nonlinear Dyn. 2011, 63, 681–697. [Google Scholar] [CrossRef]
- Machado, M.; Moreira, P.; Flores, P.; Lankarani, H.M. Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory. Mech. Mach. Theory 2012, 53, 99–121. [Google Scholar] [CrossRef]
- Goldsmith, W. Impact (Dover Civil and Mechanical Engineering), Annotated ed.; Dover Publications: Mineola, NY, USA, 2001; p. 416. [Google Scholar]
- Johnson, K.L. Contact Mechanics, Reprint ed.; Cambridge University Press: Cambridge, UK, 2008; p. 468. [Google Scholar]
- Flores, P.; Lankarani, H.M. Contact force models for multibody dynamics. In Solid Mechanics and Its Applications; Springer International Publishing: Cham, Switzerland, 2016; Volume 226. [Google Scholar] [CrossRef]
- Skrinjar, L.; Slavič, J.; Boltežar, M. A review of continuous contact-force models in multibody dynamics. Int. J. Mech. Sci. 2018, 145, 171–187. [Google Scholar] [CrossRef]
- Koshy, C.S.; Flores, P.; Lankarani, H.M. Study of the effect of contact force model on the dynamic response of mechanical systems with dry clearance joints: Computational and experimental approaches. Nonlinear Dyn. 2013, 73, 325–338. [Google Scholar] [CrossRef]
- Mindlin, R.D. Compliance of elastic bodies in contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity (Dover Books on Engineering), 4th ed.; Dover Publications: Mineola, NY, USA, 2011; p. 672. [Google Scholar]
- Deresiewicz, H. A note on Hertz’s theory of impact. Acta Mech. 1968, 6, 110–112. [Google Scholar] [CrossRef]
- Radzimovsky, E.I. Stress Distribution and Strength Condition of Two Rolling Cylinders Pressed Together; Technical Report; University of Illinois Urbana-Champaign: Champaign, IL, USA, 1953. [Google Scholar]
- Dubowsky, S. The Dynamic Response of Mechanical and Electromechanical Systems with Clearance and Nonlinear Impact Characteristics. Ph.D. Thesis, Columbia University, New York, NY, USA, 1971. [Google Scholar]
- Dubowsky, S.; Freudenstein, F. Dynamic analysis of mechanical systems with clearances Part 1: Formation of dynamic model. J. Eng. Ind. 1971, 93, 305–309. [Google Scholar] [CrossRef]
- Dubowsky, S.; Freudenstein, F. Dynamic analysis of mechanical systems with clearances Part 2: Dynamic response. J. Eng. Ind. 1971, 93, 310–316. [Google Scholar] [CrossRef]
- Lankarani, H.M.; Nikravesh, P.E. A contact force model with hysteresis damping for impact analysis of multibody systems. J. Mech. Des. 1990, 112, 369–376. [Google Scholar] [CrossRef]
- ESDU-78035. Contact Phenomena. I: Stresses, Deflections and Contact Dimensions for Normally-Loaded Unlubricated Elastic Components, Engineering Sciences Data Unit; Technical Report; 1978; ISBN 9780856792397. [Google Scholar]
- Pereira, C.; Ramalho, A.; Ambrósio, J.A.C. Experimental and numerical validation of an enhanced cylindrical contact force model. In Surface Effects and Contact Mechanics X; WIT Transactions on Engineering Sciences; De Hosson, J.M., Brebbia, C., Eds.; WIT Press: Southampton, UK, 2011; Volume 1, pp. 49–60. [Google Scholar] [CrossRef]
- Pereira, C.; Ramalho, A.; Ambrósio, J.A.C. An enhanced cylindrical contact force model. Multibody Syst. Dyn. 2015, 35, 277–298. [Google Scholar] [CrossRef]
- Flores, P.; Ambrósio, J.A.C. Revolute joints with clearance in multibody systems. Comput. Struct. 2004, 82, 1359–1369. [Google Scholar] [CrossRef]
- Flores, P.; Ambrósio, J.A.C.; Pimenta Claro, J.C.; Lankarani, H.M.; Koshy, C.S. A study on dynamics of mechanical systems including joints with clearance and lubrication. Mech. Mach. Theory 2006, 41, 247–261. [Google Scholar] [CrossRef]
- Hunt, K.H.; Crossley, F.R.E. Coefficient of restitution interpreted as damping in vibroimpact. J. Appl. Mech. 1975, 42, 440–445. [Google Scholar] [CrossRef]
- Tatara, Y.; Moriwaki, N. Study on impact of equivalent two bodies: Coefficients of restitution of spheres of brass, lead, glass, porcelain and agate, andthe material properties. Bull. JSME 1982, 25, 631–637. [Google Scholar] [CrossRef]
- Thornton, C. Coefficient of Restitution for Collinear Collisions of Elastic-Perfectly Plastic Spheres. J. Appl. Mech. 1997, 64, 383–386. [Google Scholar] [CrossRef]
- Seifried, R.; Schiehlen, W.; Eberhard, P. Numerical and experimental evaluation of the coefficient of restitution for repeated impacts. Int. J. Impact Eng. 2005, 32, 508–524. [Google Scholar] [CrossRef]
- Minamoto, H.; Kawamura, S. Moderately high speed impact of two identical spheres. Int. J. Impact Eng. 2011, 38, 123–129. [Google Scholar] [CrossRef]
- Herbert, R.G.; McWhannell, D.C. Shape and frequency composition of pulses from an impact pair. J. Eng. Ind. 1977, 99, 513–518. [Google Scholar] [CrossRef]
- Lee, T.W. Optimization of high speed geneva mechanisms. J. Mech. Des. 1981, 103, 621–630. [Google Scholar] [CrossRef]
- Lee, T.W.; Wang, A.C. On The Dynamics of Intermittent-Motion Mechanisms. Part 1: Dynamic Model and Response. J. Mech. Transm. Autom. Des. 1983, 105, 534–540. [Google Scholar] [CrossRef]
- Wang, A.C.; Lee, T.W. On the Dynamics of Intermittent-Motion Mechanisms. Part 2: Geneva Mechanisms, Ratchets, and Escapements. J. Mech. Transm. Autom. Des. 1983, 105, 541–551. [Google Scholar] [CrossRef]
- Wang, A.C. On the Kinematics and Dynamics of Intermittent Motion Mechanisms. Ph.D. Thesis, Rutgers University, New Brunswick, NJ, USA, 1983. [Google Scholar]
- Khulief, Y.A. Dynamic Analysis of Multibody Systems with Intermittent Motion. Ph.D. Thesis, University of Illinois at Chicago, Chicago, IL, USA, 1985. [Google Scholar]
- Khulief, Y.A.; Shabana, A.A. A continuous force model for the impact analysis of flexible multibody systems. Mech. Mach. Theory 1987, 22, 213–224. [Google Scholar] [CrossRef]
- Khulief, Y.A.; Shabana, A.A. Dynamic analysis of constrained system of rigid and flexible bodies with intermittent motion. J. Mech. Transm. Autom. Des. 1986, 108, 38–45. [Google Scholar] [CrossRef]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Lankarani, H.M.; Nikravesh, P.E. Continuous contact force models for impact analysis in multibody systems. Nonlinear Dyn. 1994, 5, 193–207. [Google Scholar] [CrossRef]
- Shivaswamy, S. Modeling Contact Forces and Energy Dissipation during Impact in Mechanical Systems. Ph.D. Thesis, Wichita State University, Wichita, KS, USA, 1997. [Google Scholar]
- Shivaswamy, S.; Lankarani, H.M. Impact Analysis of Plates Using Quasi-Static Approach. J. Mech. Des. 1997, 119, 376–381. [Google Scholar] [CrossRef]
- Rhee, J.; Akay, A. Dynamic response of a revolute joint with clearance. Mech. Mach. Theory 1996, 31, 121–134. [Google Scholar] [CrossRef]
- Marhefka, D.; Orin, D. A compliant contact model with nonlinear damping for simulation of robotic systems. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 1999, 29, 566–572. [Google Scholar] [CrossRef]
- Gonthier, Y.; McPhee, J.; Lange, C.; Piedœuf, J.C. A Regularized Contact Model with Asymmetric Damping and Dwell-Time Dependent Friction. Multibody Syst. Dyn. 2004, 11, 209–233. [Google Scholar] [CrossRef]
- Machado, M.; Flores, P.; Ambrósio, J.A.C. A Lookup-Table-Based Approach for Spatial Analysis of Contact Problems. J. Comput. Nonlinear Dyn. 2014, 9, 041010. [Google Scholar] [CrossRef]
- Machado, M.; Flores, P.; Pimenta Claro, J.C.; Ambrósio, J.A.C.; Silva, M.; Completo, A.; Lankarani, H.M. Development of a planar multibody model of the human knee joint. Nonlinear Dyn. 2010, 60, 459–478. [Google Scholar] [CrossRef]
- Machado, M.; Flores, P.; Ambrósio, J.A.C. Influence of the contact model on the dynamic response of the human knee joint. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2011, 225, 344–358. [Google Scholar] [CrossRef]
- Gharib, M.; Hurmuzlu, Y. A new contact force model for low coefficient of restitution impact. J. Appl. Mech. 2012, 79, 064506. [Google Scholar] [CrossRef]
- Stoianovici, D.; Hurmuzlu, Y. A Critical Study of the Applicability of Rigid-Body Collision Theory. J. Appl. Mech. 1996, 63, 307–316. [Google Scholar] [CrossRef]
- Hu, S.; Guo, X. A dissipative contact force model for impact analysis in multibody dynamics. Multibody Syst. Dyn. 2015, 35, 131–151. [Google Scholar] [CrossRef]



| Geometry | Inertia | Initial Conditions | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Name | Mass (kg) | Inertia (kg· ) | |||||||
| 68 | mm | 1 | Frame | \\ | \\ | 31 | deg | ||
| 60 | mm | 2 | Crank | 0.090 | 30.40 | 0 | |||
| 52 | mm | 3 | Pin | 0.015 | 0.48 | ||||
| 8 | mm | 4 | Slotted slider | 0.353 | 3495.6 | ||||
| 7.9 | mm | ||||||||
| 120 | deg | ||||||||
| ΔR | Lankarani | Radzimowsky | Johnson | ||||
| (mm) | K [] | n | K [] | n | K [] | n | |
| ΔR | Goldsmith | EDSU-78035 | |||||
| (mm) | K [] | n | K [] | n | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Autiero, M.; Cera, M.; Cirelli, M.; Pennestrì, E.; Valentini, P.P. Review with Analytical-Numerical Comparison of Contact Force Models for Slotted Joints in Machines. Machines 2022, 10, 966. https://doi.org/10.3390/machines10110966
Autiero M, Cera M, Cirelli M, Pennestrì E, Valentini PP. Review with Analytical-Numerical Comparison of Contact Force Models for Slotted Joints in Machines. Machines. 2022; 10(11):966. https://doi.org/10.3390/machines10110966
Chicago/Turabian StyleAutiero, Matteo, Mattia Cera, Marco Cirelli, Ettore Pennestrì, and Pier Paolo Valentini. 2022. "Review with Analytical-Numerical Comparison of Contact Force Models for Slotted Joints in Machines" Machines 10, no. 11: 966. https://doi.org/10.3390/machines10110966
APA StyleAutiero, M., Cera, M., Cirelli, M., Pennestrì, E., & Valentini, P. P. (2022). Review with Analytical-Numerical Comparison of Contact Force Models for Slotted Joints in Machines. Machines, 10(11), 966. https://doi.org/10.3390/machines10110966