Abstract
Sparse decomposition has been widely used in gear local fault diagnosis due to its outstanding performance in feature extraction. The extraction results depend heavily on the similarity between dictionary atoms and fault feature signal. However, the transient impact signal aroused by gear local defect is usually submerged in meshing harmonics and noise. It is still a challenging task to construct high-quality impact dictionary for complex actual signal. To handle this issue, a novel impact feature extraction method based on Empirical Mode Decomposition (EMD) and sparse decomposition is proposed in this paper. Firstly, EMD is employed to adaptively decompose the original signal into several Intrinsic Mode Functions (IMFs). The high-frequency resonance component is separated from meshing harmonics and part of the noise. Then, the IMF with the prominent impact features is selected as the Main Intrinsic Mode Function (MIMF) based on the kurtosis. Accordingly, the modal parameters required for impact dictionary are identified from the MIMF by correlation filtering. Finally, the transient impact component is extracted from the original signal by Match Pursuit (MP). The proposed method was adequately evaluated by a gear local fault simulation signal, and the single-stage gearbox and five-speed transmission experiments. The effectiveness and superiority of the proposed method is validated by comparison with other feature extraction techniques.
1. Introduction
The gearbox plays a vital role in the power transmission of mechanical systems, such as automotive transmissions [1] and wind turbine planetary gearbox [2,3]. Gearbox generally works under a tough environment and therefore is prone to suffer from localized faults (such as spalls and broken tooth) after longtime service. Scholars tend to diagnose faults by extracting fault features from gearbox vibration signals collected by sensors [4]. However, the transient impact signal caused by gear local fault is often accompanied by strong interference noise. Additionally, the signal-to-noise ratio (SNR) of the gear meshing harmonics is much higher than that of the impact component, which further increases the difficulty in extracting fault features [5].
Although recently developed data-driven [6] and machine learning [7] techniques avoid separating the fault signatures from complex vibration signals and have achieved great success in gear fault diagnosis, it is non-negligible that these methods need large amounts of data and are poorly interpretable. Therefore, the signal processing methods based on feature extraction still play an important role in gear fault diagnosis field. There have been various signal processing methods applied in gear fault feature extraction, including Time–Frequency Analysis (TFA) [8], Wavelet Transform (WT) [9], Spectral Kurtosis (SK) [10], Empirical Mode Decomposition (EMD) [11], Variational Mode Decomposition (VMD) [12], etc. Compared with the above methods, sparse decomposition (SD) shows more excellent performance in feature extraction. SD can sparsely represent the fault feature signal through selecting a few atoms from an appropriate dictionary and has been successfully applied in gear fault diagnosis. He at al. [13] and Yang et al. [14] employed correlation filtering to identify the modal parameters and constructed impact atom based on the impulse response function (IRF), and separated the gear localized fault features from gearbox vibration signal. Fan et al. [15] utilized Morlet wavelet in shape similar to the impact signal to construct the sparse dictionary and extracted transient features in gearbox. Cai et al. [16] constructed STFT dictionary and used the nonconvex generalized minimax-concave (GMC) penalty to enhance sparsity in the sparse approximation to extract the periodic transient component in faulty gearbox. Li et al. [17] designed the impact-type sparse dictionary consisting of the unit impulse response of multiple-degree-of-freedom vibration system, and extracted gear transient features in fixed-shaft and planetary gearboxes. Wang et al. [18] sparsely represented transient component over low Q-factor TQWTs, and extracted weak gear fault features obscured by heavy background noise and multiple harmonic interferences. Sun et al. [19] proposed a weighted sparse representation method based on the margin factor that was the more sensitive indicator to reflect the local gear fault to extract the impact features in planetary gearbox vibration signal. Cai et al. [20] proposed a reweighted generalized minimax-concave sparse regularization based on the Tunable Q-factor Wavelet Transform (TQWT) dictionary to extract transient features from the hot-milling transmission gearbox vibration signal. Deng et al. [21] proposed a novel water cycle algorithm (WCA) to identify the wavelet basis parameters and optimized the fault impulse matching algorithm (FIMA) for gear fault dictionary design. Yang et al. [22] constructed a union of redundant dictionary (URD) on the basis of the underlying prior information of the oscillate characteristics with multicomponent coupling effect and different morphological waveforms, and obtained the time–frequency distribution of the gear fault signal by combining the Wigner–Ville distribution (WVD) of each atom and corresponding sparse coefficient. The above references illustrate that the high-quality sparse dictionary whose atoms are similar to the fault feature signal could ensure the performance of sparse decomposition. However, it is not easy to construct a high-quality dictionary since the observed gearbox signal is complex and susceptible to environmental noise. The periodic impact signal aroused by gear local fault is always submerged in meshing harmonics and noise. Especially, the impact component is weak and the meshing harmonics dominate in the early stage of faults that further increases the difficulty of constructing ideal impact atoms.
To construct high-precision impact dictionaries, scholars have adopted some strategies to minimize the influence of irrelevant components. For example, the meshing harmonic components are firstly separated before identifying impact dictionary parameters in [13], and squared envelope spectrum kurtosis-based weight setting strategy is used to attenuate the effects of harmonics and noise in [20]. Obviously, these strategies do improve the performance of the techniques for extracting gear local fault features. However, this comes at the cost of adding more procedures and priors, which reduces the efficiency and practicality of the method to some extent. Therefore, it is of great significance to attenuate and even avoid the influence of irrelevant components in the gearbox vibration signal in an efficient and simple way.
Empirical Mode Decomposition (EMD) [23] can adaptively decompose the original signal into several Intrinsic Mode Functions (IMFs) from high to low frequency. As a result, various components of different frequencies in the original signal are distributed in different IMFs. Therefore, EMD has the potential to attenuate the influence of irrelevant components and has been applied in gear fault feature extraction [24]. Xia et al. [25] proposed a doubly iterative empirical mode decomposition method to separate gear fault features from irrelevant components, where the local extrema are fixed during the sifting process to improve the decomposition performance. Wang et al. [26] proposed a new noise-assisted EMD Manifold (EMDM) method that can preserve fault-related transients and suppress fault-unrelated components by nonlinearly and adaptively fusing the fault-related IMFs containing different noise via a manifold learning algorithm. Han et al. [27] decomposed the non-stationary signal into several IMFs, and selected the IMF of sensitive fault feature frequency as the input to the SVM for gear fault diagnosis. Du et al. [28] presented a new weighted-EMD de-noising technique and assigned different weights to IMFs according to their fault-related degrees for fault feature signal reconstruction in a planetary gearbox. Akram et al. [29] decomposed the original vibration signal into several IMFs by EMD and selected the IMF containing gear fault features according to operating parameters and spectrum. Inturi et al. [30] identified the IMFs containing local gear tooth defects features by examining the Pearson correlation coefficient. Li et al. [31] selected the IMF that contributes more to the gear fault source signal at the aid of mixture degree. These references validate that EMD has the potential to separate fault feature components from irrelevant components such as meshing harmonics and noise. Furthermore, the decomposition process is completely adaptive. However, it should not be ignored that EMD is prone to modal aliasing and endpoint effects that may affect the fault features extraction results.
For the aforementioned issues, a novel impact feature extraction method for gear local fault diagnosis based on EMD and sparse decomposition is proposed in this paper. EMD is employed to separate high-frequency resonance components from meshing harmonics and noise. The sparse decomposition is used to extract the local fault features from original signal. Specifically, EMD adaptively decomposes the original signal into a series of IMFs with frequencies from high to low firstly. Then, kurtosis is employed to select the IMF in which the impact component dominates as the Main IMF (MIMF). The natural frequencies and damping ratios are identified from MIMF by correlation filtering and are used to construct the impact dictionary. Since there are almost no meshing harmonics in MIMF, these modal parameters are closer to the true fault feature components. Finally, the impact fault feature component is extracted from the original signal rather than MIMF by Match Pursuit (MP). In this way, even if there is modal aliasing or end effect during EMD process, it will not affect the final extraction results. The simulation and two experimental signals verified the effectiveness and superiority of the proposed method.
The rest of this paper is structured as follows. Section 2 mainly introduces the basic theory of EMD and sparse decomposition. The construction of the impact dictionary is also mentioned. Section 3 mainly introduces the specific process of the proposed impact feature extraction method based on EMD and sparse decomposition for gear local fault diagnosis. Section 4 constructs a gear local fault simulation signal with noise to verify the effectiveness of the proposed method, and compares it with those identifying parameters directly from the original signal, and extracting fault features from the MIMF. Section 5 further verifies the superiority and effectiveness of the proposed method by the single-stage gearbox and five-speed transmission experimental data. Finally, conclusions are drawn in the last section.
2. Theoretical Background
This section introduces the basic framework of EMD and sparse decomposition, and the construction of the impact dictionary is also mentioned.
2.1. Empirical Mode Decomposition (EMD)
The EMD algorithm can self-adaptively decompose a signal vector into several high-to-low frequency IMFs and a residual series [23]:
where is the original time series, is the i-th IMF, and is the residual series that represents the trend of the signal. The conditions that must be met for IMF are as follows:
- The numbers of extreme points and zero points must be equal or at most different in one over the length of the data;
- At any data point, the average of the envelope of the local maximum and that of the local minimum must be zero.
The procedure to determine each IMF is known as the “sifting process”, and the specific process can be found in [23].
The EMD self-adaptively decomposes original signal into several IMFs, and each IMF contains the component of different frequency bands and scales. In this way, the high-frequency resonance components are separated from large-amplitude harmonics. Furthermore, since the noise signal is distributed in the whole frequency band, the energy of the noise is also dispersed into multiple IMFs.
2.2. Sparse Decomposition Based on Match Pursuit (MP)
Sparse decomposition can sparsely represent the fault feature signal through selecting a bit number of atoms from an appropriate dictionary. Specifically, a sparse signal vector can be represented as a linear combination of dictionary matrices , i.e., , where is sparse coefficient vector with only a few non-zero value. The column in the dictionary matrix is called an atom. The dictionary is redundant due to . The sparse coefficient vector can be obtained by solving the optimization problem of Equation (2).
where denotes the and is approximately sparse tolerance.
In general, Equation (2) is a NP-hard problem and cannot be solved directly. Matching Pursuit (MP) [32] is commonly used to solve the problem, which reconstructs the characteristic signal by linearly superimposing a small number of optimal atoms searched from the redundant dictionary . A signal can be decomposed into a linear superposition of atoms in the dictionary . After each greedy search, an atom that best matches the signal can be obtained, and the original signal can be decomposed by Equation (3).
where is the residual after the first pursuit.
Since and are orthogonal to each other,
where denotes inner product. After the residual is iteratively matched N times, the signal is decomposed into a linear combination of and the N-th order remainder , as expressed by Equation (5).
The iteration stops until ( is a small constant) or the iteration times exceed the number of atoms. It helps to avoid falling into infinite loop.
The feature extraction precision is closely related to the similarity between the dictionary atom and the actual signal. The impulses caused by localized fault are damped oscillation signals with the amplitude attenuates by exponential form, so an impact modulation dictionary is constructed for describing the local damage vibration response of a gear. The atom can be descripted by a single impulse response function, that is
where is the damped natural frequency of the gear and sensor system, is relative damping ratio, and A is amplitude. The damped natural frequency and relative damping ratio can be identified by correlation filtering. Correlation filtering algorithm flow and parameter setting can be consulted from [13]. The precision of the identified natural frequency and damping ratio using correlation filtering is greatly affected by interfering components such as meshing harmonics and noise.
3. The Proposed Impact Feature Extraction Method
In order to diagnose the gear local fault, an impact feature extraction method based on EMD and sparse decomposition is proposed in this section. EMD is employed to separate high-frequency resonance components from meshing harmonics and part of noise. This effectively alleviates the problem that sparse decomposition is susceptible to irrelevant components. The transient impact component is extracted from original signal rather than a certain IMF, which effectively avoids possible modal aliasing or end effects affecting the results. The flowchart of the proposed impact feature extraction method for gear local fault diagnosis is shown in Figure 1.
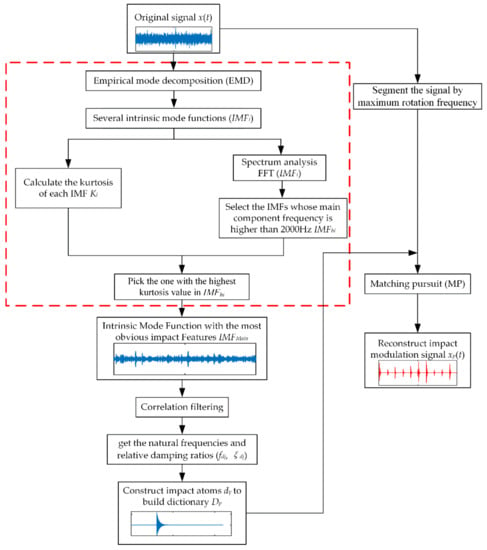
Figure 1.
The flowchart of the proposed impact feature extraction method for gear local fault diagnosis.
The details of the proposed method are summarized as follows:
- (1)
- The gearbox original vibration signal is collected at appropriate sampling frequency .
- (2)
- The vibration signal is adaptively decomposed by EMD to obtain several IMFs whose frequency range changes from high to low.
- (3)
- The first few IMFs containing few gear meshing components are selected as alternatives through the amplitude spectrum. Generally, the meshing frequencies and other harmonic components remain in a lower frequency range. Therefore, those IMFs whose frequencies are above 2000 Hz are selected for further analysis.
- (4)
- The kurtosis of the alternative IMFs is calculated according to Equation (7).where is the absolute value of each point of the signal, is the average value of the signal and is the root mean square value. The kurtosis is particularly sensitive to impact signals and usually the larger it is, the more impact components the corresponding IMF includes. Therefore, the one with the highest kurtosis among the alternative IMFs is chosen as the MIMF, which has the most prominent impact characteristics and is less affected by the meshing component.
- (5)
- The natural frequency and the damping ratio are identified by correlation filtering from MIMF, which are used to construct the impact dictionary .
- (6)
- To improve the operating efficiency, the original signal is divided into several segments based on the smallest fault feature period [13] and each segment signal is, respectively, reconstructed by MP. After splicing together all the reconstructed signals, the gear local fault feature signal is obtained.
4. Simulation Analysis
To prove the effectiveness and anti-noise performance of the proposed method, the gear local fault simulation signal containing gear meshing components and noise interference is constructed and analyzed.
4.1. Construct Fault Simulation Signal
The simulation signal is established as
where is the noise-free complex simulation signal, represents the rotational frequency and its harmonic components with the rotational frequency , represents the meshing component with amplitude modulation, where the mesh frequency is . represents the impact component containing two order modes to simulate gear local fault and the parameters are specifically set as: natural frequency , relative damping ratio , the impact moment , and the impact period . Moreover, the amplitudes of each impact in Equation (11) are set randomly as and , respectively. The sampling frequency and sampling length are set as and , respectively. To get closer to the actual situation, the Gaussian white noise is added to the simulation signal in Equation (8), and then the signal-to-noise ratio (SNR) of the impact component is −11.49 dB. The noisy simulation signal and its amplitude spectrum are given in Figure 2. It can be seen that the impact component is completely coupled with the meshing harmonic component and interference noise in time domain. In addition, the amplitudes of the natural frequency band are much lower than those of the harmonic components. The first-order natural frequency band is close to the third-order meshing frequency band in the amplitude spectrum. Therefore, it is difficult to detect the presence of the impact component from the noisy simulation signal.
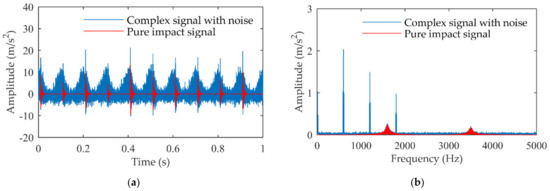
Figure 2.
The gear local fault simulation signal with noise: (a) Time domain signal and (b) amplitude spectrum.
4.2. Select the Main IMF (MIMF) Based on EMD and Kurtosis
The noisy simulation signal is adaptively decomposed into 12 IMFs by EMD. The first four IMFs and their amplitude spectrum are given in Figure 3. It can be seen that the main components of IMF4 are all within 2000 Hz and mainly contain meshing harmonics and noise. Thus, it is sufficient to select the MIMF from the first four IMFs.
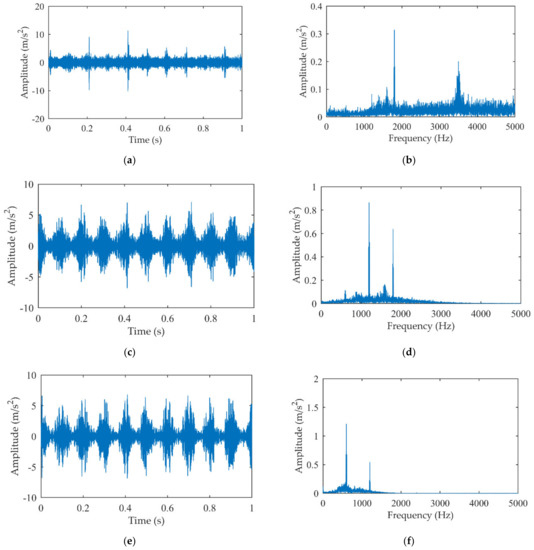
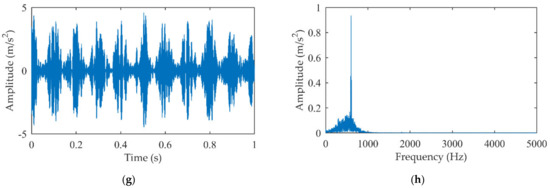
Figure 3.
The first four IMFs of the simulation signal: (a) IMF1; (b) Amplitude spectrum of IMF1; (c) IMF2; (d) Amplitude spectrum of IMF2; (e) IMF3; (f) Amplitude spectrum of IMF3; (g) IMF4; (h) Amplitude spectrum of IMF4.
The kurtosis of the first four IMFs is calculated and exhibited in Table 1. It can be seen that the kurtosis of the IMF1 is much larger than others and the natural frequency band is dominant even if there remains some harmonics in amplitude spectrum as shown in Figure 3b. Therefore, the IMF1 is selected as the MIMF. The modal parameters required for the impact dictionary will be identified from MIMF.

Table 1.
The kurtosis of the first four IMFs (Simulation).
4.3. Extracting the Fault Impact Signal
To obtain the modal parameters to construct the optimized impact dictionary, the natural frequency and relative damping ratio are identified from MIMF by correlation filtering [13]. Specifically, the MIMF is segmented by the minimum rotation period (maximum frequency conversion), i.e., . Moreover, the search ranges of the frequency and damping ratio are set as and , respectively. Since MIMF is dominated by the impact component and the interference of harmonic components is largely decreased, the modal parameters of actual faults are accurately identified. These model parameters are used to construct the optimized impact dictionary, and the impact signal is extracted from the original simulation signal rather than MIMF. The results are given in Figure 4. It can be seen that the impact component is well reconstructed and the interval is highly consistent with the theoretical impact period. In addition, the second-order natural frequency band of the impact component is clearly visible and there is no residual meshing harmonic components in the amplitude spectrum. The simulation signal illustrates that even if there is only part of the modal information available, the proposed method can still achieve satisfactory results.
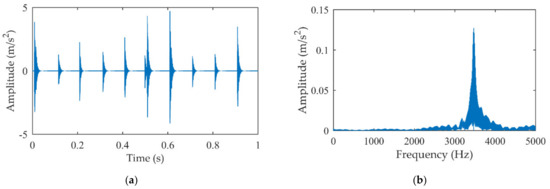
Figure 4.
The extracted impact signal by proposed method: (a) Time domain signal; (b) Amplitude spectrum.
4.4. Comparative Analysis
Before comparative analysis, we define two terms, one of which is the “traditional sparse decomposition” meaning that the dictionary parameter identification and feature extraction are all implemented in the original signal and the whole process was carried out without EMD. The other is called “EMD + MP” meaning that the dictionary parameter identification and feature extraction are all implemented in the MIMF.
To highlight the superiority of the proposed method, the traditional sparse decomposition is used to process the same simulation signal. Specifically, the natural frequency and relative damping ratio are directly identified from original signal rather than MIMF. The extracted impact component is shown in Figure 5. There are a lot of interference components appearing in the time domain except for transient impact signal as shown in Figure 5a. It leads to difficulty to identify the exact impact interval. Moreover, a large number of meshing harmonic components are visible in the amplitude spectrum. The model parameters of the dominant harmonic components are wrongly identified and added to the impact dictionary resulting in the poor extraction results.
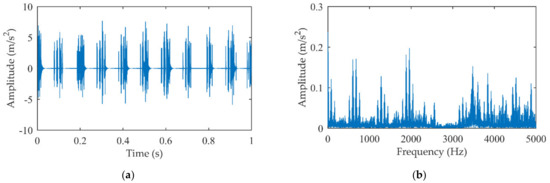
Figure 5.
The extracted impact signal by traditional sparse decomposition: (a) Time domain signal; (b) Amplitude spectrum.
The EMD + MP is also compared with the proposed method. Specifically, the modal parameters required to impact dictionary atoms are identified from MIMF and the impact component is also extracted from the MIMF. The results are given in Figure 6. There are impact waves whose number is far exceeding the theoretical value appearing in the time domain. It is almost impossible to estimate the impact interval according to Figure 6a. Although the natural frequency band triggered by impacts is still dominant in the amplitude spectrum, the signal structure is unreasonably disassembled by EMD leading to inaccurate results.
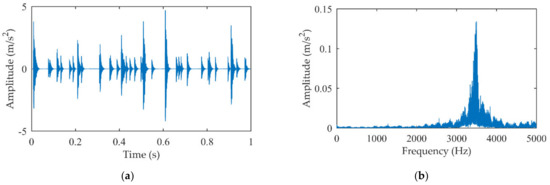
Figure 6.
The extracted impact signal by EMD + MP: (a) Time domain signal; (b) Amplitude spectrum.
To show the superiority of the proposed method scientifically, three indicators are selected to evaluate the relationship of the extracted signal with the original signal, which are, respectively, the correlation coefficient (CC), root-mean-square Error (RMSE), and relative root-mean-square error (RRMSE).
where and are the original data and the corresponding estimate data at the n-th point in the time domain; and are their mean values, respectively. Among them, the larger the value of CC is and the smaller the value of RMSE and RRMSE, the error between the extracted signal and the theoretical signal will be. The statistical indicators of the extraction results of the three methods are shown in Table 2. Obviously, the impact signal extracted by the proposed method has the biggest CC and smallest RMSE and RRMSE, which is much closer to the true value.

Table 2.
The statistical indicators of the extraction results of the three methods.
Since the modal parameters are identified only from MIMF meaning that not all model parameters are identified and introduced into the impact dictionary, the extracted impact component is partial rather than complete. This is the reason that CC is not close to 1. From another perspective, even if not all model parameters are identified, the proposed method can still achieve better results in which the impact interval can be accurately estimated. In summary, the simulation signal verifies the effectiveness and superiority of the proposed method.
5. Experimental Analysis
The single-stage gearbox and five-speed transmission experiments are further conducted to verify the effectiveness of the proposed method in this section.
5.1. The Single-Stage Gearbox Experiment
The single-stage gearbox and the fault gear are shown in Figure 7. The teeth number of the input shaft gear and output shaft gear is 32 and 44, respectively. The vibration signals are collected by the Muller BBM data acquisition system with the sampling frequency . The input shaft speed is 1000 rpm, and the observed vibration acceleration signal on the bearing house of output shaft is given in Figure 8.

Figure 7.
The single-stage gearbox test bench: (a) The single-stage gearbox; (b) The local fault gear with pitting.
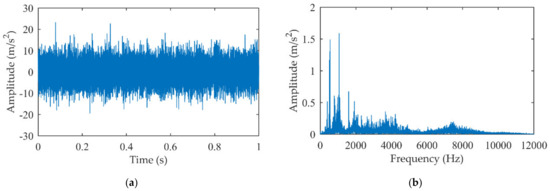
Figure 8.
The observed acceleration signal of the single-stage gearbox experiment: (a) Time domain signal; (b) Amplitude spectrum.
The experimental signal is decomposed by EMD and 15 IMFs are obtained. The first four IMFs and their amplitude spectrums are shown in Figure 9. The kurtosis values of the first four IMFs are calculated and exhibited in Table 3. As illustrated in Figure 9, the first two IMFs with higher frequencies do not contain visible gear meshing components, but IMF3 and IMF4 with lower frequencies contain harmonic components with prominent amplitudes. As the frequencies of the IMFs are from high to low, the subsequent IMFs will contain harmonic components which are harmful to the extraction of the impact signals. Therefore, the MIMF with obvious impact features should be selected from the first few IMFs. Table 3 shows that the kurtosis of IMF2 is the largest, and there is no obvious harmonic interference in IMF2 as shown in Figure 9d. There is no doubt that IMF2 was determined as the MIMF.
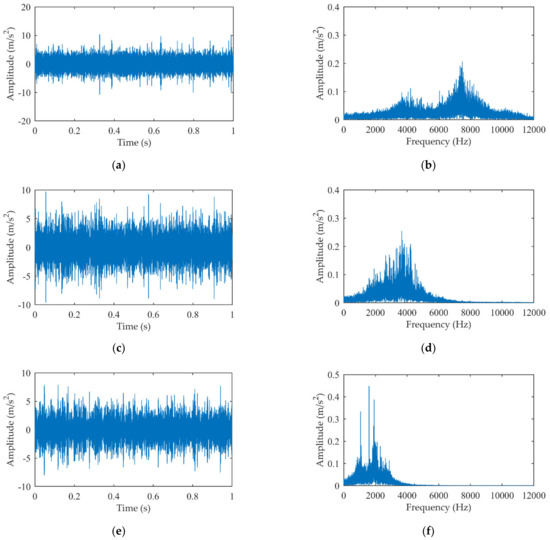
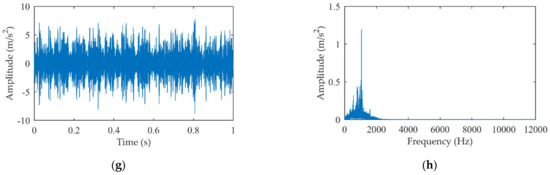
Figure 9.
The first four IMFs of the single-stage gearbox experiment signal: (a) IMF1; (b) Amplitude spectrum of IMF1; (c) IMF2; (d) Amplitude spectrum of IMF2; (e) IMF3; (f) Amplitude spectrum of IMF3; (g) IMF4; (h) Amplitude spectrum of IMF4.

Table 3.
The kurtosis of the first four IMFs (the single-stage gearbox experiment).
Set the search scopes of and as and , respectively. The MIMF is divided into several sections by the smallest rotation period of shafts . The identified modal parameters are used to construct an optimized impact dictionary. The impact signal is extracted by MP and the results are given in Figure 10. It can be seen that almost all the impacts are well reconstructed. The average time interval of the impulse responses is 0.082464 s (close to 0.0825 s, the theoretical fault period of the output shaft, the relative error is 0.04%) after using the 3σ principle to remove the gross error, which is consistent with the experimental conditions. Obviously, the proposed method which identified the modal parameters on the premise of eliminating the interference of harmonic components can reflect the characteristics of the actual impact fault signal. Thereby, the extracted periodic pulses are more accurate.
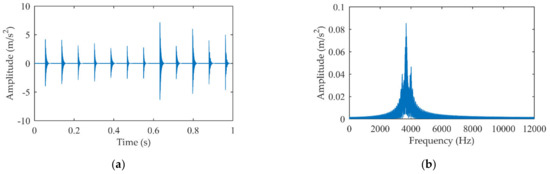
Figure 10.
The extracted impact signal by proposed method: (a) Time domain signal; (b) Amplitude spectrum.
For comparison, the impact component is also extracted by traditional sparse decomposition. The results are given in Figure 11. There is a component similar to the impact waveform appearing periodically in the time domain, but these signals decay so slowly that they cannot decay to zero in each sub-segment. Moreover, the meshing harmonic components dominate in the amplitude spectrum as shown in Figure 11b. It can be observed that the modal parameters identified have large errors and makes it impossible to extract the accurate impact signal from the experimental signal.
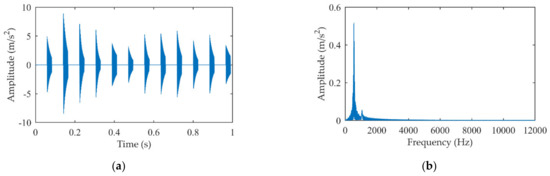
Figure 11.
The extracted impact signal by traditional sparse decomposition: (a) Time domain signal; (b) Amplitude spectrum.
Similarly, the EMD + MP is also employed to process the experimental signal, and the results are shown in Figure 12. It can be seen that although the natural frequency band is accurately identified, the impact waveform in the time domain is still incomplete because the EMD destroys the original signal structure.
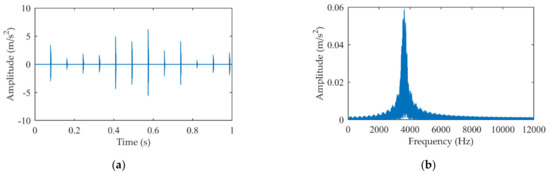
Figure 12.
The extracted impact signal by EMD + MP: (a) Time domain signal; (b) Amplitude spectrum.
5.2. The Five-Speed Transmission Experimental
The five-speed transmission experiment is implemented on the mechanical transmission test bench. The transmission and its structural diagram are shown in Figure 13, and there is a broken tooth on the output shaft of the fifth gear. The vibration signals are collected by the Muller BBM data acquisition system with the sampling frequency . The input shaft speed is 1000 rpm, and the transmission is shifted to the fifth gear. The operating parameters are given in Table 4.
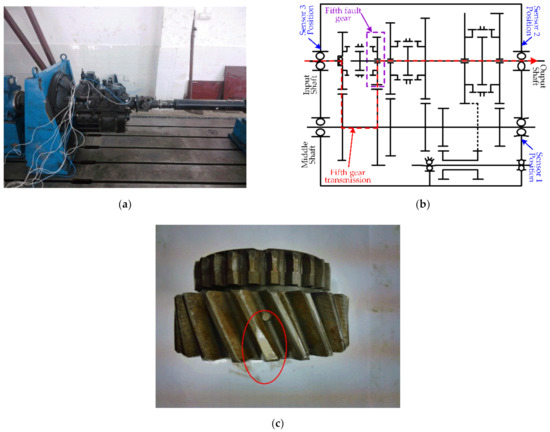
Figure 13.
The five-speed transmission test bench: (a) The five-speed transmission; (b) Drive structural diagram; (c) The local fault gear with broken tooth.

Table 4.
The operating parameter of the transmission.
In order to highlight the effectiveness of the proposed method, the acceleration signal collected on the bearing house of output shaft (sensor 2 in Figure 13b, which is far from the faulty gear) is analyzed. The measured vibration acceleration signal and its amplitude spectrum are shown in Figure 14. In this case, the fault impact component is submerged in noise and the meshing frequencies are dominant in the spectrum.
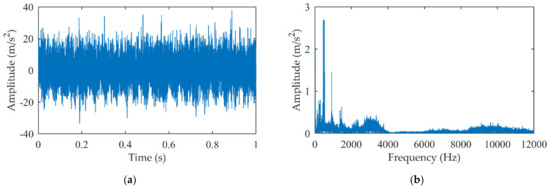
Figure 14.
The measured acceleration signal of the five-speed transmission experiment: (a) Time domain signal; (b) Amplitude spectrum.
The experimental signal is decomposed by EMD and 14 IMFs are obtained. The first four IMFs and their amplitude spectrums are given in Figure 15, and the kurtosis values of the first four IMFs are calculated and exhibited in Table 5. Noteworthy, the IMF2 with the largest kurtosis and containing no meshing harmonic component is selected as the MIMF.
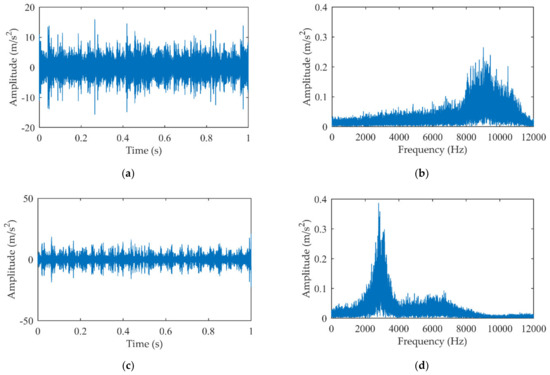
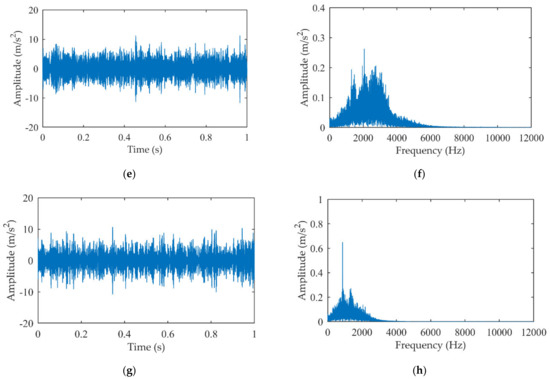
Figure 15.
The first four IMFs of the five-speed transmission experiment signal: (a) IMF1; (b) Amplitude spectrum of IMF1; (c) IMF2; (d) Amplitude spectrum of IMF2; (e) IMF3; (f) Amplitude spectrum of IMF3; (g) IMF4; (h) Amplitude spectrum of IMF4.

Table 5.
The kurtosis of the first four IMFs (the five-speed transmission experiment).
The extracted impact signal by the proposed method is given in Figure 16. The average time interval of the impulse responses is 0.045916 s (close to 0.045935 s, the theoretical fault period of the output shaft, the relative error is 0.04%) after using the 3σ principle to remove the gross error, which is consistent with the experimental conditions.
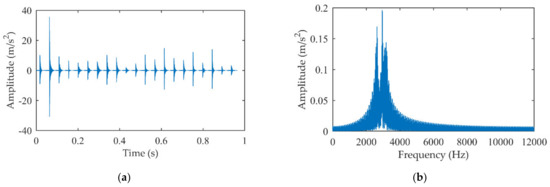
Figure 16.
The extracted impact signal by the proposed method: (a) Time domain signal; (b) Amplitude spectrum.
For comparison, the impact components are also extracted by traditional sparse decomposition, and the results are given in Figure 17. There are impact-like signals not decaying to zero in the time domain and harmonic components dominate in the amplitude spectrum. The identification of the model parameters is affected by harmonic components and interference noise, resulting in poor quality of the extracted signal.
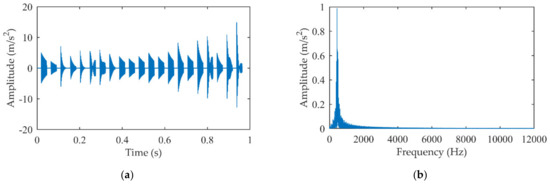
Figure 17.
The extracted impact signal by traditional sparse decomposition: (a) Time domain signal; (b) Amplitude spectrum.
Furthermore, the EMD + MP is also employed to process the same experimental signal. The results are given in Figure 18. It can be seen that the impact waveforms are well reconstructed in the time domain. However, since the MIMF only contains part of the impact component, the amplitudes of the extracted impact signal are smaller.
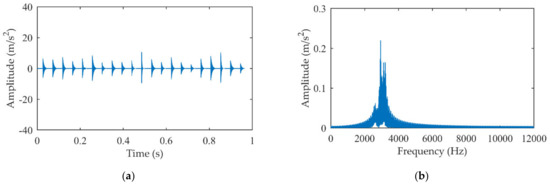
Figure 18.
The extracted impact signal by EMD + MP: (a) Time domain signal; (b) Amplitude spectrum.
The single-stage gearbox and five-speed transmission experimental signals further verify the effectiveness of the proposed method. The periodic impact signals are well extracted in the time domain, and the relative error between the average time interval and theoretical value is only 0.04%. Furthermore, compared with directly identifying modal parameters from the original signal and extracting impact components from MIMF, the proposed method shows better performance in gear local fault features extraction.
6. Conclusions
Sparse decomposition is susceptible to irrelevant components such as meshing harmonics and noise when applied in gear fault diagnosis. To handle these issues, a novel impact feature extraction method based on EMD and sparse decomposition is proposed in this article. Firstly, the observed vibration signal is adaptively decomposed into several high-to-low frequency IMFs by EMD. The high-frequency resonance component is separated from meshing harmonics. Then, the kurtosis is employed to select the one with the most prominent impact features as the MIMF. The natural frequency and relative damping ratio are identified from MIMF by the correlation filtering technique. Since getting rid of the influence of harmonic components, these modal parameters are more accurately used to construct the impact dictionary whose atoms are similar to true transient impact signals. Finally, the periodic impact component is extracted from the original signal rather than MIMF to avoid possible modal aliasing or end effects affecting the results. The proposed impact feature extraction method was fully evaluated by a noisy gear fault simulation signal. The single-stage gearbox and five-speed transmission experimental signals further verified the effectiveness and superiority of the proposed method. The relative error of the average time interval between the extracted impact signal and theoretical value is only 0.04%.
Author Contributions
Conceptualization, Z.L. and K.D.; methodology, Z.L.; software, Z.L. and G.H.; validation, Z.L., H.L. and Z.C.; formal analysis, Z.L. and C.D.; investigation, C.D.; resources, K.D. and H.L.; data curation, Z.L.; writing—original draft preparation, Z.L.; writing—review and editing, Z.L.; supervision, C.D. and Z.C.; project administration, Z.C.; funding acquisition, K.D., H.L. and Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (No. 51875206 & 51875207), Natural Science Foundation of Guangdong Province-China (No. 2020A1515010750), Opening Project of Beijing Key Laboratory of Measurement Control of Mechanical and Electrical System Technology, Beijing Information Science Technology University (No. KF20212223204), and GuangDong Basic and Applied Basic Research Foundation (No. 2021A1515110708).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- El Morsy, M.; Achtenová, G. Vehicle Gearbox Fault Diagnosis Based On Cepstrum Analysis. World Acad. Sci. Eng. Technol. Int. J. Mech. Aerosp. Ind. Mechatron. Eng. 2014, 8, 1533–1539. [Google Scholar]
- Wang, T.; Han, Q.; Chu, F.; Feng, Z. Vibration based condition monitoring and fault diagnosis of wind turbine planetary gearbox: A review. Mech. Syst. Signal Processing 2019, 126, 662–685. [Google Scholar] [CrossRef]
- Gu, H.; Liu, W.; Gao, Q.; Zhang, Y. A review on wind turbines gearbox fault diagnosis methods. J. Vibroeng. 2021, 23, 26–43. [Google Scholar]
- Jiang, F.; Ding, K.; He, G.; Sun, Y.; Wang, L. Vibration fault features of planetary gear train with cracks under time-varying flexible transfer functions. Mech. Mach. Theory 2021, 158, 104237. [Google Scholar] [CrossRef]
- Aherwar, A. An investigation on gearbox fault detection using vibration analysis techniques: A review. Aust. J. Mech. Eng. 2012, 10, 169–183. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B.; Ding, S.; Huang, B. Data-Driven Fault Diagnosis for Traction Systems in High-Speed Trains: A Survey, Challenges, and Perspect. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1700–1716. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Processing 2020, 138, 106587. [Google Scholar] [CrossRef]
- Yu, G. A Concentrated Time-Frequency Analysis Tool for Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2020, 69, 371–381. [Google Scholar] [CrossRef]
- Qin, Y.; Mao, Y.; Tang, B.; Wang, Y.; Chen, H. M-band flexible wavelet transform and its application to the fault diagnosis of planetary gear transmission systems. Mech. Syst. Signal Processing 2019, 134, 106298. [Google Scholar] [CrossRef]
- Elforjani, M.; Bechhoefer, E. Analysis of extremely modulated faulty wind turbine data using spectral kurtosis and signal intensity estimator. Renew. Energy 2018, 127, 258–268. [Google Scholar] [CrossRef]
- Cheng, J.; Yu, D.; Tang, J.; Yang, Y. Application of frequency family separation method based upon EMD and local Hilbert energy spectrum method to gear fault diagnosis. Mech. Mach. Theory 2008, 43, 712–723. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Processing 2014, 62, 531–544. [Google Scholar] [CrossRef]
- He, G.; Ding, K.; Lin, H. Gearbox coupling modulation separation method based on match pursuit and correlation filtering. Mech. Syst. Signal Processing 2016, 66–67, 597–611. [Google Scholar] [CrossRef]
- Yang, X.; Ding, K.; He, G.; Li, Y. Double-dictionary signal decomposition method based on split augmented Lagrangian shrinkage algorithm and its application in gearbox hybrid faults diagnosis. J. Sound Vib. 2018, 432, 484–501. [Google Scholar] [CrossRef]
- Fan, W.; Cai, G.; Zhu, Z.K.; Shen, C.; Huang, W.; Shang, L. Sparse representation of transients in wavelet basis and its application in gearbox fault feature extraction. Mech. Syst. Signal Processing 2015, 56, 230–245. [Google Scholar] [CrossRef]
- Cai, G.; Selesnick, I.W.; Wang, S.; Dai, W.; Zhu, Z. Sparsity-enhanced signal decomposition via generalized minimax-concave penalty for gearbox fault diagnosis. J. Sound Vib. 2018, 432, 213–234. [Google Scholar] [CrossRef]
- Li, Y.; Ding, K.; He, G.; Jiao, X. Non-stationary vibration feature extraction method based on sparse decomposition and order tracking for gearbox fault diagnosis. Meas. J. Int. Meas. Confed. 2018, 124, 453–469. [Google Scholar] [CrossRef]
- Wang, L.; Cai, G.; Wang, J.; Jiang, X.; Zhu, Z. Dual-Enhanced Sparse Decomposition for Wind Turbine Gearbox Fault Diagnosis. IEEE Trans. Instrum. Meas. 2019, 68, 450–461. [Google Scholar] [CrossRef]
- Sun, R.B.; Yang, Z.B.; Luo, W.; Qiao, B.J.; Chen, X.F. Weighted sparse representation based on failure dynamics simulation for planetary gearbox fault diagnosis. Meas. Sci. Technol. 2019, 30, 045008. [Google Scholar] [CrossRef]
- Cai, G.; Wang, S.; Chen, X.; Ye, J.; Selesnick, I.W. Reweighted generalized minimax-concave sparse regularization and application in machinery fault diagnosis. ISA Trans. 2020, 105, 320–334. [Google Scholar] [CrossRef]
- Deng, F.; Qiang, Y.; Liu, Y.; Yang, S.; Hao, R. Adaptive parametric dictionary design of sparse representation based on fault impulse matching for rotating machinery weak fault detection. Meas. Sci. Technol. 2020, 31, 065101. [Google Scholar] [CrossRef]
- Yang, B.; Liu, R.; Chen, X. Sparse Time-Frequency Representation for Incipient Fault Diagnosis of Wind Turbine Drive Train. IEEE Trans. Instrum. Meas. 2018, 67, 2616–2627. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Snin, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hubert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zuo, M.J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Processing 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Xia, S.; Zhang, J.; Ye, S.; Xu, B.; Xiang, J.; Tang, H. A mechanical fault detection strategy based on the doubly iterative empirical mode decomposition. Appl. Acoust. 2019, 155, 346–357. [Google Scholar] [CrossRef]
- Wang, J.; Du, G.; Zhu, Z.; Shen, C.; He, Q. Fault diagnosis of rotating machines based on the EMD manifold. Mech. Syst. Signal Processing 2020, 135, 106443. [Google Scholar] [CrossRef]
- Han, D.; Zhao, N.; Shi, P. Gear fault feature extraction and diagnosis method under different load excitation based on EMD, PSO-SVM and fractal box dimension. J. Mech. Sci. Technol. 2019, 33, 487–494. [Google Scholar] [CrossRef]
- Du, W.T.; Zeng, Q.; Shao, Y.M.; Wang, L.M.; Ding, X.X. Multi-scale demodulation for fault diagnosis based on a weighted-EMD de-noising technique and time–frequency envelope analysis. Appl. Sci. 2020, 10, 7796. [Google Scholar] [CrossRef]
- Akram, M.; Khushnood, S.; Tariq, S.; Ali, H.; Nizam, L. Vibration Based Gear Fault Diagnosis under Empirical Mode Decomposition and Power Spectrum Density Analysis. Adv. Sci. Technol. Res. J. 2019, 13, 192–200. [Google Scholar] [CrossRef]
- Inturi, V.; Pratyush, A.S.; Sabareesh, G.R. Detection of Local Gear Tooth Defects on a Multistage Gearbox Operating Under Fluctuating Speeds Using DWT and EMD Analysis. Arab. J. Sci. Eng. 2021, 46, 11999–12008. [Google Scholar] [CrossRef]
- Li, C.; Yu, G.; Fu, B.; Hu, H.; Zhu, X.; Zhu, Q. Fault separation and detection for compound bearing-gear fault condition based on decomposition of marginal hilbert spectrum. IEEE Access 2019, 7, 110518–110530. [Google Scholar] [CrossRef]
- Mallat, S.G.; Zhang, Z. Matching Pursuits With Time-Frequency Dictionaries. IEEE Trans. Signal Processing 1993, 41, 3397–3415. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).