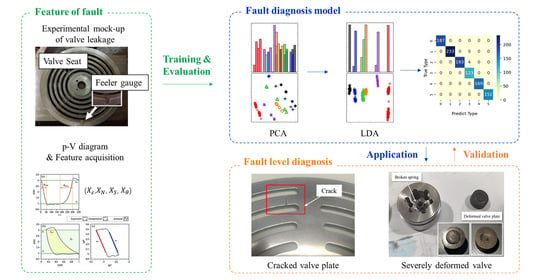
A p−V Diagram Based Fault Identification for Compressor Valve by Means of Linear Discrimination Analysis
Abstract
1. Introduction
2. Methodology
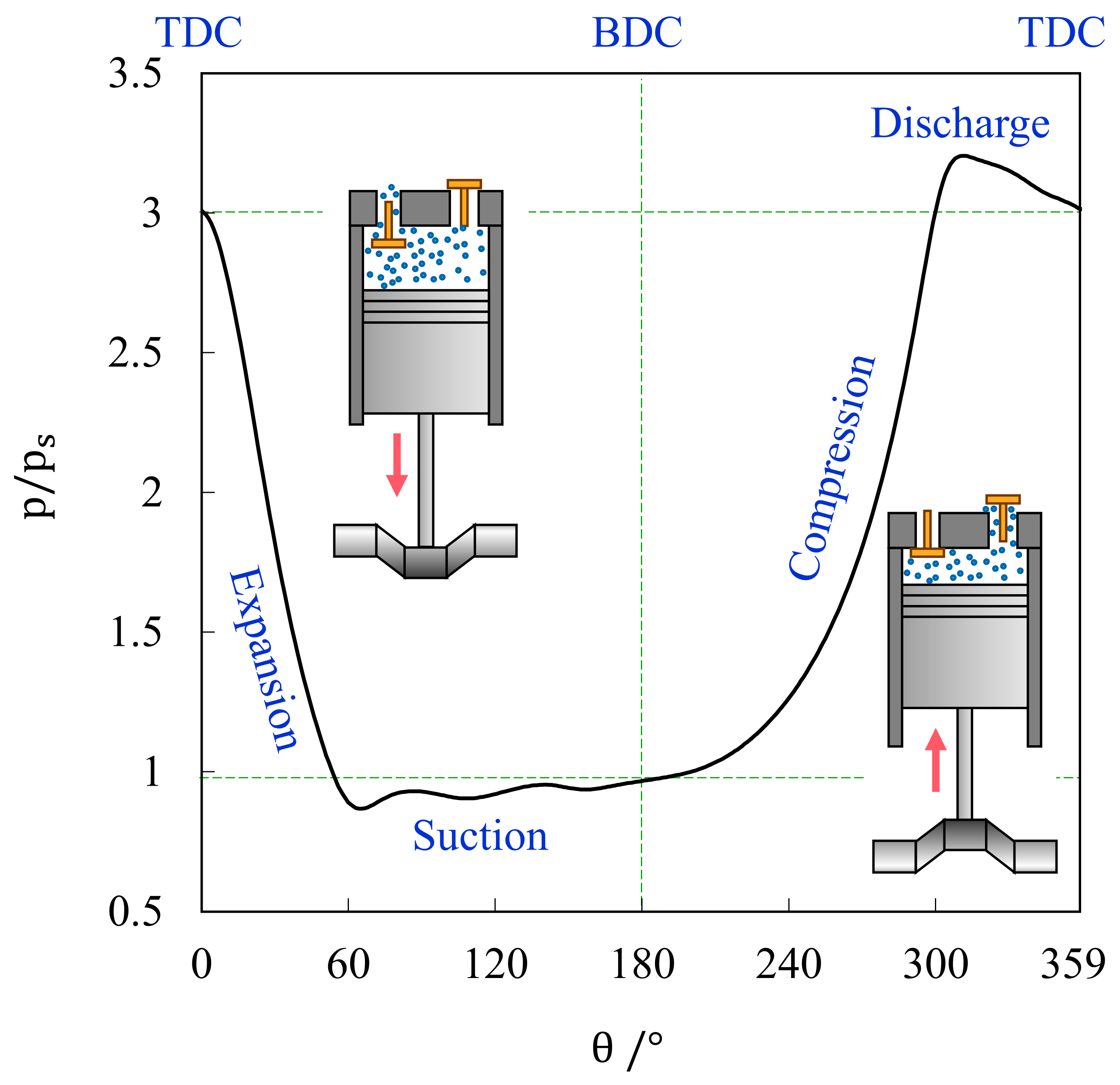
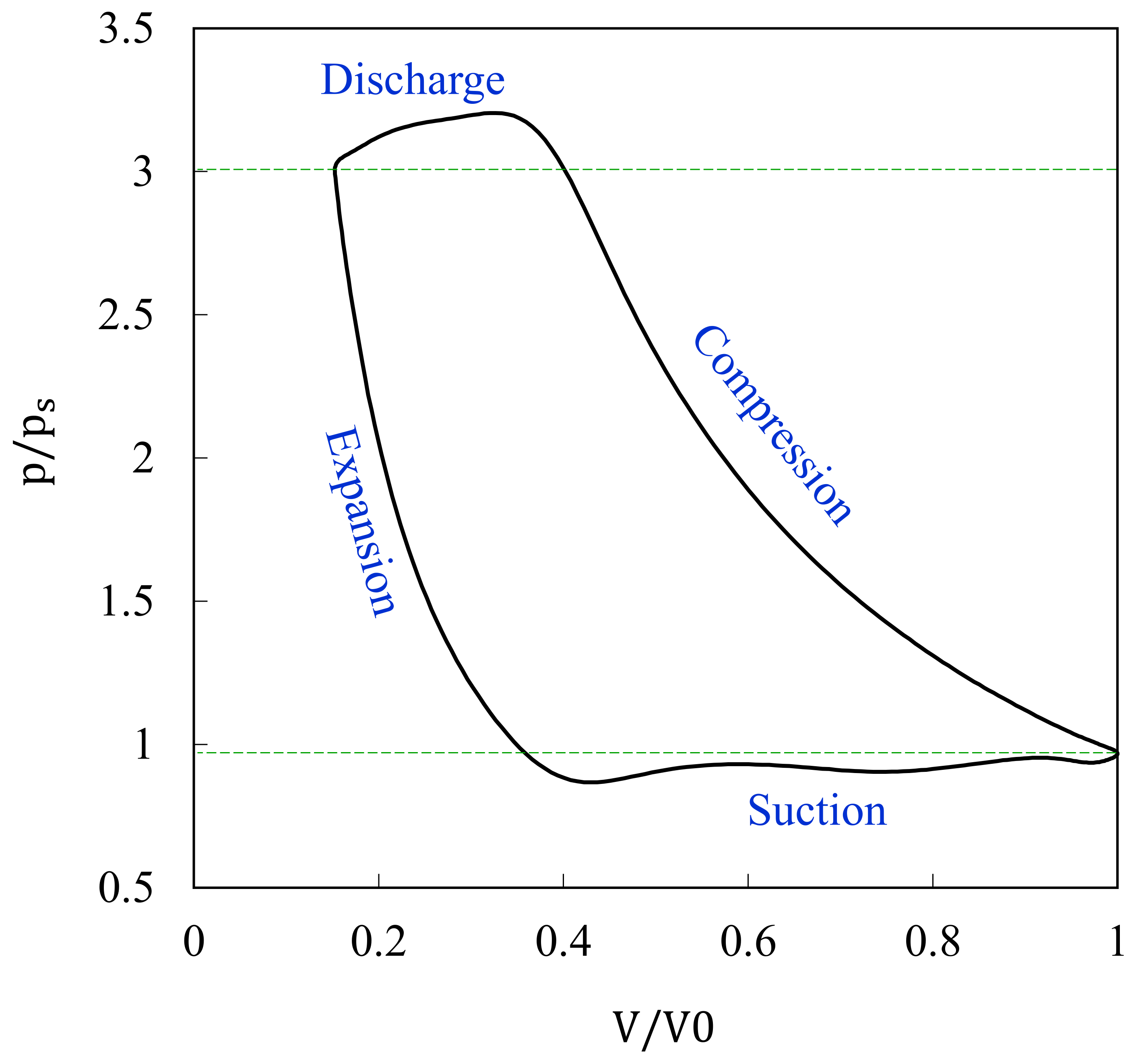
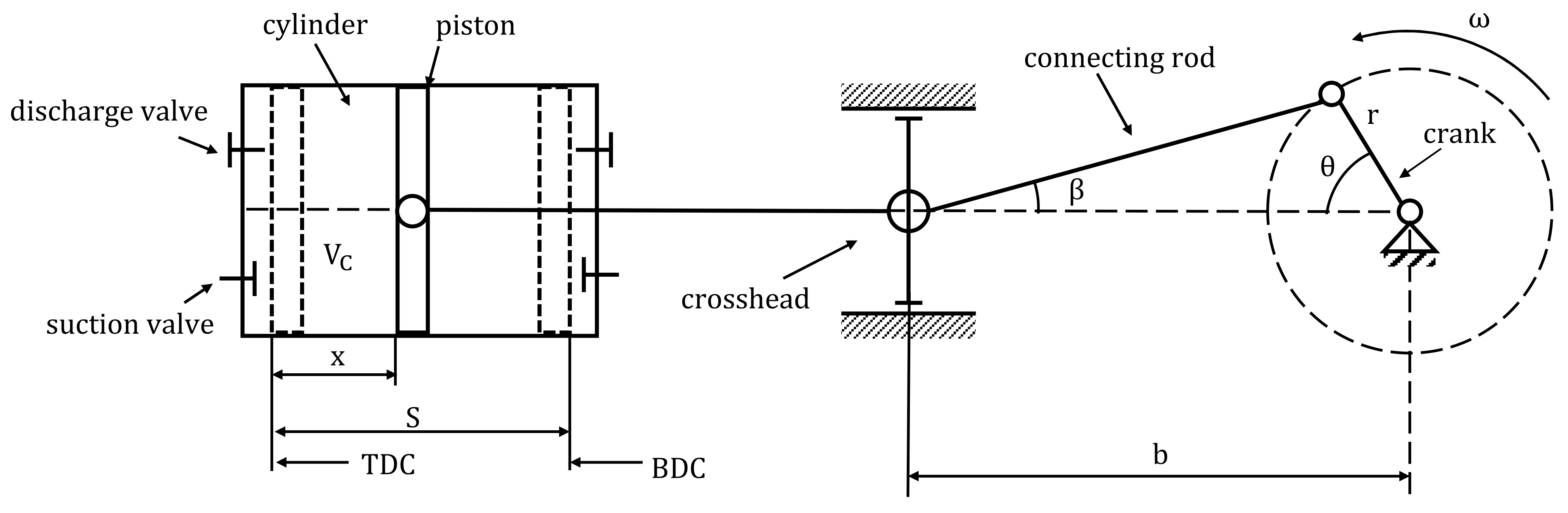
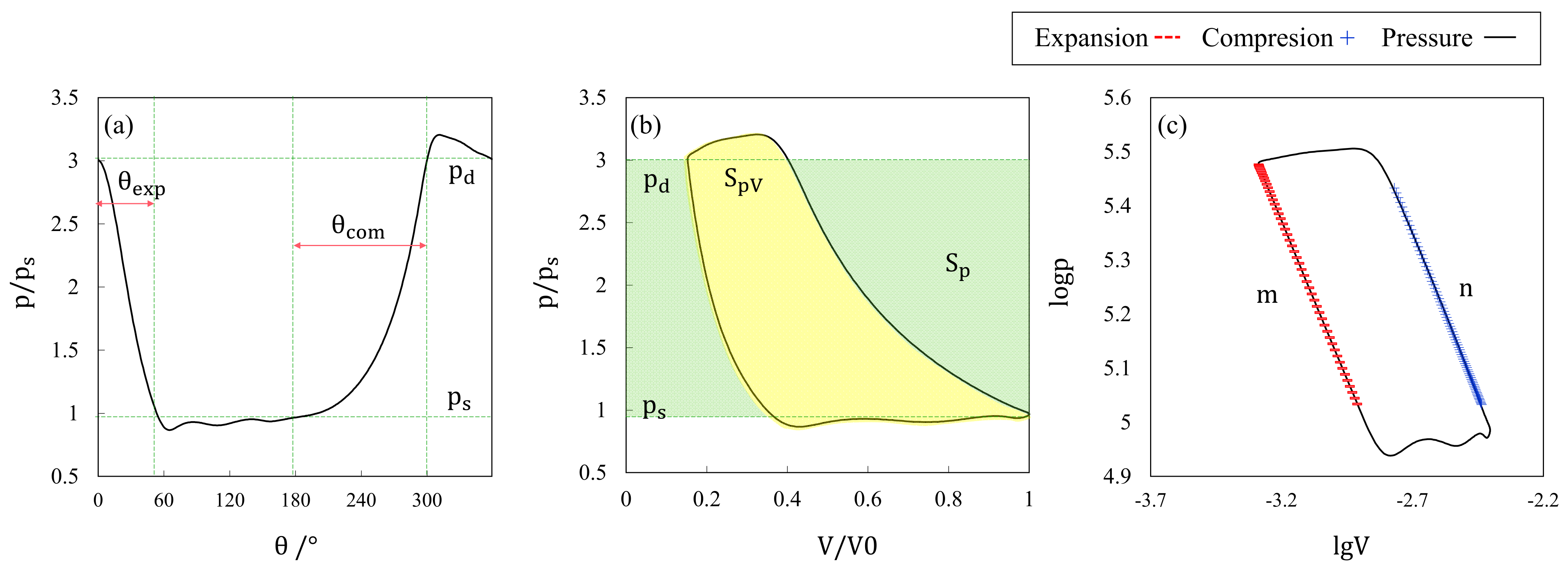
2.1. Acquisition of p−V Diagram
2.2. Feature Extraction of p−V Diagram
2.2.1. Selection of Statistical Characteristic Parameters of the p−V Diagram
- (1)
- Pressure ratio
- (2)
- Process angle coefficient
- (3)
- Area coefficient
- (4)
- Process parameter coefficient:
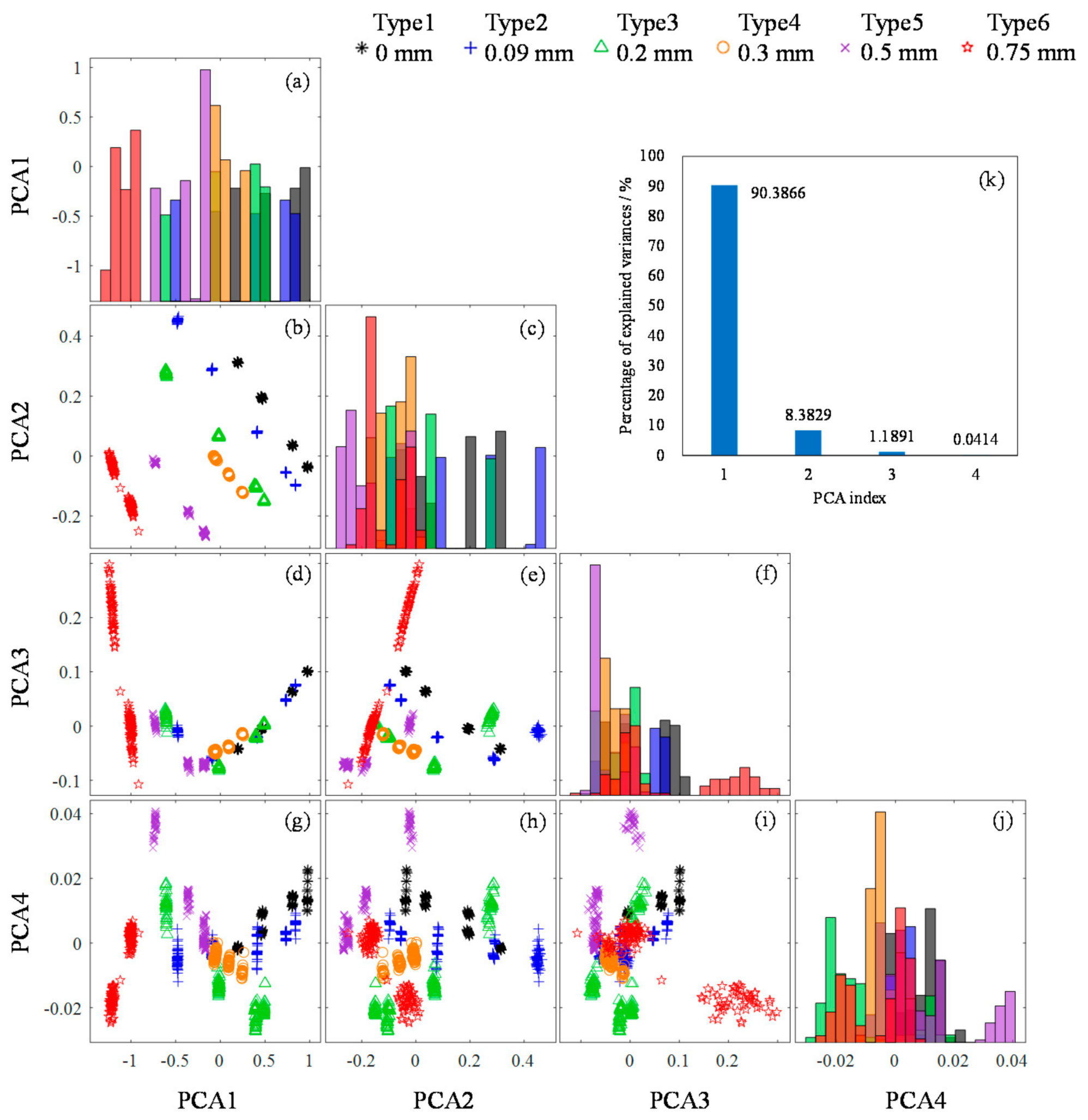
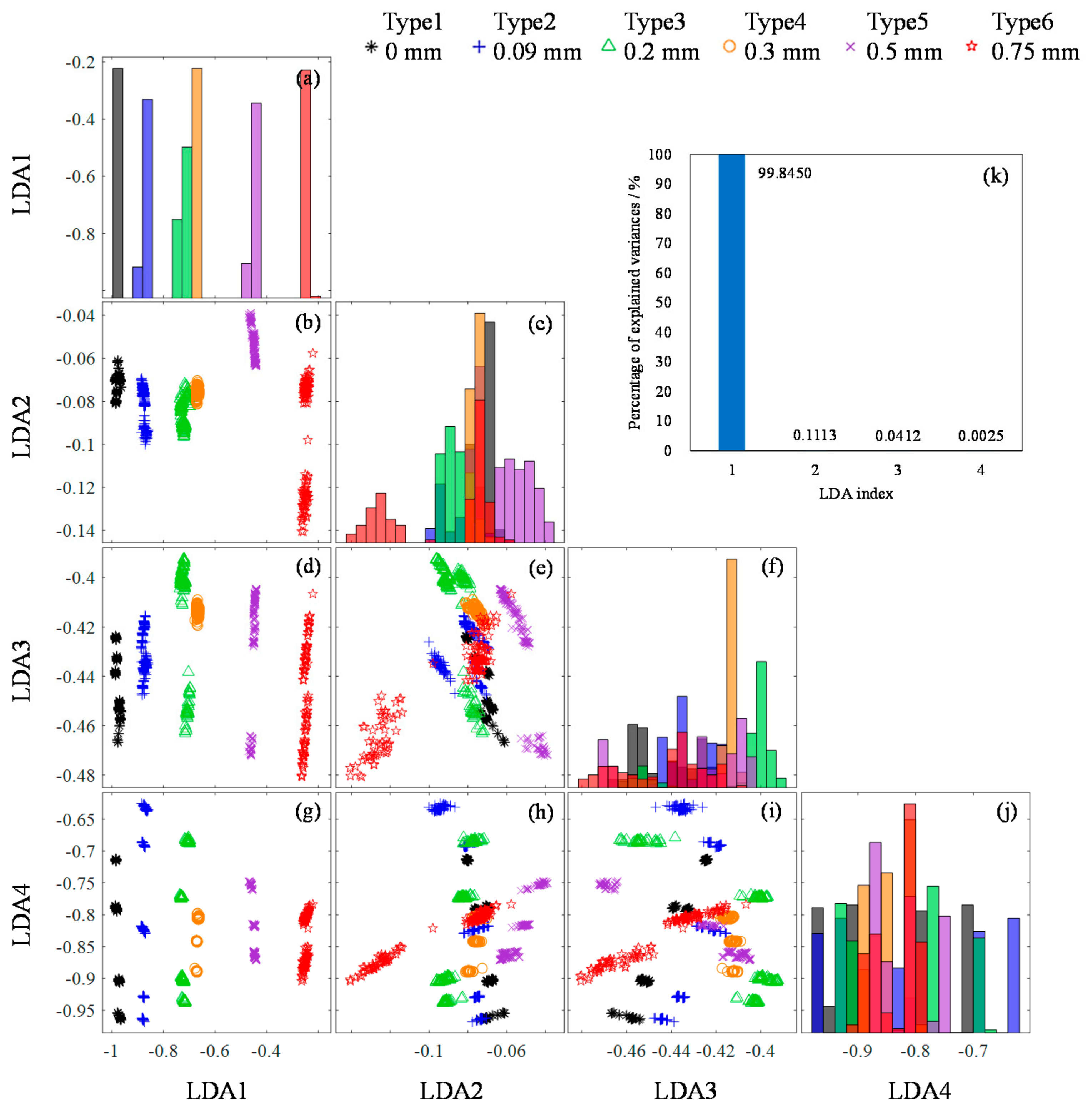
2.2.2. Feature Extraction Based on PCA-LDA
- Principal Component Analysis (PCA)
- 2.
- Linear Discriminant Analysis (LDA)
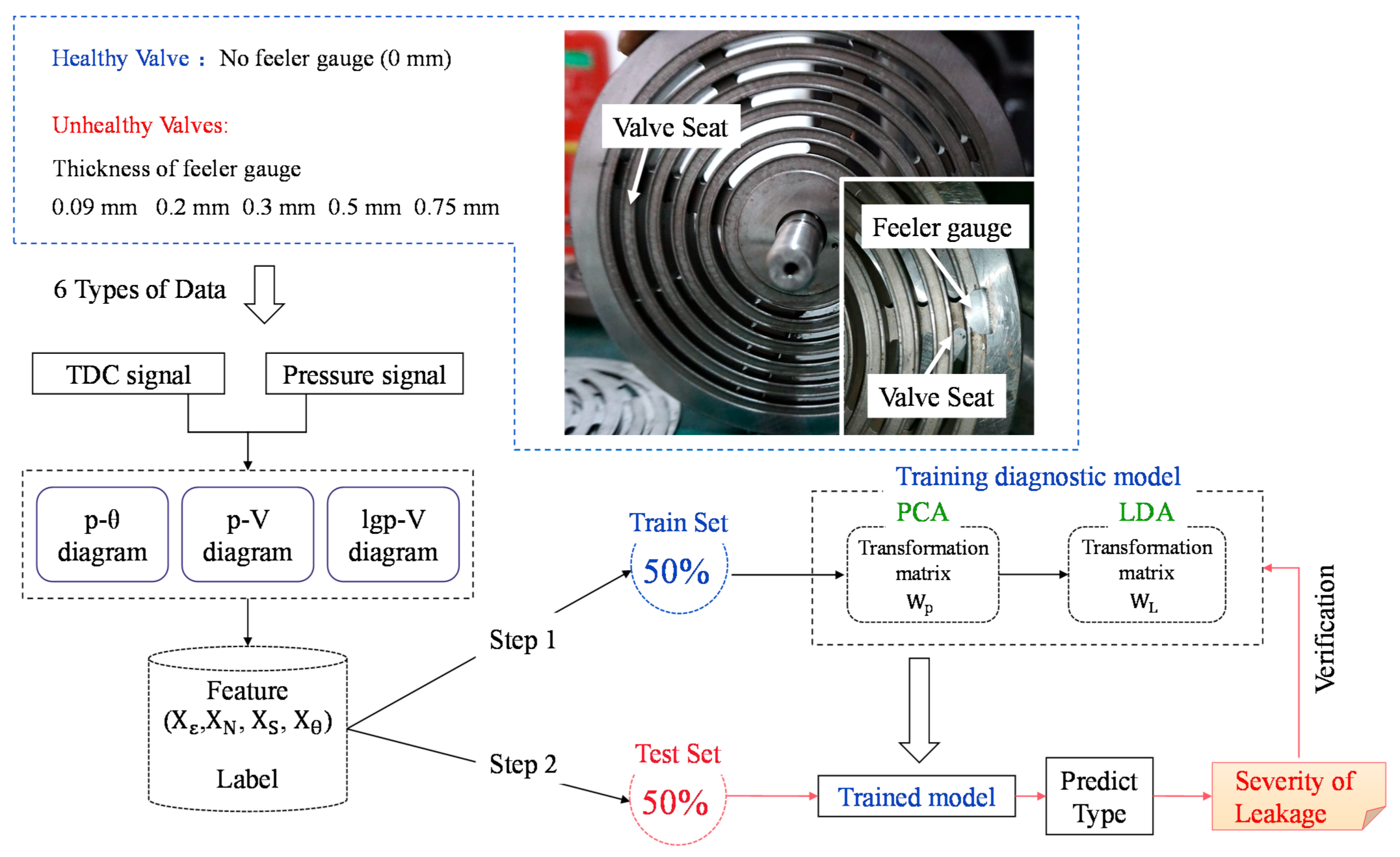
3. Experiment Setup
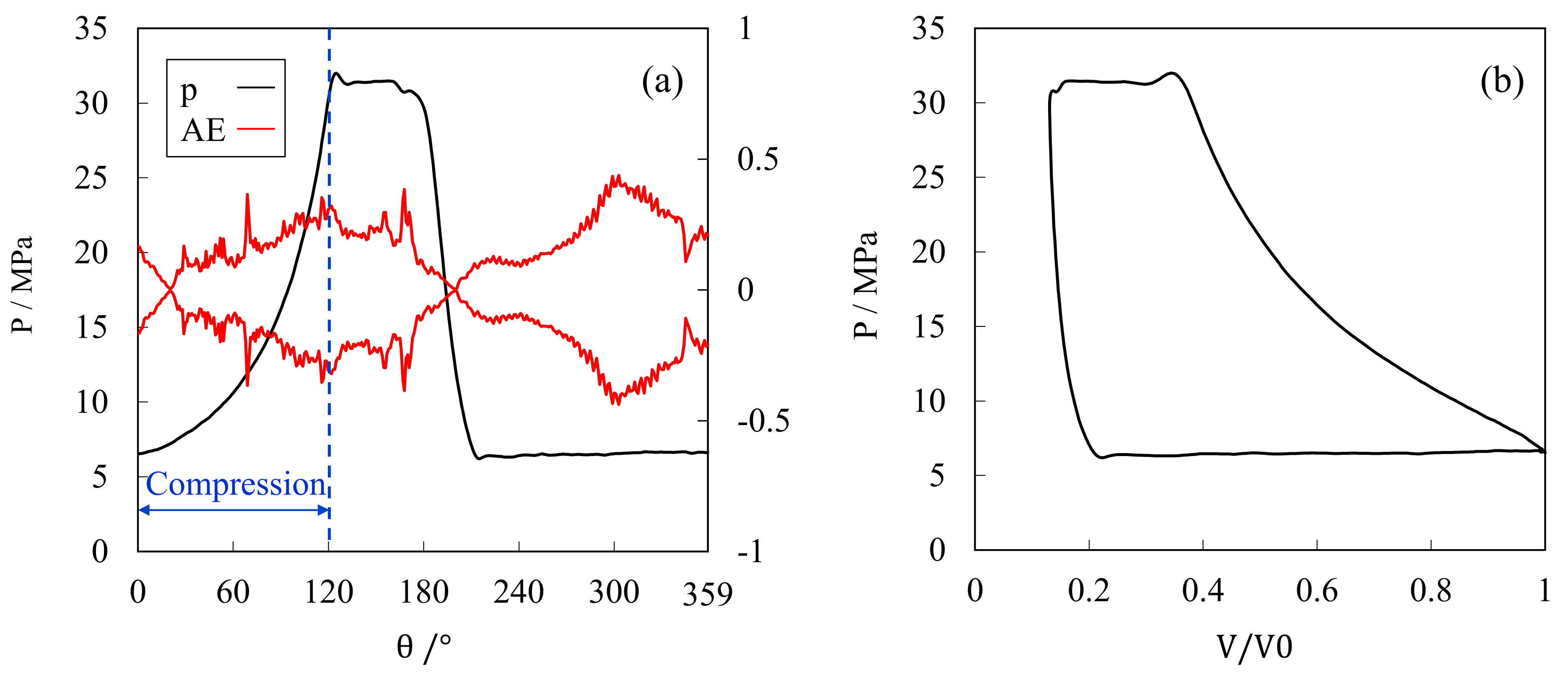
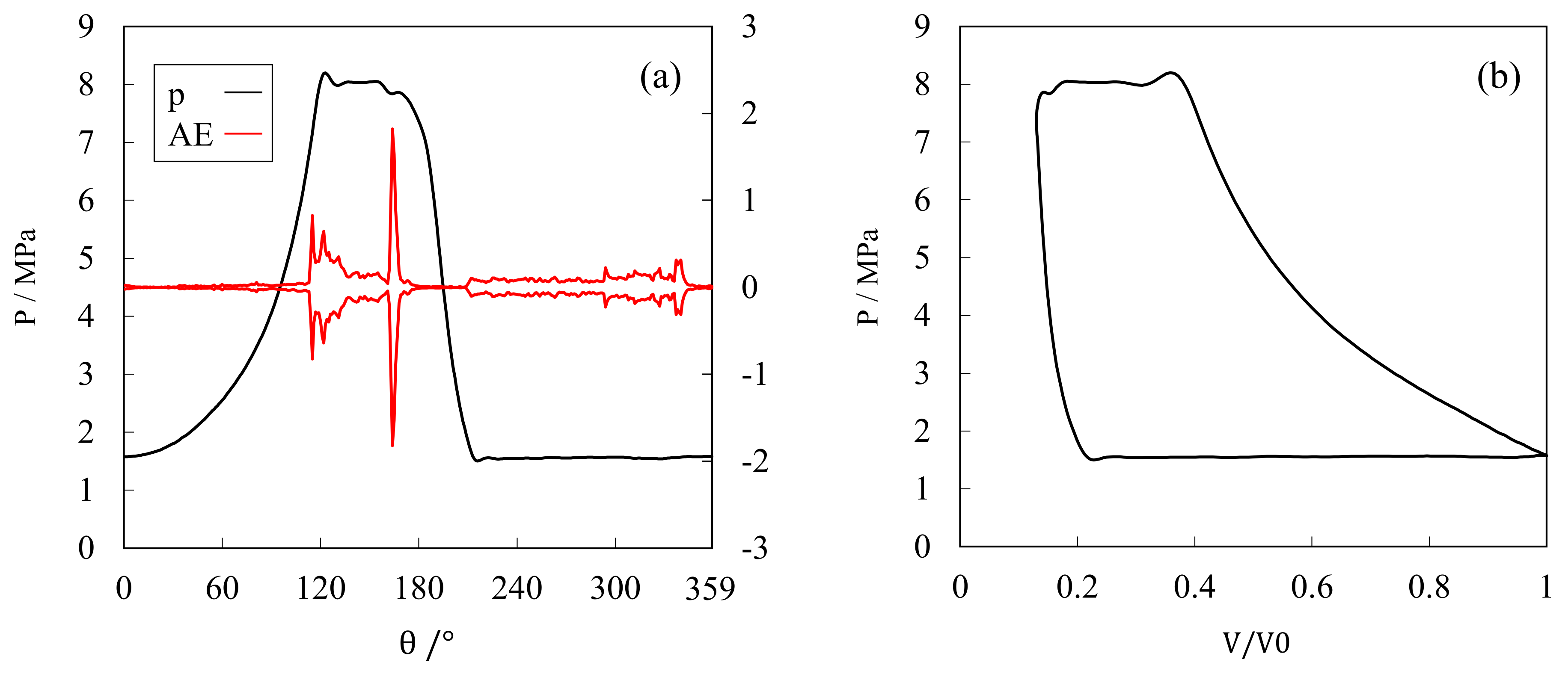
3.1. Measurement and Construction of the p−V Diagram
3.2. Experimental Mock-Up of Valve Leakage Fault
4. Results and Discussion
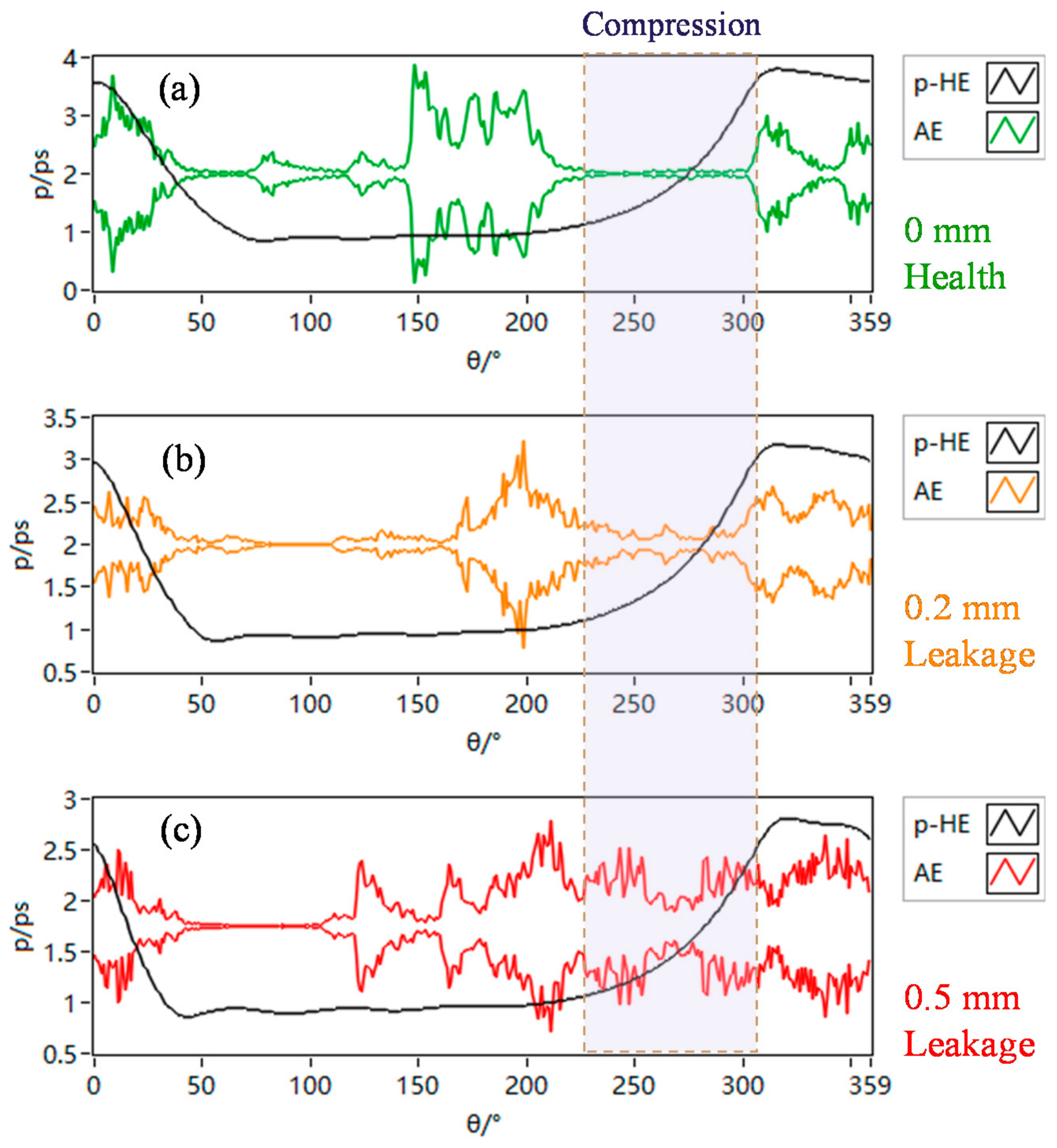
4.1. Validation of the Muck-Up of Different Valve Leakage Severity
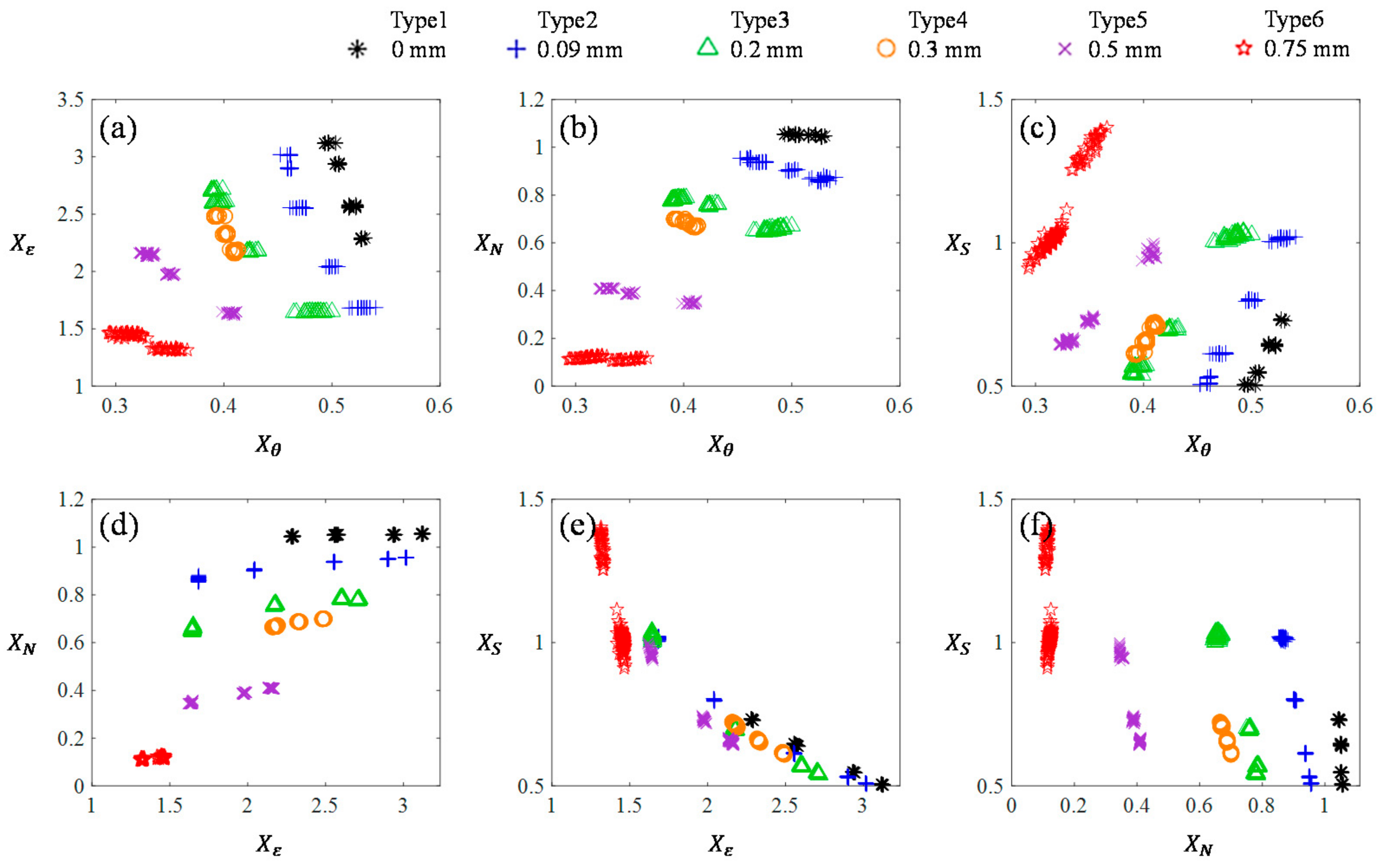
4.2. Feature Parameter Analysis
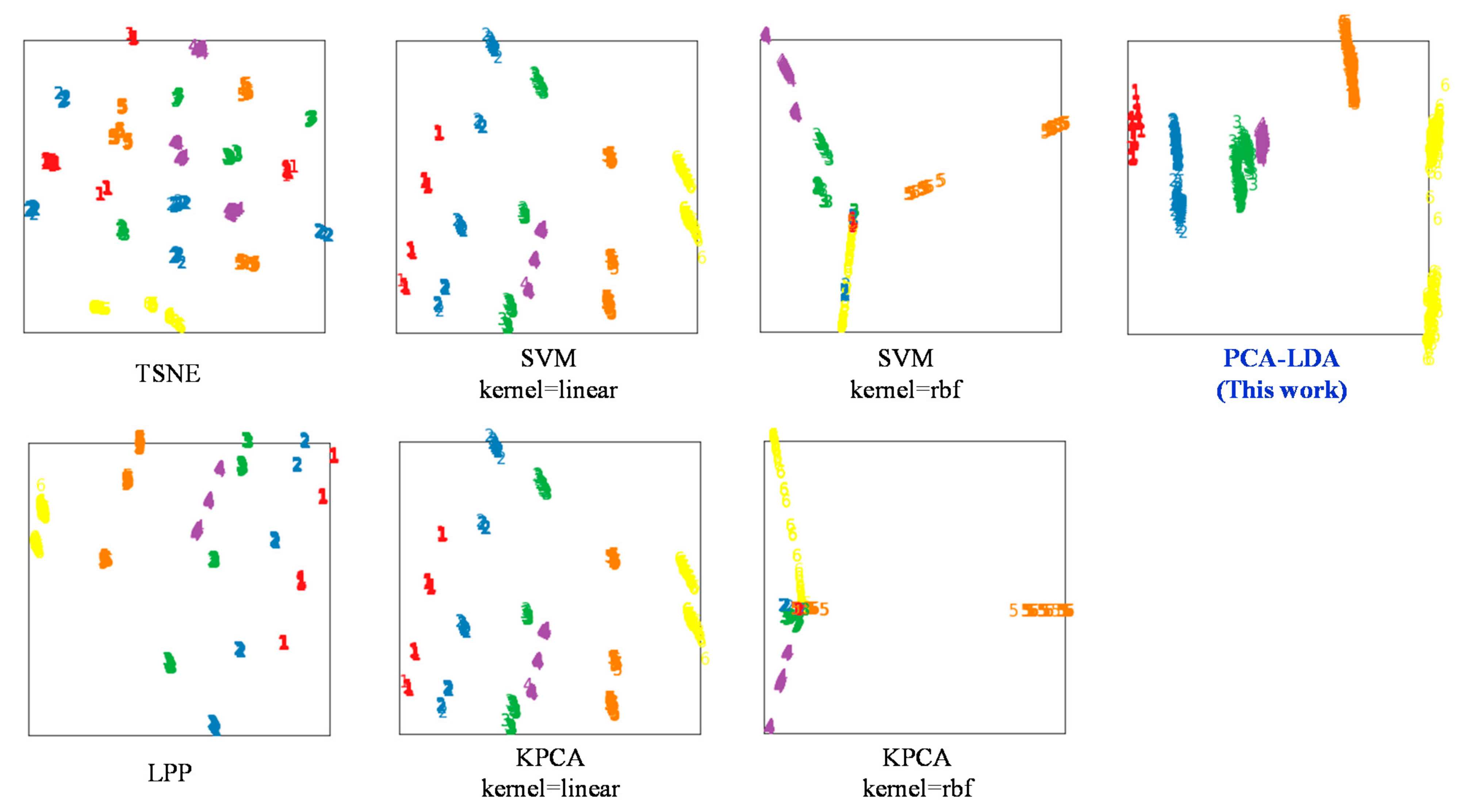
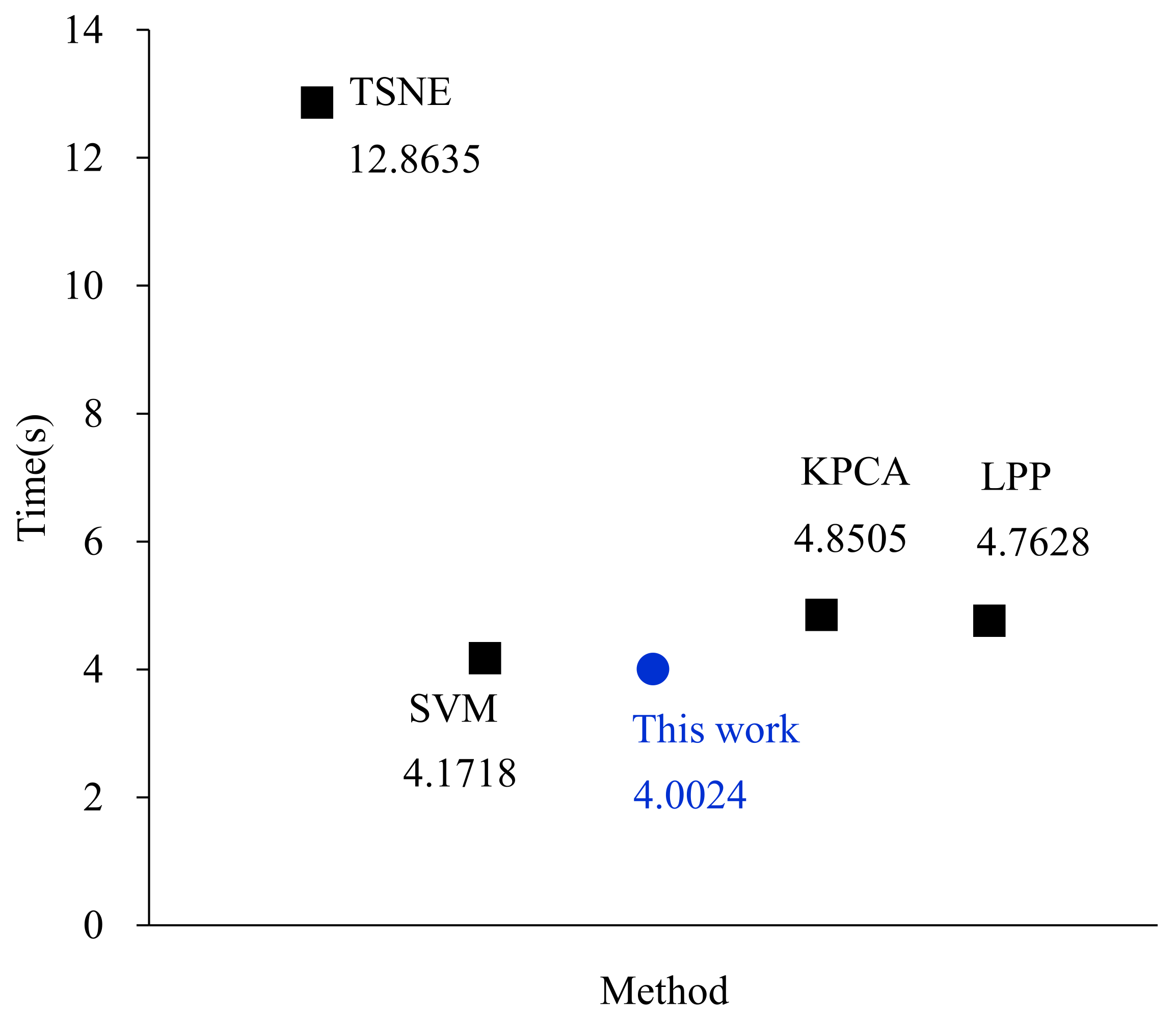
4.3. Comparisons with Other Methods
4.4. Severity Estimation of Valve Leakage
4.5. Fault Diagnosis of Valves
4.5.1. Application in the Mild Leakage Caused by the Cracked Valve Plate
4.5.2. Application in the Serious Leakage Caused by the Deformed Valve Plate
5. Conclusions
- (1)
- Four-dimensional variables composed of the pressure ratio, process angle coefficient, p−V area coefficient, and process index coefficient can be extracted from the p−V diagram to serve as the characteristics to illustrate the severity of the failure. The process index coefficient contributes to fault identification to great extent.
- (2)
- The PCA can be used to amplify and extract the preliminary features of the characteristic variables and separate the data of serious leakage faults, and the PCA-projected dataset was employed as the input parameter to the LDA classifier to achieve an optimized classification result.
- (3)
- The diagnosis and identification results of various fault data show good consistency with the actual faults including the cracked valve plate and the deformed valve in the application on the reciprocating compressor and the hydraulically driven piston compressor.
- (4)
- This finding indicates the p−V diagram-based method as an effective diagnosis tool for self-acting valve failure, which would have great potential in many application scenarios, including gas storage, hydrogen refueling station, etc.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Giorgetti, S.; Giorgetti, A.; Jahromi, R.T.; Arcidiacono, G. Machinery Foundations Dynamical Analysis: A Case Study on Reciprocating Compressor Foundation. Machines 2021, 9, 228. [Google Scholar] [CrossRef]
- PROGNOST. PROGNOST Systems GmbH Company Profile. Available online: https://www.prognost.com/2016/07/28/compressor-valve-monitoring/ (accessed on 7 December 2021).
- Loukopoulos, P.; Zolkiewski, G.; Bennett, I.; Sampath, S.; Pilidis, P.; Li, X.; Mba, D. Abrupt fault remaining useful life estimation using measurements from a reciprocating compressor valve failure. Mech. Syst. Signal Process. 2019, 121, 359–372. [Google Scholar] [CrossRef]
- Kolodziej, J.R.; Trout, J.N. An image-based pattern recognition approach to condition monitoring of reciprocating compressor valves. J. Vib. Control 2017, 24, 4433–4448. [Google Scholar] [CrossRef]
- Zhao, B.; Jia, X.; Sun, S.; Wen, J.; Peng, X. FSI model of valve motion and pressure pulsation for investigating thermodynamic process and internal flow inside a reciprocating compressor. Appl. Therm. Eng. 2018, 131, 998–1007. [Google Scholar] [CrossRef]
- Sharma, V.; Parey, A. Performance evaluation of decomposition methods to diagnose leakage in a reciprocating compressor under limited speed variation. Mech. Syst. Signal Process. 2018, 125, 275–287. [Google Scholar] [CrossRef]
- Zhou, D.; Huang, D.; Hao, J.; Ren, Y.; Jiang, P.; Jia, X. Vibration-based fault diagnosis of the natural gas compressor using adaptive stochastic resonance realized by Generative Adversarial Networks. Eng. Fail. Anal. 2020, 116, 104759. [Google Scholar] [CrossRef]
- Liang, Z.; Li, S.; Tian, J.; Zhang, L.; Feng, C.; Zhang, L. Vibration cause analysis and elimination of reciprocating compressor inlet pipelines. Eng. Fail. Anal. 2015, 48, 272–282. [Google Scholar] [CrossRef]
- Townsend, J.; Badar, M.A.; Szekerces, J. Updating temperature monitoring on reciprocating compressor connecting rods to improve reliability. Eng. Sci. Technol. Int. J. 2016, 19, 566–573. [Google Scholar] [CrossRef]
- Becerra, J.A.; Jimenez, F.J.; Torres, M.; Sanchez, D.T.; Carvajal, E. Failure analysis of reciprocating compressor crankshafts. Eng. Fail. Anal. 2011, 18, 735–746. [Google Scholar] [CrossRef]
- El-Ghamry, M.; Reuben, R.; Steel, J. The Development of Automated Pattern Recognition and Statistical Feature Isolation Techniques for the Diagnosis of Reciprocating Machinery Faults Using Acoustic Emission. Mech. Syst. Signal Process. 2003, 17, 805–823. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, C.; Jia, X.; Peng, X. Fault diagnosis of reciprocating compressor valve with the method integrating acoustic emission signal and simulated valve motion. Mech. Syst. Signal Process. 2015, 56–57, 197–212. [Google Scholar] [CrossRef]
- Chlumsky, V. Reciprocating and Rotary Compressors; SNTL-Publisher of Technical Literature: Prague, Czechoslovakia, 1965; pp. 502–506. [Google Scholar]
- Manepatil, S.S.; Tiwari, A. Fault Diagnosis of Reciprocating Compressor Using Pressure Pulsations. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 9–12 July 2018. [Google Scholar]
- Elhaj, M.; Almrabet, M.; Rgeai, M.; Ehtiwesh, I. A combined practical approach to condition monitoring of reciprocating compressor using IAS and dynamic pressure. World Acad. Sci. Eng. Technol. 2010, 63, 186–192. [Google Scholar]
- Real, M.; Pereira, E. Measuring Hermetic Compressor Valve Lift Using Fiberoptic Sensors. In Proceedings of the 7th IIR International Conference on Compressors and Coolants, Castá Papiernicka, Slovak, 30 September–2 October 2009. [Google Scholar]
- Kim, J.; Wang, S.; Park, S.; Ryu, K.; La, J. Valve Dynamic Analysis of a Hermetic Reciprocating Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 17–20 July 2006. [Google Scholar]
- Li, X.; Peng, X.; Zhang, Z.; Jia, X.; Wang, Z. A new method for nondestructive fault diagnosis of reciprocating compressor by means of strain-based p–V diagram. Mech. Syst. Signal Process. 2019, 133, 106268. [Google Scholar] [CrossRef]
- Windrock. Windrock 6400 Portable Analyzer. 2020. Available online: https://windrock.com/wp-content/uploads/2019/06/Windrock-6400-Brochure_060319_sm.pdf (accessed on 7 December 2021).
- HOERBIGER (Shanghai) Co. Ltd. Reciprocating Compressor Condition Monitoring. 2014. Available online: https://www.utilityengineers.net/specialist/Conditioning%20Monitoring.pdf (accessed on 7 December 2021).
- PROGNOST. Evaluating the Strengths and Weaknesses of the Most Common Online Condition Monitoring Technologiesm. 2014. Available online: https://www.prognost.com/wp-content/uploads/2018/03/ct2-06-14_compressor-valve-monitoring.pdf (accessed on 7 December 2021).
- Bently Nevada. OptiComp™ BN Compressor Control Suite. 2015. Available online: https://www.bakerhughesds.com/sites/g/files/cozyhq596/files/acquiadam_assets/gea30389a_opticompbrochure_printed_r2.pdf (accessed on 7 December 2021).
- Ahmed, M.; Baqqar, M.; Gu, F.; Ball, A.D. Fault Detection and Diagnosis Using Principal Component Analysis of Vibration Data from A Reciprocating Compressor. In Proceedings of the 2012 UKACC International Conference on Control, Cardiff, UK, 3–5 September 2012; pp. 461–466. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, D.; Yuan, X. LDA-based deep transfer learning for fault diagnosis in industrial chemical processes. Comput. Chem. Eng. 2020, 140, 106964. [Google Scholar] [CrossRef]
- Wang, F.; Song, L.; Zhang, L.; Li, H. Fault Diagnosis for Reciprocating Air Compressor Valve Using P−V Indicator Diagram and SVM. In Proceedings of the 3rd International Symposium on Information Science and Engineering, Shanghai, China, 24–26 December 2010; pp. 255–258. [Google Scholar] [CrossRef]
- Feng, K.; Jiang, Z.; He, W.; Ma, B. A recognition and novelty detection approach based on Curvelet transform, nonlinear PCA and SVM with application to indicator diagram diagnosis. Expert Syst. Appl. 2011, 38, 12721–12729. [Google Scholar] [CrossRef]
- Pichler, K.; Lughofer, E.; Pichler, M.; Buchegger, T.; Klement, E.; Huschenbett, M. Detecting broken reciprocating compressor valves in the PV diagram. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, NSW, Australia, 9–12 July 2013; pp. 1625–1630. [Google Scholar]
- Hanlon, P.C. Compressor Handbook; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Shen, W.D.; Tong, J.G. Thermodynamics of Engineering; Higher Education Press: Beijing, China, 2007; pp. 267–269. [Google Scholar]
- Zhang, Y.; Xu, T.; Chen, C.; Wang, G.; Zhang, Z.; Xiao, T. A hierarchical method based on improved deep forest and case-based reasoning for railway turnout fault diagnosis. Eng. Fail. Anal. 2021, 127, 105446. [Google Scholar] [CrossRef]
- Kim, H.; Drake, B.L.; Park, H. Multiclass classifiers based on dimension reduction with generalized LDA. Pattern Recognit. 2007, 40, 2939–2945. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, D.; Lyu, C.; Lu, C. Feature reconstruction based on t-SNE: An approach for fault diagnosis of rotating machinery. J. Vibroeng. 2017, 19, 5047–5060. [Google Scholar] [CrossRef][Green Version]
- Pilario, K.E.; Shafiee, M.; Cao, Y.; Lao, L.; Yang, S.H. A review of kernel methods for feature extraction in nonlinear process monitoring. Processes 2020, 8, 24. [Google Scholar] [CrossRef]
- He, X.; Niyogi, P. Locality Preserving Projections. Proc. Adv. Neural Inf. Process. Syst. 2003, 16, 153–160. [Google Scholar]
- Yang, Y.; Yu, D.; Cheng, J. A fault diagnosis approach for roller bearing based on IMF envelope spectrum and SVM. Measurement 2007, 40, 943–950. [Google Scholar] [CrossRef]
- Brun, K.; Nored, M.G.; Gernentz, R.S.; Platt, J.P. Reciprocating Compressor Valve Plate Life and Performance Analysis. In Proceedings of the Gas Machinery Conference, Covington, LA, USA, 3–5 October 2005; pp. 1–15. [Google Scholar]
- Bovsunovsky, A.P. Efficiency analysis of vibration based crack diagnostics in rotating shafts. Eng. Fract. Mech. 2017, 173, 118–129. [Google Scholar] [CrossRef]
- Sdanghi, G.; Maranzana, G.; Celzard, A.; Fierro, V. Review of the current technologies and performances of hydrogen compression for stationary and automotive applications. Renew. Sustain. Energy Rev. 2019, 102, 150–170. [Google Scholar] [CrossRef]



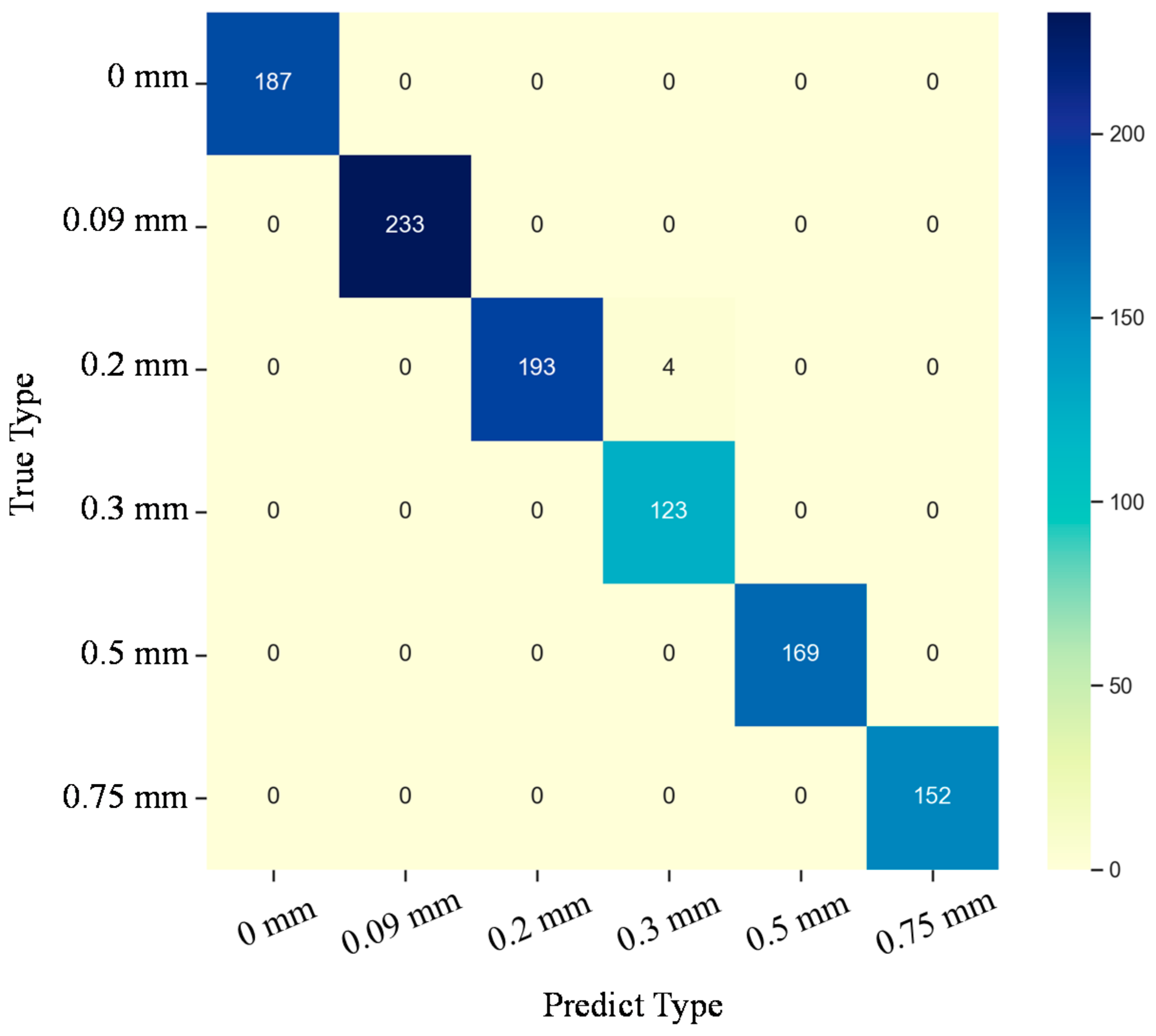
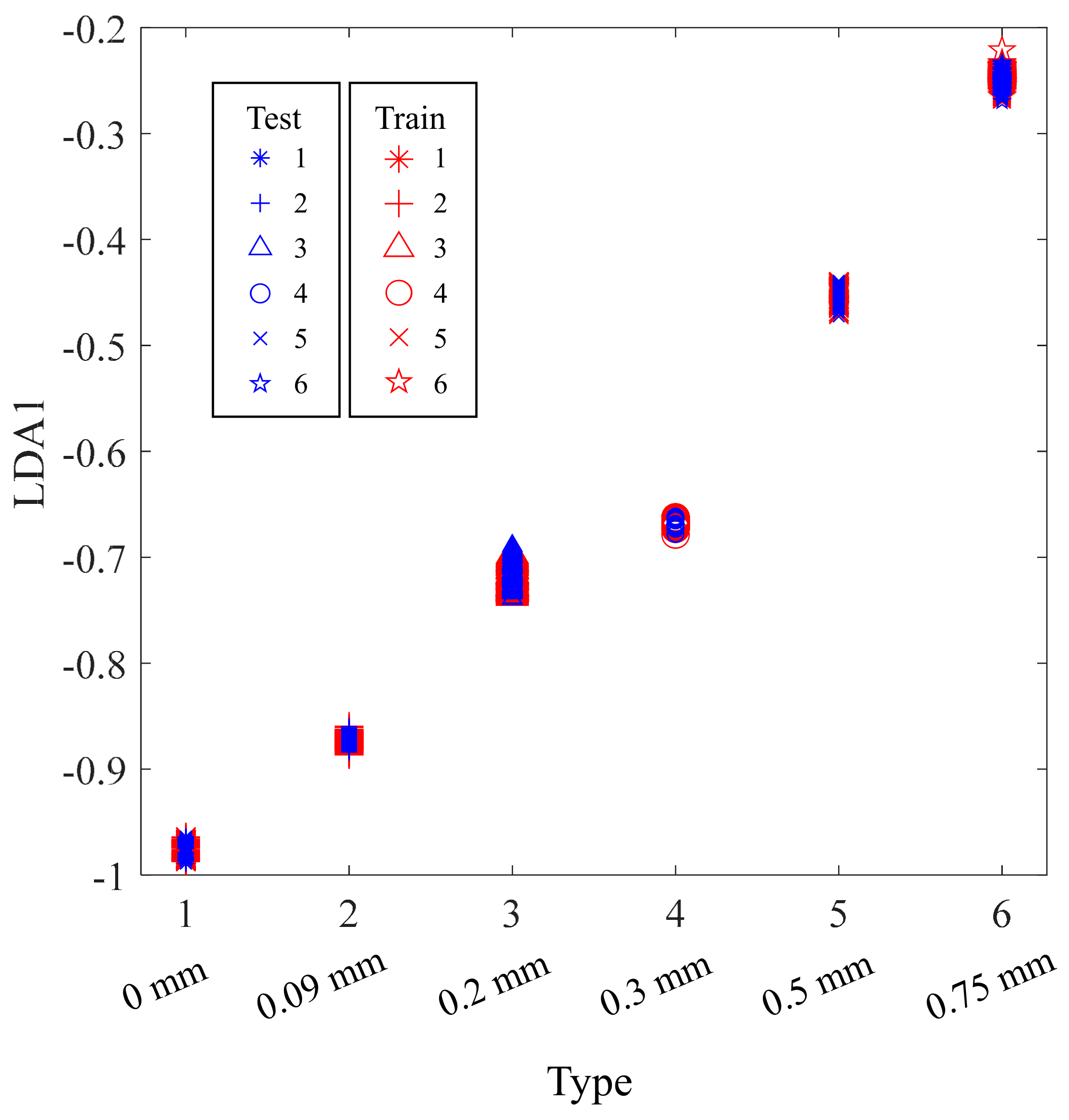
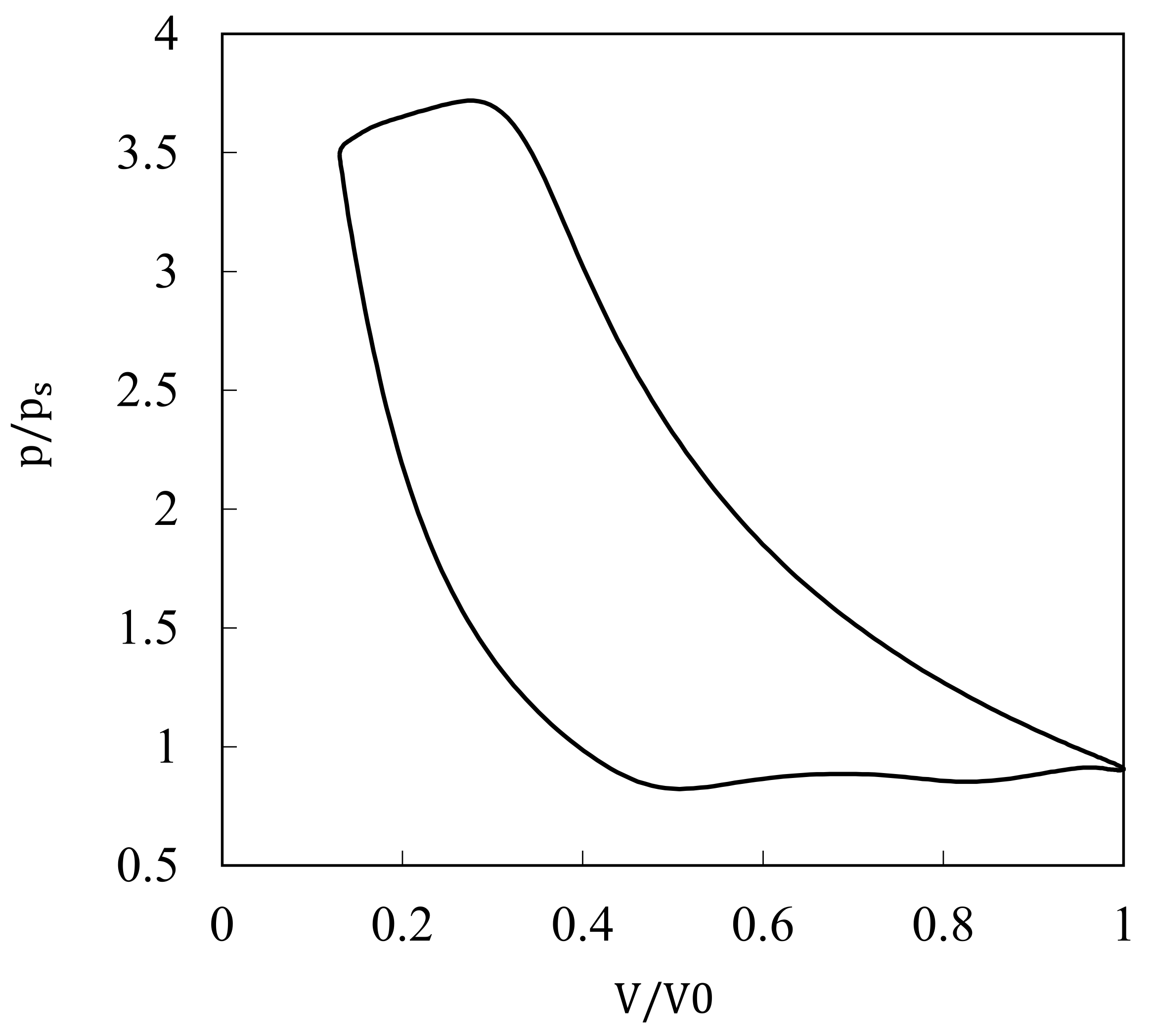
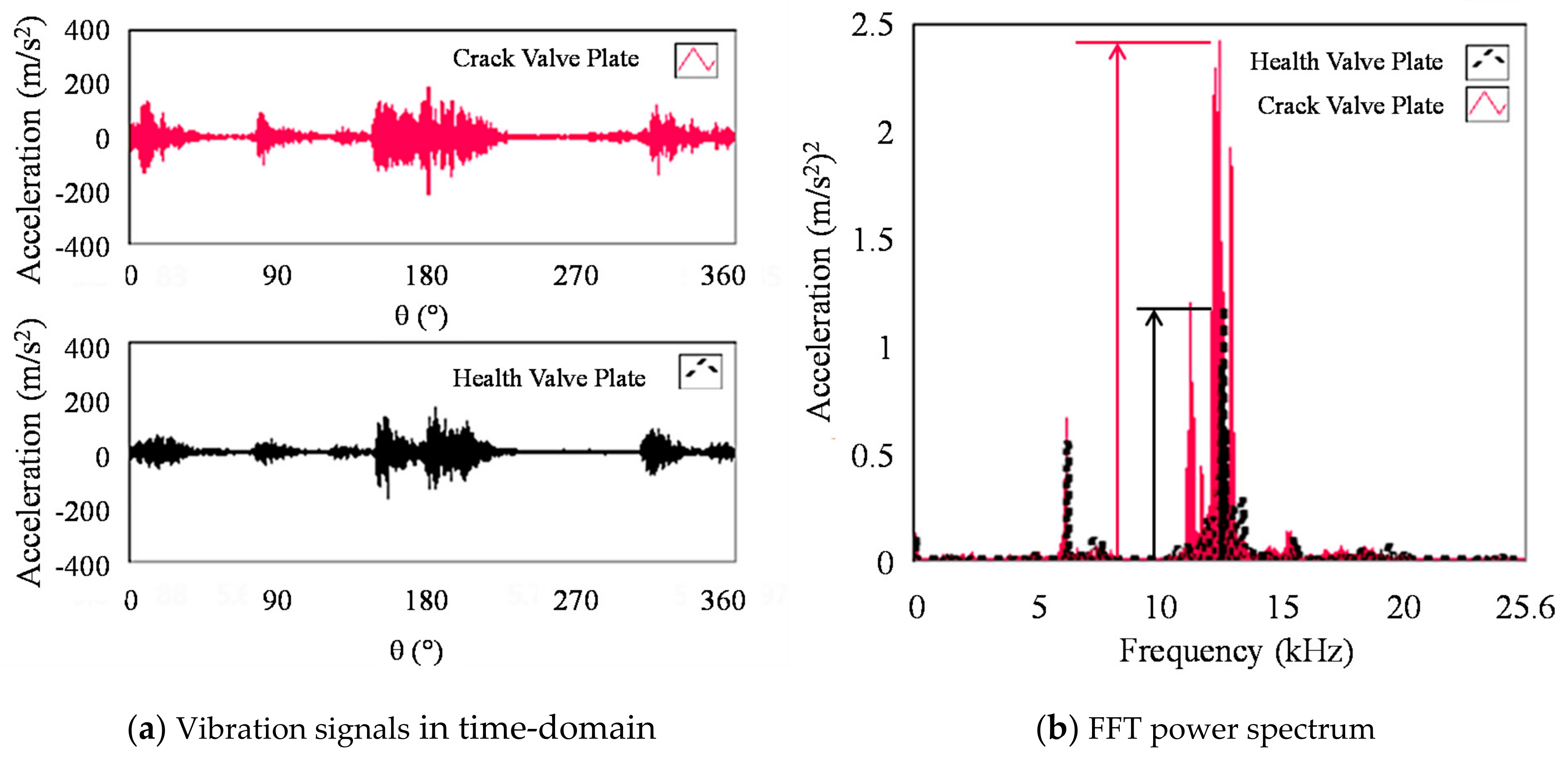



| Type | Type 1 | Type 2 | Type 3 | Type 4 | Type 5 | Type 6 |
|---|---|---|---|---|---|---|
| Thickness of gauge | 0 mm | 0.09 mm | 0.2 mm | 0.3 mm | 0.5 mm | 0.75 mm |
| Level of Fault | Health | Mild leakage | Moderate leakage | Serious leakage | ||
| data size | 365 | 463 | 357 | 282 | 372 | 283 |
| Type | Type 1 0 mm | Type 2 0.09 mm | Type 3 0.2 mm | Type 4 0.3 mm | Type 5 0.5 mm | Type 6 0.75 mm |
|---|---|---|---|---|---|---|
| Level Ratio | Health | Mild Leakage | Moderate Leakage | Serious Leakage | ||
| 1 | 0.95 | 0.92 | 0.91 | 0.86 | 0.67 | |
| 1 | 0.73 | 0.67 | 0.64 | 0.56 | 0.35 | |
| 1 | 1.55 | 1.99 | 2.12 | 3.25 | 6.02 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Ren, P.; Zhang, Z.; Jia, X.; Peng, X. A p−V Diagram Based Fault Identification for Compressor Valve by Means of Linear Discrimination Analysis. Machines 2022, 10, 53. https://doi.org/10.3390/machines10010053
Li X, Ren P, Zhang Z, Jia X, Peng X. A p−V Diagram Based Fault Identification for Compressor Valve by Means of Linear Discrimination Analysis. Machines. 2022; 10(1):53. https://doi.org/10.3390/machines10010053
Chicago/Turabian StyleLi, Xueying, Peng Ren, Zhe Zhang, Xiaohan Jia, and Xueyuan Peng. 2022. "A p−V Diagram Based Fault Identification for Compressor Valve by Means of Linear Discrimination Analysis" Machines 10, no. 1: 53. https://doi.org/10.3390/machines10010053
APA StyleLi, X., Ren, P., Zhang, Z., Jia, X., & Peng, X. (2022). A p−V Diagram Based Fault Identification for Compressor Valve by Means of Linear Discrimination Analysis. Machines, 10(1), 53. https://doi.org/10.3390/machines10010053