Vibration Responses of the Bearing-Rotor-Gear System with the Misaligned Rotor
Abstract
:1. Introduction
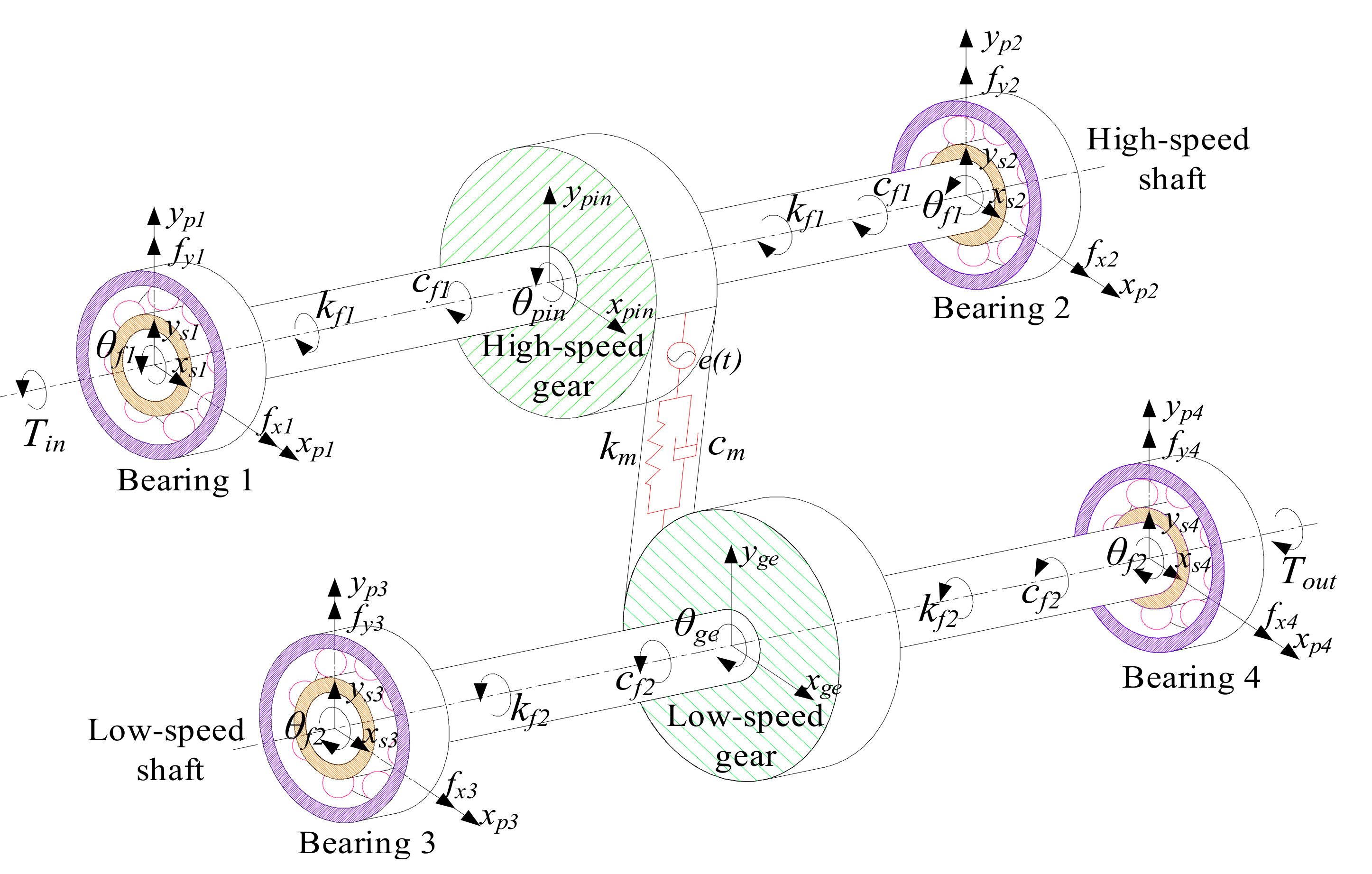
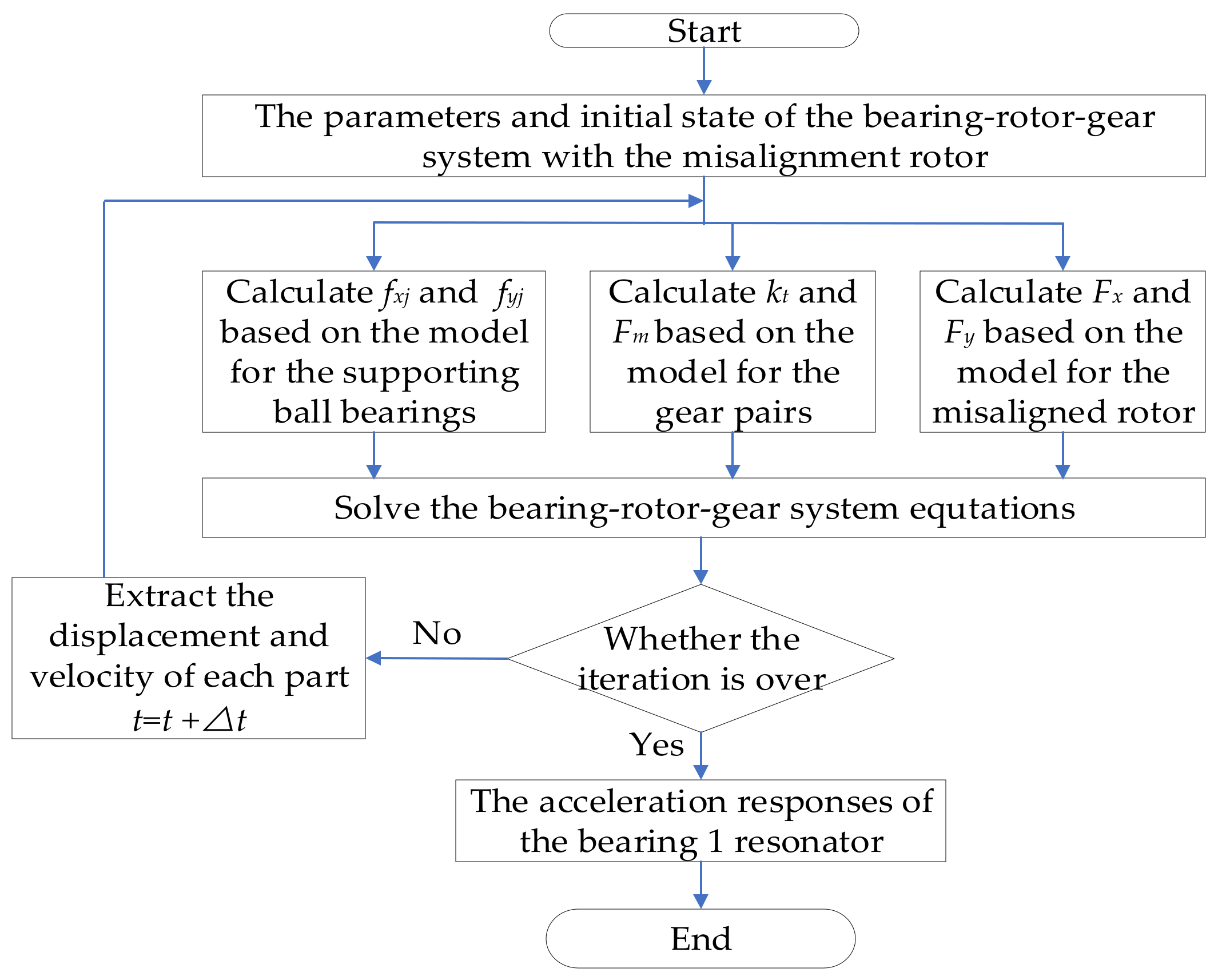
2. Dynamic Model for the Bearing-Rotor-Gear System with the Misaligned Rotor
2.1. Dynamic Model for the Bearing-Rotor-Gear System
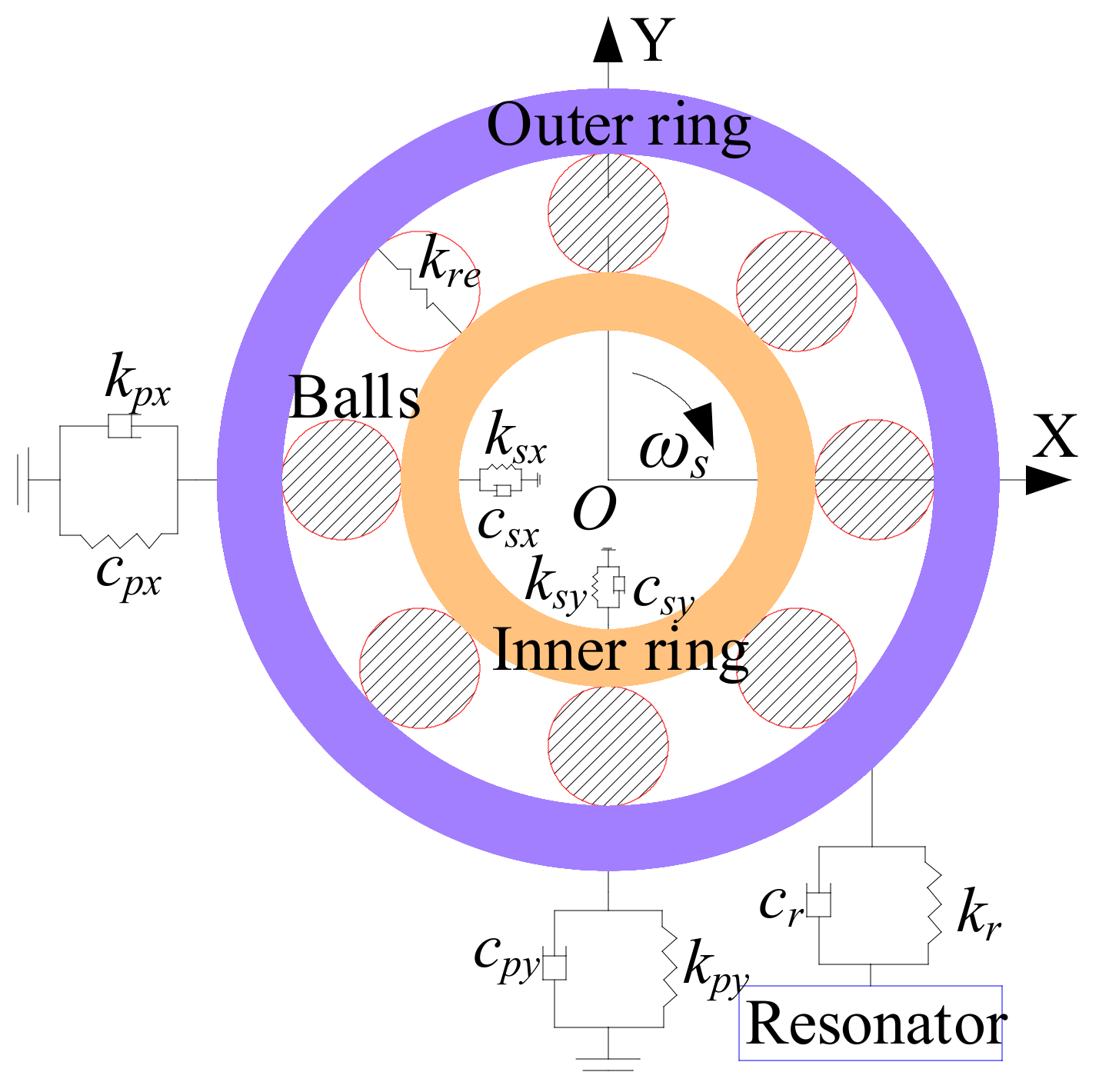
2.2. Model for the Supporting Ball Bearings
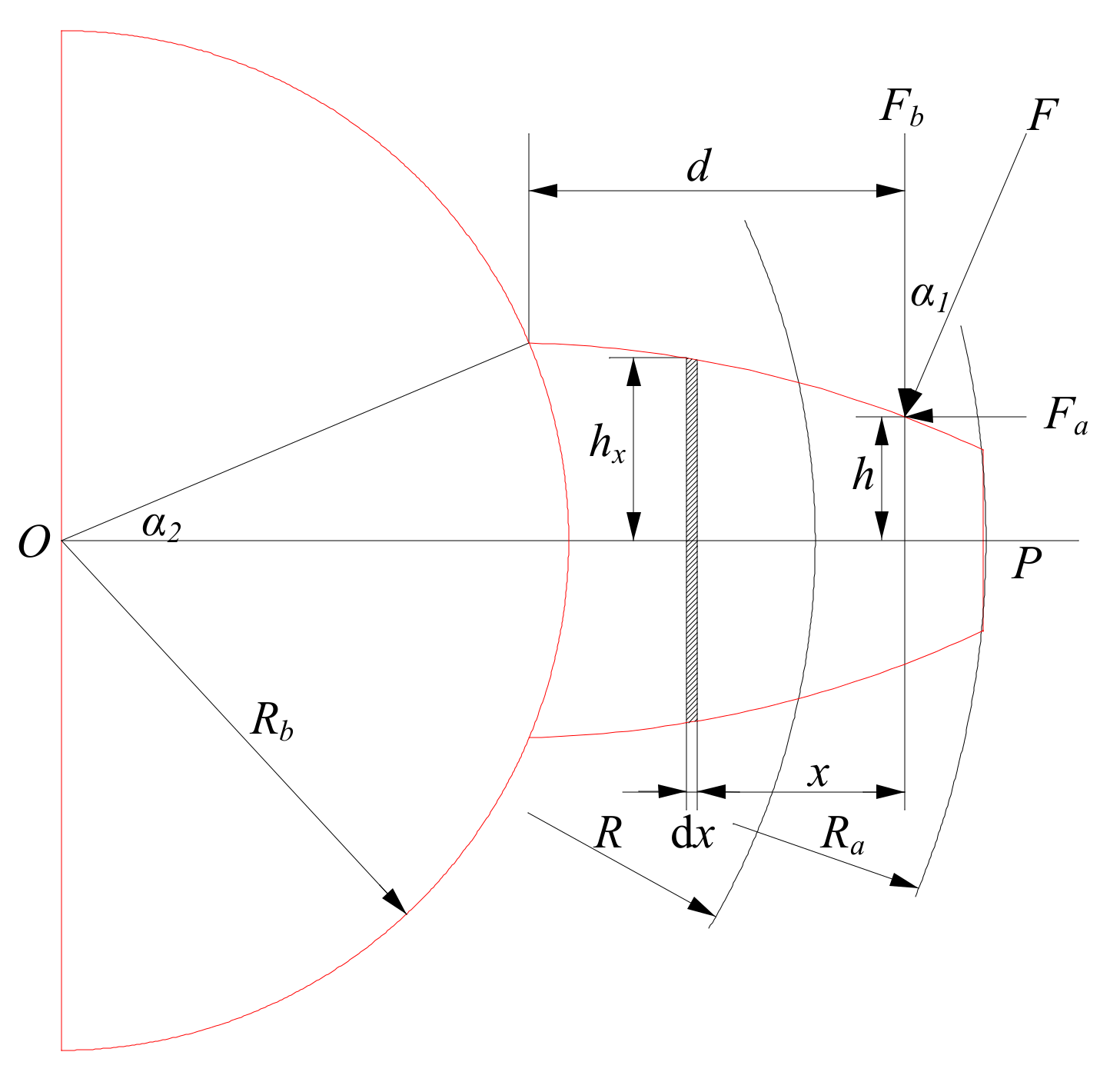
2.3. Model for the Gear Pairs
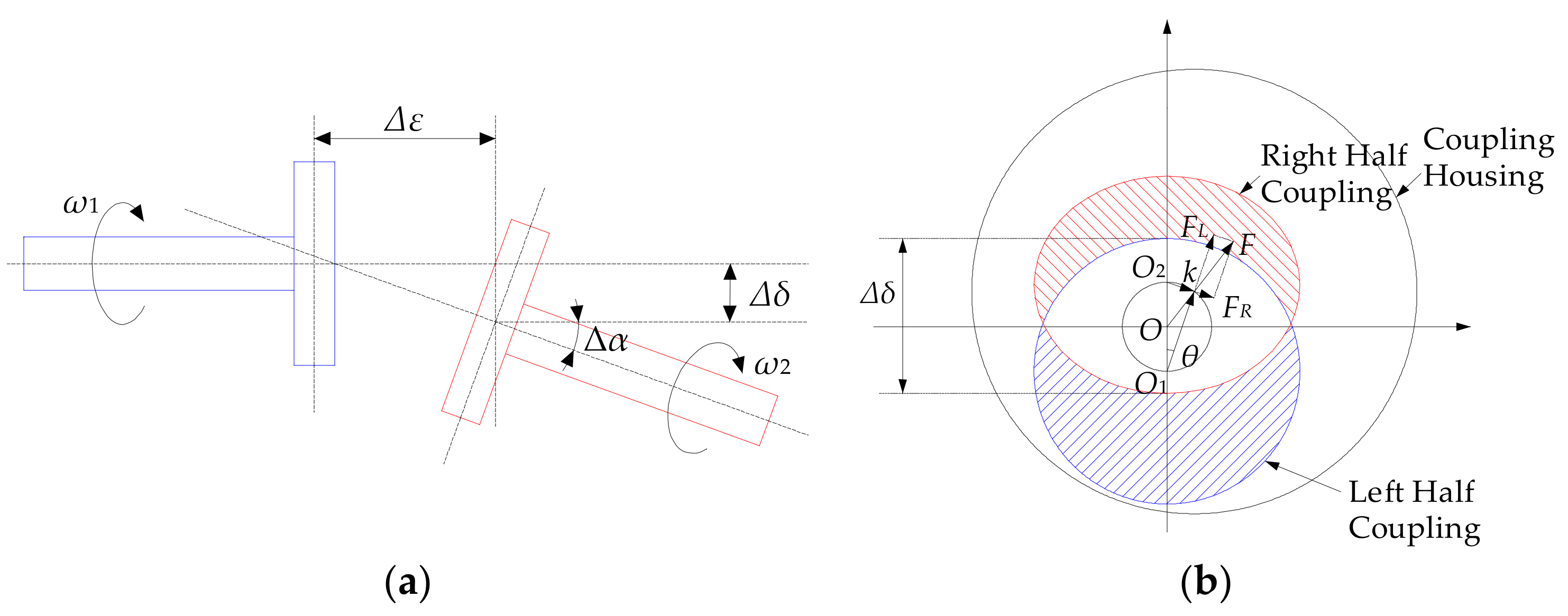
2.4. Model for the Misaligned Rotor
3. Results
4. Discussion
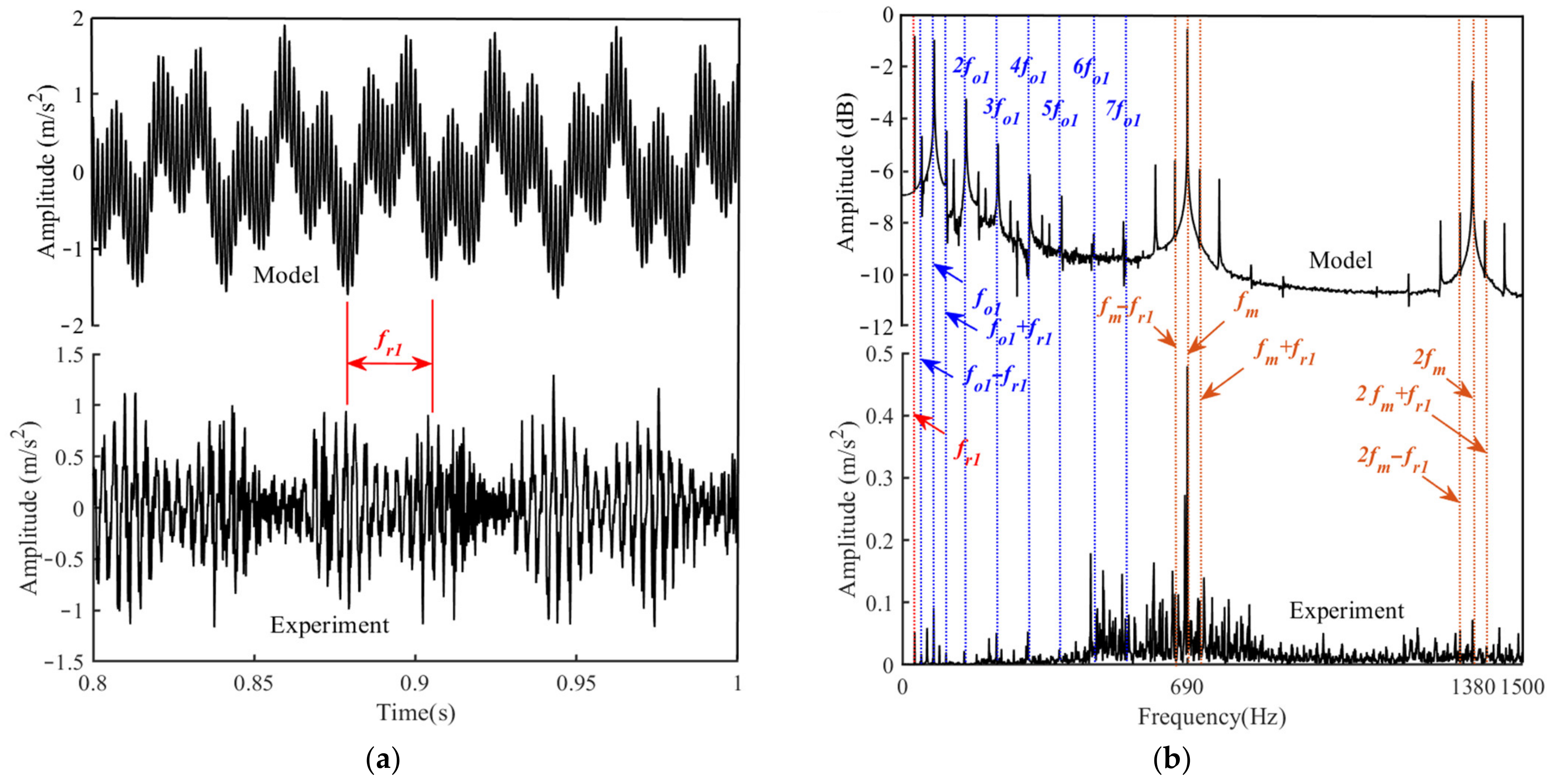
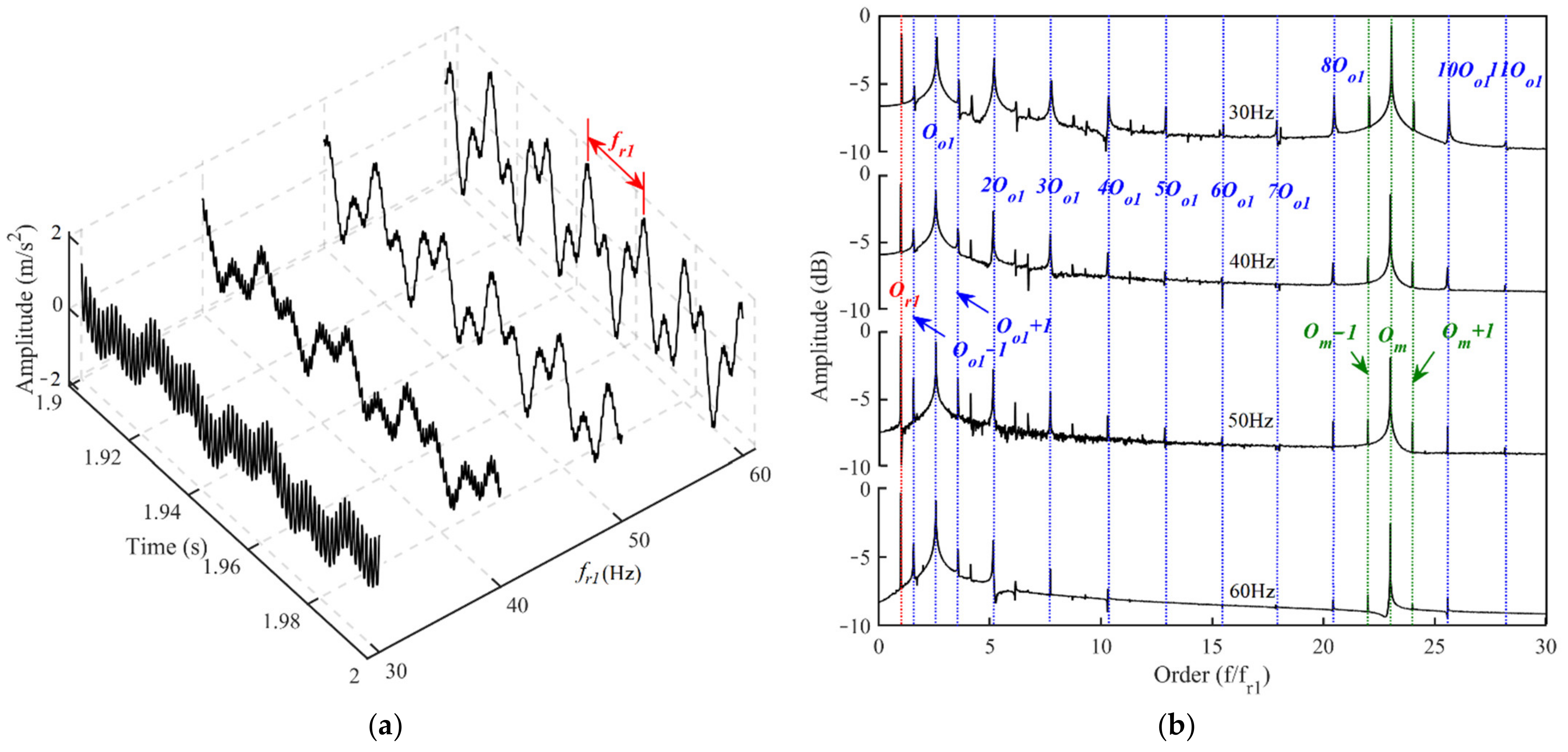
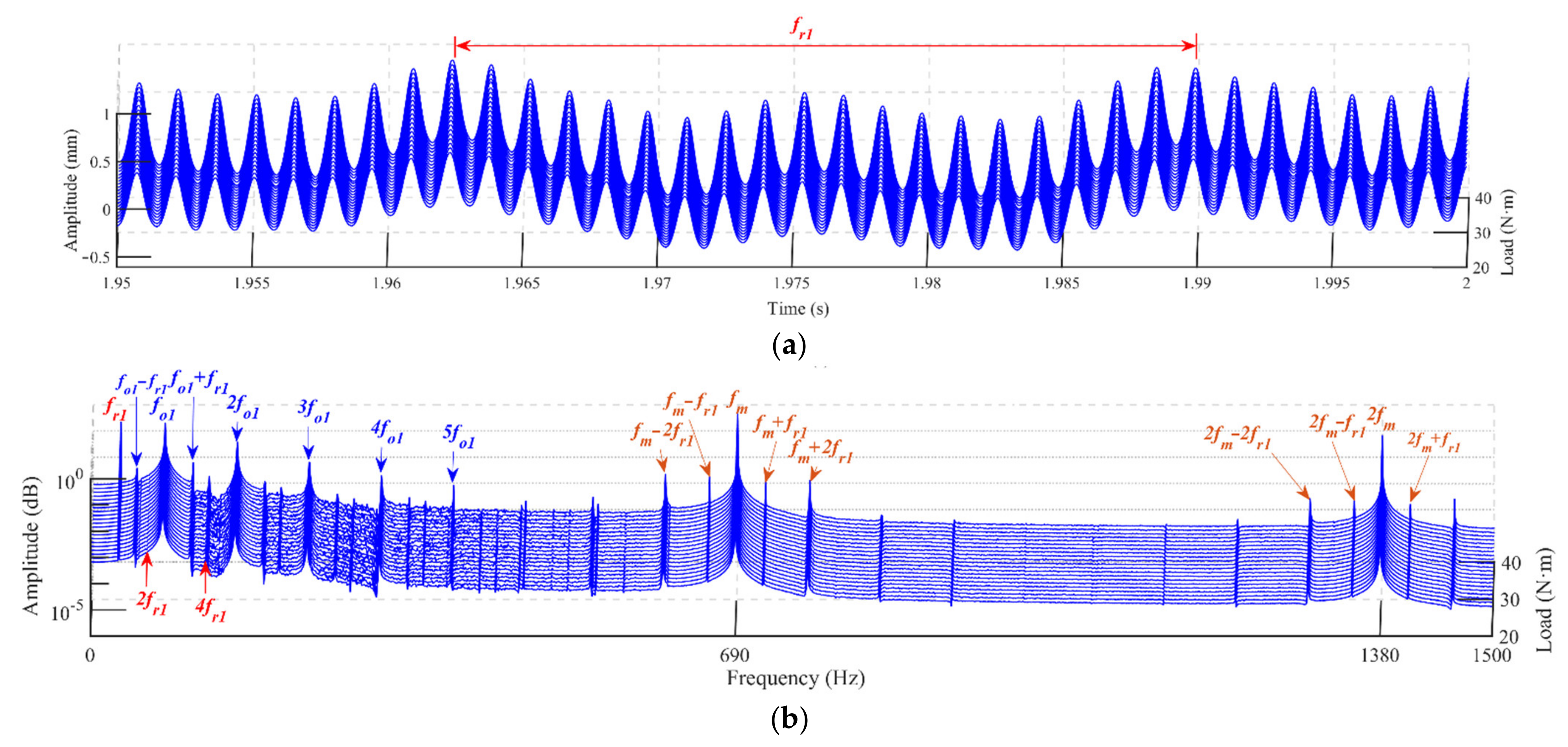
4.1. Vibration Response for the Bearing-Rotor-Gear System with the Misaligned Rotor
4.2. Influence of Speed on Vibration Responses for the Bearing-Rotor-Gear System
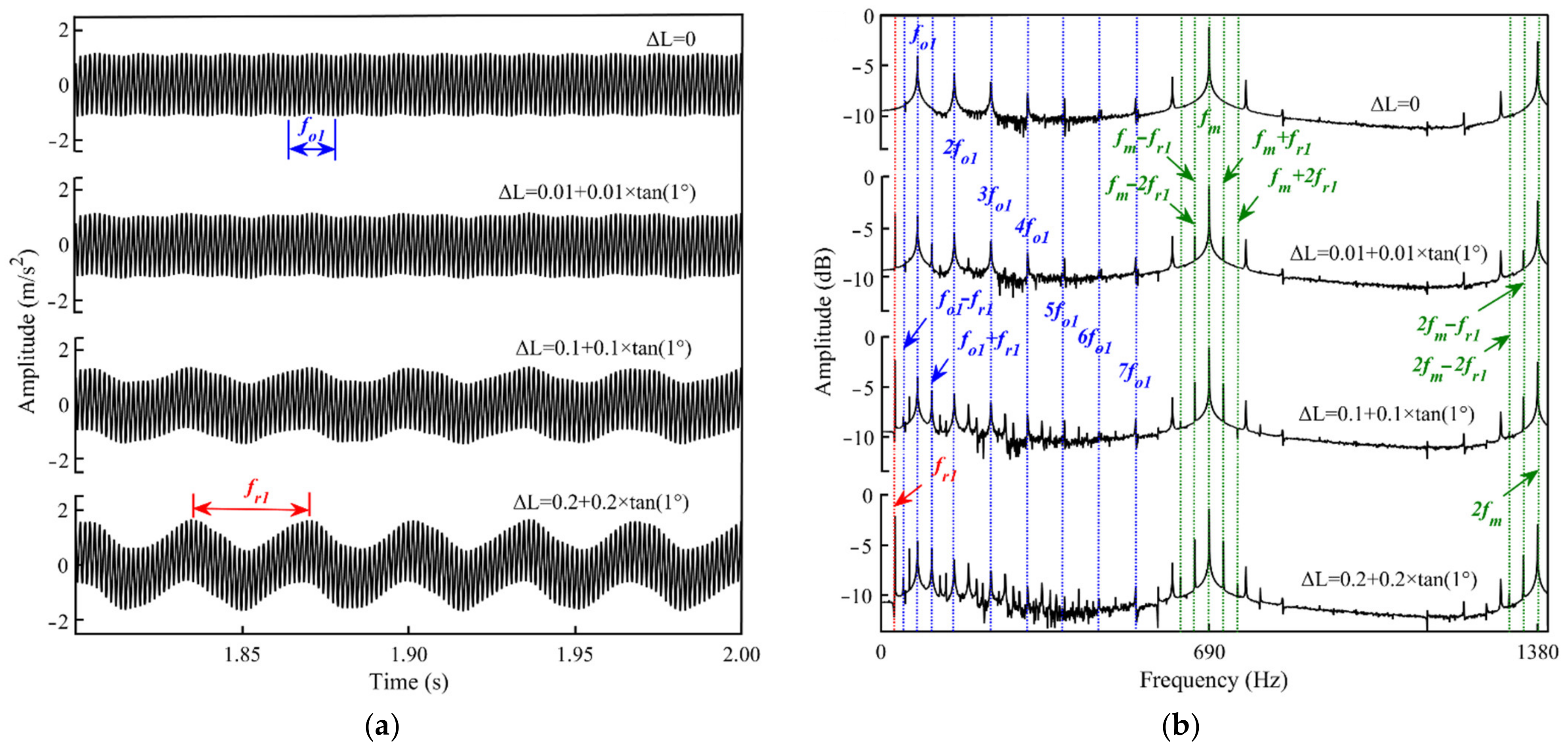
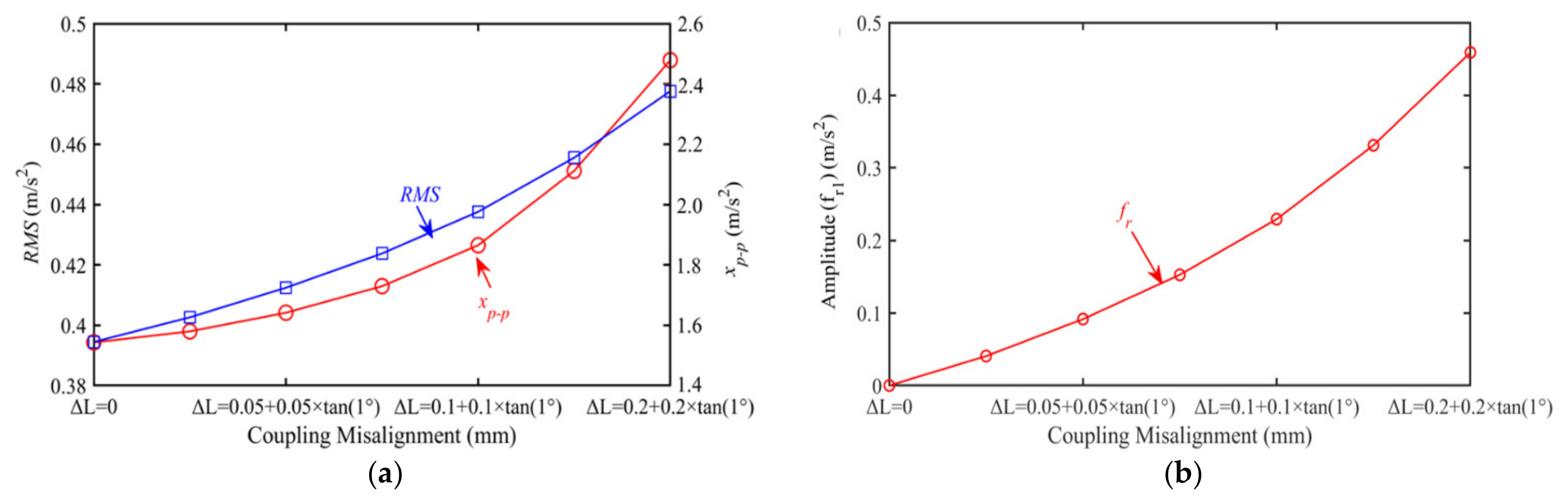
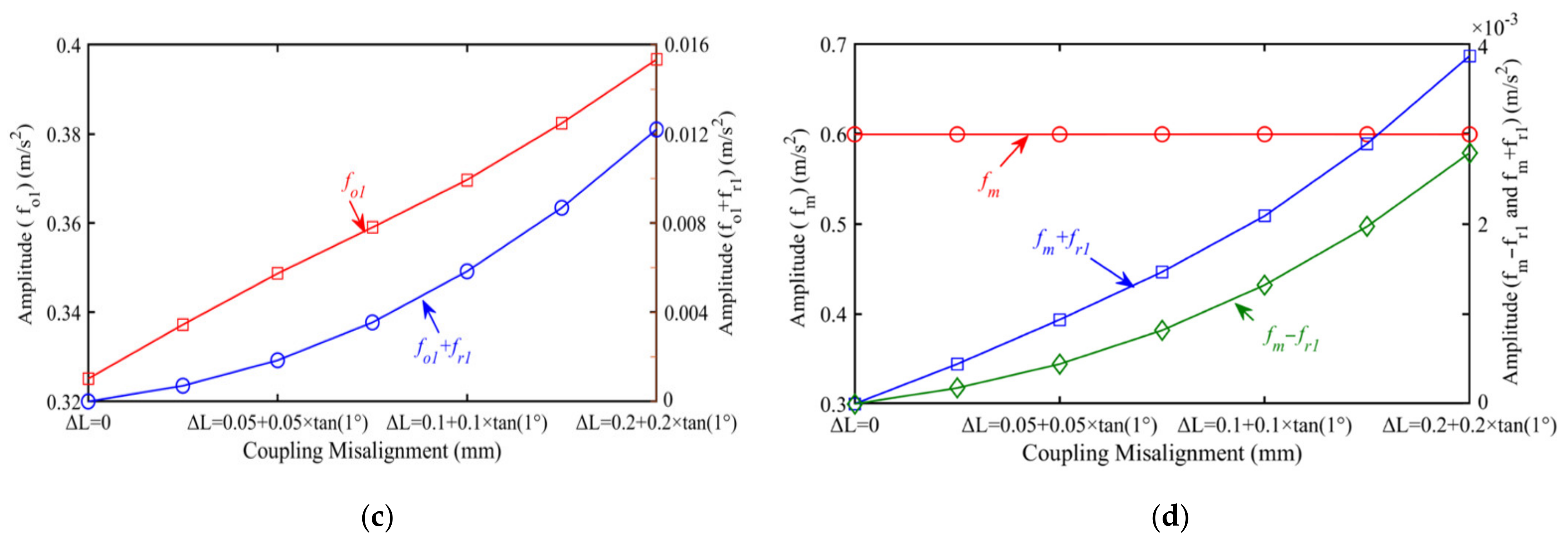
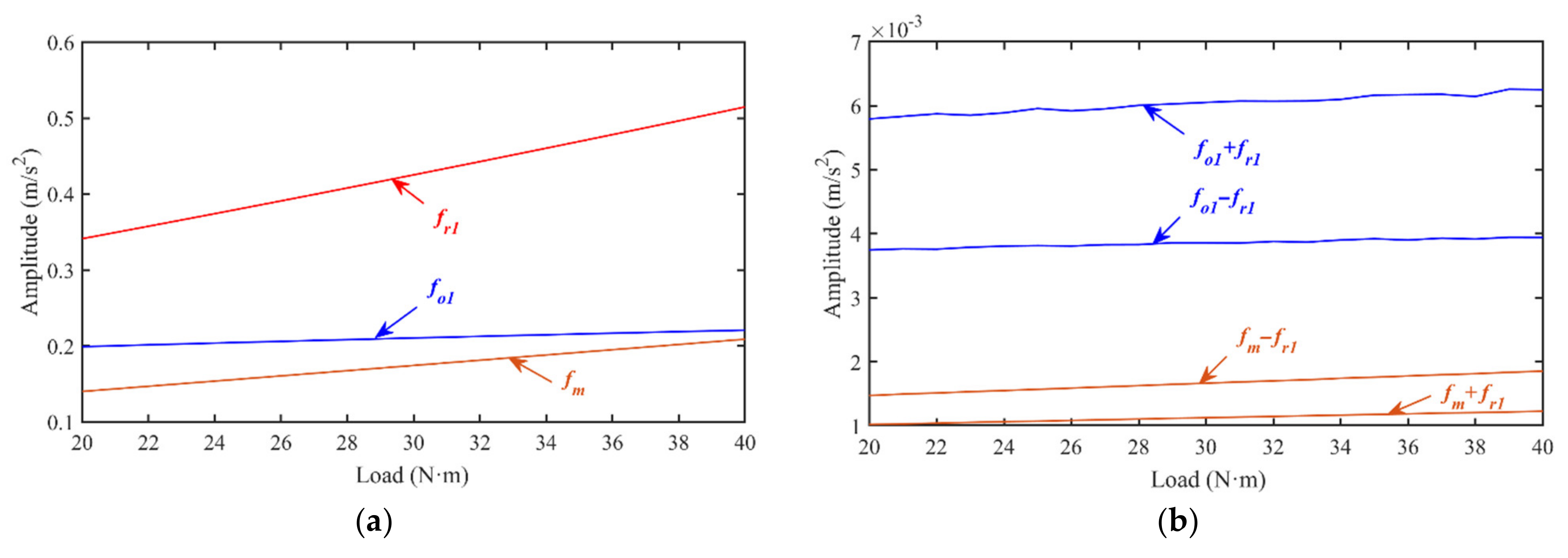
4.3. Influence of Load on Vibration Responses of the Bearing-Rotor-Gear System
5. Conclusions
- (1)
- When there are misalignment defects on the rotor, the vibration responses of the system are modulated by rotor frequencies, and there are rotor frequencies in the spectrum. Harmonic responses of gear pairs and the bearing outer raceways are excited. As the misalignment defect deepens, the high-order harmonic responses increase.
- (2)
- The modulation caused by the rotor misalignment defect is accentuated. When the input speed is raised, the vibration caused by the gear pairs is attenuated, the harmonic response and super-harmonic response of the bearings can be suppressed, and the system vibrates mainly at the fundamental frequency.
- (3)
- When the load is increasing, the amplitude of the rotor frequency, meshing frequency, and defect frequency of the bearing outer raceway are all enlarged.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- Rotor frequency
- (2)
- Bearing outer ring frequency
- (3)
- Bearing inner ring frequency
- (4)
- Meshing frequency for the gear pairs
References
- Zhou, S.; Song, G.; Ren, Z.; Wen, B. Nonlinear dynamic analysis of coupled bearing-rotor-gear system with the effect of internal and external excitations. Chin. J. Mech. Eng. 2015, 29, 281–292. [Google Scholar] [CrossRef]
- Song, C.; Bai, H.; Zhu, C.; Wang, Y.; Feng, Z.; Wang, Y. Computational investigation of off-sized bearing rollers on dynamics for hypoid gear-shaft-bearing coupled system. Mech. Mach. Theory 2021, 156, 104177. [Google Scholar] [CrossRef]
- Xiao, H.; Zhou, X.; Liu, J.; Shao, Y. Vibration transmission and energy dissipation through the gear-shaft-bearing-housing system subjected to impulse force on gear. Measurement 2017, 102, 64–79. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, B.; Kong, L.; Li, Y. Effect of the ring misalignment on the service characteristics of ball bearing and rotor system. Mech. Mach. Theory 2020, 151, 103889. [Google Scholar] [CrossRef]
- Tuckmantel, F.W.; Cavalca, K.L. Vibration signatures of a rotor-coupling-bearing system under angular misalignment. Mech. Mach. Theory 2019, 133, 559–583. [Google Scholar] [CrossRef]
- Jalan, A.K.; Mohanty, A.R. Model based fault diagnosis of a rotor-bearing system for misalignment and unbalance under steady-state condition. J. Sound Vib. 2009, 327, 604–622. [Google Scholar] [CrossRef]
- Jiang, H.; Shao, Y.; Mechefske, C.K. Dynamic characteristics of helical gears under sliding friction with spalling defect. Eng. Fail. Anal. 2014, 39, 92–107. [Google Scholar] [CrossRef]
- Wen, C.; Meng, X.; Fang, C.; Gu, J.; Xiao, L.; Jiang, S. Dynamic behaviors of angular contact ball bearing with a localized surface defect considering the influence of cage and oil lubrication. Mech. Mach. Theory 2021, 162, 104352. [Google Scholar] [CrossRef]
- Dhamande, L.S.; Chaudhari, M.B. Compound gear-bearing fault feature extraction using statistical features based on time-frequency method. Measurement 2018, 125, 63–77. [Google Scholar] [CrossRef]
- Dal, A.; Karaçay, T. Effects of angular misalignment on the performance of rotor-bearing systems supported by externally pressurized air bearing. Tribol. Int. 2017, 111, 276–288. [Google Scholar] [CrossRef]
- Xu, M.; Marangoni, R. Vibration analysis of a motor-flexible coupling-rotor system subject to misalignment and unbalance, Part I: Theoretical model and analysis. J. Sound Vib. 1994, 176, 663–679. [Google Scholar] [CrossRef]
- Xu, M.; Marangoni, R. Vibration analysis of a motor-flexible coupling-rotor system subject to misalignment and unbalance, Part Ⅱ: Experiment validation. J. Sound Vib. 1994, 176, 681–691. [Google Scholar] [CrossRef]
- Marmol, R.A.; Smalley, A.J.; Tecza, J.A. Spline Coupling Induced Nonsynchronous Rotor Vibrations. J. Mech. Des. 1980, 102, 293–303. [Google Scholar] [CrossRef]
- Lee, Y.S.; Lee, C.W. Modeling and vibration analysis of misaligned rotor-ball bearing systems. J. Sound Vib. 1999, 224, 17–32. [Google Scholar] [CrossRef]
- Al-Hussain, K.M. Dynamic stability of two rigid rotors connected by a flexible coupling with angular misalignment. J. Sound Vib. 2003, 266, 217–234. [Google Scholar] [CrossRef]
- DeSmidt, H.; Wang, K.; Smith, E. Coupled torsion-lateral stability of a shaft-disk system driven through a universal joint. J. Appl. Mech. 2002, 69, 261–273. [Google Scholar] [CrossRef]
- A1-Hussain, K.; Redmond, I. Dynamic response of two rotors connected by rigid mechanical coupling with parallel misalignment. J. Sound Vib. 2002, 249, 483–498. [Google Scholar] [CrossRef]
- Dewell, D.; Mitchell, L. Detection of a misaligned disk coupling using spectrum analysis. J. Vib. Acoust. 1984, 106, 9–16. [Google Scholar] [CrossRef]
- Sekhar, A.S.; Prabhu, B.S. Effects of coupling misalignment on vibrations of rotating machinery. J. Sound Vib. 1995, 185, 655–671. [Google Scholar] [CrossRef]
- Lees, A.W. Misalignment in rigidly coupled rotors. J. Sound Vib. 2007, 305, 261–271. [Google Scholar] [CrossRef]
- Pennacchi, P.; Vania, A.; Chatterton, S. Nonlinear effects caused by coupling misalignment in rotors equipped with journal bearings. Mech. Syst. Signal Process 2012, 30, 306–322. [Google Scholar] [CrossRef] [Green Version]
- Sawalhi, N.; Randall, R.B. Simulating gear and bearing interactions in the presence of faults. Mech. Syst. Signal Process 2008, 22, 1924–1951. [Google Scholar] [CrossRef]
- Wang, F.T.; Jing, M.Q.; Yi, J.; Dong, G.; Liu, H.; Ji, B. Dynamic modelling for vibration analysis of a cylindrical roller bearing due to localized defects on raceways. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2015, 229, 39–64. [Google Scholar] [CrossRef] [Green Version]
- Ma, R.; Chen, Y.; Cao, Q. Research on dynamics and fault mechanism of spur gear pair with spalling defect. J. Sound Vib. 2012, 331, 2097–2109. [Google Scholar] [CrossRef]
- Jia, S.X.; Howard, I. Comparison of localized spalling and crack damage from dynamic modeling of spur gear vibrations. Mech. Syst. Signal Process 2006, 20, 332–349. [Google Scholar] [CrossRef]
- Chen, Z.; Ji, P. Research on the variation of mesh stiffness and transmission error for spur gear with tooth profile modification and wear fault. Eng. Fail. Anal. 2021, 122, 105184. [Google Scholar] [CrossRef]
- Dai, H.; Long, X.; Chen, F.; Xun, C. An improved analytical model for gear mesh stiffness calculation. Mech. Mach. Theory 2021, 159, 104262. [Google Scholar] [CrossRef]
- Ma, R.; Chen, Y. Research on the dynamic mechanism of the gear system with local crack and spalling failure. Eng. Fail. Anal. 2012, 26, 12–20. [Google Scholar] [CrossRef]
- Inayat-Hussain, J.I. Nonlinear dynamics of a statically misaligned flexible rotor in active magnetic bearings. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 764–777. [Google Scholar] [CrossRef]
- Wu, K.; Liu, Z.; Ding, Q. Vibration responses of rotating elastic coupling with dynamic spatial misalignment. Mech. Mach. Theory 2020, 151, 103916. [Google Scholar] [CrossRef]
- Prabhakar, S.; Sekhar, A.S.; Mohanty, A.R. Crack versus coupling misalignment in a transient rotor system. J. Sound Vib. 2003, 266, 773–786. [Google Scholar] [CrossRef]
- Long, L.; Wen, X.; Lin, Y. Denoising of seismic signals based on empirical mode decomposition-wavelet thresholding. J. Vib. Control 2021, 27, 311–322. [Google Scholar] [CrossRef]
- Harris, T.A. Advanced Concepts of Bearing Technology, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Dai, P.; Wang, J.; Yan, S.; Huang, S.; Wang, F.; Liu, J. Vibration characteristics of the gear shaft-bearing system with compound defects under variable operating conditions. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2022, 236, 113–129. [Google Scholar] [CrossRef]


| Bearings | Types | Defect Frequency of Inner Raceway fi/Hz | Defect Frequency of Outer Raceway fo/Hz |
|---|---|---|---|
| Bearing 1 | 6304 | 132.79 | 81.13 |
| Bearing 2 | 6304 | 132.79 | 81.13 |
| Bearing 3 | 6308 | 37.71 | 21.92 |
| Bearing 4 | 6308 | 37.71 | 21.92 |
| Parameters | Driving Gear | Driven Gear |
|---|---|---|
| Pressure angle α/(°) | 20 | 20 |
| Modulus m/mm | 2 | 2 |
| Number of teeth z | 23 | 81 |
| Young’s modulus E/GPa | 216 | 216 |
| Tooth width W/mm | 24 | 24 |
| Parameters | Value |
|---|---|
| Inertia moment of input rotor If1/(kg⋅m2) | 0.0021 |
| Inertia moment of driving gear Ipin/(kg⋅m2) | 4.365 × 10−4 |
| Inertia moment of driven gear Ige/(kg⋅m2) | 8.362 × 10−4 |
| Inertia moment of output rotor If2/(kg⋅m2) | 0.0105 |
| Load Tout(N/m) | 30 |
| Average transmission error eo/m | 3.0 × 10−5 |
| Transmission fluctuation range em/m | 2.0 × 10−5 |
| Torsional stiffness of rotor kf1, kf2/(Nm/rad) | 4.4 × 105 |
| Torsional damping of rotor cf1, cf2/(Nms/rad) | 5.0 × 105 |
| Support stiffness in the bearings ksj, kpj, krj/(N/m) | 6.7 × 107 |
| Support damping in the bearings csj, cpj, crj/(Ns/m) | 1.8 × 105 |
| Mass of coupling housing mc/kg | 1 |
| Mass of driving gear mpin/kg | 0.96 |
| Mass of driven gear mge/kg | 2.88 |
| Rotation frequency of input rotor fr1/Hz | 30 |
| Meshing frequency fm/Hz | 690 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Dai, P.; Wang, J.; Niu, L. Vibration Responses of the Bearing-Rotor-Gear System with the Misaligned Rotor. Machines 2022, 10, 267. https://doi.org/10.3390/machines10040267
Wang F, Dai P, Wang J, Niu L. Vibration Responses of the Bearing-Rotor-Gear System with the Misaligned Rotor. Machines. 2022; 10(4):267. https://doi.org/10.3390/machines10040267
Chicago/Turabian StyleWang, Fengtao, Peng Dai, Jianping Wang, and Linkai Niu. 2022. "Vibration Responses of the Bearing-Rotor-Gear System with the Misaligned Rotor" Machines 10, no. 4: 267. https://doi.org/10.3390/machines10040267
APA StyleWang, F., Dai, P., Wang, J., & Niu, L. (2022). Vibration Responses of the Bearing-Rotor-Gear System with the Misaligned Rotor. Machines, 10(4), 267. https://doi.org/10.3390/machines10040267






