Abstract
Multiphase drives offer enhanced fault-tolerant capabilities compared with conventional three-phase ones. Their phase redundancy makes them able to continue running in the event of faults (e.g., open/short-circuits) in certain phases. Moreover, their greater number of degrees of freedom permits improving diagnosis and performance, not only under faults affecting individual phases, but also under those affecting the machine/drive as a whole. That is the case of failures in the dc link, resolver/encoder, control unit, cooling system, etc. Accordingly, multiphase drives are becoming remarkable contenders for applications where high reliability is required, such as electric vehicles and standalone/off-shore generation. Actually, the literature on the subject has grown exponentially in recent years. Various review papers have been published, but none of them currently cover the state-of-the-art in a comprehensive and up-to-date fashion. This two-part paper presents an overview concerning fault tolerance in multiphase drives. Hundreds of citations are classified and critically discussed. Although the emphasis is put on fault tolerance, fault detection/diagnosis is also considered to some extent, because of its importance in fault-tolerant drives. The most important recent advances, emerging trends and open challenges are also identified. Part 1 provides a comprehensive survey considering numerous kinds of faults, whereas Part 2 is focused on phase/switch open-circuit failures.
1. Introduction
Electric machines with more than three stator phases, i.e., multiphase machines, offer several substantial advantages in comparison with conventional three-phase ones [1,2]. For instance, the fact that the total power is split among a greater number of phases allows decreasing the per-phase current rating without increasing the rated voltage [2]. Another characteristic that has traditionally been valued is the smaller amount of torque ripple [2]. Furthermore, using more phases makes it possible to reduce the dc-link capacitor volume [3]. Nonetheless, nowadays, the majority of the most appreciated benefits of multiphase machines stem from their extra degrees of freedom (DOFs) with respect to the three-phase alternatives [2,4]. The latter normally have just two current DOFs, used to set the flux/torque [2], whereas the higher number in the former enables other interesting possibilities [2,4]. This additional versatility can be exploited, among many other purposes, for increased torque density [5,6,7,8,9,10], machine parameter estimation [11], multimotor drives [2,10,12,13,14,15], integrated battery chargers [16,17,18,19,20,21,22], bearingless machines [23], or, most importantly, for enhanced fault tolerance. In fact, fault tolerance is one of the research topics regarding multiphase drives that has attracted the most attention in recent years. This is illustrated, e.g., by the large amount of literature that, as shown in the classification in Table 1, addresses the detection and tolerance of faults in multiphase drives.
Accordingly, multiphase machines are often employed in applications where high reliability is important, such as off-shore wind generation (where corrective maintenance may not be easy) [24], stand-alone wind/hydro-power generation [24], aerospace (especially because of safety) [25,26], electric automotive vehicles (e.g., for limp-home mode) [17,21,22,27,28], etc. Table 2 summarizes the main kinds of applications where fault-tolerant multiphase drives are considered in recent literature. From this table, aerospace and automotive vehicles gather the most significant proportion of these publications; in any case, Table 2 also confirms that these machines are of paramount importance for high-reliability scenarios of different types.
Given that the number of industry applications and research publications on this topic has not ceased to increase, it is not surprising that numerous survey papers about multiphase drives have been put forth, most notably during the last two decades [1,2,4,16,24,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. These review papers may be broadly classified as shown in Table 3. A few of them tackle the subject of multiphase drives with very ample scope [1,2,29,30,31,32,33], providing comprehensive summaries of a wide range of aspects related to these systems: advantages, applications, modeling, harmonic mapping, control methods, fault tolerance, space-vector (SV) pulsewidth modulation (PWM), multimotor drives, etc. On the other hand, some of the existing survey papers about multiphase drives are focused on specific aspects, such as six-phase induction machines (IMs) with asymmetrical winding spatial arrangement (WSA) [42], SV PWM for five and six phases [44], integrated on-board battery chargers for electric automotive vehicles [16], traction motor drives [3,48], aircraft applications [52,53], electrical transportation (in general) [49,50,51], drives based on multiple three-phase modules [43], advanced converter topologies (matrix, multilevel, open-end windings) [4,46,52], wind-energy [54], fault tolerance and wind/stand-alone generation [24], fault-tolerant multilevel drives [47], power sharing between multiple three-phase winding sets [37], exploitation of additional DOFs [4,35,36], machine design [34,55], healthy-drive control [34], direct torque control (DTC) [38], model predictive control (MPC) [39,40,41], or fault-tolerant control for five-phase machines using reduced-order transformation matrices [45].

Table 1.
Classification of references about fault tolerance in multiphase drives (and paper sections) according to the types of faults detected and tolerated (indicated by D and T, respectively). Survey papers and books are not included in this table.
Table 1.
Classification of references about fault tolerance in multiphase drives (and paper sections) according to the types of faults detected and tolerated (indicated by D and T, respectively). Survey papers and books are not included in this table.
| References | Control Unit | Current Sensor | Dc Capacitor | Dc Volt. Sensor | Dc Volt. Excess | Dc Volt. Shortage | High-res. Connects. | Machine Cooling | Magnet Demag. | Mechanical | Resolver/Encoder | Stator SC | Supply OC/SC | Switch SC | Switch/Phase OC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [56] | DT | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| [57] | - | D | - | - | - | - | - | - | - | - | - | - | - | - | D |
| [58] | - | DT | - | DT | - | - | - | - | - | - | DT | - | - | - | DT |
| [59] | - | - | - | - | - | - | D | - | - | - | - | - | - | - | - |
| [60] | - | - | - | - | - | - | D | D | - | - | - | - | - | - | - |
| [61] | - | - | - | - | - | - | D | - | - | - | - | D | - | - | - |
| [62] | - | - | - | - | - | - | D | - | - | D | - | - | - | - | D |
| [63,64] | - | - | - | - | - | - | D | - | - | - | - | - | - | - | D |
| [65,66,67] | - | - | - | - | - | - | DT | - | - | - | - | - | - | - | - |
| [68] | - | - | - | - | - | - | DT | - | DT | - | - | - | - | - | - |
| [69] | - | - | - | - | - | - | DT | - | - | - | - | - | - | - | DT |
| [70,71,72,73] | - | - | - | - | - | - | - | D | - | - | - | - | - | - | - |
| [74,75,76,77,78] | - | - | - | - | - | - | - | - | DT | - | - | - | - | - | - |
| [79,80,81,82,83,84,85] | - | - | - | - | - | - | - | - | - | D | - | - | - | - | - |
| [86,87] | - | - | - | - | - | - | - | - | - | - | DT | - | - | - | - |
| [88,89,90,91,92] | - | - | - | - | - | - | - | - | - | - | - | D | - | - | - |
| [93,94,95,96,97,98] | - | - | - | - | - | - | - | - | - | - | - | DT | - | - | - |
| [99] | - | - | - | - | - | - | - | - | - | - | - | DT | - | DT | - |
| [100] | - | - | - | - | - | - | - | - | - | - | - | DT | - | - | DT |
| [101] | - | - | - | - | - | - | - | - | - | - | - | DT | - | - | T |
| [102] | - | - | - | - | - | - | - | - | - | - | - | - | - | D | DT |
| [103] | - | - | - | - | - | - | - | - | - | - | - | - | - | DT | DT |
| [14,104,105,106,107,108,109,110,111,112,113,114,115] | - | - | - | - | - | - | - | - | - | - | - | - | - | - | D |
| [116,117,118,119,120,121,122,123,124,125,126] | - | - | - | - | - | - | - | - | - | - | - | - | - | - | DT |
| [127] | - | - | - | - | - | - | - | - | - | - | T | - | - | - | DT |
| [128] | - | - | - | - | - | - | - | - | - | - | - | T | - | - | DT |
| [129] | - | - | T | - | - | T | - | - | T | - | - | T | - | - | - |
| [130] | - | - | T | - | - | - | - | - | - | - | T | T | - | T | T |
| [27] | - | - | T | - | - | - | - | - | - | - | - | T | - | T | T |
| [131] | - | - | - | - | T | - | - | - | - | - | - | - | - | - | - |
| [132] | - | - | - | - | T | - | - | - | - | - | - | - | - | - | T |
| [7,8,9,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160] | - | - | - | - | - | T | - | - | - | - | - | - | - | - | - |
| [161] | - | - | - | - | - | T | - | - | - | - | T | - | - | - | T |
| [162,163,164,165,166,167] | - | - | - | - | - | T | - | - | - | - | - | T | - | - | T |
| [168] | - | - | - | - | - | T | - | - | - | - | - | - | - | T | - |
| [169,170,171,172,173,174] | - | - | - | - | - | T | - | - | - | - | - | - | - | - | T |
| [175] | - | - | - | - | - | - | T | - | - | - | - | - | - | - | - |
| [176,177] | - | - | - | - | - | - | - | - | T | - | - | T | - | - | - |
| [178] | - | - | - | - | - | - | - | - | T | - | - | T | - | - | T |
| [179,180] | - | - | - | - | - | - | - | - | - | T | - | - | - | - | - |
| [181,182,183,184,185,186,187,188,189,190,191,192,193,194,195,196,197,198,199,200,201,202,203,204,205,206,207,208] | - | - | - | - | - | - | - | - | - | - | T | - | - | - | - |
| [209] | - | - | - | - | - | - | - | - | - | - | T | T | - | - | - |
| [210,211,212] | - | - | - | - | - | - | - | - | - | - | T | T | - | - | T |
| [213,214,215,216,217,218,219] | - | - | - | - | - | - | - | - | - | - | T | - | - | - | T |
| [220,221,222,223,224,225,226,227,228,229,230,231,232,233,234,235,236,237,238] | - | - | - | - | - | - | - | - | - | - | - | T | - | - | - |
| [239] | - | - | - | - | - | - | - | - | - | - | - | T | T | T | T |
| [240,241,242,243] | - | - | - | - | - | - | - | - | - | - | - | T | - | T | - |
| [244,245,246,247] | - | - | - | - | - | - | - | - | - | - | - | T | - | T | T |
| [28,248,249,250,251,252,253,254,255,256,257,258,259,260,261,262,263,264,265,266,267,268,269,270,271,272] | - | - | - | - | - | - | - | - | - | - | - | T | - | - | T |
| [273] | - | - | - | - | - | - | - | - | - | - | - | - | - | T | - |
| [13,274,275,276,277] | - | - | - | - | - | - | - | - | - | - | - | - | - | T | T |
| [15,22,278,279,280,281,282,283,284,285,286,287,288,289,290,291,292,293,294,295,296,297,298,299,300,301,302,303,304,305,306,307,308,309,310,311,312,313,314,315,316,317,318,319,320,321,322,323,324,325,326,327,328,329,330,331,332,333,334,335,336,337,338,339,340,341,342,343,344,345,346,347,348,349,350,351,352,353,354,355,356,357,358,359,360,361,362,363,364,365,366,367,368,369,370,371,372,373,374,375,376,377,378,379,380,381,382,383,384,385,386,387,388,389,390,391,392,393,394,395,396,397,398,399,400,401,402,403,404,405,406,407,408,409,410,411,412,413,414,415,416,417,418,419,420,421,422,423,424,425,426,427,428,429,430,431,432,433,434,435,436,437,438,439,440,441,442,443,444,445,446,447,448,449,450,451] | - | - | - | - | - | - | - | - | - | - | - | - | - | - | T |
| Section | Section 12.5 | Section 12.4 | Section 12.1 | Section 12.3 | Section 9 | Section 8 | Section 4 | Section 10 | Section 11 | Section 12.6 | Section 7 | Section 5 | Section 12.2 | Section 6 | Part 2 |

Table 2.
Classification of references about fault tolerance in multiphase drives according to specific applications.
Table 2.
Classification of references about fault tolerance in multiphase drives according to specific applications.
| Application | References |
|---|---|
| Aerospace | [13,14,25,26,52,53,93,98,99,100,101,130,161,167,211,212,226,227,228,229,230,231,236,237,238,240,244,246,260,265,266,267,270,272,288,303,304,305,306,307,330,391,452] |
| Automotive vehicles | [3,16,22,27,28,48,56,91,92,94,117,119,178,181,182,209,217,219,220,221,243,248,249,250,264,282,358,361,363,364,365,366,367,368,386,453] |
| Elevator | [439] |
| Marine energy | [57,291,295,371] |
| Metal industry | [269,345] |
| Ships | [203,271,332,333,417,420,440,454] |
| Wind energy | [24,54,123,287,336,340,354,409,455] |

Table 3.
Classification of survey papers focused on multiphase drives.
Table 3.
Classification of survey papers focused on multiphase drives.
| Main Topic | References |
|---|---|
| General | [1,2,29,30,31,32,33] |
| Control and PWM | [4,34,35,36,37,38,39,40,41,42,43,44,45] |
| Converter topologies | [4,43,46,52] |
| Fault tolerance | [24,45,47] |
| Machine design | [34,55] |
| Transportation | [3,16,36,48,49,50,51,52,53] |
| Wind energy | [24,54] |
There are also other review papers that, although not completely focused on multiphase drives, do include a significant part of survey about them; e.g., about fault-tolerant permanent-magnet synchronous machines (PMSMs) [456,457], more-electric aircraft [25,26,452], high-power wind-energy [455], medium-voltage supplies for ships [454], MPC [458], and integrated electric vehicle battery chargers [453,459].
In spite of the abundance of surveys about multiphase drives, and of the importance of fault tolerance in them, there is a noteworthy absence of recent review papers focusing on multiphase drives from the fault-tolerance standpoint. The publications providing an overview of this subject, although of excellent value, are at best already several years old [24,45,47]. Moreover, even though these ones address fault tolerance, the focus is specifically placed on certain subtopics: wind-energy [24], multilevel converters [47], and five-phase reduced-order transformation matrices [45]. It is also worth noting that just short-circuit (SC) and open-circuit (OC) faults in the switches or stator phases were taken into account [24,45,47], but many other kinds of failures may also arise in practical drives [58,129,460,461,462]. In this manner, the bibliographies in [24,45,47] do not bring together more than 110 references, and they do not reflect the substantial amount of work published on fault-tolerant multiphase drives during recent years.
This paper presents a comprehensive survey of the literature about fault tolerance in multiphase drives. Special attention is devoted to journal papers published in the last five years, although many older papers and conference papers are included as well for the sake of completeness. In this fashion, e.g., the new advances can be seen in perspective with respect to pre-existing publications. Although, in principle, any multiphase drive is inherently fault-tolerant because of the phase redundancy, the focus here is placed on those publications regarding multiphase drives that specifically address aspects related to fault tolerance or fault detection. Fault detection and diagnosis is here discussed to some extent because of its importance in fault-tolerant systems, but much more attention is given to fault-tolerance itself. Only voltage-source converters (VSCs), which are by far the most common, are taken into consideration. Numerous kinds of failures are discussed, including those of SC, OC, and speed-sensor types, as well as dc-link voltage excess or shortage, high-resistance connections and many others. Several hundred citations are covered with a critical point of view. The literature is classified according to the types of faults, applications, machines, topologies, methods, etc. The most relevant recent advances, emerging trends and open challenges in the state-of-the-art are highlighted, giving useful and comprehensive insight for practitioners and researchers either new or with vast experience in the field.
The paper is divided into two parts: Part 1 and Part 2. The first one presents a general overview of the fundamentals and of numerous types of faults that can occur in a multiphase drive. The second part is focused on phase and switch OC faults, which are by far the types of failure to which most publications have been devoted.
The remainder of Part 1 is organized as follows (Note that the table of contents of the paper is included in the pdf file as bookmarks). The types of faults are classified in Section 2, along with the literature on the subject. Some fundamental notions about multiphase drives are given in Section 3; in particular, the types of machines and converter topologies are reviewed, and the vector space decomposition (VSD) for machine modeling is explained. Then, faults regarding high-resistance connections (Section 4), stator SCs (Section 5), switch SCs (Section 6), resolvers/encoders (Section 7), dc-link voltage shortage (Section 8), dc-link voltage excess (Section 9), machine cooling (Section 10) and magnet demagnetization (Section 11) are addressed. Other types of faults are briefly surveyed in Section 12. The correspondence between sections and kinds of failures is also indicated in the last row of Table 1. The extension and degree of detail of each of these sections are related to the amount of existing associated literature, in accordance with this table. Section 13 compares the fault-tolerant capability of some of the most relevant multiphase drive topologies, in view of the surveyed literature and considering multiple kinds of failures. The conclusions of the paper are summarized in Section 14. Abbreviations are listed at the end.
2. Main Fault Types and Literature Classification according to Studied Topics
Since an ac drive is composed of a wide variety of complex elements, numerous types of faults can occur [24,58,460,461,462], as illustrated in the classification shown in Figure 1. For each of these faults, it is desirable to implement methods that enable effective detection/diagnosis and tolerance. The detection and identification of the type of failure is normally useful not only for fixing the defective element of the drive when possible, but also for adopting the adequate fault-tolerant measure (the main focus of this paper), or at least, to disable the drive if no tolerance is feasible or if continuing operation would lead to further damage. (Although in some cases the process of fault diagnosis may be divided into the steps of fault detection, identification (type) and isolation (location) [463], in most of the diagnosis methods available in the literature of multiphase drives the three goals are achieved simultaneously.)
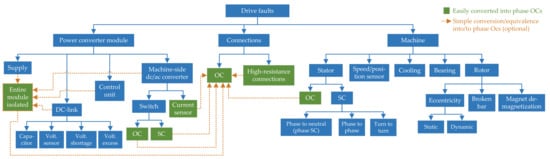
Figure 1.
Types of faults in an ac drive.
Multiphase drives have a redundancy in terms of stator phases. This implies that they inherently have a greater degree of fault-tolerance than three-phase drives to certain faults; in particular, they are especially advantageous in the face of failures that mean hampering the normal functioning of some stator phases. This is the case, principally, of SC and OC faults (or equivalent) in the dc/ac converter switches, in the machine stator windings, or in the connections between converter and machine. Accordingly, as can be observed in Table 1, most of the literature about multiphase drives is focused on these OC and SC failures. This is presumably also the reason why the recent surveys about fault-tolerant multiphase drives [24,45,47] were centered on these fault types.
In addition, SC faults are much more potentially harmful than OC ones, because large currents tend to arise [270,448]. Consequently, when SC failures occur in a converter switch or leg, they are usually transformed into phase OC faults [102,119,171,276,373,377,385,448,464,465]. This is typically completed by opening a protective element in series (e.g., a fuse) either in the converter leg [119,276,343,464,465] or in the line between the machine and converter [102,119,276,385,464,465]. Nevertheless, additional devices would be necessary just for isolating switch SC faults, and, hence, this solution is sometimes discarded due to its extra complexity, cost, size, and weight. Moreover, opening a phase implies decreasing the achievable torque for a given VSC power rating [343]. In fact, it can be seen in Table 1 that the amount of research aimed at attaining tolerance to switch SC faults, by means other than simply handling them as OCs, should not be overlooked either. On the other hand, stator SC failures cannot be easily transformed into OC ones, and hence specific approaches were devised for scenarios where tolerance to them is also sought, especially by designing the machine so as to limit the resulting SC current and its impact [240,266].
There are also other particular fault types to which multiphase drives are clearly more tolerant than three-phase ones. For instance, although a three-phase machine may be driven by three independent single-phase VSCs, multiphase machines are particularly suitable for being fed by multiple independent dc/ac converters (e.g., single- or three-phase ones). Each of these VSCs can be associated with respective separate dc links, power supplies (e.g., through ac/dc and/or dc/dc converters), or even control platforms [24,26,56]. These separate and redundant systems are often called modules. Therefore, multiphase drives can also be tolerant to faults in the components (dc links, controllers, etc.) in each of these modules. Nevertheless, with such configurations it is frequently assumed that, in case of a fault within one of these modules, the entire module is deactivated and isolated [24]. This fact may explain why there are barely any publications dealing specifically with, e.g., faults in individual control units [56] or dc links [129,130] within a modular multiphase drive system. Instead, these situations (after isolation) are normally treated in most publications identically to OC faults that occur in the corresponding phases. Similarly, in case a current-sensor fault [58] or a high-resistance connection [66] is detected in a certain phase, a possible remedy (among others) is to open the corresponding line as for an SC (e.g., using a bidirectional switch), resulting in an OC as well. It may also be highlighted that, in a respectable part of the literature about fault tolerance (although not in all of it, as discussed later), no distinction is made between faults in switch gating, OC faults in free-wheeling diodes, switch OC faults, and stator OC faults, thus treating all of these as phase OC failures for generality. In fact, it can be argued that completely opening the line in any of these OC cases is also advisable to prevent unexpected behavior or overcurrent [373].
On the other hand, there are numerous faults that do not solely affect some of the stator phases, but all of them to similar extent. This occurs, e.g., in case of shortage [138,466,467], excess [131,132] or sensor failure [58] of dc-link voltage (for single-dc-link drive), magnet demagnetization [75], as well as mechanical (e.g., eccentricity or damaged bearings/bars) [79,81,82,84,85], speed/position-sensor [182,199], or machine cooling-system failures (increasing temperature) [60,70,71,468], among others. The phase redundancy of multiphase machines, in principle, does not seem to offer inherent tolerance against these kinds of faults. In fact, in many cases the techniques to detect or tolerate such faults in conventional three-phase drives can be applied to multiphase ones without any or hardly any modifications. For instance, open-loop V/f control may be employed in IMs to tolerate speed-sensor faults [460], regardless of the phase number. In a similar fashion, many algorithms for sensorless speed/position estimation in three-phase drives, based on the fundamental (not harmonic) electromagnetic components, could be directly adopted in multiphase ones, since the machine model for such terms is (ideally) equivalent [1]. Nonetheless, existing research has revealed that, even though initially it may not seem obvious that multiphase drives provide better fault tolerance than three-phase ones to these kinds of faults not associated with particular phases, in an indirect manner the additional DOFs of the former do often allow for an advantage in this sense. For instance, these extra current DOFs can be exploited to tolerate speed/position-sensor faults [188,202], dc-link voltage shortage [138,142], dc-link voltage excess [131,132], or to monitor varying parameters related to faults such as temperature [70] or eccentricity [84], frequently with superior characteristics (e.g., without torque disturbance [70,142,188], with increased signal-to-noise ratio [84,202], etc.) in comparison with analogous techniques (if any) for three-phase machines. Accordingly, it is of great interest to survey here the research about these fault types as well, in the context of multiphase drives.
Since the classification of the methods for fault detection and tolerance depends to a great extent on the type of failure, it will be performed for each of them separately.
3. Types of Multiphase Drives and Vector Space Decomposition (VSD)
In this section, first the types of machines and stator phase configurations are reviewed in Section 3.1, and the literature about fault-tolerant multiphase drives is classified accordingly therein. Then, the main converter topologies are introduced in Section 3.2, where the literature is also classified in this regard. Finally, the general VSD is briefly explained in Section 3.3.
3.1. Types of Multiphase Machines and Stator Phase Configurations
The multiphase machines considered in this survey are mainly inner-rotor radial-flux rotary ones of the following kinds, depending on the rotor type: IMs, permanent-magnet synchronous machines (PMSMs), synchronous reluctance machines (SynRMs), and permanent-magnet-assisted SynRMs (PMaSynRMs). Switched reluctance and similar machines are excluded because of their very specific characteristics, as performed in other surveys about multiphase drives [2]. Some other particular machine types found in the existing literature about fault-tolerant multiphase drives are also included here, such as outer-rotor [27,102,117,119,229,250,257,264,361,363], dual-rotor [174,249,272,289,375], axial-flux [174,268,289,297,306,347,375], hybrid-excitation (hybrid of IM and PMSM) [94,178], and wound-field synchronous machines (WFSMs) [416].
In the following machine classification, the term “winding spatial arrangement” (WSA) is used to refer to the manner in which the different phase windings are spatially arranged in the stator, which is strongly related to the machine winding process. In contrast, the expression “stator phase connection” makes reference here to the way in which the stator phases (already wound in the stator slots) are externally connected to each other (star, pentagon, etc.) ignoring the VSC. In addition, “stator phase splitting” meant the number of phases, out of the total phase number n, that are continuously connected electrically (not by a converter high-frequency switching) to each other, e.g., through a neutral point; in this manner, the stator winding can be split into several unconnected sets. The last two concepts (stator phase connection and stator phase splitting) are related to each other, but they are not equivalent. The alternatives regarding stator phase splitting, WSA and stator phase connection are described next, in Section 3.1.1, Section 3.1.2 and Section 3.1.3, respectively.
3.1.1. Stator Phase Splitting
The stator winding may be electrically split into different groups of phases according to the following alternatives.
- If “no phase splitting” is applied, there is electrical connection between all phases (e.g., one star with one neutral point), and the stator can be considered a single n-phase winding;
- With “single-phase splitting”, there is no connection between any stator phases (e.g., open-end winding topologies), and the stator can be seen as n single-phase windings;
- With “l-phase splitting”, a stator winding of composite phase number n is composed of sets of l phases (), electrically isolated from each other. For example, stars with separate neutral points. It is common to select , given the widely spread knowledge and technology for three-phase systems [24,131,132,305,353]. Nevertheless, e.g., is sometimes chosen [303,405,421,431,432,469].
3.1.2. Stator Winding Spatial Arrangements (WSAs)
Some of the main types of stator WSAs are not suitable for prime n, but all of them can be applied to composite n. Accordingly, is chosen for illustrating the various kinds of WSAs in Figure 2. For the sake of simplicity, concentrated full-pitch windings and minimum number of pole pairs are assumed. The letters are assigned to each phase by following the alphabet in counter-clockwise direction. Red and blue colors are used to distinguish two winding sets, assuming 3-phase splitting. These diagrams would also hold for other splitting options, by simply changing these colors (although for multisector WSA then the sectors would no longer match electrically connected sets). A single color could be used for no phase splitting, or different colors for single-phase splitting. It is worth noting that for certain machines the kind of WSA may be altered by just modifying the correspondence between phases and stator coils through the external connections, without rewinding the stator [469].
The phasor diagrams with respect to time of the electrical signals that correspond to each of the WSAs from Figure 2 are represented in Figure 3. These phasor representations in Figure 3 are also valid in terms of flux spatial coordinates except for the multisector WSA, as can by deduced by comparison with Figure 2. In the following, each of the WSAs illustrated in Figure 2 and Figure 3 are discussed (Section 3.1.2.1, Section 3.1.2.2, Section 3.1.2.3 and Section 3.1.2.4), as well as the difference between overlapping and non-overlapping windings (Section 3.1.2.5).
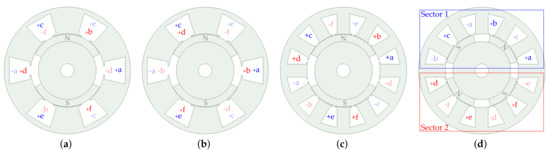
Figure 2.
Stator WSAs in a six-phase machine, using blue and red colors for each three-phase winding set (assuming three-phase splitting). Concentrated full-pitch windings are considered for simplicity. (a) Symmetrical WSA. (b) No-phase-shift WSA. (c) Asymmetrical WSA. (d) Multisector (two-sector) WSA.
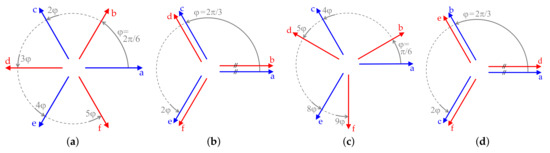
Figure 3.
Phasor representation of phase angles with respect to time corresponding to different stator WSAs in a six-phase machine (cf. Figure 2). These diagrams are also valid with respect to space for all WSAs except multisector WSA. (a) Symmetrical WSA. (b) No-phase-shift WSA. (c) Asymmetrical WSA. (d) Multisector (two-sector) WSA.
3.1.2.1. Symmetrical WSA
In the symmetrical WSA (see Figure 2a and Figure 3a), the stator windings are arranged symmetrically in space, i.e., with electrical radians between consecutive phases [2]. This is valid for either prime or composite n. For instance, conventional three-phase machines typically have symmetrical WSA. This kind of WSA provides especially good performance under phase OC faults in terms of minimum torque derating [312], as discussed in Part 2.
3.1.2.2. No-Phase-Shift WSA
For composite n, winding sets can be installed without any spatial phase shift between them (see Figure 2b and Figure 3b) [312], i.e., a no-phase-shift WSA. When identical electrical signals are applied to all winding sets, this type of WSA yields very similar behavior to an l-phase machine. Accordingly, it is less prone to current distortion than symmetrical and asymmetrical WSAs, its dc-link utilization is higher and its control is simpler [470,471]. However, the amount of torque derating under phase OC faults is worse [312].
3.1.2.3. Asymmetrical WSA
Another alternative for composite n, is to set the displacement between winding sets as (see Figure 2c and Figure 3c), producing an asymmetrical WSA [2]. Compared with other WSAs, this one is advantageous in order to increase torque density and reduce torque ripple, because odd time and space harmonics are distributed among more independent subspaces [1]. On the other hand, its control is often more complex and the current distortion [mainly producing stator copper loss (SCL)] tends to be more noticeable [470,471].
3.1.2.4. Multisector WSA
The winding sets for composite n may be instead placed in different stator sectors, yielding a multisector WSA [443]. In Figure 2d, there are sectors, one associated with each three-phase winding set: top (blue) and bottom (red). The electrical angles coincide for corresponding stator phases of all sectors (see Figure 3d), but not the mechanical ones (see Figure 2d) [346].
In Figure 3d there is one stator pole pair in each of the sectors. A multisector WSA with more stator poles can be wound so that there are still sectors, by setting more pole pairs per sector [56,247,261,346,450]. For instance, in Figure 4a there are two pole pairs in each sector. Another alternative would be to distribute the pole pairs of each winding set among several sectors, i.e., so that more than sectors are used in total [230,247,261,450]. For example, in Figure 4b there is still one pole per sector, but there are four sectors instead of two. In the latter case, the mechanical imbalance under faults affecting certain phases is less severe [230,450].
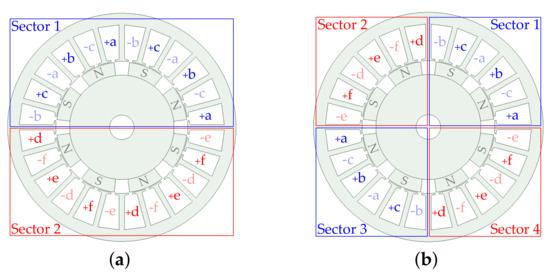
Figure 4.
Types of multisector WSAs for a six-phase machine with eight pole pairs. (a) Two pole pairs per sector. (b) One pole pair per sector.
In a machine based on l-phase sectors, similarly to a no-phase-shift WSA with l-phase windings, it is possible to supply all of them by a single l-phase VSC for simplicity [374]. However, the reliability in the face of VSC faults is then reduced compared with multiple l-phase VSCs.
Multisector WSA is often employed for bearingless machines, because it allows adjusting the radial force by the extra DOFs [23]. If the objective is to exploit the DOFs for fault tolerance, the fact that a multisector WSA offers less coupling between phases (of different sectors) than the aforesaid WSAs is helpful in this regard. Notwithstanding, multisector WSA exhibit some shortcomings under faults, as pointed out concerning six-phase PMSMs and IMs in [258,259,261,436], respectively: additional flux distortion, greater unbalanced radial force and larger current for the same output power under phase OCs, as well as higher torque ripple for three-phase SC fault. These disadvantages were nonetheless shown to be less relevant for a six-phase SynRM in [247].
3.1.2.5. Overlapping and Non-Overlapping Windings
Any of the aforementioned types of WSA can be performed using overlapping or non-overlapping windings, by suitably changing the coil pitch. Figure 5 illustrates the difference between these two options, for with symmetrical WSA. In particular, note that the couple of coils explicitly drawn in Figure 5a overlap in space, but those in Figure 5b do not. The winding layouts depicted in the examples in Figure 2 are also overlapping.
The specific overlapping winding shown in Figure 5a is distributed, because it has several (two) slots per pole per phase, in contrast to that in Figure 2a, which has one (known as concentrated, or concentrated full-pitch) [2,472]. When double layer is adopted, as in Figure 5a, the selection of which phase is placed in the bottom or top layer for each slot affects the values of the inductances, e.g., the mutual inductance between three-phase winding sets [473,474].
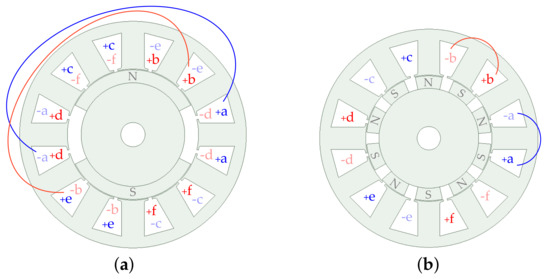
Figure 5.
Difference between overlapping and non-overlapping windings, for a six-phase machine with symmetrical WSA. (a) Overlapping. (b) Non-overlapping (namely, FSCW).
Among non-overlapping windings, fractional-slot concentrated windings (FSCWs), where each coil is wound around a single tooth, are relatively common. The number of rotor poles is usually greater or lower than the stator-slot number by 1 or 2 units [178,264,453]. In particular, the example illustrated in Figure 5b represents a single-layer 12-slot/10-pole FSCW. In a multisector FSCW, the relation between the rotor-pole and stator-slot numbers should also be studied for each sector [27].
FSCWs, especially with single layer, offer large self-inductance and high electrical, magnetic, thermal, and mechanical isolation between phases [2,232,266,472]. Consequently, FSCWs are frequently employed without electrical connection between phases (single-phase splitting, without neutral) [26,89,91,96,128,162,240,241,248,263,266,267,365]. For these reasons, FSCWs are particularly convenient when tolerance to stator SCs is sought [240,266], as will be further discussed later. Other advantages of FSCWs are, e.g., short end windings, high torque density, low cogging torque and high slot fill factor [27,220,475]. Their main drawback is the greater magnetomotive-force distortion (possibly attenuated by Halbach array magnets [241]), which can lead to, e.g., torque ripple [233], increased eddy-current losses (which can be reduced by core lamination and magnet segmentation) and high risk of magnet demagnetization (due to the temperature rise caused by these losses) [229]. Because of the air-gap flux distortion, FSCWs are normally only used in PMSMs, never in IMs [2,34,259]. In addition, FSCWs typically offer lower reluctance torque [270,476].
The difference between single- and double-layer FSCWs can be observed in Figure 6 for the same number of slots. These alternatives are also referred to as alternate-teeth-wound or all-teeth-wound FSCWs, respectively. Double-layer FSCWs provide a lower degree of isolation between phases (slots are shared), but also less magnetomotive-force distortion [233,258,398].
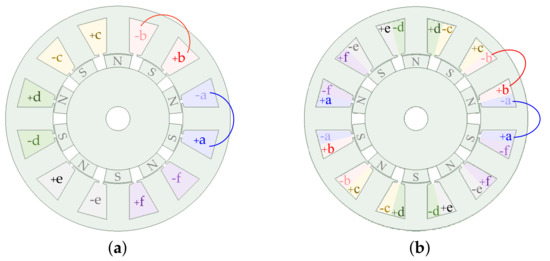
Figure 6.
Difference between single- and double-layer FSCWs, for a six-phase machine with symmetrical WSA. (a) Single layer. (b) Double layer.
In any case, FSCWs that do not follow the basic patterns shown in Figure 6 are often employed as well. For instance, when there are two coils per phase as in Figure 6b, the polarity of the coils in one half of the machine may be inverted [220], or the two coils of each phase may be placed next to each other [221]. In contrast to FSCWs, which are non-overlapping, fractional-slot overlapping windings are also possible [425,477], although much less common.
3.1.3. Stator Phase Connections
In machines with no phase splitting or with l-phase splitting of the stator, the connections between stator-phase endings can be performed in different ways. The most usual stator phase connection is star [478] with either one or neutral points. Regarding symmetrical WSA (see Figure 3a), it is possible to set different types of stator phase connections [344,389,390,478,479]. These alternatives are denoted by the variable , which indicates the series connection (ignoring the converter) of each pair of phases with a spatial step between them equal to [344,408]. In this manner, may be defined as the stator phase interconnection step. For instance, for , there are (star), (pentagon), and (pentacle) connections [141,344,389,390,408,410,411,412,428,478]. For , there are (star), (hexagon) and (double-delta) connections, as shown in Figure 7 [344,408]. In general, corresponds to no phase splitting when there is a single neutral point, and to l-phase splitting when n is composite and there are isolated neutral points. If n is composite, -phase splitting is obtained for integer with (e.g., in Figure 7c), and no phase splitting otherwise.
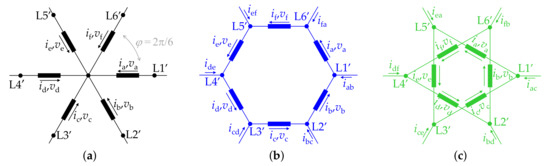
Figure 7.
Stator phase connections in a six-phase machine with symmetrical WSA [408]. (a) (star). (b) (hexagon). (c) (double delta).
In a machine with WSA other than symmetrical, besides using single-phase splitting or star connection, it may also be possible to set connections analogous to . For instance, double-delta connection could be set in a six-phase motor with asymmetrical WSA. Nonetheless, to the knowledge of the authors, these possibilities have barely been explored so far, with the exception of a multisector WSA based on three deltas [270].
Different types of stator phase connections may be combined in a single multiphase machine, as performed previously, e.g., with star/delta configurations in three-phase machines [480]. Several publications have studied the combination of star- and pentagon-connected five-phase windings in ten-phase machines [421,431,432,481]. This configuration permits obtaining a trade-off between the advantages and disadvantages of these two connection types [421] and reducing the harmonic content [421,481]. Similarly, hybrid pentacle-star five-phase connections can also yield less harmonic distortion [482]. Although these machines are intrinsically ten-phase ones, only five external terminals need to be connected [421], which means improving converter simplicity but reducing reliability concerning converter faults. Analogously, special connection types have also been devised so that other n-phase machines can be driven by converters with fewer legs than n (besides other advantages); e.g., a nine-phase six-terminal IM [355,422,430], twelve-phase six-terminal IM [426] and five-phase three-terminal PMSM [475]. Moreover, an n-phase machine with symmetrical WSA can be fully operated by an -leg converter if half of the stator phases are connected in anti-phase with the other half [229], or by just l legs in case of a no-phase-shift or multisector WSA (as aforesaid) with l-phase winding sets connected in parallel [374].
3.1.4. Literature Classification according to Machine Type and Stator Configuration
Table 4 and Table 5 classify many of the references about fault tolerance in multiphase drives depending on the studied machine types. The papers that present the theory in a general manner, for multiple n values or configurations, are, in most cases, sorted in the tables depending on the machines tested experimentally. In these tables, a dash indicates that it is unclear or does not apply. From Table 4 and Table 5, it can be stated that five- and six-phase machines have been the focus of a lot of research concerning fault tolerance. Although higher phase numbers, such as provide further enhanced fault tolerance [344], presumably the increased complexity has prevented them from a significant rise in popularity for the moment. Concerning the rotor type, IMs and PMSMs are predominant in this context. Regarding the stator phase connections and splitting, it can be seen in Table 4 and Table 5 that stator windings connected in star (), either with three-phase or no splitting, as well as those independently driven (single-phase splitting), are particularly usual in fault-tolerant multiphase drives. Symmetrical and asymmetrical are the most widely-spread WSAs, followed by multisector WSA, whereas no-phase-shift WSA is barely taken into account. Machines either with FSCWs (mainly PMSMs) or without FSCWs are common. Although FSCWs are considered for asymmetrical WSAs in some cases, in the literature concerning fault tolerance FSCWs are used more often in multisector WSAs and, mostly, in symmetrical WSAs.

Table 4.
Classification of references about fault tolerance in multiphase drives according to the type of machine and stator configuration (Section 3.1), for .
Table 4.
Classification of references about fault tolerance in multiphase drives according to the type of machine and stator configuration (Section 3.1), for .
| n | WSA | FSCW | Splitting | Rotor | References | |
|---|---|---|---|---|---|---|
| 4 | Sym. | No | No | 0 | IM | [310] |
| 4 | Sym. | Yes | 1-ph. | − | PMSM | [163,165,228,239,266] |
| 4 | Sym. | Yes | No | 0 | PMSM | [232] |
| 5 | Sym. | No | 1-ph. | − | IM | [193,194,362,406,451] |
| 5 | Sym. | No | 1-ph. | − | PMSM | [273,403] |
| 5 | Sym. | No | No | 0 | IM | [9,41,69,114,115,116,138,142,150,151,152,153,189,190,202,218,253,310,317,318,319,320,321,322,323,324,325,326,327,328,329,410,411,427,428,429] |
| 5 | Sym. | No | No | 0 | PMaSynRM | [84,104,309,404,483] |
| 5 | Sym. | No | No | 0 | WFSM | [416] |
| 5 | Sym. | No | No | 1 | IM | [410,411,412,428] |
| 5 | Sym. | No | No | 1 | WFSM | [416] |
| 5 | Sym. | No | No | − | PMaSynRM | [423] |
| 5 | Sym. | No | No | 0 | PMSM | [8,68,76,77,78,86,105,106,136,141,200,201,208,216,217,249,250,251,252,333,383,384,385,386,387,388,389,390,391,392,393,394,395,396,400,402,414,440,448] |
| 5 | Sym. | No | No | 1 | PMSM | [141,389,390] |
| 5 | Sym. | No | No | 2 | PMSM | [141,390] |
| 5 | Sym. | Yes | 1-ph. | − | PMSM | [89,90,91,95,127,130,133,162,163,164,187,226,227,233,234,241,248,263,264,267,268,304,363,365,444,445] |
| 5 | Sym. | Yes | 1-ph. | − | Hybrid excit. | [94] |
| 5 | Sym. | Yes | No | 0 | PMSM | [59,92,102,111,117,118,119,166,219,232,254,255,256,257,262,357,358,359,360,361,366,367,379,380,381,397,398,446,447] |
| 5 | Sym. | Yes | − | − | PMSM | [209,297,442] |
| 5 | Sym. | − | No | 0 | PMSM | [57,107,108,110,175,181,186,369,370,371] |
| 5 | Sym. | − | No | 0 | RL load | [149,155,159] |
| 5 | Sym. | − | No | 0 | − | [148] |
| 5 | Sym. | − | − | − | PMSM | [182,291,295] |
| 6 | Asym. | No | 1-ph. | − | IM | [415] |
| 6 | Asym. | No | 3-ph. | 0 | IM | [80,81,82,83,112,113,126,131,132,143,144,145,146,156,157,158,161,173,202,203,204,205,206,207,261,310,311,312,334,335,336,337,338,339,340,341,342,343,433,434,435,436] |
| 6 | Asym. | No | 3-ph. | 0 | PMSM | [28,58,63,64,65,70,71,72,73,74,75,87,88,103,109,134,135,137,154,170,171,176,177,179,276,277,278,279,280,281,282,283,284,285,286,287,288] |
| 6 | Asym. | No | 3-ph. | 0 | SynRM | [247] |
| 6 | Asym. | No | 3-ph. | 0 | WFSM | [15,417,454] |
| 6 | Asym. | No | No | 0 | IM | [144,213,214,310,311,312,334,341,342,343,382,433,434,435,437,438] |
| 6 | Asym. | No | No | 0 | PMSM | [137,170,171,313,314,315,356] |
| 6 | Asym. | No | No | Other | PMSM | [372] |
| 6 | Asym. | No | Other | Other | IM | [413] |
| 6 | Asym. | No | − | − | PMSM | [368] |
| 6 | Asym. | Yes | 1-ph. | − | PMSM | [220] |
| 6 | Asym. | Yes | 3-ph. | 0 | PMSM | [215,258,259,419] |
| 6 | Asym. | Yes | No | 0 | PMSM | [351] |
| 6 | Asym. | − | 3-ph. | 0 | PMSM | [121,122,125,139,191,192,299,300] |
| 6 | Asym. | − | No | 0 | PMSM | [347,348,349] |
| 6 | Multisec. | No | 3-ph. | 0 | IM | [261,418,436] |
| 6 | Multisec. | No | 3-ph. | 0 | PMSM | [179,230,305] |
| 6 | Multisec. | No | 3-ph. | 0 | SynRM | [247,450] |
| 6 | Multisec. | No | − | − | PMSM | [425] |
| 6 | Multisec. | Yes | 3-ph. | 0 | PMSM | [56,215,246,258,259,346] |
| 6 | Multisec. | Yes | No | 0 | PMSM | [346] |
| 6 | No-ph. | No | 3-ph. | 0 | IM | [312,424] |
| 6 | No-ph. | No | 3-ph. | 0 | PMSM | [169,316] |
| 6 | No-ph. | No | No | 0 | IM | [312] |
| 6 | No-ph. | − | No | 0 | PMSM | [302] |
| 6 | Sym. | No | 1-ph. | − | IM | [271] |
| 6 | Sym. | No | 3-ph. | 0 | IM | [62,79,82,202,312,344,377,407,408] |
| 6 | Sym. | No | 3-ph. | 0 | SynRM | [308] |
| 6 | Sym. | No | 3-ph. | 2 | IM | [344,408] |
| 6 | Sym. | No | No | 0 | IM | [120,123,172,261,275,292,312,344,377,436] |
| 6 | Sym. | No | No | 0 | PMSM | [331] |
| 6 | Sym. | No | No | 0 | SynRM | [308] |
| 6 | Sym. | No | No | 1 | IM | [344,408] |
| 6 | Sym. | No | Other | Other | PMSM | [13,14,345] |
| 6 | Sym. | No | − | 0 | IM | [293,294] |
| 6 | Sym. | No | − | − | PMSM | [297] |
| 6 | Sym. | Yes | 1-ph. | − | PMSM | [93,96,99,128,163,210,211,212,223,240,265] |
| 6 | Sym. | Yes | 3-ph. | 0 | PMSM | [100,101,215,222,229,230,258,259,260,265,419] |
| 6 | Sym. | Yes | No | 0 | PMSM | [101,232,330] |
| 6 | Sym. | Yes | − | − | Hybrid excit. | [178] |
| 6 | Sym. | Yes | − | − | PMSM | [221,225,231,441] |
| 6 | Sym. | − | 1-ph. | − | PMSM | [13] |

Table 5.
Classification of references about fault tolerance in multiphase drives according to the type of machine and stator configuration (Section 3.1), for .
Table 5.
Classification of references about fault tolerance in multiphase drives according to the type of machine and stator configuration (Section 3.1), for .
| n | WSA | FSCW | Splitting | Rotor | References | |
|---|---|---|---|---|---|---|
| 7 | Sym. | No | No | 0 | IM | [66,67,160,183,184,185,197,296,310,350] |
| 7 | Sym. | No | No | 0 | PMSM | [174,289,375,376] |
| 9 | Asym. | No | 3-ph. | 0 | IM | [353,354] |
| 9 | Asym. | No | 3-ph. | 0 | PMSM | [22,137] |
| 9 | Asym. | No | 3-ph. | 0 | WFSM | [454] |
| 9 | Asym. | No | No | 0 | PMSM | [137,301] |
| 9 | Asym. | No | No | Other | IM | [355,422,430] |
| 9 | Asym. | No | Other | Other | PMSM | [301] |
| 9 | Multisec. | No | 3-ph. | 0 | PMaSynRM | [97,98,129,167,224,235,236,237,238,242,243,244,245,270] |
| 9 | Multisec. | No | 3-ph. | 0 | PMSM | [61,124,180,195,196,443] |
| 9 | Multisec. | No | 3-ph. | 1 | PMaSynRM | [270] |
| 9 | Multisec. | No | No | 0 | PMaSynRM | [374] |
| 9 | Multisec. | Yes | 3-ph. | 0 | PMSM | [409] |
| 9 | Sym. | No | 1-ph. | − | IM | [274] |
| 9 | Sym. | No | 3-ph. | 0 | IM | [140,269,352] |
| 9 | Sym. | No | 3-ph. | 0 | PMSM | [439] |
| 9 | Sym. | No | No | 0 | IM | [60,290,298,332,352,449] |
| 9 | Sym. | No | No | 0 | PMSM | [198,199] |
| 9 | Sym. | No | − | − | PMSM | [188] |
| 9 | Sym. | Yes | 3-ph. | 0 | PMSM | [147] |
| 10 | Asym. | No | No | Other | IM | [421,431,432] |
| 10 | Sym. | Yes | 1-ph. | − | PMSM | [272] |
| 10 | − | No | 5-ph. | 0 | IM | [405] |
| 11 | Sym. | No | No | 0 | IM | [399] |
| 12 | Asym. | No | 3-ph. | 0 | IM | [373,378,401] |
| 12 | Asym. | No | 6-ph. | 0 | IM | [373] |
| 12 | Asym. | No | No | 0 | IM | [373] |
| 12 | Asym. | Yes | 3-ph. | 0 | PMSM | [420] |
| 12 | Multisec. | Yes | 3-ph. | 0 | PMSM | [168] |
| 12 | Multisec. | Yes | 2-ph. | Other | PMSM | [364] |
| 12 | Sym. | No | 3-ph. | 0 | PMSM | [143] |
| 12 | Sym. | No | 3-ph. | 4 | PMSM | [344] |
| 12 | Sym. | No | 4-ph. | 3 | PMSM | [344] |
| 12 | Sym. | No | 6-ph. | 2 | PMSM | [344,408] |
| 12 | Sym. | No | No | 0 | PMSM | [344,408] |
| 12 | Sym. | No | No | 1 | PMSM | [344,408] |
| 12 | Sym. | No | No | 5 | PMSM | [344] |
| 12 | Sym. | Yes | 3-ph. | 0 | PMSM | [306] |
| 12 | − | No | 6-ph. | Other | IM | [426] |
| 12 | − | No | No | Other | IM | [426] |
| 15 | Asym. | Yes | 5-ph. | 0 | PMSM | [303] |
| 18 | Multisec. | No | 3-ph. | 0 | PMSM | [307] |
| 24 | Multisec. | Yes | 3-ph. | 0 | PMSM | [27] |
3.2. Types of Multiphase Voltage-Source-Converter (VSC) Topologies
Multiphase machines offer the advantage that they are able to work under faults (e.g., OCs) in certain phases with a conventional two-level n-phase half-bridge (HB) VSC topology (see Figure 8a), as for healthy drive. Nevertheless, sometimes they are driven by other types of VSCs, either to further increase the postfault performance or to obtain additional features for certain applications. Many of the VSC schemes found in fault-tolerant multiphase drives are illustrated in Figure 8 and Figure 9, which correspond to non-modular and modular VSCs, respectively. The literature on the subject is classified accordingly in Table 6. The ideal voltage sources shown in Figure 8 and Figure 9 could be replaced by loads or other elements, depending on the application. The possibility of reconfiguring the VSC topology after faults (e.g., by extra bidirectional switches) is ignored for the moment; it will be addressed later.
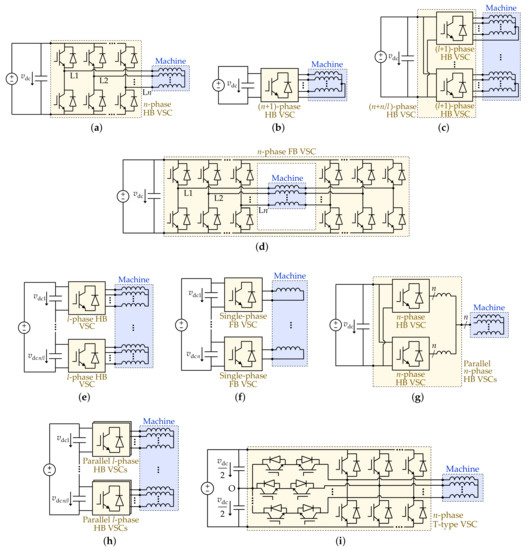
Figure 8.
VSC non-modular topologies in multiphase ac drives, ignoring postfault reconfiguration. (a) Single n-phase HB VSC. (b) Single (n+1)-phase HB VSC. (c) Single (n+)-phase HB VSC. (d) Single n-phase FB VSC for open-end windings. (e) Series dc-side connection of l-phase HB VSCs. (f) Series dc-side connection of single-phase FB VSCs. (g) Parallel n-phase HB VSCs. (h) Series dc-side connection of parallel l-phase HB VSCs. (i) Single n-phase T-type three-level VSC.
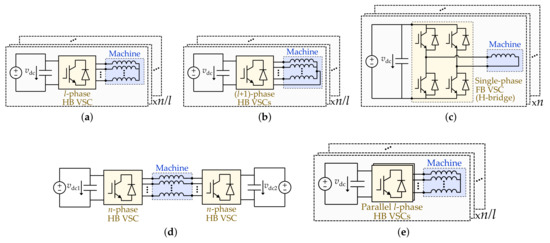
Figure 9.
VSC modular topologies in multiphase ac drives, ignoring postfault reconfiguration. (a) Multiple independent l-phase HB VSCs. (b) Multiple independent (l+1)-phase HB VSCs. (c) Multiple independent single-phase FB VSCs (H-bridges). (d) Dual n-phase HB VSC for open-end windings. (e) Multiple independent parallel l-phase HB VSCs.
A slight variant of the traditional configuration from Figure 8a is the HB VSC with one additional leg, which is connected to the stator neutral point, as shown in Figure 8b in order to obtain an extra (zero-sequence) current DOF [361]. Evidently, the single n-phase VSC from Figure 8a is also suitable for feeding machines with certain stator phase splitting, such as stars of l phases, [312,343]. This implies fewer current DOFs, which, in turn, also means, e.g., simpler current control and better dc-link utilization [312]. If other VSC legs are included, for providing connections (current paths) to the respective neutral points, a single HB VSC of n+ phases (legs) results [303], which is represented in Figure 8c.
As briefly mentioned in Section 2, some of the typical topologies in multiphase machines are the ones composed of multiple three-phase HB VSCs or multiple single-phase full-bridge (FB) VSC (i.e., H-bridges) using separate dc links, which are depicted in Figure 9a and Figure 9b, respectively. It can be seen in Table 6 that these topologies are in fact some of the most popular ones, other than using a single n-phase HB VSC. Note that, in Figure 9a, l is used instead of 3 for generality. Even though using two VSC legs per phase (as in FB VSCs) instead of one implies doubling the number of switches, in the former scenario each of them needs to withstand lower voltage [240]. Adopting an FB VSC also enables the circulation and control of zero-sequence current. Nonetheless, the scheme from Figure 9a can be slightly modified so that the VSC modules have legs, including connections (zero-sequence current paths) to the stator neutral points, as shown in Figure 9b [236,346].
When both terminals of each stator phase of the machine are available (open-end windings), besides the aforementioned possibility of using independent H-bridges, it is also common to employ an n-phase FB VSC with single dc link (see Figure 8d), or to supply each winding side by a separate n-phase HB VSC (see Figure 9d). The former allows a zero-sequence current DOF, whereas the latter makes it possible to synthesize the phase voltages by using more steps, thus reducing the current ripple and the dv/dt [413]. From Table 6, using a single FB VSC is a widely-spread solution for .

Table 6.
Classification of references about fault tolerance in multiphase drives according to the VSC topology (Section 3.2), ignoring postfault reconfiguration.
Table 6.
Classification of references about fault tolerance in multiphase drives according to the VSC topology (Section 3.2), ignoring postfault reconfiguration.
| VSC Topology | Figure | n | References |
|---|---|---|---|
| Single n-phase HB diode rectifier | 8a * | 5 | [57,295,416] |
| Single n-phase HB diode rectifier | 8a * | 6 | [454] |
| Single n-phase HB VSC | 8a | − | Most of the others. |
| Single (n+1)-phase HB VSC | 8b | 5 | [361] |
| Single (n+)-phase HB VSC | 8c | 15 | [303] |
| Single n-phase FB VSC for open-end windings | 8d | 5 | [91,94,128,133,193,248,263,267,362,363,403,406] |
| Single n-phase FB VSC for open-end windings | 8d | 6 | [13,28,234,364,451] |
| Single n-phase FB VSC for open-end windings | 8d | 10 | [272] |
| Series dc-side connection of 3-phase HB diode rectifiers | 8e * | 6 | [417] |
| Series dc-side connection of 3-phase HB diode rectifiers | 8e * | 9 | [454] |
| Series dc-side connection of 3-phase HB VSCs | 8e | 9 | [409] |
| Series dc-side connection of 1-phase FB VSCs | 8f | − | [54] |
| Parallel 6-phase HB VSCs | 8g | 6 | [341] |
| Series dc-side connection of parallel 3-phase HB VSCs | 8h | 6 | [340] |
| Single n-phase T-type three-level VSC | 8i | 6 | [103,276,277,279] |
| Multiple independent 3-phase HB VSCs | 9a | 6 | [56,173,215,222,230,265,305,436] |
| Multiple independent 3-phase HB VSCs | 9a | 9 | [61,97,98,167,180,224,235,238,242,243,244,245,353,439,443] |
| Multiple independent 3-phase HB VSCs | 9a | 12 | [168] |
| Multiple independent 3-phase HB VSCs | 9a | 18 | [307] |
| Multiple independent 3-phase HB VSCs | 9a | 24 | [27] |
| Multiple independent (l+1)-phase HB VSCs | 9b | 6 | [346] |
| Multiple independent (l+1)-phase HB VSCs | 9b | 9 | [236] |
| Multiple independent 1-phase FB VSCs (H-bridges) | 9c | 4 | [165,228,266] |
| Multiple independent 1-phase FB VSCs (H-bridges) | 9c | 5 | [89,95,130,162,164,233,264,304] |
| Multiple independent 1-phase FB VSCs (H-bridges) | 9c | 6 | [93,96,99,210,211,212,223,227,240,265,271] |
| Dual n-phase HB VSC for open-end windings | 9d | 5 | [194,273] |
| Dual n-phase HB VSC for open-end windings | 9d | 6 | [220] |
| Multiple independent parallel 3-phase HB VSCs | 9e | 6 | [339,340] |
| 3-phase HB VSC + 3 phase FB VSC | − | 6 | [413] |
| 5-phase HB VSC + 5-phase HB diode rectifier | − | 10 | [405] |
An interesting, although less usual, multiphase topology is that based on series connection of the dc links of several three-phase VSCs (see Figure 8e) [409,484]. This can be particularly attractive for off-shore wind farms using a high-voltage dc connection, allowing the use of generators and semiconductors with reduced voltage rating and avoiding bulky grid-side transformers [409,484]. Another application is generation for medium-voltage electrical distribution in ships [454]. A variant of this configuration is illustrated in Figure 8f, where each of the VSCs is a single-phase FB [54].
An n-phase machine may be supplied by two n-leg HB VSCs in parallel using interfacing inductors, as in Figure 8g. This is not only advantageous in terms of fault tolerance to converter faults (due to redundancy), but also regarding the required switch current rating, which is thereby reduced [340]. This feature can be very appropriate for high-power applications [340]. Furthermore, interleaving PWM can be implemented in the parallel VSCs to decrease current harmonics [485]. Although there are other topologies based on installing redundant legs connected in parallel [275,465], in those ones the extra legs are not used during normal operation (lacking the associated benefits), and postfault reconfiguration is applied by means of additional bidirectional switches.
Analogously, each of the l-phase VSCs in the topologies from Figure 8e and Figure 9a may be replaced by parallel l-phase VSCs (see Figure 8f and Figure 9e), as in [340].
In addition to the phase redundancy offered by multiphase drives, switch state redundancy can be achieved/increased by adopting a multilevel VSC [465]. (Switch state redundancy means that certain output voltage SVs can be obtained by more than one possible combination of switching states [465].) This is particularly convenient in the face of switch failures. The fault tolerance of T-type three-level VSCs (see Figure 8i) has been addressed in some publications [103,276,277,279], where this capability is exploited. However, to the authors’ knowledge, fault tolerance in other multiphase multilevel topologies has not been tackled in detail so far. Multiphase diode neutral-point-clamped VSCs are briefly considered for diagnosis of switch OCs in [115] and for tolerance of phase OCs in [47,288,371], but the switch state redundancy is not exploited for tolerating switch faults. Throughout this paper, the multiphase machines are assumed to be supplied by two-level VSCs, unless the opposite is explicitly mentioned. Nevertheless, the majority of the available methods for tolerating faults other than switch failures are equally valid regardless of the VSC number of levels.
Many of these VSC topologies are suitable for special drive configurations, such as multimotor drives, where several machines are controlled by a single VSC. In particular, Moraes et al., present a method for diagnosis of OC faults for a six-phase two-motor drive fed by a six-phase FB VSC [14]. Later, they compare, in [13], the fault tolerance of a drive comprising two six-phase machines depending on whether it is based on two six-phase FB VSCs sharing a dc link (no connection between phases of different machines) or a six-phase FB VSC (connecting the phases of both machines in series). Control strategies for tolerating phase OCs have also been proposed for drives composed of a six-leg HB VSC and two synchronous machines with their stator phases in series: a six-phase and a three-phase one in [345], and two six-phase ones in [15]. The tolerance to open-phase faults of a multisector nine-phase PMaSynRM fed by a single three-leg HB VSC is studied in [374]. The fault-tolerant topology devised in [364] may also be mentioned, where a six-phase FB VSC is employed for an integrated battery charger using a six-phase machine with open-end windings and an unconventional kind of connection among the stator phases.
There are also some other types of VSC setups without postfault reconfiguration in fault-tolerant multiphase drives that are not reflected in Figure 8 and Figure 9. For instance, for a machine with various winding sets, different kinds of VSCs can be employed for each of them; e.g., in [413] a three-phase HB VSC is used for one set and an FB VSC for the other one. In [415], for the HB VSC at one of the sides of Figure 9d is split into two three-phase ones, with separate dc links. The tolerance to phase OCs of an induction generator composed of two five-phase stars, with one star excited by an HB PWM inverter and another one feeding an HB diode rectifier, is addressed in [405]. On the other hand, other VSC topologies [101,171,239,274,275,316,343,346,372,408,411,413,465] rely to a great extent on postfault reconfiguration and they will hence be discussed later.
Concerning other aspects of VSC technology, it may be pointed out that some of the fault-tolerant multiphase drives in the literature consist of VSCs integrated in the machines [27,306] or are based on wide-bandgap devices [306].
Finally, it is worth mentioning that an interesting multiphase topology based on legs and series connection of the end windings has recently been proposed by Li et al., in [486]. Essentially, it is based on setting but splitting one of the series phase connections so that two VSC legs instead of one are used for the corresponding pair of stator terminals. However, its fault tolerance is yet to be studied.
3.3. General Vector Space Decomposition (VSD) for Multiphase Drives
The VSD is commonly employed to transform the electrical variables of the machine and VSC to a set of subspaces with much clearer physical meaning and decoupling. A stator electrical variable u (voltage or current), expressed as an array of per-phase values, can be transformed to a VSD - subspace as [214,313]
where T means transpose and denotes the angle in electrical radians corresponding to each stator phase with respect to a common reference (see Figure 3). For instance, for with asymmetrical WSA (see Figure 3c): , , , , , and . The gain in (1) keeps the current and voltage amplitude after the transformation; it can be replaced by to maintain instead the power/torque values without readjusting the power/torque formulas as a function of n.
The machine model in the - subspace describes the behavior related to the space harmonic of order h, which can be positive or negative depending on the direction of rotation. In particular, the fundamental magnetomotive-force component is ideally given only by the stator current in the - plane. Moreover, if voltages/currents are balanced, each time harmonic order h is also mapped into a certain subspace in accordance with (1) [214,487,488]. (For a given multiphase machine, balanced means that the voltage/current waveform has the same shape in all stator phases, but in each phase being shifted in time by the time interval that corresponds to the fundamental component according to Figure 3.)
The complete VSD transform is obtained differently depending on the WSA. Let us consider first symmetrical and asymmetrical WSAs. Customarily, odd h values from 1 up to are used in (1) for asymmetrical WSA, and both odd and even h values from 0 to for symmetrical WSA [214]. For h higher than these, the same subspaces are obtained in (1) as for lower h, and, thus, they can be ignored when deriving the VSD transform. The rows resulting from (1) for said h values can be combined into an n x n VSD transform. The subspaces corresponding to and in symmetrical WSA, or to and in asymmetrical WSA, represent the zero sequences. For all these zero sequences except for asymmetrical WSA, one of the two dimensions in (1) becomes null, and the two factors in the gain should be removed from (1) [214]. The zero sequence corresponding to the case of having the same signal in all phases is often denoted by [1]. The VSD subspaces other than zero sequences and - plane are frequently called secondary [34,109,126,319,341,434,435,489], x-y [1,2,142,143,435] or no-torque [142,143,487] planes.
If non-linear effects, such as saturation [490] and rotor-slot harmonics [202], are neglected during healthy operation, the VSD subspaces from (1) are decoupled (orthogonal), except in one particular case: asymmetrical WSA with single neutral point, where certain cross-coupling is present between planes, such that [488]. Coupling between VSD subspaces due to faults is addressed later. In any case, even if there is VSD cross-coupling between current/voltages, the VSD mapping of space (not time) harmonics normally still obeys (1), unless there are, e.g., stator SC (not OC) faults that alter the spatial winding distribution.
In no-phase-shift and multisector WSAs, all odd and even harmonic orders are mapped into a reduced number of VSD subspaces, with dimensions lower than the actual number of DOFs (i.e., n). Hence, when deriving the complete VSD transform, other specific transformations different from (1) may be defined in those cases for DOFs not included in (1) that do not correspond to any balanced integer order harmonic. For instance, the sequence of the angles associated with some of the winding sets/sectors can be inverted in (1) for these other DOFs [312].
Alternatively, in machines with l-phase splitting, instead of (1) sometimes it is preferred to use the same VSD as for an l-phase machine for each l-phase set, regardless of the WSA. This is especially common [but not as much as (1)] for 3-phase splitting, because of the well-consolidated three-phase technology [353]. Decoupling terms may be added to achieve independent control of each l-phase winding [173,353], although this is not necessary when magnetic coupling between them can be disregarded (e.g., with FSCWs) [409]. Nonetheless, for the explanations through this paper it is assumed that the general VSD is employed instead, unless the opposite is explicitly mentioned.
For simplicity, it is often assumed that all winding space harmonics other than are negligible, i.e., that the windings are sinusoidally distributed [24]. In that case, only - involves electromechanical conversion. In practice, especially for single-layer windings and low slot-per-pole-per-phase values, there are certain non-negligible space harmonics. Thus, a more realistic assumption is to consider that there is one space harmonic per VSD subspace (at least where odd h exist) while using (1) [7,174,289,296,375,376,433], at the expense of less generality and extra complexity. However, in case torque ripple or other effects associated with higher-order space harmonics are to be studied, several space harmonics per subspace need to be considered [214,491]. Moreover, VSD can also be applied to the rotor of IMs to take into account the behavior of each harmonic in the rotor; in particular, for squirrel-cage rotors, each bar may be considered as a rotor phase [214,491,492].
The electromagnetic flux and torque are obtained by the interaction between the current (time) harmonics and space harmonics within the same VSD subspace [491]. In general, for a given subspace, current and space harmonics generate average torque if they are of the same order and sequence (positive/negative), and otherwise they cause torque ripple [2]. Nevertheless, even if a certain current component is mapped into a VSD subspace where no space harmonics exist, it produces SCL, decreasing the drive efficiency [487,493,494].
In subspaces where current can flow, other than -, the impedance is often much lower than in -. This is especially true if the windings are distributed very sinusoidally, because then the impedance in these secondary subspaces is only given by the stator resistance and stator leakage inductance. Although in presence of space harmonics in the secondary subspaces there is certain coupling with the rotor and hence higher impedance, it is still considerably lower than in the plane of the fundamental component. Hence, even small voltage components can produce undesired large currents that need to be taken into account and/or compensated [139,143,202,487,488,493,494].
It may also be remarked that the VSD matrix is closely related to the symmetrical components (or Fortescue) one, which additionally is able to separate the positive and negative sequences within each plane, provided complex inputs are employed [11].
4. High-Resistance Connections
This kind of problem means that there is an unusually large value of resistance in one or several phases. If no proper measures are taken, this condition may lead to torque ripple and more severe faults, such as phase OCs or even SCs between conductors or to the ground [66,67]. The main causes, detection methods and tolerance approaches regarding high-resistance connections are illustrated in Figure 10.
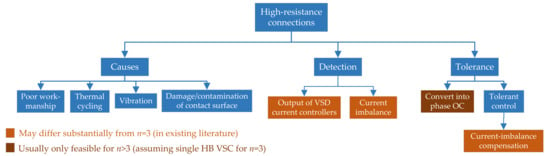
Figure 10.
Causes, detection methods, and tolerance approaches for high-resistance connections in multiphase drives.
4.1. Causes of High-Resistance Connections
Some of the reasons that can produce high-resistance connections are damage or contamination of the contact surfaces (e.g., oxidization), vibration, thermal cycling, and poor workmanship [61,66].
4.2. Detection of High-Resistance Connections
Detection of high-resistance connections is usually based on calculating the degree of stator electrical dissymmetry, either in terms of voltage or current imbalance, and checking whether a certain threshold is surpassed. Broadly speaking, in case there is closed-loop current control ensuring zero steady-state current error at the VSD components affected by the imbalance, the detection algorithms rely on the voltage references (current-control output) [65,66,67,68]. Otherwise, if there is no current control with said capability, they normally monitor the dissymmetry of the measured currents [59,62,63,69]. As an exception, the methods focused on the zero sequence/s are based on measuring the zero-sequence voltage, provided the corresponding current cannot flow (isolated neutral points) [61]. These statements are in agreement with the summary of detection techniques and their properties displayed in Table 7. It can also be distinguished between the detection approaches that employ a single fault index [65] or those that use several [59,61,63,66,67,68,69]. Computing various indices instead of one allows identifying the particular phase/s [59,63,66,67,68,69], or at least the specific winding set [61], that has extra resistance. In exchange, this implies some additional complexity. In the following, these strategies are explained in more detail, following roughly the order in Table 7.

Table 7.
Methods for detecting high-resistance connections (Section 4) in multiphase applications in the literature.
Table 7.
Methods for detecting high-resistance connections (Section 4) in multiphase applications in the literature.
| References | Machine | Current Control | Monitored Signals | x-y Current Ref. | Finds Fault Location | Needs Extra * Sensors | Diagnoses Other Faults | Smooth Postfault Torque | ||
|---|---|---|---|---|---|---|---|---|---|---|
| n | WSA | Rotor | ||||||||
| Rossi et al. [65] | 6 | Asym. | SPMSM | - & x-y rotating PI | x-y voltage | 0 | No | No | No | Yes |
| Zarri et al. [66,67] | Odd | Sym. | IM | - & x-y rotating PI | - & x-y voltage | 0 | Phase | No | No | Yes |
| Tani et al. [68] | 5 | Sym. | SPMSM | - & x-y rotating PI | x-y voltage | 0 | Phase | No | Demagn. | Yes |
| Salas-Biedma et al. [69] | 5 | Sym. | IM | - DTC | - & x-y current | − | Phase | No | Phase OC | Yes |
| Farag et al. [62] | 6 | Sym. | IM | - & x-y current | - & x-y current | − | Phase | No | Ph. OC, bars | − |
| Chen et al. [59] | 5 | Sym. | SPMSM | - rotating PI | - & x-y current | − | Phase | No | No | No |
| Gonçalves et al. [63,64] | 6 | Asym. | SPMSM | - & x-y predictive | x-y current | Any | Phase | No | Phase OC | No |
| Hu et al. [61] | 9 | 3-sect. | PMaSynRM | Rotating PI per star | Zero-seq. voltage | 0 | Set | Voltage | Turn SC | No |
| Sun et al. [60] | Any | As./sym. | Any | - rot. PI & x-y PI | Phase dc voltage | dc | Phase | Voltage | Overheat. | No |
* In addition to usual stator-current sensors.
Rossi et al., address in [65] the case of six-phase surface-mounted PMSMs (SPMSMs) with asymmetrical WSA in the presence of harmonic disturbances. Namely, it is proposed to monitor the amplitude of either the fundamental positive- or negative-sequence voltage-reference component in the - (x-y) plane to detect dissymmetry events. However, this technique cannot establish which phases offer greater resistance. Conversely, in [66,67], Zarri et al., suggest identifying the affected phase/s by computing certain combinations of the VSD unbalanced fundamental voltage references (PI outputs) in IMs with symmetrical WSA and any odd phase number. The main difference between [66,67] is that the extended method in the latter is able to identify the phases with imbalance also in case they are several. A similar approach is presented by Tani et al., in [68], but this one also detects magnet-demagnetization faults, by monitoring other frequency components of the control output at the same time.
However, since these techniques [65,66,67,68] rely on the voltage references imposed by closed-loop control to ensure zero current, they cannot be applied to most of the so-called reconfigurationless fault-tolerant controllers (discussed in Part 2), which do not include closed loops in the secondary VSD subspaces (to avoid postfault reconfiguration) [323,335,336,337,338]. Diagnosis of high-resistance connections can be effectively attained with said control strategies by monitoring certain relations (indices) between the VSD stator currents, as performed by Salas-Biedma et al., in [69]. When resistance imbalance arises, the x-y current increases, making it possible to identify the faulty phase/s. In such conditions, the uncompensated x-y current and associated SCL may decrease the efficiency, but the torque is still smooth, provided space harmonics are negligible. Analogous indices are employed in [62] for a symmetrical six-phase IM, where phase OCs and broken rotor bars are diagnosed as well, although no details about the type of control are given.
An alternative current-based solution is devised by Chen et al., in [59] for five-phase PMSMs, under the assumption that the balanced fundamental current component is the only one controlled (by PI blocks) with zero steady-state error. That is, not only the current in the secondary subspaces is actually left uncontrolled, but also the negative-sequence - fundamental current. Consequently, some torque pulsation due to this current has to be accepted with this technique when the fault occurs, even if space harmonics are disregarded. Nevertheless, concerning the advantages of this method in comparison with previous ones, the authors of [59] claim that the one from [67] is complex when detecting high resistance in multiple phases.
On the other hand, if current references different from zero are set for components other than the balanced fundamental one (so as to exploit the extra DOFs), most of the aforesaid detection approaches are no longer valid. A diagnosis method suitable for high-resistance connections and phase-OC faults in such a scenario for six-phase PMSMs with asymmetrical WSA is proposed by Gonçalves et al., in [63]. It is based on monitoring the amplitudes of the unbalanced fundamental current errors, while running predictive current finite-control-set MPC (FCS-MPC). As a shortcoming, these uncompensated currents are expected to cause torque oscillations. This approach is enhanced in [64] so that the increased resistance is estimated and smaller resistance imbalance may be detected. A variant based on monitoring the deviation from the currents predicted by the healthy machine model is also presented in [64].
An entirely different technique is presented by Hu et al. [61]. In said paper, attention is brought to the fact that stator SC faults (in particular, turn SCs) also cause resistance dissymmetry, and, hence, special care should be devoted to distinguish between turn SC and high-resistance connections. The method is tested in a multisector nine-phase PMaSynRM with three independent three-phase windings. It is proposed to measure the (zero-sequence) voltage between the neutral of each three-phase winding and the neutral of an additional star-connected three-phase resistor network of high impedance. When turn SC or high-resistance connections arise in a certain winding set, the zero-sequence fundamental voltage increases triggering the alarm, and the type of fault is identified by exploiting the fact that the zero-sequence high-frequency voltage only rises substantially for turn SC. As reflected in Table 7, the most important disadvantage of this method in comparison with the other ones is the fact that extra hardware (including one voltage sensor per star) is required. Moreover, torque ripple is also obtained in this case, unless the controller is reconfigured afterward. It may also be pointed out that, among the methods shown in Table 7, this is the one that could be most easily applied to a conventional three-phase machine.
Finally, concerning the procedure proposed by Sun et al. [60], it can be noted that, although it is mainly considered in the context of overheating prevention (later discussed in Section 10), such a method could also be applied for detecting high-resistance connections [60]. The per-phase resistance is estimated by injecting dc current into the x-y planes and sequentially measuring the voltage drop across each stator phase. Although the dc injection does not generate torque oscillations, the - current imbalance caused by resistance dissymmetry is not compensated. Further details about this technique are given in Section 10.2.
4.3. Tolerance to High-Resistance Connections
When this type of situation is detected, the maintenance personnel should be informed so that the connections are checked and fixed when feasible [66,67]. In the meantime, it is possible to continue driving the machine with undisturbed performance (avoiding torque ripple) by using a control technique able to compensate the current imbalance. This can be completed, e.g., by means of proportional-integral (PI) controllers rotating in both positive- and negative-sequence directions in each VSD subspace with fundamental frequency, as in [65,66,67,68], similarly to what is often applied under phase OC faults (discussed in Part 2) [296,311]. The DTC method adopted in [69], which was originally proposed in [323], also provides smooth torque in presence of resistance dissymmetry. This discussion is consistent with the last column of Table 7.
The high-resistance connections imply that some phase voltages have to be raised to impose the same current references. If this effect is very pronounced, it might result in overmodulation and, hence, in harmonics and torque ripple, unless special precautions are taken (see Section 8).
These control methods [65,66,67,68,69] (see Table 7) for preventing torque pulsation under resistance dissymmetry in principle do not need reconfiguration after high resistances arise: they can be implemented in such a manner also for healthy operation, and they work satisfactorily both in the presence and absence of resistance imbalance. This differs from the scenario of OCs, where the current references and the number of controlled DOFs are usually modified after the failure, except in the recent reconfigurationless techniques (such as [69], which avoids torque ripple without modifications under high resistances or phase OCs). Nonetheless, even though avoiding torque oscillations during high-resistance connections without identifying the affected phase/s is easier than for phase OC faults, it can still be of interest to alter the current references so as to maximize the efficiency, as proposed by Hang et al. [175] (using hysteresis control), analogously to the so-called minimum-loss strategy (MLS) for phase OCs [24,311,312].
In any case, since continued operation with high-resistance connections may lead to more serious failures, such as SCs [66,67], a more conservative decision is to set in OC the affected phase/s as for switch SC faults (e.g., by opening extra bidirectional switches), and then to apply tolerant strategies suitable for phase OC faults (surveyed in Part 2), until the deficient connections are fixed.
4.4. Concluding Remarks about High-Resistance Connections
From the preceding discussion, it can be concluded that most of the available methods for detecting high-resistance connections in multiphase drives are based, without extra hardware, on monitoring the current-measurement [59,62,63,64,69] or voltage-reference [65,66,67,68] imbalance. The latter is more suitable when closed-loop current control is included at the unbalanced components for ensuring smooth torque (tolerance). In any case, under the assumption that only the - plane contributes to the torque, it is possible to omit closed-loop control in the secondary subspaces and monitor the respective current, while avoiding torque ripple by proper - control [69]. On the other hand, if it is desired to minimize the losses under resistance dissymmetry, the phase currents may be reconfigured for this purpose, using suitable control of all the current DOFs [175].
Some of these techniques are able to detect and distinguish other faults as well, such as phase/switch OC [62,63,64,69], stator SC [61], overheating [60], magnet demagnetization [68], and broken rotor bars [62].
The possibility of having non-zero ac current references in several VSD subspaces is considered just in [63,64] so far, in spite of the interest of exploiting these extra DOFs for, e.g., increasing the average torque [5,6,7].
It would be desirable to continue performing research following and combining these new trends, by devising innovative methods for detecting and tolerating high-resistance connections together with many other fault types, even if there are non-zero ac references for current components other than the balanced fundamental. Avoiding torque ripple or overcurrent due to overmodulation when a phase voltage rises because of a high-resistance connection may also be addressed in the future. Further research can be performed in order to extrapolate the existing strategies for providing high performance under phase OC faults to the scenarios where the increased stator resistances are not infinite, as in high-resistance connections.
5. Stator SC Faults
SC faults in the stator windings can be of the following types (see Figure 1): phase-to-phase, phase-to-neutral, or turn-to-turn (also known as turn or interturn faults) [269]. If the stator does not include neutral points (e.g., for full-bridge VSCs), the term “phase-to-neutral SC” can be replaced by “phase SC” (more general), for which both terminals of a given phase are shorted [266]. Phase-to-phase faults can arise between terminals of two phases, between coils of different phases within a certain stator slot (mainly for windings with two or more layers) or between end windings (if overlapping) [129,262]; they may also occur through the stator core, but it is less likely [129]. A turn fault means that one or several turns of a certain phase are shorted. Turn fault is the most troublesome kind of stator SC, especially for PMSMs and when the SC involves a single turn of a certain phase [93,96,99,129,167,240]. Moreover, the severity of turn faults depends on the location of the shorted turns (unless vertical rectangular winding is adopted [223,495]), and it is particularly critical if such turns are close to a slot opening [95,129,223,227,495]. The most important causes, detection techniques and tolerant approaches concerning stator SCs are displayed in Figure 11 and are surveyed in the following.
Figure 11.
Causes, detection methods and tolerance approaches for stator SC faults in multiphase drives.
5.1. Causes of Stator SC Faults
Stator SC faults mainly occur due to breakdown of the insulation material, which, in turn, is typically caused by a combination of the following types of stress during the operating life of the machine [496]: thermal (aging, overload, and cycling), electrical (dielectric, tracking, corona, and transient voltage), mechanical (coil vibration and rotor striking the stator), and environmental (moisture, chemicals, and other foreign particles) stress. These stresses can be aggravated by manufacturing defects (e.g., in insulation) [497] and by phenomena, such as voltage surges, electrostatic discharge, high dv/dt, deficient cooling, and poor maintenance [223].
5.2. Detection of Stator SC Faults
Detection of any kind of stator SC is normally important, so that the most suitable measures are timely implemented. Nonetheless, detecting turn faults is particularly critical, because as aforesaid stator currents tend to be very large in such circumstances, rapidly causing significant temperature rise, which can lead to magnet demagnetization (for PMSM) and further damage of the machine insulation unless remedial actions are applied in time [97,98,225,237]. The methods proposed in the literature for detecting stator SC failures in multiphase drives are summarized in Table 8 and surveyed next. The techniques are roughly sorted in the table according to the type of signal/s being monitored, which is also the order that is followed in the subsequent discussion.

Table 8.
Methods for detecting stator SCs (Section 5.2) in multiphase applications in the literature.
Table 8.
Methods for detecting stator SCs (Section 5.2) in multiphase applications in the literature.
| References | Machine | Types of Stator SCs | Identifies Location of SC | Monitored Signal/s | Extra Sensors * | Differs from | Robust to Other Faults | |||
|---|---|---|---|---|---|---|---|---|---|---|
| n | WSA | Rotor | FSCW | |||||||
| Jiang et al. [100] | 6 | Sym. | SPMSM | Yes | Phase | Phase | Ph. current | No | No | Phase OC |
| Jiang et al. [101] | 6 | Sym | SPMSM | Yes | Phase | Phase | Ph. current & neutral-point volt. | 1 volt. per star | No | No |
| Haylock et al. [93] | 6 | Sym. | SPMSM | Yes | Turn | Phase | Ph. current | No | No | No |
| Haylock et al. [99] | 6 | Sym. | SPMSM | Yes | Turn/ph. | Phase | Ph. current & on-state IGBT volt. | 1 volt. per IGBT | No | IGBT |
| Gritli et al. [88] | 6 | Asym. | SPMSM | No | Turn | No | x-y volt./curr. 1st/3rd harmonics | No | Yes | No |
| Immovilli et al. [89] | 5 | Sym. | SPMSM | Yes | Turn | Phase | Product - & x-y volt./current | No | Yes | Ecc., demag. |
| Cui et al. [94] | 5 | Sym. | IPMSM | Yes | Turn | No | Torque estimation error | Torque | No | No |
| Wu et al. [96] | 6 | Sym. | SPMSM | Yes | 1 turn | Ph., top/bot. | High-freq. ph. current (injected) | No | No | No |
| Sen et al. [90,92] | 5 | Sym. | SPMSM | Yes | Turn | Phase | PWM ripple ph. current | Analog circuit | No | No |
| Fan et al. [91] | 5 | Sym. | IPMSM | Yes | Turn | No | Zero-sequence current | No | Slightly | No |
| Wang et al. [97] | 9 | 3-sect. | PMaSynRM | No | Turn | Sector | Instant. active/reactive power | Yes | Slightly | No |
| Hu et al. [61] | 9 | 3-sect. | PMaSynRM | No | Turn | Phase | Zero-sequence voltage | 1 volt. per star | No | High-resist. |
* In addition to usual stator-current sensors. † Although several of these detection methods are identical for n = 3, most of them had not been proposed for n = 3 in the past, and many of these papers also have significant research contribution on other aspects. ‡ Only including those that have been proved.
In [100], Jiang et al., detect stator SC faults by simply checking if the phase current is several times greater than rated. However, assuming that the machine is properly designed for tolerating SC faults, only very severe ones (or none) could be detected in this manner. Later, this technique is improved to some extent in [101], for machines based on several star-connected winding sets, by adding the condition that under fault the measured voltage of the corresponding stator neutral point should deviate substantially from half the dc-link voltage value. To avoid false alarms due to noise, the current absolute value in each phase is averaged during several control samples [101], at the expense of some additional detection time.
Haylock et al. [93] propose to predict the stator current in a six-phase PMSM by means of a look-up table, with flux linkage and position as inputs. When the actual phase current deviates from the predicted one at the PWM frequency (which sees much lower reactance than the fundamental), a turn fault is diagnosed. Since this is checked in each PWM cycle, the detection is fast [93]. For detecting stator phase SCs (or switch SCs), the on-state switch voltage may also be monitored at the same time, because its value is related to the phase-current magnitude [99].
Gritli et al. [88] analyze the voltage and current spectrum in both the - and - (x-y) planes of an asymmetrical six-phase SPMSM with distributed windings. It is concluded that the magnitudes of the fundamental and third-order voltage/current harmonics in the - plane can be used as indicators of turn failures, although the fault location is not identified.
Immovilli et al. [89] present an index based on the product of the - and x-y vectors for detecting turn SCs in five-phase PMSMs. Voltage or current SVs can be used depending on whether the current is controlled or not. Turn faults imply an increase in this index at both dc and second-order components. The affected phase may be identified based on the direction of the SV in the x-y plane. The method is tested in a five-phase SPMSM with single-layer 20-slot 18-pole FSCW. It is also shown that other types of faults, such as eccentricity and magnet demagnetization lead to different behavior and, thus, do not cause fault alarms, at least for this particular machine.
Cui et al. [94] propose to detect turn faults by monitoring the average torque error (between estimated and measured torque) in a five-phase hybrid-excitation interior PMSM (IPMSM) fed by FB VSC. The main shortcomings of this method are the requirement of a torque sensor and the inability to identify the faulty phase.
It is shown by Wu et al. [96] that a single-turn fault can be detected online by injecting a high-frequency square-wave voltage in the axis and measuring the associated high-frequency current. A change in the corresponding impedance would signify a turn SC, depending on its location (top/bottom of slot). However, the additional current produces undesired noise and vibrations [92].
Instead of injecting supplementary high-frequency signals, it is possible to detect turn SCs by monitoring the changes in high-frequency admittance through the rms value of the PWM current ripple, as performed by Sen et al., in [92]. Unless it is possible to acquire the current measurements with considerable accuracy and sampling frequency, special analog filters are required. The proposal is applied to a five-phase SPMSM with single-layer 10-slot 12-pole FSCW. This approach is later improved in [90], by means of a new fault indicator (ratio between adjacent phases), in terms of robustness to imbalance and different operating conditions, including transients.
However, many of these techniques are based on the assumption that the resistance between shorted turns is zero (worst case), and the severity is not quantified. A method for detecting the severity of turn faults in a five-phase IPMSM with single-layer open-end FSCW fed by a single FB VSC is presented by Fan et al., in [91]. The magnitude and phase angle of the zero-sequence current is monitored, while PWM with zero common-mode voltage is employed. The number of SC turns and the value of the associated fault resistance (insulation resistance) are obtained through an iterative calculation based on this current and a couple of two-dimensional look-up tables. Identification of the affected phase is not performed. It is important to establish beforehand the threshold value of the insulation resistance such that irreversible damage occurs, which is assessed in [98] for a nine-phase PMaSynRM by analyzing its electromagnetic and thermal behavior.
In [97], Wang et al., propose to monitor the second-harmonic magnitude of the instantaneous active (for generation mode) or reactive (for motoring mode) power of each sector of a three-sector nine-phase PMaSynRM. A turn SC is diagnosed in a given set if the value of this parameter for such set is much higher than in the healthy sets and in comparison with the values expected for healthy machine (according to a look-up table). However, the method is not suitable for low speeds, unlike, e.g., the one from [93,99] (based on PWM ripple).
Hu et al. [61] point out that it is also of interest to distinguish between turn SCs and high-resistance connections, because they both give rise to similar symptoms; namely, imbalance in the low-frequency components. Accordingly, they propose to check the zero-sequence voltage in a nine-phase PMaSynRM by using an extra sensor per winding set, and to diagnose these types of faults depending on whether the high-frequency zero-sequence voltage increases substantially (turn fault) or only the fundamental one does (high-resistance connections). The effectiveness of the turn-SC detection is also verified during transient conditions.
From the preceding survey and the summary reflected in Table 8, several conclusions can be drawn. Nearly all of these alternatives are able to identify the faulty phase [89,90,92,93,96,99,100,101] or at least its winding set [97]. Most of them are focused on turn SC [61,88,89,90,91,92,93,94,96,97,99], which is actually the most troublesome type of stator SC. Some of these procedures do not need extra sensors or circuits [88,89,91,93,96,97,100]. The capability of these methods to distinguish from other failures is limited, with just some exceptions [61,89,99,100]. All the ones shown in Table 8 are proposed for PMSMs. Only a few of the existing techniques exploit the particular characteristics (secondary subspaces) of multiphase drives in comparison with three-phase ones [88,89]. Thus, future research may attempt to take advantage of the extra DOFs of these drives so as to improve the features (e.g., discrimination from other faults) of many of the existing approaches, also in cases different from turn SCs in PMSMs. Further details about the detection methods for stator SCs in three-phase machines can be found, e.g., in [498,499].
5.3. Tolerance to Stator SC Faults
As shown in Figure 11, multiple approaches exist to tolerate stator SCs. They are rarely employed individually; on the contrary, in the literature several of them are usually combined in a certain application. In multiphase drives, enhancement of the tolerance to stator SCs is completed by special drive topologies or topology reconfigurations (surveyed in Section 5.3.1), by careful machine design (Section 5.3.2), by advanced current control (Section 5.3.3), and (on rare occasions) by including extra elements to physically shunt the rotor flux in slots affected by SC faults (Section 5.3.4).
5.3.1. Drive Topologies
The tolerance to stator SCs can be enhanced to a great extent by specific drive configurations, especially concerning the VSC topologies. The solutions found in the literature for this purpose are surveyed next, and they are summarized in Table 9 following roughly the same order as in the text.

Table 9.
Methods based on drive topology for tolerating stator SC faults (Section 5.3.1) in multiphase applications in the literature.
Table 9.
Methods based on drive topology for tolerating stator SC faults (Section 5.3.1) in multiphase applications in the literature.
| References | Method Description | n | WSA | Splitting | VSC Topology | Figure | SC Types |
|---|---|---|---|---|---|---|---|
| Mecrow et al. [93,99,240] | 1-phase SC | 6 | Sym. | 1-phase | Independent H bridges | 9c | Turn |
| Arumugam et al. [223] | 1-phase SC & vertical winding | 6 | Sym. | 1-phase | Independent H bridges | 9c | Turn |
| Wang et al. [97,98,129,243,245] | 3-phase SC | 9 | Multisec. | 3-phase | Independent 3-phase HBs | 9a | Turn |
| Xu et al. [265] | 3-phase SC | 6 | Sym. | 3-phase | Independent 3-phase HBs | 9a | Phase |
| Arumugam et al. [222] | 3-phase SC & vertical winding | 6 | Sym. | 3-phase | Independent 3-phase HBs | 9a | Turn |
| Wang et al. [236] | 3-phase & neutral SC | 9 | Multisec. | 3-phase | Independent (l+1)-phase HBs | 9b | Turn |
| Shi et al. [270] | Delta connections | 9 | Multisec. | 3-phase | Independent 3-phase HBs | 9a | Turn |
| Various [94,248,263,267] | Zero-sequence control | 5 | Sym. | 1-phase | Single n-phase FB | 8d | Phase/turn |
| Guo et al. [128] | Zero-sequence control | 6 | Sym. | 1-phase | Single n-phase FB | 8d | Phase |
| Many | Zero-sequence control | − | − | 1-phase | Independent H bridges | 9c | Phase/turn |
| Jiang et al. [101] | Extra leg to neutrals & 0-seq. control | 6 | Sym. | 3-phase | Single (n+1)-phase HB + 2 switches | 12 | Phase |
| Si et al. [239] | Zero-sequence control | 4 | Sym. | 1-phase | Dual n-phase HB + 6 switches | 13 | Phase |
| Mohammadpour and Parsa [252] | Opening shorted phase | 5 | Sym. | No | Single n-phase HB | 8a | Phase |
5.3.1.1. Topology Reconfiguration for Applying Terminal SC
In some scenarios of stator SCs, applying an external SC by means of the VSC switches can alleviate the undesired effects of such faults, assuming that the machine is properly designed (addressed shortly, in Section 5.3.2) to yield acceptable SC current after this procedure. This strategy could be understood as a reconfiguration of the drive topology. Either single- or three-phase external SCs are often performed. For instance, in case of a turn failure in a PMSM supplied by FB VSC/s (e.g., independent H-bridges), it is common to deliberately SC the terminals of the corresponding phase by means of two top or two bottom switches. In this manner, the extremely high current that tends to arise in said case is prevented, and instead the current through the phase and faulted turns becomes more similar to a phase SC fault, which is much lower and easier to accommodate [93,99,240]. The fact that the SC current caused by turn fault is reduced by the external SC is because the resulting current naturally counteracts the flux linkage in the shorted turn/s [129]. This effect may also be understood as a balanced sharing of the flux linkage by all the turns of the respective phase winding [222,223]. In any case, even after such action, the current through the shorted turn/s can be, to some extent, higher than for phase SC failures, depending on the specific coil (if there is more than one coil per phase) and turn location (except for vertical winding [222,223,495]). Hence, it is advisable to consider the worst-case scenario in this regard during the machine design [167], to adopt FSCWs using vertical conductors [222,223,495] or to implement advanced turn-fault mitigation procedures based on current control (discussed later, in Section 5.3.3.2) instead of a simple terminal SC [224].
In PMSMs based on multiple (isolated) three-phase star-connected winding sets with a stator SC (of any type) in one or two phases, it can be an attractive option to impose SC, also, on the other phases of the same winding set (i.e., three top or three bottom switches on) [97,98,129,222,243,245,265]. On the one hand, the current induced in the shorted healthy phases tends to reduce the flux and current through the faulty turns/coils [129]; on the other hand, a balanced SC can be less harmful than an unbalanced one [230]. For example, even though the brake torque is normally higher for a three-phase SC than for a single-phase SC, in most cases the torque ripple is much lower for the former, due to the greater degree of symmetry in the stator excitation [27,247,258,265].
If each three-phase winding set is fed by a VSC with four legs (as in Figure 9b, for ), it is possible to not only turn on three switches of said VSC after the SC failure, but also one of the leg connected to the neutral point (i.e., four top or four bottom switches per VSC) [236]. This is particularly helpful for decreasing SC current under turn faults, as further discussed shortly.
Nevertheless, the excessive current peaks and the torque ripple produced by a stator SC can be compensated by using suitable postfault current techniques (explained in Section 5.3.3) without applying external SC to any phases, thus avoiding the associated drawbacks such as the increased braking torque or the loss of DOFs.
5.3.1.2. Topologies Allowing Reduction in Shorted-Turn Flux Linkage by Uncontrolled Zero-Sequence Current
In case HB VSCs are adopted, the tolerance to stator SC faults may be improved by the type of stator phase connection. It has been shown in [270], taking a nine-phase PMaSynRM driven by three-phase HB VSCs as an example, that using three deltas yields lower current under turn faults than three stars. This is explained by the fact that the zero-sequence current flowing within the loops in the former case contributes to reduce the flux linkage in the shorted turn/s, even though the circulating current cannot be actively controlled.
Another possibility to allow zero-sequence current flow, without resorting to phase connections different from star (e.g., delta) or to FB VSCs (increased complexity), is to install a four-leg VSC for each three-phase star-connected set (see Figure 9b, for ), as performed in [236] for the same nine-phase PMaSynRM used in [270]. The fourth leg is simply employed to suitably clamp the neutral point to the dc-link positive or negative rail after a turn fault arises, creating an external SC with the other three terminals of the same winding set [236]. Similarly to using delta stator connections [270], this alternative also results in reduced flux linkage through the shorted turns and hence smaller SC current (by about ), in comparison with the absence of zero-sequence current (SC involving three terminals instead of four). Note that, for a nine-phase machine such as that in [236,270], a nine-phase FB VSC would mean six additional legs compared with using three four-leg VSCs. Furthermore, the fourth leg of each VSC in the latter option can be of lower current rating than the other legs [236].
Based on the aforementioned, it can be concluded that, although VSC topologies other than FB VSCs are usually simpler, it is advisable to also equip the former with paths for the zero-sequence current so as to reduce the turn-fault current.
5.3.1.3. Topologies Allowing Increase in DOFs by Controlled Zero-Sequence Current
On the other hand, the additional zero-sequence current path/s can be employed in a different manner. Instead of using them so that the SC current under turn faults is passively decreased, they may be exploited for increasing the number of actively controlled current DOFs under stator SC (or OC) fault; then, the SC current magnitude, torque capability, and maximum allowable number of phase failures can, thereby, be improved [101]. This approach is possible in FB VSCs without any modifications. FB VSCs are, in fact, relatively common in drives tolerant to stator SCs: e.g., using multiple H-bridges (which also offer high electrical isolation between phases for dc-link faults or switch SCs) [89,93,95,96,99,130,162,164,165,210,211,212,223,227,228,233,240,264,265,266,271] or a single FB VSC [94,128,248,263,267].
However, FB VSCs have shortcomings associated with the high number of extra devices and low dc-link utilization. Jiang et al. [101] proposed a particular alternative topology (see Figure 12) allowing zero-sequence current control for a symmetrical six-phase PMSM with two stars, using seven legs. One leg is saved in comparison with two four-leg VSCs, and five legs with respect to an FB VSC. Two bidirectional switches (S1 and S2) are included so that the seventh leg is connected to the neutral point of a three-phase winding set having a phase SC, or to both sets (if both have faults) at the same time. This connection is completed through an additional inductor L. The two insulated-gate bipolar transistors (IGBTs) of each leg corresponding to a faulty phase are turned off, because phase SC is considered instead of turn SC. The leg connected to the neutral point/s is not used for clamping; instead, it is actively switched at high-frequency. In any case, it may be noted that, provided the control is properly adapted, under phase SC the only difference between switching with the normal leg connected to the faulty phase or with the additional one is the inductor in series with the latter, which helps avoiding excessive currents. For a turn SC, although not discussed in [236], both legs connected to the ends of the faulty phase might be kept switching. Regarding the dc-link utilization, it is better for this topology than for FB VSCs, at least while the stator neutral points are not connected to each other. The fuses shown in Figure 12 are mainly helpful in the face of switch SCs, as later explained in Section 6.3.1.2.
Figure 12.
Fault-tolerant six-phase topology from [101].
A different VSC topology is proposed in [239] (see Figure 13), considering a four-phase SPMSM with single-layer FSCW and open-end windings. This VSC has 8 legs with 2 IGBTs per leg (similarly to a four-phase FB VSC; see Figure 8d), 4 extra diodes (besides the 16 free-wheeling ones), and 8 additional switches for increasing the number of possible reconfigurations. Two SC or OC faults (in stator windings, switches, power supplies, etc.) can be simultaneously accommodated by appropriately reconfiguring the VSC by means of these extra switches. If there is just a stator SC, the zero-sequence current may be exploited as an extra DOF for enhanced postfault performance, as for a four-phase FB VSC. In case of a switch OC or SC fault, the VSC can be in effect modified from FB (eight operative legs) to HB (four operative legs), with a neutral point being created at one side of the open-end windings by the corresponding four VSC legs (further discussed later in Section 6.3.1.5). Then, a stator SC (or OC) fault can still be tolerated, as for a four-phase PMSM with star connection and four-leg HB VSC. Faults in one of the power supplies (or corresponding dc-link capacitors, if any) can also be tolerated (further discussed in Section 12.1 and Section 12.2), unlike for a single four-phase FB VSC or for the topology from Figure 12. Therefore, although this topology is actually more complex than an FB VSC, it provides even better degree of fault tolerance. It can also be remarked that it is advisable to include dc-link capacitors next to the VSC legs in Figure 13 or additional semiconductors in order to ensure paths for the dc-side current when it is instantaneously reversed. The fuses included in Figure 13 are relatively common in fault-tolerant multiphase drives, and their purpose will become clearer after the explanations given in Section 6.3.1.2 and Section 12.2 regarding switch and supply SC faults, respectively.
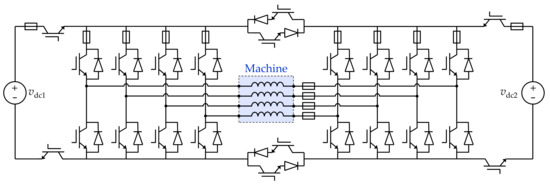
Figure 13.
Fault-tolerant four-phase topology from [239].
Concerning the control methods for exploiting the additional current DOFs for tolerating stator SCs, they will be discussed in Section 5.3.3.
5.3.1.4. Topologies Allowing Opening of a Shorted Phase
When a turn fault is present, letting current flow through the affected phase contributes to mitigate its effect (discussed in Section 5.3.1.1 and Section 5.3.3.2). In contrast, when an SC arises between the terminals of a certain phase, it would be convenient to open the electrical path through the corresponding stator winding so as to avoid current through it, particularly in case the machine is not specifically designed for ensuring low SC current and small coupling between phases (explained later in Section 5.3.2). This functionality can be attained by including switches connected in series with all or some of the stator phases [252]. Nonetheless, it is not easy to install switches within the machine in this manner, and this procedure cannot overcome the most harmful types of stator SCs (turn faults). Accordingly, it is rarely used in practice.
5.3.2. Machine Design
On the subject of enhancing the tolerance to stator SCs by machine design, some general guidelines based on the literature are first summarized in Section 5.3.2.1. Then, the publications on the topic are individually surveyed in (roughly) chronological order in Section 5.3.2.2, highlighting the main particularities of each one.
5.3.2.1. General Guidelines
In order to tolerate stator SC faults, it is crucial to design the machine in a special manner with this objective in mind. Broadly speaking, high isolation (thermal, magnetic, electrical, and mechanical) between phases should be sought, and it should be ensured that the current and, hence, temperature are kept within reasonable margins after the failures [240,266]. Table 10 summarizes the kinds of multiphase machines that have been employed for tolerating stator SCs in the literature. Recall that the term splitting refers to the number of stator phases electrically connected to each other (see Section 3.1), and that switched reluctance and similar machines are not covered in this paper. Other than those machine types, it can be seen in this table that most of the SC-tolerant machines are by far PMSMs, which are often preferred because of their high power density [266]. In exchange, the magnet flux cannot be deactivated in case of SC fault in PMSMs [242], and, thus, special care should be put in the PMSM design to ensure acceptable currents in such conditions. Regarding the machine inductances, mainly the following two aspects should be taken into account in the PMSM design to comply with the aforementioned.
- On the one hand, the self-inductance should be large, to limit the current in the affected phases so as to prevent excessive SCL and magnet demagnetization [225,230]. It can be designed so that the phase current is equal to rated in case of SC across the phase winding (1-p.u. self-inductance) [93,266,272], or even lower [258]. If the machine has saliency, this is especially important for the self-inductance in the axis, aligned with the back-EMF [240]. Furthermore, for limiting the SC current it is also recommendable to take into account the worst-case scenario (highest current) of turn fault in the machine design, while assuming that at least external SC (see Section 5.3.1.1) is applied to the affected phase/s to reduce the effect [167];
- On the other hand, the mutual inductance between phases should be very small, so that the voltage and current induced by the faulty phases in the healthy ones is minimized (magnetic decoupling).
To satisfy both conditions at the same time (high self-inductance and low mutual inductance), the leakage inductance should be very large, at the expense of greater machine size [240]. This is attained, e.g., by setting non-overlapping stator windings with a single phase winding per slot, as in single-layer (i.e., alternate-teeth-wound) FSCWs [see Figure 6a] [240,266]. Moreover, the geometry design can also help for these purposes; e.g., the phase inductance can be increased by shaping the stator tooth tips [27] and by using deep stator slots [264], the rotor can be designed for low mutual coupling through it (e.g., deep magnets with nonmagnetic retaining sleeves in case of PMSMs) [240,266], the stator and pole numbers for FSCWs can be chosen to optimize these inductances as well [226,232,233], etc. In addition, the stator resistance also plays an important part in limiting the current in SC faults involving few turns [93].
Single-layer FSCWs, besides yielding large self-inductance and low mutual inductance, are also attractive for tolerating stator SCs because of their high degree of mechanical, thermal and electrical isolation between phases [240,264,266]. Double-layer (i.e., all-teeth-wound) FSCWs [see Figure 6b] also offer these fault-tolerant characteristics, although to a lower extent, especially with regard to electrical isolation [258]. In any case, the tolerance in double-layer FSCWs can be enhanced by including coil separators in each slot [259]. Furthermore, double-layer FSCWs are more difficult to manufacture [475]. However, single-layer FSCW results in greater magnetomotive-force distortion (as mentioned earlier) [233,264,398], torque ripple [233,258,264], magnetic saturation [398], eddy-current loss [229,398] and Joule loss [475] compared with double-layer FSCW [258]. As shown in the summary displayed in Table 10, most of the multiphase machines used for tolerating stator SCs are based on FSCWs, using either single or double layer.

Table 10.
Types of multiphase machines employed for tolerating stator SC faults (Section 5.3) in the literature.
Table 10.
Types of multiphase machines employed for tolerating stator SC faults (Section 5.3) in the literature.
| n | WSA | FSCW | Layers | Stator Slots | Coils/Phase | Rotor Poles | Splitting | Rotor Type | References |
|---|---|---|---|---|---|---|---|---|---|
| 4 | Sym. | Yes | Single | 8 | 1 | 6 | 1-phase | SPMSM | [228,266] |
| 4 | Sym. | Yes | Single | 8 | 1 | 10 | 1-phase | SPMSM | [163,165] |
| 4 | Sym. | Yes | Single | 8 | 1 | 12 | 1-phase | SPMSM | [239] |
| 5 | Sym. | No | Double | 15 | 3 | 4 | No | IPMSM | [251,252] |
| 5 | Sym. | No | Single | 40 | 8 | 4 | No | IM | [253] |
| 5 | Sym. | Yes | Double | 10 | 2 | 8 | No | SPMSM | [234] |
| 5 | Sym. | Yes | Double | 20 | 4 | 18 | No | SPMSM | [254] |
| 5 | Sym. | Yes | Hybrid | 10 | 2 | 12 | 1-phase | IPMSM | [267] |
| 5 | Sym. | Yes | Hybrid | 40 | 4 | 44 | No | Dual-rotor SPMSM | [249] |
| 5 | Sym. | Yes | Single | - | - | 10 | 1-phase | SPMSM | [268] |
| 5 * | Sym. | Yes | Single | 10 | 1 | 8 | 1-phase | Dual-rotor SPMSM | [272] |
| 5 | Sym. | Yes | Single | 10 | 1 | 8 | 1-phase | SPMSM | [165,241] |
| 5 | Sym. | Yes | Single | 10 | 1 | 12 | 1-phase | SPMSM | [95,162,163,164,165] |
| 5 | Sym. | Yes | Single | 10 | 1 | 12 | No | SPMSM | [166] |
| 5 | Sym. | Yes | Single | 20 | 2 | 18 | 1-phase | IPMSM | [248,263] |
| 5 | Sym. | Yes | Single | 20 | 2 | 18 | 1-phase | SPMSM | [130,233] |
| 5 | Sym. | Yes | Single | 20 | 2 | 18 | No | Outer-rotor IPMSM | [250] |
| 5 | Sym. | Yes | Single | 20 | 2 | 18 | − | IPMSM | [209] |
| 5 | Sym. | Yes | Single | 20 | 2 | 22 | No | Outer-rotor IPMSM | [250,255,256,257] |
| 5 | Sym. | Yes | Single | 40 | 4 | 28 | 1-phase | SPMSM | [226,227] |
| 5 | Sym. | Yes | Single | 40 | 4 | 42 | 1-phase | Outer-rotor IPMSM | [264] |
| 6 | 2-sector | No | Double | 36 | 6 | 8 | 3-phase | SynRM | [247] |
| 6 | 2-sector | No | Double | 48 | 2 | 4 | 3-phase | IM | [261] |
| 6 | 2-sector | Yes | Double | 12 | 2 | 10 | 3-phase | IPMSM/SPMSM | [258,259] |
| 6 | 2-sector | Yes | Double | 18 | 3 | 12 | 3-phase | SPMSM | [246] |
| 6 | 2-sector | Yes | Single | 12 | 1 | 10 | 3-phase | IPMSM/SPMSM | [258] |
| 6 | 4-sector | No | Double | 36 | 6 | 8 | 3-phase | SynRM | [247] |
| 6 | 2-sector | No | Double | 48 | 2 | 4 | 3-phase | IM | [261] |
| 6 | 4-sector | No | Single | 24 | 2 | 8 | 3-phase | SPMSM | [230] |
| 6 | Asym. | No | Double | 18 | 3 | 8 | 3-phase | IPMSM | [28,176,177,477] |
| 6 | Asym. | No | Double | 36 | 2 | 8 | 3-phase | SynRM | [247] |
| 6 | Asym. | No | Double | 48 | 2 | 4 | 3-phase | IM | [261] |
| 6 | Asym. | Yes | Single | 24 | 2 | 22 | 1-phase | SPMSM | [96,220] |
| 6 | Asym. | Yes | Single | 24 | 2 | 22 | − | SPMSM | [225] |
| 6 | Asym./sym. | Yes | Single | 12 | 1 | 10 | 3-phase | IPMSM/SPMSM | [258] |
| 6 | Asym./sym. | Yes | Double | 12 | 2 | 10 | 3-phase | IPMSM/SPMSM | [258,259] |
| 6 | Sym. | No | Double | 48 | 2 | 4 | 1-phase | IM | [271] |
| 6 | Sym. | No | Double | 48 | 2 | 4 | 3-phase | IM | [261] |
| 6 | Sym. | Yes | Double | 24 | 4 | 28 | 3-phase | Outer-rotor SPMSM | [229] |
| 6 | Sym. | Yes | Single | 12 | 1 | 8 | 1-phase | SPMSM | [93,99,212,240] |
| 6 | Sym. | Yes | Single | 12 | 1 | 10 | 1-phase | SPMSM | [128,163,165,210,211,265] |
| 6 | Sym. | Yes | Single | 12 | 1 | 10 | 3-phase | SPMSM | [100,101,260] |
| 6 | Sym. | Yes | Single | 12 | 1 | 10 | 3-phase | SPMSM | [231] |
| 6 | Sym. | Yes | Single | 12 | 1 | 10 | − | Hybrid-excit. PMSM | [178] |
| 6 | Sym. | Yes | Single | 12 | 1 | 14 | 1-phase | SPMSM | [165,223] |
| 6 | Sym. | Yes | Single | 12 | 1 | 14 | 3-phase | SPMSM | [222] |
| 6 | Sym. | Yes | Single | 24 | 2 | 14 | − | IPMSM | [221] |
| 6 | Sym. | Yes | Single | 36 | 3 | 16 | 3-phase | SPMSM | [230] |
| 9 | 3-sector | No | Single | 36 | 2 | 6 | 3-phase | PMaSynRM | [97,98,129,167,224,235,236,237,238,242,243,244,245,270] |
| 9 | Sym. | No | Single | 54 | 1 | 6 | 3-phase | IM | [269] |
| 24 | 8-sector | Yes | Double | 72 | 3 | 64 | 3-phase | Outer-rotor SPMSM | [27] |
* This machine is a ten-phase PMSM with the stator split into two five-phase winding sets. The data in this row are for each of them.
In multisector machines [see Figure 2d and Figure 4], since the stator windings of a given phase only occupy slots of a specific sector of the stator, a significant thermal, mechanical, magnetic and electrical isolation is achieved between phases of different sectors (even for overlapping windings). Moreover, thermal insulation material may be placed between the machine sectors to further enhance the decoupling between them and hence the fault tolerance [267]. It can be observed in Table 10 (second column) that various multiphase machines based on multisector WSA have been proposed in the literature for tolerating stator SC faults.
In general, to ensure tolerance to stator SCs it is important as well to design an effective cooling system, so that the heat produced by these faults is properly dissipated [240,244]. In this manner, the required thermal decoupling between phases is also attained more easily [240]. The braking torque due to SC faults should also be taken into consideration in the design process, not only due to the associated decrease in achievable torque, but also because of safety risk, e.g., for electric vehicles [27].
5.3.2.2. Chronological Overview
In an early publication [240], Mecrow et al., discuss general guidelines to design a multiphase PMSM tolerant to SC (and OC) faults. Although switched reluctance machines had previously been used to tolerate SC failures because of their natural fault tolerance, PMSMs offer higher power density. This paper [240] provides the basis for most of the general rules just given in Section 5.3.2.1 for designing fault-tolerant drives. By using FSCWs and H-bridges, high isolation between phases and large self-inductance is achieved. In particular, a symmetrical six-phase SPMSM with 12-slot 8-pole FSCW (see Table 10) is designed in this manner. It is advised to select the phase number n as a compromise between the increased VSC complexity and the required VSC overrating. It is assumed in [240] that the VSCs are overrated so as to be able to provide rated torque after single-phase SC, although it is also possible, as in many other publications, to avoid VSC overrating and instead accept postfault torque derating [24], or to define a trade-off between both options [130]. A similar PMSM design, but of higher power (), is later presented in [99] for an an aircraft fuel pump. Further analysis of the machine parameters is given. The penalties (e.g., extra material) in comparison with an analogous three-phase PMSM are quantified.
The same research group designs and tests in [266] a 16-kW four-phase PMSM with single-layer FSCWs, fed by four H-bridges, also for an aircraft fuel pump. More attention is paid in this case to the stator and oil temperature under healthy and faulty operation. The machine is able to yield rated power under phase OC and SC faults, with just moderate increase in stator-winding temperature. Moreover, in this application the fuel acts as a coolant, permitting high loading. Based on this PMSM, a similar machine of even higher rated power ( instead of ) is afterward designed [228], with special care to reduce losses and to improve efficiency.
Atallah et al. [165] provide insight about advisable slot-pole numbers in four-, five- and six-phase modular PMSMs with single-layer FSCW and a single coil per phase. Multiple possibilities are compared in terms of cogging torque, total harmonic distortion (THD) of back-EMF and magnitude of back-EMF fundamental. It is also emphasized that the amount of harmonic orders affecting the torque ripple decreases with increasing phase number. Based on this study, the selected options are five-phase 10-slot 8-pole/12-pole FSCW and six-phase FSCW with 12-slot 10-pole/14-pole FSCW. Analysis of the eddy-current loss in the permanent magnets is given in [163].
Mitcham et al., present in [226] a set of recommended slot-pole combinations for SC-tolerant single-layer FSCWs with n between 3 and 10. This set of values yields negligible magnetic coupling between phases, as well as reduced stray loss and torque ripple. Otherwise, unnecessarily deep magnets and deep slot openings would be required to yield sufficient magnetic decoupling. In contrast to [165], in [226] the possibility of one coil per phase is ignored. Adopting one of these preferred FSCW options (40-slot 28-pole FSCW; see Table 10), a five-phase PMSM is proposed as a generator for an aircraft gas turbine. Subsequently, it is shown in [227] that this 250-kW bar-wound PMSM, as opposed to the 16-kW wire-wound PMSM from [240], requires more advanced control measures to limit the turn-fault current to acceptable magnitude (Section 5.3.3).
Bianchi et al. [233] discuss design considerations for fractional-slot windings in three-phase and multiphase synchronous machines, including SynRMs, SPMSMs and IPMSMs. Special attention is paid to FSCWs. The study is based on the diagram of the star of slots. Many of the aforesaid conclusions from previous publications are confirmed, especially regarding the remarkable suitability of single-layer FSCWs for tolerating SCs. It is also shown that FSCWs are in principle reasonable for SPMSMs but not for machines with small air-gap (e.g., IPMSMs and SynRMs), because in the latter case the increased magnetomotive-force distorsion (peak value, high-order harmonics and subharmonics) is more likely to cause saturation and hence greater torque ripple and rotor losses. In addition, rules are given for transforming a double-layer FSCW into a single-layer one, and for selecting single- and double-layer FSCWs with null mutual inductance between phases (considering odd n); namely, it is advised to set even for double layer and even for single layer, with Q being the slot number, p being the number of pole pairs, and t being the greatest common divisor of Q and p.
Gerada et al., address in [253] the question of whether it is also possible to achieve stator-SC tolerance in a multiphase IM. A star-connected five-phase IM with distributed windings, including third space harmonic, is studied under faults by means of the so-called dynamic mesh reluctance model. It is shown that, for a turn failure in a certain phase, the magnetizing flux is reduced to a greater extent as the number of shorted turns increases; thus, if many turns are faulted, larger current [using rotor-field-oriented control (RFOC)] is required to yield the same torque. On the other hand, the SC current is much greater when the shorted turns are few, as in PMSMs. In any case, even if the current control is adjusted after the turn failure (discussed later in Section 5.3.3.2), the IM is not able to work satisfactorily with significant load torque in this situation [253].
Barcaro et al. [258] compare for various single-layer and double-layer FSCW layouts (including symmetrical and two-sector WSAs) in healthy and faulty (stator SC/OC) conditions. Both SPMSMs and IPMSMs are considered, although more results are provided for the latter. The FSCWs are of 10-slot 12-pole type in all cases. Some of the results are summarized in Table 11. It is checked that, as it could be expected, the mutual inductance between both star-connected three-phase winding sets is lower for two-sector than for symmetrical WSA. The tested faults are OC or SC in an entire three-phase winding set, and SC fault in one phase (with OCs in the other two phases of the same winding). It should be noted that the behavior of symmetrical WSA under three-phase OC fault is equivalent to that of an asymmetrical WSA under the same type of failure. One of the main conclusions drawn in [258] is that symmetrical WSA is able to achieve higher maximum torque than two-sector WSA when one three-phase winding is in OC. The magnitude of SC current is smaller for the two-sector WSA, although for both SWAs it is lower than rated. The torque ripple is similar in both WSAs under OC or single-phase SC, but under three-phase SC it is notably better for symmetrical WSA. Concerning the unbalanced radial force under OC, it is much larger for two-sector than for symmetrical WSA. Although some of these outcomes may seem to be related to OC faults and not to SC ones, it is worth highlighting that they are actually associated with SC failures in the sense that the winding layouts being tested (all of them FSCWs) are particularly conceived for tolerating SCs. Based on the results of the comparison (see Table 11), it was concluded that the symmetrical WSA is preferable, as long as the moderately higher mutual inductance and SC current is acceptable [258].

Table 11.
Comparison of stator configurations for six-phase 12-slot 10-pole PMSMs for tolerating stator SCs (using FSCWs) [258,259].
Table 11.
Comparison of stator configurations for six-phase 12-slot 10-pole PMSMs for tolerating stator SCs (using FSCWs) [258,259].
| WSA | * | 3-Phase OC | 1-Phase SC, 2-Phase OC | 3-Phase SC | ||||
|---|---|---|---|---|---|---|---|---|
| Radial Force | Torque Ripple | Maximum Torque | Torque Ripple | SC Current | Torque Ripple | SC Current | ||
| Symmetrical | Low | Low | Low | High | High | Low | Low | Low |
| Two-sector | Very low | High | Low | Low | High | Very low | High | Very low |
* Mutual inductance between three-phase winding sets.
The preceding study [258] is continued in [259], focusing on the case of the IPMSM with double-layer FSCW. The conclusions regarding OC and SC faults are further validated. It is explained that the larger postfault maximum torque provided by symmetrical WSA compared with two-sector WSA is due to the lower flux saturation in the former. Moreover, analysis of thermal overload is added. It is shown that the symmetrical WSA allows increasing the phase current (and hence torque) under OCs to a much greater extent than the two-sector WSA without exceeding the maximum temperature.
Vaseghi et al. [230] study different stator winding layouts for six-phase PMSMs based on two star-connected three-phase sets. On the one hand, four-sector WSA with distributed windings, with each set of three-phase currents supplied to two opposite stator sectors [analogously to Figure 4b], is considered. This four-sector WSA is more balanced under faults than two-sector WSA [cf. Figure 4a]. On the other hand, symmetrical WSA with a special FSCW (3 concentrated coils of a phase in 6 adjacent slots) is also evaluated. In the latter, the number of turns per slot is obtained by solving an optimization problem targeted at minimizing the back-EMF harmonics. It is concluded that the PMSM with FSCW and symmetrical WSA produces more balanced SC currents, due to the higher symmetry of its inductance matrix, as well better magnetic decoupling. It is also shown that, disregarding saliency and assuming mostly inductive stator impedance at high speed, in general the braking torque due to SC current can be neglected at high speed, because the SC current is then nearly orthogonal to the back-EMF.
Alberti et al. [261] compare four stator layouts with overlapping windings in a six-phase IM under three-phase stator SCs and OCs. Symmetrical and asymmetrical WSAs yield higher torque for OC failures than multisector WSA, but only in the latter the SC current is admissible. It is also concluded that the SC current is smaller for two-sector WSA than for four-sector WSA. Although satisfactory behavior under stator SCs is obtained, turn SC faults are not considered in this IM [261], in contrast to [253].
Villani et al. [130] propose a five-phase PMSM drive with single-layer 20-slot 18-pole FSCW and quasi-trapezoidal back-EMF for an aircraft flap actuator. Each phase is fed by an independent H-bridge. The SC current is limited to rated by the machine design. Tolerant methods for other types of faults are also incorporated.
Arumugam et al. [222,223] highlight that using vertical rectangular winding is very advisable in terms of turn fault tolerance. Namely, the dependency of the resulting current on the turn-fault position is thereby reduced. In this manner, the largest potential SC current is hence substantially decreased as well. Otherwise, with conventional windings, the machine self-inductance may have to be increased even further, resulting in poorer performance; or more advanced control methods should be implemented (subsequently discussed in Section 5.3.3.2) [223]. This advantage of vertical windings comes however at the expense of increased ac losses (especially at high frequencies), which may require more careful geometry design [222].
In the context of direct-drive outer-rotor in-wheel motors for electric vehicles, a PMSM based on eight three-phase star-connected sectors is proposed by Ifedi et al., in [27]. Each subunit includes an integrated three-phase VSC with the respective dc-bus capacitor and is overrated by one seventh so that rated torque can be provided if one of them fails. The braking torque under SC fault in one module is only about one eighth of rated torque. Similarly to previous works, it is observed that the torque ripple is smaller for three-phase SC than for single-phase SC, at the expense of greater average braking torque, but in this machine these figures are reasonably low in both cases. It is also shown that, however, the SC current in case of a single shorted turn is excessive (although with small drag torque) and likely to cause thermal overheating. Additionally in agreement with [230], it is concluded that the braking torque decreases with speed. The SC current increases with speed up to a certain (moderate) value, where it ceases to rise as the stator resistance becomes negligible with respect to the inductive reactance. Analytical expressions are given for the drag torque and the SC current. Thanks to the magnetic decoupling between phases, the back-EMF drops just by in a phase adjacent to one with SC.
Cavagnino et al. [229] propose a six-phase outer-rotor PMSM with double-layer FSCWs for working as a generator inside an aeroengine. The study is focused on the thermal behavior and the cooling system, based on air flowing axially through the (relatively large) air-gap, forced by an air compressor. Six stator holes, necessary for the cooling, also permit magnet-temperature optical monitoring. The efficiency and the risk of magnet demagnetization under SC are evaluated as well.
Chen et al., [250] compare two five-phase outer-rotor PMSMs for electric vehicles: one with 20-slot 18-pole FSCW and spoke-type magnets, and another one with 20-slot 22-pole FSCW and V-shape magnets. The FSCWs are of single layer in both designs. It is concluded that, although both machines offer high fault tolerance, the former provides lower cost (for given air-gap flux density) and the latter results in smaller torque ripple, longer speed range and lower demagnetization risk.
Wu et al. [225] address the design of a six-phase PMSM with asymmetrical WSA and 24-slot 22-pole FSCW. The suitable machine dimensions to avoid magnet demagnetization under SC fault, in terms of magnet height and air-gap length, are assessed. Analytical expressions are given to predict the SC current and the associated torque, including transient and steady-state terms. In the event of a single-phase SC, the symmetry with another phase (two-phase symmetry) is exploited to reduce the torque pulsation. In [220], the study is extended, using the same machine, by taking into account the back-EMF third-order harmonic. It is pointed out that the peak of the SC current depends considerably on the phase shift between the back-EMF fundamental and third-order components, assuming that FB VSC is adopted. For example, designing the PMSM for flat-top back-EMF implies sharp-top SC current with large maximum value. On the other hand, even though the steady-state SC current barely varies with speed, its transient peak value decreases rapidly as the machine enters the field-weakening speed range. Nonetheless, when turn faults are considered instead of phase SCs, the steady-state SC current does increase substantially with speed (at least below the base speed) [96]. Given the significant third-order current harmonic under SC due to the back-EMF harmonic of the PMSM design, the torque oscillation is notable unless the current control is specifically conceived to alleviate it [96,220] (discussed later on).
Tong et al. [221] evaluate the option of using two consecutive coils for the same phase, wound in opposite directions, in single-layer FSCWs. It is concluded that this kind of layout results in less magnetic coupling between phases, especially when it is desired to obtain very high power density (which may lead to flux saturation for other winding types). However, the winding factors are lower, and it is proposed to employ unequal tooth widths to overcome this problem.
Zhang et al. [178] propose an SC-tolerant six-phase IPMSM with 12-slot 10-pole single-layer FSCWs. Excitation windings are inserted in the stator slots, yielding hybrid excitation. These extra windings are only fed in case a magnet demagnetization fault is detected. The magnetomotive-force harmonics due to the single-layer FSCWs, as well as the cogging torque, are attenuated by using asymmetrical (eccentric) air gap and unequal tooth width.
Prieto et al., present in [232] selection criteria for the phase, slot and pole numbers of multiphase PMSMs with FSCWs, so that negligible mutual inductance and high self-inductance are obtained. Both single- and double-layer windings are considered. Odd and even phase numbers between 3 and 7 are studied for double layer, whereas the even ones are ignored for single layer. Analytical expressions of the inductances are given. It is concluded that, for double layer, the odd phase numbers are preferred in this regard. On the other hand, single layer yields lower mutual inductance between phases, as aforementioned. In all these cases, certain relations between the number of stator slots Q and rotor pole pairs p are also advised; namely, it is recommended to set even for single layer (consistent with [233]), and to set for double layer with odd n.
A six-phase PMSM with 12-slot 10-pole single-layer FSCW is proposed by Jiang et al., in [100] for an aircraft fuel pump. Two three-phase VSCs are employed for driving the machine, instead of six H-bridges. The back-EMF harmonics and the cogging torque are reduced by modifying the permanent-magnet shape. Further information about the design procedure and the machine parameters are provided in [231].
In [477], although SC faults are not discussed, fractional-slot winding layouts with lower magnetomotive-force harmonic content than conventional FSCWs are devised, at the expense of some overlapping between different phase windings (but still much less than for distributed windings). Nonetheless, for these layouts it is relatively easy to insert coil separators in the end-windings. For the particular case of , the proposed 18-slot 8-pole winding involves three series-connected coils for each phase, with coil span of two slot pitches instead of one. An IPMSM with said winding is manufactured and tested. The spatial phase shift between the two three-phase winding sets is instead of as in conventional asymmetrical WSA, for optimizing the harmonic attenuation and the torque capability. Patel et al., present further analysis and details of this machine in [28] in the context of electric vehicles, including stator SC and OC faults. The low coupling between the two winding sets is exploited for performing independent control of each of them. If a stator SC of any type arises in a certain phase, SC is also applied to the other two phases of the same winding, as in other publications (see Section 5.3.1.1). This situation causes certain unbalanced magnetic pull that is not present in healthy drive, but it is claimed to be acceptable, given that this condition is only used during limp-home mode. The SC current is nearly identical to rated, with just excess. The degree of magnet demagnetization in this IPMSM under terminal SCs affecting three or six phases is analyzed in [176,177]. It is concluded that it is much lower than for a six-phase IPMSM with distributed windings [176]. In addition, the loss of torque capability after the resulting demagnetization is of small relevance, whereas it is significant for other faults, such as voltage reversal (although improbable [176]) due to, e.g., certain position-sensor failures [177].
Zhang et al. [263] propose and compare two IPMSMs with single-layer FSCWs for electric vehicles: a 12-slot 10-pole FSCW for and a 20-slot 18-pole FSCW for . Numerous figures of merit are evaluated, including SC current, back-EMF distortion, torque ripple, efficiency, flux-weakening capability, complexity, etc. The supply is based on a single n-phase FB VSC, using open-end windings. As in the previous work [178] of the authors, unequal tooth width and rotor asymmetry are optimized to reduce back-EMF distortion and torque ripple. In addition, the dimensions are set so as to maximize efficiency and minimize mass, while complying with the SC current limit. For , the magnitude of the third-order back-EMF harmonic is also reduced by design. It is concluded that, although both machines offer good performance and fault-tolerance, the five-phase PMSM exhibits lower mutual-to-self-inductance ratio, smaller torque ripple under SC and OC faults, better power density, less permanent-magnet material, and wider flux-weakening speed range than the three-phase PMSM, although with higher VSC and control complexity and slightly lower efficiency. Later, the machine design is improved in [209] by increasing saliency, so that it becomes more suitable for sensorless operation while keeping the high-tolerance to SCs (even slightly enhanced). In particular, flux-intensifying () behavior is obtained by adopting consequent-pole N–N permanent magnets, increasing eccentricity, adequately shaping the magnets, and adding a correctional tooth top. This also implies better torque-speed region and smaller risk of magnet demagnetization [209].
Special designs for tolerance to stator SC failures have also been proposed for dual-rotor PMSMs [249,272]. Guo et al. [272] consider a PMSM with two 8-pole rotors mounted on the same shaft, each of them with the corresponding five-phase single-layer 10-slot FSCW stator, supplied by 10 different phase currents. This results in more isolation and fault tolerance than a single ten-phase stator. Furthermore, a circumferential displacement is set between both segments so that cogging torque is reduced by [272]. On the other hand, the PMSM developed by Chen et al. [249] has an inner rotor and an outer one, in addition to a common stator yoke with an inner and outer five-phase winding. Both windings are fed by the same five-phase currents, unlike in [272]. The combination of inner rotor with inner stator winding can be regarded as an inner motor, whereas the outer rotor and winding form an outer motor [249]. This is of interest for hybrid and electric vehicles, mainly because they allow power split without mechanical gears. For fault-tolerant applications, this machine has to be designed so that not only high decoupling is obtained between different phases of the same motor, but also between both motors. Initially, single-layer FSCWs are used for both inner and outer stator windings, with identical slot/pole numbers. Several possibilities of slot/pole combinations are evaluated, and 40-slot 44-pole FSCW is finally chosen because torque and self/mutual inductance ratio rises with the pole number. It is also shown that congruent magnetization of the magnets in both rotors is preferred over in-opposition magnetization, since the former reduces flux saturation and, hence, results in lower magnetic coupling between motors and greater torque. Similarly, increasing the stator yoke thickness also decreases flux saturation and motor coupling, but the power density is lowered. In addition, while keeping the same number of slots and poles, single-layer, double-layer and a hybrid between both FSCWs (using ten modules, with 3 coils of the same phase wound around 3 adjacent teeth) are also compared. The hybrid proposal yields better magnetic decoupling, but worse torque ripple.
Up to this point, most of the aforementioned multiphase SC-tolerant machines are PMSMs. However, an inherent problem of PMSMs, as stated above, is that the magnet field cannot be turned off when a fault occurs. As a consequence, the SC current tends to be particularly large [242] and uncontrolled rectification may occur, producing further damage (e.g., if the generated power is excessive, or if the sudden braking torque causes a mechanical accident) [244]. For this reason, Wang et al. [244] propose a nine-phase fault-tolerant drive in which most of the output torque is due not to permanent magnets but to reluctance, i.e., a PMaSynRM. On the other hand, to increase isolation between phases without resorting to FSCWs (with extra back-EMF distortion and rotor losses), the stator overlapping winding is based on three sectors, each of them driven by a three-phase HB VSC. For the machine design it is considered, similarly to other publications, that if an SC or OC fault occurs in a certain phase, the other phases of the same three-phase set are, respectively, shorted (see Section 5.3.1.1) or opened by means of the corresponding VSC switches. Despite installing overlapping windings instead of FSCWs, the SC current is still of small magnitude, thanks to the low permanent-magnet flux. Extensive experimental tests are performed in [244], including thermal results during SC faults, and even more experiments are discussed later in [242]. A modeling approach of this PMaSynRM using four-dimensional tables and taking into account the behavior under SC and OC faults is presented in [245], and extended in [235]. In [129], significant attention is paid to different types of stator SC faults, and other kinds of drive failures are also addressed. Further details about the design optimization (efficiency, turn-fault current and temperature, rotor dynamics, mechanical stress, etc.) are given in [167]. Comprehensive thermal modeling and evaluation of the PMaSynRM under stator SC faults can be found in [98,237,238], which is important not only for the machine design but also for assessing how fast turn faults should be detected and mitigated.
Chen et al. [267] propose a five-phase PMSM with open-end 10-slot 12-pole FSCWs fed by ten-leg FB VSC for the liquid-oxygen engine of a rocket, working at very low temperature (SCL becomes less important compared with iron loss). The stator teeth and yoke are set small to reduce iron losses. The stator winding differs from conventional single- or double-layer FSCWs; namely, each phase consists of two coils wound around consecutive teeth in opposite directions (to reduce mutual coupling, as in [221]), while coils of different phases are separated by another tooth, which has shorter width. The presence of this small tooth improves the isolation between phases, also in terms of magnetic coupling, because the mutual inductance is further reduced in this manner. In addition, thermal insulation is placed in both sides of each small tooth. It is also shown that IPMSMs are preferred over SPMSMs in the sense that the former result in much smaller SC current and hence lower risk of demagnetization.
Wang et al. [268] propose an axial-flux coreless PMSM with single-layer FSCW, fed by independent H-bridges. The machine structure consists of multiple stator and rotor discs alternated along the axial direction. Alternatives with four, five, and six phases are analyzed, and the five-phase one is selected because of its better characteristics. A multi-objective optimization procedure is presented as well. It is shown that under turn SC faults the air-gap flux is barely affected, not only due to the FSCW, but also because of the high magnetic resistance associated with the absence of core [268] (at the cost of greater magnet volume for given flux linkage [500]).
Li et al. [262] perform a reliability analysis based on Markov model of several kinds of multiphase windings, taking stator SC and OC faults into account. Phase numbers n of three, four, five, six, and nine are compared, as well as single-layer FSCW, double layer FSCW, single-layer distributed winding, and double-layer distributed winding. The mean time between failures is computed for each case, considering operation with torque below of rated as a failure. SC faults are assumed to be converted into OC ones if they are severe, and otherwise they are neglected. It is concluded that, for a given n, the four studied configurations can be sorted from highest to lowest reliability in the same order as they have just been mentioned. This is consistent with the fact that SCs between end windings and between different coils within a slot normally only occur for overlapping and double-layer windings, respectively. Regarding the phase number, it is shown that reliability increases with n for FSCWs, but for overlapping windings it depends on the failure rate of each type of fault.
Wang et al. [246] compare numerous six-phase PMSM designs with FSCWs for a fault-tolerant aircraft starter generator. A multi-objective optimization process based on a genetic algorithm is employed for selecting the optimum design. The slot/pole combinations with low winding factor are discarded. The main figures of merit being considered are electrical, magnetic, and thermal isolation; efficiency; weight; and peak SC current. Among the various alternatives, a two-sector double-layer 18-slot 12-pole FSCW is chosen because of its high power density (7.9 kW/Kg) and postfault performance (limited SC current). The permanent magnets are installed as a Halbach array. Huang et al. [241] briefly point out (the paper is focused on current control) that Halbach array magnets can be adopted for reducing the back-EMF distortion of a five-phase SPMSM with single-layer 10-slot 8-pole FSCW.
Park et al. [247] compare three alternative overlapping winding layouts for a six-phase SynRM with 36 slots and 8 pole pairs (see Table 10): asymmetrical WSA, two-sector WSA [similarly to Figure 4a] and four-sector WSA [see Figure 4b]. Although the four-sector arrangement is the least common, it is analogous to, e.g., that studied in [230] for a PMSM, in [261,436] for an IM, and in [450] for another SynRM. In both two-sector and four-sector WSAs the mutual inductance between three-phase sets is very small. Under stator/switch OCs and SCs, the torque ripple is lower and average torque is much higher for multisector WSAs than for asymmetrical WSA. As an exception, torque ripple is lower for the latter under three-phase SC, and, in healthy conditions, the mean torque is moderately greater for the latter because of its larger winding factor. In summary, it is concluded that in general the multisector WSAs are preferred for the fault-tolerant six-phase SynRM [247] over the asymmetrical WSA. Interestingly, this differs to some extent from the conclusion drawn by the same research group in [258,259] regarding six-phase PMSMs (where symmetrical is preferred over multisector WSA), because of the different types of machines (SynRM versus PMSM).
5.3.3. Current Control
In addition to adopting suitable drive topologies, topology reconfigurations and machine designs, special current control strategies may also be implemented to further improve the performance in the event of stator SCs (see Figure 11). In particular, as surveyed next, current control can be used to reduce the SC current under phase (Section 5.3.3.1) or turn (Section 5.3.3.2) SCs, or to compensate the torque ripple caused by phase (Section 5.3.3.3) or turn (Section 5.3.3.4) SCs. The various techniques of each of these four kinds of approaches are summarized in Table 12, Table 13, Table 14, and Table 15, respectively, following the same order as in the text.

Table 12.
Current control method for reducing SC current under phase SCs (Section 5.3.3.1) in multiphase applications in the literature.
Table 12.
Current control method for reducing SC current under phase SCs (Section 5.3.3.1) in multiphase applications in the literature.
| Reference | Machine | Special Current References | Current Controller | Salient Features |
|---|---|---|---|---|
| Mohammadpour and Parsa [252] | PMSM | In healthy phases, for reducing SC current | Hysteresis | General; large current |

Table 13.
Current control methods for reducing SC current under turn SCs (Section 5.3.3.2) in multiphase applications in the literature.
Table 13.
Current control methods for reducing SC current under turn SCs (Section 5.3.3.2) in multiphase applications in the literature.
| References | Machine | VSC Leg/s of Faulty ph. | Special Current References | Current Controller | Salient Features |
|---|---|---|---|---|---|
| Mitcham/Arumugam et al. [223,227] | PMSM | Switching | In faulty ph., 90 lagging back-EMF | − | Simple |
| Wu et al. [96] | Asym. 6-ph. SPMSM | Switching | with 1st and 3rd harmonics | − | 3rd harm. |
| Wang et al. [224] | 3×3-ph. PMaSynRM | Switching | In faulty set, for reducing SC current | − | 3-sector |
| Gerada et al. [253] | IM | Switching | Reduced | Hyst. or multiple PI | IM; idle |
5.3.3.1. Reduction in SC Current under Phase SC
An SC between the terminals of a certain phase does not require further action if the machine is properly designed (see Section 5.3.2) to ensure low SC current in such a case. Nonetheless, it is possible to set specific current references in the healthy phases so as to cancel the flux linkage (and hence current) through the entire shorted phase, as considered for PMSMs with (using FB VSC) in [501] and with any n in [252]. However, in many PMSM drives this option may require huge current amplitudes in the healthy phases, especially if the magnetic coupling between phases is low, and is thus deemed of limited practical interest [252].
5.3.3.2. Reduction in SC Current under Turn Fault
As discussed in Section 5.3.1.1, in case of turn fault in a PMSM, an SC can be applied to the affected phase/s by the VSC switches, so that the flux linkage through the shorted turn/s is naturally reduced and, hence, the SC current decreases as well [240]. However, often the resulting SC current is still higher than rated, especially with turn fault/s close to the slot opening in PMSMs using conventional conductors (e.g., stranded windings or horizontal rectangular bars) instead of vertical ones [223,227,495], or in machines with distributed (overlapping) windings [167,224]. Moreover, even if the fault current does not surpass the rated value, it is still of great interest to reduce it by means of the drive topology (already explained in Section 5.3.1) or control (as discussed next), so that the machine torque density and efficiency can be enhanced [236].
Mitcham et al. [227] propose a control method for turn-fault mitigation (see Table 13), considering a five-phase PMSM with FSCW and horizontal rectangular conductors. Instead of applying a terminal SC, the current of the phase affected by the turn failure is controlled (by the respective VSC leg) with a certain magnitude and with phase angle of lagging the back-EMF, so as to decrease the flux linkage through the shorted turns. In this machine [227], injecting a phase current of about rated magnitude in this manner is enough to reduce the current through a shorted turn to nearly rated, in the worst-case scenario (one shorted turn close to air gap). In order to accommodate this additional current, the drive should be overrated or its output power substantially derated after fault [223]. To avoid imposing the requirement of detecting which specific turn/s suffer a fault, it is suggested [227] to set the amount of current injection such that the best result is obtained for most of the potential turn-fault scenarios.
Arumugam et al. [223], besides comparing different SC-tolerance methods, adapts the preceding turn-fault alleviation technique [227] to conventional (stranded) conductors instead of horizontal bars. It is, however, pointed out that, due to model uncertainties, it is difficult to achieve a significant reduction in the SC current in this manner. Theoretically, the ideal current to be supplied depends on the number of shorted turns and on the failure location. For this reason, the authors recommend in [223] to instead use vertical rectangular conductors and simply apply terminal SC to the faulty phase through the VSC without special current control, as in [222] (reviewed in Section 5.3.1.1).
Wu et al. [96] show that injecting negative -axis current with both fundamental and third-order components can substantially reduce the peak SC current if the machine has non-negligible third-order back-EMF harmonic. A six-phase SPMSM with single-layer FSCW, asymmetrical WSA, fed by H-bridges and with a shorted turn is considered.
For a nine-phase three-sector PMaSynRM with overlapping windings and a turn fault in one of its three-phase winding sets, Wang et al., propose in [224] to inject adequate stator currents (computed by two linear equations) in the affected three-phase set, so that the flux linkage through the shorted turns is reduced. In this manner, the associated SC current decreases as well (compared with, e.g., applying a three-phase terminal SC; see Section 5.3.1.1), analogously to the aforementioned approaches for conventional (not multisector) PMSMs with FSCWs [223,227]. A remarkable characteristic of this method [224] is that it does not require knowledge of the specific fault location, just which of the winding sets is the affected one. The currents in the other two winding sets (healthy) are still controlled to yield the required torque, in contrast to similar approaches for [502], where torque capability was lost.
In the preceding cases, the SC current was due to magnet flux linked by the shorted turns, which cannot be deactivated. Synchronous machines without magnets (e.g., switched reluctance or SynRMs) do not have this drawback, but their power density is lower [240]. In IMs, as shown in [253] for and , the rotor flux is naturally reduced by the shorted turns to some extent, and it can be further decreased through , so as to bring down the fault current to an acceptable magnitude. However, torque capability is then lost, with the IM being only able to operate in idle mode [253].
5.3.3.3. Reduction in Torque Ripple under Phase SC
Broadly speaking, under stator SC faults the air-gap magnetic field should be kept as close as possible to healthy operation, in order to avoid torque pulsation [101,239]. In particular, if space harmonics are neglected, this means that the stator current should describe a circle in the - plane. Moreover, the remaining current DOFs are often set so as to also minimize the drive losses (typically focusing on SCL) while obeying the voltage and current constraints; this is frequently referred to as MLS. In addition to the system restrictions present during healthy operation (maximum values, absence of zero-sequence current path, etc.), the event of OC or SC faults introduces extra constraints (coupling between variables) that should also be regarded. The current references, VSD transform, current control scheme and modulation method should satisfy all these conditions after a fault occurs. This is analogous to the scenario of phase OCs, which will be discussed in Part 2. Given that the literature about OC faults is far broader than about SC ones, the reader may acquire in Part 2 a much deeper understanding concerning the concepts about deriving optimum control for avoiding torque fluctuations under fault conditions. In fact, some of the control techniques surveyed here concerning torque ripple minimization during SC faults are also suitable for phase OCs, and they will be described in more detail in Part 2; in contrast, the following description mainly focuses on the particularities related to stator SCs.
Most publications about control for smooth torque with stator SCs are centered on the particular case of phase SCs. They are summarized in Table 14. One of the main features of these SCs, unlike turn faults [224,227], is that under phase SCs the current through the faulted phase cannot be directly controlled [257]. For a phase SC, even if the converter leg corresponding to a shorted phase is switching, it does not have influence on the SC current. That is, a current DOF is lost. This aspect is similar to the behavior under phase OC; nonetheless, the SC current causes additional torque pulsation, which further complicates achieving ripple-free torque compared with OC failures [257].

Table 14.
Current control methods for reducing torque ripple under phase SCs (Section 5.3.3.3) in multiphase applications in the literature.
Table 14.
Current control methods for reducing torque ripple under phase SCs (Section 5.3.3.3) in multiphase applications in the literature.
| References | Machine | Special Current References | Current Controller | Salient Features |
|---|---|---|---|---|
| Ede et al. [163] | PMSM | MLS | − | − |
| Atallah/Wang et al. [164,165] | PMSM | MLS | − | Field-weakening |
| Sun et al. [162] | 5-ph. SPMSM | MLS | Multiple PI | Field-weakening |
| Bianchi et al. [254] | 5-ph. SPMSM | Cancel 2nd & 4th torque harms. | − | Simple; 3rd harm. |
| Mohammadpour et al. [251] | PMSM | Iterative learning control | Multiple PI | Robust |
| Xu et al. [265] | Sym. 6-ph. SPMSM | Robust speed control | Multiple PI | Robust; ripple |
| Guo et al. [272] | Dual 5-ph. SPMSM | Robust speed control | − | Robust |
| Mohammadpour & Parsa [252] | PMSM | MLS | Hysteresis | General; harms. |
| Wu et al. [220] | Asym. 6-ph. SPMSM | MLS | Hysteresis | 3rd harm. |
| Sen et al. [166] | PMSM | MLS | Per-ph. multi-resonant | Field-weak.; harms. |
| Zhou/Chen et al. [255,257] | 5-ph. IPMSM | − | Reduced VSD + PI + SC curr. FF | Fast; sensors; not robust |
| Zhou et al. [256] | 5-ph. IPMSM | − | DTC * + disturbance observer | Robust |
| Jiang et al. [101] | Sym. 6-ph. SPMSM | − | RFOC + modified SV PWM | Topology |
| Si et al. [239] | 4-ph. SPMSM | Constant torque (single solution) | − | Topology |
| Huang et al. [241] | 5-ph. SPMSM | Equal phase-current amplitudes | − | High torque; not MLS |
| Yin et al. [234] | 5-ph. SPMSM | No -axis current constraint | − | High torque; not MLS |
* Note that, strictly speaking, in DTC the current is not controlled directly.
Two decades ago, Ede et al. [163] presented an approach to generate the optimum current references for a multiphase PMSM under phase SC or OC faults. The method of Lagrange multipliers is used to minimize the SCL (it is an MLS) while providing ripple-free torque. Although the current limits are not included in the definition of the optimization problem, it is advised in [163] to repeat the process when it is observed that some of the solution per-phase values do not comply with them, limiting the respective variables. (The limitation of currents and voltages to their maximum values is effectively included in the optimization problem as inequality constraints in the so-called full-range MLS (FRMLS), explained in Part 2 with regard to generation of current references for phase OC faults). The field-weakening operation is taken into account in [165] by adding to the Lagrange function the magnitude of the ac voltages, weighted by a certain factor that depends on speed and torque; however, maximum torque-speed region and minimum SCL per point of operation is not completely guaranteed in this manner. The results are obtained for a four-phase PMSM with single-layer 8-slot 10-pole FSCW in [165], and for a five-phase PMSM with single-layer 10-slot 12-pole FSCW in [164]. No details are given about the current controller adopted to track these references.
The strategy from [164,165] is further enhanced by Sun et al., in [162]. More specifically, the torque-speed region is extended by adaptively adjusting the weight factor of the ac voltages in the Lagrange function of the optimization problem. This modification is applied in closed-form formulas for the current references that were priorly obtained offline by solving said minimization problem. In each sample, the variation introduced in the weight factor depends on the deviation between the reference and estimated torque. In any case, minimum SCL for each scenario is still not ensured. PI current control is implemented in each phase.
Instead of solving a complex optimization problem, Bianchi et al. [254] propose to compute the current of a phase affected by terminal SC (based on the machine model) and then to solve for the other phase currents so that the second- and fourth-order harmonics of the torque ripple are cancelled. For this purpose, the third-order current harmonic is taken into account. The most salient feature of this approach is its simplicity, although it may not be the optimum solution in terms of minimum torque ripple and losses. A five-phase PMSM with double-layer 20-slot 18-pole FSCW is considered. No attention is paid here, either, to the control scheme for tracking the current references.
Mohammadpour et al. [251] devise a technique to generate suitable current references for tolerating phase SC or OC failures while adaptively rejecting torque ripple. The references are obtained based on iterative learning control, using the measured/estimated torque error as input. This scheme is able to compensate torque oscillations due to uncertain causes, without information about the nature of the fault. In exchange, the SCL is not necessarily the lowest possible. Alternatively, this adaptive method can be combined in parallel with a non-adaptive one that does minimize the SCL, provided the fault is properly diagnosed. The proposal is tested in a five-phase PMSM with star connection and current control based on PI controllers and SV PWM.
Other methods for automatically adapting the current references under stator SCs/OCs without fault information are presented by Guo et al. [272] and Xu et al. [265]. The current references are provided by a speed controller based on robust control law, and the main goal is to ensure satisfying transient responses when the fault occurs, before it is detected. Namely, the settling time and the peak of the speed deviation after the fault are substantially reduced, in comparison with conventional linear control. Further research is expected in order to enhance the current and torque ripple, especially for the technique from [265].
A general procedure is proposed by Mohammadpour and Parsa in [252] to obtain the optimum current references under stator SCs or OCs. Torque ripple and SCL are effectively minimized by using Lagrangian multipliers. Thanks to the use of instantaneous values, harmonics are implicitly taken into consideration. A great variety of fault scenarios are evaluated for five-phase PMSMs: various stator phase connections (star, pentagon, and pentacle), simultaneous faults in adjacent or non-adjacent phases, etc. The optimum solutions for a given drive can be obtained offline for multiple fault conditions, and stored in look-up tables for online execution. However, the current and voltage maximum values are not taken into account in the optimization problem, unlike the so-called FRMLSs that would be later proposed for phase OCs (discussed in Part 2). Experimental evaluation is performed with a five-phase star-connected PMSM driven by hysteresis current control.
A control method is designed by Wu et al., in [220] for minimizing torque ripple in an asymmetrical six-phase PMSM with FSCW driven by dual VSC using open-end windings (not considered, e.g., in [252]) and with non-negligible space harmonics (mainly third-order) under a stator phase SC. Analytical expressions are derived, by using a Lagrange multiplier, for the optimum current references in the healthy phases, which are imposed by hysteresis control. The copper loss and torque pulsation are notably reduced when the back-EMF third-order harmonic is taken into account in the references rather than ignored.
Sen et al. [166] propose to use multi-resonant current control in per-phase coordinates to track the references (unbalanced and distorted), overcoming inability of conventional PI controllers [162] to follow this kind of reference, and avoiding the problems associated with the variable switching frequency of hysteresis control (electromagnetic interference, switching loss, etc.). Special attention is paid to the controller design. A five-phase PMSM with single-layer FSCW and star connection is considered. A third-order harmonic is taken into account in the back-EMF and stator current. The current references are set similarly to previously mentioned publications where the magnitude of the ac voltages were included in the Lagrange function [162,164,165], but in this case an additional current constraint (null zero-sequence current) is included because of the usage of star connection and HB VSC instead of FB VSC. Furthermore, the online adaptation of the weight factor for the ac voltages is performed based on the excess of VSC output voltage instead of the torque error.
Zhou et al. [257] develop a control method for providing smooth torque in a five-phase star-connected IPMSM with FSCW (the one from [250]) under phase SC. The phase SC failure is treated as a combination of a phase OC (the current of faulty phase cannot be controlled) and an SC one (torque ripple due to SC current). The VSD transform is replaced by a reduced-order one to tackle the former (based on [381]), and the latter is addressed by adding a feed-forward (FF) compensation to the control scheme. Synchronous PI current control is implemented in each subspace. The FF term is based on the measurement of the SC current through the shorted phase. In addition to preventing pulsating torque, this approach also provides fast dynamic performance. A few years later, the method from [257] was extended for double-phase faults in [255]. A difficulty for implementing these proposals is that measuring the current within the shorted phase windings is not straightforward [256]. Moreover, although these techniques [255,257] are effective and fast, the FF compensation may not completely cancel the disturbance in case of significant uncertainties, such as machine and converter non-idealities. For this purpose, it may be possible to simply combine the fast dynamic response of the proposed FF compensation with additional control poles in the - plane for ensuring complete steady-state disturbance cancellation. The latter part (extra poles) would be analogous to existing fault-tolerant control methods for [503] or [166], where both positive- and negative-sequence components are controlled with zero steady-state error by corresponding synchronous PI controllers. Another possibility, proposed in [256] for a five-phase PMSM controlled by DTC, is to add a torque disturbance observer, which is able to compensate disturbance uncertainties without measuring the SC current/s.
In [101] (Jiang et al.), the two three-phase star-connected winding sets of a six-phase PMSM with FSCW are controlled independently, using RFOC and a VSC including a redundant leg (see Figure 12). When a phase SC arises, the voltage vector table of the SV PWM is modified to provide the same - components as in healthy operation.
Current references for smooth torque in a four-phase PMSM under terminal SC are provided in [239] by Si et al., when the machine is star-connected and supplied by an HB VSC (obtained, e.g., after reconfiguration in Figure 13 due to certain device faults [239]). These references are the only possible solution for keeping the magnetomotive force as in healthy conditions, given that only two current DOFs remain.
Huang et al. [241] propose a technique for generating the current references, for a five-phase PMSM with single-layer FSCW under phase SC driven by FB VSC, so that the amplitudes of all healthy phase currents are identical. Similarly to the so-called maximum-torque strategy (MTS) for stator OCs [24], this means that the SCL and, hence, heat dissipation is distributed evenly among healthy phases, and that the achievable postfault torque (without VSC oversizing) is maximized [241]. In contrast to conventional MTS for phase OCs, the non-zero current of the faulty phase (which affects torque) is taken into account in the derivation, and the relative phase angles of the phase currents are adjusted with the torque reference as another DOF. However, the resulting SCL is not minimized, unlike for MLS. Back-EMF harmonics are disregarded, since they are reduced by using Halbach array magnets.
Another strategy for generating phase-current references with equal amplitude for a five-phase SPMSM is presented by Yin et al. [234]. The main contribution is that the -axis current is set optimally for maximizing the torque, instead of setting it to zero.
Apart from the control methods reflected in Table 14, Wang et al. [243] present a detailed analysis of the behavior of the nine-phase three-sector PMaSynRM from [244] under phase OC/SC faults, emphasizing the need to include additional current control poles in order to compensate second-order torque oscillations. A control technique to tackle this goal may be addressed in the future.
5.3.3.4. Reduction in Torque Ripple under Turn Fault
All the aforementioned current-control techniques for torque ripple minimization under SC faults are focused on the particular case of phase SC (except a brief mention of turn faults in [252]), i.e., SC between both terminals of a stator phase. Nonetheless, there are also a few publications (see Table 15) where this control problem is addressed for turn faults instead of phase SCs.

Table 15.
Current control methods for reducing torque ripple under turn SCs (Section 5.3.3.4) in multiphase applications in the literature.
Table 15.
Current control methods for reducing torque ripple under turn SCs (Section 5.3.3.4) in multiphase applications in the literature.
| References | Machine | VSC Leg/s of Faulty ph. | Special Current References | Current Controller | Salient Features |
|---|---|---|---|---|---|
| Mohammadpour and Parsa [252] | PMSM | Switching | MLS | Hysteresis | General; harms. |
| Wu et al. [96] | Asym. 6-ph. SPMSM | Terminal SC | MLS | Hysteresis | Low SC current |
| Cui et al. [94] | 5-ph. IPMSM | Switching | − | - PI + zero-seq. current FF | Fast |
| Fan et al. [248] | 5-ph. IPMSM | Open | − | Reduced VSD + PI + voltage FF | Fast; open leg |
The general method proposed by Mohammadpour and Parsa in [252] for deriving current references for minimum copper loss and torque oscillations can be applied for shorted turns, since some recommendations are also given in this regard therein. However, the references are tracked by hysteresis control, whose variable switching frequency may increase electromagnetic interference and switching loss [166,257], as aforesaid. Moreover, minimization of the flux-linkage and current through specific shorted turns (e.g., as in [224,227]; see Section 5.3.3) is not studied. Similarly, current references derived by using Lagrange multipliers are imposed by Wu et al., in [96] by means of hysteresis control, although in this case terminal SC is simultaneously applied in the faulted phase to reduce the SC current.
A technique for compensating torque pulsation under turn faults is devised by Cui et al., in [94] for a five-phase hybrid-excitation IPMSM with open-end single-layer FSCWs fed by FB VSC using SV PWM. Namely, it is found that the torque ripple is due to an oscillating -axis current disturbance introduced by the turn SC into the - plane, and accordingly it is proposed to cancel this component in the FF manner, based on the zero-sequence current. Conventional PI current controllers in positive-sequence rotating frame are included in the - plane. The main differences with [257], besides dealing with turn faults instead of phase SCs, are that the FF term is computed from the zero-sequence current instead of the SC current, and that the VSD complete transform is employed instead of a reduced one. However, active minimization of the current within the shorted turns [224,227] is not taken into account in [94] either.
The same authors provided further work on this subject in [248], for a similar type of ac drive. In this case, when the turn fault is detected, the connections between the VSC and the respective phase are opened, to avoid the current through the healthy part of the phase. In addition, a voltage sensor is then connected to the terminals of this phase. This voltage measurement is employed to obtain an estimate of the disturbance introduced by the fault into the - plane, so as to compensate it by means of an FF, analogously to their previous work [94]. A reduced-order VSD transform is adopted during fault operation, with PI controllers in each subspace. Although opening the phase affected by the fault was previously considered in [257], the latter paper addressed phase SC faults, where the SC current cannot be directly controlled by the converter. In contrast to phase SCs, for turn faults the faulted phase can be shorted [240] or its current can be controlled by the respective VSC leg/s [224,227] to mitigate the flux linkage in the shorted turns and, hence, avoid excessive current through them; thus, the fact that this possibility is not exploited in [248] can be considered a shortcoming of this strategy.
It is worth mentioning that, as pointed out regarding the FF technique from [255,257] for phase SCs, the steady-state behavior under uncertainties of these FF methods for turn faults [94,248] might be straightforwardly improved by adding extra control poles [166,503] or a disturbance observer [256] as well. In addition, it would be of interest to improve these control approaches, aimed at constant torque during SC faults, by combining them with control strategies to minimize the current through the shorted turns (see Section 5.3.3).
5.3.4. Flux Shunt
It is possible to install and opportunely activate a physical mechanism to decouple from the rotor flux certain stator slot/s affected by SCs, either mechanically or electrically [223]. The mechanical shunt is able to short a slot opening with magnetic wedges, by means of a spring. However, the spring may jam, reducing reliability. In addition, this approach results in smaller fill factor and increased copper loss [223]. On the other hand, an electrical shunt is based on placing magnetic wedges and an auxiliary control winding in the slot opening. During normal operation this winding is energized, so that the wedges are saturated and, hence, the rotor flux is linked by the slot winding turns. In case of fault, the auxiliary winding supply is disconnected and the rotor flux is thus shunt. In addition to reduced fill factor and additional copper loss, this technique also implies a reduction in the average torque for healthy operation [223]. Due to these drawbacks, barely any applications of these methods are reported in the literature.
5.4. Concluding Remarks about Stator SC Faults
Stator SCs are especially troublesome faults that require specific and elaborate measures to be tolerated, especially for PMSMs and for SCs involving just a few turns.
This kind of fault may be detected in multiphase drives by adopting methods analogous to some of those for three-phase drives [498,499], principally in those cases where each phase or three-phase set is treated independently. In fact, many of the detection techniques proposed for multiphase machines are presumably also valid for three-phase ones, such as those based on monitoring the torque [94] or either the low-frequency [100,101] or high-frequency [90,92,93,96,99] components of the phase (not VSD) currents. Some others, which rely on the instantaneous power [97], zero-sequence voltage [61], or zero-sequence current (for FB VSC) [91], could also be extrapolated to three-phase systems without significant modifications. On the other hand, there are some approaches that keep track of the asymmetries produced by the stator SC in the secondary VSD planes [88,89], thus exploiting the particular features of multiphase drives. In any case, most of the detection methods are designed specifically for turns SCs in PMSMs [88,89,90,91,92,93,94,96,99], and only some of them [61,89,99,100] have been proved to be able to distinguish from other (although few) faults.
Concerning tolerance, in the first place, it is critical to design the machine with stator SCs in mind, which has attracted much attention in scientific publications up to present days. Namely, a substantial degree of magnetic, electric, thermal, and mechanical isolation between phases is normally sought. Moreover, high self-inductance is desirable for limiting SC current in PMSMs. These properties are most notably provided by FSCWs [240,266]. Although FSCWs are in principle not suitable for IMs, they yield excellent performance in, e.g., PMSMs, SynRMs and PMaSynRMs. Using multisector WSA also exhibits better decoupling between phases (of different sectors) than conventional winding arrangements and is, thus, another possible solution for this kind of failures [27]. In addition, using vertical conductors within slots can also be helpful for preventing excessive SC current in case of turn faults close to a slot opening, at the expense of higher ac losses [223,227,495]. From Table 10, the most popular multiphase machines for tolerating stator SCs are arguably symmetrical six-phase SPMSMs with single-layer 12-slot 10-pole FSCW [100,101,128,163,165,210,211,231,265]. A lot of research has also been performed recently about a nine-phase three-sector PMaSynRM with overlapping windings [97,98,129,167,224,235,236,237,238,242,243,244,245,270], although this one has only been employed by a single research group in the literature so far. Based on the preceding survey, it can also be pointed out that innovative machine structures and winding layouts are still being designed nowadays for multiphase drives with tolerance to stator SCs with excellent unprecedented features (see, e.g., [209,244,249,267,268,272]).
Traditionally, a common procedure to reduce the SC current in the event of a turn failure is to externally apply an SC to the affected phase [93,99,240] or winding set [27,230,236,247,258,265] by means of the VSC switches. In any case, even lower fault current can be obtained by actively controlling the current in such phase/s for this purpose, as later proposed in various publications [96,223,224,227,253]. Current control for compensating torque ripple under SC faults has also been addressed in the literature, for both phase SCs [101,162,163,164,165,166,220,239,251,252,254,255,256,257,265,272] and turn SCs [94,96,248,252]. The investigation of current control techniques under stator SCs for either of these two objectives (reducing current in shorted turns or torque ripple) is emerging as a strong trend in the recent literature. However, devising control approaches for simultaneously achieving both goals at the same time has not (or scarcely) been considered so far and may be the subject of future work. It may also be interesting to combine the control techniques based on adding extra poles and those based on feed-forward terms in order to bring together their respective advantages in terms of robustness to uncertainties and fast response.
Allowing the flow of zero-sequence current often makes it possible to increase the tolerance to this kind of fault. For instance, in case of adopting three-phase HB VSCs, it is recommended to include zero-sequence current paths (e.g., using delta connections or legs for neutral-point clamping) [236,270], so that the zero-sequence flux-linkage through shorted turns (and thus SC current) is naturally reduced. Alternatively, it may be decided to employ a VSC that permits actively controlling the zero-sequence current for enhanced postfault performance at the expense of a higher number of devices, such as FB VSCs [89,93,94,95,96,99,128,130,162,164,165,210,211,212,223,227,228,233,240,248,263,264,265,266,267,271] or more advanced VSC topologies [101,239].
It can be noted that there are some accomplishments that have been achieved for stator OC faults (addressed in Part 2) and not (or barely) for SC faults, which may, therefore, also be tackled for the latter more exhaustively in the next few years. Some of these possibilities include, e.g., control techniques able to provide high postfault performance without fault detection and scheme reconfiguration (reconfiguration-less methods, proposed in [126,280,323,332,335,336,337,338] for stator OCs and just in [251,265,272] for SCs), or strategies for generating postfault current references with minimum losses at each possible operating point in the full speed-torque range taking the maximum current/voltage values into account in the optimization problem (i.e., FRMLSs, as in [22,170,214,300,308,313,314,315,319,326,343,344,352,355,356,408] for stator OCs).
Moreover, since IMs are regarded as poor candidates for tolerating stator SCs (especially turn SCs), it might also be desirable to perform further research (e.g., extending the work from [253,261]) with the goal of improving their characteristics in this regard.
Finally, it is worth pointing out that most of the literature is focused on SCs between both terminals of a stator phase or between turns of a given phase, but SCs between coils or terminals of different phases [129] have received almost no attention for the moment.
6. Switch SC Faults
Any switch of a VSC in a motor drive may suffer an SC fault. Similarly to other types of failures, this is expected to degrade the drive behavior substantially and lead to further damage if it is not properly handled. In fact, switch SCs can be considered more dangerous than, e.g., switch or stator OCs, since SCs can easily result in very high currents through the VSC and machine. Regardless of whether the SC arises in a transistor itself or in its corresponding free-wheeling diode, the effect of the SC failure is in general equivalent in both cases and can be treated in the same manner. Figure 14 summarizes the most relevant methods from the literature for detecting and tolerating switch SCs in multiphase drives, as well as the causes that give rise to these failures.
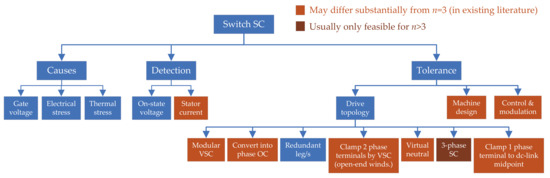
Figure 14.
Causes, detection methods, and tolerance approaches for switch SC faults in multiphase drives.
6.1. Causes of Switch SC Faults
SC faults in switches such as IGBTs are normally caused by either a wrong gate voltage (e.g., due to driver malfunction) or by an intrinsic failure produced by excessive voltage, current, or temperature [504].
6.2. Detection of Switch SC Faults
When a switch SC occurs, it is crucial to detect it soon and turn off the other switch of the leg to prevent dc-link SC [168,273]. In addition, other tolerant actions (surveyed shortly) may be applied after the failure is detected. Fortunately, modern switch drivers are usually able to detect SCs (e.g., by specific hardware circuits [504]) and they provide a signal to indicate these faults [119,168]. This may be the main reason why the recent literature about detection of switch SCs is scarce. Nevertheless, a few publications dealing with this topic can be found in the context of multiphase drives [99,103].
In [99], switch SCs are detected by simply monitoring the on-state voltage drop across each switch and comparing it with its expected value. The method is able to distinguish between switch SCs and other types of faults, such as stator SCs.
Salehifar et al. [102] propose to trigger the fault alarm when the cost function of a current FCS-MPC surpasses a predefined threshold. The faulty switch is located by a phase-current observer based on the machine model. SC and OC faults are distinguished depending on whether the respective phase current is null.
The case of an asymmetrical six-phase PMSM driven by a n-phase T-type three-level VSC [see Figure 8i] is studied by Wang et al., in [103]. In the first step, the faulty phase is identified by means of the current trajectory in the x-y plane. In this stage, a subset of possible phase OC, switch OC and switch SC possible faults are also selected. Then, in the second step, the current value in that particular phase is also used to identify the specific faulty switch and type of failure.
6.3. Tolerance to Switch SC Faults
In accordance with Figure 14, the strategies to tolerate switch SCs can be mainly divided into those related to the drive topology (Section 6.3.1), the machine design (Section 6.3.2), or to the control and modulation (Section 6.3.3).
6.3.1. Drive Topologies
Among the methods for tolerating switch SCs, those concerning the VSC topologies and their postfault reconfiguration have received special attention in the literature.
6.3.1.1. Increasing Isolation by VSC Modularity
Supplying the machine via separate VSC modules improves the electrical isolation, which is, in principle, helpful for tolerating switch SC (and other) faults [27]. This is especially important if it is decided to avoid extra devices for isolating the shorted switches from the rest of the VSC, although it is also helpful, e.g., in case these elements are actually included but they also fail. Otherwise, e.g., if the VSC is not modular and two shorted switches are not isolated, they can cause an SC of the dc link that would affect the entire drive instead of just a VSC module [27].
The highest degree of VSC modularity and hence of electrical isolation is obtained by using H-bridge modules to feed each phase [240]. For instance, multiple H-bridges are considered in [99,130,240] for tolerating switch SC faults in multiphase drives. This benefit in isolation comes at the expense, however, of increased complexity, cost, size, and losses [373]. Additionally, the conventional tolerant action for non-isolated switch SCs when using H-bridges, i.e., clamping both terminals of the affected phase to a dc-link rail, can lead to high uncontrolled zero-sequence currents (discussed in Section 6.3.1.4) [13]. Using three-phase HB VSCs or two n-leg HB VSCs, e.g., does not offer as much electrical isolation as single-phase ones; nevertheless, the isolation (modularity) is still higher than in an n-phase VSC with common dc link, it is simpler than installing n H-bridges [244,373], and it avoids the zero-sequence current associated with FB VSCs [13,273]. For multiphase drives that are tolerant to switch SCs, topologies based on three-phase HB VSCs are employed in [27,168,235,243], and dual HB VSCs in [273].
Nonetheless, obtaining electrical isolation between VSC modules may not be straightforward in some applications. Isolation transformers may be needed for this purpose, e.g., if the various dc links are supplied by rectifiers connected to the same grid. It is easier, e.g., if the power is provided by separate isolated buses in an aircraft [25] or isolated batteries in an electric vehicle [505]. Furthermore, in addition to electrical isolation, enough physical and thermal isolation should be set between power electronic devices to minimize fault propagation in case of an SC through one of them [99].
The design of a VSC with high modularity and isolation can be combined with reconfiguration of the VSC after the fault takes place, as in the methods displayed in Table 16. The main purpose of the reconfiguration is to convert the SC faults into phase OCs (first row of the table) or to allow more suitable phase currents through all phases (other rows). These reconfiguration strategies are explained in the following.

Table 16.
Methods based on drive topology reconfigurations for tolerating switch SC faults in multiphase applications in the literature.
Table 16.
Methods based on drive topology reconfigurations for tolerating switch SC faults in multiphase applications in the literature.
| References | VSC Topology | Reconfiguration | Figure | Valid for H-Bridges | Special Machine | Torque Derating | Voltage * Derating |
|---|---|---|---|---|---|---|---|
| Many | Any + 1-4 fuses or 1 switch per line | Convert into phase OC | 15b–e | Yes | No | Yes | No |
| Kumar et al. [275] | Any + 1, n, legs & , switches | Replace faulty leg by redundant | − | Yes | No | No | No |
| Mecrow et al. [99,240] | One or multiple FBs | Clamp both terminals of stator ph. | 16 | Yes | Yes | Yes | Yes |
| Nguyen et al. [273] | Dual HB | Clamp both terminals of stator ph. | 17 | No | No | No | Yes |
| Nguyen et al. [273] | Dual HB | Create virtual neutral point | 18 | No | No | No | Yes |
| Si et al. [239] | Dual HB + (2+3n) fuses & 6 switches | Create virtual neutral point | 13 | No | No | No | Yes |
| Reddy et al. [274] | HBs + 2 extra switches | Create virtual neutral point | − | No | No | No | Yes |
| Wang et al. [243,245] | HBs | Impose 3-phase SC | − | No | Yes | Yes | Yes |
| Wang et al. [103,277] | Any + 1,2 fuses & 1 switch per leg | Clamp terminal to dc-bus midpt. O | 15g,h | Yes | No | No | Yes |
| Yepes et al. [343] | Any + 1,2 fuses & 1 switch per leg | Alternate phase OC/clamping to O | 15g,h | Yes | No | If ↑ volt. | If ↑ torq. |
* The voltage drop across the stator impedance is disregarded.
6.3.1.2. Conversion of Switch SC Fault into Phase OC
As mentioned in Section 2, in the literature it is commonly assumed that switch SC faults are transformed into phase OC ones [102,119,171,277,373,377,385,448,464,465], which are easier to handle and are discussed in Part 2. Considering for the sake of illustration a single leg of a conventional two-level VSC based on IGBTs as in Figure 15a, this conversion into phase OC can be easily completed by opening a bidirectional switch between the corresponding converter leg and stator terminal as depicted in Figure 15b [102,119,385,464,465,506]. This switch may be replaced by a fast fuse [see Figure 15c], which would also open the line in case of a fault, because of the resulting overcurrent [385].
Alternatively, the fuses can be placed in series with each of the IGBTs, as depicted in Figure 15d. Then, phase OC is obtained when these fuses are blown out, either as a consequence of the fault itself or by intentionally turning on the healthy IGBT of the same leg for this purpose [119,343,464,465,506]. This configuration [see Figure 15d] is robust to SCs in both switches of the same leg, unlike the previous ones [see Figure 15b,c]. Note that the topologies from Figure 15b,d could be combined [119]. On the other hand, one of the two fuses from Figure 15d might instead be located in the line, as shown in Figure 15e or in Figure 13.
A fuse may be placed next to just one of the IGBTs of each leg, as represented in Figure 15f. This is the case, e.g., of the VSC topology from Figure 12 [101]. This option is also valid for preventing dc-link SC in case of double switch SC in a certain leg [101]. If an SC fault occurs in the IGBT with the fuse, the latter is burnt and the other IGBT is turned off, then phase OC results. Otherwise, for SCs involving the opposite IGBT, phase OC is not obtained. Then, other fault-tolerant procedures can be applied afterward, such as those described later in Section 6.3.1.4, Section 6.3.1.5 and Section 6.3.1.6.
Another possibility for blowing the fuses from the aforesaid configurations is to close an additional bidirectional switch between the midpoints of the leg and dc link. For instance, the schemes from Figure 15c,d would then become as illustrated in Figure 15g,h [343,465,506]. A similar procedure may also be applied to other VSC topologies, such as T-type ones [103,277]. In the schemes from Figure 15g,h, if the bidirectional switch is kept closed afterward, the phase is not in OC; instead, it can conduct, thus avoiding torque derating, although at the expense of voltage derating. The latter approach is further discussed shortly, in Section 6.3.1.7.

Figure 15.
Schematic of two-level VSC dc link and an arbitrary leg [343]. (a) Without extra elements. (b) With a bidirectional switch per line. (c) With a fuse per line. (d) With a fuse per IGBT. (e) With a fuse per line and leg. (f) With a fuse per leg. (g) With a fuse per line and a bidirectional switch to connect to the dc-link midpoint O. (h) With a fuse per IGBT and a bidirectional switch to connect to the dc-link midpoint O.
6.3.1.3. Redundant VSC Legs
The same performance as in healthy drive, without derating, can be attained under a switch SC if the affected VSC leg is replaced by a redundant one. Drive topologies allowing this kind of reconfiguration are, e.g., those including one or n redundant legs and also a couple of extra bidirectional switches per line for the connection/disconnection of each leg [275,464,465]. This means bidirectional switches for an n-leg HB VSC or for an FB VSC. However, this option has barely been considered for multiphase machines, presumably because it implies a significant increase in complexity and cost, while the enhancement in performance compared with other alternatives is not as significant as in three-phase drives. Similarly, there are also three-phase topologies [465] based on parallel or series connections of individual switches, but to the knowledge of the authors they have not been used with multiphase drives, because of the same reasons.
6.3.1.4. Clamping Both Terminals of a Stator Phase through VSC
In principle, in case of open-end windings, an alternative to installing redundant legs (extra complexity) or converting a switch SC fault into a phase OC (extra elements and torque derating) would be to simply turn off the gating signals of the other three switches connected to the affected stator phase. It would also be possible to turn off the opposite switch of the same leg and keep switching the leg at the other side of the phase. However, the resulting phase current has relatively large dc (limited only by stator resistance) and peak values, as shown in [240,273] for topologies based on independent H-bridges (disabling three switches) and based on dual HB VSC (disabling one switch), respectively. In this regard, it is preferable, e.g., to apply SC through the VSC (two top or two bottom switches) across the terminals of the corresponding stator phase, provided FB VSCs (e.g., H-bridges) are used. This approach is depicted in Figure 16. In this manner, there is no current dc component and the current rms value is acceptable [99,240]. This improvement is related to the fact that current paths in both directions are thereby allowed through the stator phase, as opposed to the case of opening the other switches, where the phase current would only be able to circulate in one direction [240].
Figure 16.
Tolerance to a switch SC by clamping both terminals of a stator phase through an FB VSC (causing phase SC), as in [99,240].
The scenario just described resembles that of a terminal SC (phase SC) fault, which has been discussed in Section 5 (with other types of stator SC faults). The main difference is that in this case the SC current does not only flow through the affected stator phase as in phase SC failures, but also through the VSC [240]. It is also similar to the case in which a terminal SC is externally applied by the VSC to a given phase with stator turn failure (explained in Section 5.3.1.1), where there is actually increased current also through the VSC; but then the turn SC gives rise to especially high current through the shorted turns, in contrast to switch SCs. However, applying an SC across a phase requires a special design of the machine, so that it is able to properly withstand this condition, as explained earlier with regard to stator SC faults. Otherwise, the uncontrolled zero-sequence path tends to make the resulting current especially high [13].
If the dc links at each side of the stator phase are not connected to each other, as in a dual HB VSC [see Figure 9d], then this same approach (two top or two bottom switches on; see Figure 17) can be applied without causing zero-sequence current and phase SC, thus avoiding the requirement of a special machine. Then, the current through this stator phase can be controlled by the remaining working legs (all phase currents are related by the condition that their sum is zero), making it possible to obtain the same phase currents as in a healthy drive [273]. In any case, the available voltage is reduced after the fault compared with healthy operation. Furthermore, for the topology based on two HB VSCs, which is used to apply this technique, there is less electrical isolation than for multiple H-bridges [99,240], and, hence, less tolerance to, e.g., DC-side faults.
Figure 17.
Tolerance to a switch SC by clamping both terminals of a stator phase through HB VSCs (no phase SC), as in [273].
6.3.1.5. Creating Virtual Neutral Point through Dual HB VSCs
Another possibility to tolerate switch SCs is based on using a dual HB VSC and setting an artificial neutral point at the HB that contains the switch SC [273], as illustrated in Figure 18. Then, the machine can be controlled as a star-connected one driven by a single HB VSC. Unlike the preceding techniques, based on clamping certain stator terminals to the positive or negative poles of the dc link/s, this one cannot be easily applied to VSCs based on single-phase modules. In addition, the maximum achievable voltage across a stator phase is not as high as for those techniques.
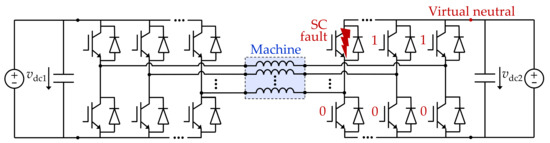
Figure 18.
Tolerance to a switch SC by creating a virtual neutral point through an HB VSC in a drive based on open-end windings supplied by two HB VSCs.
The four-phase topology shown in Figure 13 [239] can be used to create a neutral point in an HB VSC with switch SC as aforesaid, but its extra elements allow for other potential reconfigurations. For example, in absence of SCs the additional bidirectional switches can be set so that the topology behaves as a single FB VSC (with an extra current DOF) and is, thus, able to tolerate two simultaneous phase OCs, which would not be possible with a dual four-phase HB VSC. This idea of conveniently changing between single-FB or dual-HB VSC could be straightforwardly extrapolated to higher phase numbers, as discussed in Part 2.
The approach based on creating an artificial neutral point can also be applied in pole-phase modulated machines based on open-end windings. This is performed in [274] for a nine-phase IM. A nine-leg HB VSC is used at one side of the windings, and three three-leg HB VSCs at the other side. In case of a switch fault in the nine-leg VSC, other eight switches of the same VSC are employed to set the virtual neutral point. Otherwise, if there is a switch failure in the three-leg VSCs, a virtual neutral point is set in each of them, and they are all connected by means of two bidirectional switches when three-phase instead of nine-phase operation is desired.
6.3.1.6. Applying Three-Phase SC through VSC
Similarly to the case of stator SCs (see Section 5.3.1.1), in the scenario of a switch SC in a machine with multiple three-phase star-connected winding sets it is possible to impose a three-phase SC by means of the VSC to the corresponding three-phase winding [168,243,245]. In principle, this procedure may produce a more balanced situation than having an SC in a single phase. In any case, although an SC in a stator phase is difficult to be removed, for a switch SC it is relatively easy to reconfigure the drive so as to keep the same currents through all phases as in healthy operation (e.g., by using dual HB VSCs and applying a suitable corrective action [273], as discussed earlier). Thus, the option of applying a three-phase SC is much less attractive for a switch SC than for a stator SC. Furthermore, even if the VSC is not reconfigured, the imbalance associated with an SC in a single phase can be compensated by suitable control techniques [168] without imposing SCs in other phases, as explained later in Section 6.3.3.
6.3.1.7. Allowing Current Flow through All Phases Avoiding Shorted Switches
Some of the aforesaid tolerant approaches allow current flow through all phases still after a switch SC, but by conducting significant current through the faulty switch. This is the case, e.g., for the methods just described in Section 6.3.1.4, Section 6.3.1.5 and Section 6.3.1.6. However, it might be preferred to avoid using the shorted switch to conduct current, since it may exhibit abnormal behavior and resistance [103,277]. For this purpose, it is possible to isolate the faulty switch e.g., blowing a fuse by briefly turning on the bidirectional switch in Figure 15h and then simply turn on the opposite switch/es of the same leg/s, in order to obtain analogous behavior.
Current flow through a phase affected by a switch SC may instead be obtained by, e.g., keeping on an extra bidirectional switch placed between the phase terminal and the dc-link midpoint [see Figure 15g,h]. This has been performed, e.g., for an asymmetrical six-phase drive driven by a two-level VSC in [343] and by a T-type three-level VSC in [103,277]. However, in this situation the maximum output ac voltage (and, hence, maximum speed) of the converter is roughly halved (assuming star connection), and special care should then be taken to avoid damage in the dc-link or excessive oscillations in the dc-link voltage [343,465]. It can also be noted that in the case of a T-type VSC the phase terminal could be clamped to the dc-link midpoint by means of the two switches (e.g., IGBTs) that are included between both points by default in this topology [see Figure 8i] [276]. Nevertheless, using instead an additional bidirectional switch (e.g., a TRIAC) for this purpose is suggested mainly for avoiding current flow through a switch with SC (if one of those two is faulty) [103,277].
It has recently been proposed in [343] to open or close such bidirectional switch between the dc-link and leg midpoints in a two-level VSC [see Figure 15g,h] depending on the operating conditions. In this manner, either the achievable torque (closed switch) or voltage (open switch) can be ideally as high as in healthy drive, as reflected in Table 16. Nonetheless, since the behavior is the same as for switch OC faults (switch SCs are assumed to be isolated), this will be reviewed in more detail in Part 2.
6.3.2. Machine Design
In case of applying a method to tolerate switch SCs that implies increasing the current through the machine phases (e.g., imposing single-phase [99,240] or three-phase [243,245] SCs; see Section 6.3.1.4 and Section 6.3.1.6), it is important to ensure that the machine is designed so that this condition is suitably tolerated. For this purpose, in general the recommendations given in Section 5.3.2 for phase SC faults can also be applied in this situation. In fact, most of the publications that address machine design under switch SCs also study the scenario of stator SCs [99,130,240,242,243,244,245,246,247], and they have, thus, already been reviewed in Section 5.3.2.
6.3.3. Control and Modulation
If the drive topology is modified for improving the tolerance to switch SCs, often the control or modulation method has to be adapted accordingly. For this reason, in some of the papers where specific topologies or topology reconfigurations are presented for switch SCs (see Section 6.3.1), the suitable control/modulation strategies are also discussed [13,243,273]. Moreover, due to the behavior similarity between stator and switch SCs in certain cases (e.g., after applying a terminal single- or three-phase SC), the comments provided about the control techniques under stator SCs of some of these papers (see Section 5.3.3) [241,243] are also adequate for switch SCs.
The necessary changes in the SV PWM algorithm under switch faults for a T-type three-level VSC driving an asymmetrical six-phase PMSM are discussed in [103], considering RFOC based on PI controllers. The voltage SVs that are missing as a consequence of switch SCs are taken into account so that they are suitably replaced by other SVs. The maximum speed is reduced according to the available voltage region. It is ensured that the voltage at the dc-link midpoint is balanced, which requires special attention in this topology. Similarly, the postfault selection of voltage SVs is addressed for the same type of drive in [277], but using deadbeat predictive current control.
The voltage SVs in a twelve-phase IPMSM fed by four three-phase HB VSCs are adapted in [168] for a switch SC fault. The machine has four three-phase stars, arranged in the stator as four sectors, and using double-layer 12-slot 8-pole FSCW. In addition, to avoid windup of the PI current controllers, the integration is disabled when the output voltage is limited. The voltage SVs of each three-phase module are treated independently. Even though the torque contribution by a three-phase VSC with a switch SC unavoidably contains ripple, such ripple is compensated by adding adequate ac terms in the torque references of the healthy VSCs. Flux saturation is taken into account in the controller. Compared with the conventional option of imposing a three-phase SC to the winding set with a switch SC (Section 6.3.1.6), this approach provides the same average output torque with lower phase-current peaks, and thus higher postfault maximum torque.
6.4. Concluding Remarks about Switch SC Faults
SC failures in switches have not received as much attention in the existing literature as other types of faults in multiphase drives such as stator SCs or phase OCs. On the one hand, the switch drivers are commonly able to detect switch SCs [119,168]. On the other hand, regarding tolerance, the main reason for the lack of specific publications about switch SCs is arguably that these faults may be easily converted into phase OCs by simply opening the corresponding current path, and then the tolerance methods for the latter can be directly applied [102,119,130,171,277,373,377,385,448,464,465]. However, in practice this implies reducing the achievable torque compared with healthy conditions [24,312,344], assuming that the VSC rating is not set higher than needed for normal operation. Furthermore, the devices for switch isolation may also fail.
Instead of opening the affected phase, in a conventional VSC topology it is possible to turn on certain VSC switches (among the ones used in healthy drive) so that there is still current through all phases after the fault. Actually, most of the research about tolerance to switch SCs in multiphase drives is devoted to this kind of procedure. As reflected in Table 16, this can be performed, e.g., by clamping both terminals of a stator phase through the VSC [99,240,273], by imposing a three-phase SC (if ) [243,245], by creating an artificial neutral point in drives based on HB VSCs [239,273,274], or by connecting one phase terminal to the dc-link midpoint [103,277,343]. Among these strategies, the ones that permit individual control of all phase currents [103,239,273,274,277,343] are particularly convenient, since in principle they do not imply any postfault torque derating, although usually they do cause some decrease in the maximum voltage. In this respect, it has been recently proposed [343] during postfault conditions to alternate between phase OC and phase-terminal clamping depending on whether high voltage or high torque is required. Further research may be performed on this subject in order to seek, e.g., even better performance or simpler application of this idea.
Increasing the VSC modularity and isolation between VSC units, if possible, is in principle also advisable for improving the reliability in the phase of switch SCs. For example, topologies based on multiple H-bridges [130,240], dual HB VSCs [273], or multiple three-phase HB VSCs [27,168,235,243] are common in fault-tolerant drives.
In any case, the tolerant action that is typically applied for non-isolated switch SCs when using FB VSCs, such as H-bridges, is based on imposing an SC on a stator phase by means of the VSC, causing uncontrolled zero-sequence current. This implies that the machine should be specially designed for withstanding this demanding situation, similarly to stator SCs [99,130,240,242,243,244,245,246,247]. Moreover, even if the machine is such that overcurrent is then prevented, the resulting zero-sequence current gives rise to undesired effects, such as increased losses. Therefore, for non-isolated switch SCs it seems preferable to resort to topologies based on HBs and to tolerance procedures (devised for such VSCs) that do not force phase SCs [103,239,273,274,277,343]. This differs from the case of tolerance to stator SCs, for which special machine design is almost unavoidable, and the zero-sequence current is helpful for improving the postfault behavior (see Section 5).
Other special VSC topologies have also been presented, e.g., for replacing a faulty leg by a redundant one [275,465] or for enhancing the postfault performance under various simultaneous faults [239]. Since the latter [239] permits alternating between FB and dual-HB configurations, it can also be very convenient for overcoming the aforementioned incongruity that the zero-sequence current path is desirable for stator SCs but not for non-isolated switch SCs.
Concerning control and modulation, the respective techniques should be adapted to the postfault VSC configuration [13,103,168,241,243,273,277]. In particular, they can be modified so that the effects of missing voltage SVs are taken into account [103,168,277] and so that the resulting torque ripple is compensated [168]. Nevertheless, it may be desirable to, e.g., conduct future research so as to obtain high-performance drive control after switch SCs in a simpler manner and with minimum reconfiguration.
7. Speed/Position-Sensor Faults
A significant part of ac drives nowadays relies on the speed or position of the rotor, which is frequently measured by resolvers or encoders. Most often this fact is because of its requirement for closed-loop current (vector) or speed control [507], which yields better performance than open-loop (scalar) control. Moreover, although conventional open-loop V/f control works for IMs, it does not for synchronous machines. On the other hand, even in IMs driven by simple V/f control, the speed may be useful for monitoring purpose [508]. Failure of the speed/position sensor is not expected to be critical in the latter case (monitoring), but in a drive with closed-loop control such fault usually means that normal operation cannot continue. In fact, the abnormal behavior of the machine after said sensor fails may compromise the mechanical and electrical (e.g., back-EMF rise with speed) integrity of the system [58]. For these reasons, encoders and resolvers represent a possible source of faults that needs to be taken into account [58,87,127,130,182,197,199,208,213,215,216]. Although the reasons that produce these failures do not depend on n and the three-phase tolerance approaches in many cases are also valid for , the extra DOFs of multiphase machines offer valuable potential for obtaining enhanced performance in such conditions. Figure 19 illustrates the principal causes, detection methods and tolerant techniques for encoder/resolver faults.
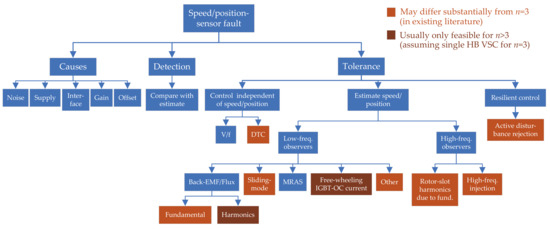
Figure 19.
Causes, detection methods, and tolerance approaches for speed/position-sensor faults in multiphase drives.
7.1. Causes of Speed/Position-Sensor Faults
Some of the typical failures in incremental encoders are inconsistent number of pulses per turn (e.g., due to noise) and total/intermittent signal loss (e.g., supply/interface fault). Concerning resolvers and absolute encoders, faults usually consist in zero output, gain drop, offset, or high noise [87,509].
7.2. Detection of Speed/Position-Sensor Faults
The most common method for detection of encoder/resolver faults is based on comparing the speed measurement with a speed estimate, as indicated in Figure 19. When the difference between them exceeds a certain threshold, the alarm flag is set. Special care should be taken to select this threshold so that no false alarms occur. This approach can be applied for any phase number. Regarding multiphase drives, it has been performed for six-phase PMSMs with asymmetrical WSA, based on an extended sliding-mode observer [87] and on a voltage-model-based stator-flux observer [58]. It has also been performed by means of sliding-mode observer for a five-phase PMSM in [86].
It is worth noting that, in case a deviation is detected between the actual speed and its estimate, it is necessary to distinguish whether such difference arises due to an actual encoder/resolver failure or because of a different type of fault (e.g., phase OCs) that affects the inputs (and, hence, output) of the speed observer [58]. This distinction can be achieved, e.g., by running several speed observers based on different variables or by including additional algorithms to diagnose other faults [58,212].
The same speed/position observers employed for detecting resolver/encoder failure can be used afterward for tolerating this condition, as explained shortly.
7.3. Tolerance to Speed/Position-Sensor Faults
A simple solution for tolerating resolver/encoder failure is to replace the closed-loop control by V/f control [460], which does not require speed/position information. In any case, this comes at the expense of worsening the drive performance, and in addition it is not suitable for synchronous machines. Similarly, DTC (or similar schemes) is generally considered to be inherently encoderless (especially if low-speed operation is ignored), and, thus, it is in principle adequate for such fault; however, if the speed/position has to be controlled by an outer loop, an estimate/measurement of the actual speed/position is in fact needed nonetheless [200,204].
The most widely spread approach to control a drive when a resolver/encoder is not available consists in estimating the frequency/position (of rotor, rotor flux, stator flux, or back-EMF) by an observer as a function of other variables (stator current, stator voltage references, etc.), instead of based on the rotor speed/position-sensor measurements. These sensorless techniques are frequently implemented to be used at all times, avoiding the complexity and cost of buying, installing and maintaining the sensor [507]. Nevertheless, it is also reasonable to resort to these observers just in case of sensor fault [58,87,127,130,197,199,208,213,216], because usually they are not as accurate and robust to uncertainties (e.g., flux saturation) as sensors [510], or they have additional shortcomings, such as introducing torque ripple (e.g., those based on signal injection) [511].
The encoderless observers may be roughly classified into those based on low- or high-frequency components, in agreement with Figure 19. The former includes the fundamental and low-order harmonics, such as the third, fifth, and seventh, whereas greater harmonic orders are considered as high frequencies. In most cases, low-frequency observers rely, to a great extent, on the machine model and parameters, whereas high-frequency ones do not. Note that, for the sake of illustration, the classification of estimation algorithms displayed in this figure is not completely strict; e.g., some observers based on sliding mode or on model reference adaptive systems (MRASs) are also back-EMF/flux observers. On the other hand, Table 17 reflects many of the strategies found in the existing literature for multiphase applications that are tolerant to encoder/resolver faults, sorted by the types of methods. Low-frequency observers are surveyed first in Section 7.3.1, high-frequency observers next in Section 7.3.2, and resilient control is briefly discussed finally in Section 7.3.3.

Table 17.
Speed/position-sensorless methods (Section 7) in multiphase applications in the literature.
Table 17.
Speed/position-sensorless methods (Section 7) in multiphase applications in the literature.
| References | Method Description | Machine | Differs from * | Proved to Work with Other Simult. Faults | Works at & Near 0 r/min | Extra Loss/Ripple | ||
|---|---|---|---|---|---|---|---|---|
| n | WSA | Rotor | ||||||
| Nguyen et al. [186] | Adaptive linear neural network | 5 | Sym. | PMSM | No | No | No | No |
| Olivieri et al. [130,187] | Back-EMF Luenberger observ. | 5 | Sym. | PMSM | No | No | No | No |
| Olivieri et al. [127] | Back-EMF Luenberger observ. (designed for ph. OC) | 5 | Sym. | PMSM | Yes | Phase OC | No | No |
| Xu et al. [210,211] | Back-EMF non-orthog. observ. (2 arbitrary phases) | 6 | Sym. | PMSM | Yes | Stator SC/OC | No | No |
| Imai et al. [196] | Back-EMF disturb. observ. (extended for saliency) | 9 | Multisec. | PMSM | Yes | No | No | No |
| Belie et al. [217] | Back-EMF 3rd-harm. observ. (PMSM with ph. OCs) | 5 | Sym. | PMSM | Yes | Phase OC | No | No |
| Stiscia et al. [198] | Back-EMF 3rd-harm. observ. (healthy PMSM) | 9 | Sym. | PMSM | Yes | No | No | No |
| Slunjski et al. [199] | Back-EMF 5th-harm. observ. (healthy PMSM) | 9 | Sym. | PMSM | Yes | No | No | No |
| Taheri et al. [206,207] | Extended Kalman filter | 6 | Asym. | IM | Yes | No | No | No |
| Tian et al. [216] | Free-wheeling current under IGBT fault | 5 | Sym. | PMSM | Yes | Switch OC | No | No |
| Zhang et al. [209] | High-freq. inject. (flux-intensifying PMSM) | 5 | Sym. | PMSM | No | No | Yes | Yes |
| Liu et al. [201] | High-freq. inject. ( square wave) | 5 | Sym. | PMSM | Yes | No | Yes | Yes |
| Tian et al. [208] | High-freq. inject. (system delay & stator resistance) | 5 | Sym. | PMSM | Yes | No | Yes | Yes |
| Barcaro et al. [215] | High-freq. inject. (various stator configs.) | 6 | As./sym./mul. | PMSM | No | Phase OC | Yes | Yes |
| Almarhoon et al. [191] | High-freq. inject. (stat. frame inject.; 0-seq. meas.) | 6 | Asym. | PMSM | Yes | No | Yes | Yes |
| Almarhoon et al. [192] | High-freq. inject. (synch. frame inject.; 0-seq. meas.) | 6 | Asym. | PMSM | Yes | No | Yes | Yes |
| Imai et al. [195] | High-freq. inject. (standstill; SPMSM) | 9 | Multisec. | PMSM | Yes | No | Yes | Yes |
| Ramezani et al. [188] | High-freq. inject. (- rotating sine wave) | 9 | Sym. | PMSM | Yes | No | Yes | Yes |
| Guzman et al. [181] | Minimization of torque error | 5 | Sym. | PMSM | No | No | No | No |
| Khadar et al. [193] | MRAS (flux-based; + parameter estimation) | 5 | Sym. | IM | No | No | No | No |
| Khadar et al. [194] | MRAS (sliding mode; + parameter estimation) | 5 | Sym. | IM | No | No | No | No |
| Holakooie et al. [204] | MRAS (sliding mode) | 6 | Asym. | IM | No | No | No | No |
| Holakooie et al. [205] | MRAS (sliding mode; + rotor-time-constant est.) | 6 | Asym. | IM | No | No | No | No |
| Listwan et al. [197] | MRAS (flux-based and current¤t-based) | 7 | Sym. | IM | No | No | No | No |
| Hezzi et al. [182] | Resilient control based on active dist. rejection | 5 | Sym. | PMSM | Yes | No | No | No |
| Amin et al. [203] | Rotor-flux robust simplified dynamic observer | 6 | Asym. | IM | No | No | No | No |
| Mengoni et al. [183] | Rotor-flux 3rd-harm. observ. (healthy IM) | 7 | Sym. | IM | Yes | No | No | Yes |
| Mengoni et al. [184,185] | Rotor-flux 3rd-harm. observ. (healthy IM; ↓ speed) | 7 | Sym. | IM | Yes | No | Yes | Yes |
| Yepes et al. [202] | Rotor-slot harm. due to fund. current (healthy) | Any | Asym./sym. | IM | Yes | No | No | No |
| Yepes et al. [214] | Rotor-slot harm. due to fund. current (phase OC) | Any | Asym./sym. | IM | Yes | Phase OC | No | No |
| Kong et al. [218] | Sliding-mode observ. (+ stator-resist. estimation) | 5 | Sym. | IM | Yes | Phase OC | No | No |
| Mossa et al. [189] | Sliding-mode observ. (+ rotor-resist. estimation) | 5 | Sym. | IM | Yes | No | No | No |
| Zhang et al. [219] | Sliding-mode observ. (volt. FF; active resist.) | 5 | Sym. | PMSM | No | Phase OC | No | No |
| Bensalem et al. [86] | Sliding-mode observ. (including 3rd space harm.) | 5 | Sym. | PMSM | Yes | No | No | No |
| Geng et al. [213] | Sliding-mode observ. (reduced-order transf.) | 6 | Asym. | IM | Yes | Phase OC | No | No |
| Xiao et al. [87] | Sliding-mode observ. (load-torque est. & rejection) | 6 | Asym. | PMSM | No | No | No | No |
| Zheng et al. [190] | St.-flux variable-structure observ. | 5 | Asym. | IM | No | No | No | No |
| Parsa et al. [200] | St.-flux volt.-model observ. (load angle included) | 5 | Sym. | PMSM | No | No | No | No |
| Green et al. [212] | St.-flux volt.-model observ. (per phase) | 6 | Sym. | PMSM | Yes | Stator SC/OC | No | No |
| Wang et al. [58] | St.-flux volt.-model observ. (= st.-flux & rotor freqs.) | 6 | Asym. | PMSM | No | No | No | No |
| Bojoi et al. [161] | St.-flux Gopinath observ. (fault: ignore rotor model) | 6 | Asym. | IM | Yes | Phase OC | No | No |
* It should be noted that, although several of these sensorless methods are identical for n = 3, some of them had not been proposed for n = 3 in the past, and many of these papers also have significant research contribution on aspects different from the sensorless algorithms. † For given machine, this sensorless method does not imply extra losses, but choosing a machine with larger rotor-slot current harmonics does yield higher losses than adopting other machines.
7.3.1. Encoderless Low-Frequency Observers
The survey of speed/position-sensorless observers based on low-frequency signals is organized in agreement with Figure 19. Among back-EMF/flux observers, which are widely spread (see Table 17), the following types are distinguished: stator-flux fundamental observers (Section 7.3.1.1), rotor-flux fundamental observers (Section 7.3.1.2), back-EMF fundamental observers (Section 7.3.1.3), rotor-flux harmonic observers (Section 7.3.1.4), and back-EMF harmonic observers (Section 7.3.1.5). Other common observers are those based on sliding-mode and MRAS, which are reviewed in Section 7.3.1.6 and Section 7.3.1.7, respectively. An interesting strategy specific for an IGBT OC is based on monitoring the corresponding free-wheeling current, as explained in Section 7.3.1.8. There are also other types of low-frequency observers for speed/position estimation that do not fit into these categories, which are addressed in Section 7.3.1.9.
7.3.1.1. Stator-Flux Fundamental Observers
Knowledge of the stator-flux vector (position and magnitude) is particularly useful for certain control strategies, such as DTC [58,200] and direct-flux vector control [512]. In three-phase machines (either asynchronous or synchronous), a classical method to obtain the stator flux is based on solving it from the equation of the stator equivalent circuit (voltage model), i.e., by integrating the difference between the stator voltage and the stator current times stator resistance, which represents the back-EMF [512,513,514,515,516]. To ensure stability, the integrator is typically replaced by a low-pass filter [515]. This open-loop estimation by the voltage model is prone to error at low speeds due to small back-EMF (proportional to speed) and to stator-resistance uncertainty [513]. Alternatively, the stator flux may instead be obtained by means of the stator current and the rotor magnetic model (current model) [515,516]. This open-loop observer works satisfactorily at low speeds, but it requires the rotor position/speed, and at high speeds it is more sensitive to machine parameters than the voltage model [514,517]. All the aforementioned also applies in case the voltage and current models are employed to observe rotor flux instead of stator flux, e.g., for direct (Recall that, in IMs, for indirect RFOC the position of the rotor flux is calculated with respect to the rotor position, whereas for direct RFOC the rotor flux position is either directly measured or (usually) directly calculated from the terminal measurements [516]. In synchronous machines, the rotor flux and the rotor itself are always aligned) RFOC, which acts in a reference frame aligned with the rotor field [513,514,515,516].
In an early paper [212], Green et al., proposed a method to estimate speed, position, and stator flux for a six-phase symmetrical PMSM with FSCWs, with each phase being fed by an independent H-bridge. The stator flux is calculated by means of the conventional open-loop - voltage model, based on the stator voltage references and the measured stator currents. Then, a stator current estimate is obtained by using a look-up table, depending on the estimated values of stator flux and position. In turn, the position is calculated by means of another look-up table, as a function of the stator flux and the error between the actual and estimated stator current. Since the machine has FSCWs (see Section 3.1.2), the mutual inductance between phases is neglected. Two alternatives are studied: either providing a position estimate for each individual phase, or a position estimate based on the information of all phases simultaneously (through a least-squares algorithm). In principle, the latter (all-phase estimation) is more accurate in the absence of OC/SC faults, but in presence of such failures the healthy phases are much less affected when using the former (per-phase estimation). In view of this outcome, it is then proposed to automatically discard, in the all-phase estimation, the position values provided by phases, such that the corresponding error in phase-current estimation exceeds a certain threshold [212]. Thus, a combination of the advantages of both approaches is thereby attained.
In [58], both of the aforesaid classical open-loop stator-flux observers (voltage and current models) from three-phase machines are simultaneously implemented in the - plane of a six-phase PMSM. In addition to calculating the stator-flux variables for performing DTC, these two observers are exploited in [58] for fault detection and tolerance. More specifically, in case of speed-sensor fault, the speed is assumed to be identical (it is a synchronous machine) to the frequency of stator flux that is estimated by the voltage model [58]. That is, the angle that exists between stator flux and rotor (load angle) during transients [200] is neglected. The speed value is fed back to the outer speed loop so that it is controlled in closed loop. Regarding the speed and flux behavior, in this case no particular characteristics stem from the fact that it is a machine with more than three phases; nevertheless, the other fault types (discussed in Part 2 and in Section 12.3 and Section 12.4) from which speed-sensor failure is distinguished in the diagnosis in [58] do depend on the phase number. Parsa and Toliyat [200] had also proposed to use the - voltage model to estimate the speed of a multiphase PMSM (in this case, ) controlled by DTC. Nevertheless, in [200] the expressions to estimate the load angle during abrupt torque transients (if any) were given.
Instead of the open-loop voltage and current models, it is common in three-phase machines to merge the two of them, so that the advantages of the former for high speeds and of the latter for low speeds are combined in the flux estimation [512,513,514,515,516]. The resulting scheme is often known as Gopinath [513] or reduced-order [515] observer. It is usually considered a closed-loop observer [514,516], as opposed to the conventional open-loop current and voltage models. Inspired by this solution, Bojoi et al. [161] treat a six-phase IM as a combination of two three-phase IMs, and for each of them a closed-loop stator-flux observer analogous to said Gopinath observer is implemented. The rotor part (current model), which needs the rotor position, is, in fact, shared by both three-phase observers of the six-phase drive, whereas the stator part (voltage model) is different for each of the two winding sets. The estimated stator flux for each three-phase set is employed to perform direct flux-vector control separately. Given that an IM is considered, the rotor speed cannot be simply assumed to match the stator-flux frequency, as performed in [58] for a PMSM. Instead, if the encoder fails, the rotor model is ignored in the stator-flux observers and the observer gain is reduced (giving priority to the voltage model over the current one) to avoid too large a phase error [161]. In this manner, satisfactory behavior is obtained in case of encoder fault, even if it is combined with phase OCs. However, the machine just works as a generator with torque reference; a speed estimate would have to be added if closed-loop speed control were desired. Moreover, since the current model in the flux observers is disabled, the control performance may not be as good as with working encoder, especially at low speeds.
A different type of model-based stator-flux observer is presented in [190], for a five-phase IM driven by DTC. Namely, it is a variable-structure observer, whose behavior is more non-linear than the previous ones. In fact, it is closely related to sliding-mode observers, which are discussed later on. The fundamental stator flux and the speed are estimated based on the - stator voltage and current [190]. Thus, it is also expected to work similarly for . No comparison is provided with other observers, because the focus of the paper [190] is on the DTC strategy.
7.3.1.2. Rotor-Flux Fundamental Observers
A six-phase asymmetrical IM driven by backstepping control is considered in [203]. Said control, besides the speed value, also requires rotor-flux estimation. Two estimates of the rotor-flux - vector are calculated, based on the conventional voltage and current models. The speed is obtained as a function of the cross product between both rotor-flux vectors, and is fed back to the aforesaid current model. From this description, it could be noted that this method resembles a flux-based model reference adaptive system (MRAS) [518], which will be further discussed later in Section 7.3.1.7. Nevertheless, in this case is substantially more elaborate [203] than in existing MRASs for this purpose. In fact, this novel observer, called robust simplified dynamic observer, is proved in [203] to yield better speed accuracy than state-of-the-art MRAS speed estimators.
7.3.1.3. Back-EMF Fundamental Observers
In synchronous machines the phase angle of the fundamental back-EMF is directly related to the rotor position, and, hence, the latter can easily be obtained from the former, if adequately estimated.
The conventional model-based observers [519] for the estimation of the flux or back-EMF (and from it, of speed/position) in synchronous machines are not able to take advantage of the additional position information contained in saliency (e.g., in IPMSMs). For the latter purpose, the concept of extended back-EMF was presented for three-phase synchronous machines in [520], and a closed-loop disturbance observer was also proposed to track this signal. Regarding multiphase drives, an extended back-EMF observer was developed for a three-sector nine-phase PMSM in [196], so that the individual parameters of each stator sector are taken into account in the observer. However, operation under other types of faults (e.g., OC or SC) was not considered.
A back-EMF Luenberger-like observer for a five-phase SPMSM is devised in [187]. This observer is also included in [130], and later extended for phase OCs in [127]. In the latter [127], depending on the affected phase, the VSD transform is replaced by a suitable reduced-order transform, so that the fundamental back-EMF and its phase angle (using a phase-locked loop) are properly extracted in spite of the fault.
Nguyen et al. [186] adopt the Luenberger-like observer from [127] for a healthy situation, but they replace the phase-locked loop by an algorithm for position estimation (from back-EMF) based on an adaptive linear neural network (Adaline). Adaline is a particularly simple type of neutral network that is not too computationally demanding. This modification is shown to yield faster response and lower ripple than the phase-locked loop, especially at low speed. In any case, comparison with more advanced phase-locked loops remains to be completed. Since just healthy operation and fundamental back-EMF are considered, the study is not expected to change substantially for other n.
More recently, in [210,211], the rotor position of a five-phase PMSM under stator OC/SC faults is estimated by an observer based on robust law that tracks the non-orthogonal back-EMF of two healthy phases. The high-frequency noise is attenuated by means of a second-order low-pass filter whose bandwidth is adjusted with the speed reference [211]. The rotor position is extracted from the two filtered back-EMF waveforms by a phase-locked loop designed to work with non-orthogonal input signals [210,211]. Finally, the phase delay introduced by the low-pass filter in the rotor estimation is compensated by a simple formula [211].
7.3.1.4. Rotor-Flux Harmonic Observers
The preceding observers are all based solely on the fundamental component of the electromagnetic variables. Nonetheless, in many multiphase machines, a significant third-order space harmonic interacts with a stator VSD plane different from - and with potential current flow. Thus, this component may also be excited and exploited for extracting a speed estimate. This possibility has been first tackled by Mengoni et al., in [183]. In said paper, a third-order current harmonic is injected in a secondary plane to excite the third-order flux harmonic in such a manner that the torque is not altered. In principle most kinds of observers could be applied to this third-order harmonic; a linear closed-loop rotor-flux estimator based on the voltage (stator) model is adopted in this case [183]. An observer of third-order rotor-flux harmonic provides, apart from the rotor speed, also the phase angle of this rotor-flux component. This angle is employed for the synchronization of the current controller in the secondary plane. In turn, the rotor speed estimated from the third harmonic is used in an observer of the fundamental rotor flux, from which the angle for the field-oriented fundamental current control is obtained. The reference magnitude of the third-order current harmonic should be selected as a trade-off between accuracy and performance degradation due to losses and iron saturation, while respecting the drive voltage and current constraints.
Later, in [184], the same authors improve this approach by making it suitable for low and zero speeds. This is an important property, because in these conditions the fundamental back-EMF (used in many methods) is zero or extremely small and, hence, very difficult to observe (see penultimate column of Table 17). It is attained in [184] by increasing (from zero) the phase shift between the third-harmonic stator and rotor flux, so that the third-harmonic slip also rises and thereby the stator frequency of the third-harmonic flux does not decrease below a certain predefined threshold. This is allowed by the fact that the electromagnetic components in the - and - planes do not need to obey any synchronization in phase or frequency with respect to each other. However, this technique introduces additional losses, and it only works for positive rotor speeds. Moreover, the dynamics may be worsened to some extent because at low/zero speed the third-order current harmonic introduces torque disturbances that need to be compensated by the closed-loop speed controller. Although only simulation results were given in [184], experimental results can be found in [185].
7.3.1.5. Back-EMF Harmonic Observers
Belie et al. [217] proposed to employ observers for the fundamental and third-order harmonics of the back-EMF, for a five-phase PMSM under single or double phase OC faults. The effective separation of both harmonics is achieved by applying appropriate reduced-order transformations depending on the phase-OC scenario. The rotor position and speed can then be estimated from any of these two frequency components of the back-EMF. The adopted back-EMF observer and phased-locked loop are based on those from [127] (see Section 7.3.1.3), but with the differences that in [217] they are adequately used also for the harmonic back-EMF and under double phase OCs, instead of just for fundamental back-EMF and single phase OC.
In [198], the rotor position is estimated from the back-EMF third harmonic in a nine-phase PMSM with symmetrical WSA, in absence of phase OCs. Given that in this case the VSD planes are decoupled (no phase OCs) and zero reference is set for the third-harmonic closed-loop current control, the corresponding back-EMF is simply assumed to be roughly identical to the respective components of the voltage references. In this manner, machine parameters, such as stator resistances and inductances are not needed for this purpose, in contrast to most low-frequency observers. In turn, the rotor position can be obtained from this back-EMF by using a phase-locked loop. Further work on this subject has been performed in [199], in the context of a drive where harmonic injection is performed for increasing the torque density. It is proposed therein to set to zero the reference of the fifth-order (not the third-order) current harmonic when an encoder fault occurs, so that the output of the corresponding current controller can be adopted as an estimation of the back-EMF fifth harmonic. A phase-locked loop is then applied to the latter in order to yield the rotor position.
7.3.1.6. Sliding-Mode Observers
Sliding-mode observers exhibit excellent performance in terms of accuracy, dynamic behavior, and robustness to parameter variations and plant non-linearity [521]. On the other hand, special care should be taken to prevent chattering [194,219].
A sliding-mode observer is proposed for a five-phase IM in [218]. It is based on the fundamental - machine model, taking into account the imbalance due to a phase OC. Apart from the speed, the stator resistance is considered as an unknown parameter, to be also estimated by the observer. The other parameters are assumed invariable. This method is unaffected by faults or third-order harmonic injection.
Another sliding-mode observer for five-phase IMs is presented in [189], but estimating the rotor resistance (besides speed) instead of the stator one (assumed constant). The voltages and currents in both VSD subspaces are used as inputs [189]. Both planes are taken into account in the observer for the estimation, under the hypothesis of sinusoidally distributed windings. The occurrence of other faults simultaneously with speed/position-sensor ones is not studied, unlike in [218]. Similarly to [189], an observer with four voltage and current inputs is devised in [86] for a five-phase drive. The main differences with respect to [189] are that a PMSM is studied instead of an IM, that a third-order space harmonic is included in the machine model of the secondary plane, and that no machine parameters other than speed are adapted with operation.
Zhang et al. [219] propose a sliding-mode observer for a five-phase IPMSM. It is based on a previous method for [522], which offers low chattering and reduced phase error thanks to the adoption of a sigmoid function and an inner back-EMF observer, respectively. In [219] the disturbance rejection of this solution is substantially enhanced by adding an FF of measured output voltage and an active resistance. This improvement in the robustness to disturbances makes this observer suitable for phase OC faults. The speed is computed from the back-EMF estimate provided by the observer. In contrast to, e.g., the sliding-mode observer from [218], which was also tolerant to phase OCs in a five-phase drive, the one from [219] does not need to alter the observer implementation depending on the specific phase that is faulty. This observer is based on the - machine model and can be easily applied to any phase number, including .
A sliding-mode speed estimator for six-phase asymmetrical IMs is devised in [213]. Chattering is prevented by using a piecewise saturation function. Under phase OCs, suitable reduced-order transformations are employed. Although this kind of postfault transformation is used in many publications, the resulting machine model in the fundamental plane depends on the specific faulty phase/s, unlike for the conventional full-order VSD transform. In this paper [213], the speed observer is adequately designed so that, in spite of this problem, the speed value is still accurate when OC faults occur.
Load-torque estimation is included in the sliding-mode speed observer of an asymmetrical six-phase PMSM without SC/OC faults in [87], so that improved rejection of torque disturbances is attained. The -axis current is used as an input, and the values of inertia and amplitude of rotor flux (per unit of speed) are required. The observer is just based on the - plane and it could be applied to other n without modifications.
7.3.1.7. Model Reference Adaptive Systems (MRASs)
As illustrated in Figure 20, an MRAS estimator consists of two cooperating subsystems: the reference model and the adaptive model. The former does not depend on the sought variable (e.g., ), whereas the latter does. A function (error function) of the outputs (X and ) of both models is used through an adaptation mechanism (e.g., a PI controller) to adjust an estimate of the sought signal, fed back to the adaptive model, until such error function is zero [518]. Usually the model outputs X and are vectors and is implemented as the cross product; when the X and vectors are aligned, . One of the main advantages of MRAS-based speed estimators in comparison with other alternatives is their relatively low complexity and computational burden [204]. Numerous types of MRAS speed estimators have been proposed for ac drives in the past, especially for IMs. Their popularity has decreased in recent decades because of their sensitivity to model uncertainties (causing oscillations or instability) [515,523], but they still receive notable attention. A recent comprehensive review about them in (three-phase) IMs can be found in [518]. The MRAS speed estimators found in the literature about multiphase drives are summarized in Table 18, specifying how the general MRAS scheme from Figure 20 is particularized in each case.
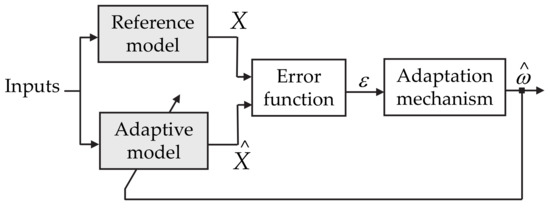
Figure 20.
General illustration of a speed estimator based on MRAS.

Table 18.
Speed/position-sensorless methods based on MRAS (Section 7.3.1.7) in multiphase applications in the literature.
Table 18.
Speed/position-sensorless methods based on MRAS (Section 7.3.1.7) in multiphase applications in the literature.
| References | Machine | Reference Model | Adaptive Model | Model Output | Adapted Parameter | ||
|---|---|---|---|---|---|---|---|
| n | WSA | Rotor | |||||
| Khadar et al. [193] | 5 | Sym. | IM | Conventional voltage model | Conventional current model | Rotor flux | Speed |
| Listwan and Pieńkowski [197] | 7 | Sym. | IM | Actual machine | Hybrid voltage-current model | Current | Speed |
| Holakooie et al. [204,205] | 6 | Asym. | IM | 2nd-order sliding-mode observer | Conventional current model | Rotor flux | Speed |
| Khadar et al. [194] | 5 | Sym. | IM | Sigmoid-based sliding-mode observer | Conventional current model | Rotor flux | Speed |
In conventional flux-based MRAS [518], the reference and adaptive models correspond with the machine voltage (stator) and current (rotor) models, respectively. The error function is based on the rotor-flux estimates provided by both models. The adaptation law is simply a PI controller, which modifies the speed of the current model. This kind of MRAS has been adopted for the - plane of a five-phase IM in [193] (see Table 18), and the MRAS parameters are also updated by values of stator resistance, rotor resistance, and magnetizing inductance estimated by additional observers.
Two kinds of MRAS estimators are compared in [197] for a seven-phase IM controlled by DTC using SV PWM (with two large voltage vectors) and operating under encoder failure. Namely, the ones compared are the aforesaid conventional flux-based MRAS and the advanced current¤t-based MRAS from [524] (concerning ), which is known to have less sensitivity to parameter deviations and better suitability in a wide speed range. Although the SV PWM in [197] depends on the phase number, the MRAS estimators do not, because they are just based on the behavior of the fundamental component in the - plane. In current¤t-based MRAS, the stator current measurements taken from the actual machine are used as the model reference, and the adaptive model provides stator currents estimated by means of a hybrid voltage-current model (see Table 18) [197,524]. For both types of MRASs under study in [197], the adaptive model is adjusted by means of the speed estimate, and the resulting speed value is employed to compute the speed error for the outer speed controller. In any case, the MRAS is not only used for estimating speed; since DTC needs the torque and stator flux as well, these values can also be obtained from the reference model in the MRAS. From the analysis in [197], it is concluded that in the seven-phase IM under encoder fault the current¤t-based MRAS yields smaller ripple in speed, torque and current waveforms than the flux-based MRAS.
Inspired by the conventional - flux-based MRAS with reference model based on stator circuit and adaptive model based on rotor circuit, Holakooie et al. [204] have proposed to replace the linear expressions of said reference model by a second-order sliding-mode observer (see Table 18). This is addressed in the context of a six-phase IM with asymmetrical WSA, controlled by DTC based on virtual voltage vectors (minimum in x-y) and a sliding-mode speed controller. It is proved that the novel MRAS speed estimator offers much better robustness to dc offsets and resistance mismatches [204]. The fact that an MRAS can benefit from the inherent robustness of sliding mode is of special relevance, given that the sensitivity to uncertainties is as aforementioned the main shortcoming of conventional MRAS-based observers [515,523]. On the other hand, the typical chattering problem of sliding-mode observers is avoided by the second-order character (super-twisting algorithm) of the one proposed in this case [204]. Later, this MRAS speed estimator [204] has been combined in parallel with an additional MRAS for estimating the rotor time constant [205]. In order to allow the latter estimation, a low-frequency harmonic is also injected in the rotor flux [205].
A structure similar to the one from [204] is also devised in [194], for five-phase IMs. The chattering problem is prevented by using a sigmoid function without resorting to super-twisting algorithm. In addition, simple estimators based on the IM model are also proposed for the stator and rotor resistances. These parameter estimates are employed to adjust the models in the MRAS speed estimator so as to further improve its robustness and accuracy.
In accordance with Table 17, it can be noted that none of these MRAS-based speed estimators would differ substantially for or other n, since they are entirely based on the fundamental - machine model.
7.3.1.8. Free-Wheeling Current of OC IGBT
Tian et al. [216] proposed to extract the position information from the current that circulates through the free-wheeling diode of an IGBT with OC fault, for a five-phase PMSM. This is allowed by the fact that this free-wheeling current is affected by the back-EMF. Namely, a frequency-locked loop based on second-order generalized integrators (which work as a band-pass filter around the fundamental frequency) is applied to said current. This novel technique based on the free-wheeling current is shown to exhibit better dynamics than a conventional back-EMF/rotor-flux sliding-mode observer. Moreover, the implementation of the former requires specification of much fewer machine parameters. However, inaccuracy may arise in some cases (e.g., for relatively high compared with permanent-magnet excitation current) due to the assumption that the free-wheeling current is in phase with the back-EMF. In addition, it is only suitable for single IGBT OC faults, and not for low speeds. Encoder/resolver faults in absence of IGBT OCs may be tolerated using this technique by deliberately opening one switch, but at the expense of power derating.
7.3.1.9. Other Low-Frequency Observers
There are other observers based on low-frequency components that are used for speed/position estimation in multiphase ac drives and do not fit in the preceding categories.
Taheri et al. [206] have proposed a control strategy (loss-model control) for improving the efficiency of asymmetrical six-phase IMs. Since conventional loss-model control is very sensitive to model uncertainties, they suggest adapting its parameters by means of an extended Kalman filter. Among many other variables, this filter also estimates the speed, and, thus, it could be used in the event of encoder/resolver failures. The machine model in both - and x-y planes is taken into account, thus differing from . Space harmonics are neglected in the model. This Kalmar filter was later simplified so as to reduce the computational burden [207].
Another option was devised in [181], for a five-phase SPMSM. The rotor position is found by iteratively reducing the error between the measured torque and the torque computed based on the position estimate. This technique also works in the absence of torque measurement, if the error is instead obtained as the difference between the torque estimates of the current and previous samples. Space harmonics are disregarded and only the - variables are employed for the estimation. The improvement of aspects, such as accuracy, robustness, and computational burden was left as future work.
7.3.2. Encoderless High-Frequency Observers
In accordance with Figure 19, mainly two types of high-frequency speed/position estimators can be found in the literature about multiphase drives: those based on rotor-slot harmonics produced by the fundamental current (Section 7.3.2.1), and those based on high-frequency injection (Section 7.3.2.2).
7.3.2.1. Based on Rotor-Slot Harmonics Due to Fundamental Current
One of the conventional methods to obtain the rotor speed in three-phase IMs is based on tracking the frequencies of the rotor-slot current harmonics produced by the stator fundamental current [525,526,527,528,529,530,531,532]. More specifically, the lowest-order ones (principal slot harmonics) are usually preferred, because of their relatively greater magnitude. However, in three-phase IMs these harmonics are typically very small, which makes it particularly difficult to obtain accurate speed values in this manner [533]. Furthermore, as previously established in [529], the combinations of rotor-slot and pole-pair numbers have to be carefully chosen to ensure that said harmonics are mapped into the - plane so as to produce corresponding current components; such combinations had been assessed for , but not for higher n. To address these obstacles, it was shown in [202] that multiphase machines offer an excellent opportunity to exploit the rotor-slot harmonics for speed estimation, because the resulting current components are relatively large when these harmonics are mapped into low-impedance x-y planes; furthermore, the combinations of rotor-slot, pole-pair and phase numbers for satisfying this condition for were given as well.
For the sake of illustration, Figure 21 and Figure 22 show the complex spectrum per VSD plane of stator current for a six-phase IM with symmetrical and asymmetrical WSA, respectively [202]. Both IMs have been obtained by rewinding with one pole pair identical three-phase IMs, with 18 rotor and 24 stator slots [202]. The results using two different loads are included for each machine: one for lower (red) and another one for higher (blue) value of slip gain . It can be seen that the symmetrical six-phase IM (see Figure 21) behaves similarly to a conventional three-phase machine with observable principal slot harmonics [529], i.e., the principal slot harmonics (of frequencies and ) are mapped into the - plane, yielding small current components that, besides producing torque ripple, are difficult to distinguish from noise and from other harmonics. Conversely, the six-phase IM with asymmetrical WSA (see Figure 22) exhibits principal slot harmonics in the - (i.e., x-y) plane that are relatively large and, hence, easy to measure and track. It can also be observed that the frequencies of these harmonics vary with the slip [see Figure 22b], as expected, thus allowing to estimate the speed [202]. The main drawback associated with this improvement is that the drive losses are increased, but the extra loss is not expected to be significant in most cases [202].
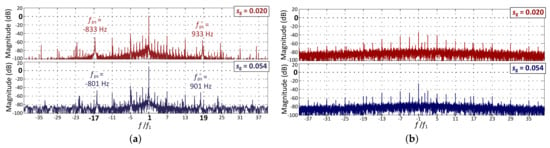
Figure 21.
Complex spectrum of stator current for six-phase IM with symmetrical SWA, one pole pair and 18 rotor slots [202]. In the label of the horizontal axis, f represents any frequency and the fundamental frequency. (a) - plane. (b) - (i.e., x-y) plane.
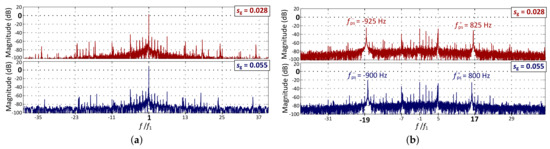
Figure 22.
Complex spectrum of stator current for six-phase IM with asymmetrical SWA, one pole pair and 18 rotor slots [202]. In the label of the horizontal axis, f represents any frequency and the fundamental frequency. (a) - plane. (b) - (i.e., x-y) plane.
In absence of OC and SC faults, the phase currents are practically balanced and a principal slot harmonic in a certain phase can be tracked with just one current sensor. Alternatively, if a sufficient number of phase currents are measured, a principal slot harmonic in an x-y plane [see Figure 22b] can be tracked, with less possibilities of interference with - harmonics.
However, under phase OC faults, the resulting current constraints make it necessary to impose fundamental current in secondary subspaces (further discussed in Part 2) and introduce very significant current imbalance. As a consequence, as shown later in [214], the principal slot harmonics are no longer located in just one subspace and with either positive or negative sequence; instead, although the frequency in absolute value is not altered, these harmonics are distributed among several subspaces and positive/negative sequences. This also means that their amplitude is different in each phase current. Accordingly, a novel scheme (see Figure 23) was proposed in [214] to estimate the speed based on the principal slot harmonics under phase OCs.
Broadly speaking, the strategy from [214], illustrated in Figure 23, is based on obtaining an estimate of a principal-slot-harmonic frequency from each phase current (analogously to [526]), and then selecting the most accurate (lowest error covariance) one at each instant. A set of filters is applied to each phase current, consisting of a notch filter to remove the fundamental component at , a bandpass filter approximately centered at the principal slot harmonic, and an adaptive notch filter that automatically adjusts its center frequency to said harmonic. The center frequency of the bandpass filter is calculated based on and the electromagnetic-torque reference . The outputs of the adaptive notch filter of phase are the corresponding error covariance and the scalar , related to the center frequency of this filter. is a binary signal that can be used to accelerate the response of the adaptive notch filter during transients. Note that in the selection, it is imposed that should be between two bounds, and [214]. Once the value associated with the lowest error covariance is chosen, the corresponding frequency is computed, and finally the rotor-speed estimate is obtained from and .
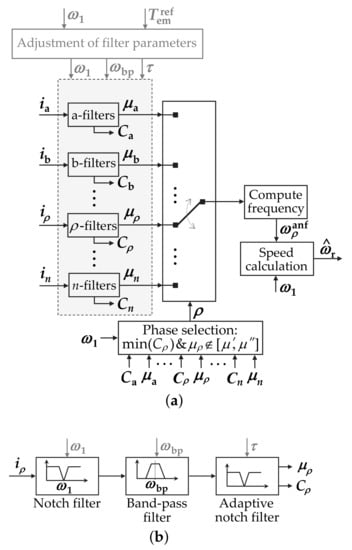
Figure 23.
Speed estimation method based on rotor-slot harmonics due to fundamental current, suitable for phase OC faults [214]. (a) General view. (b) Set of filters in an arbitrary phase .
7.3.2.2. High-Frequency Signal Injection
As reflected in Table 17, most of the preceding methods are not suitable for operation at zero and very low speed (with the exception, e.g., of [184,185]; see Section 7.3.1.4), because the majority of them rely on the back-EMF, which usually is practically zero in such conditions. In synchronous machines, knowledge of the initial position is normally required for starting, unlike in IMs. In any case, in IMs, accurate information about the flux position at zero or very low speeds is often desirable as well, especially for high torque capability [534,535]. The initial position of synchronous machines could be obtained by specific low-cost Hall-effect sensors, damper windings, or by initially running the machine in open-loop manner or by external means [536,537]; however, these options are not advisable in many applications [537]. Alternatively, it is possible to inject a high-frequency signal that permits to estimate the rotor position without these shortcomings. Basically, these strategies are based on exploiting the high-frequency saliency that naturally arises, e.g., in three-phase PMSMs [510,538,539,540] or IMs [534,535,541,542,543], in many cases even in those machines that do not exhibit saliency at the fundamental frequency. This high-frequency saliency is due to deterministic rotor salient modulation or to flux saturation [541]. For , there are mainly two options for the high-frequency injection: rotating signal in stationary frame or pulsating signal (sine or square wave) in an axis (usually ) of the synchronous frame [510], both within the - plane. In case of stationary-frame rotating injection, the main alternatives for obtaining the position information are based on demodulating and extracting (through filtering) the resulting high-frequency negative-sequence current or zero-sequence voltage [542]. The latter option is more accurate but needs extra hardware [542]. For -axis pulsating injection, demodulation and filtering is most often performed in the -axis current [510]. It is worth highlighting that using square wave instead of sinusoidal injection implies that the high-frequency and fundamental components can be farther from each other in the spectrum, thus becoming much easier to separate them and reducing the need to diminish the control bandwidth [543]; however, the higher injection frequency may mean worsening the audible noise, iron loss, measurement resolution, and dc-link utilization [208]. On the other hand, for non-salient PMSMs, pulsating injection in synchronous frame is more suitable than rotating stationary-frame injection [209]. Although these approaches have mostly been investigated for three phases, many of them have also been applied/extended to multiphase machines in some publications, as summarized in Table 19 and surveyed in the following.

Table 19.
Speed/position-sensorless methods based on high-frequency injection (Section 7.3.2.2) in multiphase applications in the literature.
Table 19.
Speed/position-sensorless methods based on high-frequency injection (Section 7.3.2.2) in multiphase applications in the literature.
| References | Machine | Injected Signal | Measurement | ||
|---|---|---|---|---|---|
| n | WSA | Rotor | |||
| Zhang et al. [209] | 5 | Sym. | IPMSM | Rotating sine wave in - stat. frame | Negative-seq. - current |
| Ramezani and Ojo [188] | 9 | Sym. | IPMSM | Rotating sine wave in - stat. frame | - current harmonic |
| Almarhoon et al. [191] | 6 | Asym. | IPMSM | Rotating sine waves in double - stat. frames | Zero-seq. voltage |
| Barcaro et al. [215] | 6 | Asym./sym./mult. | IPMSM | Pulsating sine wave in axis | current harmonic |
| Imai et al. [195] | 9 | Multisec. | SPMSM | Pulsating sine wave in q axis of one sector | d axis of same sector |
| Almarhoon et al. [192] | 6 | Asym. | IPMSM | Pulsating sine waves in double d axes | Zero-seq. voltage |
| Liu et al. [201] | 5 | Sym. | IPMSM | Pulsating square wave in axis | - current harmonic |
| Tian et al. [208] | 5 | Sym. | IPMSM | Pulsating square/sine wave in axis | current harmonic |
Barcaro et al., estimate the rotor position of a six-phase IPMSM with double-layer FSCWs in both healthy and open-phase conditions [215]. In a healthy situation, the two three-phase winding sets are connected in series and supplied by three-phase currents. Under OC fault, only half of the windings are employed, either as a two-sector machine [see Figure 3d] with one faulty sector or as an asymmetrical/symmetrical six-phase machine [see Figure 3a,c] with one faulty three-phase winding. In the latter case, two alternative winding connections are also studied. The low-frequency (apparent) and high-frequency (differential) saliencies are theoretically and experimentally assessed, yielding high values (suitable for the sensorless method) for all the configurations. The position and speed are obtained analogously to previous three-phase methods [539]: high-frequency voltage is added in the axis within the - plane, and the estimated rotor position is adaptively adjusted (e.g., by a PI block) so that the high-frequency current is nullified, which means that the position error is cancelled.
In the context of a five-phase IPMSM with trapezoidal back-EMF, Tian et al., propose an improved position estimator based on pulsating sinusoidal injection in axis [208]. Zero average current references are assumed in the and axes. A detailed high-frequency model taking into account the system delays, the stator resistance and the influence of the injection frequency (unlike previous publications) is presented. Although the high-frequency signals are injected and measured in the - plane, the coupling with the - plane is also taken into consideration in the model. Based on this model, it is shown that, by simply injecting the high-frequency voltage in phase with the measured -axis current (instead of the axis corresponding to estimated position), more accurate position is attained in both transient and steady state.
A rotating high-frequency signal has also been added in the - plane (stationary frame) of a nine-phase symmetrical IPMSM with non-negligible space harmonics [188]. The fact that the extra signal is injected in a plane different from the fundamental (-) allows reducing the generation of torque ripple (due to low third back-EMF harmonic) and also simplifying the filtering required for extracting the resulting high-frequency current. In any case, a low-pass filter is still necessary, in the - plane. A full-order machine model is presented, including harmonics and cross-coupling. For the position estimation, a Luenberger observer is applied to the filtered - harmonic current.
High-frequency injection with low torque ripple was achieved in [201] also by adding the signal in the - plane, in a five-phase IPMSM. In this case the injected voltage is a square wave, injected in the synchronous axis. Consequently, in practice the main difference with respect to [188] is that low-pass filters are not necessary, hence avoiding the associated phase lag [201]. In this manner, the advantages of low-torque ripple (due to - injection) [188] and excellent dynamics (due to square-wave injection, as for ) [543] are simultaneously combined in a single drive [201].
The initial position of the rotor is estimated in [195] by high-frequency injection for a nine-phase PMSM including space harmonics. In contrast to [188] (also for nine-phase PMSM), it is an SPMSM instead of an IPMSM. Moreover, it is a three-sector WSA [195] instead of symmetrical WSA [188]. As a consequence of the multisector WSA, the mutual inductance is not the same for every pair of phases within a sector. The high-frequency voltage is added in the synchronous q axis of one of the three sectors, and the d-axis current corresponding to the same sector is extracted to calculate the position. However, this method is not suitable for speed different from zero.
The sensorless position estimation by high-frequency injection has also been addressed from the motor-design perspective [209]. A previous design of a five-phase PMSM [263], in which the back-EMF harmonics common for single-layer FSCWs are reduced by unequal tooth width and asymmetrical air-gap, is adopted as a starting point. In [209], flux barriers are adequately designed so that flux-intensifying behavior is attained (), increasing saliency over the original machine. Consequently, the accuracy of the high-frequency position estimation is improved, besides reducing the risk of demagnetization and extending the torque-speed range. Moreover, in the new design, flux saturation is less significant thanks to the air barriers, and hence the position estimation is less sensitive to load variations. In the new machine, sensorless position estimation is performed by the aforementioned three-phase method of rotating - injection and - negative-sequence current extraction [542], as indicated in Table 19.
As previously mentioned, a particular type of three-phase position estimation using high-frequency injection is based on setting the high-frequency signal as a rotating voltage in the - plane (stationary frame) and computing the rotor position from zero-sequence voltage measurements [540,542]. Compared with calculating the position from the resulting negative-sequence component, using the zero sequence provides faster and more accurate estimation [542]. However, this typically requires several voltage sensors or one voltage sensor with a resistor network; furthermore, relatively complex algorithms are required to cancel oscillations that tend to arise in the estimation [191]. Almarhoon et al., propose a technique to apply this kind of sensorless position estimation without these drawbacks in a six-phase asymmetrical PMSM with two stator neutral points [191]. Only a single voltage sensor is needed, between both neutrals, and without extra resistors. In addition, the sixth-order zero-sequence oscillations are cancelled by setting a phase shift between the waveforms injected in each three-phase set.
Later, the same authors as in [191] have proposed a similar method in [192], but based on -axis pulsating injection instead of stationary-frame rotating injection (see Table 19). The position is also obtained from a voltage sensor placed between both stator neutral points. It is shown that, in this case, the phase shift between high-frequency signals in order to cancel the zero-sequence sixth-order oscillations should be .
In any case, although high-frequency injection makes it possible to accurately obtain the rotor position even at zero and very low speeds, this approach also exhibits some drawbacks [208,511]. Namely, it generates extra losses, torque ripple, and acoustic noise [208,511]. Furthermore, the maximum-voltage and maximum-speed capabilities might also be decreased [208,511], and the risk of magnet demagnetization in PMSMs may be increased [208]. For these reasons, it is often recommended to employ these methods at zero/low speed, but resort to other sensorless techniques at higher speed [511].
7.3.3. Encoderless Resilient Control
Instead of monitoring the difference between measured and estimated speed and changing the control scheme when a sensor failure is thereby detected, it is proposed in [182] to employ a resilient control method that is able to automatically compensate the effect of such fault as an external disturbance. In particular, it is completed by means of active disturbance-rejection control for a five-phase PMSM. The model of the machine in both planes is taken into account. In any case, adaptation of this approach for other n is expected to be relatively simple. Satisfactory rejection of torque disturbances is also provided. Nonetheless, it should be noted that the tested speed-sensor faults are just emulated by relatively small measurement disturbances (e.g., ).
7.4. Concluding Remarks about Speed/Position-Sensor Faults
From the preceding review and the summary in Table 17, several outcomes can be drawn concerning tolerance to encoder/resolver failures in multiphase drives.
The problems associated with faults in these sensors may be avoided by not installing them in the ac drives, and by using at all times a sensorless speed/position observer or a control method (e.g., V/f or DTC without speed control) that does not require this information. However, in many cases, for better performance (accuracy, dynamic response, absence of torque ripple, etc.), it is preferable to actually include the speed/position sensor and just resort to these tolerant techniques in case of encoder/resolver malfunction [58,87,127,197,199,208,213,216].
Most of the numerous encoderless methods available for three-phase drives may be directly applied to the - plane of a multiphase machine with barely any modification, given that the behavior of such a plane is usually identical as for , as long as space harmonics are disregarded. Similarly, many of the novel sensorless techniques proposed and tested with multiphase machines could easily be used in machines of other n, including . This is especially true regarding the existing MRAS observers, as indicated in Table 17. In any case, the existing publications have revealed that the extra DOFs of multiphase drives can be exploited to obtain additional advantages, with respect to , for tolerance of speed/position-sensor faults, such as the following.
- The combination of rotor-slot, pole-pair, and phase numbers can be chosen so that the rotor-slot harmonics of IMs are mapped in a low-impedance subspace, thus yielding larger current components that are much easier to track (for speed estimation) than for [202,214];
- By setting to zero the current reference of a secondary plane of a PMSM with certain back-EMF harmonics, a back-EMF harmonic and its phase angle (rotor position) can easily be obtained from the respective voltage references without the need of machine parameters, such as inductances and resistances [198,199], unlike for ;
- Concerning position estimation from zero-sequence voltage during high-frequency injection, the DOFs of a six-phase machine can be set so that it is carried out with less extra hardware and with smaller measurement ripple than for [191,192];
- High-frequency injection can be performed in a secondary plane, instead of in -, to reduce the associated torque ripple and the measurement filtering [188,201];
- In a multiphase IM, the rotor position/speed can be estimated even at zero/low speed by exciting a low-order (e.g., third-order) space harmonic in a secondary subspace, without resorting to high-frequency injection and the associated problems (e.g., acoustic noise) [184,185].
It is also worth of notice that, in a modular drive, which is typical in fault-tolerant multiphase applications, position/speed estimates can be separately obtained for each module, even if each of them consists of a single phase [212].
Tolerance to OC and SC faults is, in fact, a property that is strongly associated with multiphase machines, in contrast to three-phase ones. For , it is hence of uttermost importance to ensure that the drive is able to work not only under encoder/resolver failures, but also when such faults are present in combination with OC or SC faults. Some of the sensorless methods proposed for multiphase drives are suitable for such conditions [127,161,210,211,213,214,215,216,217,218,219,544]. However, many of the most advanced sensorless strategies, such as [185,192,199,201], are not suitable for OC and SC faults, and, thus, their extension to such scenarios in the near future is of substantial interest.
In the particular case of MRAS-based speed estimators, there is a recognizable trend to improve their robustness to parameter uncertainties by using sliding-mode reference observers, while taking care to avoid chattering [194,204,205]. Nevertheless, this is not only specific of multiphase drives; it also affects three-phase ones.
Another interesting possibility to handle these faults, recently suggested [182], is to implement a resilient control method that automatically adapts to encoder/resolver failures without fault detection and switching between techniques, but this kind of approach has barely been studied for multiphase drives so far.
Finally, it should be noted that, in spite of the wide variety of strategies that are tolerant to speed/position-sensor faults in multiphase drives (see Table 17), the performance of most of them has not been compared in a quantitative manner. A comparison of many of these state-of-the-art techniques in a given multiphase application by means of specific figures of merit (e.g., accuracy, transient response, torque ripple, etc.) would also be of great interest for the research community and industry.
8. DC-Link Voltage Shortage
If the dc-link voltage of an ac drive decreases, it may not be possible to provide large enough ac voltage in the VSC machine side. The same problem arises if the required ac voltage increases too much, even if is constant. In both cases the requested modulation index m becomes excessive, with m being defined as the ratio of the amplitude of the - fundamental voltage reference over [138,149,151,152,159]. Several undesired effects may be caused by these situations, such as the following ones.
- Since the machine back-EMF tends to increase with speed, if decreases then the maximum speed and power are reduced as well [141,171];
- If the modulation index increases beyond the linear modulation range, overmodulation occurs. This means that low-order voltage harmonics are introduced, the VSD subspaces become coupled in terms of voltage, and the conventional PWM and control methods are no longer able to work properly [8,9,134,135,137,138,139,142,143,145,147,148,149,150,151,152,154,155,156,158,159,167];
- If the VSC ac voltage is reduced, the difference between its magnitude and that of the machine back-EMF may become substantially greater. As a consequence, overcurrent may occur [129,545].
The main causes, detection methods and tolerant approaches for shortage are summarized in Figure 24.
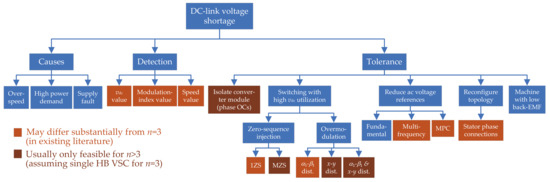
Figure 24.
Causes, detection methods and tolerance approaches for dc-link voltage shortage in multiphase drives.
8.1. Causes of DC-Link Voltage Shortage
One of the possible reasons for this type of problem is related to speed. If speed (and, hence, back-EMF) becomes higher than expected, may not be enough for driving the machine without taking special measures [129,141,546]. This is especially critical for PMSMs, where the magnet flux (producing large back-EMF) cannot be deactivated [129]. Overspeed, in turn, can be due to, e.g., encoder damage [546], high torque/speed reference in the ac drive [7,141], excessive mechanical power from a different machine coupled to the same shaft, sudden decrease in external load torque, etc.
DC-link voltage shortage may also be caused by a large demand of active power, e.g., by fast accelerations [547] or by other loads connected to the dc-link or power supply (if any) [169]. Alternatively, if there is not an increment in the active-power demand, shortage can be produced when a failure occurs in the power supply, assuming that the machine works as a motor [169,466,467,548,549]; e.g., a voltage sag in the grid [467,548,549].
Undesired variations (e.g., decrease) in are especially likely when the dc-link capacitance is low, which is an attractive feature for reducing bulky capacitors and the associated cost [467].
Furthermore, even if the drive is working properly in a scenario with phase-to-phase back-EMF higher than (e.g., in the so-called field-weakening speed range), excessive stator currents and active power may be obtained because of uncontrolled rectification if the switches are turned off, e.g., due to a control fault. This situation is particularly troublesome in the case of SPMSMs, whose back-EMF is high and it remains after disabling the switch control [129].
A shortage in the capability to produce sufficient ac voltage can also be caused by other faults in the drive, such as switch SCs [103,168,277]. This is addressed in the part of the paper corresponding to that type of failure (Section 6.3.3).
8.2. Detection of DC-Link Voltage Shortage
A shortage can be straightforwardly detected by monitoring the value of [169], the modulation index [133,138,143,147,148,149,150,151,152,153,154,155,156,157,158,159], or the speed [141]. The last option may be troublesome when relying on the hypothesis that is constant, because it may not hold in practice.
8.3. Tolerance to DC-Link Voltage Shortage
In accordance with the classification shown in Figure 24, the survey of methods to tolerate shortage faults is organized as follows. First, the possibility of isolating VSC modules is addressed in Section 8.3.1. Increasing the dc-link utilization by injecting one or multiple zero sequences is discussed in Section 8.3.2. Overmodulation methods based on square-wave switching or PWM are reviewed in Section 8.3.3. Reducing the ac voltage references to restore the PWM linear range or to respect voltage constraints with current FCS-MPC is explained in Section 8.3.4 and Section 8.3.5, respectively. Concerning topology reconfiguration, modification of the stator phase connections is described in Section 8.3.6. Finally, the convenience of adopting a machine with small back-EMF for tolerating uncontrolled rectification during shortage is discussed in Section 8.3.7.
8.3.1. Isolation of VSC Module
One of the most disruptive procedures to handle a drop is disabling the affected VSC module/s [169]. If there is a single machine-side VSC with one dc-link, this would normally interrupt the operation. Thus, in such case, this approach is not a fault-tolerant method; nevertheless, it can help preventing further damage, such as overcurrent, e.g., if decreased due to a supply fault and the supply is suddenly restored [169].
If there are independent dc-links, it is enough to disable and isolate just the corresponding VSCs, so that the machine can still work, with OCs in the respective phases.
In the particular scenario where the dc-links of several machine-side VSCs are connected in series [see Figure 8e,f,h], disabling certain VSC module/s can help tolerating shortage faults. This is because then the dc-link voltage in each of the active VSCs can be increased while keeping the same total [409].
8.3.2. Zero-Sequence Voltage Injection: 1ZS and MZS
DC-link utilization is a concept very closely related to this type of fault. Higher dc-link utilization means that greater stator phase voltage can be provided with given [2]. This feature is not only desirable for tolerating shortage faults, but also for obtaining advantageous characteristics in healthy operation, such as extended speed range [141], lower rating for given machine [138,142], or greater ability to track abrupt changes in the torque reference [550]. Nonetheless, even though many of the publications surveyed here about enhancing dc-link utilization are not specifically focused on drops caused by faults, they are included because their methods and studies can be equally applied to such faulty situation. Moreover, in several of them the proposals are actually tested in the experiments by applying reductions [137,138,142,143,154,157,158].
A popular and simple method to improve dc-link utilization is based on injecting zero-sequence voltage signals that reduce the amplitude of the phase-voltage references without causing extra current, because the corresponding impedance is ideally infinite [2]. In particular, the zero sequence, equally distributed among all phases, can normally be added without producing current, except in FB topologies or if there is a current path, e.g., between the stator neutral point/s and the converter. When applied by carrier-based (CB) PWM, the most common technique for this purpose is often known as min–max method [172,448], based on setting the zero sequence as [10]
where is the vector of n pole-voltage references for the VSC ac side. (The pole voltages are the voltages between the VSC ac-side terminals and the dc-link midpoint.) Regarding implementation, (2) can be added to all phases before performing CB PWM (see Figure 25), e.g., although it may also be equivalently applied by means of SV PWM [2,154,448]. In this manner, one zero sequence (1ZS), , is injected.
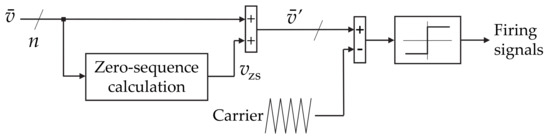
Figure 25.
Block diagram of the CB PWM implementation of zero-sequence injection 1ZS or MZS, using (2) for computing [343].
If there are multiple l-phase winding sets with (star connection) and isolated neutral points, or with (see Section 3.1.3) and forming loops of phases (with ), i.e., l-phase splitting, then multiple zero sequences (MZSs) can be included without associated current, by applying (2) to the voltages corresponding to each winding set [137,143,154,551]. MZS yields even better dc-link utilization than 1ZS. This fact can be observed in Figure 26, which shows the improvement in dc-link utilization of several methods with respect to simple PWM without any injection or clipping (balanced sinusoidal modulating signals) [143]. Since the maximum modulation index with the latter is (normalized by ), the percentage values shown in this figure could be understood as increments in hundredths of p.u. over In particular, it can be seen that the plots of MZS (black) in Figure 26 are always equal or higher than those of 1ZS (beige). When using MZS with and three-phase splitting, the extra exploitation is the same as for 1ZS with , i.e., [2]. This also holds for other WSAs with three-phase splitting other than symmetrical and asymmetrical, despite not being explicitly indicated in Figure 26. Regarding MZS and asymmetrical WSA, note that only three-phase winding sets () are considered in this figure, because it is by far the most common l option. The same dc-link utilization as for 1ZS with n phases and symmetrical WSA would be obtained for 1ZS with phases and k winding sets using either no-phase-shift WSA or multisector WSA. As reflected in Figure 26, in the cases where the zero sequence would only be composed of even-order harmonics (e.g., 1ZS for even n with symmetrical WSA), these harmonics are in practice of zero magnitude and, hence, no benefit in this regard is attained by its injection, at least if non-ideal imbalance is neglected. Figure 26 also illustrates that the voltage gain provided by 1ZS with respect to conventional PWM tends to become lower with increasing n, as known from preceding publications, such as [147,150].
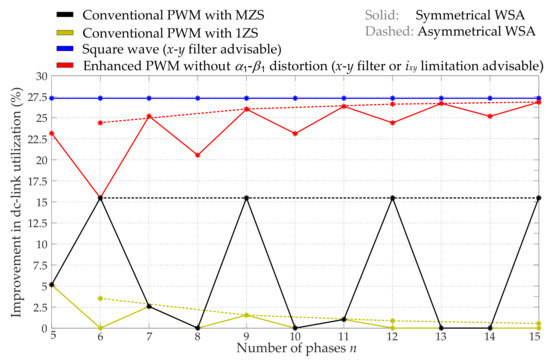
Figure 26.
Improvement in dc-link utilization, by various switching techniques, with respect to conventional PWM without zero sequence (i.e., sinusoidal modulating signals) [143].
8.3.3. Overmodulation
Let us neglect non-ideal effects of the converter switching such as dead time, device voltage drop and turn-on/off times. Then, the linear modulation range corresponds with modulation index values, such that the low-frequency current-producing components of the actual ac voltages match those of the voltage references (frequently, just - positive-sequence fundamental) [138,151,152,154]. For instance, in agreement with Figure 26, when using sinusoidal balanced voltage references in combination with MZS in machines with multiple three-phase winding sets, the linear modulation range spans up to a modulation index of For , its limit is at When the modulation index exceeds the linear modulation range (black/beige lines in Figure 26), overmodulation occurs, which means that current-producing voltages have to be included, thus affecting to certain extent the machine performance (at least its SCL, and often also the torque ripple) [138,151,152,154,159].
The literature about overmodulation is surveyed next, focusing consecutively on square-switching with passive x-y filters (Section 8.3.3.1), combination of PWM with x-y filters (Section 8.3.3.2), overmodulation by using PWM (Section 8.3.3.3), overmodulation PWM with automatic current limitation (Section 8.3.3.4), and, finally, overmodulation with closed-loop and multifrequency control (Section 8.3.3.5).
8.3.3.1. Square-Wave Switching and Passive x-y Filters
Considering an n-phase two-level HB VSC, the most extreme case of overmodulation happens when square waves are applied in each of the pole voltages. This is achieved by turning on the upper and lower switch of each leg during half the fundamental period, sequentially. In three-phase VSCs, it is known as six-step operation. In addition to the high dc-link utilization, this method is also advantageous in terms of simplicity and low switching frequency [145]. It provides a modulation index of as much as regardless of n and WSA, as shown in Figure 26 (blue). However, the resulting voltages contain significant low-frequency current-producing distortion. This is particularly troublesome in the secondary subspaces, where large undesired currents arise due to the extremely low impedance [145,150].
If the drive is only conceived for square-wave switching, the magnitude of the fundamental voltage can only be regulated by varying the dc-link voltage [150]. Thus, if drops due to a fault, the machine operation is substantially altered. In any case, ac drives using solely square-wave switching, although popular many decades ago, they were mostly replaced by PWM gradually [2]. In a PWM-based VSC, switching with square waveforms can be used occasionally to tolerate shortage faults, because under this condition the modulation index required to provide the same fundamental phase voltage increases, resulting in square-wave switching in the worst-case scenario.
A solution for attenuating the undesired currents considerably when using square voltage waveforms was devised in [140] for various phase numbers. Namely, special custom-made passive filters using multiple cores are inserted between the VSC and machine, so that large impedance is obtained in the secondary VSD subspaces, without affecting the - plane. Accordingly, they can be understood as x-y filters [143]. Examples of x-y filters based on [140] are depicted in Figure 27 [142,143], where and denote distinct self-inductances. A similar concept is applied to a six-phase IM with asymmetrical WSA in [145], but the filter is incorporated in a compact fashion in the machine stator by inserting magnetic rings in the coil ends. Additionally, for the same type of machine, in [474], although it is not focused on overmodulation or square voltages, it is proposed to increase the x-y impedance by using full coil pitch and special design of the stator slot shape, instead of additional filters. Later, in [144], which addresses square-wave switching for identical n and WSA, it is suggested to use an external passive x-y filter based on a single iron core, very small and easy to manufacture.
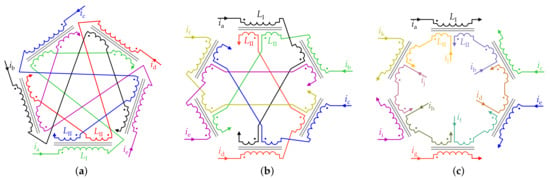
Figure 27.
Examples of passive x-y filters, based on [140]. (a) For symmetrical WSA [142]. (b) For asymmetrical WSA [143]. (c) For symmetrical WSA [143].
8.3.3.2. Combination of Passive x-y Filters and PWM
When using these passive x-y filters (or equivalent designs) with square voltage waveforms, only the x-y harmonics due to the square waves are attenuated by the filters. This prevents excessive SCL, the associated requirement of increasing the current rating, and the torque ripple due to interaction between x-y space (if any) and time harmonics [145]. However, the low-order harmonics introduced by the square waveforms into the - plane are not filtered, despite producing torque ripple. To overcome this problem, it is proposed in [142] for to combine an x-y filter with a (novel) CB PWM method. The latter is designed so that no low-order - harmonics are produced, while the injected x-y harmonics are optimum so as to yield the highest dc-link utilization. Consequently, no torque ripple is introduced, the resulting maximum modulation index is nearly as high as for square wave ( versus ), and the filtered x-y currents are almost negligible [142]. Moreover, this PWM method is very simple, e.g., in comparison with other PWM techniques (discussed shortly) able to achieve the same dc-link utilization, as shown in Figure 28 and Table 20. Online computation of square-root or trigonometric functions is not needed. In addition, this simplicity is also allowed by the fact that, since the performance is very satisfactory with x-y filter even for , there is no need to reduce the x-y injection as a function of the phase angle or when m decreases. In this manner, this method is particularly suitable for drives where high dc-link utilization is desired in prolonged or frequent manner. This technique was extended to machines of other n, with either symmetrical or asymmetrical WSA, in [143]. The resulting dc-link utilization is represented also in Figure 26, using red color. It can be seen that the improvement in comparison with 1ZS and MZS is substantial in all cases except with symmetrical WSA, and it becomes closer to that of square-wave switching as n rises [143]. However, the addition of the passive x-y filters increases the cost, size and weight of the system, and hampers the potential of exploiting the current DOFs for other purposes such as fault tolerance [138].
Moreover, although [142,143] address specifically the optimum combination of x-y filters with PWM, numerous PWM methods able to work during overmodulation had already been proposed in the past (e.g., those included in Figure 28 and Table 20), some of them with some superior characteristics, as reviewed next.
8.3.3.3. Overmodulation by Using PWM
Concerning SV PWM, in general its basic principle, either in linear or overmodulation range, consists in selecting some of the voltage vectors corresponding to the VSC possible switching states and computing the respective times of application, depending on the angle and amplitude of the reference - voltage SV at each instant (sample).
One of the oldest and simplest SV PWM methods suitable for overmodulation is based on using only the two largest active voltage vectors that are the nearest to the reference voltage vector in the - plane [146,148]. (The term “active” excludes the so-called zero voltage vectors, which are null in the - plane). For instance, for , this permits achieving a maximum m of without - low-frequency distortion [148]. However, in absence of additional filtering, the resulting undesired x-y currents are very large [148]. The performance offered by this SV PWM method is equivalent to the aforementioned CB one proposed in [142] with x-y filter (see Section 8.3.3.2); nevertheless, the latter PWM is much simpler in terms of computations (see Figure 28), principally thanks to its lack of online trigonometric and square-root functions [143].

| References | Method Description | n | WSA | VSC | Unneeded Dis-Tortion * | Minimum | Autom. i Limitation | Compu-Tational Complex. |
|---|---|---|---|---|---|---|---|---|
| Various [140,144,145] | Square-wave switching | Any | Any | HB | Yes | No | No | Very low |
| Various [146,148] | SV PWM with 2 large vectors | Any | Any | HB | No | No | No | Medium |
| Iqbal and Levi [148] | SV PWM with 2 large and 2 med. vectors | 5 | Sym. | HB | No | No | No | Medium |
| Carrasco and Silva [149] | SV PWM with min. | 5 | Sym. | HB | No | Yes | No | Very high |
| Duran et al. [151] | SV PWM with min. and no common mode | 5 | Sym. | HB | No | Yes | No | Very high |
| Prieto et al. [152] | SV PWM with low and no common mode | Odd | Sym. | HB | No | No | No | Very high |
| Bu et al. [159] | SV PWM with linear injection | 5 | Sym. | HB | No | No | No | Medium |
| Priestley et al. [133] | SV PWM for FB VSC | 5 | Sym. | FB | No | No | No | Very high |
| Yazdani et al. [156] | SV PWM with double 3-phase VSD | 6 | Asym. | HB | Yes | No | No | Very high |
| Zhu et al. [139] | SV PWM with double 3-phase VSD | 6 | Asym. | HB | Yes | No | No | High |
| Zhou et al. [154] | SV PWM with 6-phase VSD | 6 | Asym. | HB | No | Yes | No | Very high |
| Paul and Basu [157] | SV PWM with double 3-phase VSD (limited m) | 6 | Asym. | HB | No | Yes | No | High |
| Paul and Basu [158] | SV PWM with double 3-phase VSD (extended m) | 6 | Asym. | HB | No | Yes | No | High |
| Yang et al. [160] | SV PWM with sequential optimization scheme | Any | Sym. | HB | No | No | No | Very high |
| Yepes et al. [137] | CB PWM for multifrequency current control | Any | As./sym. | FB/HB | Yes | No | No | Low |
| Komrska et al. [155] | CB PWM with high utilization | Any | Sym. | HB | No | No | No | Medium |
| Yepes et al. [142,143] | Simple CB PWM with high utilization | Any | As./sym. | HB | No | No | No | Low |
| Vancini et al. [153] | CB PWM extended from | 5 | Sym. | HB | No | Yes | No | Low |
| Yepes et al. [138] | CB PWM with adaptive x-y current limitation | 5 | Sym. | HB | No | No | Yes | Medium |
* The methods with “No” in this column have α1-β1 distortion in conditions where it is unavoidable for any method: either due to very high modulation index m (e.g., m > 1.231 for n = 5) [151,153] or to excessive/rated SCL [138]; but with such methods there is no α1-β1 distortion in other conditions. † Complexity depends on the adopted platform and implementation; assumptions similar to those in [143] are considered here in this regard. ‡ Although this method is not based on finding the global minimum in terms of for each , it has been shown in [160] that at least for a certain n = 7 machine it yields lower x-y distortion than the other existing methods.
Iqbal and Levi [148] propose an SV PWM method for using four active voltage vectors: two large and two medium ones. The computations are performed differently depending on whether m is within the linear (<1.052) or overmodulation (>1.052) regions. No - low-order harmonics are produced. The x-y low-frequency distortion with four vectors is lower than with the conventional overmodulation technique based on two large vectors, as long as the m is below its maximum , where both strategies are equivalent [148].
A more advanced SV PWM method for overmodulation in five-phase drives is presented by Carrasco and Silva in [149]. This technique also combines two medium and two large voltage vectors, avoiding - low-frequency voltage distortion. Nevertheless, although in [148] the four vectors were used for any m except , in this case [149] some of these vectors are ignored depending on the - vector of the voltage reference. More importantly, for each position of , the solution adopted in [149] ensures that the x-y low-order voltage harmonics are minimum, unlike the preceding one from [148]. This solution is obtained by minimization based on Lagrange multipliers. As shown in [149], the method devised therein exhibits much smaller x-y components, even at the maximum m of
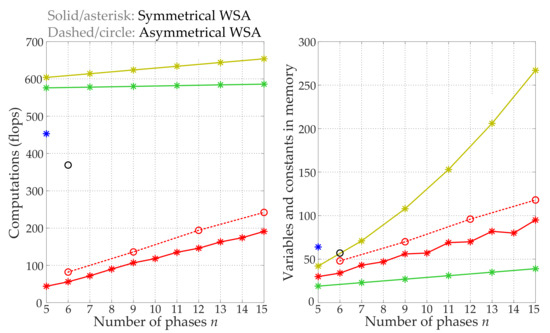
Figure 28.
Computational burden, in terms of number of floating-point operations (flops) and constants/variables in memory, among several overmodulation methods that avoid - low-frequency distortion [143]: two large neighboring voltage vectors [146,148,152] (green), SV PWM with minimum x-y distortion and no common mode for [151] (blue), SV PWM with minimum x-y distortion and no common mode for odd n [152] (beige), SV PWM with minimum x-y distortion for with asymmetrical WSA [158] (black), and simple CB PWM with high dc-link utilization [142,143] (red).
On the other hand, nearly at the same time as [149], Duran et al., proposed another overmodulation SV PWM method for in [151]. Two alternatives are presented: one based on (up to) two medium and two large voltage vectors, and another one based on (up to) four large voltage vectors. In contrast to previous approaches, here special care is taken to avoid zero voltage vectors, so that high-frequency common-mode voltage is notably reduced, especially in the latter option. Reducing high-frequency common-mode voltage in the machine decreases the risk of potential problems, such as parasitic currents in bearings and damage of winding insulation [151,552]. The low-frequency x-y voltage is effectively minimized (as mathematically proved), while satisfying the condition of small high-frequency common mode. In this manner, reduced x-y and no - low-frequency distortion is obtained up to , with small high-frequency common-mode voltage. Operation with m beyond is also achieved (up to square-wave switching), in contrast to previous SV PWM approaches, although at the unavoidable cost of introducing - harmonics. The latter implies that torque ripple arises, and that the m requested at the PWM input and the actual one at the converter ac-side (output) may no longer match [138,153].
The same authors as in [151] have later developed a general SV PWM methodology [152] suitable for overmodulation in n-phase machines of any odd with symmetrical WSA. For this purpose, voltage vectors adjacent to the - voltage reference are exploited [152]. Similarly to [151], zero voltage vectors are avoided. On the other hand, differently from [151], all the voltage vectors are used in the entire overmodulation range, reducing their application proportionally (except of the largest ones) instead of ignoring some of them in the most demanding regions. Operation with - harmonic injection up to square-wave switching is not considered. In addition to the generality of the new method, it is also claimed to be simpler [152] than those in [149,151] for . In this regard, it can be observed in Figure 28 [143] that, e.g., for this technique [152] involves fewer variables and constants than the one from [151]. It was also shown in [152] that for the low-frequency x-y distortion is smaller than with the methods from [148]. However, it is not ensured that the presented solution [152] corresponds with the actual global minimum of all possibilities for given reference and n.
In [160], a universal overmodulation SV PWM technique is developed for any n, although the study is focused on . Up to active voltage vectors are employed. This strategy is based on sequentially disabling the usage of the voltage vectors of lower magnitude, as increases. Thus, this approach resembles in this regard those proposed in [149,151] for , but in this case also for other n. Conversely to five-phase drives, for higher n there are several x-y planes instead of one. In the new method [160], the progressive loss of DOFs, when discarding the lower voltage vectors, imply injecting harmonics in the x-y planes corresponding to higher h in the VSD transform (see Section 3.3). The resulting x-y distortion is not mathematically demonstrated to be the minimum possible, but it is experimentally shown [160] to be substantially smaller for than preceding techniques, including the one from [152] (of similar complexity). Moreover, the switching frequency is lower as well.
Another SV PWM method for overmodulation in five-phase drives is presented in [159], also based on four active voltage vectors. Instead of minimizing low-order harmonics in the x-y plane, it injects a third-order x-y harmonic whose amplitude follows a linear relation with the excess of m with respect to Three different values are considered for the slope of this relation, distinguishing between three overmodulation regions depending on m. The main advantage with respect to preceding five-phase techniques, such as [151,152] is its simplicity. However, the x-y low-frequency distortion is larger, and it still relies on online computation of trigonometric functions (as most SV PWM methods), which are often considered very resource consuming [143,553]. In fact, SV PWM methods are usually much more computationally demanding than CB equivalents [554]. Furthermore, many control platforms include dedicated hardware modules for CB PWM, but not for SV PWM [142].
In [155], an overmodulation CB PWM method is proposed for any number of phases and DOFs. The signals to be compared with the carrier (modulating signals) are generated by minimizing the infinite norm of the vector of leg voltages, for given - voltage reference. When a single DOF is considered, the obtained solution is equivalent to 1ZS. For DOFs, it matches the conventional SV PWM based on two large voltage vectors. Thus, the performance in terms of current harmonics is inferior to advanced SV PWM methods with minimum distortion, such as those from [149,151,152]. In any case, it has the merit of being designed for CB instead of SV PWM, and also of its generality in terms of n and DOFs. However, the implementation is not straightforward, especially for cases other than the particular one detailed therein (). In this regard, the aforementioned CB PWM techniques proposed in [142,143] with x-y filters (see Section 8.3.3.2), although also equivalent to using two large vectors, are advantageous in the sense that simple closed-form expressions for direct implementation are presented.
Overmodulation by CB PWM for is also studied in [153]. In said paper, well-consolidated overmodulation strategies for three-phase drives are extended to five phases; namely, the so-called minimum-distance, minimum-phase-error, SV (referring to 1ZS, but clipping the modulating signals to when needed), and Bolognani’s PWM methods. Closed-form expressions of the modulating signals are included. Injection of - harmonics is avoided and x-y distortion is minimized in all of them (behaving equivalently) up to , except for 1ZS with clipping, which in this range offers smaller current THD but with torque ripple and reduced actual m. For a higher value of the requested m (), the methods can be sorted from lowest to highest switching frequency, from highest to lowest current THD, and from greatest to lowest difference between requested and actual m, in the following order: Bolognani’s, minimum distance, minimum phase error, and 1ZS with clipping. It is also shown that the actual m obtained by minimum phase error does not surpass ; by minimum distance, it tends to when the requested one tends to infinite; by Bologani’s, it reaches (square-wave switching) as soon as the requested one does; and by 1ZS with clipping, it rises with the requested one much more slowly than for the other techniques. As reflected in Table 20, these overmodulation methods are simpler than most other in the literature, in agreement with the fact that they are CB.
Overmodulation PWM for six-phase machines with asymmetrical WSA and two stator neutral points (three-phase splitting) has also received considerable attention [146,154,156,157,158]. Gopakumar et al. [146] attain high dc-link utilization (up to ) without torque ripple by using just two large voltage vectors. This is obtained, however, at the expense of significant current-producing x-y harmonics, similarly to the aforementioned analogous approach for [148]. Yazdani et al., propose in [156] an SV PWM method that avoids low-order current-producing voltage harmonics in the linear modulation range (up to ), and includes both - and x-y distortion during overmodulation (between and ). It is based on combining three-phase PWM techniques for each of the two winding sets, using a vector classification algorithm. The main drawback of this technique [156] is that torque ripple is produced by the - injection even for low degree of overmodulation () [154,157,158]. In [139], another overmodulation SV PWM technique considering the two winding sets separately is presented. For m between and only the angle of the SV is changed at each instant, whereas between and just its modulus is altered. Linear relation between the actual and requested m is achieved for any m. Similarly to [156], - harmonics are introduced as soon as Zhou et al. [154] instead treat the machine as a whole (six-dimensional VSD transform) and up to four active voltage vectors are employed in the overmodulation range with minimum x-y and no - low-frequency voltage distortion, until Two important shortcomings of this strategy [154] can be pointed out: it is relatively complex [157] and the x-y minimization is performed by considering just that two medium and two large active vectors are used [158]. The first problem is tackled in [157], which presents a PWM method based on double three-phase PWM, with similar performance but lower computational burden. In any case, the maximum m is limited to [157]. A further step is taken in [158] by the same authors, where is reached and the optimization problem is not restricted to specific vector types, thus being more general. In fact, 16 possible PWM techniques with equivalent low-frequency behavior are derived in [158], out of which one matches the previous one from [154]. Another of these 16 PWM methods is selected and compared with that from [154], showing that the new one has smaller high-frequency current ripple [158]. This new technique distinguishes between two overmodulation regions: in one of them (from to ), it uses two large, one medium, and two small active vectors; in the other one (from to ), two large and two medium active vectors. Furthermore, it can also be implemented as a double three-phase PWM [158]. The comparison between all the other potential PWM solutions found in [158] was left for future research.
At this point, it is worth emphasizing that the maximum m provided by all these overmodulation SV and CB PWM methods based on avoiding injection of - low-order harmonics for HB VSCs [142,143,146,148,149,151,152,153,154,155,157,158,159] coincides with the red lines shown in Figure 26.
A minimum-phase-error overmodulation technique based on CB PWM is presented in [137] for any phase number and various drive topologies, although the paper is focused on closed-loop multifrequency current control. In contrast to [153], the minimum-phase-error saturation is applied to all subspaces as soon as m exceeds the 1ZS or MZS maximum, instead of resorting to it just when - saturation is unavoidable (i.e., for [153]). Thus, with this strategy [137] the - voltage vector is altered for smaller m (above those corresponding to the 1ZS or MZS maximum) than in [153]. In particular, the amount of useful active power (related to -) is modified to a greater extent than with the minimum-phase-error method of [153]. Furthermore, the maximum actual m is lower than in [153]. Nevertheless, this CB-PWM strategy [137] admits non-zero x-y voltage references, so that it is able to partially compensate x-y voltage disturbances, unlike [153]. It should also be noted that, although the computational complexity of this PWM approach [137] is low (as displayed in Table 20), that of the associated multifrequency current control is much higher [137].
Overmodulation SV PWM is addressed in [133] in the context of a five-phase PMSM with open-end windings supplied by a single FB VSC [see Figure 8d]. In this scenario, the voltage reference provided by the closed-loop current control does not only contain an - component, but also x-y and (zero sequence) voltages. This is performed with the aim of cancelling undesired x-y and low-frequency currents that could produce torque ripple in presence of space harmonics in such subspaces. This means, however, that the fundamental voltage attainable during overmodulation is not as high as in PWM methods without said capability or in HB VSCs [133]. That is, this PWM is not able to reach the dc-link utilization represented by the red lines in Figure 26. Moreover, the high-frequency current ripple is larger than with conventional unipolar CB PWM [133].
8.3.3.4. Automatic x-y Current Limitation
From the preceding discussion (summarized in Table 20), it can be stated that most multiphase PWM methods for overmodulation, assuming just - voltage reference, are based on injecting only x-y current-producing harmonics and avoiding low-frequency - distortion, at least until m is so high that the latter is not possible ( for ) [142,143,146,148,149,151,152,153,154,155,157,158,159]. However, given the typically very low impedance in the machine secondary subspaces, this approach leads to large x-y currents that easily surpass the drive rating and compromise its integrity [138,142,150].
Although some multiphase PWM overmodulation strategies do add low-order - harmonics when m does not make it necessary (as discussed mostly in Section 8.3.3.3, and briefly in Section 8.3.3.5 and Section 8.3.4.2) [137,139,148,153,156,487], most of them are not able to select the proportion between - and x-y harmonics so as to optimally provide the least - (torque/flux) alteration while complying with the drive current rating.
Recently, a novel overmodulation method for (see Figure 29) is presented in [143] to address this aspect. Priority is given to avoiding - distortion as well, but when the phase current (equivalently, the total SCL) tends to surpass its rating, the x-y injection is automatically reduced and adequately (to the necessary extent) replaced by - harmonics. Hence, the generation of torque ripple is minimized, but without risk of overheating. Thus, adding passive x-y filters (or similar) [140,142,143,144,145] (see Section 8.3.3.2) is not required. In fact, as shown in the comparison of Table 20, this is so far the only available overmodulation method for that includes current limitation. The computation of the x-y voltage references for maximum dc-link utilization is based on the simple CB PWM method from [142], but these references are multiplied (yielding ) by a factor , which is within , with . When these x-y components are not enough to avoid clipping of the modulating signals to , the - voltage is saturated with an - minimum-phase-error criterion. The factor is adjusted by an integrator, whose input can be either the amount of - voltage saturation or the excess in the square root of the actual x-y SCL with respect to its maximum allowable value. Certain gains and are introduced to set the dynamics of the resulting closed loop. The former input is selected unless there is excessive SCL (), with certain thresholds to avoid chattering [143]. In this manner, steady-state - distortion is only introduced when it is strictly necessary to prevent overcurrent, as intended. The maximum actual (output) modulation index that can be achieved is between and , depending on the allowable x-y current injection.
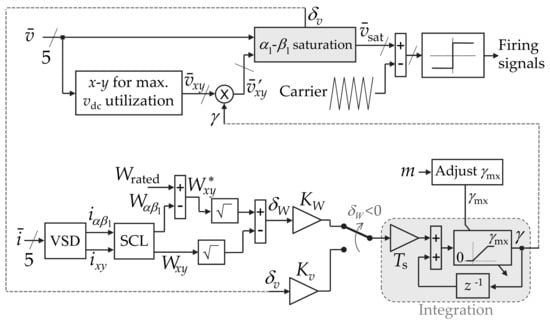
Figure 29.
Overmodulation method with adaptive x-y current limitation proposed in [143] for to provide minimum - distortion while preventing excessive x-y current. is sampling period, is rated SCL, is - SCL, is x-y SCL, and is the maximum allowable x-y SCL (depending on and ) [143].
In any case, it should be noted that this method relies on the assumption that changing varies the SCL in the x-y plane to a much greater extent than in -. This only holds as long as the x-y impedance is actually much smaller than the - one. Thus, e.g., this strategy is expected to work much better for machines with distributed windings than for full-pitch or fractional-slot concentrated windings.
8.3.3.5. Closed-Loop and Multifrequency Control under Overmodulation
Most of the overmodulation methods just reviewed in the sections between Section 8.3.3.1 and Section 8.3.3.4 rely on the assumption of open-loop V/f control and that the voltage references (inputs of the overmodulation algorithms) are zero in all VSD subspaces but the - plane [138,139,140,142,143,144,145,146,148,149,151,152,153,154,156,157,158,159,160]. When these hypotheses do not hold, additional modifications are then necessary for ensuring proper functioning during overmodulation. In fact, although a few of the aforesaid overmodulation techniques (e.g., [137]) were actually employed with closed-loop or multifrequency control in the past, it was performed by adding extra operations. This additional difficulty is mainly due to the following problems.
- Although open-loop control is reliable and simple [334], it is, in principle, only suitable for IMs, and its performance is usually inferior to closed-loop control in terms of efficiency, transient behavior, etc. Hence, closed-loop control is frequently preferred. However, during overmodulation, the actual low-frequency voltage components may differ to a great extent from the requested ones. That is, the plant seen by the current control (e.g., when using RFOC) becomes substantially non-linear. Consequently, in case of closed loop, the dynamics are likely to be worsened or even become unstable. In particular, saturating the output of a closed-loop linear controller with integral terms is known to cause unconstrained increase (wind-up) in the accumulated error in them [555,556]. In this manner, in a VSC with this type of control, the voltage reference tends to rise without limits when the actual ac voltage is saturated [557]. This increase aggravates the distortion associated with the output saturation, and it can also cause very long transient and large overshoot when the cause of saturation is eventually removed (e.g., recover) [556,557,558].
- As previously mentioned, most overmodulation algorithms assume that there is only - voltage reference. Non-zero voltage references are highly advisable in secondary subspaces where current can flow. This is mainly because, as a consequence of the corresponding low impedance, even small uncompensated voltage disturbances (due to dead times, asymmetries, saturation, back-EMF harmonics, etc.) give rise to large undesired currents [134,135,137,139,487,488,493,494]. Alternative reasons for including multifrequency (multi-subspace) voltages are, e.g., enhancing the torque density by harmonic injection [5,6,7,8,9,10] or driving several machines by a single VSC [2,10,12]. In any of these cases, the output of the multifrequency current control consists of non-zero voltage references in multiple subspaces and frequencies, so as to cancel the effect of the voltage disturbances and/or impose required currents.
In the first place, note that problem 1 listed above, regarding the effect of voltage saturation on closed-loop current control, is not exclusive of multiphase drives. For understanding better the methods available for multiphase drives, it is convenient to survey, first, some of the three-phase ones, briefly. For typically only the - and -axis currents are controlled, by using PI controllers; hence, wind-up protection can be easily obtained by applying to them conventional anti-wind-up techniques of PI control [559,560]. One of the most common of such techniques is known as back-calculation, where the difference between the saturated and unsaturated output is fed back to the corresponding integrator input [555]. The gain of this feedback can be chosen (, with being the proportional gain) so that the controller output becomes equal to the saturated output value almost instantaneously (ideally) [559,560]. Back-calculation anti-wind-up for PI current control in synchronous - frame is depicted in Figure 30. In this figure, bold typeface denotes complex vectors of the form . A similar effect is obtained by simply disabling the integration when voltage saturation occurs [168,561]. It is worth noting that these kinds of wind-up protection often mean maintaining the magnitude of the output voltage reference and staying in overmodulation in practice, not decreasing the output so as to return to the linear modulation range. If instead reducing the ac voltage references for avoiding overmodulation (and associated distortion) is preferred, it would require other operations in the control scheme, which are discussed later, in Section 8.3.4.
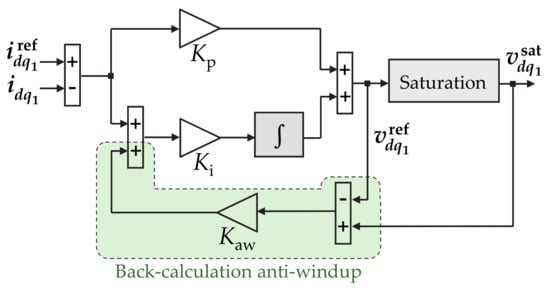
Figure 30.
Anti-wind-up based on back-calculation for synchronous PI current control with output voltage saturation in - plane, as for [559,560].
In addition, in many cases it is not sufficient to control in closed loop just the positive-sequence fundamental component, even in three-phase drives. Controlling multiple frequencies in the - plane of a three-phase ac drive is often performed in order to reduce torque/speed ripple [545,562,563,564], and hence including wind-up protection for such type of control is of interest as well. Anti-wind-up strategies have been applied/proposed for multifrequency (Controllers able to track both the positive and negative sequences of a certain frequency, such as resonant controllers [565,566], are here also considered as multifrequency) current controllers in three-phase VSCs, either roughly maintaining the magnitude of the control outputs during overmodulation [558,565,566,567,568,569,570] or reducing the requested modulation index in order to return to linear modulation (also explained later) [545,557,571,572]. Within the former group of anti-wind-up methods, some of them are based on simply using back-calculation [565,566,570], as for single-frequency control. However, applying back-calculation to multifrequency control without additional measures can lead to important output distortion under voltage saturation, including harmonic orders not present in the voltage references [557]. For , this problem is avoided in [545,557,568,571,572] by using various different solutions, which cannot be directly applied to drives with more than three phases.
Concerning multiphase drives, anti-wind-up methods have also been implemented in them, either reducing [7,135,137] or not [334,487] the requested modulation index so as to return to the linear range. The former will be reviewed in Section 8.3.4. Regarding [334,487], although the anti-wind-up protection is not the focus of these papers, it is briefly mentioned in them that it is completed by using back-calculation similarly to .
On the other hand, a simple solution for the aforesaid problems 1 and 2 is presented by Zhu et al., in [139] for a six-phase PMSM with asymmetrical WSA using RFOC. Three different operating regions are distinguished. In the first one, called sinusoidal current modulation area, is sufficient for synthesizing the voltage references of the - and x-y planes ( and ) with closed-loop current control enabled in both. In the second one, called sinusoidal voltage modulation area, is enough for synthesizing (circular trajectory) and not ; hence, the x-y current control is disabled and the reference is set to zero. In the last one, which is the overmodulation area, neither nor can be synthesized, and one of the overmodulation PWM methods reviewed in Section 8.3.3 is employed [139]. In addition, although it is not discussed therein [139], to prevent wind-up of the - field-oriented current control during overmodulation, anti-windup methods as for three-phase drives [559,560] may be adopted. No wind-up protection is required for the x-y control, since it is turned off before output saturation occurs. It should be noted that transition may occur between the first and third operating regions without working in the second one, because setting may actually reduce the voltage available in the - plane with respect to in some cases, instead of increasing it. It is also worth pointing out that, since the x-y closed-loop is completely deactivated for high modulation index, the resulting undesired currents may be too large. In applications where control simplicity is not a priority, it may be preferable to find a better compromise between dc-link utilization and current distortion when addressing problems 1 and 2. Steps in this direction, by suitably reducing the multifrequency voltage references, have been taken for multiphase drives in a few publications so far [134,135,137], which are discussed shortly.
8.3.4. Reducing AC Voltage References to Restore Linear Modulation in PWM-Based Control
Under shortage, unless other actions (e.g., drive reconfiguration) are taken to remedy this failure, the switching (e.g., PWM) and control methods in the control platform should be adapted to tolerate it. Special measures for the generation of switching signals in this situation were surveyed in Section 8.3.2 and Section 8.3.3. Namely, the zero-sequence (1ZS and MZS) methods from Section 8.3.2 increase the dc-link utilization without altering (normally) the low-frequency stator current, while the overmodulation techniques from Section 8.3.3 introduce current-producing low-frequency voltage distortion in order to yield higher modulation indices. However, even if the overmodulation methods are designed optimally and controller wind-up is effectively prevented, current distortion is unavoidable when operating in the overmodulation range. There is an interesting three-phase voltage saturation technique [568] that avoids introducing frequency components not present in the voltage references under overmodulation, even during transients. Nonetheless, besides other limitations, such as potential overcurrent [545], this method [568] does produce distortion during overmodulation in the sense that the magnitudes of the frequency components in the actual voltages and currents differ from those that are in fact in the references. That is, as aforesaid, low-frequency current distortion is unavoidable in practice during overmodulation.
Consequently, instead of maintaining overmodulation, in practice a different approach is often preferred (see Figure 24): reducing the ac voltage references (inputs of the overmodulation methods) in order to return to the linear modulation range and, hence, decrease the amount of output distortion. In any case, it is worth emphasizing that, even if this option is chosen, when using closed-loop control a suitable overmodulation method such as those in Section 8.3.3 is usually still necessary. It is needed for driving the machine during the time interval consumed in restoring linear modulation. On the other hand, for open-loop control the voltage references may be instantaneously decreased to prevent overmodulation, avoiding the need of overmodulation algorithms.
This reduction in the voltage references is carried out differently depending on whether these references consist of a single frequency or of multiple frequencies, and also on whether open- or closed-loop control is employed. Accordingly, the following scenarios are next discussed separately: only fundamental voltage reference either in open or in closed loop (Section 8.3.4.1), multifrequency closed-loop current control for disturbance compensation (Section 8.3.4.2), for torque-density enhancement (Section 8.3.4.3) or for other applications such as multimotor drives, torque-ripple mitigation or speed-sensorless operation by x-y injection (Section 8.3.4.4).
8.3.4.1. Fundamental Frequency
When an IM is driven by simple open-loop V/f control with single fundamental frequency, under shortage the modulus of can be directly decreased, while either keeping the fundamental frequency (reducing flux) or lowering it as well (reducing speed). This is valid for both three-phase and multiphase drives.
Regarding closed-loop control based on conventional RFOC, if the distortion caused by voltage saturation is deemed unacceptable, it is common to reduce the reference by decreasing the -axis current (field weakening) [559,560]. In particular, for , the magnitude of is often lowered until it matches the radius of the circle inscribed in the - hexagonal boundary, avoiding overmodulation [560]. This is especially suitable when only the - fundamental positive sequence is controlled. This type of field weakening is illustrated in Figure 31 for the - plane for any n, considering that current control is performed by just PI controllers in and axes. It can be combined with the anti-wind-up technique shown in Figure 30 [560]. Under phase OC faults, fundamental-frequency currents must be present in the secondary subspaces; accordingly, their effect on the dc-link utilization may also be taken into account for calculating (e.g., by offline numerical optimization) optimum current references for all VSD subspaces, such that overmodulation does not occur [170] (discussed in Part 2).
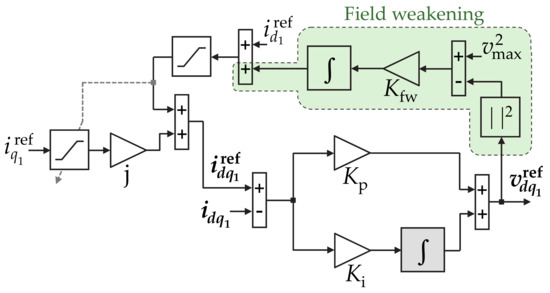
Figure 31.
Field weakening for RFOC synchronous PI current control in - plane, as for [560]. The maximum steady-state voltage-reference modulus usually matches the radius of a circumference inscribed in the - output-voltage boundary. Instead of squared voltage values before , a square root may be applied [7], at the cost of more computations [560]. Anti-wind-up (not shown) may also be needed for the integrator in the field-weakening feedback [7].
A different option, although less usual, is to implement a control scheme where the flux is directly controlled, instead of being indirectly regulated by the current as in field-oriented control. This happens, e.g., in DTC and direct flux vector control [512,573]. Thanks to the direct regulation of the stator flux, the field-weakening operation can be easily achieved by reducing the flux reference, depending on the dc-link voltage and synchronous speed, without adding extra loops such as the one shown in Figure 31. Moreover, since the -axis current is also directly regulated in direct flux vector control, overcurrent can be straightforwardly prevented as well through the current references, unlike in DTC [512,573]. This kind of approach has been satisfactorily employed for multiphase IMs in [161,173], even under phase OCs (see Part 2).
8.3.4.2. Multifrequency Control for Disturbance Compensation
When the control scheme is designed so as to cancel/attenuate harmonic disturbances, the voltage references are composed of various frequency components. For three-phase multifrequency current control, it is proposed in [557] to dynamically readjust the current references under overmodulation until the trajectory of the - voltage reference does not exceed its hexagonal boundary (realizable references), returning to linear modulation. The scheme is illustrated in Figure 32. More specifically, in this process the magnitude of all voltage-reference frequency components are reduced by the same proportion, so that the shape of the voltage trajectory is kept, simply scaled down (see Figure 33). In this manner, no extra voltage harmonics, caused by clipping to the hexagon, are introduced in steady state. In this sense, this kind of approach is often referred to as distortion-free saturation [137,545,557,568,572]. Instead of full compensation of the drive harmonic disturbances as in normal operation, during the shortage partial compensation of voltage disturbances is accomplished. Since the unconstrained rise of the output is prevented, this procedure also serves as anti-wind-up protection. The direction in which the current references are modified is calculated based on the voltage references and the plant model, so that the shape of the voltage trajectory is not altered, as intended. During the transient reduction in the modulation index, overmodulation is performed by instantaneously scaling down the magnitude of the voltage-reference SV (without phase error) so that it is constrained within the hexagon. In any case, other overmodulation techniques could be used during this transient. Later, in [572], it was proposed to add certain operations [included with yellow shade in Figure 32a] based on internal model control [555], so that the effect of the plant non-linearity due to saturation is removed from the current feedback during the transient current-reference readjustment, thus improving dynamics. It was also shown that the method provides good performance even under significant plant parameter variations [572].
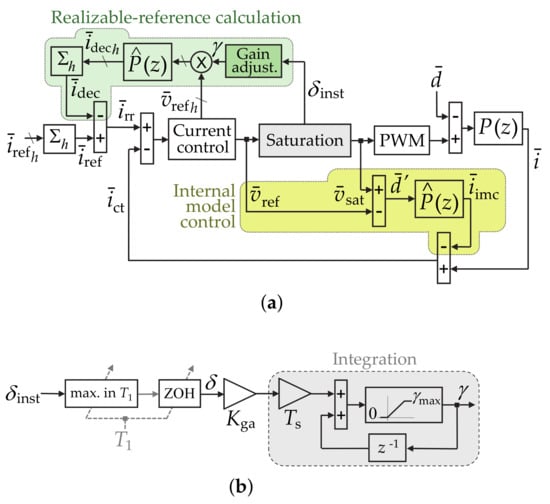
Figure 32.
Simplified representation of the multifrequency distortion-free method used for three-phases in [137,557,572] and for n phases in [545]. Coordinate transformations are omitted. In this figure, a dash over a line indicates multiple harmonics h, not values for several phases; the latter is just denoted by overbar in the corresponding variable. and denote the actual plant and its nominal model, respectively. and are fundamental and sampling period, respectively. and are the instantaneous and per-, respectively, excess with respect to the output-voltage boundary. represents the realizable references. d is voltage disturbance. ZOH stands for zero-order hold. (a) General view. (b) Content of gain-adjustment block.
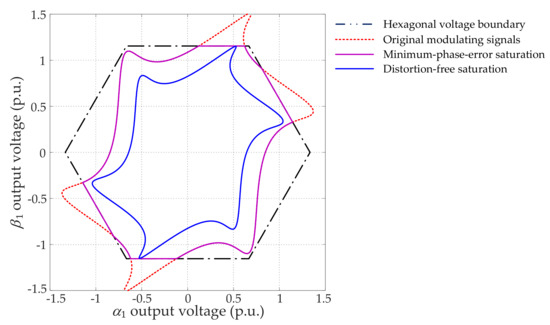
Figure 33.
Comparison for between the - output-voltage trajectories provided by conventional minimum-phase-error saturation (solid magenta) and by the multifrequency distortion-free method (solid blue) from [137,545,557,572] (see Figure 32), for original voltage references (dashed red) containing fifth- and seventh-order harmonics, as well as positive- and negative-sequence fundamental. Min–max zero-sequence injection based on (2) is considered in all cases.
This multifrequency approach [557,572] was extended from three-phase to multiphase drives in [137], where multiple topologies and any phase number are taken into account. Its features are summarized in Table 21, with other multiphase strategies. The fact that the closed-loop x-y current control is still operative during shortage, partially compensating disturbances, permits obtaining better current THD than with the strategies that do not include (or disable) x-y control. Instead of a two-dimensional hexagon as in [137,557,572] (), a multidimensional output-voltage boundary () is considered and fully exploited in [137]. During the transient process of returning from overmodulation to linear modulation range, it is necessary to apply an overmodulation PWM method; the one used in [137] during this time interval can be understood as multiphase minimum-phase-error CB PWM, as mentioned in Section 8.3.3.3.

Table 21.
Multiphase methods for reducing multifrequency voltage references with partial disturbance compensation during shortage (Section 8.3.4.2).
Table 21.
Multiphase methods for reducing multifrequency voltage references with partial disturbance compensation during shortage (Section 8.3.4.2).
| References | n | WSA | Unneeded Fundamental Reduction | Depends on Relative Phase between Harmonics | Periodically Disables Harmonic Control | Needs Measurement |
|---|---|---|---|---|---|---|
| Yepes et al. [137] | Any | Asym./sym. | Yes | No | No | Yes |
| Karttunen et al. [135] | 6 | Asym. | No | Yes | Yes | Yes |
| Feng et al. [134] | 6 | Asym. | No | Yes | Yes | No |
A different strategy for reducing multiphase ac voltage references with multiple frequencies under shortage is proposed by Karttunen et al., in [135], focused on a six-phase PMSM with asymmetrical WSA. As in [137,557,572], the main purpose is to adapt the current references so that overmodulation and associated extra harmonic orders are avoided in steady state. Partial compensation of disturbances during shortage is also attained. Conventional techniques are adopted in [135] for anti-wind-up and SV PWM. The principal advantage of this method [135] in comparison with [137], for certain applications, is that the magnitude of the fundamental component is not modified when it is sufficient to just alter the harmonics. On the other hand, this implies additional complexity, because in this case, depending on the relative phase between the vectors of each frequency, the voltage margin available for the fundamental may either increase or decrease as a certain harmonic is reduced. This holds even if the harmonic under consideration is in a different VSD plane from the fundamental, since all VSD subspaces are coupled in terms of voltage saturation [10], similarly to the fact that the zero-sequence third-order harmonic alters the - hexagonal boundary for . Moreover, this method [135] requires measuring and storing the current harmonics present when their control is disabled, for each operating point.
Feng et al., present a different technique [134] for performing closed-loop multifrequency current control under voltage constraints, also in a six-phase PMSM with asymmetrical WSA. The proposed strategy resembles the preceding two multiphase multifrequency methods [135,137] in the sense that the current references are modified so that the voltage references decrease. Priority is given to adjust the harmonics while maintaining the fundamental component, as in [135]. Additionally, similarly to [135], the harmonic control is initially disabled in order to obtain extra information about the current components in such condition. This information is then exploited to progressively change the harmonic amplitude using the optimum phase angle. Even though, in [135], the output voltage excess with respect to needs to be continuously monitored while adjusting the harmonics, in [134] is not needed, because the condition of voltage saturation is instead confirmed by checking whether harmonic current increases with the corresponding voltage. However, this method [134] relies on the assumption that reducing the harmonic compensation decreases the degree of voltage saturation, but in reality the opposite may also occur [135,570]. Furthermore, with this approach it may be necessary to periodically disable the harmonic control and restart the process to find the new optimum current references.
8.3.4.3. Multifrequency Control for Enhancement of Torque Density
In addition to harmonic disturbance compensation, the topic of reducing multifrequency voltage references to avoid shortage (by either open- or closed-loop control) has also been tackled in the context of increasing torque density by harmonic injection. This is particularly common in multiphase machines with full-pitch concentrated windings.
It is worth remarking that, although the multifrequency methods proposed in [134,135] are suitable for harmonic disturbance compensation and not for non-zero current-harmonic tracking, the one from [137] can be employed for either application.
Levi et al., present an approach for assessing the output-voltage boundaries for any odd n in [10], which is extended for even n in [574]. The resulting volume for avoiding overmodulation in an machine is illustrated in Figure 34, where , and denote the modulation indices in the -, -, and - planes, respectively. These limits could be directly applied to control a drive in open loop without entering overmodulation in this kind of application. However, the additional actions needed for closed-loop control are not discussed. Furthermore, since the boundaries are computed by disregarding the frequencies and phase shifts of the VSD voltages (assuming the worst-case scenario), the capability provided by the available dc-link voltage is actually underestimated (not fully exploited) for cases other than the most unfavorable one.
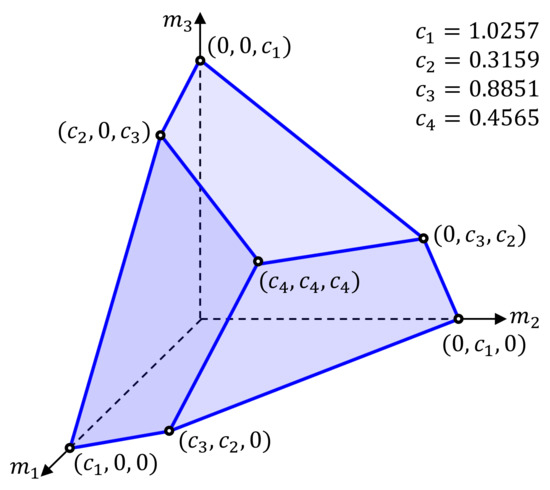
Figure 34.
Volume corresponding to linear PWM operation (no overmodulation) in a seven-phase machine, considering optimum zero-sequence (i.e., 1ZS) injection and the worst-case scenario in terms of phase shifts or frequencies of the voltages in each VSD subspace [10].
Considering fundamental and third-order current and space harmonics, Mengoni et al. [7] divided the operation of a multiphase IM drive into four main regions as the modulation index m (or equivalently, speed) increases:
- (I)
- Both fundamental and third-order current components are exploited;
- (II)
- The third-order current harmonic is gradually reduced to avoid overmodulation;
- (III)
- Said harmonic is completely avoided, and field-weakening is applied to the fundamental if necessary;
- (IV)
- With available and field-weakening, it is no longer possible to provide maximum current, and, hence, the output power is reduced.
Using closed-loop control, this reduction in the third- and first-order current references is performed analogously to Figure 31 in each corresponding plane, with priority given to the fundamental [7]. The constraints regarding current and air-gap flux density are also respected at all times, which were not considered in [137]. In absence of overmodulation, the current references are set following a maximum-torque-per-ampere trajectory taking into account both frequency components. A drawback of this method is that, for simplicity, the phase shifts of the voltage components are assumed to be those of the worst scenario for calculating the conditions of shortage, similarly to [10] (the drive operates within the plane from Figure 34 [7]); consequently, the dc-link voltage is not fully exploited [9].
A different method [9] for tolerating shortage for drives with high torque density, based on multifrequency FCS-MPC, will be addressed in Section 8.3.5.
8.3.4.4. Multifrequency Control for other Applications
There are also other multiphase applications where conventional overmodulation methods are not suitable due to the need of multifrequency voltage references.
This is the case of multimotor drives, where various machines with sinusoidally distributed windings are driven by means of a single VSC [10,574]. The output-voltage boundaries established in [10,574] are also valid for this application, with the same assumptions as the aforementioned ones for enhanced torque density. These limits can be of great help, e.g., for selecting the necessary dc-link voltage in the design stage of a multimotor drive for any possible combination of operating conditions of certain machines. It would also be possible to employ these limitations for controlling a multimotor drive in open loop without overmodulation. However, decreasing the requested output with closed-loop control so as to restore linear modulation under shortage has not been addressed so far in the specific context of a multimotor application. In any case, among the multifrequency techniques reviewed in Section 8.3.4.2 and Section 8.3.4.3, it can be inferred that the one from [137] is particularly suitable for allowing simultaneous operation of all the machines when decreases. The other solutions [7,134,135], based on removing one frequency component while preserving other/s, would often mean stopping at least one of the machines.
Another example of multiphase multifrequency application is the injection of a third-order harmonic into an x-y plane for closed-loop speed-sensorless operation [183,184,185] (explained in Section 7.3.1.4). Mengoni et al., propose to give priority to the x-y harmonic when shortage arises, so that the proper estimation of the rotor flux position is preserved [183,184,185]. That is, the - voltage reference is saturated to a circle of reduced radius in order to satisfy this condition. However, no details are given therein concerning how anti-wind-up is then performed and about whether the ac voltage and current references are decreased for avoiding overmodulation (the action of the saturator) in steady state or not. None of the aforementioned strategies based on reduction in ac references [7,134,135,137] would be adequate for this application, since none of them give priority to the x-y voltage over the - one.
Current harmonics may also be injected for mitigating torque ripple, which is particularly important for machines with non-sinusoidal back-EMF under phase OC or SC faults. The computation of optimum current references is a common task for tolerating phase OC/SC faults in drives based on RFOC, and the voltage constraints may be included in the optimization problem for allowing field-weakening operation in such conditions. This is addressed in [162,164,165,166] for both SC and OC failures, and in [174] for OC ones, all of them with PMSMs. Further details in this regard are given in Part 2. Among these publications, anti-windup protection for the current control (per-phase resonant controllers) is described in [166], based on [575].
8.3.5. Consideration of Voltage Constraints in Current FCS-MPC
Numerous methods have been surveyed in the preceding sections for operating in overmodulation (Section 8.3.3) and also for reducing the voltage references so as to return to linear modulation in PWM-based VSCs (Section 8.3.4) when shortage occurs. However, all these techniques relied on either PWM (mostly) or applying square-wave switching. In other situations, alternative solutions should be applied.
Yu et al. [136] present a current FCS-MPC with improved dc-link utilization for a five-phase PMSM. A popular type of current FCS-MPC is that based on virtual voltage vectors, where several VSC voltage SVs are combined in each sampling period so as to cancel the average x-y components in such period. However, this approach has limited voltage capability. To overcome this problem, it is suggested in [136] to combine three large VSC voltage vectors so that the low-frequency x-y voltage is cancelled, but this condition is relieved as the m increases in order to extend the available range.
Bermúdez et al., have proposed a current FCS-MPC method for five-phase PMSMs [8] and IMs [9] with first- and third-order harmonic injection (for full-pitch concentrated windings) that is also able to respect the dc-link voltage constraint. Using the machine model, the current references are generated at each instant so that this limitation is not violated. Namely, this FCS-MPC strategy is based on two cascaded stages.
- In the first one, the optimum current references are obtained by minimizing a cost function involving the SCL and torque error, under the drive constraints: mainly the voltage (peak phase-to-phase voltage below ) and current (peak line current below switch maximum current) restrictions. Conversely to [7], which addresses a similar application with linear control (discussed in Section 8.3.4.3), the dc-link utilization is not unnecessarily reduced by simplifications in this regard. Furthermore, in this case the voltage constraint is taken into consideration in the optimization of the current references, unlike in [7];
- In the second stage, the cost function related to the squared current errors is minimized to find the optimum switching vectors.
Since FCS-MPC does not need integral actions, anti-windup protections are not necessary in the current control [576]. Despite all these benefits and the inherently fast response of FCS-MPC, these solutions suffer from the same shortcomings as most FCS-MPC-based methods [576,577,578,579]: they are computationally demanding, exhibit variable switching frequency, they are prone to steady-state error and do not compensate unknown voltage disturbances. They are, nonetheless, the only existing multiphase multifrequency current FCS-MPC techniques so far, to the authors’ knowledge, that take into account the voltage constraints. With regard to the classification of tolerance methods shown in Figure 24 for shortage, note that these approaches [8,9] can be included among those that reduce (limit) the ac voltage references.
8.3.6. Reconfiguration of Stator Phase Connection
It is known that, in three-phase drives, dc-link utilization (and, hence, maximum speed) can be increased by changing the type of stator phase connection from (star) to (delta). Analogously, it was proposed in [141] to progressively change from (star) to (pentagon) and to (pentacle) in a five-phase PMSM drive as the speed rises. Obviously, the same procedure could be applied to tolerate a significant reduction without reducing the speed. Following this sequence, the minimum value required for ensuring linear modulation decreases from of twice the back-EMF amplitude to , and then to , respectively [see Figure 35a]. In this manner, the dc-link utilization with respect to star is increased by or for or , respectively [see Figure 35b]. On the other hand, the maximum phase current is lowered by exactly the same proportion, assuming that the maximum line current withstood by the converter does not change. In Figure 35, negligible stator-impedance voltage drop, symmetrical SWA and zero-sequence injection 1ZS are assumed [344]. The main shortcomings of this technique are the need of additional switches for altering the stator phase connections, the associated time delays, the potential current peaks during changeover, and the required modifications in the control algorithm [141].
It may be inferred that, since more possibilities are available for higher n, this strategy [141] may be extended to greater n by incorporating other reconfiguration steps. For instance, it follows from Figure 35 that a machine with could be modified from to in up to four steps ( is avoided), if deemed convenient. Thus, small drop could be tolerated without reducing the maximum torque as much. However, the system complexity increases with the number of steps.
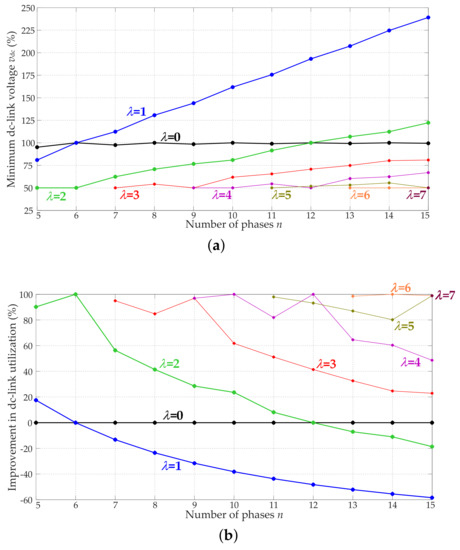
Figure 35.
Comparison of dc-link utilization depending on the type of stator phase connection and the phase number n. (a) Expressed as minimum dc-link voltage required for ensuring operation in the linear modulation range, normalized by twice the magnitude of the back-EMF [344]. (b) Expressed as improvement with respect to star ().
8.3.7. Tolerance to Uncontrolled Rectification by Machines with Low Back-EMF
In case the shortage is tolerated by suitable control or modulation techniques (Section 8.3.2, Section 8.3.3, Section 8.3.4 and Section 8.3.5), uncontrolled rectification is likely to occur if the switch gating is suddenly disabled because of a fault. Then, excessive current/power may arise. Wang et al., point out in [129] that this problem can be tolerated more easily by adopting a machine with low back-EMF (for given total torque), such as a PMaSynRM, as opposed to an SPMSM. Regarding IMs, they are also more suitable than SPMSMs in this context given that their back-EMF tends to decrease after the switches are turned off; however, the transient current is still expected to be higher than in PMaSynRMs, because of their relatively large back-EMF. Among the previous techniques to tolerate high modulation indices, those based on altering the stator phase connections (Section 8.3.6) can be appropriate for handling uncontrolled rectification as well.
8.4. Concluding Remarks about DC-Link Voltage Shortage
Operation under shortage has been addressed in numerous publications in recent years. Several kinds of approaches have been studied for this purpose.
The tolerance to drops has been increased by extensive research about switching methods suitable for overmodulation (see Table 20), which do not require altering the drive topology. Most of these publications were focused on five- and six-phase drives based on two-level HB VSCs using SV PWM. Nevertheless, new trends point toward the development of novel overmodulation techniques based on CB PWM [137,138,142,143,153,155], which is inherently much simpler. Overmodulation for other topologies and phase numbers are currently being studied as well, e.g., [160] and FB VSCs [133]. The latest publications, such as [160], reveal that there is still considerable scope for reducing the resulting low- and high-frequency distortion in many types of multiphase drives. A significant part of the available techniques (e.g., the 16 ones found in [158]) have not been compared in detail yet. The necessity of automatically adjusting the proportion between - and x-y injection to avoid overcurrent has also been recently pointed out, although so far a solution has only been presented for [138]. Moreover, most of the existing overmodulation algorithms assume that there is only voltage reference in the - plane, which is often false in practical multiphase drives.
Some publications have proposed to reduce the ac voltage references for PWM so as to return to linear modulation when overmodulation occurs. This requires special attention when the voltage references contain various frequencies (distributed among more than one subspace), as shown in [7,134,135,137,183,184,185], mainly because multiple possibilities exist depending on which frequency components are considered of priority.
Concerning current FCS-MPC, the voltage constraints can also be taken into account in order to perform satisfactorily under this kind of faults, but this possibility has only been studied in three papers about multiphase machines for the moment [8,9,136].
Other existing methods to increase dc-link utilization in multiphase drives rely on reconfiguring the topology, by modifying the stator phase connections [141]. Although this is very effective, it requires special designs with higher complexity and cost. Nevertheless, since the extra margin provided in this manner is quite large, it is still of interest to continue performing further research on this type of approaches. In addition, they are also effective in case the switch gating is no longer working (e.g., after controller faults), unlike those based on control or modulation.
Designing machines able to yield large torque with low back-EMF, such as PMaSynRMs, is also helpful for preventing uncontrolled rectification with high current when -shortage and control failures occur simultaneously [129].
In summary, the literature on the subject of tolerance to situations with reduced dc-link voltage has increased substantially during the last few years, but numerous challenges remain open and this new research trend is expected to continue vigorously in the near future.
9. DC-Link Voltage Excess
If the dc-link voltage surpasses its rating, elements of the power system, such as semiconductors and capacitors can be damaged [580]. The increase in dv/dt also aggravates the stress of the machine insulation, bearing currents, skin-effect losses and core losses [581]. Furthermore, in such case may exceed the range of the respective voltage sensor, degrading the drive control performance. Thus, this kind of situation should be mended as soon as possible.
In a grid-connected back-to-back VSC, often dc-link overvoltage can be easily prevented or remedied by injecting sufficient active power to the grid. However, this procedure is not always possible. That is the case, e.g., in topologies where the dc-link is supplied by a grid-side diode rectifier, which is, in fact, common in motor drives because of its reliability and its lower cost and complexity [131,467]. Similarly, in motors fed by back-to-back topologies based on two VSCs, if some of the grid-side VSC switches are damaged, the free-wheeling diodes avoid drop, but the direction of the active power flow cannot be reversed when needed. Other scenarios with unidirectional power flow are, e.g., those where the power source itself cannot absorb active power.
9.1. Causes of DC-Link Voltage Excess
As displayed in Figure 36, one of the main causes of dc-link overvoltage in motor drives is continued or intense motor braking [131,547]. Even in drives where braking is not expected to produce this effect, it could actually happen if the normal procedure to prevent it suffers a fault; this is the case, e.g., of switch failures in a grid-side PWM rectifier. Excessive can also be the result of an abnormal behavior of the power source; e.g., in case of voltage swells in the grid when charging the dc-link through an uncontrolled grid-tied rectifier [580], or grid voltage dips when the machine operates as a generator (including motor braking) [131,582].
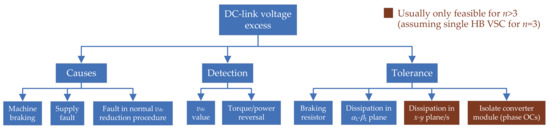
Figure 36.
Causes, detection methods and tolerance approaches for dc-link voltage excess in multiphase drives.
9.2. Detection of DC-Link Voltage Excess
The detection of dc-link overvoltage is usually straightforward, since is measured in most ac drives for adjusting the modulation index or for protection. Comparing the value with a certain threshold should be sufficient to detect this kind of failure. If excess is just expected to occur due to motor braking, this situation can be detected by checking whether the sign of the torque [132] or stator active power [131] is reversed (assuming no normal procedure is available to dissipate it).
9.3. Tolerance to DC-Link Voltage Excess
A traditional method to restore is by dissipating the active power excess in a resistive load (braking resistor) in parallel with the dc-link, by means of an additional electronically controlled switch. However, this implies including extra hardware, which is not desirable in many cases because of the associated increase in size and cost [131]. Moreover, even if this approach is implemented, it is still convenient to include an alternative strategy for this purpose, in case the former fails (e.g., due to a fault in the corresponding switch).
There are also other methods for handling excess in three-phase drives, not reflected in Figure 36. Most of them are based on increasing the losses of the machine, so as to decrease . However, since these solutions were specifically designed for motors, in which current normally can only flow in the - plane, the flux and torque are hence disturbed, or otherwise the algorithm becomes complicated [131].
In contrast, Duran et al., suggested in [131] to mend the increase by dissipating active power in the secondary subspaces of multiphase machines. Under the assumption of sinusoidally distributed windings, the impact of this technique on the flux and torque can be disregarded. Given the low impedance in said subspaces, the dc-link utilization is barely affected. However, this approach produces an increase in the machine temperature. Thus, the extra injection should be removed in case it is prolonged and the temperature rises too much.
This technique [131] is extended to drives under phase OCs in [132]. As explained therein, active power can be dissipated in the machine secondary subspaces to prevent dc-link overvoltage without disturbing the flux and torque, even with phase OC faults, as long as at least three current DOFs remain available.
As a last resort, if no other solution for a excess remains possible, the affected VSC can be isolated. Then, the corresponding phases behave as OCs and drops to zero, effectively avoiding further/any damage.
9.4. Concluding Remarks about DC-Link Voltage Excess
In summary, in a multiphase drive it is possible to tolerate dc-link overvoltage by dissipating active power in the machine stator with much less impact (ideally zero) on the torque than in a three-phase drive. The torque disturbance can normally be avoided even under phase OC faults. However, only the specific multiphase scenario of six-phase motors with asymmetrical WSA and a single dc-link [131,132] has been analyzed so far.
10. Machine-Cooling Faults
The temperature of a machine should be kept within acceptable ranges to avoid degradation of components, such as the isolation, wires, core, and bearings [468], or magnet demagnetization in PMSMs [72,583]. Normally, the rated current of a machine is established so that it can be maintained during long periods of time without causing overheating. Cooling systems are usually installed as well to avoid excessive temperature rise, typically based on either a simple fan or on ducts/vents using air or other fluids. If a failure occurs in the cooling system and the temperature becomes too high, it is critical to detect it and adopt suitable actions to avoid further damage [468].
10.1. Causes of Machine-Cooling Faults
When the heat dissipation from the machine is obstructed, it can be said that the cooling system behaves abnormally and there is a fault in it. As illustrated in Figure 37, this can be due to, e.g., breaking of a fan, dirt build-up in the windings, clogged or covered fins/casing, or obstruction of coolant flow in duct/vent [468]. Alternatively, even if strictly speaking there is no failure in the cooling system itself, overheating may be caused by too much heat dissipation within the machine (e.g., overcurrent or certain braking procedures [131]) or by excessively-high ambient temperature [584].
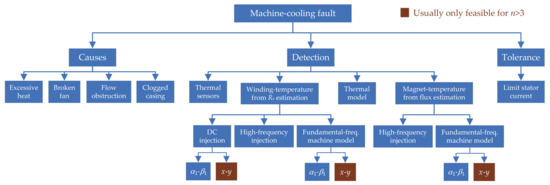
Figure 37.
Causes, detection methods, and tolerance approaches for machine-cooling fault in multiphase drives.
10.2. Detection of Machine-Cooling Faults
The literature about thermal monitoring in three-phase machines is broad. Thermal sensors can be installed, but they are not cost effective, especially in small machines [468]. In addition, such sensors are highly undesirable in some applications [584]. Furthermore, even if a temperature sensor is present, it is still convenient to implement an algorithm for the estimation of this variable in case there is a sensor failure.
Although temperature varies to some extent depending on the location within the machine, it is more frequently estimated at the stator windings [584]. There are principally two sensorless approaches for monitoring the stator-winding temperature [468,584]: employing a thermal model or estimating the stator resistance. The former is not sensitive to abnormal cooling, and, hence, the latter is clearly more suitable for detecting this situation [468,584]. The stator resistance may be obtained from the fundamental voltages and currents, but the magnitude of the stator-resistance voltage drop is often small compared with the reactances and back-EMF, and, hence, the resulting estimate is sensitive to uncertainties and prone to inaccuracy [585]. High-frequency currents due to PWM or deliberate injection may also be used, but they can be affected by uncertainties related to skin effect, eddy currents, winding capacitances and other parasitic phenomena [586]. Consequently, it is often preferred to calculate the resistance by injecting a dc signal in the machine stator, which is easier to distinguish from the ac components and less dependent on unknown or varying factors [585]. However, a well-known shortcoming of this DC-injection technique is that it causes torque ripple in three-phase machines, because the dc current can only be injected into the torque-producing - plane. Thus, it is necessary to seek a trade-off between magnitude of torque oscillations and estimation accuracy [468,584,585]. Some other variants have been proposed, where the injected signal is projected with a specific proportion between the and axes so that ideally no torque ripple is produced. This can be achieved by combining a certain second-order harmonic with the dc component in stationary frame [587,588]. In any case, with these techniques the torque oscillations are not completely removed, due to simplifications or uncertainties in the machine model, as well as imperfect decoupling between the and axes (especially in transients).
To overcome this problem of dc injection for three-phase drives, it is proposed by Baneira et al., in [70] (summarized in Table 22) to instead add the dc signal in the secondary x-y plane of a six-phase machine, so that the torque is not disturbed (see Figure 38). Namely, it is tested in a six-phase PMSM with asymmetrical WSA and two isolated neutral points. Positive and negative polarity can be applied consecutively in time to remove the influence of dc offsets. The resulting average voltage is extracted by means of a specific circuit between two phases of the same three-phase winding set, based on an analog low-pass filter and an isolation amplifier [70]. In any case, if such a physical device is undesired, the dc voltage could be computed from the VSC voltage references, analogously to other three-phase techniques [585]. More recently, Sun et al. [60] present a method able to individually estimate the resistance of each stator phase of a multiphase machine, instead of assuming a single stator-resistance value for the entire machine. Interestingly, this strategy is devised in a general manner, regardless of the phase number. The mean voltages are measured by physical second-order RC filters for each phase. The outputs of these filters are sequentially applied to a single amplifier and analog-to-digital converter by means of a multiplexer [60]. It is worth mentioning that, although this paper [60] is focused on temperature monitoring, said approach could also be used for detecting high-resistance connections (see Section 4).

Table 22.
Methods for detecting machine-cooling faults (Section 10.2) in multiphase applications in the literature.
Table 22.
Methods for detecting machine-cooling faults (Section 10.2) in multiphase applications in the literature.
| References | Machine | x-y Injected Frequency | Causes Torque Ripple | Assumes Uniform Temperature | Estimated Temperature | Uses Extra Hardware | ||
|---|---|---|---|---|---|---|---|---|
| n | WSA | Rotor | ||||||
| Baneira et al. [70] | 6 | Asym. | IPMSM | dc | No | Yes | Stator winding | Yes |
| Sun et al. [60] | Any | Asym./sym. | Any | dc | No | No | Stator winding | Yes |
| Li et al. [71] | 6 | Asym. | IPMSM | Fund. | No | Yes | Stator winding | No |
| Feng et al. [72] | 6 | Asym. | IPMSM | Fund. | No | Yes | Magnets | No |
| Li et al. [73] | 6 | Asym. | IPMSM | Fund. | No | Yes | Magnets and winding | No |
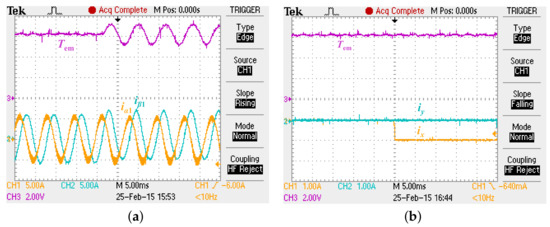
Figure 38.
Effect of injecting dc current (for temperature estimation) on the electromagnetic torque , depending on whether it is added in the (a) - plane (as for ) or (b) x-y plane, for a six-phase PMSM with asymmetrical WSA [70].
In [71], Li et al., estimate the average winding temperature of an asymmetrical six-phase PMSM by means of dc injection not in the x-y stationary frame, but in a synchronous frame - rotating at the fundamental frequency within the x-y plane (see Table 22). That is, a fundamental component is added in x-y stationary frame. The phase angle of the x-y current is set to the same value as for the - current. Compared with stationary-frame dc injection, this alternative enables automatic cancellation of the disturbance introduced by the switch dead times [71], which is particularly convenient for avoiding voltage sensors and instead relying on the voltage references for the estimation without adding a dead-time compensation method. However, other converter non-linear effects, such as those due to device voltage drop and turn-on/off time [585] are not automatically compensated. Moreover, since the injected signal is ac, additional uncertain losses (e.g., stray load loss) may affect the estimation accuracy [70]. A Kalman filter is also included for improving (smoothing) the estimation of the temperature variation with time [71].
On the other hand, a method for monitoring the temperature of the magnets (instead of stator-winding temperature) in a six-phase PMSM with asymmetrical WSA is proposed by Feng et al., in [72]. Differently from the three-phase techniques existing for this purpose, this one exploits the extra DOFs provided by so as to cancel the impact of parameter uncertainties (those of resistances and inductances) on the estimation accuracy. Similarly to [71], the injected x-y current reference corresponds with dc components with respect to an x-y synchronous frame - rotating with fundamental frequency. In this case, the x-y current is selected appropriately as a function of the current in the main plane (using a look-up table) to yield said cancellation of resistance/inductance uncertainties, as well as of dead-time effects. The magnitude of back-EMF is computed based on the average current and voltage in the four axes of the - and - frames. The permanent-magnet temperature is finally estimated by means of the relation between its value and the back-EMF [72]. Later, simultaneous estimation of stator-winding and magnet temperatures is attained in [73] for the same kind of PMSM, also by means of x-y fundamental injection. In contrast to [72], look-up tables are avoided and dead-time effect is cancelled in a simpler and more effective manner. Identical phase angle is used for the current references in both planes, as in [71].
10.3. Tolerance to Machine-Cooling Faults
When a failure of this type is detected, the drive may be turned off until it is repaired, to avoid more serious damage; nevertheless, certain degree of tolerance is preferable. In this regard, a possible fault-tolerant solution is to adaptively limit the magnitude of the stator current depending on the significance of the measured/estimated temperature increase, so that the thermal thresholds of the machine are not surpassed for excessive time during operation. For instance, this has been completed for three-phase PMSMs, actively managing the winding and end-winding temperature [589] or the rotor temperature [590]. Although currently no specific methods for this purpose have been reported for multiphase machines, it is reasonable to expect that it could be performed for them analogously, based, e.g., on temperature estimates obtained by the aforementioned multiphase monitoring techniques [60,70,71,72,73].
10.4. Concluding Remarks about Machine-Cooling Faults
Although the literature about temperature monitoring is very extensive in three-phase machines, this topic has barely been addressed yet for multiphase drives [60,70,71,72,73]. The initial attempts in this regard, based on dc or fundamental x-y injection, have revealed that the increase in DOFs of multiphase machines make it possible to provide substantial improvements. On the one hand, performing the injection in the secondary subspaces of these machines allows decreasing the undesired torque pulsation [60,70,71,72,73]. On the other hand, the extra DOFs can be exploited so as to enhance the robustness to parameter uncertainties and converter non-idealities, while avoiding the use of extra hardware and voltage measurements [71,72,73].
Given the relevance of the aforesaid advantages offered by multiphase machines for detection of machine-cooling faults, further research on this topic is expected in the near future. The existing methods may be extended to machines different from asymmetrical six-phase PMSMs, which so far have been the focus of most of these papers (see Table 22). It is also important to consider the coexistence with other drive faults and the scenario of non-uniform temperature distribution (completed just in [60]). The suitability for this purpose of the techniques discussed in Section 4, originally designed for detecting high-resistance connections, can be studied in detail. Novel strategies for tolerating cooling failures, based on the temperature estimates, may be developed as well.
11. Permanent-Magnet Demagnetization
Irreversible demagnetization in PMSMs may take place in various manners [74,583]. If it affects the entire volume of all the magnets equally, it is referred to as uniform demagnetization. If it affects to a greater extent some of the magnet parts (e.g., trailing edges), or just some of the magnets, it is called local demagnetization. The former (uniform) implies a reduction in the amplitude of the back-EMF waveform, and, hence, a decrease in the output torque for given stator current [74,129,177]. The latter (local) additionally leads to a distortion of the back-EMF waveform and to torque ripple [68,74,77]. The most relevant causes, detection methods and tolerance approaches for magnet demagnetization are illustrated in Figure 39.
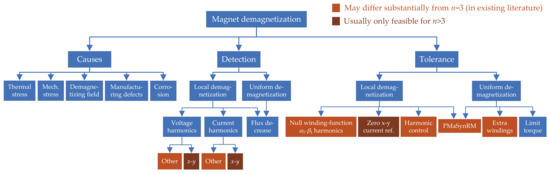
Figure 39.
Causes, detection methods, and tolerance approaches for magnet demagnetization in multiphase drives.
11.1. Causes of Permanent-Magnet Demagnetization
This problem can arise as a consequence of various reasons. For instance, it can be caused by manufacturing defects, corrosion or mechanical stress (e.g., cracked magnets) [74,75,78,583]. Nonetheless, one of the most common origins of demagnetization is excessive temperature [72,74,75,78,129,177,267,583], e.g., due to a failure of the machine cooling system or to large current. The latter may be produced, e.g., by stator SCs [75,78,129,176,177,267], converter SCs [75,78,583], heavy load [129], or position-sensor faults [176,177]. Magnet demagnetization is often alternatively produced by intense magnetic field induced by high-current along the negative -axis direction [74,78,129,176,177,267,583]. Accordingly, recommendations, such as those given in Section 5 to prevent overcurrent under stator SCs, or those pointed out in Section 7 and Section 10 regarding position-sensor and cooling failures, respectively, are, hence, also helpful in avoiding demagnetization. For instance, it is shown in [176] that a six-phase IPMSM with FSCW is less affected by demagnetization than a similar IPMSM with distributed windings under identical SC faults, mainly as a consequence of the fact that in the former the stator SC current is smaller (see Section 5.3.2).
11.2. Detection of Permanent-Magnet Demagnetization
Detecting irreversible demagnetization and its severity is useful for, e.g., assessing the amount of performance degradation associated with it, the urgency for replacing the faulty machine, and the maximum torque that can be set without causing overcurrent (which would worsen the demagnetization) [591]. In addition, monitoring the status of the magnet field is also helpful for preventing that reversible demagnetization evolves into irreversible [75]. As depicted in Figure 39, the diagnosis of demagnetization may be performed differently depending on whether it occurs locally or uniformly.
Since local demagnetization can give rise to back-EMF harmonics, these may be used for diagnosis of this kind of fault. The specific components to be monitored depend to a great extent of the machine design [74,77,78]. The methods available in the literature for detection of local demagnetization in multiphase drives, based on this principle, are summarized in Table 23. If a certain space harmonic is not contained in the stator winding function, the respective back-EMF harmonic does not arise after demagnetization. Conversely, if a given back-EMF harmonic is minimized in healthy conditions by instead selecting adequately the magnet pole arc, this harmonic is expected to increase as a consequence of demagnetization, and it could, thus, be used for demagnetization detection [77,78]. Furthermore, even if a back-EMF harmonic is not reduced by design in any manner, demagnetization could be detected by checking potential changes in its magnitude and phase [77]. In any case, if it is decided to avoid minimizing a certain harmonic during the design of the winding function (for allowing demagnetization diagnosis), it is advisable to do it for a back-EMF harmonic in a secondary subspace where significant current reference is not expected, so that torque pulsation does not occur when demagnetization arises [78]. This recommendation is respected in all the approaches displayed in Table 23, where the monitored harmonics belong to the (only) x-y plane and the x-y current reference is set to zero.

Table 23.
Methods for detecting magnet demagnetization (Section 11.2) in multiphase applications in the literature.
Table 23.
Methods for detecting magnet demagnetization (Section 11.2) in multiphase applications in the literature.
| References | Machine | Current Control with Zero Error at Monitored Harmonic | Monitored Harmonics | x-y Current Reference | Needs Extra * Sensors | Diagnoses Other Faults | Smooth Postfault Torque | ||
|---|---|---|---|---|---|---|---|---|---|
| n | WSA | Rotor | |||||||
| Gritli et al. [77,78] | 5 | Sym. | SPMSM | No | th x-y voltage/current | 0 | No | No | Yes |
| Casadei et al. [76] | 5 | Sym. | SPMSM | Yes | th x-y voltage | 0 | No | No | Yes |
| Tani et al. [68] | 5 | Sym. | SPMSM | Yes | th x-y voltage | 0 | No | High resist. | Yes |
| Mengoni et al. [74] | 6 | Asym. | SPMSM | Yes | 5th x-y voltage | 0 | No | No | Yes |
| Gritli et al. [75] | 6 | Asym. | SPMSM | Yes | 5th and th x-y voltage | 0 | No | No | Yes |
* In addition to usual stator-current sensors.
Similarly to other faults, such as high-resistance connections, it is shown in [77] by Gritli et al., that detection of local demagnetization should preferably be based on current-measurement or voltage-reference (control-output) harmonics depending on whether there is small or large impact of closed-loop current control on the corresponding frequencies, respectively. In agreement with this fact, it is proposed by Casadei et al., in [76] to detect local demagnetization of a five-phase SPMSM by monitoring the output of PI controllers rotating synchronously with the back-EMF seventh-order harmonic in the x-y plane. Furthermore, this technique is improved upon in [68] so that it is able to distinguish these faults from high-resistance connections, which mainly affect the fundamental component (see Section 4.2). Later, the same authors also monitor the seventh harmonic in [78] for detecting demagnetization, but argue that it is better to use the current spectrum instead of the voltage spectrum for this purpose, while using a current controller with low gain at this frequency. In particular, it is shown that the current harmonic is less influenced by the speed value than the voltage one, at least for the drive under study, with relatively small control bandwidth and for speeds in the range between and of rated speed [78].
Analogously to [68], Mengoni et al., manage to detect local demagnetization in [74] by also monitoring the amplitude of a back-EMF harmonic (control output) while employing a multifrequency current controller providing zero steady-state current error at the respective frequency. In this case, it is completed for a fifth-order harmonic, which is mapped into the x-y plane of an asymmetrical six-phase SPMSM. Furthermore, the fault severity is assessed by estimating the portion of magnet that is demagnetized. Further work is presented in [75], where a fault index is defined not only based on the fifth harmonic, but including information from the seventh-order one as well (also in x-y).
However, the preceding approaches are not suitable for uniform decrease in the magnet field. Regarding detection of uniform demagnetization, it should be noted that this type of fault is expected to be very similar regardless of the number of phases. Namely, it is principally reflected as a drop in the fundamental back-EMF component in the - plane. Therefore, it may be detected by applying identical methods to those employed in three-phase PMSMs, such as those described in [583]. For instance, the back-EMF reduction could be diagnosed by monitoring the magnitude of the back-EMF fundamental or by inserting search coils in the machine. These methods are sensitive to local demagnetization as well [583], but combining them with the aforementioned ones [68,74,75,76,77,78], specific for partial demagnetization, can be of interest for distinguishing between uniform or local kinds of demagnetization.
11.3. Tolerance to Permanent-Magnet Demagnetization
The techniques available in the literature for tolerating demagnetization faults in multiphase drives are summarized in Table 24. To prevent torque oscillations under local demagnetization, Gritli et al. [78] recommend to minimize the back-EMF harmonics of the healthy machine that are mapped into the - plane not by the geometry of the magnets and their field, but by nullifying the respective components of the winding function. For example, this is achieved in [75] by shortening the stator winding pitch by one slot so as to cancel the - eleventh-order space harmonic in an asymmetrical six-phase SPMSM. Moreover, as pointed out in several publications [68,74,76,77,78], the current references in the secondary subspaces where back-EMF components arise after demagnetization should be set to zero in order not to cause torque ripple. If a certain non-zero current reference is desired (e.g., for torque density enhancement [5,6,7,8,9,10]), it may be nullified just after a demagnetization fault is detected. In any case, smooth torque might be attained even in the presence of non-zero current and back-EMF harmonics in the same VSD subspace by setting suitable harmonic current references, analogously to similar approaches for three-phase PMSMs [563], at the expense of greater complexity and sensitiveness to uncertainties.

Table 24.
Methods for tolerating magnet demagnetization (Section 11.3) in multiphase applications in the literature.
Table 24.
Methods for tolerating magnet demagnetization (Section 11.3) in multiphase applications in the literature.
| References | Method Description | Reduces Torque Ripple Due to Local Demagnetization | Reduces Impact of Flux Decrease |
|---|---|---|---|
| Gritli et al. [74,75,78] | Null winding-function - harmonics | Yes | No |
| Gritli et al. [68,74,75,76,77,78] | Zero x-y current reference | Yes | No |
| Zhang et al. [178] | Extra windings | No | Yes |
| Wang et al. [129] | Adopt PMaSynRM | Yes | Yes |
The decrease in fundamental back-EMF due to magnet-demagnetization faults is tolerated in [178] by Zhang et al., by exciting extra windings that are inserted for this purpose in the stator slots of a six-phase symmetrical IPMSM.
Wang et al. [129] show that, in contrast to PMSMs, a PMaSynRM is particularly suitable for avoiding problems related to demagnetization, because in this kind of machine the torque provided by the magnets is only a small proportion of the total output torque. Similarly, it could be stated that an IPMSM is more tolerant to demagnetization than an SPMSM thanks to its reluctance torque. Moreover, embedding the magnets in the rotor makes them more protected both mechanically and magnetically [592].
Finally, it should be emphasized that it is highly advisable to limit the torque reference depending on the degree of demagnetization, to prevent worsening this condition because of the increased current requirement, as in three-phase drives [583].
11.4. Concluding Remarks about Permanent-Magnet Demagnetization
A relatively significant amount of research has been devoted to the detection of local demagnetization in multiphase PMSMs by monitoring the voltage or current harmonics that arise in the secondary subspaces when this problem occurs [68,74,75,76,77,78]. Compensating the x-y current harmonics in closed loop and monitoring the voltage ones (control output) [68,74,75,76] is preferred in terms of reduced losses, although the magnitudes of these components depend to a great extent on the speed [78]. On the other hand, uniform demagnetization might be diagnosed by keeping track of the magnitude of the fundamental - back-EMF or flux, analogously to three-phase drives [583]. As shown in Table 23, discrimination of faults different from demagnetization has only been addressed concerning high-resistance connections [68]. Further research should be performed for discerning other kinds of faults in the context of multiphase drives.
Concerning tolerance, a remarkable conclusion is that multiphase drives are inherently less prone to torque oscillations caused by local demagnetization. One of the reasons is that, as happens with harmonics generated by other causes [2], the back-EMF harmonics in the - plane are fewer and of higher order than in three-phase drives. Another argument in this regard is that in multiphase machines it is possible to nullify the winding-function - harmonics and not the x-y ones, so that demagnetization can be detected by means of the latter without occurrence of torque pulsation. For this purpose, however, the current-reference in the secondary subspace/s should be set to zero [68,74,76,77,78], at least when demagnetization takes place. Nevertheless, even if these conditions are not met in a given multiphase drive, torque ripple minimization under local demagnetization may be tackled by setting suitable harmonic current references, similarly to three-phase drives with back-EMF harmonics [563].
The impact of the decrease in output torque as a consequence of magnet demagnetization can be diminished by adopting other machine structures, such as those with extra windings [178] or with embedded magnets and significant reluctance torque [129]. In exchange, the torque density may be worsened in comparison with machines that rely mainly on the magnet flux [240]. Additionally, the maximum torque reference should be limited to avoid a vicious cycle that could keep worsening the problem [583].
In any case, the existing publications (see Table 24) about tolerating magnet demagnetization in multiphase PMSMs are scarce, and, hence, more research effort on this topic in the coming years should be sought.
12. Other Types of Faults
Finally, it is worth discussing briefly some other kinds of drive faults that, although still scarcely addressed in the literature about multiphase drives, are of relevance as well.
12.1. DC-Link Capacitor Faults
A fault in a dc-link capacitor can be of various types: aging, OC, or SC [27,129,593]. Capacitor aging implies that the capacitance decreases and (mainly) the equivalent series resistance increases [129,594], which, in turn, worsens the current ripple [129]. DC-link capacitor OC leads to poor filtering in the dc bus and even instability [129]. Capacitor SC fault causes, most notably, overcurrent [27].
The main causes of failures in dc-link capacitors are electrical, thermal and mechanical (vibration) stress, as well as humidity [129,593,594].
To the knowledge of the authors, the detection of dc-link capacitor faults has not been addressed in the specific context of multiphase drives. In the future, it may be attempted to extrapolate existing detection methods for three-phase drives (e.g., based on monitoring the capacitor equivalent series resistance [594]) to higher phase numbers, or otherwise design special techniques exploiting the additional DOFs of multiphase drives to this end. On the other hand, a few publications have addressed the tolerance to capacitor failures in drives with more than three phases, as discussed in the following.
If the drive is supplied by a single dc source, it is possible to use several VSC modules (e.g., H-bridges or l-phase FBs) with their dc-link capacitors connected in parallel, in order to increase the tolerance to capacitor faults. A fuse can be inserted between each dc-link and the common supply line (see Figure 40), to prevent that a failure in one of these capacitors could cause the source to trip [27,130]. Capacitor aging or OC may not necessarily lead to high dc current and blow the respective fuse, but then the effect of the healthy capacitors in parallel may attenuate to some extent the performance degradation of the faulty module. Notwithstanding, the defective capacitor may worsen the behavior of the other VSCs in parallel.
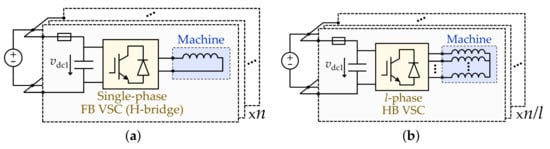
Figure 40.
Topologies for tolerating dc-link capacitor faults based on modular VSC with fuses and parallel capacitors. (a) For H-bridge modules, as in [130]. (b) For l-phase HB modules, as in [27].
An alternative solution is to install independent capacitors and dc sources for each module [e.g., as in Figure 9a–c,e] and turn the respective VSC off when an OC or aging failure occurs in its capacitor [129], completely avoiding the associated ripple. The same action can be applied in the scenario of a supply fault. In fact, these topologies also allow for better tolerance to faults in the power supplies (as indicated in Table 25) than the preceding one, which had a single dc source. When the faulty VSC module is disabled, the drive can be operated as for phase OC faults. In any case, the improvement provided in dc-side fault tolerance by this option comes at the expense of drawbacks, such as greater physical complexity and inferior performance in terms of SCL and maximum torque (once a VSC is turned off). The latter is due to the loss of current DOFs, as discussed in Part 2 and in Section 13.
If the capacitor fault is of SC type, for either of these topologies from Table 25, it may not be sufficient to just turn off the corresponding VSC module. In such scenario, an SC is in effect present at the stator terminals, through the free-wheeling diodes. This problem can be solved by opening the affected lines by means of extra elements (e.g., bidirectional switches), similarly to the case of switch SCs (see Section 6.3.1.2). Otherwise, the stator current can be kept within reasonable margins in spite of the SC by adopting a suitable machine design [27], as explained regarding stator SCs in Section 5.3.2.

Table 25.
Methods for tolerating dc-link capacitor faults (Section 12.1) in multiphase applications in the literature.
Table 25.
Methods for tolerating dc-link capacitor faults (Section 12.1) in multiphase applications in the literature.
| References | Topology | Figure | Tolerates Capacitor SC | Tolerates Capacitor OC | Tolerates Capacitor Aging | Tolerates Supply Fault |
|---|---|---|---|---|---|---|
| Various [27,130] | VSC modules with capacitors in parallel, using fuses | 40 | Yes | Partially | Partially | No |
| Wang et al. [129] | Independent VSC modules | 9a–c,e | Yes | Yes | Yes | Yes |
12.2. DC-Link Power-Supply Faults
There are a few publications about fault tolerance in multiphase drives that discuss the particular case of failures in the power supply, such as [239], or the survey paper [25]. Concerning supply OCs or SCs, they are normally very similar to the scenario where the same fault type occurs in the dc-link capacitor (just reviewed), since the latter is typically in parallel with the supply (see Figure 8 and Figure 9). Thus, as with capacitor faults, modularity (independent supplies) is also convenient for tolerating supply OCs and SCs [25,239], and analogous actions can be applied when these failures arise.
If the supply fault is not OC/SC, but means a lower or higher supply voltage than expected, it can be understood as a shortage or excess in the dc-link voltage (e.g., due to a grid-voltage sag/swell), as discussed in Section 8.1 and Section 9.1, respectively. Accordingly, these problems can be tackled similarly to those ones (see Section 8.3 and Section 9.3).
The topology proposed in [239] (see Figure 13) is especially advantageous for supply faults (see Table 26), at the cost of a few extra devices. With this VSC scheme, it is possible to obtain identical performance as for healthy drive when one of the supplies is no longer working properly, rather than having to disable the corresponding VSC legs. Namely, in such a case, the faulty supply is isolated by means of the fuse and bidirectional switches in series with it in this topology, while the two dc-links at both sides of the windings are connected to each other by the switches placed between them.

Table 26.
Methods for tolerating dc-link power-supply OC/SC faults (Section 12.2) in multiphase applications in the literature.
Table 26.
Methods for tolerating dc-link power-supply OC/SC faults (Section 12.2) in multiphase applications in the literature.
| Topology | Figure | Performance Degradation | Refs. |
|---|---|---|---|
| Independent VSC modules | 9 | Torque derating | [25] |
| Dual HB + (2+3n) fuses and 6 switches | 13 | No | [239] |
12.3. DC-Link Voltage-Sensor Faults
Sensor failure is one of the most common problems in ac drives [595]. It is a consequence, e.g., of the aging of the sensor components, which can be accelerated by harsh external conditions in terms of humidity, temperature, etc. [596]. It can be of various types, including gain drop, offset, intermittent interruption or total outage [597].
Failure of the dc-link voltage sensor is addressed by Wang et al., in [58] in the context of a six-phase PMSM with asymmetrical WSA and two neutral points driven by DTC. In general, with this type of control, is employed for estimating the stator flux. Hence, a significant deviation in these values caused by a sensor fault can lead to drive breakdown if no actions are taken. It is proposed in [58] to check whether the variation of the measurement with respect to the previous sample has changed over a certain threshold, in order to detect said situations rapidly. Just in case the sensor fault produces a relatively small variation, a second check is performed: if the stator-flux values estimated by voltage- and current-based observers are too different from each other, and the x-y current magnitude does not increase notably after a fundamental period (for current-sensor fault, it would), then it is concluded that there is a sensor fault.
Regarding tolerance to sensor fault after being diagnosed, it can be performed by applying the difference between both stator-flux estimates to a PI controller, whose output then yields the error between the actual and measured values [58].
12.4. Current-Sensor Faults
Current-sensor faults are also studied in [58] for the same scenario just described, i.e., a DTC-based asymmetrical six-phase PMSM drive. In presence of a fault of this kind, although the actual x-y currents do not increase (there is no x-y closed-loop control), the measured x-y values do. In particular, the trajectory described by the measured x-y current becomes a straight line, whose slope depends on the specific sensor that is faulty. Phase OC faults also produce linear x-y current trajectories, but with slopes different from the previous case. This behavior also differs from that of switch OC faults, where the linear current trajectory only is seen in one half of the x-y plane, instead of both halves. These characteristics are assessed and exploited for the diagnosis in [58], which takes one fundamental period.
The tolerance to a current-sensor fault is attained in [58] by estimating the current corresponding to the faulty sensor. Namely, it is calculated based on the assumption that the actual x-y current is nearly zero. Nonetheless, special care should be taken regarding the x-y current due to system non-ideal behavior (dead time, asymmetries, saturation, etc.), which is known to become typically very large in multiphase drives if left uncompensated [134,135,137,139,487,488,493,494]. Alternatively, to avoid implementing current estimation algorithms, as well as undesired effects (e.g., torque ripple) that could arise under estimation inaccuracies, the line corresponding to the faulty sensor could be opened and a method tolerant to phase OCs (see Part 2) could be then adopted, at the expense of requiring isolation devices and torque derating.
A different method for diagnosing current sensor faults is presented by Yao et al., in [57], for five-phase PMSMs. It is based on monitoring the current an applying empirical mode decomposition, Hilbert transform, variable-parameter particle swarm optimization and support vector machine. This technique is able to distinguish from phase OCs. Although the effectiveness of this procedure is proved by simulation results, it is complex and relatively slow. Furthermore, the behavior under varying or uncertain conditions is left for further research.
12.5. Control-Unit Faults
The sources of control-units failures can be related to either hardware or software, such as chip defects, low/high supply voltage, memory problems, overflow or calculation errors [56]. The consequences can be of different types. The system can be easily designed so that, if a control platform is completely turned off spontaneously due to a fault, the generated gating signals open all the corresponding VSC switches. In this regard, it may also be helpful to employ a different controller, or even redundant ones, for each VSC module [25,56]. However, the aforesaid problems do not necessarily mean immediate and total disabling of the control unit. Torque and current deviations caused by calculation errors are particularly difficult to detect and handle [56].
In the 2012 survey paper [25], Bennett et al., recommend assigning a different microprocessor to each lane of a modular drive, so as to improve the tolerance to a controller fault. Communication between the various processors is used for proper diagnosis of different types of failures. The switches to turn off the modules are controlled by the other units as well, through a voting system.
Noh et al. [56] studied a two-sector six-phase PMSM with FSCWs driven by two independent three-phase modules in an electric vehicle. Each module comprised a separate battery, a three-phase VSC and a couple of microcontrollers (main and auxiliary). That is, there were four microcontrollers in total. The torque command was computed individually in each of the four microcontrollers, based on the same inputs. The two main microcontrollers included both torque and current controllers, but the only part that was redundant with the auxiliary ones was the calculation of torque commands. The various torque references were compared in the two auxiliary units. If it was observed that one of the four torque commands was substantially different from the others, the respective microcontroller was labeled as faulty. In case the microcontroller with the failure was a main (not auxiliary) one, the corresponding module was isolated and afterward just the other three-phase sector of the PMSM was supplied. If the torque commands were similar and yet there was certain current differences between the two three-phase modules (e.g., due to deviation in measurement gains), the current values were then readjusted so that they became identical for both modules again [56].
12.6. Mechanical Faults
Mechanical faults comprise rotor eccentricity, breakage of bars or end rings in IM cage rotors, damage in the bearings or gearbox, misaligned or bent shaft, etc. [598,599,600,601]. Defective magnets are occasionally also considered mechanical failures, but this problem has already been discussed, within the ambit of magnet demagnetization, in Section 11. The literature about eccentricity, broken bars, and bearing faults is surveyed next.
12.6.1. Eccentricity
Eccentricity faults can be classified into static or dynamic eccentricity. For static eccentricity, the rotor rotates around the axis at the geometrical center of the rotor, but the latter is fixed and displaced from the central axis of the stator. For dynamic eccentricity, the rotation axis matches the axis of symmetry of the stator, but not the one of the rotor. In the former kind, the angular position of the minimum air-gap length does not vary with time, whereas in the latter it does. Usually, both types occur at the same time, which is known as mixed eccentricity [79].
These problems are mainly caused by bearing defects and shaft misalignment [79], although some level of eccentricity due to manufacturing tolerances is unavoidable, which tends to be aggravated with continued operation [598].
Both static and dynamic eccentricity lead to a proliferation of space harmonics in the air-gap flux [602]. Each of these harmonics is actually seen or not as a voltage harmonic in the machine stator depending on the magnitude of the corresponding harmonic in the stator winding function [603]. Furthermore, even if a certain voltage harmonic is present, it does not produce a current component when it is mapped in a VSD subspace where current flow is not possible (e.g., zero sequence for isolated neutral points). Moreover, the frequencies of these voltage/current components may be modified by the dynamic eccentricity [602]. Monitoring these voltage or current symptoms is one of the most common approaches for eccentricity detection in three-phase machines [598]. As with other faults, the voltage harmonics (e.g., in the PWM references) should be monitored instead of the current ones if there is a closed-loop current controller with significant gain at them (which happens especially at low frequencies) [79]. Detection of mixed eccentricity based on the per-phase voltage/current symptoms for a symmetrical six-phase IM with two isolated neutral points is performed by Andriamalala et al., in [79] (see the summary in Table 27). In any case, for this machine the symptoms are analogous to those of conventional three-phase IMs. Later, Mouche et al. [80] propose to detect static eccentricity by measuring the voltage between the two neutral points of an asymmetrical six-phase IM with three-phase splitting, at the expense of an extra sensor. Choi et al. [84] show, supported by tests with a five-phase PMaSynRM, that the accuracy in the detection of mixed eccentricity by current monitoring increases by combining the information of a greater number of phase currents.
It is important to remark that the eccentricity symptoms in the voltage/current signals can be predicted for any phase number by combining the equations from [602], which describe the space harmonics due to eccentricity and the associated time frequencies, with the expression that defines in which stator VSD subspace is mapped each space harmonic order in general (regardless of its origin) [140,214]. Comprehensive analysis and tests in this regard are provided in [604]. From this study, it can also be inferred that, as the space harmonics are distributed among a greater variety of VSD subspaces as the phase number rises, it becomes increasingly easy to discriminate between faults (e.g., static/dynamic eccentricities).

Table 27.
Methods for detecting eccentricity faults (Section 12.6.1) in multiphase applications in the literature.
Table 27.
Methods for detecting eccentricity faults (Section 12.6.1) in multiphase applications in the literature.
| References | Machine | Monitored Spectrum | Eccentricity | Needs Extra * Sensors | Differs from n = 3 | ||
|---|---|---|---|---|---|---|---|
| n | WSA | Rotor | |||||
| Andriamalala et al. [79] | 6 | Sym. | IM | Phase current/voltage | Mixed | No | No |
| Maouche et al. [80] | 6 | Sym. | IM | Voltage between neutrals | Static | 1 volt. | Yes |
| Choi et al. [84] | 5 | Sym. | PMaSynRM | Combined phase currents | Mixed | No | Yes |
| Malvar [604] | 5 | Sym. | IM | VSD current/voltage | Mixed | No | Yes |
* In addition to usual stator-current sensors.
When it is detected that eccentricity exceeds an acceptable threshold, it is advisable to fix it as soon as possible, in order to prevent vibrations, unbalanced magnetic pull, shaft currents and further damage, such as bearing wear and rotor-stator rub [79,598]. In any case, if it is decided to continue operating during a certain time before correcting the eccentricity, in some cases it is possible to apply tolerant measures to attenuate the undesired effects. For instance, Keller et al. [179], after showing for a six-phase IPMSM that an asymmetrical WSA is much less prone to performance degradation due to static eccentricity than a two-sector WSA, present a control method to mitigate such effects in the latter. Yang et al. [180] reduce the vibration and radial force due to dynamic eccentricity in a nine-phase three-sector IPMSM by injecting suitable compensation currents. These actions [179,180] resemble to some extent the deliberate generation of radial force in multisector machines for a different purpose: bearingless operation [23]. On the other hand, it may be possible to extrapolate to multiphase drives the approach from [605], where the impact of eccentricity is substantially attenuated in a three-phase IPMSM by setting parallel connections of the stator coils.
12.6.2. Broken Rotor Bars
One or several bars of an IM cage rotor may crack or break due to phenomena, such as thermal (e.g., hot spots), mechanical (e.g., vibration), and environmental (e.g., humidity) stress [85,462,601]. Similarly to eccentricity faults, bar breakage also generates space harmonics (hence, voltage/current distortion), but with particular frequency characteristics that may be used to distinguish them [462,492,601]. The harmonics caused by broken bars also give rise to undesired torque and speed ripple [82,85].
As indicated in Table 28, the harmonic spectrum of the current and torque signals of six-phase IMs with either symmetrical or asymmetrical WSA under one broken bar are analyzed by Maouche et al. [82] so that it can be used for diagnosis. The current signature for the asymmetrical WSA is further studied in [83], where it is concluded that special care should be taken to avoid misdiagnosis because of the non-ideal converter/machine asymmetries and the effect of the closed-loop current control. Abdel-Mageed et al. [85] show that an asymmetrical six-phase IM exhibits larger stator-current symptoms with one or two broken bars than a similar three-phase IM (analogously to, e.g., rotor slot harmonics; see Section 7.3.2.1); in addition, they propose to use neural networks for the fault detection. On the other hand, Farag et al. [62] show that the indices used for detecting phase OCs or high-resistance connections (based on x-y current) are robust to bar breakage in a symmetrical six-phase IM, while the broken bars could be detected from the - or phase current spectrum as in a three-phase IM.

Table 28.
Methods for detecting broken bars (Section 12.6.2) in multiphase applications in the literature.
Table 28.
Methods for detecting broken bars (Section 12.6.2) in multiphase applications in the literature.
| References | Machine | Monitored Spectrum | Broken Bars | Needs Extra * Sensors | Differs from n = 3 | ||
|---|---|---|---|---|---|---|---|
| n | WSA | Rotor | |||||
| Maouche et al. [82] | 6 | Asym./sym. | IM | Phase current or torque | 1 | No | Yes |
| Maouche et al. [83] | 6 | Asym. | IM | Phase current | 1 | No | Yes |
| Abdel-Mageed et al. [85] | 6 | Asym. | IM | Phase current (neural network) | 1, 2 | No | Yes |
| Farag et al. [62] | 6 | Sym. | IM | - or phase current | 1, 2, 3 | No | No |
* In addition to usual stator-current sensors.
12.6.3. Bearing Faults
Damage in the bearings can happen because of causes including vibration, rotor eccentricity, corrosion, bearing currents, improper lubrication or installation, contamination of external particles, etc. [462]. In turn, this failure leads to an increase in machine problems, such as eccentricity and vibration [462]. In fact, vibration monitoring is one of the most common approaches for the detection of bearing faults [81,462]. Nonetheless, it is preferable to avoid the use of additional transducers and instead rely on the current measurements, which nowadays are typically found in available ac drives.
Bearings consist of an inner and an outer ring, with balls or rollers between them [462]. The possibility of monitoring the stator phase-current harmonics for detection of damage in the outer ring is analyzed in [81] for an asymmetrical six-phase IM. Namely, it is shown that side-band harmonics around the fundamental and rotor-slot harmonics can be employed for this purpose. To the knowledge of the authors, the diagnosis (or tolerance) of bearing faults in multiphase drives has not been tackled yet by any other publications, and it is thus a topic of special interest for future research.
12.7. Concluding Remarks about Other Types of Faults
There are certain kinds of faults that have barely been studied yet in the context of multiphase drives. That is the case of failures in the sensors of dc-link voltage or stator current, in the power supplies, dc capacitors and control units, as well as mechanical faults, such as eccentricity, broken bars, and bearing damage. The detection and tolerance of these problems can be expected to increase the lifetime, reduce the necessary maintenance and improve the performance of these drives. Therefore, further research on this topic is of paramount importance. The possibility of future work addressing the exploitation of the extra DOFs of multiphase machines to this end is particularly promising. In fact, the initial attempts that are available reveal that multiphase drives offer excellent features in this regard, such as enhanced tolerance to controller faults by using different control units for multiple modules [25,56], monitoring with reduced signal-to-noise ratio for eccentricity [84] or bar-breakage [85] detection, easier discrimination between fault symptoms thanks to the distribution of harmonics among a greater number of VSD subspaces [604], or the capability to compensate the effects of eccentricity [179,180]. Furthermore, even though the handling of some faults does not seem in principle easier than for three phases, it does anyway require specific analysis for higher phase numbers, because of the considerable differences; e.g., the current trajectories in VSD subspaces under current-sensor faults, which has only been addressed for asymmetrical six-phase machines so far [58].
13. Comparison of Drive Topologies Considering Multiple Fault Types
In view of the survey carried out in this paper for each class of fault, it is of interest to compare, at this point, in a general manner, the fault-tolerant capability depending on the drive topology for multiple kinds of failures. The number of current DOFs available for the drive control is an important figure of merit that can be used for this purpose. In the first place, recall that smooth torque can be achieved as long as at least two current DOFs remain [2]. In addition, broadly speaking, a higher number of stator current DOFs under faults has the following beneficial implications for a certain machine, assuming that the controller is suitably designed.
- Greater achievable ripple-free torque, i.e., smaller derating, if any (see Part 2) [311,312,343,356];
- Lower SCL (see Part 2) [343,356];
- Better attenuation of the high current and torque ripple due to stator SCs (see Section 5) [101,252];
- Better signal-to-noise ratio [84] and discrimination between faults [604] for diagnosis based on stator current (see, e.g., Section 12.6.1);
- Enhanced possibilities for exploiting these DOFs for special purposes (in combination with fault tolerance), such as high-torque-density control [5,6,7,8,9,10], tolerance to encoder faults [86,185,188,199,214], or parameter estimation [11].
Accordingly, it can be stated that, usually, the higher the number of current control DOFs of an ac drive under a certain fault, the greater the degree of tolerance of the drive to such fault. On the other hand, an increased number of current DOFs for given machine has the following shortcomings, that should also be taken into account.
- Worse dc-link utilization (fewer voltage components can be added without causing current) [24,143,311,312,606], which means poorer tolerance to dc-link voltage shortage (see Section 8);
- Some current DOFs may give rise to significant uncontrolled current if, after a switch SC, current can still flow through the corresponding path but it is not controllable (no longer a DOF), e.g., the zero-sequence current in FB VSCs (see Section 6.3.1.4) [273];
- Drive non-idealities, such as undesired asymmetries and harmonics can cause troublesome current components through these DOFs, either at low or high frequencies, worsening torque pulsation and efficiency even in healthy operation unless special measures are taken (e.g., specific control, extra inductors, etc.) [101,488];
- More complex control and modulation techniques [311,312,606].
Table 29 shows the stator current DOFs for the main VSC topologies considered in the literature about fault-tolerant multiphase drives (cf. Section 3.2), where the integer variable denotes the number of faults (for each column). For some of the VSC schemes several types of stator phase splitting (cf. Section 3.1.1) are studied, one per row. The categories of faults that are explicitly indicated in the table are those that normally alter the number of current DOFs: stator phase OCs, OC legs (i.e., legs with all switches kept open, either due to switch OCs or to isolation, e.g., after switch SCs), SCs between any stator phase terminals (terminal SCs), dc-link power-supply faults, and dc-link capacitor faults. The expressions given for phase OCs are also suitable for the cases where other types of faults (control units, current sensors, etc.) are converted into this kind of situation, in agreement with Figure 1. Other faults, such as SCs between internal points (not terminals) of the stator windings, or the other failures reviewed in this paper, do not alter the current DOF number and, thus, are not reflected in the table. Note that a single switch OC in a certain leg is normally converted into OC leg, except for multilevel VSCs, such as T-type ones, where the affected leg can still be employed without losing a DOF [103,276,277]. For each scenario in Table 29, the DOF expressions are obtained based on the discussion given in the corresponding sections of this paper (also including Part 2, concerning phase/switch OC faults).

Table 29.
Number of stator current DOFs of different combinations of VSC topologies and stator phase splitting for an n-phase machine depending on the fault scenario, for failures that alter the current DOFs, other than non-isolated switch SCs.
Table 29.
Number of stator current DOFs of different combinations of VSC topologies and stator phase splitting for an n-phase machine depending on the fault scenario, for failures that alter the current DOFs, other than non-isolated switch SCs.
| VSC Topology | Stator Splitting | Figure | Stator Current DOFs | ||||
|---|---|---|---|---|---|---|---|
| Healthy Drive | Phase OCs or Terminal SCs | OC legs ( Parallel Pairwise) | Supply Faults | Capacitor Faults | |||
| Single n-phase HB VSC | No | 8a | 0 | 0 | |||
| Single n-phase HB VSC | l-phase | − | 0 | 0 | |||
| Single (n+1)-phase HB VSC | No | 8b | n | 0 | 0 | ||
| Single (n+)-phase HB VSC | l-phase | 8c | n | 0 | 0 | ||
| Single n-phase FB VSC | Single-ph. | 8d | n | 0 | 0 | ||
| Series dc-side connect. of l-phase HBs | l-phase | 8e | 0 | ||||
| Series dc-side connect. of H-bridges | Single-ph. | 8f | n | 0 | |||
| Parallel n-phase HB VSCs | No | 8g | 0 | 0 | |||
| Parallel n-phase HB VSCs | l-phase | − | 0 | 0 | |||
| Series dc-side connect. of parallel l-ph. HBs | l-phase | 8h | 0 | ||||
| Single n-phase T-type three-level VSC | No | 8i | 0 | 0 | |||
| Single n-phase T-type three-level VSC | l-phase | − | 0 | 0 | |||
| Multiple independent l-phase HBs | l-phase | 9a | |||||
| Multiple independent (l+1)-phase HBs | l-phase | 9b | n | ||||
| Multiple independent H-bridges | Single-ph. | 9c | n | ||||
| Dual n-phase HB VSC | Single-ph. | 9d | ;0 if | ;0 if | |||
| Multiple independent parallel l-ph. HBs | l-phase | 9e | |||||
From Table 29, for phase OCs or terminal SCs the number of faults matches the number of current DOFs lost with respect to healthy conditions. In the case of OC legs in VSC topologies consisting of VSCs connected in parallel pairwise [see, e.g., Figure 8g], the even number is defined to represent how many of the OC legs are in parallel. As shown in Table 29, in said configurations the DOFs are only reduced by , because a line supplied by an OC leg can still conduct current as long as the leg in parallel with it is still operative. For instance, for a topology based on two parallel n-phase HB VSCs as in Figure 8g, means that just one current DOF is lost, even if, e.g., . It can also be observed in Table 29 that the DOF reduction under supply or capacitor faults is times the DOF number of each VSC module, when these failures are tolerated by deactivating the corresponding modules. For topologies based on series dc-side connection of VSCs, faulty dc-link capacitors are assumed to be transformed into SCs (bypassed), at the cost of reducing the total dc-link voltage or increasing the voltage rating of each module beforehand [409,454].
It has been occasionally assumed in the past that an independent three-phase HB VSC [see Figure 9a] should be completely deactivated when it is affected by a single-phase OC. Presumably, this misconception may be due to the common approach of studying a multi-three-phase drive as a set of independent three-phase modules. From this perspective, a two-phase HB VSC yields significant torque ripple (assuming dc-link voltage ripple is prevented), which is undesired and should be avoided. In reality, when the multiphase drive is conceived as a whole, it is possible to suitably adjust the currents in the other VSC modules so as to compensate said torque ripple. In this manner, all VSCs can still work, with only one current DOF less (as reflected in Table 29), instead of three. This reasoning is applied, e.g., in [169] to a six-phase drive based on a pair of isolated three-phase HB VSCs under a phase OC, or in [168] to a twelve-phase machine fed by four HB VSCs under one switch SC. It is also similar to the operation of a machine fed by independent single-phase H-bridges, where the active power of a VSC unit would also be oscillating if considered individually, while the overall active power is smooth.
If there are switch SCs and they are not isolated (OC legs), other approaches are possible, as discussed in Section 6.3.1. Redundant legs [275,464,465] or additional bidirectional switches for dc-link-midpoint clamping [103,277,343] may be employed for avoiding the loss of any DOFs. Alternatively, other solutions can be applied in certain topologies without using extra hardware, not even for isolating the shorted switches. Namely, in configurations based on open-end windings, both terminals of a phase affected by a switch SC can be clamped to the positive/negative rail of the dc-link/s (see Section 6.3.1.4) [99,240,273], and in dual HB VSCs it is possible to set a virtual neutral point in the respective module [273]. The current DOFs for these possibilities are displayed in Table 30. It is assumed that the switch SCs arise in different legs and phases. This table also shows that in this situation uncontrolled current paths are present in FB VSCs, producing larger undesired current than in dual-HB ones [13,273]
For the sake of illustration, the values obtained from Table 29 and Table 30 are shown in Table 31 and Table 32, respectively, for the particular scenario of with (), which is arguably one of the most common in the literature.

Table 30.
Number of stator current DOFs and uncontrolled current paths of different VSC topologies and reconfigurations for an n-phase machine under non-isolated switch SCs (in different legs and phases).
Table 30.
Number of stator current DOFs and uncontrolled current paths of different VSC topologies and reconfigurations for an n-phase machine under non-isolated switch SCs (in different legs and phases).
| VSC Topology | Stator Splitting | Figure | Stator Current DOFs for Healthy Drive | Switch SCs (Different Legs and Phases) | ||
|---|---|---|---|---|---|---|
| Reconfiguration (cf. Section 6.3.1 | Stator Current DOFs | Uncontrolled Current Paths | ||||
| Single n-phase FB VSC | Single-ph. | 8d | n | Clamp both ph. terminals | ||
| Multiple independent H-bridges | Single-ph. | 9c | n | Clamp both ph. terminals | ||
| Dual n-phase HB VSC | Single-ph. | 9d | Clamp both ph. terminals | ; if | 0; if | |
| Dual n-phase HB VSC | Single-ph. | 9d | Virtual neutral * | 0 | ||
* Only valid if all switch SCs occur in the same HB VSC.

Table 31.
Values obtained from Table 29 for the particular case of with ().
Table 31.
Values obtained from Table 29 for the particular case of with ().
| VSC Topology | Stator Splitting | Figure | Stator Current DOFs | |||
|---|---|---|---|---|---|---|
| Healthy Drive | 1 OC Phase/leg or Terminal SC | 1 Supply Fault | 1 Capacitor Fault | |||
| Single n-phase HB VSC | No | 8a | 5 | 3 | 0 | 0 |
| Single n-phase HB VSC | 3-phase | − | 3 | 2 | 0 | 0 |
| Single (n+1)-phase HB VSC | No | 8b | 6 | 5 | 0 | 0 |
| Single (n+)-phase HB VSC | 3-phase | 8c | 6 | 5 | 0 | 0 |
| Single n-phase FB VSC | Single-ph. | 8d | 6 | 5 | 0 | 0 |
| Series dc-side connect. of l-phase HBs | 3-phase | 8e | 4 | 4 | 0 | 2 |
| Series dc-side connect. of H-bridges | Single-ph. | 8f | 6 | 5 | 0 | 5 |
| Parallel n-phase HB VSCs | No | 8g | 5 | 5 | 0 | 0 |
| Parallel n-phase HB VSCs | 3-phase | − | 4 | 4 | 0 | 0 |
| Series dc-side connect. of parallel l-ph. HBs | 3-phase | 8h | 4 | 4 | 0 | 2 |
| Single n-phase T-type three-level VSC | No | 8i | 5 | 4 | 0 | 0 |
| Single n-phase T-type three-level VSC | 3-phase | − | 4 | 3 | 0 | 0 |
| Multiple independent l-phase HBs | 3-phase | 9a | 4 | 3 | 2 | 2 |
| Multiple independent (l+1)-phase HBs | 3-phase | 9b | 6 | 5 | 3 | 3 |
| Multiple independent H-bridges | Single-ph. | 9c | 6 | 5 | 5 | 5 |
| Dual n-phase HB VSC | Single-ph. | 9d | 5 | 4 | 5 | 5 |
| Multiple independent parallel l-ph. HBs | 3-phase | 9e | 4 | 4 | 2 | 2 |

Table 32.
Values obtained from Table 30 for the particular case of with .
Table 32.
Values obtained from Table 30 for the particular case of with .
| VSC Topology | Stator Splitting | Figure | Stator Current DOFs for Healthy Drive | 1 Switch SC | ||
|---|---|---|---|---|---|---|
| Reconfiguration (cf. Section 6.3.1 | Stator Current DOFs | Uncontrolled Current Paths | ||||
| Single n-phase FB VSC | Single-ph. | 8d | n | Clamp both ph. terminals | 1 | |
| Multiple independent H-bridges | Single-ph. | 9c | n | Clamp both ph. terminals | 1 | |
| Dual n-phase HB VSC | Single-ph. | 9d | Clamp both ph. terminals | 0 | ||
| Dual n-phase HB VSC | Single-ph. | 9d | Virtual neutral | 0 | ||
This analysis also holds if stator phase connections different from star (see Section 3.1.3) are adopted, for VSC topologies where it is possible. Nonetheless, the uncontrolled current paths (loops) that exist within the stator windings for some (e.g., delta connections) can be helpful for naturally mitigating the SC current through shorted turns in case of turn SC faults (see Section 5.3.1.2) [270]. Furthermore, unlike the uncontrolled current paths of FB VSCs (see Table 30), the ones associated with stator phase connections are not excited by switch SCs.
From Table 29, Table 30, Table 31 and Table 32, it can be seen that in general VSC modularity is convenient for increasing the postfault current DOFs and, thus, the tolerance to many of the common drive faults. Setting single-phase splitting, which is the highest degree of modularity in the stator windings, is also advantageous in this regard, and it is normally associated with highly modular VSC topologies, such as FB and dual-HB ones. These benefits of drive modularity in terms of fault tolerance are usually acknowledged in the literature [2,24,27,240]. Nevertheless, they come at the expense of greater complexity and cost [373], not only because of the extra devices, but often also due to the requirement (if sought) of ensuring isolation between modules. Moreover, there are some important shortcomings of VSC and machine modularity, concerning fault tolerance, that are often overlooked and should be emphasized, as follows.
- In topologies not based on open-end windings, increasing the modularity and isolation of the machine stator by splitting the windings into sets of fewer phases (e.g., 3-phase sets) results in reduced current DOFs and hence worse tolerance to the aforesaid fault types;
- Adopting FB VSCs such as independent H-bridges in order to attain high modularity can be counterproductive for non-isolated switch SC failures, where the uncontrolled zero-sequence paths are excited leading to increased SC current;
- The extra current DOFs provided by H-bridges tend to exhibit undesired currents due to non-idealities, even for healthy drive;
- H-bridges imply inferior dc-link utilization, and, thus, lower tolerance to faults that mean reduced dc-bus voltage/s.
As a consequence, if a considerable degree of tolerance to multiple kinds of faults and performance is sought in a multiphase drive, an attractive option is to install a reconfigurable topology, so that it is possible to adequately alternate between the benefits of modular and non-modular schemes for each scenario during the machine operation. Advances in this direction have been presented during the last few years, e.g., based on alternating between FB and dual-HB VSCs for open-end windings [239], or on modification of the stator phase splitting [101,170,343].
In any case, for a given number of current DOFs, there are also other aspects of a drive topology that can make it preferable for fault tolerance. For instance, as discussed in Part 2, the performance under phase OCs depends to a great extent on the stator phase connections (as well as the dc-link utilization) [344,408] and on the specific phases that are affected [312,356,408]. Accordingly, topology reconfiguration in these terms has also been recently proposed for enhancing the postfault capability [408].
Developing new multiphase topologies or reconfiguration strategies with superior tolerance to multiple faults is a promising field of research for future work, particularly if performed in combination with smooth transitions (if any) and simplicity.
14. Conclusions
In this two-part paper, a comprehensive survey is presented on the topic of fault tolerance in multiphase drives. In Part 1, multiple types of faults have been considered, including high-resistance connections, switch and stator SCs, speed/position-sensor faults, dc-link voltage shortage and excess, machine-cooling faults, magnet demagnetization, capacitor, and supply faults, current- and voltage-sensor faults, control-unit failures, mechanical faults, etc. Phase and switch OCs are discussed in depth in Part 2. Since fault detection/diagnosis is crucial in a fault-tolerant drive, this aspect is also discussed for each kind of failure, in addition to the tolerant actions.
The literature on the subject has been classified according to different criteria, such as studied faults, types of machines and converters, fault-diagnosis and -tolerant methods, etc. These categorizations are helpful for researchers and practitioners, where they may immediately identify the papers dealing with the specific aspects of their interest, as well as the pros and cons of each of the existing detection/tolerance strategies.
From this division of the literature, it can be concluded that, although most of the available publications are focused on stator OC and (secondly) stator SC failures, an especially significant amount of research has been presented recently regarding encoder faults (e.g., speed/position estimation) and dc-link voltage shortage (e.g., overmodulation). The many other aforementioned kinds of faults have also been studied in some papers in the context of multiphase drives, particularly during the last few years, although to a smaller extent. In any case, there is still scope for much further research for all classes of failures. Based on the existing papers, remarkable emerging trends and open challenges have been identified in this review for each of these faults.
New literature has brought special attention to the fact that the extra DOFs of multiphase machines can be exploited not only for increasing the tolerance to faults that affect certain phases, but also for improving the detection and tolerance of most possible types of failures (even those affecting all phases), in comparison with three-phase drives. For instance, easier discrimination between fault symptoms can thereby be attained in the diagnosis of multiphase drives, as well as better signal-to-noise ratio in the current monitoring (e.g., for fault detection, speed estimation, etc.). Another example in this respect is the fact that less torque pulsation may be obtained when injecting signals for detection (e.g., of overheating) or tolerance (e.g., to encoder faults, dc-link overvoltage, etc.) purpose, or when harmonics arise due to faults (e.g., demagnetization, overmodulation, etc.). This advantageous behavior is a consequence of the various orthogonal subspaces where the electromagnetic variables are distributed.
Even though it has traditionally been assumed that increasing modularity leads to better fault tolerance, an overview taking into account numerous scenarios makes it possible to put this statement into perspective and to realize that it is not entirely true. Several exceptions, based on the existing literature, have been pointed out. Splitting electrically the stator windings into sets of lower phase numbers imply decreasing the current DOFs and, hence, the tolerance to many of the possible faults, except when setting single-phase stator splitting by means of open-end windings. Nevertheless, adopting open-end winding topologies and FB VSCs, such as individual H-bridges, often gives rise to undesired zero-sequence currents, which become especially troublesome when excited by switch SCs. Furthermore, the schemes based on FB VSCs provide lower dc-link utilization, and, therefore, worse tolerance to failures that mean reduced dc-bus voltage. In view of these aspects, it becomes understandable that new trends have emerged to improve the overall performance and tolerance by reconfiguring the drive depending on the kind of fault and operating conditions, e.g., by altering the degree of converter and machine modularity as appropriate.
Converting switch SCs into phase OCs by isolating the faulty legs has also been a popular approach. Presumably this may be one of the main reasons why the specific case of switch SCs has not been studied profusely in multiphase drives yet. Notwithstanding, this solution means reducing (derating) the achievable torque or increasing the converter rating a priori. Consequently, further investigation of novel techniques for tolerating switch SCs without opening the corresponding phases should be pursued.
Concerning stator SCs, the most common tolerance approach used to be applying an external SC to one or several phases, so that the flux linkage through the shorted turn/coils is passively decreased and the machine imbalance is mitigated. In contrast, recent papers have shown that it is preferable to keep switching as many converter legs as possible, and employ the respective current DOFs to actively reduce the resulting SC current or torque ripple by suitable current control strategies. However, both control goals have not been considered together yet. Moreover, it would be highly desirable to attempt attaining for stator SCs analogous advances to those that have recently been carried out for phase OCs, such as reconfiguration-less or FRMLS tolerant control. Obtaining IMs with satisfactory performance under stator SCs (especially turn SCs) is an important pending task as well.
It has also been noted that there are barely any publications about fault diagnosis and tolerance in multiphase multilevel topologies. A few recent works have been put forth regarding faults in some specific three-level converters such as T-type ones, but most multilevel configurations are yet to be studied under failures. This is particularly important for switch OCs/SCs, where these alternatives behave differently from two-level converters and offer promising prospects thanks to the switch state redundancy.
One of the main subjects to be dealt with in the future is the simultaneous consideration of numerous faults in a certain drive. The majority of the research efforts address one specific kind of failure, or a few of them at best, and, hence, in most cases there is no assurance that the proposed techniques would be able to work properly under different failures. Taking into account all (or nearly all) the potential faults, occurring either simultaneously or not, is thus expected to be of great interest for improving both the diagnosis and the tolerance of multiphase drives.
Given that the secondary DOFs of multiphase machines are frequently exploited for purposes other than fault tolerance, such as torque density enhancement, multimotor drives, integrated battery chargers, bearingless machines or parameter estimation, it is also of paramount relevance to perform further research on the adequate combination of these applications and fault diagnosis/tolerance, which have received little attention in conjunction yet. Actually, several current research efforts point in this direction.
In summary, the excellent fault-tolerant potential offered by multiphase machines has sparked considerable research that has not ceased to proliferate at an ever-increasing rate. Although some decades ago these drives were only considered more tolerant to faults that affected specific phases, the recent evidence that they are in fact preferable for many other failures as well have contributed to this renewed interest. Nonetheless, the latest publications also make evident that only the top of the iceberg has been addressed for the moment, and there are many open challenges that are still to be tackled in the years to come.
Author Contributions
Conceptualization, all authors.; methodology, all authors; software, A.G.Y., O.L. and I.G.-P.; validation, all authors; formal analysis, A.G.Y., O.L. and I.G.-P.; investigation, A.G.Y., O.L. and I.G.-P.; resources, all authors; data curation, A.G.Y., O.L. and I.G.-P.; writing—original draft preparation, A.G.Y., O.L. and I.G.-P.; writing—review and editing, all authors; visualization, A.G.Y., O.L. and I.G.-P.; supervision, A.G.Y., M.J.D. and J.D.-G.; project administration, A.G.Y., M.J.D. and J.D.-G.; funding acquisition, A.G.Y., M.J.D. and J.D.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Government of Galicia under the grants ED431F 2020/07 and GPC-ED431B 2020/03, in part by the Ministry of Science, Innovation and Universities under the Ramon-y-Cajal Grant RYC2018-024407-I, in part by the Spanish State Research Agency (AEI) under project PID2019-105612RB-I00/AEI/10.13039/501100011033, and in part by the Government of Andalusia under project UMA20-FEDERJA-039.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors would like to thank Nicola Bianchi and Hang Seng Che for answering questions about their publications on the topic.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 1ZS | One zero sequence |
| CB | Carrier-based |
| DOF | Degree of freedom |
| DTC | Direct torque control |
| EMF | Electromotive force |
| FB | Full-bridge |
| FCS-MPC | Finite-control-set model predictive control |
| FF | Feed forward |
| flop | Floating-point operation |
| FRMLS | Full-range minimum-loss strategy |
| FSCW | Fractional-slot concentrated winding |
| HB | Half-bridge |
| IGBT | Insulated-gate bipolar transistor |
| IM | Induction machine |
| IPMSM | Interior permanent-magnet synchronous machine |
| MLS | Minimum-loss strategy |
| MPC | Model predictive control |
| MRAS | Model Reference Adaptive System |
| MTS | Maximum-torque strategy |
| MZS | Multiple zero sequence |
| OC | Open circuit |
| PI | Proportional-integral |
| PMaSynRM | Permanent-magnet-assisted synchronous reluctance machine |
| PMSM | Permanent-magnet synchronous machine |
| PWM | Pulsewidth modulation |
| RFOC | Rotor-field-oriented control |
| SC | Short circuit |
| SCL | Stator copper loss |
| SPMSM | Surface-mounted permanent-magnet synchronous machine |
| SV | Space vector |
| SynRM | Synchronous reluctance machine |
| THD | Total harmonic distortion |
| VSC | Voltage-source converter |
| VSD | Vector space decomposition |
| WFSM | Wound-field synchronous machine |
| WSA | Winding spatial arrangement |
| ZOH | Zero-order hold |
References
- Levi, E.; Bojoi, R.; Profumo, F.; Toliyat, H.A.; Williamson, S. Multiphase induction motor drives—A technology status review. IET Electric Power Appl. 2007, 1, 489–516. [Google Scholar] [CrossRef] [Green Version]
- Levi, E. Multiphase electric machines for variable-speed applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Tahaa, W.; Azerb, P.; Callegaro, A.D.; Emadi, A. Multiphase traction inverters: State-of-the-art review and future trends. IEEE Access 2022, 10, 4580–4599. [Google Scholar] [CrossRef]
- Levi, E. Advances in converter control and innovative exploitation of additional degrees of freedom for multiphase machines. IEEE Trans. Ind. Electron. 2016, 63, 433–448. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Khalik, A.S.; Masoud, M.I.; Ahmed, S.; Massoud, A.M. Effect of current harmonic injection on constant rotor volume multiphase induction machine stators: A comparative study. IEEE Trans. Ind. Appl. 2012, 48, 2002–2013. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Masoud, M.I.; Williams, B.W. Improved flux pattern with third harmonic injection for multiphase induction machines. IEEE Trans. Power Electron. 2012, 27, 1563–1578. [Google Scholar] [CrossRef]
- Mengoni, M.; Zarri, L.; Tani, A.; Parsa, L.; Serra, G.; Casadei, D. High-torque-density control of multiphase induction motor drives operating over a wide speed range. IEEE Trans. Ind. Electron. 2015, 62, 814–825. [Google Scholar] [CrossRef]
- Bermúdez, M.; Gomozov, O.; Kestelyn, X.; Barrero, F.; Nguyen, N.; Semail, E. Model predictive optimal control considering current and voltage limitations: Real-time validation using OPAL-RT technologies and five-phase permanent magnet synchronous machines. Math. Comput. Simul. 2019, 158, 148–161. [Google Scholar] [CrossRef] [Green Version]
- Bermúdez, M.; Martín, C.; Barrero, F.; Kestelyn, X. Predictive controller considering electrical constraints: A case example for five-phase induction machines. IET Electr. Power Appl. 2019, 13, 1079–1088. [Google Scholar] [CrossRef] [Green Version]
- Levi, E.; Dujic, D.; Jones, M.; Grandi, G. Analytical determination of dc-bus utilization limits in multiphase VSI supplied ac drives. IEEE Trans. Energy Convers. 2008, 23, 433–443. [Google Scholar] [CrossRef] [Green Version]
- Yepes, A.G.; Riveros, J.A.; Doval-Gandoy, J.; Barrero, F.; Lopez, O.; Bogado, B.; Jones, M.; Levi, E. Parameter identification of multiphase induction machines with distributed windings–Part 1: Sinusoidal excitation methods. IEEE Trans. Energy Convers. 2012, 27, 1056–1066. [Google Scholar] [CrossRef]
- Levi, E.; Jones, M.; Vukosavic, S.N.; Toliyat, H.A. A novel concept of a multiphase, multimotor vector controlled drive system supplied from a single voltage source inverter. IEEE Trans. Power Electron. 2004, 19, 320–335. [Google Scholar] [CrossRef]
- dos Santos Moraes, T.; Nguyen, N.K.; Semail, E.; Meinguet, F.; Guerin, M. Dual-multiphase motor drives for fault-tolerant applications: Power electronic structures and control strategies. IEEE Trans. Power Electron. 2018, 33, 572–580. [Google Scholar] [CrossRef] [Green Version]
- dos Santos Moraes, T.J.; Trabelsi, M.; Nguyen, N.K.; Semail, E.; Meinguet, F.; Guerin, M. Inverter open circuit faults diagnosis in series-connected six-phases permanent magnet drive. In Proceedings of the 2017 IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017; pp. 188–194. [Google Scholar] [CrossRef] [Green Version]
- Gupta, N.; Gopika, T.G.; Kaarthik, R.S. Modeling and decoupled control of series-connected split-phase synchronous machines with open-circuit fault. IEEE Trans. Ind. Appl. 2020, 56, 325–334. [Google Scholar] [CrossRef]
- Subotic, I.; Bodo, N.; Levi, E.; Dumnic, B.; Milicevic, D.; Katic, V. Overview of fast on-board integrated battery chargers for electric vehicles based on multiphase machines and power electronics. IET Electr. Power Appl. 2016, 10, 217–229. [Google Scholar] [CrossRef]
- Subotic, I.; Bodo, N.; Levi, E.; Jones, M. Onboard integrated battery charger for EVs using an asymmetrical nine-phase machine. IEEE Trans. Ind. Electron. 2015, 62, 3285–3295. [Google Scholar] [CrossRef]
- Subotic, I.; Bodo, N.; Levi, E.; Jones, M.; Levi, V. Isolated chargers for EVs incorporating six-phase machines. IEEE Trans. Ind. Electron. 2016, 63, 653–664. [Google Scholar] [CrossRef] [Green Version]
- Subotic, I.; Bodo, N.; Levi, E. Single-phase on-board integrated battery chargers for EVs based on multiphase machines. IEEE Trans. Power Electron. 2016, 31, 6511–6523. [Google Scholar] [CrossRef] [Green Version]
- Subotic, I.; Bodo, N.; Levi, E. An EV drive-train with integrated fast charging capability. IEEE Trans. Power Electron. 2016, 31, 1461–1471. [Google Scholar] [CrossRef] [Green Version]
- Bodo, N.; Levi, E.; Subotic, I.; Espina, J.; Empringham, L.; Johnson, C.M. Efficiency evaluation of fully integrated on-board EV battery chargers with nine-phase machines. IEEE Trans. Energy Convers. 2017, 32, 257–266. [Google Scholar] [CrossRef]
- Abdel-Majeed, M.S.; Eldeeb, H.M.; Metwly, M.Y.; Abdel-Khalik, A.S.; Hamad, M.S.; Hamdy, R.A.; Ahmed, S. Postfault operation of onboard integrated battery charger via a nine-phase EV-drive train. IEEE Trans. Ind. Electron. 2021, 68, 5626–5637. [Google Scholar] [CrossRef]
- Sala, G.; Valente, G.; Formentini, A.; Papini, L.; Gerada, D.; Zanchetta, P.; Tani, A.; Gerada, C. Space vectors and pseudoinverse matrix methods for the radial force control in bearingless multisector permanent magnet machines. IEEE Trans. Ind. Electron. 2018, 65, 6912–6922. [Google Scholar] [CrossRef]
- Duran, M.; Barrero, F. Recent advances in the design, modeling and control of multiphase machines–Part 2. IEEE Trans. Ind. Electron. 2016, 63, 459–468. [Google Scholar] [CrossRef]
- Bennett, J.W.; Atkinson, G.J.; Mecrow, B.C.; Atkinson, D.J. Fault-tolerant design considerations and control strategies for aerospace drives. IEEE Trans. Ind. Electron. 2012, 59, 2049–2058. [Google Scholar] [CrossRef]
- Cao, W.; Mecrow, B.C.; Atkinson, G.J.; Bennett, J.W.; Atkinson, D.J. Overview of electric motor technologies used for more electric aircraft (MEA). IEEE Trans. Ind. Electron. 2012, 59, 3523–3531. [Google Scholar] [CrossRef]
- Ifedi, C.J.; Mecrow, B.C.; Brockway, S.T.M.; Boast, G.S.; Atkinson, G.J.; Kostic-Perovic, D. Fault-tolerant in-wheel motor topologies for high-performance electric vehicles. IEEE Trans. Ind. Appl. 2013, 49, 1249–1257. [Google Scholar] [CrossRef]
- Patel, V.I.; Wang, J.; Nugraha, D.T.; Vuletić, R.; Tousen, J. Enhanced availability of drivetrain through novel multiphase permanent-magnet machine drive. IEEE Trans. Ind. Electron. 2016, 63, 469–480. [Google Scholar] [CrossRef]
- Singh, G. Multi-phase induction machine drive research—A survey. Electr. Power Syst. Res. 2002, 61, 139–147. [Google Scholar] [CrossRef]
- Levi, E.; Jones, M. A literature survey of state-of-the art in multiphase ac drives. In Proceedings of the UPEC, Stafford, UK, 9–11 September 2002; pp. 505–510. [Google Scholar]
- Huang, J.; Kang, M.; Yang, J.; Jiang, H.; Liu, D. Multiphase machine theory and its applications. In Proceedings of the ICEMS, Wuhan, China, 17–20 October 2008; pp. 1–7. [Google Scholar]
- Liu, Z.; Li, Y.; Zheng, Z. A review of drive techniques for multiphase machines. CES Trans. Elect. Mach. Syst. 2018, 2, 243–251. [Google Scholar] [CrossRef]
- Gupta, S.K.; Singh, O.; Khan, M.A.; Kushwaha, A.K. A review on developments of polyphase machines. J. Inf. Optim. Sci. 2020, 41, 327–343. [Google Scholar] [CrossRef]
- Barrero, F.; Duran, M.J. Recent advances in the design, modeling and control of multiphase machines–Part 1. IEEE Trans. Ind. Electron. 2016, 63, 449–458. [Google Scholar] [CrossRef]
- Parsa, L. On advantages of multi-phase machines. In Proceedings of the 31st Annual Conference of IEEE Industrial Electronics Society, 2005. IECON 2005, Raleigh, NC, USA, 6–10 November 2005; pp. 1574–1579. [Google Scholar] [CrossRef]
- Parsa, L.; Toliyat, H.A. Five-phase permanent magnet motor drives for ship propulsion applications. In Proceedings of the IEEE Electric Ship Technologies Symposium, Philadelphia, PA, USA, 27 July 2005; pp. 371–378. [Google Scholar] [CrossRef]
- Zoric, I.; Zabaleta, M.; Jones, M.; Levi, E. Techniques for power sharing between winding sets of multiple three-phase machines. In Proceedings of the 2017 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Nottingham, UK, 20–21 April 2017; pp. 208–215. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Tani, A.; Zarri, L. Direct torque control for induction machines: A technology status review. In Proceedings of the 2013 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Paris, France, 11–12 March 2013; pp. 117–129. [Google Scholar] [CrossRef]
- Tenconi, A.; Rubino, S.; Bojoi, R. Model predictive control for multiphase motor drives–A technology status review. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018 -ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 732–739. [Google Scholar] [CrossRef]
- Gonçalves, P.; Cruz, S.; Mendes, A. Finite control set model predictive control of six-phase asymmetrical machines–An overview. Energies 2019, 12, 4693. [Google Scholar] [CrossRef] [Green Version]
- Bermudez, M.; Martín, C.; Gonzalez-Prieto, I.; Duran, M.J.; Arahal, M.R.; Barrero, F. Predictive current control in electrical drives: An illustrated review with case examples using a five-phase induction motor drive with distributed windings. IET Electric Power Appl. 2020, 14, 1291–1310. [Google Scholar] [CrossRef]
- Bojoi, R.; Farina, F.; Profumo, F.; Tenconi, A. Dual-three phase induction machine drives control–A survey. IEEJ Trans. Ind. Appl 2006, 126, 420–429. [Google Scholar] [CrossRef]
- Alosa, C.; Immovilli, F.; Lorenzani, E. Modular multi-three-phase electric drives for enhanced reliability and current ripple minimization. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 7108–7114. [Google Scholar] [CrossRef]
- Oleschuk, V.; Grandi, G.; Dragonas, F.A. Five-phase and six-phase converters with synchronized PWM: An overview. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 283–288. [Google Scholar] [CrossRef]
- Vu, D.T.; Nguyen, N.K.; Semail, E. An overview of methods using reduced-ordered transformation matrices for fault-tolerant control of 5-phase machines with an open phase. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, Australia, 13–15 February 2019; pp. 1557–1562. [Google Scholar] [CrossRef] [Green Version]
- Levi, E.; Bodo, N.; Dordevic, O.; Jones, M. Recent advances in power electronic converter control for multiphase drive systems. In Proceedings of the 2013 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Paris, France, 11–12 March 2013; pp. 158–167. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Wang, Y.; Chen, J.; Cheng, M. Fault tolerant control of multiphase multilevel motor drives–Technical review. Chin. J. Electr. Eng. 2017, 3, 76–86. [Google Scholar] [CrossRef]
- Salem, A.; Narimani, M. A review on multiphase drives for automotive traction applications. IEEE Trans. Transp. Electrific. 2019, 5, 1329–1348. [Google Scholar] [CrossRef]
- Bojoi, R.; Cavagnino, A.; Tenconi, A.; Tessarolo, A.; Vaschetto, S. Multiphase electrical machines and drives in the transportation electrification. In Proceedings of the 2015 IEEE 1st International Forum on Research and Technologies for Society and Industry Leveraging a better tomorrow (RTSI), Turin, Italy, 16–18 September 2015; pp. 205–212. [Google Scholar] [CrossRef]
- Bojoi, R.; Rubino, S.; Tenconi, A.; Vaschetto, S. Multiphase electrical machines and drives: A viable solution for energy generation and transportation electrification. In Proceedings of the 2016 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 20–22 October 2016; pp. 632–639. [Google Scholar] [CrossRef]
- Menon, R.; Kadam, A.H.; Azeez, N.A.; Williamson, S.S. A comprehensive survey on permanent magnet synchronous motor drive systems for electric transportation applications. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 6627–6632. [Google Scholar] [CrossRef]
- Bojoi, R.; Neacsu, M.G.; Tenconi, A. Analysis and survey of multi-phase power electronic converter topologies for the more electric aircraft applications. In Proceedings of the International Symposium on Power Electronics Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 20–22 June 2012; pp. 440–445. [Google Scholar] [CrossRef]
- Bojoi, R.; Boggero, L.; Comino, S.; Fioriti, M.; Tenconi, A.; Vaschetto, S. Multiphase drives for hybrid-electric propulsion in light aircrafts: A viable solution. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 613–619. [Google Scholar] [CrossRef]
- Peng, X.; Liu, Z.; Jiang, D. A review of multiphase energy conversion in wind power generation. Renew. Sust. Energ. Rev. 2021, 147, 111172. [Google Scholar] [CrossRef]
- Laksar, J.; Cermak, R.; Hruska, K. Challenges in the electromagnetic design of multiphase machines: Winding and equivalent circuit parameters. Energies 2021, 14, 7335. [Google Scholar] [CrossRef]
- Noh, Y.; Kim, W.; Lee, J. The optimal current ratio control of redundant electric drive systems and diagnostic strategies for disagreement. IEEE Access 2021, 9, 32115–32130. [Google Scholar] [CrossRef]
- Yao, G.; Pang, S.; Ying, T.; Benbouzid, M.; Ait-Ahmed, M.; Benkhoris, M.F. VPSO-SVM-based open-circuit faults diagnosis of five-phase marine current generator sets. Energies 2020, 13, 6004. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Xu, Z.; Cheng, M.; Wang, W.; Hu, Y. Comprehensive diagnosis and tolerance strategies for electrical faults and sensor faults in dual three-phase PMSM drives. IEEE Trans. Power Electron. 2019, 34, 6669–6684. [Google Scholar] [CrossRef]
- Chen, H.; He, J.; Guan, X.; Demerdash, N.A.O.; El-Refaie, A.; Lee, C.H.T. High-resistance connection diagnosis in five-phase PMSMs based on the method of magnetic field pendulous oscillation and symmetrical components. IEEE Trans. Ind. Electron. 2022, 69, 2288–2299. [Google Scholar] [CrossRef]
- Sun, J.; Li, C.; Zheng, Z.; Wang, K.; Li, Y. Online estimation of per-phase stator resistance based on dc-signal injection for condition monitoring in multiphase drives. IEEE Trans. Ind. Electron. 2022, 69, 2227–2239. [Google Scholar] [CrossRef]
- Hu, R.; Wang, J.; Mills, A.R.; Chong, E.; Sun, Z. Detection and classification of turn fault and high resistance connection fault in permanent magnet machines based on zero sequence voltage. IEEE Trans. Power Electron. 2020, 35, 1922–1933. [Google Scholar] [CrossRef]
- Farag, K.; Shawier, A.; Abdel-Khalik, A.S.; Ahmed, M.M.; Ahmed, S. Applicability analysis of indices-based fault detection technique of six-phase induction motor. Energies 2021, 14, 5905. [Google Scholar] [CrossRef]
- Gonçalves, P.F.C.; Cruz, S.M.A.; Mendes, A.M.S. Diagnosis of open-phase faults and high resistance connections in six-phase PMSM drives. In Proceedings of the 2020 International Conference on Smart Energy Systems and Technologies (SEST), Istanbul, Turkey, 7–9 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Gonçalves, P.F.C.; Cruz, S.M.A.; Mendes, A.M.S. Online diagnostic method for the detection of high-resistance connections and open-phase faults in six-phase PMSM drives. IEEE Trans. Ind. Appl. 2022, 58, 345–355. [Google Scholar] [CrossRef]
- Rossi, C.; Gritli, Y.; Pilati, A.; Rizzoli, G.; Tani, A.; Casadei, D. High resistance fault-detection and fault-tolerance for asymmetrical six-phase surface-mounted ac permanent magnet synchronous motor drives. Energies 2020, 13, 3089. [Google Scholar] [CrossRef]
- Zarri, L.; Mengoni, M.; Gritli, Y.; Tani, A.; Filippetti, F.; Serra, G.; Casadei, D. Detection and localization of stator resistance dissymmetry based on multiple reference frame controllers in multiphase induction motor drives. IEEE Trans. Ind. Electron. 2013, 60, 3506–3518. [Google Scholar] [CrossRef]
- Mengoni, M.; Zarri, L.; Tani, A.; Gritli, Y.; Serra, G.; Filippetti, F.; Casadei, D. Online detection of high-resistance connections in multiphase induction machines. IEEE Trans. Power Electron. 2015, 30, 4505–4513. [Google Scholar] [CrossRef]
- Tani, A.; Gritli, Y.; Mengoni, M.; Zarri, L.; Sala, G.; Bellini, A.; Serra, G. Detection of magnet demagnetization and high-resistance connections in five-phase surface-mounted permanent magnet generators. In Proceedings of the 2015 IEEE 10th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Guarda, Portugal, 1–4 September 2015; pp. 487–493. [Google Scholar] [CrossRef]
- Salas-Biedma, P.; Gonzalez-Prieto, I.; Duran, M.J.; Bermudez, M.; Barrero, F. Multiphase current imbalance localisation method applied to natural fault-tolerant strategies. IET Electric Power Appl. 2020, 14, 1421–1429. [Google Scholar] [CrossRef]
- Baneira, F.; Yepes, A.G.; Lopez, O.; Doval-Gandoy, J. Estimation method of stator winding temperature for dual three-phase machines based on dc-signal injection. IEEE Trans. Power Electron. 2016, 31, 5141–5148. [Google Scholar] [CrossRef]
- Li, Z.; Feng, G.; Lai, C.; Tian, J.; Li, W.; Kar, N.C. Dual dc current injection-based stator winding temperature tracking for dual three-phase permanent magnet synchronous machine using Kalman filter. IET Electric Power Appl. 2019, 13, 1726–1733. [Google Scholar] [CrossRef]
- Feng, G.; Lai, C.; Li, W.; Li, Z.; Kar, N.C. Efficient permanent magnet temperature modeling and estimation for dual three-phase PMSM considering inverter nonlinearity. IEEE Trans. Power Electron. 2020, 35, 7328–7340. [Google Scholar] [CrossRef]
- Li, Z.; Feng, G.; Lai, C.; Li, W.; Kar, N.C. Current injection-based simultaneous stator winding and PM temperature estimation for dual three-phase PMSMs. IEEE Trans. Ind. Appl. 2021, 57, 4933–4945. [Google Scholar] [CrossRef]
- Mengoni, M.; Vancini, L.; Tani, A.; Gritli, Y.; Zarri, L.; Rossi, C. On-line detection of magnet demagnetization in asymmetrical six-phase surface-mounted permanent magnet synchronous motor drives. In Proceedings of the 2019 IEEE 12th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Toulouse, France, 27–30 August 2019; pp. 188–194. [Google Scholar] [CrossRef]
- Gritli, Y.; Mengoni, M.; Rizzoli, G.; Rossi, C.; Tani, A.; Casadei, D. Rotor magnet demagnetisation diagnosis in asymmetrical six-phase surface-mounted ac PMSM drives. IET Electric Power Appl. 2020, 14, 1747–1755. [Google Scholar] [CrossRef]
- Casadei, D.; Filippetti, F.; Mengoni, M.; Gritli, Y.; Serra, G.; Tani, A.; Zarri, L. Detection of magnet demagnetization in five-phase surface-mounted permanent magnet generators. In Proceedings of the 2012 3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 25–28 June 2012; pp. 841–848. [Google Scholar] [CrossRef]
- Gritli, Y.; Tani, A.; Mengoni, M.; Zarri, L.; Serra, G.; Filippetti, F.; Casadei, D. Effect of the closed-loop control on the diagnosis of rotor demagnetization in five-phase surface-mounted permanent magnet generators. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 2349–2354. [Google Scholar] [CrossRef]
- Gritli, Y.; Tani, A.; Rossi, C.; Casadei, D. Assessment of current and voltage signature analysis for the diagnosis of rotor magnet demagnetization in five-phase ac permanent magnet generator drives. Math. Comput. Simul. 2019, 158, 91–106. [Google Scholar] [CrossRef]
- Andriamalala, R.N.; Razik, H.; Baghli, L.; Sargos, F.M. Eccentricity fault diagnosis of a dual-stator winding induction machine drive considering the slotting effects. IEEE Trans. Ind. Electron. 2008, 55, 4238–4251. [Google Scholar] [CrossRef]
- Maouche, Y.; Oumaamar, M.; Nemmour, A.L.; Khezzar, A. Voltage signatures between two sub-windings in dual three-phase induction motor under static air-gap eccentricity. In Proceedings of the 2013 8th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2013; pp. 258–262. [Google Scholar] [CrossRef]
- Kaikaa, M.Y.; Yasmine Kecita, Z. Modeling of multiphase induction motors under outer raceway bearing fault. In Proceedings of the 2018 6th International Conference on Control Engineering and Information Technology (CEIT), Istanbul, Turkey, 25–27 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Maouche, Y.; Boussaid, A.; Boucherma, M.; Khezzar, A. Analytical study of pulsating torque and harmonic components in rotor current of six-phase induction motor under healthy and faulty conditions. In Proceedings of the 2013 9th IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives (SDEMPED), Valencia, Spain, 27–30 August 2013; pp. 295–301. [Google Scholar] [CrossRef]
- Maouche, Y.; Oumaamar, M.E.K.; Khezzar, A.; Razik, H. Analysis of stator current of dual-three phase induction motor drive under broken bar fault condition. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 560–564. [Google Scholar] [CrossRef]
- Choi, S.; Haque, M.S.; Arafat, A.; Toliyat, H.A. Detection and estimation of extremely small fault signature by utilizing multiple current sensor signals in electric machines. IEEE Trans. Ind. Appl. 2017, 53, 2805–2816. [Google Scholar] [CrossRef]
- Abdel-Mageed, B.S.; Shalaby, M.S.; Seoudy, H.M. Study of broken rotor bar fault for asymmetrical six-phase induction motor. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Bensalem, Y.; Abbassi, R.; Jerbi, H. Fuzzy logic based-active fault tolerant control of speed sensor failure for five-phase PMSM. J. Electr. Eng. Technol. 2021, 16, 287–299. [Google Scholar] [CrossRef]
- Xiao, L.; Zhang, L.; Gao, F.; Qian, J. Robust fault-tolerant synergetic control for dual three-phase PMSM drives considering speed sensor fault. IEEE Access 2020, 8, 78912–78922. [Google Scholar] [CrossRef]
- Gritli, Y.; Mengoni, M.; Rossi, C.; Tani, A.; Casadei, D.; Serra, G. Experimental assessment of winding inter-turn short-circuits fault signatures in six-phase ac permanent magnet synchronous motors. IET Renew. Power Gener. 2020, 14, 2791–2800. [Google Scholar] [CrossRef]
- Immovilli, F.; Bianchini, C.; Lorenzani, E.; Bellini, A.; Fornasiero, E. Evaluation of combined reference frame transformation for interturn fault detection in permanent-magnet multiphase machines. IEEE Trans. Ind. Electron. 2015, 62, 1912–1920. [Google Scholar] [CrossRef]
- Hu, R.; Wang, J.; Sen, B.; Mills, A.R.; Chong, E.; Sun, Z. Pwm ripple currents based turn fault detection for multiphase permanent magnet machines. IEEE Trans. Ind. Appl. 2017, 53, 2740–2751. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Li, C.; Zhu, W.; Zhang, X.; Zhang, L.; Cheng, M. Stator winding interturn short-circuit faults severity detection controlled by OW-SVPWM without CMV of a five-phase FTFSCW-IPM. IEEE Trans. Ind. Appl. 2017, 53, 194–202. [Google Scholar] [CrossRef]
- Sen, B.; Wang, J. Stator interturn fault detection in permanent-magnet machines using PWM ripple current measurement. IEEE Trans. Ind. Electron. 2016, 63, 3148–3157. [Google Scholar] [CrossRef] [Green Version]
- Haylock, J.; Mecrow, B.; Jack, A.; Atkinson, D. Operation of fault tolerant machines with winding failures. IEEE Trans. Energy Convers. 1999, 14, 1490–1495. [Google Scholar] [CrossRef]
- Cui, R.; Fan, Y.; Li, C. On-line inter-turn short-circuit fault diagnosis and torque ripple minimization control strategy based on OW five-phase BFTHE-IPM. IEEE Trans. Energy Convers. 2018, 33, 2200–2209. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, J.; Howe, D.; Jewell, G. Analytical prediction of the short-circuit current in fault-tolerant permanent-magnet machines. IEEE Trans. Ind. Electron. 2008, 55, 4210–4217. [Google Scholar] [CrossRef]
- Wu, F.; EL-Refaie, A.M.; Zheng, P. Diagnosis and remediation of single-turn short circuit in a multiphase FSCW PM machine based on T-type equivalent circuit. IEEE Trans. Ind. Appl. 2020, 56, 158–169. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Griffo, A.; Sen, B. Stator turn fault detection by second harmonic in instantaneous power for a triple-redundant fault-tolerant PM drive. IEEE Trans. Ind. Electron. 2018, 65, 7279–7289. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Wang, J.; Hu, R.; Wang, B. Electromagnetic and thermal behavior of a triple redundant 9-phase PMASynRM with insulation deterioration fault. IEEE Trans. Ind. Appl. 2020, 56, 6374–6383. [Google Scholar] [CrossRef]
- Haylock, J.A.; Mecrow, B.C.; Jack, A.G.; Atkinson, D.J. Operation of a fault tolerant PM drive for an aerospace fuel pump application. IEE Proc.-Electr. Power Appl. 1998, 145, 441–448. [Google Scholar] [CrossRef]
- Jiang, X.; Huang, W.; Cao, R.; Hao, Z.; Jiang, W. Electric drive system of dual-winding fault-tolerant permanent-magnet motor for aerospace applications. IEEE Trans. Ind. Electron. 2015, 62, 7322–7330. [Google Scholar] [CrossRef]
- Jiang, X.; Li, Q.; Huang, W.; Cao, R. A dual-winding fault-tolerant motor drive system based on the redundancy bridge arm. IEEE Trans. Ind. Electron. 2019, 66, 654–662. [Google Scholar] [CrossRef]
- Salehifar, M.; Moreno-Eguilaz, M.; Putrus, G.; Barras, P. Simplified fault tolerant finite control set model predictive control of a five-phase inverter supplying BLDC motor in electric vehicle drive. Electr. Power Syst. Res. 2016, 132, 56–66. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Wang, Z.; Xu, Z.; He, J.; Zhao, W. Diagnosis and tolerance of common electrical faults in T-type three-level inverters fed dual three-phase PMSM drives. IEEE Trans. Power Electron. 2020, 35, 1753–1769. [Google Scholar] [CrossRef]
- Arafat, A.; Choi, S.; Baek, J. Open-phase fault detection of a five-phase permanent magnet assisted synchronous reluctance motor based on symmetrical components theory. IEEE Trans. Ind. Electron. 2017, 64, 6465–6474. [Google Scholar] [CrossRef]
- Meinguet, F.; Semail, E.; Gyselinck, J. An on-line method for stator fault detection in multi-phase PMSM drives. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Meinguet, F.; Sandulescu, P.; Aslan, B.; Lu, L.; Nguyen, N.; Kestelyn, X.; Semail, E. A signal-based technique for fault detection and isolation of inverter faults in multi-phase drives. In Proceedings of the 2012 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Bengaluru, India, 16–19 December 2012; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Trabelsi, M.; Nguyen, N.K.; Semail, E. Real-time switches fault diagnosis based on typical operating characteristics of five-phase permanent-magnetic synchronous machines. IEEE Trans. Ind. Electron. 2016, 63, 4683–4694. [Google Scholar] [CrossRef] [Green Version]
- Trabelsi, M.; Semail, E.; Nguyen, N.K. Experimental investigation of inverter open-circuit fault diagnosis for biharmonic five-phase permanent magnet drive. IEEE J. Emerg. Sel. Topics Power Electron. 2018, 6, 339–351. [Google Scholar] [CrossRef] [Green Version]
- Gonçalves, P.F.C.; Cruz, S.M.A.; Mendes, A.M.S. Open-phase fault diagnosis in six-phase PMSM drives based on the harmonics of the measured secondary subspace currents. In Proceedings of the IECON 2020 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 4863–4868. [Google Scholar] [CrossRef]
- Kong, J.; Wang, K.; Zhang, J.; Zhang, H. Multiple open-switch fault diagnosis for five-phase permanent magnet machine utilizing currents in stationary reference frame. IEEE Trans. Energy Convers. 2021, 36, 314–324. [Google Scholar] [CrossRef]
- Chen, H.; He, J.; Demerdash, N.A.O.; Guan, X.; Lee, C.H.T. Diagnosis of open-phase faults for a five-phase PMSM fed by a closed-loop vector-controlled drive based on magnetic field pendulous oscillation technique. IEEE Trans. Ind. Electron. 2021, 68, 5582–5593. [Google Scholar] [CrossRef]
- Duran, M.J.; Gonzalez-Prieto, I.; Rios-Garcia, N.; Barrero, F. A simple, fast, and robust open-phase fault detection technique for six-phase induction motor drives. IEEE Trans. Power Electron. 2018, 33, 547–557. [Google Scholar] [CrossRef]
- Mesai-Ahmed, H.; Jlassi, I.; Marques Cardoso, A.J.; Bentaallah, A. Multiple open-circuit faults diagnosis in six-phase induction motor drives, using stator current analysis. IEEE Trans. Power Electron. 2022, 37, 7275–7285. [Google Scholar] [CrossRef]
- Torabi, N.; Sundaram, V.M.; Toliyat, H.A. On-line fault diagnosis of multi-phase drives using self-recurrent wavelet neural networks with adaptive learning rates. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 570–577. [Google Scholar] [CrossRef]
- Torabi, N.; Naghavi, F.; Toliyat, H.A. Real-time fault isolation in multiphase multilevel NPC converters using active semi-supervised fuzzy clustering algorithm with pairwise constraints. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017. [Google Scholar] [CrossRef]
- Gonzalez-Prieto, I.; Duran, M.J.; Rios-Garcia, N.; Barrero, F.; Martín, C. Open-switch fault detection in five-phase induction motor drives using model predictive control. IEEE Trans. Ind. Electron. 2018, 65, 3045–3055. [Google Scholar] [CrossRef]
- Salehifar, M.; Salehi Arashloo, R.; Moreno-Eguilaz, M.; Sala, V.; Romeral, L. Observer-based open transistor fault diagnosis and fault-tolerant control of five-phase permanent magnet motor drive for application in electric vehicles. IET Power Electron. 2015, 8, 76–87. [Google Scholar] [CrossRef]
- Salehifar, M.; Moreno-Eguilaz, M. Fault diagnosis and fault-tolerant finite control set-model predictive control of a multiphase voltage-source inverter supplying BLDC motor. ISA Trans. 2016, 60, 143–155. [Google Scholar] [CrossRef] [Green Version]
- Salehifar, M.; Arashloo, R.S.; Moreno-Equilaz, J.M.; Sala, V.; Romeral, L. Fault detection and fault tolerant operation of a five phase PM motor drive using adaptive model identification approach. IEEE J. Emerg. Sel. Topics Power Electron. 2014, 2, 212–223. [Google Scholar] [CrossRef]
- Pantea, A.; Yazidi, A.; Betin, F.; Taherzadeh, M.; Carrière, S.; Henao, H.; Capolino, G. Six-phase induction machine model for electrical fault simulation using the circuit-oriented method. IEEE Trans. Ind. Electron. 2016, 63, 494–503. [Google Scholar] [CrossRef]
- Lin, F.; Hung, Y.; Hwang, J.; Tsai, M. Fault-tolerant control of a six-phase motor drive system using a Takagi–Sugeno–Kang type fuzzy neural network with asymmetric membership function. IEEE Trans. Power Electron. 2013, 28, 3557–3572. [Google Scholar] [CrossRef]
- Lin, F.; Hung, Y.; Tsai, M. Fault-tolerant control for six-phase PMSM drive system via intelligent complementary sliding-mode control using TSKFNN-AMF. IEEE Trans. Ind. Electron. 2013, 60, 5747–5762. [Google Scholar] [CrossRef]
- Pantea, A.; Yazidi, A.; Betin, F.; Carrière, S.; Sivert, A.; Vacossin, B.; Henao, H.; Capolino, G. Fault-tolerant control of a low-speed six-phase induction generator for wind turbines. IEEE Trans. Ind. Appl. 2019, 55, 426–436. [Google Scholar] [CrossRef]
- Wen, Z.; Valente, G.; Formentini, A.; Papini, L.; Gerada, C.; Zanchetta, P. Open-circuit fault control techniques for bearingless multisector permanent magnet synchronous machines. IEEE Trans. Ind. Appl. 2021, 57, 2527–2536. [Google Scholar] [CrossRef]
- Lin, F.; Sun, I.; Yang, K.; Chang, J. Recurrent fuzzy neural cerebellar model articulation network fault-tolerant control of six-phase permanent magnet synchronous motor position servo drive. IEEE Trans. Fuzzy Syst. 2016, 24, 153–167. [Google Scholar] [CrossRef]
- Garcia-Entrambasaguas, P.; Gonzalez-Prieto, I.; Duran, M.J. Single-index open-phase fault detection method for six-phase electric drives. IEEE Trans. Ind. Electron. 2020, 67, 10233–10242. [Google Scholar] [CrossRef]
- Olivieri, C. A fault-adaptive and observer-based sensorless strategy for a fault-tolerant five-phase BLDC motor. In Proceedings of the 2013 IEEE International Symposium on Sensorless Control for Electrical Drives and Predictive Control of Electrical Drives and Power Electronics (SLED/PRECEDE), Munich, Germany, 17–19 October 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Guo, H.; Guo, S.; Xu, J.; Tian, X. Power switch open-circuit fault diagnosis of six-phase fault tolerant permanent magnet synchronous motor system under normal and fault-tolerant operation conditions using the average current Park’s vector approach. IEEE Trans. Power Electron. 2021, 36, 2641–2660. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Griffo, A.; Shi, Y. Investigation into fault-tolerant capability of a triple redundant PMA SynRM drive. IEEE Trans. Power Electron. 2019, 34, 1611–1621. [Google Scholar] [CrossRef] [Green Version]
- Villani, M.; Tursini, M.; Fabri, G.; Castellini, L. High reliability permanent magnet brushless motor drive for aircraft application. IEEE Trans. Ind. Electron. 2012, 59, 2073–2081. [Google Scholar] [CrossRef]
- Duran, M.J.; Gonzalez-Prieto, I.; Barrero, F.; Levi, E.; Zarri, L.; Mengoni, M. A simple braking method for six-phase induction motor drives with unidirectional power flow in the base-speed region. IEEE Trans. Ind. Electron. 2017, 64, 6032–6041. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Prieto, I.; Duran, M.J.; Barrero, F.J. Fault-tolerant control of six-phase induction motor drives with variable current injection. IEEE Trans. Power Electron. 2017, 32, 7894–7903. [Google Scholar] [CrossRef]
- Priestley, M.; Fletcher, J.E.; Tan, C. Space-vector PWM technique for five-phase open-end winding PMSM drive operating in the overmodulation region. IEEE Trans. Ind. Electron. 2018, 65, 6816–6827. [Google Scholar] [CrossRef]
- Feng, G.; Lai, C.; Li, W.; Li, Z.; Kar, N.C. Dual reference frame based current harmonic minimization for dual three-phase PMSM considering inverter voltage limit. IEEE Trans. Power Electron. 2021, 36, 8055–8066. [Google Scholar] [CrossRef]
- Karttunen, J.; Kallio, S.; Honkanen, J.; Peltoniemi, P.; Silventoinen, P. Partial current harmonic compensation in dual three-phase PMSMs considering the limited available voltage. IEEE Trans. Ind. Electron. 2017, 64, 1038–1048. [Google Scholar] [CrossRef]
- Yu, B.; Song, W.; Guo, Y.; Saeed, M.S.R. A finite control set model predictive control for five-phase PMSMs with improved dc-link utilization. IEEE Trans. Power Electron. 2022, 37, 3297–3307. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J.; Toliyat, H.A. Multifrequency current control for n-phase machines including antiwindup and distortion-free saturation with full dc-bus utilization. IEEE Trans. Power Electron. 2019, 34, 9891–9905. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J. Overmodulation method with adaptive x-y current limitation for five-phase induction motor drives. IEEE Trans. Ind. Electron. 2022, 69, 2240–2251. [Google Scholar] [CrossRef]
- Zhu, Y.; Gu, W.; Lu, K.; Wu, Z. Vector control of asymmetric dual three-phase PMSM in full modulation range. IEEE Access 2020, 8, 104479–104493. [Google Scholar] [CrossRef]
- Klingshirn, E.A. Harmonic filters for six-phase and other multiphase motors on voltage source inverters. IEEE Trans. Ind. Appl. 1985, IA-21, 588–594. [Google Scholar] [CrossRef]
- Sadeghi, S.; Guo, L.; Toliyat, H.A.; Parsa, L. Wide operational speed range of five-phase permanent magnet machines by using different stator winding configurations. IEEE Trans. Ind. Electron. 2012, 59, 2621–2631. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J.; Toliyat, H.A. Improvement in dc-link utilization with reduced current and torque deterioration for five-phase drives by combination of circulating-current filters and simple carrier-based PWM based on closed-form expressions. IEEE Trans. Ind. Electron. 2021, 68, 960–971. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J. Simple carrier-based PWM for prolonged high dc-link utilization for symmetrical and asymmetrical n-phase ac drives. IEEE Trans. Power Electron. 2021, 36, 8696–8712. [Google Scholar] [CrossRef]
- Wang, T.; Fang, F.; Wu, X.; Jiang, X. Novel filter for stator harmonic currents reduction in six-step converter fed multiphase induction motor drives. IEEE Trans. Power Electron. 2013, 28, 498–506. [Google Scholar] [CrossRef]
- Xu, L.; Ye, L. Analysis of a novel stator winding structure minimizing harmonic current and torque ripple for dual six-step converter-fed high power ac machines. IEEE Trans. Ind. Appl. 1995, 31, 84–90. [Google Scholar] [CrossRef]
- Gopakumar, K.; Ranganthan, V.; Bhat, S. Split-phase induction motor operation from PWM voltage source inverter. IEEE Trans. Ind. Appl. 1993, 29, 927–932. [Google Scholar] [CrossRef]
- Young, P.; Preindl, M. Optimal generalized overmodulation for multiphase PMSM drives. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 500–505. [Google Scholar] [CrossRef]
- Iqbal, A.; Levi, E. Space vector modulation schemes for a five-phase voltage source inverter. In Proceedings of the 2005 European Conference on Power Electronics and Applications, Dresden, Germany, 11–14 September 2005; pp. 1–12. [Google Scholar] [CrossRef]
- Carrasco, G.; Silva, C. Space vector PWM method for five-phase two-level VSI with minimum harmonic injection in the overmodulation region. IEEE Trans. Ind. Electron. 2013, 60, 2042–2053. [Google Scholar] [CrossRef]
- Halasz, S. Overmodulation region of multi-phase inverters. In Proceedings of the 2008 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; pp. 682–689. [Google Scholar] [CrossRef]
- Duran, M.J.; Prieto, J.; Barrero, F. Space vector PWM with reduced common-mode voltage for five-phase induction motor drives operating in overmodulation zone. IEEE Trans. Power Electron. 2013, 28, 4030–4040. [Google Scholar] [CrossRef]
- Prieto, J.; Barrero, F.; Duran, M.J.; Toral Marin, S.; Perales, M.A. SVM procedure for n-phase VSI with low harmonic distortion in the overmodulation region. IEEE Trans. Ind. Electron. 2014, 61, 92–97. [Google Scholar] [CrossRef]
- Vancini, L.; Mengoni, M.; Rizzoli, G.; Sala, G.; Zarri, L.; Tani, A. Carrier-based PWM overmodulation strategies for five-phase inverters. IEEE Trans. Power Electron. 2021, 36, 6988–6999. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, G.; Su, J. PWM strategy with minimum harmonic distortion for dual three-phase permanent-magnet synchronous motor drives operating in the overmodulation region. IEEE Trans. Power Electron. 2016, 31, 1367–1380. [Google Scholar] [CrossRef]
- Komrska, T.; Glasberger, T.; Peroutka, Z. Universal PWM modulator for multiphase drives with a minimum infinity-norm approach. IEEE Trans. Ind. Electron. 2016, 63, 5979–5987. [Google Scholar] [CrossRef]
- Yazdani, D.; Ali Khajehoddin, S.; Bakhshai, A.; Joos, G. Full utilization of the inverter in split-phase drives by means of a dual three-phase space vector classification algorithm. IEEE Trans. Ind. Electron. 2009, 56, 120–129. [Google Scholar] [CrossRef]
- Paul, S.; Basu, K. A three-phase inverter based overmodulation strategy of asymmetrical six-phase induction machine. IEEE Trans. Power Electron. 2021, 36, 5802–5817. [Google Scholar] [CrossRef]
- Paul, S.; Basu, K. Overmodulation techniques of asymmetrical six-phase machine with optimum harmonic voltage injection. IEEE Trans. Ind. Electron. 2021, 68, 4679–4690. [Google Scholar] [CrossRef]
- Bu, F.; Pu, T.; Liu, Q.; Ma, B.; Degano, M.; Gerada, C. Four-degree-of-freedom overmodulation strategy for five-phase space vector pulsewidth modulation. IEEE J. Emerg. Sel. Topics Power Electron. 2021, 9, 1578–1590. [Google Scholar] [CrossRef]
- Yang, G.; Yang, J.; Li, S.; Wang, Y.; Hussain, H.; Yan, L.; Deng, R. Overmodulation strategy for seven-phase induction motors with optimum harmonic voltage injection based on sequential optimization scheme. IEEE Trans. Power Electron. 2021, 36, 14039–14050. [Google Scholar] [CrossRef]
- Bojoi, R.; Cavagnino, A.; Tenconi, A.; Vaschetto, S. Control of shaft-line-embedded multiphase starter/generator for aero-engine. IEEE Trans. Ind. Electron. 2016, 63, 641–652. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, J.; Jewell, G.W.; Howe, D. Enhanced optimal torque control of fault-tolerant PM machine under flux-weakening operation. IEEE Trans. Ind. Electron. 2010, 57, 344–353. [Google Scholar] [CrossRef]
- Ede, J.D.; Atallah, K.; Wang, J.; Howe, D. Effect of optimal torque control on rotor loss of fault-tolerant permanent-magnet brushless machines. IEEE Trans. Magn. 2002, 38, 3291–3293. [Google Scholar] [CrossRef]
- Wang, J.; Atallah, K.; Howe, D. Optimal torque control of fault-tolerant permanent magnet brushless machines. IEEE Trans. Magn. 2003, 39, 2962–2964. [Google Scholar] [CrossRef]
- Atallah, K.; Wang, J.; Howe, D. Torque-ripple minimization in modular permanent-magnet brushless machines. IEEE Trans. Ind. Appl. 2003, 39, 1689–1695. [Google Scholar] [CrossRef]
- Sen, B.; Wang, J. Stationary frame fault-tolerant current control of polyphase permanent-magnet machines under open-circuit and short-circuit faults. IEEE Trans. Power Electron. 2016, 31, 4684–4696. [Google Scholar] [CrossRef]
- Wang, B.; Hu, J.; Hua, W. Design process of a triple redundant fault tolerant PMA SynRM. IEEE Access 2019, 7, 76241–76249. [Google Scholar] [CrossRef]
- Dieterle, O.; Greiner, T.; Heidrich, P. Control of a PMSM with quadruple three-phase star-connected windings under inverter short-circuit fault. IEEE Trans. Ind.l Electron. 2019, 66, 685–695. [Google Scholar] [CrossRef]
- Shamsi-Nejad, M.; Nahid-Mobarakeh, B.; Pierfederici, S.; Meibody-Tabar, F. Fault tolerant and minimum loss control of double-star synchronous machines under open phase conditions. IEEE Trans. Ind. Electron. 2008, 55, 1956–1965. [Google Scholar] [CrossRef]
- Eldeeb, H.M.; Abdel-Khalik, A.S.; Hackl, C.M. Postfault full torque-speed exploitation of dual three-phase IPMSM drives. IEEE Trans. Ind. Electron. 2019, 66, 6746–6756. [Google Scholar] [CrossRef]
- Jing, G.; Zhou, C. Control strategy for a five-leg inverter supplying dual three-phase PMSM. IEEE Access 2020, 8, 174480–174488. [Google Scholar] [CrossRef]
- Munim, W.N.W.A.; Tousizadeh, M.; Che, H.S. Effects of zero-sequence transformations and min-max injection on fault-tolerant symmetrical six-phase drives with single isolated neutral. J. Power Electron. 2019, 19, 968–979. [Google Scholar] [CrossRef]
- Rubino, S.; Bojoi, R.; Odhano, S.A.; Zanchetta, P. Model predictive direct flux vector control of multi-three-phase induction motor drives. IEEE Trans. Ind. Appl. 2018, 54, 4394–4404. [Google Scholar] [CrossRef]
- Vu, D.T.; Nguyen, N.K.; Semail, E.; dos Santos Moraes, T.J. Control strategies for non-sinusoidal multiphase PMSM drives in faulty modes under constraints on copper losses and peak phase voltage. IET Electric Power Appl. 2019, 13, 1743–1752. [Google Scholar] [CrossRef] [Green Version]
- Hang, J.; Ren, X.; Tang, C.; Tong, M.; Ding, S. Fault-tolerant control strategy for five-phase PMSM drive system with high-resistance connection. IEEE Trans. Transport. Electrific. 2021, 7, 1390–1400. [Google Scholar] [CrossRef]
- Patel, V.I.; Wang, J.; Nair, S.S. Demagnetization assessment of fractional-slot and distributed wound 6-phase permanent magnet machines. IEEE Trans. Magn. 2015, 51, 1–11. [Google Scholar] [CrossRef]
- Nair, S.S.; Patel, V.I.; Wang, J. Post-demagnetization performance assessment for interior permanent magnet ac machines. IEEE Trans. Magn. 2016, 52, 1–10. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, Y.; Li, C.; Liu, C. Design and analysis of a new six-phase fault-tolerant hybrid-excitation motor for electric vehicles. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Keller, D.; Karayel, A.; Naumoski, H.; Parspour, N. Influence of static eccentricities on performance and control of dual three-phase permanent magnet synchronous machines. In Proceedings of the 2020 10th International Electric Drives Production Conference (EDPC), Ludwigsburg, Germany, 8–9 December 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Yang, K.; Akatsu, K.; Okazaki, K.; Miyama, Y. A method to suppress vibration due to dynamic eccentricity by using triple three-phase winding motor. In Proceedings of the 2021 IEEE International Electric Machines and Drives Conference (IEMDC), Hartford, CT, USA, 17–20 May 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Guzman, D.A.T.; Nguyen, N.K.; Trablesi, M.; Semail, E. Low speed sensorless control of non-salient poles multiphase PMSM. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, VIC, Australia, 13–15 February 2019; pp. 1563–1568. [Google Scholar] [CrossRef] [Green Version]
- Hezzi, A.; Ben Elghali, S.; Bensalem, Y.; Zhou, Z.; Benbouzid, M.; Abdelkrim, M.N. ADRC-based robust and resilient control of a 5-phase PMSM driven electric vehicle. Machines 2020, 8, 17. [Google Scholar] [CrossRef]
- Mengoni, M.; Zarri, L.; Tani, A.; Serra, G.; Casadei, D. Sensorless multiphase induction motor drive based on a speed observer operating with third-order field harmonics. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 68–74. [Google Scholar] [CrossRef]
- Mengoni, M.; Zarri, L.; Tani, A.; Serra, G.; Casadei, D. Sensorless speed observer based on third-order spatial field harmonic for multiphase induction motor drives. In Proceedings of the 2016 IEEE Symposium on Sensorless Control for Electrical Drives (SLED), Nadi, Fiji, 5–6 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Mengoni, M.; Zarri, L.; Tani, A.; Rizzoli, G.; Serra, G.; Casadei, D. Injection of third-order spatial field harmonics for sensorless speed estimation in multiphase induction motor drives. In Proceedings of the 2017 IEEE International Symposium on Sensorless Control for Electrical Drives (SLED), Catania, Italy, 18–19 September 2017; pp. 49–54. [Google Scholar] [CrossRef]
- Nguyen, N.K.; Semail, E.; De Belie, F.; Kestelyn, X. Adaline neural networks-based sensorless control of five-phase PMSM drives. In Proceedings of the IECON 2016 - 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 5741–5746. [Google Scholar] [CrossRef] [Green Version]
- Olivieri, C.; Fabri, G.; Tursini, M. Sensorless control of five-phase brushless dc motors. In Proceedings of the 2010 First Symposium on Sensorless Control for Electrical Drives, Padua, Italy, 9–10 July 2010; pp. 24–31. [Google Scholar] [CrossRef]
- Ramezani, M.; Ojo, O. The modeling and position-sensorless estimation technique for a nine-phase interior permanent-magnet machine using high-frequency injections. IEEE Trans. Ind. Appl. 2016, 52, 1555–1565. [Google Scholar] [CrossRef]
- Mossa, M.A.; Echeikh, H.; Iqbal, A.; Duc Do, T.; Al-Sumaiti, A.S. A novel sensorless control for multiphase induction motor drives based on singularly perturbed sliding mode observer-experimental validation. Appl. Sci. 2020, 10, 2776. [Google Scholar] [CrossRef] [Green Version]
- Zheng, L.; Fletcher, J.E.; Williams, B.W.; He, X. A novel direct torque control scheme for a sensorless five-phase induction motor drive. IEEE Trans. Ind. Electron. 2011, 58, 503–513. [Google Scholar] [CrossRef]
- Almarhoon, A.H.; Zhu, Z.Q.; Xu, P. Improved rotor position estimation accuracy by rotating carrier signal injection utilizing zero-sequence carrier voltage for dual three-phase PMSM. IEEE Trans. Ind. Electron. 2017, 64, 4454–4462. [Google Scholar] [CrossRef]
- Almarhoon, A.H.; Zhu, Z.Q.; Xu, P.L. Improved pulsating signal injection using zero-sequence carrier voltage for sensorless control of dual three-phase PMSM. IEEE Trans. Energy Convers. 2017, 32, 436–446. [Google Scholar] [CrossRef]
- Saad, K.; Abdellah, K.; Ahmed, H.; Iqbal, A. Investigation on SVM-backstepping sensorless control of five-phase open-end winding induction motor based on model reference adaptive system and parameter estimation. Eng. Sci. Technol. Int. 2019, 22, 1013–1026. [Google Scholar] [CrossRef]
- Khadar, S.; Abu-Rub, H.; Kouzou, A. Sensorless field-oriented control for open-end winding five-phase induction motor with parameters estimation. IEEE Open J. Ind. Electron. Soc. 2021, 2, 266–279. [Google Scholar] [CrossRef]
- Imai, K.; Valente, G.; Gerada, D. Initial position estimation method based on inductance spatial harmonic components for triple three-phase surface-mounted permanent magnet synchronous motor. Singapore, 18–21 October 2020; pp. 4845–4850. [Google Scholar] [CrossRef]
- Imai, K.; Valente, G.; Gerada, D. Position sensorless control for triple three-phase permanent magnet synchronous motor based on extended electromotive force model. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020; pp. 1977–1982. [Google Scholar] [CrossRef]
- Listwan, J.; Pieńkowski, K. Comparative analysis of control methods with model reference adaptive system estimators of a seven-phase induction motor with encoder failure. Energies 2021, 14, 1147. [Google Scholar] [CrossRef]
- Stiscia, O.; Slunjski, M.; Levi, E.; Cavagnino, A. Sensorless control of a nine-phase surface mounted permanent magnet synchronous machine with highly non-sinusoidal back-EMF. IEEE IECON 2019, 1, 1327–1332. [Google Scholar] [CrossRef]
- Slunjski, M.; Stiscia, O.; Jones, M.; Levi, E. General torque enhancement approach for a nine-phase surface PMSM with built-in fault tolerance. IEEE Trans. Ind. Electron. 2021, 68, 6412–6423. [Google Scholar] [CrossRef]
- Parsa, L.; Toliyat, H.A. Sensorless direct torque control of five-phase interior permanent-magnet motor drives. IEEE Trans. Ind. Appl. 2007, 43, 952–959. [Google Scholar] [CrossRef]
- Liu, G.; Geng, C.; Chen, Q. Sensorless control for five-phase IPMSM drives by injecting HF square-wave voltage signal into third harmonic space. IEEE Access 2020, 8, 69712–69721. [Google Scholar] [CrossRef]
- Yepes, A.G.; Baneira, F.; Malvar, J.; Vidal, A.; Pérez-Estévez, D.; Lopez, O.; Doval-Gandoy, J. Selection criteria of multiphase induction machines for speed-sensorless drives based on rotor slot harmonics. IEEE Trans. Ind. Electron. 2016, 63, 4663–4673. [Google Scholar] [CrossRef]
- Amin, M.; Aziz, G.A.A.; Durkin, J.; Al-Durra, A. A robust simplified dynamic observer-based backstepping control of six-phase induction motor for marine vessels applications. IEEE Trans. Ind. Appl. 2020, 56, 7044–7054. [Google Scholar] [CrossRef]
- Holakooie, M.H.; Ojaghi, M.; Taheri, A. Modified DTC of a six-phase induction motor with a second-order sliding-mode MRAS-based speed estimator. IEEE Trans. Power Electron. 2019, 34, 600–611. [Google Scholar] [CrossRef]
- Holakooie, M.H.; Iwanski, G. An adaptive identification of rotor time constant for speed-sensorless induction motor drives: A case study for six-phase induction machine. IEEE J. Emerg. Sel. Topics Power Electron. 2021, 9, 5452–5464. [Google Scholar] [CrossRef]
- Taheri, A.; Ren, H.P.; Holakooie, M.H. Sensorless loss model control of the six-phase induction motor in all speed range by extended kalman filter. IEEE Access 2020, 8, 118741–118750. [Google Scholar] [CrossRef]
- Li, G.; Taheri, A.; Ren, H.P.; Song, C.H. Sensorless direct torque control of the six-phase induction motor by fast reduced order extended kalman filter. Complexity 2020, 2, 1076–2787. [Google Scholar] [CrossRef]
- Tian, B.; An, Q.T.; Molinas, M. High-frequency injection-based sensorless control for a general five-phase BLDC motor incorporating system delay and phase resistance. IEEE Access 2019, 7, 162862–162873. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, X.; Gao, J.; Mao, Y. Design and analysis of new five-phase flux-intensifying fault-tolerant interior-permanent-magnet motor for sensorless operation. IEEE Trans. Ind. Electron. 2020, 67, 6055–6065. [Google Scholar] [CrossRef]
- Xu, J.; Du, Y.; Fang, H.; Guo, H.; Chen, Y. A robust observer and nonorthogonal PLL-based sensorless control for fault-tolerant permanent magnet motor with guaranteed postfault performance. IEEE Trans. Ind. Electron. 2020, 67, 5959–5970. [Google Scholar] [CrossRef]
- Xu, J.; Du, Y.; Zhang, B.; Fang, H.; Guo, H.; Chen, Y.H. Sensorless fault-tolerant control with phase delay compensation for aerospace FTPMSM drives with phase open-circuit and short-circuit faults. IEEE Trans. Ind. Electron. 2021, 68, 4576–4585. [Google Scholar] [CrossRef]
- Green, S.; Atkinson, D.; Jack, A.G.; Mecrow, B.C.; King, A. Sensorless operation of a fault tolerant PM drive. IEE Proc. Electric Power Appl. 2003, 150, 117–125. [Google Scholar] [CrossRef]
- Geng, Y.; Lai, Z.; Li, Y.; Wang, D.; Chen, R.; Zheng, P. Sensorless fault-tolerant control strategy of six-phase induction machine based on harmonic suppression and sliding mode observer. IEEE Access 2019, 7, 110086–110102. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J.; Baneira, F.; Toliyat, H.A. Speed estimation based on rotor slot harmonics in multiphase induction machines under open-phase fault. IEEE Trans. Power Electron. 2018, 33, 7980–7993. [Google Scholar] [CrossRef]
- Barcaro, M.; Faggion, A.; Bianchi, N.; Bolognani, S. Sensorless rotor position detection capability of a dual three-phase fractional-slot IPM machine. IEEE Trans. Ind. Appl. 2012, 48, 2068–2078. [Google Scholar] [CrossRef]
- Tian, B.; Molinas, M.; An, Q.; Zhou, B.; Wei, J. Freewheeling current-based sensorless field-oriented control of five-phase permanent magnet synchronous motors under insulated gate bipolar transistor failures of a single phase. IEEE Trans. Ind. Electron. 2022, 69, 213–224. [Google Scholar] [CrossRef]
- De Belie, F.; Kestelyn, X.; Nguyen, N.K. Fault-tolerant optimal-current torque-controlled five-phase PMSMs with open-circuited phases: Position self-sensing operation. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Kong, W.; Huang, J.; Li, B.; Zhao, L. Sensorless vector control of five-phase induction motor under open-phases fault. Electr. Power Compon. Syst. 2014, 42, 1039–1047. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, Y.; Li, C.; Nied, A.; Cheng, M. Fault-tolerant sensorless control of a five-phase FTFSCW-IPM motor based on a wide-speed strong-robustness sliding mode observer. IEEE Trans. Energy Convers. 2018, 33, 87–95. [Google Scholar] [CrossRef]
- Wu, F.; Tong, C.; Sui, Y.; Cheng, L.; Zheng, P. Influence of third harmonic back EMF on modeling and remediation of winding short circuit in a multiphase PM machine with FSCWs. IEEE Trans. Ind. Electron. 2016, 63, 6031–6041. [Google Scholar] [CrossRef]
- Tong, C.; Wu, F.; Zheng, P.; Yu, B.; Sui, Y.; Cheng, L. Investigation of magnetically isolated multiphase modular permanent-magnet synchronous machinery series for wheel-driving electric vehicles. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Arumugam, P.; Hamiti, T.; Brunson, C.; Gerada, C. Analysis of vertical strip wound fault-tolerant permanent magnet synchronous machines. IEEE Trans. Ind. Electron. 2014, 61, 1158–1168. [Google Scholar] [CrossRef]
- Arumugam, P.; Hamiti, T.; Gerada, C. Turn–turn short circuit fault management in permanent magnet machines. IET Electric Power Appl. 2015, 9, 634–641. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Griffo, A.; Huang, L. A turn fault mitigation strategy based on current injection technique for a triple three-phase PMA SynRM. IEEE Trans. Ind. Electron. 2020, 67, 2511–2522. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Zheng, P.; Sui, Y.; Yu, B.; Wang, P. Design and experimental verification of a short-circuit proof six-phase permanent magnet machine for safety critical applications. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Mitcham, A.J.; Antonopoulos, G.; Cullen, J.J.A. Favourable slot and pole number combinations for fault-tolerant PM machines. IEE Proc. Electr. Power Appl. 2004, 151, 520–525. [Google Scholar] [CrossRef]
- Mitcham, A.J.; Antonopoulos, G.; Cullen, J.J.A. Implications of shorted turn faults in bar wound PM machines. IEE Proc. Electr. Power Appl. 2004, 151, 651–657. [Google Scholar] [CrossRef]
- Atkinson, G.; Mecrow, B.; Jack, A.; Atkinson, D.; Sangha, P.; Benarous, M. The analysis of losses in high-power fault-tolerant machines for aerospace applications. IEEE Trans. Ind. Appl. 2006, 42, 1162–1170. [Google Scholar] [CrossRef]
- Cavagnino, A.; Li, Z.; Tenconi, A.; Vaschetto, S. Integrated generator for more electric engine: Design and testing of a scaled-size prototype. IEEE Trans. Ind. Appl. 2013, 49, 2034–2043. [Google Scholar] [CrossRef]
- Vaseghi, B.; Takorabet, N.; Caron, J.P.; Nahid-Mobarakeh, B.; Meibody-Tabar, F.; Humbert, G. Study of different architectures of fault-tolerant actuator using a two-channel PM motor. IEEE Trans. Ind. Appl. 2011, 47, 47–54. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, S.; Li, Q.; Gao, Y. Design and optimization of dual-winding fault-tolerant permanent magnet motor. CES Trans. Electr. Mach. Syst. 2019, 3, 45–53. [Google Scholar] [CrossRef]
- Prieto, B.; Martínez-Iturralde, M.; Fontán, L.; Elosegui, I. Fault-tolerant permanent magnet synchronous machine – phase, pole and slot number selection criterion based on inductance calculation. IET Electric Power Appl. 2015, 9, 138–149. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Pré, M.D.; Grezzani, G. Design considerations for fractional-slot winding configurations of synchronous machines. IEEE Trans. Ind. Appl. 2006, 42, 997–1006. [Google Scholar] [CrossRef]
- Yin, Z.; Sui, Y.; Zheng, P.; Yang, S.; Zheng, Z.; Huang, J. Short-circuit fault-tolerant control without constraint on the D-axis armature magnetomotive force for five-phase PMSM. IEEE Trans. Ind. Electron. 2022, 69, 4472–4483. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Griffo, A. Stator turn fault modeling for a triple redundant 3×3-phase PMA SynRM. IEEE Trans. Ind. Electron. 2019, 66, 4220–4230. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Griffo, A.; Hua, W. Effective turn fault mitigation by creating zero sequence current path for a triple redundant 3×3-phase PMA SynRM. IEEE Trans. Power Electron. 2019, 34, 11080–11089. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, J.; Wang, B. Electromagnetic-thermal coupled simulation under various fault conditions of a triple redundant 9-phase PMASynRM. IEEE Trans. Ind. Appl. 2020, 56, 128–137. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, J.; Wang, B. Transient 3-D lumped parameter and 3-D FE thermal models of a PMASynRM under fault conditions with asymmetric temperature distribution. IEEE Trans. Ind. Electron. 2021, 68, 4623–4633. [Google Scholar] [CrossRef]
- Si, B.; Fu, Q.; Wang, T.; Gao, C.; Zhu, J. Twofold fail-work remedy for reconfigurable driver and windings of four-phase permanent magnet fault-tolerant motor system. IEEE Trans. Power Electron. 2019, 34, 7763–7774. [Google Scholar] [CrossRef]
- Mecrow, B.C.; Jack, A.G.; Haylock, J.A.; Coles, J. Fault-tolerant permanent magnet machine drives. IEE Proc. Electr. Power Appl. 1996, 143, 437–442. [Google Scholar] [CrossRef]
- Huang, J.; Hao, Y.; Sui, Y.; Yin, Z.; Cheng, L.; Zheng, P. Compensation strategy based on rotating rhombus method for five-phase PMSM with one-phase terminal short-circuit fault. IEEE Trans. Magn. 2021, 57, 1–5. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Griffo, A.; Sen, B. Experimental assessments of a triple redundant nine-phase fault-tolerant PMA SynRM drive. IEEE Trans. Ind. Electron. 2019, 66, 772–783. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Hu, J.; Hua, W.; Wang, Z. Fault operation analysis of a triple-redundant three-phase PMA-SynRM for EV application. IEEE Trans. Transport. Electrific. 2021, 7, 183–192. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Sen, B.; Griffo, A.; Sun, Z.; Chong, E. A fault-tolerant machine drive based on permanent magnet-assisted synchronous reluctance machine. IEEE Trans. Ind. Appl. 2018, 54, 1349–1359. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Griffo, A.; Sen, B. A general modeling technique for a triple redundant 3×3-phase PMA SynRM. IEEE Trans. Ind. Electron. 2018, 65, 9068–9078. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Vakil, G.; Liu, Y.; Yang, T.; Zhang, Z.; Gerada, C. Optimization and analysis of a high power density and fault tolerant starter–generator for aircraft application. Energies 2021, 14, 113. [Google Scholar] [CrossRef]
- Park, J.K.; Babetto, C.; Berardi, G.; Hur, J.; Bianchi, N. Comparison of fault characteristics according to winding configurations for dual three-phase synchronous reluctance motor. IEEE Trans. Ind. Appl. 2021, 57, 2398–2406. [Google Scholar] [CrossRef]
- Fan, Y.; Cui, R.; Zhang, A. Torque ripple minimization for inter-turn short-circuit fault based on open-winding five phase FTFSCW-IPM motor for electric vehicle application. IEEE Trans. Veh. Technol. 2020, 69, 282–292. [Google Scholar] [CrossRef]
- Chen, H.; Liu, X.; Zhao, J.; Demerdash, N.A.O. Magnetic-coupling characteristics investigation of a dual-rotor fault-tolerant PMSM. IEEE Trans. Energy Convers. 2018, 33, 362–372. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, G.; Zhao, W.; Sun, L.; Shao, M.; Liu, Z. Design and comparison of two fault-tolerant interior-permanent-magnet motors. IEEE Trans. Ind. Electron. 2014, 61, 6615–6623. [Google Scholar] [CrossRef]
- Mohammadpour, A.; Mishra, S.; Parsa, L. Fault-tolerant operation of multiphase permanent-magnet machines using iterative learning control. IEEE J. Emerg. Sel. Topics Power Electron. 2014, 2, 201–211. [Google Scholar] [CrossRef]
- Mohammadpour, A.; Parsa, L. Global fault-tolerant control technique for multiphase permanent-magnet machines. IEEE Trans. Ind. Appl. 2015, 51, 178–186. [Google Scholar] [CrossRef]
- Gerada, C.; Bradley, K.; Sumner, M.; Wheeler, P.; Picker, S.; Clare, J.; Whitley, C.; Towers, G. The results do mesh. IEEE Ind. Appl. Mag. 2007, 13, 62–72. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Pre, M.D. Strategies for the fault-tolerant current control of a five-phase permanent-magnet motor. IEEE Trans. Ind. Appl. 2007, 43, 960–970. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, H.; Wang, G.; Liu, G. Unified decoupling vector control of five-phase permanent-magnet motor with double-phase faults. IEEE Access 2020, 8, 152646–152658. [Google Scholar] [CrossRef]
- Zhou, H.; Xu, J.; Chen, C.; Tian, X.; Liu, G. Disturbance-observer-based direct torque control of five-phase permanent magnet motor under open-circuit and short-circuit faults. IEEE Trans. Ind. Electron. 2021, 68, 11907–11917. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, G.; Zhao, W.; Yu, X.; Gao, M. Dynamic performance improvement of five-phase permanent-magnet motor with short-circuit fault. IEEE Trans. Ind. Electron. 2018, 65, 145–155. [Google Scholar] [CrossRef]
- Barcaro, M.; Bianchi, N.; Magnussen, F. Analysis and tests of a dual three-phase 12-slot 10-pole permanent-magnet motor. IEEE Trans. Ind. Appl. 2010, 46, 2355–2362. [Google Scholar] [CrossRef]
- Barcaro, M.; Bianchi, N.; Magnussen, F. Faulty operations of a PM fractional-slot machine with a dual three-phase winding. IEEE Trans. Ind. Electron. 2011, 58, 3825–3832. [Google Scholar] [CrossRef]
- Madonna, V.; Giangrande, P.; Gerada, C.; Galea, M. Thermal analysis of fault-tolerant electrical machines for aerospace actuators. IET Electric Power Appl. 2019, 13, 843–852. [Google Scholar] [CrossRef]
- Alberti, L.; Bianchi, N. Experimental tests of dual three-phase induction motor under faulty operating condition. IEEE Trans. Ind. Electron. 2012, 59, 2041–2048. [Google Scholar] [CrossRef]
- Li, W.; Cheng, M. Investigation of influence of winding structure on reliability of permanent magnet machines. CES Trans. Electr. Mach. Syst. 2020, 4, 87–95. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, Y.; Lorenz, R.D.; Nied, A.; Cheng, M. Design and comparison of three-phase and five-phase FTFSCW-IPM motor open-end winding drive systems for electric vehicles applications. IEEE Trans. Veh. Technol. 2018, 67, 385–396. [Google Scholar] [CrossRef]
- Zheng, P.; Sui, Y.; Zhao, J.; Tong, C.; Lipo, T.A.; Wang, A. Investigation of a novel five-phase modular permanent-magnet in-wheel motor. IEEE Trans. Magn. 2011, 47, 4084–4087. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, B.; Fang, H.; Guo, H. Guaranteeing the fault transient performance of aerospace multiphase permanent magnet motor system: An adaptive robust speed control approach. CES Trans. Electr. Mach. Syst. 2020, 4, 114–122. [Google Scholar] [CrossRef]
- Mecrow, B.C.; Jack, A.G.; Atkinson, D.J.; Green, S.R.; Atkinson, G.J.; King, A.; Green, B. Design and testing of a four-phase fault-tolerant permanent-magnet machine for an engine fuel pump. IEEE Trans. Energy Convers. 2004, 19, 671–678. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, B. Design and analysis of a five-phase fault-tolerant permanent magnet synchronous motor for aerospace starter-generator system. IEEE Access 2019, 7, 135040–135049. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, M.; Tang, L.; Xu, W.; Islam, M.R. Fault-tolerant analysis and design of AFPMSM with multi-disc type coreless open-end winding. IEEE Access 2020, 8, 171744–171753. [Google Scholar] [CrossRef]
- Bastos, R.R.; de Souza, T.S.; de Carvalho, M.M.; Silva, L.A.R.; Filho, B.J.C. Assessment of a nine-phase induction motor drive for metal industry applications. IEEE Trans. Ind. Appl. 2020, 56, 7217–7226. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, J.; Wang, B. Performance assessment of triple redundant nine-phase delta- and wye-connected permanent magnet-assisted synchronous reluctance motor under healthy and fault conditions. J. Eng. Technol. 2019, 2019, 3563–3567. [Google Scholar] [CrossRef]
- Apsley, J.; Williamson, S. Analysis of multiphase induction machines with winding faults. IEEE Trans. Ind. Appl. 2006, 42, 465–472. [Google Scholar] [CrossRef]
- Guo, H.; Xu, J.; Chen, Y.H. Robust control of fault-tolerant permanent-magnet synchronous motor for aerospace application with guaranteed fault switch process. IEEE Trans. Ind. Electron. 2015, 62, 7309–7321. [Google Scholar] [CrossRef]
- Nguyen, N.K.; Meinguet, F.; Semail, E.; Kestelyn, X. Fault-tolerant operation of an open-end winding five-phase PMSM drive with short-circuit inverter fault. IEEE Trans. Ind. Electron. 2016, 63, 595–605. [Google Scholar] [CrossRef] [Green Version]
- Reddy, B.P.; Rao A, M.; Sahoo, M.; Keerthipati, S. A fault-tolerant multilevel inverter for improving the performance of a pole-phase modulated nine-phase induction motor drive. IEEE Trans. Ind. Electron. 2018, 65, 1107–1116. [Google Scholar] [CrossRef]
- Kumar, P.; Rathore, V.; Yadav, K.B. Fault tolerance study of symmetrical six-phase induction drive. In Proceedings of the 2020 1st IEEE International Conference on Measurement, Instrumentation, Control and Automation (ICMICA), Kurukshetra, India, 24–26 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Cheng, M.; Hu, Y. Comprehensive investigation on remedial operation of switch faults for dual three-phase PMSM drives fed by T-3L inverters. IEEE Trans. Ind. Electron. 2018, 65, 4574–4587. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Gu, M.; Xu, Z.; Zou, Z.; Wang, W.; Cheng, M. Fault-tolerant control of common electrical faults in dual three-phase PMSM drives fed by T-type three-level inverters. IEEE Trans. Ind. Appl. 2021, 57, 481–491. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Cheng, M.; Li, S. Fault-tolerant control of dual three-phase permanent-magnet synchronous machine drives under open-phase faults. IEEE Trans. Power Electron. 2017, 32, 2052–2063. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Cheng, M.; Hu, Y. Remedial strategies of T-NPC three-level asymmetric six-phase PMSM drives based on SVM-DTC. IEEE Trans. Ind. Electron. 2017, 64, 6841–6853. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Wang, Z.; Gu, M.; Xiao, D.; He, J.; Emadi, A. Diagnosis-free self-healing scheme for open-circuit faults in dual three-phase PMSM drives. IEEE Trans. Power Electron. 2020, 35, 12053–12071. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Xu, Z.; Wang, W.; Wang, B.; Zou, Z. Deadbeat predictive current control-based fault-tolerant scheme for dual three-phase PMSM drives. IEEE J. Emerg. Sel. Topics Power Electron. 2021, 9, 1591–1604. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. Pre- and post-fault tolerant operation of a six-phase PMSM motor using FCS-MPC without controller reconfiguration. IEEE Trans. Veh. Technol. 2019, 68, 254–263. [Google Scholar] [CrossRef]
- Feng, G.; Lai, C.; Li, W.; Han, Y.; Kar, N.C. Computation-efficient solution to open-phase fault tolerant control of dual three-phase interior PMSMs with maximized torque and minimized ripple. IEEE Trans. Power Electron. 2021, 36, 4488–4499. [Google Scholar] [CrossRef]
- Feng, G.; Lai, C.; Li, W.; Tjong, J.; Kar, N.C. Open-phase fault modeling and optimized fault-tolerant control of dual three-phase permanent magnet synchronous machines. IEEE Trans. Power Electron. 2019, 34, 11116–11127. [Google Scholar] [CrossRef]
- Feng, G.; Lu, Y.; Lai, C.; Ding, B.; Kar, N. Fault tolerant maximum torque per ampere (FT-MTPA) control for dual three-phase interior PMSMs under open-phase fault. IEEE Trans. Ind. Electron. accepted for publication. 2022. [Google Scholar] [CrossRef]
- Li, W.; Feng, G.; Li, Z.; Tjong, J.; Kar, N.C. Multireference frame based open-phase fault modeling and control for asymmetrical six-phase interior permanent magnet motors. IEEE Trans. Power Electron. 2021, 36, 11712–11725. [Google Scholar] [CrossRef]
- Gonçalves, P.F.; Cruz, S.M.; Mendes, A.M. Design of a six-phase asymmetrical permanent magnet synchronous generator for wind energy applications. J. Eng. Technol. 2019, 2019, 4532–4536. [Google Scholar] [CrossRef]
- Harikumaran, J.; Buticchi, G.; Galea, M.; Wheeler, P. Open phase fault tolerant control of multi three phase machines. IEEE Open J. Power Electron. 2021, 2, 535–544. [Google Scholar] [CrossRef]
- Vu, D.T.; Nguyen, N.K.; Semail, E. Fault-tolerant control for nonsinusoidal multiphase drives with minimum torque ripple. IEEE Trans. Power Electron. 2022, 37, 6290–6304. [Google Scholar] [CrossRef]
- de Souza, T.S.; Bastos, R.R.; Cardoso Filho, B.J. Modeling and control of a nine-phase induction machine with open phases. IEEE Trans. Ind. Appl. 2018, 54, 6576–6585. [Google Scholar] [CrossRef]
- Mekri, F.; Benelghali, S.; Benbouzid, M.; Charpentier, J.F. A fault-tolerant multiphase permanent magnet generator for marine current turbine applications. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 2079–2084. [Google Scholar] [CrossRef] [Green Version]
- Kianinezhad, R.; Nahid-Mobarakeh, B.; Baghli, L.; Betin, F.; Capolino, G.A. Modeling and control of six-phase symmetrical induction machine under fault condition due to open phases. IEEE Trans. Ind. Electron. 2008, 55, 1966–1977. [Google Scholar] [CrossRef]
- Fnaiech, M.A.; Betin, F.; Capolino, G.A.; Fnaiech, F. Fuzzy logic and sliding-mode controls applied to six-phase induction machine with open phases. IEEE Trans. Ind. Electron. 2010, 57, 354–364. [Google Scholar] [CrossRef]
- Betin, F.; Capolino, G. Shaft positioning for six-phase induction machines with open phases using variable structure control. IEEE Trans. Ind. Electron. 2012, 59, 2612–2620. [Google Scholar] [CrossRef]
- Mekri, F.; Ben Elghali, S.; Benbouzid, M.E.H. Fault-tolerant control performance comparison of three- and five-phase pmsg for marine current turbine applications. IEEE Trans. Sustain. Energy 2013, 4, 425–433. [Google Scholar] [CrossRef]
- Tani, A.; Mengoni, M.; Zarri, L.; Serra, G.; Casadei, D. Control of multiphase induction motors with an odd number of phases under open-circuit phase faults. IEEE Trans. Power Electron. 2012, 27, 565–577. [Google Scholar] [CrossRef]
- Lee, K.; Li, L.; Bai, K.; Ouyang, X.; Yang, H. Harmonic model and remedy strategy of multiphase PM motor under open-circuit fault. IEEE/ASME Trans. Mechatronics 2019, 24, 1407–1419. [Google Scholar] [CrossRef]
- de Souza, T.S.; Bastos, R.R.; Cardoso Filho, B.J. Synchronous-frame modeling and dq current control of an unbalanced nine-phase induction motor due to open phases. IEEE Trans. Ind. Appl. 2020, 56, 2097–2106. [Google Scholar] [CrossRef]
- Hu, Y.; Zhu, Z.Q.; Wu, Z.Y. Modelling and vector control of dual three-phase PMSM with one-phase open. IET Electric Power Appl. 2021, 15, 847–860. [Google Scholar] [CrossRef]
- Hu, Y.; Feng, Y.; Li, X. Fault-tolerant hybrid current control of dual three-phase PMSM with one phase open. IEEE J. Emerg. Sel. Topics Power Electron. accepted for publication. 2020. [Google Scholar] [CrossRef]
- Cervone, A.; Dordevic, O.; Brando, G. General approach for modelling and control of multiphase PMSM drives. IEEE Trans. Power Electron. 2021, 36, 10490–10503. [Google Scholar] [CrossRef]
- Li, Z.; Wu, L.; Chen, Z.; Shi, Y.; Qiu, L.; Fang, Y. Single- and two-phase open-circuit fault tolerant control for dual three-phase PM motor without phase shifting. IEEE Access 2020, 8, 171945–171955. [Google Scholar] [CrossRef]
- Kuang, Z.; Wu, S.; Du, B.; Xu, H.; Cui, S.; Chan, C.C. Thermal analysis of fifteen-phase permanent magnet synchronous motor under different fault tolerant operations. IEEE Access 2019, 7, 81466–81480. [Google Scholar] [CrossRef]
- Tursini, M.; Villani, M.; Di Tullio, A.; Fabri, G.; Collazzo, F.P. Nonlinear model suitable for the offline cosimulation of fault-tolerant PM motors drives. IEEE Trans. Ind. Appl. 2017, 53, 3719–3729. [Google Scholar] [CrossRef]
- Gu, C.; Yan, H.; Yang, J.; Sala, G.; De Gaetano, D.; Wang, X.; Galassini, A.; Degano, M.; Zhang, X.; Buticchi, G. A multiport power conversion system for the more electric aircraft. IEEE Trans. Transport. Electrific. 2020, 6, 1707–1720. [Google Scholar] [CrossRef]
- Schiestl, M.; Marcolini, F.; Incurvati, M.; Capponi, F.G.; Stärz, R.; Caricchi, F.; Rodriguez, A.S.; Wild, L. Development of a high power density drive system for unmanned aerial vehicles. IEEE Trans. Power Electron. 2021, 36, 3159–3171. [Google Scholar] [CrossRef]
- Golovanov, D.; Gerada, D.; Sala, G.; Degano, M.; Trentin, A.; Connor, P.H.; Xu, Z.; La Rocca, A.; Galassini, A.; Tarisciotti, L.; et al. 4MW class high-power-density generator for future hybrid-electric aircraft. IEEE Trans. Transport. Electrific. 2021, 7, 2952–2964. [Google Scholar] [CrossRef]
- Eldeeb, H.M.; Abdel-Khalik, A.S.; Kullick, J.; Hackl, C.M. Pre- and postfault current control of dual three-phase reluctance synchronous drives. IEEE Trans. Ind. Electron. 2020, 67, 3361–3373. [Google Scholar] [CrossRef]
- Arafat, A.K.M.; Choi, S. Optimal phase advance under fault-tolerant control of a five-phase permanent magnet assisted synchronous reluctance motor. IEEE Trans. Ind. Electron. 2018, 65, 2915–2924. [Google Scholar] [CrossRef]
- Fu, J.R.; Lipo, T.A. Disturbance-free operation of a multiphase current-regulated motor drive with an opened phase. IEEE Trans. Ind. Appl. 1994, 30, 1267–1274. [Google Scholar] [CrossRef]
- Che, H.S.; Duran, M.J.; Levi, E.; Jones, M.; Hew, W.P.; Abd Rahim, N. Postfault operation of an asymmetrical six-phase induction machine with single and two isolated neutral points. IEEE Trans. Power Electron. 2014, 29, 5406–5416. [Google Scholar] [CrossRef] [Green Version]
- Munim, W.N.W.A.; Duran, M.J.; Che, H.S.; Bermúdez, M.; Gonzalez-Prieto, I.; Rahim, N.A. A unified analysis of the fault tolerance capability in six-phase induction motor drives. IEEE Trans. Power Electron. 2017, 32, 7824–7836. [Google Scholar] [CrossRef]
- Baneira, F.; Doval-Gandoy, J.; Yepes, A.G.; Lopez, O.; Pérez-Estévez, D. Control strategy for multiphase drives with minimum losses in the full torque operation range under single open-phase fault. IEEE Trans. Power Electron. 2017, 32, 6275–6285. [Google Scholar] [CrossRef]
- Baneira, F.; Doval-Gandoy, J.; Yepes, A.G.; Lopez, O.; Pérez-Estévez, D. Comparison of postfault control strategies in terms of converter losses for dual three-phase machines. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 3612–3619. [Google Scholar] [CrossRef]
- Baneira, F.; Doval-Gandoy, J.; Yepes, A.G.; Lopez, O.; Pérez-Estévez, D. Comparison of postfault strategies for current reference generation for dual three-phase machines in terms of converter losses. IEEE Trans. Power Electron. 2017, 32, 8243–8246. [Google Scholar] [CrossRef]
- Liang, Z.; Liang, D.; Kou, P.; Jia, S. Postfault control and harmonic current suppression for a symmetrical dual three-phase SPMSM drive under single-phase open-circuit fault. IEEE Access 2020, 8, 67674–67686. [Google Scholar] [CrossRef]
- Guzman, H.; Duran, M.J.; Barrero, F. A comprehensive fault analysis of a five-phase induction motor drive with an open phase. In Proceedings of the 2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012; pp. LS5b.3–1–LS5b.3–6. [Google Scholar] [CrossRef]
- Guzman, H.; Duran, M.J.; Barrero, F.; Bogado, B.; Toral, S. Speed control of five-phase induction motors with integrated open-phase fault operation using model-based predictive current control techniques. IEEE Trans. Ind. Electron. 2014, 61, 4474–4484. [Google Scholar] [CrossRef]
- Shawier, A.; Abdel-Khalik, A.S.; Hamdy, R.A.; Ahmed, K.H.; Ahmed, S. Postfault operation of five-phase induction machine with minimum total losses under single open-phase fault. IEEE Access 2020, 8, 208696–208706. [Google Scholar] [CrossRef]
- Mossa, M.A.; Echeikh, H.; Diab, A.A.Z.; Haes Alhelou, H.; Siano, P. Comparative study of hysteresis controller, resonant controller and direct torque control of five-phase IM under open-phase fault operation. Energies 2021, 14, 1317. [Google Scholar] [CrossRef]
- Guzman, H.; Duran, M.J.; Barrero, F.; Zarri, L.; Bogado, B.; Gonzalez Prieto, I.; Arahal, M.R. Comparative study of predictive and resonant controllers in fault-tolerant five-phase induction motor drives. IEEE Trans. Ind. Electron. 2016, 63, 606–617. [Google Scholar] [CrossRef]
- Bermudez, M.; Gonzalez-Prieto, I.; Barrero, F.; Guzman, H.; Kestelyn, X.; Duran, M.J. An experimental assessment of open-phase fault-tolerant virtual-vector-based direct torque control in five-phase induction motor drives. IEEE Trans. Power Electron. 2018, 33, 2774–2784. [Google Scholar] [CrossRef] [Green Version]
- Barrero, F.; Bermudez, M.; Duran, M.J.; Salas, P.; Gonzalez-Prieto, I. Assessment of a universal reconfiguration-less control approach in open-phase fault operation for multiphase drives. Energies 2019, 12, 4698. [Google Scholar] [CrossRef] [Green Version]
- Chikondra, B.; Muduli, U.R.; Behera, R.K. An improved open-phase fault-tolerant DTC technique for five-phase induction motor drive based on virtual vectors assessment. IEEE Trans. Ind. Electron. 2021, 68, 4598–4609. [Google Scholar] [CrossRef]
- Kong, W.; Kang, M.; Li, D.; Qu, R.; Jiang, D.; Gan, C. Investigation of spatial harmonic magnetic field coupling effect on torque ripple for multiphase induction motor under open fault condition. IEEE Trans. Power Electron. 2018, 33, 6060–6071. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, X.; Zheng, Z.; Jiang, D.; Li, Y. Optimized current trajectory tracking control of a five-phase induction machine under asymmetrical current limits. IEEE Trans. Power Electron. 2020, 35, 5290–5303. [Google Scholar] [CrossRef]
- Guzman, H.; Barrero, F.; Duran, M.J. IGBT-gating failure effect on a fault-tolerant predictive current-controlled five-phase induction motor drive. IEEE Trans. Ind. Electron. 2015, 62, 15–20. [Google Scholar] [CrossRef] [Green Version]
- Bermudez, M.; Gonzalez-Prieto, I.; Barrero, F.; Guzman, H.; Duran, M.J.; Kestelyn, X. Open-phase fault-tolerant direct torque control technique for five-phase induction motor drives. IEEE Trans. Ind. Electron. 2017, 64, 902–911. [Google Scholar] [CrossRef] [Green Version]
- He, S.; Sui, X.; Liu, Z.; Kang, M.; Zhou, D.; Blaabjerg, F. Torque ripple minimization of a five-phase induction motor under open-phase faults using symmetrical components. IEEE Access 2020, 8, 114675–114691. [Google Scholar] [CrossRef]
- Baudart, F.; Dehez, B.; Matagne, E.; Telteu-Nedelcu, D.; Alexandre, P.; Labrique, F. Torque control strategy of polyphase permanent-magnet synchronous machines with minimal controller reconfiguration under open-circuit fault of one phase. IEEE Trans. Ind. Electron. 2012, 59, 2632–2644. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, X.; Cheng, M. A fault-tolerant direct torque control for six-phase permanent magnet synchronous motor with arbitrary two opened phases based on modified variables. IEEE Trans. Energy Convers. 2016, 31, 549–556. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, Z.; Li, Y. Enhancing fault-tolerant ability of a nine-phase induction motor drive system using fuzzy logic current controllers. IEEE Trans. Energy Convers. 2017, 32, 759–769. [Google Scholar] [CrossRef]
- Nounou, K.; Benbouzid, M.; Marouani, K.; Charpentier, J.F.; Kheloui, A. Performance comparison of open-circuit fault-tolerant control strategies for multiphase permanent magnet machines for naval applications. Electr. Eng. 2018, 100, 1827–1836. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Hamdy, R.A.; Massoud, A.M.; Ahmed, S. Postfault control of scalar (V/f) controlled asymmetrical six-phase induction machines. IEEE Access 2018, 6, 59211–59220. [Google Scholar] [CrossRef]
- Gonzalez-Prieto, I.; Duran, M.J.; Bermudez, M.; Barrero, F.; Martín, C. Assessment of virtual-voltage-based model predictive controllers in six-phase drives under open-phase faults. IEEE J. Emerg. Sel. Topics Power Electron. 2020, 8, 2634–2644. [Google Scholar] [CrossRef]
- Gonzalez-Prieto, A.; Gonzalez-Prieto, I.; Duran, M.J.; Barrero, F. Efficient model predictive control with natural fault-tolerance in asymmetrical six-phase induction machines. Energies 2019, 12, 3989. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Prieto, A.; Aciego, J.J.; Gonzalez-Prieto, I.; Duran, M.J. Automatic fault-tolerant control of multiphase induction machines: A game changer. Electronics 2020, 9, 938. [Google Scholar] [CrossRef]
- Gonzalez-Prieto, I.; Duran, M.J.; Garcia-Entrambasaguas, P.; Bermudez, M. Field-oriented control of multiphase drives with passive fault tolerance. IEEE Trans. Ind. Electron. 2020, 67, 7228–7238. [Google Scholar] [CrossRef]
- Gonzalez-Prieto, I.; Duran, M.J.; Barrero, F.; Bermudez, M.; Guzmán, H. Impact of postfault flux adaptation on six-phase induction motor drives with parallel converters. IEEE Trans. Power Electron. 2017, 32, 515–528. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Prieto, I.; Duran, M.J.; Che, H.S.; Levi, E.; Bermudez, M.; Barrero, F. Fault-tolerant operation of six-phase energy conversion systems with parallel machine-side converters. IEEE Trans. Power Electron. 2016, 31, 3068–3079. [Google Scholar] [CrossRef] [Green Version]
- Duran, M.J.; Gonzalez-Prieto, I.; Bermudez, M.; Barrero, F.; Guzman, H.; Arahal, M.R. Optimal fault-tolerant control of six-phase induction motor drives with parallel converters. IEEE Trans. Ind. Electron. 2016, 63, 629–640. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J.; Toliyat, H. Improvement of postfault performance of multiphase drives in terms of operating region and stator copper loss. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 5819–5824. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J.; Toliyat, H.A. Strategy with smooth transitions and improved torque-speed region and stator copper loss for two-level asymmetrical six-phase induction motor drives under switch faults. IEEE Trans. Power Electron. 2021, 36, 1954–1969. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J.; Baneira, F.; Toliyat, H. Comparison of stator winding connections in multiphase drives under healthy operation and with one open converter leg. IET Electric Power Appl. 2020, 14, 584–596. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, G. Predictive DTC strategy with fault-tolerant function for six-phase and three-phase PMSM series-connected drive system. IEEE Trans. Ind. Electron. 2018, 65, 9101–9112. [Google Scholar] [CrossRef]
- Chai, F.; Gao, L.; Yu, Y.; Liu, Y. Fault-tolerant control of modular permanent magnet synchronous motor under open-circuit faults. IEEE Access 2019, 7, 154008–154017. [Google Scholar] [CrossRef]
- Lu, H.; Li, J.; Qu, R.; Ye, D.; Xiao, L. Reduction of unbalanced axial magnetic force in postfault operation of a novel six-phase double-stator axial-flux PM machine using model predictive control. IEEE Trans. Ind. Appl. 2017, 53, 5461–5469. [Google Scholar] [CrossRef]
- Lu, H.; Li, J.; Qu, R.; Ye, D. Fault-tolerant predictive current control with two-vector modulation for six-phase permanent magnet synchronous machine drives. IET Electric Power Appl. 2018, 12, 169–178. [Google Scholar] [CrossRef]
- Lu, H.; Li, J.; Qu, R.; Ye, D.; Lu, Y. Fault-tolerant predictive control of six-phase PMSM drives based on pulsewidth modulation. IEEE Trans. Ind. Electron. 2019, 66, 4992–5003. [Google Scholar] [CrossRef]
- He, S.; Sui, X.; Zhou, D.; Blaabjerg, F. Zero torque ripple operation of seven-phase concentrated-full-pitch winding induction motor under open circuit faults. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, Netherlands, 17–19 June 2020; pp. 380–385. [Google Scholar] [CrossRef]
- Ye, D.; Li, J.; Chen, J.; Qu, R.; Xiao, L. Study on steady-state errors for asymmetrical six-phase permanent magnet synchronous machine fault-tolerant predictive current control. IEEE Trans. Power Electron. 2020, 35, 640–651. [Google Scholar] [CrossRef]
- Sun, J.; Liu, Z.; Zheng, Z.; Li, Y. An online global fault-tolerant control strategy for symmetrical multiphase machines with minimum losses in full torque production range. IEEE Trans. Power Electron. 2020, 35, 2819–2830. [Google Scholar] [CrossRef]
- Rubino, S.; Dordevic, O.; Bojoi, R.; Levi, E. Modular vector control of multi-three-phase permanent magnet synchronous motors. IEEE Trans. Ind. Electron. 2021, 68, 9136–9147. [Google Scholar] [CrossRef]
- Zoric, I.; Jones, M.; Levi, E. Arbitrary power sharing among three-phase winding sets of multiphase machines. IEEE Trans. Ind. Electron. 2018, 65, 1128–1139. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Khalik, A.S.; Hamad, M.S.; Massoud, A.M.; Ahmed, S. Postfault operation of a nine-phase six-terminal induction machine under single open-line fault. IEEE Trans. Ind. Electron. 2018, 65, 1084–1096. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J.; Baneira, F.; Toliyat, H. Control strategy for dual three-phase machines with two open phases providing minimum loss in the full torque operation range. IEEE Trans. Power Electron. 2018, 33, 10044–10050. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, C.; Tao, W.; Wang, J.; Liu, G. Virtual-stator-flux-based direct torque control of five-phase fault-tolerant permanent-magnet motor with open-circuit fault. IEEE Trans. Power Electron. 2020, 35, 5007–5017. [Google Scholar] [CrossRef]
- Huang, W.; Hua, W.; Chen, F.; Yin, F.; Qi, J. Model predictive current control of open-circuit fault-tolerant five-phase flux-switching permanent magnet motor drives. IEEE J. Emerg. Sel. Topics Power Electron. 2018, 6, 1840–1849. [Google Scholar] [CrossRef]
- Huang, W.; Hua, W.; Chen, F.; Zhu, J. Enhanced model predictive torque control of fault-tolerant five-phase permanent magnet synchronous motor with harmonic restraint and voltage preselection. IEEE Trans. Ind. Electron. 2020, 67, 6259–6269. [Google Scholar] [CrossRef]
- Huang, W.; Hua, W.; Chen, F.; Hu, M.; Zhu, J. Model predictive torque control with SVM for five-phase PMSM under open-circuit fault condition. IEEE Trans. Power Electron. 2020, 35, 5531–5540. [Google Scholar] [CrossRef]
- Arashloo, R.S.; Martinez, J.L.R.; Salehifar, M.; Moreno-Eguilaz, M. Genetic algorithm-based output power optimisation of fault tolerant five-phase brushless direct current drives applicable for electrical and hybrid electrical vehicles. IET Electric Power Appl. 2014, 8, 267–277. [Google Scholar] [CrossRef]
- Khadar, S.; Abdellah, K.; Benguesmia, H. Remedial robust control of five-phase fault-tolerant induction motor with open-end winding using reduced-order transformation matrices. Model. Meas. Control. A 2019, 92, 52–59. [Google Scholar] [CrossRef]
- Sui, Y.; Zheng, P.; Yin, Z.; Wang, M.; Wang, C. Open-circuit fault-tolerant control of five-phase PM machine based on reconfiguring maximum round magnetomotive force. IEEE Trans. Ind. Electron. 2019, 66, 48–59. [Google Scholar] [CrossRef]
- Raherimihaja, H.J.; Zhang, Q.; Na, T.; Shao, M.; Wang, J. A three-phase integrated battery charger for EVs based on six-phase open-end winding machine. IEEE Trans. Power Electron. 2020, 35, 12122–12132. [Google Scholar] [CrossRef]
- Huang, J.; Zheng, P.; Sui, Y.; Zheng, J.; Yin, Z.; Cheng, L. Third harmonic current injection in different operating stages of five-phase PMSM with hybrid single/double layer fractional-slot concentrated winding. IEEE Access 2021, 9, 15670–15685. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, Y.; Cui, R.; Lorenz, R.D.; Cheng, M. Fault-tolerant direct torque control of five-phase FTFSCW-IPM motor based on analogous three-phase SVPWM for electric vehicle applications. IEEE Trans. Veh. Technol. 2018, 67, 910–919. [Google Scholar] [CrossRef]
- Ouenzerfi, S.; Zahr, H.; Trabelsi, M.; Semail, E.; Harmand, S.; Boubaker, R. 3-D multi-nodal thermal modelling for fault-tolerant machine. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, VIC, Australia, 13–15 February 2019; pp. 1551–1556. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Khalik, A.S.; Ahmed, S.; Massoud, A.M. A six-phase 24-slot/10-pole permanent-magnet machine with low space harmonics for electric vehicle applications. IEEE Trans. Magn. 2016, 52, 1–10. [Google Scholar] [CrossRef]
- Xiong, C.; Xu, H.; Guan, T.; Zhou, P. Fault-tolerant FOC for five-phase SPMSM with non-sinusoidal back EMF. IET Electric Power Appl. 2019, 13, 1734–1742. [Google Scholar] [CrossRef]
- Xiong, C.; Guan, T.; Zhou, P.; Xu, H. A fault-tolerant FOC strategy for five-phase SPMSM with minimum torque ripples in the full torque operation range under double-phase open-circuit fault. IEEE Trans. Ind. Electron. 2020, 67, 9059–9072. [Google Scholar] [CrossRef]
- Pham, H.T.; Bourgeot, J.M.; Benbouzid, M. Fault-tolerant model predictive control of 5-phase PMSG under an open-circuit phase fault condition for marine current applications. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 5760–5765. [Google Scholar] [CrossRef]
- Hu, Y.; Huang, S.; Wu, X.; Li, X. Control of dual three-phase permanent magnet synchronous machine based on five-leg inverter. IEEE Trans. Power Electron. 2019, 34, 11071–11079. [Google Scholar] [CrossRef]
- Sala, G.; Mengoni, M.; Rizzoli, G.; Degano, M.; Zarri, L.; Tani, A. Impact of star connection layouts on the control of multiphase induction motor drives under open-phase fault. IEEE Trans. Power Electron. 2021, 36, 3717–3726. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, G.; Chen, Q.; Zhao, W.; Lee, C.H.T. Fault-tolerant control of a triple redundant PMA-SynRM driven under single-phase open-circuit by mono-inverter. IEEE Trans. Power Electron. 2021, 36, 11593–11605. [Google Scholar] [CrossRef]
- Locment, F.; Semail, E.; Kestelyn, X. Vectorial approach-based control of a seven-phase axial flux machine designed for fault operation. IEEE Trans. Ind. Electron. 2008, 55, 3682–3691. [Google Scholar] [CrossRef] [Green Version]
- Cervone, A.; Slunjski, M.; Levi, E.; Brando, G. Optimal Third-Harmonic Current Injection for Asymmetrical Multiphase Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2021, 68, 2772–2783. [Google Scholar] [CrossRef] [Green Version]
- Tousizadeh, M.; Che, H.S.; Abdel-Khalik, A.S.; Munim, W.N.W.A.; Selvaraj, J.; Rahim, N.A. Effects of flux derating methods on torque production of fault-tolerant polyphase induction drives. IET Electric Power Appl. 2021, 15. [Google Scholar] [CrossRef]
- Sala, G.; Mengoni, M.; Rizzoli, G.; Zarri, L.; Tani, A. Decoupled d–q axes current-sharing control of multi-three-phase induction machines. IEEE Trans. Ind. Electron. 2020, 67, 7124–7134. [Google Scholar] [CrossRef]
- Cheng, L.; Sui, Y.; Zheng, P.; Wang, P.; Wu, F. Implementation of postfault decoupling vector control and mitigation of current ripple for five-phase fault-tolerant PM machine under single-phase open-circuit fault. IEEE Trans. Power Electron. 2018, 33, 8623–8636. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Zhao, W.; Chen, Q.; Xu, G. Third harmonic current injection in fault-tolerant five-phase permanent-magnet motor drive. IEEE Trans. Power Electron. 2018, 33, 6970–6979. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, W.; Liu, G.; Cheng, R.; Xie, Y. Remedial field-oriented control of five-phase fault-tolerant permanent-magnet motor by using reduced-order transformation matrices. IEEE Trans. Ind. Electron. 2017, 64, 169–178. [Google Scholar] [CrossRef]
- Rahman, U.; Munim, A.; Che, H.; Tousizadeh, M.; Muhammad, K. Fault tolerance of asymmetrical six-phase induction machine during single open circuit fault to three open circuit faults using GUI. Int. J. Power Electron. Drive Syst. 2020, 11, 611. [Google Scholar] [CrossRef]
- Kestelyn, X.; Semail, E. A vectorial approach for generation of optimal current references for multiphase permanent-magnet synchronous machines in real time. IEEE Trans. Ind. Electron. 2011, 58, 5057–5065. [Google Scholar] [CrossRef] [Green Version]
- Mekri, F.; Elghali, S.B.; Charpentier, J.F.; Kestelyn, X.; Benbouzid, M. A new control strategy of 5-phase PM motor under open-circuited phase based on high order sliding mode and current references real-time generation. Electr. Power Compon. Syst. 2019, 47, 261–274. [Google Scholar] [CrossRef]
- Ryu, H.M.; Kim, J.W.; Sul, S.K. Synchronous-frame current control of multiphase synchronous motor under asymmetric fault condition due to open phases. IEEE Trans. Ind. Appl. 2006, 42, 1062–1070. [Google Scholar] [CrossRef]
- Parsa, L.; Toliyat, H.A. Fault-tolerant interior-permanent-magnet machines for hybrid electric vehicle applications. IEEE Trans. Veh. Technol. 2007, 56, 1546–1552. [Google Scholar] [CrossRef]
- Dwari, S.; Parsa, L. An optimal control technique for multiphase PM machines under open-circuit faults. IEEE Trans. Ind. Electron. 2008, 55, 1988–1995. [Google Scholar] [CrossRef]
- Dwari, S.; Parsa, L. Fault-tolerant control of five-phase permanent-magnet motors with trapezoidal back EMF. IEEE Trans. Ind. Electron. 2011, 58, 476–485. [Google Scholar] [CrossRef]
- Mohammadpour, A.; Parsa, L. A unified fault-tolerant current control approach for five-phase PM motors with trapezoidal back EMF under different stator winding connections. IEEE Trans. Power Electron. 2013, 28, 3517–3527. [Google Scholar] [CrossRef]
- Mohammadpour, A.; Sadeghi, S.; Parsa, L. A generalized fault-tolerant control strategy for five-phase PM motor drives considering star, pentagon, and pentacle connections of stator windings. IEEE Trans. Ind. Electron. 2014, 61, 63–75. [Google Scholar] [CrossRef]
- Liu, G.; Song, C.; Chen, Q. FCS-MPC-based fault-tolerant control of five-phase IPMSM for MTPA operation. IEEE Trans. Power Electron. 2020, 35, 2882–2894. [Google Scholar] [CrossRef]
- Tian, B.; An, Q.; Duan, J.; Semenov, D.; Sun, D.; Sun, L. Cancellation of torque ripples with FOC strategy under two-phase failures of the five-phase PM motor. IEEE Trans. Power Electron. 2017, 32, 5459–5472. [Google Scholar] [CrossRef]
- Tian, B.; An, Q.; Duan, J.; Sun, D.; Sun, L.; Semenov, D. Decoupled modeling and nonlinear speed control for five-phase PM motor under single-phase open fault. IEEE Trans. Power Electron. 2017, 32, 5473–5486. [Google Scholar] [CrossRef]
- Tian, B.; Sun, L.; Molinas, M.; An, Q.T. Repetitive control based phase voltage modulation amendment for FOC-based five-phase PMSMs under single-phase open fault. IEEE Trans. Ind. Electron. 2021, 68, 1949–1960. [Google Scholar] [CrossRef]
- Tian, B.; Mirzaeva, G.; An, Q.; Sun, L.; Semenov, D. Fault-tolerant control of a five-phase permanent magnet synchronous motor for industry applications. IEEE Trans. Ind. Appl. 2018, 54, 3943–3952. [Google Scholar] [CrossRef]
- Tao, T.; Zhao, W.; He, Y.; Cheng, Y.; Saeed, S.; Zhu, J. Enhanced fault-tolerant model predictive current control for a five-phase PM motor with continued modulation. IEEE Trans. Power Electron. 2021, 36, 3236–3246. [Google Scholar] [CrossRef]
- Bianchi, N.; Fornasiero, E.; Bolognani, S. Thermal analysis of a five-phase motor under faulty operations. IEEE Trans. Ind. Appl. 2013, 49, 1531–1538. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Pre, M.D. Impact of stator winding of a five-phase permanent-magnet motor on postfault operations. IEEE Trans. Ind. Electron. 2008, 55, 1978–1987. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.; Masoud, M.; Ahmed, S.; Massoud, A. Calculation of derating factors based on steady-state unbalanced multiphase induction machine model under open phase(s) and optimal winding currents. Electr. Power Syst. Res. 2014, 106, 214–225. [Google Scholar] [CrossRef]
- Tao, T.; Zhao, W.; Du, Y.; Cheng, Y.; Zhu, J. Simplified fault-tolerant model predictive control for a five-phase permanent-magnet motor with reduced computation burden. IEEE Trans. Power Electron. 2020, 35, 3850–3858. [Google Scholar] [CrossRef]
- Boglietti, A.; Bojoi, I.R.; Rubino, S.; Cossale, M. Overload capability of multiphase machines under normal and open-phase fault conditions: A thermal analysis approach. IEEE Trans. Ind. Appl. 2020, 56, 2560–2569. [Google Scholar] [CrossRef]
- Chen, Q.; Zhao, W.; Liu, G.; Lin, Z. Extension of virtual-signal-injection-based MTPA control for five-phase IPMSM into fault-tolerant operation. IEEE Trans. Ind. Electron. 2019, 66, 944–955. [Google Scholar] [CrossRef]
- Priestley, M.; Farshadnia, M.; Fletcher, J.E. FOC transformation for single open-phase faults in the five-phase open-end winding topology. IEEE Trans. Ind. Electron. 2020, 67, 842–851. [Google Scholar] [CrossRef]
- Arafat, A.K.M.; Choi, S. Active current harmonic suppression for torque ripple minimization at open-phase faults in a five-phase PMa-SynRM. IEEE Trans. Ind. Electron. 2019, 66, 922–931. [Google Scholar] [CrossRef]
- Xu, H.; Huang, W.; Bu, F.; Liu, H.; Lin, X. Control of five-phase dual stator-winding induction generator with an open phase. IEEE Trans. Ind. Electron. 2019, 66, 696–706. [Google Scholar] [CrossRef]
- Liu, H.; Wang, D.; Yi, X.; Meng, F. Torque ripple suppression under open-phase fault conditions in a five-phase induction motor with harmonic injection. IEEE J. Emerg. Sel. Topics Power Electron. 2021, 9, 274–288. [Google Scholar] [CrossRef]
- Che, H.S.; Tousizadeh, M.; Duran, M.J.; Munim, W.N.W.; Rahim, N.A. Fault-tolerant symmetrical six-phase induction motor drive based on feed-forward voltage compensation. IEEE IECON 2019, 1, 6212–6216. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J. Study and active enhancement by converter reconfiguration of the performance in terms of stator copper loss, derating factor and converter rating of multiphase drives under two open legs with different stator winding connections. IEEE Access 2021, 9. [Google Scholar] [CrossRef]
- Gjerde, S.S.; Olsen, P.K.; Ljøkelsøy, K.; Undeland, T.M. Control and fault handling in a modular series-connected converter for a transformerless 100 kV low-weight offshore wind turbine. IEEE Trans. Ind. Appl. 2014, 50, 1094–1105. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Morsy, A.S.; Ahmed, S.; Massoud, A.M. Effect of stator winding connection on performance of five-phase induction machines. IEEE Trans. Ind. Electron. 2014, 61, 3–19. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Ahmed, S.; Elserougi, A.A.; Massoud, A.M. Effect of stator winding connection of five-phase induction machines on torque ripples under open line condition. IEEE/ASME Trans. Mechatronics 2015, 20, 580–593. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Ahmed, S.; Massoud, A.M. Steady-state equivalent circuit of five-phase induction machines with different stator connections under open-line conditions. IEEE Trans. Ind. Electron. 2016, 63, 4651–4662. [Google Scholar] [CrossRef]
- Melo, V.F.M.B.; Jacobina, C.B.; Rocha, N.; Braga-Filho, E.R. Fault tolerance performance of two hybrid six-phase drive systems under single-phase open-circuit fault operation. IEEE Trans. Ind. Appl. 2019, 55, 2973–2983. [Google Scholar] [CrossRef]
- Chen, Q.; Gu, L.; Lin, Z.; Liu, G. Extension of space-vector-signal-injection-based MTPA control into SVPWM fault-tolerant operation for five-phase IPMSM. IEEE Trans. Ind. Electron. 2020, 67, 7321–7333. [Google Scholar] [CrossRef]
- Melo, V.F.M.B.; Jacobina, C.B.; Rocha, N. Fault tolerance performance of dual-inverter-based six-phase drive system under single-, two-, and three-phase open-circuit fault operation. IET Power Electron. 2018, 11, 212–220. [Google Scholar] [CrossRef]
- Jordan, S.; Manolopoulos, C.D.; Apsley, J.M. Winding configurations for five-phase synchronous generators with diode rectifiers. IEEE Trans. Ind. Electron. 2016, 63, 517–525. [Google Scholar] [CrossRef]
- Sulligoi, G.; Tessarolo, A.; Benucci, V.; Baret, M.; Rebora, A.; Taffone, A. Modeling, simulation, and experimental validation of a generation system for medium-voltage dc integrated power systems. IEEE Trans. Ind. Appl. 2010, 46, 1304–1310. [Google Scholar] [CrossRef]
- Popescu, M.; Dorrell, D.G.; Alberti, L.; Bianchi, N.; Staton, D.A.; Hawkins, D. Thermal analysis of duplex three-phase induction motor under fault operating conditions. IEEE Trans. Ind. Appl. 2013, 49, 1523–1530. [Google Scholar] [CrossRef]
- Barcaro, M.; Bianchi, N.; Magnussen, F. Six-phase supply feasibility using a PM fractional-slot dual winding machine. IEEE Trans. Ind. Appl. 2011, 47, 2042–2050. [Google Scholar] [CrossRef]
- Scuiller, F.; Charpentier, J.; Semail, E. Multi-star multi-phase winding for a high power naval propulsion machine with low ripple torques and high fault tolerant ability. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–5. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Khalik, A.S.; Elgenedy, M.A.; Ahmed, S.; Massoud, A.M. An improved fault-tolerant five-phase induction machine using a combined star/pentagon single layer stator winding connection. IEEE Trans. Ind. Electron. 2016, 63, 618–628. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Ahmed, S.; Massoud, A.M. A nine-phase six-terminal concentrated single-layer winding layout for high-power medium-voltage induction machines. IEEE Trans. Ind. Electron. 2017, 64, 1796–1806. [Google Scholar] [CrossRef]
- Bonthu, S.S.R.; Choi, S.; Baek, J. Design optimization with multiphysics analysis on external rotor permanent magnet-assisted synchronous reluctance motors. IEEE Trans. Energy Convers. 2018, 33, 290–298. [Google Scholar] [CrossRef]
- Paredes, J.; Prieto, B.; Satrústegui, M.; Elósegui, I.; Gonzalez, P. Improving the performance of a 1-MW induction machine by optimally shifting from a three-phase to a six-phase machine design by rearranging the coil connections. IEEE Trans. Ind. Electron. 2021, 68, 1035–1045. [Google Scholar] [CrossRef]
- Wang, K.; Lin, H. A novel 24-slot/10-pole dual three-phase fractional-slot overlapped winding for low non-working space harmonics and stator modularization. IEEE Access 2020, 8, 85490–85503. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Massoud, A.M.; Ahmed, S. An improved torque density pseudo six-phase induction machine using a quadruple three-phase stator winding. IEEE Trans. Ind. Electron. 2020, 67, 1855–1866. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Massoud, A.M.; Ahmed, S. Application of standard three-phase stator frames in prime phase order multiphase machine construction. IEEE Trans. Ind. Electron. 2019, 66, 2506–2517. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Ahmed, S.; Elserougi, A.A.; Massoud, A.M. A voltage-behind-reactance model of five-phase induction machines considering the effect of magnetic saturation. IEEE Trans. Energy Convers. 2013, 28, 576–592. [Google Scholar] [CrossRef]
- Toliyat, H.A. Analysis and simulation of five-phase variable-speed induction motor drives under asymmetrical connections. IEEE Trans. Power Electron. 1998, 13, 748–756. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Massoud, A.M.; Ahmed, S. Nine-phase six-terminal induction machine modeling using vector space decomposition. IEEE Trans. Ind. Electron. 2019, 66, 988–1000. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Ahmed, S.; Massoud, A.M. Steady-state mathematical modeling of a five-phase induction machine with a combined star/pentagon stator winding connection. IEEE Trans. Ind. Electron. 2016, 63, 1331–1343. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Ahmed, S.; Massoud, A.M. Dynamic modeling of a five-phase induction machine with a combined star/pentagon stator winding connection. IEEE Trans. Energy Convers. 2016, 31, 1645–1656. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Hamdy, R.A.; Massoud, A.M.; Ahmed, S. Low-order space harmonic modeling of asymmetrical six-phase induction machines. IEEE Access 2019, 7, 6866–6876. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Massoud, A.M.; Ahmed, S. Effect of dc-link voltage limitation on postfault steady-state performance of asymmetrical six-phase induction machines. IEEE Trans. Ind. Electron. 2018, 65, 6890–6900. [Google Scholar] [CrossRef]
- Shata, A.M.; Abdel-Khalik, A.S.; Hamdy, R.A.; Mostafa, M.Z.; Ahmed, S. Improved mathematical modeling of six phase induction machines based on fractional calculus. IEEE Access 2021, 9, 53146–53155. [Google Scholar] [CrossRef]
- Alberti, L.; Bianchi, N. Impact of winding arrangement in dual 3-phase induction motor for fault tolerant applications. In Proceedings of the XIX International Conference on Electrical Machines—ICEM 2010, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Zhao, Y.; Lipo, T.A. Modeling and control of a multi-phase induction machine with structural unbalance–Part I: Machine modeling and multidimensional current regulation. IEEE Trans. Energy Convers. 1996, 11, 570–577. [Google Scholar] [CrossRef]
- Zhao, Y.; Lipo, T.A. Modeling and control of a multi-phase induction machine with structural unbalance–Part II: Field-oriented control and experimental verification. IEEE Trans. Energy Convers. 1996, 11, 578–584. [Google Scholar] [CrossRef]
- Jung, E.; Yoo, H.; Sul, S.K.; Choi, H.S.; Choi, Y.Y. A nine-phase permanent-magnet motor drive system for an ultrahigh-speed elevator. IEEE Trans. Ind. Appl. 2012, 48, 987–995. [Google Scholar] [CrossRef]
- Nounou, K.; Charpentier, J.F.; Marouani, K.; Benbouzid, M.; Kheloui, A. Emulation of an electric naval propulsion system based on a multiphase machine under healthy and faulty operating conditions. IEEE Trans. Veh. Technol. 2018, 67, 6895–6905. [Google Scholar] [CrossRef]
- Akay, A.; Lefley, P. Research on torque ripple under healthy and open-circuit fault-tolerant conditions in a PM multiphase machine. CES Trans. Electr. Mach. Syst. 2020, 4, 349–359. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, X.; Cai, Y.; Yang, Z. Robust design optimization of a five-phase PM hub motor for fault-tolerant operation based on Taguchi method. IEEE Trans. Energy Convers. 2020, 35, 2036–2044. [Google Scholar] [CrossRef]
- Zhang, H.; Giangrande, P.; Sala, G.; Xu, Z.; Hua, W.; Madonna, V.; Gerada, D.; Gerada, C. Thermal model approach to multisector three-phase electrical machines. IEEE Trans. Ind. Electron. 2021, 68, 2919–2930. [Google Scholar] [CrossRef]
- Liu, G.; Qu, L.; Zhao, W.; Chen, Q.; Xie, Y. Comparison of two SVPWM control strategies of five-phase fault-tolerant permanent-magnet motor. IEEE Trans. Power Electron. 2016, 31, 6621–6630. [Google Scholar] [CrossRef]
- Qiu-Liang, H.; Yong, C.; Li, X. Fault-tolerant control strategy for five-phase PMSM with third-harmonic current injection. IEEE Access 2018, 6, 58501–58509. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, G.; Zhao, W.; Qu, L.; Xu, G. Asymmetrical SVPWM fault-tolerant control of five-phase PM brushless motors. IEEE Trans. Energy Convers. 2017, 32, 12–22. [Google Scholar] [CrossRef]
- Salehi Arashloo, R.; Salehifar, M.; Romeral, L.; Sala, V. A robust predictive current controller for healthy and open-circuit faulty conditions of five-phase BLDC drives applicable for wind generators and electric vehicles. Energy Convers. Manag. 2015, 92, 437–447. [Google Scholar] [CrossRef]
- Tian, B.; Molinas, M.; An, Q. PWM investigation of a field-oriented controlled five-phase PMSM under two-phase open faults. IEEE Trans. Energy Convers. 2021, 36, 580–593. [Google Scholar] [CrossRef]
- Sun, J.; Zheng, Z.; Li, C.; Wang, K.; Li, Y. Optimal fault-tolerant control of multiphase drives under open-phase/open-switch faults based on dc current injection. IEEE Trans. Power Electron. 2022, 37, 5928–5936. [Google Scholar] [CrossRef]
- Bianchi, N.; Park, J.; Tortella, A.; Zavagnin, R. Experimental tests of dual three-phase synchronous reluctance motor under half-control mode. IEEE Trans. Ind. Appl. 2021, 57, 5887–5893. [Google Scholar] [CrossRef]
- Wang, P.; Gong, S.; Sun, X.; Liu, Z.; Jiang, D.; Qu, R. Fault-tolerant reconfiguration topology and control strategy for symmetric open-winding multiphase machines. IEEE Trans. Ind. Electron. accepted for publication. 2021. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, J.; Jiang, Y.; Geng, W.; Xu, Y. Overview and analysis of PM starter/generator for aircraft electrical power systems. CES Trans. Electr. Mach. Syst. 2017, 1, 117–131. [Google Scholar] [CrossRef]
- Metwly, M.Y.; Abdel-Majeed, M.S.; Abdel-Khalik, A.S.; Hamdy, R.A.; Hamad, M.S.; Ahmed, S. A review of integrated on-board EV battery chargers: Advanced topologies, recent developments and optimal selection of FSCW slot/pole combination. IEEE Access 2020, 8, 85216–85242. [Google Scholar] [CrossRef]
- Javaid, U.; Freijedo, F.D.; Dujic, D.; van der Merwe, W. MVDC supply technologies for marine electrical distribution systems. CPSS Trans. Power Electron. Appl. 2018, 3, 65–76. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B.; Sen, P.C.; Kouro, S.; Narimani, M. High-power wind energy conversion systems: State-of-the-art and emerging technologies. Proc. IEEE 2015, 103, 740–788. [Google Scholar] [CrossRef]
- El-Refaie, A. Fault-tolerant permanent magnet machines: A review. IET Electric Power Appl. 2011, 5, 59–74. [Google Scholar] [CrossRef]
- Zhao, W.; Xu, L.; Liu, G. Overview of permanent-magnet fault-tolerant machines: Topology and design. CES Trans. Electr. Mach. Syst. 2018, 2, 51–64. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Davari, S.A.; Rodas Benítez, J.E.; Valencia, D.F.; Elmorshedy, M.F.; Wang, F.; Tarisciotti, L.; Flores-Bahamonde, F.; et al. Latest advances of model predictive control in electrical drives—Part II: Applications and benchmarking with classical control methods. IEEE Trans. Power Electron. 2022, 37, 5047–5061. [Google Scholar] [CrossRef]
- Valente, M.; Wijekoon, T.; Freijedo, F.; Pescetto, P.; Pellegrino, G.; Bojoi, R. Integrated on-board ev battery chargers: New perspectives and challenges for safety improvement. In Proceedings of the 2021 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Modena, Italy, 8–9 April 2021; pp. 349–356. [Google Scholar] [CrossRef]
- Liu, Y.; Stettenbenz, M.; Bazzi, A.M. Smooth fault-tolerant control of induction motor drives with sensor failures. IEEE Trans. Power Electron. 2019, 34, 3544–3552. [Google Scholar] [CrossRef]
- Bellini, A.; Filippetti, F.; Tassoni, C.; Capolino, G. Advances in diagnostic techniques for induction machines. IEEE Trans. Ind. Electron. 2008, 55, 4109–4126. [Google Scholar] [CrossRef]
- Nandi, S.; Toliyat, H.A.; Li, X. Condition monitoring and fault diagnosis of electrical motors–A review. IEEE Trans. Energy Convers. 2005, 20, 719–729. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques–Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef] [Green Version]
- Welchko, B.A.; Lipo, T.A.; Jahns, T.M.; Schulz, S.E. Fault tolerant three-phase ac motor drive topologies: A comparison of features, cost, and limitations. IEEE Trans. Power Electron. 2004, 19, 1108–1116. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Xu, D.; Enjeti, P.N.; Li, H.; Hawke, J.T.; Krishnamoorthy, H.S. Survey on fault-tolerant techniques for power electronic converters. IEEE Trans. Power Electron. 2014, 29, 6319–6331. [Google Scholar] [CrossRef]
- Zhang, X.; Foo, G.H.B. Overmodulation of constant-switching-frequency-based DTC for reluctance synchronous motors incorporating field-weakening operation. IEEE Trans. Ind. Electron. 2019, 66, 37–47. [Google Scholar] [CrossRef]
- Kim, S.; Seok, J. Induction motor control with a small dc-link capacitor inverter fed by three-phase diode front-end rectifiers. IEEE Trans. Power Electron. 2015, 30, 2713–2720. [Google Scholar] [CrossRef]
- Lee, S.-B.; Habetler, T.G. A remote and sensorless thermal protection scheme for small line-connected ac machines. IEEE Trans. Ind. Appl. 2003, 39, 1323–1332. [Google Scholar] [CrossRef]
- Slunjski, M.; Dordevic, O.; Jones, M.; Levi, E. Symmetrical/asymmetrical winding reconfiguration in multiphase machines. IEEE Access 2020, 8, 12835–12844. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Abdel-Majeed, M.S.; Ahmed, S. Effect of winding configuration on six-phase induction machine parameters and performance. IEEE Access 2020, 8, 223009–223020. [Google Scholar] [CrossRef]
- Shawier, A.; Habib, A.; Mamdouh, M.; Abdel-Khalik, A.S.; Ahmed, K.H. Assessment of predictive current control of six-phase induction motor with different winding configurations. IEEE Access 2021, 9, 81125–81138. [Google Scholar] [CrossRef]
- EL-Refaie, A.M. Fractional-slot concentrated-windings synchronous permanent magnet machines: Opportunities and challenges. IEEE Trans. Ind. Electron. 2010, 57, 107–121. [Google Scholar] [CrossRef]
- Che, H.S.; Abdel-Khalik, A.S.; Dordevic, O.; Levi, E. Parameter estimation of asymmetrical six-phase induction machines using modified standard tests. IEEE Trans. Ind. Electron. 2017, 64, 6075–6085. [Google Scholar] [CrossRef] [Green Version]
- Hadiouche, D.; Razik, H.; Rezzoug, A. On the modeling and design of dual-stator windings to minimize circulating harmonic currents for VSI fed ac machines. IEEE Trans. Ind. Appl. 2004, 40, 506–515. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Ahmed, S.; Massoud, A.M.; Elserougi, A.A. An improved performance direct-drive permanent magnet wind generator using a novel single-layer winding layout. IEEE Trans. Magn. 2013, 49, 5124–5134. [Google Scholar] [CrossRef]
- Zhang, X.; Ji, J.; Zheng, J.; Zhu, X. Improvement of reluctance torque in fault-tolerant permanent-magnet machines with fractional-slot concentrated-windings. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Wang, J.; Patel, V.I.; Wang, W. Fractional-slot permanent magnet brushless machines with low space harmonic contents. IEEE Trans. Magn. 2014, 50, 1–9. [Google Scholar] [CrossRef]
- Dujic, D.; Jones, M.; Levi, E. Analysis of output current-ripple rms in multiphase drives using polygon approach. IEEE Trans. Power Electron. 2010, 25, 1838–1849. [Google Scholar] [CrossRef]
- Edelson, J.S. High Phase Order Motor with Mesh Connected Windings. U.S. Patent 6,831,430, 22 March 2004. [Google Scholar]
- Lei, Y.; Zhao, Z.; Wang, S.; Dorrell, D.G.; Xu, W. Design and analysis of star–delta hybrid windings for high-voltage induction motors. IEEE Trans. Ind. Electron. 2011, 58, 3758–3767. [Google Scholar] [CrossRef]
- Zhao, B.; Gong, J.; Tong, T.; Xu, Y.; Semail, E.; Nguyen, N.K.; Gillon, F. A novel five-phase fractional slot concentrated winding with low space harmonic contents. IEEE Trans. Magn. 2021, 57, 1–5. [Google Scholar] [CrossRef]
- Li, J.; Meng, D. Magneto-motive force and performance comparative analysis research for a novel pentacle-star hybrid winding five-phase induction motor. Prog. Electromagn. Res. C 2021, 109, 125–138. [Google Scholar] [CrossRef]
- Pazouki, E.; Islam, M.Z.; Bonthu, S.S.R.; Choi, S. Eccentricity fault detection in multiphase permanent magnet assisted synchronous reluctance motor. In Proceedings of the 2015 IEEE International Electric Machines and Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 240–246. [Google Scholar] [CrossRef]
- Che, H.S.; Levi, E.; Jones, M.; Duran, M.J.; Hew, W.P.; Rahim, N.A. Operation of a six-phase induction machine using series-connected machine-side converters. IEEE Trans. Ind. Electron. 2014, 61, 164–176. [Google Scholar] [CrossRef] [Green Version]
- Jung, H.S. Interleaved pulse width modulation based on modified carrier in parallel operation. IEEE Access 2021, 9, 1–10. [Google Scholar] [CrossRef]
- Li, A.; Jiang, D.; Liu, Z.; Sun, X.; Kong, W. Unified analysis of winding connection sequence in series-end winding topology. IEEE Trans. Ind. Appl. 2021, 57, 516–527. [Google Scholar] [CrossRef]
- Yepes, A.G.; Malvar, J.; Vidal, A.; Lopez, O.; Doval-Gandoy, J. Current harmonics compensation based on multiresonant control in synchronous frames for symmetrical n-phase machines. IEEE Trans. Ind. Electron. 2015, 62, 2708–2720. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J.; Baneira, F.; Pérez-Estévez, D.; Lopez, O. Current harmonic compensation for n-phase machines with asymmetrical winding arrangement and different neutral configurations. IEEE Trans. Ind. Appl. 2017, 53, 5426–5439. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Ahmed, S. Performance evaluation of a five-phase modular winding induction machine. IEEE Trans. Ind. Electron. 2012, 59, 2654–2669. [Google Scholar] [CrossRef]
- Jecmenica, M.; Brkovic, B.; Levi, E.; Lazarevic, Z. Interplane cross-saturation in multiphase machines. IET Electric Power Appl. 2019, 13, 1812–1822. [Google Scholar] [CrossRef] [Green Version]
- Fudeh, H.R.; Ong, C.M. Modeling and analysis of induction machines containing space harmonics Part I: Modeling and transformation. IEEE Trans. Power App. Syst. 1983, PAS-102, 2608–2615. [Google Scholar] [CrossRef]
- Bruzzese, C. Analysis and application of particular current signatures (symptoms) for cage monitoring in nonsinusoidally fed motors with high rejection to drive load, inertia, and frequency variations. IEEE Trans. Ind. Electron. 2008, 55, 4137–4155. [Google Scholar] [CrossRef]
- Jones, M.; Vukosavic, S.N.; Dujic, D.; Levi, E. A synchronous current control scheme for multiphase induction motor drives. IEEE Trans. Energy Convers. 2009, 24, 860–868. [Google Scholar] [CrossRef]
- Che, H.S.; Levi, E.; Jones, M.; Hew, W.P.; Rahim, N.A. Current control methods for an asymmetrical six-phase induction motor drive. IEEE Trans. Power Electron. 2014, 29, 407–417. [Google Scholar] [CrossRef] [Green Version]
- Arumugam, P.; Hamiti, T.; Gerada, C. Modeling of different winding configurations for fault-tolerant permanent magnet machines to restrain interturn short-circuit current. IEEE Trans. Energy Convers. 2012, 27, 351–361. [Google Scholar] [CrossRef]
- Siddique, A.; Yadava, G.S.; Singh, B. A review of stator fault monitoring techniques of induction motors. IEEE Trans. Energy Convers. 2005, 20, 106–114. [Google Scholar] [CrossRef]
- Shifat, T.A.; Hur, J.W. An effective stator fault diagnosis framework of BLDC motor based on vibration and current signals. IEEE Access 2020, 8, 106968–106981. [Google Scholar] [CrossRef]
- Zafarani, M.; Bostanci, E.; Qi, Y.; Goktas, T.; Akin, B. Interturn short-circuit faults in permanent magnet synchronous machines: An extended review and comprehensive analysis. IEEE J. Emerg. Sel. Topics Power Electron. 2018, 6, 2173–2191. [Google Scholar] [CrossRef]
- Gandhi, A.; Corrigan, T.; Parsa, L. Recent advances in modeling and online detection of stator interturn faults in electrical motors. IEEE Trans. Ind. Electron. 2011, 58, 1564–1575. [Google Scholar] [CrossRef]
- Neethu, N.; Nikam, S.P.; Singh, S.; Pal, S.; Wankhede, A.K.; Fernandes, B.G. High-speed coreless axial-flux permanent-magnet motor with printed circuit board winding. IEEE Trans. Ind. Appl. 2019, 55, 1954–1962. [Google Scholar] [CrossRef]
- Welchko, B.; Wai, J.; Jahns, T.; Lipo, T. Magnet-flux-nulling control of interior PM machine drives for improved steady-state response to short-circuit faults. IEEE Trans. Ind. Appl. 2006, 42, 113–120. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Zhang, Z.; Jiang, W.; Geng, W.; Huang, J. Three-phase current injection method for mitigating turn-to-turn short-circuit fault in concentrated-winding permanent magnet aircraft starter generator. IET Electric Power Appl. 2018, 12, 566–574. [Google Scholar] [CrossRef]
- Jeong, I.; Hyon, B.J.; Nam, K. Dynamic modeling and control for SPMSMs with internal turn short fault. IEEE Trans. Power Electron. 2013, 28, 3495–3508. [Google Scholar] [CrossRef]
- Lu, B.; Sharma, S.K. A literature review of IGBT fault diagnostic and protection methods for power inverters. IEEE Trans. Ind. Appl. 2009, 45, 1770–1777. [Google Scholar] [CrossRef]
- Muduli, U.R.; Beig, A.R.; Jaafari, K.A.; Alsawalhi, J.Y.; Behera, R.K. Interrupt-free operation of dual-motor four-wheel drive electric vehicle under inverter failure. IEEE Trans. Transport. Electrific. 2021, 7, 329–338. [Google Scholar] [CrossRef]
- Hu, K.; Liu, Z.; Yang, Y.; Iannuzzo, F.; Blaabjerg, F. Ensuring a reliable operation of two-level IGBT-based power converters: A review of monitoring and fault-tolerant approaches. IEEE Access 2020, 8, 89988–90022. [Google Scholar] [CrossRef]
- Xu, D.; Wang, B.; Zhang, G.; Wang, G.; Yu, Y. A review of sensorless control methods for ac motor drives. CES Trans. Electr. Mach. Syst. 2018, 2, 104–115. [Google Scholar] [CrossRef]
- Lima, F.; Kaiser, W.; da Silva, I.N.; de Oliveira, A.A.A. Open-loop neuro-fuzzy speed estimator applied to vector and scalar induction motor drives. Appl. Soft Comput. 2014, 21, 469–480. [Google Scholar] [CrossRef]
- Mollet, Y.; Gyselinck, J. Mechanical-state estimator for doubly-fed induction generators–Application to encoder-fault tolerance and sensorless control. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 1779–1785. [Google Scholar] [CrossRef]
- Sul, S.K.; Kwon, Y.C.; Lee, Y. Sensorless control of IPMSM for last 10 years and next 5 years. CES Trans. Electr. Mach. Syst. 2017, 1, 91–99. [Google Scholar] [CrossRef]
- Wang, G.; Valla, M.; Solsona, J. Position sensorless permanent magnet synchronous machine drives–A review. IEEE Trans. Ind. Electron. 2020, 67, 5830–5842. [Google Scholar] [CrossRef]
- Pellegrino, G.; Bojoi, R.I.; Guglielmi, P. Unified direct-flux vector control for ac motor drives. IEEE Trans. Ind. Appl. 2011, 47, 2093–2102. [Google Scholar] [CrossRef]
- Kim, J.H.; Choi, J.W.; Sul, S.K. Novel rotor-flux observer using observer characteristic function in complex vector space for field-oriented induction motor drives. IEEE Trans. Ind. Appl. 2002, 38, 1334–1343. [Google Scholar] [CrossRef]
- Jansen, P.; Lorenz, R. A physically insightful approach to the design and accuracy assessment of flux observers for field oriented induction machine drives. IEEE Trans. Ind. Appl. 1994, 30, 101–110. [Google Scholar] [CrossRef] [Green Version]
- Harnefors, L.; Hinkkanen, M. Stabilization methods for sensorless induction motor drives–A survey. IEEE J. Emerg. Sel. Topics Power Electron. 2014, 2, 132–142. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Lipo, T.A.; Novotny, D.W. Motion control with induction motors. In Power Electronics and Variable Frequency Drives; Chapter 5; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1996; pp. 209–276. [Google Scholar] [CrossRef]
- Vagati, A.; Pastorelli, M.; Franceschini, G. High performance control of synchronous reluctance motor. In Proceedings of the IAS ’96. Conference Record of the 1996 IEEE Industry Applications Conference Thirty-First IAS Annual Meeting, San Diego, CA, USA, 6–10 October 1996; Volume 1, pp. 295–303. [Google Scholar] [CrossRef]
- Korzonek, M.; Tarchala, G.; Orlowska-Kowalska, T. A review on MRAS-type speed estimators for reliable and efficient induction motor drives. ISA Trans. 2019, 93, 1–13. [Google Scholar] [CrossRef]
- Consoli, A.; Musumeci, S.; Raciti, A.; Testa, A. Sensorless vector and speed control of brushless motor drives. IEEE Trans. Ind. Electron. 1994, 41, 91–96. [Google Scholar] [CrossRef]
- Chen, Z.; Tomita, M.; Doki, S.; Okuma, S. An extended electromotive force model for sensorless control of interior permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2003, 50, 288–295. [Google Scholar] [CrossRef]
- Foo, G.; Rahman, M.F. Sensorless sliding-mode MTPA control of an IPM synchronous motor drive using a sliding-mode observer and HF signal injection. IEEE Trans. Ind. Electron. 2010, 57, 1270–1278. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, L.; Cheng, M.; Chau, K.T. Sensorless SVPWM-FADTC of a new flux-modulated permanent-magnet wheel motor based on a wide-speed sliding mode observer. IEEE Trans. Ind. Electron. 2015, 62, 3143–3151. [Google Scholar] [CrossRef] [Green Version]
- Blasco-Gimenez, R.; Asher, G.M.; Sumner, M.; Bradley, K.J. Dynamic performance limitations for MRAS based sensorless induction motor drives. Part 1: Stability analysis for the closed loop drive. IEE Proc. Electr. Power Appl. 1996, 143, 113–122. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Dybkowski, M. Stator-current-based MRAS estimator for a wide range speed-sensorless induction-motor drive. IEEE Trans. Ind. Electron. 2010, 57, 1296–1308. [Google Scholar] [CrossRef]
- Blasco, R.; Sumner, M.; Asher, G. Speed measurement of inverter fed induction motors using the FFT and the rotor slot harmonics. In Proceedings of the 1994 5th International Conference on Power Electronics and Variable-Speed Drives, London, UK, 26–28 October 1994; pp. 470–475. [Google Scholar] [CrossRef]
- Ferrah, A.; Bradley, K.J.; Hogben-Laing, P.J.; Woolfson, M.S.; Asher, G.M.; Sumner, M.; Cilia, J.; Shuli, J. A speed identifier for induction motor drives using real-time adaptive digital filtering. IEEE Trans. Ind. Appl. 1998, 34, 156–162. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Guzinski, J.; Krzeminski, Z.; Toliyat, H.A. Speed observer system for advanced sensorless control of induction motor. IEEE Trans. Energy Convers. 2003, 18, 219–224. [Google Scholar] [CrossRef]
- Keysan, O.; Ertan, H.B. Real-time speed and position estimation using rotor slot harmonics. IEEE Trans. Ind. Informat. 2013, 9, 899–908. [Google Scholar] [CrossRef]
- Nandi, S.; Ahmed, S.; Toliyat, H.A.; Mohan Bharadwaj, R. Selection criteria of induction machines for speed-sensorless drive applications. IEEE Trans. Ind. Appl. 2003, 39, 704–712. [Google Scholar] [CrossRef]
- Bellini, A.; Franceschini, G.; Tassoni, C. Monitoring of induction machines by maximum covariance method for frequency tracking. IEEE Trans. Ind. Appl. 2006, 42, 69–78. [Google Scholar] [CrossRef]
- Silva, W.L.; Nogueira Lima, A.M.; Oliveira, A. Speed estimation of an induction motor operating in the nonstationary mode by using rotor slot harmonics. IEEE Trans. Instrum. Meas. 2015, 64, 984–994. [Google Scholar] [CrossRef]
- Sahraoui, M.; Cardoso, A.J.M.; Yahia, K.; Ghoggal, A. The use of the modified Prony’s method for rotor speed estimation in squirrel-cage induction motors. IEEE Trans. Ind. Appl. 2016, 52, 2194–2202. [Google Scholar] [CrossRef]
- Hurst, K.; Habetler, T.G.; Griva, G.; Profumo, F. Zero-speed tacholess IM torque control: Simply a matter of stator voltage integration. IEEE Trans. Ind. Appl. 1998, 34, 790–795. [Google Scholar] [CrossRef]
- Ha, J.I.; Sul, S.K. Sensorless field-orientation control of an induction machine by high-frequency signal injection. IEEE Trans. Ind. Appl. 1999, 35, 45–51. [Google Scholar] [CrossRef]
- Consoli, A.; Scarcella, G.; Testa, A. A new zero-frequency flux-position detection approach for direct-field-oriented-control drives. IEEE Trans. Ind. Appl. 2000, 36, 797–804. [Google Scholar] [CrossRef]
- Matsui, N. Sensorless PM brushless dc motor drives. IEEE Trans. Ind. Electron. 1996, 43, 300–308. [Google Scholar] [CrossRef]
- Mao, S.; Liu, W.; Chen, Z.; Jiao, N.; Peng, J. Rotor position estimation of brushless synchronous starter/generators by using the main exciter as a position sensor. IEEE Trans. Power Electron. 2020, 35, 800–815. [Google Scholar] [CrossRef]
- Jang, J.H.; Sul, S.K.; Ha, J.I.; Ide, K.; Sawamura, M. Sensorless drive of surface-mounted permanent-magnet motor by high-frequency signal injection based on magnetic saliency. IEEE Trans. Ind. Appl. 2003, 39, 1031–1039. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Faggion, A. Predicted and measured errors in estimating rotor position by signal injection for salient-pole PM synchronous motors. In Proceedings of the 2009 IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 3–6 May 2009; pp. 1565–1572. [Google Scholar] [CrossRef]
- Xu, P.L.; Zhu, Z.Q. Novel carrier signal injection method using zero-sequence voltage for sensorless control of PMSM drives. IEEE Trans. Ind. Electron. 2016, 63, 2053–2061. [Google Scholar] [CrossRef]
- Briz, F.; Diez, A.; Degner, M.W. Dynamic operation of carrier-signal-injection-based sensorless direct field-oriented ac drives. IEEE Trans. Ind. Appl. 2000, 36, 1360–1368. [Google Scholar] [CrossRef]
- Garcia, P.; Briz, F.; Degner, M.W.; Diaz-Reigosa, D. Accuracy, bandwidth, and stability limits of carrier-signal-injection-based sensorless control methods. IEEE Trans. Ind. Appl. 2007, 43, 990–1000. [Google Scholar] [CrossRef]
- Yoon, Y.D.; Sul, S.K. Sensorless control for induction machines based on square-wave voltage injection. IEEE Trans. Power Electron. 2014, 29, 3637–3645. [Google Scholar] [CrossRef]
- Zafari, Y.; Shoja-Majidabad, S. Sensorless fault-tolerant control of five-phase IPMSMs via model reference adaptive systems. Automatika 2020, 61, 564–573. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J. Effective current limitation for multifrequency current control with distortion-free voltage saturation and antiwindup. IEEE Trans. Power Electron. 2020, 35, 13697–13713. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Pothi, N.; Xu, P.L.; Ren, Y. Uncontrolled generator fault protection of novel hybrid-excited doubly salient synchronous machines with field excitation current control. IEEE Trans. Ind. Appl. 2019, 55, 3598–3606. [Google Scholar] [CrossRef]
- Casadei, D.; Mengoni, M.; Serra, G.; Tani, A.; Zarri, L. A control scheme with energy saving and dc-link overvoltage rejection for induction motor drives of electric vehicles. IEEE Trans. Ind. Appl. 2010, 46, 1436–1446. [Google Scholar] [CrossRef]
- Djokic, S.; Stockman, K.; Milanovic, J.; Desmet, J.; Belmans, R. Sensitivity of ac adjustable speed drives to voltage sags and short interruptions. IEEE Trans. Power Del. 2005, 20, 494–505. [Google Scholar] [CrossRef]
- Seibel, B.; Rowan, T.; Kerkman, R. Field-oriented control of an induction machine in the field-weakening region with dc-link and load disturbance rejection. IEEE Trans. Ind. Appl. 1997, 33, 1578–1584. [Google Scholar] [CrossRef]
- Kwon, Y.C.; Kim, S.; Sul, S.K. Voltage feedback current control scheme for improved transient performance of permanent magnet synchronous machine drives. IEEE Trans. Ind. Electron. 2012, 59, 3373–3382. [Google Scholar] [CrossRef]
- Bojoi, R.; Lazzari, M.; Profumo, F.; Tenconi, A. Digital field-oriented control for dual three-phase induction motor drives. IEEE Trans. Ind. Appl. 2003, 39, 752–760. [Google Scholar] [CrossRef]
- Lopez, O.; Alvarez, J.; Malvar, J.; Yepes, A.G.; Vidal, A.; Baneira, F.; Perez-Estevez, D.; Freijedo, F.D.; Doval-Gandoy, J. Space-vector PWM with common-mode voltage elimination for multiphase drives. IEEE Trans. Power Electron. 2016, 31, 8151–8161. [Google Scholar] [CrossRef]
- Yu, Z.; Qin, M.; Chen, X.; Meng, L.; Huang, Q.; Fu, C. Computationally efficient coordinate transformation for field-oriented control using phase shift of linear hall-effect sensor signals. IEEE Trans. Ind. Electron. 2020, 67, 3442–3451. [Google Scholar] [CrossRef]
- Lopez, O.; Alvarez, J.; Yepes, A.G.; Baneira, F.; Perez-Estevez, D.; Freijedo, F.D.; Doval-Gandoy, J. Carrier-based PWM equivalent to multilevel multiphase space vector PWM techniques. IEEE Trans. Ind. Electron. 2020, 67, 5220–5231. [Google Scholar] [CrossRef]
- Kothare, M.V.; Campo, P.J.; Morari, M.; Nett, C.N. A unified framework for the study of anti-windup designs. Automatica 1994, 30, 1869–1883. [Google Scholar] [CrossRef] [Green Version]
- Goodwin, G.C.; Graebe, S.F.; Salgado, M.E. Control system design, 1st ed.; Prentice Hall PTR: Hoboken, NJ, USA, 2000. [Google Scholar]
- Harnefors, L.; Yepes, A.G.; Vidal, A.; Doval-Gandoy, J. Multifrequency current control with distortion-free saturation. IEEE J. Emerg. Sel. Topics Power Electron. 2016, 4, 37–43. [Google Scholar] [CrossRef]
- McGrath, B.P.; Holmes, D.G.; McNabb, L. A signal conditioning antiwindup approach for digital stationary frame current regulators. IEEE Trans. Ind. Appl. 2019, 55, 6036–6046. [Google Scholar] [CrossRef]
- Harnefors, L.; Nee, H.P. Model-based current control of ac machines using the internal model control method. IEEE Trans. Ind. Appl. 1998, 34, 133–141. [Google Scholar] [CrossRef]
- Harnefors, L.; Pietilainen, K.; Gertmar, L. Torque-maximizing field-weakening control: Design, analysis, and parameter selection. IEEE Trans. Ind. Electron. 2001, 48, 161–168. [Google Scholar] [CrossRef]
- Zhang, D.; Li, H.; Collins, E. Digital anti-windup PI controllers for variable-speed motor drives using FPGA and stochastic theory. IEEE Trans. Power Electron. 2006, 21, 1496–1501. [Google Scholar] [CrossRef]
- Xia, C.; Ji, B.; Yan, Y. Smooth speed control for low-speed high-torque permanent-magnet synchronous motor using proportional-integral-resonant controller. IEEE Trans. Ind. Electron. 2015, 62, 2123–2134. [Google Scholar] [CrossRef]
- Mattavelli, P.; Tubiana, L.; Zigliotto, M. Torque-ripple reduction in PM synchronous motor drives using repetitive current control. IEEE Trans. Power Electron. 2005, 20, 1423–1431. [Google Scholar] [CrossRef]
- Song, Z.; Wang, Y.; Shi, T. A dual-loop predictive control structure for permanent magnet synchronous machines with enhanced attenuation of periodic disturbances. IEEE Trans. Power Electron. 2020, 35, 760–774. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Borup, U.; Liserre, M. A new control structure for grid-connected LCL PV inverters with zero steady-state error and selective harmonic compensation. In Proceedings of the 19th Annual IEEE Applied Power Electronics Conference and Exposition, APEC ’04, Anaheim, CA, USA, 22–26 February 2004; Volume 1, pp. 580–586. [Google Scholar] [CrossRef]
- Bottrell, N.; Green, T.C. Comparison of current-limiting strategies during fault ride-through of inverters to prevent latch-up and wind-up. IEEE Trans. Power Electron. 2014, 29, 3786–3797. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Estévez, D.; Doval-Gandoy, J.; Yepes, A.G.; Lopez, O.; Baneira, F. Generalized multifrequency current controller for grid-connected converters with LCL filter. IEEE Trans. Ind. Appl. 2018, 54, 4537–4553. [Google Scholar] [CrossRef]
- Moriano, J.; Rizo, M.; Bueno, E.; Sendra, J.R.; Mateos, R. Distortion-free instantaneous multifrequency saturator for THD current reduction. IEEE Trans. Ind. Electron. 2019, 66, 5310–5320. [Google Scholar] [CrossRef]
- Moral, C.G.; Guerrero, J.M.; Fernández, D.; Reigosa, D.; Rivas, C.; Briz, F. Realizable reference antiwindup implementation for parallel controller structures. IEEE J. Emerg. Sel. Topics Power Electron. 2021, 9, 5055–5068. [Google Scholar] [CrossRef]
- Amerise, A.; Mengoni, M.; Rizzoli, G.; Zarri, L.; Tani, A.; Casadei, D. Comparison of three voltage saturation algorithms in shunt active power filters with selective harmonic control. IEEE Trans. Ind. Appl. 2020, 56, 2762–2772. [Google Scholar] [CrossRef]
- Harnefors, L.; Yepes, A.G.; Vidal, A.; Doval-Gandoy, J. Reduction of saturation-induced distortion and antiwindup in multifrequency current control. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Yepes, A.G.; Doval-Gandoy, J.; Toliyat, H.A. Multifrequency current control including distortion-free saturation and antiwindup with enhanced dynamics. IEEE Trans. Power Electron. 2018, 33, 7309–7313. [Google Scholar] [CrossRef]
- Varatharajan, A.; Pellegrino, G.; Armando, E. Direct flux vector control of synchronous motor drives: A small-signal model for optimal reference generation. IEEE Trans. Power Electron. 2021, 36, 10526–10535. [Google Scholar] [CrossRef]
- Lopez, O.; Dujic, D.; Jones, M.; Freijedo, F.D.; Doval-Gandoy, J.; Levi, E. Multidimensional two-level multiphase space vector PWM algorithm and its comparison with multifrequency space vector PWM method. IEEE Trans. Ind. Electron. 2011, 58, 465–475. [Google Scholar] [CrossRef]
- McGrath, B.P.; Parker, S.G.; Holmes, D.G. High-performance current regulation for low-pulse-ratio inverters. IEEE Trans. Ind. Appl. 2013, 49, 149–158. [Google Scholar] [CrossRef]
- Young, H.A.; Perez, M.A.; Rodriguez, J.; Abu-Rub, H. Assessing finite-control-set model predictive control: A comparison with a linear current controller in two-level voltage source inverters. IEEE Ind. Electron. Mag. 2014, 8, 44–52. [Google Scholar] [CrossRef]
- Aguilera, R.P.; Lezana, P.; Quevedo, D.E. Finite-control-set model predictive control with improved steady-state performance. IEEE Trans. Ind. Informat. 2013, 9, 658–667. [Google Scholar] [CrossRef]
- Garcia, C.F.; Silva, C.A.; Rodriguez, J.R.; Zanchetta, P.; Odhano, S.A. Modulated model-predictive control with optimized overmodulation. IEEE J. Emerg. Sel. Topics Power Electron. 2019, 7, 404–413. [Google Scholar] [CrossRef]
- Lim, C.; Levi, E.; Jones, M.; Rahim, N.; Hew, W. FCS-MPC-based current control of a five-phase induction motor and its comparison with PI-PWM control. IEEE Trans. Ind. Electron. 2014, 61, 149–163. [Google Scholar] [CrossRef]
- Lam, C.S.; Wong, M.C.; Han, Y.D. Voltage swell and overvoltage compensation with unidirectional power flow controlled dynamic voltage restorer. IEEE Trans. Power Del. 2008, 23, 2513–2521. [Google Scholar] [CrossRef]
- Habetler, T.G.; Naik, R.; Nondahl, T.A. Design and implementation of an inverter output LC filter used for dv/dt reduction. IEEE Trans. Power Electron. 2002, 17, 327–331. [Google Scholar] [CrossRef]
- Conroy, J.F.; Watson, R. Low-voltage ride-through of a full converter wind turbine with permanent magnet generator. IET Renew. Power Gener.n 2007, 1, 182–189. [Google Scholar] [CrossRef]
- Faiz, J.; Mazaheri-Tehrani, E. Demagnetization modeling and fault diagnosing techniques in permanent magnet machines under stationary and nonstationary conditions: An overview. IEEE Trans. Ind. Appl. 2017, 53, 2772–2785. [Google Scholar] [CrossRef]
- Zhang, P.; Du, Y.; Habetler, T.G.; Lu, B. A survey of condition monitoring and protection methods for medium-voltage induction motors. IEEE Trans. Ind. Appl. 2011, 47, 34–46. [Google Scholar] [CrossRef]
- Cheng, S.; Du, Y.; Restrepo, J.A.; Zhang, P.; Habetler, T.G. A nonintrusive thermal monitoring method for induction motors fed by closed-loop inverter drives. IEEE Trans. Power Electron. 2012, 27, 4122–4131. [Google Scholar] [CrossRef]
- Popov, N.Z.; Vukosavic, S.N.; Levi, E. Motor temperature monitoring based on impedance estimation at PWM frequencies. IEEE Trans. Energy Convers. 2014, 29, 215–223. [Google Scholar] [CrossRef] [Green Version]
- Baneira, F.; Doval-Gandoy, J.; Yepes, A.G.; Lopez, O. DC-current injection with minimum torque ripple in interior permanent-magnet synchronous motors. IEEE Trans. Power Electron. 2020, 35, 1176–1181. [Google Scholar] [CrossRef]
- Yoo, J.; Lee, J.; Sul, S.K.; Baloch, N.A. Stator resistance estimation using dc injection with reduced torque ripple in induction motor sensorless drives. IEEE Trans. Ind. Appl. 2020, 56, 3744–3754. [Google Scholar] [CrossRef]
- Sun, T.; Wang, J.; Griffo, A.; Sen, B. Active thermal management for interior permanent magnet synchronous machine (IPMSM) drives based on model predictive control. IEEE Trans. Ind. Appl. 2018, 54, 4506–4514. [Google Scholar] [CrossRef] [Green Version]
- Sun, T.; Yang, R.; Li, H.; Zhang, X.; Xu, T. Active motor rotor temperature management based on one-node thermal network model predictive control. IEEE Trans. Power Electron. 2020, 35, 11213–11221. [Google Scholar] [CrossRef]
- Wang, C.; Delgado Prieto, M.; Romeral, L.; Chen, Z.; Blaabjerg, F.; Liu, X. Detection of partial demagnetization fault in PMSMs operating under nonstationary conditions. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Pyrhonen, J.; Jokinen, T.; Hrabovcova, V. Design of rotating electrical machines; John Wiley & Sons: Hoboken, NJ, USA, 2008; p. 397. [Google Scholar]
- Wang, H.; Blaabjerg, F. Reliability of capacitors for dc-link applications in power electronic converters–An overview. IEEE Trans. Ind. Appl. 2014, 50, 3569–3578. [Google Scholar] [CrossRef] [Green Version]
- Pu, X.S.; Nguyen, T.H.; Lee, D.C.; Lee, K.B.; Kim, J.M. Fault diagnosis of dc-link capacitors in three-phase ac/dc PWM converters by online estimation of equivalent series resistance. IEEE Trans. Ind. Electron. 2013, 60, 4118–4127. [Google Scholar] [CrossRef]
- Najafabadi, T.A.; Salmasi, F.R.; Jabehdar-Maralani, P. Detection and isolation of speed-, dc-link voltage-, and current-sensor faults based on an adaptive observer in induction-motor drives. IEEE Trans. Ind. Electron. 2011, 58, 1662–1672. [Google Scholar] [CrossRef]
- Gong, Z.; Huang, D.; Jadoon, H.U.K.; Ma, L.; Song, W. Sensor-fault-estimation-based tolerant control for single-phase two-level PWM rectifier in electric traction system. IEEE Trans. Power Electron. 2020, 35, 12274–12284. [Google Scholar] [CrossRef]
- Jlassi, I.; Estima, J.O.; El Khil, S.K.; Bellaaj, N.M.; Cardoso, A.J.M. A robust observer-based method for IGBTs and current sensors fault diagnosis in voltage-source inverters of PMSM drives. IEEE Trans. Ind. Appl. 2017, 53, 2894–2905. [Google Scholar] [CrossRef]
- Riera-Guasp, M.; Antonino-Daviu, J.A.; Capolino, G.A. Advances in electrical machine, power electronic, and drive condition monitoring and fault detection: State of the art. IEEE Trans. Ind. Electron. 2015, 62, 1746–1759. [Google Scholar] [CrossRef]
- Zanardelli, W.G.; Strangas, E.G.; Aviyente, S. Identification of intermittent electrical and mechanical faults in permanent-magnet ac drives based on time–frequency analysis. IEEE Trans. Ind. Appl. 2007, 43, 971–980. [Google Scholar] [CrossRef]
- Yao, Y.; Xie, B.; Lei, L.; Li, Y.; Yin, Q. Signal enhancement method for mechanical fault diagnosis in flexible drive-train. IEEE Trans. Ind. Electron. 2021, 68, 2554–2563. [Google Scholar] [CrossRef]
- Ye, Z.; Wu, B.; Sadeghian, A. Current signature analysis of induction motor mechanical faults by wavelet packet decomposition. IEEE Trans. Ind. Electron. 2003, 50, 1217–1228. [Google Scholar] [CrossRef] [Green Version]
- Cameron, J.R.; Thomson, W.T.; Dow, A.B. Vibration and current monitoring for detecting airgap eccentricity in large induction motors. Proc. Inst. Elect. Eng. Part B 1986, 133, 155–163. [Google Scholar] [CrossRef]
- Nandi, S.; Ahmed, S.; Toliyat, H.A. Detection of rotor slot and other eccentricity related harmonics in a three phase induction motor with different rotor cages. IEEE Trans. Energy Convers. 2001, 16, 253–260. [Google Scholar] [CrossRef]
- Malvar, J. Analysis of Time and Space Harmonics in Symmetrical Multiphase Induction Motor Drives by Means of Vector Space Decomposition. Ph.D. thesis, Department of Electronics Technology, University of Vigo, Vigo, Spain, 2015. [Google Scholar]
- Jiang, J.W.; Bilgin, B.; Sathyan, A.; Dadkhah, H.; Emadi, A. Analysis of unbalanced magnetic pull in eccentric interior permanent magnet machines with series and parallel windings. IET Electric Power Appl. 2016, 10, 526–538. [Google Scholar] [CrossRef]
- Che, H.S.; Hew, W.P. Dual three-phase operation of single neutral symmetrical six-phase machine for improved performance. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 1176–1181. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).