Abstract
This paper recommends an alternative designing process for a superior road racing bicycle frame manufactured from composite materials that is much faster than typically used design processes. The main design goal is for the rider to be faster under the same riding conditions and with the same effort made. This performance gain is the result of a combined structural and aerodynamic optimization process used during the design process along with the selection of the materials. As the needs of the rider are the focus of this design proposal, the optimization can be carried out only after they are understood. The main difference in this approach compared to the typically used methodology is that, instead of analyzing the frame as a whole from the beginning of the design process and the CFD and CAE iterations, we examine each candidate part of the frame separately. After evaluating the parts’ performances, we select those that performed better to create a single frame. This final frame design is used to choose the appropriate layup that would meet the performance needs of the riders and the necessary safety regulations. The benefit of this approach is that the design time is reduced, allowing the product to reach the market faster. Furthermore, it is more convenient and easier to make any modifications required by marketing or regulations.
1. Introduction
After their introduction and mass production, composite materials such as polymer matrix composites have been increasingly used in mass transit applications [1] and consumer products. This was because they possessed superior properties, such as strength, fatigue life, stiffness, low weight [2], and sometimes, aesthetics. New recycling methods help with the further expanding use of these materials [3]. Pre-Impregnated Carbon Fiber Reinforced Plastic (CFRP) sheets, in particular, are a revolutionary material for composites manufacturing. They are lighter, more durable in harsh conditions, and allow more aerodynamic shapes to be manufactured. Non-CFRP frames are comprised of many separate tubes, which are then united by using different methods, such as soldering (if they are metal frames). This creates a “bumpy” surface at the tubes’ joints, which in turn may create turbulence in the flow when riding. CFRP frames may also have separate tubes, but their joints are not visible over the paint. The smooth surface allows the air to flow around it without causing turbulence. Furthermore, CFRP can be used to create a plethora of shapes that would not be easily manufactured with traditional materials, eliminating any manufacturing restrictions that non-CFRP frames face. In addition, the correct use of their orthotropic properties by the engineer can create products that are stiff in one direction and more compliant in another, leading to great design freedom. This makes them an ideal material for bicycle frame manufacturing by offering the advantages of high strength and stiffness to weight ratios, long fatigue life, low density, corrosion resistance, wear-resistance, and environmental stability [4] along with low weight. For example, a carbon/epoxy bicycle frameset may weigh less than 1 kg, and this is much less than the 5 kg weight of a same steel frame [4].
Advanced knowledge of modern CAD modeling programs, such as SolidWorks, CATIA, Creo, Siemens NX, etc., is necessary to make the design and evaluation of the initial frame easier and its modifications more flexible until a final shape is attained [5]. The creation of CAD models instead of physical prototypes during the design process is faster, costs less (both because of time saved and material waste), and allows the engineers to test much more virtual solutions compared to actual prototypes. The above factors make the creation of CAD models a much more efficient method to design products [6,7].
For an evaluation of the aerodynamic performance of the resulting bicycle frame from each iteration step during the design process, CFD is used to easily set up and solve the complex equations that describe the airflow around the bicycle [8,9]. Depending on available computing power, many different scenarios can run simultaneously, resulting in a very fast bicycle frame in less time compared to physical prototypes and wind-tunnel or real-life testing. A frame that is manufactured by taking into consideration aerodynamic principles is faster under the same conditions than a non-aerodynamic frame because it requires less effort (and therefore, energy output) by the rider [10]. These CFD tools are the same for the ones used in the analysis of various other applications, such as aircrafts [11,12], wind turbine blades [13], and underwater vehicles [14].
The design of a state-of-the-art bicycle frame also requires a precise understanding of the applied loading conditions along with a deep knowledge of the stress development and failure analysis of composite materials [15]. Based on theoretical or numerical calculations, the strength and stiffness of the bicycle structures can be predicted and modified to be made optimal before the manufacturing of the prototype takes place. Finite element analysis (FEA) is used to calculate stress/strain fields and fatigue life of the structures [16]. It is a computational tool that is widely used in the automotive industry and manufacturing of composite leaf and coil springs [15,16], suspension lower arms [17], in hovercrafts [18], bus manufacturing [2], wheelchair wheels for athletes [19], aircrafts [20], and wind turbine blades [21]. In bicycle manufacturing, application examples include the design of a composite crank [22] and frames [7,23,24,25,26,27].
The efficient selection of materials and layup for the frame requires the evaluation of its performance under different loading scenarios and material choices. This evaluation includes a variety of composite materials, a wide range of ply angles, and a different number of plies in each part of the frame [28].
This paper presents the whole process of such a project by making an introduction to all the steps needed to design and test the mechanical and aerodynamic properties of a composite road racing bicycle frame by using computational tools with user-friendly environments (with the aid of pre-processors, solvers, and post-processors). The results are visualized for faster and better reviewing.
What makes our designing process different is the manner of the approach. In such a design scenario, the designer would typically start with a given geometry for the frame (typically from bike fitting statistics) and then make a full 3D model of it. The shapes of the tubes are initially chosen for aesthetical reasons and in a way in which all the necessary components can be assembled on the frame. In the CAD environment, the components are fitted on the frame. Then, a typical-sized rider for the given bicycle frame size is fitted on the assembly of the frame and the various components. Next, CFD and FEA simulations are executed to improve the shape of the tubes. This can be performed either manually by using a parametric optimization tool or with the use of a topological optimization tool. Due to the complexity of the bicycle tube connections and their interaction with the other components and the rider, a lot of effort is needed to redesign or modify the existing parts. In addition, it is very demanding on computer time, and especially on pre- and post-processing during computational fluid dynamics analysis and finite element analysis.
Instead of using this strategy, our approach was to start by using a spaceframe model from a bike fitting analysis, which was gradually modified to be able to accommodate the necessary parts, such as the wheels. Following this, a fast FEA analysis was conducted using beam element spaceframe models to determine which part of the frame received loads in the different loading scenarios. The next step was to design various cross-sections for each tube that seemed to be able to receive the loads that each part of the frame bore. Then, these shapes were tested in CFD for aerodynamic performance as well as in bending and torsional loads for structural evaluation. The selection of the most suitable shape for each tube was made by comparing the advantages of each cross-section model and the load requirements of each part of the frame. The 3D design that derived from the combination of the selected spaceframe model and cross-sections for each tube was used to find the appropriate laminate layup that would satisfy the security regulations set by the ISO standards and would have the required lateral stiffness for performance and vertical compliance for comfort.
This approach is less time-consuming because the simulation of separate single tubes is much faster compared to designing and simulating a full model in each design iteration. Compared to full-frame analysis in each iteration, we expect that the result in CFD may be a little different, but the actual percentage of drag for the frame alone compared to the full bicycle rider combo is too small for this to matter. Any possible structural issue, for example, a stress raiser point, can be fully covered by changing the layup or changing the composite material. The above means that this method can bring the product to the market faster and with less cost for the designer and/or manufacturer, thus making it more competitive on the market.
2. Materials and Methods
2.1. Design Decisions and Strategy
In order to develop a product that appeals to a targeted end-user group and possesses sufficient mechanical properties, visual appearance, and other useful features, an effective process plan must be created in the engineering design.
This process plan starts with market needs (what do we need to do and why do we need to do it?), followed by a conceptual design (the ideas, possible solutions, materials, lay-ups, etc.), a preliminary design (sketches, a shortlist of possible solutions), and a detailed design (working drawings, more accurate data, refined cost estimates, finite element analysis, coupon tests). The process ends with the development of a prototype and, finally, the production of the design, as shown in Figure 1 [29].
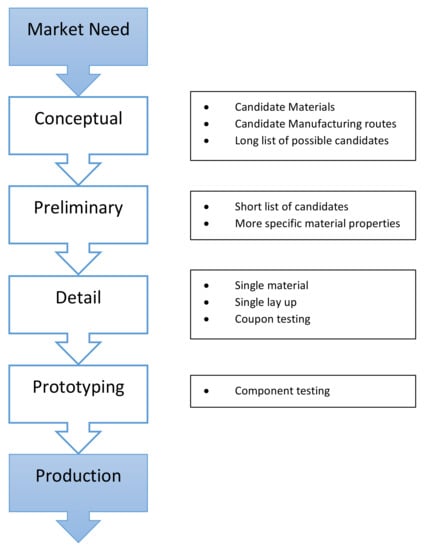
Figure 1.
Designing process flow chart adapted from [29].
The basic idea was to go through a variety of structural composite designs, perform appropriate calculations, including FEA, to determine their performance, incorporate the results into a database, work with the data to screen out infeasible solutions or those not meeting the design constraints, and, finally, identify a shortlist of solutions that best meet the design goals [29].
The design brief sets the framework for the design and provides the ‘‘need’’ that the product must satisfy. This is where the planning process comes to life, converting the latter ideas into action. A useful flow chart is shown in Figure 2, describing the whole process and making the visualization easier for the reader [29].
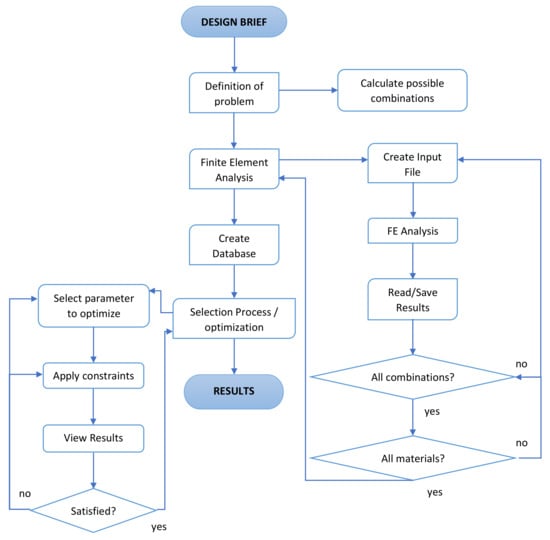
Figure 2.
Design and FEA process flowchart adapted from [29].
2.2. CAD Processing and Spaceframe Sequence
Our initial goal was to depict the frame dimensions that came from statistical bike fitting measurements and rider reviews of previous designs so that we could have a starting point for the first frame size design. The other sizes would come up later, after the completion of the prototype, and create a database for future reference and further evolution. This initial design would be changed to meet manufacturing needs and standards compliance. A basic sketch of the frame’s tubes and their names are shown in Figure 3 [30]. The design sequence is shown in Figure 4, and the design change steps are described below.
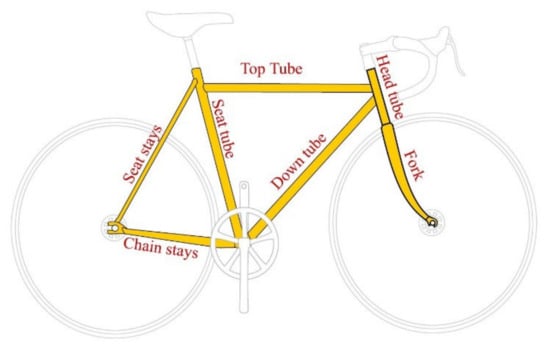
Figure 3.
Basic tube diagram of a typical frame [30]. No changes were made to the original illustration (Keithonearth, CC BY 3.0).
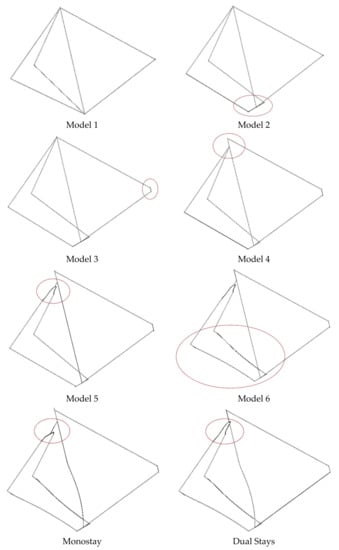
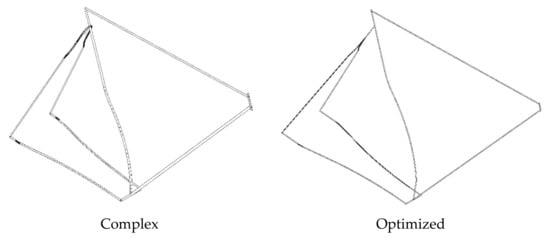
Figure 4.
Sequence of simple spaceframe design.
Firstly, we wanted the resulting frame to comply with the standards set by the UCI. From the regulations set by the UCI, the following must be true:
- The frame must be of a traditional pattern, i.e., built around the main triangle, which consists of the top tube, head tube, down tube, and seat tube.
- It shall be constructed out of straight or tapered tubular elements (which may be round, oval, flattened, teardrop-shaped, or otherwise in cross-section) such that the form of each element encloses a straight line.
- The elements of the frame shall be laid out in such a way that the joining points shall follow the following pattern: the top tube connects the top of the head tube to the top of the seat tube; the seat tube (from which the seat post shall extend) shall connect to the bottom bracket shell (which houses the bearings for the crankset); the down tube shall connect the bottom bracket shell to the bottom of the head tube.
- The rear triangles shall be formed by the chain stays, the seat stays, and the seat tube, with the seat stays anchored to the seat tube at points falling within the limits laid down for the slope of the top tube.
- The maximum height of the elements shall be 8 cm and the minimum thickness 1 cm.
- The minimum thickness of the elements of the front fork shall be 1 cm; these may be straight or curved.
- The top tube may slope, provided that this element fits within a horizontal template defined by a maximum height of 16 cm and a minimum thickness of 2.5 cm [31].
As shown in Model 1, we started with a basic bicycle frame that lacked shape and included only the basic tubing (i.e., top tube, down tube, seat tube, chain stays, and seat stays). Then, the bottom bracket was added to accommodate the crankset in Model_2. The headtube was added to house the steerer tube of the fork in Model_3. The seat stays were lowered to lower the center of gravity in Model_4 and then shaped to accommodate the wheel in Model_5. The chain stays were shaped to create clearance for the wheel and the crankset in Model_6. These first six models were each an evolution of the previous spaceframe model by adding the necessary geometries and accounting for the various parts of the bicycle. The next four models, mono-stay, dual-stay, complex, and optimized, were variations of Model_6 with small differences between each other. They all presented a curvature on the middle and bottom part of the seat tube to create the necessary space for the rear wheel to fit. In the mono-stay model, the two seat stays were united into a single tube before coming into contact with the seat tube. In the dual-stay model, the two seat stays tubes were directly connected to the seat tube. The complex model had the same set-up for the seat stays as the dual-stay model, but the bottom bracket was lowered. The optimized model further shortened the bottom bracket and the head tube lengths, while uniting the seat stays before meeting the seat tube in a mono-stay set-up. The different spaceframe models we developed and examined are shown in Figure 4. In each picture of the various models, the red line encircles the main difference compared to the previous model. As far as the complex and optimized models are concerned, the variations were many and relatively small, therefore no highlights are shown on them.
2.3. Spaceframe Modeling, Testing, and Loading Scenarios
During the changes described in Section 2.2, the spaceframe was tested to determine which loads affected each part of the frame. These loads were used as a guide when adding shape to the spaceframe to acquire optimized mechanical strength and controllable deformation phenomena. The first six models were not actually viable solutions as their shape cannot accommodate all the necessary equipment needed in a bicycle. Even though Model_6 looked like a viable solution, the short chain stays do not allow the rear wheel to fit on the frame. Only the last four models, mono-stay, dual-stays, complex, and optimized, were the real possible solutions; however, we extended the analysis to the first six models to see how the evolution of our design affected the stresses and displacements that occur on the spaceframe models.
The spaceframe was modeled using beam elements to obtain results quickly. By doing this, we get an idea of the needs of each part before applying a shape to it. We can also view a qualitative comparison between the various spaceframe models as far as maximum displacement and stresses are concerned.
There are several methods for testing a bicycle frame, suggested by approved testing methods from ISO 4210-6 standards [32] or by the literature [15,32]. The FEA tests conducted on the frame were: a horizontal forces scenario as shown in Figure 5a (with a dynamic loading force of 600 N at a frequency of 25 Hz applied on each end of the head tube); a static start-up in a hill climb scenario as shown in Figure 5b (with an overweight rider in mind, and axial loading forces of 143.6 N inwards and 1090 N downwards on each side of the bottom bracket shell); a riding scenario as shown in Figure 5c (with stable chain and seat stays and axial loading forces of 20 kgf at each side pedal connected to the bottom bracket, 70 kgf at the end of the seat tube, and two 20 kgf forces on each end of a handlebar connected to the head tube); and in the end, two frame out-of-plane loading scenarios (one with stable seat, bottom bracket, chain stays, and seat stays and axial loading forces of 600 N at the head tube, as shown in Figure 5d, and one with stable seat, chain stays, seat stays, and head tube and axial loading forces of 600 N at the bottom bracket, as shown in Figure 5e). It should be noted that each spaceframe design model scenario presented previously was tested separately for the first three loading scenarios, these being the horizontal forces, the static start-up, and the riding scenarios. Only the last four models (mono-stay, dual-stays, complex, and optimized) were tested on all five loading scenarios because they were the only viable choices. In Figure 5, the first three loading scenarios applied to the Model_6 spaceframe and the two out-of-plane loading scenarios applied to the optimized geometry spaceframe are presented. Fixed constraints and loads are represented with green and red colors, respectively.
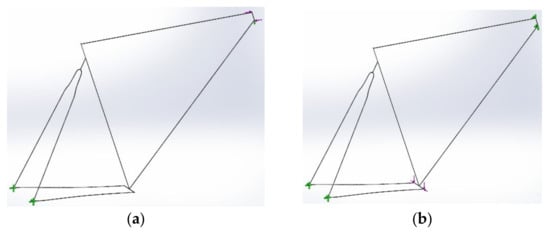
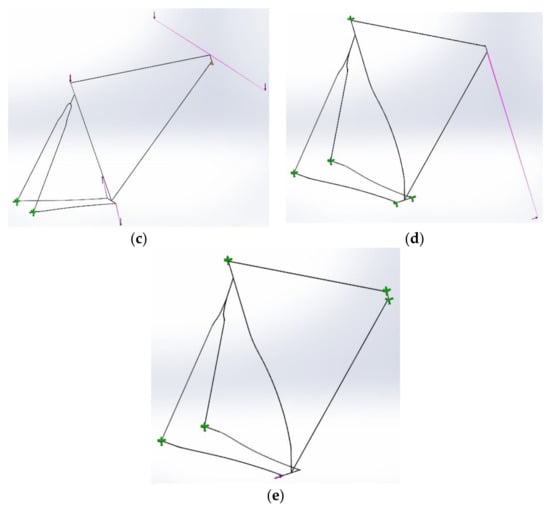
Figure 5.
Tested loading scenarios: (a) horizontal forces scenario with fixed constraints on the rear ends of the stays, simple support on the bottom end of the head tube, and forces on either end of the head tube; (b) static start-up scenario with fixed constraints on the rear ends of the stays and either end of the head tube, and loads on either end of the bottom bracket shell; (c) riding scenario with fixed constraints on the ends of stays, simple support on the bottom end of the head tube, and forces on the top of the seat tube, either end of the handlebar and the crankset; (d) out-of-plane load to head tube scenario with fixed constraints on the ends of the stays, top of seat tube, and bottom bracket shell; (e) out-of-plane load to bottom bracket shell scenario with fixed constraints on the ends of the stays and head tube.
2.4. Static Loads Analysis on the Frame Tubes
After testing the various spaceframe models in the five scenarios described above, we needed to determine the shape of each tube of the frame. To accomplish this, we designed different cross-sections for each tube. These cross-sections were initially tested using a torsional and a bending load. These static tests were used to determine the maximum stress and displacement for each cross-section and then perform a qualitative comparison among them. As we simply wanted to see the effect of the tube shape on the distribution of stresses and whether it could create an area of high stress, we decided to use the same material and layup recipe for the simulations; this was T300 Woven, and the laminate recipe was [(45F/0F)2]T [±45/0–90]2.
The cross-sections that were designed for each tube of the frame are listed below and shown in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.
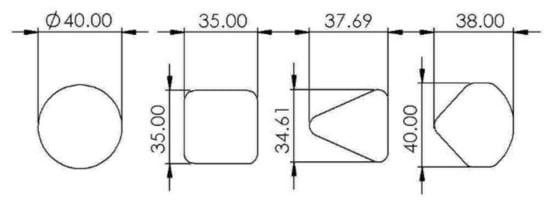
Figure 6.
Top tube cross-sections from left to right: circular 40 mm, rectangular 35 × 35 mm, triangular, and complex.

Figure 7.
Down tube cross-sections from left to right: oval 39 × 79, oval 45 × 79, oval 51 × 79, circular 60.7 mm, rectangular 50 × 50, complex 1, and complex 2.

Figure 8.
Seat tube cross-sections from left to right: complex 1, complex 2, complex 3, complex 4, and circular 34.9 mm and 53 mm.
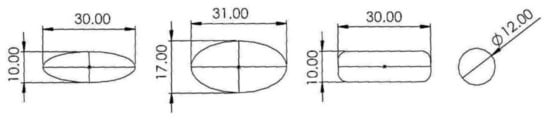
Figure 9.
Seat stay cross-sections from left to right: oval 10 × 30, oval 17 × 30, rectangular 10 × 30, and circular 12 mm.

Figure 10.
Chain stay cross-sections from left to right: oval 15 × 45, oval 20 × 60, rectangular 15 × 45, rectangular 20 × 60, and circular 18 mm.
The cross-sections designed for the top tube, shown in Figure 6, were:
- A circular cross-section, with 40 mm diameter.
- A square cross-section, 35 mm × 35 mm.
- A triangular cross-section with 37.69 mm height and 34.61 mm width.
- A complex geometry cross-section with 38 mm height and 40 mm width.
The cross-sections designed for the down tube, shown in Figure 7, were:
- Three oval-shaped cross-sections with 79 mm height and width 39, 45, and 51 mm, respectively.
- A circular cross-section with 60.7 mm diameter.
- A square cross-section, 50 mm × 50 mm.
- Two complex geometry cross-sections with 79 mm height and 45 and 48 mm width, respectively.
The cross-sections designed for the seat tube, shown in Figure 8, were:
- Four complex geometry cross-sections with the same height (60 mm) and various widths, as shown in Figure 8.
- Two circular cross-sections with 34.9 mm and 53 mm diameter, respectively.
The cross-sections designed for the seat stays, shown in Figure 9, were:
- Two oval-shaped cross-sections, 10 × 30 mm and 17 × 31 mm, respectively.
- A rectangular cross-section, 10 × 30 mm.
- A circular cross-section with 12 mm diameter.
The cross-sections designed for the chain stays, shown in Figure 10, were:
- Two oval-shaped cross-sections, 15 × 45 mm and 20 × 60 mm, respectively.
- Two rectangular cross-sections, 15 × 45 mm and 20 × 60 mm, respectively.
- A circular cross-section with 18 mm diameter.
In order to run the simulations, all the cross-sections were positioned vertically. A fixed constraint was applied to the bottom end of the tube and the loads (a bending load of 250 N and a torsional load of 50 Nm) were applied to the top end of the tube.
2.5. CFD (Computational Fluid Dynamics) Analysis of the Frame’s Tubes
In order to aerodynamically test the cross-sections that we designed for each tube, first, we needed to determine which velocities and yaw angles we needed to use for the simulations.
If the air is still while the rider is driving, the rider still perceives the air as moving with a velocity equal to his. This means that if the rider is driving with wind, the overall velocity of air Vin that the rider perceives is the summary of both the velocity of the wind Vw and the velocity of the rider Vr. The angle between the rider’s direction and the wind velocity Vin is called the yaw angle (ay). This is also depicted in Figure 11.

Figure 11.
Total wind velocity as perceived by the rider.
The next step was to select the wind velocity Vw that a cyclist may drive through. Using a wind atlas [33] similar to the one shown in Figure 12 as a guide, we can estimate that the most common wind velocity is between 3 m/s and 8 m/s, which is the equivalent of 3 and 4 Beaufort. We decided to use 5 m/s or 18 km/h wind velocity in our simulations because it is in the middle of the range.
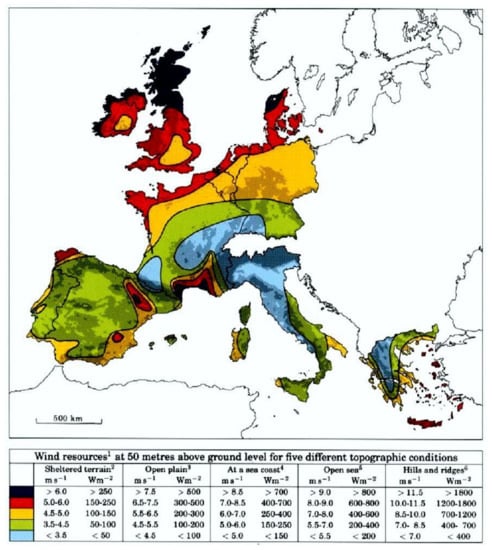
Figure 12.
Wind atlas of Europe [33] 1989 DTU Wind Energy, formerly Risø National Laboratory.
The velocity of the rider is chosen to represent a typical velocity he might achieve in a race. Under still wind conditions, a cyclist may develop a speed of 45 km/h; therefore, this would be one of our design points in the CFD analysis. In the case of a resisting wind of 18 km/h, like the one we chose earlier, we considered a rider velocity of 32 km/h.
The yaw angle of the total perceived wind is the next variable we needed to specify to fully describe our CFD analysis. From Figure 13, it is obvious that the most common yaw angles are between −12 and 12 degrees. We decided to use three different yaw angles in our simulations, 2°, 7°, and 12°.
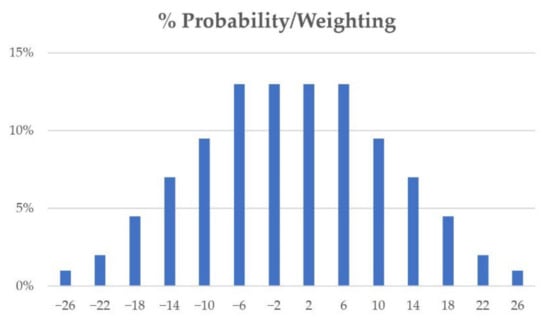
Figure 13.
Probability/weighting of each yaw angle.
Table 1 lists the four design points we used for the CFD analysis as well as the values of the different variables. We also listed the weight for the drag and the side force, this being the same for each design point. This is because we wanted to account for both of these forces and not solely for the drag in our analysis, as the side force impacts the overall stability of the bicycle and rider and also the sense of security of the cyclist.

Table 1.
The four design points and their weights.
We know from Figure 12 and the wind atlas that a zero-wind velocity is not commonly encountered, therefore we only gave this a 10% weight in the overall analysis. The rest of the design points were given weights according to their probability, as shown in Figure 13. For yaw angles 2° and 7°, the probability is almost the same, whereas, for 12°, the probability is more than half of that for 2° and 7°. That is why design point 2 was given a 20% weight and both design points 3 and 4 were each given a 35% weight.
Each of the cross-sections for the tubes was given the appropriate length and direction, as indicated from a bike fitting analysis. For each cross-section, we created a file with four design points where the computational area, the mesh, and the orientation of the model were the same but the velocities in the × direction (driving direction of the cyclist) and the Y direction (vertical to the driving direction) changed according to the conditions specified in Table 1.
The computational domain was checked to ensure that it encompassed the entire tube; however, as the orientation of the various tube models varies, so does the size of the domain. The mesh we used was a structured Cartesian mesh that had a basic mesh size of 5 × 5 × 5 mm with a level four refinement level, which means that the mesh size near the surface of the tube is 0.625 × 0.625 × 0.625 mm.
The final step involved the start of the simulation and monitoring the process until its finalization. Figure 14 shows the flow lines around chosen cross-sections of the seat tube in design point 1 CFD analysis.
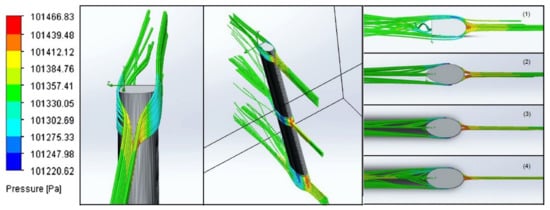
Figure 14.
Flow and pressure area lines on seat tube cross-sections in design point 1. From left to right: the two left pictures show the flow lines around the complex 1 cross-section from different views. The next three pictures show the flow lines around the complex 4, complex 3, and complex 1 cross-sections as viewed from above. The different colors represent the variation of pressure caused when the air flows around the models (red indicates high pressure, blue is low, and green is atmospheric pressure).
2.6. Final CAD Model
Using the results of these initial simulations, we were able to create the final CAD model of the bicycle frame. The optimized spaceframe model has the best overall behavior when subjected to the aforementioned spaceframe loading scenarios, which is explained in the results section. Taking into consideration the results for each tube cross-section, the final frame is depicted in Figure 15.

Figure 15.
Final frame model.
The joint areas where two or more tubes meet were created by initially joining the tubes and then creating smooth transitions between them. To avoid stress raising areas, flow separation, and detachment of the boundary layer from the surface, the joints were selected to have large curvature and G2 continuity with the surrounding surfaces.
2.7. Final CAD Model Loading Scenarios
A new set of experimental simulations was created to represent the safety requirements for bicycles set by ISO 4210 [34]. Those experimental simulations, which are depicted in Figure 16, consisted of five different scenarios:
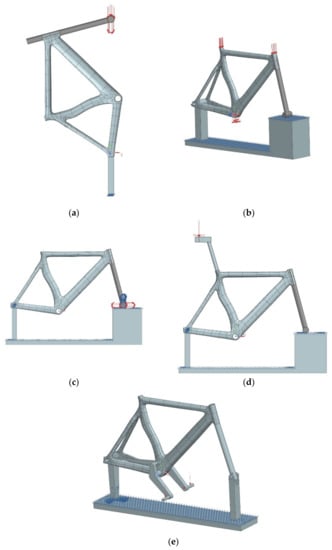
Figure 16.
(a) FE method preview of drop mass test, (b) FE test method preview of the falling frame, (c) FE test method preview of horizontal forces, (d) FE test method preview of vertical force through the seat tube, (e) FE test method preview of pedaling forces.
- Drop mass;
- Falling frame;
- Horizontal forces;
- Vertical force through the seat post;
- Pedaling forces.
The red arrows represent the direction of the loads applied in each scenario.
The drop mass test, depicted in Figure 16a, is an impact test wherein a dummy fork is assembled on the vertically supported frame and a 22.5 kg mass is dropped 212 mm above the end of the fork. The mass is released and allowed to bounce on the end of the fork until it comes to rest on it. The wheelbase is measured before and after the impact. We used a non-linear dynamic simulation with an implicit solver, where the falling mass was placed directly above the end of the fork just before the contact point. The load is the velocity that the mass acquires because of the drop.
The falling frame test, as shown in Figure 16b, is also an impact test. The frame with the assembled fork is constrained and able to rotate around the axle of the rear wheel. Three masses are placed on the frame: a 30 kg mass on the seat post, a 10 kg mass on top of the steering head, and a 50 kg mass on the bottom bracket. The wheelbase is measured with the three masses and the end of the fork resting on the floor. The lower end of the fork is then raised 200 mm above the floor, and the assembly is allowed to fall freely to impact the floor; the wheelbase is remeasured when the assembly comes to a rest. In this case, we again used a nonlinear dynamic simulation with an implicit solver, where the assembled frame fork was placed just before the lower part of the fork comes into contact with the floor. The loads are the angular velocity due to the rotation of the assembly under the gravitational acceleration and the static forces due to the masses fastened on the frame.
Figure 16c features the horizontal forces test, which is a fatigue test wherein a horizontal force of 600 N in a forward and a rearward direction is applied at the lower part of the fork for 100,000 cycles, with a maximum frequency of 10 Hz. In this case, the load applied is a nonlinear dynamic force and the simulation takes into account the large displacements that occur.
The test of the vertical force through the seat post is another fatigue test and is presented in Figure 16d. A dynamic vertical force of 1200 N is applied on the dummy seat post 70 mm behind the intersection of the ax of the seat post and the flat part for 50,000 cycles, with a maximum frequency of 10 Hz. In this case, the load applied is a nonlinear dynamic force and the simulation takes into account the large displacements that occur.
The pedaling forces test, shown in Figure 16e, is also a fatigue test wherein dynamic forces of 1100 N are applied on each side of a dummy crankset, whose geometry is specified by the ISO. Both of the cranks are 175 mm long and are inclined forwards and downwards at an angle of 45° to the horizontal. The crank is secured by a rod that connects the top of the dummy crankset to the rear axle replacing the chain. Each pedal spindle is subjected to a repeated downward force at a position 150 mm from the centerline of the frame in a vertical, transverse plane and inclined at 7.5° to the fore/aft plane of the frame. The forces are applied to the pedals for 100,000 test cycles. In this case, the load applied is a nonlinear dynamic force consisting of two components, one downward and one inward, to account for the 7.5° angle; the simulation takes into account the large displacements that occur.
For the simulations, the fork and all the peripheral parts were modeled as solid parts made of steel with a 3D CTETRA (10) mesh. Their element size varied according to their dimensions, curvature, and overall geometry. The frame was modeled as a sheet part where each tube had a different 2D mesh to account for the various layup recipes and orientations of each section of the frame. The 2D mesh in every case was a CTRIA3 mesh with a 1.5 mm element size, which was able to accurately represent all the small features of the frame without increasing the computational time disproportionally. To simulate the overlap of the layup at the junctions between the tubes, a different 2D mesh was created in each case where the layup recipe contained the plies of both the recipes of the respective tubes taking into account their different orientation.
2.8. Material Layup and Stacking Orientation
After the work described above and 3D modeling the frame, to create a competitive bicycle frame we had to choose the final fabrication materials and specify the layup stacking sequence to achieve an optimal combination of weight and strength. Besides, we had to make a necessary compromise between these factors and the fact that the structure had to pass the requirements of approved testing methods, as described above.
The materials tested in this process were the TORAYCA M46J Woven, M46J UD, T300 Woven, and T700 UD in sheet form and pre-impregnated with resin [35,36,37]. The first two stacking scenarios shown in Table 2 and Table 3 were quasi-isotropic types with a material layup recipe of [(0F/45F)2]T and M46J Woven and T300 Woven, respectively, as testing materials applied to the whole frame. The reason was to create a comparison between displacement and compression and tensile stresses so that the material layup could be upgradable at each tube of the frame and we would then have an indication of which material to use.

Table 2.
Quasi-isotropic layup using M46J Woven fabric.

Table 3.
Quasi-isotropic layup using T300 Woven fabric.
These quasi-type stacking scenarios were the benchmark to check further stacking scenarios, under the same conditions as the FE analysis, to better understand how material selection, sequence, and orientation affect the final results. Each tube of the frame has its own orientation, therefore the angle of each layer is relevant to the element orientation of each tube.
The two quasi-isotropic scenarios were used as a basis for the development of the stacking scenarios. Depending on the distribution of the strain energy in the optimized geometry spaceframe model, extra plies were gradually added on the tubes that bore most of the stresses. Next, the load that each ply bore as well as its direction were evaluated. For instance, if a woven ply bore stressed only in direction 11, it was replaced by a unidirectional ply in the direction that was loaded to remove any unnecessary mass. In some stacking scenarios, each woven ply was replaced by two unidirectional ones to check for any differentiation between the use of the woven and their equivalent unidirectional materials. The difference between the effects of the two sets of materials, T300 Woven with T700 UD and M46J Woven with M46J UD, on the overall behavior of the frame was also tested. The next step was to check the displacements for the various loading cases, which we wanted to minimize. In the case of the pedaling test, an attempt was made to ensure that the displacements caused by applying the forces on either side of the bottom bracket were similar; this is why the layup recipe on the chain stays was differentiated.
Table 4 shows stacking scenario 1. The material used in this scenario was the T300 Woven fabric. This time, there was a differentiation in the layup recipe of the various tubes of the frame, creating two groups: the first group consisting of the headtube, downtube, seat tube, and chain stay right with a [(45F/0F)3]T layup recipe, and the second group consisting of the top tube, seat stay left and right, and chain stay left with [(45F/0F)2]T.

Table 4.
Stacking scenario 1.
T300 Woven was also used in stacking scenario 2, as shown in Table 5. We now had three different groups; the first with a [(45F/0F)4]T layup recipe on the headtube and chain stay right, the second with a [(45F/0F)3]T recipe on the downtube and chain stay left, and, finally, the third group with [(45F/0F)2]T on the top tube, seat tube, and both seat stays.

Table 5.
Stacking scenario 2.
In stacking scenario 3 (Table 6), we introduced a unidirectional material; thus, apart from the T300 Woven fabric, we also had the T700 UD. Apart from for the top tube and both the seat stays that used the same layup recipe [45F/0/45F/0F]T, each of the other tubes had a different sequence. The head tube followed the [(45F/0F)4]T layup recipe and the seat tube followed [45F/0/0F/02]T. The downtube used the [(45F/0)3]T, the left chain stay used the [(45F/0)2/45F/0F]T, and the right chain stay used the [(45F/0)2/45F/0F/45F/0]T.

Table 6.
Stacking scenario 3.
Stacking scenario 4 in Table 7 had the same headtube, downtube, and seat tube recipes as stacking scenario 3. The top tube and both seat stays had a [45F/0/45F]T recipe, the left chain stay a [(45F/0)3]T recipe, and the right chain stay a [(45F/0)4]T recipe. The materials used were the T300 Woven and the T700 UD.

Table 7.
Stacking scenario 4.
In stacking scenario 5 of Table 8, the only material used was the M46J UD. The headtube followed a [(±45/0/90)3]T recipe, the top tube and both seat stays a [±45/0]T recipe, the downtube a [(±45/0)3]T recipe, the seat tube a [±45/0/90/03]T recipe, the left chain stay a [(±45/0)2]T recipe, and lastly, the right chain stay a [(±45/0)3]T recipe.

Table 8.
Stacking scenario 5.
Stacking scenario 6, shown in Table 9, had many similarities to stacking scenario 4. The main difference was that the materials used in this case were M46J Woven and M46J UD on the headtube, downtube, seat tube, and both the chain stays and T300 Woven and T700 UD on the top tube and both of the seat stays. However, most of the recipes on the tubes remained the same except for the headtube, which had a [(45F/0F)3]T layup.

Table 9.
Stacking scenario 6.
Stacking scenario 7, in Table 10, was also very similar to stacking scenario 4. The only difference here was that instead of the T300 Woven, we used the M46J Woven, and instead of the T700 UD, we used the M46J UD.

Table 10.
Stacking scenario 7.
Table 11 shows stacking scenario 8, which also used the M46J Woven and M46J UD materials and had many similarities to stacking scenario 7. The layup recipes for the down tube, seat tube, and both the chain stays remained the same, whereas the headtube had [(45F/0F)3]T layup and the top tube and both seat stays had [45F/0F]T.

Table 11.
Stacking scenario 8.
In stacking scenario 9 of Table 12, there was a significant increase in the material in each tube. Specifically, the headtube had the [(45F/0F)6]T layup recipe, the top tube and both seat stays had [(45F/0)3]T, the downtube and left chain stay had [(45F/0)4]T, the right chain stay had [(45F/0)5]T, and the seat tube had [45F/0/0F/02/45F/0/0F/0]T.

Table 12.
Stacking scenario 9.
Finally, stacking scenario 10, presented in Table 13, was basically the same as stacking scenario 5, but instead of the M46J UD, the material used was the T700 UD. The headtube followed a [(±45/0/90)3]T recipe, the top tube and both seat stays a [±45/0]T, the downtube a [(±45/0)3]T, the seat tube a [±45/0/90/03]T, the left chain stay a [(±45/0)2]T, and lastly, the right chain stay a [(±45/0)3]T recipe.

Table 13.
Stacking scenario 10.
3. Results and Discussion
3.1. Spaceframe Models’ Results and Selection
The simulation results of all the tests that were executed during the design process of the bicycle road frame are presented in this section of the paper. They include tables, charts, and comments. The material used for these simulations was an isotropic test material and the failure criterion used was the Von Mises. As these simulations do not use composite materials, the Von Mises failure criterion was adequate for this part of the study. Furthermore, the resulting stresses and displacements are of low importance because they are only used for a qualitative comparison between the different spaceframe models.
In the beginning, all the spaceframe geometries were tested in three loading scenarios and the final four models in five loading scenarios. The results of displacements, stresses, and strain energy distribution are shown in Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25.
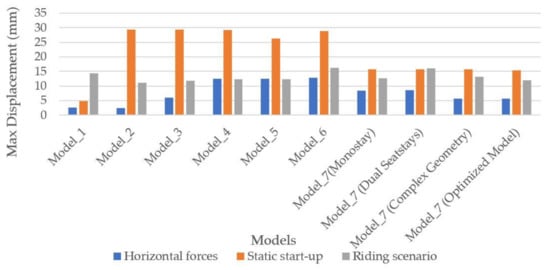
Figure 17.
Maximum displacement per model in horizontal impact, in static start-up, and in riding scenarios.
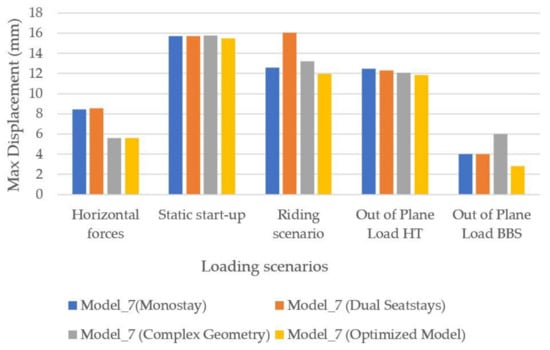
Figure 18.
Maximum displacement per model in horizontal impact, static startup, riding, out-of-plane load in the headtube, and out-of-plane load in the bottom bracket shell scenarios.
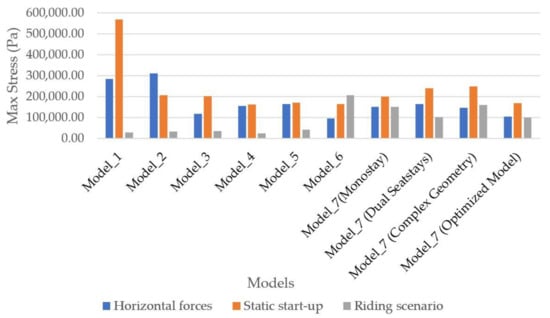
Figure 19.
Maximum stress of horizontal impact, static start-up, and riding scenarios per model.
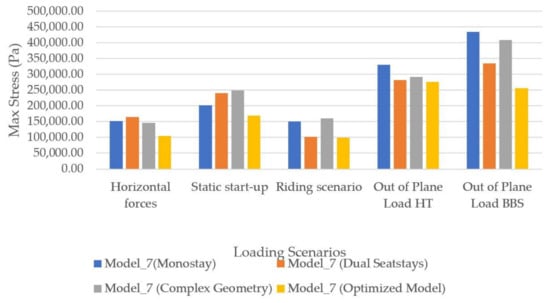
Figure 20.
Maximum stress per model in horizontal forces, static start-up, riding, out-of-plane load in the headtube, and out-of-plane load in the bottom bracket shell scenarios.
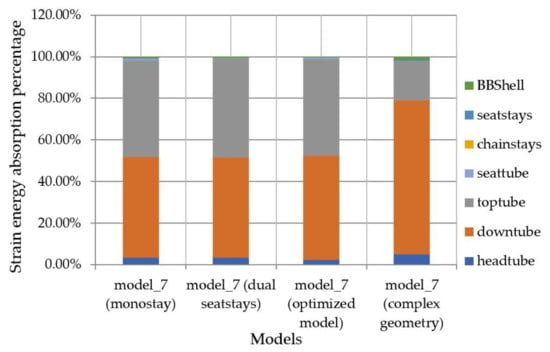
Figure 21.
Absorption of strain energy and its distribution in out-of-plane loads on head tube scenario.
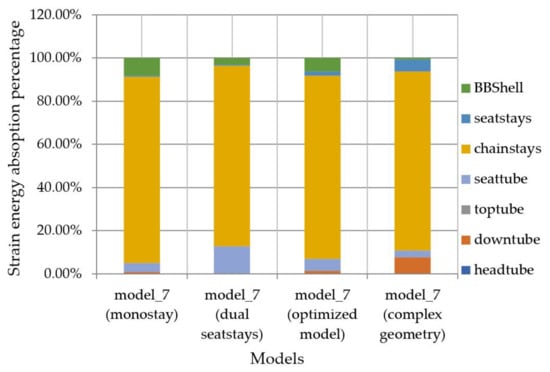
Figure 22.
Absorption of strain energy and its distribution in out-of-plane loads on bottom bracket shell scenario.
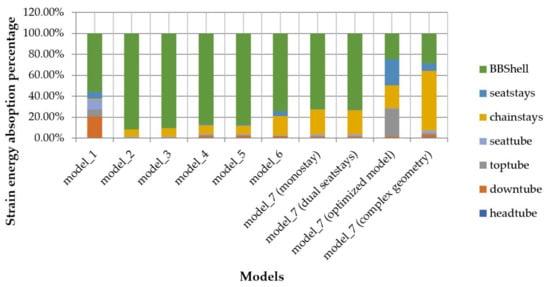
Figure 23.
Absorption of strain energy and its distribution in a static start-up scenario.
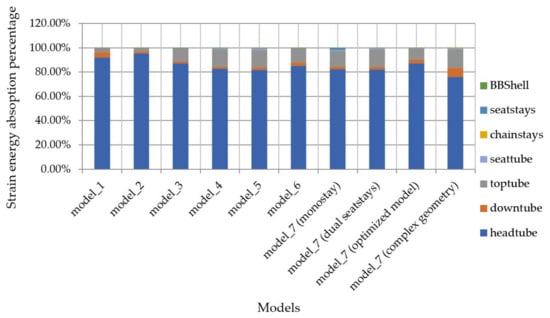
Figure 24.
Absorption of strain energy and its distribution in a horizontal forces scenario.
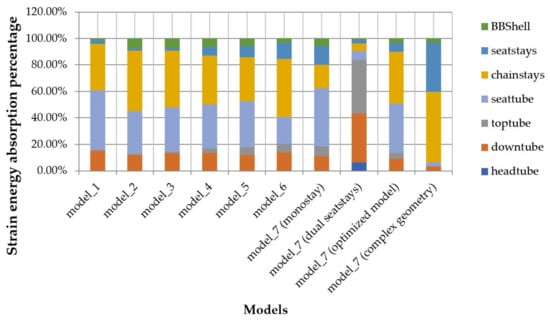
Figure 25.
Absorption of strain energy and its distribution in the riding scenario.
As the 2D bike fitting sketch result, from which we start, becomes an actual 3D spaceframe road bicycle frame, it is obvious that the maximum displacements change a lot in the beginning as the frame takes shape, and less in the final models, in which changes do not have such a big impact (Figure 17).
The last four models (mono-stay, dual-stays, complex, and optimized) were also tested on the out-of-plane load in the headtube and the out-of-plane load in the bottom bracket shell tests. The results of all the loading cases tested on the last four models are presented on Figure 18. As the design evolves, small but measurable gains are noticed. The redesigned optimized model had the least displacement in all tests. Less displacement in the frame means that the wheels do not lose their alignment during heavy pedaling sessions, which translates into less watts needed from the rider under the same speed and riding conditions.
Another important factor is the max stress that comes as a result of the loading. With less stress, less material is needed in the actual frame, which makes it lighter. The evolution of the stresses as they change from the beginning to the final model is presented in Figure 19.
Following the same procedure as with the maximum displacement figures, Figure 20 presents the results of the maximum stresses for the last four spaceframe models in all the loading cases, including the scenarios with the out-of-plane loads to the head tube and bottom bracket shell. The optimized model did not only have the least displacements, as noted before, but was also better in all the loading scenarios.
The end of this phase of the design process involved the examination of the energy that each part of the frame receives during the various loading cases. These results would be used during the selection of a suitable cross-section for each part of the frame.
In the out-of-plane load to the head tube case, it is obvious that most of the load is absorbed by the downtube and top tube, which, when combined, are actually part of the head tube. This means that the ends of the top and down tubes that connect to the head tube need to be reinforced to account for such loads, such as when sprinting out of the saddle. The strain energy distribution in the out-of-plane load to the head tube case is presented in Figure 21.
In Figure 22, the results of the out-of-plane loading of the bottom bracket shell indicate that most of the load is carried by the chain stays. This means that the chain stays have to be stiff enough so as to not deform during hard pedaling.
The static start-up scenario simulates the start of a ride from zero speed where the rider pushes at the pedals and most of the load is carried through the bottom bracket shell and the chain stays, as shown in Figure 23. Again, this means that these parts have to be reinforced.
In the horizontal forces, as shown in Figure 24, the headtube received most of the load, with the top tube and downtube receiving less. Similar to the out-of-plane headtube loading scenario, the area between the headtube, downtube, and top tube must be reinforced.
Finally, in Figure 25, a realistic riding scenario depicts the load distribution during normal riding. The optimized model had a good distribution of strain energy among the different tubes. It is interesting to see that the optimized and the complex geometries have a much different distribution, although the actual loads are not so different. Specifically, the strain energy percentage that is absorbed in the seat stays of the complex geometry seems to be absorbed by the seat tube of the optimized geometry. This is due to the mono-stay formation of the seat stays in the optimized spaceframe model, which lets the seat tube carry most of the load. This depicts the importance of the design process.
After reviewing the results of displacements, stresses, and strain energy distributions for all the spaceframe models, it is obvious that the optimized geometry model offers the lowest displacements paired with the lowest stresses and the evenest distribution of strain energy compared to all the other models. This geometry was used as the basis for the creation of the final CAD model of the frame.
3.2. Tubes’ Cross-Sections Results and Selection
After deciding on the basic geometry of our bicycle frame, the next step was to determine the shape of each tube of the frame. To this end, we examined both the results of the static loads tests, one bending and one torsional, as well as the results of our CFD analysis. The selection of the final tube cross-section depended on the overall stresses and displacements developed in the statis tests, the surface area of each model, which basically determines the weight of the tube, and the weighted results of the aerodynamic tests.
The surface area and results of the tests of the two static loads for each model are presented in Table 14. The results of the CFD analysis for each tube of the frame are presented using the graphs of Figure 26, Figure 27, Figure 28, Figure 29 and Figure 30. Finally, in Table 15, we present an evaluation of each tube cross-section to support the selection for the different frame parts.

Table 14.
Static analysis of all tubes under bending and torsional loads.
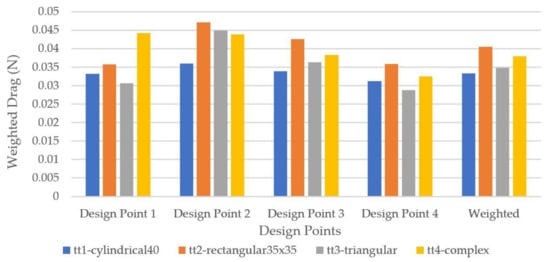
Figure 26.
Weighted drag on top tube cross-sections.
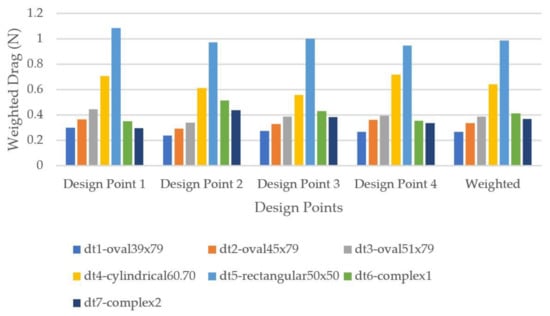
Figure 27.
Weighted drag force on down tube cross-sections.
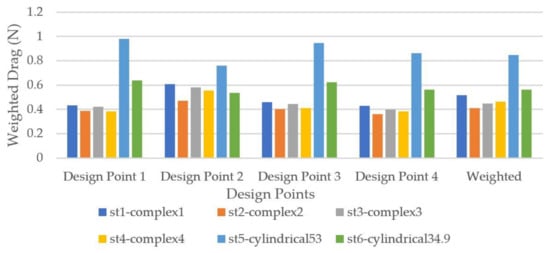
Figure 28.
Weighted drag force on seat tube cross-sections.
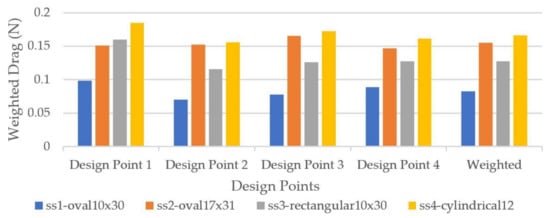
Figure 29.
Weighted drag force on seat stay cross-sections.
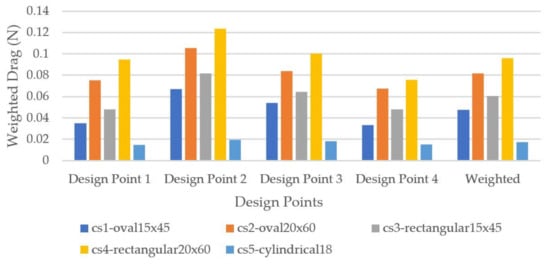
Figure 30.
Weighted drag force on chain stay cross-sections.

Table 15.
Evaluation of each cross-section.
From the static loads’ tests results, we can select the tubes that combine the least mass, which is related to the surface area, the least developed stresses, and displacements. We mostly used the bending load test results because the loads that appear on the various tests that we tested the different spaceframe models on caused bending on the tubes of the frame.
As far as the top tube models are concerned, the cylindrical and the rectangular models have the best stresses and displacements, even though they are heavier than the triangular and complex models. From the down tube models, the oval 51 × 79 model seems to have the best structural behavior while being the heaviest of the cross-sections. The cylindrical and the rectangular models are the lightest and have the best results in torsion but not in bending loads. From the tests on the seat tube models, the cylindrical and the complex 1 models seem to have the best structural characteristics while also having the biggest surface area and, subsequently, the biggest mass. For the seat stays, the models that show the lowest stresses and displacements are firstly the oval 17 × 31 followed by the rectangular 10 × 30, which are also the two heaviest cross-sections. Finally, the oval 20 × 60 and the rectangular 20 × 60 cross-sections are the structurally best choices for the chain stays.
The results of the CFD analysis for each tube of the frame are presented using the graphs of Figure 26, Figure 27, Figure 28, Figure 29 and Figure 30. For each design point, the resulting value of each model was 0.85× (Drag) + 0.15× (Side Force). The weighted drag results utilized the resulting values of each design point following this formula: 0.1× (design_point1) + 0.2× (design_point2) + 0.35× (design_point3) + 0.35× (design_point4).
From the results of the aerodynamic tests on the top tube cross-sections shown in Figure 26, the two models that show the best behavior are the cylindrical and the triangular models. While the triangular model may have a lower value in design point 1 and design point 4, the overall weighted drag of the cylindrical cross-section is lower.
The aerodynamic results for the tests on the down tube cross-sections are presented in Figure 27. The oval 39 × 79 cross-section has the best aerodynamic behavior of the down tube models, as stems from the CFD analysis. The models that follow closely behind are the other two oval cross-sections and the two complex ones. This remains the same over the four design points.
In the seat tube CFD analysis, whose results are shown in Figure 28, the model that shows the worst behavior is the cylindrical 53 cross-section; the rest seem to have small differences across the four design points, and so any of them is a viable option.
From the results of the aerodynamic tests on the seat stays cross-sections, which are shown in Figure 29, the one that appears to have the lowest overall weighted drag is the oval 10 × 30, followed by the rectangular 10 × 30.
Lastly, from the results of the aerodynamic tests on the chain stay cross-sections presented in Figure 30, the cylindrical 18 model has the least weighted drag for the chain stay models, followed by the oval 15 × 45.
Table 15 shows an evaluation of each cross-section of the various tubes of the frame based on the results of the structural and aerodynamic tests and their comparison.
The symbols of Table 15 have the following meanings:
- ✓ indicates a good behavior–result
- ✓✓ indicates a very good behavior–result
- ✕ indicates a bad behavior–result
- ✕✕ indicates a very bad behavior–result
- ✕✕✕ indicates an unacceptable result.
After evaluating the results of all the tests, both aerodynamic and structural, we were able to select the most suitable cross-section for each part of the frame. For the top tube, the obvious solution is the cylindrical 40 mm as it performs well in all the tests. For the down tube, which is one of the frame parts with the biggest amount of airflow, we decided to combine the three oval-shaped cross-sections in order to benefit from the great aerodynamic behavior and low mass of the oval 39 × 79 while also keeping the low displacements, and therefore increased stiffness, of oval 51 × 79. The seat tube is a very important element of the frame because of its angle and position. From the structural tests, two cross-sections, complex 1 and the cylindrical 53, showed promise. However, in the CFD analysis, the cylindrical 53 showed the highest drag in all the cases, therefore it had to be discarded as a possible solution. This means that complex 1 was the model we decided upon, despite its higher mass. The seat stay geometry was selected to be the oval 30 mm × 10 mm because it showed the least drag in all the design points of the CFD analysis. The high displacements of this model are actually welcome because this part of the frame has to absorb the vibration while riding. As for the chain stays, a very good solution was the combination of the oval and the rectangular cross-sections to achieve reduced aerodynamic drag force by designing the oval 20 mm × 60 mm as the outside diameter of the chain stay. Necessary stiffness was achieved by designing the inside diameter as a rectangular model with a 20 mm × 60 mm cross-section.
3.3. Stacking Scenarios’ Results and Selection
Having created the final CAD model of the frame, the next step was the selection of the most suitable layup and stacking order. We had to take into consideration the various parameters that the final frame must meet:
- The frame must be able to withstand the various loadings that occur during a ride, as indicated by the ISO standards, which means the stresses that develop in each test are allowable.
- The weight must be kept low, which means the stacking recipe must have a reduced number of plies.
- The deformations on the head tube, down tube, bottom bracket, lower part of the seat tube, and chain stays must be small so as to achieve minimized power loss while riding.
- The deformations on the top tube and seat stays are encouraged to be bigger to allow the absorption of the vibrations caused during the ride, which contributes to the rider’s comfort.
In order to evaluate the stress results of each layup recipe, Table 16 shows the allowable stresses, both tensile and compressive, for each material in all the directions. Note that the woven materials had the same allowable stresses in directions 11 and 22 because they have the same fibers in both of those directions. For the unidirectional materials, it is apparent that the allowable stresses in direction 22 were significantly lower than those of direction 11 as they only had fibers aligned along direction 11.

Table 16.
Allowable tensile and compressive stresses for each material.
The results of the various stacking scenarios for each loading case were produced using the maximum stress failure criterion. Table 17, Table 18, Table 19, Table 20, Table 21, Table 22, Table 23, Table 24, Table 25, Table 26, Table 27 and Table 28 present the results of the different stacking scenarios across the five loading cases of ISO and Table 29 shows the weights of each stacking recipe.

Table 17.
Stress and displacement results of M46J Woven quasi-isotropic scenario.

Table 18.
Stress and displacement results of T300 Woven quasi-isotropic scenario.

Table 19.
Stress and displacement results of stacking scenario 1.

Table 20.
Stress and displacement results of stacking scenario 2.

Table 21.
Stress and displacement results of stacking scenario 3.

Table 22.
Stress and displacement results of stacking scenario 4.

Table 23.
Stress and displacement results of stacking scenario 5.

Table 24.
Stress and displacement results of stacking scenario 6.

Table 25.
Stress and displacement results of stacking scenario 7.

Table 26.
Stress and displacement results of stacking scenario 8.

Table 27.
Stress and displacement results of stacking scenario 9.

Table 28.
Stress and displacement results of stacking scenario 10.

Table 29.
Weight of each stacking recipe.
The resulting stresses and displacements of the M46J Woven quasi-isotropic scenario for all the loading scenarios are shown in Table 17. No stress exceeded the allowable stresses of Table 16.
In Table 18, the stresses and displacements listed are the results of the T300 Woven quasi-isotropic scenario for the five loading cases. Again, all the stresses were below the allowable levels of Table 16. The displacements had small variations from the M46J Woven quasi-isotropic scenario results.
The results of stacking scenario 1 for each loading test are presented in Table 19. Once again, all the stresses were within the allowable values for each material and significantly lower compared to the two previous stacking scenarios. The displacements also improved, especially in the drop mass, falling frame, vertical forces, and pedaling tests.
The results of stacking scenario 2 are presented in Table 20. There were some small variations from the previous scenario and all the stresses were allowable.
In the results of stacking scenario 3, presented in Table 21, there was a slight increase in the resulting stresses without any of them exceeding the allowable stresses of Table 16.
After evaluating the results of stacking scenario 4, presented in Table 22, the stresses appeared to be elevated compared to the results of stacking scenario 3 while still remaining within the allowable limits. There was also a slight elevation on the displacements, especially in the drop mass, vertical forces, and pedaling scenarios.
In the results of stacking scenario 5, shown in Table 23, there was a slight decrease in all the displacements, with a simultaneous increase in the stresses. While the resulting stresses were still in the allowable limits, the minimum stress of 11 in the pedaling forces test was approaching the limit of 600 MPa.
The results of stacking scenario 6, shown in Table 24, were similar to those of stacking scenario 5 in most of the loading cases. The most apparent differentiation is in the vertical forces and pedaling tests, where the displacements were lower and the high stresses were diminished in most cases. The exception was located in the Min 22 and Max 22 stresses in the pedaling forces test where there was an increase; however, these values were well within the allowable range.
In stacking scenario 7, whose results are presented in Table 25, there was a further decrease in the displacements and stresses of the drop mass, falling frame, and horizontal forces tests and an increase in the displacement and stresses of the vertical forces test. The results for the pedaling test were similar between stacking scenarios 6 and 7.
After reviewing the results of stacking scenario 8, shown in Table 26, and comparing them to those of stacking scenario 7, the displacements in drop mass and falling frame tests were lower and the stresses were slightly elevated. The horizontal forces and pedaling forces tests had very similar results in both scenarios. The vertical forces test showed a slight increase in the displacement and stresses. All the stresses were below the allowable limits.
In stacking scenario 9, whose results are displayed in Table 27, there was a further decrease in the displacements and the stresses in the drop mass, horizontal forces, and pedaling forces tests. The vertical forces test showed similar stresses, with a slight increase in the displacement, while the falling frame results presented a decrease in the stresses and a minor increase in the displacement. All the stresses were allowable.
The results of stacking scenario 10, shown in Table 28, when compared to those of stacking scenario 9, showed a significant increase in most of the stresses and displacements in all the loading cases. Nevertheless, the stresses did not approach the limits set by the materials presented in Table 16.
The final comparison between the various stacking scenarios was regarding the weight of the frame that each lay-up recipe would result in. Table 29 presents the weights of the various resulting frames.
The lightest stacking recipes were the two quasi-isotropic recipes with M46J Woven and T300 Woven. However, the displacements they exhibited were not as low as those of other tested recipes. The second-lightest scenario was the 8th stacking recipe. The stresses that occurred in the five loading cases are all kept in the mid-to-low range. In addition, the displacements were some of the lowest across all the test recipes. The only scenario that displayed lower displacements in some of the tests (drop mass and pedaling tests) was the 9th stacking recipe, but this comes at the cost of additional mass (almost 50% more mass). There were other recipes that had relative low weight, such as stacking scenarios 1, 4, 6, and 7, but the displacements they developed were inferior to those of stacking scenario 8.
When further investigating the results of stacking scenario 8, we can see that the developing stresses in the various loading cases were nowhere near the limit set for the materials used. When we tried to remove some of the plies that did not contribute much to the overall structure, meaning that the load they bore was kept at low levels, the displacements that occurred were significantly higher. Therefore, we decided that this was the best solution for our frame.
4. Conclusions
In this paper, the main project was to indicate the design method of manufacturing a competitive road bicycle frame with a combination of lightness, strength, and aerodynamic efficiency using carbon/epoxy composite sheets. This superior blend of materials transmits its mechanical attributes to the bicycle by applying it with a proper sequence and direction on each part of the frame to pass approved tests of static and dynamic loading scenarios.
Firstly, through the use of spaceframe models, the basic geometry of the frame was determined to be the optimized geometry because this produced reduced displacements and stresses compared to the other models and the absorption of the strain energy was well distributed across the different tubes of the frame.
The next step was to determine the shape of each tube of the bicycle. To this end, both structural (bending and torsional) and aerodynamic tests were simulated for various cross-sections for each part of the frame. After evaluating the results, the cross-sections that were chosen were: the circular cross-section with 40 mm diameter for the top tube, a combination of two oval cross-sections (39 × 79 and 51 × 79) for the down tube, complex 1 for the seat tube, the oval 30 mm × 10 mm cross-section for the seat stays, and a combination of the oval and rectangular 20 mm × 60 mm cross-sections for the chain stays.
Having selected the appropriate geometry and the cross-sections for each tube, the final model of the frame was created. With the use of the five tests set by the ISO standards, various stacking scenarios were tested to determine the layup recipe that best combined low weight, high stiffness along the down tube, bottom bracket, and chain stays, and absorption of vibrations while riding. The laminate recipe that was chosen was stacking scenario 8, which presented the second lowest mass and some of the lowest displacements among the other layup recipes.
The joints of the tubes on the frame were created as smooth surfaces connecting the surrounding tubes and were not a primary subject of this study. Spending more time on the evaluation of their shape would be counterintuitive to the development of this new time-saving design process when considering the small gains the change in those areas would offer to the overall performance of the frame. In the future, the shape of the joints could be the parameter of a new aerodynamic and structural study.
Author Contributions
Conceptualization, A.G.K.; data curation, A.G.K. and C.S.N.; formal analysis, A.G.K.; funding acquisition, A.G.K.; investigation, A.G.K. and C.S.N.; methodology, A.G.K. and D.E.M.; project administration, A.G.K. and D.E.M.; resources, A.G.K. and D.E.M.; software, A.G.K.; supervision, A.G.K. and D.E.M.; validation, A.G.K., D.E.M. and C.S.N.; visualization, A.G.K. and C.S.N.; writing—original draft, A.G.K.; writing—review and editing, C.S.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw/processed data required to reproduce these findings cannot be shared at this time due to technical or time limitations.
Acknowledgments
In this section, we need to acknowledge the help provided during this research by two NTUA students, Alexandros Chronis and Evangelos Goulas, who helped process the data as well as write and proofread the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sajan, S.; Selvaraj, D.P. A review on polymer matrix composite materials and their applications. Mater. Today Proc. 2021, 47, 5493–5498. [Google Scholar] [CrossRef]
- Ning, H.; Vaidya, U.; Janowski, G.M.; Husman, G. Design, manufacture, and analysis of a thermoplastic composite frame structure for mass transit. Compos. Struct. 2007, 80, 105–116. [Google Scholar] [CrossRef]
- May, D.; Goergen, C.; Friedrich, K. Multifunctionality of polymer composites based on recycled carbon fibers: A review. Adv. Ind. Eng. Polym. Res. 2021, 4, 70–81. [Google Scholar] [CrossRef]
- Daniel, I.M.; Ishai, O. Engineering Mechanics of Composite Materials; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Fuerle, F.; Sienz, J. Decomposed surrogate-based optimization of carbon-fiber bicycle frames using Optimum Latin Hypercubes for constrained design spaces. Comput. Struct. 2013, 119, 48–59. [Google Scholar] [CrossRef]
- Covill, D.; Allard, P.; Drouet, J.-M.; Emerson, N. An Assessment of Bicycle Frame Behaviour under Various Load Conditions Using Numerical Simulations. Procedia Eng. 2016, 147, 665–670. [Google Scholar] [CrossRef]
- Khutal, K.; Kathiresan, G.; Ashok, K.; Simhachalam, B.; Jebaseelan, D.D. Design Validation Methodology for Bicycle Frames Using Finite Element Analysis. Mater. Today Proc. 2020, 22, 1861–1869. [Google Scholar] [CrossRef]
- Fintelman, D.M.; Hemida, H.; Sterling, M.; Li, F.-X. CFD simulations of the flow around a cyclist subjected to crosswinds. J. Wind. Eng. Ind. Aerodyn. 2015, 144, 31–41. [Google Scholar] [CrossRef]
- Malizia, F.; Blocken, B. Bicycle aerodynamics: History, state-of-the-art and future perspectives. J. Wind. Eng. Ind. Aerodyn. 2020, 200, 104–134. [Google Scholar] [CrossRef]
- Malizia, F.; Blocken, B. Cyclist aerodynamics through time: Better, faster, stronger. J. Wind. Eng. Ind. Aerodyn. 2021, 214, 104673. [Google Scholar] [CrossRef]
- Della Vecchia, P.; Nicolosi, F. Aerodynamic guidelines in the design and optimization of new regional turboprop aircraft. Aerosp. Sci. Technol. 2014, 38, 88–104. [Google Scholar] [CrossRef]
- Panagiotou, P.; Kaparos, P.; Yakinthos, K. Winglet design and optimization for a MALE UAV using CFD. Aerosp. Sci. Technol. 2014, 39, 190–205. [Google Scholar] [CrossRef]
- Idahosa, U.; Golubev, V.V.; Balabanov, V.O. An Automated Optimal Design of a Fan Blade Using an Integrated CFD/MDO Computer Environment. Eng. Appl. Comput. Fluid Mech. 2008, 2, 141–154. [Google Scholar] [CrossRef][Green Version]
- Joung, T.-H.; Sammut, K.; He, F.; Lee, S.-K. Shape optimization of an autonomous underwater vehicle with a ducted propeller using computational fluid dynamics analysis. Int. J. Nav. Archit. Ocean. Eng. 2012, 4, 44–56. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Rezaei, D. Analysis and optimization of a composite leaf spring. Compos. Struct. 2003, 60, 317–325. [Google Scholar] [CrossRef]
- Choi, B.-L.; Choi, B.-H. Numerical method for optimizing design variables of carbon-fiber-reinforced epoxy composite coil springs. Compos. Part B 2015, 82, 42–49. [Google Scholar] [CrossRef]
- Kim, D.-H.; Choi, D.-H.; Kim, H.-S. Design optimization of a carbon fiber reinforced composite automotive lower arm. Compos. Part B 2014, 58, 400–407. [Google Scholar] [CrossRef]
- Amiruddin, A.K.; Sapuan, S.M.; Jaafar, A.A. Analysis of glass fiber reinforced epoxy composite hovercraft hull base. Mater. Des. 2008, 29, 1453–1458. [Google Scholar] [CrossRef]
- Kalyanasundaram, S.; Lowe, A.; Watters, A.J. Finite element analysis and optimization of composite wheelchair wheels. Compos. Struct. 2006, 75, 393–399. [Google Scholar] [CrossRef]
- Hansen, L.U.; Horst, P. Multilevel optimization in aircraft structural design evaluation. Compos. Struct. 2008, 86, 104–118. [Google Scholar] [CrossRef]
- Song, F.; Ni, Y.; Tan, Z. Optimization Design, Modeling and Dynamic Analysis for Composite Wind Turbine Blade. Procedia Eng. 2011, 16, 369–375. [Google Scholar] [CrossRef]
- Chang, R.R.; Wu, W.J.; Jia, S.Y.; Tan, H.M. Design and Manufacturing of a Laminated Composite Bicycle Crank. Procedia Eng. 2013, 67, 497–505. [Google Scholar] [CrossRef]
- Lin, C.-C.; Huang, S.-J.; Liu, C.-C. Structural analysis and optimization of bicycle frame designs. Adv. Mech. Eng. 2017, 9, 1687814017739513. [Google Scholar] [CrossRef]
- Sani, M.S.M.; Nazri, N.A.; Zahari, S.N.; Abdullah, N.A.Z.; Priyandoko, G. Dynamic Study of Bicycle Frame Structure. Mater. Sci. Eng. 2016, 160, 012009. [Google Scholar] [CrossRef]
- Chung, C.-P.; Lee, C.-F. Parameters Decision on the Product Characteristics of a Bike Frame. Procedia—Soc. Behav. Sci. 2012, 40, 107–115. [Google Scholar] [CrossRef][Green Version]
- Covill, D.; Begg, S.; Elton, E.; Milne, M.; Morris, R.; Katz, T. Parametric finite element analysis of bicycle frame geometries. Procedia Eng. 2014, 72, 441–446. [Google Scholar] [CrossRef][Green Version]
- Devaiah, B.B.; Purohit, R.; Rana, R.S.; Parashar, V. Stress Analysis of a Bicycle Frame. Mater. Today Proc. 2018, 5, 18920–18926. [Google Scholar] [CrossRef]
- Liu, T.J.-C.; Wu, H.-C. Fiber direction and stacking sequence design for bicycle frame made of carbon epoxy laminate. Mater. Des. 2010, 31, 1971–1980. [Google Scholar] [CrossRef]
- Aceves, C.M.; Skordos, A.A.; Sutcliffe, M.P.F. Design selection methodology for composite structures. Mater. Des. 2008, 29, 418–426. [Google Scholar] [CrossRef]
- Keithonearth, CC BY 3.0. Available online: https://commons.wikimedia.org/w/index.php?curid=4914154 (accessed on 12 January 2022).
- Clarification Guide of the UCI Technical Regulation—05.10.2021 version. 2021. Available online: https://www.uci.org/equipment/bh2JJzw1eB0n876rX2iB1 (accessed on 12 January 2021).
- Peterson, L.A.; Londry, K.J. Finite-element structural analysis: A new tool for bicycle frame design. Bike Tech 1986, 5, 2. [Google Scholar]
- European Wind Atlas. Available online: https://www.wasp.dk/wind-atlas/european-wind-atlas (accessed on 12 January 2022).
- ISO 4210-6, Cycles-Safety Requirements for bicycles Part 6, ISO 2014. Available online: https://www.iso.org/standard/78081.html (accessed on 12 January 2022).
- M46J Data Sheet, TORAYCA. Available online: https://www.toraycma.com/wp-content/uploads/M46J-Technical-Data-Sheet-1.pdf.pdf (accessed on 12 January 2022).
- T300 Data Sheet, TORAYCA. Available online: https://www.toraycma.com/wp-content/uploads/T300-Technical-Data-Sheet-1.pdf.pdf (accessed on 12 January 2022).
- T700S Data Sheet, TORAYCA. Available online: https://www.toraycma.com/wp-content/uploads/T700S-Technical-Data-Sheet-1.pdf.pdf (accessed on 12 January 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).