Method for Adjusting Torsional Natural Frequencies of Powertrains with Novel Coupling Design

Abstract

Torsional vibrations are inherently present in every rotating powertrain. In resonant conditions, torsional vibrations can be significantly amplified. A typical method to reduce the torsional vibration particularly at resonance is to modify the torsional natural frequencies with the component design. Commonly, a straightforward method for the modification is the adjustment of the torsional stiffness of a coupling. This study presents a method to modify the torsional natural frequencies using a coupling design with continuously adjustable torsional stiffness. The presented coupling design is investigated with torsional analysis and experimental measurements. Torsional analysis was utilized to predict the effects of varying the coupling stiffness to the torsional natural frequencies of a powertrain. The experimental measurements were conducted by attaching the adjustable stiffness coupling to the powertrain and measuring the change in the torsional natural frequencies while the torsional stiffness of the coupling was adjusted. The torsional natural frequencies were determined from the measurements by identifying the resonance induced torsional vibrations from the vibration response of the powertrain. The torsional vibrations were excited to the system by a load motor. The measurements showed that the first torsional natural frequency of the powertrain changed from 15.6 Hz to 43.0 Hz as the torsional stiffness of the coupling was adjusted. The results of the torsional analysis and the experimental measurements were compared to determine the performance of the realized coupling. The results indicated that the torsional natural frequencies determined by torsional analysis agree well with the experimentally measured results. The prediction errors were generally below $\pm 5\%$, which is typically considered as a margin for accurate torsional analysis.

1. Introduction

Torsional vibrations are observed in every rotating system. Common sources for torsional vibration excitation include variable effective inertia in internal combustion engines and reciprocating compressors, process loads in pumps, and propulsion excitation in ship propellers. The most severe torsional vibration is typically detected at resonance, where the frequency of the excitation coincides with the torsional natural frequency of the system. The magnitude of torsional vibration at resonance is typically high since torsional systems have commonly low damping levels [1]. Resonance may cause significant problems such as excessive wear, gear damage, or cracks in powertrain components. In the worst cases, shafts have fractured completely due to high loads or fatigue [2]. Common methods for reducing the magnitude of resonant vibration introduce more damping to the system, and modification of the excitation frequencies or the natural frequencies.

To avoid resonance, powertrains are designed to have a safety margin between the torsional natural frequencies and the excitation frequencies. The torsional natural frequencies of rotating systems are estimated by torsional analysis, and its use is a standard practice in the design of powertrains [3]. Thus, large quantity of literature has been published related to the topic and various software have the capabilities of determining the torsional natural frequencies of rotating systems. However, the excitation frequencies can be difficult to predict. Common once and twice per revolution excitations caused by conditions such as misalignment are typically present in every rotating system and thus are easy to consider. Hence, individual components or processes can generate excitations with frequencies that can be unpredictable during the design phase of the powertrain. Thus, it can be difficult to determine if resonance will actually manifest during operation.

If unexpected resonant torsional vibrations are detected, they cannot usually be feasibly mitigated by modifying the excitation frequencies. Controlling the excitation frequencies is difficult, since they are usually inherently produced by the machine operation [4]. However, their magnitude can be reduced in some cases by introducing additional damping. Thus, unexpected resonance related torsional vibration problems can usually be solved by adjusting the natural frequencies of the system. Commonly used methods for the adjustment are the modification of the torsional stiffness of a coupling and the modification of the inertia of the components in the powertrain. The adjustment of torsional natural frequencies has been successfully used to reduce resonance induced torsional vibrations in various case studies. Almasi [5], Holdrege et al. [6] and Murray et al. [7] proposed changes to the torsional stiffness of the coupling in the powertrain. Modifications to the inertia of the powertrain components were done by Howes et al. [8], Feng et al. [9], and Wang [10]. However, adjustment of torsional natural frequencies with these methods is inherently time-consuming and expensive, as commonly disassembly and modification of powertrain components is required.

There has been limited research conducted for the development of methods to adjust the torsional natural frequencies of powertrains. The present study is intended to address this gap in research literature. This study presents a method for adjustment of the torsional natural frequencies in continuous range using an adjustable coupling design. The coupling design allows the tuning of the torsional stiffness of the coupling without disassembly. The torsional stiffness is adjusted by changing the effective length of the torque transferring cantilever beams in the coupling. The static torsional stiffness of this coupling design was studied in recent research by the authors [11]. Cantilever beams has also been utilized in coupling designs earlier by Kołodziej et al. [12] and Ning [13]. Other methods for torsional stiffness adjustment for couplings has been presented in literature and patents. A coupling design with pneumatically adjusted torsional stiffness has been presented by Homišin et al. [14], while Brosowske [15] introduced a coupling design utilizing hydraulics for the adjustment. Lee et al. [16] has demonstrated a coupling design, which adjusts the torsional stiffness using magnetorheological elastomer. They created a simulation model of the coupling and verified its ability to adjust torsional natural frequencies by experimental measurements.

As discussed earlier, a research considering the static torsional stiffness of the coupling design has been done by the authors [11]. It showed how the static torsional stiffness of the adjustable coupling can be determined by analytical calculations, finite element method (FEM) simulations and measurements. The present study investigated how accurately the stiffness determined by these three methods can represent the coupling in dynamic torsional analysis, and in a comparison with experiments. It is essential to determine the accuracy of the coupling stiffness for use in torsional analysis to properly validate the coupling design for industrial and research use. The accurate prediction by torsional analysis significantly increases confidence in the practical implementation of the coupling design, since it confirms that the actual behavior of the coupling will be consistent with the behavior predicted by torsional analysis. This allows the powertrain to be optimized for multiple different torsional natural frequencies during its design. If unexpected resonance manifests, the powertrain can be adjusted to another torsional natural frequency predetermined during its design phase. Thus, it is possible to avoid the excitation frequency that is causing the resonance and unexpected resonance can be mitigated.

Secondary goal in this study was to determine the non-linearity of the torsional stiffness of the coupling in dynamic environment. The non-linearity in couplings is commonly used to describe the phenomena where the coupling stiffness increases or decreases when torque load is varied. The non-linear behavior of the coupling stiffness is important to consider, since unexpected resonant vibrations can occur if the torsional natural frequencies change significantly as a function of torque. For example, the torsional stiffness of couplings with elastomeric inserts is typically non-linear [17]. The non-linearity of the coupling design was studied by measuring the changes in torsional natural frequencies of the powertrain while varying the torque load.

The results demonstrate that the first torsional natural frequency was significantly modified by adjusting the coupling stiffness. Free manipulation of the lowest torsional natural frequency of the powertrain was possible between 15.6 and 43.0 $\mathrm{Hz}$. The errors in predicted torsional natural frequencies from the torsional analysis compared to the measured torsional natural frequencies were small, generally below $\pm 5\%$, when measured torsional stiffness range was used to represent the adjustable coupling in the torsional analysis. If the prediction error of below $\pm 5\%$, the torsional analysis model is typically considered to be correctly modeled [3,18]. Thus, the results validated the method to be effective and predictable. Potential applications for the presented method include torsional resonance control for industrial powertrains and research use considering vibrations, resonance, and natural frequencies.

2. Materials and Methods

2.1. Torsional Analysis

Torsional analysis was used to predict the torsional natural frequencies of the powertrain. The torsional analysis was done using an open-source torsional finite element analysis software “openTorsion” [19]. Using this software, the components of the powertrain were discretized to inertia and torsional stiffness elements. These elements were assembled to form global inertia and stiffness matrices. The effect of damping is negligible to torsional natural frequencies in most torsional systems, thus it was not considered in the analysis [3], considering also that the powertrain did not include any particular damping elements. The torsional analysis is based on the fundamental equation of motion for rotatingsystems

$$M\ddot{\theta }+K\theta =T,$$

(1)

where M is moment of inertia matrix, $\theta$ is the angular displacement vector, K is the torsional stiffness matrix and T is the vector representation of external torques applied to the system.

Torsional natural frequencies and vibration mode shapes were determined from the global inertia and stiffness matrices using eigenvalue analysis. As the system is considered freely vibrating, the external torque T is zero. The torsional natural frequencies can be solved as a linear eigenvalue problem from the basic equation of rotating motion. The natural frequencies are square roots of the eigenvalues, and the vibration mode shapes are the eigenvectors. They can be solved from equation

$$[K-{\omega }_i^{2}M]\left\{{\mathrm{\Phi }}_i\right\}=0i=1,2,\cdots$$

(2)

where $\omega$ is the torsional natural frequency and $\mathrm{\Phi }$ is the corresponding vibration mode shape.

The inertia and torsional stiffness matrices of each component were assembled to form moment of inertia and torsional stiffness matrices for the system. They are presented in Equation (3). These matrices represent the total inertia and torsional stiffness of the whole system. The assembled system matrices are used in the eigenvalue analysis presented earlier in Equation (2) to determine the torsional natural frequencies and mode shapes.

$$M=\left[\begin{array}{cccc}{J}_1& & & \\ & J_2& & \\ & & \ddots & \\ & & & J_n\end{array}\right],K=\left[\begin{array}{cccc}{K}_1& -K_1& & \\ -K_1& K_1+K_2& -K_2& \\ & & \ddots & \\ & & -K_n& K_n\end{array}\right]$$

(3)

where J is the inertia of a component and K is the torsional stiffness of a component.

2.2. Powertrain Test Setup

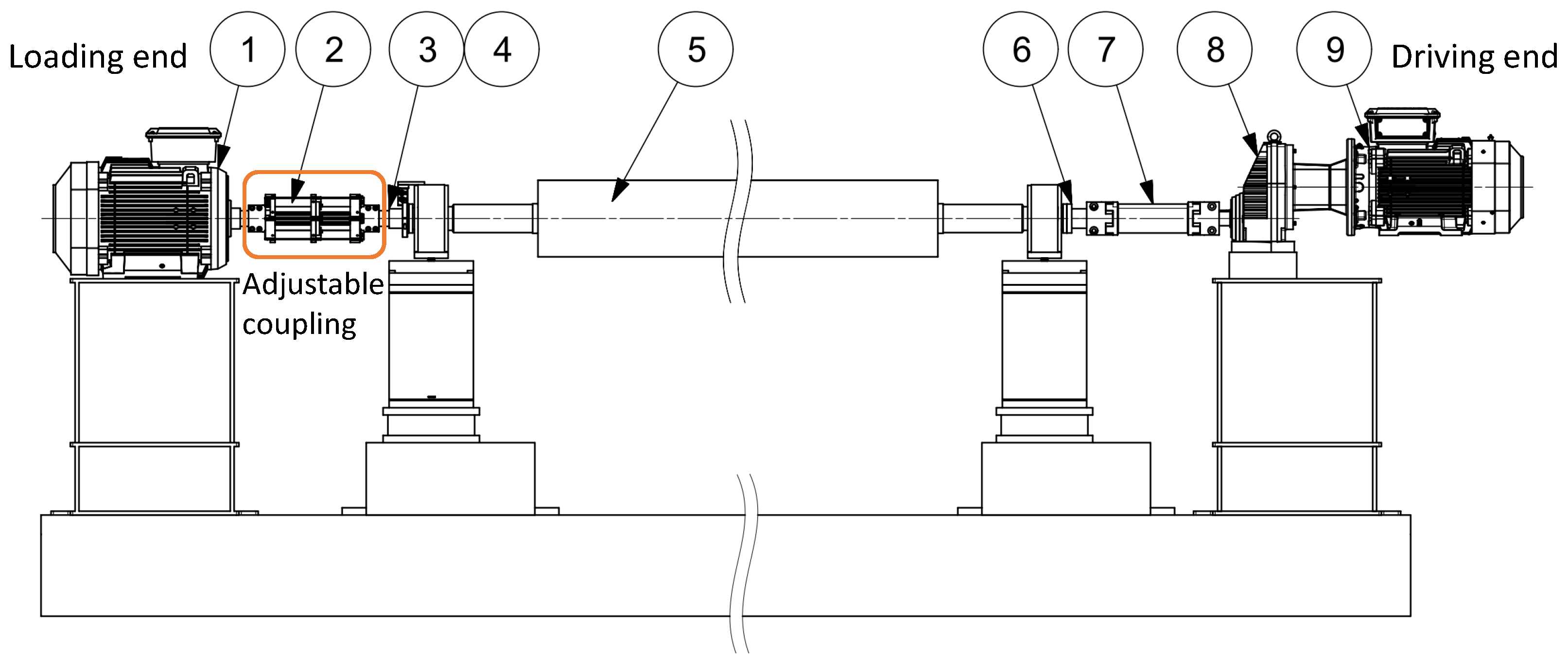
A rotor test bench was used as the powertrain in the study. The components of the analysed powertrain are presented in Figure 1. The powertrain consisted of two variable speed drive (VSD) electric motors, a gear unit, a test rotor, a torque transducer, an elastomer coupling and the coupling with adjustable torsional stiffness. In the experiment, one of the electric motors was an induction motor and it was utilized as a driving motor to rotate the system at constant speed. The gear unit was connected to the driving motor and the torque was transmitted through the gear unit to the test rotor by the elastomer coupling. The other motor was a synchronous reluctance motor and it was used as the loading motor to excite the system with torsional vibrations. Both motors had nominal power of 37 $\mathrm{kW}$ and nominal torque of 236 N·m. The coupling with adjustable torsional stiffness was mounted between the loading motor and the torque transducer. The torque transducer was mounted to the rotor. The torque transducer was used to detect the torsional vibration response near the coupling. A paper machine roll mounted on two roller bearings was used as the test rotor in the experiment.

2.3. Coupling with Adjustable Torsional Stiffness

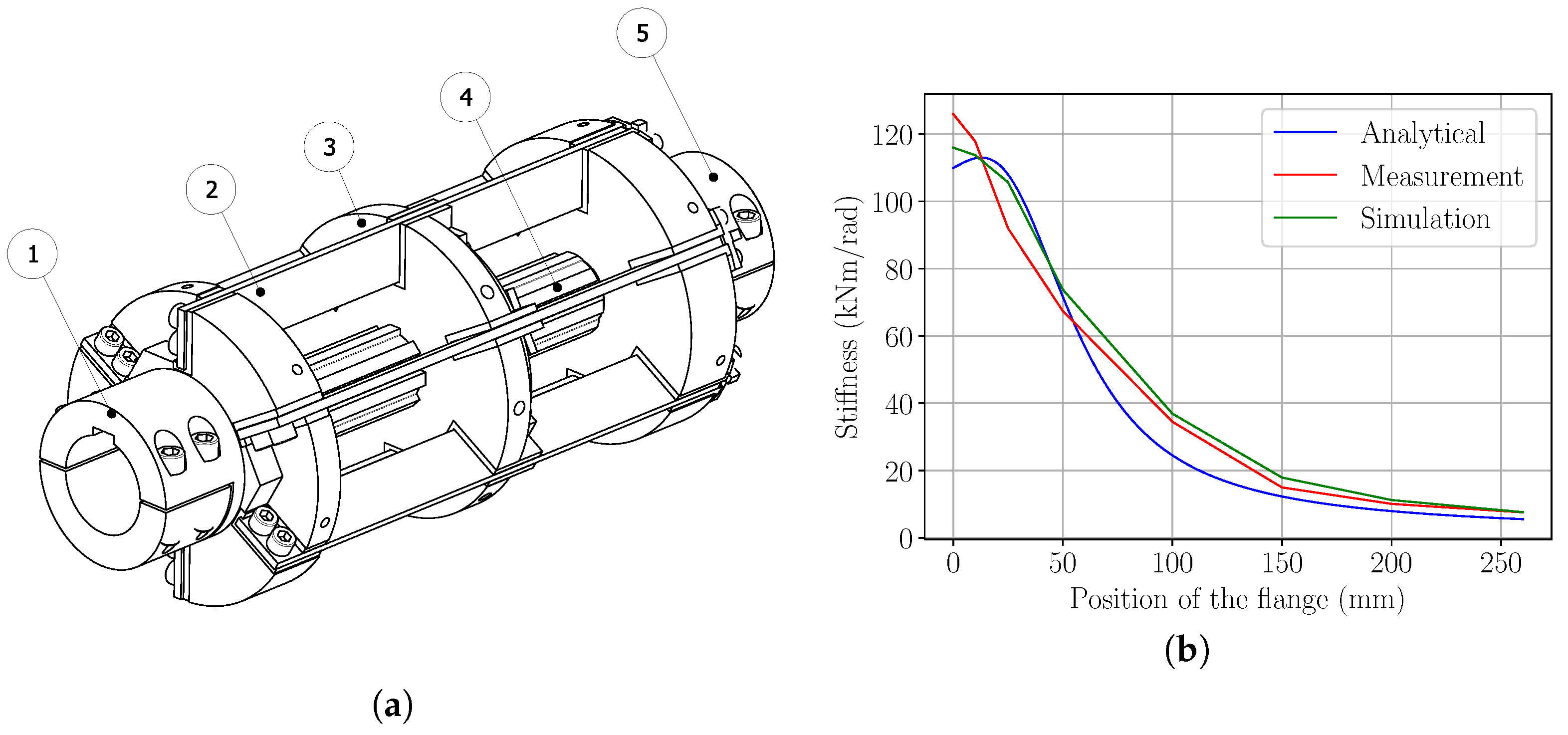
The main parts of the coupling assembly are presented in Figure 2a. The torsional stiffness of the coupling can be adjusted by changing the effective lengths of the beams (part number 2) and the middle shaft (part number 4) by moving the adjustable flange (part number 3). The torsional stiffness is at its highest when the adjustable flange is near the input half and the lowest when it is near the output half. The beams have rectangular cross-section profile but their profile could be designed to be tapered or wider to vary the ratio of torsional stiffness change. The coupling design is presented in detail in earlier study [11]. The study determined the static torsional stiffness of this coupling design by analytical calculations, FEM simulations, and experimental measurements (Figure 2b).

2.4. Torsional Analysis Model

The torsional analysis model of the powertrain was constructed by simplifying the powertrain components to inertia elements and torsional stiffness elements. Moreover, a gear element was used to take into account the gear ratio of the gear unit. The model consisted a total of 21 inertia elements, 20 torsional stiffness elements and 1 gear element. Next the discretization and the modeling of the powertrain are described in detail. All relevant parameters for the finite element analysis are presented in

Table 2. Parameters used in the finite element analysis.

Parameter	Value	Unit
Driving motor inertia	0.196	kg$·$m${}^2$
Loading motor inertia	0.575	kg$·$m${}^2$
Elastomer coupling inertia	0.045	kg$·$m${}^2$
Adjustable coupling inertia	0.147	kg$·$m${}^2$
Torque transducer inertia	0.002	kg$·$m${}^2$
Gear unit inertia	0.007	kg$·$m${}^2$
Elastomer coupling stiffness	40.5	kN$·$m/rad
Adjustable coupling stiffness	8–126	kN$·$m/rad
Torque transducer stiffness	180	kN$·$m/rad
Gear ratio	1.95	-
Shear modulus of steel	80	GPa
Density of steel	7800	kg/m${}^3$

.

The driving and loading motors were modeled as inertia elements with no torsional stiffness.

The coupling with adjustable torsional stiffness and the elastomeric coupling were modeled as elements with inertia and torsional stiffness. The torsional stiffness of the coupling is presented in Section 2.3 in Figure 2b, and it was used to represent the adjustable coupling in the analysis. Penetration factor of 1/3 was applied to all shaft-to-hub connections, as this value is recommended in the relevant standards [3,20].

The gear unit imposes constraints to the powertrain. These constraints are enforced to the model with a transformation matrix to include the effect of the gear ratio to the analysis [21]. Apart from the transformation matrix, the gear unit was considered as a inertia element with no torsional stiffness.

The torque transducer was modeled as a inertia with torsional stiffness. The test rotor, the torque transducer and the shaft end flanges are shown in Figure 3. Each of the element corresponds to a single section of the rotor with certain diameter and length. The corresponding elements and their dimensions are presented in Figure 3. The inertia and torsional stiffness for each element were calculated using basic formulas for circular cross-section (as in [21]).

The powertrain was simple to model accurately, since the test rotor in the powertrain had the highest inertia of all components by a significant margin. The high inertia of the rotor separates the loading and driving sides of the powertrain and diminishes the effect of the driving side components on the measurements as the vibrations are isolated mostly to the loading side of the powertrain. Thus, it significantly reduces the possible non-linear effects of the elastomeric coupling and the gear unit to the measured torsional natural frequencies. It has been shown by Wang et al. [22] that accurate prediction of the torsional natural frequencies can be difficult in powertrains with components that have complex non-linearities.

3. Measurement Procedure and Data Analysis

The powertrain test setup is presented in Figure 4. The torsional natural frequencies of the powertrain were measured by exciting the system with the load motor, while the driving motor was used to rotate the powertrain at constant velocity 100 rpm clockwise. A pseudorandom binary sequence (PRBS) was used to generate the torque excitation signal. The PRBS produces an excitation signal with a binary amplitude and random phase. When the excitation signal is fed to the loading motor, the motor creates very short pulses of torque with random phases. Thus, the loading motor excites the system at a wide frequency bandwidth. The pseudorandom excitation appears as white noise in the measurements and the excitation itself does not appear dominant in the results. Thus, the high amplitude torsional vibrations caused by resonance can be identified by measuring the torque and the torsional natural frequencies can be determined from the vibration peaks.

The dynamic properties of the adjustable coupling were studied by varying the PRBS excitation magnitudes. The effect of cyclic loading was also investigated. The goal was to identify if the measured torsional natural frequencies would change when the loading magnitude and type were adjusted. Hence, it was the possible to measure any non-linear behavior of the torsional stiffness of the coupling.

As the powertrain was rotating at constant 100 rpm clockwise, the cyclic loading was generated by using the loading motor to apply a constant counterclockwise torque and cycle the PRBS excitation to alternate the loading between clockwise and counterclockwise directions.

The used terms for the modified torque magnitude parameters are torque gain and constant load torque. The torque gain is the magnitude of the PRBS torque applied by the loading motor and the constant load torque is the magnitude of the constant torque produced by the loading motor. The varied PRBS excitation magnitude is presented as percentages of the maximum motor torque of 236 N·m. Three different torque gains 5%, 10%, and 15% and two different constant load torques 0% and 5% were used.

The torque gain in the results is the magnitude of the PRBS torque and constant load torque is the magnitude of the constant opposing torque produced by the loading motor. The varied PRBS excitation magnitude is presented as percentages of the maximum motor torque of 236 N·m. Three different torque gains 5%, 10%, and 15% and two different constant load torques 0% and 5% were used.

The torque response was measured with contactless flange type torque transducer. The flange has a built in strain gauge, which is excited with alternating current to contactlessly measure the strain. The accuracy class of the torque transducer was 0.05. However, the main purpose of the measurements was to detect the resonance, hence the measurement error of the torque transducer was not considered in the measurements.

The torque transducer was connected to an amplifier and from the amplifier to data acquisition (DAQ) card. The DAQ was installed on a computer, which had a software for the measurement data processing and PRBS excitation control. The software was used to request the PRBS excitation from VSD system controlling the load motor.

10 different samples were measured with each combination of torque gains and constant load torques. The length of one measurement sample was 10 s. The rotating speed of the powertrain was not varied during the measurements, as the torsional natural frequencies were assumed not to be affected by the rotational speed. This assumption is common in torsional vibration analysis and it is cited in various sources (as in [21,23]). However, this assumption is a potential source of uncertainty in the experimental measurements.

A 4 $\mathrm{kHz}$ sampling frequency for the torque transducer was used during the measurements and a low-pass filter with 1 $\mathrm{kHz}$ cutoff frequency was applied to prevent aliasing. Torque request update frequency of the VSD system was 200 $\mathrm{Hz}$.

The measurement procedure was completed as follows:

• The coupling was set to its highest torsional stiffness.
• The powertrain was accelerated to 100 rpm with the driving motor.
• PRBS excitation was applied with the loading motor for 10 s to measure one sample. A total of 10 samples was measured.
• The torque gain and constant load torque were modified.
• New measurements were taken until all possible torque gain and constant load combinations were exhausted.
• The rotation of the system was stopped and the torsional stiffness of the coupling was adjusted.
• Steps 2–6 were repeated until the whole stiffness range of the coupling had been measured.

The Discrete Fourier Transform (DFT) was used to transform the measurement data from time domain to frequency domain. The torsional natural frequencies were determined from the transformed data by identifying the torque peaks caused by torsional resonance. The torsional natural frequencies determined from each series of 10 samples were averaged to single values to reduce the effect of possible uncertainties and random variation.

4. Results and Discussion

4.1. Changes in Torsional Natural Frequency

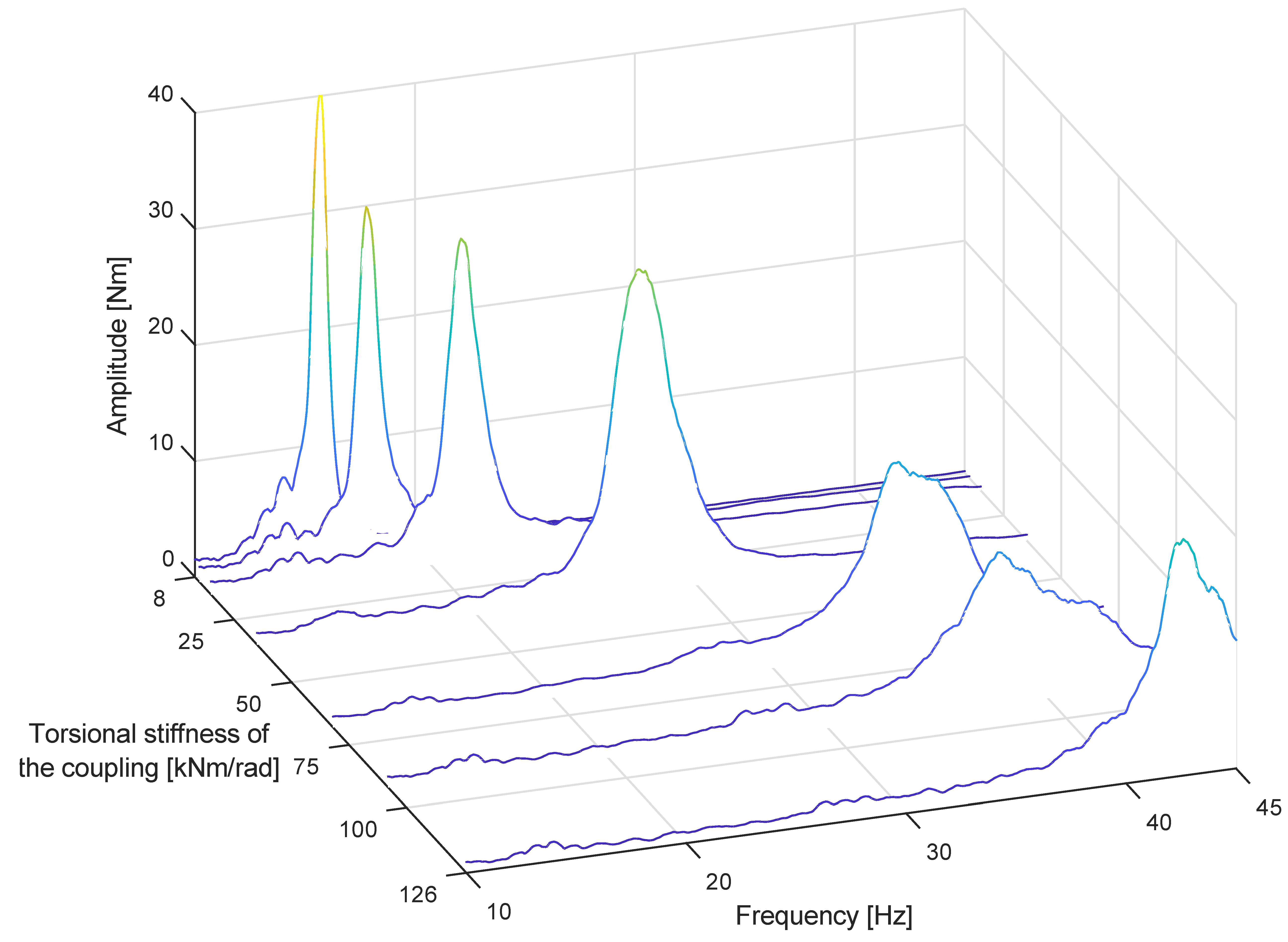
The changes in the measured torsional natural frequency are presented as a function of the torsional stiffness of the adjustable coupling in Figure 5. The measurement results were averaged and plotted in frequency domain. Only the first torsional natural frequency was considered in the results, since it is most significantly affected by the torsional stiffness of the adjustable coupling.

4.2. Comparison of Torsional Analysis to Measurements

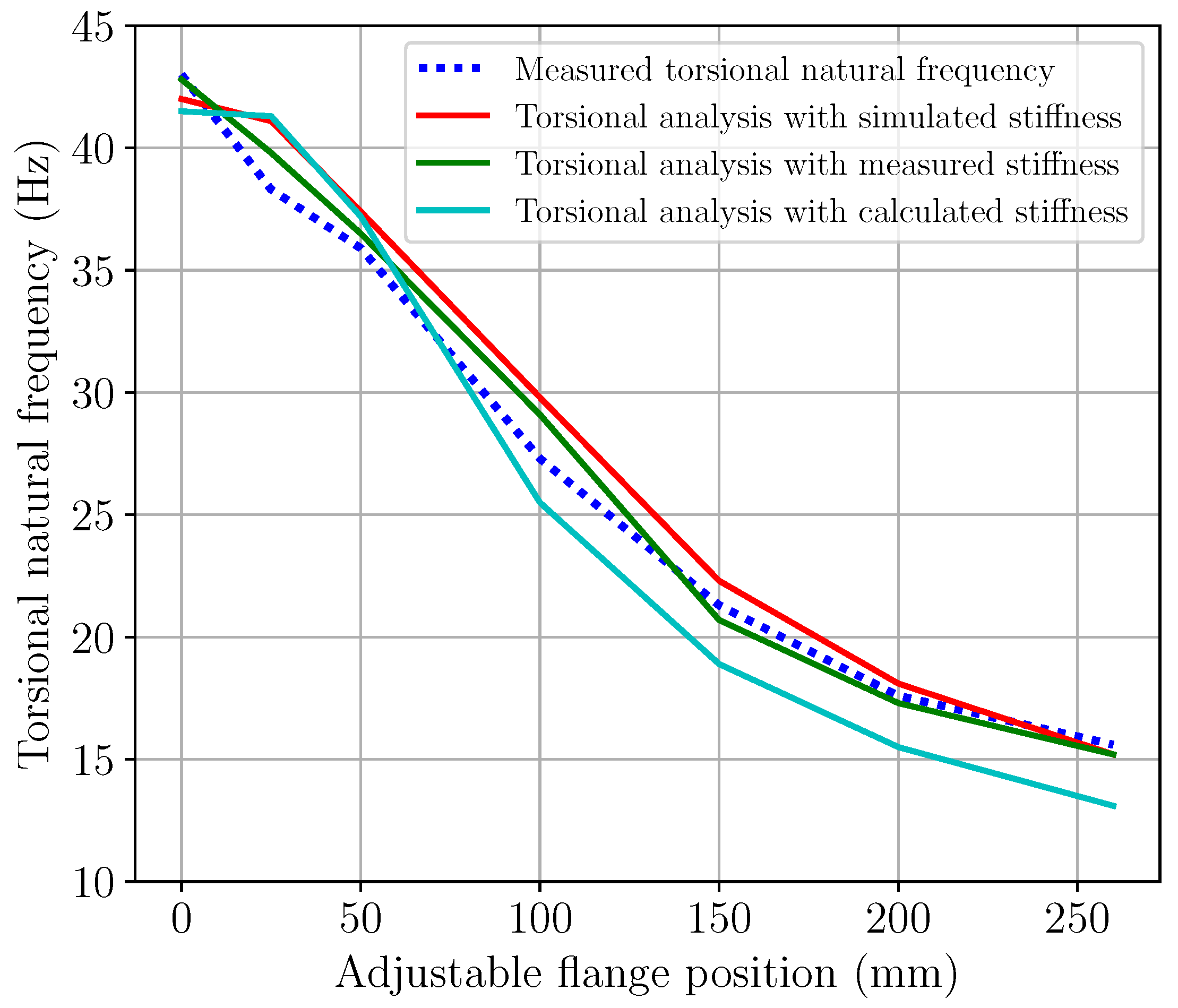
Figure 6 presents the comparison between predicted and experimentally measured torsional natural frequencies. The torsional natural frequencies are plotted as a function of adjustable flange position, which determines the torsional stiffness of the coupling. The torsional natural frequency values used were averaged from the measurements with different constant load torque and gain values. These average values are shown in

Table 3. The torsional natural frequencies measured using different excitation magnitudes. Gain is the torque magnitude of the PRBS excitation and constant torque is the magnitude of constant torque opposing the rotation of the powertrain. Torque magnitudes are presented as percentages from the maximum motor torque of 236 N·m.

Constant	Torque	Adjustable Flange Position [mm]
Torque	Gain	0	25	50	100	150	200	260
		Measured torsional natural frequency [Hz]
0%	5%	44.5	38.8	35.0	27.0	21.3	17.8	15.6
0%	10%	42.4	37.7	35.7	27.6	21.5	17.5	15.7
0%	15%	43.4	40.6	36.9	28.2	21.7	17.7	15.7
5%	5%	43.1	37.2	35.9	26.7	21.0	17.4	15.6
5%	10%	42.4	37.5	35.5	26.5	21.0	17.4	15.6
5%	15%	42.3	38.1	36.5	27.8	21.6	17.7	15.6
Mean		43.0	38.3	35.9	27.3	21.3	17.6	15.6
Std. deviation		0.9	1.3	0.7	0.6	0.3	0.2	0.1

.

The comparison suggests that the effect of the adjustable coupling on the investigated torsional natural frequency was accurately predicted with torsional analysis. The differences between torsional natural frequencies determined by the torsional analysis and the measurements were mostly under $\pm 5\%$, which is the range commonly considered for high quality torsional analysis [3,18]. Thus, the results suggests that the powertrain and the coupling are modeled correctly.

The total range of torsional natural frequency adjustment was wide. At lowest coupling stiffness the first torsional natural frequency was 15.6 $\mathrm{Hz}$ and at highest stiffness 43.0 $\mathrm{Hz}$. However, it needs to be considered that the relative stiffness between the coupling and the powertrain components also affects the range of torsional natural frequency adjustment. If the combined torsional stiffness of the powertrain differs significantly from the adjustable torsional stiffness of the coupling, the range that the torsional natural frequency changes increases. Thus, the change in torsional natural frequencies also depends on the torsional stiffness difference between the powertrain components and the coupling.

4.3. Accuracy of Coupling Stiffness in Torsional Analysis

When the measured torsional stiffness values of the coupling are used in the torsional analysis, the results correspond well with the measured torsional natural frequencies. This is an expected result, since measuring the torsional stiffness is likely to produce the most realistic stiffness estimates.

The comparison shows that the torsional stiffness range determined with FEM can be used with good accuracy in the torsional analysis. This is a significant result, since it suggest that the behavior of the coupling can be predicted accurately with simulations by combining FEM and torsional analysis. This reduces uncertainties in early stages of the powertrain design process and shows that the coupling design is robust and can be accurately dimensioned and modeled. Accurate modeling is important, since it has been shown that inaccurate and incorrect modeling of the torsional stiffness values for couplings is a common cause of errors in torsional analysis [22].

The deviation between the predicted and measured torsional natural frequencies increases when the analytically calculated torsional stiffness is used in the torsional analysis. The deviation increases significantly at higher adjustable flange positions. The increase in the deviation is likely caused by the error in the analytical torsional stiffness calculations, as presented in the earlier study [11]. The error in analytical calculations increases significantly when the effective length of the beams in the coupling increases. Thus, the torsional stiffness range determined by analytical calculations can potentially be used accurately in torsional analysis if the effective length of the beams in the coupling is relatively short.

4.4. Nonlinear Behavior of the Coupling

Secondary goal in the present study was to determine the nonlinear behavior of the coupling. The study was conducted by investigating if the excitation magnitude has an effect on the measured torsional natural frequencies. The effect of the PRBS excitation magnitude and the cyclic loading on the the measured torsional natural frequencies is presented in Table 3. Each presented torsional natural frequency value is averaged from series of 10 measurement samples.

As the excitation magnitude is increased, variation between $3\%$ to $5\%$ in the torsional natural frequencies can be observed when the adjustable flange position is between 25 to 100 $\mathrm{mm}$. Minor changes are observed also with cyclic loading. The changes are small but yet noticeable as typically $\pm 5\%$ deviation is considered to be the definition of accurate prediction in torsional analysis [3,18]. However, uncertainties such as spectral leakage in DFT can also contribute to the magnitude of the differences. The non-linearity seems to decrease as the adjustable flange position is increased. This higher non-linearity is likely to be caused by the lower stiffness of the plastic parts, which are used as guides for the beams. As the stiffness of the beams is high so is their stiffness relative to the plastic parts. Thus, the plastic is mostly deforming during the vibration causing the non-linearity. As the stiffness of the beams is decreased, the relative stiffness between the beams and the plastic parts decreases causing the non-linear behavior to gradually fade. Thus, it can be deduced that increasing the torque magnitude produces non-linearity especially when the coupling stiffness is high.

4.5. Comparison to Magnetorheological Elastomer Coupling Study

Coupling designs with difficult to model materials or phenomena can cause errors in prediction of torsional natural frequencies. Thus, it is highly beneficial that the modeling of the coupling would be simple. A study conducted by Lee and Kim [16] presented a coupling design, which used magnetorheological elastomer to adjust the torsional stiffness. Similarly as in the present study, Lee and Kim mounted their coupling to a test bench, predicted the first torsional natural frequency with simulations, and measured the prediction accuracy by using an experimental test setup. The error between predicted and measured torsional natural frequency was approximately 8% at lowest coupling stiffness and approximately 17% at highest stiffness. Lee and Kim consider that the errors are caused by limitations in the simulations and the modeling of the magnetorheological elastomer.

As shown by the study of magnetorheological elastomer coupling, modeling problems can cause significant errors between the predicted and measured torsional natural frequencies. The errors can over the desired range of $\pm 5\%$ and thus cause unexpected resonant vibrations when used in industrial machinery. These prediction errors were mostly under $\pm 5\%$ for the presented adjustable coupling in this study. This is likely to be attributed to the commonly known and simple modeling of the cantilever beams used for the torsional stiffness adjustment.

4.6. Uncertainties and Limitations in the Study

As shown by the results, torsional analysis predicted accurately the change in the torsional natural frequencies as the coupling stiffness was adjusted. Despite of the good prediction accuracy, the torsional analysis model and the test setup both have some uncertainties and limitations. These uncertainties and limitations need to be acknowledged and accounted for as the results of the study are interpreted.

The vibration excitation has some uncertainty, as the true characteristics of the VSD system controlling the loading motor are unknown. The VSD system can have some unknown properties or restrictions. For example, the VSD system could restrict the maximum frequency for PRBS type signals that request the motor torque to vary rapidly between clockwise and counterclockwise direction. Moreover, the loading motor itself may also not be able to properly produce the requested oscillating torque. Thus, it is difficult to estimate if the excitation produced by the loading motor is actually what is requested. However, the main goal was to excite the torsional natural frequencies. They can be excited also with other excitation signal types and the results are likely similar [24]. Thus, it was considered that this uncertainty does not significantly affect the quality or the repeatability of the study.

Particular limitation in the study is the assumption that the torsional natural frequencies are stable and not change as a function of rotational speed. This is a common assumption in torsional analysis [21,23]. The torsional stiffness of most components do not change as a function of rotational speed and that validates the assumption. This study considers a novel coupling design and thus the assumption may not be valid. The results show minor changes in torsional natural frequencies when the torque magnitude is manipulated. These minor non-linearities could could also change torsional natural frequencies at higher rotational speeds where typically higher total torque output is required and applied to the powertrain. Thus, studying the variation of torsional natural frequency relative to rotational speed should be a focus for a further study since it is a cause of uncertainty in the behavior of the coupling.

5. Conclusions

In the industry, determining the torsional natural frequencies during the design of powertrains is known well due to the large amount of resources related to the topic. However, it can be much more difficult to determine if resonant torsional natural vibrations really appear during machine use since the excitation frequencies are often unknown or difficult to determine during machine design. The coupling design presented in this study can be used to address this problem as coupling allows the machine to be optimized for operation in multiple different torsional natural frequencies. Thus, the coupling design allows the utilization of well known methods for determining the torsional natural frequencies and mitigates the effect of excitation frequencies, which can be difficult to determine.

The results suggest that the coupling design can be used to adjust the torsional natural frequencies in a wide range. The torsional natural frequency of the powertrain was freely manipulated between 15.6 $\mathrm{Hz}$ and 43.0 $\mathrm{Hz}$ by adjusting the torsional stiffness of the coupling. Moreover, the result suggest that torsional analysis can be used to accurately predict the range in which the torsional natural frequency adjustment can be made. The errors between predicted and measured torsional natural frequencies were below $\pm 5\%$ for most adjustable flange positions. Accurate predictability is highly desirable when the method is applied in practice. The present study also identified minor non-linear behavior of the coupling in dynamic conditions, which was considered to be limited.

The coupling in its current form can be implemented for research, product development, factory acceptance testing and torsional vibration control in industrial machinery. Potential industrial applications are, for example: Modifying the torsional natural frequency for combustion engine powertrain during skipfire operation, avoiding resonance in reciprocating machinery when running on wide rotation speed range, and preventing resonant torsional vibrations during synchronous motor startup.