Effect of the Computational Model and Mesh Strategy on the Springback Prediction of the Sandwich Material
Abstract
:1. Introduction
2. Materials and Methods
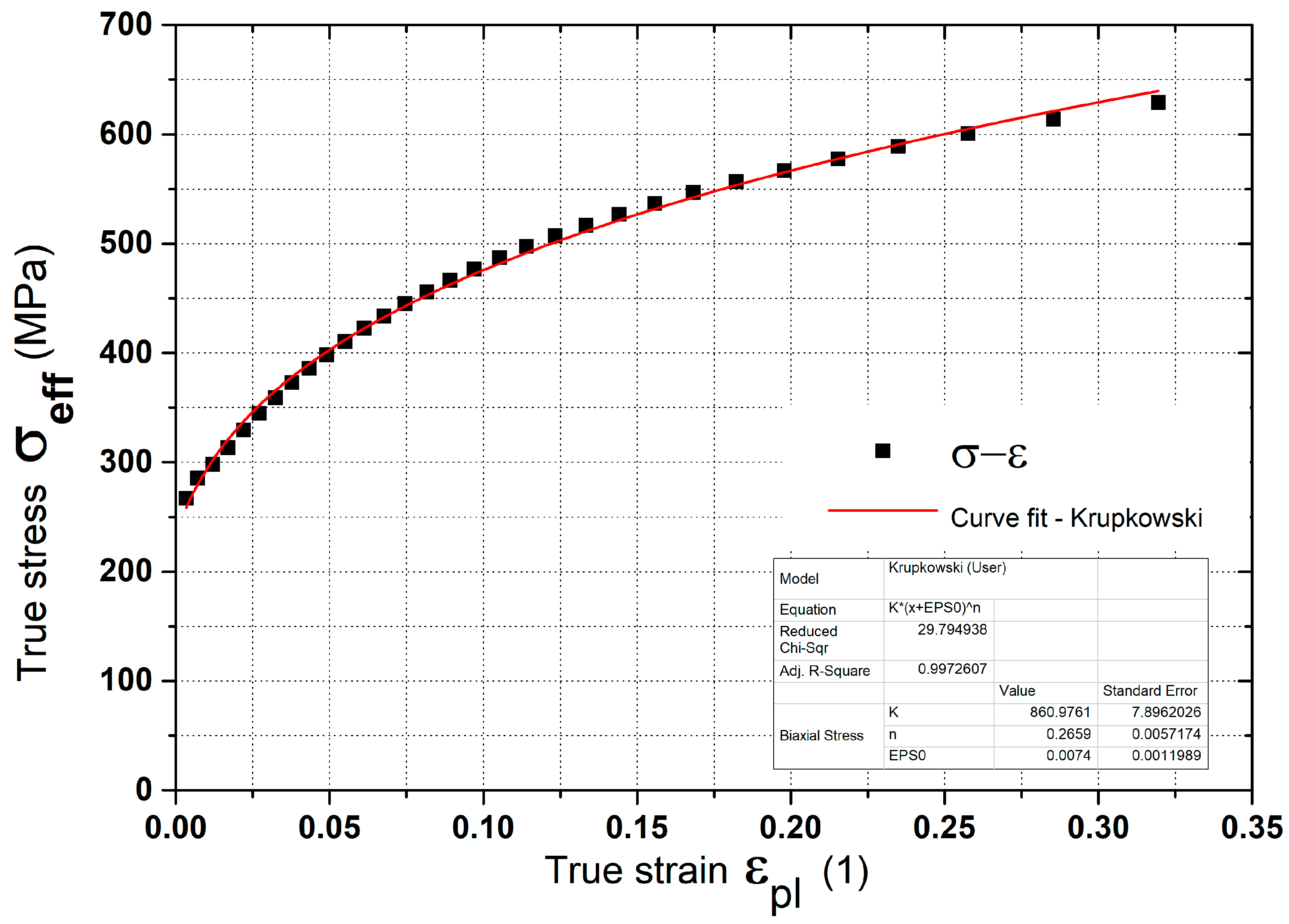
2.1. Static Tensile Test
- σ—true stress (effective stress) (MPa)
- K—strength coefficient (MPa)
- εpl—true plastic strain (1)
- ε0—offset true strain (pre-strain) (1)
- n—strain hardening exponent (1)
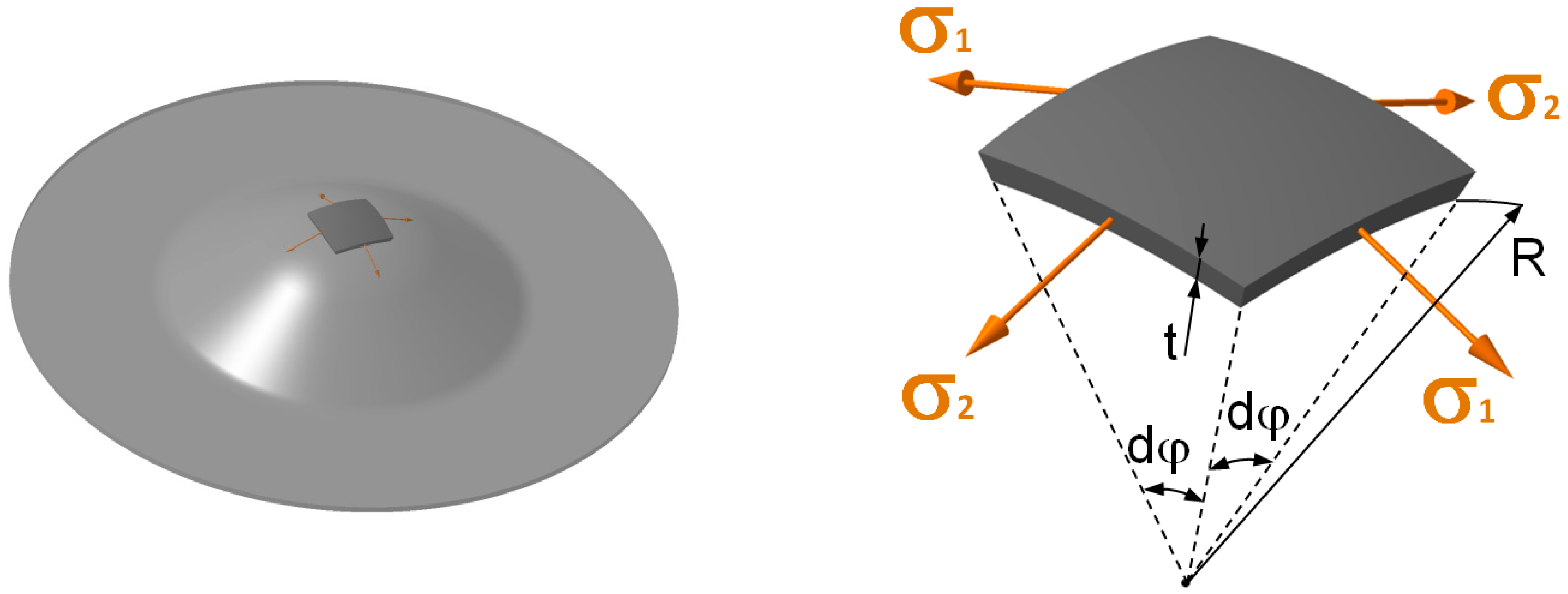
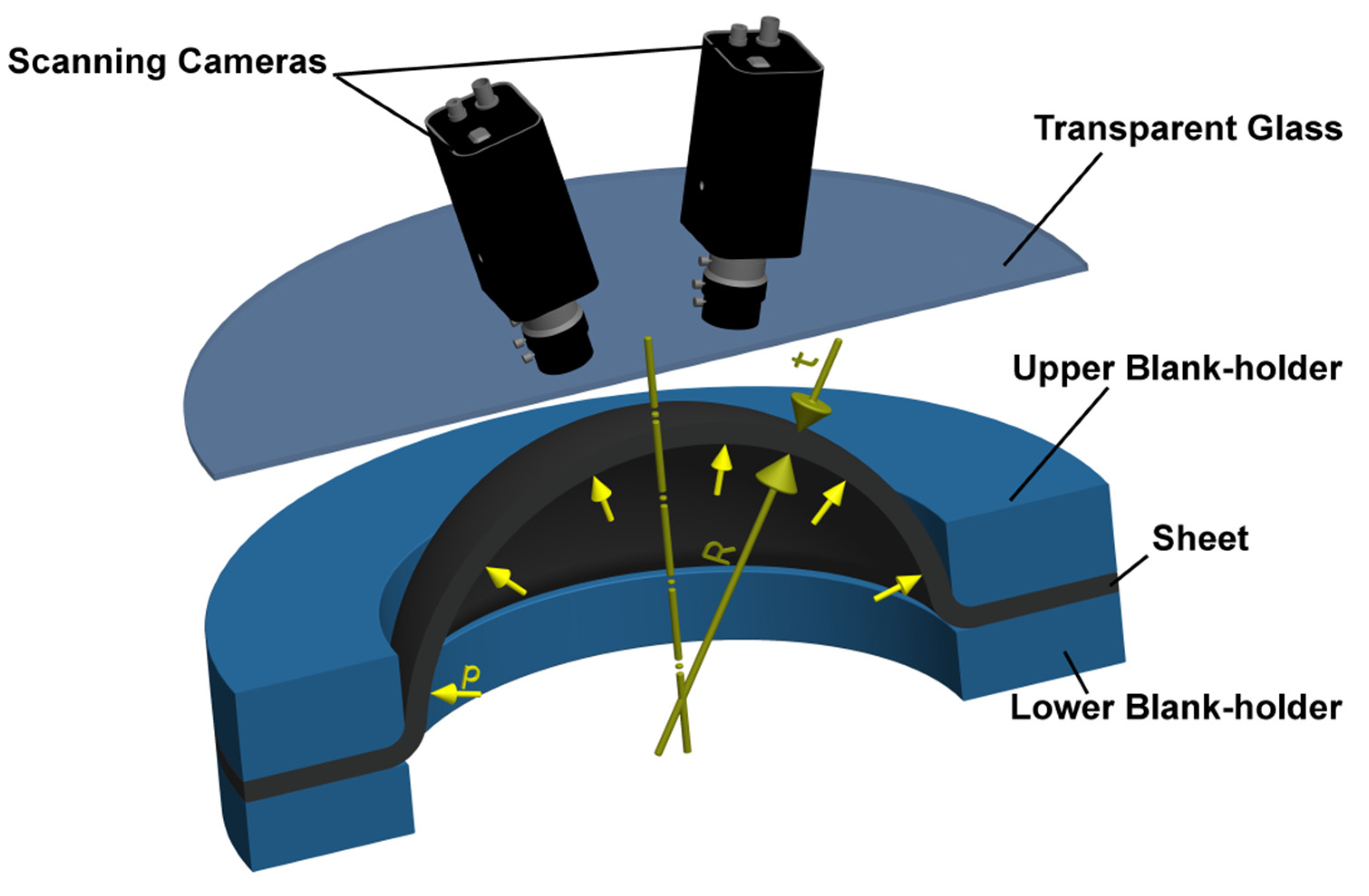
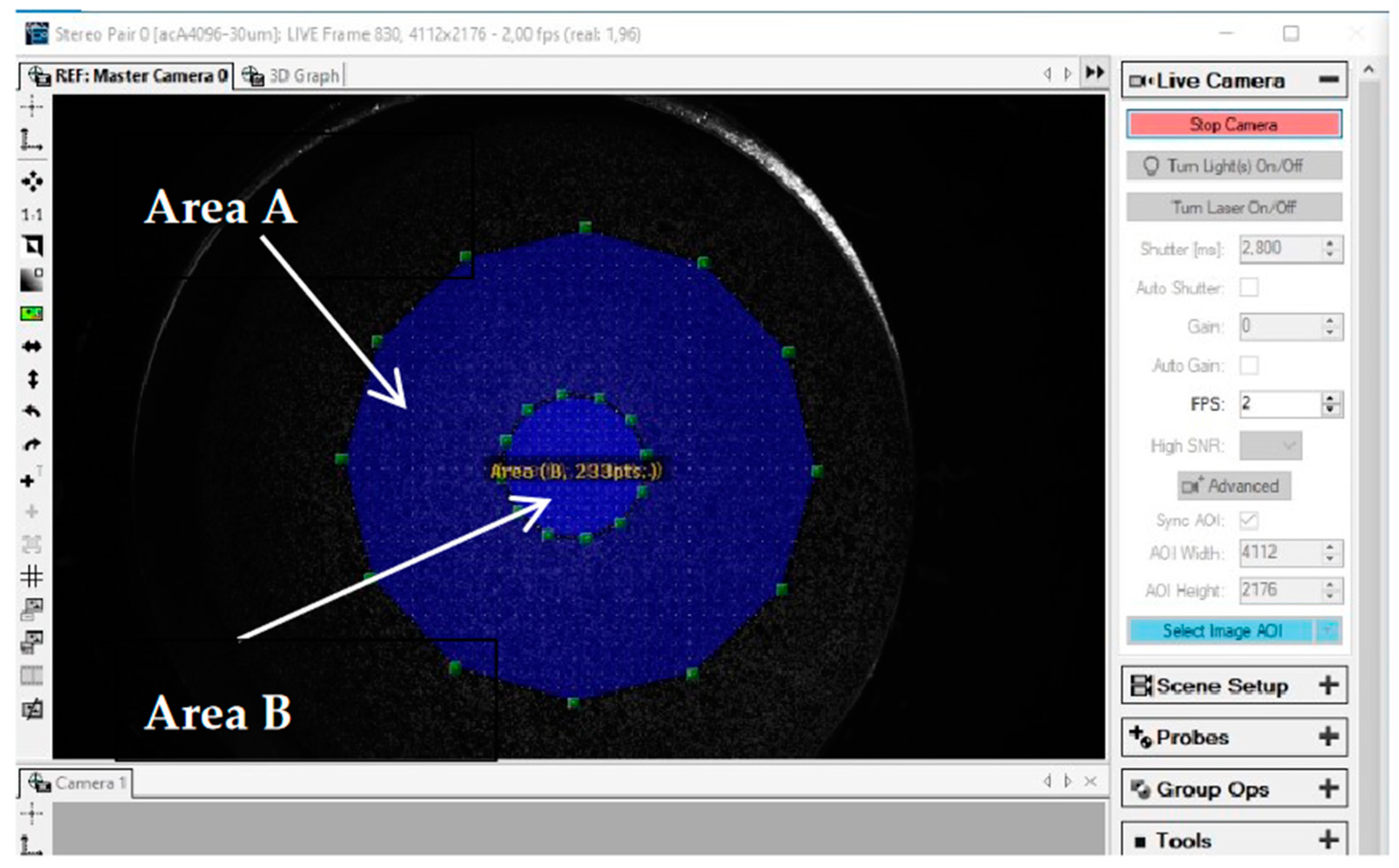
2.2. Hydraulic Bulge Test
- p—hydraulic pressure (MPa)
- R—radius of curvature (mm)
- t—actual thickness of specimen (mm)
- ε1,2,3—principal strains (1)
- t—actual thickness (mm)
- t0—initial thickness (mm)
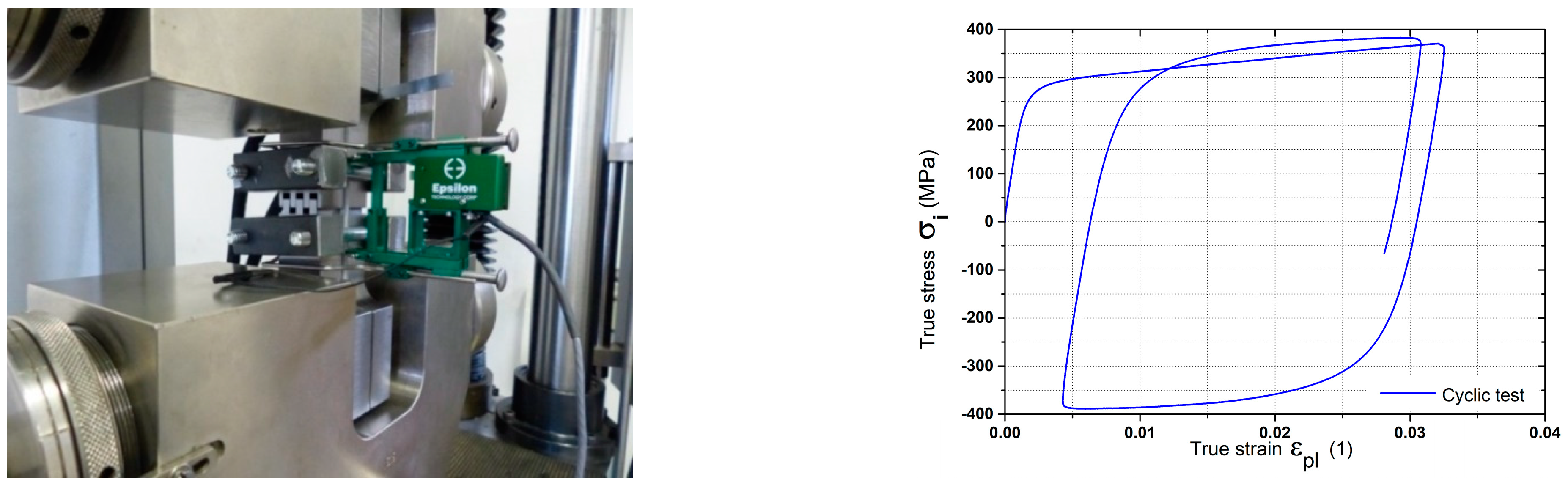
2.3. Cyclic Test
2.4. U-Bending of the Specimens
3. Numerical Simulation
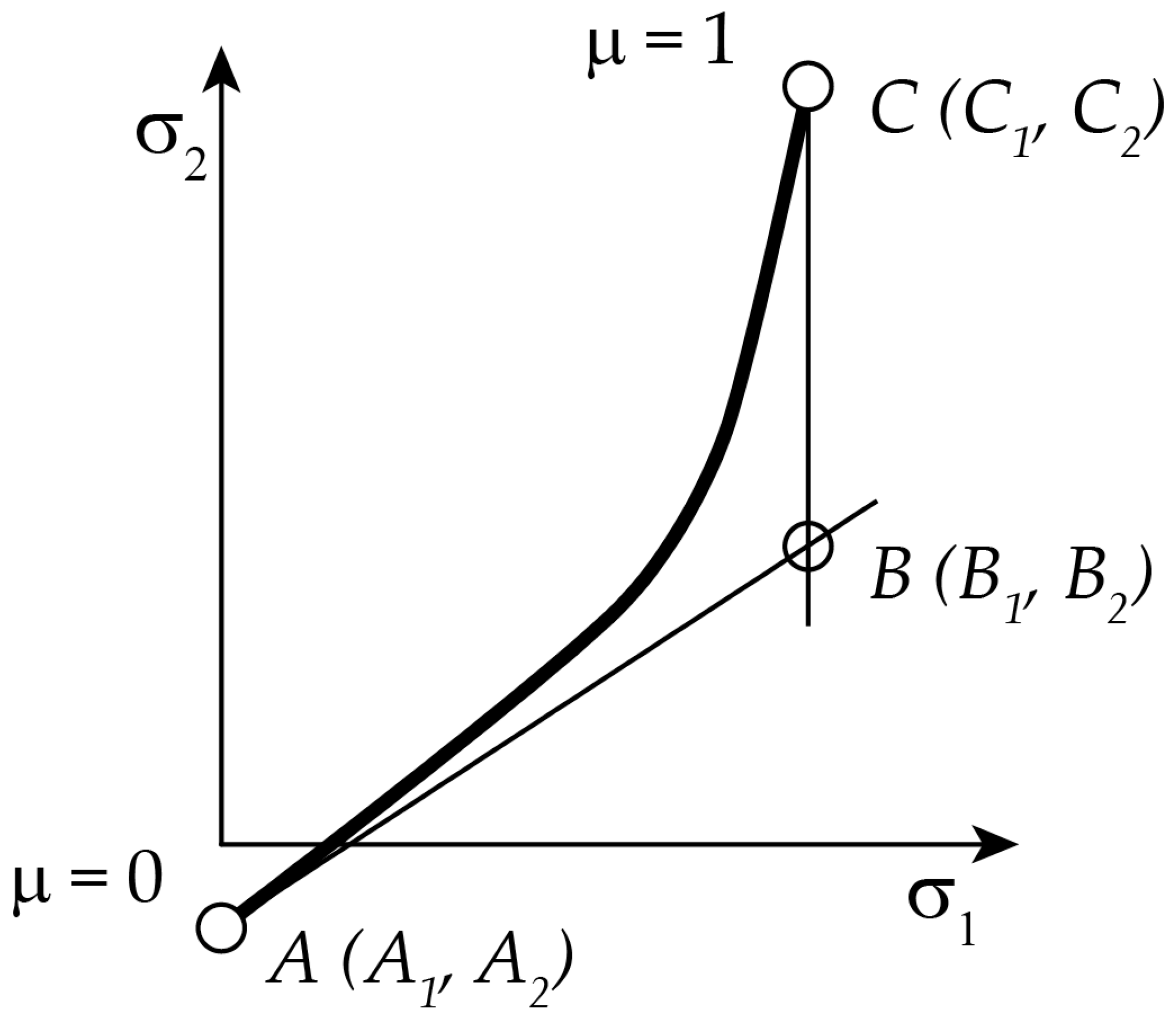
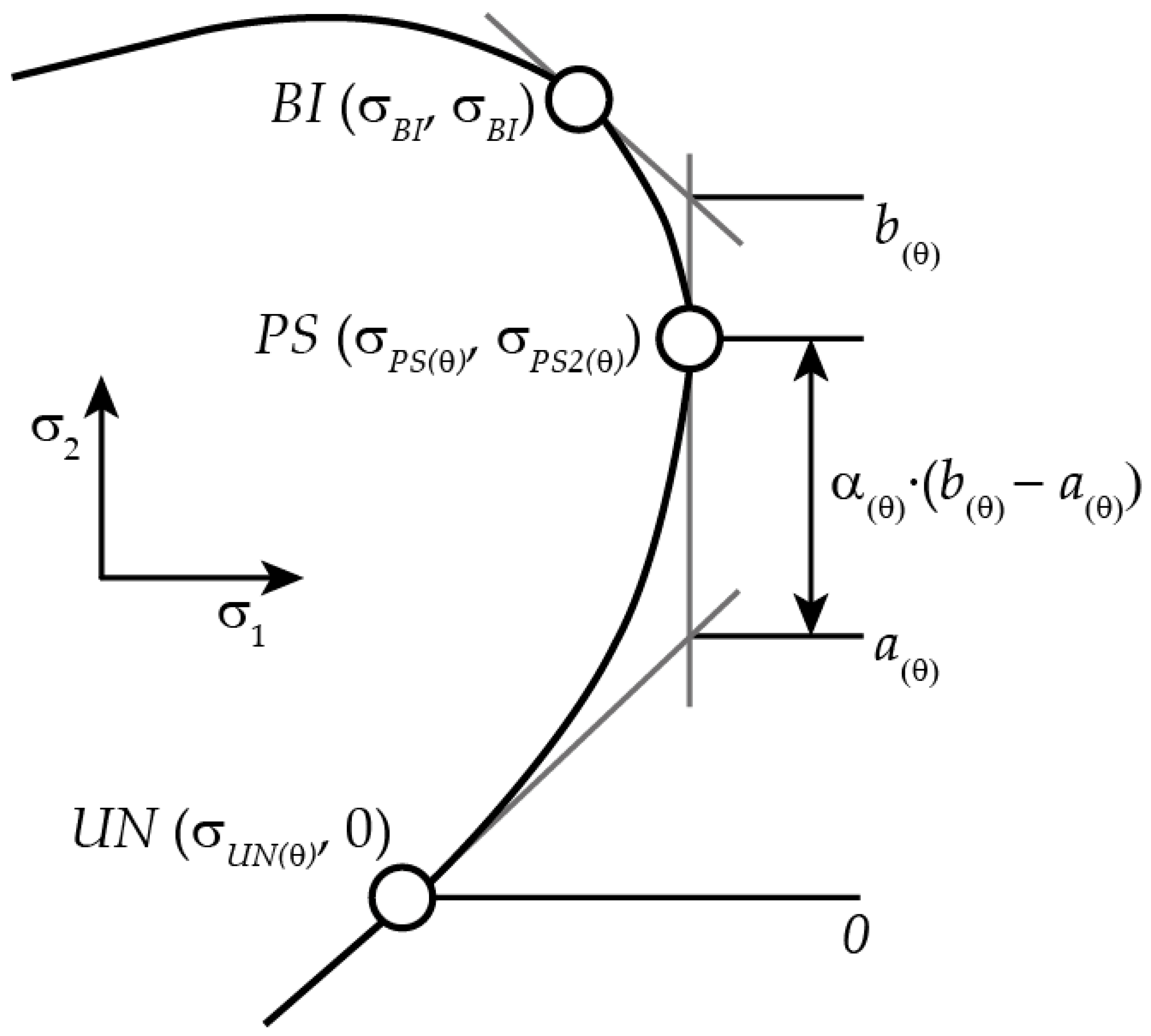
3.1. Vegter Yield Criterion
- s = sin (2θ)
- c = cos (2θ)
3.2. Kinematic Hardening Law
3.3. Definition of the Material Model in the Software PAM-STAMP 2G
3.3.1. Vegter Yield Criterion in Combination with the Isotropic Hardening Law
- x—weighted average of the monitored quantity
- x0, x45, x90—measured values in the relevant directions
3.3.2. Vegter Yield Criterion in Combination with the Kinematic Hardening Law
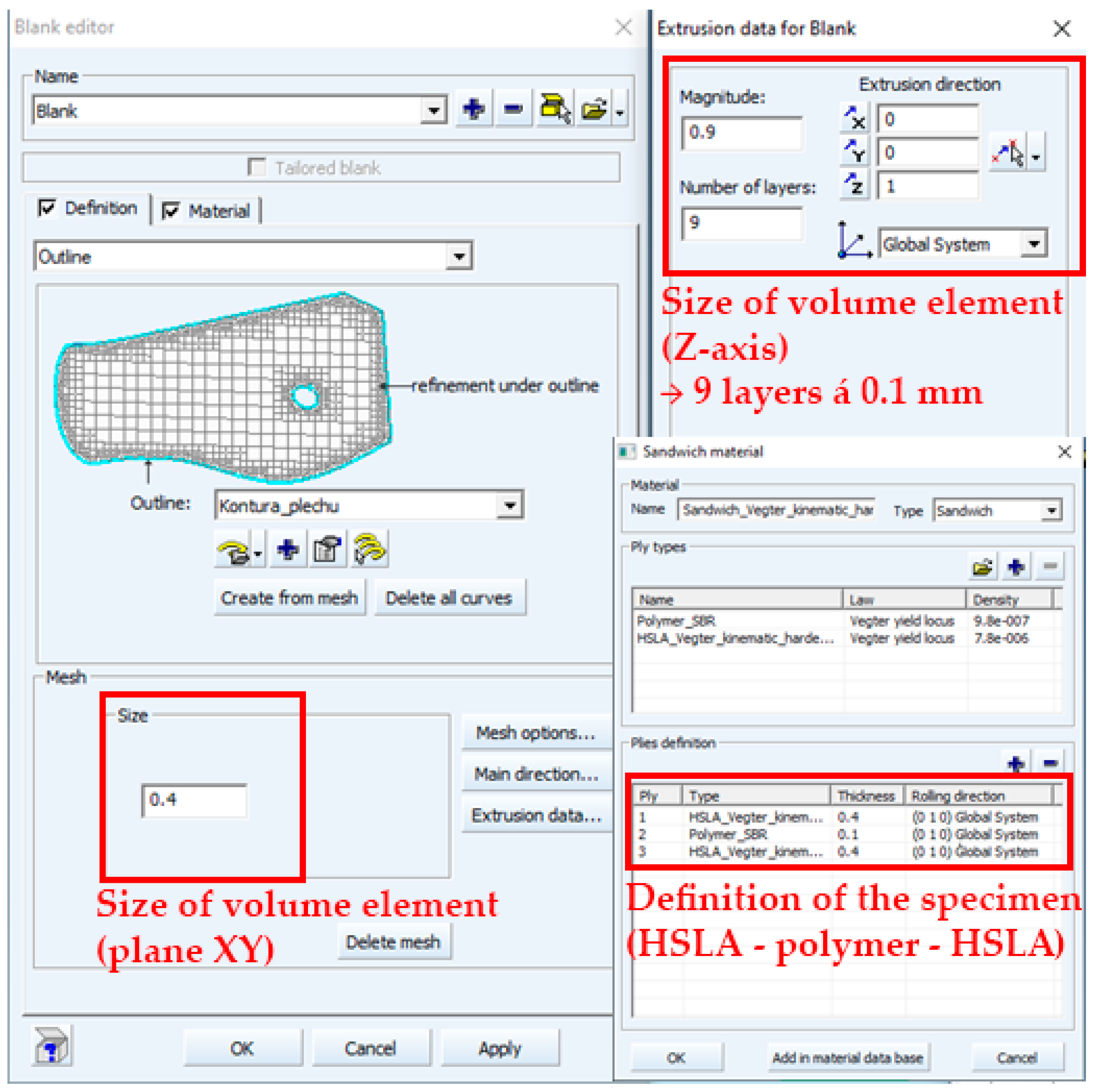
3.3.3. Vegter Yield Criterion in Combination with the Kinematic Hardening Law: Volume Element of the Deformation Mesh
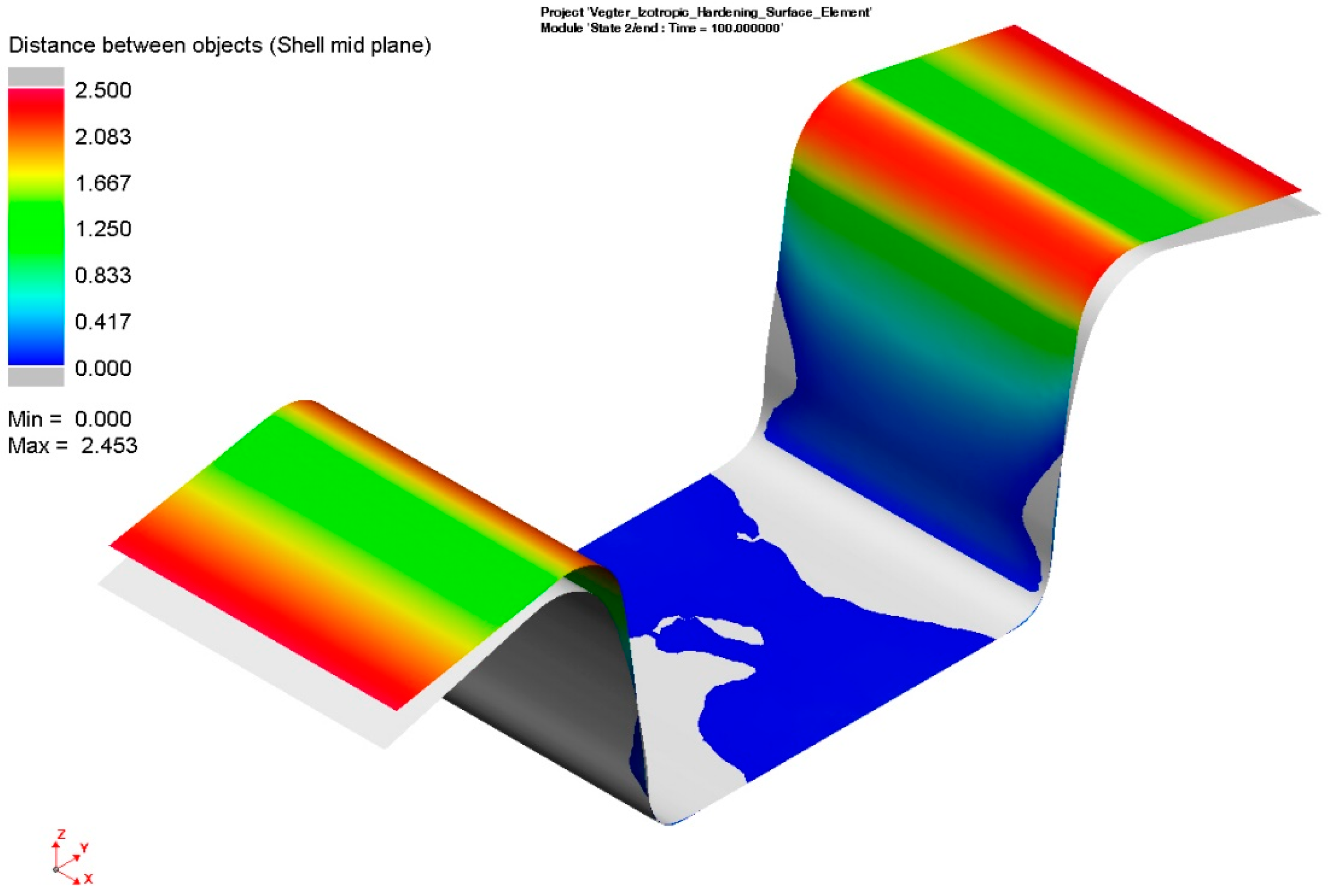
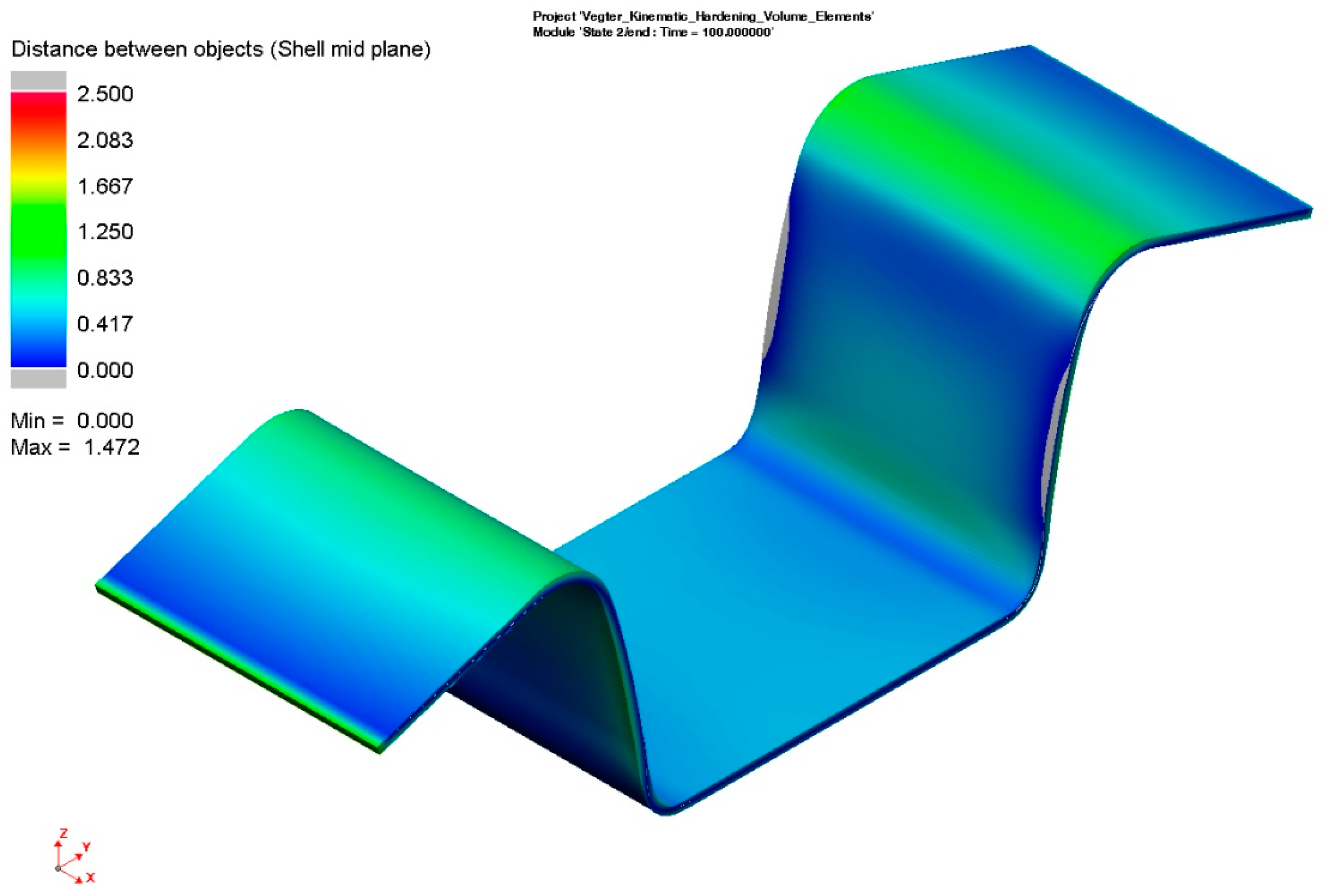
4. Results from the Finite Element Analysis (FEA)
5. Discussion
6. Conclusions
- The isotropic hardening law cannot be used to correctly predict the springback of sandwich material in cases where the stress state changes during the forming process.
- The kinematic hardening law provides a more accurate springback prediction compared to the isotropic hardening model regardless of the surface or volume element selection for the computational mesh.
- The choice of the meshing strategy does not have any significant effect on the FEA result when the kinematic hardening law is used. The surface and volume elements give almost exactly comparable results for the springback prediction of the sandwich material.
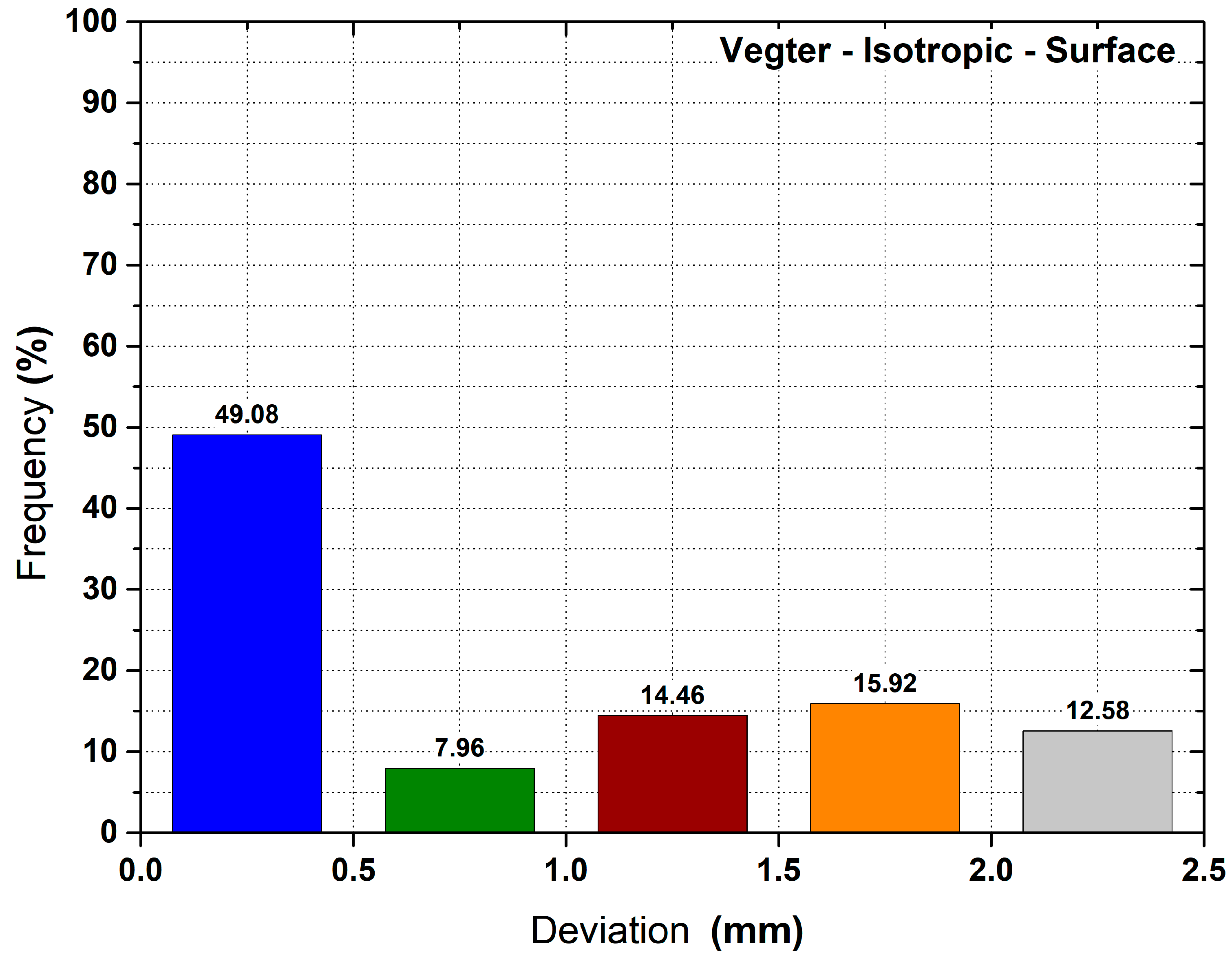
- From a quantitative point of view (using histograms of surfaces’ deviations, see Figure 26, Figure 27 and Figure 28), it was confirmed that the kinematic hardening law (regardless of the element type) has significantly higher accuracy in springback prediction than the isotropic hardening law. In addition to that, both kinematic hardening laws (surface and volume type of mesh) have almost 90% of the surfaces’ deviations up to 0.5 mm compared to the isotropic hardening law, where only 46% can be found up to 0.5 mm.
- The definition of the sandwich material using layers of volume elements in the deformation mesh does not provide a significant improvement of the FEM result.
- In the numerical simulation of forming the sandwich material, the measured values of the mechanical quantities can be related to the entire sheet (sandwich) thickness, and it is not necessary to distinguish the different deformation and stress behaviour of the individual layers.
- From the calculation accuracy point of view, it does not make any sense to use volume elements of the deformation mesh for the thin sheets. Such an approach leads only to a significant increase in computational time.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fischer, S. Aluminium foldcores for sandwich structure application: Mechanical properties and FE-simulation. Thin Walled Struct. 2015, 90, 31–41. [Google Scholar] [CrossRef]
- Grygorowicz, M.; Magnucki, K.; Malinowski, M. Elastic buckling of a sandwich beam with variable mechanical properties of the core. Thin Walled Struct. 2015, 87, 127–132. [Google Scholar] [CrossRef]
- Sivaram, A.R.; Manikandan, N.; Krishnakumar, S.K.; Rajavel, R.; Krishnamohan, S.; Vijayaganth, G. Experimental study on aluminium based sandwich composite with polypropylene foam sheet. Mater. Today Proc. 2020, 24, 746–753. [Google Scholar] [CrossRef]
- Arbaoui, J.; Schmitt, Y.; Pierrot, J.-L.; Royer, F.-X. Numerical simulation and experimental bending behaviour of multi-layer sandwich structures. J. Theor. Appl. Mech. 2014, 52, 431–442. [Google Scholar]
- Li, X.; Lin, Y.; Lu, F. Numerical simulation on in-plane deformation characteristics of lightweight aluminum honeycomb under direct and indirect explosion. Materials 2019, 12, 2222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Li, Z.; Xiong, W. Numerical study on three-point bending behavior of honeycomb sandwich with ceramic tile. Compos. Part B Eng. 2019, 167, 63–70. [Google Scholar] [CrossRef]
- Xie, S.; Feng, Z.; Zhou, H.; Wang, D. Three-point bending behavior of nomex honeycomb sandwich panels: Experiment and simulation. Mech. Adv. Mater. Struct. 2021, 28, 1917–1931. [Google Scholar] [CrossRef]
- Bi, G.; Yin, J.; Wang, Z.; Jia, Z. Micro fracture behavior of composite honeycomb sandwich structure. Materials 2021, 14, 135. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, M.; Huang, Y.; Sang, L.; Hou, W. Experimental and numerical investigation of thermoplastic honeycomb sandwich structures under bending loading. Thin Walled Struct. 2020, 155, 106961. [Google Scholar] [CrossRef]
- Wu, X.; Yu, H.; Guo, L.; Zhang, L.; Sun, X.; Chai, Z. Experimental and numerical investigation of static and fatigue behaviors of composites honeycomb sandwich structure. Compos. Struct. 2019, 213, 165–172. [Google Scholar] [CrossRef]
- Yu, G.-C.; Feng, L.-J.; Wu, L.-Z. Thermal and mechanical properties of a multifunctional composite square honeycomb sandwich structure. Mater. Des. 2016, 102, 238–246. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Hui, D. Blast resistance and parametric study of sandwich structure consisting of honeycomb core filled with circular metallic tubes. Compos. Part B Eng. 2018, 145, 261–269. [Google Scholar] [CrossRef]
- Gladkovsky, S.V.; Kuteneva, S.V.; Sergeev, S.N. Microstructure and mechanical properties of sandwich copper/steel composites produced by explosive welding. Mater. Charact. 2019, 154, 294–303. [Google Scholar] [CrossRef]
- Nilsson, P.; Al-Emrani, M.; Atashipour, S.R. Fatigue-strength assessment of laser welds in corrugated core steel sandwich panels. J. Constr. Steel Res. 2020, 164, 105797. [Google Scholar] [CrossRef]
- Nilsson, P.; Hedegård, J.; Al-Emrani, M.; Atashipour, S.R. The impact of production-dependent geometric properties on fatigue-relevant stresses in laser-welded corrugated core steel sandwich panels. Weld World 2019, 63, 1801–1818. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.S.; Yoon, J.H.; Yoo, J.T. Application of solid state joining technologies in aerospace parts. Key Eng. Mater. 2020, 837, 69–73. [Google Scholar] [CrossRef]
- Pragana, J.P.; Contreiras, T.R.; Bragança, I.M.; Silva, C.M.; Alves, L.M.; Martins, P.A. Joining by forming of metal–polymer sandwich composite panels. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 2089–2098. [Google Scholar] [CrossRef]
- Ablat, M.A.; Qattawi, A. Numerical simulation of sheet metal forming: A review. Int. J. Adv. Manuf. Technol. 2017, 89, 1235–1250. [Google Scholar] [CrossRef]
- Zajkani, A.; Hajbarati, H. An analytical modeling for springback prediction during U-bending process of advanced high-strength steels based on anisotropic nonlinear kinematic hardening model. Int. J. Adv. Manuf. Technol. 2017, 90, 349–359. [Google Scholar] [CrossRef]
- Li, Y.; Liang, Z.; Zhang, Z.; Zou, T.; Li, D.; Ding, S.; Xiao, H.; Shi, L. An analytical model for rapid prediction and compensation of springback for chain-die forming of an AHSS U-channel. Int. J. Mech. Sci. 2019, 159, 195–212. [Google Scholar] [CrossRef]
- Hajbarati, H.; Zajkani, A. A novel analytical model to predict springback of DP780 steel based on modified Yoshida-Uemori two-surface hardening model. Int. J. Mater. 2019, 12, 441–455. [Google Scholar] [CrossRef]
- Yang, X.; Choi, C.; Sever, N.K.; Altan, T. Prediction of springback in air-bending of advanced high strength steel (DP780) considering Young’s modulus variation and with a piecewise hardening function. Int. J. Mech. Sci. 2016, 105, 266–272. [Google Scholar] [CrossRef]
- Liu, J.; Xue, W. Unconstrained bending and springback behaviors of aluminum-polymer sandwich sheets. Int. J. Adv. Manuf. Technol. 2017, 91, 1517–1529. [Google Scholar] [CrossRef]
- Gautam, V.; Raut, V.M.; Kumar, D.R. Analytical prediction of springback in bending of tailor-welded blanks incorporating effect of anisotropy and weld zone properties. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2018, 232, 294–306. [Google Scholar] [CrossRef]
- Zhang, Z.K.; Wu, J.J.; Guo, R.C.; Wang, M.Z.; Li, F.F.; Guo, S.C.; Wang, Y.A.; Liu, W.P. A semi-analytical method for the springback prediction of thick-walled 3D tubes. Mater. Des. 2016, 99, 57–67. [Google Scholar] [CrossRef]
- Jin, L.; Yang, Y.-F.; Li, R.-Z.; Cui, Y.-W.; Jamil, M.; Li, L. study on springback straightening after bending of the U-section of TC4 material under high-temperature conditions. Materials 2020, 13, 1895. [Google Scholar] [CrossRef]
- Wasif, M.; Iqbal, S.A.; Tufail, M.; Karim, H. Experimental analysis and prediction of springback in V-bending process of high-tensile strength steels. Trans. Indian Inst. Met. 2020, 73, 285–300. [Google Scholar] [CrossRef]
- Panthi, S.K.; Ramakrishnan, N. Semi analytical modeling of springback in arc bending and effect of forming load. Trans. Nonferrous Met. Soc. China 2011, 21, 2276–2284. [Google Scholar] [CrossRef]
- Han, Y.S.; Yang, W.H.; Choi, K.Y.; Kim, B.H. A Study on the effect of input parameters on springback prediction accuracy. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2011; Volume 1383, pp. 1137–1142. [Google Scholar] [CrossRef]
- Mertin, C.; Stellmacher, T.; Schmitz, R.; Hirt, G. Enhanced springback prediction for bending of high-strength spring steel using material data from an inverse modelling approach. Procedia Manuf. 2019, 29, 153–160. [Google Scholar] [CrossRef]
- Gu, B.; He, J.; Li, S.; Chen, Y.; Li, Y. Cyclic sheet metal test comparison and parameter calibration for springback prediction of dual-phase steel sheets. J. Manuf. Sci. Eng. 2017, 139, 91010. [Google Scholar] [CrossRef]
- Li, Y.; Li, A.; Yue, Z.; Qiu, L.; Badreddine, H.; Gao, J.; Wang, Y. Springback prediction of AL6061 pipe in free bending process based on finite element and analytic methods. Int. J. Adv. Manuf. Technol. 2020, 109, 1789–1799. [Google Scholar] [CrossRef]
- Seo, K.-Y.; Kim, J.-H.; Lee, H.-S.; Kim, J.H.; Kim, B.-M. Effect of constitutive equations on springback prediction accuracy in the TRIP1180 cold stamping. Metals 2018, 8, 18. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Cao, J.; Chai, X.; Liu, J.; Zhao, R.; Kong, N. Investigation of forming parameters on springback for ultra high strength steel considering Young’s modulus variation in cold roll forming. J. Manuf. Process. 2017, 29, 289–297. [Google Scholar] [CrossRef]
- Pouraliakbar, H.; Khalaj, G.; Jandaghi, M.R.; Khalaj, M.J. Study on the correlation of toughness with chemical composition and tensile test results in microalloyed API pipeline steels. J. Min. Metall. B Metall. 2015, 51, 173–178. [Google Scholar] [CrossRef]
- Jamli, M.R.; Farid, N.M. The sustainability of neural network applications within finite element analysis in sheet metal forming: A review. Measurement 2019, 138, 446–460. [Google Scholar] [CrossRef]
- Angsuseranee, N.; Pluphrach, G.; Watcharasresomroeng, B.; Songkroh, A. Springback and sidewall curl prediction in U-bending process of AHSS through finite element method and artificial neural network approach. Songklanakarin J. Sci. Technol. 2018, 40, 534–539. [Google Scholar]
- Miranda, S.S.; Barbosa, M.R.; Santos, A.D.; Pacheco, J.B.; Amaral, R.L. Forming and springback prediction in press brake air bending combining finite element analysis and neural networks. J. Strain Anal. Eng. Des. 2018, 53, 584–601. [Google Scholar] [CrossRef]
- Zhu, Y.X.; Liu, Y.L.; Yang, H.; Li, H.P. Development and application of the material constitutive model in springback prediction of cold-bending. Mater. Des. 2012, 42, 245–258. [Google Scholar] [CrossRef]
- Chatti, S.; Fathallah, R. A study of the variations in elastic modulus and its effect on springback prediction. Int. J. Mater. 2014, 7, 19–29. [Google Scholar] [CrossRef]
- Jung, J.; Jun, S.; Lee, H.-S.; Kim, B.-M.; Lee, M.-G.; Kim, J.H. Anisotropic hardening behaviour and springback of advanced high-Strength steels. Metals 2017, 7, 480. [Google Scholar] [CrossRef] [Green Version]
- Baara, W.A.B.; Baharudin, B.T.H.T.B.; Anuar, M.K.; Ismail, M.I.S. Effect of elastic module degradation measurement in different sizes of the nonlinear isotropic–kinematic yield surface on springback prediction. Metals 2019, 9, 511. [Google Scholar] [CrossRef] [Green Version]
- Mulidrán, P.; Spišák, E.; Tomáš, M.; Slota, J.; Majerníková, J. Numerical prediction and reduction of hat-shaped part springback made of dual-phase AHSS steel. Metals 2020, 10, 1119. [Google Scholar] [CrossRef]
- Mulidrán, P.; Šiser, M.; Slota, J.; Spišák, E.; Sleziak, T. Numerical prediction of forming car body parts with emphasis on springback. Metals 2018, 8, 435. [Google Scholar] [CrossRef] [Green Version]
- Trzepiecinski, T.; Lemu, H.G. Effect of computational parameters on springback prediction by numerical simulation. Metals 2017, 7, 380. [Google Scholar] [CrossRef] [Green Version]
- Naofal, J.; Naeini, H.M.; Mazdak, S. Effects of hardening model and variation of elastic modulus on springback prediction in roll forming. Metals 2019, 9, 1005. [Google Scholar] [CrossRef] [Green Version]
- Sumikawa, S.; Ishiwatari, A.; Hiramoto, J.; Urabe, T. Improvement of springback prediction accuracy using material model considering elastoplastic anisotropy and Bauschinger effect. J. Mater. Process. Technol. 2016, 230, 1–7. [Google Scholar] [CrossRef]
- Slota, J.; Šiser, M.; Dvorák, M. Experimental and numerical analysis of springback behavior of aluminum alloys. Strength Mater. 2017, 49, 565–574. [Google Scholar] [CrossRef]
- Vegter, H.; van den Boogaard, A.H. A plane stress yield function for anisotropic sheet material by interpolation of biaxial stress states. Int. J. Plast. 2006, 22, 557–580. [Google Scholar] [CrossRef]
- ESI Group. Pam-Stamp 2020.5 User’s Guide; ESI Group: Paris, France, 2020. [Google Scholar]
- Yoshida, F.; Uemori, T. A model of large-strain cyclic plasticity and its application to springback simulation. Int. J. Mech. Sci. 2003, 45, 1687–1702. [Google Scholar] [CrossRef]
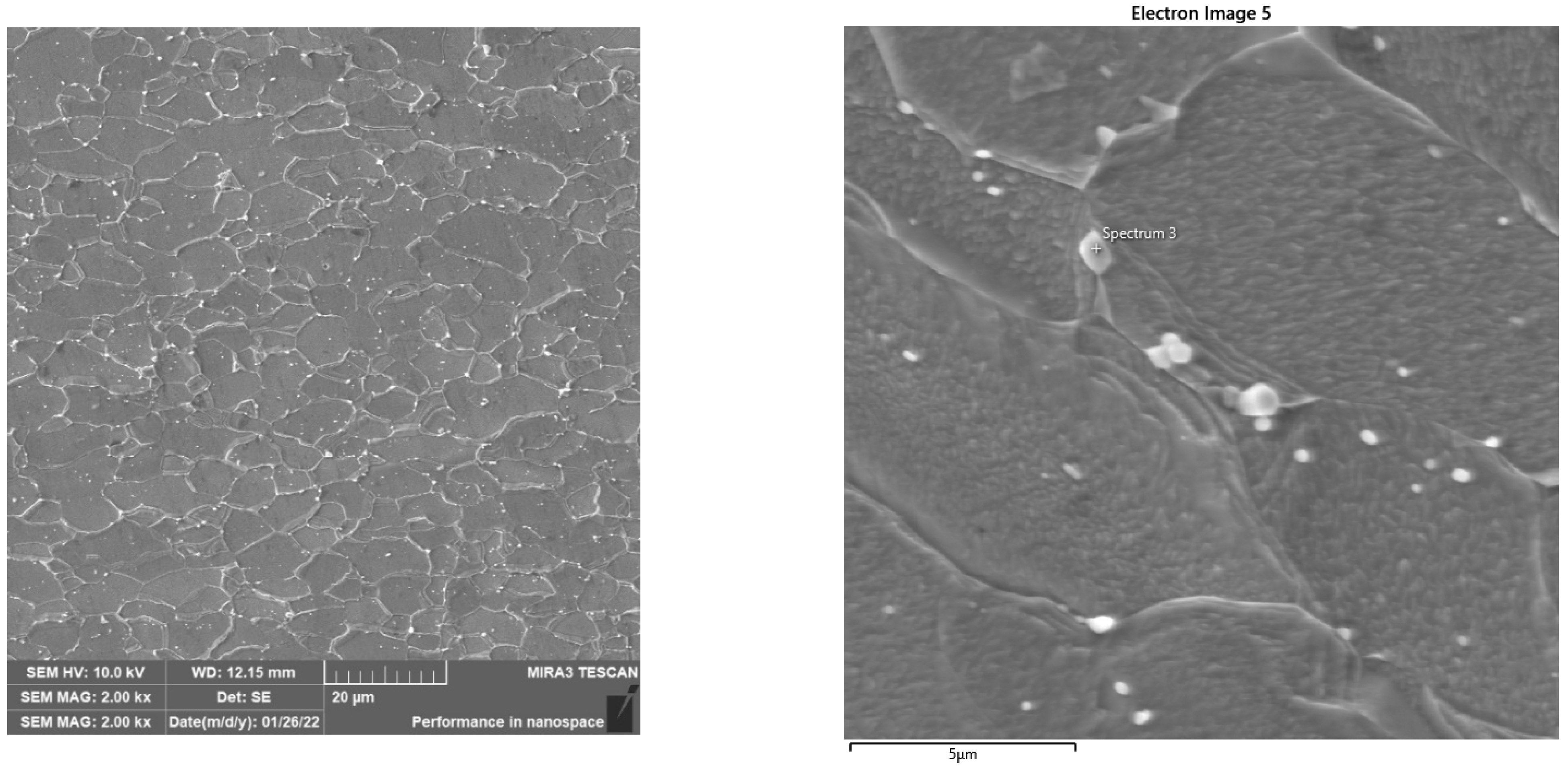
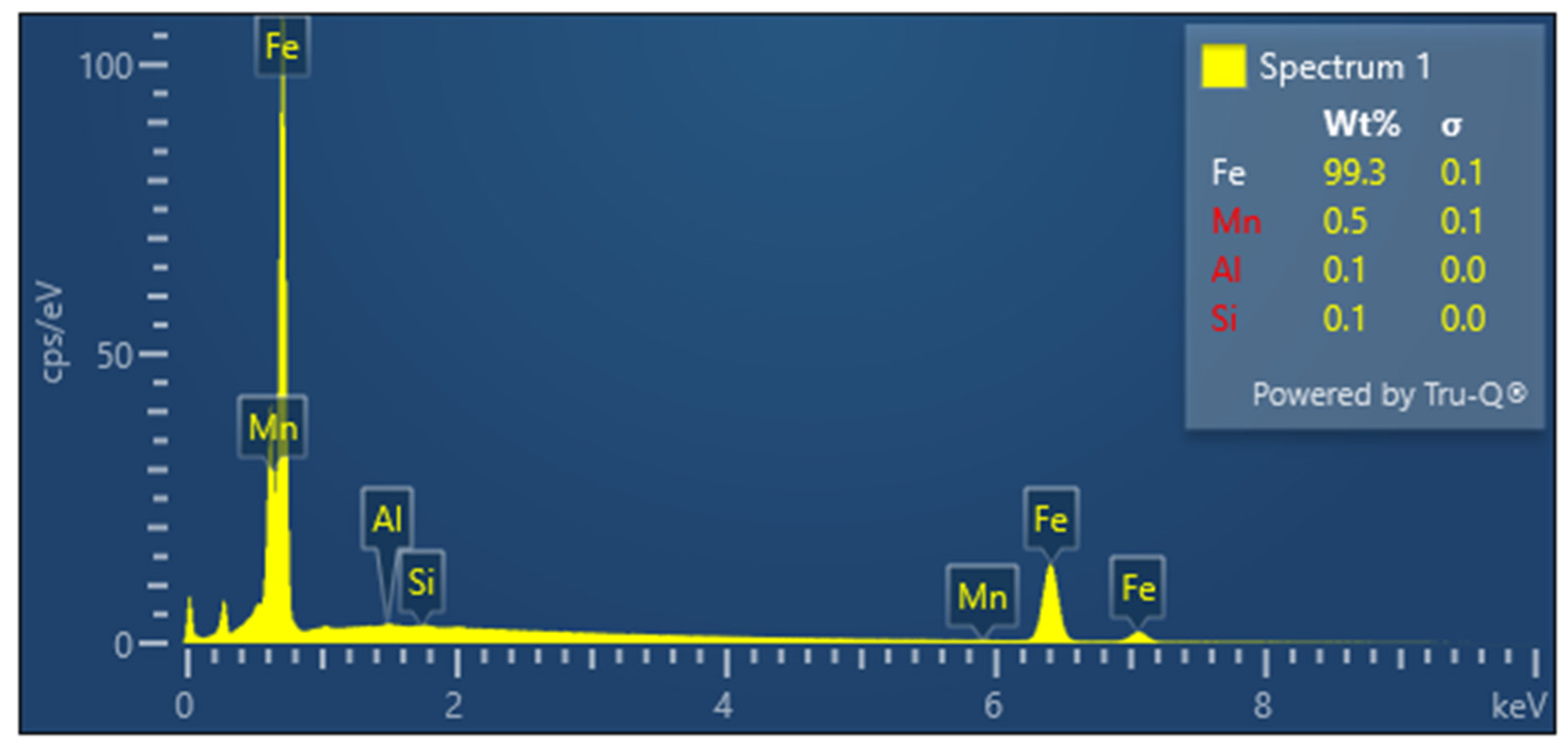

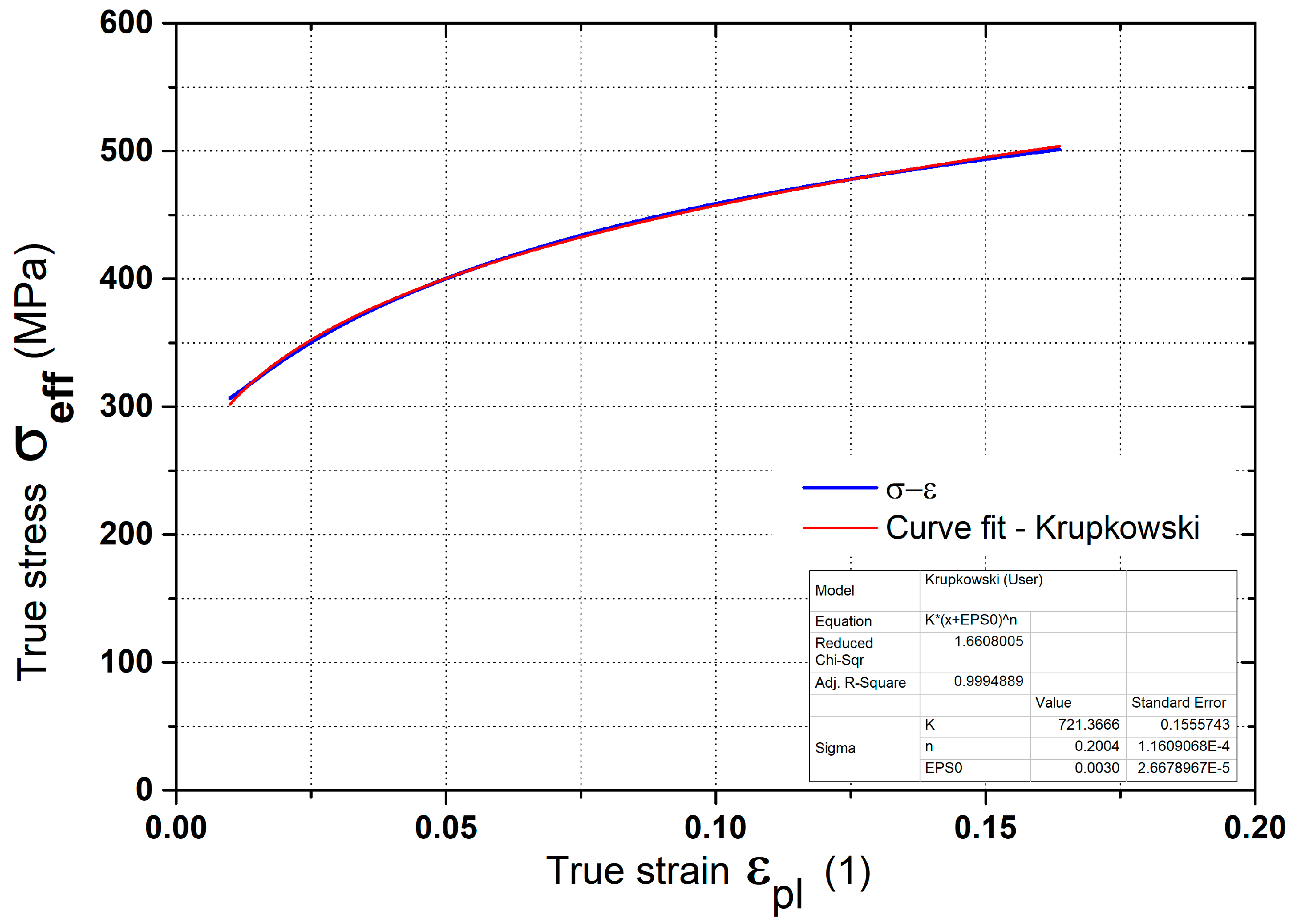













| Chemical Element | C | Si | Mn | Al | P | S | Ti | Nb |
|---|---|---|---|---|---|---|---|---|
| Composition [wt%] | 0.097 | 0.406 | 0.746 | 0.211 | 0.016 | 0.013 | 0.122 | 0.074 |
| Direction | Rp0.2 (MPa) | Rm (MPa) | Ag (%) | A80mm (%) | r10–20 (1) | E (MPa) |
|---|---|---|---|---|---|---|
| 0° | 291.7 | 426.5 | 17.8 | 23.1 | 1.335 | 174,283 |
| 45° | 299.6 | 418.3 | 18.9 | 27.1 | 1.515 | 183,718 |
| 90° | 307.7 | 428.5 | 18.1 | 26.6 | 1.622 | 179,928 |
| Direction | K (MPa) | n (1) | ε0 (1) |
|---|---|---|---|
| 0° | 720.6 | 0.1995 | 0.0030 |
| 45° | 707.6 | 0.2025 | 0.0065 |
| 90° | 726.9 | 0.2039 | 0.0067 |
| Material | K (MPa) | n (1) | ε0 (1) |
|---|---|---|---|
| Sandwich | 865.1 | 0.267 | 0.0076 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solfronk, P.; Sobotka, J.; Koreček, D. Effect of the Computational Model and Mesh Strategy on the Springback Prediction of the Sandwich Material. Machines 2022, 10, 114. https://doi.org/10.3390/machines10020114
Solfronk P, Sobotka J, Koreček D. Effect of the Computational Model and Mesh Strategy on the Springback Prediction of the Sandwich Material. Machines. 2022; 10(2):114. https://doi.org/10.3390/machines10020114
Chicago/Turabian StyleSolfronk, Pavel, Jiří Sobotka, and David Koreček. 2022. "Effect of the Computational Model and Mesh Strategy on the Springback Prediction of the Sandwich Material" Machines 10, no. 2: 114. https://doi.org/10.3390/machines10020114
APA StyleSolfronk, P., Sobotka, J., & Koreček, D. (2022). Effect of the Computational Model and Mesh Strategy on the Springback Prediction of the Sandwich Material. Machines, 10(2), 114. https://doi.org/10.3390/machines10020114






