Abstract
This investigation attempts to study a possible controller in improving the dynamic stability of capacitive microstructures through mitigating the effects of disturbances and uncertainties in their resultant dynamic behavior. Consequently, a nonsingular terminal sliding mode control strategy is suggested in this regard. The main features of this particular control strategy are its high response speed and its non-reliance on powerful controller forces. The stability of the controller was investigated using Lyapunov theory. For this purpose, a suitable Lyapunov function was introduced to prove the stability of a controller, and the singularity conditions and methods to overcome these conditions are presented. The achieved results proved the high capability of the applied technique in stabilizing of the microstructure as well as mitigating the effects of disturbances and uncertainties.
1. Introduction
The industry of Micro Electro Mechanical System (MEMS) has been among the most significant businesses in the recent last decades, gaining the attention of numerous researchers all over the world. MEMS structures, such as micro-switches [1,2,3,4], micro-capacitors [5,6,7], micro-gyroscopes [8,9,10,11], micro-sensors [12,13,14], and micro-actuators [15,16,17,18,19], are essentially used in various industrial fields, such as aerospace, micro-electronics, telecommunication, and medical [20,21]. Their wider scopes of applications and popularity comes principally from their small-scale features, their low energy/power consumption, their ability of batch fabrication, and their high response speed.
The development and progress for these tiny structures depend on their suitable design and correct prediction of their respective electro-mechanical behaviors and characteristics. One of the primary challenges of these structures are their variant dynamic characteristics, useful in certain applications but limiting their use in others. One can observe a significant increase in the study of the mechanical and dynamical behaviors of these structures [22,23,24,25,26] in the recently published literature.
One of the important concerns concerning the dynamic behavior analysis of these structures are the effects of external disturbances and uncertainties. As for most microstructures, the governing dynamic equation is nonlinear; this nonlinearity can lead to numerous dynamic instabilities, such as dynamic pull-in [27,28,29,30], bifurcations, dynamic hysteresis, fractal and chaotic behaviors [31,32,33,34,35,36]. Disturbances and uncertainties, in addition to nonlinearity, drastically intensify such instabilities.
Reducing disturbances requires altering the microstructure packaging and its isolation; however, such adjustments/modifications cannot cancel all the unwanted disturbances at all ranges of frequencies. Moreover, reducing uncertainties requires improved fabrication processes [37,38], including lithography, etching, and others, but this would significantly increase the manufacturing costs of these tiny structures. Bearing in mind these challenges, it was proven that uncertainties and disturbances cannot be completely eliminated from macro-scale structures [39,40,41]; thus, their elimination is even more challenging in microstructures.
The common studies on examining microstructure dynamical behavior do not include disturbance and uncertainty effects [42,43,44,45]. For example, dynamical analysis of MEM structures incorporating micro-beams have been studied without considering uncertainties or disturbances [4,46,47,48,49]. Some studies in the case of vibration analysis of micro-plates that neglect uncertainties and disturbances have been provided in references [50,51,52,53,54]. Additional to the abovementioned works, some relevant vibration analysis of micro gyroscopes without considering uncertainty and disturbances are available in [55,56,57,58].
Contrary to these works, few studies have investigated such effects and attempted their mitigation. As an example, the robust active control method is an efficient technique for reducing and eliminating the effects of disturbance and uncertainty effects [59,60]. Furthermore, the Sliding Mode Control (SMC) is one of the primary robust control strategies offering a particularly strong robustness against disturbances and uncertainties [61,62,63,64,65,66]. This control method has also the merit of being computationally cheap and simple as compared to other robust control methods, and it can be combined with fuzzy and artificial intelligent methods [67,68,69,70,71].
Rahmani et al. [72] studied dynamic analysis of MEMS gyroscopes using a sliding mode controller. They considered external disturbances as an unwanted factor that disturbs the vibration of the structure and used a Lyapunov function to extract the control parameters. Robust dynamic analysis of MEMS Probing was presented in ref. [73]. In this work, H-infinity method was employed to mitigate uncertainties and noises. He and Geng [74] studied the dynamics and robust control of a torsional gyroscope subjected to electrostatic force with considering structural uncertainties.
They applied an observer-based robust controller on the basis of linear matrix inequalities to fulfilment of this work. The stability of a micro gyroscope, including model uncertainties and external disturbances, was investigated in ref. [75]. The implemented strategy was based on applying of a robust adaptive fuzzy controller. Qin et al. [76] applied a nonlinear feedback control method with integral sliding mode to alleviate the effects of external disturbance of micro ultrasonic transducer. They used particle swarm optimization for tuning the control parameters.
Darbasi et al. [77] investigated the dynamic analysis of a micro ultrasonic transducer subjected to external disturbances and uncertainty. They applied sliding model control to stabilize the microstructure. Robust dynamic analysis and disturbance rejection of an electrostatically micro-tunable capacitor was studied in ref. [78] by means of an adaptive sliding mode controller.
Among the SMC methods, Nonsingular Terminal SMC (NTSMC) represents the most efficient control technique offering fast or finite-time convergence without requiring a strong controlling force [79,80,81,82]. Considering the reputation and effectiveness of this method, there have been significant studies to improve it in controlling the dynamic response of mechanical structures [83,84,85]. Contrary to the majority of studies on control of mechanical structures, there have been few studies on microstructure control and eliminating the effects of disturbance and uncertainty.
Owing to the importance of controlling the responses of microstructure and the efficiency of the NTSMC control strategy as well as its high response speed, this study investigates the stabilization of micro-capacitors in the presence of disturbances and uncertainties. For this purpose, a dynamical system that covers the dynamic equations of most microstructures is considered. This equation includes uncertainty and disturbance terms, and, in reality, these terms may not be negligible.
However, as mentioned before, most of the studies did not take these factors into account. In the continuation of the study, a suitable sliding surface for the design of NTSMC is presented, and the existence conditions for singularity are also discussed in detail. The relation of the control inputs are presented and based on the presented Lyapunov function. The stability of the Lyapunov function and, consequently, the stability of the NTSMC are examined. The Lyapunov function and its derivative in the singular and nonsingular regions are investigated.
Additionally, we aims to examine the effect of the main controller parameters on the dynamic behavior of the micro-capacitors. The main controlling parameters consist of the electrostatic forces applied to the microstructure to possibly overcome the disturbance effects in the neighborhood of the fixed-point and prevent its distancing from this zone. The major findings of this study are then summarized in indicating the vast potential of the NTSMC method in controlling the dynamic behavior of capacitive microstructures under the effects of disturbances and uncertainties.
The effects of controller and microstructure parameters on the amplitude of vibration, phase plane associated with the sliding surface, the magnitude of the control parameter or the applied voltages are fully investigated. In addition, the ability of the controller to stabilize the microstructure in the presence of uncertainty and noise is investigated, and the effect of noise intensity on the dynamic behavior of the system, extent of the phase plane and its effects on applied voltages are discussed in detail.
The present study is structured as follows: The next section discusses the NTSMC controller and its stabilizing based on Lyapunov theory. In Section 2.1, the studied microstructure and its governing dynamic equations are presented. The obtained results related to dynamic behavior, stabilization, and the control of microstructure are presented in Section 3. Section 4 presents the concluding remarks of this paper.
2. Nonsingular Terminal Sliding Mode Control
Below, the NTSMC design process for a dynamical system governed by a second order differential equation [86] is presented. Equation (1) shows the general form of governing differential equation of the examined system:
where represents the vector of state space; and both express the smooth functions, respectively; and represent the uncertainty and the external factor of disturbance; and denotes the controlling factor. For the investigated case, it is assumed that where . The purpose of designing a NTSMC is to determine the control law of so that the dynamic system of Equation (1) is stable in the vicinity of . Therefore, the NTSMC manifold for the mentioned design is considered as follows [86,87]:
where is the controller parameter, and and are positive odd numbers satisfying the following condition . A control law determination is based on the fulfilment of the following condition: . In fact, for this particular case, a Lyapunov function is considered as , and representing the condition of stability of Lyapunov function or . Given the equations of (1) and (2), we have:
Considering , for and , there is a singularity situation for , and it can be written as follows:
The above state cannot occur in the neighborhood of and , and therefore:
The purpose of the NTSMC controller is to assure a control condition that does not cause a singularity on . For this reason, and according to [86], the control law can be expressed as follows:
where , represents the saturation function considering , and is a positive number.
In the continuation of this section, the stability of the Lyapunov function is discussed. As previously said, should be negative () in order for the system to be stable. If this condition is satisfied, the Lyapunov function and, consequently, the controller, will be stable.
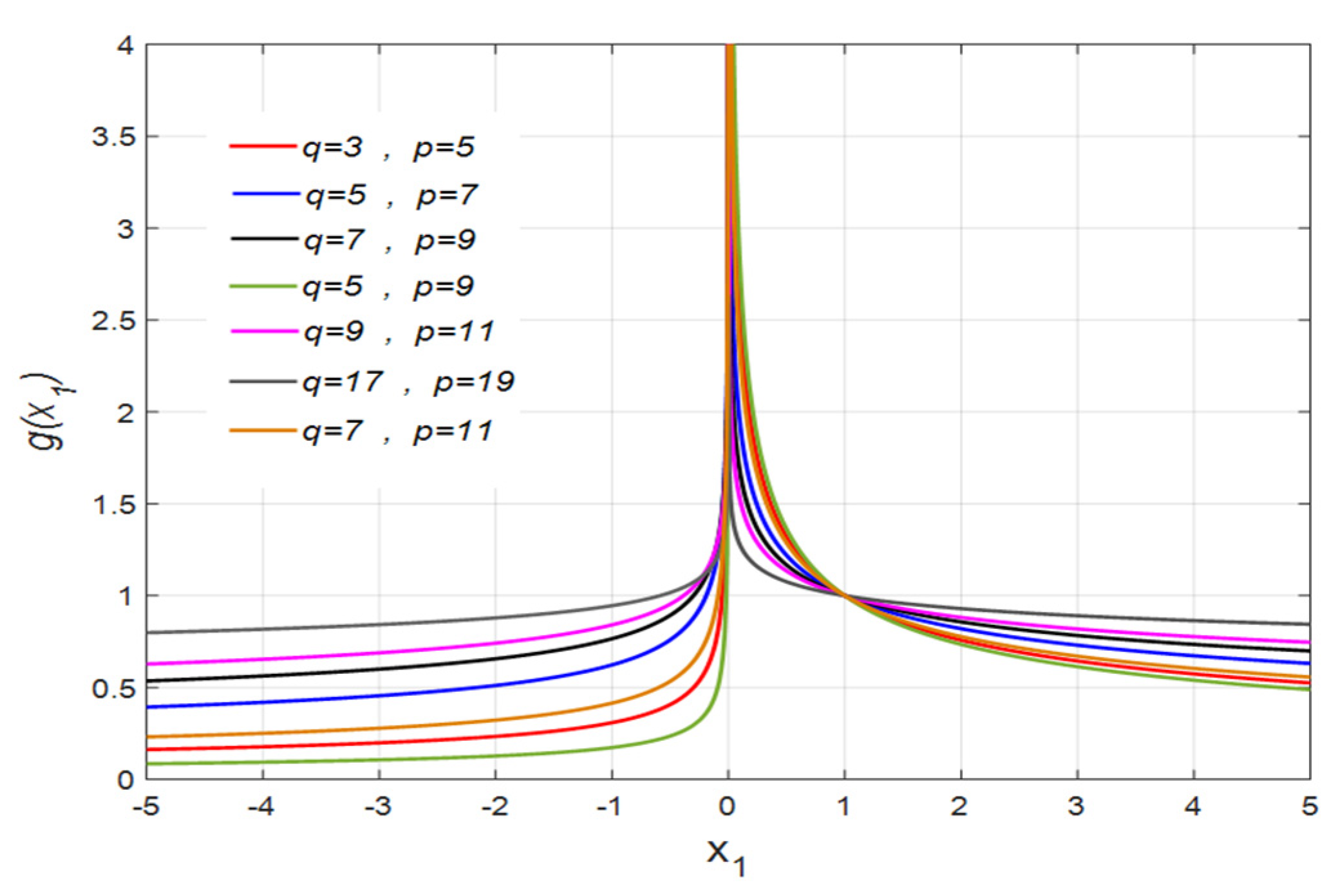
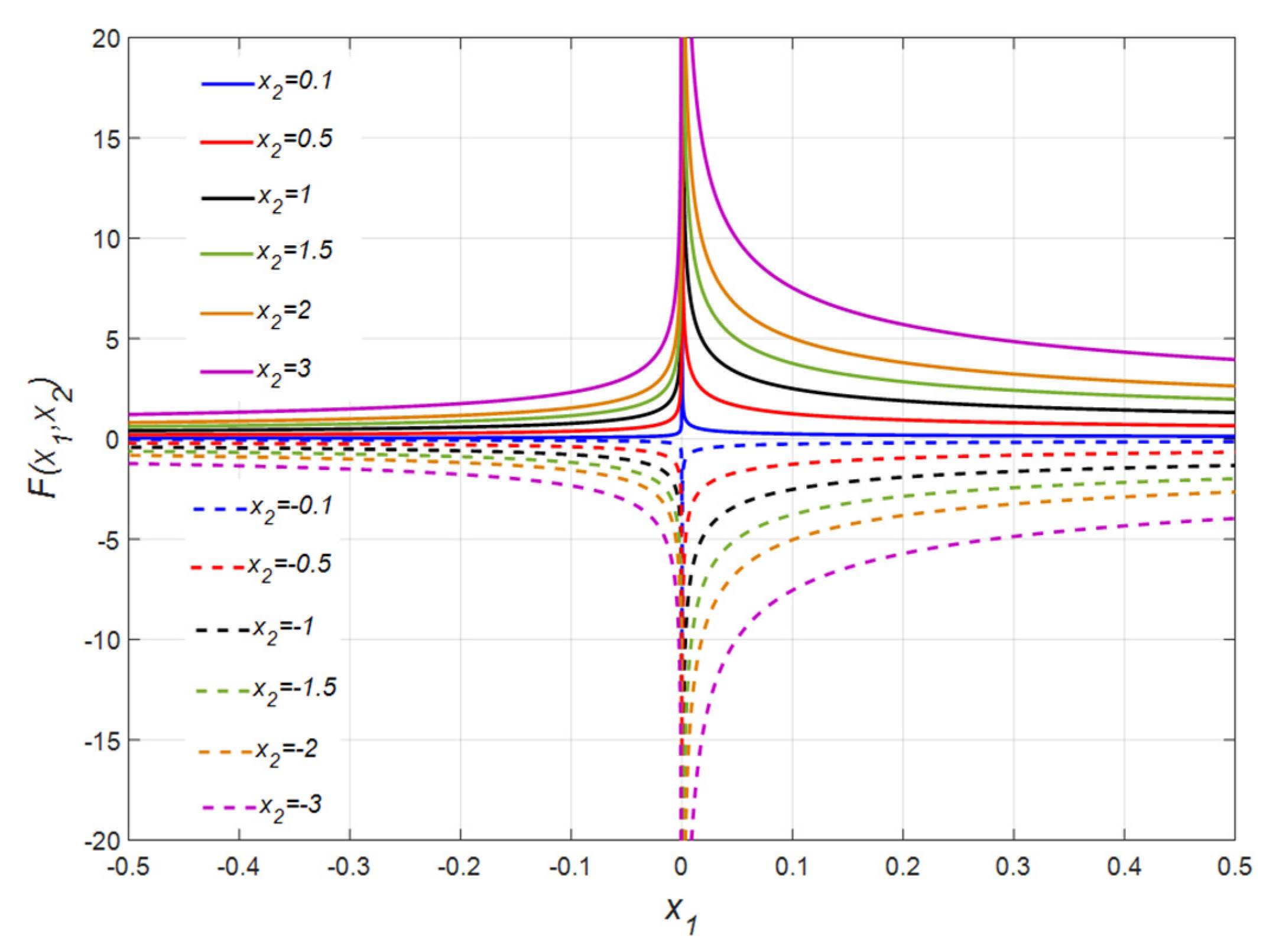
The term in Equation (3) is important, and this element may result in singularity. Figure 1 and Figure 2 illustrate the fluctuation of and versus .
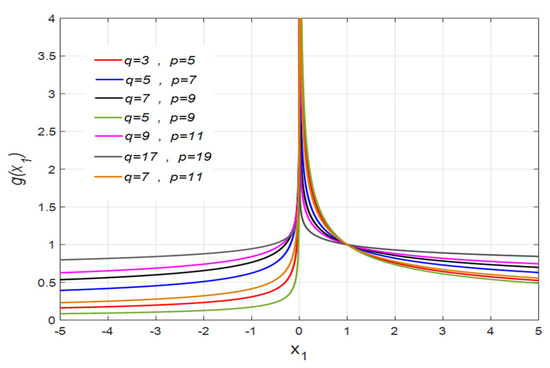
Figure 1.
for different values of and .
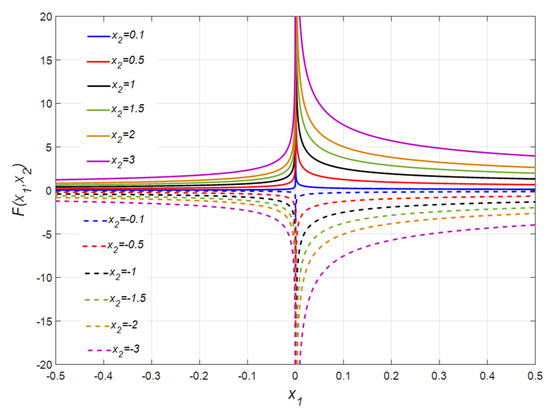
Figure 2.
for different values of ( and ).
The following conclusions can be found from these figures.
It is important to thoroughly analyze the term . To facilitate the examination of the Lyapunov function’s stability, we focus on the following two areas on the plane.
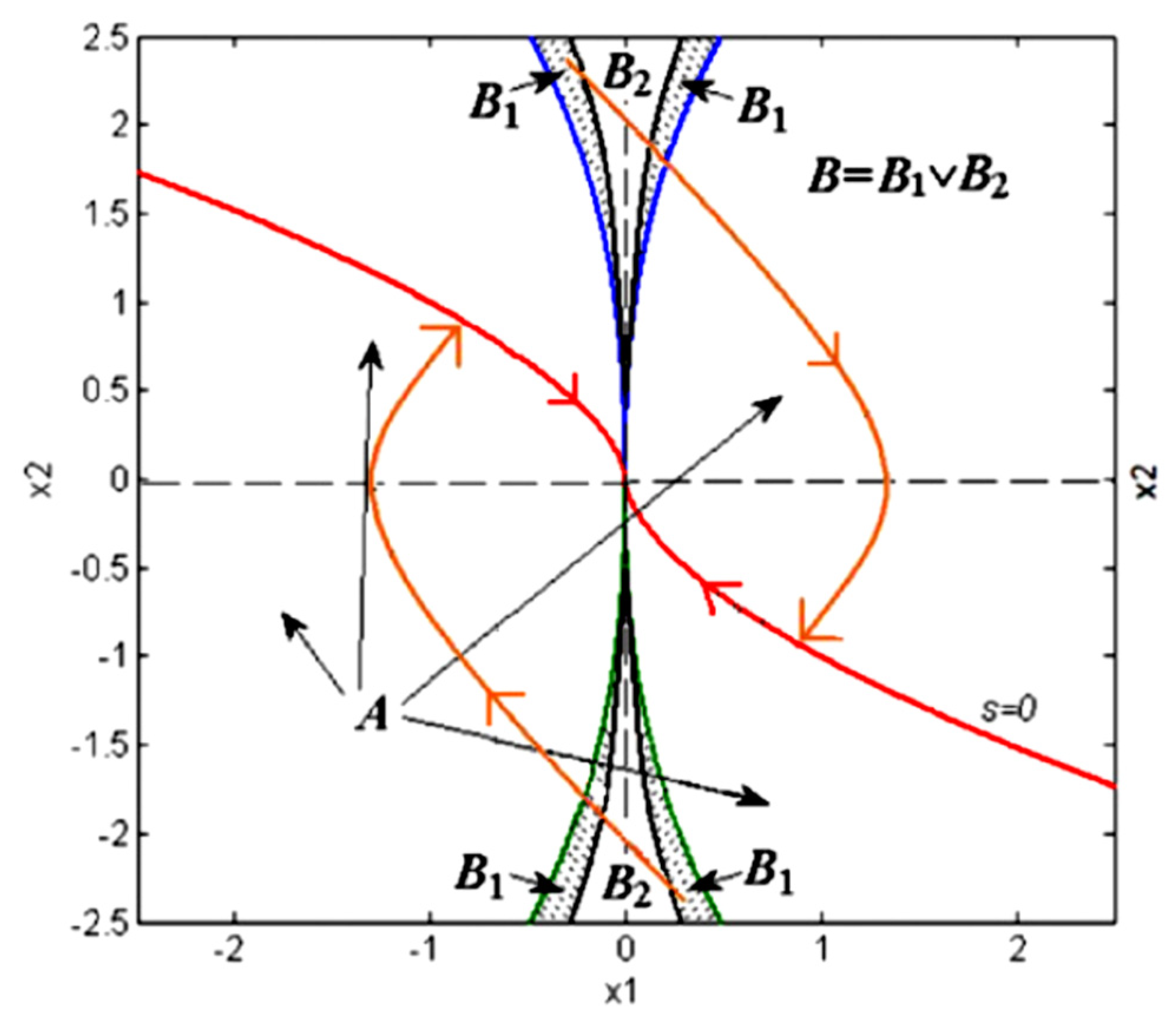
As previously stated, . The regions of A and B, as well as the curve, are represented in Figure 3.
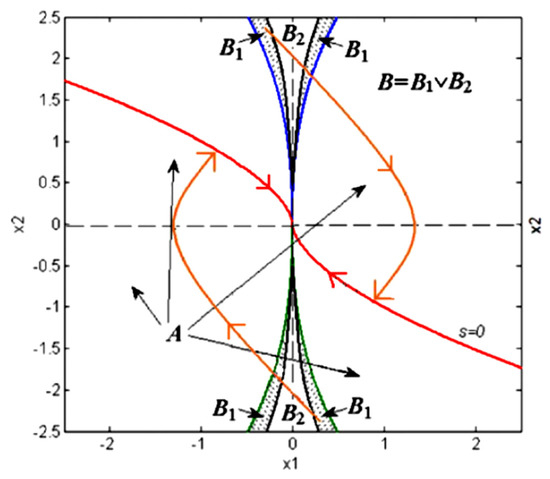
Figure 3.
Singular and nonsingular areas (, , ). Reprinted with permission from ref. [86]. 2013 Elsevier.
As can be seen in the illustration, is always in the district of A. As a result, there is no singularity on the diagram.
If state is in the area . Then the condition is met. Thus: . In this case, and by substituting the preceding term in Equation (6), can be obtained as (see Equation (3)):
Considering Equation (7) and according to and , the following relation can be extracted for :
Therefore, for the area of , the stability condition holds true.
For the area of , the following relation is valid.
According to Equation (6) and substituting Equation (9) in it, and using Equation (3) we have:
As shown in Figure 3, the is union of and . If the state is placed in the area of , the is equal with . For the region of ; Given that , , and considering that the gain generally has some margin; therefore, in the area , as the same as area of A, still holds true [86]. If passes from to , the condition of is disturbed, and, in the area , for while , singularity happens.
Calculating the boundaries of and is difficult and requires an in-depth understanding of the bounds of uncertainties and disturbances [86]. However, significant here is that the area of is a transition region in which the state does not persist indefinitely. Furthermore, as illustrated below, the state passes through this transient situation and reaches the stability region of A [86].
Using in Equation (1) and integrating from there, we find:
If is in the , there are two scenarios.
In case (1) for , according to the Equation (11), increases monotonically until crossing the border of and entering the region in a finite time (see Figure 3). As mentioned before is a stable region, where satisfies the stability of the Lyapunov condition.
For case (2), if , then decreases monotonically to enter the region of , and the scenario presented in case 1 is repeated, and the stability of the Lyapunov function is guaranteed, and the state reaches .
For such design, should be considered in the following range [86]:
The saturation function can be expressed as follows:
2.1. Micro-Capacitor Dynamic Model Governing Equation
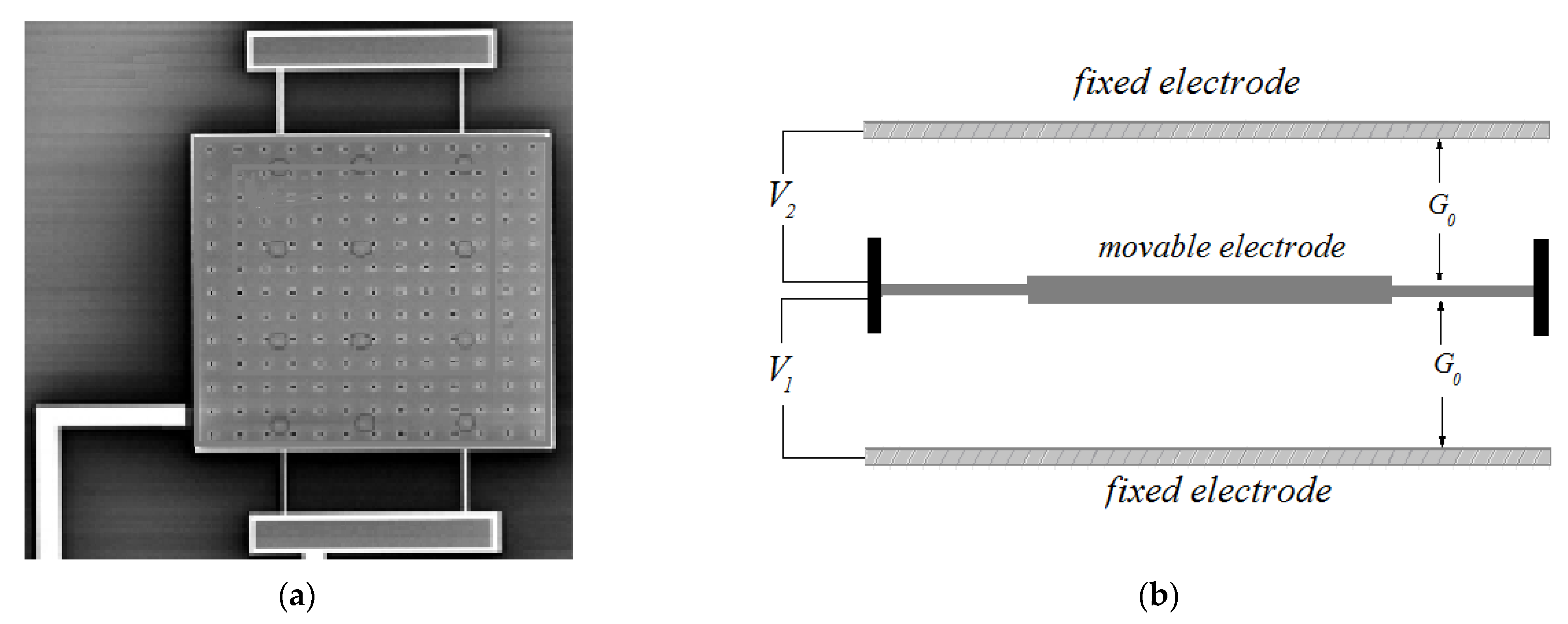
In this part, the schematic view of studied micro-capacitor is presented consisting of a conductive movable plate suspended between two conductive upper and lower fixed plates, Figure 4. The top view of the moving plate is shown in Figure 4a, consisting of a rectangular plate detained by four carrier beams. Given the length l, thickness h and width b of each rectangular beam, their respective equivalent stiffness coefficients can be calculated as follows: and , where symbolizes the rectangular beam second moment of inertia.
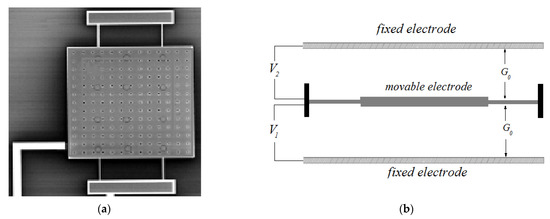
Figure 4.
Schematic view of studied microstructure. (a) Schematic view of movable electrode from top view [88], (b) front view of micro structure.
Correspondingly, the front view of the structure shown in Figure 4b, illustrates the moving electrode, which is located at a distance from its fixed upper and lower electrodes, and two electrical potentials and are applied to the moving electrode from both lower and upper actuating electrodes. The material of the moving electrode is considered to be homogeneous with a Young’s modulus E, mass density , and cross section area . In this investigation, we considered , , , , , , and .
The simple one-degree of freedom mathematical model governing the dynamic behavior of the above micro-capacitor can be written as follows [88]:
where , , , , and denote the equivalent mass of the movable electrode, damping coefficient, electrostatic force, external disturbance, and inherent uncertainty, respectively. Moreover, denotes time, and is the displacement of the movable plate with respect to the lower electrode. The resultant electrostatic force on the movable plate can be expressed as follows assuming a parallel-plates theory with negligible fringing-fields effects [88]:
where designates the air permittivity in the vacuum.
For the sake of normalizing the above dynamic equation, we consider the following non-dimensional parameters and . Therefore, the dynamic equation, Equation (14) can be written as follows:
where , , and are parameters defined as follows:
Now considering and , Equation (16) can be re-written in state space form as follows:
where
Comparing Equation (18) with standard form of the presented state space form of Equation (1), we have:
An important point in designing of controller is that the nonlinear term is expressed in the form of electrostatic force or . According to Equation (19), it is clear that Equation (18) becomes nonlinear due to the presence of terms and . It should also be considered that electrostatic force is inherently attractive and applied voltages create attractive forces. As mentioned in Section 2.1; applying a voltage of causes the movable electrode to move towards the lower electrode.
Given that the positive direction and are toward the lower electrode; therefore, applying causes more instability of the structure and moves the electrode away from the fixed point. Therefore, in these conditions, must be applied to attract the movable electrode towards a fixed point or stability region. Therefore, depending on the position of the moving electrode, the can be or .
In other words, and do not act simultaneously. As will be presented in the results section; at any given time, only one of the voltages is non-zero. According to the above explanations and depending on the position of the movable electrode, the nonlinear term is or and also the control factor means or .
3. Results and Discussions
In this section, the generated results for controlling the above micro-capacitor are presented and discussed. It is assumed next that the micro-plate capacitor is first subjected to a disturbance of the following form: and with an inherent uncertainty represented by the following function . The simulation is for a span of , and, in some cases, for more clear trends, we present the results with a shorter timing range. The purpose of this motion is to reduce the effects of disturbance on the dynamic behavior of the microstructure. It is worth noting that, due to the fact that the disturbance is permanent without any decaying, it is not possible to completely eliminate its effects, and the controller can only mitigate them.
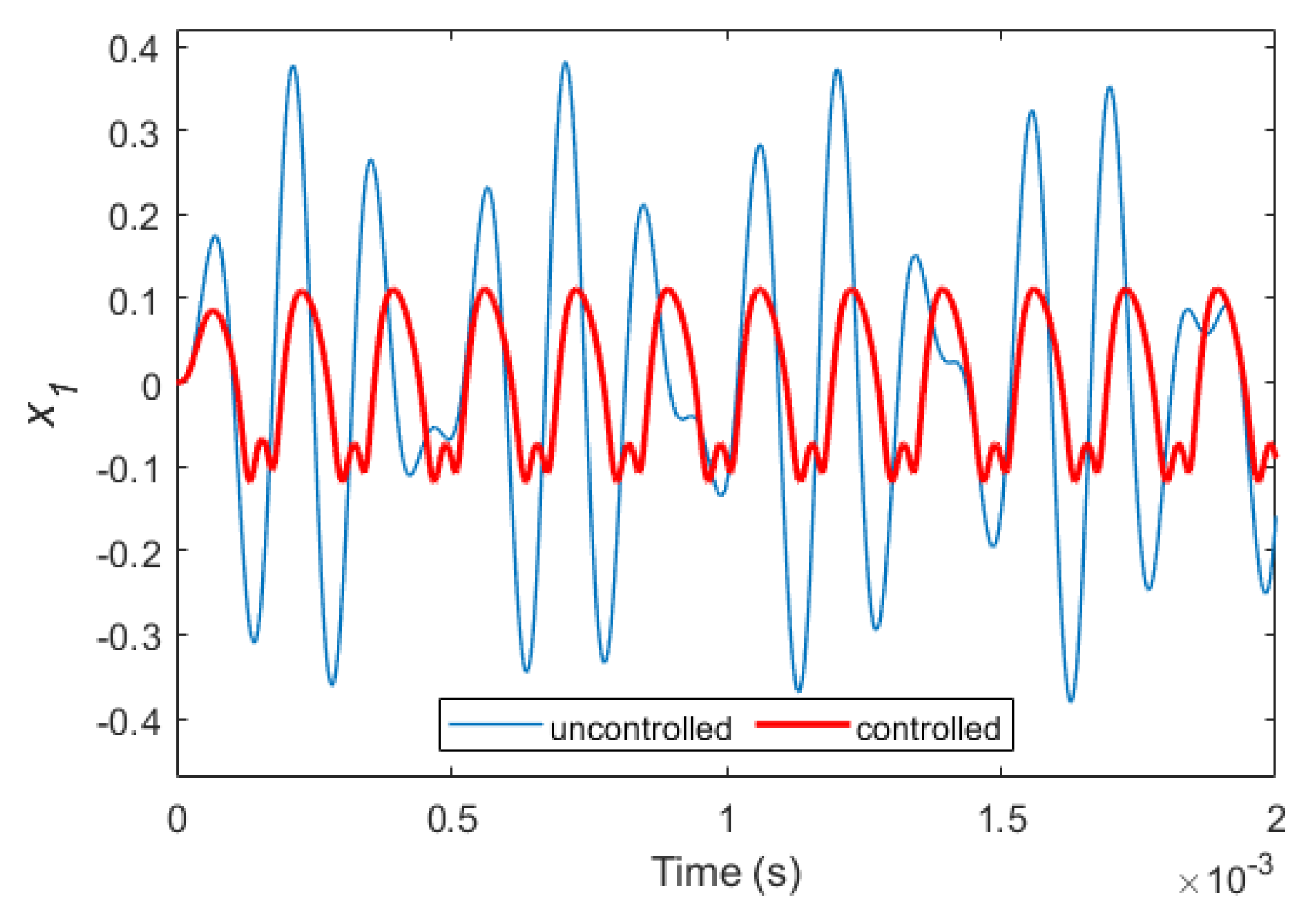
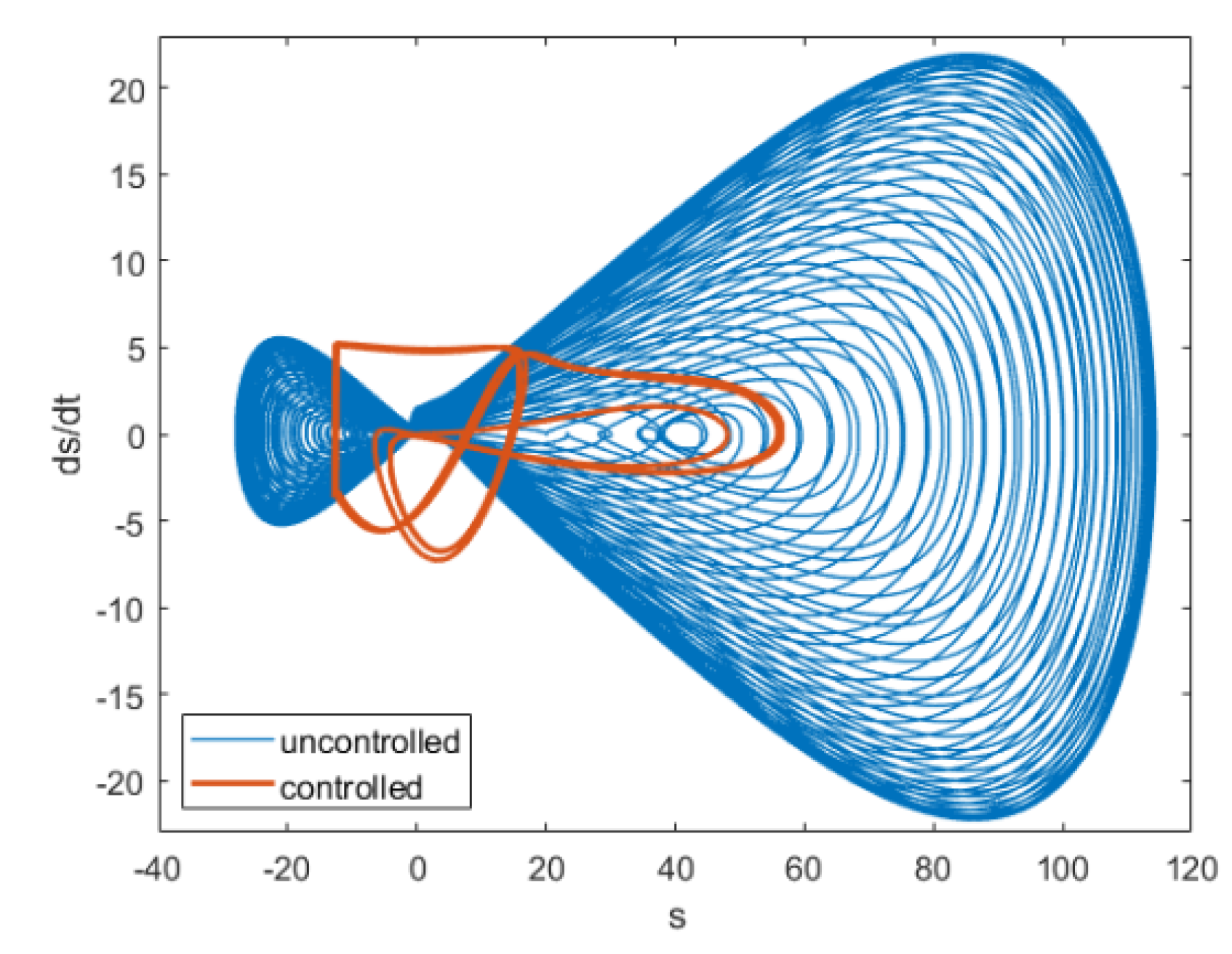
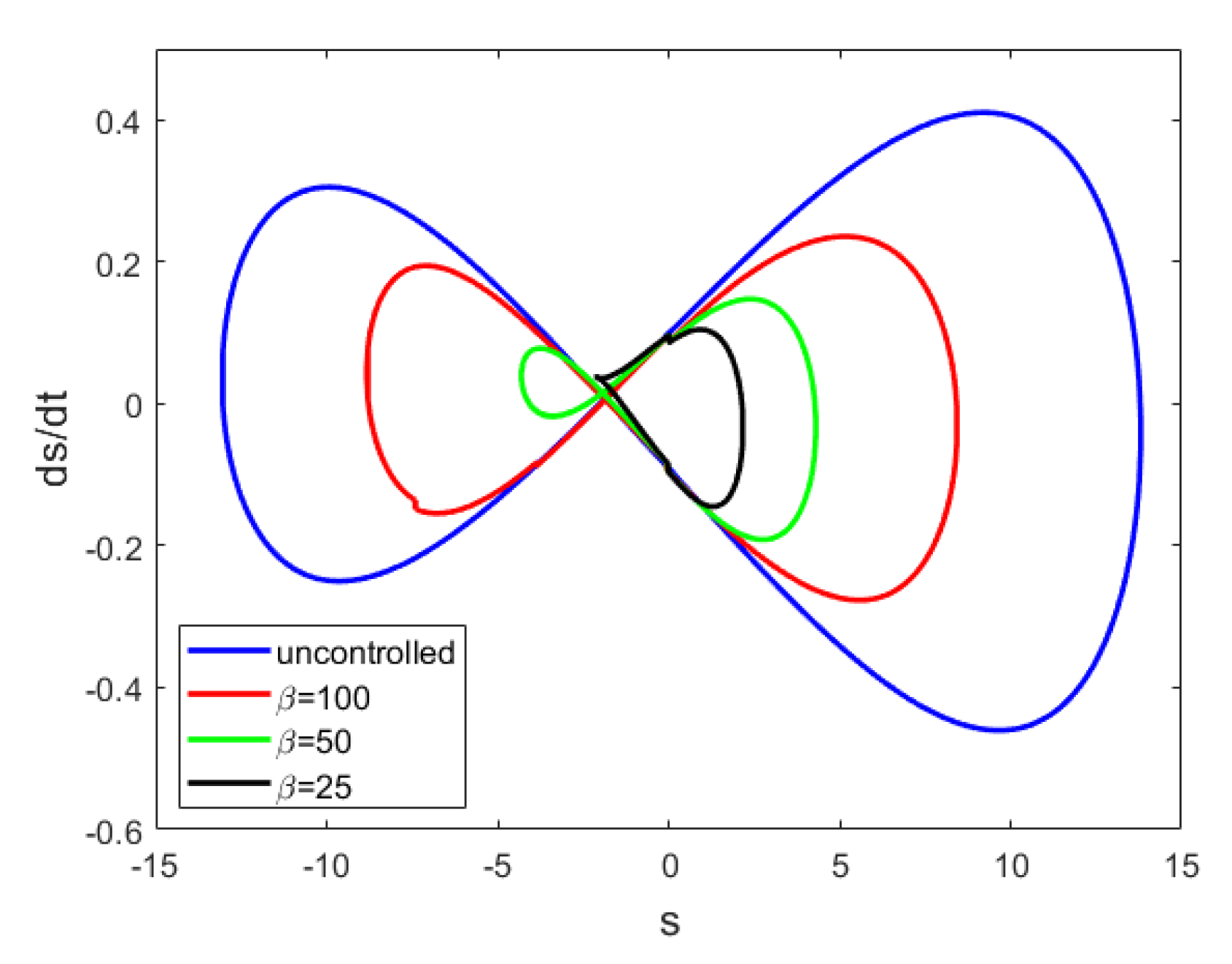
Figure 5 shows the variation of versus time for both controlled and uncontrolled situations. As it is clear from this figure; the controller is able to significantly reduce the effects of disturbance. The specifications of the controller for this simulation are , , and . The phase portrait for a manifold of and its time derivative variation is drawn in Figure 6. As can be seen from this figure, with the application of the control law, the phase limit becomes significantly more compacted.
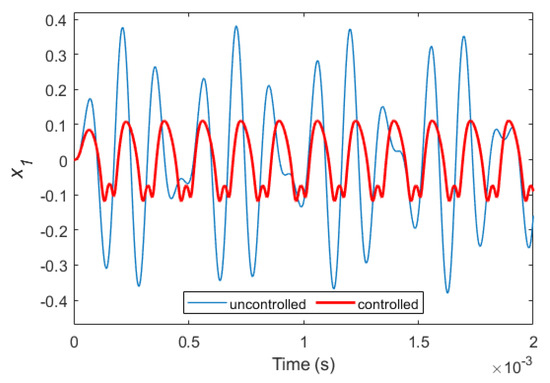
Figure 5.
Variation of versus time for controlled and uncontrolled systems considering , , and .
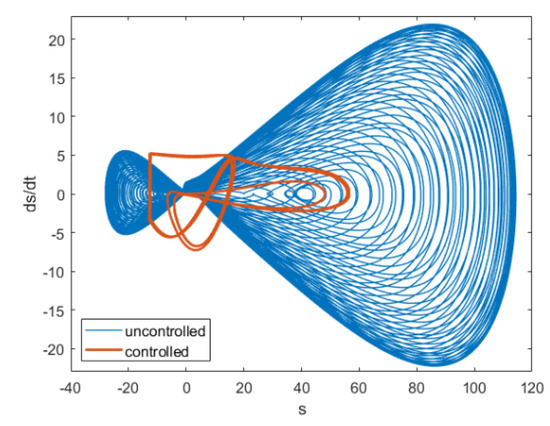
Figure 6.
The relevant phase portrait for manifold and of Figure 2.
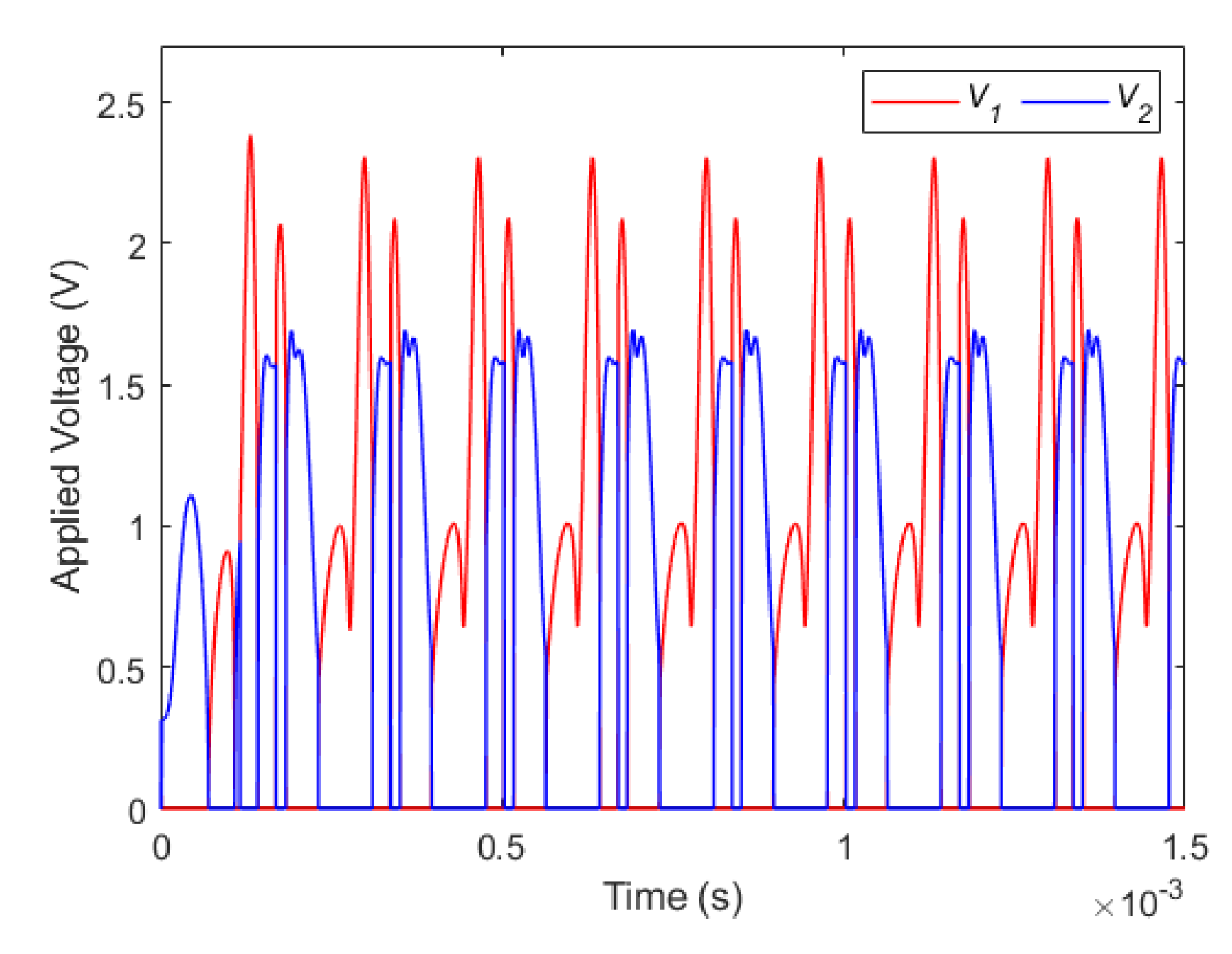
Correspondingly, the variation of control parameters and are both depicted in the Figure 7. As can be seen from this figure, the control voltage does not exceed 2.5 volts, which is a reasonable applied DC load amplitude for MEMS capacitors.
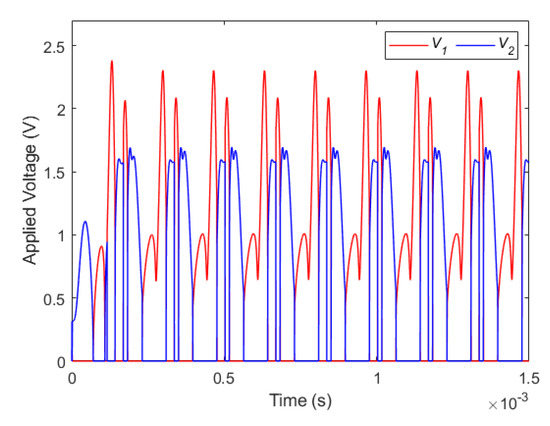
Figure 7.
Variation of the control parameters and considering , , and .
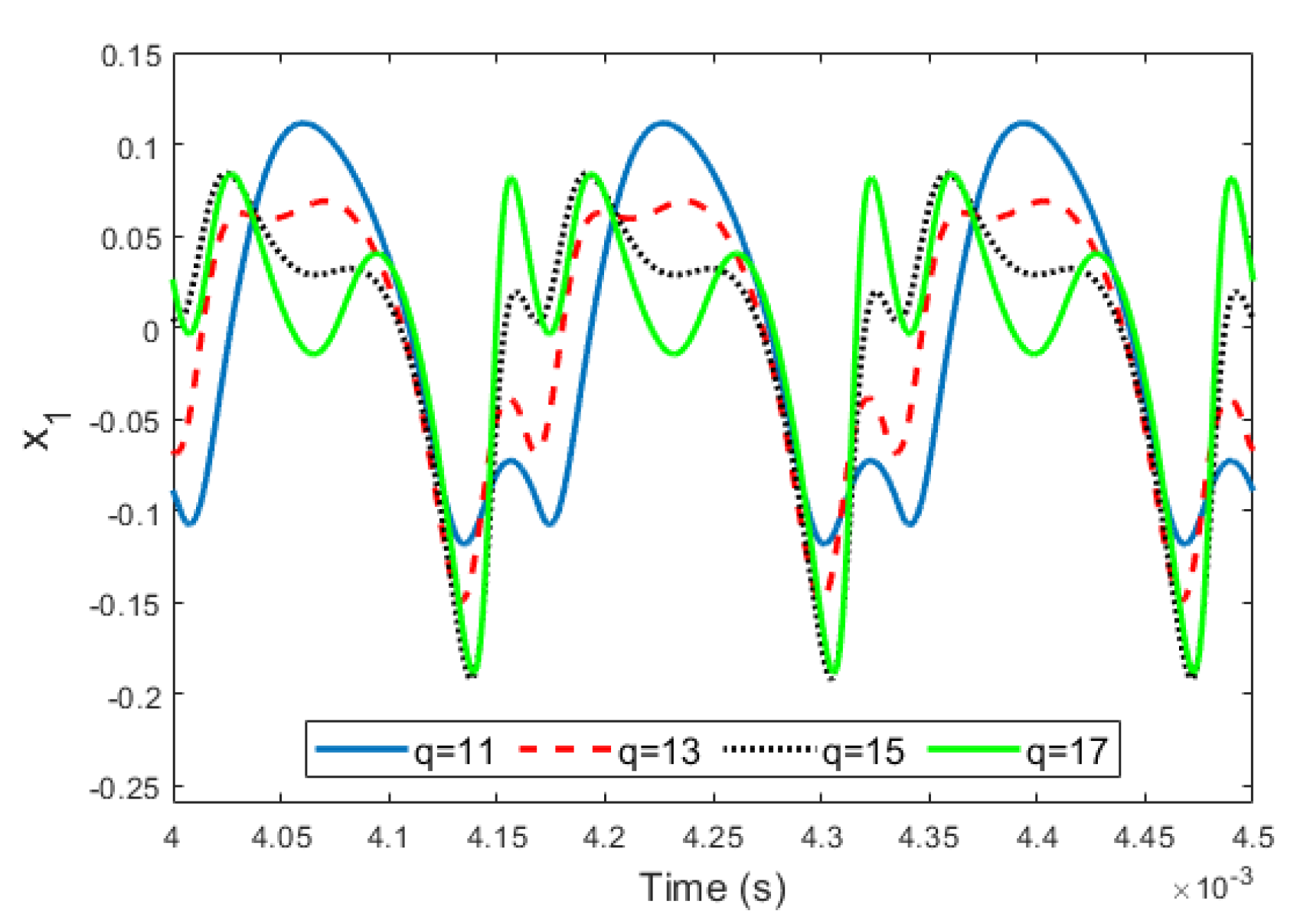
The variation of the parameter versus time for various amounts of was extracted and is shown in Figure 8. From this figure, the upper and lower amplitudes of decrease with increase of , and the structure tends to oscillate near the fixed point. For instance, for , varies in range of , but for , vibrates in the domain. Furthermore, the phase diagrams for different values of are illustrated in Figure 9. It is clear from this figure that, with the increase of , the relevant phase plane expands.
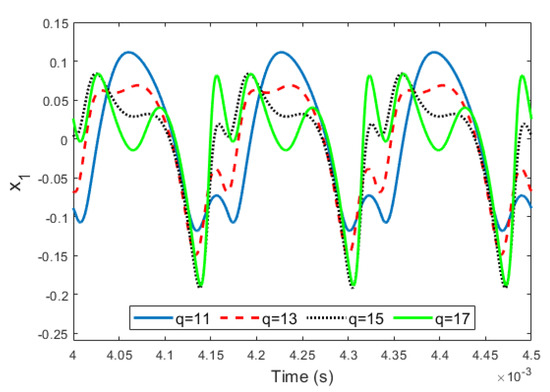
Figure 8.
Variation of the parameter versus time for various amounts of , , and .
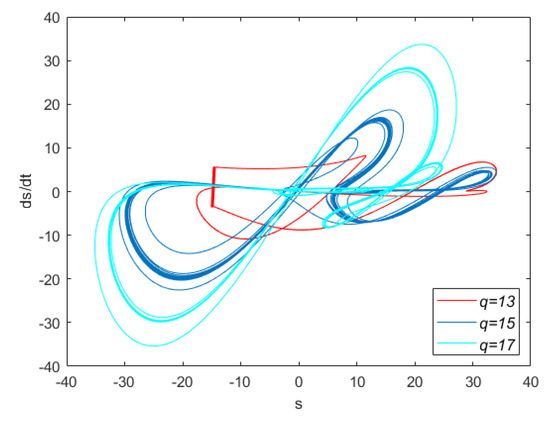
Figure 9.
The phase portrait for manifold and for various amounts of , , and .
In this paper, the main purpose of robustness is to keep around a fixed-point or . As shown in this section, this is possible by applying a control process to improve the stability of the system around a fixed-point. As shown, by changing the control parameters, the phase portrait can be contracted. Therefore, robustness can be considered from two perspectives. (1) System stabilization around fixed-point or . (2) In the controlled mode, robustness can be considered as limiting the phase portrait on the plane.
More explanations and results in this field are provided in the continuation of this section. On the other hand, a noteworthy point in this design is the absence of the chatting phenomenon. As presented in this section, the chatting phenomenon, which is a problem in the design of sliding mode controllers, does not appear here. However, as can be seen in studies related to MEMS structure control, such phenomena are clearly visible [78].
Similarly, the maximum applied voltages and for different are presented in Table 1. From this table, the values of the applied voltages increase with the increase of , and approaches 2. According to the results presented in this table as well as Figure 8 and Figure 9, the controller design is preferable to choosing less or choosing close to one.

Table 1.
The maximum applied voltages and for various amounts of , , and .
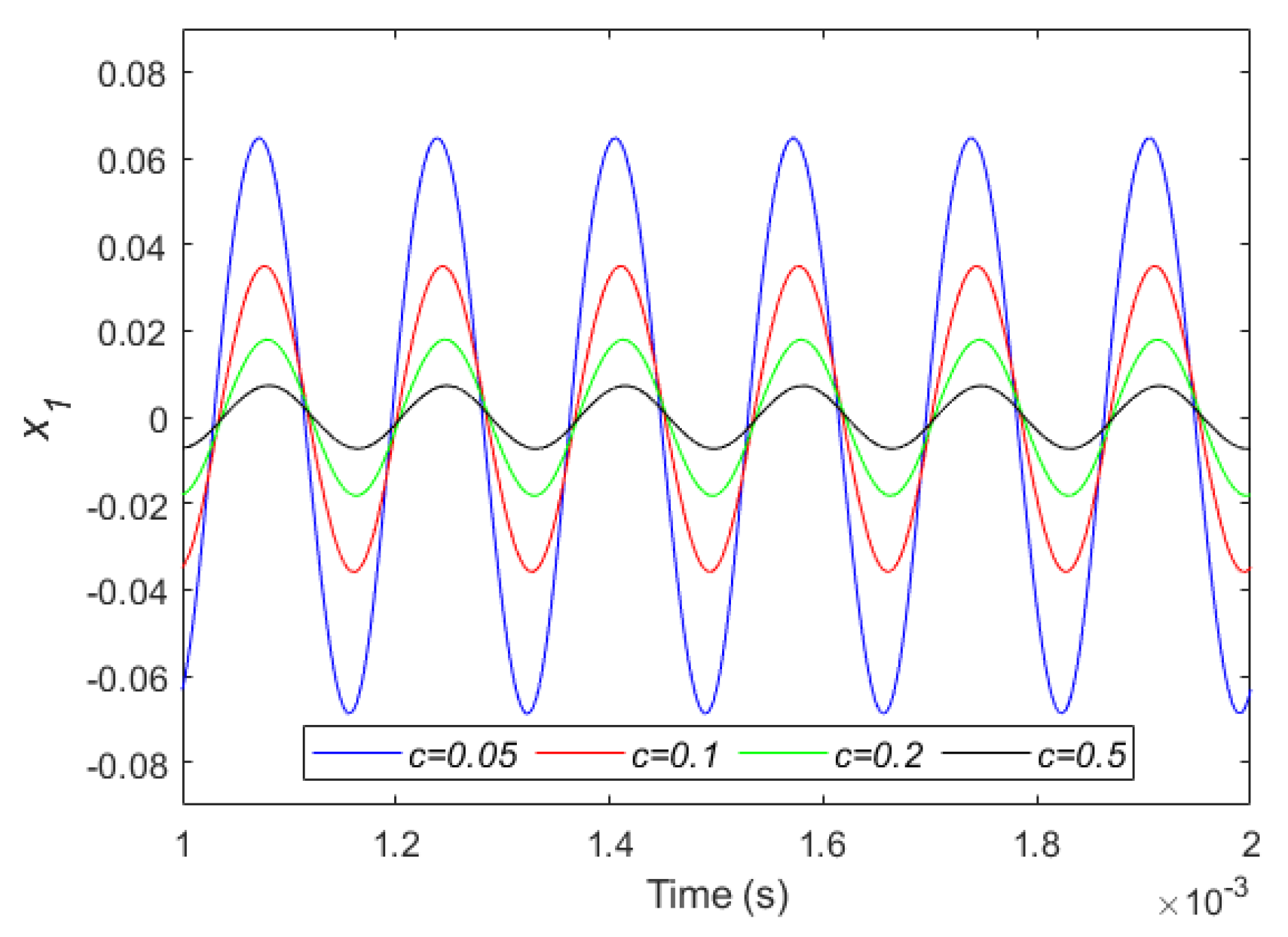
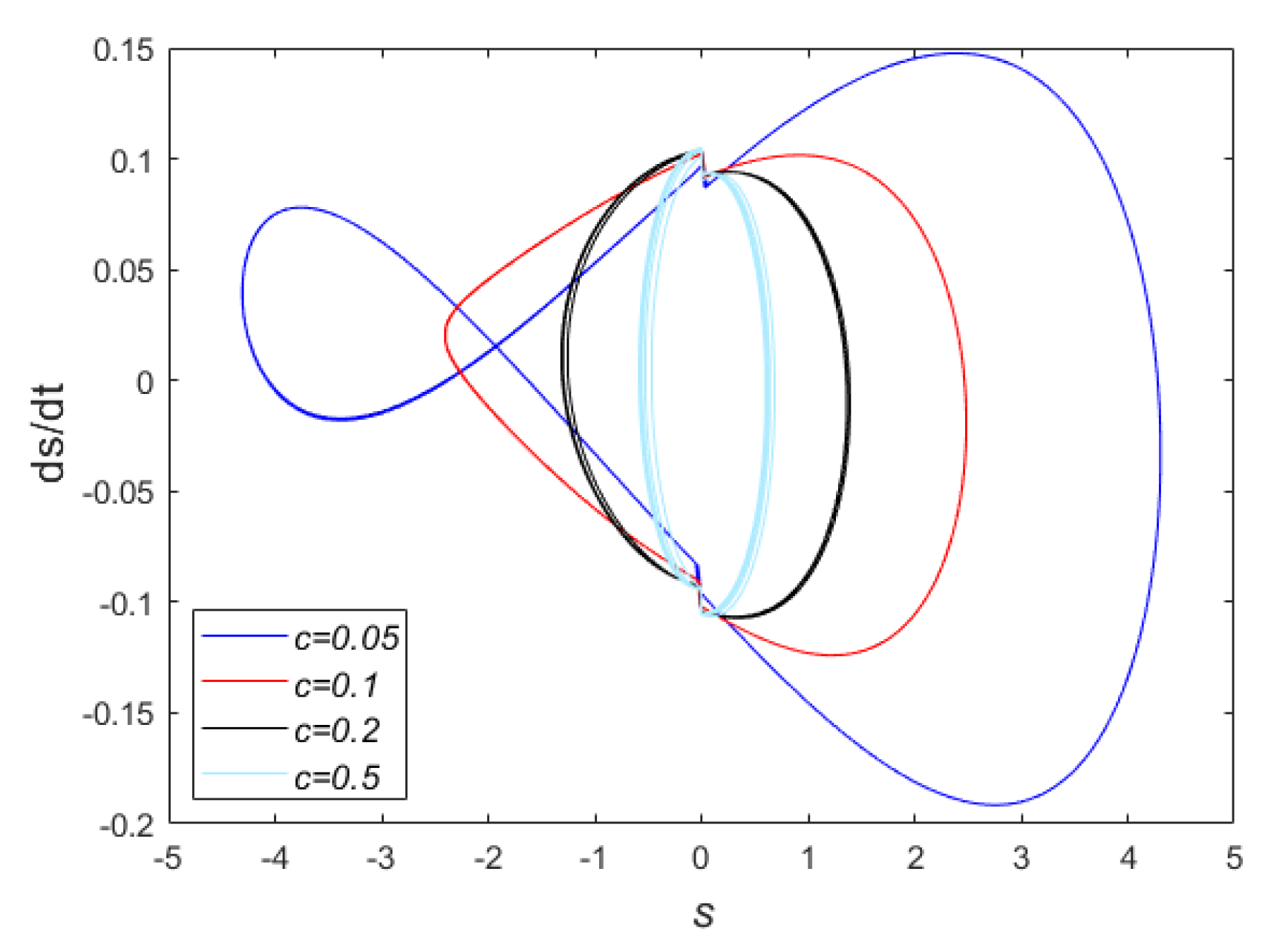
Subsequently, the effects of the damping coefficient on the control of the micro-capacitor are investigated. For this case, we considered , , and . The diagram of for various damping coefficients is demonstrated in Figure 10. As can be seen from this figure, the amplitude decreases with the increase of the damping coefficient. Correspondingly, the phase plane is also depicted for this simulation in Figure 11. This figure shows, with an increase of , that the related phase diagram considerably constricts in the vicinity of origin.
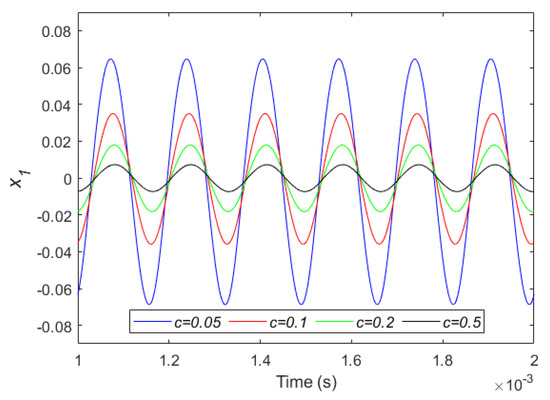
Figure 10.
Variation of versus time for various amounts of and considering , , and .
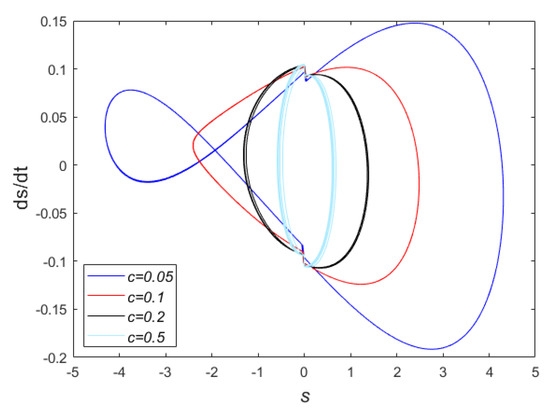
Figure 11.
The phase portrait of manifold and for various amounts of and considering , , and .
The maximum values of the applied voltages for this simulation are summarized in Table 2. As can be seen from the table, with the increase of the damping coefficient, the maximum values of the applied voltages become smaller. Moreover, the effect of the parameter on the control of the microstructure is also studied, and the phase trajectories are drawn for different . For this case, the damping coefficient is . It is clear from Figure 12 that, with increase of , the amplitudes of and are increased. The maximum values of and are shown in Table 3. As it is clear from this table, increasing causes an increase in the maximum amount of applied voltage. Therefore, in identical conditions, the preference is to choose a small .

Table 2.
The maximum applied voltages and for various amounts of and considering , , and .
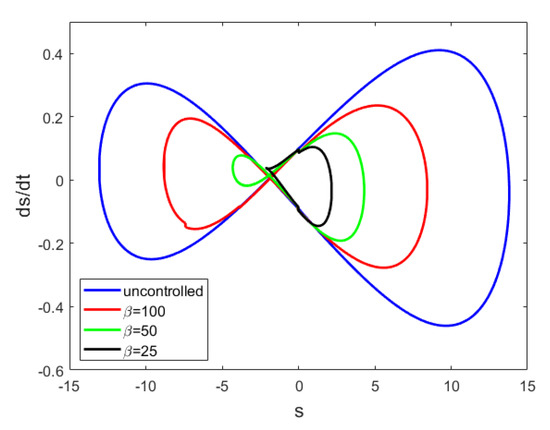
Figure 12.
The phase portrait of manifold and for various amounts of and considering , , and .

Table 3.
The maximum applied voltages and for various amounts of and considering , , and .
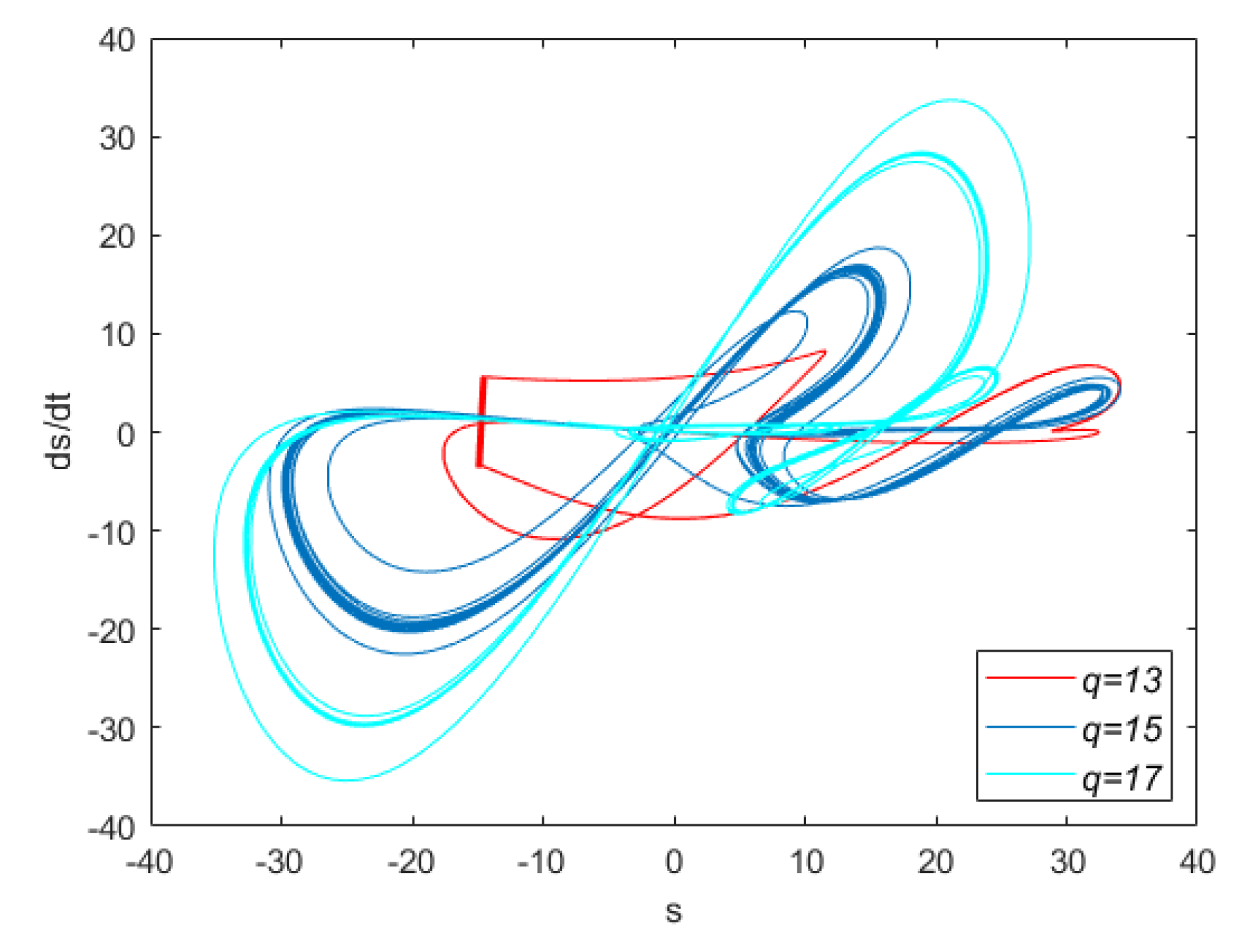
In the continuation of this section, the effects of disturbance on the robustness of the controller and the existence region of the sliding mode controller are explored. The noise under consideration is , where denotes the noise’s amplitude. This analysis takes into account the specifications , and . The maximum applicable for the designed controller is 1.05.
This means that will be followed by , and the moving electrode will make contact with one of the stationary electrodes.
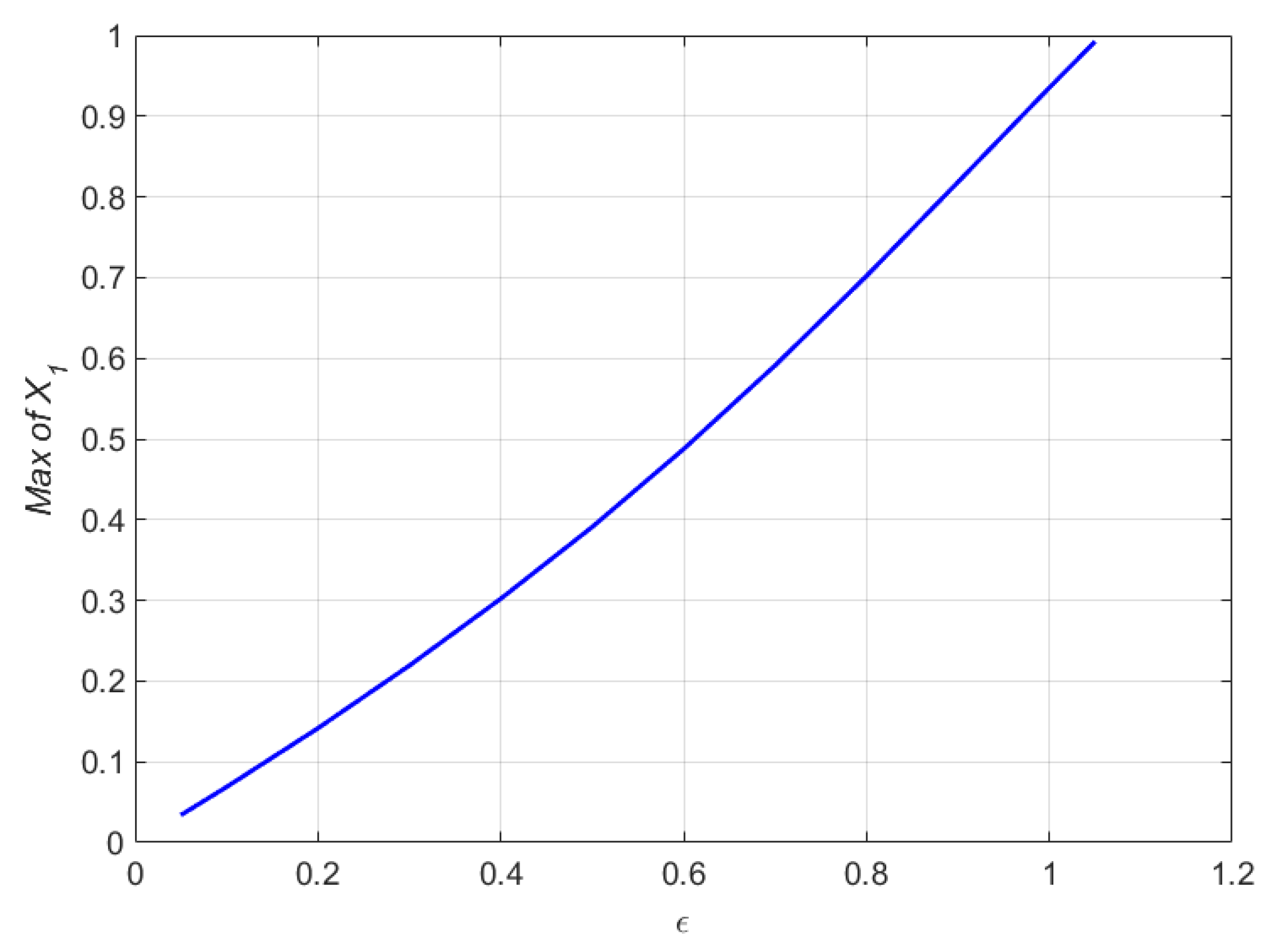
Figure 13 illustrates the highest variance in vs. . As can be seen from the graph, raising raises the maximum value of , while increasing raises the maximum value of to 1. As a result, the sliding mode controller’s stability region is established for . For , the controller is unable to maintain the microstructure’s stability.
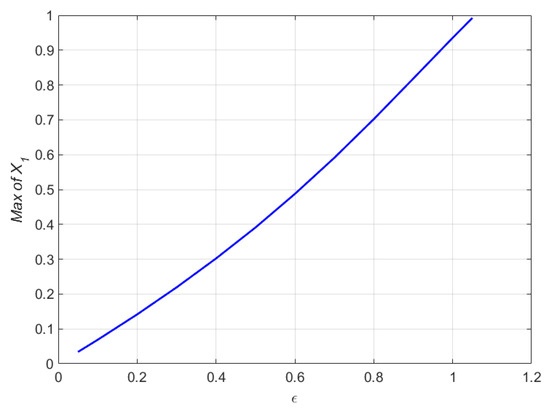
Figure 13.
The maximum variation of versus for , and .
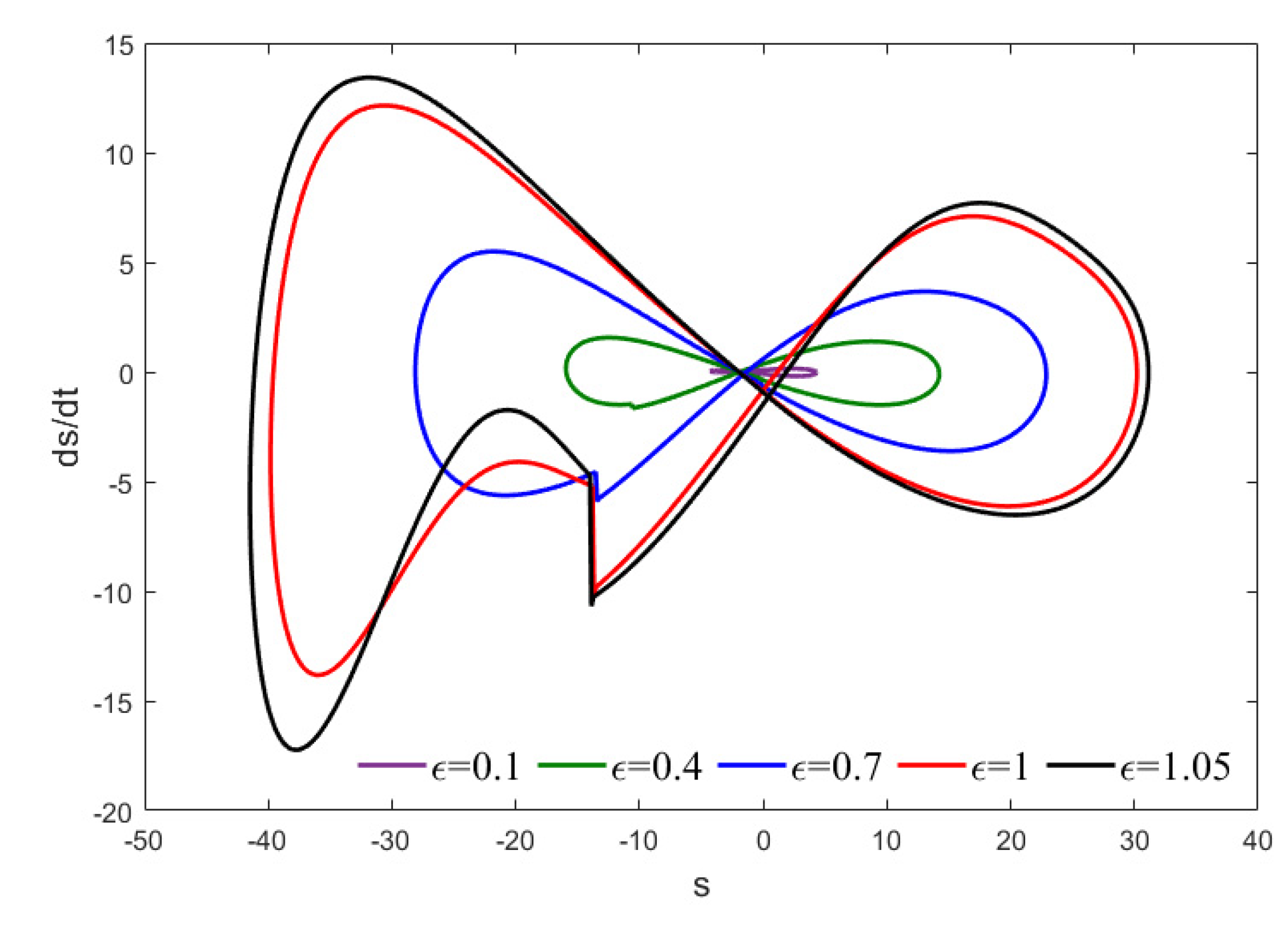
Figure 14 depicts phase images for various values. As illustrated in this figure, as increases, the associated phase diagram also expands dramatically. Additionally, the phase diagrams take on a distinct shape as a result of the nonlinear character of the applied electrostatic field.
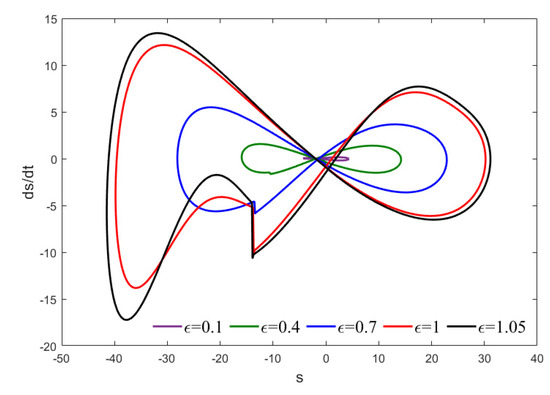
Figure 14.
The phase portraits of for different values of .
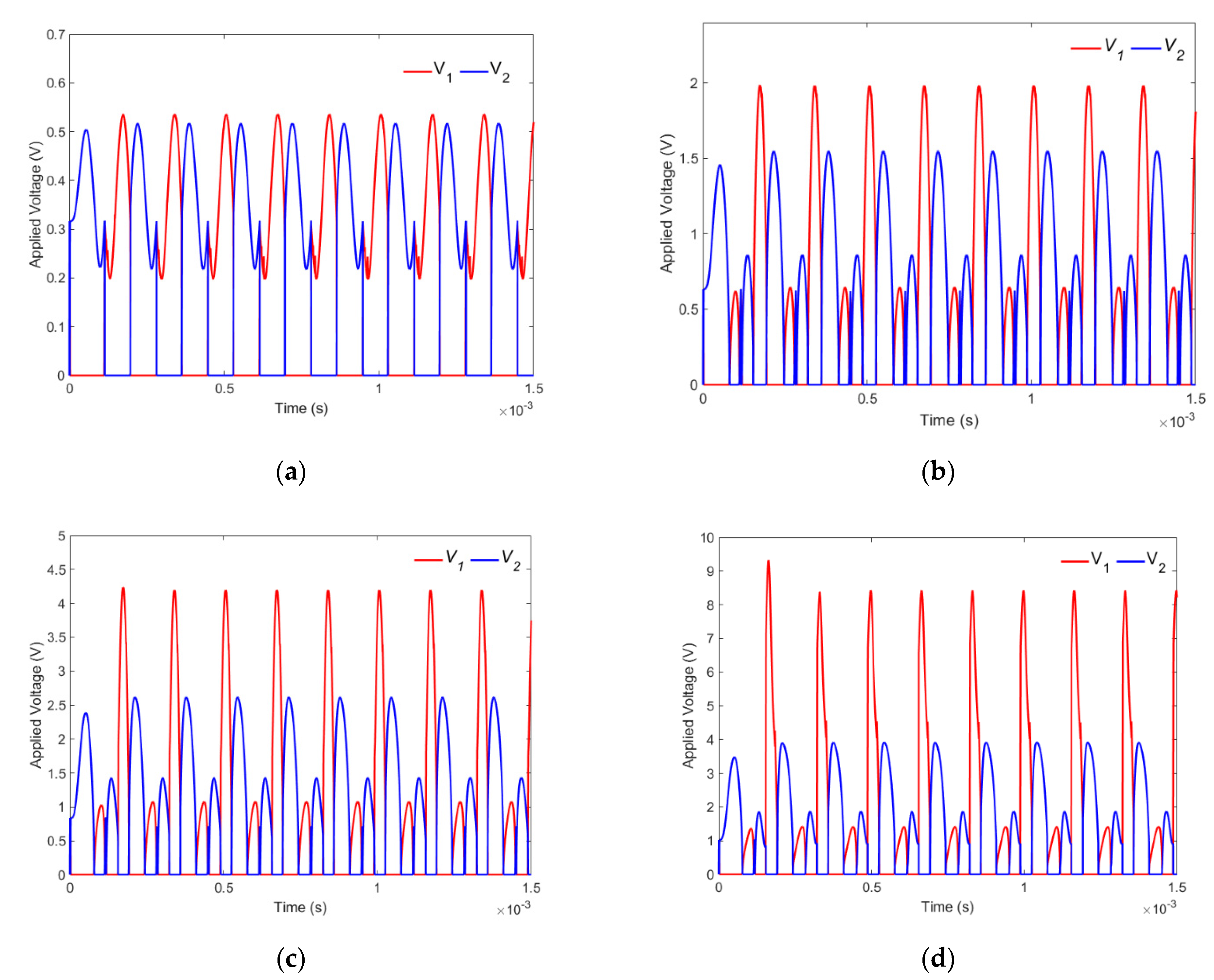
Now, we will explore the influence of on the quantity of applied voltage. Figure 15a–d illustrates the applied voltages and for various . increases the voltage amplitude greatly, although the pace of this amplitude increase for is more than that for , as demonstrated in these figures. For example, whereas the and amplitudes are about similar for , it is clear from Figure 15b,c that the amplitude is much greater than the amplitude for , , and .
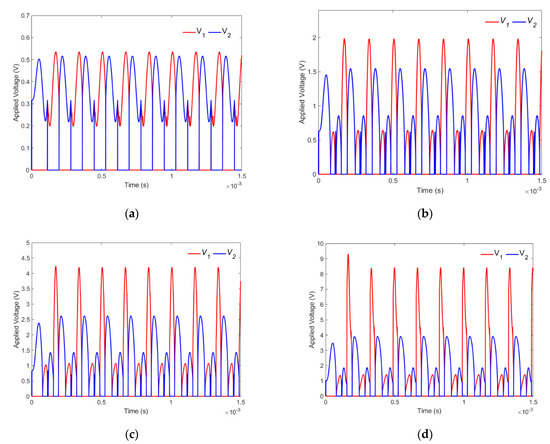
Figure 15.
The diagrams of applied voltages and versus time for different . (a) ; (b) ; (c) ; (d) .
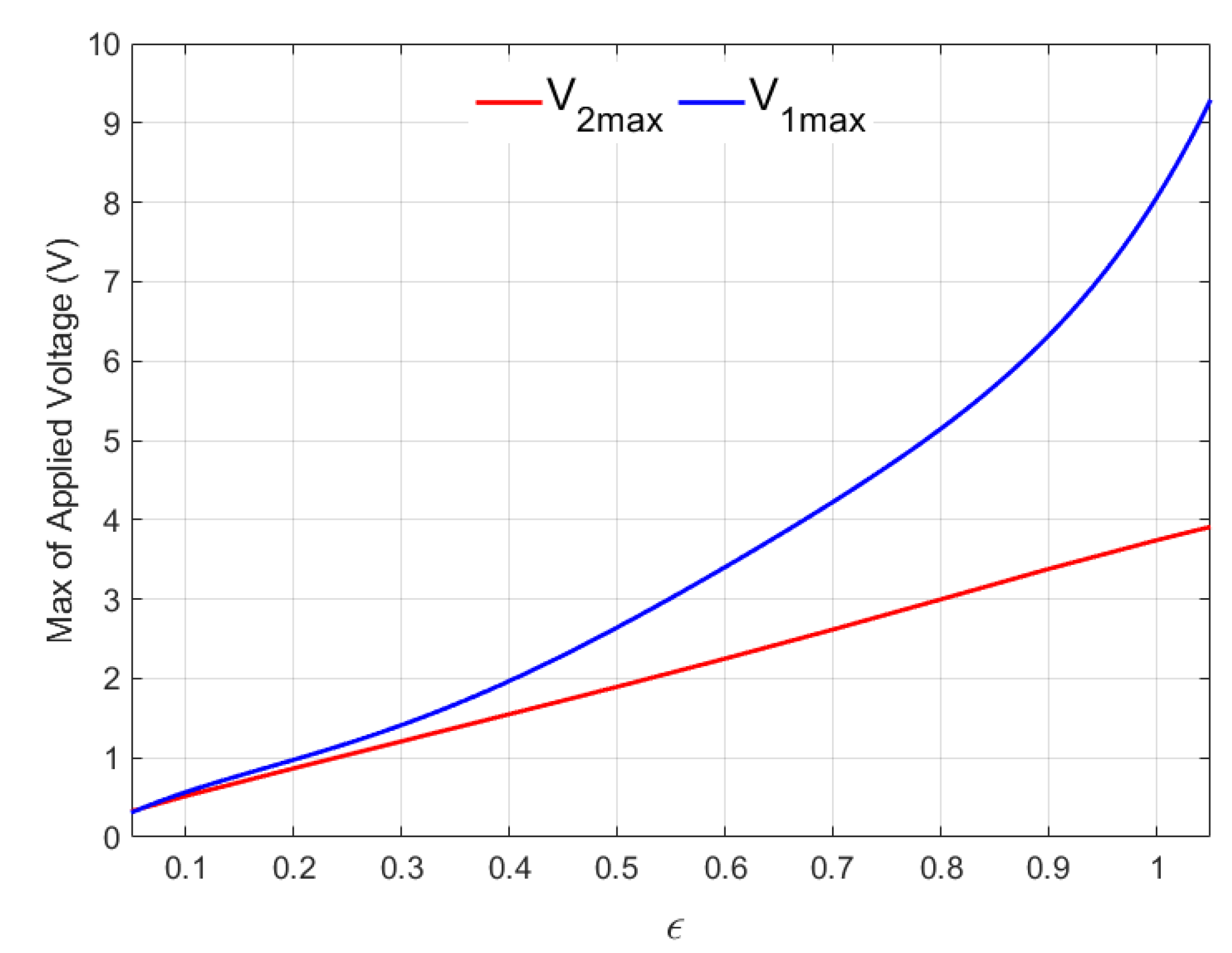
Figure 16 depicts the variances of and for for further examination. As may be seen in this diagram, for , . However, with higher levels of , the exceeds the . Additionally, as illustrated in this figure, increases in are nearly linear, whereas changes in are nonlinear, and the rate of increase of is more noticeable with greater .
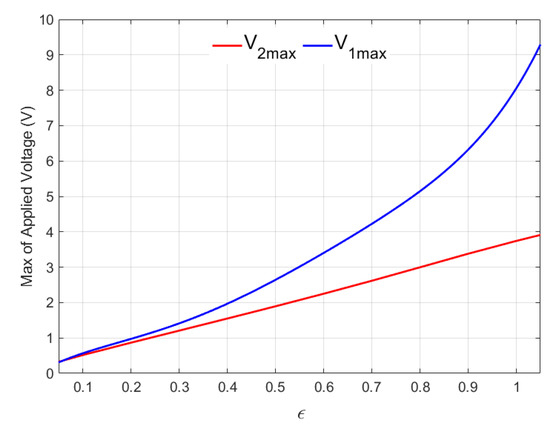
Figure 16.
Maximum values of and for .
4. Conclusions
Given the importance of active control of microstructures as well as mitigating the unwanted effects of disturbances and uncertainties in such tiny structures, this study investigated a control strategy seeking mainly their stabilization in the vicinity of a fixed point. Indeed, the nonsingular TSMC was considered in this regard, which is an efficient and fast method with high robustness.
In addition to the aforementioned advantages, the lack of need for a strong control force is another respectable feature of this particular control strategy. This controller is of a second-order type, where determination of its control law in mitigating the effects of disturbances and uncertainties were examined for the case of a micro-capacitor. The control forces in such a capacitor were performed through the electrostatic forces regulated by the assumed electric potentials.
The effects of control parameters on the dynamic behavior and the control forces as well as the phase trajectory of the sliding surface manifold were studied. The obtained results showed high capability of the control method in stabilizing the microstructure as well as considerably reducing the effects of disturbances and uncertainties. The results also showed a significant contraction of the phase portrait for the controlled system compared to uncontrolled system.
Furthermore, we confirmed that, with increasing , the phase diagram became more contracted, and the level of control force was significantly reduced. Moreover, the effect of the damping coefficient on the active control together with dynamic behavior of the system was studied. The results showed that, through increasing the damping coefficient, the phase diagram became more compact, and the maximum control force decreased. We also demonstrated that changing the parameter had a significant effect on the behavior of the controlled system and increasing caused expansion in the phase diagram and a decrease of the maximum level of control force.
Author Contributions
Conceptualization, A.A. and H.M.; methodology, A.A., H.M., and H.M.O.; software, H.M. and O.R.B.S.; validation, A.A. and H.M.O.; formal analysis, A.A. and O.R.B.S.; investigation, A.A., H.M., and H.M.O.; resources, O.R.B.S.; data curation, A.A. and O.R.B.S.; writing—original draft preparation, H.M.; writing—review and editing, H.M.O.; visualization, O.R.B.S.; supervision, A.A.; project administration, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The related data are presented within the manuscript.
Conflicts of Interest
The authors declare they have no conflict of interest.
References
- Peng, Y.; Sun, Y.; Luo, G.; Wu, G.; Zhang, T. Recent Advancements in Inertial Micro-Switches. Electronics 2019, 8, 648. [Google Scholar] [CrossRef] [Green Version]
- Gorgani, H.H.; Adeli, M.M.; Hosseini, M. Pull-in behavior of functionally graded micro/nano-beams for MEMS and NEMS switches. Microsyst. Technol. 2019, 25, 3165–3173. [Google Scholar] [CrossRef]
- Shojaei-Asanjan, D.; Bakri-Kassem, M.; Mansour, R.R. Analysis of thermally actuated RF-MEMS switches for power limiter applications. J. Microelectromech. Syst. 2019, 28, 107–113. [Google Scholar] [CrossRef]
- Sedighi, H.M.; Shirazi, K.; Changizian, M. Effect of the amplitude of vibrations on the pull-in instability of double-sided actuated microswitch resonators. J. Appl. Mech. Tech. Phys. 2015, 56, 304–312. [Google Scholar] [CrossRef]
- Liang, S.; Teng, F.; Hao, W.; Gu, W.; Sun, P.; Zhai, S.; Yang, X. Fabrication of flexible, foldable Ag/Bi2S3 nanoflowers-based asymmetric micro-capacitor. Micro Nano Lett. 2020, 15, 614–617. [Google Scholar] [CrossRef]
- Wang, C.-P.; Chou, C.-P.; Chang, T.-L.; Chou, C.-Y. Micromachining of graphene based micro-capacitor using picosecond laser ablation. Microelectron. Eng. 2018, 189, 69–73. [Google Scholar] [CrossRef]
- Rezazadeh, G.; Mobki, H. Design of direct exponential observers for fault detection of nonlinear mems tunable capacitor. Int. J. Eng. 2015, 28, 634–641. [Google Scholar]
- Xu, B.; Zhang, P. Minimal-learning-parameter technique based adaptive neural sliding mode control of MEMS gyroscope. Complexity 2017, 2017, 6019175. [Google Scholar] [CrossRef] [Green Version]
- Fei, J.; Liang, X. Adaptive backstepping fuzzy neural network fractional-order control of microgyroscope using a nonsingular terminal sliding mode controller. Complexity 2018, 2018, 5246074. [Google Scholar] [CrossRef] [Green Version]
- Jin, L.; Qin, S.-Y.; Zhang, R.; Li, M.-W. High-sensitivity tunneling magneto-resistive micro-gyroscope with immunity to external magnetic interference. Sci. Rep. 2020, 10, 16441. [Google Scholar] [CrossRef]
- Zeng, L.; Yu, Z.; Zhang, H.; Zhang, X.; Chen, H. A high sensitive multi-parameter micro sensor for the detection of multi-contamination in hydraulic oil. Sens. Actuators A Phys. 2018, 282, 197–205. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, X.; Ye, Z.; Zhang, J.; Cao, F.; Zhang, J. A fabrication of iridium oxide film pH micro-sensor on Pt ultramicroelectrode and its application on in-situ pH distribution of 316 L stainless steel corrosion at open circuit potential. Sens. Actuators B Chem. 2018, 255, 1974–1982. [Google Scholar] [CrossRef]
- Ghouila-Houri, C.; Gallas, Q.; Garnier, E.; Merlen, A.; Viard, R.; Talbi, A.; Pernod, P. High temperature gradient calorimetric wall shear stress micro-sensor for flow separation detection. Sens. Actuators A Phys. 2017, 266, 232–241. [Google Scholar] [CrossRef] [Green Version]
- Nazemi, H.; Joseph, A.; Park, J.; Emadi, A. Advanced micro-and nano-gas sensor technology: A review. Sensors 2019, 19, 1285. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Admassu, D.; Durowade, T.; Gao, W.; Velicu, S.; Sivananthan, S. Adhesive wafer bonding of micro-actuators with SU-8 photoresist. Microsyst. Technol. 2020, 27, 3293–3297. [Google Scholar] [CrossRef]
- Ak, C.; Yildiz, A.; Akdagli, A. A novel expression obtained by using artificial bee colony algorithm to calculate pull-in voltage of fixed-fixed micro-actuators. Microsyst. Technol. 2018, 24, 2137–2145. [Google Scholar] [CrossRef]
- Rakotondrabe, M. Smart Materials-Based Actuators at the Micro/Nano-Scale: Characterization, Control and Applications; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-6683-3. [Google Scholar]
- Ouakad, H.M.; Bahadur, I.M. Bi-stability behavior in electrostatically actuated non-contact based micro-actuator. Microsyst. Technol. 2020, 26, 2961–2969. [Google Scholar] [CrossRef]
- Moory-Shirbani, M.; Sedighi, H.M.; Ouakad, H.M.; Najar, F. Experimental and mathematical analysis of a piezoelectrically actuated multilayered imperfect microbeam subjected to applied electric potential. Compos. Struct. 2018, 184, 950–960. [Google Scholar] [CrossRef]
- Osiander, R.; Darrin, M.A.G.; Champion, J.L. MEMS and Microstructures in Aerospace Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Choudhary, V.; Iniewski, K. Mems: Fundamental Technology and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Daeichin, M.; Ozdogan, M.; Towfighian, S.; Miles, R. Dynamic response of a tunable MEMS accelerometer based on repulsive force. Sens. Actuators A Phys. 2019, 289, 34–43. [Google Scholar] [CrossRef]
- Hajjaj, A.Z.; Alcheikh, N.; Younis, M.I. The static and dynamic behavior of MEMS arch resonators near veering and the impact of initial shapes. Int. J. Non-Linear Mech. 2017, 95, 277–286. [Google Scholar] [CrossRef] [Green Version]
- Pallay, M.; Daeichin, M.; Towfighian, S. Dynamic behavior of an electrostatic MEMS resonator with repulsive actuation. Nonlinear Dyn. 2017, 89, 1525–1538. [Google Scholar] [CrossRef]
- Skrzypacz, P.; Kadyrov, S.; Nurakhmetov, D.; Wei, D. Analysis of dynamic pull-in voltage of a graphene MEMS model. Nonlinear Anal. Real World Appl. 2019, 45, 581–589. [Google Scholar] [CrossRef] [Green Version]
- Madinei, H.; Mobki, H. State estimation of MEMs capacitor using taylor expansion. Int. J. Eng. 2015, 28, 764–770. [Google Scholar]
- Ozdogan, M.; Towfighian, S.; Miles, R.N. Modeling and Characterization of a Pull-in Free MEMS Microphone. IEEE Sens. J. 2020, 20, 6314–6323. [Google Scholar] [CrossRef] [Green Version]
- Radi, E.; Bianchi, G.; Nobili, A. Bounds to the pull-in voltage of a MEMS/NEMS beam with surface elasticity. Appl. Math. Model. 2020, 91, 1211–1226. [Google Scholar] [CrossRef]
- Daeichin, M.; Miles, R.; Towfighian, S. Lateral pull-in instability of electrostatic MEMS transducers employing repulsive force. Nonlinear Dyn. 2020, 100, 1927–1940. [Google Scholar] [CrossRef]
- Sedighi, H.M.; Daneshmand, F.; Yaghootian, A. Application of Iteration Perturbation Method in studying dynamic pull-in instability of micro-beams. Lat. Am. J. Solids Struct. 2014, 11, 1078–1089. [Google Scholar] [CrossRef] [Green Version]
- Azizi, A.; Mobki, H.; Rezazadeh, G. Bifurcation behavior of a capacitive micro-beam suspended between two conductive plates. Int. J. Sens. Netw. Data Commun. 2016, 5, 1–10. [Google Scholar]
- Azizi, A.; Fard, N.M.; Mobki, H.; Arbi, A. Bifurcation behaviour and stability analysis of a nano-beam subjected to electrostatic pressure. Appl. Comput. Math. 2018, 7, 1–11. [Google Scholar] [CrossRef]
- Siewe, M.S.; Hegazy, U.H. Homoclinic bifurcation and chaos control in MEMS resonators. Appl. Math. Model. 2011, 35, 5533–5552. [Google Scholar] [CrossRef]
- Han, J.; Zhang, Q.; Wang, W. Static bifurcation and primary resonance analysis of a MEMS resonator actuated by two symmetrical electrodes. Nonlinear Dyn. 2015, 80, 1585–1599. [Google Scholar] [CrossRef]
- Aghababa, M.P. Chaos in a fractional-order micro-electro-mechanical resonator and its suppression. Chin. Phys. B 2012, 21, 100505. [Google Scholar] [CrossRef]
- Miandoab, E.M.; Pishkenari, H.N.; Yousefi-Koma, A.; Tajaddodianfar, F. Chaos prediction in MEMS-NEMS resonators. Int. J. Eng. Sci. 2014, 82, 74–83. [Google Scholar] [CrossRef]
- Galetto, M.; Schiavi, A.; Genta, G.; Prato, A.; Mazzoleni, F. Uncertainty evaluation in calibration of low-cost digital MEMS accelerometers for advanced manufacturing applications. CIRP Ann. 2019, 68, 535–538. [Google Scholar] [CrossRef]
- Ghodssi, R.; Lin, P. MEMS Materials and Processes Handbook; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 1. [Google Scholar]
- Wang, Z.-F.; Shen, S.-L.; Modoni, G. Enhancing discharge of spoil to mitigate disturbance induced by horizontal jet grouting in clayey soil: Theoretical model and application. Comput. Geotech. 2019, 111, 222–228. [Google Scholar] [CrossRef]
- Jo, N.H.; Jeon, C.; Shim, H. Noise reduction disturbance observer for disturbance attenuation and noise suppression. IEEE Trans. Ind. Electron. 2016, 64, 1381–1391. [Google Scholar] [CrossRef]
- Wang, D.; He, H.; Mu, C.; Liu, D. Intelligent critic control with disturbance attenuation for affine dynamics including an application to a microgrid system. IEEE Trans. Ind. Electron. 2017, 64, 4935–4944. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Kong, L.; Shen, H.; Zhang, X. Size-dependent static and dynamic analysis of Reddy-type micro-beams by strain gradient differential quadrature finite element method. Thin-Walled Struct. 2020, 148, 106496. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Younis, M.I. The dynamic behavior of MEMS arch resonators actuated electrically. Int. J. Non-Linear Mech. 2010, 45, 704–713. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. Nonlinear behaviour of electrically actuated MEMS resonators. Int. J. Eng. Sci. 2013, 71, 137–155. [Google Scholar] [CrossRef]
- Younis, M.I. MEMS Linear and Nonlinear Statics and Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 20. [Google Scholar]
- Ouakad, H.M.; Sedighi, H.M. Static response and free vibration of MEMS arches assuming out-of-plane actuation pattern. Int. J. Non-Linear Mech. 2019, 110, 44–57. [Google Scholar] [CrossRef]
- Ale Ali, N.; Mohammadi, A.K. Effect of thermoelastic damping in nonlinear beam model of MEMS resonators by differential quadrature method. J. Appl. Comput. Mech. 2015, 1, 112–121. [Google Scholar]
- Wei, D.; Li, X. Finite element solutions of cantilever and fixed actuator beams using augmented lagrangian methods. J. Appl. Comput. Mech. 2018, 4, 125–132. [Google Scholar]
- ILGAMOV, M.A.; KHAKIMOV, A.G. Influence of Pressure on the Frequency Spectrum of Micro and Nanoresonators on Hinged Supports. J. Appl. Comput. Mech. 2021, 7, 977–983. [Google Scholar]
- Ghodrati, B.; Yaghootian, A.; Ghanbar Zadeh, A.; Mohammad-Sedighi, H. Lamb wave extraction of dispersion curves in micro/nano-plates using couple stress theories. Waves Random Complex Media 2018, 28, 15–34. [Google Scholar] [CrossRef]
- Kalhori, H.; Halkon, B.; Abbasnejad, B.; Li, B.; Shooshtari, A. Nonlinear Vibration of an Electrostatically Excited Capacitive Microplate. In Vibration Engineering for a Sustainable Future; Springer: Berlin/Heidelberg, Germany, 2021; pp. 3–9. [Google Scholar]
- Saadatmand, M.; Shooshtari, A. Nonlinear vibration analysis of a circular micro-plate in two-sided NEMS/MEMS capacitive system by using harmonic balance method. Acta Mech. Sin. 2019, 35, 129–143. [Google Scholar] [CrossRef]
- Liu, C.-C. The stability and non-linear vibration analysis of a circular clamped microplate under electrostatic actuation. Smart Sci. 2017, 5, 132–139. [Google Scholar] [CrossRef]
- Karamanli, A.; Aydogdu, M. Vibration of functionally graded shear and normal deformable porous microplates via finite element method. Compos. Struct. 2020, 237, 111934. [Google Scholar] [CrossRef]
- Li, W.; Yang, X.-D.; Zhang, W.; Ren, Y. Parametric amplification performance analysis of a vibrating beam micro-gyroscope with size-dependent and fringing field effects. Appl. Math. Model. 2021, 91, 111–124. [Google Scholar] [CrossRef]
- Moghimi Zand, M.; Ostadi Moghaddam, A. Pull-in instability and vibrations of a beam micro-gyroscope. J. Comput. Appl. Mech. 2014, 45, 29–34. [Google Scholar]
- Ouakad, H.M. Nonlinear structural behavior of a size-dependent MEMS gyroscope assuming a non-trivial shaped proof mass. Microsyst. Technol. 2020, 26, 573–582. [Google Scholar] [CrossRef]
- Gill, W.A.; Ali, D.; An, B.H.; Syed, W.U.; Saeed, N.; Al-shaibah, M.; Elfadel, I.M.; Al Dahmani, S.; Choi, D.S. MEMS multi-vibrating ring gyroscope for space applications. Microsyst. Technol. 2020, 26, 2527–2533. [Google Scholar] [CrossRef]
- Liu, K.-Z.; Yao, Y. Robust Control: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Ebihara, Y.; Peaucelle, D.; Arzelier, D. S-Variable Approach to LMI-Based Robust Control; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Azar, A.T.; Zhu, Q. Advances and Applications in Sliding Mode Control Systems; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Vaidyanathan, S.; Lien, C.-H. Applications of Sliding Mode Control in Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2017; Volume 709. [Google Scholar]
- Precup, R.-E.; Radac, M.-B.; Dragos, C.-A.; Preitl, S.; Petriu, E.M. Model-free tuning solution for sliding mode control of servo systems. In 2014 IEEE International Systems Conference Proceedings; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Precup, R.-E.; Preitl, S.; Szabo, C.; Gyurko, Z.; Szemes, P. Sliding mode navigation control in intelligent space. In IEEE International Symposium on Intelligent Signal Processing; IEEE: Piscataway, NJ, USA, 2003. [Google Scholar]
- Hedrea, E.-L.; Precup, R.-E.; Bojan-Dragos, C.-A.; Petriu, E.M.; Roman, R.-C. Tensor Product–Based Model Transformation and Sliding Mode Control of Electromagnetic Actuated Clutch System. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019. [Google Scholar]
- Preitl, S.; Precup, R.-E.; Fodor, J.; Bede, B. Iterative feedback tuning in fuzzy control systems. Theory and applications. Acta Polytech. Hung. 2006, 3, 81–96. [Google Scholar]
- Aparanji, V.M.; Wali, U.V.; Aparna, R. Multi-Layer Auto Resonance Network for Robotic Motion Control. Int. J. Artif. Intell. 2020, 18, 19–44. [Google Scholar]
- Precup, R.-E.; Teban, T.-A.; Albu, A.; Borlea, A.-B.; Zamfirache, I.A.; Petriu, E.M. Evolving fuzzy models for prosthetic hand myoelectric-based control. IEEE Trans. Instrum. Meas. 2020, 69, 4625–4636. [Google Scholar] [CrossRef]
- Precup, R.E.; Tomescu, M.L.; Petriu, E.M. A Unified Anti-Windup Technique for Fuzzy and Sliding Mode Controllers. Int. J. Comput. Commun. Control 2015, 10, 83–95. [Google Scholar] [CrossRef]
- Precup, R.-E.; Roman, R.-C.; Hedrea, E.-L.; Petriu, E.M.; Bojan-Dragos, C.-A. Data-Driven Model-Free Sliding Mode and Fuzzy Control with Experimental Validation. Int. J. Comput. Commun. Control 2021, 16, 1–17. [Google Scholar] [CrossRef]
- Rahmani, M.; Rahman, M.H.; Nosonovsky, M. A new hybrid robust control of MEMS gyroscope. Microsyst. Technol. 2020, 26, 853–860. [Google Scholar] [CrossRef]
- Zhang, X.; Koo, B.; Salapaka, S.M.; Dong, J.; Ferreira, P.M. Robust control of a MEMS probing device. IEEE/ASME Trans. Mechatron. 2012, 19, 100–108. [Google Scholar] [CrossRef]
- He, G.; Geng, Z. Dynamics and robust control of an underactuated torsional vibratory gyroscope actuated by electrostatic actuator. IEEE/ASME Trans. Mechatron. 2014, 20, 1725–1733. [Google Scholar] [CrossRef]
- Fei, J.; Zhou, J. Robust adaptive control of MEMS triaxial gyroscope using fuzzy compensator. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 1599–1607. [Google Scholar]
- Qin, Y.; Sun, W.; Yeow, J.T. A robust control approach for MEMS capacitive micromachined ultrasonic transducer. Trans. Inst. Meas. Control 2019, 41, 107–116. [Google Scholar] [CrossRef]
- Darbasi, S.; Mirzaei, M.J.; Abazari, A.M.; Rezazadeh, G. Adaptive under-Actuated Control for Capacitive Micro-Machined Ultrasonic Transducer Based on an Accurate Nonlinear Modeling. Available online: https://www.researchsquare.com/article/rs-756261/v1 (accessed on 5 October 2021).
- Mobki, H.; Sabegh, A.M.; Azizi, A.; Ouakad, H.M. On the implementation of adaptive sliding mode robust controller in the stabilization of electrically actuated micro-tunable capacitor. Microsyst. Technol. 2020, 26, 3903–3916. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Trajectory tracking control of AUVs via adaptive fast nonsingular integral terminal sliding mode control. IEEE Trans. Ind. Inform. 2019, 16, 1248–1258. [Google Scholar] [CrossRef]
- Xiong, J.-J.; Zhang, G.-B. Global fast dynamic terminal sliding mode control for a quadrotor UAV. ISA Trans. 2017, 66, 233–240. [Google Scholar] [CrossRef]
- Mu, C.; He, H. Dynamic behavior of terminal sliding mode control. IEEE Trans. Ind. Electron. 2017, 65, 3480–3490. [Google Scholar] [CrossRef]
- Aghababa, M.P.; Feizi, H. Nonsingular terminal sliding mode approach applied to synchronize chaotic systems with unknown parameters and nonlinear inputs. Chin. Phys. B 2012, 21, 060506. [Google Scholar] [CrossRef]
- Chen, G.; Song, Y.; Guan, Y. Terminal sliding mode-based consensus tracking control for networked uncertain mechanical systems on digraphs. IEEE Trans. Neural Netw. Learn. Syst. 2016, 29, 749–756. [Google Scholar] [CrossRef] [PubMed]
- Shotorbani, A.M.; Ajami, A.; Zadeh, S.G.; Aghababa, M.P.; Mahboubi, B. Robust terminal sliding mode power flow controller using unified power flow controller with adaptive observer and local measurement. IET Gener. Transm. Distrib. 2014, 8, 1712–1723. [Google Scholar] [CrossRef]
- Mobayen, S.; Javadi, S. Disturbance observer and finite-time tracker design of disturbed third-order nonholonomic systems using terminal sliding mode. J. Vib. Control 2017, 23, 181–189. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Han, F. On nonsingular terminal sliding-mode control of nonlinear systems. Automatica 2013, 49, 1715–1722. [Google Scholar] [CrossRef]
- Liu, W.; Feng, Z.; Bi, A. A novel nonsingular terminal sliding mode control combined with global sliding surface for uncertain nonlinear second-order systems. Trans. Inst. Meas. Control 2020, 42, 1294–1300. [Google Scholar] [CrossRef]
- Mobki, H.; Jalilirad, M.; Moradi, M.V.; Azizi, A. Multi input versus single input sliding mode for closed-loop control of capacitive micro structures. SN Appl. Sci. 2019, 1, 676. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).