1. Introduction
The notion of pseudo-orbits very often appears in the several branches of modern theory of dynamical systems, and, especially, the pseudo-orbit shadowing property usually plays an important role in the investigation of stability theory and ergodic theory as well as expansivity. Let be a compact metric space, and let be a homeomorphism. For , a sequence of points is called a δ-pseudo-orbit of f if for all .
Denote by the restriction of f to a subset A of X. Let be a closed f-invariant set, that is, . We say that has the shadowing property if for every , there is such that for any and -pseudo-orbit of f, there is -shadowing the pseudo-orbit, that is, for all . Notice that only -pseudo-orbits of f “contained in ” can be -shadowed, but shadowing point is “not necessarily” contained in . We say that f has the shadowing property if in the above definition. Since X is compact, it is not hard to show that if has the shadowing property, then every pseudo-orbit can be shadowed by some true orbit.
The notion of expansivity has been intensively studied by several researchers, mainly from the topological view point, and lots of important fruitful results were obtained. Nowadays, expansive theory of dynamical systems has been well developed in both of the geometric theory and ergodic theory of dynamical systems as well as that of shadowing theory. Recently, the notion of the expansive measures was introduced by Morales and Sirvent [
1] as a generalization of the notion of expansivity from the measure theoretical view point, and they exhibit the effectiveness of the use of it in expansive theory of dynamical systems (see [
2,
3,
4] among others).
In this paper, inspired by the work of Morales and Sirvent, we introduce the notion of shadowable measures for a homeomorphism of a compact metric space as a generalization of the shadowing property from the measure theoretical view point, and consider the set of diffeomorphisms of a closed differentiable manifolds possessing the shadowable measures. The notion of such kind of measures is recently introduced by Lee and Morales [
2], and they consider the shadowability of pseudo-orbits of a dynamical system from the measure theoretical view point. In our opinion, however, the introduced measure does not properly reflect the behavior of pseudo-orbits of the system. In fact, for a given pseudo-orbit
of the system, they measure only the initial point
of the pseudo-orbit, whole of the pseudo-orbit is not considered (see ([
2], Definition 2.5)).
Recall that is a compact metric space and is a homeomorphism of X. Let (the n-times of direct product) be the sequences of points of X with length n, and denote by the space of Borel probability measures of X. For any (which is not necessarily f-invariant), let (n-times) be the direct product measure of . For any , denote by the space of -pseudo-orbits of f, and for , denote by the set of -pseudo-orbits -shadowed by some point.
We say that
is a
shadowable measure of
f (or simply,
f is
-
shadowable) if for any
, there exists
such that
for any
(if
A is a subset of
X, then we define the shadowable measure for
by the same manner). Observe that if
has the shadowing property, then
f is
-shadowable for any
. Denote by
the support of
. Then, since
X is compact, we can see that if
f is
-shadowable and
, then
has the shadowing property (see Lemma 1 in
Section 3).
Let
M be a closed
manifold, and let
be the space of diffeomorphisms of
M endowed with the
-topology. In this paper, we denote by
the set of
possessing the shadowing property. It is well-known that
if and only if
f satisfies both Axiom A and the strong transversality condition (see [
5,
6,
7] among others), where
means the
-interior of the set.
Hereafter, let
be the set of periodic points of
, and let
be the set of non-wandering points of it. Let
be a closed
f-invariant set. Recall that
is
hyperbolic if the tangent bundle
has a
-invariant splitting
with constants
and
such that
for all
and
. It is well-known that if
is hyperbolic, then
has the shadowing property (see [
8]). Recall that the shadowing point is not necessarily contained in
.
We say that
f satisfies
Axiom A if
is hyperbolic and
. The
stable manifold of a point
x is the set
The
unstable manifold of
x is also defined analogously for
. It is well-known that if
is hyperbolic, then
and
are both immersed manifolds for each
(for instance, see [
8]). Let
f satisfies Axiom A. We say that
f satisfies the strong transversality condition if all the stable and the unstable manifolds are transverse at any point of their intersection.
To describe our results, let us introduce some notation on probability measures of
M. Let us endow
with the weak topology. It is well-known that the set of
f-invariant measures,
, is a non-empty compact subset of
. We say that
is
atomic if there exists a point
such that
(denote by
the set of atomic measures of
M). It is known that the set of non-atomic measures is a residual set in
(see [
9]).
We define two subsets and of as follows from a measure-theoretical view point and characterize them in the context of geometric theory of differentiable dynamical systems.
, and
,
Recall that if
, then
f is
-shadowable for any
. Thus
In this paper, we prove the following two theorems.
Theorem 1. if and only if f satisfies both Axiom A and the strong transversality condition.
The proof is based on the main result of [
7], and the result is obtained by proving that
(see
Section 3).
Denote by
the set of
such that there is a
-neighborhood
of
f with property that every
is hyperbolic. It is proved by Hayashi [
10] that
if and only if
f satisfies both Axiom A and no-cycle condition. The proof of the second result is based on Hayashi, and the result is obtained by proving that
(see
Section 4).
Theorem 2. if and only if f satisfies both Axiom A and the no-cycle condition.
Owing to the above two theorems, the relationship between uniform hyperbolicity and -robustness of the existence of shadowable measures turns out to be clear.
2. Examples
Recall that if a dynamical system has the shadowing property, then any probability mesasure is shadowable. The dynamical systems considered in this section do not have the shadowing property. First two examples have a measure that is not shadowable, but the last example has a shadowable measure.
Example 1. (The identity map of the unit interval).
Let
I be the unit interval
, and let
be the identity map, that is,
for
. It is well-known that the identity map of
I does not have the shadowing property. Let
be the Lebesgue probability measure on
I. Then we can see that there exists
such that for any
and
, there is a subset
with the property that
and non of any element in
can be
-shadowed.
For any integer
and
, denote by
. First we put
for
, and then set
for
. It is easy to see that for any
,
so that
is a
-pseudo-orbit of
. Set
Since is the identity map, it is not hard to show that there exists (say, ) such that for any -pseudo-orbit of , there is n such that cannot be -shadowed by any point .
Example 2. (Rotation maps of the unit circle).
Let
, and define a metric on
by
For , let be a rotation map defined by .
Then the map
does not have the shadowing property. In fact, the identity map
does not have the shadowing property. For any (small)
, put
. Then since
for any
, the sequence
is a
-pseudo-orbit of
. It is easy to see that the pseudo-orbit cannot be
-shadowed by
-orbit for any
.
Observe that if
is small enough, then
Thus, it is not hard to show that the rotation map does not have the shadowing property as in the case .
Let be the usual Lebesgue probability measure on so that is -invariant. Then, as in the case of the identity map of the unit interval I, the measure of the set of non-shadowable pseudo-orbits is positive.
As stated before, the last example does not have the shadowing property, but has a shadowable measure. For the description, we need some notations.
Let
be a surface, and let
satisfy Axiom A. The so-called
-transversality condition for
f is introduced by [
11]. Roughly speaking, we say that the stable manifold
and the unstable manifold
of
are
-transverse at
z if these sets cross at
z as the graph of the function
crosses the
x-axis at the origin in the
-plane. We say that
f satisfies the
-transversality condition if all the stable and the unstable manifolds are
-transverse at any point of their intersection. It is proved therein that
f satisfies the
-transversality condition if and only if
f has the shadowing property.
Example 3. (Axiom A diffeomorphisms with no-cycles).
We represent two-torus
as the square
with identified opposite sides in the Euclidean space
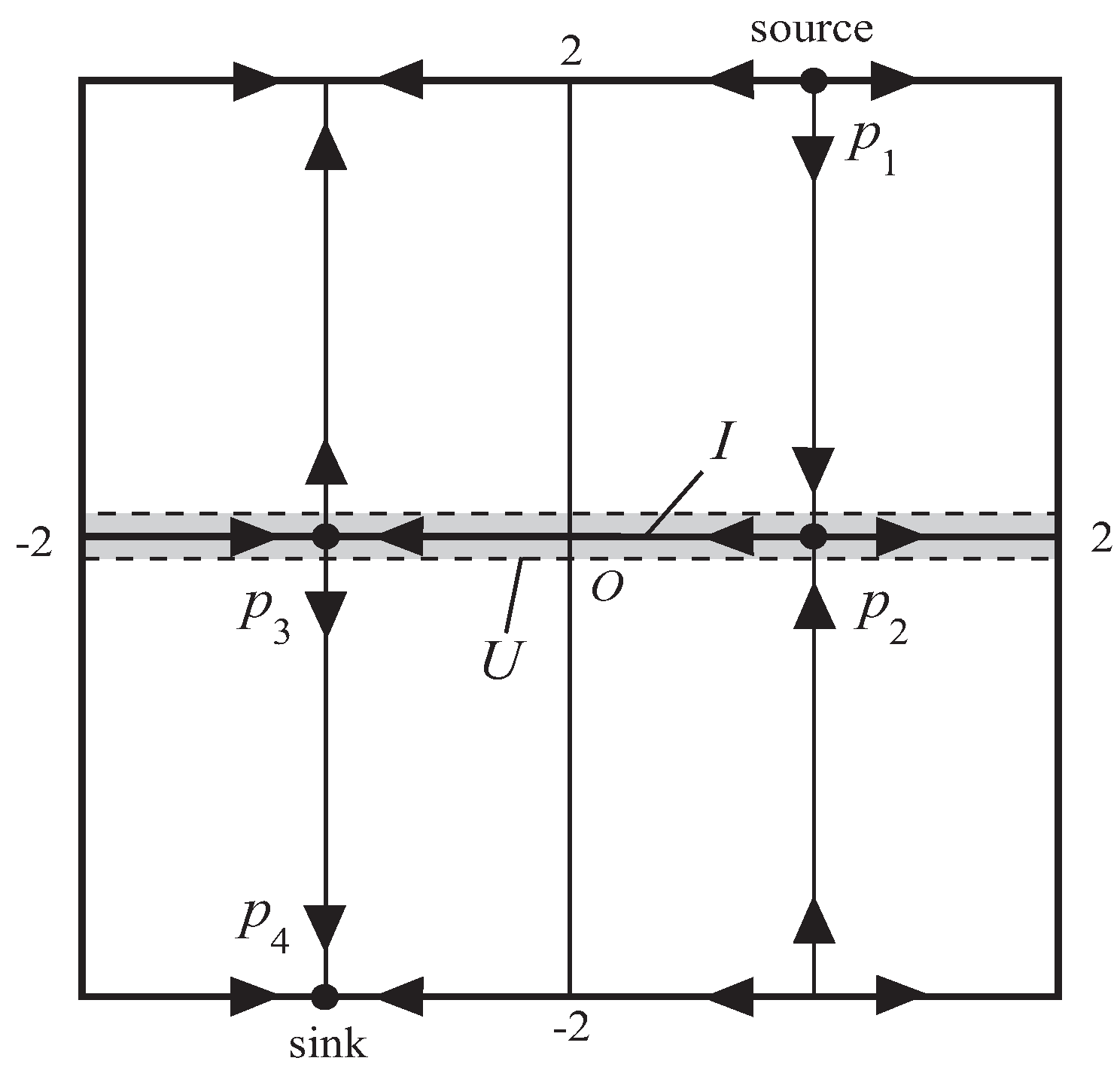
. Let
be a diffeomorphism with the following properties (see
Figure 1):
- (1)
the non-wandering set of g is the union of 4 hyperbolic fixed points, that is, , where is a source, is a sink, and are saddles;
- (2)
with respect to coordinates , the following conditions hold:
- (2.1)
,
- (2.2)
,
where
and
are the stable and unstable manifolds
, respectively, defined as usual;
there exist neighborhoods of such that
there exists a neighborhood V of the point such that and is affine on ,
the eigenvalues of are with , , and the eigenvalues of are with .
Please note that g satisfies both Axiom A and the no-cycle condition (i.e., it is -stable) but does not have the shadowing property. Indeed, since , the stable manifold and the unstable manifold are not -transverse, and thus g does not have the shadowing property. However, we show herewith that there exists shadowable measure for g.
Indeed, put
and let
U be a small neighborhood of
I (see
Figure 1). Define
as the Lebesgue measure on
such that
and
. Observe that for any
and
, we can construct a
-pseudo-orbit
of
g starting at a neighborhood of
, passing through
I, and arriving at a neighborhood of
. It is easy to see that there exists
such that for any
, there exists this kind of
-pseudo-orbit
which cannot be
-shadowed by any orbit of
g. Since
, the
-measure of the set of such a kind of
-pseudo-orbits is 0.
On the other hand, since
g is, in a sense, hyperbolic in the outside of
U, we can see that any pseudo-orbit can be shadowed by an orbit of
g. For, since
is a sink fixed point, there is a neighbourhood
of
and
such that for any
,
. For any
, choose
small enough so that
. Let
be a
-pseudo-orbit of
g contained in
. If
for some
, then
by the choice of
. Moreover, since
, we have
By continuing this manner, we can see that for any . Thus, we have the following.
Claim 1. For any , there is such that any δ-pseudo-orbit of g which is contained in can be ϵ-shadowed by some point.
Observe that since is a source fixed point, a similar property also holds in a neighbourhoof of with respect to . The assertion of the following claim can be easily checked.
Claim 2. There are a constant and such that for any δ-pseudo-orbit of g , ifthen . It is not hard to show that for any , there exists such that any -pseudo-orbit of g with can be -shadowed some point. Combining this fact with the assertion of Claim 1, we can see that the map g has the shadowing property in the outside of U. Thus is a shadowable measure.
4. Proof of Theorem 2
In what follows, we give a proof of Theorem 2. Recall that
if and only if
f satisfies both Axiom A and no-cycle condition by [
10]. Thus, to get the conclusion, it is enough to show that
. Suppose
. The existence of the non-hyperbolic periodic point of
f easily gives a small periodic curve with period
l for some
-nearby
f such that the restriction of the map
to the curve is the identity map (see End of the proof of Theorem 2 below). From this, we will show that periodic points of any
g,
-nearby
f, are all hyperbolic. This kind of result was first obtained by the first author in ([
12], Proposition 1). To show this fact we use the next lemma several times.
Lemma 2. Let and let be given. Then there is such that for a finite set , a neighborhood U of and linear maps satisfying for all , there are and such that
- (a)
if , and
- (b)
if for all .
Observe that the assertion
implies that
and that
for all
. The proof is essentially contained in the proof of ([
13], Lemma 1).
End of the proof of Theorem 2. Suppose , and we show that . By contradiction, assume that and we shall derive a contradiction. Since , there exists a -neighborhood of f such that for any and any , g is -shadowable. On the other hand, it follows from the assumption that there are and non-hyperbolic periodic point p of g.
At first, by Lemma 2, with a small modification of the map g with respect to the -topology, we may assume that has only one eigenvalue with modulus equal to 1 (or only one pair of complex conjugated eigenvalues, see Case 2 below). Denote by the eigenspace corresponding to .
Case 1. .
In this case, we suppose further that
for simplicity (the other case is similar). Then, by Lemma 2, there are
and
such that
and
if
for
, and
if
. We can choose
such that
and
Define a small arc with its center at
p by
Here is the -ball in centered at the origin . Since the eigenvalue of is 1, we have
,
, and
is the identity map.
Denote by
the eigenspace corresponding to the eigenvalues of
with modulus less than 1, and by
the eigenspace corresponding to the eigenvalues with modulus more than 1. Then
For
we define
If we put
for
, then, we may assume
by reducing
if necessary.
Let
be a normalized Lebesgue measure on
. We define
by
for any Borel set
C of
M. Observe that
.
Let
. By the continuity of
, there exists
such that
implies
for
and
. Choose an integer
such that
. Then there are points
such that
- (i)
,
- (ii)
for ,
- (iii)
.
For any
and
, we set
The set
is defined by
Then it is easily checked that
and
. We show that
Let
and
satisfy
for
. Since
we have
for
and
. If we put
, then we have
Since
we have
, which is a contradiction.
Therefore we have . But this contradicts with .
Case 2. .
In the proof of the second case, to avoid notational complexity, we consider only the case
. As in the first case, by Lemma 2, there are
and
such that
and
if
. With a small modification of the map
, we may suppose that there is
(the minimum number) such that
for any
by Lemma 2.
Take
such that
, and set
Then is an arc such that
Let
be the normalized Lebesgue measure on
and set
for a Borel set
C.
Then . As in the first case, we can prove that is not -shadowable, which contradicts the fact that . Thus, Theorem 2 is proved.