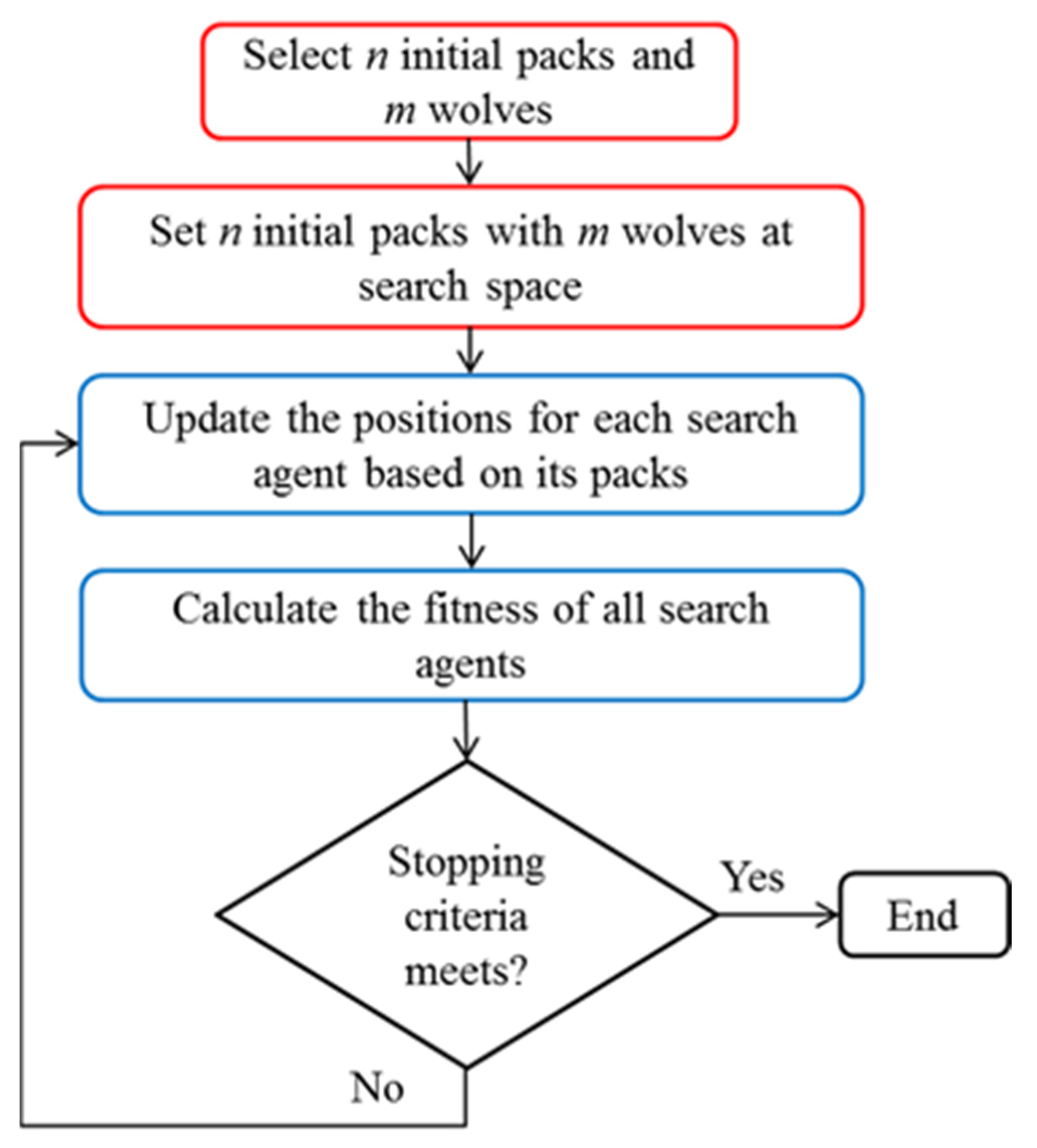
Figure 1.
Flow chart of conventional FWA-GWO.
Figure 1.
Flow chart of conventional FWA-GWO.
Figure 2.
Example of initialization with 4 packs.
Figure 2.
Example of initialization with 4 packs.
Figure 3.
Pseudocode of conventional FWA-GWO.
Figure 3.
Pseudocode of conventional FWA-GWO.
Figure 4.
Flow chart of the EF-FWA-GWO.
Figure 4.
Flow chart of the EF-FWA-GWO.
Figure 5.
Conditional decision for implementation.
Figure 5.
Conditional decision for implementation.
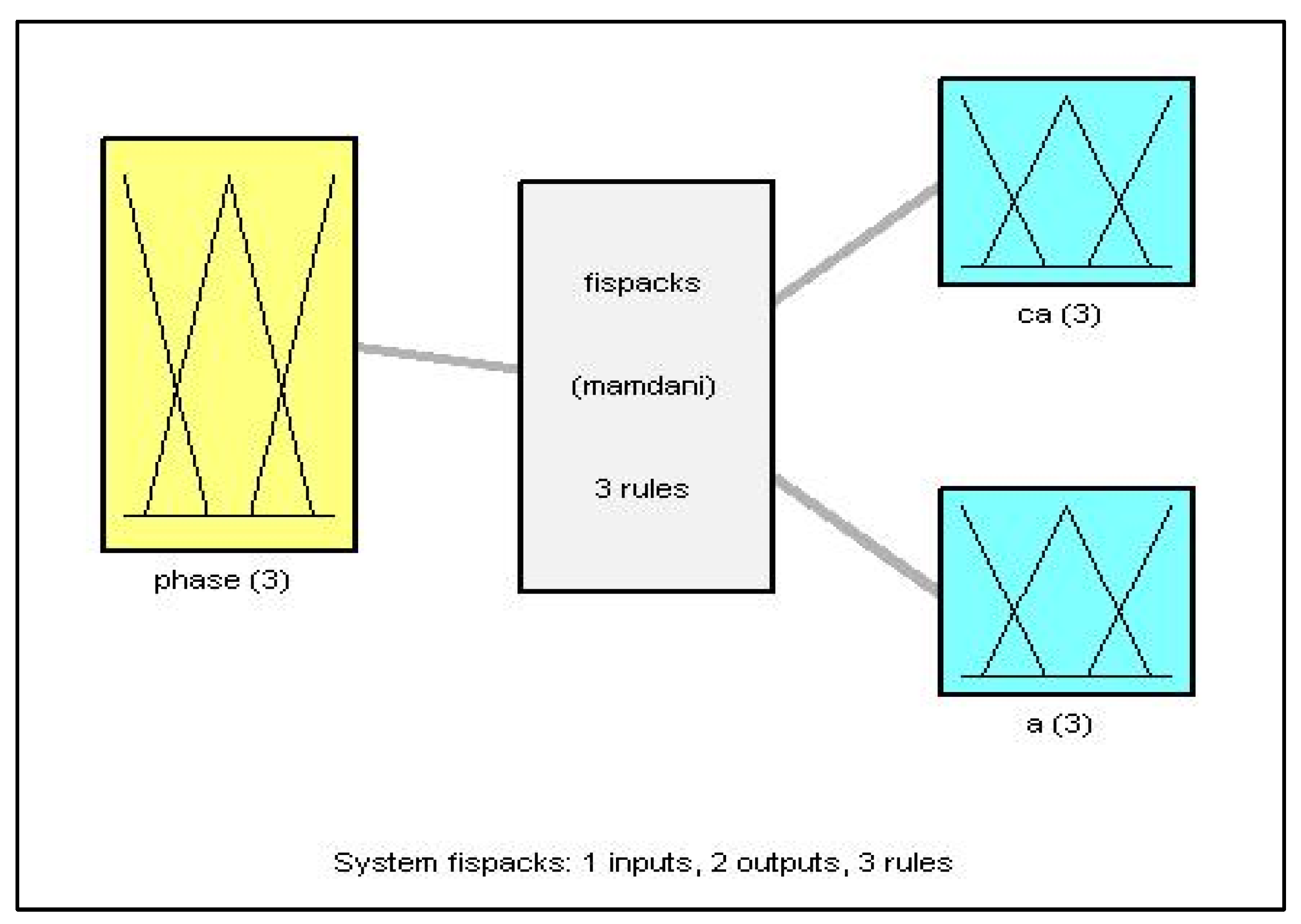
Figure 6.
Triangular FIS “FisPacks”.
Figure 6.
Triangular FIS “FisPacks”.
Figure 7.
Gaussian FIS “FisPacks”.
Figure 7.
Gaussian FIS “FisPacks”.
Figure 8.
Triangular Input Variable “Phase” in the FIS “FisPacks”.
Figure 8.
Triangular Input Variable “Phase” in the FIS “FisPacks”.
Figure 9.
Triangular Output Variable “ca” in the FIS “FisPacks”.
Figure 9.
Triangular Output Variable “ca” in the FIS “FisPacks”.
Figure 10.
Triangular Output Variable “a” in the FIS “FisPacks”.
Figure 10.
Triangular Output Variable “a” in the FIS “FisPacks”.
Figure 11.
Gaussian Input Variable “Phase” in the FIS “FisPacks”.
Figure 11.
Gaussian Input Variable “Phase” in the FIS “FisPacks”.
Figure 12.
Gaussian Input Variable “ca” in the FIS “FisPacks”.
Figure 12.
Gaussian Input Variable “ca” in the FIS “FisPacks”.
Figure 13.
Gaussian Input Variable “a” in the FIS “FisPacks”.
Figure 13.
Gaussian Input Variable “a” in the FIS “FisPacks”.
Figure 14.
Fuzzy rules in FIS “FisPacks”.
Figure 14.
Fuzzy rules in FIS “FisPacks”.
Figure 15.
Surface of “ca” parameter of the first FIS.
Figure 15.
Surface of “ca” parameter of the first FIS.
Figure 16.
Surface of “a” parameter of the first FIS.
Figure 16.
Surface of “a” parameter of the first FIS.
Figure 17.
Triangular FIS “FisAmplitude”.
Figure 17.
Triangular FIS “FisAmplitude”.
Figure 18.
Gaussian FIS “FisAmplitude”.
Figure 18.
Gaussian FIS “FisAmplitude”.
Figure 19.
Triangular Output Variable “amplitude” in the FIS “FispAmplitude”.
Figure 19.
Triangular Output Variable “amplitude” in the FIS “FispAmplitude”.
Figure 20.
Triangular Output Variable “a” in the FIS “FispAmplitude”.
Figure 20.
Triangular Output Variable “a” in the FIS “FispAmplitude”.
Figure 21.
Gaussian Output Variable “amplitude” in the FIS “FispAmplitude”.
Figure 21.
Gaussian Output Variable “amplitude” in the FIS “FispAmplitude”.
Figure 22.
Gaussian Output Variable “a” in the FIS “FispAmplitude”.
Figure 22.
Gaussian Output Variable “a” in the FIS “FispAmplitude”.
Figure 23.
Fuzzy Rules of “FisAmplitude”.
Figure 23.
Fuzzy Rules of “FisAmplitude”.
Figure 24.
Surface of “amplitude” parameter of the second FIS.
Figure 24.
Surface of “amplitude” parameter of the second FIS.
Figure 25.
Surface of “a” parameter of the second FIS.
Figure 25.
Surface of “a” parameter of the second FIS.
Figure 26.
Graphical representations of benchmark functions.
Figure 26.
Graphical representations of benchmark functions.
Figure 27.
Fixed-dimension multimodal mathematical functions in 3D versions.
Figure 27.
Fixed-dimension multimodal mathematical functions in 3D versions.
Figure 28.
Results analysis.
Figure 28.
Results analysis.
Figure 29.
Autonomous mobile robot model.
Figure 29.
Autonomous mobile robot model.
Figure 30.
FIS for the Fuzzy controller.
Figure 30.
FIS for the Fuzzy controller.
Figure 31.
Input variable of the FIS in EF-FWAGWO.
Figure 31.
Input variable of the FIS in EF-FWAGWO.
Figure 32.
Output variable of the FIS in EF-FWAGWO.
Figure 32.
Output variable of the FIS in EF-FWAGWO.
Figure 33.
Best experiment obtained by EF-FWAGWO with a 0.3254 MSE.
Figure 33.
Best experiment obtained by EF-FWAGWO with a 0.3254 MSE.
Table 1.
Number of packs during different phases.
Table 1.
Number of packs during different phases.
| Phase | Number of Packs |
|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 1 | 1 | 2 | 2 | 3 | 3 | 4 |
| 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Table 2.
Triangular Input Variable “Phase” parameters.
Table 2.
Triangular Input Variable “Phase” parameters.
| Linguistic Values | Parameters |
|---|
| Low | [−0.4, 0, 0.4] |
| Medium | [0.1, 0.5, 0.9] |
| High | [0.6, 1, 1.4] |
Table 3.
Triangular Output Variable “ca” parameters.
Table 3.
Triangular Output Variable “ca” parameters.
| Linguistic Values | Parameters |
|---|
| Low | [−28.6, −7, 14.6] |
| Medium | [−1.6, 20, 41.6] |
| High | [25.4, 47, 68.6] |
Table 4.
Triangular Output Variable “a” parameters for first FIS.
Table 4.
Triangular Output Variable “a” parameters for first FIS.
| Linguistic Values | Parameters |
|---|
| Low | [−0.9, 0, 0.9] |
| Medium | [0.225, 1.125, 2.025] |
| High | [1.35, 2.25, 3.15] |
Table 5.
Gaussian Output Variable “phase” parameters.
Table 5.
Gaussian Output Variable “phase” parameters.
| Linguistic Variables | Parameters |
|---|
| Low | [0.1699, 6.93 × 10−18] |
| Medium | [0.1699, 0.5] |
| High | [0.1699, 1] |
Table 6.
Gaussian Output Variable “ca” parameters.
Table 6.
Gaussian Output Variable “ca” parameters.
| Linguistic Values | Parameters |
|---|
| Low | [9.173, −7] |
| Medium | [9.173, 20] |
| High | [9.173, 40] |
Table 7.
Gaussian Output Variable “a” parameters.
Table 7.
Gaussian Output Variable “a” parameters.
| Linguistic Variables | Parameters |
|---|
| Low | [0.3822, 6.939 × 10−18] |
| Medium | [0.3822, 1.125] |
| High | [0.3822, 2.25] |
Table 8.
Triangular Output Variable “amplitude” parameters.
Table 8.
Triangular Output Variable “amplitude” parameters.
| Linguistic Values | Parameters |
|---|
| Low | [−0.9, 0, 0.9] |
| Medium | [0.225, 1.125, 0.025] |
| High | [1.35, 2.25, 3.15] |
Table 9.
Triangular Output Variable “a” parameter in second FIS.
Table 9.
Triangular Output Variable “a” parameter in second FIS.
| Linguistic Values | Parameters |
|---|
| Low | [−0.9, 0, 0.9] |
| Medium | [0.225, 1.125, 0.025] |
| High | [1.35, 2.25, 3.15] |
Table 10.
Gaussian Output Variable “amplitude” parameters.
Table 10.
Gaussian Output Variable “amplitude” parameters.
| Linguistic Values | Parameters |
|---|
| Low | [0.3822, 6.939 × 10−18] |
| Medium | [0.3822, 1.125] |
| High | [0.3822, 2.25] |
Table 11.
Gaussian Output Variable “a” parameters.
Table 11.
Gaussian Output Variable “a” parameters.
| Linguistic Variables | Parameters |
|---|
| Low | [0.3822, 6.939 × 10−18] |
| Medium | [0.3822, 1.125] |
| High | [0.3822, 2.25] |
Table 12.
Features of benchmark functions.
Table 12.
Features of benchmark functions.
| Function | Range | fmin |
|---|
| [−100, 100] | 0 |
| [−100, 100] | 0 |
| [−100, 100] | 0 |
| [−100, 100] | 0 |
| [−100, 100] | 0 |
| [−100, 100] | 0 |
| [−100, 100] | −39.17 |
| [−100, 100] | 0 |
| [−100, 100] | 0 |
| [−100, 100] | 0 |
| [−100, 100] | 0 |
| [−100, 100] | 0 |
| [−100, 100] | 0 |
Table 13.
Fixed-dimension multimodal functions.
Table 13.
Fixed-dimension multimodal functions.
| Function | Dim | Range | fmin |
|---|
| 2 | [−65, 65] | 1 |
| 4 | [−5, 5] | 0.00030 |
| 2 | [−5, 5] | −1.0316 |
| 2 | [−2, 2] | 3 |
| 3 | [1, 3] | −3.86 |
| 6 | [0, 1] | −3.32 |
| 4 | [0, 10] | −10.1532 |
| 4 | [0, 10] | −10.4028 |
| 4 | [0, 10] | −10.5363 |
Table 14.
Comparison of version 1 between conventional FWA GWO and the Fuzzy FWA-GWO in 30 dimensions.
Table 14.
Comparison of version 1 between conventional FWA GWO and the Fuzzy FWA-GWO in 30 dimensions.
| Function | Hybrid V1 | STD | Hybrid FV1 | STD | Z-Value |
|---|
| F1 | 6.43 × 10−28 | 1.17 × 10−27 | 1.1948 × 10−31 | 2.41 × 10−31 | −3.9240 |
| F2 | 1.70 × 10−16 | 1.63 × 10−16 | 2.13 × 10−18 | 2.98 × 10−18 | −7.3536 |
| F3 | 8.47 × 10−4 | 0.0025 | 3.07 × 10−4 | 0.0007 | −1.4900 |
| F4 | 0.0383 | 0.0584 | 0.0080 | 0.0146 | −3.5971 |
| F5 | 27.6283 | 0.5878 | 27.5833 | 0.5480 | −0.3996 |
| F6 | 0.8856 | 0.4284 | 0.9831 | 0.5835 | 0.9619 |
| F7 | −775.8908 | 98.3576 | −751.4547 | 99.0596 | −1.2501 |
| F8 | 1.7697 | 6.7631 | 20.6972 | 74.5578 | 1.8055 |
| F9 | 9641.80 | 11,406.71 | 18,071.97 | 29,673.06 | 1.8938 |
| F10 | 1.731 | 2.2942 | 2.7775 | 6.4951 | 1.0849 |
| F11 | 5.8606 | 9.4934 | 8.7885 | 10.5125 | 1.4761 |
| F12 | 0.0693 | 0.0297 | 0.1155 | 0.0713 | 4.2727 |
| F13 | 0 | 0 | 0.00 | 0.00 | |
Table 15.
Comparison of version 2 between conventional FWA GWO and the Fuzzy FWA-GWO in 30 dimensions.
Table 15.
Comparison of version 2 between conventional FWA GWO and the Fuzzy FWA-GWO in 30 dimensions.
| Function | Hybrid V2 | STD | Hybrid FV2 | STD | Z-Value |
|---|
| F1 | 1.84 × 10−22 | 7.49 × 10−22 | 8.4637 × 10−26 | 2.8773 × 10−25 | −1.7536 |
| F2 | 1.17 × 10−13 | 1.20 × 10−13 | 1.84 × 10−15 | 1.65 × 10−15 | −6.8525 |
| F3 | 0.0044 | 0.0166 | 4.19 × 10−4 | 0.0007 | −1.7112 |
| F4 | 0.0409 | 0.044 | 0.0062 | 0.0083 | −5.5262 |
| F5 | 27.5222 | 0.5276 | 27.7630 | 0.7437 | 1.8863 |
| F6 | 0.5746 | 0.3179 | 0.6856 | 0.4105 | 1.5274 |
| F7 | −811.8833 | 98.7647 | −846.9459 | 114.8316 | −1.6532 |
| F8 | 7.55 × 10−5 | 1.91 × 10−4 | 3.76 × 10−5 | 4.51 × 10−5 | −1.3791 |
| F9 | 15,241.4387 | 16,021.8731 | 8564.5959 | 10,302.3794 | −2.5032 |
| F10 | 1.3627 | 2.0485 | 10.3246 | 19.3669 | 3.2863 |
| F11 | 1.71 × 10−11 | 4.23 × 10−11 | 2.62 × 10−13 | 3.28 × 10−13 | −2.8426 |
| F12 | 0.0705 | 0.0316 | 0.1213 | 0.1184 | 2.9641 |
| F13 | 0 | 0 | 0.00 | 0.00 | |
Table 16.
Comparison of version 3 between conventional FWA GWO and the Fuzzy FWA-GWO in 30 dimensions.
Table 16.
Comparison of version 3 between conventional FWA GWO and the Fuzzy FWA-GWO in 30 dimensions.
| Function | Hybrid V3 | STD | Hybrid FV3 | STD | Z-Value |
|---|
| F1 | 1.8 × 10−18 | 2.7 × 10−18 | 5.7 × 10−21 | 3.0 × 10−20 | −4.6926 |
| F2 | 4.19 × 10−11 | 3.52 × 10−11 | 4.58 × 10−13 | 5.19 × 10−13 | −8.4070 |
| F3 | 0.0095 | 0.0241 | 6.50 × 10−4 | 0.0017 | −2.6161 |
| F4 | 0.0248 | 0.0207 | 0.0046 | 0.0038 | −6.8395 |
| F5 | 27.7054 | 0.5847 | 27.6202 | 0.5759 | −0.7418 |
| F6 | 0.59297 | 0.35281 | 0.5904 | 0.3383 | −0.0376 |
| F7 | −753.7345 | 291.2693 | −981.3364 | 116.3217 | −5.1824 |
| F8 | 0.1544 | 0.6904 | 0.0013 | 0.0024 | −1.5838 |
| F9 | 6439.18 | 23,019.40 | 5305.38 | 10,361.15 | −0.3208 |
| F10 | 3.1066 | 3.9244 | 10.0339 | 18.1246 | 2.6677 |
| F11 | 1.33 × 10−9 | 1.34 × 10−9 | 2.67 × 10−11 | 3.21 × 10−11 | −6.9436 |
| F12 | 0.0416 | 0.0249 | 0.0295 | 0.0284 | −2.2874 |
| F13 | 9.33 × 10−17 | 2.21 × 10−16 | 0.00 | 0.00 | −3.0149 |
Table 17.
Comparison of version 1 between conventional FWA GWO and the Fuzzy FWA-GWO in 60 dimensions.
Table 17.
Comparison of version 1 between conventional FWA GWO and the Fuzzy FWA-GWO in 60 dimensions.
| Function | Hybrid V1 | STD | Hybrid FV1 | STD | Z-Value |
|---|
| F1 | 6.78 × 10−18 | 1.14 × 10−17 | 7.92 × 10−20 | 3.29 × 10−19 | −4.1959 |
| F2 | 1.55 × 10−11 | 1.28 × 10−11 | 3.68 × 10−13 | 2.20 × 10−13 | −8.4412 |
| F3 | 2.3311 | 2.0824 | 4.0899 | 7.5120 | 1.6113 |
| F4 | 3.2579 | 1.1983 | 2.2917 | 1.4838 | −3.6177 |
| F5 | 57.9631 | 0.7311 | 58.0651 | 0.6640 | 0.7376 |
| F6 | 4.3132 | 0.7794 | 5.0155 | 0.9131 | 4.1778 |
| F7 | −1273.7126 | 157.2159 | −1382.53 | 293.7782 | −2.3323 |
| F8 | 975.1898 | 2020.46 | 5260.53 | 14,248.47 | 2.1266 |
| F9 | 123,474.29 | 105,804.6 | 137,306.33 | 147,064.20 | 0.5452 |
| F10 | 5.3125 | 6.2564 | 9.1421 | 8.5493 | 2.5815 |
| F11 | 13.3142 | 10.0509 | 9.5331 | 10.6785 | −1.8413 |
| F12 | 0.1571 | 0.1423 | 0.1323 | 0.0836 | −1.0752 |
| F13 | 1.04 × 10−16 | 3.11 × 10−16 | 0.00 | 0.00 | −2.3881 |
Table 18.
Comparison of version 2 between conventional FWA GWO and the Fuzzy FWA-GWO in 60 dimensions.
Table 18.
Comparison of version 2 between conventional FWA GWO and the Fuzzy FWA-GWO in 60 dimensions.
| Function | Hybrid V2 | STD | Hybrid FV2 | STD | Z-Value |
|---|
| F1 | 4.61 × 10−14 | 1.31 × 10−13 | 1.66 × 10−16 | 3.18 × 10−16 | −2.5041 |
| F2 | 2.37 × 10−9 | 1.37 × 10−9 | 1.36 × 10−10 | 8.73 × 10−11 | −11.6228 |
| F3 | 13.7898 | 15.3383 | 10.5559 | 12.5115 | −1.1668 |
| F4 | 1.1251 | 0.3469 | 0.6500 | 0.3190 | −7.1991 |
| F5 | 57.9556 | 0.6457 | 58.0125 | 0.6017 | 0.4605 |
| F6 | 3.8645 | 0.7918 | 4.1065 | 0.8431 | 1.4942 |
| F7 | −1572.6017 | 164.5944 | −1446.4868 | 181.8827 | 3.6716 |
| F8 | 1.9391 | 13.6862 | 0.0372 | 0.2033 | −0.9923 |
| F9 | 97,623.32 | 73,980.79 | 161,436.30 | 194,085.14 | 2.1940 |
| F10 | 6.8427 | 5.1627 | 16.0706 | 11.3228 | 5.2957 |
| F11 | 3.68 × 10−7 | 1.23 × 10−6 | 2.377 × 10−8 | 8.097 × 10−8 | −1.9943 |
| F12 | 0.5661 | 0.4146 | 0.3825 | 0.3618 | −2.3831 |
| F13 | 1.07 × 10−14 | 2.42 × 10−14 | 3.58 × 10−17 | 8.30 × 10−17 | −3.1470 |
Table 19.
Comparison of version 3 between conventional FWA GWO and the Fuzzy FWA-GWO in 60 dimensions.
Table 19.
Comparison of version 3 between conventional FWA GWO and the Fuzzy FWA-GWO in 60 dimensions.
| Function | Hybrid V3 | STD | Hybrid FV3 | STD | Z-Value |
|---|
| F1 | 8.17 × 10−11 | 1.91 × 10−10 | 2.44 × 10−13 | 4.59 × 10−13 | −3.0456 |
| F2 | 1.24 × 10−7 | 1.01 × 10−7 | 4.79 × 10−9 | 2.72 × 10−9 | −8.4257 |
| F3 | 3.9614 | 5.0226 | 2.9745 | 5.3663 | −0.9589 |
| F4 | 1.2317 | 0.6411 | 0.6592 | 0.4376 | −5.2667 |
| F5 | 58.5643 | 0.5194 | 57.9718 | 0.7475 | −4.6488 |
| F6 | 4.6116 | 1.0565 | 3.6102 | 1.0798 | −4.7338 |
| F7 | −2020.5185 | 251.665 | −2036.4981 | 121.8630 | −0.4081 |
| F8 | 81.8637 | 197.114 | 7.2381 | 12.4364 | −2.6983 |
| F9 | 231,548.53 | 432,289.99 | 197,193.30 | 269,419.40 | −0.4817 |
| F10 | 21.6702 | 30.8963 | 30.6226 | 38.9509 | 1.2859 |
| F11 | 5.10 × 10−6 | 9.24 × 10−6 | 2.26 × 10−7 | 1.87 × 10−7 | −3.7664 |
| F12 | 0.0723 | 0.0566 | 0.0839 | 0.0610 | 0.9979 |
| F13 | 3.14 × 10−11 | 1.31 × 10−10 | 5.81 × 10−7 | 3.23 × 10−6 | 1.2826 |
Table 20.
Comparison of version 1 between conventional FWA GWO and the Fuzzy FWA-GWO in 90 dimensions.
Table 20.
Comparison of version 1 between conventional FWA GWO and the Fuzzy FWA-GWO in 90 dimensions.
| Function | Hybrid V1 | STD | Hybrid FV1 | STD | Z-Value |
|---|
| F1 | 3.59 × 10−13 | 1.05 × 10−12 | 1.31 × 10−15 | 2.63 × 10−15 | −2.4328 |
| F2 | 1.71 × 10−9 | 9.38 × 10−10 | 1.19 × 10−10 | 9.03 × 10−11 | −12.0566 |
| F3 | 170.1456 | 208.229 | 190.2772 | 522.9864 | 0.2554 |
| F4 | 9.7444 | 3.1814 | 9.6617 | 3.8646 | −0.1179 |
| F5 | 88.8722 | 0.4571 | 88.6116 | 0.3810 | −3.1269 |
| F6 | 8.869 | 1.4223 | 9.0872 | 1.9827 | 0.6386 |
| F7 | −2958.527 | 123.562 | −2594.0221 | 281.0649 | 8.4784 |
| F8 | 32,391.5762 | 49,298.17 | 82,287.85 | 162,803.28 | 2.0948 |
| F9 | 427,794.09 | 576,474.77 | 340,907.53 | 484,611.35 | −0.8239 |
| F10 | 19.1615 | 20.626 | 23.8487 | 21.2635 | 1.1300 |
| F11 | 14.8326 | 9.8082 | 17.2033 | 8.2971 | 1.3178 |
| F12 | 0.4483 | 0.5499 | 0.0737 | 0.0549 | −4.8404 |
| F13 | 6.11 × 10−12 | 3.76 × 10−11 | 1.34 × 10−14 | 5.34 × 10−14 | −1.1579 |
Table 21.
Comparison of version 2 between conventional FWA GWO and the Fuzzy FWA-GWO in 90 dimensions.
Table 21.
Comparison of version 2 between conventional FWA GWO and the Fuzzy FWA-GWO in 90 dimensions.
| Function | Hybrid V2 | STD | Hybrid FV2 | STD | Z-Value |
|---|
| F1 | 3.18 × 10−10 | 7.68 × 10−10 | 3.63 × 10−12 | 4.35 × 10−12 | −2.9194 |
| F2 | 1.45 × 10−7 | 1.02 × 10−7 | 1.35 × 10−8 | 6.96 × 10−9 | −9.1854 |
| F3 | 218.3702 | 141.9908 | 168.5144 | 152.0538 | −1.7114 |
| F4 | 3.2032 | 0.9551 | 2.5327 | 0.7804 | −3.8825 |
| F5 | 89.5622 | 5.1037 | 88.4004 | 0.3822 | −1.6212 |
| F6 | 9.038 | 1.2308 | 9.5703 | 1.2616 | 2.1568 |
| F7 | −2382.765 | 133.511 | −2293.44 | 162.75 | 3.0304 |
| F8 | 1.334 | 5.1118 | 0.0456 | 0.1678 | −1.7990 |
| F9 | 353,505.71 | 442,838.28 | 337,757.79 | 295,953.954 | −0.2111 |
| F10 | 28.204 | 20.3175 | 51.6813 | 41.4278 | 3.6336 |
| F11 | 2.01 × 10−4 | 4.50 × 10−4 | 6.44 × 10−6 | 1.11 × 10−5 | −3.0867 |
| F12 | 1.3641 | 0.5779 | 0.7542 | 0.3633 | −6.3806 |
| F13 | 1.21 × 10−9 | 4.38 × 10−9 | 2.73 × 10−12 | 1.01 × 10−11 | −1.9684 |
Table 22.
Comparison of version 3 between conventional FWA GWO and the Fuzzy FWA-GWO in 90 dimensions.
Table 22.
Comparison of version 3 between conventional FWA GWO and the Fuzzy FWA-GWO in 90 dimensions.
| Function | Hybrid V3 | STD | Hybrid FV3 | STD | Z-Value |
|---|
| F1 | 6.02 × 10−7 | 9.58 × 10−7 | 3.22 × 10−9 | 5.05 × 10−9 | −4.4636 |
| F2 | 4.35 × 10−6 | 2.27 × 10−6 | 2.86 × 10−7 | 1.92 × 10−7 | −12.7412 |
| F3 | 68.9997 | 71.6442 | 64.5839 | 82.3960 | −0.2888 |
| F4 | 3.6878 | 1.6607 | 3.1730 | 1.5990 | −1.5949 |
| F5 | 90.1465 | 1.4684 | 88.5058 | 0.5688 | −7.4406 |
| F6 | 7.5438 | 2.503 | 6.5657 | 2.0512 | −2.1584 |
| F7 | −2485.267 | 427.572 | −2287.9810 | 169.6956 | 3.0627 |
| F8 | 397.2208 | 835.3509 | 115.9959 | 179.6233 | −2.3505 |
| F9 | 541,955.02 | 846,552.82 | 827,106.07 | 823,110.85 | 1.7247 |
| F10 | 64.8371 | 63.4859 | 68.3618 | 62.0739 | 0.2835 |
| F11 | 3.00 × 10−4 | 4.00 × 10−4 | 4.28 × 10−5 | 1.06 × 10−4 | −4.4369 |
| F12 | 0.2455 | 0.7294 | 0.4034 | 0.5814 | 1.2092 |
| F13 | 8.60 × 10−7 | 4.95 × 10−6 | 3.38 × 10−9 | 1.34 × 10−8 | −1.2358 |
Table 23.
Comparison of version 1 between conventional FWA-GWO and Fuzzy FWAGWO with fixed dimensions multimodal functions.
Table 23.
Comparison of version 1 between conventional FWA-GWO and Fuzzy FWAGWO with fixed dimensions multimodal functions.
| Function | Hybrid V1 | STD | Hybrid FV1 | STD |
|---|
| F14 | 2.7499 | 2.8626 | 3.5215 | 3.3115 |
| F15 | 7.42 × 10−4 | 2.70 × 10−4 | 8.06 × 10−4 | 4.55 × 10−4 |
| F16 | −1.0315 | 5.60 × 10−4 | −1.0316 | 1.17 × 10−6 |
| F17 | 3.0007 | 8.20 × 10−4 | 3.0007 | 7.60 × 10−4 |
| F18 | −3.8612 | 0.0024 | −3.8611 | 0.0024 |
| F19 | −3.3124 | 0.0449 | −3.3151 | 0.0213 |
| F20 | −5.3093 | 0.6601 | −5.0480 | 0.0041 |
| F21 | −5.2378 | 0.5854 | −5.2016 | 0.6736 |
| F22 | −5.3646 | 0.4713 | −5.2136 | 0.4032 |
Table 24.
Comparison of version 2 between conventional FWA-GWO and Fuzzy FWAGWO with fixed dimensions multimodal functions.
Table 24.
Comparison of version 2 between conventional FWA-GWO and Fuzzy FWAGWO with fixed dimensions multimodal functions.
| Function | Hybrid V2 | STD | Hybrid FV2 | STD |
|---|
| F14 | 4.1664 | 3.7214 | 4.3546 | 4.1228 |
| F15 | 7.00 × 10−4 | 3.18 × 10−4 | 8.43 × 10−4 | 4.08 × 10−4 |
| F16 | −1.0316 | 2.61 × 10−5 | −1.0316 | 1.98 × 10−4 |
| F17 | 3.0009 | 9.83 × 10−4 | 3.0006 | 6.26 × 10−4 |
| F18 | −3.8612 | 0.0022 | −3.8612 | 0.0024 |
| F19 | −3.3093 | 0.0484 | −3.3045 | 0.0566 |
| F20 | −5.5335 | 0.9876 | −5.0547 | 0.0414 |
| F21 | −5.3205 | 0.6697 | −5.1542 | 0.2801 |
| F22 | −5.5058 | 0.7676 | −5.1389 | 0.1022 |
Table 25.
Comparison of version 3 between conventional FWA-GWO and Fuzzy FWAGWO with fixed dimensions multimodal functions.
Table 25.
Comparison of version 3 between conventional FWA-GWO and Fuzzy FWAGWO with fixed dimensions multimodal functions.
| Function | Hybrid V3 | STD | Hybrid FV3 | STD |
|---|
| F14 | 4.1664 | 3.7214 | 4.3546 | 4.1228 |
| F15 | 7.00 × 10−4 | 3.18 × 10−4 | 8.43 × 10−4 | 4.08 × 10−4 |
| F16 | −1.0316 | 2.61 × 10−5 | −1.0316 | 1.98 × 10−4 |
| F17 | 3.0009 | 9.83 × 10−4 | 3.0006 | 6.26 × 10−4 |
| F18 | −3.8612 | 0.0022 | −3.8612 | 0.0024 |
| F19 | −3.3093 | 0.0484 | −3.3045 | 0.0566 |
| F20 | −5.5335 | 0.9876 | −5.0547 | 0.0414 |
| F21 | −5.3205 | 0.6697 | −5.1542 | 0.2801 |
| F22 | −5.5058 | 0.7676 | −5.1389 | 0.1022 |
Table 26.
Comparison of version 1 between conventional FWGWO and Fuzzy FWAGWO Version 1 with 60 dimensions in benchmark functions.
Table 26.
Comparison of version 1 between conventional FWGWO and Fuzzy FWAGWO Version 1 with 60 dimensions in benchmark functions.
| Function | FWGWO | STD | Hybrid FV1 | STD |
|---|
| F1 | 5.16 × 10−18 | 1.93 × 10−16 | 7.92 × 10−20 | 3.29 × 10−19 |
| F2 | 1.7400 | 60.1000 | 4.0899 | 7.5120 |
| F3 | 1.02 × 10−3 | 3.06 × 10−3 | 2.2917 | 1.4838 |
| F4 | 90.00 | 17.40 | 58.0651 | 0.6640 |
| F5 | 3.02 × 10−2 | 2.42 × 10−2 | 5.0155 | 0.9131 |
| F9 | 4.43 × 10−2 | 8.31 × 10−2 | 9.1421 | 8.5493 |
| F10 | 4.21 × 10−10 | 5.61 × 10−10 | 9.5331 | 10.6785 |
| F11 | 1.11 × 10−17 | 1.20 × 10−16 | 0.00 | 0.00 |
| F12 | 2.13 × 10−3 | 6.89 × 10−3 | 0.1323 | 0.0836 |
Table 27.
Comparison of version 2 between conventional FWGWO and Fuzzy FWAGWO Version 2 with 60 dimensions in benchmark functions.
Table 27.
Comparison of version 2 between conventional FWGWO and Fuzzy FWAGWO Version 2 with 60 dimensions in benchmark functions.
| Function | FWGWO | STD | Hybrid FV2 | STD |
|---|
| F1 | 5.16 × 10−18 | 1.93 × 10−16 | 1.66 × 10−16 | 3.18 × 10−16 |
| F2 | 1.7400 | 60.1000 | 10.5559 | 12.5115 |
| F3 | 1.02 × 10−3 | 3.06 × 10−3 | 0.6500 | 0.3190 |
| F4 | 90.000 | 17.400 | 58.0125 | 0.6017 |
| F5 | 0.0302 | 0.0242 | 4.1065 | 0.8431 |
| F9 | 0.0443 | 0.0831 | 16.0706 | 11.3228 |
| F10 | 4.21 × 10−10 | 5.61 × 10−10 | 2.38 × 10−8 | 8.10 × 10−8 |
| F11 | 1.11 × 10−17 | 1.20 × 10−16 | 3.58 × 10−17 | 8.30 × 10−17 |
| F12 | 2.13 × 10−3 | 6.89 × 10−3 | 0.3825 | 0.3618 |
Table 28.
Comparison of version 3 between conventional FWGWO and Fuzzy FWAGWO Version 2 with 60 dimensions in benchmark functions.
Table 28.
Comparison of version 3 between conventional FWGWO and Fuzzy FWAGWO Version 2 with 60 dimensions in benchmark functions.
| Function | FWGWO | STD | Hybrid FV3 | STD |
|---|
| F1 | 5.16 × 10−18 | 1.93 × 10−16 | 2.44 × 10−13 | 4.59 × 10−13 |
| F2 | 1.7400 | 60.1000 | 2.9745 | 5.3663 |
| F3 | 1.02 × 10−3 | 3.06 × 10−3 | 0.6592 | 0.4376 |
| F4 | 9.00 × 101 | 1.74 × 101 | 57.9718 | 0.7475 |
| F5 | 3.02 × 10−2 | 2.42 × 10−2 | 3.6102 | 1.0798 |
| F9 | 4.43 × 10−2 | 8.31 × 10−2 | 30.6226 | 38.9509 |
| F10 | 4.21 × 10−10 | 5.61 × 10−10 | 2.26 × 10−7 | 1.87 × 10−7 |
| F11 | 1.11 × 10−17 | 1.20 × 10−16 | 5.81 × 10−7 | 3.23 × 10−6 |
| F12 | 2.13 × 10−3 | 6.89 × 10−3 | 0.0839 | 0.0610 |