Multi-Strategy-Improved Growth Optimizer and Its Applications
Abstract
1. Introduction
- Using the Circle-OBL initialization strategy for initializing better-distributed populations makes the performance of the algorithm improve.
- The exploration strategy improves the global exploration performance of the algorithm by learning self-knowledge over a radius R and improving population diversity by learning the differences between individuals.
- The exploitation strategy leads to an improvement in the convergence speed and convergence accuracy of the algorithm through the bootstrapping of the optimal individuals.
- CODGBGO is proposed by combining the above strategies, and it is confirmed to be a promising optimization method by numerical optimization, feature selection, and engineering optimization.
2. The Theory of Growth Optimizer
2.1. Learning Stage
2.2. Reflection Stage
2.3. Implementation of GO for Optimization
| Algorithm 1: The pseudocode of the GO algorithm |
 |
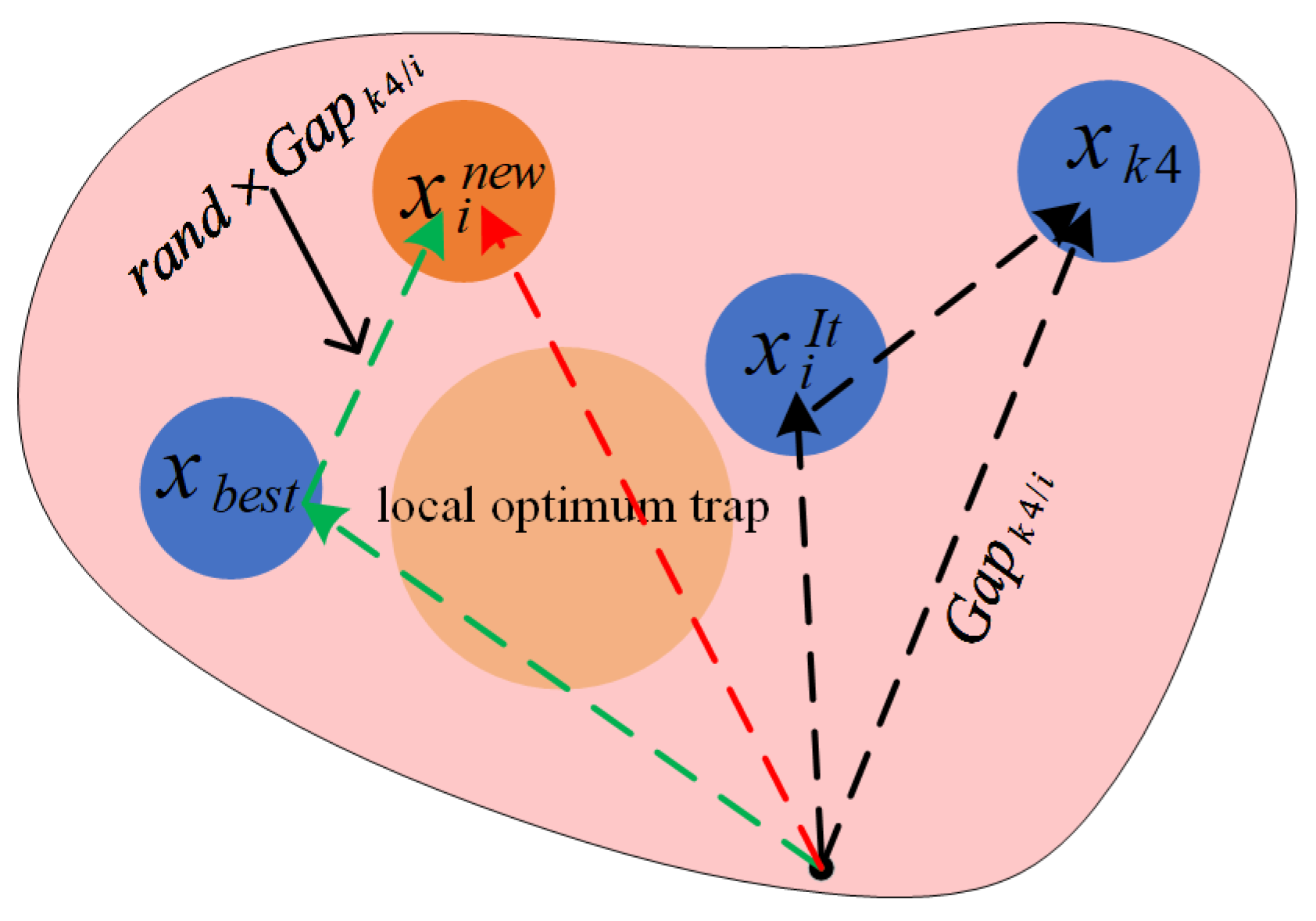
3. A Multi-Strategy Enhanced Growth Optimizer
3.1. Circle-OBL Initialization Strategy
3.2. Exploration Strategy
3.3. Exploitation Strategy
3.4. Implementation of CODGBGO for Optimization
| Algorithm 2: The pseudocode of the CODGBGO algorithm |
 |
3.5. Compytional Complexity
4. Experimental Results
4.1. Comparison Algorithm and CEC Benchmark Problems
4.2. Effectiveness of Strategies and Parameter Settings
4.2.1. Effectiveness of Strategies
4.2.2. Parameter {α,β} Settings
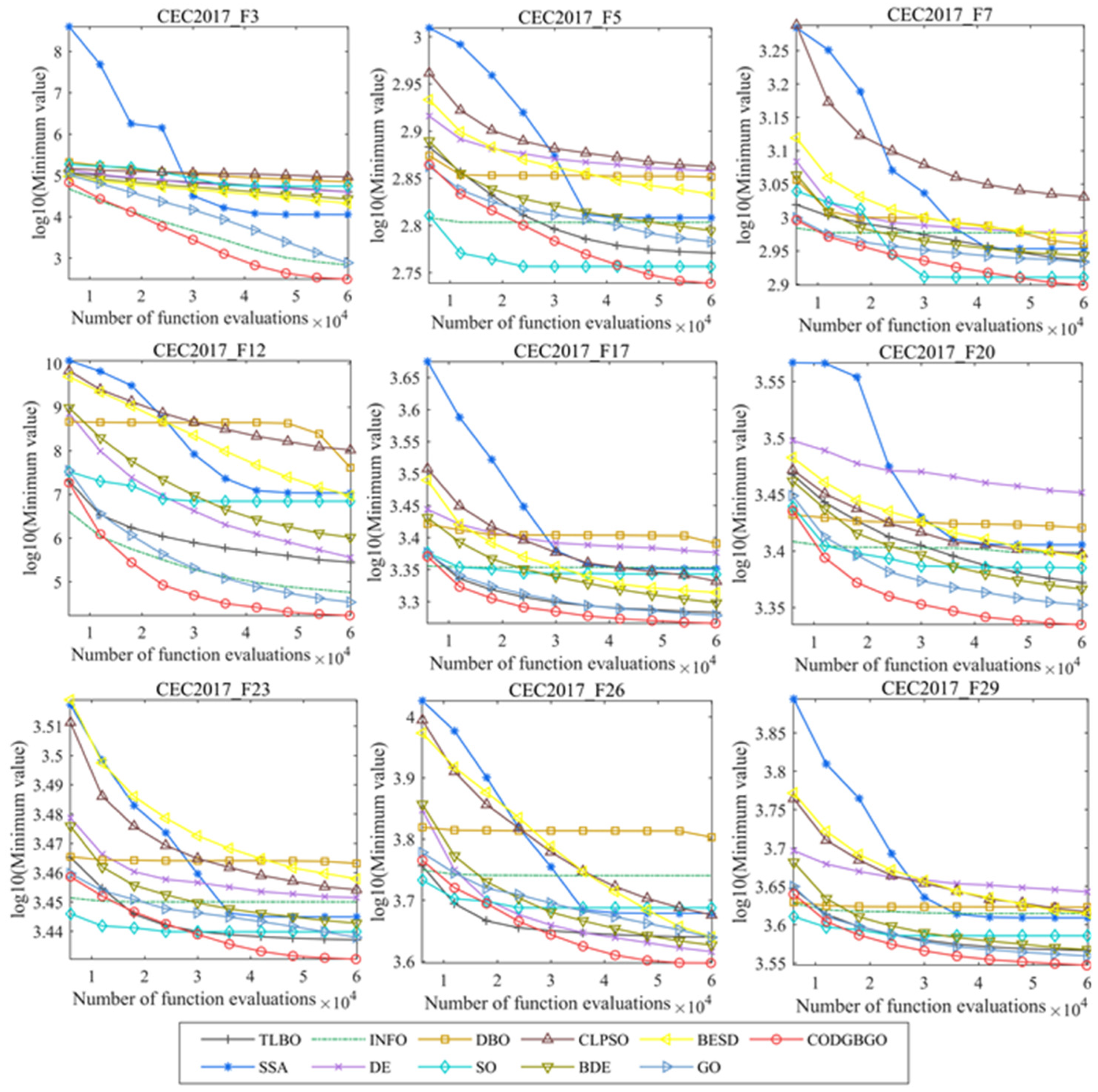
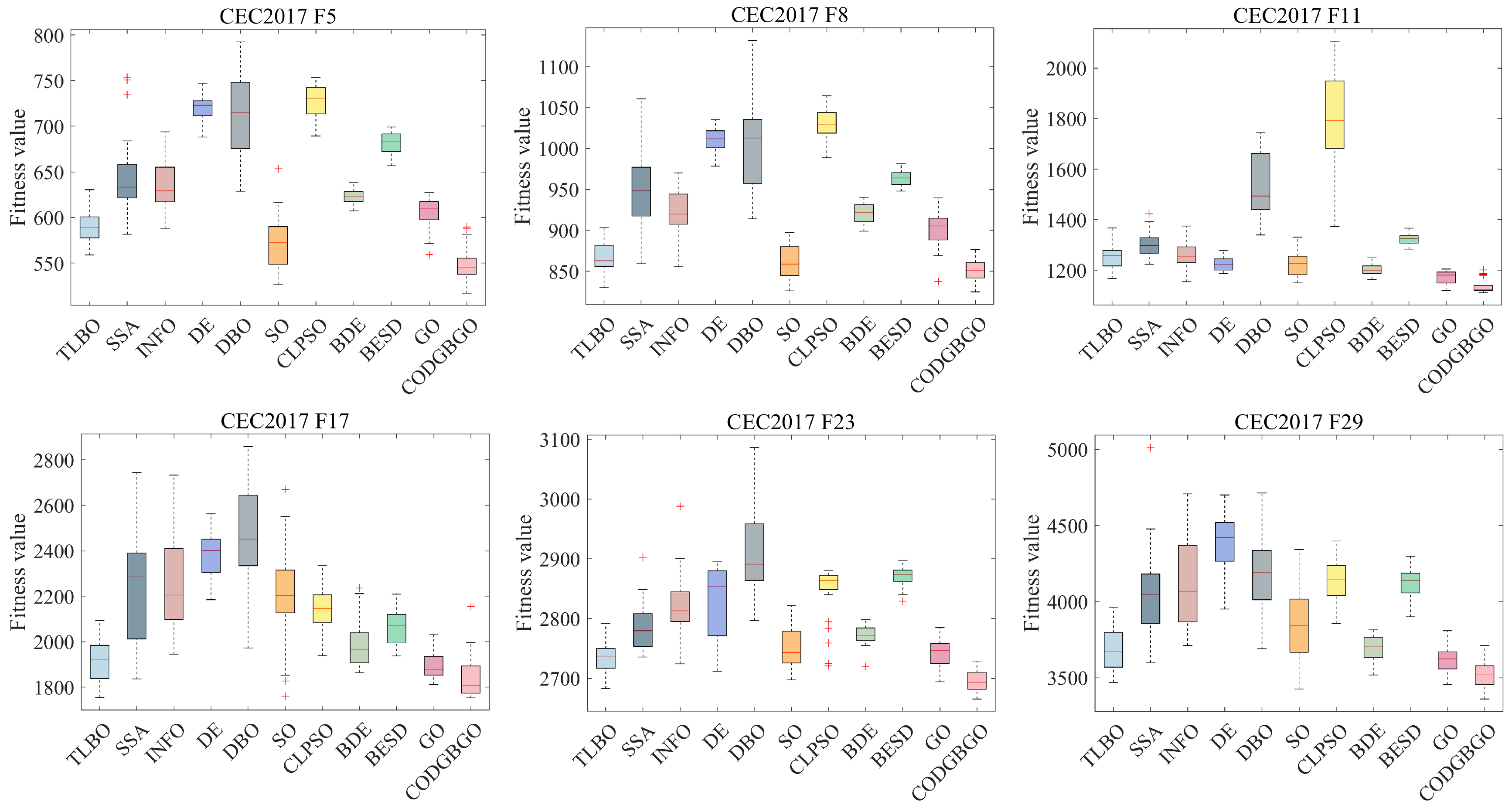
4.3. Experimental Results
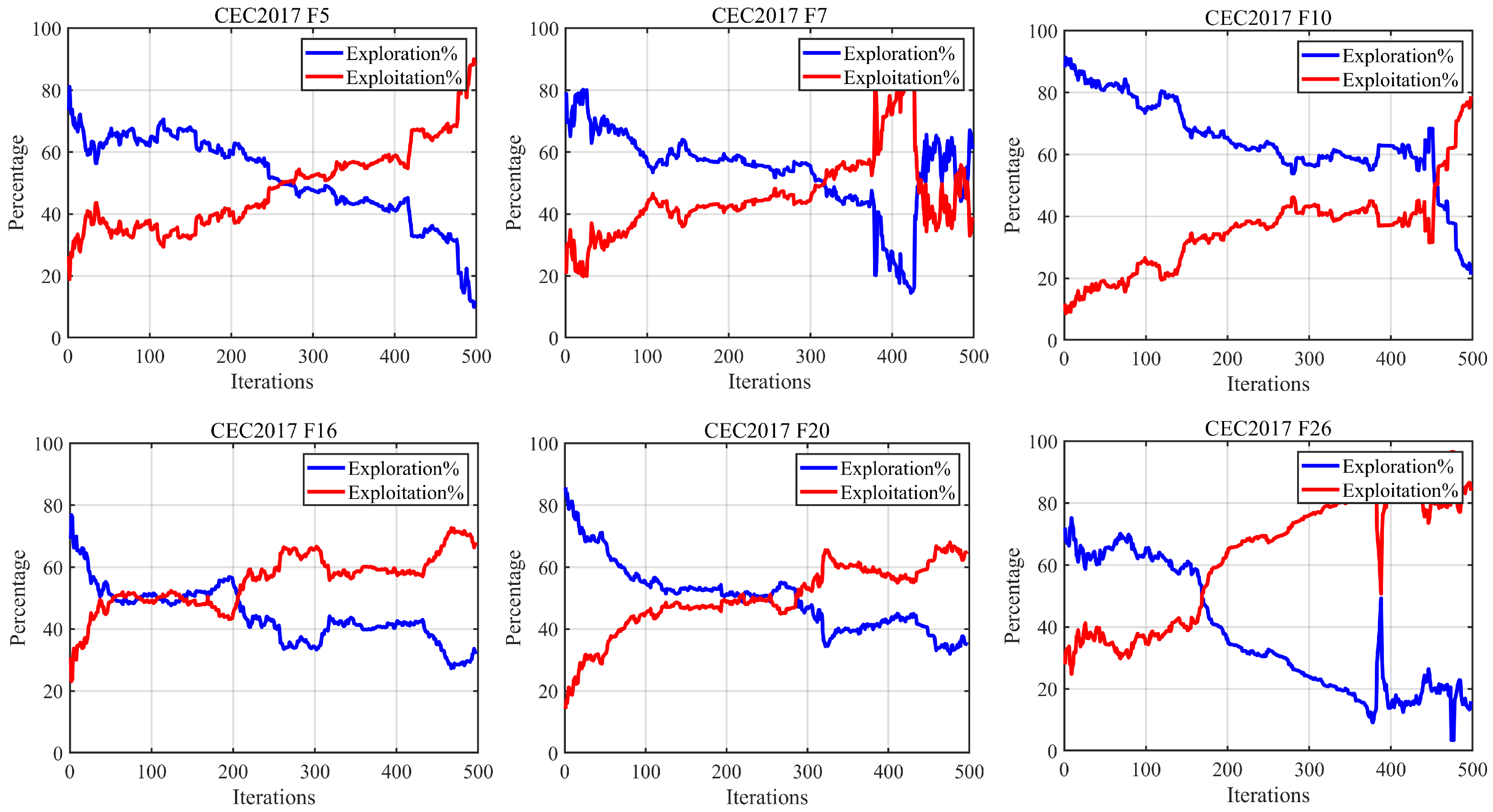
4.3.1. Population Diversity Analysis
4.3.2. Exploration and Exploitation Analysis
4.3.3. Numerical Analysis
4.3.4. Convergence and Stability Analysis
4.3.5. Nonparametric Analysis
4.3.6. Expanded Analysis
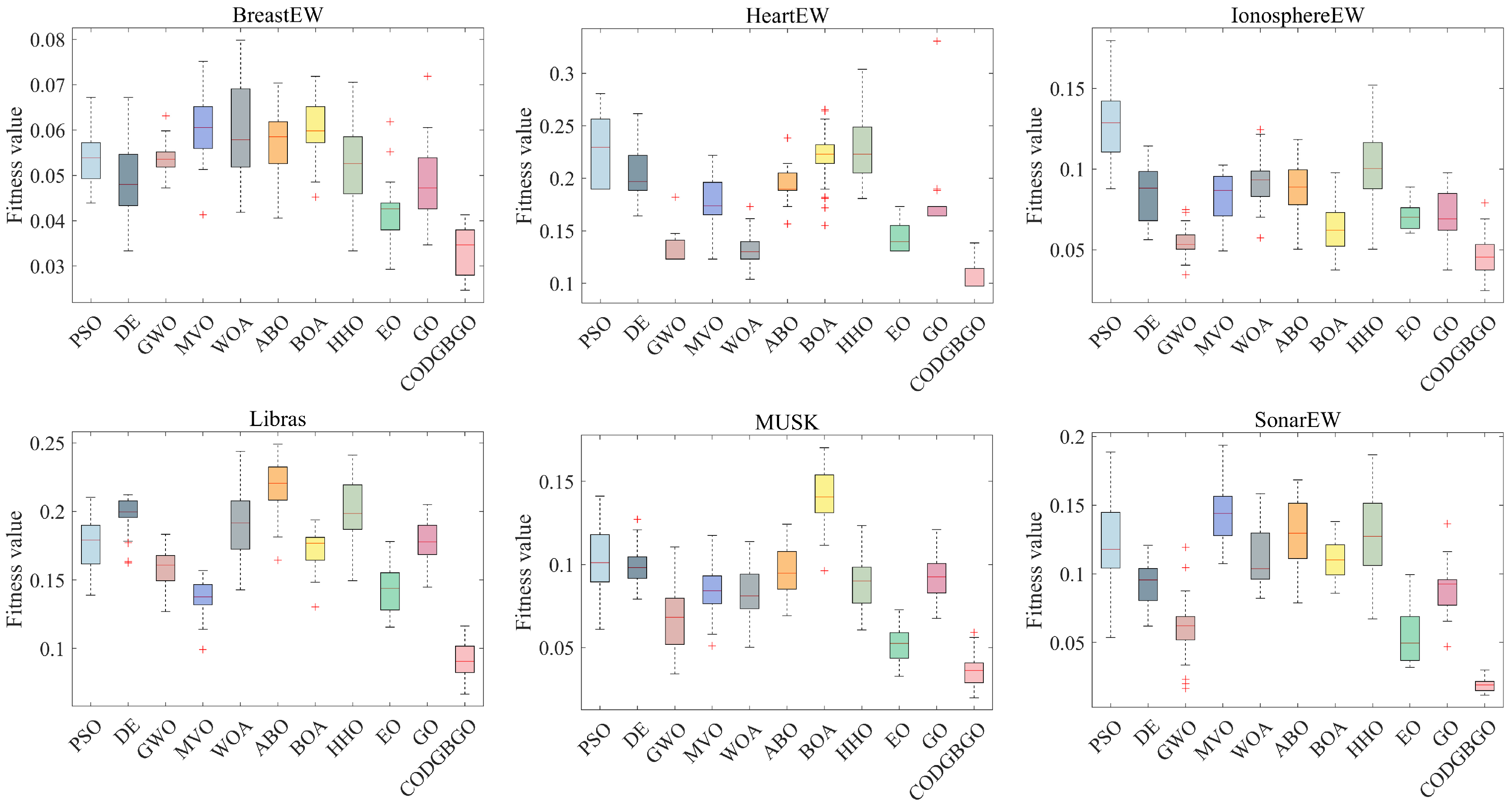
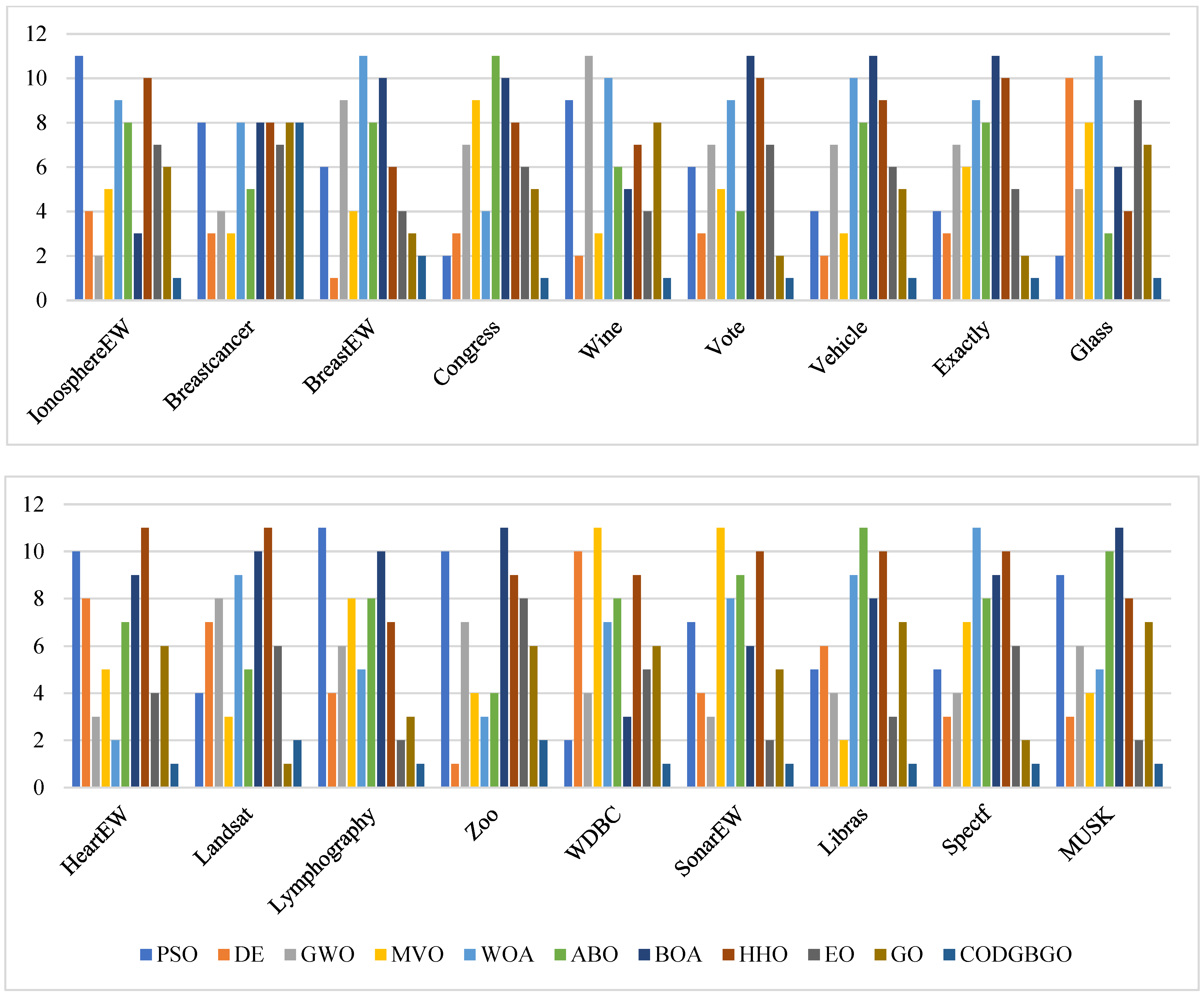
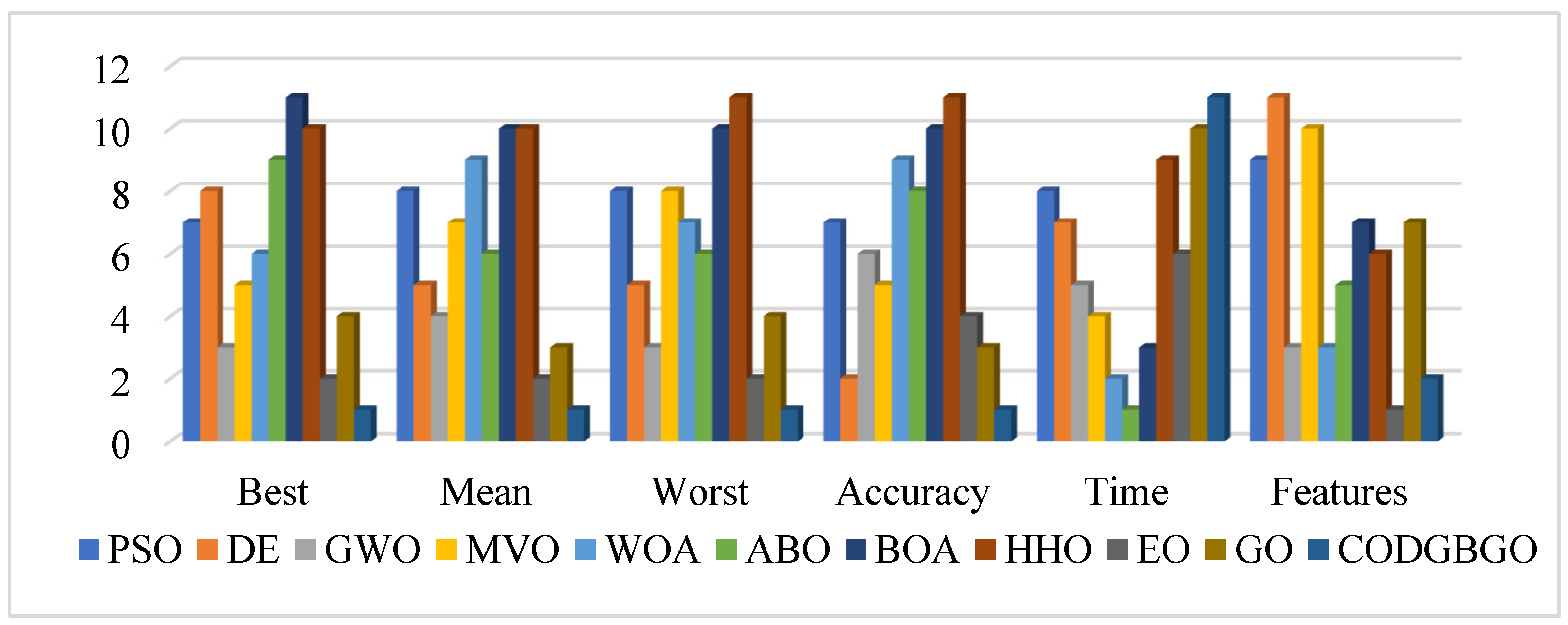
4.4. Results for Feature Selection Problems
4.4.1. Establishment of an Optimization Model
4.4.2. Experimental Analyses
4.5. Results for Constrained Engineering Application Problems
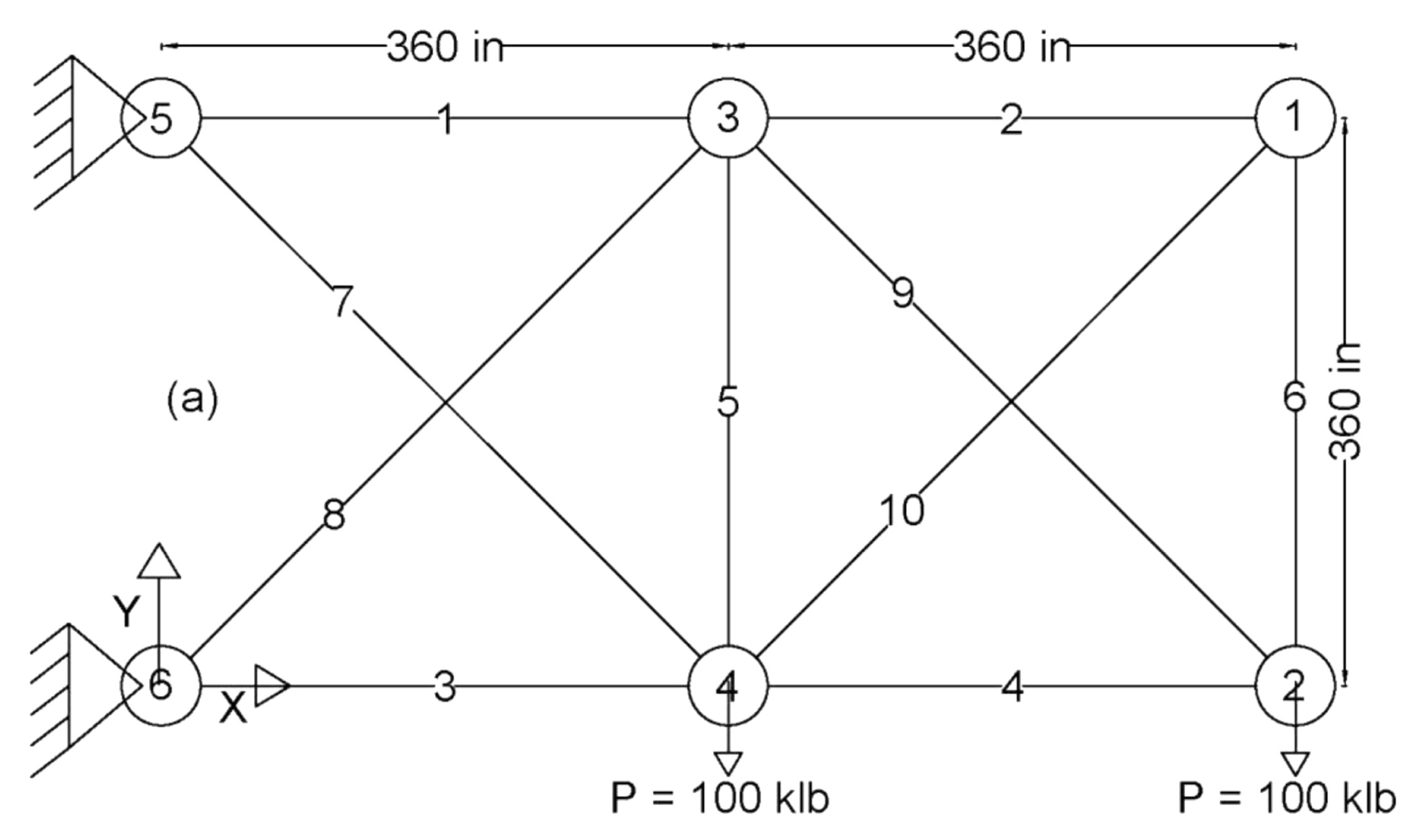
4.5.1. Results on 10-Bar Truss Design [61]
4.5.2. Results on Tension/Compression Spring Design [62]
4.5.3. Results on Weight Minimization of a Speed Reducer [63]
4.5.4. Results on Welded Beam Design [64]
5. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hussien, A.G.; Oliva, D.; Houssein, E.H.; Juan, A.A.; Yu, X. Binary Whale Optimization Algorithm for Dimensionality Reduction. Mathematics 2020, 8, 1821. [Google Scholar] [CrossRef]
- Hao, Y.; Helo, P.; Shamsuzzoha, A. Virtual Factory System Design and Implementation: Integrated Sustainable Manufacturing. Int. J. Syst. Sci. Oper. Logist. 2018, 5, 116–132. [Google Scholar] [CrossRef]
- Simpson, A.R.; Dandy, G.C.; Murphy, L.J. Genetic algorithms compared to other techniques for pipe optimization. J. Water Resour. Plan. Manag. 1994, 120, 423–443. [Google Scholar] [CrossRef]
- Gharaei, A.; Hoseini Shekarabi, S.A.; Karimi, M. Modelling And Optimal Lot-Sizing of the Replenishments in Constrained, Multi-Product and Bi-Objective EPQ Models with Defective Products: Generalised Cross Decomposition. Int. J. Syst. Sci. Oper. Logist. 2020, 7, 262–274. [Google Scholar] [CrossRef]
- Hussien, A.G.; Hassanien, A.E.; Houssein, E.H.; Amin, M.; Azar, A.T. New Binary Whale Optimization Algorithm for Discrete Optimization Problems. Eng. Optim. 2020, 52, 945–959. [Google Scholar] [CrossRef]
- Sayyadi, R.; Awasthi, A. An Integrated Approach Based on System Dynamics and ANP for Evaluating Sustainable Transportation Policies. Int. J. Syst. Sci. Oper. Logist. 2020, 7, 182–191. [Google Scholar] [CrossRef]
- Schwefel, H.-P.; Beyer, H.-G. Evolution Strategies-A Comprehensive Introduction Evolution Strategies A Comprehensive Introduction. ACM Comput. Classif. 2002, 1, 3–52. [Google Scholar]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Fleming, P.J.; Fonseca, C.M. Genetic algorithms in control systems engineering. IFAC Proc. Vol. 1993, 26, 605–612. [Google Scholar] [CrossRef]
- Azizi, M.; Talatahari, S.; Gandomi, A.H. Fire Hawk Optimizer: A Novel Metaheuristic Algorithm. Artif. Intell. Rev. 2023, 56, 287–363. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mohammed, H.; Rashid, T. FOX: A FOX-Inspired Optimization Algorithm. Appl. Intell. 2023, 53, 1030–1050. [Google Scholar] [CrossRef]
- Chopra, N.; Mohsin Ansari, M. Golden Jackal Optimization: A Novel Nature-Inspired Optimizer for Engineering Applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Erol, O.K.; Eksin, I. A New Optimization Method: Big Bang-Big Crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Kushwaha, N.; Pant, M.; Kant, S.; Jain, V.K. Magnetic Optimization Algorithm for Data Clustering. Pattern Recognit. Lett. 2018, 115, 59–65. [Google Scholar] [CrossRef]
- Kaveh, A.; Bakhshpoori, T. Water Evaporation Optimization: A Novel Physically Inspired Optimization Algorithm. Comput. Struct. 2016, 167, 69–85. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Atom Search Optimization and Its Application to Solve a Hydrogeologic Parameter Estimation Problem. Knowl. Based Syst. 2019, 163, 283–304. [Google Scholar] [CrossRef]
- Shabani, A.; Asgarian, B.; Salido, M.; Asil Gharebaghi, S. Search and Rescue Optimization Algorithm: A New Optimization Method for Solving Constrained Engineering Optimization Problems. Expert Syst. Appl. 2020, 161, 113698. [Google Scholar] [CrossRef]
- Mousavirad, S.J.; Ebrahimpour-Komleh, H. Human Mental Search: A New Population-Based Metaheuristic Optimization Algorithm. Appl. Intell. 2017, 47, 850–887. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Elsayed, A.M.; El-Sehiemy, R.A.; Abdelaziz, A.Y. Equilibrium Optimization Algorithm for Network Reconfiguration and Distributed Generation Allocation in Power Systems. Appl. Soft Comput. 2021, 98, 106867. [Google Scholar] [CrossRef]
- Turkoglu, B.; Uymaz, S.A.; Kaya, E. Binary Artificial Algae Algorithm for Feature Selection [Formula Presented]. Appl. Soft Comput. 2022, 120, 108630. [Google Scholar] [CrossRef]
- Hu, G.; Du, B.; Wang, X.; Wei, G. An Enhanced Black Widow Optimization Algorithm for Feature Selection. Knowl. Based Syst. 2022, 235, 107638. [Google Scholar] [CrossRef]
- Xu, M.; Song, Q.; Xi, M.; Zhou, Z. Binary Arithmetic Optimization Algorithm for Feature Selection. Soft Comput. 2023, 27, 11395–11429. [Google Scholar] [CrossRef]
- Hu, G.; Zhong, J.; Du, B.; Wei, G. An Enhanced Hybrid Arithmetic Optimization Algorithm for Engineering Applications. Comput. Methods Appl. Mech. Eng. 2022, 394, 114901. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, H.; Zhan, Z.H.; Li, J.; Zhang, H. Growth Optimizer: A Powerful Metaheuristic Algorithm for Solving Con-tinuous and Discrete Global Optimization Problems. Knowl. Based Syst. 2023, 261, 110206. [Google Scholar] [CrossRef]
- Aribia, H.B.; El-Rifaie, A.M.; Tolba, M.A.; Shaheen, A.; Moustafa, G.; Elsayed, F.; Elshahed, M. Growth Optimizer for Parameter Identification of Solar Photovoltaic Cells and Modules. Sustainability 2023, 15, 7896. [Google Scholar] [CrossRef]
- Hakmi, S.H.; Alnami, H.; Moustafa, G.; Ginidi, A.R.; Shaheen, A.M. Modified Rime-Ice Growth Optimizer with Polynomial Differential Learning Operator for Single- and Double-Diode PV Parameter Estimation Problem. Electronics 2024, 13, 1611. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Q.; Bu, X.; Zhang, H. Quadruple Parameter Adaptation Growth Optimizer with Integrated Distribution, Confrontation, and Balance Features for Optimization. Expert Syst. Appl. 2024, 235, 121218. [Google Scholar] [CrossRef]
- Fatani, A.; Dahou, A.; Abd Elaziz, M.; Al-qaness, M.A.A.; Lu, S.; Alfadhli, S.A.; Alresheedi, S.S. Enhancing Intrusion Detection Systems for IoT and Cloud Environments Using a Growth Optimizer Algorithm and Conventional Neural Networks. Sensors 2023, 23, 4430. [Google Scholar] [CrossRef]
- Altay, O. Chaotic Slime Mould Optimization Algorithm for Global Optimization. Artif. Intell. Rev. 2022, 55, 3979–4040. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Elhosseini, M.A. Large Scale Salp-Based Grey Wolf Optimization for Feature Selection and Global Optimization. Neural Comput. Appl. 2022, 34, 8989–9014. [Google Scholar] [CrossRef]
- Ahmad, M.F.; Isa, N.A.M.; Lim, W.H.; Ang, K.M. Differential Evolution with Modified Initialization Scheme Using Chaotic Oppositional Based Learning Strategy. Alex. Eng. J. 2022, 61, 11835–11858. [Google Scholar] [CrossRef]
- Li, X.D.; Wang, J.S.; Hao, W.K.; Zhang, M.; Wang, M. Chaotic Arithmetic Optimization Algorithm. Appl. Intell. 2022, 52, 16718–16757. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, T.; Ye, X.; Heidari, A.A.; Liang, G.; Chen, H.; Pan, Z. Differential Evolution-Assisted Salp Swarm Algorithm with Chaotic Structure for Real-World Problems. Eng. Comput. 2023, 39, 1735–1769. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubalovsky, S.; Trojovsky, P. Northern Goshawk Optimization: A New Swarm-Based Algorithm for Solving Optimization Problems. IEEE Access. 2021, 9, 162059–162080. [Google Scholar] [CrossRef]
- Yang, Q.; Yan, J.Q.; Gao, X.D.; Xu, D.D.; Lu, Z.Y.; Zhang, J. Random Neighbor Elite Guided Differential Evolution for Global Numerical Optimization. Inf. Sci. 2022, 607, 1408–1438. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive Learning Particle Swarm Optimizer for Global Optimization of Multimodal Functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Civicioglu, P.; Besdok, E. Bezier Search Differential Evolution Algorithm for Numerical Function Optimization: A Comparative Study with CRMLSP, MVO, WA, SHADE and LSHADE. Expert Syst. Appl. 2021, 165, 113875. [Google Scholar] [CrossRef]
- Civicioglu, P.; Besdok, E. Bernstein-Levy Differential Evolution Algorithm for Numerical Function Optimization. Neural Comput. Appl. 2023, 35, 6603–6621. [Google Scholar] [CrossRef]
- Malik, N.A.; Chang, C.L.; Chaudhary, N.I.; Raja, M.A.Z.; Cheema, K.M.; Shu, C.M.; Alshamrani, S.S. Knacks of Fractional Order Swarming Intelligence for Parameter Estimation of Harmonics in Electrical Systems. Mathematics 2022, 10, 1570. [Google Scholar] [CrossRef]
- Mehmood, K.; Chaudhary, N.I.; Khan, Z.A.; Cheema, K.M.; Raja, M.A.Z. Variants of Chaotic Grey Wolf Heuristic for Robust Identification of Control Autoregressive Model. Biomimetics 2023, 8, 141. [Google Scholar] [CrossRef] [PubMed]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-Learning-Based Optimization: A Novel Method for Constrained Mechanical Design Optimization Problems. CAD Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-Verse Optimizer: A Nature-Inspired Algorithm for Global Optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A Bio-Inspired Optimizer for Engineering Design Problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Qi, X.; Zhu, Y.; Zhang, H. A New Meta-Heuristic Butterfly-Inspired Algorithm. J. Comput. Sci. 2017, 23, 226–239. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly Optimization Algorithm: A Novel Approach for Global Optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung Beetle Optimizer: A New Meta-Heuristic Algorithm for Global Optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Noshadian, S.; Chen, H.; Gandomi, A.H. INFO: An Efficient Optimization Algorithm Based on Weighted Mean of Vectors. Expert Syst. Appl. 2022, 195, 116516. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A Novel Meta-Heuristic Optimization Algorithm. Knowl. Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- IEEE Computational Intelligence Society; Institute of Electrical and Electronics Engineers. Behavioral Study of the Surrogate Model-aware Evolutionary Search Framework. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation, Beijing, China, 6–11 July 2014; ISBN 9781479914883. [Google Scholar]
- Institute of Electrical and Electronics Engineers; IEEE Computational Intelligence Society. Hybrid Single and Multiobjective Optimization for Engineering Design without Exact Specifications. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC): 2020 Conference Proceedings, Glasgow, UK, 19–24 July 2020; ISBN 9781728169293. [Google Scholar]
- Li, Y.; Han, T.; Zhou, H.; Tang, S.; Zhao, H. A Novel Adaptive L-SHADE Algorithm and Its Application in UAV Swarm Resource Configuration Problem. Inf. Sci. 2022, 606, 350–367. [Google Scholar] [CrossRef]
- Azizi, M.; Aickelin, U.; Khorshidi, H.A.; Shishehgarkhaneh, M.B. Shape and Size Optimization of Truss Structures by Chaos Game Optimization Considering Frequency Constraints. J. Adv. Res. 2022, 41, 89–100. [Google Scholar] [CrossRef] [PubMed]
- Tzanetos, A.; Blondin, M. A Qualitative Systematic Review of Metaheuristics Applied to Tension/Compression Spring Design Problem: Current Situation, Recommendations, and Research Direction. Eng. Appl. Artif. Intell. 2023, 118, 105521. [Google Scholar] [CrossRef]
- Kumar, A.; Wu, G.; Ali, M.Z.; Mallipeddi, R.; Suganthan, P.N.; Das, S. A Test-Suite of Non-Convex Constrained Optimization Problems from the Real-World and Some Baseline Results. Swarm Evol. Comput. 2020, 56, 100693. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. Artificial Bee Colony Algorithm for Large-Scale Problems and Engineering Design Optimization. J. Intell. Manuf. 2012, 23, 1001–1014. [Google Scholar] [CrossRef]





| Index | Types | Name | Optimum |
|---|---|---|---|
| CEC2017_F1 | Unimodal | Shifted and Rotated Bent Cigar Function | 100 |
| CEC2017_F3 | Shifted and Rotated Zakharov Function | 300 | |
| CEC2017_F4 | Multimodal | Shifted and Rotated Rosenbrock’s Function | 400 |
| CEC2017_F5 | Shifted and Rotated Rastrigin’s Function | 500 | |
| CEC2017_F6 | Shifted and Rotated Expanded Scaffer’s F6 Function | 600 | |
| CEC2017_F7 | Shifted and Rotated Lunacek Bi-Rastrigin Function | 700 | |
| CEC2017_F8 | Shifted and Rotated Non-Continuous Rastrigin’s Function | 800 | |
| CEC2017_F9 | Shifted and Rotated Lévy Function | 900 | |
| CEC2017_F10 | Shifted and Rotated Schwefel’s Function | 1000 | |
| CEC2017_F11 | Hybrid | Hybrid function 1 (N = 3) | 1100 |
| CEC2017_F12 | Hybrid function 1 (N = 3) | 1200 | |
| CEC2017_F13 | Hybrid function 3 (N = 3) | 1300 | |
| CEC2017_F14 | Hybrid function 4 (N = 4) | 1400 | |
| CEC2017_F15 | Hybrid function 5 (N = 4) | 1500 | |
| CEC2017_F16 | Hybrid function 6 (N = 4) | 1600 | |
| CEC2017_F17 | Hybrid function 6 (N = 5) | 1700 | |
| CEC2017_F18 | Hybrid function 6 (N = 5) | 1800 | |
| CEC2017_F19 | Hybrid function 6 (N = 5) | 1900 | |
| CEC2017_F20 | Hybrid function 6 (N = 6) | 2000 | |
| CEC2017_F21 | Composition | Composition function 1 (N = 3) | 2100 |
| CEC2017_F22 | Composition function 2 (N = 3) | 2200 | |
| CEC2017_F23 | Composition function 3 (N = 4) | 2300 | |
| CEC2017_F24 | Composition function 4 (N = 4) | 2400 | |
| CEC2017_F25 | Composition function 5 (N = 5) | 2500 | |
| CEC2017_F26 | Composition function 6 (N = 5) | 2600 | |
| CEC2017_F27 | Composition function 7 (N = 6) | 2700 | |
| CEC2017_F28 | Composition function 8 (N = 6) | 2800 | |
| CEC2017_F29 | Composition function 9 (N = 3) | 2900 | |
| CEC2017_F30 | Composition function 10 (N = 3) | 3000 | |
| Search range: [−100,100] |
| Index | Types | Name | Optimum |
|---|---|---|---|
| CEC2020_F1 | Unimodal | Shifted and Rotated Bent Cigar Function | 100 |
| CEC2020_F2 | Multimodal | Shifted and Rotated Schwefel’s Function | 1100 |
| CEC2020_F3 | Shifted and Rotated Lunacek bi-Rastrigin Function | 700 | |
| CEC2020_F4 | Expanded Rosenbrock’s plus Griewangk’s Function | 1900 | |
| CEC2020_F5 | Hybrid | Hybrid Function 1 (N = 3) | 1700 |
| CEC2020_F6 | Hybrid Function 2 (N = 4) | 1600 | |
| CEC2020_F7 | Hybrid Function 3 (N = 5) | 2100 | |
| CEC2020_F8 | Composition | Composition Function 1 (N = 3) | 2200 |
| CEC2020_F9 | Composition Function 2 (N = 4) | 2400 | |
| CEC2020_F10 | Composition Function 3 (N = 5) | 2500 | |
| Search range: [−100, 100] |
| Algorithms | Proposed Time | Parameters Settings | Citations | Type |
|---|---|---|---|---|
| Particle Swarm Optimization (PSO) [40] | 1995 | 81,387 | classical | |
| Differential Evolution (DE) [41] | 1997 | 33,925 | classical | |
| Comprehensive Learning Particle Swarm Optimizer (CLPSO) [42] | 2006 | 2838 | Improved | |
| Bezier Search Differential Evolution (BESD) [43] | 2021 | 40 | Improved | |
| Bernstein-levy Differential Evolution (BDE) [44] | 2023 | 3 | Improved | |
| Fractional Order Particle Swarm Optimization (FOPSO) [45] | 2022 | 18 | Improved | |
| Improved Chaotic Grey Wolf Optimizer (ICGWO) [46] | 2023 | 15 | Improved | |
| Teaching Learning-Based Optimization (TLBO) [47] | 2011 | 3438 | high citation | |
| Grey Wolf Optimizer (GWO) [48] | 2014 | 11,102 | high citation | |
| Multi-Verse Optimizer (MVO) [49] | 2016 | 2094 | high citation | |
| Whale Optimization Algorithm (WOA) [11] | 2016 | 7672 | high citation | |
| Salp Swarm Algorithm (SSA) [50] | 2017 | 3284 | high citation | |
| Harris Hawks Optimization (HHO) [51] | 2019 | 3048 | high citation | |
| Artificial Butterfly Optimization (ABO) [52] | 2017 | 67 | popular | |
| Butterfly Optimization Algorithm (BOA) [53] | 2019 | 813 | popular | |
| Equilibrium Optimizer (EO) [54] | 2020 | 1177 | popular | |
| Dung Beetle Optimizer (DBO) [55] | 2023 | 38 | new | |
| INFO [56] | 2022 | 258 | new | |
| Snake Optimizer (SO) [57] | 2022 | 198 | new | |
| Growth Optimizer (GO) | 2023 | 11 | new | |
| LSHADE [58] | 2014 | 671 | superior | |
| Improved Multi-Operator Differential Evolution (IMODE) [59] | 2020 | 106 | superior | |
| Adaptive L-SHADE algorithm (ALSHADE) [60] | 2022 | 6 | superior |
| Problems | GO | COGO | DGGO | BGO | CODGBGO |
|---|---|---|---|---|---|
| CEC2017_F1 | 3.53 | 3.43 | 2.23 | 2.93 | 2.87 |
| CEC2017_F3 | 4.37 | 3.67 | 1.53 | 3.97 | 1.47 |
| CEC2017_F4 | 3.13 | 2.90 | 3.27 | 3.30 | 2.40 |
| CEC2017_F5 | 3.77 | 4.30 | 3.90 | 1.33 | 1.70 |
| CEC2017_F6 | 2.23 | 2.40 | 2.80 | 3.83 | 3.73 |
| CEC2017_F7 | 4.07 | 4.20 | 3.67 | 1.50 | 1.57 |
| CEC2017_F8 | 3.87 | 3.97 | 4.03 | 1.33 | 1.80 |
| CEC2017_F9 | 2.53 | 2.47 | 1.93 | 4.40 | 3.67 |
| CEC2017_F10 | 3.70 | 4.17 | 4.13 | 1.53 | 1.47 |
| CEC2017_F11 | 3.73 | 3.43 | 3.43 | 2.40 | 2.00 |
| CEC2017_F12 | 4.10 | 2.90 | 2.23 | 2.97 | 2.80 |
| CEC2017_F13 | 3.60 | 2.87 | 2.40 | 4.03 | 2.10 |
| CEC2017_F14 | 4.03 | 3.60 | 2.50 | 2.97 | 1.90 |
| CEC2017_F15 | 3.50 | 3.43 | 2.67 | 3.30 | 2.10 |
| CEC2017_F16 | 3.83 | 2.90 | 3.60 | 2.80 | 1.87 |
| CEC2017_F17 | 3.60 | 3.10 | 3.43 | 2.53 | 2.33 |
| CEC2017_F18 | 4.23 | 4.00 | 1.47 | 3.57 | 1.73 |
| CEC2017_F19 | 4.00 | 3.80 | 2.60 | 3.03 | 1.57 |
| CEC2017_F20 | 3.47 | 2.90 | 3.43 | 2.83 | 2.37 |
| CEC2017_F21 | 3.90 | 4.27 | 3.83 | 1.53 | 1.47 |
| CEC2017_F22 | 4.00 | 3.13 | 2.53 | 3.87 | 1.47 |
| CEC2017_F23 | 3.80 | 3.90 | 3.63 | 1.97 | 1.70 |
| CEC2017_F24 | 4.00 | 4.30 | 3.57 | 1.73 | 1.40 |
| CEC2017_F25 | 3.03 | 2.20 | 3.20 | 3.10 | 3.47 |
| CEC2017_F26 | 3.63 | 3.43 | 3.13 | 2.57 | 2.23 |
| CEC2017_F27 | 2.27 | 2.93 | 3.03 | 3.27 | 3.50 |
| CEC2017_F28 | 2.70 | 2.83 | 2.83 | 3.10 | 3.53 |
| CEC2017_F29 | 3.67 | 3.93 | 3.40 | 1.70 | 2.30 |
| CEC2017_F30 | 4.40 | 3.50 | 2.00 | 3.33 | 1.77 |
| Mean Rank | 3.61 | 3.41 | 2.98 | 2.78 | 2.22 |
| Final Rank | 5 | 4 | 3 | 2 | 1 |
| Problems | {0.7, 0.9} | {0.7, 0.95} | {0.7, 0.85} | {0.8, 0.85} | {0.8, 0.9} | {0.9, 0.85} | {0.9, 0.9} | {0.9, 0.95} | {0.8, 0.95} |
|---|---|---|---|---|---|---|---|---|---|
| CEC2017_F1 | 5.03 | 5.17 | 5.90 | 5.37 | 4.13 | 5.40 | 4.40 | 4.43 | 5.17 |
| CEC2017_F3 | 4.40 | 4.60 | 3.87 | 3.20 | 4.83 | 6.80 | 5.73 | 6.17 | 5.40 |
| CEC2017_F4 | 4.70 | 5.43 | 5.77 | 4.30 | 4.17 | 5.17 | 5.20 | 5.33 | 4.93 |
| CEC2017_F5 | 4.77 | 4.43 | 6.10 | 5.20 | 5.17 | 5.87 | 4.73 | 4.07 | 4.67 |
| CEC2017_F6 | 4.90 | 3.87 | 7.10 | 6.73 | 4.27 | 6.83 | 4.90 | 3.20 | 3.20 |
| CEC2017_F7 | 4.40 | 4.67 | 4.83 | 4.93 | 5.43 | 5.90 | 5.47 | 5.20 | 4.17 |
| CEC2017_F8 | 5.50 | 3.77 | 5.83 | 4.97 | 5.57 | 6.40 | 4.53 | 4.60 | 3.83 |
| CEC2017_F9 | 5.20 | 3.17 | 5.83 | 6.13 | 5.57 | 6.97 | 4.93 | 3.23 | 3.97 |
| CEC2017_F10 | 5.03 | 5.70 | 3.67 | 4.83 | 4.60 | 4.43 | 4.60 | 6.07 | 6.07 |
| CEC2017_F11 | 4.37 | 5.93 | 4.77 | 4.83 | 4.10 | 5.73 | 4.70 | 5.07 | 5.50 |
| CEC2017_F12 | 5.57 | 5.73 | 5.50 | 5.83 | 4.37 | 5.87 | 4.23 | 4.30 | 3.60 |
| CEC2017_F13 | 4.63 | 5.30 | 5.60 | 4.63 | 4.77 | 5.80 | 5.53 | 4.27 | 4.47 |
| CEC2017_F14 | 5.03 | 4.77 | 5.07 | 4.33 | 4.80 | 5.07 | 5.13 | 6.50 | 4.30 |
| CEC2017_F15 | 5.30 | 5.43 | 4.20 | 4.17 | 5.73 | 4.73 | 5.50 | 5.57 | 4.37 |
| CEC2017_F16 | 5.57 | 5.17 | 3.80 | 5.13 | 4.43 | 4.13 | 5.77 | 5.40 | 5.60 |
| CEC2017_F17 | 4.93 | 5.23 | 4.63 | 5.03 | 5.10 | 4.73 | 4.07 | 5.93 | 5.33 |
| CEC2017_F18 | 4.87 | 4.73 | 5.30 | 4.40 | 4.07 | 5.30 | 5.13 | 5.63 | 5.57 |
| CEC2017_F19 | 5.60 | 4.80 | 4.90 | 4.93 | 4.93 | 4.83 | 4.30 | 5.50 | 5.20 |
| CEC2017_F20 | 5.40 | 4.53 | 5.40 | 5.40 | 5.00 | 5.43 | 4.67 | 4.57 | 4.60 |
| CEC2017_F21 | 3.87 | 4.37 | 5.07 | 6.57 | 5.63 | 5.83 | 5.57 | 4.00 | 4.10 |
| CEC2017_F22 | 4.23 | 4.70 | 4.47 | 4.18 | 4.53 | 5.23 | 5.90 | 6.48 | 5.27 |
| CEC2017_F23 | 4.90 | 4.00 | 5.77 | 6.13 | 4.60 | 5.50 | 5.97 | 4.20 | 3.93 |
| CEC2017_F24 | 4.47 | 3.97 | 5.53 | 5.63 | 5.73 | 5.37 | 5.27 | 4.67 | 4.37 |
| CEC2017_F25 | 4.50 | 5.17 | 5.37 | 5.30 | 5.10 | 5.63 | 5.57 | 3.93 | 4.43 |
| CEC2017_F26 | 5.43 | 3.57 | 5.67 | 5.77 | 4.50 | 6.33 | 5.20 | 4.27 | 4.27 |
| CEC2017_F27 | 5.13 | 5.37 | 4.73 | 4.93 | 5.37 | 5.40 | 4.30 | 4.97 | 4.80 |
| CEC2017_F28 | 5.13 | 5.13 | 5.37 | 4.80 | 4.87 | 4.80 | 4.83 | 5.67 | 4.40 |
| CEC2017_F29 | 4.23 | 4.50 | 5.57 | 5.27 | 4.73 | 5.90 | 4.03 | 5.70 | 5.07 |
| CEC2017_F30 | 5.67 | 5.13 | 5.43 | 4.83 | 4.17 | 5.33 | 4.83 | 5.57 | 4.03 |
| Mean Rank | 4.92 | 4.77 | 5.21 | 5.10 | 4.84 | 5.54 | 5.00 | 4.98 | 4.64 |
| Final Rank | 4 | 2 | 8 | 7 | 3 | 9 | 6 | 5 | 1 |
| Problems | Metric | TLBO | SSA | INFO | DE | DBO | SO | CLPSO | BDE | BESD | GO | CODGBGO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CEC2017_F1 | Mean | 4.53 × 103 | 3.29 × 103 | 1.05 × 102 | 1.26 × 105 | 7.13 × 106 | 1.63 × 104 | 1.85 × 109 | 4.95 × 105 | 3.07 × 108 | 1.62 × 102 | 1.54 × 102 |
| Std | 4.89 × 103 | 3.95 × 103 | 7.16 × 100 | 5.43 × 104 | 1.13 × 107 | 1.40 × 104 | 3.86 × 108 | 2.67 × 105 | 9.21 × 107 | 2.01 × 102 | 1.46 × 102 | |
| CEC2017_F3 | Mean | 4.03 × 104 | 1.14 × 104 | 6.84 × 102 | 4.00 × 104 | 7.03 × 104 | 5.50 × 104 | 9.29 × 104 | 2.70 × 104 | 2.13 × 104 | 7.70 × 102 | 3.09 × 102 |
| Std | 8.00 × 103 | 4.68 × 103 | 1.53 × 103 | 7.37 × 103 | 1.64 × 104 | 1.07 × 104 | 1.56 × 104 | 6.04 × 103 | 3.76 × 103 | 5.10 × 102 | 8.78 × 100 | |
| CEC2017_F4 | Mean | 4.97 × 102 | 5.03 × 102 | 4.79 × 102 | 4.91 × 102 | 5.47 × 102 | 5.19 × 102 | 7.74 × 102 | 5.07 × 102 | 5.94 × 102 | 4.41 × 102 | 4.28 × 102 |
| Std | 3.64 × 101 | 1.82 × 101 | 2.62 × 101 | 8.80 × 100 | 4.33 × 101 | 4.05 × 101 | 4.30 × 101 | 2.19 × 101 | 2.54 × 101 | 3.26 × 101 | 3.10 × 101 | |
| CEC2017_F5 | Mean | 5.90 × 102 | 6.43 × 102 | 6.36 × 102 | 7.21 × 102 | 7.10 × 102 | 5.71 × 102 | 7.28 × 102 | 6.23 × 102 | 6.81 × 102 | 6.06 × 102 | 5.48 × 102 |
| Std | 1.73 × 101 | 4.24 × 101 | 3.01 × 101 | 1.28 × 101 | 4.79 × 101 | 2.70 × 101 | 1.77 × 101 | 8.45 × 100 | 1.15 × 101 | 1.84 × 101 | 1.66 × 101 | |
| CEC2017_F6 | Mean | 6.07 × 102 | 6.47 × 102 | 6.18 × 102 | 6.09 × 102 | 6.30 × 102 | 6.01 × 102 | 6.23 × 102 | 6.01 × 102 | 6.21 × 102 | 6.00 × 102 | 6.00 × 102 |
| Std | 4.34 × 100 | 1.17 × 101 | 8.90 × 100 | 2.69 × 100 | 8.18 × 100 | 6.00 × 10−1 | 2.68 × 100 | 2.06 × 10−1 | 2.81 × 100 | 7.81 × 10−3 | 2.92 × 10−2 | |
| CEC2017_F7 | Mean | 8.61 × 102 | 8.98 × 102 | 9.49 × 102 | 9.48 × 102 | 9.13 × 102 | 8.14 × 102 | 1.07 × 103 | 8.77 × 102 | 9.35 × 102 | 8.58 × 102 | 7.91 × 102 |
| Std | 4.16 × 101 | 5.80 × 101 | 5.35 × 101 | 1.35 × 101 | 7.17 × 101 | 3.18 × 101 | 2.59 × 101 | 1.24 × 101 | 1.42 × 101 | 1.14 × 101 | 1.90 × 101 | |
| CEC2017_F8 | Mean | 8.68 × 102 | 9.49 × 102 | 9.20 × 102 | 1.01 × 103 | 1.00 × 103 | 8.60 × 102 | 1.03 × 103 | 9.21 × 102 | 9.64 × 102 | 9.03 × 102 | 8.52 × 102 |
| Std | 1.83 × 101 | 4.41 × 101 | 2.69 × 101 | 1.33 × 101 | 6.23 × 101 | 1.81 × 101 | 1.64 × 101 | 1.21 × 101 | 9.94 × 100 | 2.24 × 101 | 1.27 × 101 | |
| CEC2017_F9 | Mean | 1.20 × 103 | 4.39 × 103 | 2.80 × 103 | 1.13 × 103 | 5.57 × 103 | 1.06 × 103 | 4.49 × 103 | 9.63 × 102 | 1.92 × 103 | 9.01 × 102 | 9.03 × 102 |
| Std | 2.76 × 102 | 1.49 × 103 | 6.58 × 102 | 2.97 × 102 | 2.30 × 103 | 1.07 × 102 | 6.86 × 102 | 5.94 × 101 | 3.24 × 102 | 1.19 × 100 | 2.95 × 100 | |
| CEC2017_F10 | Mean | 8.12 × 103 | 5.01 × 103 | 5.10 × 103 | 8.57 × 103 | 5.48 × 103 | 5.13 × 103 | 7.51 × 103 | 5.26 × 103 | 6.67 × 103 | 7.04 × 103 | 4.54 × 103 |
| Std | 4.02 × 102 | 7.43 × 102 | 6.12 × 102 | 2.98 × 102 | 7.92 × 102 | 2.04 × 103 | 2.62 × 102 | 1.76 × 102 | 2.46 × 102 | 4.36 × 102 | 6.17 × 102 | |
| CEC2017_F11 | Mean | 1.25 × 103 | 1.30 × 103 | 1.26 × 103 | 1.23 × 103 | 1.54 × 103 | 1.22 × 103 | 1.80 × 103 | 1.20 × 103 | 1.32 × 103 | 1.17 × 103 | 1.14 × 103 |
| Std | 4.93 × 101 | 5.10 × 101 | 4.65 × 101 | 2.63 × 101 | 1.28 × 102 | 4.63 × 101 | 1.86 × 102 | 2.13 × 101 | 2.10 × 101 | 2.66 × 101 | 2.80 × 101 | |
| CEC2017_F12 | Mean | 2.82 × 105 | 1.08 × 107 | 5.73 × 104 | 3.61 × 105 | 4.14 × 107 | 7.01 × 106 | 1.05 × 108 | 1.04 × 106 | 9.41 × 106 | 3.43 × 104 | 1.69 × 104 |
| Std | 3.43 × 105 | 9.93 × 106 | 3.70 × 104 | 1.30 × 105 | 6.31 × 107 | 1.07 × 107 | 2.78 × 107 | 6.60 × 105 | 3.50 × 106 | 2.79 × 104 | 8.16 × 103 | |
| CEC2017_F13 | Mean | 1.45 × 104 | 1.09 × 105 | 1.78 × 104 | 2.27 × 103 | 2.81 × 106 | 1.17 × 106 | 2.75 × 107 | 2.16 × 104 | 1.16 × 105 | 4.22 × 103 | 1.90 × 103 |
| Std | 1.25 × 104 | 6.58 × 104 | 1.37 × 104 | 2.08 × 102 | 5.92 × 106 | 1.36 × 106 | 1.75 × 107 | 1.33 × 104 | 4.89 × 104 | 1.10 × 104 | 1.19 × 103 | |
| CEC2017_F14 | Mean | 1.56 × 104 | 3.48 × 104 | 2.37 × 103 | 1.49 × 103 | 7.24 × 104 | 3.83 × 104 | 8.63 × 104 | 1.74 × 103 | 2.06 × 103 | 1.48 × 103 | 1.46 × 103 |
| Std | 1.62 × 104 | 3.23 × 104 | 1.53 × 103 | 7.27 × 100 | 9.64 × 104 | 6.00 × 104 | 4.94 × 104 | 1.91 × 102 | 3.11 × 102 | 1.06 × 101 | 1.47 × 101 | |
| CEC2017_F15 | Mean | 8.45 × 103 | 7.78 × 104 | 3.98 × 103 | 1.62 × 103 | 7.81 × 104 | 1.49 × 105 | 1.09 × 106 | 5.62 × 103 | 5.12 × 103 | 1.62 × 103 | 1.58 × 103 |
| Std | 6.89 × 103 | 5.31 × 104 | 4.13 × 103 | 2.34 × 101 | 6.62 × 104 | 2.51 × 105 | 6.83 × 105 | 5.05 × 103 | 9.80 × 102 | 4.24 × 101 | 3.21 × 101 | |
| CEC2017_F16 | Mean | 2.58 × 103 | 2.76 × 103 | 2.55 × 103 | 3.46 × 103 | 3.10 × 103 | 2.51 × 103 | 3.02 × 103 | 2.67 × 103 | 3.04 × 103 | 2.46 × 103 | 2.22 × 103 |
| Std | 3.96 × 102 | 3.32 × 102 | 3.19 × 102 | 1.94 × 102 | 4.48 × 102 | 3.06 × 102 | 1.57 × 102 | 1.53 × 102 | 1.07 × 102 | 1.72 × 102 | 1.85 × 102 | |
| CEC2017_F17 | Mean | 1.92 × 103 | 2.25 × 103 | 2.26 × 103 | 2.38 × 103 | 2.46 × 103 | 2.20 × 103 | 2.15 × 103 | 1.99 × 103 | 2.06 × 103 | 1.90 × 103 | 1.85 × 103 |
| Std | 9.02 × 101 | 2.45 × 102 | 2.24 × 102 | 1.02 × 102 | 2.06 × 102 | 2.07 × 102 | 9.02 × 101 | 9.75 × 101 | 8.35 × 101 | 5.95 × 101 | 9.11 × 101 | |
| CEC2017_F18 | Mean | 5.79 × 105 | 5.13 × 105 | 3.28 × 104 | 2.27 × 103 | 1.85 × 106 | 1.23 × 106 | 1.04 × 106 | 4.50 × 104 | 5.47 × 104 | 3.94 × 103 | 1.93 × 103 |
| Std | 4.43 × 105 | 3.80 × 105 | 2.10 × 104 | 1.82 × 102 | 2.72 × 106 | 1.36 × 106 | 3.76 × 105 | 2.09 × 104 | 1.59 × 104 | 3.41 × 103 | 5.00 × 101 | |
| CEC2017_F19 | Mean | 8.00 × 103 | 1.84 × 106 | 3.39 × 103 | 1.95 × 103 | 1.06 × 106 | 2.00 × 105 | 1.60 × 106 | 6.07 × 103 | 7.12 × 103 | 1.96 × 103 | 1.93 × 103 |
| Std | 6.13 × 103 | 1.15 × 106 | 2.99 × 103 | 5.65 × 100 | 1.38 × 106 | 4.62 × 105 | 1.09 × 106 | 4.17 × 103 | 1.85 × 103 | 8.45 × 101 | 7.15 × 100 | |
| CEC2017_F20 | Mean | 2.36 × 103 | 2.54 × 103 | 2.50 × 103 | 2.83 × 103 | 2.63 × 103 | 2.43 × 103 | 2.50 × 103 | 2.33 × 103 | 2.48 × 103 | 2.25 × 103 | 2.16 × 103 |
| Std | 1.35 × 102 | 2.00 × 102 | 1.65 × 102 | 1.06 × 102 | 1.80 × 102 | 1.54 × 102 | 9.13 × 101 | 6.95 × 101 | 8.06 × 101 | 1.02 × 102 | 9.22 × 101 | |
| CEC2017_F21 | Mean | 2.37 × 103 | 2.44 × 103 | 2.43 × 103 | 2.51 × 103 | 2.52 × 103 | 2.37 × 103 | 2.50 × 103 | 2.42 × 103 | 2.47 × 103 | 2.41 × 103 | 2.35 × 103 |
| Std | 2.03 × 101 | 3.73 × 101 | 2.76 × 101 | 1.57 × 101 | 4.66 × 101 | 1.87 × 101 | 5.21 × 101 | 1.41 × 101 | 8.89 × 100 | 1.55 × 101 | 1.61 × 101 | |
| CEC2017_F22 | Mean | 2.56 × 103 | 3.32 × 103 | 4.58 × 103 | 3.32 × 103 | 5.22 × 103 | 3.73 × 103 | 3.04 × 103 | 2.31 × 103 | 2.43 × 103 | 2.50 × 103 | 2.30 × 103 |
| Std | 1.35 × 103 | 1.88 × 103 | 2.10 × 103 | 1.46 × 103 | 1.94 × 103 | 2.03 × 103 | 2.34 × 102 | 8.07 × 100 | 2.53 × 101 | 1.12 × 103 | 7.36 × 10−1 | |
| CEC2017_F23 | Mean | 2.74 × 103 | 2.79 × 103 | 2.82 × 103 | 2.83 × 103 | 2.91 × 103 | 2.75 × 103 | 2.85 × 103 | 2.77 × 103 | 2.87 × 103 | 2.74 × 103 | 2.69 × 103 |
| Std | 2.30 × 101 | 3.89 × 101 | 5.39 × 101 | 5.74 × 101 | 7.42 × 101 | 3.19 × 101 | 4.38 × 101 | 1.49 × 101 | 1.50 × 101 | 2.32 × 101 | 1.67 × 101 | |
| CEC2017_F24 | Mean | 2.91 × 103 | 2.93 × 103 | 2.96 × 103 | 3.04 × 103 | 3.06 × 103 | 2.90 × 103 | 3.04 × 103 | 2.95 × 103 | 3.03 × 103 | 2.95 × 103 | 2.88 × 103 |
| Std | 2.12 × 101 | 3.20 × 101 | 4.24 × 101 | 1.49 × 101 | 8.10 × 101 | 3.58 × 101 | 1.88 × 101 | 1.69 × 101 | 1.86 × 101 | 1.71 × 101 | 1.60 × 101 | |
| CEC2017_F25 | Mean | 2.90 × 103 | 2.91 × 103 | 2.90 × 103 | 2.89 × 103 | 2.95 × 103 | 2.89 × 103 | 3.07 × 103 | 2.89 × 103 | 2.99 × 103 | 2.89 × 103 | 2.89 × 103 |
| Std | 1.66 × 101 | 2.15 × 101 | 1.84 × 101 | 6.11 × 10−1 | 4.56 × 101 | 1.48 × 101 | 3.71 × 101 | 7.63 × 100 | 1.63 × 101 | 1.02 × 100 | 1.56 × 100 | |
| CEC2017_F26 | Mean | 4.36 × 103 | 4.77 × 103 | 5.50 × 103 | 4.13 × 103 | 6.35 × 103 | 4.87 × 103 | 4.74 × 103 | 4.23 × 103 | 4.36 × 103 | 4.36 × 103 | 3.96 × 103 |
| Std | 1.09 × 103 | 8.63 × 102 | 1.33 × 103 | 2.27 × 102 | 1.12 × 103 | 3.95 × 102 | 6.38 × 102 | 9.30 × 102 | 7.63 × 102 | 3.04 × 102 | 4.04 × 102 | |
| CEC2017_F27 | Mean | 3.24 × 103 | 3.26 × 103 | 3.26 × 103 | 3.23 × 103 | 3.27 × 103 | 3.26 × 103 | 3.27 × 103 | 3.24 × 103 | 3.37 × 103 | 3.20 × 103 | 3.21 × 103 |
| Std | 2.11 × 101 | 4.69 × 101 | 2.93 × 101 | 7.35 × 100 | 4.11 × 101 | 1.67 × 101 | 7.69 × 100 | 5.13 × 100 | 1.69 × 101 | 9.68 × 100 | 1.03 × 101 | |
| CEC2017_F28 | Mean | 3.23 × 103 | 3.26 × 103 | 3.18 × 103 | 3.22 × 103 | 3.38 × 103 | 3.27 × 103 | 3.50 × 103 | 3.24 × 103 | 3.38 × 103 | 3.16 × 103 | 3.19 × 103 |
| Std | 2.37 × 101 | 3.04 × 101 | 5.01 × 101 | 1.02 × 101 | 7.41 × 101 | 4.35 × 101 | 5.20 × 101 | 1.72 × 101 | 3.07 × 101 | 6.24 × 101 | 6.24 × 101 | |
| CEC2017_F29 | Mean | 3.69 × 103 | 4.07 × 103 | 4.12 × 103 | 4.39 × 103 | 4.20 × 103 | 3.85 × 103 | 4.14 × 103 | 3.69 × 103 | 4.12 × 103 | 3.62 × 103 | 3.53 × 103 |
| Std | 1.37 × 102 | 2.83 × 102 | 3.06 × 102 | 1.88 × 102 | 2.84 × 102 | 2.45 × 102 | 1.43 × 102 | 8.32 × 101 | 1.09 × 102 | 8.50 × 101 | 9.22 × 101 | |
| CEC2017_F30 | Mean | 1.10 × 104 | 5.51 × 106 | 8.87 × 103 | 1.80 × 104 | 2.42 × 106 | 4.18 × 105 | 3.60 × 106 | 2.28 × 104 | 3.63 × 105 | 6.82 × 103 | 5.32 × 103 |
| Std | 4.44 × 103 | 3.42 × 106 | 3.35 × 103 | 5.35 × 103 | 4.31 × 106 | 1.10 × 106 | 1.51 × 106 | 1.34 × 104 | 1.57 × 105 | 9.44 × 102 | 3.24 × 102 | |
| MeanRank | 4.97 | 7.24 | 5.72 | 6.38 | 9.72 | 5.90 | 9.66 | 4.90 | 7.55 | 2.76 | 1.21 | |
| FinalRank | 4 | 8 | 5 | 7 | 11 | 6 | 10 | 3 | 9 | 2 | 1 | |
| Rank First | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 24 |
| Problems | Metric | TLBO | SSA | INFO | DE | DBO | SO | CLPSO | BDE | BESD | GO | CODGBGO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CEC2017_F1 | Mean | 3.63 × 107 | 7.02 × 103 | 7.88 × 104 | 4.29 × 107 | 4.41 × 108 | 1.90 × 107 | 1.13 × 1010 | 4.35 × 107 | 4.59 × 109 | 4.31 × 103 | 7.58 × 103 |
| Std | 1.09 × 108 | 8.47 × 103 | 3.99 × 105 | 1.49 × 107 | 2.97 × 108 | 4.48 × 107 | 1.54 × 109 | 1.34 × 107 | 9.72 × 108 | 5.09 × 103 | 8.08 × 103 | |
| CEC2017_F3 | Mean | 1.60 × 105 | 1.01 × 105 | 1.99 × 104 | 1.97 × 105 | 2.13 × 105 | 1.33 × 105 | 2.27 × 105 | 1.04 × 105 | 8.33 × 104 | 3.73 × 104 | 1.31 × 104 |
| Std | 2.23 × 104 | 2.97 × 104 | 6.91 × 103 | 2.91 × 104 | 4.47 × 104 | 1.38 × 104 | 2.50 × 104 | 1.75 × 104 | 1.26 × 104 | 1.35 × 104 | 4.70 × 103 | |
| CEC2017_F4 | Mean | 5.99 × 102 | 5.89 × 102 | 5.38 × 102 | 6.00 × 102 | 8.12 × 102 | 6.60 × 102 | 1.89 × 103 | 6.47 × 102 | 1.23 × 103 | 5.19 × 102 | 5.17 × 102 |
| Std | 5.49 × 101 | 4.67 × 101 | 5.47 × 101 | 3.84 × 101 | 1.70 × 102 | 6.83 × 101 | 1.74 × 102 | 2.59 × 101 | 1.26 × 102 | 5.87 × 101 | 4.12 × 101 | |
| CEC2017_F5 | Mean | 6.95 × 102 | 8.38 × 102 | 8.07 × 102 | 9.53 × 102 | 9.13 × 102 | 6.34 × 102 | 9.98 × 102 | 7.90 × 102 | 9.09 × 102 | 7.84 × 102 | 6.32 × 102 |
| Std | 2.82 × 101 | 5.35 × 101 | 4.61 × 101 | 1.94 × 101 | 7.88 × 101 | 4.36 × 101 | 1.94 × 101 | 1.58 × 101 | 1.94 × 101 | 3.30 × 101 | 3.68 × 101 | |
| CEC2017_F6 | Mean | 6.21 × 102 | 6.56 × 102 | 6.40 × 102 | 6.26 × 102 | 6.56 × 102 | 6.04 × 102 | 6.40 × 102 | 6.03 × 102 | 6.41 × 102 | 6.00 × 102 | 6.00 × 102 |
| Std | 4.80 × 100 | 9.77 × 100 | 9.47 × 100 | 5.75 × 100 | 8.02 × 100 | 2.01 × 100 | 3.96 × 100 | 5.95 × 10−1 | 3.98 × 100 | 1.01 × 10−1 | 1.45 × 10−1 | |
| CEC2017_F7 | Mean | 1.07 × 103 | 1.14 × 103 | 1.30 × 103 | 1.22 × 103 | 1.16 × 103 | 9.39 × 102 | 1.59 × 103 | 1.08 × 103 | 1.26 × 103 | 1.08 × 103 | 8.98 × 102 |
| Std | 6.20 × 101 | 1.27 × 102 | 1.07 × 102 | 1.86 × 101 | 1.48 × 102 | 4.11 × 101 | 5.46 × 101 | 2.65 × 101 | 3.16 × 101 | 1.84 × 101 | 4.87 × 101 | |
| CEC2017_F8 | Mean | 1.01 × 103 | 1.11 × 103 | 1.10 × 103 | 1.25 × 103 | 1.23 × 103 | 9.49 × 102 | 1.30 × 103 | 1.09 × 103 | 1.21 × 103 | 1.09 × 103 | 9.14 × 102 |
| Std | 2.68 × 101 | 7.77 × 101 | 5.42 × 101 | 2.33 × 101 | 6.39 × 101 | 5.28 × 101 | 3.12 × 101 | 2.01 × 101 | 2.07 × 101 | 2.16 × 101 | 2.99 × 101 | |
| CEC2017_F9 | Mean | 6.86 × 103 | 1.28 × 104 | 7.97 × 103 | 6.81 × 103 | 1.96 × 104 | 1.77 × 103 | 1.98 × 104 | 2.32 × 103 | 1.19 × 104 | 9.49 × 102 | 1.06 × 103 |
| Std | 2.92 × 103 | 2.96 × 103 | 1.70 × 103 | 2.72 × 103 | 7.92 × 103 | 4.09 × 102 | 2.77 × 103 | 4.48 × 102 | 1.44 × 103 | 4.57 × 101 | 2.05 × 102 | |
| CEC2017_F10 | Mean | 1.46 × 104 | 8.04 × 103 | 8.10 × 103 | 1.52 × 104 | 8.85 × 103 | 1.01 × 104 | 1.29 × 104 | 9.85 × 103 | 1.23 × 104 | 1.35 × 104 | 8.23 × 103 |
| Std | 3.93 × 102 | 1.18 × 103 | 9.15 × 102 | 3.74 × 102 | 1.84 × 103 | 2.57 × 103 | 3.31 × 102 | 4.10 × 102 | 3.38 × 102 | 3.94 × 102 | 9.60 × 102 | |
| CEC2017_F11 | Mean | 1.35 × 103 | 1.58 × 103 | 1.31 × 103 | 1.41 × 103 | 2.70 × 103 | 1.48 × 103 | 5.43 × 103 | 1.54 × 103 | 2.28 × 103 | 1.28 × 103 | 1.22 × 103 |
| Std | 6.00 × 101 | 1.07 × 102 | 6.18 × 101 | 3.59 × 101 | 1.78 × 103 | 1.05 × 102 | 1.28 × 103 | 1.19 × 102 | 2.50 × 102 | 2.57 × 101 | 3.47 × 101 | |
| CEC2017_F12 | Mean | 3.55 × 106 | 7.64 × 107 | 1.94 × 106 | 7.53 × 106 | 4.43 × 108 | 5.73 × 107 | 1.93 × 109 | 1.80 × 107 | 3.49 × 108 | 5.66 × 105 | 3.39 × 105 |
| Std | 6.30 × 106 | 3.87 × 107 | 1.10 × 106 | 3.68 × 106 | 3.73 × 108 | 6.76 × 107 | 5.54 × 108 | 8.58 × 106 | 9.08 × 107 | 4.14 × 105 | 2.95 × 105 | |
| CEC2017_F13 | Mean | 8.57 × 103 | 1.75 × 105 | 7.50 × 103 | 6.61 × 104 | 1.95 × 107 | 5.51 × 106 | 4.50 × 108 | 1.34 × 105 | 1.11 × 107 | 9.39 × 103 | 5.66 × 103 |
| Std | 5.31 × 103 | 1.05 × 105 | 3.80 × 103 | 1.77 × 104 | 2.78 × 107 | 6.05 × 106 | 1.68 × 108 | 2.17 × 105 | 5.75 × 106 | 8.55 × 103 | 6.40 × 103 | |
| CEC2017_F14 | Mean | 1.36 × 105 | 1.94 × 105 | 1.31 × 104 | 1.67 × 103 | 1.50 × 106 | 4.78 × 105 | 2.15 × 106 | 3.68 × 104 | 6.42 × 104 | 1.71 × 103 | 1.61 × 103 |
| Std | 1.10 × 105 | 1.35 × 105 | 1.50 × 104 | 2.15 × 101 | 1.94 × 106 | 1.19 × 106 | 9.50 × 105 | 2.53 × 104 | 2.81 × 104 | 7.07 × 101 | 3.67 × 101 | |
| CEC2017_F15 | Mean | 8.25 × 103 | 5.70 × 104 | 1.09 × 104 | 2.80 × 103 | 5.76 × 106 | 1.01 × 106 | 7.54 × 107 | 2.29 × 104 | 2.77 × 105 | 3.46 × 103 | 3.22 × 103 |
| Std | 6.30 × 103 | 2.34 × 104 | 7.18 × 103 | 2.63 × 102 | 2.36 × 107 | 1.58 × 106 | 3.16 × 107 | 1.82 × 104 | 1.25 × 105 | 4.41 × 103 | 3.47 × 103 | |
| CEC2017_F16 | Mean | 3.13 × 103 | 3.69 × 103 | 3.50 × 103 | 5.35 × 103 | 4.40 × 103 | 3.59 × 103 | 4.36 × 103 | 3.86 × 103 | 4.20 × 103 | 3.79 × 103 | 3.08 × 103 |
| Std | 4.59 × 102 | 5.27 × 102 | 4.75 × 102 | 2.23 × 102 | 5.98 × 102 | 7.99 × 102 | 3.15 × 102 | 1.80 × 102 | 2.69 × 102 | 3.34 × 102 | 4.17 × 102 | |
| CEC2017_F17 | Mean | 2.92 × 103 | 3.40 × 103 | 3.25 × 103 | 4.08 × 103 | 4.12 × 103 | 3.19 × 103 | 3.89 × 103 | 3.23 × 103 | 3.34 × 103 | 3.05 × 103 | 2.74 × 103 |
| Std | 2.99 × 102 | 3.74 × 102 | 3.52 × 102 | 1.75 × 102 | 4.02 × 102 | 4.31 × 102 | 2.38 × 102 | 1.93 × 102 | 1.35 × 102 | 1.52 × 102 | 2.29 × 102 | |
| CEC2017_F18 | Mean | 1.95 × 106 | 2.48 × 106 | 1.25 × 105 | 8.20 × 104 | 5.88 × 106 | 5.31 × 106 | 7.48 × 106 | 5.90 × 105 | 7.89 × 105 | 2.51 × 104 | 7.92 × 103 |
| Std | 1.32 × 106 | 2.21 × 106 | 9.12 × 104 | 2.83 × 104 | 6.86 × 106 | 4.90 × 106 | 4.05 × 106 | 5.11 × 105 | 3.60 × 105 | 1.51 × 104 | 5.77 × 103 | |
| CEC2017_F19 | Mean | 1.84 × 104 | 3.30 × 106 | 1.54 × 104 | 2.27 × 103 | 5.29 × 106 | 6.62 × 105 | 1.54 × 107 | 2.05 × 104 | 1.14 × 105 | 2.28 × 103 | 2.08 × 103 |
| Std | 8.69 × 103 | 2.57 × 106 | 1.08 × 104 | 1.18 × 102 | 7.55 × 106 | 1.23 × 106 | 6.95 × 106 | 7.84 × 103 | 3.26 × 104 | 4.59 × 102 | 7.73 × 101 | |
| CEC2017_F20 | Mean | 3.73 × 103 | 3.18 × 103 | 3.31 × 103 | 4.19 × 103 | 3.61 × 103 | 3.11 × 103 | 3.40 × 103 | 3.29 × 103 | 3.51 × 103 | 3.22 × 103 | 2.99 × 103 |
| Std | 2.42 × 102 | 3.99 × 102 | 3.53 × 102 | 1.71 × 102 | 4.12 × 102 | 4.90 × 102 | 1.53 × 102 | 1.59 × 102 | 1.52 × 102 | 1.87 × 102 | 2.10 × 102 | |
| CEC2017_F21 | Mean | 2.50 × 103 | 2.61 × 103 | 2.58 × 103 | 2.75 × 103 | 2.79 × 103 | 2.45 × 103 | 2.78 × 103 | 2.59 × 103 | 2.69 × 103 | 2.58 × 103 | 2.41 × 103 |
| Std | 4.04 × 101 | 7.03 × 101 | 5.79 × 101 | 2.42 × 101 | 9.89 × 101 | 4.42 × 101 | 1.79 × 101 | 1.65 × 101 | 1.75 × 101 | 3.64 × 101 | 3.04 × 101 | |
| CEC2017_F22 | Mean | 1.40 × 104 | 9.51 × 103 | 9.70 × 103 | 1.66 × 104 | 1.09 × 104 | 1.32 × 104 | 1.40 × 104 | 1.11 × 104 | 1.30 × 104 | 1.45 × 104 | 8.96 × 103 |
| Std | 5.15 × 103 | 1.63 × 103 | 9.94 × 102 | 4.20 × 102 | 1.31 × 103 | 2.56 × 103 | 1.99 × 103 | 2.27 × 103 | 1.68 × 103 | 2.37 × 103 | 2.41 × 103 | |
| CEC2017_F23 | Mean | 2.98 × 103 | 3.03 × 103 | 3.13 × 103 | 3.19 × 103 | 3.36 × 103 | 2.95 × 103 | 3.24 × 103 | 3.05 × 103 | 3.27 × 103 | 2.99 × 103 | 2.84 × 103 |
| Std | 4.59 × 101 | 7.99 × 101 | 7.16 × 101 | 2.61 × 101 | 9.04 × 101 | 7.45 × 101 | 2.96 × 101 | 2.07 × 101 | 3.67 × 101 | 5.07 × 101 | 3.13 × 101 | |
| CEC2017_F24 | Mean | 3.17 × 103 | 3.15 × 103 | 3.27 × 103 | 3.34 × 103 | 3.43 × 103 | 3.09 × 103 | 3.41 × 103 | 3.26 × 103 | 3.42 × 103 | 3.20 × 103 | 3.02 × 103 |
| Std | 8.19 × 101 | 5.26 × 101 | 9.83 × 101 | 2.52 × 101 | 9.34 × 101 | 8.84 × 101 | 2.29 × 101 | 3.16 × 101 | 3.05 × 101 | 5.69 × 101 | 2.88 × 101 | |
| CEC2017_F25 | Mean | 3.14 × 103 | 3.08 × 103 | 3.06 × 103 | 3.07 × 103 | 3.51 × 103 | 3.11 × 103 | 4.42 × 103 | 3.14 × 103 | 3.68 × 103 | 3.03 × 103 | 3.03 × 103 |
| Std | 4.32 × 101 | 4.06 × 101 | 2.90 × 101 | 2.09 × 101 | 1.28 × 103 | 4.18 × 101 | 2.05 × 102 | 2.92 × 101 | 1.13 × 102 | 3.62 × 101 | 3.62 × 101 | |
| CEC2017_F26 | Mean | 7.81 × 103 | 5.57 × 103 | 9.22 × 103 | 8.14 × 103 | 1.00 × 104 | 6.25 × 103 | 8.30 × 103 | 7.01 × 103 | 8.76 × 103 | 5.63 × 103 | 4.88 × 103 |
| Std | 1.74 × 103 | 2.36 × 103 | 2.39 × 103 | 6.20 × 102 | 1.61 × 103 | 5.67 × 102 | 1.01 × 103 | 1.92 × 102 | 1.11 × 103 | 6.90 × 102 | 2.95 × 102 | |
| CEC2017_F27 | Mean | 3.57 × 103 | 3.55 × 103 | 3.65 × 103 | 3.53 × 103 | 3.75 × 103 | 3.59 × 103 | 3.72 × 103 | 3.55 × 103 | 4.20 × 103 | 3.25 × 103 | 3.29 × 103 |
| Std | 1.45 × 102 | 1.14 × 102 | 1.70 × 102 | 1.23 × 102 | 2.11 × 102 | 8.92 × 101 | 5.44 × 101 | 4.87 × 101 | 8.02 × 101 | 5.61 × 101 | 5.38 × 101 | |
| CEC2017_F28 | Mean | 3.42 × 103 | 3.35 × 103 | 3.32 × 103 | 3.34 × 103 | 5.39 × 103 | 3.41 × 103 | 5.03 × 103 | 3.47 × 103 | 4.38 × 103 | 3.29 × 103 | 3.30 × 103 |
| Std | 5.39 × 101 | 2.83 × 101 | 3.43 × 101 | 3.02 × 101 | 2.19 × 103 | 4.49 × 101 | 2.79 × 102 | 4.42 × 101 | 1.57 × 102 | 2.37 × 101 | 2.18 × 101 | |
| CEC2017_F29 | Mean | 4.48 × 103 | 5.38 × 103 | 4.97 × 103 | 5.83 × 103 | 5.47 × 103 | 4.46 × 103 | 5.74 × 103 | 4.28 × 103 | 5.37 × 103 | 4.02 × 103 | 3.75 × 103 |
| Std | 2.98 × 102 | 5.12 × 102 | 4.32 × 102 | 2.47 × 102 | 5.22 × 102 | 4.56 × 102 | 3.15 × 102 | 1.61 × 102 | 2.04 × 102 | 2.29 × 102 | 2.08 × 102 | |
| CEC2017_F30 | Mean | 9.43 × 105 | 9.89 × 107 | 9.06 × 105 | 6.57 × 106 | 2.41 × 107 | 1.59 × 107 | 1.18 × 108 | 3.91 × 106 | 4.65 × 107 | 7.96 × 105 | 7.70 × 105 |
| Std | 1.42 × 105 | 2.55 × 107 | 2.09 × 105 | 1.49 × 106 | 1.74 × 107 | 2.24 × 107 | 4.28 × 107 | 7.51 × 105 | 8.21 × 106 | 1.00 × 105 | 1.39 × 105 | |
| MeanRank | 5.17 | 6.00 | 4.86 | 6.83 | 9.41 | 5.24 | 10.03 | 5.55 | 8.24 | 3.34 | 1.31 | |
| FinalRank | 4 | 7 | 3 | 8 | 10 | 5 | 11 | 6 | 9 | 2 | 1 | |
| Rank First | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 24 |
| Problems | Metric | TLBO | SSA | INFO | DE | DBO | SO | CLPSO | BDE | BESD | GO | CODGBGO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CEC2017_F1 | Mean | 6.64 × 109 | 1.82 × 105 | 2.06 × 107 | 7.10 × 109 | 4.61 × 1010 | 6.02 × 107 | 7.23 × 1010 | 2.18 × 109 | 4.57 × 1010 | 2.47 × 107 | 2.21 × 107 |
| Std | 3.12 × 109 | 1.96 × 105 | 6.46 × 107 | 1.84 × 109 | 4.83 × 1010 | 1.07 × 108 | 6.83 × 109 | 4.04 × 108 | 5.52 × 109 | 9.71 × 106 | 1.24 × 107 | |
| CEC2017_F3 | Mean | 4.80 × 105 | 3.96 × 105 | 1.71 × 105 | 6.53 × 105 | 5.70 × 105 | 3.32 × 105 | 6.45 × 105 | 3.25 × 105 | 2.66 × 105 | 3.01 × 105 | 1.70 × 105 |
| Std | 5.54 × 104 | 1.11 × 105 | 2.44 × 104 | 9.49 × 104 | 2.04 × 105 | 1.93 × 104 | 5.03 × 104 | 3.01 × 104 | 1.55 × 104 | 6.52 × 104 | 2.53 × 104 | |
| CEC2017_F4 | Mean | 1.65 × 103 | 8.84 × 102 | 8.94 × 102 | 1.48 × 103 | 6.19 × 103 | 1.01 × 103 | 1.04 × 104 | 1.29 × 103 | 6.04 × 103 | 7.74 × 102 | 7.60 × 102 |
| Std | 3.22 × 102 | 6.50 × 101 | 1.48 × 102 | 1.91 × 102 | 6.09 × 103 | 1.54 × 102 | 1.49 × 103 | 9.55 × 101 | 6.34 × 102 | 4.17 × 101 | 4.72 × 101 | |
| CEC2017_F5 | Mean | 1.14 × 103 | 1.36 × 103 | 1.26 × 103 | 1.66 × 103 | 1.64 × 103 | 9.94 × 102 | 1.81 × 103 | 1.35 × 103 | 1.64 × 103 | 1.36 × 103 | 1.04 × 103 |
| Std | 8.68 × 101 | 1.32 × 102 | 6.52 × 101 | 4.38 × 101 | 2.03 × 102 | 1.71 × 102 | 4.11 × 101 | 3.51 × 101 | 2.35 × 101 | 3.42 × 101 | 1.07 × 102 | |
| CEC2017_F6 | Mean | 6.42 × 102 | 6.67 × 102 | 6.54 × 102 | 6.60 × 102 | 6.68 × 102 | 6.15 × 102 | 6.69 × 102 | 6.14 × 102 | 6.69 × 102 | 6.05 × 102 | 6.07 × 102 |
| Std | 4.98 × 100 | 6.82 × 100 | 6.68 × 100 | 7.82 × 100 | 7.97 × 100 | 3.02 × 100 | 3.86 × 100 | 1.44 × 100 | 3.38 × 100 | 9.15 × 10−1 | 2.01 × 100 | |
| CEC2017_F7 | Mean | 2.09 × 103 | 2.02 × 103 | 2.61 × 103 | 2.25 × 103 | 2.40 × 103 | 1.37 × 103 | 3.58 × 103 | 1.81 × 103 | 2.42 × 103 | 1.76 × 103 | 1.52 × 103 |
| Std | 1.66 × 102 | 1.97 × 102 | 2.32 × 102 | 9.08 × 101 | 3.89 × 102 | 5.48 × 101 | 1.59 × 102 | 4.45 × 101 | 1.03 × 102 | 4.03 × 101 | 1.02 × 102 | |
| CEC2017_F8 | Mean | 1.52 × 103 | 1.65 × 103 | 1.63 × 103 | 1.99 × 103 | 2.02 × 103 | 1.31 × 103 | 2.11 × 103 | 1.66 × 103 | 1.98 × 103 | 1.66 × 103 | 1.36 × 103 |
| Std | 7.93 × 101 | 1.50 × 102 | 9.69 × 101 | 5.32 × 101 | 1.78 × 102 | 1.75 × 102 | 5.30 × 101 | 3.96 × 101 | 2.88 × 101 | 3.69 × 101 | 1.11 × 102 | |
| CEC2017_F9 | Mean | 4.52 × 104 | 3.00 × 104 | 2.17 × 104 | 4.69 × 104 | 4.66 × 104 | 6.21 × 103 | 9.05 × 104 | 2.45 × 104 | 4.75 × 104 | 5.21 × 103 | 7.28 × 103 |
| Std | 8.32 × 103 | 3.55 × 103 | 2.40 × 103 | 8.12 × 103 | 2.03 × 104 | 1.58 × 103 | 8.77 × 103 | 4.25 × 103 | 3.95 × 103 | 1.94 × 103 | 3.42 × 103 | |
| CEC2017_F10 | Mean | 3.18 × 104 | 1.62 × 104 | 1.68 × 104 | 3.25 × 104 | 1.93 × 104 | 3.15 × 104 | 2.79 × 104 | 2.41 × 104 | 2.82 × 104 | 3.14 × 104 | 2.22 × 104 |
| Std | 5.55 × 102 | 2.06 × 103 | 1.70 × 103 | 5.48 × 102 | 3.83 × 103 | 9.29 × 102 | 6.95 × 102 | 5.79 × 102 | 4.35 × 102 | 6.53 × 102 | 1.43 × 103 | |
| CEC2017_F11 | Mean | 4.46 × 104 | 1.88 × 104 | 3.63 × 103 | 3.93 × 104 | 1.43 × 105 | 8.18 × 104 | 1.30 × 105 | 3.13 × 104 | 4.91 × 104 | 4.03 × 103 | 2.62 × 103 |
| Std | 1.08 × 104 | 6.80 × 103 | 5.47 × 102 | 7.47 × 103 | 4.98 × 104 | 1.99 × 104 | 2.50 × 104 | 7.28 × 103 | 8.33 × 103 | 6.43 × 102 | 1.81 × 102 | |
| CEC2017_F12 | Mean | 2.33 × 108 | 6.00 × 108 | 2.93 × 107 | 2.19 × 108 | 2.15 × 109 | 2.50 × 108 | 1.89 × 1010 | 4.92 × 108 | 6.13 × 109 | 2.16 × 107 | 1.22 × 107 |
| Std | 2.10 × 108 | 2.91 × 108 | 1.60 × 107 | 8.45 × 107 | 7.57 × 108 | 2.85 × 108 | 3.65 × 109 | 1.22 × 108 | 9.88 × 108 | 6.63 × 106 | 6.70 × 106 | |
| CEC2017_F13 | Mean | 2.07 × 104 | 8.79 × 104 | 2.19 × 104 | 1.04 × 106 | 1.21 × 108 | 1.28 × 107 | 2.17 × 109 | 1.21 × 106 | 3.06 × 108 | 5.63 × 103 | 8.05 × 103 |
| Std | 8.46 × 103 | 3.31 × 104 | 3.61 × 104 | 5.75 × 105 | 1.30 × 108 | 1.31 × 107 | 5.39 × 108 | 6.14 × 105 | 7.45 × 107 | 3.36 × 103 | 6.08 × 103 | |
| CEC2017_F14 | Mean | 1.38 × 106 | 2.92 × 106 | 3.54 × 105 | 2.91 × 105 | 1.01 × 107 | 7.61 × 106 | 2.27 × 107 | 2.33 × 106 | 2.17 × 106 | 2.19 × 104 | 9.00 × 103 |
| Std | 6.81 × 105 | 1.61 × 106 | 1.80 × 105 | 9.76 × 104 | 9.56 × 106 | 6.51 × 106 | 7.02 × 106 | 1.31 × 106 | 6.00 × 105 | 1.80 × 104 | 1.15 × 104 | |
| CEC2017_F15 | Mean | 5.68 × 103 | 7.87 × 104 | 4.69 × 103 | 1.74 × 105 | 1.44 × 107 | 2.87 × 106 | 5.02 × 108 | 1.00 × 105 | 2.40 × 107 | 5.38 × 103 | 3.27 × 103 |
| Std | 3.51 × 103 | 2.97 × 104 | 2.75 × 103 | 6.10 × 104 | 4.14 × 107 | 4.44 × 106 | 1.75 × 108 | 7.34 × 104 | 9.34 × 106 | 5.19 × 103 | 1.69 × 103 | |
| CEC2017_F16 | Mean | 5.64 × 103 | 6.89 × 103 | 6.00 × 103 | 1.09 × 104 | 8.75 × 103 | 8.44 × 103 | 1.03 × 104 | 8.53 × 103 | 1.04 × 104 | 8.94 × 103 | 5.86 × 103 |
| Std | 9.37 × 102 | 9.34 × 102 | 6.61 × 102 | 4.20 × 102 | 9.88 × 102 | 2.03 × 103 | 7.67 × 102 | 3.99 × 102 | 3.63 × 102 | 5.64 × 102 | 6.87 × 102 | |
| CEC2017_F17 | Mean | 4.93 × 103 | 5.75 × 103 | 5.81 × 103 | 7.50 × 103 | 8.46 × 103 | 5.90 × 103 | 9.89 × 103 | 6.37 × 103 | 6.81 × 103 | 6.23 × 103 | 5.11 × 103 |
| Std | 5.64 × 102 | 6.17 × 102 | 5.49 × 102 | 3.18 × 102 | 1.16 × 103 | 1.47 × 103 | 8.83 × 102 | 2.80 × 102 | 2.65 × 102 | 4.14 × 102 | 6.93 × 102 | |
| CEC2017_F18 | Mean | 2.75 × 106 | 4.21 × 106 | 4.11 × 105 | 2.61 × 106 | 2.12 × 107 | 1.01 × 107 | 2.90 × 107 | 2.82 × 106 | 2.61 × 106 | 2.32 × 105 | 1.65 × 105 |
| Std | 1.44 × 106 | 2.26 × 106 | 2.20 × 105 | 6.22 × 105 | 2.05 × 107 | 1.21 × 107 | 7.53 × 106 | 9.69 × 105 | 6.06 × 105 | 9.28 × 104 | 7.46 × 104 | |
| CEC2017_F19 | Mean | 4.36 × 103 | 1.39 × 107 | 6.72 × 103 | 3.98 × 105 | 2.29 × 107 | 5.97 × 106 | 6.08 × 108 | 9.75 × 104 | 2.93 × 107 | 4.61 × 103 | 3.31 × 103 |
| Std | 2.54 × 103 | 9.33 × 106 | 4.37 × 103 | 1.92 × 105 | 2.39 × 107 | 7.51 × 106 | 1.75 × 108 | 5.47 × 104 | 9.69 × 106 | 3.62 × 103 | 1.86 × 103 | |
| CEC2017_F20 | Mean | 7.09 × 103 | 5.40 × 103 | 5.55 × 103 | 7.84 × 103 | 6.06 × 103 | 6.88 × 103 | 6.26 × 103 | 6.36 × 103 | 6.84 × 103 | 6.81 × 103 | 5.57 × 103 |
| Std | 3.13 × 102 | 6.23 × 102 | 5.44 × 102 | 3.10 × 102 | 7.10 × 102 | 4.56 × 102 | 4.14 × 102 | 2.73 × 102 | 2.81 × 102 | 3.47 × 102 | 5.70 × 102 | |
| CEC2017_F21 | Mean | 3.06 × 103 | 3.12 × 103 | 3.19 × 103 | 3.46 × 103 | 3.80 × 103 | 2.83 × 103 | 3.64 × 103 | 3.20 × 103 | 3.47 × 103 | 3.16 × 103 | 2.83 × 103 |
| Std | 1.18 × 102 | 1.38 × 102 | 1.47 × 102 | 5.06 × 101 | 1.35 × 102 | 1.90 × 102 | 3.98 × 101 | 3.65 × 101 | 3.80 × 101 | 4.23 × 101 | 1.16 × 102 | |
| CEC2017_F22 | Mean | 3.34 × 104 | 1.92 × 104 | 1.98 × 104 | 3.48 × 104 | 2.22 × 104 | 3.17 × 104 | 3.03 × 104 | 2.67 × 104 | 3.09 × 104 | 3.33 × 104 | 2.50 × 104 |
| Std | 4.79 × 103 | 1.54 × 103 | 1.93 × 103 | 5.24 × 102 | 3.05 × 103 | 2.55 × 103 | 7.53 × 102 | 5.89 × 102 | 3.98 × 102 | 6.27 × 102 | 1.15 × 103 | |
| CEC2017_F23 | Mean | 3.60 × 103 | 3.59 × 103 | 3.79 × 103 | 4.07 × 103 | 4.35 × 103 | 3.38 × 103 | 4.07 × 103 | 3.65 × 103 | 4.37 × 103 | 3.36 × 103 | 3.21 × 103 |
| Std | 1.27 × 102 | 1.64 × 102 | 1.28 × 102 | 7.13 × 101 | 1.94 × 102 | 1.16 × 102 | 6.18 × 101 | 3.14 × 101 | 5.86 × 101 | 8.32 × 101 | 4.91 × 101 | |
| CEC2017_F24 | Mean | 4.35 × 103 | 4.14 × 103 | 4.59 × 103 | 4.52 × 103 | 5.26 × 103 | 4.05 × 103 | 4.79 × 103 | 4.23 × 103 | 5.06 × 103 | 4.03 × 103 | 3.70 × 103 |
| Std | 1.68 × 102 | 1.59 × 102 | 2.56 × 102 | 6.90 × 101 | 2.41 × 102 | 1.67 × 102 | 5.08 × 101 | 5.11 × 101 | 8.05 × 101 | 1.02 × 102 | 7.94 × 101 | |
| CEC2017_F25 | Mean | 4.24 × 103 | 3.60 × 103 | 3.51 × 103 | 4.15 × 103 | 6.35 × 103 | 3.73 × 103 | 1.24 × 104 | 4.08 × 103 | 7.09 × 103 | 3.44 × 103 | 3.41 × 103 |
| Std | 2.25 × 102 | 7.97 × 101 | 5.82 × 101 | 1.43 × 102 | 4.65 × 103 | 1.41 × 102 | 1.15 × 103 | 1.41 × 102 | 3.49 × 102 | 4.57 × 101 | 6.71 × 101 | |
| CEC2017_F26 | Mean | 2.27 × 104 | 1.44 × 104 | 2.26 × 104 | 1.87 × 104 | 2.47 × 104 | 1.36 × 104 | 2.14 × 104 | 1.57 × 104 | 2.47 × 104 | 1.28 × 104 | 1.00 × 104 |
| Std | 3.09 × 103 | 3.15 × 103 | 4.12 × 103 | 8.12 × 102 | 2.53 × 103 | 1.73 × 103 | 8.55 × 102 | 5.41 × 102 | 1.14 × 103 | 1.11 × 103 | 8.84 × 102 | |
| CEC2017_F27 | Mean | 4.22 × 103 | 3.87 × 103 | 3.91 × 103 | 3.86 × 103 | 4.18 × 103 | 3.84 × 103 | 4.51 × 103 | 4.01 × 103 | 5.31 × 103 | 3.42 × 103 | 3.43 × 103 |
| Std | 2.45 × 102 | 1.40 × 102 | 2.73 × 102 | 2.03 × 102 | 2.15 × 102 | 1.21 × 102 | 1.08 × 102 | 7.65 × 101 | 1.37 × 102 | 3.67 × 101 | 4.26 × 101 | |
| CEC2017_F28 | Mean | 5.13 × 103 | 3.68 × 103 | 3.62 × 103 | 4.41 × 103 | 1.76 × 104 | 4.31 × 103 | 1.58 × 104 | 5.05 × 103 | 1.04 × 104 | 3.53 × 103 | 3.53 × 103 |
| Std | 6.61 × 102 | 9.50 × 101 | 7.47 × 101 | 3.36 × 102 | 5.79 × 103 | 3.45 × 102 | 1.33 × 103 | 3.29 × 102 | 5.32 × 102 | 5.10 × 101 | 3.76 × 101 | |
| CEC2017_F29 | Mean | 7.82 × 103 | 9.56 × 103 | 7.66 × 103 | 1.06 × 104 | 1.03 × 104 | 7.28 × 103 | 1.46 × 104 | 8.35 × 103 | 1.14 × 104 | 8.25 × 103 | 6.72 × 103 |
| Std | 6.19 × 102 | 9.87 × 102 | 6.62 × 102 | 3.48 × 102 | 1.46 × 103 | 1.07 × 103 | 1.01 × 103 | 2.88 × 102 | 3.46 × 102 | 5.06 × 102 | 7.14 × 102 | |
| CEC2017_F30 | Mean | 4.26 × 105 | 1.22 × 108 | 9.77 × 104 | 1.80 × 106 | 8.40 × 107 | 1.04 × 106 | 1.06 × 109 | 4.06 × 106 | 3.47 × 108 | 5.73 × 104 | 3.34 × 104 |
| Std | 3.61 × 105 | 5.26 × 107 | 1.05 × 105 | 5.53 × 105 | 1.33 × 108 | 6.90 × 105 | 2.67 × 108 | 1.17 × 106 | 1.08 × 108 | 2.85 × 104 | 1.15 × 104 | |
| MeanRank | 5.76 | 4.90 | 4.07 | 7.55 | 8.72 | 5.07 | 9.93 | 5.86 | 8.79 | 3.59 | 1.76 | |
| FinalRank | 6 | 4 | 3 | 8 | 9 | 5 | 11 | 7 | 10 | 2 | 1 | |
| Rank First | 2 | 4 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 5 | 14 |
| Problems | TLBO | SSA | INFO | DE | DBO | SO | CLPSO | BDE | BESD | GO |
|---|---|---|---|---|---|---|---|---|---|---|
| CEC2017_F1 | 2.67 × 10−9/− | 4.18 × 10−9/− | 1.50 × 10−2/+ | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.70 × 10−2/− |
| CEC2017_F3 | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.22 × 10−2/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− |
| CEC2017_F4 | 3.82 × 10−9/− | 3.02 × 10−11/− | 4.69 × 10−8/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.15 × 10−10/− | 3.02 × 10−11/− | 7.39 × 10−11/− | 3.02 × 10−11/− | 3.27 × 10−2/− |
| CEC2017_F5 | 1.86 × 10−9/− | 4.50 × 10−11/− | 3.69 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.01 × 10−4/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.78 × 10−10/− |
| CEC2017_F6 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.01 × 10−4/+ |
| CEC2017_F7 | 1.55 × 10−9/− | 7.39 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.37 × 10−10/− | 4.03 × 10−3/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.08 × 10−11/− |
| CEC2017_F8 | 4.71 × 10−4/− | 6.70 × 10−11/− | 2.15 × 10−10/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 8.50 × 10−2/= | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 5.57 × 10−10/− |
| CEC2017_F9 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.08 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 6.55 × 10−4/+ |
| CEC2017_F10 | 3.02 × 10−11/− | 2.51 × 10−2/− | 1.30 × 10−3/− | 3.02 × 10−11/− | 9.51 × 10−6/− | 5.59 × 10−1/= | 3.02 × 10−11/− | 1.61 × 10−6/− | 3.02 × 10−11/− | 3.02 × 10−11/− |
| CEC2017_F11 | 1.61 × 10−10/− | 3.02 × 10−11/− | 1.33 × 10−10/− | 7.39 × 10−11/− | 3.02 × 10−11/− | 9.26 × 10−9/− | 3.02 × 10−11/− | 2.92 × 10−9/− | 3.02 × 10−11/− | 1.64 × 10−5/− |
| CEC2017_F12 | 4.50 × 10−11/− | 3.02 × 10−11/− | 4.57 × 10−9/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.62 × 10−3/− |
| CEC2017_F13 | 3.47 × 10−10/− | 3.02 × 10−11/− | 2.61 × 10−10/− | 1.43 × 10−8/− | 3.02 × 10−11/− | 6.07 × 10−11/− | 3.02 × 10−11/− | 4.50 × 10−11/− | 3.02 × 10−11/− | 4.22 × 10−4/− |
| CEC2017_F14 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.20 × 10−9/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.19 × 10−6/− |
| CEC2017_F15 | 3.02 × 10−11/− | 3.02 × 10−11/− | 6.07 × 10−11/− | 3.57 × 10−6/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.71 × 10−4/− |
| CEC2017_F16 | 1.17 × 10−4/− | 1.31 × 10−8/− | 1.34 × 10−5/− | 3.02 × 10−11/− | 2.61 × 10−10/− | 7.20 × 10−5/− | 3.02 × 10−11/− | 2.15 × 10−10/− | 3.02 × 10−11/− | 1.53 × 10−5/− |
| CEC2017_F17 | 1.24 × 10−3/− | 7.77 × 10−9/− | 1.33 × 10−10/− | 3.02 × 10−11/− | 4.50 × 10−11/− | 1.31 × 10−8/− | 2.15 × 10−10/− | 3.01 × 10−7/− | 1.17 × 10−9/− | 3.67 × 10−3/− |
| CEC2017_F18 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.08 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.33 × 10−10/− |
| CEC2017_F19 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 7.39 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.31 × 10−8/− |
| CEC2017_F20 | 2.20 × 10−7/− | 1.78 × 10−10/− | 1.69 × 10−9/− | 3.02 × 10−11/− | 1.33 × 10−10/− | 1.85 × 108/− | 5.49 × 10−11/− | 2.83 × 10−8/− | 5.49 × 10−11/− | 2.27 × 10−3/− |
| CEC2017_F21 | 6.53 × 10−7/− | 3.69 × 10−11/− | 3.69 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.25 × 10−5/− | 6.70 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 6.70 × 10−11/− |
| CEC2017_F22 | 1.29 × 10−9/− | 1.86 × 10−9/− | 1.11 × 10−4/− | 3.02 × 10−11/− | 5.57 × 10−10/− | 1.61 × 10−10/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 5.00 × 10−9/− |
| CEC2017_F23 | 1.20 × 10−8/− | 3.02 × 10−11/− | 3.34 × 10−11/− | 4.98 × 10−11/− | 3.02 × 10−11/− | 4.20 × 10−10/− | 4.08 × 10−11/− | 4.08 × 10−11/− | 3.02 × 10−11/− | 9.26 × 10−9/− |
| CEC2017_F24 | 2.00 × 10−5/− | 8.48 × 10−9/− | 3.47 × 10−10/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.30 × 10−3/− | 3.02 × 10−11/− | 4.50 × 10−11/− | 3.02 × 10−11/− | 6.07 × 10−11/− |
| CEC2017_F25 | 9.06 × 10−8/− | 5.07 × 10−10/− | 3.57 × 10−6/− | 1.17 × 10−3/− | 3.02 × 10−11/− | 5.60 × 10−7/− | 3.02 × 10−11/− | 9.92 × 10−11/− | 3.02 × 10−11/− | 1.45 × 10−1/= |
| CEC2017_F26 | 1.03 × 10−2/− | 9.53 × 10−7/− | 1.86 × 10−6/− | 1.58 × 10−1/= | 3.82 × 10−9/− | 1.21 × 10−10/− | 9.06 × 10−8/− | 2.71 × 10−2/− | 8.77 × 10−2/= | 8.15 × 10−5/− |
| CEC2017_F27 | 7.12 × 10−9/− | 2.87 × 10−10/− | 1.21 × 10−10/− | 2.87 × 10−10/− | 7.39 × 10−11/− | 6.07 × 10−11/− | 3.02 × 10−11/− | 4.98 × 10−11/− | 3.02 × 10−11/− | 1.68 × 10−3/+ |
| CEC2017_F28 | 4.22 × 10−4/− | 9.83 × 10−8/− | 2.77 × 10−1/= | 7.62 × 10−3/− | 3.34 × 10−11/− | 3.08 × 10−8/− | 3.02 × 10−11/− | 5.97 × 10−5/− | 3.02 × 10−11/− | 3.39 × 102/+ |
| CEC2017_F29 | 1.25 × 10−5/− | 8.15 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.08 × 10−11/− | 2.38 × 10−7/− | 3.02 × 10−11/− | 8.35 × 10−8/− | 3.02 × 10−11/− | 2.25 × 10−4/− |
| CEC2017_F30 | 4.08 × 10−11/− | 3.02 × 10−11/− | 1.61 × 10−10/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 9.92 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.16 × 10−10/− |
| +/−/= | 0/29/0 | 0/29/0 | 1/27/1 | 0/28/1 | 0/29/0 | 0/27/2 | 0/29/0 | 0/29/0 | 0/28/1 | 4/24/1 |
| Problems | TLBO | SSA | INFO | DE | DBO | SO | CLPSO | BDE | BESD | GO |
|---|---|---|---|---|---|---|---|---|---|---|
| CEC2017_F1 | 3.02 × 10−11/− | 4.73 × 10−1/= | 6.31 × 10−1/= | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.09 × 10−1/= |
| CEC2017_F3 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.83 × 10−5/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.55 × 10−9/− |
| CEC2017_F4 | 2.78 × 10−7/− | 8.84 × 10−7/− | 4.36 × 10−2/− | 1.01 × 10−8/− | 3.02 × 10−11/− | 1.96 × 10−10/− | 3.02 × 10−11/− | 3.69 × 10−11/− | 3.02 × 10−11/− | 8.07 × 10−1/= |
| CEC2017_F5 | 7.69 × 10−8/− | 3.02 × 10−11/− | 3.69 × 10−11/− | 3.02 × 10−11/− | 3.69 × 10−11/− | 9.47 × 10−1/= | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.08 × 10−11/− |
| CEC2017_F6 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.00 × 10−3/+ |
| CEC2017_F7 | 1.46 × 10−10/− | 8.15 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 5.49 × 10−11/− | 3.77 × 10−4/− | 3.02 × 10−11/− | 3.69 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− |
| CEC2017_F8 | 1.21 × 10−10/− | 5.49 × 10−11/− | 3.34 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.84 × 10−2/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− |
| CEC2017_F9 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.07 × 10−9/− | 3.02 × 10−11/− | 4.08 × 10−11/− | 3.02 × 10−11/− | 4.46 × 10−4/+ |
| CEC2017_F10 | 3.02 × 10−11/− | 5.20 × 10−1/= | 5.69 × 10−1/= | 3.02 × 10−11/− | 2.46 × 10−1/= | 6.20 × 104/− | 3.02 × 10−11/− | 8.48 × 10−9/− | 3.02 × 10−11/− | 3.02 × 10−11/− |
| CEC2017_F11 | 3.82 × 10−10/− | 3.02 × 10−11/− | 3.08 × 10−8/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 5.53 × 10−8/− |
| CEC2017_F12 | 8.10 × 10−10/− | 3.02 × 10−11/− | 3.16 × 10−10/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.03 × 10−2/− |
| CEC2017_F13 | 5.56 × 10−4/− | 3.02 × 10−11/− | 9.52 × 10−4/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.82 × 10−10/− | 3.02 × 10−11/− | 9.92 × 10−11/− | 3.02 × 10−11/− | 1.03 × 10−2/− |
| CEC2017_F14 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.16 × 10−7/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.96 × 10−8/− |
| CEC2017_F15 | 1.09 × 10−5/− | 3.34 × 10−11/− | 1.73 × 10−7/− | 2.53 × 10−4/+ | 3.02 × 10−11/− | 3.82 × 10−10/− | 3.02 × 10−11/− | 5.07 × 10−10/− | 3.02 × 10−11/− | 3.18 × 10−1/= |
| CEC2017_F16 | 6.31 × 10−1/= | 1.09 × 10−5/− | 2.68 × 10−4/− | 3.02 × 10−11/− | 8.89 × 10−10/− | 4.03 × 10−3/− | 1.33 × 10−10/− | 5.00 × 10−9/− | 3.16 × 10−10/− | 1.47 × 10−7/− |
| CEC2017_F17 | 2.42 × 10−2/− | 9.76 × 10−10/− | 6.01 × 10−8/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.77 × 10−5/− | 3.02 × 10−11/− | 1.17 × 10−9/− | 4.08 × 10−11/− | 1.60 × 10−7/− |
| CEC2017_F18 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.20 × 10−7/− |
| CEC2017_F19 | 5.49 × 10−11/− | 3.02 × 10−11/− | 5.49 × 10−11/− | 6.52 × 10−9/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.89 × 10−4/− |
| CEC2017_F20 | 1.78 × 10−10/− | 4.36 × 10−2/− | 3.18 × 10−4/− | 3.02 × 10−11/− | 9.83 × 10−8/− | 3.95 × 10−1/= | 1.01 × 10−8/− | 1.29 × 10−6/− | 3.82 × 10−10/− | 9.21 × 10−5/− |
| CEC2017_F21 | 1.86 × 10−9/− | 3.34 × 10−11/− | 3.69 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 6.20 × 10−4/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.34 × 10−11/− |
| CEC2017_F22 | 3.32 × 10−6/− | 4.04 × 10−1/= | 3.63 × 10−1/= | 3.02 × 10−11/− | 1.43 × 10−5/− | 3.08 × 10−8/− | 1.07 × 10−9/− | 9.06 × 10−8/− | 2.02 × 10−8/− | 5.07 × 10−10/− |
| CEC2017_F23 | 6.70 × 10−11/− | 3.34 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.03 × 10−9/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.78 × 10−10/− |
| CEC2017_F24 | 1.78 × 10−10/− | 6.70 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.04 × 10−4/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.98 × 10−11/− |
| CEC2017_F25 | 1.96 × 10−10/− | 3.09 × 10−6/− | 1.06 × 10−3/− | 4.35 × 10−5/− | 9.92 × 10−11/− | 1.29 × 10−9/− | 3.02 × 10−11/− | 5.49 × 10−11/− | 3.02 × 10−11/− | 7.51 × 10−1/= |
| CEC2017_F26 | 8.48 × 10−9/− | 1.86 × 10−1/= | 8.48 × 10−9/− | 3.02 × 10−11/− | 5.57 × 10−10/− | 6.70 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.43 × 10−5/− |
| CEC2017_F27 | 8.15 × 10−11/− | 5.49 × 10−11/− | 7.39 × 10−11/− | 1.46 × 10−10/− | 4.50 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.68 × 10−4/+ |
| CEC2017_F28 | 6.70 × 10−11/− | 2.83 × 10−8/− | 4.43 × 10−3/− | 3.32 × 10−6/− | 3.02 × 10−11/− | 3.69 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.77 × 10−1/= |
| CEC2017_F29 | 5.49 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 5.00 × 10−9/− | 3.02 × 10−11/− | 7.39 × 10−11/− | 3.02 × 10−11/− | 1.25 × 10−4/− |
| CEC2017_F30 | 1.09 × 10−5/− | 3.02 × 10−11/− | 1.03 × 10−2/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.50 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 8.50 × 10−2/= |
| +/−/= | 0/28/1 | 0/25/4 | 0/26/3 | 1/28/0 | 0/28/1 | 0/27/2 | 0/29/0 | 0/29/0 | 0/29/0 | 3/20/6 |
| Problems | TLBO | SSA | INFO | DE | DBO | SO | CLPSO | BDE | BESD | GO |
|---|---|---|---|---|---|---|---|---|---|---|
| CEC2017_F1 | 3.02 × 10−11/− | 3.02 × 10−11/+ | 7.74 × 10−6/+ | 3.02 × 10−11/− | 3.02 × 10−11/− | 7.04 × 10−7/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.05 × 10−1/= |
| CEC2017_F3 | 3.02 × 10−11/− | 3.02 × 10−11/− | 9.12 × 10−1/= | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.69 × 10−11/− |
| CEC2017_F4 | 3.02 × 10−11/− | 1.41 × 10−9/− | 1.47 × 10−7/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.96 × 10−10/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 7.73 × 10−2/= |
| CEC2017_F5 | 6.91 × 10−4/− | 9.76 × 10−10/− | 3.47 × 10−10/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.33 × 10−1/= | 3.02 × 10−11/− | 3.34 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− |
| CEC2017_F6 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 7.39 × 10−11/− | 3.02 × 10−11/− | 3.34 × 10−11/− | 3.02 × 10−11/− | 3.56 × 10−4/+ |
| CEC2017_F7 | 3.02 × 10−11/− | 6.70 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.08 × 10−8/+ | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.34 × 10−11/− |
| CEC2017_F8 | 4.11 × 10−7/− | 2.44 × 10−9/− | 8.89 × 10−10/− | 3.02 × 10−11/− | 3.69 × 10−11/− | 3.18 × 10−1/= | 3.02 × 10−11/− | 5.49 × 10−11/− | 3.02 × 10−11/− | 7.39 × 10−11/− |
| CEC2017_F9 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 5.40 × 10−1/= | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.32 × 10−2/+ |
| CEC2017_F10 | 3.02 × 10−11/− | 8.99 × 10−11/+ | 4.50 × 10−11/+ | 3.02 × 10−11/− | 4.31 × 10−8/+ | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.87 × 107/− | 3.02 × 10−11/− | 3.02 × 10−11/− |
| CEC2017_F11 | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.07 × 10−9/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.34 × 10−11/− |
| CEC2017_F12 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.96 × 10−8/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.69 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.61 × 10−6/− |
| CEC2017_F13 | 2.83 × 10−8/− | 3.02 × 10−11/− | 5.61 × 10−5/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.01 × 10−1/= |
| CEC2017_F14 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 6.28 × 10−6/− |
| CEC2017_F15 | 7.20 × 10−5/− | 3.02 × 10−11/− | 3.34 × 10−3/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 7.39 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.06 × 10−2/− |
| CEC2017_F16 | 2.12 × 10−1/= | 2.43 × 10−5/− | 4.55 × 10−1/= | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.15 × 10−6/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− |
| CEC2017_F17 | 2.34 × 10−1/= | 1.60 × 10−3/− | 1.11 × 10−4/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 9.05 × 10−2/= | 3.02 × 10−11/− | 2.87 × 10−10/− | 3.34 × 10−11/− | 1.01 × 10−8/− |
| CEC2017_F18 | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.80 × 10−7/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.86 × 10−3/− |
| CEC2017_F19 | 2.61 × 10−2/− | 3.02 × 10−11/− | 8.29 × 10−6/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.98 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.29 × 10−1/= |
| CEC2017_F20 | 4.98 × 10−11/− | 3.79 × 10−1/= | 7.17 × 10−1/= | 3.02 × 10−11/− | 6.38 × 10−3/− | 9.76 × 10−10/− | 1.34 × 105/− | 1.60 × 107/− | 1.61 × 10−10/− | 2.15 × 10−10/− |
| CEC2017_F21 | 3.08 × 10−8/− | 9.76 × 10−10/− | 2.61 × 10−10/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.63 × 10−1/= | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.34 × 10−11/− |
| CEC2017_F22 | 5.57 × 10−10/− | 3.02 × 10−11/+ | 1.21 × 10−10/+ | 3.02 × 10−11/− | 5.53 × 10−8/+ | 3.34 × 10−11/− | 3.02 × 10−11/− | 1.20 × 10−8/− | 3.02 × 10−11/− | 3.02 × 10−11/− |
| CEC2017_F23 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.25 × 10−7/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.92 × 10−9/− |
| CEC2017_F24 | 3.02 × 10−11/− | 3.69 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.61 × 10−10/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.09 × 10−10/− |
| CEC2017_F25 | 3.02 × 10−11/− | 1.29 × 10−9/− | 3.81 × 10−7/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 6.07 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 1.50 × 10−2/− |
| CEC2017_F26 | 3.02 × 10−11/− | 8.48 × 10−9/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.15 × 10−10/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.37 × 10−10/− |
| CEC2017_F27 | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.84 × 101/= |
| CEC2017_F28 | 3.02 × 10−11/− | 6.52 × 10−9/− | 2.32 × 10−6/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.55 × 10−1/= |
| CEC2017_F29 | 4.11 × 10−7/− | 5.49 × 10−11/− | 1.64 × 10−5/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 5.19 × 10−2/= | 3.02 × 10−11/− | 6.70 × 10−11/− | 3.02 × 10−11/− | 1.17 × 10−9/− |
| CEC2017_F30 | 3.34 × 10−11/− | 3.02 × 10−11/− | 7.04 × 10−7/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 2.84 × 10−4/− |
| +/−/= | 0/27/2 | 3/25/1 | 3/23/3 | 0/29/0 | 2/27/0 | 1/22/6 | 0/29/0 | 0/29/0 | 0/29/0 | 2/21/6 |
| Dimensions | 30D | 50D | 100D | |||
|---|---|---|---|---|---|---|
| Algorithms | Mean Rank | Final Rank | Mean Rank | Final Rank | Mean Rank | Final Rank |
| TLBO | 5.05 | 3 | 5.31 | 5 | 5.77 | 6 |
| SSA | 7.08 | 8 | 6.08 | 7 | 5.13 | 5 |
| INFO | 5.51 | 5 | 4.82 | 3 | 3.99 | 3 |
| DE | 6.51 | 7 | 7.02 | 8 | 7.67 | 8 |
| DBO | 8.91 | 10 | 8.69 | 10 | 8.49 | 9 |
| SO | 5.58 | 6 | 5.10 | 4 | 5.01 | 4 |
| CLPSO | 9.60 | 11 | 9.84 | 11 | 9.87 | 11 |
| BDE | 5.30 | 4 | 5.61 | 6 | 5.78 | 7 |
| BESD | 7.79 | 9 | 8.39 | 9 | 8.77 | 10 |
| GO | 3.03 | 2 | 3.38 | 2 | 3.63 | 2 |
| CODGBGO | 1.65 | 1 | 1.75 | 1 | 1.87 | 1 |
| Dimensions | 10D | 20D | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithms | Algorithms | ||||||||
| Problems | ALSHADE | IMODE | LSHADE | CODGBGO | ALSHADE | IMODE | LSHADE | CODGBGO | |
| CEC2020_F1 | Mean | 1.00 × 102 | 1.00 × 102 | 1.00 × 102 | 1.00 × 102 | 1.00 × 102 | 1.00 × 102 | 1.00 × 102 | 1.00 × 102 |
| Std | 0.00 × 100 | 2.64 × 10−15 | 0.00 × 100 | 1.50 × 10−10 | 2.04 × 10−14 | 5.91 × 10−12 | 1.20 × 10−12 | 9.49 × 10−5 | |
| CEC2020_F2 | Mean | 1.15 × 103 | 1.16 × 103 | 1.12 × 103 | 1.11 × 103 | 1.21 × 103 | 1.30 × 103 | 1.28 × 103 | 1.12 × 103 |
| Std | 6.99 × 101 | 5.43 × 101 | 2.25 × 101 | 5.19 × 100 | 4.01 × 101 | 9.85 × 101 | 8.29 × 101 | 8.88 × 100 | |
| CEC2020_F3 | Mean | 7.13 × 102 | 7.17 × 102 | 7.12 × 102 | 7.12 × 102 | 7.26 × 102 | 7.29 × 102 | 7.27 × 102 | 7.26 × 102 |
| Std | 8.45 × 10−1 | 2.28 × 100 | 9.45 × 10−1 | 1.36 × 101 | 1.43 × 101 | 1.98 × 100 | 7.90 × 10−1 | 3.47 × 10−13 | |
| CEC2020_F4 | Mean | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 | 1.90 × 103 |
| Std | 1.07 × 10−1 | 2.25 × 10−1 | 7.01 × 10−2 | 7.91 × 10−2 | 1.89 × 10−1 | 2.84 × 10−1 | 2.13 × 10−1 | 4.63 × 10−13 | |
| CEC2020_F5 | Mean | 1.72 × 103 | 1.73 × 103 | 1.70 × 103 | 1.70 × 103 | 2.16 × 103 | 2.07 × 103 | 2.01 × 103 | 1.93 × 103 |
| Std | 3.07 × 101 | 4.53 × 101 | 1.42 × 100 | 3.33 × 10−1 | 2.20 × 102 | 1.02 × 102 | 2.75 × 100 | 2.82 × 100 | |
| CEC2020_F6 | Mean | 1.60 × 103 | 1.60 × 103 | 1.60 × 103 | 1.60 × 103 | 1.60 × 103 | 1.60 × 103 | 1.60 × 103 | 1.60 × 103 |
| Std | 3.00 × 10−1 | 2.03 × 100 | 3.00 × 10−1 | 2.88 × 10−1 | 2.59 × 10−1 | 3.44 × 10−1 | 3.53 × 10−1 | 0.00 × 100 | |
| CEC2020_F7 | Mean | 2.10 × 103 | 2.10 × 103 | 2.10 × 103 | 2.10 × 103 | 2.22 × 103 | 2.16 × 103 | 2.15 × 103 | 2.16 × 103 |
| Std | 2.60 × 10−1 | 3.11 × 10−1 | 3.18 × 101 | 1.79 × 10−1 | 1.02 × 102 | 6.29 × 101 | 5.23 × 101 | 3.01 × 100 | |
| CEC2020_F8 | Mean | 2.30 × 103 | 2.31 × 103 | 2.31 × 103 | 2.31 × 103 | 2.31 × 103 | 2.31 × 103 | 2.31 × 103 | 2.31 × 103 |
| Std | 2.50 × 101 | 4.55 × 10−13 | 4.31 × 10−13 | 4.31 × 10−13 | 0.00 × 100 | 7.97 × 10−13 | 6.86 × 10−13 | 0.00 × 100 | |
| CEC2020_F9 | Mean | 2.72 × 103 | 2.66 × 103 | 2.68 × 103 | 2.74 × 103 | 2.81 × 103 | 2.82 × 103 | 2.81 × 103 | 2.84 × 103 |
| Std | 4.26 × 101 | 1.13 × 102 | 9.39 × 101 | 4.35 × 100 | 4.83 × 100 | 6.04 × 101 | 1.66 × 100 | 1.33 × 101 | |
| CEC2020_F10 | Mean | 2.92 × 103 | 2.91 × 103 | 2.91 × 103 | 2.90 × 103 | 2.92 × 103 | 2.92 × 103 | 2.91 × 103 | 2.91 × 103 |
| Std | 2.33 × 101 | 1.72 × 101 | 1.72 × 101 | 4.54 × 10−1 | 1.09 × 101 | 1.69 × 101 | 1.72 × 10−2 | 3.05 × 10−2 | |
| Mean Rank | 2.4 | 2.8 | 2.1 | 1.4 | 2.3 | 2.9 | 2.2 | 1.4 | |
| Final Rank | 3 | 4 | 2 | 1 | 3 | 4 | 2 | 1 | |
| Rank First | 2 | 2 | 1 | 8 | 1 | 2 | 4 | 8 | |
| Dimensions | 10D | 20D | ||||
|---|---|---|---|---|---|---|
| Algorithms | Algorithms | |||||
| Problems | ALSHADE | IMODE | LSHADE | ALSHADE | IMODE | LSHADE |
| CEC2020_F1 | 1.63 × 10−11/+ | 1.63 × 10−11/+ | 1.63 × 10−11/+ | 1.21 × 10−12/+ | 3.16 × 10−12/+ | 7.82 × 10−12/+ |
| CEC2020_F2 | 1.42 × 10−4/− | 2.36 × 10−9/− | 7.39 × 10−4/− | 1.37 × 10−8/− | 9.26 × 10−10/− | 2.15 × 10−12/− |
| CEC2020_F3 | 4.87 × 10−4/− | 7.41 × 10−11/− | 4.34 × 10−2/− | 1.22 × 10−12/− | 1.01 × 10−12/− | 3.90 × 10−13/− |
| CEC2020_F4 | 2.40 × 10−11/− | 2.40 × 10−11/− | 5.93 × 10−11/− | 7.15 × 10−9/− | 3.36 × 10−11/− | 1.21 × 10−12/− |
| CEC2020_F5 | 5.18 × 10−5/− | 3.87 × 10−4/− | 2.21 × 10−3/− | 2.34 × 10−5/− | 3.73 × 10−11/− | 4.29 × 10−14/− |
| CEC2020_F6 | 3.47 × 10−1/= | 7.47 × 10−2/= | 6.93 × 10−1/= | 1.81 × 10−7/− | 2.05 × 10−5/− | 1.21 × 10−12/− |
| CEC2020_F7 | 1.47 × 10−1/= | 1.22 × 10−1/= | 3.53 × 10−1/= | 2.06 × 10−2/− | 1.55 × 10−1/= | 2.34 × 10−5/+ |
| CEC2020_F8 | 1.61 × 10−1/= | 3.34 × 10−1/= | 3.34 × 10−1/= | 3.34 × 10−1/= | 3.34 × 10−1/= | 3.34 × 10−1/= |
| CEC2020_F9 | 1.55 × 10−8/+ | 1.64 × 10−6/+ | 3.61 × 10−11/+ | 9.92 × 10−11/+ | 1.22 × 10−2/+ | 3.02 × 10−11/+ |
| CEC2020_F10 | 6.70 × 10−3/− | 2.71 × 10−1/= | 6.25 × 10−1/= | 1.72 × 10−12/− | 1.07 × 10−9/− | 1.35 × 10−12/− |
| +/−/= | 2/5/3 | 2/4/4 | 2/4/4 | 2/7/1 | 2/6/2 | 3/7/0 |
| Dimensions | 10D | 20D | ||
|---|---|---|---|---|
| Algorithms | Mean Rank | Final Rank | Mean Rank | Final Rank |
| ALSHADE | 2.58 | 3 | 2.55 | 2 |
| IMODE | 2.78 | 4 | 2.87 | 4 |
| SHADE | 2.35 | 2 | 2.59 | 3 |
| CODGBGO | 2.28 | 1 | 1.99 | 1 |
| Datasets | Number of Features | Number of Classifications | Dataset Size |
|---|---|---|---|
| IonosphereEW | 34 | 2 | 351 |
| Breastcancer | 9 | 2 | 699 |
| BreastEW | 30 | 2 | 569 |
| Congress | 16 | 2 | 435 |
| Wine | 13 | 3 | 178 |
| Vote | 16 | 2 | 435 |
| Vehicle | 18 | 4 | 846 |
| Exactly | 13 | 2 | 1000 |
| Glass | 9 | 7 | 214 |
| HeartEW | 13 | 2 | 270 |
| Landsat | 36 | 6 | 2000 |
| Lymphography | 18 | 4 | 148 |
| Zoo | 16 | 7 | 101 |
| WDBC | 30 | 2 | 569 |
| SonarEW | 60 | 2 | 208 |
| Libras | 90 | 15 | 360 |
| Spectf | 44 | 2 | 267 |
| MUSK | 166 | 2 | 476 |
| Datasets | Metric | PSO | DE | GWO | MVO | WOA | ABO | BOA | HHO | EO | GO | CODGBGO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IonosphereEW | Best | 0.0878 | 0.0562 | 0.0345 | 0.0492 | 0.0573 | 0.0503 | 0.0375 | 0.0503 | 0.0603 | 0.0375 | 0.0246 |
| Mean | 0.1278 | 0.0858 | 0.0545 | 0.0826 | 0.0919 | 0.0865 | 0.0641 | 0.1017 | 0.0714 | 0.0708 | 0.0476 | |
| Worst | 0.1797 | 0.1143 | 0.0750 | 0.1025 | 0.1245 | 0.1183 | 0.0977 | 0.1521 | 0.0889 | 0.0977 | 0.0790 | |
| Rank | (11/11/11) | (8/7/7) | (2/2/1) | (5/6/6) | (9/9/9) | (6/8/8) | (4/3/5) | (6/10/10) | (10/5/3) | (3/4/4) | (1/1/2) | |
| Breastcancer | Best | 0.0592 | 0.0528 | 0.0592 | 0.0592 | 0.0611 | 0.0592 | 0.0639 | 0.0416 | 0.0463 | 0.0546 | 0.0398 |
| Mean | 0.0626 | 0.0547 | 0.0603 | 0.0607 | 0.0684 | 0.0612 | 0.0696 | 0.0672 | 0.0468 | 0.0569 | 0.0422 | |
| Worst | 0.0805 | 0.0592 | 0.0722 | 0.0722 | 0.0916 | 0.0740 | 0.0787 | 0.0879 | 0.0481 | 0.0657 | 0.0463 | |
| Rank | (6/8/9) | (4/3/3) | (6/5/5) | (6/6/5) | (10/10/11) | (6/7/7) | (11/11/8) | (2/9/10) | (3/2/2) | (5/4/4) | (1/1/1) | |
| BreastEW | Best | 0.0439 | 0.0333 | 0.0472 | 0.0413 | 0.0419 | 0.0406 | 0.0452 | 0.0333 | 0.0293 | 0.0346 | 0.0246 |
| Mean | 0.0532 | 0.0488 | 0.0535 | 0.0602 | 0.0597 | 0.0574 | 0.0601 | 0.0531 | 0.0415 | 0.0489 | 0.0325 | |
| Worst | 0.0672 | 0.0672 | 0.0632 | 0.0752 | 0.0798 | 0.0704 | 0.0719 | 0.0706 | 0.0619 | 0.0719 | 0.0413 | |
| Rank | (9/6/4) | (3/3/4) | (11/7/3) | (7/11/10) | (8/9/11) | (6/8/6) | (10/10/8) | (3/5/7) | (2/2/2) | (5/4/8) | (1/1/1) | |
| Congress | Best | 0.0166 | 0.0250 | 0.0394 | 0.0601 | 0.0269 | 0.0623 | 0.0582 | 0.0476 | 0.0313 | 0.0353 | 0.0063 |
| Mean | 0.0215 | 0.0389 | 0.0452 | 0.0747 | 0.0275 | 0.0744 | 0.0788 | 0.0551 | 0.0371 | 0.0371 | 0.0063 | |
| Worst | 0.0313 | 0.0623 | 0.0519 | 0.0914 | 0.0353 | 0.0787 | 0.0974 | 0.0996 | 0.0373 | 0.0394 | 0.0063 | |
| Rank | (2/2/2) | (3/6/7) | (7/7/6) | (10/10/9) | (4/3/3) | (11/9/8) | (9/11/10) | (8/8/11) | (5/4/4) | (6/5/5) | (1/1/1) | |
| Wine | Best | 0.0308 | 0.0231 | 0.0565 | 0.0231 | 0.0411 | 0.0565 | 0.0308 | 0.0231 | 0.0231 | 0.0565 | 0.0231 |
| Mean | 0.0717 | 0.0427 | 0.0711 | 0.0449 | 0.0687 | 0.0606 | 0.0639 | 0.0664 | 0.0420 | 0.0656 | 0.0259 | |
| Worst | 0.1336 | 0.0642 | 0.1079 | 0.1053 | 0.1851 | 0.0745 | 0.1079 | 0.1387 | 0.0899 | 0.0899 | 0.0385 | |
| Rank | (6/11/9) | (1/3/2) | (9/10/7) | (1/4/6) | (8/9/11) | (9/5/3) | (6/6/7) | (1/8/10) | (1/2/4) | (9/7/4) | (1/1/1) | |
| Vote | Best | 0.0332 | 0.0269 | 0.0269 | 0.0228 | 0.0332 | 0.0166 | 0.0746 | 0.0394 | 0.0269 | 0.0250 | 0.0063 |
| Mean | 0.0399 | 0.0334 | 0.0269 | 0.0388 | 0.0367 | 0.0175 | 0.0932 | 0.0557 | 0.0269 | 0.0280 | 0.0067 | |
| Worst | 0.0541 | 0.0438 | 0.0269 | 0.0769 | 0.0435 | 0.0435 | 0.1388 | 0.0996 | 0.0269 | 0.0500 | 0.0188 | |
| Rank | (8/9/8) | (5/6/6) | (5/3/2) | (3/8/9) | (8/7/4) | (2/2/4) | (11/11/11) | (10/10/10) | (5/3/2) | (4/5/7) | (1/1/1) | |
| Vehicle | Best | 0.2575 | 0.2519 | 0.2563 | 0.2468 | 0.2568 | 0.2626 | 0.2621 | 0.2572 | 0.2568 | 0.2514 | 0.2308 |
| Mean | 0.2730 | 0.2710 | 0.2770 | 0.2660 | 0.2933 | 0.2857 | 0.2988 | 0.2966 | 0.2687 | 0.2746 | 0.2463 | |
| Worst | 0.3100 | 0.2950 | 0.3047 | 0.2947 | 0.3272 | 0.3105 | 0.3427 | 0.3334 | 0.3052 | 0.2943 | 0.2623 | |
| Rank | (9/5/7) | (4/4/4) | (5/7/5) | (2/2/3) | (6/9/9) | (11/8/8) | (10/11/11) | (8/10/10) | (6/3/6) | (3/6/2) | (1/1/1) | |
| Exactly | Best | 0.0462 | 0.0462 | 0.0462 | 0.0462 | 0.0462 | 0.0462 | 0.2177 | 0.0628 | 0.0462 | 0.0462 | 0.0462 |
| Mean | 0.1256 | 0.1047 | 0.2058 | 0.2006 | 0.2537 | 0.2183 | 0.2886 | 0.2662 | 0.1711 | 0.0781 | 0.0603 | |
| Worst | 0.3040 | 0.2704 | 0.2912 | 0.3143 | 0.2912 | 0.2912 | 0.2912 | 0.3387 | 0.2905 | 0.2912 | 0.2635 | |
| Rank | (1/4/9) | (1/3/2) | (1/7/4) | (1/6/10) | (1/9/4) | (1/8/4) | (11/11/4) | (10/10/11) | (1/5/3) | (1/2/4) | (1/1/1) | |
| Glass | Best | 0.2373 | 0.2905 | 0.2587 | 0.2698 | 0.2690 | 0.2373 | 0.2373 | 0.2484 | 0.2802 | 0.2690 | 0.1833 |
| Mean | 0.2438 | 0.2982 | 0.2745 | 0.2941 | 0.2952 | 0.2469 | 0.2890 | 0.2799 | 0.2952 | 0.2838 | 0.1894 | |
| Worst | 0.2810 | 0.3230 | 0.3016 | 0.3452 | 0.3333 | 0.2802 | 0.3341 | 0.3238 | 0.3119 | 0.3016 | 0.2476 | |
| Rank | (2/2/3) | (11/11/7) | (6/4/4) | (9/8/11) | (7/10/9) | (2/3/2) | (2/7/10) | (5/5/8) | (10/9/6) | (7/6/4) | (1/1/1) | |
| HeartEW | Best | 0.1897 | 0.1641 | 0.1231 | 0.1231 | 0.1038 | 0.1564 | 0.1551 | 0.1808 | 0.1308 | 0.1641 | 0.0974 |
| Mean | 0.2287 | 0.2052 | 0.1332 | 0.1754 | 0.1324 | 0.1928 | 0.2210 | 0.2291 | 0.1421 | 0.1742 | 0.1038 | |
| Worst | 0.2808 | 0.2615 | 0.1821 | 0.2218 | 0.1731 | 0.2385 | 0.2654 | 0.3038 | 0.1731 | 0.3308 | 0.1385 | |
| Rank | (11/10/9) | (8/8/7) | (3/3/4) | (3/6/5) | (2/2/2) | (7/7/6) | (6/9/8) | (10/11/10) | (5/4/2) | (8/5/11) | (1/1/1) | |
| Landsat | Best | 0.1117 | 0.1194 | 0.1122 | 0.1088 | 0.1061 | 0.1059 | 0.1292 | 0.1183 | 0.1083 | 0.1048 | 0.1010 |
| Mean | 0.1214 | 0.1325 | 0.1196 | 0.1201 | 0.1204 | 0.1160 | 0.1395 | 0.1436 | 0.1160 | 0.1122 | 0.1109 | |
| Worst | 0.1343 | 0.1495 | 0.1268 | 0.1339 | 0.1386 | 0.1240 | 0.1498 | 0.1623 | 0.1257 | 0.1228 | 0.1240 | |
| Rank | (7/8/7) | (10/9/9) | (8/5/5) | (6/6/6) | (4/7/8) | (3/4/2) | (11/10/10) | (9/11/11) | (5/3/4) | (2/2/1) | (1/1/2) | |
| Lymphography | Best | 0.1375 | 0.0898 | 0.1042 | 0.1065 | 0.0699 | 0.1264 | 0.1153 | 0.0755 | 0.0644 | 0.0644 | 0.0533 |
| Mean | 0.1890 | 0.1189 | 0.1181 | 0.1581 | 0.1152 | 0.1598 | 0.1741 | 0.1314 | 0.0860 | 0.0929 | 0.0649 | |
| Worst | 0.2506 | 0.1741 | 0.1519 | 0.2251 | 0.1885 | 0.1941 | 0.2418 | 0.2052 | 0.1153 | 0.1320 | 0.0954 | |
| Rank | (11/11/11) | (6/6/5) | (7/5/4) | (8/8/9) | (4/4/6) | (10/9/7) | (9/10/10) | (5/7/8) | (2/2/2) | (2/3/3) | (1/1/1) | |
| Zoo | Best | 0.0375 | 0.0438 | 0.0375 | 0.0375 | 0.0375 | 0.0375 | 0.0625 | 0.0500 | 0.0438 | 0.0438 | 0.0375 |
| Mean | 0.0875 | 0.0505 | 0.0667 | 0.0690 | 0.0668 | 0.0607 | 0.1323 | 0.0938 | 0.0746 | 0.0614 | 0.0516 | |
| Worst | 0.1475 | 0.0950 | 0.1213 | 0.1525 | 0.1075 | 0.0888 | 0.1788 | 0.1725 | 0.0825 | 0.0825 | 0.0825 | |
| Rank | (1/9/8) | (7/1/5) | (1/5/7) | (1/7/9) | (1/6/6) | (1/3/4) | (11/11/11) | (10/10/10) | (7/8/1) | (7/4/1) | (1/2/1) | |
| WDBC | Best | 0.0372 | 0.0791 | 0.0385 | 0.0552 | 0.0465 | 0.0532 | 0.0419 | 0.0545 | 0.0498 | 0.0498 | 0.0372 |
| Mean | 0.0527 | 0.0877 | 0.0457 | 0.0943 | 0.0642 | 0.0601 | 0.0575 | 0.0781 | 0.0528 | 0.0631 | 0.0393 | |
| Worst | 0.0778 | 0.1004 | 0.0678 | 0.1269 | 0.0830 | 0.0750 | 0.0758 | 0.0971 | 0.0704 | 0.0771 | 0.0578 | |
| Rank | (1/3/7) | (11/10/10) | (3/2/2) | (10/11/11) | (5/8/8) | (8/6/4) | (4/5/5) | (9/9/9) | (6/4/3) | (6/7/6) | (1/1/1) | |
| SonarEW | Best | 0.0536 | 0.0620 | 0.0167 | 0.1075 | 0.0822 | 0.0789 | 0.0859 | 0.0672 | 0.0320 | 0.0470 | 0.0117 |
| Mean | 0.1225 | 0.0922 | 0.0609 | 0.1457 | 0.1127 | 0.1293 | 0.1111 | 0.1295 | 0.0546 | 0.0893 | 0.0192 | |
| Worst | 0.1887 | 0.1209 | 0.1195 | 0.1937 | 0.1584 | 0.1684 | 0.1381 | 0.1867 | 0.0995 | 0.1364 | 0.0300 | |
| Rank | (5/8/10) | (6/5/4) | (2/3/3) | (11/11/11) | (9/7/7) | (8/9/8) | (10/6/6) | (7/10/9) | (3/2/2) | (4/4/5) | (1/1/1) | |
| Libras | Best | 0.1389 | 0.1625 | 0.1269 | 0.0992 | 0.1428 | 0.1644 | 0.1303 | 0.1494 | 0.1156 | 0.1447 | 0.0667 |
| Mean | 0.1770 | 0.1979 | 0.1581 | 0.1376 | 0.1885 | 0.2185 | 0.1727 | 0.1984 | 0.1435 | 0.1783 | 0.0913 | |
| Worst | 0.2103 | 0.2122 | 0.1833 | 0.1569 | 0.2439 | 0.2492 | 0.1939 | 0.2411 | 0.1781 | 0.2050 | 0.1164 | |
| Rank | (6/6/7) | (10/9/8) | (4/4/4) | (2/2/2) | (7/8/10) | (11/11/11) | (5/5/5) | (9/10/9) | (3/3/3) | (8/7/6) | (1/1/1) | |
| Spectf | Best | 0.0681 | 0.0602 | 0.0544 | 0.1076 | 0.0963 | 0.0985 | 0.1145 | 0.1076 | 0.0669 | 0.0511 | 0.0511 |
| Mean | 0.1073 | 0.1140 | 0.0926 | 0.1416 | 0.1506 | 0.1213 | 0.1484 | 0.1469 | 0.0930 | 0.0817 | 0.0748 | |
| Worst | 0.1496 | 0.1496 | 0.1360 | 0.1745 | 0.1913 | 0.1551 | 0.1689 | 0.1936 | 0.1280 | 0.1304 | 0.1111 | |
| Rank | (6/5/5) | (4/6/5) | (3/3/4) | (9/8/9) | (7/11/10) | (8/7/7) | (11/10/8) | (9/9/11) | (5/4/2) | (1/2/3) | (1/1/1) | |
| MUSK | Best | 0.0610 | 0.0792 | 0.0342 | 0.0510 | 0.0503 | 0.0692 | 0.0963 | 0.0606 | 0.0328 | 0.0676 | 0.0199 |
| Mean | 0.1020 | 0.0981 | 0.0681 | 0.0843 | 0.0816 | 0.0960 | 0.1424 | 0.0894 | 0.0516 | 0.0913 | 0.0366 | |
| Worst | 0.1411 | 0.1272 | 0.1106 | 0.1175 | 0.1138 | 0.1243 | 0.1703 | 0.1234 | 0.0728 | 0.1210 | 0.0591 | |
| Rank | (7/10/10) | (10/9/9) | (3/3/3) | (5/5/5) | (4/4/4) | (9/8/8) | (11/11/11) | (6/6/7) | (2/2/2) | (8/7/6) | (1/1/1) | |
| Mean Rank | Best | 6.0556 | 6.2222 | 4.7778 | 5.5000 | 5.7778 | 6.6111 | 8.4444 | 7.0556 | 4.5000 | 4.9444 | 1.0000 |
| Mean | 7.1111 | 6.0556 | 4.7222 | 6.9444 | 7.3333 | 6.7778 | 8.7778 | 8.7778 | 3.7222 | 4.6667 | 1.0556 | |
| Worst | 7.5556 | 5.7778 | 4.0556 | 7.5556 | 7.3333 | 5.9444 | 8.2222 | 9.5000 | 2.9444 | 4.6667 | 1.1111 | |
| Final Rank | Best | 7 | 8 | 3 | 5 | 6 | 9 | 11 | 10 | 2 | 4 | 1 |
| Mean | 8 | 5 | 4 | 7 | 9 | 6 | 10 | 10 | 2 | 3 | 1 | |
| Worst | 8 | 5 | 3 | 8 | 7 | 6 | 10 | 11 | 2 | 4 | 1 |
| Datasets | PSO | DE | GWO | MVO | WOA | ABO | BOA | HHO | EO | GO |
|---|---|---|---|---|---|---|---|---|---|---|
| IonosphereEW | 2.80 × 10−11/− | 6.88 × 10−10/− | 1.56 × 10−2/− | 1.04 × 10−9/− | 7.07 × 10−11/− | 1.48 × 10−9/− | 6.83 × 10−5/− | 2.42 × 10−10/− | 1.26 × 10−8/− | 7.75 × 10−7/− |
| Breastcancer | 6.85 × 10−12/− | 6.83 × 10−12/− | 1.86 × 10−12/− | 3.38 × 10−12/− | 7.62 × 10−12/− | 6.81 × 10−12/− | 9.99 × 10−12/− | 4.77 × 10−8/− | 5.61 × 10−8/− | 6.29 × 10−12/− |
| BreastEW | 2.21 × 10−11/− | 7.23 × 10−10/− | 2.05 × 10−11/− | 2.78 × 10−11/− | 2.33 × 10−11/− | 2.83 × 10−11/− | 2.30 × 10−11/− | 3.80 × 10−10/− | 1.24 × 10−6/− | 2.67 × 10−10/− |
| Congress | 8.56 × 10−13/− | 1.10 × 10−12/− | 5.51 × 10−13/− | 1.10 × 10−12/− | 6.14 × 10−14/− | 5.29 × 10−13/− | 9.74 × 10−13/− | 7.32 × 10−13/− | 2.71 × 10−14/− | 2.03 × 10−13/− |
| Wine | 2.85 × 10−10/− | 5.29 × 10−8/− | 7.33 × 10−12/− | 1.99 × 10−6/− | 1.06 × 10−11/− | 3.21 × 10−12/− | 1.99 × 10−11/− | 2.39 × 10−9/− | 3.69 × 10−5/− | 4.43 × 10−12/− |
| Vote | 1.33 × 10−12/− | 1.50 × 10−12/− | 2.71 × 10−14/− | 1.57 × 10−12/− | 3.00 × 10−13/− | 1.61 × 10−12/− | 1.63 × 10−12/− | 1.54 × 10−12/− | 2.71 × 10−14/− | 3.86 × 10−13/− |
| Vehicle | 8.02 × 10−10/− | 2.58 × 10−10/− | 1.28 × 10−10/− | 5.52 × 10−8/− | 8.10 × 10−11/− | 2.71 × 10−11/− | 3.84 × 10−11/− | 4.48 × 10−11/− | 3.56 × 10−7/− | 5.60 × 10−11/− |
| Exactly | 7.22 × 10−5/− | 4.90 × 10−6/− | 1.38 × 10−6/− | 1.68 × 10−7/− | 2.80 × 10−11/− | 2.25 × 10−9/− | 3.54 × 10−13/− | 1.93 × 10−12/− | 1.04 × 10−4/− | 5.87 × 10−1/= |
| Glass | 2.42 × 10−10/− | 1.25 × 10−12/− | 2.12 × 10−12/− | 2.34 × 10−12/− | 2.61 × 10−12/− | 2.87 × 10−10/− | 8.94 × 10−12/− | 2.96 × 10−12/− | 1.17 × 10−12/− | 2.01 × 10−12/− |
| HeartEW | 1.08 × 10−11/− | 1.13 × 10−11/− | 4.53 × 10−11/− | 1.72 × 10−11/− | 4.17 × 10−9/− | 1.11 × 10−11/− | 1.12 × 10−11/− | 1.16 × 10−11/− | 3.47 × 10−11/− | 5.04 × 10−12/− |
| Landsat | 1.52 × 10−7/− | 4.05 × 10−11/− | 9.38 × 10−8/− | 1.86 × 10−5/− | 9.13 × 10−6/− | 6.00 × 10−4/− | 2.99 × 10−11/− | 3.85 × 10−11/− | 6.17 × 10−4/− | 3.55 × 10−1/= |
| Lymphography | 2.16 × 10−11/− | 3.18 × 10−11/− | 1.91 × 10−11/− | 2.15 × 10−11/− | 1.13 × 10−10/− | 2.12 × 10−11/− | 2.20 × 10−11/− | 3.78 × 10−11/− | 5.95 × 10−6/− | 3.37 × 10−7/− |
| Zoo | 3.01 × 10−7/− | 6.93 × 10−2/= | 7.37 × 10−2/= | 2.38 × 10−3/− | 9.68 × 10−4/− | 4.64 × 10−2/− | 6.34 × 10−11/− | 9.31 × 10−9/− | 5.00 × 10−6/− | 2.52 × 10−2/− |
| WDBC | 4.35 × 10−9/− | 2.99 × 10−12/− | 7.54 × 10−9/− | 4.21 × 10−12/− | 2.89 × 10−11/− | 2.38 × 10−11/− | 3.48 × 10−10/− | 4.37 × 10−12/− | 5.34 × 10−9/− | 2.26 × 10−11/− |
| SonarEW | 2.88 × 10−11/− | 2.87 × 10−11/− | 1.06 × 10−9/− | 2.88 × 10−11/− | 2.89 × 10−11/− | 2.89 × 10−11/− | 2.89 × 10−11/− | 2.89 × 10−11/− | 2.87 × 10−11/− | 2.84 × 10−11/− |
| Libras | 2.99 × 10−11/− | 2.99 × 10−11/− | 2.98 × 10−11/− | 7.31 × 10−11/− | 3.00 × 10−11/− | 3.00 × 10−11/− | 2.97 × 10−11/− | 3.00 × 10−11/− | 3.64 × 10−11/− | 2.99 × 10−11/− |
| Spectf | 4.06 × 10−8/− | 2.26 × 10−8/− | 3.75 × 10−4/− | 3.66 × 10−11/− | 7.28 × 10−11/− | 6.79 × 10−11/− | 2.97 × 10−11/− | 4.01 × 10−11/− | 1.88 × 10−4/− | 9.16 × 10−2/= |
| MUSK | 3.00 × 10−11/− | 3.00 × 10−11/− | 2.38 × 10−8/− | 4.95 × 10−11/− | 1.04 × 10−10/− | 3.00 × 10−11/− | 3.00 × 10−11/− | 3.01 × 10−11/− | 3.43 × 10−6/− | 3.00 × 10−11/− |
| (+/−/=) | (0/18/0) | (0/17/1) | (0/17/1) | (0/18/0) | (0/18/0) | (0/18/0) | (0/18/0) | (0/18/0) | (0/18/0) | (0/15/3) |
| Datasets | PSO | DE | GWO | MVO | WOA | ABO | BOA | HHO | EO | GO | CODGBGO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| IonosphereEW | 89.1429 | 94.7143 | 95.5714 | 94.5714 | 91.0476 | 92.4286 | 94.9524 | 90.3333 | 93.0952 | 93.9524 | 96.1905 |
| 11 | 4 | 2 | 5 | 9 | 8 | 3 | 10 | 7 | 6 | 1 | |
| Breastcancer | 96.5468 | 97.7458 | 96.8825 | 97.2422 | 95.2038 | 96.8585 | 95.5635 | 96.0671 | 98.1775 | 96.5947 | 99.0168 |
| 8 | 3 | 4 | 3 | 8 | 5 | 8 | 8 | 7 | 8 | 8 | |
| BreastEW | 97.4631 | 99.2035 | 96.5782 | 97.6696 | 96.1357 | 96.7257 | 96.2242 | 97.4631 | 97.6696 | 98.1121 | 99.1150 |
| 6 | 1 | 9 | 4 | 11 | 8 | 10 | 6 | 4 | 3 | 2 | |
| Congress | 99.6935 | 97.9693 | 96.4368 | 94.2912 | 97.7778 | 93.3716 | 93.6782 | 95.3640 | 96.6667 | 97.0115 | 100.0000 |
| 2 | 3 | 7 | 9 | 4 | 11 | 10 | 8 | 6 | 5 | 1 | |
| Wine | 95.9048 | 99.8095 | 95.5238 | 98.2857 | 95.6190 | 96.5714 | 96.8571 | 96.3810 | 98.0952 | 96.1905 | 100.0000 |
| 9 | 2 | 11 | 3 | 10 | 6 | 5 | 7 | 4 | 8 | 1 | |
| Vote | 97.8161 | 99.2720 | 97.7011 | 98.0077 | 96.7816 | 98.7739 | 91.9540 | 96.0536 | 97.7011 | 99.6169 | 100.0000 |
| 6 | 3 | 7 | 5 | 9 | 4 | 11 | 10 | 7 | 2 | 1 | |
| Vehicle | 74.3393 | 75.0099 | 72.1893 | 74.9310 | 71.4596 | 71.7949 | 70.3550 | 71.7357 | 73.3136 | 73.8462 | 76.2919 |
| 4 | 2 | 7 | 3 | 10 | 8 | 11 | 9 | 6 | 5 | 1 | |
| Exactly | 90.8833 | 94.6667 | 80.1000 | 82.1000 | 73.7167 | 78.6833 | 69.3333 | 72.3000 | 85.4333 | 96.0000 | 98.4000 |
| 4 | 3 | 7 | 6 | 9 | 8 | 11 | 10 | 5 | 2 | 1 | |
| Glass | 78.1746 | 71.2698 | 73.5714 | 72.3810 | 70.0794 | 77.3016 | 72.6190 | 74.2063 | 72.1429 | 72.4603 | 82.6984 |
| 2 | 10 | 5 | 8 | 11 | 3 | 6 | 4 | 9 | 7 | 1 | |
| HeartEW | 77.8395 | 81.7284 | 87.6543 | 84.0123 | 89.5679 | 82.2222 | 78.5802 | 77.1605 | 87.2840 | 83.8889 | 91.9136 |
| 10 | 8 | 3 | 5 | 2 | 7 | 9 | 11 | 4 | 6 | 1 | |
| Landsat | 90.3833 | 89.4500 | 89.3167 | 90.6083 | 89.2417 | 90.3417 | 87.4333 | 87.2000 | 89.5917 | 91.0417 | 90.7000 |
| 4 | 7 | 8 | 3 | 9 | 5 | 10 | 11 | 6 | 1 | 2 | |
| Lymphography | 83.2184 | 91.7241 | 89.0805 | 86.3218 | 90.8046 | 86.3218 | 84.2529 | 88.2759 | 93.7931 | 93.5632 | 96.2069 |
| 11 | 4 | 6 | 8 | 5 | 8 | 10 | 7 | 2 | 3 | 1 | |
| Zoo | 94.3333 | 99.6667 | 96.5000 | 97.3333 | 98.0000 | 97.3333 | 90.0000 | 94.6667 | 95.6667 | 96.8333 | 98.5000 |
| 10 | 1 | 7 | 4 | 3 | 4 | 11 | 9 | 8 | 6 | 2 | |
| WDBC | 96.5782 | 93.3038 | 95.9292 | 92.2714 | 94.1003 | 94.0708 | 95.9587 | 93.3628 | 95.2212 | 94.3068 | 97.0796 |
| 2 | 10 | 4 | 11 | 7 | 8 | 3 | 9 | 5 | 6 | 1 | |
| SonarEW | 90.2439 | 95.2846 | 95.4472 | 88.0488 | 89.9187 | 88.9431 | 90.8130 | 88.6992 | 95.6911 | 93.0081 | 100.0000 |
| 7 | 4 | 3 | 11 | 8 | 9 | 6 | 10 | 2 | 5 | 1 | |
| Libras | 84.5833 | 84.3519 | 85.0463 | 89.4444 | 81.5741 | 78.5648 | 83.5648 | 80.5556 | 85.8333 | 83.7037 | 92.4537 |
| 5 | 6 | 4 | 2 | 9 | 11 | 8 | 10 | 3 | 7 | 1 | |
| Spectf | 92.8302 | 93.1447 | 92.9560 | 88.9937 | 84.7170 | 88.4906 | 86.2893 | 85.7862 | 92.5157 | 94.8428 | 95.5975 |
| 5 | 3 | 4 | 7 | 11 | 8 | 9 | 10 | 6 | 2 | 1 | |
| MUSK | 93.5088 | 96.1053 | 95.0526 | 95.4737 | 95.2982 | 92.6316 | 86.9474 | 93.8596 | 96.8070 | 94.2807 | 99.2281 |
| 9 | 3 | 6 | 4 | 5 | 10 | 11 | 8 | 2 | 7 | 1 | |
| Mean Rank | 6.3889 | 4.2778 | 5.7778 | 5.6111 | 7.7778 | 7.2778 | 8.4444 | 8.7222 | 5.1667 | 4.9444 | 1.5556 |
| Final Rank | 7 | 2 | 6 | 5 | 9 | 8 | 10 | 11 | 4 | 3 | 1 |
| Datasets | PSO | DE | GWO | MVO | WOA | ABO | BOA | HHO | EO | GO | CODGBGO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| IonosphereEW | 10.2333 | 13.0000 | 4.9667 | 11.4667 | 3.8667 | 6.2333 | 6.3333 | 5.0000 | 3.1333 | 5.5667 | 4.5333 |
| 9 | 11 | 4 | 10 | 2 | 7 | 8 | 5 | 1 | 6 | 3 | |
| Breastcancer | 2.8333 | 3.1000 | 2.9000 | 3.2333 | 2.2667 | 2.9667 | 2.6667 | 2.8667 | 2.7333 | 2.3667 | 3.0000 |
| 5 | 10 | 7 | 11 | 1 | 8 | 3 | 6 | 4 | 2 | 9 | |
| BreastEW | 9.1000 | 12.5000 | 6.8000 | 11.7667 | 7.4667 | 8.3667 | 7.8333 | 9.0667 | 6.1667 | 9.5667 | 7.3667 |
| 8 | 11 | 2 | 10 | 4 | 6 | 5 | 7 | 1 | 9 | 3 | |
| Congress | 3.0000 | 3.3000 | 2.1000 | 3.7333 | 1.2000 | 2.3667 | 3.5000 | 2.1333 | 1.1333 | 1.6333 | 1.0000 |
| 8 | 9 | 5 | 11 | 3 | 7 | 10 | 6 | 2 | 4 | 1 | |
| Wine | 4.5333 | 5.3333 | 4.0000 | 3.8333 | 3.8000 | 3.8667 | 4.6333 | 4.4000 | 3.2333 | 4.0667 | 3.3667 |
| 9 | 11 | 6 | 4 | 3 | 5 | 10 | 8 | 1 | 7 | 2 | |
| Vote | 3.2333 | 4.3000 | 1.0000 | 3.3333 | 1.2333 | 1.0333 | 3.3333 | 3.2333 | 1.0000 | 3.9333 | 1.0667 |
| 6 | 11 | 1 | 8 | 5 | 3 | 8 | 6 | 1 | 10 | 4 | |
| Vehicle | 7.5667 | 8.3000 | 4.8000 | 7.2667 | 6.5667 | 5.7333 | 5.7667 | 7.6000 | 5.1333 | 7.0667 | 5.9333 |
| 9 | 11 | 1 | 8 | 6 | 3 | 4 | 10 | 2 | 7 | 5 | |
| Exactly | 5.6667 | 7.3667 | 3.4667 | 5.1333 | 2.2333 | 3.4333 | 1.6333 | 2.2000 | 5.2000 | 5.4667 | 5.9667 |
| 9 | 11 | 5 | 6 | 3 | 4 | 1 | 2 | 7 | 8 | 10 | |
| Glass | 4.2667 | 3.5667 | 3.3000 | 4.1000 | 2.3333 | 3.8333 | 3.8333 | 4.3000 | 4.0000 | 3.2333 | 3.0333 |
| 2 | 6 | 6 | 2 | 7 | 3 | 3 | 1 | 1 | 1 | 1 | |
| HeartEW | 3.8000 | 5.3000 | 2.8667 | 4.1000 | 5.0000 | 4.2667 | 3.6667 | 3.0667 | 3.6000 | 3.8000 | 4.0333 |
| 6 | 1 | 9 | 3 | 1 | 1 | 3 | 4 | 3 | 2 | 1 | |
| Landsat | 12.5333 | 13.5000 | 8.4333 | 12.8000 | 8.5000 | 10.4667 | 9.5000 | 10.2333 | 8.0333 | 11.3667 | 9.8000 |
| 3 | 1 | 8 | 1 | 6 | 2 | 4 | 2 | 3 | 1 | 1 | |
| Lymphography | 6.8333 | 8.0000 | 3.5667 | 6.3000 | 5.8333 | 6.6000 | 5.8333 | 4.6667 | 5.4333 | 6.3000 | 5.5333 |
| 10 | 11 | 1 | 7 | 5 | 9 | 5 | 2 | 3 | 7 | 4 | |
| Zoo | 5.8333 | 7.6000 | 5.6333 | 7.2000 | 7.8000 | 5.8667 | 6.7667 | 7.3333 | 5.7000 | 5.2667 | 6.1000 |
| 4 | 10 | 2 | 8 | 11 | 5 | 7 | 9 | 3 | 1 | 6 | |
| WDBC | 6.5667 | 8.2333 | 2.7333 | 7.4333 | 3.3333 | 2.0333 | 6.3333 | 5.5000 | 2.9333 | 3.5667 | 3.9000 |
| 9 | 11 | 2 | 10 | 4 | 1 | 8 | 7 | 3 | 5 | 6 | |
| SonarEW | 20.8333 | 29.8333 | 11.9333 | 22.8667 | 13.2000 | 17.8667 | 17.0333 | 16.7000 | 9.4667 | 15.8333 | 11.5000 |
| 9 | 11 | 3 | 10 | 4 | 8 | 7 | 6 | 1 | 5 | 2 | |
| Libras | 34.4000 | 51.3667 | 21.1667 | 38.3667 | 20.3667 | 23.0667 | 22.3333 | 21.0667 | 14.3667 | 28.5000 | 21.0000 |
| 9 | 11 | 5 | 10 | 2 | 7 | 6 | 4 | 1 | 8 | 3 | |
| Spectf | 18.8333 | 23.0000 | 12.8333 | 18.7000 | 5.7333 | 7.8000 | 11.0000 | 8.3667 | 11.2667 | 15.5333 | 15.5000 |
| 10 | 11 | 6 | 9 | 1 | 2 | 4 | 3 | 5 | 8 | 7 | |
| MUSK | 72.2667 | 104.7333 | 39.2000 | 72.3333 | 65.2000 | 49.2667 | 41.3667 | 56.7000 | 37.9333 | 66.0333 | 49.2000 |
| 9 | 11 | 2 | 10 | 7 | 5 | 3 | 6 | 1 | 8 | 4 | |
| Mean Rank | 7.4444 | 9.3889 | 4.1667 | 7.6667 | 4.1667 | 4.7778 | 5.5000 | 5.2222 | 2.3889 | 5.5000 | 4.0000 |
| Final Rank | 9 | 11 | 3 | 10 | 3 | 5 | 7 | 6 | 1 | 7 | 2 |
| Datasets | PSO | DE | GWO | MVO | WOA | ABO | BOA | HHO | EO | GO | CODGBGO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| IonosphereEW | 3.3108 | 3.1722 | 3.3264 | 3.1784 | 2.9800 | 2.1202 | 3.2604 | 4.9315 | 3.3270 | 6.5616 | 6.6642 |
| Breastcancer | 3.6709 | 3.5429 | 3.4315 | 3.4680 | 3.0807 | 2.2683 | 3.4019 | 5.7813 | 3.4697 | 6.8237 | 6.9120 |
| BreastEW | 3.3533 | 3.2018 | 3.5022 | 3.2243 | 3.1798 | 2.2524 | 3.3439 | 5.2125 | 3.4673 | 6.6059 | 6.9163 |
| Congress | 3.3494 | 3.2961 | 3.2631 | 3.3033 | 2.6290 | 2.0781 | 3.2823 | 4.5191 | 3.1994 | 6.5350 | 6.4676 |
| Wine | 3.1881 | 3.1710 | 3.1694 | 3.1464 | 2.9201 | 2.1440 | 3.1045 | 4.6576 | 3.1517 | 6.3121 | 6.3179 |
| Vote | 3.3267 | 3.3109 | 3.2309 | 3.2795 | 2.6670 | 2.0366 | 3.2974 | 4.6792 | 3.3187 | 6.5316 | 6.6233 |
| Vehicle | 3.6556 | 3.6239 | 3.5830 | 3.6427 | 3.3595 | 2.4563 | 3.5264 | 5.4494 | 3.5911 | 7.4301 | 7.4114 |
| Exactly | 3.7490 | 3.7573 | 3.6516 | 3.7003 | 3.0622 | 2.2741 | 3.5822 | 5.0219 | 3.6353 | 7.3639 | 7.6153 |
| Glass | 3.2112 | 3.1554 | 3.1348 | 3.1633 | 2.7608 | 2.1511 | 2.9145 | 4.8530 | 3.1383 | 6.2397 | 6.2764 |
| HeartEW | 3.2382 | 3.2001 | 3.2068 | 3.1889 | 2.9947 | 2.1126 | 3.0886 | 4.7290 | 3.2077 | 6.4120 | 6.5637 |
| Landsat | 4.3829 | 4.4849 | 4.6258 | 4.2721 | 4.2646 | 2.9833 | 4.4782 | 7.0426 | 4.6445 | 8.6532 | 9.0210 |
| Lymphography | 3.1431 | 3.1904 | 3.1270 | 3.1329 | 2.8913 | 2.1470 | 3.1233 | 4.5939 | 3.1329 | 6.2383 | 6.2533 |
| Zoo | 3.2060 | 3.0961 | 3.0762 | 3.0675 | 2.9377 | 2.0992 | 3.1017 | 4.8683 | 3.2445 | 6.1870 | 6.2997 |
| WDBC | 3.3966 | 3.2996 | 3.3730 | 3.3750 | 2.9942 | 2.0821 | 3.3059 | 5.0062 | 3.3910 | 6.8395 | 6.8839 |
| SonarEW | 3.0436 | 3.0531 | 3.0037 | 3.0109 | 2.9500 | 2.1247 | 3.0362 | 4.6112 | 3.0677 | 6.0004 | 6.1562 |
| Libras | 3.2948 | 3.3294 | 3.1570 | 3.2474 | 3.0417 | 2.2046 | 3.1727 | 4.8582 | 3.1632 | 6.3859 | 6.3510 |
| Spectf | 3.0568 | 3.0503 | 3.0780 | 3.0571 | 2.8979 | 2.0055 | 3.0874 | 4.7757 | 3.1155 | 5.9824 | 6.1543 |
| MUSK | 3.6771 | 3.8192 | 3.3378 | 3.5578 | 3.3299 | 2.3570 | 3.3974 | 5.3402 | 3.3292 | 7.1061 | 6.8958 |
| Mean time | 3.4030 | 3.3753 | 3.3488 | 3.3342 | 3.0523 | 2.2165 | 3.3058 | 5.0517 | 3.3664 | 6.6782 | 6.7657 |
| Mean Rank | 8 | 7 | 5 | 4 | 2 | 1 | 3 | 9 | 6 | 10 | 11 |
| Algorithms | Optimal | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GO | 0.003526 | 0.001473 | 0.003511 | 0.001466 | 0.000065 | 0.000456 | 0.002384 | 0.002362 | 0.001224 | 0.001250 | 524.4727 |
| INFO | 0.003560 | 0.001477 | 0.003443 | 0.001485 | 0.000065 | 0.000455 | 0.002361 | 0.002359 | 0.001228 | 0.001283 | 524.5944 |
| SSA | 0.003571 | 0.001596 | 0.003558 | 0.001489 | 0.000065 | 0.000447 | 0.002432 | 0.002200 | 0.001206 | 0.001235 | 525.0305 |
| TLBO | 0.003493 | 0.001466 | 0.003537 | 0.001454 | 0.000065 | 0.000457 | 0.002394 | 0.002368 | 0.001233 | 0.001243 | 524.4853 |
| BESD | 0.003514 | 0.001515 | 0.003449 | 0.001451 | 0.000115 | 0.000455 | 0.002411 | 0.002330 | 0.001239 | 0.001297 | 526.6039 |
| DE | 0.003536 | 0.001470 | 0.003509 | 0.001511 | 0.000065 | 0.000454 | 0.002315 | 0.002394 | 0.001233 | 0.001245 | 524.5510 |
| PSO | 0.003578 | 0.001473 | 0.003455 | 0.001521 | 0.000065 | 0.000453 | 0.002297 | 0.002400 | 0.001267 | 0.001224 | 524.5765 |
| SO | 0.003552 | 0.001476 | 0.003445 | 0.001433 | 0.000065 | 0.000458 | 0.002433 | 0.002334 | 0.001236 | 0.001266 | 524.5727 |
| FOPSO | 0.003599 | 0.001420 | 0.003452 | 0.001539 | 0.000065 | 0.000455 | 0.002234 | 0.002503 | 0.001292 | 0.001176 | 524.7809 |
| ICGWO | 0.003211 | 0.001594 | 0.003734 | 0.001469 | 0.000065 | 0.000495 | 0.002890 | 0.002145 | 0.001243 | 0.001277 | 538.3172 |
| CODGBGO | 0.003515 | 0.001471 | 0.003511 | 0.001472 | 0.000065 | 0.000456 | 0.002368 | 0.002371 | 0.001244 | 0.001241 | 524.4511 |
| Algorithms | Best | Worst | Mean | Std |
|---|---|---|---|---|
| GO | 524.472692 | 530.626625 | 524.972147 | 1.205804 |
| INFO | 524.594363 | 536.501563 | 527.520947 | 3.520433 |
| SSA | 525.030465 | 536.997795 | 529.502118 | 3.881703 |
| TLBO | 524.485260 | 530.858513 | 525.462996 | 2.132384 |
| BESD | 526.603949 | 531.093229 | 529.159895 | 1.163149 |
| DE | 524.550988 | 525.206518 | 524.754413 | 0.154388 |
| PSO | 524.576532 | 533.737282 | 528.496080 | 3.450720 |
| SO | 524.572671 | 535.307127 | 527.344681 | 2.970005 |
| FOPSO | 524.780922 | 537.102061 | 529.847788 | 3.819223 |
| ICGWO | 541.278051 | 573.614056 | 552.856617 | 7.635963 |
| CODGBGO | 524.451125 | 524.602817 | 524.463803 | 0.034718 |
| Algorithms | Optimal | |||
|---|---|---|---|---|
| GO | 0.051610 | 0.354815 | 11.401536 | 0.012665 |
| INFO | 0.051879 | 0.361303 | 11.025125 | 0.012666 |
| SSA | 0.050000 | 0.315802 | 14.245195 | 0.012826 |
| TLBO | 0.051520 | 0.352659 | 11.531001 | 0.012666 |
| BESD | 0.051768 | 0.358525 | 11.191061 | 0.012674 |
| DE | 0.051696 | 0.356874 | 11.279811 | 0.012665 |
| PSO | 0.051861 | 0.360861 | 11.050136 | 0.012666 |
| SO | 0.051636 | 0.355443 | 11.364087 | 0.012665 |
| FOPSO | 0.051654 | 0.355874 | 11.338620 | 0.012665 |
| ICGWO | 0.050000 | 0.317212 | 14.230810 | 0.012872 |
| CODGBGO | 0.051701 | 0.356996 | 11.272677 | 0.012665 |
| Algorithms | Best | Worst | Mean | Std |
|---|---|---|---|---|
| GO | 0.012665 | 0.012742 | 0.012672 | 1.423895 × 10−5 |
| INFO | 0.012666 | 0.012734 | 0.012686 | 1.642346 × 10−5 |
| SSA | 0.012728 | 0.013977 | 0.012920 | 2.356985 × 10−4 |
| TLBO | 0.012666 | 0.012732 | 0.012683 | 1.585319 × 10−5 |
| BESD | 0.012674 | 0.012792 | 0.012727 | 2.427097 × 10−5 |
| DE | 0.012665 | 0.012666 | 0.012665 | 2.013640 × 10−7 |
| PSO | 0.012666 | 0.014329 | 0.013268 | 5.261813 × 10−4 |
| SO | 0.012665 | 0.013907 | 0.012835 | 2.417478 × 10−4 |
| FOPSO | 0.012665 | 0.014304 | 0.013264 | 5.067277 × 10−4 |
| ICGWO | 0.013111 | 0.016786 | 0.014086 | 1.306659 × 10−3 |
| CODGBGO | 0.012665 | 0.012676 | 0.012666 | 1.957407 × 10−6 |
| Algorithms | Optimal | |||||||
|---|---|---|---|---|---|---|---|---|
| GO | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424466 |
| INFO | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424466 |
| SSA | 3.500072 | 0.700000 | 17.000000 | 7.660034 | 8.087044 | 3.358114 | 5.286784 | 3007.818687 |
| TLBO | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424466 |
| BESD | 3.503719 | 0.700002 | 17.001660 | 7.340884 | 7.755843 | 3.351224 | 5.288070 | 2998.504231 |
| DE | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424479 |
| PSO | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424466 |
| SO | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424466 |
| FOPSO | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424466 |
| ICGWO | 3.600000 | 0.700000 | 17.000000 | 8.300000 | 8.300000 | 3.353812 | 5.500000 | 3197.929838 |
| CODGBGO | 3.500000 | 0.700000 | 17.000000 | 7.300000 | 7.715320 | 3.350541 | 5.286654 | 2994.424466 |
| Algorithms | Best | Worst | Mean | Std |
|---|---|---|---|---|
| GO | 2994.424466 | 2994.424466 | 2994.424466 | 1.850085 × 10−12 |
| INFO | 2994.424466 | 2994.424466 | 2994.424466 | 1.850085 × 10−12 |
| SSA | 3007.818687 | 3124.932806 | 3035.033900 | 2.585991 × 101 |
| TLBO | 2994.424466 | 2994.424466 | 2994.424466 | 1.850085 × 10−12 |
| BESD | 2998.504231 | 3005.944928 | 3002.199777 | 1.751670 × 100 |
| DE | 2994.424479 | 2994.424576 | 2994.424525 | 3.035569 × 10−5 |
| PSO | 2994.424466 | 2994.424466 | 2994.424466 | 1.850085 × 10−12 |
| SO | 2994.424466 | 2996.185353 | 2994.499642 | 3.245885 × 10−1 |
| FOPSO | 2994.424466 | 3033.701596 | 2995.733703 | 7.050461 × 100 |
| ICGWO | 3218.393654 | 3218.393654 | 3218.393654 | 4.547474 × 10−13 |
| CODGBGO | 2994.424466 | 2994.424466 | 2994.424466 | 1.850085 × 10−12 |
| Algorithms | Optimal | ||||
|---|---|---|---|---|---|
| GO | 0.198832 | 3.337365 | 9.192024 | 0.198832 | 1.670218 |
| INFO | 0.198832 | 3.337365 | 9.192024 | 0.198832 | 1.670218 |
| SSA | 0.196408 | 3.378769 | 9.210326 | 0.198747 | 1.674474 |
| TLBO | 0.198832 | 3.337365 | 9.192024 | 0.198832 | 1.670218 |
| BESD | 0.198250 | 3.368697 | 9.188929 | 0.199399 | 1.677316 |
| DE | 0.198832 | 3.337367 | 9.192024 | 0.198832 | 1.670218 |
| PSO | 0.198832 | 3.337365 | 9.192024 | 0.198832 | 1.670218 |
| SO | 0.198832 | 3.337365 | 9.192024 | 0.198832 | 1.670218 |
| FOPSO | 0.198832 | 3.337365 | 9.192024 | 0.198832 | 1.670218 |
| ICGWO | 0.198308 | 3.457363 | 9.478214 | 0.201282 | 1.752510 |
| CODGBGO | 0.198832 | 3.337365 | 9.192024 | 0.198832 | 1.670218 |
| Algorithms | Best | Worst | Mean | Std |
|---|---|---|---|---|
| GO | 1.670218 | 1.670218 | 1.670218 | 1.086776 × 10−8 |
| INFO | 1.670218 | 1.670218 | 1.670218 | 1.129203 × 10−15 |
| SSA | 1.674474 | 1.831619 | 1.749027 | 5.575776 × 10−2 |
| TLBO | 1.670218 | 1.670218 | 1.670218 | 1.129203 × 10−15 |
| BESD | 1.677316 | 1.691348 | 1.683443 | 3.948120 × 10−3 |
| DE | 1.670218 | 1.670219 | 1.670218 | 2.127735 × 10−7 |
| PSO | 1.670218 | 1.711166 | 1.672234 | 8.154641 × 10−3 |
| SO | 1.670218 | 1.679417 | 1.670570 | 1.673049 × 10−3 |
| FOPSO | 1.670218 | 2.330363 | 1.860656 | 2.038525 × 10−1 |
| ICGWO | 1.752510 | 2.140073 | 1.888851 | 7.733192 × 10−2 |
| CODGBGO | 1.670218 | 1.670218 | 1.670218 | 9.433468 × 10−12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, R.; Yu, L.; Li, S.; Wu, F.; Zhang, T.; Yuan, P. Multi-Strategy-Improved Growth Optimizer and Its Applications. Axioms 2024, 13, 361. https://doi.org/10.3390/axioms13060361
Xie R, Yu L, Li S, Wu F, Zhang T, Yuan P. Multi-Strategy-Improved Growth Optimizer and Its Applications. Axioms. 2024; 13(6):361. https://doi.org/10.3390/axioms13060361
Chicago/Turabian StyleXie, Rongxiang, Liya Yu, Shaobo Li, Fengbin Wu, Tao Zhang, and Panliang Yuan. 2024. "Multi-Strategy-Improved Growth Optimizer and Its Applications" Axioms 13, no. 6: 361. https://doi.org/10.3390/axioms13060361
APA StyleXie, R., Yu, L., Li, S., Wu, F., Zhang, T., & Yuan, P. (2024). Multi-Strategy-Improved Growth Optimizer and Its Applications. Axioms, 13(6), 361. https://doi.org/10.3390/axioms13060361







