An RBF Method for Time Fractional Jump-Diffusion Option Pricing Model under Temporal Graded Meshes
Abstract
1. Introduction
2. Preliminaries
- For any constant function (c is a constant) .
- For any , we have
- For , we have , but .
- Fractional integrals and derivatives satisfy the linearity property:
- (a)
- (b)
are some positive constants.
3. Option Pricing Model
3.1. TFPIDE for European Option
3.2. LCP for American Option
4. The Discrete Problem
4.1. Nonuniform Fractional Discretization along Time
4.2. Spatial Discretization
4.3. Discretization of the Integral Operator
5. Stability and Convergence Analysis
5.1. Stability Analysis
5.2. Convergence Analysis
6. Numerical Experiments and Empirical Analysis
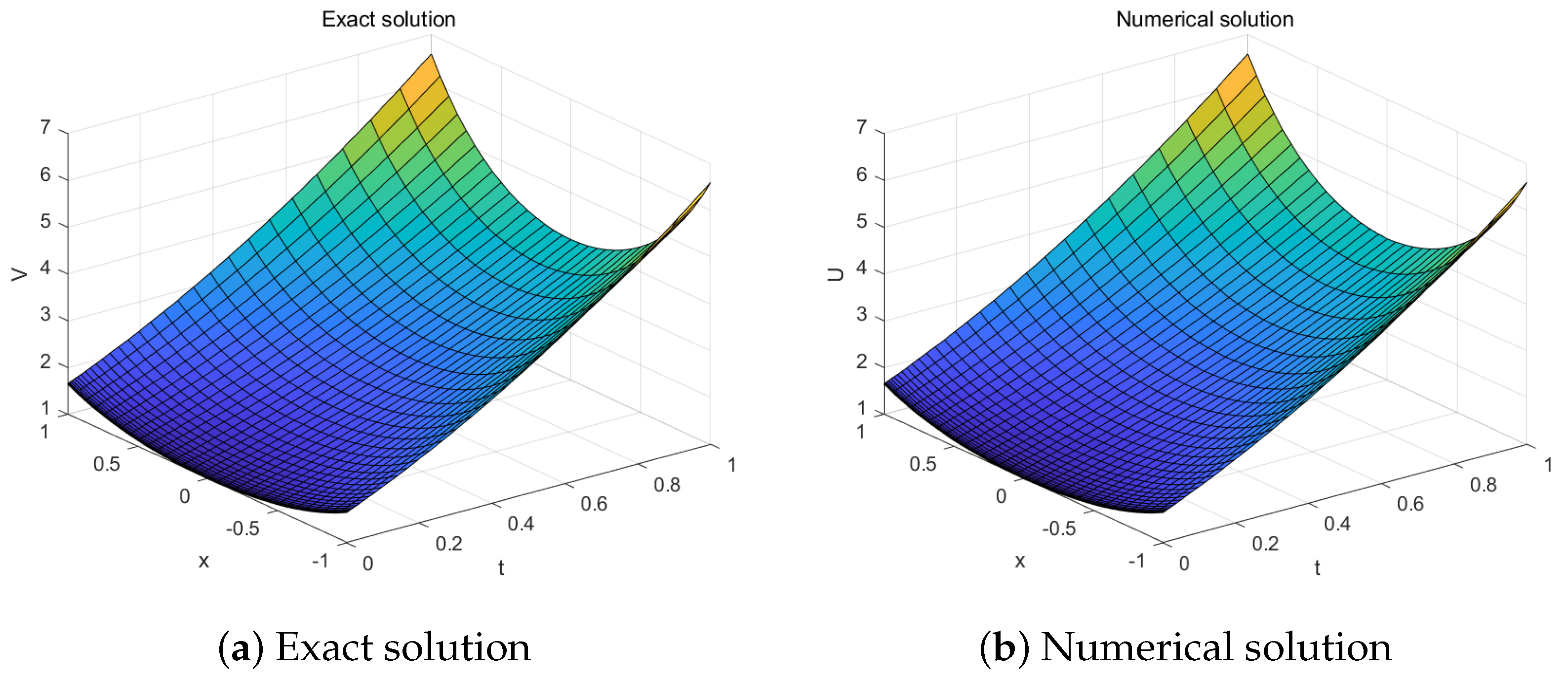
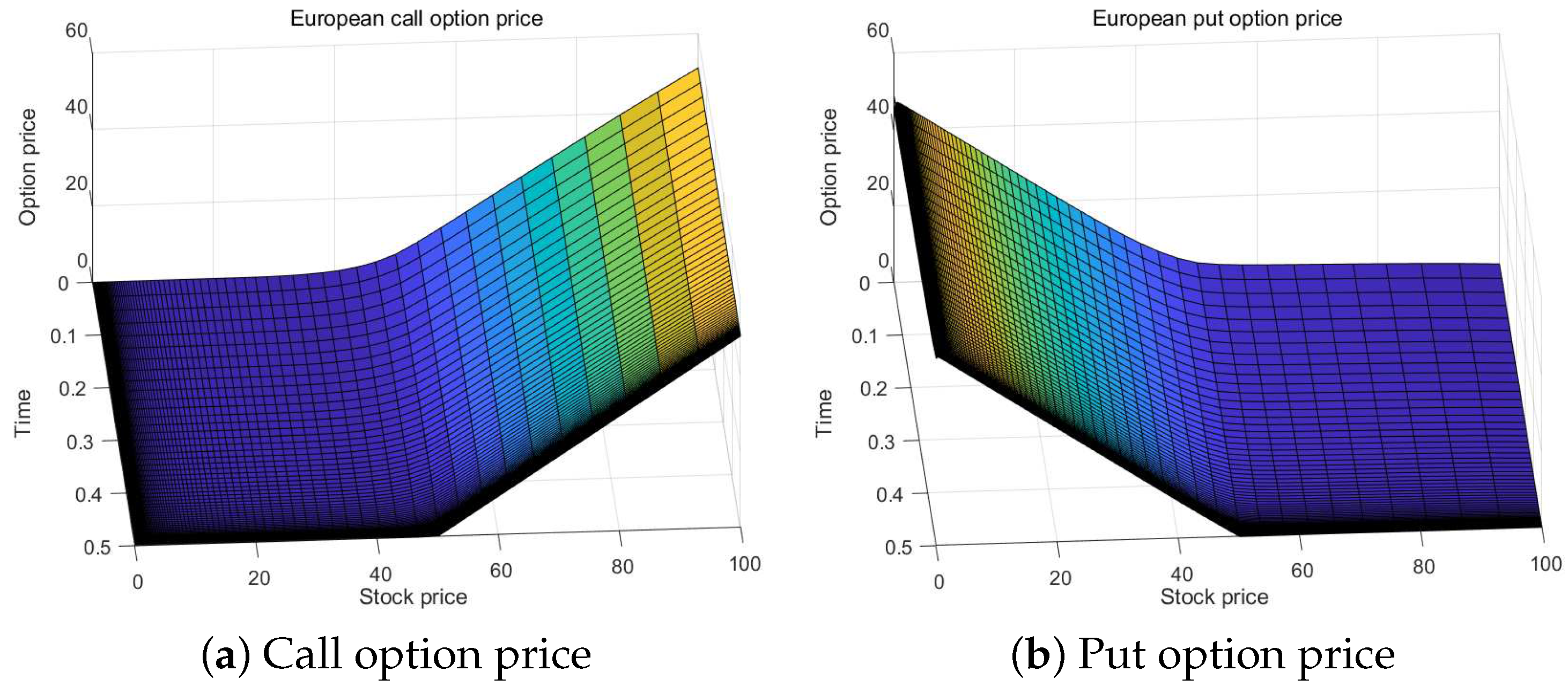
6.1. Numerical Experiments
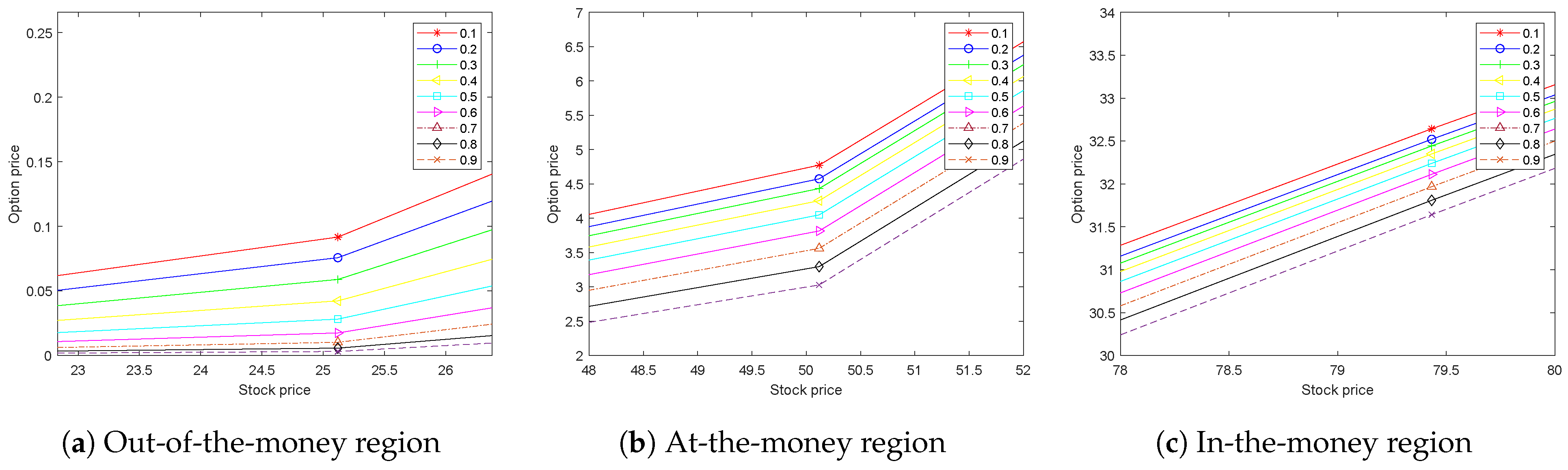
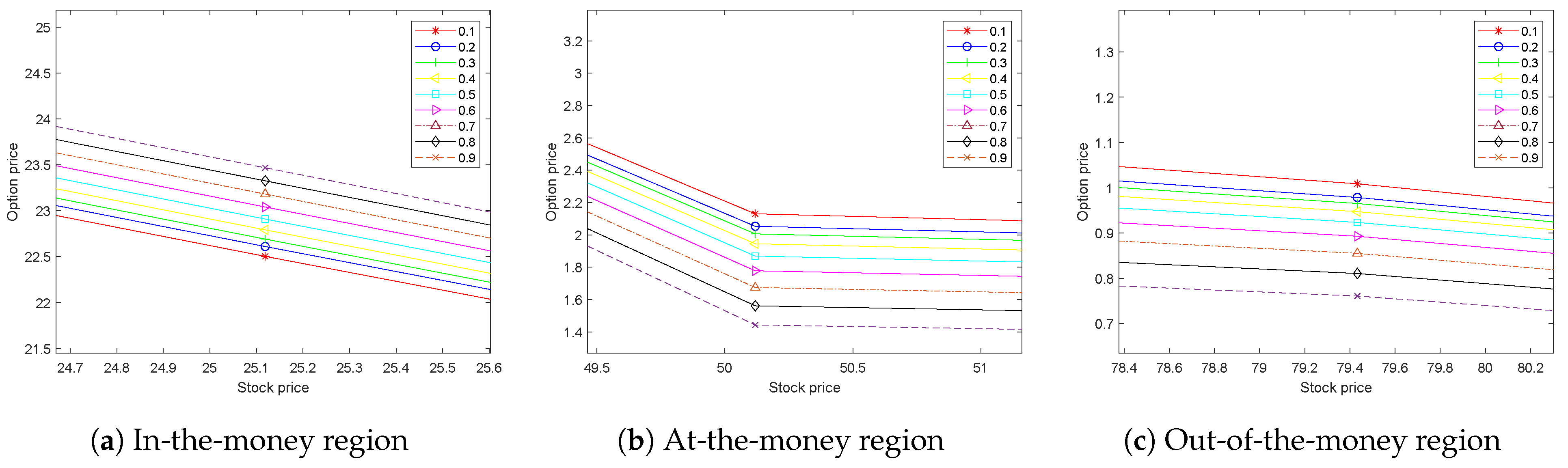
6.2. Empirical Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Polit. Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- TunÇ, O.; TunÇ, C. On the asymptotic stability of solutions of stochastic differential delay equations of second order. J. Taibah Univ. Sci. 2019, 13, 875–882. [Google Scholar] [CrossRef]
- Zouine, A.; Imzegouan, C.; Bouzahir, H.; Tunç, C. General decay stability of nonlinear delayed hybrid stochastic system with switched noises. Appl. Set-Valued Anal. Opt. 2024, 6, 157–177. [Google Scholar]
- Merton, R.C. Option pricing when underlying stock returns are discontinuous. J. Financ. Econ. 1976, 3, 125–144. [Google Scholar] [CrossRef]
- Kou, S.G. A jump-diffusion model for option pricing. Manag. Sci. 2002, 48, 1086–1101. [Google Scholar] [CrossRef]
- Toivanen, J. Numerical valuation of European and American options under Kou’s jump-diffusion model. SIAM J. Sci. Comput. 2008, 30, 1949–1970. [Google Scholar] [CrossRef]
- Salmi, S.; Toivanen, J. IMEX schemes for pricing options under jump-diffusion models. Appl. Numer. Math. 2014, 84, 33–45. [Google Scholar] [CrossRef]
- Christara, C.C.; Leung, N.C.-H. Option pricing in jump diffusion models with quadratic spline collocation. Appl. Math. Comput. 2016, 279, 28–42. [Google Scholar]
- Rad, J.A.; Parand, K. Pricing American options under jump-diffusion models using local weak form meshless techniques. Int. J. Comput. Math. 2017, 94, 1694–1718. [Google Scholar]
- Kwon, Y.; Lee, Y. A second-order tridiagonal method for American options under jump-diffusion models. SIAM J. Sci. Comput. 2011, 33, 1860–1872. [Google Scholar] [CrossRef]
- Saib, A.A.E.F.; Tangman, D.Y.; Bhuruth, M. A new radial basis functions method for pricing American options under Merton’s jump-diffusion model. Int. J. Comput. Math. 2012, 89, 1164–1185. [Google Scholar] [CrossRef]
- Chan, R.T.L.; Hubbert, S. Options pricing under the one-dimensional jump-diffusion model using the radial basis function interpolation scheme. Rev. Deriv. Res. 2014, 17, 161–189. [Google Scholar] [CrossRef]
- Haghi, M.; Mollapourasl, R.; Vanmaele, M. An RBF-FD method for pricing American options under jump-diffusion models. Comput. Math. Appl. 2018, 76, 2434–2459. [Google Scholar] [CrossRef]
- Carpinterj, A.; Mainardi, F. Fractals and Fractional Calculus in Continuum Mechanics; Springer: New York, NY, USA, 1997. [Google Scholar]
- Wyss, W. The fractional Black-Scholes equations. Fract. Calc. Appl. Anal. 2000, 3, 51–61. [Google Scholar]
- Chen, W.; Xu, X.; Zhu, S. Analytically pricing double barrier options based on a time-fractional Black-Scholes equation. Comput. Math. Appl. 2015, 69, 1407–1419. [Google Scholar] [CrossRef]
- Huang, J.; Cen, Z.; Zhao, J. An adaptive moving mesh method for a time-fractional Black-Scholes equation. Adv. Differ. Equ. 2019, 1, 516. [Google Scholar] [CrossRef]
- Rezaei, M.; Yazdanian, A.R.; Ashrafi, A.; Mahmoudi, S.M. Numerical pricing based on fractional Black-Scholes equation with time-dependent parameters under CEV model: Double barrier options. Comput. Math. Appl. 2021, 90, 104–111. [Google Scholar] [CrossRef]
- Elbeleze, A.A.; Kılıçman, A.; Taib, B.M. Homotopy perturbation method for fractional Black-Scholes European option pricing equations using Sumudu transform. Math. Probl. Eng. 2013, 2013, 524852. [Google Scholar] [CrossRef]
- Prathumwan, D.; Trachoo, K. On the solution of two-dimensional fractional Black-Scholes equation for European put option. Adv. Differ. Equ. 2020, 2020, 146. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. European Vanilla Option Pricing Model of Fractional Order without Singular Kernel. Fractal Fract. 2018, 2, 3. [Google Scholar] [CrossRef]
- Fadugba, S.E. Homotopy analysis method and its applications in the valuation of European call options with time-fractional Black-Scholes equation. Chaos Solitons Fract. 2020, 141, 110351. [Google Scholar] [CrossRef]
- Haq, S.; Hussain, M. Selection of shape parameter in radial basis functions for solution of time-fractional Black-Scholes models. Appl. Math. Comput. 2018, 335, 248–263. [Google Scholar] [CrossRef]
- Song, L. A semianalytical solution of the fractional derivative model and its application in financial market. Complexity 2018, 2018, 1872409. [Google Scholar] [CrossRef]
- Song, L.; Wang, W. Solution of the fractional Black-Scholes option pricing model by finite difference method. Abstr. Appl. Anal. 2013, 1–2, 194286. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Numerical solution of time-fractional Black-Scholes equation. Comput. Appl. Math. 2017, 36, 1699–1715. [Google Scholar] [CrossRef]
- Jumarie, G. Derivation and solutions of some fractional Black-Scholes equations in coarse-grained space and time. Application to Merton’s optimal portfolio. Comput. Math. Appl. 2010, 59, 1142–1164. [Google Scholar] [CrossRef]
- Yang, X.Z.; Wu, L.F.; Sun, S.Z.; Zhang, X. A universal difference method for time-space fractional Black-Scholes equation. Adv. Differ. Equ. 2016, 2016, 71. [Google Scholar]
- Zhang, H.; Liu, F.; Turner, I.; Yang, Q. Numerical solution of the time fractional Black-Scholes model governing European options. Comput. Math. Appl. 2016, 71, 1772–1783. [Google Scholar] [CrossRef]
- Cen, H.D.; Huang, J.; Xu, A.M.; Le, A. Numerical approximation of a time-fractional Black-Scholes equation. Comput. Math. Appl. 2018, 75, 2874–2887. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y.; Sabermahani, S. Hahn hybrid functions for solving distributed order fractional Black-Scholes European option pricing problem arising in financial market. Math. Method Appl. Sci. 2023, 46, 6558–6577. [Google Scholar] [CrossRef]
- Maddouri, F. Stability and convergence analysis of a numerical method for solving a ζ-Caputo time fractional Black–Scholes model via European options. Comput. Econ. 2024. [Google Scholar] [CrossRef]
- De Staelen, R.H.; Hendy, A.S. Numerically pricing double barrier options in a time-fractional Black-Scholes model. Comput. Math. Appl. 2017, 74, 1166–1175. [Google Scholar] [CrossRef]
- Abdi, N.; Aminikhah, H.; Sheikhani, A.R. High-order compact finite difference schemes for the time-fractional Black-Scholes model governing European options. Chaos Solitons Fract. 2022, 162, 112423. [Google Scholar] [CrossRef]
- Roul, P.; Goura, V.M.K.P. A compact finite difference scheme for fractional Black-Scholes option pricing model. Appl. Numer. Math. 2021, 166, 40–60. [Google Scholar] [CrossRef]
- Roul, P. Design and analysis of a high order computational technique for time-fractional Black-Scholes model describing option pricing. Math. Methods Appl. Sci. 2022, 45, 5592–5611. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Machado, J.A.T. Localized kernel-based meshless method for pricing financial options underlying fractal transmission system. Math. Methods Appl. Sci. 2024, 47, 3247–3260. [Google Scholar] [CrossRef]
- Delpasand, R.; Hosseini, M.M. An efficient method for solving two-asset time fractional Black-Scholes option pricing model. J. Korean Soc. Ind. Appl. Math. 2022, 26, 121–137. [Google Scholar]
- Ford, N.J.; Yan, Y. An approach to construct higher order time discretization schemes for time fractional partial differential equations with nonsmooth data. Fract. Calc. Appl. Anal. 2017, 20, 1076–1105. [Google Scholar] [CrossRef]
- Soleymani, F.; Zhu, S. Error and stability estimates of a time-fractional option pricing model under fully spatial-temporal graded meshes. J. Comput. Appl. Math. 2023, 425, 115075. [Google Scholar] [CrossRef]
- Yang, P.; Xu, Z.L. Numerical valuation of European and American options under fractional Black-Scholes model. Fractal Fract. 2022, 6, 143. [Google Scholar] [CrossRef]
- Mohapatra, J.; Santra, S.; Ramos, H. Analytical and numerical solution for the time fractional Black-Scholes model under jump-diffusion. Comput. Econ. 2024, 63, 1853–1871. [Google Scholar] [CrossRef]
- Chen, Y.; Li, L. An efficient IMEX compact scheme for the coupled time fractional integro-differential equations arising from option pricing with jumps. Comput. Econ. 2024. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Mathematics in Science and Engineering; Academic Press, Inc.: San Diego, CA, USA, 1999. [Google Scholar]
- Stynes, M.; O’Riordan, E.; Gracia, J.L. Error analysis of a fnite diference method on graded meshes for a time-fractional difusion equation. SIAM J. Numer. Anal. 2017, 55, 1057–1079. [Google Scholar] [CrossRef]
- Imran, M.A.; Shah, N.A.; Khan, I.; Aleem, M. Applications of non-integer Caputo time fractional derivatives to natural convection flow subject to arbitrary velocity and Newtonian heating. Neural Comput. Appk. 2018, 30, 1589–1599. [Google Scholar] [CrossRef]





| Exact | 1.3333 | 1.1408 | 1.7168 | 2.0053 | 4.7979 |
| RBF | 1.3321 | 1.1394 | 1.7097 | 1.9988 | 4.7885 |
| Error | 0.0012 | 0.0013 | 0.0072 | 0.0065 | 0.0094 |
| 0.7 | Error | |||||
| Order | 1.29 | 1.28 | 1.29 | 1.29 | ||
| CPU (s) | 0.0146 | 0.0213 | 0.0281 | 0.0385 | 0.1064 | |
| 0.5 | Error | |||||
| Order | 1.48 | 1.53 | 1.51 | 1.49 | ||
| CPU (s) | 0.0161 | 0.0209 | 0.0291 | 0.0388 | 0.1013 | |
| 0.3 | Error | |||||
| Order | 1.71 | 1.71 | 1.68 | 1.71 | ||
| CPU (s) | 0.0152 | 0.0207 | 0.0270 | 0.0487 | 0.1057 |
| K | RBF | FD | ||
|---|---|---|---|---|
| Error | CPU (s) | Error | CPU (s) | |
| 140 | 2.0599 | 0.058 | 2.0617 | 0.058 |
| 150 | 0.057 | 0.0017 | 0.056 | |
| 160 | 0.5899 | 0.057 | 0.5917 | 0.057 |
| 170 | 0.7100 | 0.058 | 0.7100 | 0.056 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, W.; Xu, Z.; Sun, Y. An RBF Method for Time Fractional Jump-Diffusion Option Pricing Model under Temporal Graded Meshes. Axioms 2024, 13, 674. https://doi.org/10.3390/axioms13100674
Gong W, Xu Z, Sun Y. An RBF Method for Time Fractional Jump-Diffusion Option Pricing Model under Temporal Graded Meshes. Axioms. 2024; 13(10):674. https://doi.org/10.3390/axioms13100674
Chicago/Turabian StyleGong, Wenxiu, Zuoliang Xu, and Yesen Sun. 2024. "An RBF Method for Time Fractional Jump-Diffusion Option Pricing Model under Temporal Graded Meshes" Axioms 13, no. 10: 674. https://doi.org/10.3390/axioms13100674
APA StyleGong, W., Xu, Z., & Sun, Y. (2024). An RBF Method for Time Fractional Jump-Diffusion Option Pricing Model under Temporal Graded Meshes. Axioms, 13(10), 674. https://doi.org/10.3390/axioms13100674




