1. Introduction
In all the fields of science and engineering, numerical methods have great significance for solving nonlinear equations. Implicit equations, also known as nonlinear transcendental equations, require iterative techniques to approximate their solutions because they lack analytical solutions. The fact that numerical approaches can handle complex and non-analytic functions is a major justification for using them to solve these equations. In general, models containing nonlinear equations are used to describe nonlinear phenomena, and they are not limited to academia but are found in a variety of fields including problems of steering and reactors [
1,
2], transport theory [
3], economics modeling problems, neuro-physiology [
4], social sciences, engineering, and business. In [
5,
6,
7,
8], fluid flow, combustion, the triangulation of GPS signals, economic modeling, and kinematics are some more complex problems with nonlinear equations. As a result, numerical techniques with higher orders of convergence and lower computational expenses must be used to solve them. The dynamics of systems with multiple components that interact are often described by nonlinear equations, which present significant challenges for analytical solutions. Iterative techniques for approximation solutions can be derived by breaking down these complicated structures into smaller, more manageable components using numerical methods. In this way, Newton’s method [
9] is one of the oldest methods with quadratic convergence, and it is optimal. According to the conjecture of Kung and Traub [
10], the order of convergence of an optimal iterative method without memory is at least
, where
n denotes the number of function evaluations. A number of researchers have used different techniques to develop optimal iterative methods in order to reach this bound. For example, Kou et al. [
11], Sharma et al. [
12], Nadeem et al. [
13], Panday et al. [
14], Kansal et al. [
15], Qureshi et al. [
16], Jaiswal et al. [
17], and Choubey et al. [
18] have employed combination technique to derive optimal higher order iterative schemes for solving nonlinear equations.
Although the objective of recent studies has been either to propose modifications of the existing methods or to develop new ones, iterative techniques have been designed as a workaround for determining the initial values of solutions to the nonlinear equations in the following form:
where
is a continuously differentiable nonlinear function and
D is an open interval. As accurate solutions are rarely found for such equations, iterative approaches suffer from issues including divergence at all, non-convergence, slow convergence, inefficiency, and failure. As a result, researchers worldwide are committed to improving and developing higher-order multi-point iterative techniques that can overcome the above problems. Multi-point techniques theoretically outperform one-point techniques in terms of effectiveness and system compatibility.
In this paper, a two-step, fourth-order, and optimal iterative method is developed for solving nonlinear equations. With the goal of achieving the optimal convergence order, the proposed method requires just one evaluation of function, in addition to two evaluations of its first derivative. We also have a relatively straightforward framework for our method. Furthermore, we also suggest a main theorem that illustrates convergence to the fourth order when the number of roots is known in advance. Additionally, we demonstrate the numerical effectiveness of our approach on real-world examples such as a quarter car suspension model, a hanging object, a series circuit analogue problem, a vertical stress problem, a chemical engineering problem and a blood rheology model. We provide numerical and graphical examples to further highlight how our approaches behave in contrast to the existing methods.
The rest of the paper is structured as follows: After the introduction,
Section 2 presents a concise overview of various existing methods documented in the literature.
Section 3 details the development and convergence analysis of our proposed fourth-order method.
Section 4 delves into the stability analysis of specific methods using the basins of attraction technique. In
Section 5, we present numerical results for certain methods in the real domain, along with comparative analyses. Finally,
Section 6 concludes the paper.
2. Brief Overview of Some Existing Methods
Before proceeding with the discussion and derivation of the proposed method, we will first review some of the frequently used methods found in the literature. These established methods will later serve as benchmarks to compare against the results obtained from our proposed method. By doing so, we aim to highlight the effectiveness and potential advantages of our new approach. Additionally, we will examine their respective performance metrics and computational costs to provide a comprehensive evaluation. In nutshell, we use the following fourth-order optimal methods as follows.
King [
19,
20] proposed the following two-point iterative technique with optimal fourth order of convergence requiring to evaluate only three functional evaluations, given as (
)
Kou et al. presented [
11] a fourth-order iterative method with the help of composing the Newton–Steffensen method [
21] and Potra–Ptak method [
22]. Their method is given by (
)
In 2012, Chun et al. [
23] developed fourth-order optimal iterative method given as
:
In 2015, Junjua et al. [
24] proposed the following fourth-order optimal iterative algorithm, denoted as
:
In 2019, Chicharro et al. [
25] devised a fourth-order optimal iterative method as follows:
We denote scheme (
6) by
.
In 2020, Sharma et al. [
26] developed a fourth-order optimal iterative method as
:
where
.
In 2023, Qureshi et al. [
16] developed an optimal fourth-order method with the help of a combination technique given as
:
In 2023, Panday et al. [
14] proposed a fourth-order optimal iterative algorithm by taking the linear combination of two existing third-order methods given as
:
In 2024, Abdullah et al. [
27] developed a new root finding algorithm of the fourth order satisfying the Kung and Traub conjecture given as
:
Again in 2024, Qureshi et al. [
28] developed an optimal fourth-order method by merging two existing third-order algorithms with the the aid of a linear combination technique given as
:
4. Basins of Attraction
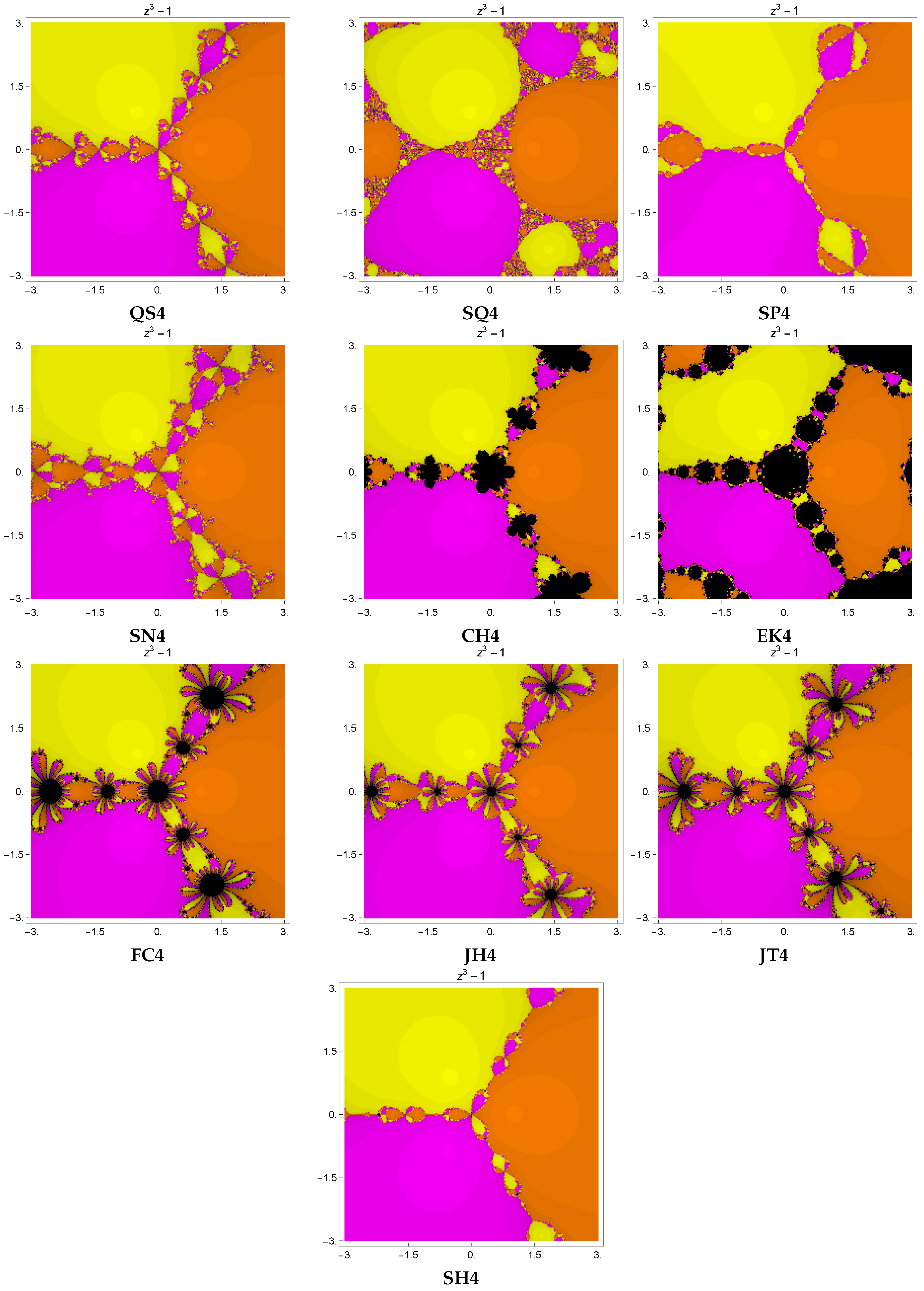
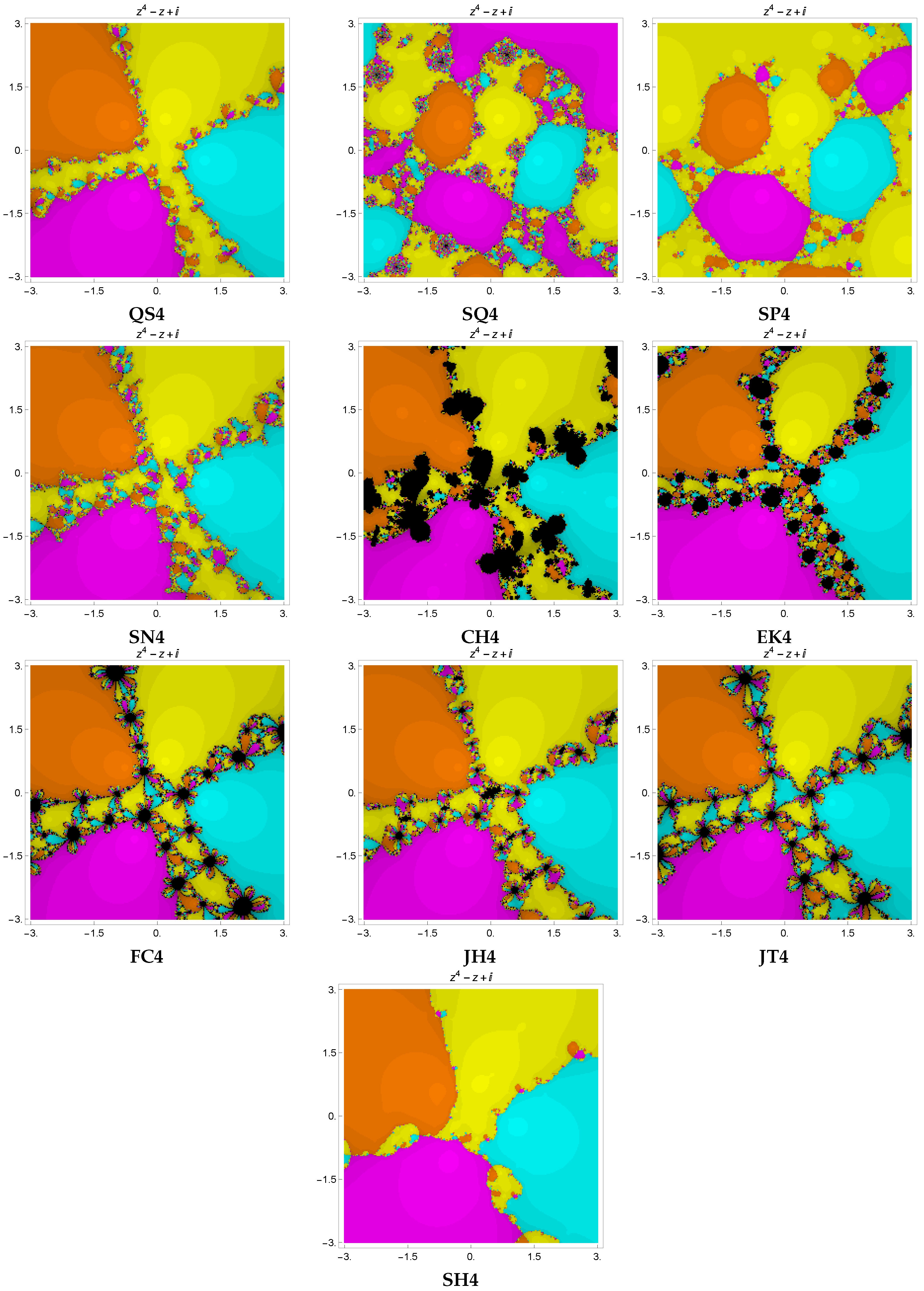
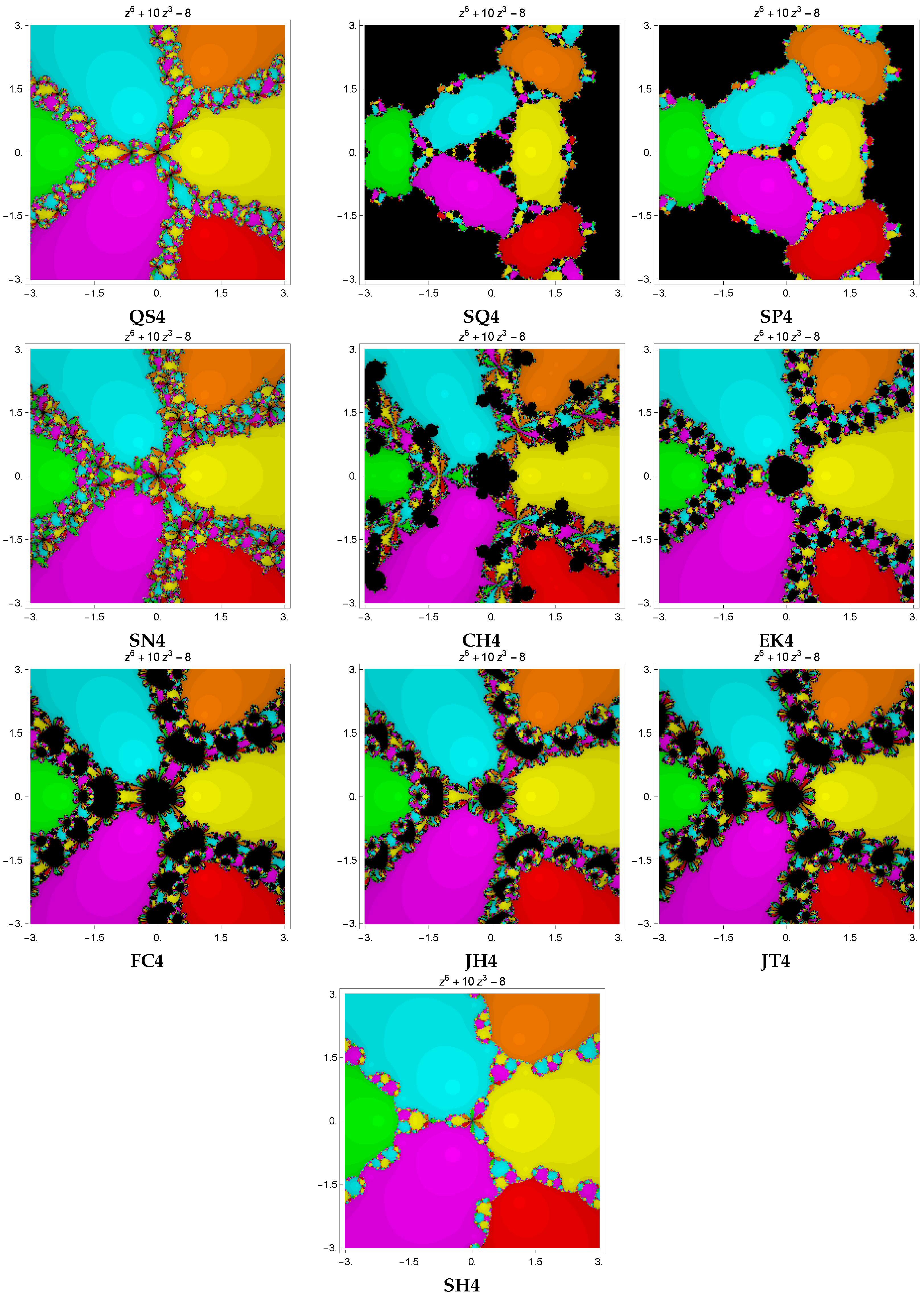
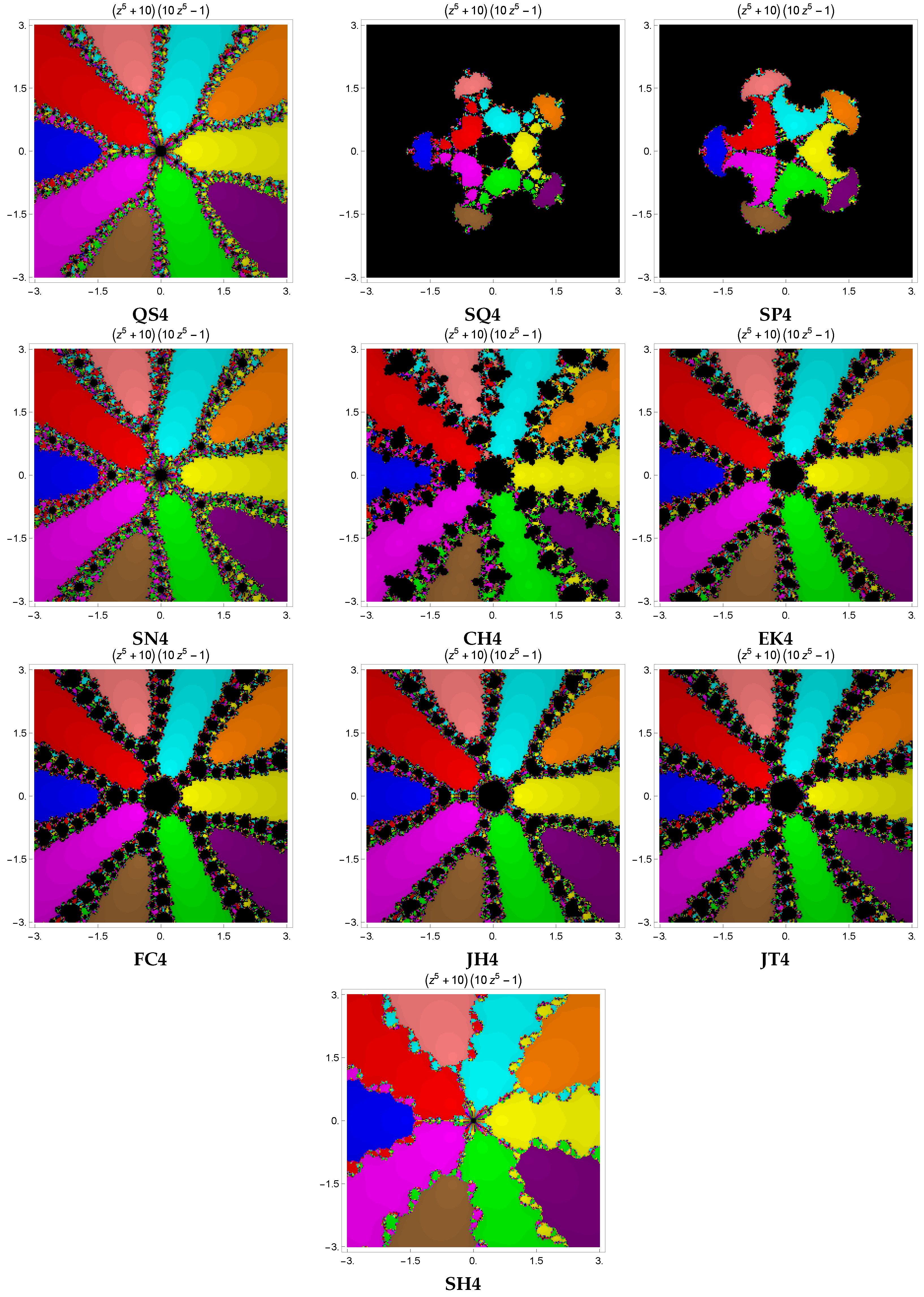
In this section, we investigate the dynamic properties of several fourth-order iterative techniques for solving the nonlinear equation
, in which the function
operates in a complex plane of complex geometry. In 1879, Cayley [
30] initiated the exploration of Newton’s technique by plotting basins of attraction for a quadratic polynomial
. Firstly, Stewart in [
30] presented the study of basins of attractions for the visual comparisons of different iteration techniques. He displayed the attraction basins of the roots of a polynomial obtained by different iterative procedures. He compared Newton’s scheme with numerous other methods of different orders, such as Leguerre’s method, Popovski’s method and Halley’s method.
The basins of attraction technique is a way to illustrate how different initial points impact the iterative method’s behavior. An iterative method can converge to the required root regardless of the order of convergence provided an appropriate initial estimate is given. Therefore, evaluating an iterative method’s stability using one or more initial estimates on different test functions does not yield a complete picture of the method’s stability. The convergence region of the basins of attraction of the root allows us to evaluate different iterative techniques. An iterative technique which provides less divergence (black dots) and wider regions of convergence is regarded as stable and reliable.
In order to plot the basins of attraction, we select a square region in the complex plane, labeled as I, that encompasses all of the roots of the complex polynomial under consideration. For a given initial point , distinct colors are allocated to different roots to which an iterative method converges. The presence of black-colored dots in the images indicates that the method did not succeed in finding a solution within the specified conditions, including the maximum number of iterations and the predetermined error threshold allowed to find the solution. The color brightness varies according to the number of iterations needed for convergence; a darker color indicates that more iterations are needed for the iterative technique to converge, while a brighter color specifies that fewer iterations are needed. We assume a maximum of 15 iterations and a tolerance of in this section. The number of black points in column number 3 shows that non-convergent points have a significant impact on the average number of iterations per point because they always require the maximum number of iterations allowed. Column 5 indicates the time it took to arrive at the solution, while column 4 displays the average number of iterations per point.
Example 1. Consider the nonlinear functionhaving roots 1, and . The basins are depicted in Figure 1. The distinct methods , , and of the same order were compared with the new iterative approach . One can observe from Table 1 that our proposed method produces fewer black points as compared to others. Furthermore, a mean number of iterations is lower for than for the rest of the iterative techniques. Example 2. Consider the nonlinear function:The basins are depicted in Figure 2. The distinct methods , , , and of the same order were compared with the new iterative approach . One can observe from Table 2 that basins of attraction for the proposed method contain fewer black points as compared to others. Furthermore, the mean number of iterations is lower for than for the rest of the techniques. Example 3. Consider the nonlinear function:having roots ,, , , and . The basins are depicted in Figure 3. The distinct methods , , and of the same order were compared with the new iterative approach . One can observe from Table 3 that basins of attraction for the proposed method contain fewer black points as compared to others. Furthermore, the mean number of iterations is less for than for the rest of the techniques. Example 4. Consider the nonlinear function:having roots
. The basins are depicted in Figure 4. The distinct methods , , and of the fourth order are compared with the new iterative approach . One can observe from Table 4 that the basins of attraction for the proposed method have fewer black points as compared to others. Furthermore, mean number of iterations is less for than for the rest of the techniques. Moreover,
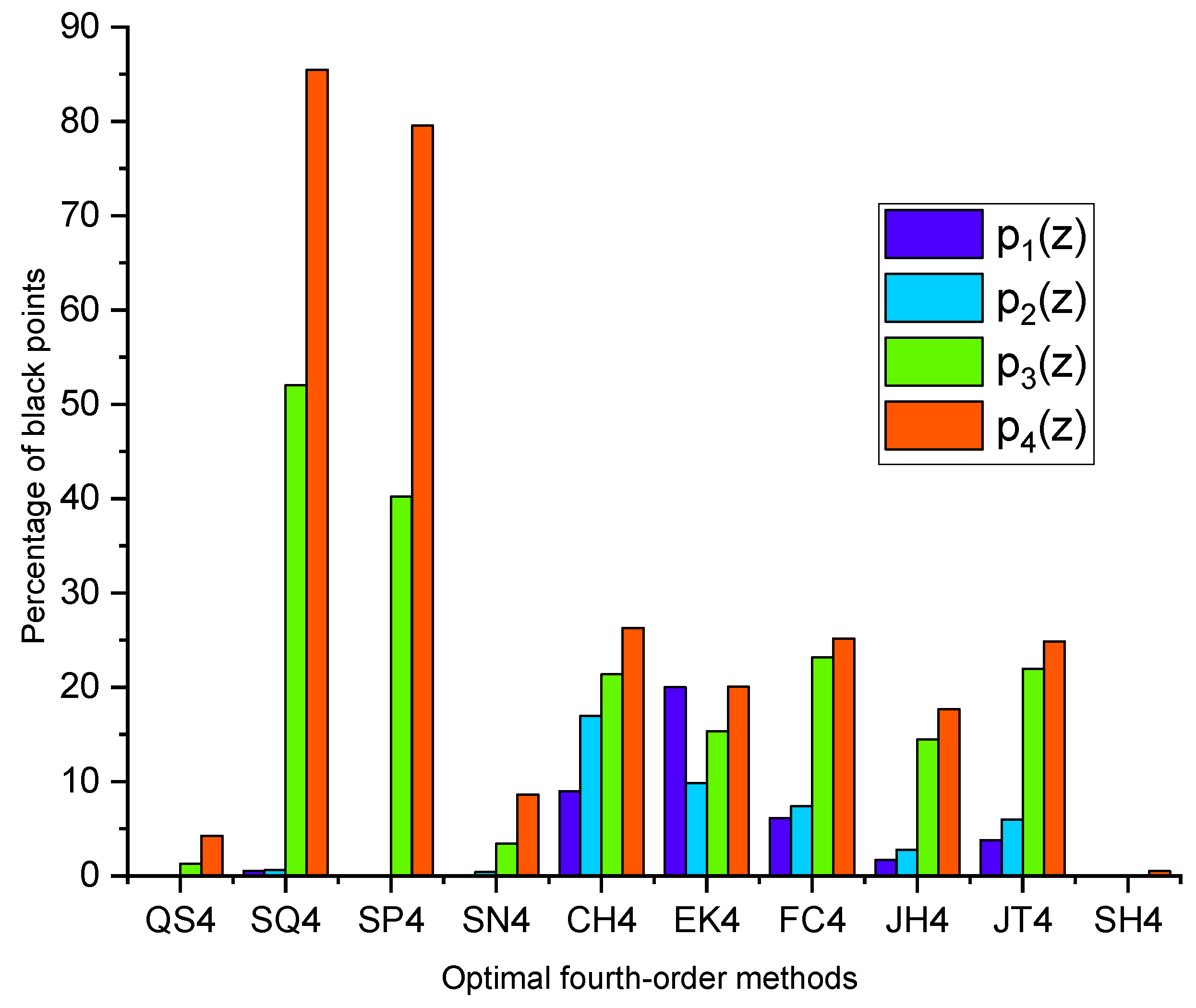
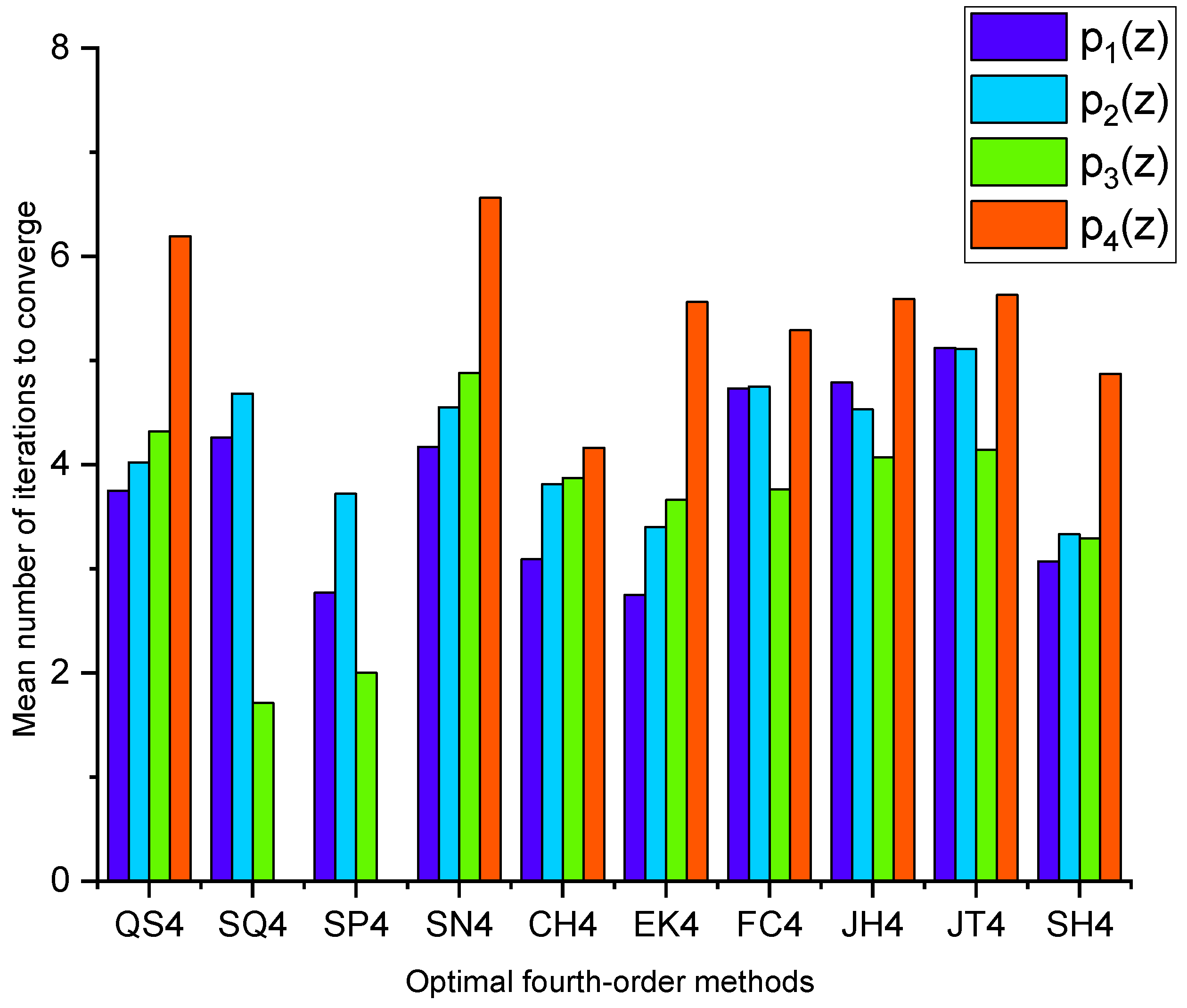
Figure 5 and
Figure 6 depict the graphical comparison among various iterative methods based on the number of black points and the mean number of iterations required for convergence, respectively.
From
Table 1,
Table 2,
Table 3 and
Table 4 and
Figure 1,
Figure 2,
Figure 3 and
Figure 4, it is evident that our proposed method
excels by demonstrating larger basins of attraction and fewer divergent points compared to other methods. Furthermore, it is observed from
Table 3 and
Table 4 and
Figure 3 and
Figure 4 that for Examples 3 and 4, most of the recently available optimal iterative algorithms failed to converge for solving highly complex problems since they provide a large number of black dots and a small area of convergence while the presented method remains effective in these circumstances.
5. Numerical Experiments
In this numerical study, we investigate numerical comparison of several iterative methods for solving some application-oriented nonlinear equations. To evaluate the performance of our recently developed iterative approach and to demonstrate its applications, some real-life application-based problems and their numerical solutions found by applying several iterative schemes are presented in this section.
The programming package
was used for all numerical computations and the results were rounded to 2000 significant digits to obtain accurate results.
Table 5,
Table 6,
Table 7,
Table 8,
Table 9 and
Table 10 show the absolute residual error
, the absolute error in the approximation of the root ((
) for the initial three iterations, the computational order of convergence
and the CPU time in seconds, for the different methods. Additionally, the CPU time (measured in seconds) required by each method is computed to achieve the stopping criterion condition
. The computational order of convergence (COC) is given by the formula [
19]:
All of the comparison results are shown in
Table 5,
Table 6,
Table 7,
Table 8,
Table 9 and
Table 10.
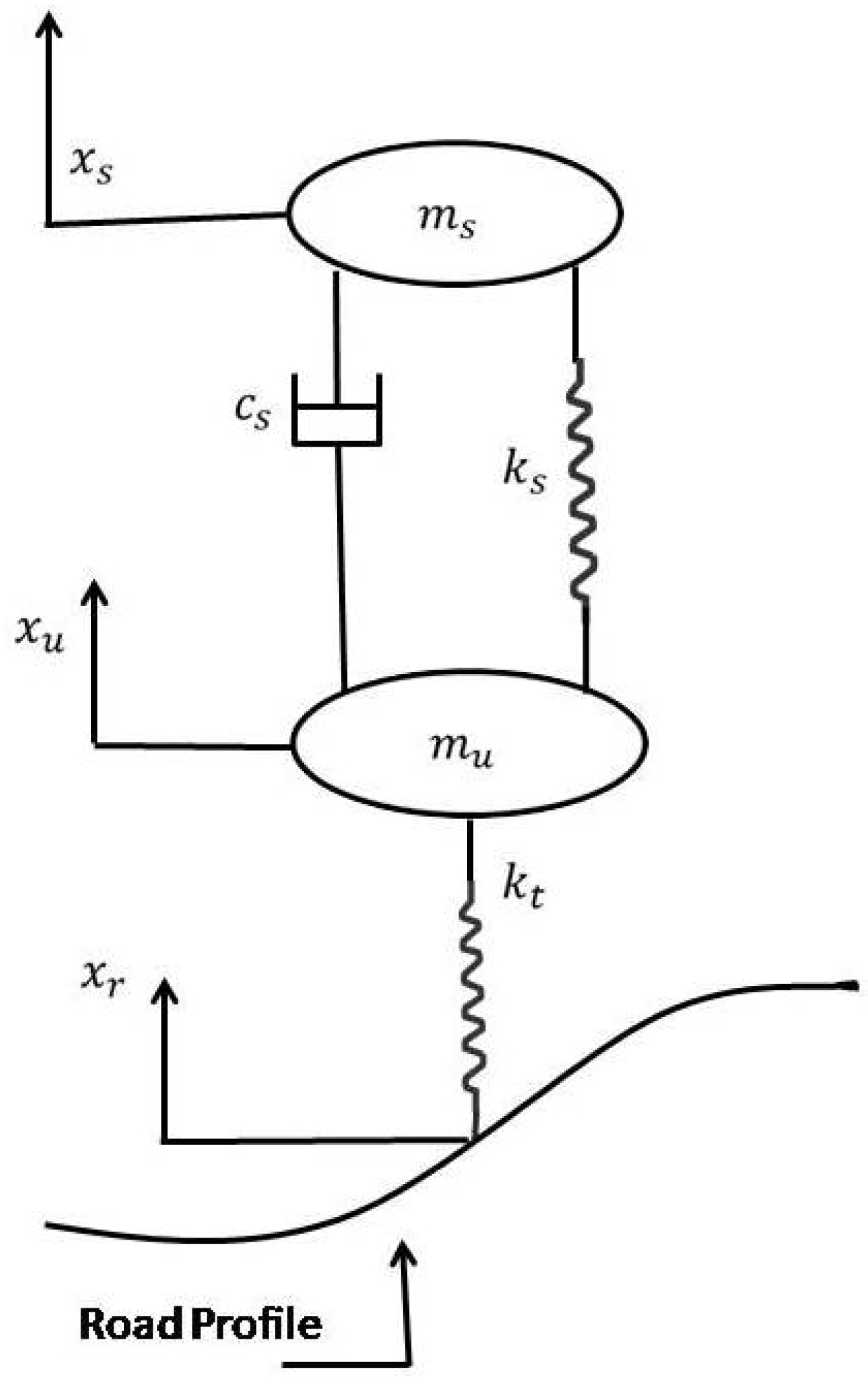
Problem 1: Quarter car suspension model [
31]. The shock absorber (also called a damper) is an important component of the suspension system that controls the dynamic response of the vehicle’s mass as well as the mass of the suspension system (Konieczny [
32] and Pulvirenti [
33]). The shock absorber’s nonlinear properties make it one of the suspension system’s most intricate parts. An asymmetric nonlinear hysteresis loop [
34] characterizes the damping force generated by the damper. The vehicle’s features are simulated in this study using a quarter-car model with two degrees of freedom. Comparing the effects of linear and nonlinear damping properties enables an investigation of the damper’s impact. Simple models, even linear and independently linear ones, are insufficient to adequately characterise the behavior of the damper. The mass motion equations are as follows [
35]:
The spring stiffness and suspension coefficients in the tire stiffness system are represented by the symbols
and
, respectively.
and
stand for the masses above and below the springs, and
and
for their respective displacements. According to [
31], the following polynomial is used to estimate the damping force coefficient
F in Equation (
30),
measuring the acceleration, velocity, and displacement of a mass over time (refer to
Figure 7), where
are exact roots of (
31) up to ten decimal places.
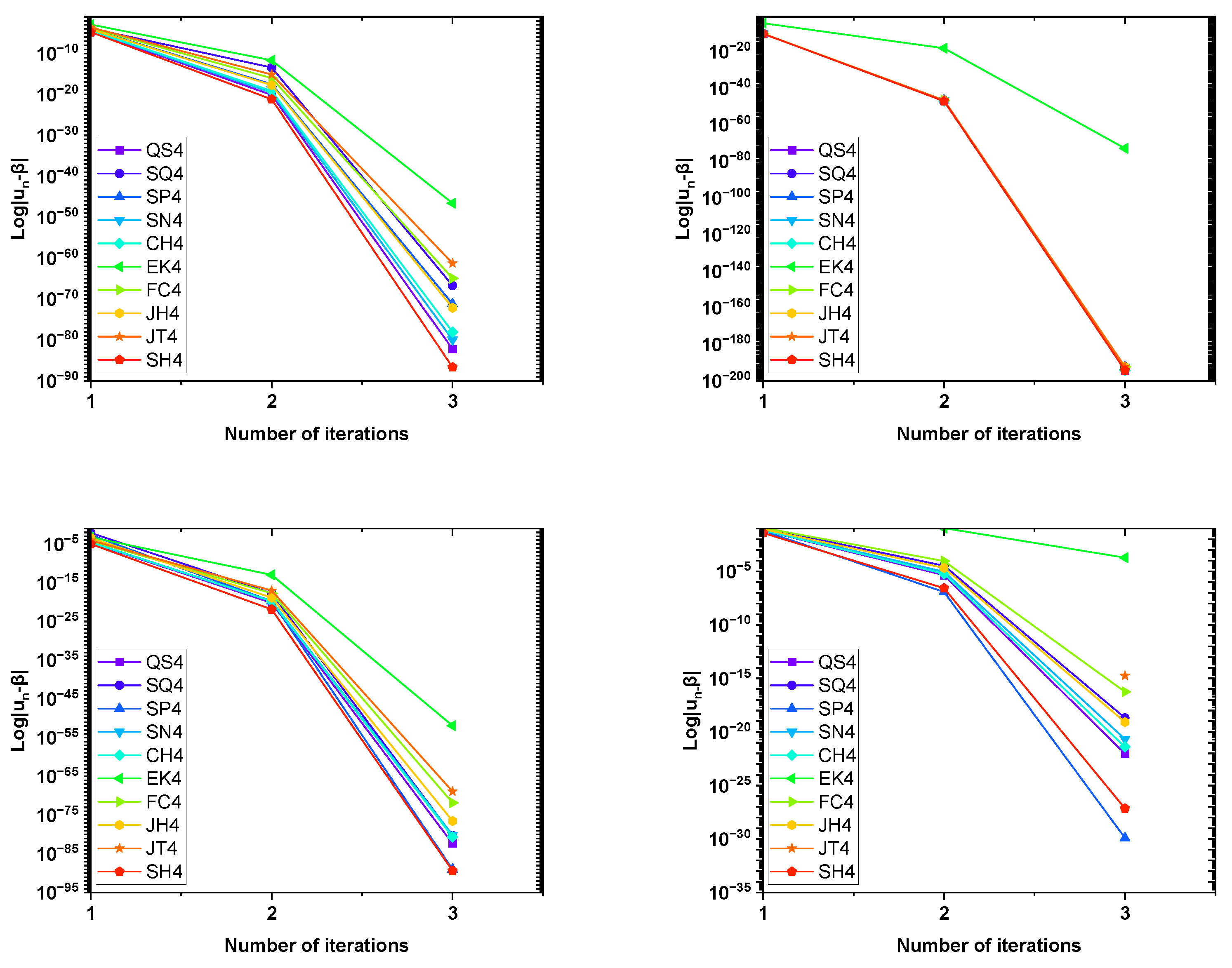
Table 5 provides an in-depth comparison of various fourth-order optimal algorithms applied to the quarter car suspension model described in (
31). Our proposed method,
, demonstrates outstanding performance by achieving the smallest absolute error after the third iteration (
) and the lowest final function value (
), indicating remarkable accuracy in the shortest
time (
s), showcasing its efficiency in comparison with the other methods
,
,
,
and
.
Problem 2: Hanging Object. The following nonlinear initial value problem originates from a situation in which a chain tied to an object on the ground is pushed upwards vertically by constant forces opposing gravity [
36]:
By utilizing the method discussed in [
37], a polynomial is employed to replicate Equation (
32) as follows:
where
denotes the exact solution of (
33) up to four decimal places.
Table 6 provides the comparison of various fourth-order optimal algorithms applied to the hanging object problem given by (
33). The proposed method,
, shows better performance by achieving the smallest absolute error after the third iteration (
) and the lowest final function value (
) in the shortest
time (
s), showcasing its efficiency.
Problem 3: Series circuit series analogue. Suppose we have a flexible spring with a mass m hanging from its free end, suspended vertically from a solid support. The mass attached to the spring controls how much it stretches or elongates; varied masses will result in different spring lengths. In accordance with Hooke’s law, a spring operates in the opposite direction of elongation and produces a restoring force,
F, that is exactly proportional to the amount of elongation. In short,
, where
k denotes the spring constant, serves as the proportionality constant. The differential equation for an undamped spring mass system is symbolized by
, which is mathematically represented as per [
37]:
By utilizing the method discussed in [
37], the polynomial is employed to replicate Equation (
34) as follows:
denote the exact solution of (
35) up to nine decimal places.
Table 7 provides a comparison of various fourth-order optimal algorithms applied to the series circuit analogue problem described in (
35). The proposed method
demonstrates outstanding performance in comparison with other methods,
,
,
,
and
, by achieving the smallest absolute error after the third iteration (
) and the lowest final function value (
), indicating remarkable accuracy. Moreover,
provides these results in the shortest
time (
s), showcasing its efficiency.
Problem 4: Civil Engineering Problem. You are designing a bookshelf with a height ranging from 8.5 inches to 11 inches and a total length of 29 inches. The shelf is made of wood with a Young’s Modulus of 3.66 Msi. It has a width of 12 inches and a thickness of 3/8 inches. Determine the maximum vertical deflection of the shelf in the figure:
The mathematical equation for the deflection of the shelf can be expressed as
In this example,
u represents the position along the length of the beam. Therefore, to determine the optimal deflection, we need to find
and perform the second derivative test, and thus,
The critical point for the deflection of the shelf, denoted as
, occurs at a position of
along the length of the beam. To determine the optimal deflection, we apply the second derivative test from single-variable calculus:
Now, at .
Hence, the minimum deflection of the shelf is at
Table 8 provides an in-depth comparison of various fourth-order optimal algorithms applied to the civil engineering problem described in (
37). The performance of our proposed method,
, is better than that of other methods like
,
,
,
and
, as it produces the smallest absolute error after the third iteration (
) and the lowest final function value (
), indicating remarkable accuracy in the shortest
time (
s), showcasing its efficiency.
Problem 5: Chemical Engineering Problem [
27]. The concentration of
determines the acidity of a solution containing
in
:
The following nonlinear model is obtained by defining
x as 104 times the hydronium ion concentration
as
where
are all the desired roots of Equation (
40).
Table 9 provides the numerical comparison of various fourth-order optimal algorithms applied to the chemical engineering problem described in (
40). Our proposed method,
, demonstrates outstanding performance by achieving the smallest absolute error after the third iteration (
) and the lowest final function value (
), indicating remarkable accuracy. Moreover,
delivers these results in the shortest
time (
s), showcasing its efficiency in comparison with
,
and
.
Problem 6: Blood rheology model [
38]. Blood rheology is the field of medical science that studies the physical and flow characteristics of blood. Blood’s non-Newtonian behavior often leads to its description as a Casson fluid. A simple fluid, such as blood or water, flows through a tube in a way that produces a velocity gradient along the tube walls. This fluid moves as a cohesive plug with little deformation, in accordance with the flow characteristics of a Casson fluid. Upon investigating the plug flow of Caisson fluid, particular attention is directed towards the following nonlinear equation:
where
u denotes the plug flow of Caisson fluid flow. One root of the Equation (
41) is
Table 10 provides an in-depth comparison of various fourth-order optimal algorithms applied to the blood rheology model described in (
41). The proposed method,
, demonstrates efficient performance by achieving the smallest absolute error after the third iteration (
), (
) and the lowest final function value (
), (
), respectively, indicating remarkable accuracy. Moreover,
delivers these results in the shortest
time (
s), showcasing its efficiency in comparison with other methods,
,
,
and
.
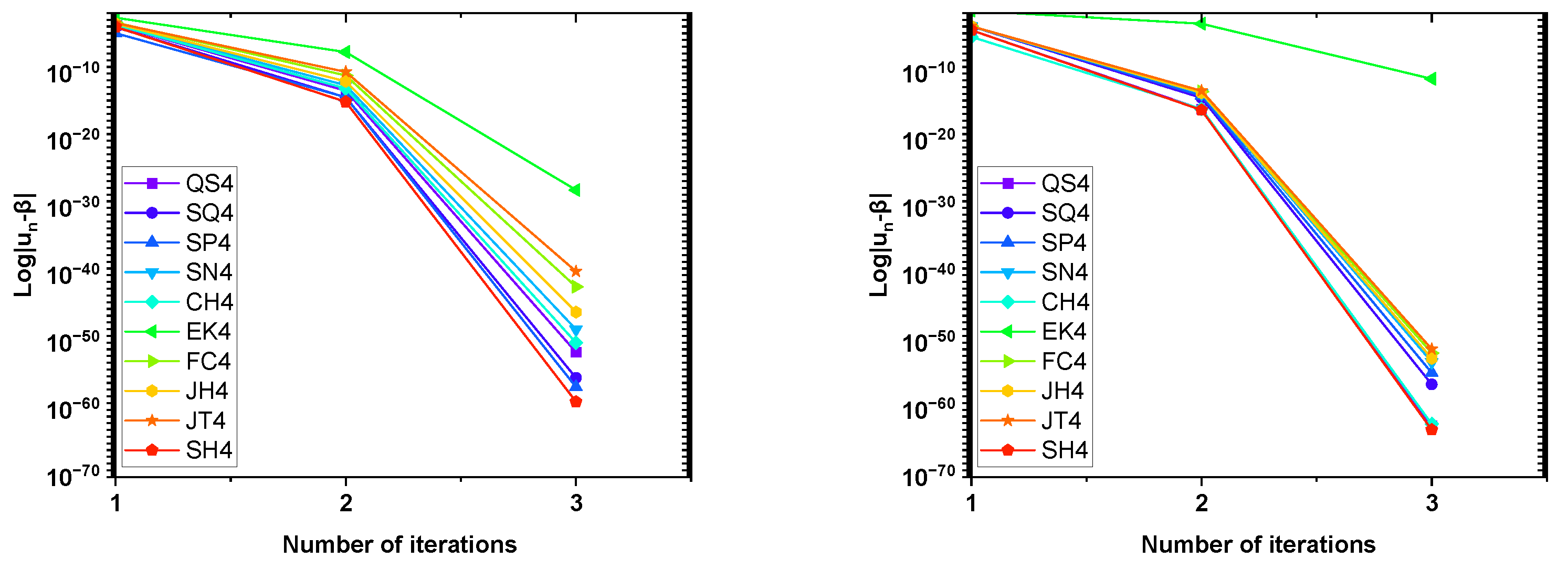
Furthermore,
Figure 5,
Figure 6 and
Figure 8 illustrate the graphical comparison of the different fourth-order optimal methods based on a percentage of black points, the mean number of iterations for methods to converge, and the absolute error in consecutive iterations represented as
after completing three iterations, respectively. The
Figure 5,
Figure 6 and
Figure 8 show that the proposed method
is highly competitive, demonstrating fast convergence towards the root in less CPU time and possesses superior accuracy compared to other well-known methods.