A Clustering-Based Approach to Detecting Critical Traffic Road Segments in Urban Areas
Abstract
1. Introduction
- We introduce an approach to automatic threshold value estimation based on knee-point detection. In general, a knee point in considered the operational point at which the system achieves the trade-off between cost and performance dependent on a tunable parameter. Thus, the traffic accident data are clustered repetitively by varying threshold value , and the operational threshold value is selected with respect to the introduced internal evaluation measure. Various knee-point detection algorithms have already been applied to determine the optimal number of clusters, cf. [21,22,23]. However, the criteria for the evaluation of clustering results are usually defined in a domain-independent manner, e.g., based on the within-cluster dispersion, between-cluster dispersion, etc. In contrast to those approaches, this paper proposes a novel domain-specific criterion for evaluating the clustering results, which promotes the stability of clustering results through time and inter-period accident spatial collocation, and penalizes the size of selected clusters.
- We propose an adaptation of the Kneedle algorithm [24] aimed at the automatic determination of the operational threshold value.
- In our approach, an urban area (e.g., a city) encompasses a set of possibly diverse administrative units (e.g., municipalities), each of which exercises traffic control jurisdiction over its roads. Thus, the criteria for the determination of critical road segments may differ among different administrative units. One of the novelties of the proposed approach is that traffic analysis is conducted for each administrative unit separately, but the clustering results are evaluated at the level of the entire urban area.
- For the purpose of illustration, the proposed approach is applied to data on traffic accidents with injuries or death that occurred in three of the largest cities of Serbia over the three-year period [25,26,27], as summarized in Table 2. For each accident, only its unique identification number and positional coordinates are taken into account. In an external validation, the obtained clustering results are positively evaluated with respect to the locations of traffic cameras.
2. Evaluation Measure for Traffic Accident Clustering
- Stability of clustering results through time;
- Inter-period accident spatial collocation;
- Area covered by the selected clusters.
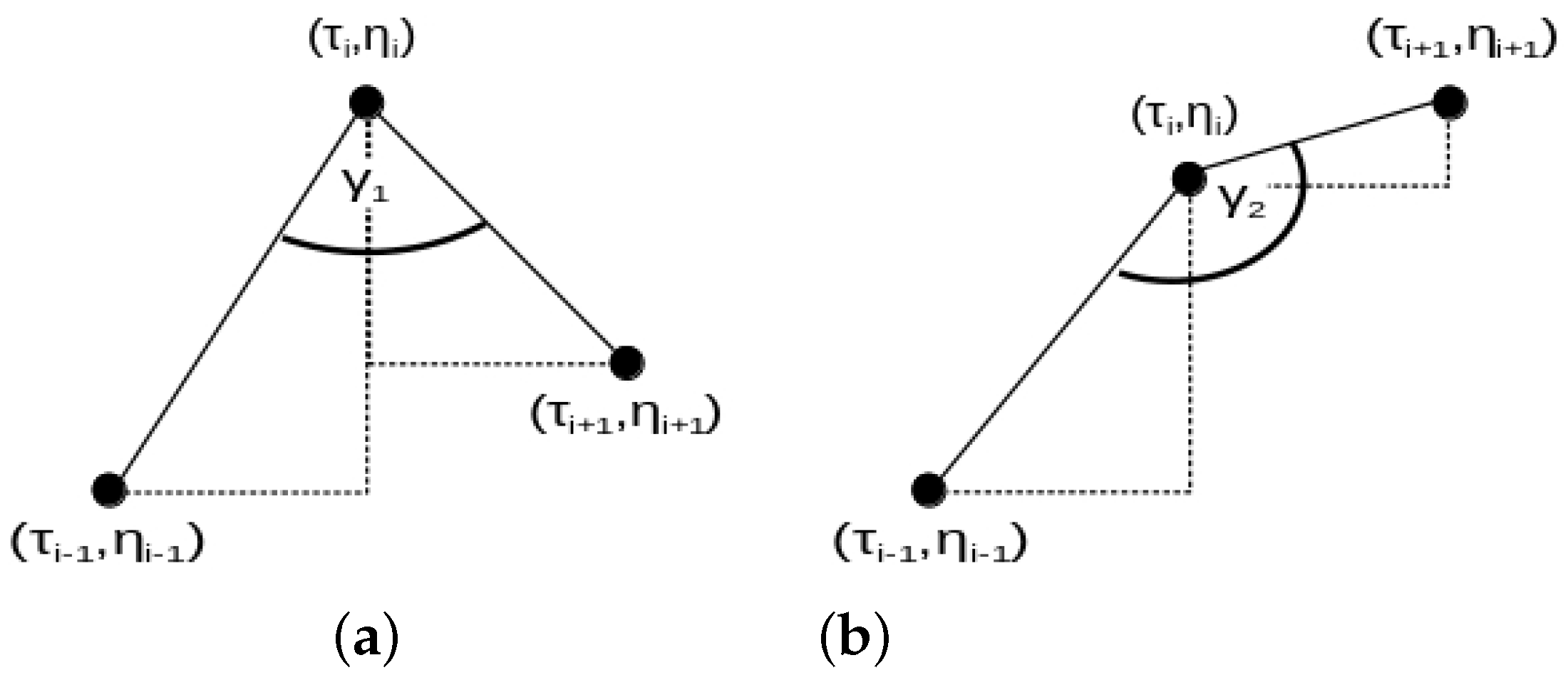
2.1. Stability of Clustering Results through Time
- 1.
- The clustering algorithm [19] is applied to data on traffic accidents that occurred in municipality over period .
- 2.
- We calculate the shares (i.e., percentage) of all traffic accidents that occurred in municipality over period and , respectively, that belong to the clusters selected in Step 1. We denote these shares as and .
- The municipality of Zvezdara (denoted as m);
- Threshold value ;
- Period runs from January 2019 to December 2020;
- Period runs from January 2021 to December 2021.
- 1.
- 2.
- The four selected clusters contain 257 traffic accidents. Thus, the share of the traffic accidents that occurred in the municipality over period that belong to the selected clusters is
- 3.
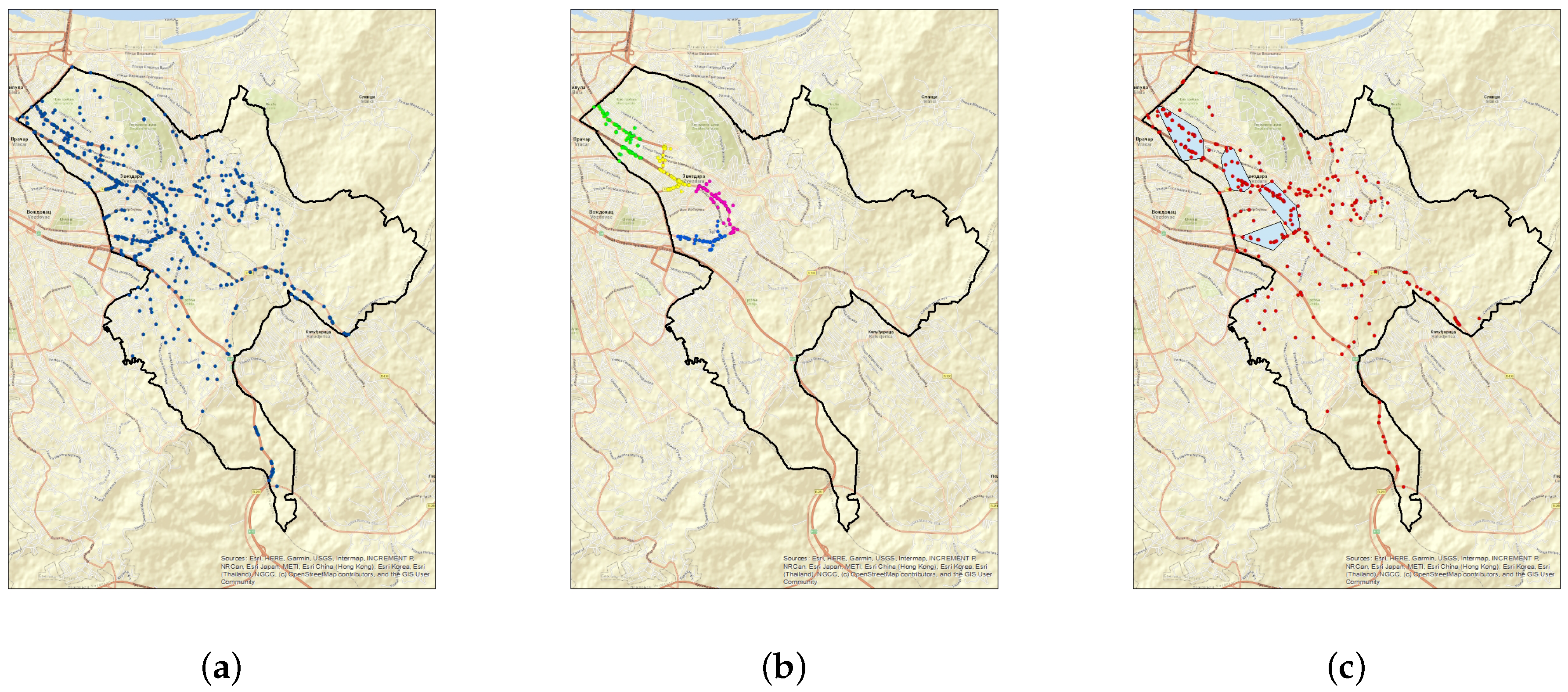
- Over period , 317 traffic accidents with injuries or death occurred in the municipality of Zvezdara. Figure 1c shows a map of all these traffic accidents. In addition, each of the clusters given in Figure 1a is represented as the minimum bounding box of its convex hull in Figure 1c. The number of accidents occurred over this period that belong to the areas covered by the clusters selected in Step 1 is 131. The share of the captured traffic accidents is
2.2. Inter-Period Accident Spatial Collocation
- The total number of accidents with injuries or death over period is 4072.
- The number of accidents that occurred over this period that belong to the areas covered by the clusters obtained when the clustering algorithm was applied to the set of all traffic accidents with injuries or death occurred over period is 1588.
2.3. Relative Size of Selected Clusters
2.4. Integrated Measure for Traffic Accident Clustering
- represents the stability of the clustering results;
- represents the inter-period accident spatial collocation index;
- represents the city-level relative size of selected clusters.
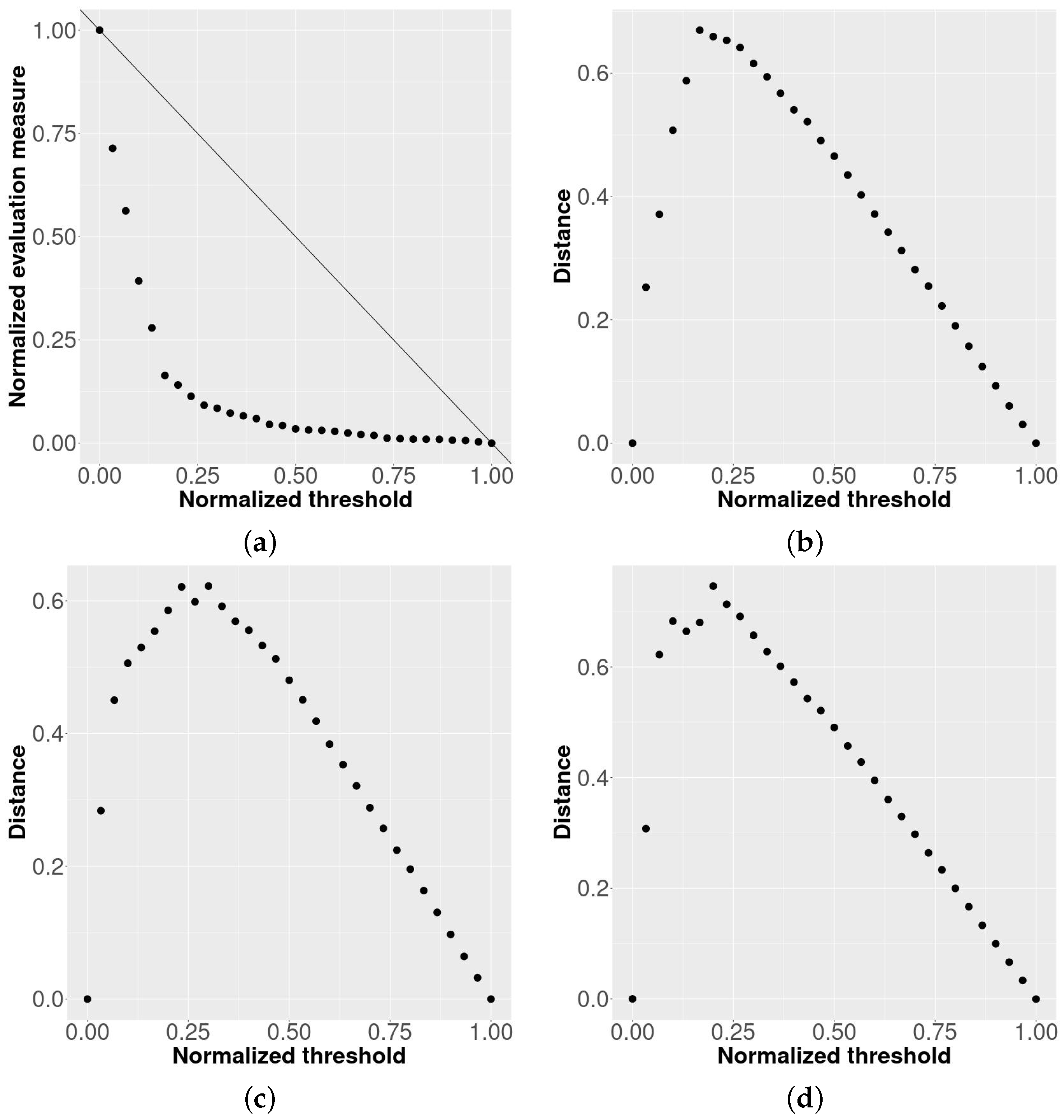
3. Threshold Selection
4. Results
5. Discussion
- Data availability: The information on the locations of traffic cameras as of August 2020 can be derived from the publicly available information provided by the Ministry of Interior of the Republic of Serbia [28].
- External criterion: The locations are determined based on expert analysis performed by a third party and independently of this study. The camera locations are indicative, inter alia, of traffic hotspots and may be used as an external evaluation criterion.
- Time appropriateness: We consider the locations of traffic cameras in an early installation phase, under the assumption that the installation has started with the most critical traffic hotspots. In addition, the clusters are obtained by applying the clustering algorithm on traffic accidents that occurred over period . The selected “ground-truth” moment (i.e., August 2020) is close in time to the end of period .
- The considered cameras were not put into official use during periods and , i.e., they did not influence the traffic participant behavior during these periods.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Guo, X.; Su, B.; Sun, Y.; Zhu, Y. Multi-Lane Traffic Load Clustering Model for Long-Span Bridge Based on Parameter Correlation. Mathematics 2023, 11, 274. [Google Scholar] [CrossRef]
- Zang, J.; Jiao, P.; Liu, S.; Zhang, X.; Song, G.; Yu, L. Identifying Traffic Congestion Patterns of Urban Road Network Based on Traffic Performance Index. Sustainability 2023, 15, 948. [Google Scholar] [CrossRef]
- Shang, Q.; Yu, Y.; Xie, T. A Hybrid Method for Traffic State Classification Using K-Medoids Clustering and Self-Tuning Spectral Clustering. Sustainability 2022, 14, 11068. [Google Scholar] [CrossRef]
- Hernández, H.; Alberdi, E.; Pérez-Acebo, H.; Álvarez, I.; García, M.J.; Eguia, I.; Fernández, K. Managing Traffic Data through Clustering and Radial Basis Functions. Sustainability 2021, 13, 2846. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, N.; Wang, R.; Malekian, R. A Method for Traffic Congestion Clustering Judgment Based on Grey Relational Analysis. ISPRS Int. J. Geo-Inf. 2016, 5, 71. [Google Scholar] [CrossRef]
- Esenturk, E.; Turley, D.; Wallace, A.; Khastgir, S.; Jennings, P. A data mining approach for traffic accidents, pattern extraction and test scenario generation for autonomous vehicles. Int. J. Transp. Sci. Technol. 2022; in press, corrected proof. [Google Scholar] [CrossRef]
- Esenturk, E.; Wallace, A.G.; Khastgir, S.; Jennings, P. Identification of Traffic Accident Patterns via Cluster Analysis and Test Scenario Development for Autonomous Vehicles. IEEE Access 2022, 10, 6660–6675. [Google Scholar] [CrossRef]
- Niu, Z.; Wang, Y.; Sun, S. Correlation Analysis of Traffic Accident Factors based on Mean Clustering. In ICCSIE ’22, Proceedings of the 7th International Conference on Cyber Security and Information Engineering, Brisbane Australia, 23–25 September 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 569–575. [Google Scholar] [CrossRef]
- Bokaba, T.; Doorsamy, W.; Paul, B.S. Comparative Study of Machine Learning Classifiers for Modelling Road Traffic Accidents. Appl. Sci. 2022, 12, 828. [Google Scholar] [CrossRef]
- Wang, D.; Huang, Y.; Cai, Z. A two-phase clustering approach for traffic accident black spots identification: Integrated GIS-based processing and HDBSCAN model. Int. J. Inj. Control. Saf. Promot. 2023; published online. [Google Scholar] [CrossRef]
- Li, Y.; Huang, M. Identification of Critical Road Links Based on Static and Dynamic Features Fusion. Appl. Sci. 2023, 13, 5994. [Google Scholar] [CrossRef]
- Chen, S.; Cheng, K.; Yang, J.; Zang, X.; Luo, Q.; Li, J. Driving Behavior Risk Measurement and Cluster Analysis Driven by Vehicle Trajectory Data. Appl. Sci. 2023, 13, 5675. [Google Scholar] [CrossRef]
- Shah, M.A.; Zeeshan Khan, F.; Abbas, G.; Abbas, Z.H.; Ali, J.; Aljameel, S.S.; Khan, I.U.; Aslam, N. Optimal Path Routing Protocol for Warning Messages Dissemination for Highway VANET. Sensors 2022, 22, 6839. [Google Scholar] [CrossRef] [PubMed]
- Rampinelli, A.; Calderón, J.F.; Blazquez, C.A.; Sauer-Brand, K.; Hamann, N.; Nazif-Munoz, J.I. Investigating the Risk Factors Associated with Injury Severity in Pedestrian Crashes in Santiago, Chile. Int. J. Environ. Res. Public Health 2022, 19, 11126. [Google Scholar] [CrossRef] [PubMed]
- Lilhore, U.K.; Imoize, A.L.; Li, C.-T.; Simaiya, S.; Pani, S.K.; Goyal, N.; Kumar, A.; Lee, C.-C. Design and Implementation of an ML and IoT Based Adaptive Traffic-Management System for Smart Cities. Sensors 2022, 22, 2908. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.; Kim, I.; Han, K.; Kim, J. Comprehensive Analysis of Traffic Accidents in Seoul: Major Factors and Types Affecting Injury Severity. Appl. Sci. 2022, 12, 1790. [Google Scholar] [CrossRef]
- Baek, J. Highway Regional Classification Method Based on Traffic Flow Characteristics for Highway Safety Assessment. Sensors 2022, 22, 86. [Google Scholar] [CrossRef] [PubMed]
- Bajada, T.; Attard, M. A typological and spatial analysis of pedestrian fatalities and injuries in Malta. Res. Transp. Econ. 2021, 86, 101023. [Google Scholar] [CrossRef]
- Gnjatović, M.; Košanin, I.; Maček, N.; Joksimović, D. Clustering of Road Traffic Accidents as a Gestalt Problem. Appl. Sci. 2022, 12, 4543. [Google Scholar] [CrossRef]
- Shih, F.Y. Image Processing and Pattern Recognition: Fundamentals and Techniques; Wiley-IEEE Press: Hoboken, NJ, USA, 2010. [Google Scholar]
- Zhao, Q.; Hautamaki, V.; Fränti, P. Knee Point Detection in BIC for Detecting the Number of Clusters. In Advanced Concepts for Intelligent Vision Systems (ACIVS 2008); Blanc-Talon, J., Bourennane, S., Philips, W., Popescu, D., Scheunders, P., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5259, pp. 664–673. [Google Scholar] [CrossRef]
- Islam, M.R.; Jenny, I.J.; Nayon, M.; Islam, M.R.; Amiruzzaman, M.; Abdullah-Al-Wadud, M. Clustering algorithms to analyze the road traffic crashes. In Proceedings of the 2021 International Conference on Science & Contemporary Technologies (ICSCT), Dhaka, Bangladesh, 5–7 August 2021. [Google Scholar]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Satopää, V.; Albrecht, J.; Irwin, D.; Raghavan, B. Finding a “Kneedle” in a Haystack: Detecting Knee Points in System Behavior. In ICDCSW ’11, Proceedings of the 2011 31st International Conference on Distributed Computing Systems Workshops, Washington, DC, USA, 20–24 June 2011; Association for Computing Machinery: Minneapolis, MN, USA, 2011; pp. 166–171. [Google Scholar] [CrossRef]
- Republic of Serbia. Data on Traffic Accidents for 2021 for the Territory of all Police Administrations and Municipalities. Available online: https://data.gov.rs/s/resources/podatsi-o-saobratshajnim-nezgodama-po-politsijskim-upravama-i-opshtinama/20220125-085458/nez-opendata-2021-20220125.xlsx (accessed on 1 March 2022).
- Republic of Serbia. Data on Traffic Accidents for 2020 for the Territory of all Police Administrations and Municipalities. Available online: https://data.gov.rs/s/resources/podatsi-o-saobratshajnim-nezgodama-po-politsijskim-upravama-i-opshtinama/20210208-095135/nez-opendata-2020-20210125.xlsx (accessed on 1 March 2022).
- Republic of Serbia. Data on Traffic Accidents for 2019 for the Territory of all Police Administrations and Municipalities. Available online: https://data.gov.rs/s/resources/podatsi-o-saobratshajnim-nezgodama-po-politsijskim-upravama-i-opshtinama/20200127-133136/nez-opendata-2019-20200125.xlsx (accessed on 1 March 2022).
- Ministry of Interior, Republic of Serbia. List of Locations of Video Surveillance System Camera Sites in the City of Belgrade. Available online: http://www.mup.rs/wps/wcm/connect/56a5cf77-df71-440a-a5bd-0d5f92ec8336/lat-Tabela-prelazi.pdf?MOD=AJPERES&CVID=ng1rX1 (accessed on 12 March 2023). (In Serbian).

| Ref. | Task | Clustering Approach |
|---|---|---|
| [1] | traffic load analysis | improved k-means clustering algorithm |
| [2] | traffic congestion analysis | self-organizing maps neural network |
| [3] | traffic state classification | k-medoids algorithm |
| [4] | road network level identification | k-means algorithm |
| [5] | traffic congestion analysis | grey relational clustering model |
| [6] | traffic accidents and pattern extraction | ROCK algorithm |
| [7] | traffic accident pattern identification | COOLCAT algorithm |
| [8] | traffic accident factor analysis | k-means algorithm |
| [9] | road traffic accident modeling | a comparative study of machine learning classifiers |
| [10] | traffic accident black spots identification | HDBSCAN algorithm |
| [11] | traffic congestion analysis | k-means algorithm |
| [12] | driving behavior risk analysis | k-means algorithm |
| [13] | optimal path routing | a modified K-medoids algorithm |
| [14] | analysis of pedestrian crash fatalities and severe injuries | KDE method |
| [15] | traffic-management system | DBSCAN agorithm |
| [16] | severity of traffic accident analysis | DBSCAN algorithm |
| [17] | highway safety assessment | k-means algorithm |
| [18] | pedestrian crash severity analysis | KDE method |
| [19] | detection of road segments of spatially prolonged and high traffic accident risk | a clustering algorithm based on the Gestalt principle of proximity |
| City | 2019 | 2020 | 2021 | Total |
|---|---|---|---|---|
| Beograd | 4684 | 3720 | 4072 | 12,476 |
| Novi Sad | 1710 | 1464 | 1574 | 4748 |
| Niš | 607 | 521 | 528 | 1656 |
| Total | 7001 | 5705 | 6174 | 18,880 |
| Municipality | ||||||
|---|---|---|---|---|---|---|
| # Accidents | # Selected Accidents | Share [%] | # Accidents | # Selected Accidents | Share [%] | |
| Barajevo | 123 | 54 | 43.902 | 51 | 21 | 41.176 |
| Grocka | 295 | 105 | 35.593 | 150 | 40 | 26.667 |
| Lazarevac | 281 | 98 | 34.875 | 123 | 31 | 25.203 |
| Mladenovac | 206 | 59 | 28.641 | 113 | 30 | 26.549 |
| Novi beograd | 1126 | 401 | 35.613 | 537 | 186 | 34.637 |
| Obrenovac | 376 | 129 | 34.309 | 220 | 59 | 26.818 |
| Palilula | 962 | 308 | 32.017 | 384 | 132 | 34.375 |
| Rakovica | 297 | 105 | 35.354 | 141 | 44 | 31.206 |
| Savski venac | 572 | 311 | 54.371 | 270 | 155 | 57.407 |
| Sopot | 100 | 28 | 28.000 | 49 | 10 | 20.408 |
| Stari grad | 316 | 263 | 83.228 | 176 | 145 | 82.386 |
| Surčin | 231 | 86 | 37.229 | 125 | 30 | 24.000 |
| Voždovac | 879 | 324 | 36.860 | 447 | 177 | 39.597 |
| Vračar | 412 | 272 | 66.019 | 182 | 139 | 76.374 |
| Zemun | 800 | 257 | 32.125 | 393 | 126 | 32.061 |
| Zvezdara | 631 | 257 | 40.729 | 317 | 131 | 41.325 |
| Čukarica | 797 | 258 | 32.371 | 394 | 132 | 33.503 |
| Total | 8404 | 3315 | 39.446 | 4072 | 1588 | 38.998 |
| Municipality | # Selected Clusters | Area of Selected Clusters [km] | Municipality Area [km] | Relative Cluster Size [%] |
|---|---|---|---|---|
| Barajevo | 19 | 0.011 | 212.831 | 0.005% |
| Grocka | 22 | 0.072 | 299.349 | 0.024% |
| Lazarevac | 21 | 0.123 | 382.540 | 0.032% |
| Mladenovac | 9 | 0.151 | 338.764 | 0.045% |
| Novi Beograd | 1 | 7.057 | 40.756 | 17.316% |
| Obrenovac | 3 | 0.644 | 409.588 | 0.157% |
| Palilula | 2 | 4.563 | 450.351 | 1.013% |
| Rakovica | 7 | 0.222 | 30.025 | 0.739% |
| Savski venac | 2 | 2.321 | 14.082 | 16.484% |
| Sopot | 11 | 0.003 | 270.506 | 0.001% |
| Stari grad | 1 | 2.232 | 5.376 | 41.527% |
| Surčin | 20 | 0.053 | 288.303 | 0.018% |
| Voždovac | 3 | 2.233 | 148.409 | 1.505% |
| Vračar | 1 | 2.424 | 2.911 | 83.256% |
| Zemun | 8 | 1.500 | 149.682 | 1.002% |
| Zvezdara | 4 | 1.612 | 31.087 | 5.186% |
| Čukarica | 6 | 1.280 | 156.909 | 0.815% |
| Total | 140 | 26.502 | 3231.469 | 0.820% |
| Threshold Value | Stability of Clustering Results | Relative Size of Selected Clusters | Inter-Period Spatial Collocation | Integrated Measure for Traffic Accident Clustering |
|---|---|---|---|---|
| 100 | 0.980 | 0.001 | 0.297 | 302.465 |
| 110 | 0.982 | 0.001 | 0.286 | 220.035 |
| 120 | 0.975 | 0.002 | 0.327 | 176.388 |
| 130 | 0.980 | 0.002 | 0.319 | 127.509 |
| 140 | 0.981 | 0.004 | 0.368 | 94.753 |
| 150 | 0.978 | 0.005 | 0.329 | 61.536 |
| 160 | 0.987 | 0.007 | 0.363 | 54.953 |
| 170 | 0.990 | 0.008 | 0.390 | 47.082 |
| 180 | 0.991 | 0.010 | 0.416 | 40.827 |
| 190 | 0.992 | 0.011 | 0.440 | 38.685 |
| 200 | 0.993 | 0.013 | 0.454 | 35.308 |
| 210 | 0.994 | 0.014 | 0.466 | 33.419 |
| 220 | 0.993 | 0.015 | 0.461 | 31.504 |
| 230 | 0.994 | 0.017 | 0.477 | 27.453 |
| 240 | 0.995 | 0.019 | 0.510 | 26.685 |
| 250 | 0.996 | 0.022 | 0.532 | 24.345 |
| 260 | 0.996 | 0.024 | 0.569 | 23.539 |
| 270 | 0.996 | 0.025 | 0.591 | 23.275 |
| 280 | 0.997 | 0.026 | 0.587 | 22.600 |
| 290 | 0.997 | 0.028 | 0.594 | 21.453 |
| 300 | 0.997 | 0.029 | 0.589 | 20.412 |
| 310 | 0.997 | 0.030 | 0.601 | 19.732 |
| 320 | 0.998 | 0.035 | 0.629 | 17.872 |
| 330 | 0.998 | 0.036 | 0.637 | 17.489 |
| 340 | 0.998 | 0.037 | 0.641 | 17.186 |
| 350 | 0.998 | 0.037 | 0.642 | 17.118 |
| 360 | 0.999 | 0.038 | 0.647 | 17.047 |
| 370 | 0.999 | 0.040 | 0.661 | 16.406 |
| 380 | 0.999 | 0.041 | 0.667 | 16.178 |
| 390 | 0.999 | 0.045 | 0.682 | 15.263 |
| 400 | 0.999 | 0.048 | 0.690 | 14.371 |
| Municipality | # Selected Clusters | Area of Selected Clusters [km] | Municipality Area [km] | Relative Cluster Size [%] |
|---|---|---|---|---|
| Barajevo | 19 | 0.008197 | 212.831 | 0.004% |
| Grocka | 57 | 0.045736 | 299.349 | 0.015% |
| Lazarevac | 21 | 0.085380 | 382.540 | 0.022% |
| Mladenovac | 14 | 0.049522 | 338.764 | 0.015% |
| Novi Beograd | 1 | 3.575020 | 40.756 | 8.772% |
| Obrenovac | 3 | 0.516352 | 409.588 | 0.126% |
| Palilula | 2 | 4.257652 | 450.351 | 0.945% |
| Rakovica | 6 | 0.132195 | 30.025 | 0.440% |
| Savski Venac | 2 | 1.855433 | 14.082 | 13.176% |
| Sopot | 11 | 0.003422 | 270.506 | 0.001% |
| Stari Grad | 1 | 1.196700 | 5.376 | 22.260% |
| Surčin | 41 | 0.035323 | 288.303 | 0.012% |
| Vozdovac | 4 | 1.324443 | 148.409 | 0.892% |
| Vracar | 2 | 1.171392 | 2.911 | 40.240% |
| Zemun | 8 | 0.653254 | 149.682 | 0.436% |
| Zvezdara | 6 | 1.064036 | 31.087 | 3.423% |
| Čukarica | 5 | 0.898991 | 156.909 | 0.573% |
| Total | 203 | 16.873 | 3231.469 | 0.522% |
| Municipality | # Selected Clusters | Area of Selected Clusters [km] | Municipality Area [km] | Relative Cluster Size [%] |
|---|---|---|---|---|
| Bač | 6 | 0.010 | 367.268 | 0.003% |
| Bačka Palanka | 19 | 0.052 | 589.496 | 0.009% |
| Bački Petrovac | 7 | 0.001 | 158.257 | 0.000% |
| Beočin | 8 | 0.001 | 184.105 | 0.001% |
| Bečej | 21 | 0.036 | 486.196 | 0.007% |
| Novi Sad | 2 | 2.523 | 698.816 | 0.361% |
| Srbobran | 13 | 0.005 | 283.939 | 0.002% |
| Sremski Karlovci | 8 | 0.001 | 50.538 | 0.002% |
| Temerin | 14 | 0.031 | 169.525 | 0.019% |
| Titel | 1 | 0.000 | 260.600 | 0.000% |
| Vrbas | 10 | 0.131 | 375.326 | 0.035% |
| Žabalj | 18 | 0.003 | 399.566 | 0.001% |
| Total | 127 | 2.794 | 4023.633 | 0.069% |
| Municipality | # Selected Clusters | Area of Selected Clusters [km] | Municipality Area [km] | Relative Cluster Size [%] |
|---|---|---|---|---|
| Aleksinac | 6 | 0.116 | 706.335 | 0.016% |
| Doljevac | 10 | 0.001 | 121.275 | 0.001% |
| Gadžin Han | 1 | 0.000 | 324.931 | 0.000% |
| Merošina | 2 | 0.000 | 193.089 | 0.000% |
| Niš | 2 | 1.594 | 449.929 | 0.354% |
| Niška Banja | 5 | 0.002 | 146.185 | 0.001% |
| Ražanj | 2 | 0.000 | 288.512 | 0.000% |
| Svrljig | 6 | 0.001 | 496.894 | 0.000% |
| Total | 34 | 1.714 | 2727.151 | 0.063% |
| Municipality | # Camera Poles | # Cameras | # Covered Camera Poles | Share of Covered Camera Poles [%] | # Covered Cameras | Share of Covered Cameras [%] |
|---|---|---|---|---|---|---|
| Novi Beograd | 73 | 219 | 13 | 17.81 | 31 | 14.16 |
| Palilula | 7 | 17 | 4 | 57.14 | 10 | 58.82 |
| Savski venac | 13 | 20 | 9 | 69.23 | 15 | 75.00 |
| Stari grad | 15 | 42 | 12 | 80.00 | 35 | 83.33 |
| Vračar | 5 | 10 | 4 | 80.00 | 9 | 90.00 |
| Voždovac | 14 | 19 | 8 | 57.14 | 11 | 57.89 |
| Zemun | 24 | 57 | 9 | 37.50 | 22 | 38.60 |
| Zvezdara | 2 | 6 | 2 | 100.00 | 6 | 100.00 |
| Čukarica | 1 | 2 | 1 | 100.00 | 2 | 100.00 |
| Total | 154 | 392 | 62 | 40.26 | 141 | 35.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Košanin, I.; Gnjatović, M.; Maček, N.; Joksimović, D. A Clustering-Based Approach to Detecting Critical Traffic Road Segments in Urban Areas. Axioms 2023, 12, 509. https://doi.org/10.3390/axioms12060509
Košanin I, Gnjatović M, Maček N, Joksimović D. A Clustering-Based Approach to Detecting Critical Traffic Road Segments in Urban Areas. Axioms. 2023; 12(6):509. https://doi.org/10.3390/axioms12060509
Chicago/Turabian StyleKošanin, Ivan, Milan Gnjatović, Nemanja Maček, and Dušan Joksimović. 2023. "A Clustering-Based Approach to Detecting Critical Traffic Road Segments in Urban Areas" Axioms 12, no. 6: 509. https://doi.org/10.3390/axioms12060509
APA StyleKošanin, I., Gnjatović, M., Maček, N., & Joksimović, D. (2023). A Clustering-Based Approach to Detecting Critical Traffic Road Segments in Urban Areas. Axioms, 12(6), 509. https://doi.org/10.3390/axioms12060509






