A Note on Eigenvalues and Asymmetric Graphs

Abstract

This note is intended as a contribution to the study of quantitative measures of graph complexity that use entropy measures based on symmetry. Determining orbit sizes of graph automorphism groups is a key part of such studies. Here we focus on an extreme case where every orbit contains just a single vertex. A permutation of the vertices of a graph G is an automorphism if, and only if, the corresponding permutation matrix commutes with the adjacency matrix of G. This fact establishes a direct connection between the adjacency matrix and the automorphism group. In particular, it is known that if the eigenvalues of the adjacency matrix of G are all distinct, every non-trivial automorphism has order 2. In this note, we add a condition to the case of distinct eigenvalues that makes the graph asymmetric, i.e., reduces the automorphism group to the identity alone. In addition, we prove analogous results for the Google and Laplacian matrices. The condition is used to build an O(n³) algorithm for detecting identity graphs, and examples are given to demonstrate that it is sufficient, but not necessary.

1. Introduction

Studies of algebraic and spectral properties of graphs have blossomed since the 1970s (see [1,2,3]). This note introduces the eigenvectors of a graph that imply that the automorphism group is trivial. The proof builds on the result of Mowshowitz [4] that every non-trivial automorphism of a graph with all distinct eigenvalues has order 2. When the eigenvalues of a graph are distinct, we show that additional conditions imposed on the eigenvectors guarantees that the automorphism group is trivial. This condition imposed on the eigenvectors is sufficient but not necessary, as shown by examples.

The research reported here is motivated by the needs of symmetry-based quantitative measures of graph complexity. Such measures compute the entropy of a probability distribution over the orbits of the automorphism group (for a review of this topic, see [5]). The probability of an orbit is defined as the ratio of orbit size to the number n of vertices in the graph. Identity graphs constitute a special case for which each orbit has probability $1/n$, which gives the maximum entropy value of $log\left(n\right)$ . The determination of identity graphs is thus of interest in the study of symmetry-based measures of complexity.

The paper is organized as follows. In Section 2, we introduce mathematical preliminaries. In Section 3, we present the main results and derive conditions for determining whether a graph with distinct eigenvalues is an identity graph. Examples are given to illustrate the method. In Section 4, we complement the result in Section 3 by proving that the Laplacian matrix and Google matrix can be substituted for the adjacency matrix in the hypotheses of the main theorem. Moreover, properties of the Google matrix are contrasted with those of the adjacency matrix in relation to graph automorphisms. In Section 5, we show that the algorithm for determining identity graphs based on our main results has complexity $O\left(n^3\right)$. The concluding section points towards possible extensions of the results reported here.

2. Preliminaries

In this section, we introduce some mathematical preliminaries. All graphs are taken to be simple, connected and finite. See [5,6] for the graph theory terminology used in this note. Let G be a graph and $A=\left(a_{ij}\right)$ its adjacency matrix. Then, the characteristic polynomial of G is given by

$$\chi (G,\lambda )=det(\lambda I-A).$$

The eigenvalues of G are the roots of this polynomial. The spectrum of G, denoted by $Spec\left(G\right)$, is given by

$$Spec\left(G\right)=\left\{\right|{\lambda }_1{|}^{m_1},|{\lambda }_2{|}^{m_2},\cdots ,|{\lambda }_r{|}^{m_r}\},$$

where $m_i$ for $(1\le i\le r)$ is the multiplicity of eigenvalue ${\lambda }_i$ and ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_r$.

An eigenvalue ${\lambda }_i$ of G is called simple if its algebraic multiplicity $m_i=1$. The vector $X_i$ is called the eigenvector of graph G corresponding to ${\lambda }_i$, if $A{X}_i={\lambda }_i{X}_i$.

An automorphism of a graph G is a permutation $\pi$ of $V\left(G\right)$ satisfying $uv\in E\left(G\right)$ if, and only if, $\pi \left(u\right)\pi \left(v\right)\in E\left(G\right)$. The set of all automorphisms of G, under the operation of composition, is the automorphism group of G, denoted by $Aut\left(G\right)$. A graph that has only the identity automorphism is called an identity (or asymmetric) graph.

Let A be the adjacency matrix of simple graph G, and S the stochastic (or transition) matrix, defined by

$$S=D^{-1}A,$$

where $D=\left(d_{ij}\right)$ is a diagonal matrix in which $d_{ii}$ is the degree of vertex i. The Laplacian matrix of graph G is defined by

$$L=D-A.$$

The Google matrix M is given by

$$M=\alpha S+(1-\alpha )e{v}^T,$$

where $\alpha \in (0,1)$, $v^T>0$ is a probability vector, e is the column vector of all 1s, and n is the order of graph G [7]. In this paper, we use the uniform probability vector $v^T=\frac{1}{n}{e}^T$. The PageRank vector ${\pi }^T$ is the normalized dominant eigenvector of M corresponding to the dominant eigenvalue ${\lambda }_1=1$. Note that M is a stochastic matrix, so ${\lambda }_1=1$. Thus, determining PageRank requires solving the following for ${\pi }^T$.

$$\begin{array}{cc}\hfill {\pi }^T& ={\pi }^{T}M,\hfill \\ \hfill {\pi }^{T}e& =1.\hfill \end{array}$$

3. Main Results

The work presented here builds on the following results.

(1) Let A be the adjacency matrix of a graph G, and $\pi$ a permutation of $V\left(G\right)$. Then, $\pi$ is an automorphism of G if, and only if, $AP=PA$, where P is the permutation matrix representing $\pi$ [4,8].

(2) If all the eigenvalues of a graph G are distinct, every non-trivial automorphism of G has order 2 [4].

With these observations as a foundation, we first establish the following.

Lemma 1.

Let G be a simple graph with n distinct eigenvalues ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$, and suppose $X_1,X_2,\cdots ,X_n$ are their corresponding eigenvectors. If, for two vertices, $v_i,v_j\in V\left(G\right)$, and, for every eigenvector, $X_k$ , $x_{ik}\ne \mp x_{jk},k=1,2,\cdots ,n$, then there is no $P\in Aut\left(G\right)$, such that $P\left(v_i\right)=v_j$ (or for every $P\in Aut\left(G\right)$, $P\left(v_i\right)\ne v_j$).

Proof. 

If P is an automorphism, then $AP=PA$. Let $A{X}_k={\lambda }_k{X}_k$ for $k=1,2,\cdots ,n$ , so that $PA{X}_k={\lambda }_{k}P{X}_k$ and $AP{X}_k={\lambda }_{k}P{X}_k$. Hence, $P{X}_k$ is also an eigenvector of ${\lambda }_k$. Because ${\lambda }_k$ is a simple eigenvalue, the dimension of its eigenspace is one, which means $X_k$ and $P{X}_k$ are linearly dependent. Therefore, there exists a scalar $\mu \in \mathbb{R}$, such that $P{X}_k=\mu X_k$. Now, ${\left(P{X}_k\right)}^t\left(P{X}_k\right)={\mu }^2\left|\right|X_k{\left|\right|}^2$, and thus, $X_k^t{P}^{t}P{X}_k={\mu }^2\left|\right|X_k{\left|\right|}^2$, so that ${\mu }^2=1$, which implies $\mu =\mp 1$. From this we conclude

$$P{X}_k=\mp X_k.$$

(1)

Now, suppose there is a permutation $P\in Aut\left(G\right)$, such that $P\left(v_i\right)=v_j,P\left(v_j\right)=v_i$. This implies

$$P{X}_k=P\left[\begin{array}{c}⋮\\ x_{ik}\\ ⋮\\ x_{jk}\\ ⋮\end{array}\right]=\left[\begin{array}{c}⋮\\ x_{jk}\\ ⋮\\ x_{ik}\\ ⋮\end{array}\right]\ne \left[\begin{array}{c}⋮\\ \mp x_{ik}\\ ⋮\\ \mp x_{jk}\\ ⋮\end{array}\right],$$

or

$$P{X}_k\ne \mp X_k,$$

(2)

which gives a contradiction, concluding the proof. □

Example 1.

$G_1$, shown in Figure 1, is a simple graph with $Spec\left(G_1\right)=\{-1.8478,-7.6537\times {10}^{-1},1.3727\times {10}^{-16},8.6537\times {10}^{-1},1.8478\}$, whose corresponding eigenvectors are columns of the following matrix X.

$$X=\left[\begin{array}{ccccc}0.2760\times {10}^{-1}& -6.5328\times {10}^{-1}& 5.2313\times {10}^{-17}& 6.5328\times {10}^{-1}& 2.7060\times {10}^{-1}\\ -0.50000\times {10}^{-1}& -0.50000\times {10}^{-1}& 1.4174\times {10}^{-16}& -0.50000\times {10}^{-1}& -0.50000\times {10}^{-1}\\ 6.5328\times {10}^{-1}& 2.7060\times {10}^{-1}& 1.4105\times {10}^{-16}& 2.7060\times {10}^{-1}& 6.5328\times {10}^{-1}\\ -0.35355\times {10}^{-1}& -3.5355\times {10}^{-1}& -7.0711\times {10}^{-1}& -3.5355\times {10}^{-1}& 3.5355\times {10}^{-1}\\ -0.35355\times {10}^{-1}& -3.5355\times {10}^{-1}& 7.0711\times {10}^{-1}& -3.5355\times {10}^{-1}& 3.5355\times {10}^{-1}\end{array}\right]$$

The magnitudes of entries $1,2$, and 3 in all vectors $X_k$ are distinct. According to Lemma 1, there is no $P\in Aut\left(G_1\right)$, such that $P\left(v_1\right)=v_2$ and $P\left(v_2\right)=v_1$. Additionally, for vertices $v_1,v_3$ and $v_2,v_3$, there is no $P\in Aut\left(G_1\right)$, such that $P\left(v_1\right)=v_3$ and $P\left(v_3\right)=v_1$ or $P\left(v_2\right)=v_3$ and $P\left(v_3\right)=v_2$.

Note that the vertices $v_1$ and $v_2$ of $G_1$ are not in the same orbit. The orbits are $\left\{v_1\right\}$, $\left\{v_2\right\}$, $\left\{v_3\right\}$, and $\{v_4,v_5\}$.

Theorem 1.

Let G be a simple graph with n distinct eigenvalues ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$, and suppose $X_1,X_2,\cdots ,X_n$ are their corresponding eigenvectors. If, for every two vertices, $v_i,v_j\in V\left(G\right)$, and, for every eigenvector, $X_k$, $x_{ik}\ne \mp x_{jk}$, then G is an identity graph.

Proof. 

Since all eigenvalues are simple, Lemma 1 indicates that for every ${\lambda }_s(s=1,2,\cdots ,n)$ and $P\in Aut\left(G\right)$, we have

$$P{X}_s=\mp X_s.$$

(3)

From Result 2, we have $P^2=I$ for every $P\in Aut\left(G\right)$. There are two cases to consider, namely, $P=I$ or $P\ne I$. Now we will show that $P\ne I$ cannot be true. For this purpose, let $P\ne I$.

If $P\ne I$, there exists $X_k$ and $v_i,v_j\in V\left(G\right)$, such that $P\left(v_i\right)=v_j$, $P\left(v_j\right)=v_i$.

Clearly,

$$P{X}_k=P\left[\begin{array}{c}⋮\\ x_{ik}\\ ⋮\\ x_{jk}\\ ⋮\end{array}\right]=\left[\begin{array}{c}⋮\\ x_{jk}\\ ⋮\\ x_{ik}\\ ⋮\end{array}\right]\ne \left[\begin{array}{c}⋮\\ \mp x_{ik}\\ ⋮\\ \mp x_{jk}\\ ⋮\end{array}\right],$$

or

$$P{X}_k\ne \mp X_k.$$

(4)

From (3) and (4), we conclude that G is an identity graph. □

In other words, the graph G is an identity graph, whenever no two rows of matrix X are $\mp 1$ times each other, where the multiplication is performed element-wise.

Remark 1.

Figure 2 gives an example of an identity graph that does not satisfy the hypotheses of Theorem 1. In this case, there are two vertices, $v_i,v_j\in V\left(G\right)$, with $x_{ik}=\mp x_{jk}$ for some values of k. So, the converse of Theorem 1 is not true.

Example 2.

The Frucht graph shown in Figure 2 is an identity graph with distinct eigenvalues. For the two vertices $v_2,v_{12}\in V\left(G\right)$, we have $X_{2k}=\mp X_{12k}$ for all $k=1,2,\cdots n$.

$$X=\left[\begin{array}{cccccccccccc}4.37\times {10}^{-1}& -3.53\times {10}^{-1}& -9.44\times {10}^{-16}& -4.36\times {10}^{-2}& 1.66\times {10}^{-1}& 2.79\times {10}^{-16}& 2.04\times {10}^{-1}& 6.30\times {10}^{-1}& 4.11\times {10}^{-16}& -3.11\times {10}^{-1}& 1.84\times {10}^{-1}& -2.88\times {10}^{-1}\\ -1.97\times {10}^{-1}& 3.53\times {10}^{-1}& 2.67\times {10}^{-1}& 1.35\times {10}^{-1}& -5.00\times {10}^{-1}& -2.67\times {10}^{-1}& 2.04\times {10}^{-1}& 1.43\times {10}^{-1}& -2.67\times {10}^{-1}& -4.00\times {10}^{-1}& -2.17\times {10}^{-1}& -2.88\times {10}^{-1}\\ 1.66\times {10}^{-1}& 9.09\times {10}^{-16}& -4.81\times {10}^{-1}& 4.03\times {10}^{-1}& 1.66\times {10}^{-1}& 1.18\times {10}^{-1}& -4.08\times {10}^{-1}& -1.14\times {10}^{-1}& -3.33\times {10}^{-1}& -1.78\times {10}^{-1}& -3.60\times {10}^{-1}& -2.88\times {10}^{-1}\\ -4.99\times {10}^{-2}& -1.07\times {10}^{-15}& 6.00\times {10}^{-1}& -1.64\times {10}^{-1}& 1.66\times {10}^{-1}& 2.14\times {10}^{-1}& -4.08\times {10}^{-1}& 2.38\times {10}^{-1}& -1.48\times {10}^{-1}& 3.56\times {10}^{-1}& -2.83\times {10}^{-1}& -2.88\times {10}^{-1}\\ 1.47\times {10}^{-1}& 3.53\times {10}^{-1}& -3.33\times {10}^{-1}& -2.99\times {10}^{-1}& 1.66\times {10}^{-1}& -4.81\times {10}^{-1}& 2.04\times {10}^{-1}& 9.45\times {10}^{-2}& -1.18\times {10}^{-1}& 4.89\times {10}^{-1}& -6.63\times {10}^{-1}& -2.88\times {10}^{-1}\\ -9.75\times {10}^{-2}& -3.53\times {10}^{-1}& 2.67\times {10}^{-1}& 4.64\times {10}^{-1}& 1.66\times {10}^{-1}& -2.67\times {10}^{-1}& 2.04\times {10}^{-1}& -3.32\times {10}^{-1}& -2.67\times {10}^{-1}& 2.22\times {10}^{-1}& 3.49\times {10}^{-1}& -2.88\times {10}^{-1}\\ -3.14\times {10}^{-1}& 3.53\times {10}^{-1}& -1.48\times {10}^{-1}& -1.03\times {10}^{-1}& 1.66\times {10}^{-1}& 6.00\times {10}^{-1}& 2.04\times {10}^{-1}& 1.99\times {10}^{-2}& -2.14\times {10}^{-1}& -4.45\times {10}^{-2}& 4.26\times {10}^{-1}& -2.88\times {10}^{-1}\\ 3.94\times {10}^{-1}& -2.42\times {10}^{-16}& 5.65\times {10}^{-17}& -2.70\times {10}^{-1}& -5.00\times {10}^{-1}& 1.20\times {10}^{-16}& -4.08\times {10}^{-1}& -2.87\times {10}^{-1}& -4.15\times {10}^{-17}& 7.27\times {10}^{-16}& 4.34\times {10}^{-1}& -2.88\times {10}^{-1}\\ -5.11\times {10}^{-1}& 2.03\times {10}^{-16}& -1.18\times {10}^{-1}& 3.16\times {10}^{-2}& 1.66\times {10}^{-1}& -3.33\times {10}^{-1}& -4.08\times {10}^{-1}& 1.63\times {10}^{-1}& 4.81\times {10}^{-1}& -1.78\times {10}^{-1}& 2.09\times {10}^{-1}& -2.88\times {10}^{-1}\\ 3.64\times {10}^{-1}& 3.53\times {10}^{-1}& 2.14\times {10}^{-1}& 2.68\times {10}^{-1}& 1.66\times {10}^{-1}& 1.48\times {10}^{-1}& 2.04\times {10}^{-1}& -2.58\times {10}^{-1}& 6.00\times {10}^{-1}& -4.45\times {10}^{-2}& -1.43\times {10}^{-1}& -2.88\times {10}^{-1}\\ -1.42\times {10}^{-1}& -3.53\times {10}^{-1}& -2.77\times {10}^{-16}& -5.56\times {10}^{-1}& 1.66\times {10}^{-1}& 3.49\times {10}^{-16}& 2.04\times {10}^{-1}& -4.41\times {10}^{-1}& -4.35\times {10}^{-16}& -3.11\times {10}^{-1}& -3.17\times {10}^{-1}& -2.88\times {10}^{-1}\\ -1.97\times {10}^{-1}& -3.53\times {10}^{-1}& -2.67\times {10}^{-1}& 1.35\times {10}^{-1}& 5.00\times {10}^{-1}& 2.67\times {10}^{-1}& 2.04\times {10}^{-1}& 1.43\times {10}^{-1}& 2.67\times {10}^{-1}& 4.00\times {10}^{-1}& -2.17\times {10}^{-1}& -2.88\times {10}^{-1}\end{array}\right]$$

This is an example of a regular graph with a trivial automorphism group, which does not satisfy the hypotheses of the theorem.

Example 3.

The graph H with six vertices, shown in Figure 3, has six distinct eigenvalues, but clearly is not an identity graph, and for every eigenvector $X_k$, $x_{4k}=\mp x_{5k}$.

$$X=\left[\begin{array}{cccccc}3.5355\times {10}^{-1}& 1.6919\times {10}^{-1}& 1.0201\times {10}^{-1}& -6.9971\times {10}^{-1}& 5.4806\times {10}^{-1}& 2.1450\times {10}^{-1}\\ 3.5355\times {10}^{-1}& 1.6919\times {10}^{-1}& 1.0201\times {10}^{-1}& 6.9971\times {10}^{-1}& 5.4806\times {10}^{-1}& 2.1450\times {10}^{-1}\\ -7.0711\times {10}^{-1}& -2.2720\times {10}^{-1}& -7.2569\times {10}^{-17}& 2.7365\times {10}^{-19}& 2.9010\times {10}^{-1}& 6.0351\times {10}^{-1}\\ 3.5355\times {10}^{-1}& -3.9639\times {10}^{-1}& -6.9971\times {10}^{-1}& -1.0201\times {10}^{-1}& -2.5796\times {10}^{-1}& 3.8901\times {10}^{-1}\\ 3.5355\times {10}^{-1}& -3.9639\times {10}^{-1}& 6.9971\times {10}^{-1}& 1.0201\times {10}^{-1}& -2.5796\times {10}^{-1}& 3.8901\times {10}^{-1}\\ 7.0944\times {10}^{-17}& 7.5953\times {10}^{-1}& -1.2692\times {10}^{-16}& -1.8504\times {10}^{-17}& -4.2664\times {10}^{-1}& 4.9102\times {10}^{-1}\end{array}\right]$$

Like the Frucht graph, this one does not satisfy the hypotheses of the theorem, but its automorphism group is not trivial.

Example 4.

The tree $T_7$ is the smallest identity tree that satisfies the hypotheses of Theorem 1, show in Figure 4. For this tree, $Spec\left(T_7\right)=\{-1.9696,-1.2856,-6.8404\times {10}^{-1},2.0733\times {10}^{-17},$$6.8404\times {10}^{-1},$$1.2856,1.9696\}$, and the corresponding eigenvectors are columns of the following matrix X:

$$X=\left[\begin{array}{ccccccc}3.0301\times {10}^{-1}& 1.6123\times {10}^{-1}& -4.6424\times {10}^{-1}& -5.7735\times {10}^{-1}& -4.6424\times {10}^{-1}& -1.6123\times {10}^{-1}& -3.0301\times {10}^{-1}\\ -5.9682\times {10}^{-1}& -2.0727\times {10}^{-1}& 3.1756\times {10}^{-1}& -9.9820\times {10}^{-1}& -3.1756\times {10}^{-1}& -2.0727\times {10}^{-1}& -5.9682\times {10}^{-1}\\ 4.0825\times {10}^{-1}& 4.0825\times {10}^{-1}& 4.0825\times {10}^{-1}& 9.1733\times {10}^{-17}& 4.0825\times {10}^{-1}& -4.0825\times {10}^{-1}& -4.0825\times {10}^{-1}\\ -2.0727\times {10}^{-1}& -3.1756\times {10}^{-1}& -5.9682\times {10}^{-1}& 4.4603\times {10}^{-17}& 5.9682\times {10}^{-1}& -3.1756\times {10}^{-1}& -2.0727\times {10}^{-1}\\ 4.6424\times {10}^{-1}& -3.0301\times {10}^{-1}& -1.6123\times {10}^{-1}& 5.7735\times {10}^{-1}& -1.6123\times {10}^{-1}& 3.0301\times {10}^{-1}& -4.6424\times {10}^{-1}\\ -3.1756\times {10}^{-1}& 5.9682\times {10}^{-1}& -2.0727\times {10}^{-1}& -1.0053\times {10}^{-16}& 2.0727\times {10}^{-1}& 5.9682\times {10}^{-1}& -3.1756\times {10}^{-1}\\ 1.6123\times {10}^{-1}& -4.6424\times {10}^{-1}& 3.0301\times {10}^{-1}& -5.7735\times {10}^{-1}& 3.0301\times {10}^{-1}& 4.6424\times {10}^{-1}& -1.6123\times {10}^{-1}\end{array}\right]$$

Theorem 2.

Under the assumptions of Theorem 1, if there exists an eigenvector $X_s$ for which $x_{is}\ne \mp x_{js}$ for every i and j, then G is an identity graph.

Proof. 

Assume that there exists an eigenvector $X_s$, such that $x_{is}\ne \mp x_{js}$ for all $i,j=1,2,\cdots ,n$ (or all magnitudes of all its entries are distinct). Now, for an arbitrary $P\in Aut\left(G\right)$, we will show that $P=I$.

Claim: ${\left(P{X}_s\right)}_i=x_{is},\forall i,j=1,2,\cdots ,n$, or $P=I$. Since $x_{js}\ne \mp x_{is}$ for all $i=1,2,\cdots ,n$, if ${\left(P{X}_s\right)}_i=x_{js}$, then $P{X}_s\ne \mp X_s$. As shown in the proof of Lemma 1, for all eigenvectors $X_k$ and for all $P\in Aut\left(G\right)$, $P{X}_k=\mp X_k$, giving a contradiction that concludes the proof.

□

Example 5.

The graph K with eight vertices, shown in Figure 5, has eight distinct eigenvalues $\{3.2883,$$-2.2624,-1.6616,1.1854,9.0901\times {10}^{-1},-1.8366\times {10}^{-16},-8.0897\times {10}^{-1},-6.4966\times {10}^{-1}\}$. Consider eigenvector $X_1$. For $i,j=1,2,\cdots ,n$ , $x_{i1}\ne \mp x_{j1}$, so K is an identity graph.

$$X_1=\left[\begin{array}{c}-9.2418\times {10}^{-2}\\ -3.0390\times {10}^{-1}\\ -4.5776\times {10}^{-1}\\ -2.8217\times {10}^{-1}\\ -4.7007\times {10}^{-1}\\ -3.5669\times {10}^{-1}\\ -2.4505\times {10}^{-1}\\ -4.4911\times {10}^{-1}\end{array}\right]$$

4. Laplacian and Google Matrices

4.1. Adjacency Matrix and Laplacian Matrix

In this subsection, we show that the Laplacian matrix can be substituted for the adjacency matrix in our main theorem. First we prove that the eigenvalues of adjacency matrix $A=A\left(G\right)$ are distinct if, and only if, the eigenvalues of matrix L are distinct; then, we prove $PL=LP$ for every P in the automorphism group of G. Finally, we adapt Theorem 1, using the Laplacian matrix in place of the adjacency matrix.

Lemma 2.

Let L be the Laplacian matrix of graph G. If all the eigenvalues of adjacency matrix A are distinct, then for every eigenvalue $\mu \in Spec\left(L\right)$ there exists an eigenvalue ${\lambda }_j\in Spec\left(A\right)$, $j=1,2,\cdots ,n$ of the following form:

$$\mu =\frac{\left({\sum }_{k=1}^n{d}_k{x}_{kj}{\gamma }_{jk}\right)-{\lambda }_j}{{\sum }_{k=1}^n{x}_{kj}{\gamma }_{jk}}$$

where ${\beta }_A=\{X_1,X_2,\cdots ,X_n\}$ is the basis for ${\mathbb{R}}^n$, and $X_j,j=1,2,\cdots ,n$ are eigenvectors corresponding to ${\lambda }_j$. Additionally, ${\gamma }_{jk}$ is j’th component of vector $e_k$ in the basis ${\beta }_A$, and $d_k$ is the degree of vertex $v_k$.

Proof. 

Let $\mu$ be an eigenvalue of Laplacian matrix L (defined as $L=D-A$) and Y its eigenvector. Thus, $LY=\mu Y$. Since all the eigenvalues of the adjacency matrix are distinct, there exist scalars $c_i$, such that $Y={\sum }_{i=1}^n{c}_i{X}_i$. Hence,

$$\begin{array}{cc}\hfill L\left(\sum _{i=1}^n{c}_i{X}_i\right)& =\mu \left(\sum _{i=1}^n{c}_i{X}_i\right)\hfill \\ \hfill (D-A)\left(\sum _{i=1}^n{c}_i{X}_i\right)& =\mu \left(\sum _{i=1}^n{c}_i{X}_i\right)\hfill \\ \hfill \left(\sum _{i=1}^n{c}_{i}D{X}_i\right)-\left(\sum _{i=1}^n{c}_{i}A{X}_i\right)& =\mu \left(\sum _{i=1}^n{c}_i{X}_i\right)\hfill \\ \hfill \left(\sum _{i=1}^n{c}_{i}D{X}_i\right)-\left(\sum _{i=1}^n{c}_i\mu X_i\right)& =\left(\sum _{i=1}^n{c}_{i}A{X}_i\right)\hfill \\ \hfill \sum _{i=1}^n{c}_i(D-\mu I)X_i& =\sum _{i=1}^n{c}_{i}A{X}_i.\hfill \end{array}$$

$⟹c_j(D-\mu I)X_j=c_{j}A{X}_j$ for $j=1,2,\cdots ,n.$

$$\begin{array}{cc}\hfill A{X}_j& =(d_1-\mu )\left[\begin{array}{c}{x}_{1j}\\ 0\\ 0\\ ⋮\\ 0\end{array}\right]+(d_2-\mu )\left[\begin{array}{c}0\\ x_{2j}\\ 0\\ ⋮\\ 0\end{array}\right]+\cdots +(d_n-\mu )\left[\begin{array}{c}0\\ 0\\ 0\\ ⋮\\ x_{nj}\end{array}\right]\hfill \\ \hfill & =(d_1-\mu )x_{1j}\left[\begin{array}{c}1\\ 0\\ 0\\ ⋮\\ 0\end{array}\right]+(d_2-\mu )x_{2j}\left[\begin{array}{c}0\\ 1\\ 0\\ ⋮\\ 0\end{array}\right]+\cdots +(d_n-\mu )x_{nj}\left[\begin{array}{c}0\\ 0\\ 0\\ ⋮\\ 1\end{array}\right].\hfill \\ \hfill ⟹A{X}_j& =(d_1-\mu )x_{1j}{e}_1+(d_2-\mu )x_{2j}{e}_2+\cdots +(d_1-\mu )x_{nj}{e}_n.\hfill \end{array}$$

Let $e_k={\sum }_{k=1}^n{\gamma }_{ik}{X}_i$.

$$⟹A{X}_j=(d_1-\mu )x_{1j}\left(\sum _{k=1}^n{\gamma }_{i1}{X}_i\right)+(d_2-\mu )x_{2j}\left(\sum _{k=1}^n{\gamma }_{i2}{X}_i\right)+\cdots +(d_1-\mu )x_{nj}\left(\sum _{k=1}^n{\gamma }_{in}{X}_i\right).$$

$$\begin{array}{cc}\hfill A{X}_j=& [(d_1-\mu )x_{1j}{\gamma }_{11}+(d_2-\mu )x_{2j}{\gamma }_{12}+\cdots +(d_n-\mu )x_{nj}{\gamma }_{1n}]X_1+\hfill \\ \hfill & \cdots +[(d_1-\mu )x_{1j}{\gamma }_{j1}+(d_2-\mu )x_{2j}{\gamma }_{j2}+\cdots +(d_n-\mu )x_{nj}{\gamma }_{jn}]X_j+\hfill \\ \hfill & \cdots +[(d_1-\mu )x_{1j}{\gamma }_{n1}+(d_2-\mu )x_{2j}{\gamma }_{n2}+\cdots +(d_n-\mu )x_{nj}{\gamma }_{nn}]X_n.\hfill \end{array}$$

Here,

$${\lambda }_j{X}_j=[(d_1-\mu )x_{1j}{\gamma }_{j1}+(d_2-\mu )x_{2j}{\gamma }_{j2}+\cdots +(d_n-\mu )x_{nj}{\gamma }_{jn}]X_j.$$

Therefore,

$${\lambda }_j=\sum _{k=1}^n(d_k-\mu )x_{kj}{\gamma }_{jk}=\sum _{k=1}^n{d}_k{x}_{kj}{\gamma }_{jk}-\sum _{k=1}^n\mu x_{kj}{\gamma }_{jk},$$

$⟶{\sum }_{k=1}^n{d}_k{x}_{kj}{\gamma }_{jk}-{\lambda }_j=\mu {\sum }_{k=1}^n{x}_{kj}{\gamma }_{jk}$.

This implies that

$$\mu =\frac{{\sum }_{k=1}^n{d}_k{x}_{kj}{\gamma }_{jk}-{\lambda }_j}{{\sum }_{k=1}^n{x}_{kj}{\gamma }_{jk}}.$$

□

Note that $L=D-A$, and thus, $A=D-L$, so the procedure in the proof of Lemma 2 can be readily adapted to prove the following Lemma.

Lemma 3.

Let L be the Laplacian matrix of graph G. If all the eigenvalues of Laplacian matrix L are distinct, then for every eigenvalue $\lambda \in \sigma \left(A\right)$ there exists an eigenvalue ${\mu }_j\in \sigma \left(L\right)$, $j=1,2,\cdots ,n$ of the following form:

$$\lambda =\frac{\left({\sum }_{k=1}^n{d}_k{y}_{kj}{\gamma }_{jk}\right)-{\mu }_j}{{\sum }_{k=1}^n{y}_{kj}{\gamma }_{jk}}$$

where ${\beta }_L=\{Y_1,Y_2,\cdots ,Y_n\}$ is the basis for ${\mathbb{R}}^n$, and $Y_j,j=1,2,\cdots ,n$ are eigenvectors corresponding to ${\mu }_j$. Additionally, ${\gamma }_{jk}$ is j’th component of vector $e_k$ in the basis ${\beta }_A$, and $d_k$ is the degree of vertex $v_k$.

The proof follows directly from Lemmas 2 and 3. An immediate consequence is the following Theorem.

Theorem 3.

All the eigenvalues of adjacency matrix A are distinct if, and only if, all the eigenvalues of Laplacian matrix L are distinct.

Lemma 4.

Let G be a simple graph, A its adjacency matrix, and L the Laplacian matrix. If the eigenvalues of L are distinct, then for every $P\in Aut\left(G\right)$, $PL=LP$.

Proof. 

$PL=P(D-A)=PD-PA=DP-AP=(D-A)P=LP$. □

Theorem 4.

Let L be the Laplacian matrix of simple graph G, and suppose L has the n distinct eigenvalues ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$. Suppose further that $X_1,X_2,\cdots ,X_n$ are the corresponding eigenvectors. If, for every two vertices, $v_i,v_j\in V\left(G\right)$, and, for every eigenvector, $X_k,k=1,2,\cdots ,n$$x_{ik}\ne \mp x_{jk}$, then G is an identity graph.

4.2. Adjacency Matrix and Google Matrix

In this subsection, we show that the Google matrix M can be substituted for the adjacency matrix in our main theorem. First we prove that the eigenvalues of adjacency matrix A are distinct if, and only if, the eigenvalues of matrix S are distinct, and then the eigenvalues of the Google matrix M are distinct. Next we prove $PS=SP$ and $PM=MP$ for every P in the automorphism group of a simple graph G. Finally, we adapt Theorem 1 using the Google matrices in place of the adjacency matrix.

Lemma 5.

If all the eigenvalues of adjacency matrix A are distinct, then for every eigenvalue $\mu \in Spec\left(S\right)$ there exists an eigenvalue ${\lambda }_j\in Spec\left(A\right)$, $j=1,2,\cdots ,n$ of the following form:

$$\mu =\frac{{\lambda }_j}{{\sum }_{k=1}^n{d}_k{x}_{kj}{\gamma }_{jk}}$$

where ${\beta }_A=\{X_1,X_2,\cdots ,X_n\}$ is the basis for ${\mathbb{R}}^n$, and $X_j,j=1,2,\cdots ,n$ are eigenvectors corresponding to ${\lambda }_j$. Additionally, ${\gamma }_{jk}$ is the j’th component of vector $e_k$ in the basis ${\beta }_A$.

Proof. 

Let $\mu$ be an eigenvalue of stochastic matrix S (defined in Section 2) and Y its eigenvector. Thus, $SY=\mu Y$. Since all the eigenvalues of the adjacency matrix are distinct, there exist scalars $c_i$, such that $Y={\sum }_{i=1}^n{c}_i{X}_i$. Hence,

$$\begin{array}{cc}\hfill S\left(\sum _{i=1}^n{c}_i{X}_i\right)& =\mu \sum _{i=1}^n{c}_i{X}_i\hfill \\ \hfill D^{-1}A\left(\sum _{i=1}^n{c}_i{X}_i\right)& =\mu \sum _{i=1}^n{c}_i{X}_i\hfill \\ \hfill \sum _{i=1}^n{c}_{i}A{X}_i& =\mu D\sum _{i=1}^n{c}_i{X}_i,\hfill \end{array}$$

which implies $c_{j}A{X}_j=\mu c_{j}D{X}_j$ for $j=1,\cdots ,n$.

Since $D=\left(d_{ij}\right)$ is a diagonal matrix in which $d_{ii}$ is the degree of vertex i (elsewhere denoted by $d_i$), then

$$\begin{array}{cc}\hfill A{X}_j& =\mu d_1\left[\begin{array}{c}{x}_{1j}\\ 0\\ 0\\ ⋮\\ 0\end{array}\right]+\mu d_2\left[\begin{array}{c}0\\ x_{2j}\\ 0\\ ⋮\\ 0\end{array}\right]+\cdots +\mu d_n\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ x_{nj}\end{array}\right]\hfill \\ \hfill & =\mu (d_1{x}_{1j}\left[\begin{array}{c}1\\ 0\\ 0\\ ⋮\\ 0\end{array}\right]+\mu d_2{x}_{2j}\left[\begin{array}{c}0\\ 1\\ 0\\ ⋮\\ 0\end{array}\right]+\cdots +\mu d_n{x}_{nj}\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\end{array}\right]),\hfill \end{array}$$

so

$$A{X}_j=\mu (d_1{x}_{1j}{e}_1+\mu d_2{x}_{2j}{e}_2+\cdots +\mu d_n{x}_{nj}{e}_n).$$

Setting $e_k={\sum }_{i=1}^n{\gamma }_{ik}{X}_i$, we have

$$\begin{array}{cc}\hfill {\lambda }_j{X}_j=& \mu (d_1{x}_{1j}\sum _{i=1}^n{\gamma }_{i1}{X}_i+d_2{x}_{2j}\sum _{i=1}^n{\gamma }_{i2}{X}_i+\cdots +d_n{x}_{nj}\sum _{i=1}^n{\gamma }_{in}{X}_i),\hfill \\ \hfill ⟹{\lambda }_j{X}_j=& \mu (d_1{x}_{1j}{\gamma }_{11}+d_2{x}_{2j}{\gamma }_{12}+\cdots +d_n{x}_{nj}{\gamma }_{1n})X_1+\cdots \hfill \\ \hfill & \cdots +\mu (d_1{x}_{1j}{\gamma }_{j1}+d_2{x}_{2j}{\gamma }_{j2}+\cdots +d_n{x}_{nj}{\gamma }_{jn})X_j+\cdots \hfill \\ \hfill & +\cdots +\mu (d_1{x}_{1j}{\gamma }_{n1}+d_2{x}_{2j}{\gamma }_{n2}+\cdots +d_n{x}_{nj}{\gamma }_{nn})X_n,\hfill \end{array}$$

which implies

$${\lambda }_j=\mu (d_1{x}_{1j}{\gamma }_{j1}+d_2{x}_{2j}{\gamma }_{j2}+\cdots +d_n{x}_{nj}{\gamma }_{jn}).$$

From this we conclude that

$${\lambda }_j=\mu \left(\sum _{k=1}^n{d}_k{x}_{kj}{\gamma }_{jk}\right),$$

or

$$\mu =\frac{{\lambda }_j}{{\sum }_{k=1}^n{d}_k{x}_{kj}{\gamma }_{jk}},j=1,\cdots ,n.$$

□

Lemma 6.

If all the eigenvalues of matrix S are distinct, then for every eigenvalue $\lambda \in Spec\left(A\right)$ there exists an eigenvalue ${\mu }_j\in Spec\left(S\right)$, $j=1,\cdots ,n$ of the form

$$\lambda =\frac{{\mu }_j}{{\sum }_{k=1}^n\frac{1}{d_k}{y}_{kj}{\gamma }_{jk}},$$

where ${\beta }_S=\{Y_1,Y_2,\cdots ,Y_n\}$ is the basis for ${\mathbb{R}}^n$, and $Y_j$, $j=1,2,\cdots ,n$ are corresponding eigenvectors ${\mu }_j$. Moreover, ${\gamma }_{jk}$ is the j’th components of vector $e_k$ in the basis ${\beta }_S$.

Proof. 

Let $\lambda \in \sigma \left(A\right)$, so $AX=\lambda X$, where X is an eigenvector corresponding to $\lambda$. Then, it follows that

$$\begin{array}{cc}\hfill D^{-1}AX& =\lambda D^{-1}X\hfill \\ \hfill SX& =\lambda D^{-1}X.\hfill \end{array}$$

Now, if $X={\sum }_{i=1}^n{c}_i{Y}_i$,

$$S\left(\sum _{i=1}^n{c}_i{Y}_i\right)=\lambda D^{-1}\left(\sum _{i=1}^n{c}_i{Y}_i\right),$$

$$⟶\sum _{i=1}^n{c}_{i}S{Y}_i=\sum _{i=1}^n\lambda D^{-1}{c}_i{Y}_i.$$

(5)

Thus,

$$S{Y}_j=\lambda D^{-1}{Y}_j$$

(6)

for $j=1,2,\cdots ,n$.

From (5) and (6), it follows that

$$\begin{array}{cc}\hfill \lambda D^{-1}{Y}_j& =\lambda (\frac{1}{d_1}\left[\begin{array}{c}{y}_{1j}\\ 0\\ 0\\ ⋮\\ 0\end{array}\right]+\frac{1}{d_2}\left[\begin{array}{c}0\\ y_{2j}\\ 0\\ ⋮\\ 0\end{array}\right]+\cdots +\frac{1}{d_n}\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ y_{nj}\end{array}\right]),\hfill \\ \hfill & =\lambda (\frac{1}{d_1}{y}_{1j}\left[\begin{array}{c}1\\ 0\\ 0\\ ⋮\\ 0\end{array}\right]+\frac{1}{d_2}{y}_{2j}\left[\begin{array}{c}0\\ 1\\ 0\\ ⋮\\ 0\end{array}\right]+\cdots +\frac{1}{d_n}{y}_{nj}\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\end{array}\right]),\hfill \\ \hfill & =\lambda (\frac{1}{d_1}{y}_{1j}{e}_1+\frac{1}{d_2}{y}_{2j}{e}_2+\cdots +\frac{1}{d_n}{y}_{nj}{e}_n).\hfill \end{array}$$

If $e_k={\sum }_{i=1}^n{\gamma }_{ik}{Y}_i$, then

$$S{Y}_j=\lambda (\frac{1}{d_1}{y}_{1j}\sum _{i=1}^n{\gamma }_{i1}{Y}_i+\frac{1}{d_2}{y}_{2j}\sum _{i=1}^n{\gamma }_{i2}{Y}_i+\cdots +\frac{1}{d_n}{y}_{nj}\sum _{i=1}^n{\gamma }_{in}{Y}_i),$$

$$S{Y}_j=\lambda \left(\sum _{k=1}^n\left(\sum _{i=1}^n\frac{1}{d_k}{y}_{kj}{\gamma }_{ik}{Y}_i\right)\right).$$

Since $S{Y}_j={\mu }_j{Y}_j$, it follows that

$$\begin{array}{cc}\hfill {\mu }_j{Y}_j& =\lambda \left(\sum _{k=1}^n\frac{1}{d_k}{y}_{kj}{\gamma }_{jk}\right)Y_j,\hfill \\ \hfill ⟹{\mu }_j& =\lambda \sum _{k=1}^n\frac{1}{d_k}{y}_{kj}{\gamma }_{jk},\hfill \end{array}$$

or

$$\lambda =\frac{{\mu }_j}{{\sum }_{k=1}^n\frac{1}{d_k}{y}_{kj}{\gamma }_{jk}}.$$

□

Theorem 5.

([7]). If the spectrum of stochastic matrix S is $\{1,{\lambda }_2,{\lambda }_3,\cdots ,{\lambda }_n\}$, then the spectrum of the Google matrix $M=\alpha S+\frac{(1-\alpha )}{n}e{e}^T$ is $\{1,\alpha {\lambda }_2,\alpha {\lambda }_3,\cdots ,\alpha {\lambda }_n\}$.

The proof follows directly from Theorem 5 and Lemmas 5 and 6. An immediate consequence is the following theorem.

Theorem 6.

If all the eigenvalues of adjacency matrix A are distinct, then all the eigenvalues of Google matrix M are distinct.

Lemma 7.

Let G be a simple graph, A its adjacency matrix, and $S=D^{-1}A$ the stochastic matrix. If the eigenvalues of A are distinct, then for every $P\in Aut\left(G\right)$, $PS=SP$.

Proof. 

Let D be a diagonal matrix whose diagonal entries are the degrees of the vertices of graph G. Since the eigenvalues of A are distinct, $P^2=I$ for every $P\in Aut\left(G\right)$[4]. So, $P{D}^{-1}=D^{-1}P$. Thus,

$$PS=P{D}^{-1}A=D^{-1}PA=D^{-1}AP=SP.$$

□

Theorem 7.

Let S be the stochastic (or transition) matrix of simple graph G, and suppose S has the n distinct eigenvalues ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$. Suppose further that $X_1,X_2,\cdots ,X_n$ are the corresponding eigenvectors. If, for every two vertices, $v_i,v_j\in V\left(G\right)$, and, for every eigenvector, $X_k$, $x_{ik}\ne \mp x_{jk}$, then G is an identity graph.

The proof is essentially the same as that for the main theorem, and yields the following Corollary.

Corollary 1.

Let G be a simple graph, with adjacency matrix A and Google matrix M. If the eigenvalues of A are distinct, then for every $P\in Aut\left(G\right)$, $PM=MP$.

The following theorem is an immediate consequence of Theorem 6 and Corollary 1.

Theorem 8.

Let M be the Google matrix of simple graph G whose adjacency matrix A has n distinct eigenvalues. Suppose M has the n distinct eigenvalues ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$, and that $X_1,X_2,\cdots ,X_n$ are the corresponding eigenvectors. If, for every two vertices, $v_i,v_j\in V\left(G\right)$, there exists an eigenvector $x_k$, such that $x_{ik}\ne \mp x_{jk}$, then G is an identity graph.

The next result is similar to Theorem 2 concerning the eigenvectors of the Google matrix.

Theorem 9.

Under the assumptions of Theorem 8, if there exists an eigenvector $X_s$ of the Google matrix for which $x_{is}\ne \mp x_{js}$ for every i and j, then G is an identity graph.

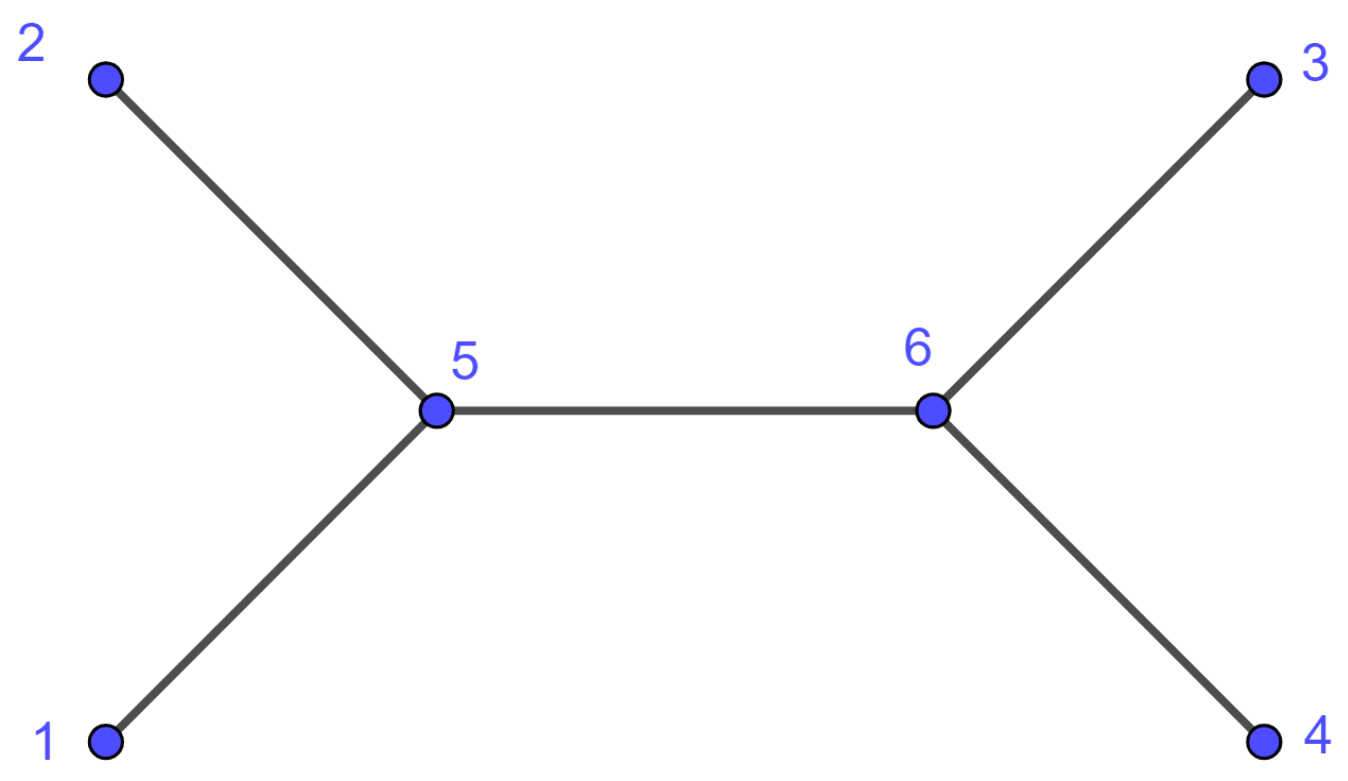
The eigenvector corresponding to eigenvalue $\mu =1$ of the Google matrix is called the PageRank vector [7], and all of its entries are positive. As we have proven in [9], if two entries $i,j$ of the PageRank vector are distinct, then there is no $P\in Aut\left(G\right)$, which maps vertex $v_i$ to vertex $v_j$. This result does not hold for eigenvectors of the adjacency matrix, as shown in the following example.

Example 6.

Graph $T_6$ in Figure 6 has the following eigenvalues: $Spec\left(A\right)=\{-2,-1,-3.3425\times {10}^{-49},4.7246\times {10}^{-32},1,2\}$. The corresponding eigenvectors are the columns of matrix X.

$$X=\left[\begin{array}{cccccc}-2.8868\times {10}^{-1}& -4.0825\times {10}^{-1}& -7.0711\times {10}^{-1}& -6.7240\times {10}^{-17}& -4.0825\times {10}^{-1}& 2.8868\times {10}^{-1}\\ -2.8868\times {10}^{-1}& -4.0825\times {10}^{-1}& 7.0711\times {10}^{-1}& 8.5228\times {10}^{-18}& -4.0825\times {10}^{-1}& 2.8868\times {10}^{-1}\\ 2.8868\times {10}^{-1}& -4.0825\times {10}^{-1}& 2.1131\times {10}^{-17}& 7.0711\times {10}^{-1}& 4.0825\times {10}^{-1}& 2.8868\times {10}^{-1}\\ 2.8868\times {10}^{-1}& -4.0825\times {10}^{-1}& -5.9205\times {10}^{-17}& -7.0711\times {10}^{-1}& 4.0825\times {10}^{-1}& 2.8868\times {10}^{-1}\\ 5.7735\times {10}^{-1}& 4.0825\times {10}^{-1}& 3.8074\times {10}^{-17}& -1.7512\times {10}^{-16}& -4.0825\times {10}^{-1}& 5.7735\times {10}^{-1}\\ -5.7735\times {10}^{-1}& 4.0825\times {10}^{-1}& 2.9388\times {10}^{-33}& -5.4857\times {10}^{-17}& 4.0825\times {10}^{-1}& 5.7735\times {10}^{-1}\end{array}\right]$$

For the eigenvectors $X_3$, $x_{33}\ne \mp x_{43}$. Additionally, for $X_4$, we observe that $x_{14}\ne \mp x_{24}$. However, as shown in Figure 6, vertices $v_3,v_4$ and $v_1,v_2$ are in the same orbit.

As this example shows, the Google matrix may offer more information than the adjacency matrix about the automorphism group. In particular, if two entries $i,j$ of an adjacency matrix eigenvector $X_k$ are distinct, there may or may not be an automorphism mapping $v_i$ to $v_j$. However, if such is the case for the PageRank vector corresponding to the eigenvector of ${\mu }_1=1$, then there is no automorphism mapping $v_i$ to $v_j$ in the graph.

5. Complexity Analysis

In this section, we analyze the complexity of an algorithm based on Theorem 1. As shown in Section 3, Theorem 1 provides a sufficient condition for identifying identity graphs. To make effective use of this theorem, it is sufficient to determine, for all pairs of rows $R_i$, $R_j$ of matrix X, whether the condition $|R_{ik}|\ne |R_{jk}|$, $k=1,2,\cdots ,n$, holds. Applying Theorem 1, we show that the algorithm is of order $O\left(n^3\right)$.

Proof. 

The first step is to compute the eigenvalues of the $n\times n$ adjacency matrix of the graph. This computation is of order $O\left(n^3\right)$. Now it is enough to prove that the computation required to determine whether or not any two rows are $\mp 1$ times each other is at most $O\left(n^3\right)$. □

Two additional procedures are required. One is to check the condition for all $\left(\genfrac{}{}{0.0pt}{}{n}{2}\right)$ pairs of rows. This can be performed in $O\left(n^2\right)$ operations. The other is needed to compare corresponding entries in rows $R_i$ and $R_j$. This requires $O\left(n\right)$ computations. These two procedures require $O\left(n^2\right)$ operations. Combined with the eigenvalue computation, this gives a total of $O\left(n^3\right)$, which concludes the proof.

6. Conclusions

In this note, we prove a theorem showing that a condition imposed on the eigenvectors of an adjacency matrix with all distinct eigenvalues is sufficient to ensure an identity graph. In addition, we prove that the Google and Laplacian matrices can be substituted for the adjacency matrix in the theorem. So, essentially the same hypothesis regarding eigenvectors serves as a sufficient condition to apply to the adjacency, Google, and Laplacian matrices for the automorphism group of the graph to be trivial. We also show that the Google matrix offers more information than the adjacency matrix about graph automorphisms. Using the machinery of this theorem, we constructed an $O\left(n^3\right)$ algorithm for determining identity graphs.

The results reported in this paper are meant as a contribution to quantitative studies of graph and network complexity based on symmetry. Asymmetric graphs have maximum entropy, so this case is of special interest. The algorithm proposed here is a relatively efficient procedure for identifying such graphs.

In future work, we will explore sufficient and necessary conditions for the eigenvectors of the adjacency matrix for the automorphism group of a simple graph to have a specific structure. In particular, we will investigate alternative conditions that reduce the complexity of identity graph determination, and examine adjacency matrix connections with other automorphism group structures.

Moreover, we plan to investigate the relationship between adjacency matrix and automorphism group structure, where the matrix entries are elements of a finite field such as GF(2). Restricting the field is expected to simplify the construction of solutions to the matrix equation $PA=AP$ for the purpose of determining the automorphism group.