Convergence of Parameterized Variable Metric Three-Operator Splitting with Deviations for Solving Monotone Inclusions

Abstract

In this paper, we propose a parameterized variable metric three-operator algorithm for finding a zero of the sum of three monotone operators in a real Hilbert space. Under some appropriate conditions, we prove the strong convergence of the proposed algorithm. Furthermore, we propose a parameterized variable metric three-operator algorithm with a multi-step inertial term and prove its strong convergence. Finally, we illustrate the effectiveness of the proposed algorithm with numerical examples.

1. Introduction

Let H be a real Hilbert space with inner product $⟨·,·⟩$ and the induced norm $\parallel ·\parallel$. We consider the following monotone inclusion problem of the sum of three operators: find $x\in H$ such that

$$0\in Ax+Bx+Cx,$$

(1)

where $A,B:H\to 2^H$ are maximally monotone operators and $C:H\to H$ is a $\beta$-cocoercive operator, $\beta >0$. There have been numerous algorithms for solving the problem (1) when $B=0$ because of the wide applications of this problem in compressed sensing, image recovery, sparse optimization, machine learning, etc.; see [1,2,3,4,5,6,7], to name a few. Although in theory these algorithms can be used to solve the problem (1) by bundling $A+B+C$ as $T+C$ with $T=A+B$, ${(\mathrm{Id}+T)}^{-1}$ is hard to compute in practice. For the past few years, problem (1) has received a lot of attention, and several algorithms have been constructed for solving it.

In 2017, Davis and Yin [8] proposed the following three-operator algorithm:

$$\left\{\begin{array}{c}{z}_k=J_{\gamma A}\left(x_k\right),\hfill \\ y_k=J_{\gamma B}(2z_k-x_k-\gamma C{z}_k),\hfill \\ x_{k+1}=x_k+{\lambda }_k(y_k-z_k).\hfill \end{array}\right.$$

(2)

Here $J_{\gamma A}={(\mathrm{Id}+\gamma A)}^{-1}$, $J_{\gamma B}={(\mathrm{Id}+\gamma B)}^{-1}$, $\gamma \in (0,2\beta )$, ${\lambda }_k\in (0,\frac{4\beta -\gamma }{2\beta })$. Expression (2) also has the form

$$x_{k+1}=(1-{\lambda }_k)x_k+{\lambda }_{k}T{x}_k,$$

(3)

where the averaged operator T is defined by

$$T=J_{\gamma B}(2J_{\gamma A}-\mathrm{Id}-\gamma C\circ J_{\gamma A})+\mathrm{Id}-J_{\gamma A}.$$

(4)

Then [8] proved that the sequence $\left\{x_k\right\}$ generated by (2) converges weakly to a fixed point $x^{*}$ of T under some suitable conditions by utilizing the averageness of T. In turn, $J_{\gamma A}\left(x^{*}\right)$ solves problem (1).

Soon after, Cui, Tang and Yang [9] put forward the inertial version of the algorithm (2):

$$\left\{\begin{array}{c}{w}_k=x_k+{\theta }_k(x_k-x_{k-1}),\hfill \\ z_k=J_{\gamma A}\left(w_k\right),\hfill \\ y_k=J_{\gamma B}(2z_k-w_k-\gamma C{z}_k),\hfill \\ x_{k+1}=w_k+{\lambda }_k(y_k-z_k),\hfill \end{array}\right.$$

(5)

to improve the convergence speed of the algorithm (2). For the problem (1) in which $C=0$, B is monotone and L-Lipschitz continuous, Malitsky and Tam [10] proposed the forward-reflected-backward algorithm to solve problem (1), which consists of iterating

$$x_{k+1}=J_{\gamma A}(x_k-2\gamma B{x}_k+\gamma B{x}_{k-1}-\gamma C{x}_k).$$

(6)

Under some appropriate conditions, they proved the convergence of (6). Furthermore, Zong et al. [11] introduced the inertial semi-forward-reflected-backward splitting algorithm to address (1):

$$x_{k+1}=J_{\gamma A}(x_k-{\gamma }_{k}B{x}_k+{\gamma }_{k-1}(B{x}_k-B{x}_{k-1})-\alpha (x_k-x_{k-1})-{\gamma }_{k}C{x}_k),$$

(7)

and proved the weak convergence of the algorithm. Zhang and Chen [12] proposed the parameterized three-operator splitting algorithm:

$$\left\{\begin{array}{c}{z}_k=J_{\gamma A}\left(x_k\right),\hfill \\ y_k=J_{\gamma B}([2-\gamma (2-\alpha )]z_k-x_k-\gamma C{z}_k),\hfill \\ x_{k+1}=x_k+{\lambda }_k(y_k-z_k),\hfill \end{array}\right.$$

(8)

which generalizes the parameterized Douglas–Rachford algorithm [13]. They proved that the sequence generated by the regularization of (8) converges to the least-norm solution of problem (1). Other algorithms for solving (1) have also been investigated in recent years; see [14,15,16].

In order to speed up the convergence of iterative algorithms, scholars often use acceleration techniques. The inertial extrapolation technique and variable metric technique are two popular acceleration methods. The inertial extrapolation technique, or heavy ball method [17], has been widely studied in past decades; please see [18,19,20,21,22,23] and the references therein. The variable metric technique is a method to improve the convergence speed of the corresponding algorithm by changing the step size in each iteration. This method has been widely used in various optimization problems in the past decades. To solve the monotone inclusion problem of the sum of two operators, Rockafeller [24] first combined the variable metric strategy with the forward-backward algorithm in 1997. For solving the monotone inclusion of the sum of two operators, Combettes [25] proposed the following variable metric forward-backward splitting algorithm

$$\left\{\begin{array}{c}{y}_k=x_k-{\gamma }_k{U}_k(B_k{x}_k+b_k),\hfill \\ x_{k+1}=x_k+{\lambda }_k(J_{{\gamma }_k{U}_{k}A}\left(y_k\right)+a_k-x_k),\hfill \end{array}\right.$$

(9)

where $\left\{a_k\right\}$ and $\left\{b_k\right\}$ are absolutely summable sequences in H, $\left\{U_k\right\}$ is a linear bounded self-adjoint positive operator sequence defined on H, and proved its strong convergence. Bonettini [26] proposed an inexact inertial variable metric proximity gradient algorithm. In [27], the author studied the variable metric forward-backward splitting algorithm for convex minimization problems without the Lipschitz continuity assumption of the gradient and proved the weak convergence of the iteration. Further, in [28], Audrey and Yves proposed a variable metric forward-backward-based algorithm for solving problems of the sum of two nonconvex functions. In [29], the authors addressed the weak convergence of a nonlinearly preconditioned forward-backward splitting method for the sum of a maximally hypermonotone operator A and a hypercocoercive operator B. For other applications of variable metric techniques, see [30,31,32] and the references therein.

Inspired by the above work, we propose a parameterized variable metric three-operator algorithm and a multi-step inertial parameterized variable metric three-operator algorithm. Furthermore, instead of requiring the averageness or nonexpansiveness of the operator, we directly analyze the convergence of the proposed iterative algorithm.

The rest of this paper is organized as follows. In Section 2, we recall some basic definitions and important lemmas. In Section 3, we propose the parameterized variable metric three-operator algorithm and prove its strong convergence. Then we introduce a multi-step inertial parameterized variable metric three-operator algorithm and prove a strong convergence result of it. In Section 4, we show the performance of the proposed iterative algorithm under different parameters and illustrate the feasibility of the algorithm with numerical examples.

2. Preliminaries

In this section, we list the necessary symbols, notations, definitions and lemmas and certify some results used in this paper. Let $B\left(H\right)$ be the space of bounded linear operators from H to H. Set $S\left(H\right)=\{L\in B\left(H\right)|L=L^{*}\}$, where $L^{*}$ denotes the adjoint of L, and $P_{\alpha }\left(H\right)=\{L\in S\left(H\right)|⟨Lx,x⟩\ge \alpha ⟨x,x⟩\}$, $\alpha >0$. Given $M\in P_{\alpha }\left(H\right)$, define the M-inner product ${⟨·,·⟩}_M$ on H by ${⟨x,y⟩}_M=⟨Mx,y⟩$ for all $x,y\in H$. So the corresponding M-norm on H is defined as ${\parallel x\parallel }_M=\sqrt{⟨Mx,x⟩}$ for all $x\in H$. The strong convergence of a sequence $\left\{z_n\right\}$ is denoted by → and the symbol ⇀ means weak convergence. $\mathrm{Id}$ means the identity operator. ${\ell }_{+}^1\left(\mathbb{N}\right)$ denotes the set of sequences $\left\{{\eta }_n\right\}$ in $[0,+\infty )$ such that ${\displaystyle \sum _{n\in \mathbb{N}}}{\eta }_n<+\infty$. Let $T:H\to H$ be an operator. We denote the fixed point set of T by $\mathrm{Fix}\left(T\right)$, that is, $\mathrm{Fix}\left(T\right)=\{x\in H|Tx=x\}$. Let $A:H\to 2^H$ be a set-valued operator. We denote its graph and domain by $\mathrm{gra}A=\left\{\right(x,u)\in H\times H|u\in Ax\}$ and $\mathrm{dom}A=\{x\in H|Ax\ne ⌀\}$, respectively. In this paper, let S be the solution set of problem (1) and we always assume that $S\ne \varnothing$.

Definition 1.

Let $T:H\to H$ be an operator. T is said to be

$\left(i\right)$ ([33]) τ-cocoercive, $\tau >0$ if

$$⟨Tx-Ty,x-y⟩\ge {\tau \parallel Tx-Ty\parallel }^2,\forall x,y\in H;$$

$\left(ii\right)$ ([34]) demiregular at $x\in H$ if $\forall \left\{x_n\right\}\subset H$ with $x_n\rightharpoonup x$ and $T{x}_n\to Tx$ as $n\to \infty$, it follows that $x_n\to x$ as $n\to \infty$.

Definition 2

([33]). Let $A:H\to 2^H$ be an operator. A is said to be

$\left(i\right)$ monotone if

$$⟨x-y,u-v⟩\ge 0,\forall (x,u)\in \mathrm{gra}A,\forall (y,v)\in \mathrm{gra}A.$$

$\left(ii\right)$ strictly monotone if

$$x\ne y\Rightarrow ⟨x-y,u-v⟩>0,\forall (x,u)\in \mathrm{gra}A,\forall (y,v)\in \mathrm{gra}A.$$

$\left(iii\right)$ β-strongly monotone if

$$⟨x-y,u-v⟩\ge {\beta \parallel x-y\parallel }^2,\forall (x,u)\in \mathrm{gra}A,\forall (y,v)\in \mathrm{gra}A.$$

$\left(iv\right)$ maximally monotone if $\forall (x,u)\in H\times H$

$$(x,u)\in \mathrm{gra}A\iff ⟨x-y,u-v⟩\ge 0,\forall (y,v)\in \mathrm{gra}A.$$

$\left(v\right)$ uniformly monotone with modulus $\varphi :{\mathbb{R}}_{+}\to [0,+\infty ]$ if ϕ is increasing and vanishes only at 0 and

$$⟨x-y,u-v⟩\ge \varphi (\parallel x-y\parallel ),\forall (x,u)\in \mathrm{gra}A,\forall (y,v)\in \mathrm{gra}A.$$

Definition 3

([33]). Let D be a nonempty subset of H. Let $\left\{x_n\right\}$ be a sequence in H. $\left\{x_n\right\}$ is called Fej$\acute{e}$r monotone with respect to D if

$$\parallel x_{n+1}-\widehat{x}\parallel \le \parallel x_n-\widehat{x}\parallel ,\forall \widehat{x}\in D,\forall n\ge 0.$$

Lemma 1

([33]). Let $A:H\to 2^H$ be a maximally monotone operator and let $M:H\to H$ be a linear bounded self-adjoint and strongly monotone operator. Then

$\left(i\right)$ $M^{-1}A$ is maximally monotone operator.

$\left(ii\right)$ $\forall \lambda >0$, $J_{\lambda M^{-1}A}={(\mathrm{Id}+\lambda M^{-1}A)}^{-1}$ is firmly nonexpansive with respect to M-norm, that is,

$${⟨J_{\lambda M^{-1}A}x-J_{\lambda M^{-1}A}y,x-y⟩}_M\ge {\parallel J_{\lambda M^{-1}A}x-J_{\lambda M^{-1}A}y\parallel }_M^2,\forall x,y\in H.$$

$\left(iii\right)$ $J_{M^{-1}A}={(M+A)}^{-1}M$.

Lemma 2

([35]). Let $x\in H$, $y\in H$, $z\in H$, we have

$$\begin{array}{c}\hfill 2⟨x-y,x-z⟩={\parallel x-y\parallel }^2{+\parallel x-z\parallel }^2-{\parallel y-z\parallel }^2.\end{array}$$

Lemma 3

([33]). Let Ω be a nonempty subset of H. Let $\left\{x_n\right\}$ be a sequence in H. If the following conditions hold:

$\left(i\right)$ $\forall x\in \Omega$, $\underset{n\to \infty }{lim}\parallel x_n-x\parallel$ exists;

$\left(ii\right)$ every weak sequential cluster point of $\left\{x_n\right\}$ is in Ω.

• Then the sequence $\left\{x_n\right\}$ converges weakly to a point in Ω.

Lemma 4

([36]). Let $\left\{{\alpha }_n\right\}$ be a sequence in $[0,+\infty )$, $\left\{{\eta }_n\right\}\in {\ell }_{+}^1\left(\mathbb{N}\right)$, $\left\{{\delta }_n\right\}\in {\ell }_{+}^1\left(\mathbb{N}\right)$ such that

$${\alpha }_{n+1}\le (1+{\eta }_n){\alpha }_n+{\delta }_n,\forall n\in \mathbb{N}.$$

Then $\left\{{\alpha }_n\right\}$ converges.

3. Iterative Algorithms and Convergence Analyses

In this section, we propose the parameterized variable metric three-operator algorithm and multi-step inertial parameterized variable metric three-operator algorithm to solve the approximate solution of the problem (1). The weak and strong convergence results are obtained. Both algorithms require the following assumptions:

Assumption 1.

$A,B:H\to 2^H$ are maximally monotone operators, $C:H\to H$ is a β-cocoercive operator, $\beta >0$.

Assumption 2.

$D\in B\left(H\right)$ and the solution set of $\mathrm{zer}(A+B+C+(2\mathrm{Id}-D\left)\right)$ is nonempty.

The following Proposition is mainly used to prove the convergence of the proposed algorithm.

Proposition 1.

Let $A,B:H\to 2^H$ be maximally monotone operators, $C:H\to H$ be a β-cocoercive operator and $\beta >0$. Let $D\in B\left(H\right)$, $M\in P_{\alpha }\left(H\right)$ and $\gamma >0$. Denote by

$$\begin{array}{cc}\hfill J_{\gamma A}^M& ={(M+\gamma A)}^{-1},\hfill \\ \hfill K_M& =\{z\in H|J_{\gamma A}^{M}z=J_{\gamma B}^M(2M{J}_{\gamma A}^{M}z-z-\gamma C{J}_{\gamma A}^{M}z-\gamma (2\mathrm{Id}-D)J_{\gamma A}^{M}z)\}.\hfill \end{array}$$

Then $\mathrm{zer}(A+B+C+(2\mathrm{Id}-D))=J_{\gamma A}^M\left(K_M\right)$ and $K_M=\mathrm{Fix}\left(T\right)$, where $T=\mathrm{Id}-J_{\gamma A}^M+J_{\gamma B}^M(2M{J}_{\gamma A}^M-\mathrm{Id}-\gamma C{J}_{\gamma A}^M-\gamma (2\mathrm{Id}-D)J_{\gamma A}^M)$. Moreover,

$$\mathrm{Fix}\left(T\right)=\{Mx+\gamma a|x\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D\left)\right),a\in Ax\cap (-Bx-Cx-(2\mathrm{Id}-D\left)x\right)\}.$$

(10)

Proof of Proposition 1.

Let $x\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D\left)\right)$. We have

$$\begin{array}{cc}\hfill & 0\in (A+B+C+(2\mathrm{Id}-D\left)\right)x\hfill \\ \hfill & \iff 0\in \gamma (A+B+C+(2\mathrm{Id}-D\left)\right)x\hfill \\ \hfill & \iff \exists z\in H \mathrm{with} z-Mx\in \gamma Ax \mathrm{such} \mathrm{that} Mx-z\in \gamma Bx+\gamma Cx+\gamma (2\mathrm{Id}-D)x\hfill \\ \hfill & \Rightarrow x=J_{\gamma A}^{M}z \mathrm{and} 2Mx-z-\gamma Cx-\gamma (2\mathrm{Id}-D)x\in Mx+\gamma Bx\hfill \\ \hfill & \iff x=J_{\gamma A}^{M}z \mathrm{and} x=J_{\gamma B}^M(2Mx-z-\gamma Cx-\gamma (2\mathrm{Id}-D)x)\hfill \\ \hfill & \iff z\in K_M \mathrm{and} x\in J_{\gamma A}^M\left(K_M\right).\hfill \end{array}$$

In turn, if $x\in J_{\gamma A}^M\left(K_M\right)$, there exists $z\in K_M$ such that $x=J_{\gamma A}^{M}z$. Each of the above steps can be worked backward. It follows that $\mathrm{zer}(A+B+C+(2\mathrm{Id}-D))=J_{\gamma A}^M\left(K_M\right)$.

That $K_M=\mathrm{Fix}\left(T\right)$ is a trivial result.

Next, we show that (10) holds.

$$\begin{array}{cc}\hfill & z\in K_M\hfill \\ \hfill & \iff \exists x\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D)),x=J_{\gamma A}^{M}z,x=J_{\gamma B}^M(2Mx-z-\gamma Cx-\gamma (2\mathrm{Id}-D)x)\hfill \\ \hfill & \iff z-Mx\in \gamma Ax,Mx-z\in \gamma Bx+\gamma Cx+\gamma (2\mathrm{Id}-D)x\hfill \\ \hfill & \iff \exists a\in Ax\cap (-Bx-Cx-(2\mathrm{Id}-D\left)x\right),z=Mx+\gamma a\hfill \\ \hfill & \iff z\in \mathrm{Fix}\left(T\right).\hfill \end{array}$$

The proof is completed. □

Proposition 2.

Let $A,B:H\to 2^H$ be maximally monotone operators, $C:H\to H$ be an operator. Let $\alpha >0$, $\gamma >0$, $M_1$, $M_2\in P_{\alpha }\left(H\right)$. Given $z,\widehat{z}\in H$, denote by

$$\begin{array}{c}x=J_{\gamma A}^{M_1}z,\\ \widehat{x}=J_{\gamma A}^{M_2}\widehat{z},\end{array}\begin{array}{c}y=J_{\gamma B}^{M_1}(2M_{1}x-z-\gamma Cx-\gamma (2\mathrm{Id}-D)x),\\ \widehat{y}=J_{\gamma B}^{M_2}(2M_2\widehat{x}-\widehat{z}-\gamma C\widehat{x}-\gamma (2\mathrm{Id}-D)\widehat{x}).\end{array}$$

(11)

Then we have

$$\begin{array}{cc}0\le \hfill & ⟨z-\widehat{z},(x-y)-(\widehat{x}-\widehat{y})⟩-\alpha {\parallel (x-y)-(\widehat{x}-\widehat{y})\parallel }^2\hfill \\ \hfill & +\gamma ⟨y-\widehat{y},(2\mathrm{Id}-D)\widehat{x}-(2\mathrm{Id}-D)x⟩-\gamma ⟨y-\widehat{y},Cx-C\widehat{x}⟩\hfill \\ \hfill & +⟨y-\widehat{y},(M_2-M_1)(\widehat{y}-\widehat{x})⟩+⟨(M_2-M_1)\widehat{x},(x-y)-(\widehat{x}-\widehat{y})⟩.\hfill \end{array}$$

(12)

Further, if A or B is uniformly monotone with modulus ϕ, then the above inequality holds with 0 on the left replaced by $\gamma \varphi (\parallel x-\widehat{x}\parallel )$ or $\gamma \varphi (\parallel y-\widehat{y}\parallel )$.

Proof of Proposition 2.

According to (11), we have

$$\begin{array}{c}z-M_{1}x\in \gamma Ax,\\ \widehat{z}-M_2\widehat{x}\in \gamma A\widehat{x},\end{array}\begin{array}{c}2M_{1}x-z-\gamma Cx-\gamma (2\mathrm{Id}-D)x-M_{1}y\in \gamma By,\\ 2M_2\widehat{x}-\widehat{z}-\gamma C\widehat{x}-\gamma (2\mathrm{Id}-D)\widehat{x}-M_2\widehat{y}\in \gamma B\widehat{y}.\end{array}$$

By the monotonicity of A, B we obtain

$$0\le ⟨x-\widehat{x},z-M_{1}x-(\widehat{z}-M_2\widehat{x})⟩,$$

$$\begin{array}{cc}\hfill 0& \le ⟨y-\widehat{y},2M_{1}x-z-\gamma Cx-\gamma (2\mathrm{Id}-D)x-M_{1}y\hfill \\ \hfill & -(2M_2\widehat{x}-\widehat{z}-\gamma C\widehat{x}-\gamma (2\mathrm{Id}-D)\widehat{x}-M_2\widehat{y})⟩\hfill \\ \hfill & =-⟨y-\widehat{y},z-M_{1}x-(\widehat{z}-M_2\widehat{x})⟩-\gamma ⟨y-\widehat{y},Cx-C\widehat{x}⟩\hfill \\ \hfill & +⟨y-\widehat{y},M_2\widehat{y}-M_2\widehat{x}+\gamma (2\mathrm{Id}-D)\widehat{x}-(M_{1}y-M_{1}x+\gamma (2\mathrm{Id}-D)x)⟩.\hfill \end{array}$$

Adding the above two inequalities, we obtain

$$\begin{array}{cc}\hfill 0& \le ⟨z-M_{1}x-(\widehat{z}-M_2\widehat{x}),(x-y)-(\widehat{x}-\widehat{y})⟩-\gamma ⟨y-\widehat{y},Cx-C\widehat{x}⟩\hfill \\ \hfill & +⟨y-\widehat{y},M_2\widehat{y}-M_2\widehat{x}+\gamma (2\mathrm{Id}-D)\widehat{x}-(M_{1}y-M_{1}x+\gamma (2\mathrm{Id}-D)x)⟩\hfill \\ \hfill & =⟨z-\widehat{z},(x-y)-(\widehat{x}-\widehat{y})⟩-⟨M_{1}x-M_2\widehat{x},(x-y)-(\widehat{x}-\widehat{y})⟩-\gamma ⟨y-\widehat{y},Cx-C\widehat{x}⟩\hfill \\ \hfill & +⟨y-\widehat{y},M_2\widehat{y}-M_2\widehat{x}-(M_{1}y-M_{1}x)⟩+\gamma ⟨y-\widehat{y},(2\mathrm{Id}-D)(\widehat{x}-x)⟩.\hfill \end{array}$$

Notice that

$$\begin{array}{cc}\hfill & -⟨M_{1}x-M_2\widehat{x},(x-y)-(\widehat{x}-\widehat{y})⟩\hfill \\ \hfill & =-⟨M_{1}x-M_1\widehat{x},(x-y)-(\widehat{x}-\widehat{y})⟩-⟨M_1\widehat{x}-M_2\widehat{x},(x-y)-(\widehat{x}-\widehat{y})⟩\hfill \\ \hfill & =-{⟨x-\widehat{x},(x-y)-(\widehat{x}-\widehat{y})⟩}_{M_1}-⟨M_1\widehat{x}-M_2\widehat{x},(x-y)-(\widehat{x}-\widehat{y})⟩\hfill \end{array}$$

and that

$$\begin{array}{cc}\hfill & ⟨y-\widehat{y},M_2\widehat{y}-M_2\widehat{x}-(M_{1}y-M_{1}x)⟩\hfill \\ \hfill & =⟨y-\widehat{y},M_1\widehat{y}-M_1\widehat{x}-(M_{1}y-M_{1}x)⟩+⟨y-\widehat{y},M_2\widehat{y}-M_1\widehat{y}-(M_2\widehat{x}-M_1\widehat{x})⟩\hfill \\ \hfill & ={⟨y-\widehat{y},(x-y)-(\widehat{x}-\widehat{y})⟩}_{M_1}+⟨y-\widehat{y},(M_2-M_1)(\widehat{y}-\widehat{x})⟩.\hfill \end{array}$$

By $M_1\in P_{\alpha }\left(H\right)$, we have,

$$\begin{array}{cc}\hfill 0& \le ⟨z-\widehat{z},(x-y)-(\widehat{x}-\widehat{y})⟩-{\parallel (x-y)-(\widehat{x}-\widehat{y})\parallel }_{M_1}^2\hfill \\ \hfill & +\gamma ⟨y-\widehat{y},(2\mathrm{Id}-D)\widehat{x}-(2\mathrm{Id}-D)x⟩-\gamma ⟨y-\widehat{y},Cx-C\widehat{x}⟩\hfill \\ \hfill & +⟨y-\widehat{y},(M_2-M_1)(\widehat{y}-\widehat{x})⟩+⟨(M_2-M_1)\widehat{x},(x-y)-(\widehat{x}-\widehat{y})⟩\hfill \\ \hfill & \le ⟨z-\widehat{z},(x-y)-(\widehat{x}-\widehat{y})⟩-\alpha {\parallel (x-y)-(\widehat{x}-\widehat{y})\parallel }^2\hfill \\ \hfill & +\gamma ⟨y-\widehat{y},(2\mathrm{Id}-D)\widehat{x}-(2\mathrm{Id}-D)x⟩-\gamma ⟨y-\widehat{y},Cx-C\widehat{x}⟩\hfill \\ \hfill & +⟨y-\widehat{y},(M_2-M_1)(\widehat{y}-\widehat{x})⟩+⟨(M_2-M_1)\widehat{x},(x-y)-(\widehat{x}-\widehat{y})⟩.\hfill \end{array}$$

Further, if A or B is uniformly monotone, we just need to replace 0 with $\gamma \varphi (\parallel x-\widehat{x}\parallel )$ or $\gamma \varphi (\parallel y-\widehat{y}\parallel )$ from (12). □

3.1. Parameterized Variable Metric Three-Operator Algorithm

In this subsection, we study the following parameterized variable metric three-operator algorithm and its convergence.

Pick any $z_0\in H$,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_n=J_{\gamma A}^{M_n}{z}_n,\hfill \\ y_n=J_{\gamma B}^{M_n}(2M_n{x}_n-z_n-\gamma C{x}_n-\gamma (2\mathrm{Id}-D)x_n),\hfill \\ z_{n+1}=z_n+{\mu }_n(y_n-x_n),n\ge 0,\hfill \end{array}\right.\end{array}$$

(13)

where $J_{\gamma A}^{M_n}={(M_n+\gamma A)}^{-1}$, $M_n\in P_{\alpha }\left(H\right),\forall n\in \mathbb{N}$, $\alpha >0$. $\gamma >0$.

Theorem 1.

Let $\left\{z_n\right\}$ be generated by Algorithm (13). Suppose that the following conditions hold:

(C1) $\parallel D\parallel \in [0,2)$, $\gamma \in (0,\frac{4\alpha \beta (2-\parallel D\parallel )}{{2-\parallel D\parallel +\beta \parallel 2\mathrm{Id}-D\parallel }^2})$;

(C2) ${\displaystyle \sum _{n=0}^{\infty }}{\mu }_n=+\infty$, $0<{\mu }_n\le \underset{n\to \infty }{lim\; sup}{\mu }_n=\overline{\mu }\le 2\alpha -\gamma (\frac{1}{2\beta }+\frac{{\parallel 2\mathrm{Id}-D\parallel }^2}{2(2-\parallel D\parallel )})$;

(C3) $M\in P_{\alpha }\left(H\right)$, ${\displaystyle \sum _{n=0}^{\infty }}\frac{1}{{\mu }_n}\parallel M-M_n\parallel <+\infty$.

• Then we have

1. 

$\left\{z_n\right\}$ is bounded;

2. 

$y_n-x_n\to 0$, $z_n\rightharpoonup z^{*}\in K_M$, $x_n\rightharpoonup x^{*}$, $y_n\rightharpoonup x^{*}$, $C{x}_n\to C{x}^{*}$, where $x^{*}=J_{\gamma A}^M{z}^{*}\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D))$, $K_M$ is defined as Proposition 1;

3. 

Suppose that one of the following holds:

(a) 

A is uniformly monotone on every nonempty bounded subset of $\mathrm{dom}A$;

(b) 

B is uniformly monotone on every nonempty bounded subset of $\mathrm{dom}B$;

(c) 

$\forall x\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D\left)\right)$, C is demiregular at x,

then $x_n,y_n\to x^{*}$.

Proof of Theorem 1.

1. Set $w_n=y_n-x_n$. By (13), we have

$$\begin{array}{c}(x_n,z_n-M_n{x}_n)\in \mathrm{gra}\gamma A,\hfill \\ (y_n,2M_n{x}_n-z_n-\gamma C{x}_n-\gamma (2\mathrm{Id}-D)x_n-M_n{y}_n)\in \mathrm{gra}\gamma B.\hfill \end{array}$$

(14)

Let $x\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D\left)\right)$. Then there exist $p\in K_M$ and $p_n\in K_{M_n}$, respectively, such that $x=J_{\gamma A}^M\left(p\right)$ and $x=J_{\gamma A}^{M_n}\left(p_n\right)$ in view of Proposition 1, where $K_{M_n}=\{p_n\in H|J_{\gamma A}^{M_n}{p}_n=J_{\gamma B}^{M_n}(2M_n{J}_{\gamma A}^{M_n}{p}_n-p_n-\gamma C{J}_{\gamma A}^{M_n}{p}_n-\gamma (2\mathrm{Id}-D)J_{\gamma A}^{M_n}{p}_n)\}$. By taking $z=p_n$, $\widehat{z}=z_n$, $M_1=M_2=M_n$ and noting that $\widehat{x}=x_n$, $\widehat{y}=y_n$, $x=y$ in Proposition 2, we obtain

$$\begin{array}{cc}0\le \hfill & ⟨p_n-z_n,w_n⟩-\alpha {\parallel w_n\parallel }^2-\gamma ⟨x-y_n,Cx-C{x}_n⟩\hfill \\ \hfill & +\gamma ⟨x-y_n,(2\mathrm{Id}-D)x_n-(2\mathrm{Id}-D)x⟩.\hfill \end{array}$$

(15)

Multiplying the first two terms on the right of (15) by $2{\mu }_n$, we obtain

$$\begin{array}{cc}\hfill & 2{\mu }_n(⟨p_n-z_n,w_n⟩-\alpha \parallel w_n{\parallel }^2)\hfill \\ =\hfill & 2⟨p_n-z_n,z_{n+1}-z_n⟩-2\alpha {\mu }_n{\parallel w_n\parallel }^2\hfill \\ =\hfill & \parallel z_n-p_n{\parallel }^2-\parallel z_{n+1}-p_n{\parallel }^2+{\mu }_n({\mu }_n-2\alpha ){\parallel w_n\parallel }^2.\hfill \end{array}$$

(16)

Since C is a $\beta$-cocoercive operator, it follows from Young’s inequality that

$$\begin{array}{cc}\hfill & -\gamma ⟨x-y_n,Cx-C{x}_n⟩\hfill \\ =\hfill & -\gamma ⟨x-x_n,Cx-C{x}_n⟩+\gamma ⟨w_n,Cx-C{x}_n⟩\hfill \\ \le \hfill & -\beta \gamma \parallel Cx-C{x}_n{\parallel }^2+\gamma ⟨w_n,Cx-C{x}_n⟩\hfill \\ \le \hfill & -\beta \gamma \parallel Cx-C{x}_n{\parallel }^2+\beta \gamma \parallel Cx-C{x}_n{\parallel }^2+\frac{\gamma }{4\beta }{\parallel w_n\parallel }^2\hfill \\ =\hfill & \frac{\gamma }{4\beta }{\parallel w_n\parallel }^2.\hfill \end{array}$$

(17)

Furthermore, the last term of (15) can be expressed by utilizing Young’s inequality again as

$$\begin{array}{cc}\hfill & \gamma ⟨x-y_n,(2\mathrm{Id}-D)x_n-(2\mathrm{Id}-D)x⟩\hfill \\ =\hfill & -\gamma ⟨y_n-x_n,(2\mathrm{Id}-D)x_n-(2\mathrm{Id}-D)x⟩-\gamma ⟨x_n-x,(2\mathrm{Id}-D)x_n-(2\mathrm{Id}-D)x⟩\hfill \\ \le \hfill & \gamma ⟨w_n,(2\mathrm{Id}-D)x-(2\mathrm{Id}-D)x_n⟩-2\gamma \parallel x_n{-x\parallel }^2+\gamma \parallel D\parallel \parallel x_n{-x\parallel }^2\hfill \\ \le \hfill & \gamma (\frac{ϵ}{2}\parallel w_n{\parallel }^2+\frac{1}{2ϵ}{\parallel 2\mathrm{Id}-D\parallel }^2\parallel x-x_n{\parallel }^2)+(\gamma \parallel D\parallel -2\gamma )\parallel x_n{-x\parallel }^2\hfill \\ =\hfill & \gamma [\parallel D\parallel -2+\frac{1}{2ϵ}{\parallel 2\mathrm{Id}-D\parallel }^2]\parallel x_n{-x\parallel }^2+\frac{\gamma ϵ}{2}{\parallel w_n\parallel }^2\hfill \\ \le \hfill & \frac{\gamma ϵ}{2}{\parallel w_n\parallel }^2,\hfill \end{array}$$

(18)

where the positive constant $ϵ$ satisfies

$$\frac{{\parallel 2\mathrm{Id}-D\parallel }^2}{2(2-\parallel D\parallel )}\le ϵ\le \frac{4\alpha \beta -\gamma -2\beta {\mu }_n}{2\beta \gamma },$$

(19)

which implies that $\parallel D\parallel -2+\frac{1}{2ϵ}{\parallel 2\mathrm{Id}-D\parallel }^2\le 0$.

Now, substituting (16)–(18) into (15), we derive

$$\begin{array}{c}\hfill 0\le \parallel z_n-p_n{\parallel }^2-\parallel z_{n+1}-p_n{\parallel }^2+{\mu }_n({\mu }_n-2\alpha +\frac{\gamma }{2\beta })\parallel w_n{\parallel }^2+\gamma ϵ{\mu }_n{\parallel w_n\parallel }^2.\end{array}$$

Thereby,

$$\begin{array}{c}\hfill \parallel z_{n+1}-p_n{\parallel }^2+{\mu }_n(2\alpha -\frac{\gamma }{2\beta }-{\mu }_n-\gamma ϵ)\parallel w_n{\parallel }^2\le {\parallel z_n-p_n\parallel }^2.\end{array}$$

(20)

It yields

$$\begin{array}{c}\hfill \parallel z_{n+1}-p_n\parallel \le \parallel z_n-p_n\parallel \end{array}$$

since $2\alpha -\frac{\gamma }{2\beta }-{\mu }_n-\gamma ϵ>0$ by (19). Hence, we obtain from $x=J_{\gamma A}^M\left(p\right)=J_{\gamma A}^{M_n}\left(p_n\right)$ and Proposition 1 that $p_n-p=(M_n-M)x$ and

$$\begin{array}{cc}\hfill \parallel z_{n+1}-p\parallel & \le \parallel z_{n+1}-p_n\parallel +\parallel p_n-p\parallel \hfill \\ \hfill & \le \parallel z_n-p\parallel +2\parallel p_n-p\parallel \hfill \\ \hfill & \le \parallel z_n-p\parallel +2\parallel M_n-M\parallel \parallel x\parallel .\hfill \end{array}$$

Note that ${\displaystyle \sum _{n=0}^{\infty }}\parallel M-M_n\parallel <+\infty$ because ${\displaystyle \sum _{n=0}^{\infty }}\frac{1}{\overline{\mu }}\parallel M-M_n\parallel \le {\displaystyle \sum _{n=0}^{\infty }}\frac{1}{{\mu }_n}\parallel M-M_n\parallel <+\infty$. Thus we have $\underset{n\to \infty }{lim}\parallel z_n-p\parallel$ exists by Lemma 4. As a result, $\left\{z_n\right\}$ is bounded.

In addition, we have by applying Lemma 1

$$\begin{array}{cc}\hfill \parallel x_n{-x\parallel }^2& =\parallel J_{\gamma A}^{M_n}{z}_n-J_{\gamma A}^{M_n}{p}_n{\parallel }^2\hfill \\ \hfill & \le \frac{1}{\alpha }{\parallel J_{\gamma A}^{M_n}{z}_n-J_{\gamma A}^{M_n}{p}_n\parallel }_{M_n}^2\hfill \\ \hfill & =\frac{1}{\alpha }{\parallel J_{\gamma {M_n}^{-1}A}{M_n}^{-1}{z}_n-J_{\gamma {M_n}^{-1}A}{M_n}^{-1}{p}_n\parallel }_{M_n}^2\hfill \\ \hfill & \le \frac{1}{\alpha }{\parallel {M_n}^{-1}{z}_n-{M_n}^{-1}{p}_n\parallel }_{M_n}^2\hfill \\ \hfill & \le \frac{1}{\alpha }\parallel {M_n}^{-1}\parallel \parallel z_n-p_n{\parallel }^2\hfill \\ \hfill & \le \frac{1}{{\alpha }^2}(\parallel z_n-p\parallel +\parallel p-p_n{\parallel )}^2\hfill \\ \hfill & <\infty .\hfill \end{array}$$

So $\left\{x_n\right\}$ is a bounded sequence. Similarly, $\left\{y_n\right\}$ is bounded.

2. In Proposition 2, we take $z=z_{n+1}$, $\widehat{z}=z_n$, $M_1=M_{n+1}$, $M_2=M_n$, then $x=x_{n+1}$, $y=y_{n+1}$, $\widehat{x}=x_n$ and $\widehat{y}=y_n$. Thus,

$$\begin{array}{cc}0\le \hfill & ⟨z_{n+1}-z_n,w_n-w_{n+1}⟩-\alpha {\parallel w_{n+1}-w_n\parallel }^2-\gamma ⟨y_{n+1}-y_n,C{x}_{n+1}-C{x}_n⟩\hfill \\ \hfill & +\gamma ⟨y_{n+1}-y_n,(2\mathrm{Id}-D)(x_n-x_{n+1})⟩\hfill \\ \hfill & +⟨y_{n+1}-y_n,(M_n-M_{n+1})(y_n-x_n)⟩+⟨(M_n-M_{n+1})x_n,w_n-w_{n+1}⟩\hfill \\ \hspace{1em}\le \hfill & ⟨z_{n+1}-z_n,w_n-w_{n+1}⟩-\alpha {\parallel w_{n+1}-w_n\parallel }^2-\gamma ⟨y_{n+1}-y_n,C{x}_{n+1}-C{x}_n⟩\hfill \\ \hfill & +\parallel M_{n+1}-M_n\parallel [\parallel y_n-y_{n+1}\parallel \parallel w_n\parallel +\parallel x_n\parallel \parallel w_{n+1}-w_n\parallel ]\hfill \\ \hfill & +\gamma ⟨y_{n+1}-y_n,(2\mathrm{Id}-D)(x_n-x_{n+1})⟩.\hfill \end{array}$$

(21)

Similar to (17) and (18), we obtain the following estimations of the third and the last terms of the right side in (21), respectively,

$$\begin{array}{cc}\hfill & -\gamma ⟨y_{n+1}-y_n,C{x}_{n+1}-C{x}_n⟩\hfill \\ =\hfill & -\gamma ⟨w_{n+1}-w_n,C{x}_{n+1}-C{x}_n⟩-\gamma ⟨x_{n+1}-x_n,C{x}_{n+1}-C{x}_n⟩\hfill \\ \le \hfill & \beta \gamma \parallel C{x}_{n+1}-C{x}_n{\parallel }^2+\frac{\gamma }{4\beta }\parallel w_{n+1}-w_n{\parallel }^2-\beta \gamma {\parallel C{x}_{n+1}-C{x}_n\parallel }^2\hfill \\ =\hfill & \frac{\gamma }{4\beta }{\parallel w_{n+1}-w_n\parallel }^2\hfill \end{array}$$

(22)

and

$$\begin{array}{cc}\hfill & \gamma ⟨y_{n+1}-y_n,(2\mathrm{Id}-D)(x_n-x_{n+1})⟩\hfill \\ =\hfill & -\gamma ⟨w_{n+1}-w_n,(2\mathrm{Id}-D)(x_{n+1}-x_n)⟩-\gamma ⟨x_{n+1}-x_n,(2\mathrm{Id}-D)(x_{n+1}-x_n)⟩\hfill \\ \le \hfill & \gamma (\frac{ϵ}{2}\parallel w_{n+1}-w_n{\parallel }^2+\frac{1}{2ϵ}\parallel 2\mathrm{Id}-D{\parallel }^2\parallel x_{n+1}-x_n{\parallel }^2)\hfill \\ \hfill & -2\gamma \parallel x_{n+1}-x_n{\parallel }^2+\gamma \parallel D\parallel \parallel x_{n+1}-x_n{\parallel }^2\hfill \\ =\hfill & \gamma (\frac{1}{2ϵ}{\parallel 2\mathrm{Id}-D\parallel }^2+\parallel D\parallel -2)\parallel x_{n+1}-x_n{\parallel }^2+\frac{\gamma ϵ}{2}{\parallel w_{n+1}-w_n\parallel }^2\hfill \\ \le \hfill & \frac{\gamma ϵ}{2}{\parallel w_{n+1}-w_n\parallel }^2,\hfill \end{array}$$

(23)

where $ϵ$ is given by (19).

Multiplying (21) by 2 and substituting (22) and (23) into (21), we conclude that

$$\begin{array}{cc}\hfill 0& \le 2⟨z_{n+1}-z_n,w_n-w_{n+1}⟩-2\alpha {\parallel w_{n+1}-w_n\parallel }^2\hfill \\ \hfill & +\frac{\gamma }{2\beta }\parallel w_{n+1}-w_n{\parallel }^2+\gamma ϵ{\parallel w_{n+1}-w_n\parallel }^2\hfill \\ \hfill & +2\parallel M_{n+1}-M_n\parallel [\parallel y_n-y_{n+1}\parallel \parallel w_n\parallel +\parallel x_n\parallel \parallel w_{n+1}-w_n\parallel ]\hfill \\ \hfill & =2{\mu }_n⟨w_n,w_n-w_{n+1}⟩+\left(\frac{\gamma }{2\beta }+\gamma ϵ-2\alpha \right){\parallel w_{n+1}-w_n\parallel }^2\hfill \\ \hfill & +2\parallel M_{n+1}-M_n\parallel [\parallel y_n-y_{n+1}\parallel \parallel w_n\parallel +\parallel x_n\parallel \parallel w_{n+1}-w_n\parallel ]\hfill \\ \hfill & ={\mu }_n\parallel w_n{\parallel }^2-{\mu }_n\parallel w_{n+1}{\parallel }^2+\left(\frac{\gamma }{2\beta }+\gamma ϵ-2\alpha +{\mu }_n\right){\parallel w_{n+1}-w_n\parallel }^2\hfill \\ \hfill & +2\parallel M_{n+1}-M_n\parallel [\parallel y_n-y_{n+1}\parallel \parallel w_n\parallel +\parallel x_n\parallel \parallel w_{n+1}-w_n\parallel ].\hfill \end{array}$$

From ${\mu }_n>0$, we have

$$\begin{array}{cc}\hfill \parallel w_{n+1}{\parallel }^2& \le \parallel w_n{\parallel }^2-\frac{1}{{\mu }_n}\left(2\alpha -\frac{\gamma }{2\beta }-\gamma ϵ-{\mu }_n\right){\parallel w_{n+1}-w_n\parallel }^2\hfill \\ \hfill & +\frac{2}{{\mu }_n}\parallel M_{n+1}-M_n\parallel [\parallel y_n-y_{n+1}\parallel \parallel w_n\parallel +\parallel x_n\parallel \parallel w_{n+1}-w_n\parallel ]\hfill \\ \hfill & \le \parallel w_n{\parallel }^2+\frac{2}{{\mu }_n}\parallel M_{n+1}-M_n\parallel [\parallel y_n-y_{n+1}\parallel \parallel w_n\parallel +\parallel x_n\parallel \parallel w_{n+1}-w_n\parallel ]\hfill \end{array}$$

since $2\alpha -\frac{\gamma }{2\beta }-\gamma ϵ-{\mu }_n\ge 0$ by (19). Let

$${\delta }_n=\frac{2}{{\mu }_n}\parallel M_{n+1}-M_n\parallel [\parallel y_n-y_{n+1}\parallel \parallel w_n\parallel +\parallel x_n\parallel \parallel w_{n+1}-w_n\parallel ].$$

We have ${\displaystyle \sum _{n=0}^{\infty }}{\delta }_n<+\infty$ by virtue of the fact that ${\displaystyle \sum _{n=0}^{\infty }}\frac{1}{{\mu }_n}\parallel M_{n+1}-M_n\parallel <+\infty$ and $\left\{x_n\right\}$, $\left\{y_n\right\}$, $\left\{w_n\right\}$ are bounded sequences. Therefore, $\{\parallel w_n\parallel \}$ converges from Lemma 4.

Next, we show that $w_n=y_n-x_n$ converges to 0 as n goes to infinity.

Rearranging terms in (20), we have

$$\begin{array}{cc}\hfill & {\mu }_n(2\alpha -\frac{\gamma }{2\beta }-{\mu }_n-\gamma ϵ){\parallel w_n\parallel }^2\hfill \\ \le \hfill & \parallel z_n-p_n{\parallel }^2-{\parallel z_{n+1}-p_n\parallel }^2\hfill \\ \le \hfill & \parallel z_n-p_n{\parallel }^2-\parallel z_{n+1}-p_{n+1}{\parallel }^2-\parallel p_n-p_{n+1}{\parallel }^2+2\parallel z_{n+1}-p_{n+1}\parallel \parallel p_n-p_{n+1}\parallel \hfill \\ \le \hfill & \parallel z_n-p_n{\parallel }^2-\parallel z_{n+1}-p_{n+1}{\parallel }^2-{\parallel (M_n-M_{n+1})x\parallel }^2\hfill \\ \hfill & +2[\parallel z_{n+1}-p\parallel +\parallel p-p_{n+1}\parallel ]\parallel (M_n-M_{n+1})x\parallel \hfill \\ =\hfill & \parallel z_n-p_n{\parallel }^2-\parallel z_{n+1}-p_{n+1}{\parallel }^2-{\parallel (M_n-M_{n+1})x\parallel }^2\hfill \\ \hfill & +2[\parallel z_{n+1}-p\parallel +\parallel (M-M_{n+1})x\parallel ]\parallel (M_n-M_{n+1})x\parallel \hfill \\ \le \hfill & \parallel z_n-p_n{\parallel }^2-\parallel z_{n+1}-p_{n+1}{\parallel }^2+\Omega \parallel (M_n-M_{n+1})x\parallel ,\hfill \end{array}$$

(24)

where $\Omega ={sup}_n\left\{2\right[\parallel z_{n+1}-p\parallel +\parallel (M-M_{n+1})x\parallel ]-\parallel (M_n-M_{n+1})x\parallel \}<\infty$ due to the boundedness of $\left\{z_n\right\}$ and (C2), (C3).

Summing on both sides of (24) from 0 to k, we obtain as k goes to infinity

$$\begin{array}{c}\hfill \sum _{n=0}^{\infty }{\mu }_n(2\alpha -\frac{\gamma }{2\beta }-{\mu }_n-\gamma ϵ){\parallel w_n\parallel }^2\le \parallel z_0-p_0{\parallel }^2+\Omega \sum _{n=0}^{\infty }\parallel (M_n-M_{n+1})x\parallel \hfill \\ \hfill <\infty .\hfill \end{array}$$

(25)

By ${\displaystyle \sum _{n=0}^{\infty }}{\mu }_n=+\infty$ and (19), it has ${\displaystyle \sum _{n=0}^{\infty }}{\mu }_n(2\alpha -\frac{\gamma }{2\beta }-{\mu }_n-\gamma ϵ)=+\infty$. Thus, $\underset{n\to \infty }{lim\; inf}\parallel w_n\parallel =0$ in view of (25). Hence, $\underset{n\to \infty }{lim}\parallel w_n\parallel =0$, that is $y_n-x_n\to 0$ as $n\to \infty$.

For simplicity, denote by $v_n=\gamma C\left(x_n\right)$. From 1., $\left\{z_n\right\}$, $\left\{x_n\right\}$, and $\left\{v_n\right\}$ are bounded sequences. Assume that $(z^{*},x^{*},v^{*})$ is a weak limit point of the sequence $\left\{(z_n,x_n,v_n)\right\}$. Then there exists its subsequence $\left\{(z_{n_k},x_{n_k},v_{n_k})\right\}$ such that $(z_{n_k},x_{n_k},v_{n_k})\rightharpoonup (z^{*},x^{*},v^{*})$.

Define $F:H^3\to 2^{H^3}$ by

$$\begin{array}{c}\hfill F=\left(\begin{array}{c}{\left(\gamma A\right)}^{-1}\\ {\left(\gamma C\right)}^{-1}\\ \gamma B+\gamma (2\mathrm{Id}-D)\end{array}\right)+\left(\begin{array}{ccc}0& 0& -\mathrm{Id}\\ 0& 0& -\mathrm{Id}\\ \mathrm{Id}& \mathrm{Id}& 0\end{array}\right).\end{array}$$

Then F is a maximally monotone operator (see [33] (Example 20.35, Corollary 25.5(i))). From (14), we obtain

$$\left(\begin{array}{c}{x}_{n_k}-y_{n_k}\\ x_{n_k}-y_{n_k}\\ M_{n_k}(x_{n_k}-y_{n_k})+\gamma (2\mathrm{Id}-D)(y_{n_k}-x_{n_k})\end{array}\right)\in F\left(\begin{array}{c}{z}_{n_k}-M_{n_k}{x}_{n_k}\\ v_{n_k}\\ y_{n_k}\end{array}\right).$$

Noting that $z_{n_k}-M_{n_k}{x}_{n_k}\rightharpoonup z^{*}-M{x}^{*}$, $v_{n_k}\rightharpoonup v^{*}$, $y_{n_k}\rightharpoonup x^{*}$ by $w_{n_k}\to 0$, and that $\mathrm{gra}F$ is sequentially closed in $H^{weak}\times H^{strong}$, we deduce

$$\begin{array}{c}\hfill \left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)\in \left(\left(\begin{array}{c}{\left(\gamma A\right)}^{-1}\\ {\left(\gamma C\right)}^{-1}\\ \gamma B+\gamma (2\mathrm{Id}-D)\end{array}\right)+\left(\begin{array}{ccc}0& 0& -\mathrm{Id}\\ 0& 0& -\mathrm{Id}\\ \mathrm{Id}& \mathrm{Id}& 0\end{array}\right)\right)\left(\begin{array}{c}{z}^{*}-M{x}^{*}\\ v^{*}\\ x^{*}\end{array}\right).\end{array}$$

In other words,

$$\begin{array}{c}{x}^{*}=J_{\gamma A}^M{z}^{*},v^{*}=\gamma C{x}^{*},x^{*}=J_{\gamma B}^M(2M{x}^{*}-z^{*}-\gamma C{x}^{*}-\gamma (2\mathrm{Id}-D)x^{*}).\end{array}$$

Thus $z^{*}\in K_M$. This gives $z_n\rightharpoonup z^{*}\in K_M$ according to Lemma 3. Furthermore, $x^{*}=J_{\gamma A}^M{z}^{*}\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D))$ by Proposition 1. Since $z^{*}$ is the unique weak limit point of $\left\{z_n\right\}$, $x^{*}=J_{\gamma A}^M{z}^{*}$ and $v^{*}=\gamma C{x}^{*}$ are the unique weak limit points of $\left\{x_n\right\}$, $\left\{v_n\right\}$, respectively. So, $x_n\rightharpoonup x^{*}$, $v_n\rightharpoonup v^{*}$. By $w_n\to 0$, we have $y_n\rightharpoonup x^{*}$.

Taking $z=z^{*}$, $\widehat{z}=z_n$, $M_1=M$ and $M_2=M_n$ in Proposition 2 and applying (17) and (18), we have

$$\begin{array}{cc}\hfill 0& \le ⟨z^{*}-z_n,w_n⟩-\alpha \parallel w_n{\parallel }^2+\frac{\gamma ϵ}{2}\parallel w_n{\parallel }^2-\beta \gamma {\parallel C{x}^{*}-C{x}_n\parallel }^2\hfill \\ \hfill & +\gamma ⟨w_n,C{x}^{*}-C{x}_n⟩+⟨x^{*}-y_n,(M_n-M)w_n⟩+⟨(M_n-M)x_n,w_n⟩.\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill \beta \gamma \parallel C{x}^{*}-C{x}_n{\parallel }^2& \le ⟨z^{*}-z_n,w_n⟩+(\frac{\gamma ϵ}{2}-\alpha ){\parallel w_n\parallel }^2+\gamma ⟨w_n,C{x}^{*}-C{x}_n⟩\hfill \\ \hfill & +⟨x^{*}-y_n,(M_n-M)w_n⟩+⟨(M_n-M)x_n,w_n⟩\hfill \\ \hfill & \to 0,\mathrm{as} n\to \infty .\hfill \end{array}$$

That is, $C{x}_n\to C{x}^{*}$ as $n\to \infty$.

3. As seen in 2., there exists $x^{*}\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D))$ such that $x_n\rightharpoonup x^{*}$ as $n\to \infty$.

$\left(a\right)$ Set $O=\left\{x^{*}\right\}\cup \left\{x_n\right\}$. Obviously, O is a bounded subset of $\mathrm{dom}A$. Since A is uniformly monotone on O, which means that there exists an increasing function ${\varphi }_A:{\mathbb{R}}_{+}\to [0,+\infty ]$ satisfying that ${\varphi }_A\left(x\right)=0$ if and only if $x=0$, which allows us to write the result of Proposition 2 as if we set $z=z^{*}$, $\widehat{z}=z_n$, $M_1=M$, $M_2=M_n$ 

$$\begin{array}{cc}\hfill \gamma {\varphi }_A(\parallel x^{*}-x_n\parallel )& \le ⟨z^{*}-z_n,w_n⟩-\alpha {\parallel w_n\parallel }^2-\gamma ⟨x^{*}-y_n,C{x}^{*}-C{x}_n⟩\hfill \\ \hfill & +\gamma ⟨x^{*}-y_n,(2\mathrm{Id}-D)(x_n-x^{*})⟩\hfill \\ \hfill & +⟨x^{*}-y_n,(M_n-M)w_n⟩+⟨(M_n-M)x_n,w_n⟩.\hfill \end{array}$$

Hence, we have by using (18) and the results of 2.

$$\begin{array}{cc}\hfill 0& \le \gamma {\varphi }_A(\parallel x^{*}-x_n\parallel )\hfill \\ \hfill & \le ⟨z^{*}-z_n,w_n⟩-\alpha \parallel w_n{\parallel }^2-\gamma ⟨x^{*}-y_n,C{x}^{*}-C{x}_n⟩+\frac{\gamma ϵ}{2}{\parallel w_n\parallel }^2\hfill \\ \hfill & +⟨x^{*}-y_n,(M_n-M)w_n⟩+⟨(M_n-M)x_n,w_n⟩\hfill \\ \hfill & \to 0,\mathrm{as} n\to \infty ,\hfill \end{array}$$

where $ϵ$ is a positive constant satisfying (19). $\underset{n\to \infty }{lim}\parallel x_n-x^{*}\parallel =0$ follows from $\underset{n\to \infty }{lim}\parallel {\varphi }_A(\parallel x^{*}-x_n\parallel )\parallel =0$ and the definition of ${\varphi }_A$. Moreover, $\left\{y_n\right\}$ converges strongly to $x^{*}$ holds due to $\underset{n\to \infty }{lim}\parallel y_n-x_n\parallel =0$.

(b) The proof is the same as (a).

(c) From 2., we have $x_n\rightharpoonup x^{*}\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D))$ and $C{x}_n\to C{x}^{*}$. The demiregularity of C at $x^{*}$ guarantees $x_n\to x^{*}$ as $n\to \infty$. □

Remark 1.

$\left(i\right)$ The operator T defined in Proposition 1 is similar in form to the operators that appeared in [8] (Proposition 2.1) and [12] (Lemma 3.4), but it is no longer an averaged operator. We prove the weak and strong convergence results of the proposed algorithm in this more general case.

$\left(ii\right)$ Algorithm (13) can be seen as a generalization of (8). In fact, if we choose $M_n=\mathrm{Id}$ and $D=\alpha$, $\alpha \in (0,2)$, Algorithm (13) becomes (8).

3.2. Multi-Step Inertial Parameterized Variable Metric Three-Operator Algorithm

In this subsection, we present the multi-step inertial parameterized variable metric three-operator algorithm, which combines Algorithm (13) and the multi-step inertial technique. Meanwhile, we show the convergence of the proposed algorithm.

Let $s\in {\mathbb{N}}_{+}$ and $U=\{0,\cdots ,s-1\}$. Let ${\left\{{\theta }_{i,n}\right\}}_{i\in U}\in {(-1,1)}^s$. Choose $z_0\in H$, $z_{-i-1}=z_0$, $i\in U$ and set

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{v}_n=z_n+{\displaystyle \sum _{i\in U}}{\theta }_{i,n}(z_{n-i}-z_{n-i-1}),\hfill \\ x_n=J_{\gamma A}^{M_n}{v}_n,\hfill \\ y_n=J_{\gamma B}^{M_n}(2M_n{x}_n-v_n-\gamma C{x}_n-\gamma (2\mathrm{Id}-D)x_n),\hfill \\ z_{n+1}=v_n+{\mu }_n(y_n-x_n),n\ge 0,\hfill \end{array}\right.\end{array}$$

(26)

where $J_{\gamma A}^{M_n}={(M_n+\gamma A)}^{-1}$, $M_n\in P_{\alpha }\left(H\right)$.

Theorem 2.

Let $\left\{z_n\right\}$ be defined by Algorithm (26), $K_M$ be defined as Proposition 1. Set $\parallel D\parallel \in [0,2)$, $\gamma \in (0,\frac{4\alpha \beta (2-\parallel D\parallel )}{{2-\parallel D\parallel +\beta \parallel 2\mathrm{Id}-D\parallel }^2})$ and provided the following conditions hold:

(C3) ${\displaystyle \sum _{n=0}^{\infty }}{\mu }_n=+\infty$, $0<\underline{\mu }\le {\mu }_n\le 2\alpha -\frac{\gamma }{2\beta }(1+\frac{{\beta \parallel 2\mathrm{Id}-D\parallel }^2}{2-\parallel D\parallel })$;

(C4) $M_n\in P_{\alpha }\left(H\right)$ such that ${\displaystyle \sum _{n=0}^{\infty }}\parallel M-M_n\parallel <+\infty$;

(C5) $\overline{{\theta }_i}=su{p}_{n\in \mathbb{N}}|{\theta }_{i,n}|$, ${\displaystyle \sum _{i\in U}}\overline{{\theta }_i}<1$, $\underset{n\to \infty }{lim}{\theta }_{i,n}\ne 0$ and

$$\sum _{n=1}^{+\infty }\underset{i\in U}{max}|{\theta }_{i,n}|\sum _{i\in U}\parallel z_{n-i}-z_{n-i-1}\parallel <+\infty .$$

(27)

Then the following assertions hold:

1. 

For every $q\in K_M$, $\underset{n\to \infty }{lim}\parallel z_n-q\parallel$ exists;

2. 

$\left\{z_n\right\}$, $\left\{v_n\right\}$ converge weakly to the same point of $K_M$, $\left\{x_n\right\}$, $\left\{y_n\right\}$ converge weakly to the same point of $\mathrm{zer}(A+B+C+(2\mathrm{Id}-D\left)\right)$;

3. 

Suppose that one of the following holds:

(a) 

A is uniformly monotone on every nonempty bounded subset of $\mathrm{dom}A$;

(b) 

B is uniformly monotone on every nonempty bounded subset of $\mathrm{dom}B$;

(c) 

$\forall x\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D\left)\right)$, C is demiregular at x,

• then $\left\{x_n\right\}$, $\left\{y_n\right\}$ converge strongly to the same point of $\mathrm{zer}(A+B+C+(2\mathrm{Id}-D\left)\right)$.

Proof of Theorem 2.

1. Given $q\in K_M$, arbitrarily, there exists $\overline{x}\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D))$ such that $\overline{x}=J_{\gamma A}^M\left(q\right)$, and for this $\overline{x}$, there exists $q_n\in K_{M_n}$ such that $\overline{x}=J_{\gamma A}^{M_n}\left(q_n\right)$ according to Proposition 1. We choose $z=q_n$, $\widehat{z}=v_n$, $M_1=M_2=M_n$ in Proposition 2. Then we have $x=y=\overline{x}$, $\widehat{x}=x_n$, $\widehat{y}=y_n$, and

$$\begin{array}{cc}0\le \hfill & ⟨q_n-v_n,y_n-x_n⟩-\alpha {\parallel y_n-x_n\parallel }^2-\gamma ⟨\overline{x}-y_n,C\overline{x}-C{x}_n⟩\hfill \\ \hfill & +\gamma ⟨\overline{x}-y_n,(2\mathrm{Id}-D)x_n-(2\mathrm{Id}-D)\overline{x}⟩.\hfill \end{array}$$

(28)

Applying Lemma 2, we have

$$\begin{array}{cc}\hfill & 2{\mu }_n(⟨q_n-v_n,y_n-x_n⟩-\alpha \parallel y_n-x_n{\parallel }^2)\hfill \\ =\hfill & 2⟨q_n-v_n,z_{n+1}-v_n⟩-2\alpha {\mu }_n{\parallel y_n-x_n\parallel }^2\hfill \\ =\hfill & \parallel v_n-q_n{\parallel }^2-\parallel z_{n+1}-q_n{\parallel }^2+{\mu }_n({\mu }_n-2\alpha ){\parallel y_n-x_n\parallel }^2.\hfill \end{array}$$

(29)

As same as (17) and (18), we obtain

$$\begin{array}{cc}-\gamma ⟨\overline{x}-y_n,C\overline{x}-C{x}_n⟩\hfill & \le -\beta \gamma \parallel C\overline{x}-C{x}_n{\parallel }^2+\gamma ⟨y_n-x_n,C\overline{x}-C{x}_n⟩\hfill \\ \hfill & \le \frac{\gamma }{4\beta }{\parallel y_n-x_n\parallel }^2,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill \gamma ⟨\overline{x}-y_n,(2\mathrm{Id}-D)x_n-(2\mathrm{Id}-D)\overline{x}⟩& \le \frac{\gamma ϵ}{2}{\parallel y_n-x_n\parallel }^2,\hfill \end{array}$$

(31)

where $\frac{{\parallel 2\mathrm{Id}-D\parallel }^2}{2(2-\parallel D\parallel )}\le ϵ\le \frac{4\alpha \beta -\gamma -2\beta {\mu }_n}{2\beta \gamma }$.

Combining (28)–(31), we have

$$\begin{array}{c}\hfill 0\le \parallel v_n-q_n{\parallel }^2-\parallel z_{n+1}-q_n{\parallel }^2+{\mu }_n({\mu }_n-2\alpha +\frac{\gamma }{2\beta }+\gamma ϵ){\parallel y_n-x_n\parallel }^2,\end{array}$$

from which it follows that

$$\begin{array}{c}\hfill \parallel z_{n+1}-q_n{\parallel }^2+{\mu }_n(2\alpha -\frac{\gamma }{2\beta }-{\mu }_n-\gamma ϵ)\parallel y_n-x_n{\parallel }^2\le {\parallel v_n-q_n\parallel }^2.\end{array}$$

Since $2\alpha -\frac{\gamma }{2\beta }-{\mu }_n-\gamma ϵ\ge 0$, it has

$$\begin{array}{c}\hfill \parallel z_{n+1}-q_n{\parallel }^2\le {\parallel v_n-q_n\parallel }^2,\end{array}$$

which implies

$$\begin{array}{cc}\hfill \parallel z_{n+1}-q_n\parallel & \le \parallel v_n-q_n\parallel \hfill \\ \hfill & \le \parallel z_n-q_n\parallel +\parallel \sum _{i\in U}{\theta }_{i,n}(z_{n-i}-z_{n-i-1})\parallel \hfill \\ \hfill & \le \parallel z_n-q\parallel +\parallel q-q_n\parallel +\underset{i\in U}{max}|{\theta }_{i,n}|\sum _{i\in U}\parallel z_{n-i}-z_{n-i-1}\parallel \hfill \\ \hfill & \le \parallel z_n-q\parallel +\parallel M-M_n\parallel \parallel \overline{x}\parallel +\underset{i\in U}{max}|{\theta }_{i,n}|\sum _{i\in U}\parallel z_{n-i}-z_{n-i-1}\parallel .\hfill \end{array}$$

By (C4), (C5) and Lemma 4, we have $\underset{n\to \infty }{lim}\parallel z_n-q\parallel$ exists and $\left\{z_n\right\}$ is bounded. Hence, $\left\{v_n\right\}$, $\left\{x_n\right\}$ and $\left\{\gamma C{x}_n\right\}$ are bounded.

2. Since $\underset{n\to \infty }{lim}{\theta }_{i,n}\ne 0$ and (27) holds, for all $i\in U$, it has

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}|{\theta }_{i,n}|\parallel z_{n-i}-z_{n-i-1}\parallel =0.\end{array}$$

Particularly,

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel z_{n+1}-z_n\parallel =0.\end{array}$$

(32)

Further, we have

$$\begin{array}{c}\hfill \parallel z_{n+1}-v_n\parallel \le \parallel z_{n+1}-z_n\parallel +\sum _{i\in U}|{\theta }_{i,n}|\parallel z_{n-i}-z_{n-i-1}\parallel \to 0,asn\to \infty .\end{array}$$

(33)

By (32) and (33), we have

$$\begin{array}{cc}\hfill 0\le \parallel z_n-v_n\parallel & =\parallel \sum _{i\in U}{\theta }_{i,n}(z_{n-i}-z_{n-i-1})\parallel \hfill \\ \hfill & \le \sum _{i\in U}|{\theta }_{i,n}|\parallel z_{n-i}-z_{n-i-1}\parallel ,\hfill \end{array}$$

which indicates that $\parallel z_n-v_n\parallel \to 0$.

Since $\underset{n\to \infty }{lim}\parallel y_n-x_n\parallel =\underset{n\to \infty }{lim}\frac{1}{{\mu }_n}\parallel z_{n+1}-v_n\parallel =0$. Then, $y_n-x_n\to 0$.

Set $u_n=\gamma C{x}_n$. Let $(\overline{z},\overline{x},\overline{u})$ be a weak limit point of the sequence $\left\{(z_n,x_n,u_n)\right\}$. Then there exists a subsequence $\left\{(z_{n_k},x_{n_k},u_{n_k})\right\}$ such that $(z_{n_k},x_{n_k},u_{n_k})\rightharpoonup (\overline{z},\overline{x},\overline{u})$. Without loss of generality, we assume that $\exists \left\{v_{n_k}\right\}\subset \left\{v_n\right\}$ such that $v_{n_k}\rightharpoonup \overline{z}$. In addition, we have $M_{n_k}\to M$ as $k\to \infty$ by (C4).

Define a maximally monotone operator $F:H^3\to 2^{H^3}$ by

$$\begin{array}{c}\hfill F=\left(\begin{array}{c}{\left(\gamma A\right)}^{-1}\\ {\left(\gamma C\right)}^{-1}\\ \gamma B+\gamma (2\mathrm{Id}-D)\end{array}\right)+\left(\begin{array}{ccc}0& 0& -\mathrm{Id}\\ 0& 0& -\mathrm{Id}\\ \mathrm{Id}& \mathrm{Id}& 0\end{array}\right).\end{array}$$

By (26), we have

$$\begin{array}{c}(x_n,v_n-M_n{x}_n)\in \mathrm{gra}\gamma A,\\ (y_n,2M_n{x}_n-v_n-\gamma C{x}_n-\gamma (2\mathrm{Id}-\gamma D)x_n-M_n{y}_n)\in \mathrm{gra}\gamma B.\end{array}$$

(34)

Therefore, from (34), we obtain

$$\left(\begin{array}{c}{x}_{n_k}-y_{n_k}\\ x_{n_k}-y_{n_k}\\ M_{n_k}(x_{n_k}-y_{n_k})+\gamma (2\mathrm{Id}-D)(y_{n_k}-x_{n_k})\end{array}\right)\in F\left(\begin{array}{c}{v}_{n_k}-M_{n_k}{x}_{n_k}\\ u_{n_k}\\ y_{n_k}\end{array}\right).$$

Since $\mathrm{gra}F$ is sequentially closed in $H^{weak}\times H^{strong}$,

$$\begin{array}{c}\hfill \left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)\in \left(\left(\begin{array}{c}{\left(\gamma A\right)}^{-1}\\ {\left(\gamma C\right)}^{-1}\\ \gamma B+\gamma (2\mathrm{Id}-D)\end{array}\right)+\left(\begin{array}{ccc}0& 0& -\mathrm{Id}\\ 0& 0& -\mathrm{Id}\\ \mathrm{Id}& \mathrm{Id}& 0\end{array}\right)\right)\left(\begin{array}{c}\overline{z}-M\overline{x}\\ \overline{u}\\ \overline{x}\end{array}\right),\end{array}$$

it yields that

$$\begin{array}{c}\overline{x}=J_{\gamma A}^M\overline{z},\overline{u}=\gamma C\overline{x},\overline{x}=J_{\gamma B}^M(2M\overline{x}-\overline{z}-\gamma C\overline{x}-\gamma (2\mathrm{Id}-D)\overline{x}).\end{array}$$

Hence, $\overline{z}\in K_M$. Using Lemma 3, $v_n\rightharpoonup \overline{z}\in K_M$. Meanwhile, $z_n\rightharpoonup \overline{z}\in K_M$ by $\parallel z_n-v_n\parallel \to 0$. Furthermore, $\overline{x}=J_{\gamma A}^M\overline{z}\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D))$ by Proposition 1. From that $z_n\rightharpoonup \overline{z}$, $\overline{x}=J_{\gamma A}^M\overline{z}$ and $\overline{u}=\gamma C\overline{x}$, we conclude that $x_n\rightharpoonup \overline{x}$, $u_n\rightharpoonup \overline{u}$. Using $y_n-x_n\to 0$, we obtain $y_n\rightharpoonup \overline{x}$.

By (30) and (31) and Proposition 2 with $z=\overline{z}$, $\widehat{z}=v_n$, $M_1=M$, $M_2=M_n$, we have

$$\begin{array}{cc}\hfill \beta \gamma \parallel C\overline{x}-C{x}_n{\parallel }^2& \le ⟨\overline{z}-v_n,y_n-x_n⟩+(\frac{\gamma ϵ}{2}-\alpha ){\parallel y_n-x_n\parallel }^2+\gamma ⟨y_n-x_n,C\overline{x}-C{x}_n⟩\hfill \\ \hfill & +⟨\overline{x}-y_n,(M_n-M)(y_n-x_n)⟩+⟨(M_n-M)x_n,y_n-x_n⟩.\hfill \end{array}$$

Hence, $C{x}_n\to C\overline{x}$.

3. Taking $z=\overline{z}$, $\widehat{z}=v_n$, $M_1=M$, $M_2=M_n$ and using similar arguments in the proof of 3. in Theorem 1, we obtain $x_n\to \overline{x}$ and $y_n\to \overline{x}$, where $\overline{x}\in \mathrm{zer}(A+B+C+(2\mathrm{Id}-D))$. □

Remark 2.

If ${\theta }_{i,n}\in [0,1)$, (27) reduces to

$$\sum _{n=1}^{+\infty }\underset{i\in U}{max}{\theta }_{i,n}\sum _{i\in U}\parallel z_{n-i}-z_{n-i-1}\parallel <+\infty .$$

(35)

(35) can be implemented by the following simple online updating rule

$${\theta }_{i,n}=min\{{\theta }_i,b_{i,n}\},$$

where ${\theta }_i\in [0,1)$, $\left\{b_{i,n}\right\}$ and $\{max{b}_{i,n}{\displaystyle \sum _{i\in U}}\parallel z_{n-i}-z_{n-i-1}\parallel \}$ are summable sequences for each $i\in U$. For example, one can choose

$$\begin{array}{c}\hfill b_{i,n}=\frac{b_i}{n^{1+\delta }{\displaystyle \sum _{i\in U}}\parallel z_{n-i}-z_{n-i-1}\parallel },b_i>0,\delta >0.\end{array}$$

4. Numerical Results

We consider the following LASSO problem with a nonnegative constraint:

$$\underset{x\in {\mathbb{R}}^N}{min}\{\frac{1}{2}{\parallel Ax-b\parallel }^2+{\parallel x\parallel }_1+{\iota }_c\left(x\right)\},$$

(36)

where $A\in {\mathbb{R}}^{J\times N}$, $b\in {\mathbb{R}}^{J\times 1}$, $C=\{x\in {\mathbb{R}}^N|x_i\ge 0,i=1,2,\cdots ,N\}$. Let ${\iota }_C\left(x\right)$ be the indicator function of the closed convex set C, that is,

$$\begin{array}{c}\hfill {\iota }_C\left(x\right)=\left\{\begin{array}{cc}\hfill & 0,x\in C,\hfill \\ \hfill & +\infty ,\mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

Set $f_1\left(x\right)={\parallel x\parallel }_1$, $f_2\left(x\right)={\iota }_c\left(x\right)$ and $f_3\left(x\right)=\frac{1}{2}{\parallel Ax-b\parallel }^2$. Obviously, $\nabla f_3\left(x\right)=A^T(Ax-b)$, $\nabla f_3\left(x\right)$ is $\parallel A^{T}A\parallel$-Lipschitz continuous and the i-th component of $J_{{\gamma }_n\partial f_1}^{M}x$ is

$$\begin{array}{cc}\hfill \left(J_{{\gamma }_n\partial f_1}^{M}x\right){}_i& =\left(J_{{\gamma }_n{M}^{-1}\partial f_1}{M}^{-1}x\right){}_i\hfill \\ \hfill & =\left(pro{x}_{{\gamma }_{n}M{f}_1}{M}^{-1}x\right){}_i=\left\{\begin{array}{cc}\hfill & \frac{x_i}{m_i}-\frac{{\gamma }_n}{m_i},\frac{x_i}{m_i}>\frac{{\gamma }_n}{m_i},\hfill \\ \hfill & \frac{x_i}{m_i}+\frac{{\gamma }_n}{m_i},\frac{x_i}{m_i}<\frac{{\gamma }_n}{m_i},\hfill \\ \hfill & 0,otherwise,\hfill \end{array}\right.\hfill \end{array}$$

where $M=diag(m_1,m_2,\cdots ,m_N)$. Similarly, we have

$$\begin{array}{c}\hfill J_{{\gamma }_n\partial f_2}^M\left(x\right)=J_{{\gamma }_n{M}^{-1}\partial f_2}\left(M^{-1}x\right)=pro{x}_{{\gamma }_{n}M{f}_2}\left(M^{-1}x\right)=P_C\left(M^{-1}x\right).\end{array}$$

Problem (36) is equivalent to the problem of finding $x\in {\mathbb{R}}^N$ such that

$$\begin{array}{c}\hfill 0\in \partial f_1\left(x\right)+\partial f_2\left(x\right)+\nabla f_3\left(x\right).\end{array}$$

Select any initial value $z_0,z_{-1},z_{-2}\in {\mathbb{R}}^N$, $U=\{1,2\}$, $i\in U$, ${\theta }_{1,n}={\theta }_{2,n}=min\{0.1,\frac{n-1}{n+2}\}$. Set $J=N=20$, $\mathrm{E}\in {\mathbb{R}}^{20\times 20}$, $M_n=M=2\mathrm{E}$, $\alpha =\frac{1}{2}$, $L=\parallel A^{T}A\parallel$, $\zeta =\frac{4\alpha (2-\parallel D\parallel )}{{L(2-\parallel D\parallel )+\parallel 2\mathrm{E}-D\parallel }^2}$, and take $\parallel z_{n+1}-z_n\parallel <$ eps as the stopping criteria. In the following, we denote Algorithm (13) as PVMTO and Algorithm (26) as MIPVMTO.

In Algorithms (13) and (26) take $D=k\mathrm{E}$, $k\in [0.009,1.999]$, and take $\gamma =\frac{1}{2}\zeta$, ${\mu }_n=0.499$, eps $={10}^{-5}$. In Figure 1 and Figure 2, we show the effect of the parameter D on the CPU time and iteration numbers of the PVMTO and the MIPVMTO. As can be seen from the figure, compared with PVMTO, MIPVMTO has a great improvement in the number of iterations and CPU. Furthermore, we list the CPU time of PVMTO and MIPVMTO at different stopping criteria and different D in Table 1.

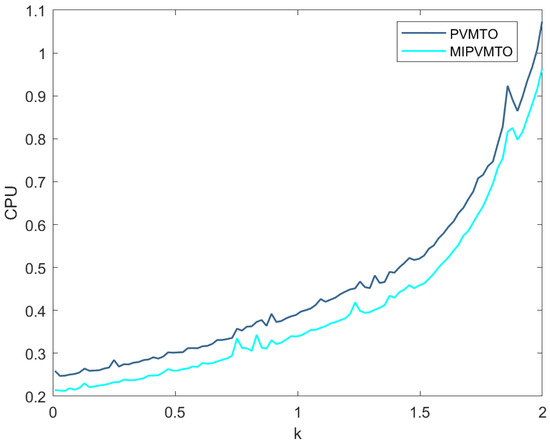
Figure 1. The effect of $D=k\mathrm{E}$ on CPU (s).

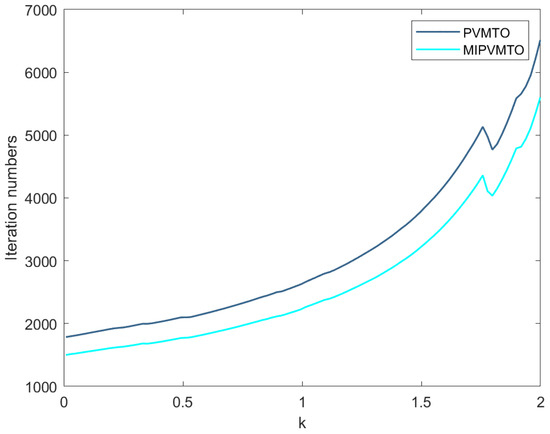
Figure 2. The effect of $D=k\mathrm{E}$ on iteration numbers.

Table 1. Numerical results of the PVMTO (Algorithm (13)) and the MIPVMTO (Algorithm (26)).

	PVMTO				MIPVMTO
eps	$\mathit{D}$	Iter	$\parallel {\mathit{x}}_{\mathit{n}}\parallel$	CPU ($\mathit{s}$)	$\mathit{D}$	Iter	$\parallel {\mathit{x}}_{\mathit{n}}\parallel$	CPU ($\mathit{s}$)
${10}^{-3}$	0.00999E	531	0.892097	0.075116	0.00999E	473	0.896813	0.101615
	0.50659E	564	0.909472	0.079004	0.50659E	526	0.917201	0.078163
	1.00499E	624	0.932223	0.083093	1.00499E	592	0.942767	0.080023
	1.50599E	725	0.965979	0.098467	1.50599E	615	0.969368	0.088909
	1.91199E	745	0.987424	0.103177	1.91199E	668	0.994628	0.093426
	1.93599E	746	0.988654	0.102805	1.93599E	676	0.996532	0.095638
	1.95699E	747	0.989739	0.106307	1.95699E	685	0.998393	0.092109
	1.97899E	749	0.990939	0.097910	1.97899E	696	1.000491	0.094137
	1.98999E	750	0.991522	0.098771	1.98999E	702	1.001613	0.093303
	1.99999E	750	0.991941	0.098490	1.99999E	707	1.002606	0.094370
	2.00000E	750	0.991941	0.113851	2.00000E	750	0.991941	0.113851
${10}^{-4}$	0.00999E	1114	0.869743	0.159736	0.00999E	958	0.870160	0.131419
	0.50659E	1223	0.880358	0.165580	0.50659E	1063	0.880900	0.142245
	1.00499E	1487	0.893068	0.193978	1.00499E	1314	0.893768	0.175073
	1.50599E	1878	0.909894	0.245709	1.50599E	1675	0.910860	0.224609
	1.91199E	2523	0.928138	0.328125	1.91199E	2249	0.929321	0.302159
	1.93599E	2538	0.929595	0.342751	1.93599E	2297	0.931024	0.324058
	1.95699E	2586	0.931119	0.350296	1.95699E	2302	0.932462	0.309686
	1.97899E	2635	0.932768	0.347120	1.97899E	2357	0.934105	0.315834
	1.98999E	2623	0.933456	0.341721	1.98999E	2388	0.934962	0.318405
	1.99999E	2652	0.934230	0.349495	1.99999E	2417	0.935759	0.321433
	2.00000E	2652	0.934231	0.314799	2.00000E	2652	0.934231	0.314799
${10}^{-5}$	0.00999E	2017	0.893855	0.518356	0.00999E	1692	0.893916	0.237726
	0.50659E	2370	0.915375	0.312055	0.50659E	1990	0.915430	0.267332
	1.00499E	2998	0.939446	0.389901	1.00499E	2520	0.939509	0.340453
	1.50599E	4365	0.968586	0.563529	1.50599E	3667	0.968661	0.485276
	1.91199E	6464	0.999046	0.832374	1.91199E	5530	0.999158	0.735078
	1.93599E	6717	1.001373	0.864062	1.93599E	5748	1.001488	0.765171
	1.95699E	6957	1.003502	1.488362	1.95699E	5956	1.003622	2.570363
	1.97899E	7229	1.005861	3.010892	1.97899E	6190	1.005987	2.856389
	1.98999E	7374	1.007065	3.209643	1.98999E	6315	1.007196	2.881690
	1.99999E	7511	1.008205	3.351171	1.99999E	6433	1.008341	2.996621
	2.00000E	7511	1.008206	3.024831	2.00000E	7511	1.008206	3.024831

In Algorithms (13) and (26) take $D=0.009\mathrm{E}$, $e\in [\frac{0.999}{20},\frac{19.999}{20}]$, ${\mu }_n=0.999-e$, $\gamma =e\zeta$ and eps $={10}^{-5}$. The effect of choosing different $\gamma$ on the number of iterations of the two algorithms is shown in Figure 3. It can be concluded that, when $\gamma =\frac{1}{2}\zeta$, the number of iterations of our two proposed algorithms is the least, and the number of iterations of MIPVMTO is less than that of the PVMTO.

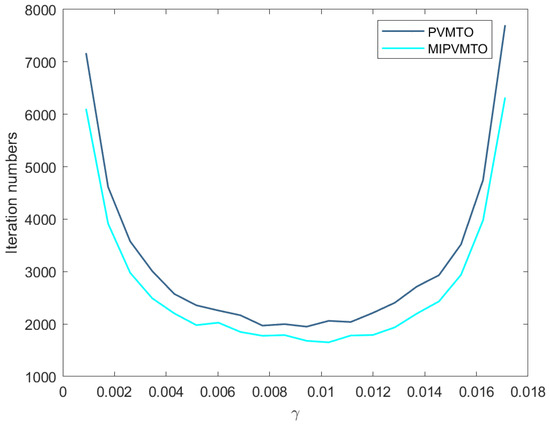
Figure 3. Different $\gamma$ with $\parallel z_{n+1}-z_n\parallel <{10}^{-5}$.

In Algorithms (13) and (26) take $D=0.009\mathrm{E}$, $M_n=M=2\mathrm{E}$ and $\gamma =\frac{1}{2}\zeta$, ${\mu }_n=0.499$. In Figure 4, we compare the number of iterations of PVMTO and MIPVMTO under different stopping criteria, and it can be seen that the parameterized variable metric three-operator algorithm with inertia term has more advantages.

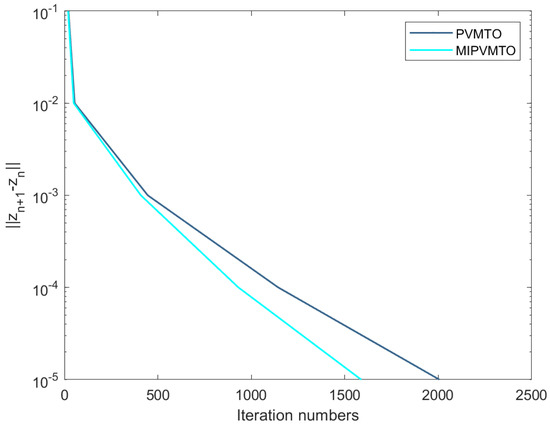
Figure 4. Numerical results with different stopping criterion.

5. Conclusions

In this paper, we propose a parameterized variable metric three-operator algorithm to solve the monotone inclusion problem involving the sum of three operators and prove the strong convergence of the algorithm under some appropriate conditions. The multi-step inertial parameterized variable metric three-operator algorithm is also proposed and its strong convergence is analyzed in order to speed up the parameterized variable metric three-operator algorithm. To a certain extent, the proposed algorithm can be seen as a generalization of the parameterized three-operator algorithm [12]. The constructed numerical examples show the efficiency of the proposed algorithms and the effects of the choices of the parameter operator D on running time. In future development, we can consider proving that the regularization of parameterized variable metric three-operator algorithm converges to the least norm solution of the sum of three maximally monotone operators as shown in [12] and show the real applications of the algorithms in practice. Another direction of consideration is to study the self-adaption version of the currently proposed algorithms.