A Modified Gamma Model: Properties, Estimation, and Applications
Abstract
1. Introduction
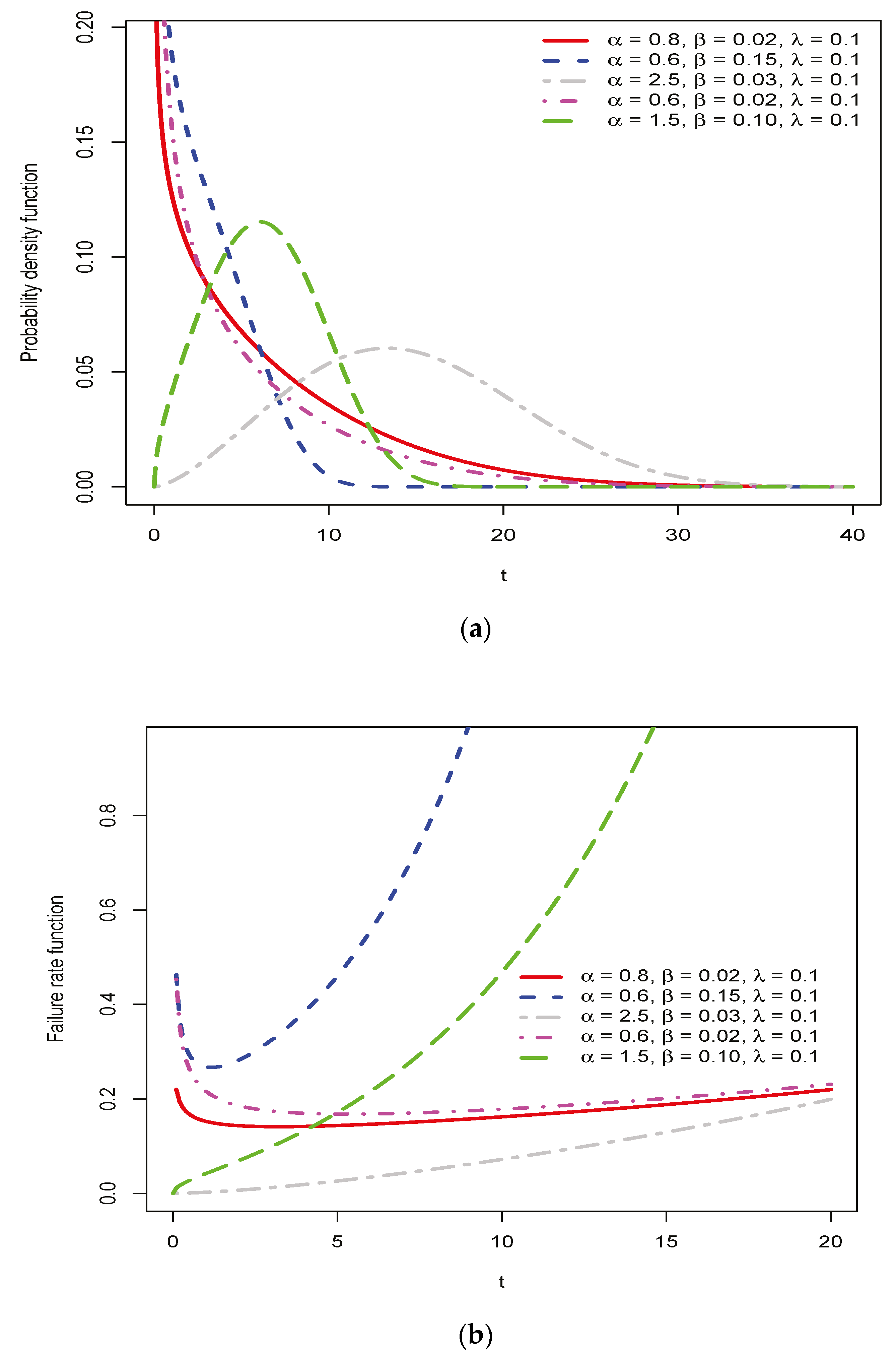
2. Model Formulation
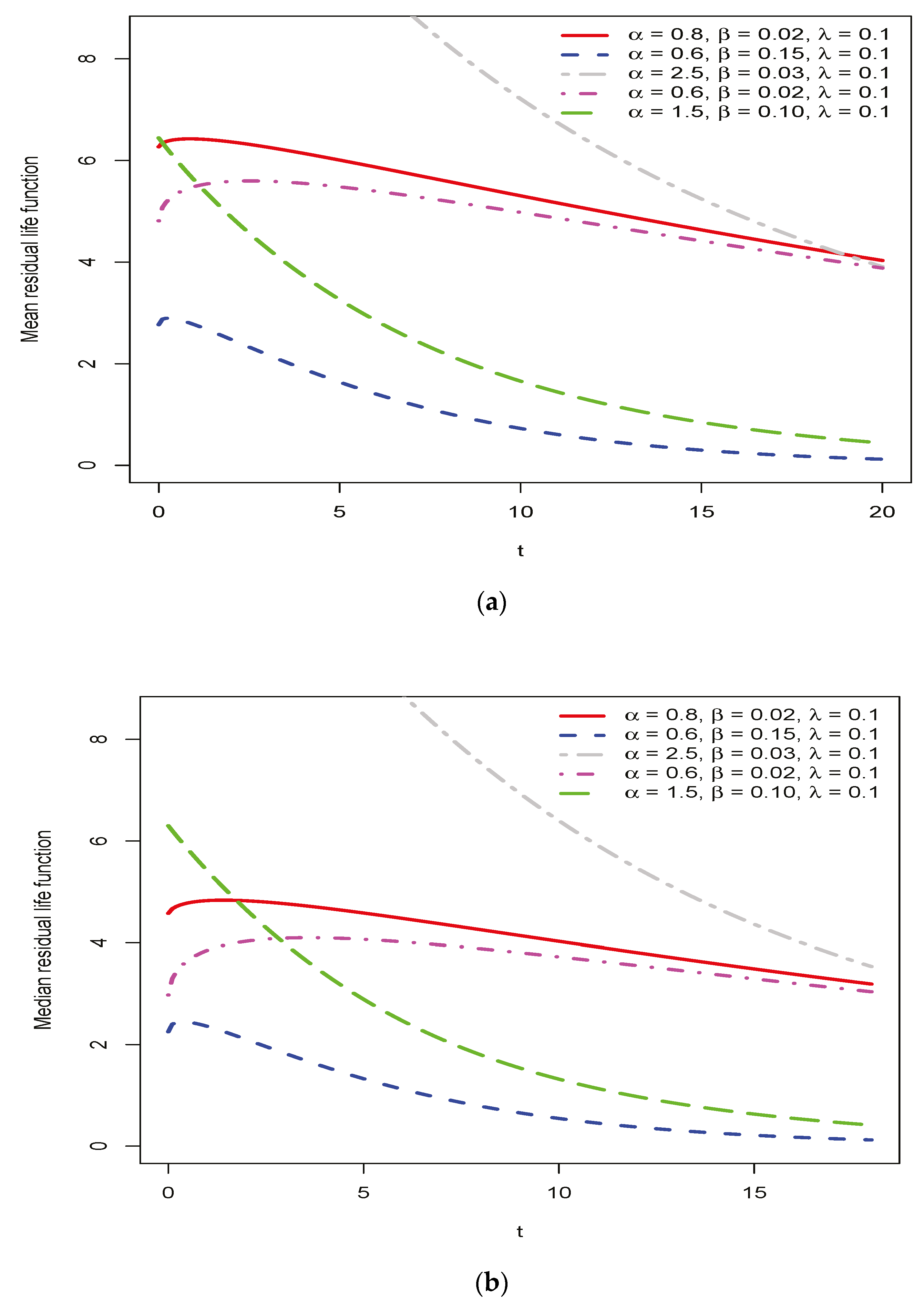
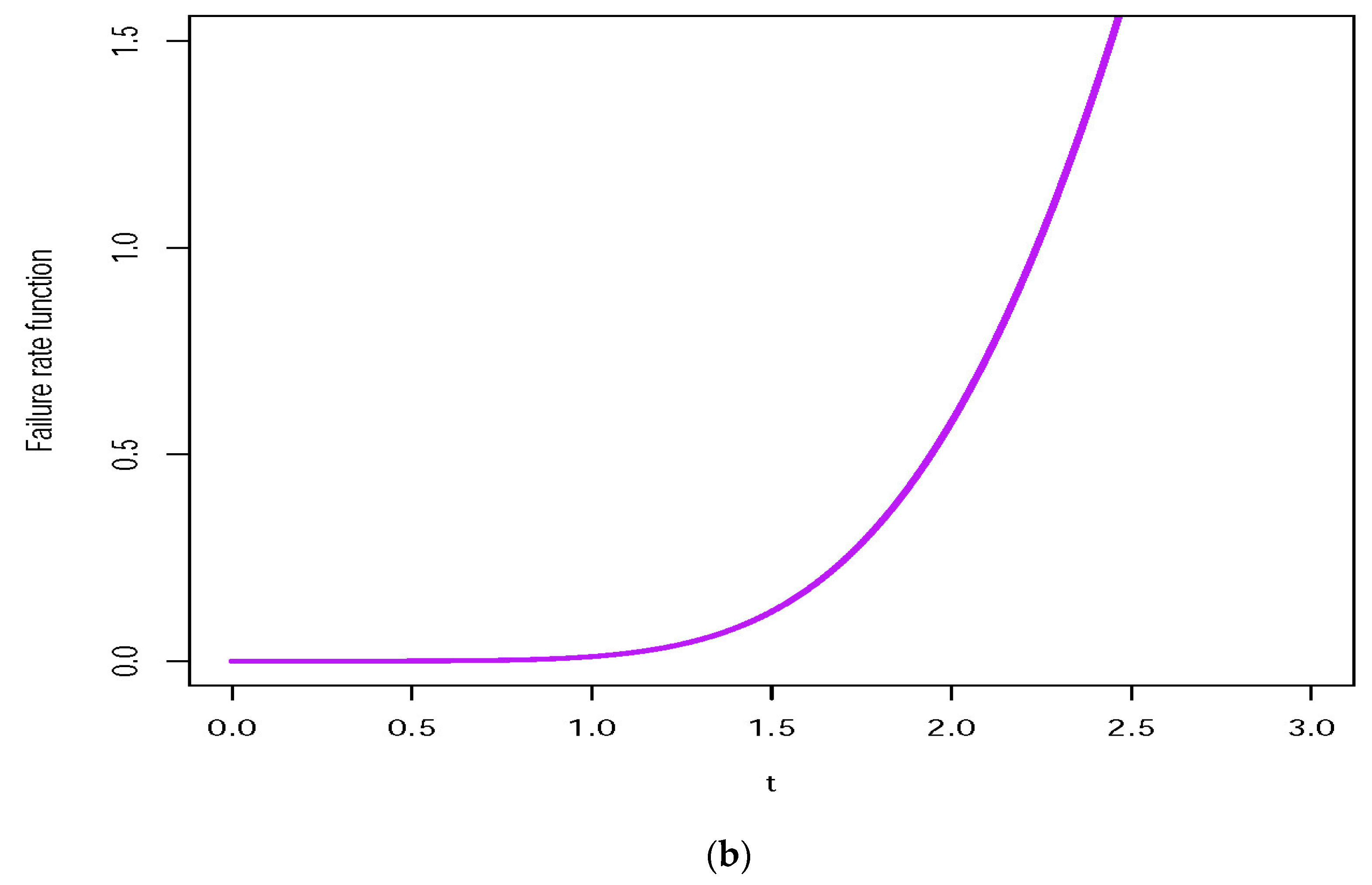
Dynamic Measures
3. Parameters Estimation
3.1. Maximum Likelihood Method
3.2. Least Squared Error Method
3.3. Anderson-Darling Method
3.4. Quantile Based Method
4. Investigation of the Estimator’s Behavior
- All estimators are consistent and efficient for estimating the model parameters.
- The AD estimator, a weighted form of the LSE method, outperforms the LSE estimator.
- The QB estimator has a very small MSE but does not improve significantly with sample size.
5. Applications
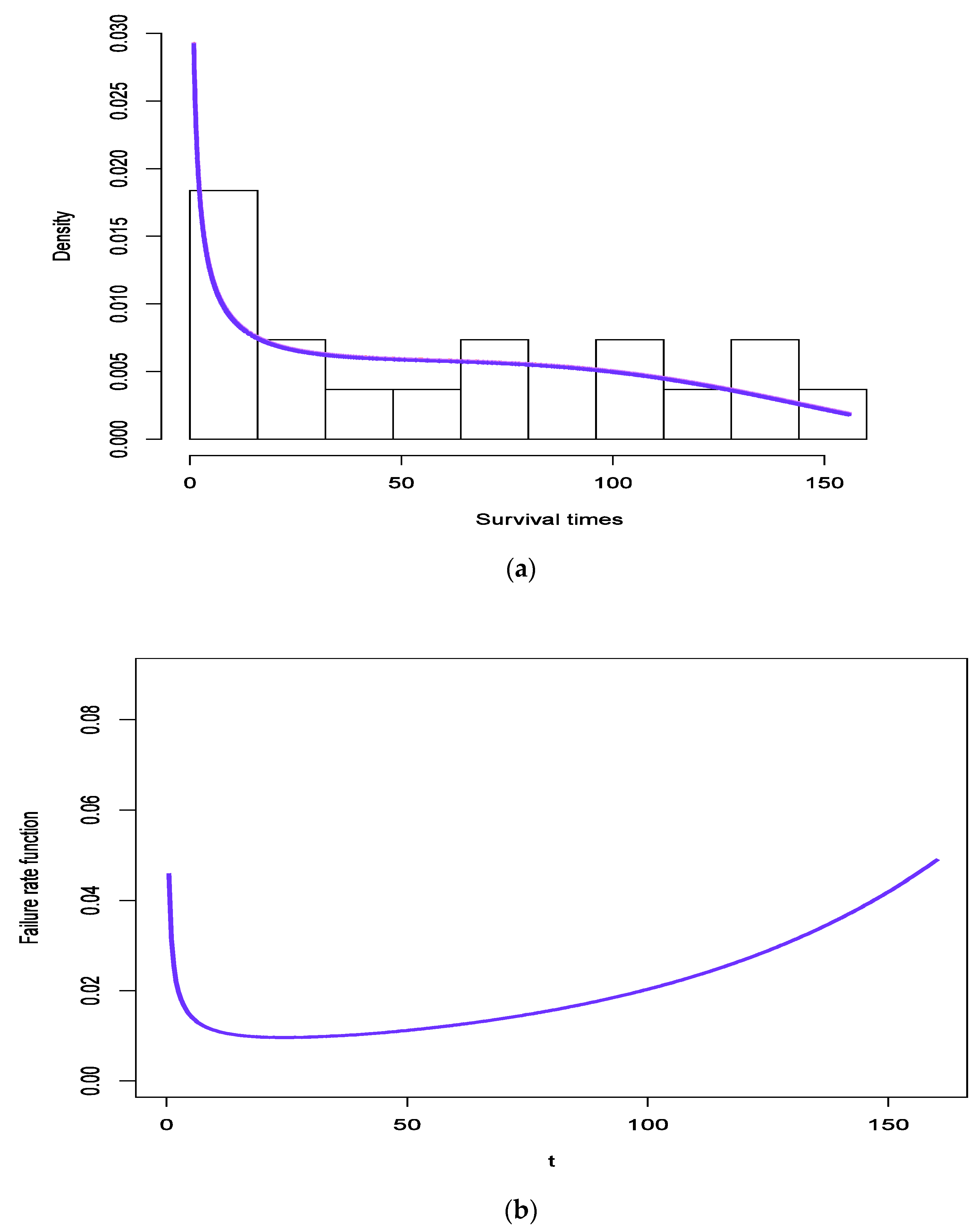
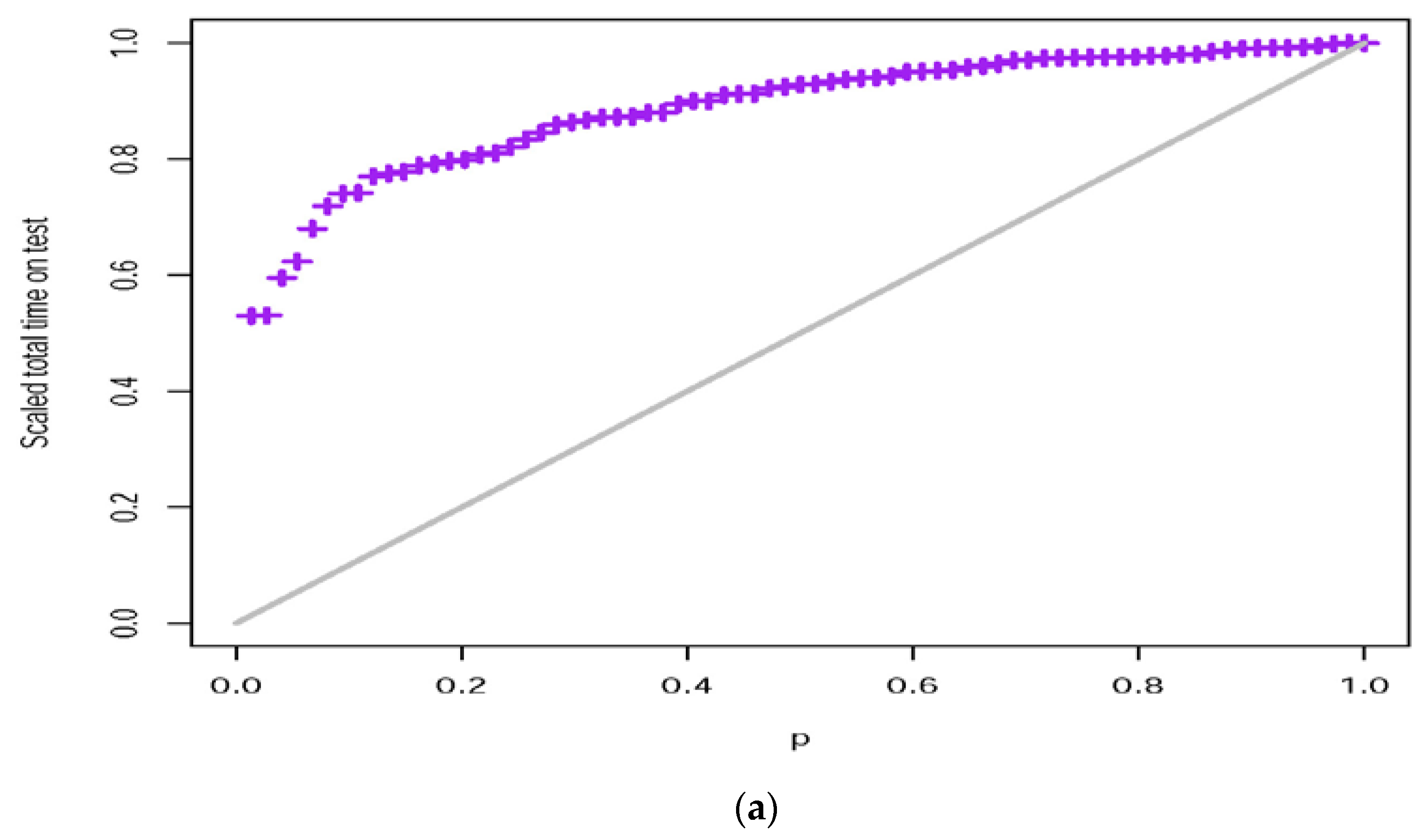
5.1. Application 1 Survival Times of AG Positive Patients Data
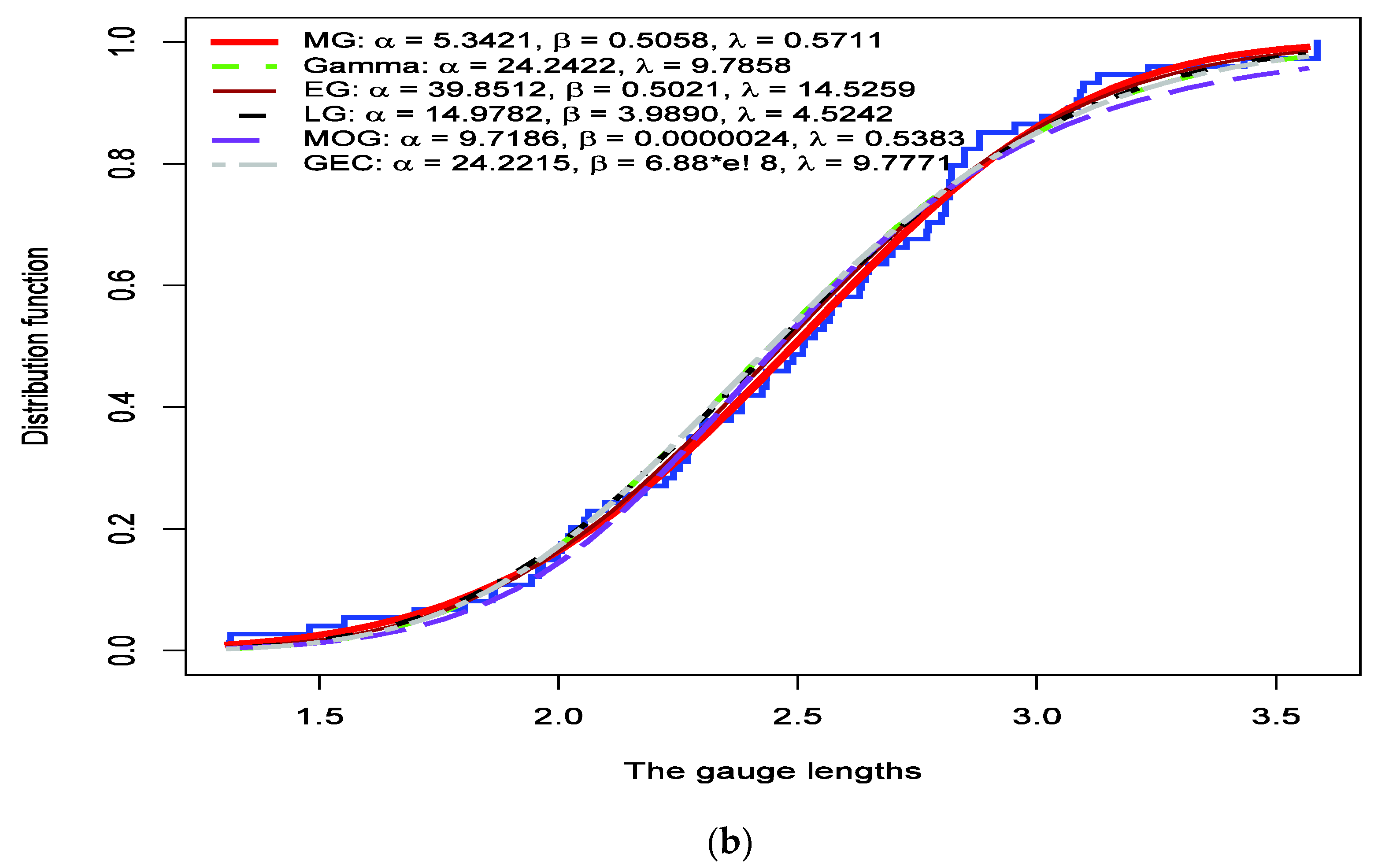
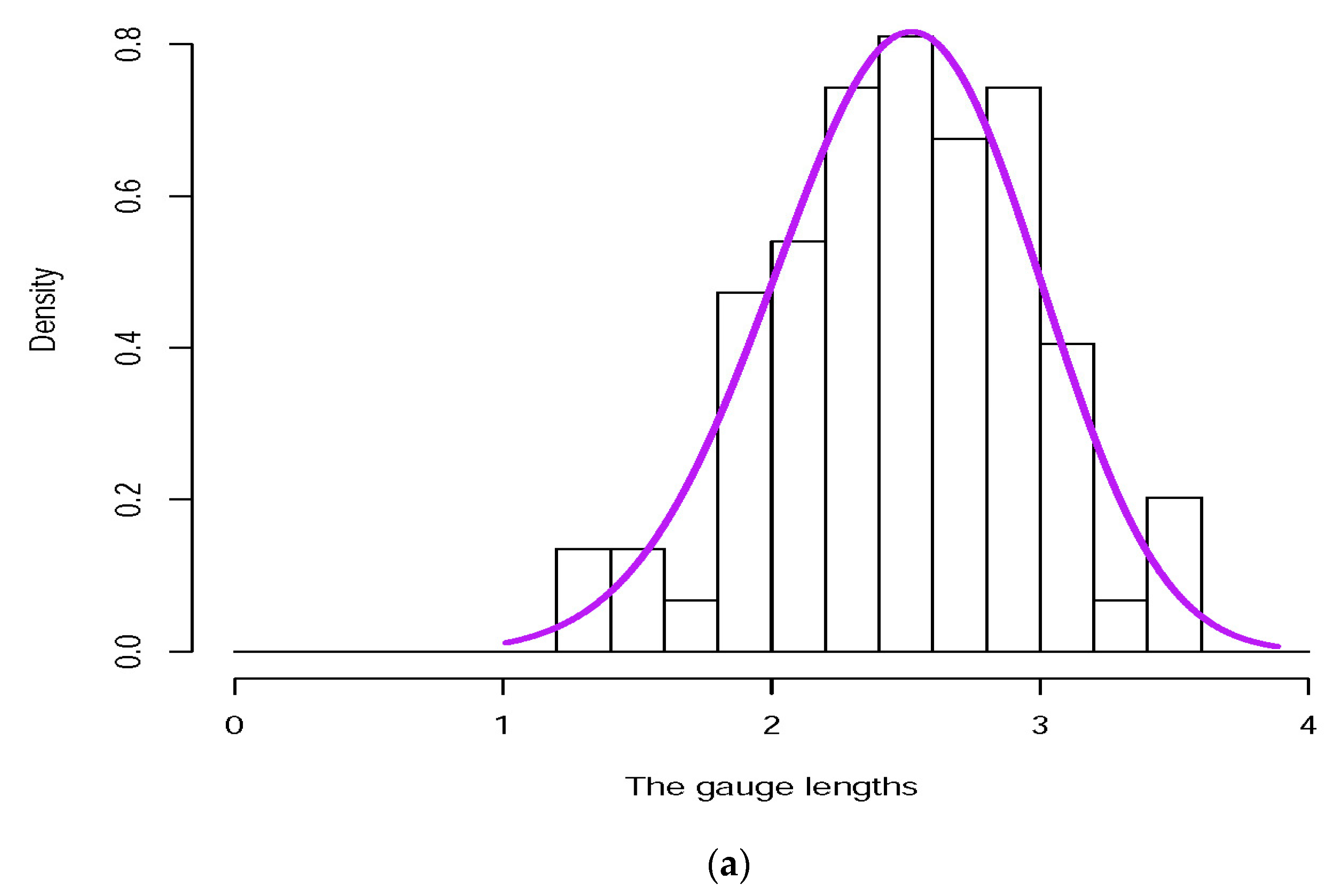
5.2. Application 2 The Gauge Lengths Data
6. Conclusions
- Bayesian and E-Bayesian estimation based on complete and different censoring schemes;
- Proposing a bivariate family of this model to extend the univariate case.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Petty, G.W.; Huang, W. The modified gamma size distribution applied to inhomogeneous and nonspherical particles: Key relationships and conversions. J. Atmos. Sci. 2011, 68, 1460–1473. [Google Scholar] [CrossRef]
- Belikov, A.V. The number of key carcinogenic events can be predicted from cancer incidence. Sci. Rep. 2017, 7, 12170. [Google Scholar] [CrossRef] [PubMed]
- Boland, P.J. Statistical and Probabilistic Methods in Actuarial Science; Chapman and Hall (CRC): Boca Raton, FL, USA, 2007. [Google Scholar]
- Aksoy, H. Use of gamma distribution in hydrological analysis. Turk. J. Eng. Environ. Sci. 2000, 24, 419–428. [Google Scholar]
- Wright, M.C.M.; Winter, I.M.; Forster, J.J.; Bleeck, S. Response to best-frequency tone bursts in the ventral cochlear nucleus is governed by ordered inter-spike interval statistics. Hear. Res. 2014, 317, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Williams, M.M.R. On the modified gamma distribution for representing the size spectra of coagulating aerosol particles. J. Colloid Interface Sci. 1985, 103, 516–527. [Google Scholar] [CrossRef]
- Ong, J.T.; Shan, Y.Y. Modified gamma model for Singapore rain drop size distribution. IGARSS’97. In Proceedings of the 1997 IEEE International Geoscience and Remote Sensing Symposium Proceedings. Remote Sensing—A Scientific Vision for Sustainable Development, Singapore, 3–8 August 1997; Volume 4, pp. 1757–1759. [Google Scholar]
- Muralidharan, K.; Kale, B.K. Modified gamma distribution with singularity at zero. Commun. Stat.-Simul. Comput. 2002, 31, 143–158. [Google Scholar] [CrossRef]
- Gebrenegus, G. The extended generalized gamma model and its special cases: Applications to modeling marriage durations. Qual. Quant. 2005, 39, 71–85. [Google Scholar]
- Nadarajah, S.; Gupta, A.K. The exponentiated gamma distribution with application to drought data. Calcutta Stat. Assoc. Bull. 2007, 59, 29–54. [Google Scholar] [CrossRef]
- Shawky, A.I.; Bakoban, R.A. Exponentiated gamma distribution: Different methods of estimations. J. Appl. Math. 2012, 2012, 284296. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Lima, M.S.; Gomes, A.E. The gamma extended Weibull distribution. J. Stat. Distrib. Appl. 2016, 5, 1–19. [Google Scholar] [CrossRef]
- Feroze, N.; Elbatal, I. Beta exponentiated gamma distribution: Some properties and estimation. Pak. J. Stat. Oper. Res. 2016, 12, 141–154. [Google Scholar] [CrossRef][Green Version]
- Barriga, G.D.; Cordeiro, G.M.; Dey, D.K.; Cancho, V.G.; Louzada, F.; Suzuki, A.K. The Marshall-Olkin generalized gamma distribution. Commun. Stat. Appl. Methods 2018, 25, 245–261. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Mead, M.; Nassar, M.M.; Dey, S. A generalization of generalized gamma distributions. Pak. J. Stat. Oper. Res. 2018, 14, 121–138. [Google Scholar] [CrossRef]
- Altun, E.; Korkmaz, M.C.; El-Morshedy, M.; Eliwa, M.S. The extended gamma distribution with regression model and applications. AIMS Math. 2021, 6, 2418–2439. [Google Scholar] [CrossRef]
- Saboor, A.; Rahman, G.; Ali, H.; Nisar, K.S.; Abdeljawad, T. Properties and Applications of a New Extended Gamma Function Involving Confluent Hypergeometric Function. J. Math. 2021, 2021, 2491248. [Google Scholar] [CrossRef]
- Lai, C.D.; Xie, M.; Murthy, D.N.P. A modified Weibull distribution. IEEE Trans. Reliab. 2003, 52, 33–37. [Google Scholar] [CrossRef]
- Lai, C.D.; Xie, M. Stochastic Ageing and Dependence for Reliability; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Feigl, P.; Zelen, M. Estimation of exponential survival probabilities with concomitant information. Biometrics 1965, 21, 826–838. [Google Scholar] [CrossRef] [PubMed]
- Alfaer, N.M.; Gemeay, A.M.; Aljohani, H.M.; Afify, A.Z. The extended log-logistic distribution: Inference and actuarial applications. Mathematics 2021, 9, 1386. [Google Scholar] [CrossRef]
- Afify, A.Z.; Cordeiro, G.M.; Shafique Butt, N.; Ortega, E.M.; Suzuki, A.K. A new lifetime model with variable shapes for the hazard rate. Braz. J. Probab. Stat. 2017, 31, 516–541. [Google Scholar] [CrossRef]

| Method | 80 | 150 | |||
|---|---|---|---|---|---|
| B | MSE | B | MSE | ||
| ML | 1.1, 0.01, 0.1 | 0.0086 | 0.04794 | 0.0054 | 0.02583 |
| 0.0046 | 0.00017 | 0.0021 | 0.00007 | ||
| −0.0009 | 0.00125 | 0.0003 | 0.00072 | ||
| 1, 0.1, 0.05 | 0.0681 | 0.10696 | 0.0219 | 0.04698 | |
| 0.0051 | 0.00191 | 0.0045 | 0.00093 | ||
| 0.0120 | 0.00212 | 0.0044 | 0.00079 | ||
| 2, 0.5, 0.01 | 0.7002 | 5.2393 | 0.3272 | 1.76903 | |
| 0.0495 | 0.06745 | 0.02533 | 0.03287 | ||
| 0.05366 | 0.02518 | 0.0201 | 0.00395 | ||
| QB | 1.1, 0.01, 0.1 | −0.0014 | 0.00492 | 0.0002 | 0.00403 |
| −0.000013 | |||||
| −0.00012 | |||||
| 1, 0.1, 0.05 | −0.0039 | 0.00328 | −0.0021 | 0.00032 | |
| −0.00038 | −0.0002 | ||||
| −0.00020 | −0.00010 | ||||
| 2, 0.5, 0.01 | −0.0054 | 0.01338 | 0.0009 | 0.01311 | |
| −0.0014 | 0.00087 | 0.00024 | 0.00081 | ||
| Method | 80 | 150 | |||
|---|---|---|---|---|---|
| B | MSE | B | MSE | ||
| LSE | 1.1, 0.01, 0.1 | −0.0475 | 0.0705 | −0.0190 | 0.03801 |
| 0.0091 | 0.00051 | 0.0044 | 0.00020 | ||
| −0.0052 | 0.00193 | −0.0020 | 0.00110 | ||
| 1, 0.1, 0.05 | 0.01710 | 0.16723 | 0.0089 | 0.09612 | |
| 0.0204 | 0.00534 | 0.0123 | 0.00241 | ||
| 0.0117 | 0.00363 | 0.0064 | 0.00189 | ||
| 2, 0.5, 0.01 | 0.1615 | 0.92601 | 0.1485 | 0.65873 | |
| 0.0299 | 0.02355 | 0.0167 | 0.01754 | ||
| 0.0112 | 0.00104 | 0.0089 | 0.00064 | ||
| AD | 1.1, 0.01, 0.1 | −0.0870 | 0.05139 | −0.0458 | 0.02675 |
| 0.0079 | 0.00030 | 0.0042 | 0.00013 | ||
| −0.0113 | 0.00132 | −0.0062 | 0.00078 | ||
| 1, 0.1, 0.05 | −0.0867 | 0.08498 | −0.0474 | 0.04829 | |
| 0.0266 | 0.00348 | 0.0133 | 0.00138 | ||
| −0.0042 | 0.00133 | −0.00211 | 0.00079 | ||
| 2, 0.5, 0.01 | −0.1091 | 0.85380 | −0.0697 | 0.59151 | |
| 0.0794 | 0.03572 | 0.0540 | 0.02315 | ||
| 0.0074 | 0.00112 | 0.0052 | 0.00058 | ||
| 65 | 156 | 100 | 134 | 16 | 108 | 121 | 4 | 39 | 143 |
| 56 | 26 | 22 | 1 | 1 | 5 | 65 |
| Model | AIC | BIC | K-S p-Value | CVM p-Value | AD p-Value | |||
|---|---|---|---|---|---|---|---|---|
| MG | 0.4225 | 0.0140 | 0.0013 | 175.67 | 178.17 | 0.1015 0.9948 | 0.0384 0.9459 | 0.2695 0.9588 |
| Gamma | 0.7716 | — | 0.0123 | 177.74 | 179.41 | 0.1464 0.8591 | 0.0758 0.7229 | 0.5217 0.7223 |
| LG | 0.8235 | 0.9319 | 0.0125 | 179.72 | 182.22 | 0.1466 0.8584 | 0.0785 0.7227 | 0.5197 0.7243 |
| EG | 0.6295 | 0.1839 | 0.0736 | 179.54 | 182.04 | 0.1437 0.8739 | 0.0678 0.7717 | 0.4690 0.7763 |
| MOG | 0.7761 | 1.1059 | 0.0131 | 179.61 | 182.11 | 0.1457 0.8630 | 0.0720 0.7458 | 0.5186 0.7254 |
| GEC | 0.4549 | 0.0125 | 0.00044 | 179.81 | 182.31 | 0.1444 0.8705 | 0.0680 0.7704 | 0.4658 0.7795 |
| 1.312 | 1.314 | 1.479 | 1.552 | 1.700 | 1.803 | 1.861 | 1.865 | 1.944 | 1.958 |
| 1.966 | 1.997 | 2.006 | 2.021 | 2.027 | 2.055 | 2.063 | 2.098 | 2.140 | 2.179 |
| 2.224 | 2.240 | 2.253 | 2.270 | 2.272 | 2.274 | 2.301 | 2.301 | 2.359 | 2.382 |
| 2.426 | 2.434 | 2.435 | 2.382 | 2.478 | 2.554 | 2.514 | 2.511 | 2.490 | 2.535 |
| 2.566 | 2.570 | 2.586 | 2.629 | 2.800 | 2.773 | 2.770 | 2.809 | 3.585 | 2.818 |
| 2.642 | 2.726 | 2.697 | 2.684 | 2.648 | 2.633 | 3.128 | 3.090 | 3.096 | 3.233 |
| 2.821 | 2.880 | 2.848 | 2.818 | 3.067 | 2.821 | 2.954 | 2.809 | 3.585 | 3.084 |
| 3.012 | 2.880 | 2.848 | 3.433 |
| Model | AIC | BIC | K-S p-Value | CVM p-Value | AD p-Value | |||
|---|---|---|---|---|---|---|---|---|
| MG | 5.3421 | 0.5058 | 0.5711 | 108.34 | 115.25 | 0.0582 0.9632 | 0.0265 0.9866 | 0.2087 0.9878 |
| Gamma | 24.2422 | — | 9.7858 | 110.33 | 114.94 | 0.0681 0.8821 | 0.0864 0.6570 | 0.5642 0.6818 |
| LG | 39.8512 | 0.5021 | 14.5259 | 110.76 | 117.67 | 0.0619 0.9387 | 0.0726 0.7368 | 0.4633 0.7839 |
| EG | 14.9782 | 3.9890 | 4.5242 | 109.49 | 116.41 | 0.0557 0.9758 | 0.0474 0.8932 | 0.3246 0.9183 |
| MOG | 9.7186 | 0.0000024 | 0.5383 | 115.17 | 122.08 | 0.0631 0.9301 | 0.0767 0.7124 | 0.6256 0.6235 |
| GEC | 24.2215 | 6.88 × 10−8 | 9.7771 | 112.33 | 119.24 | 0.0680 0.8830 | 0.0863 0.6577 | 0.5639 0.6822 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshehri, M.A.; Kayid, M. A Modified Gamma Model: Properties, Estimation, and Applications. Axioms 2023, 12, 262. https://doi.org/10.3390/axioms12030262
Alshehri MA, Kayid M. A Modified Gamma Model: Properties, Estimation, and Applications. Axioms. 2023; 12(3):262. https://doi.org/10.3390/axioms12030262
Chicago/Turabian StyleAlshehri, Mashael A., and Mohamed Kayid. 2023. "A Modified Gamma Model: Properties, Estimation, and Applications" Axioms 12, no. 3: 262. https://doi.org/10.3390/axioms12030262
APA StyleAlshehri, M. A., & Kayid, M. (2023). A Modified Gamma Model: Properties, Estimation, and Applications. Axioms, 12(3), 262. https://doi.org/10.3390/axioms12030262







