A Compound Class of Inverse-Power Muth and Power Series Distributions
Abstract
1. Introduction
2. The Model
2.1. Model Construction
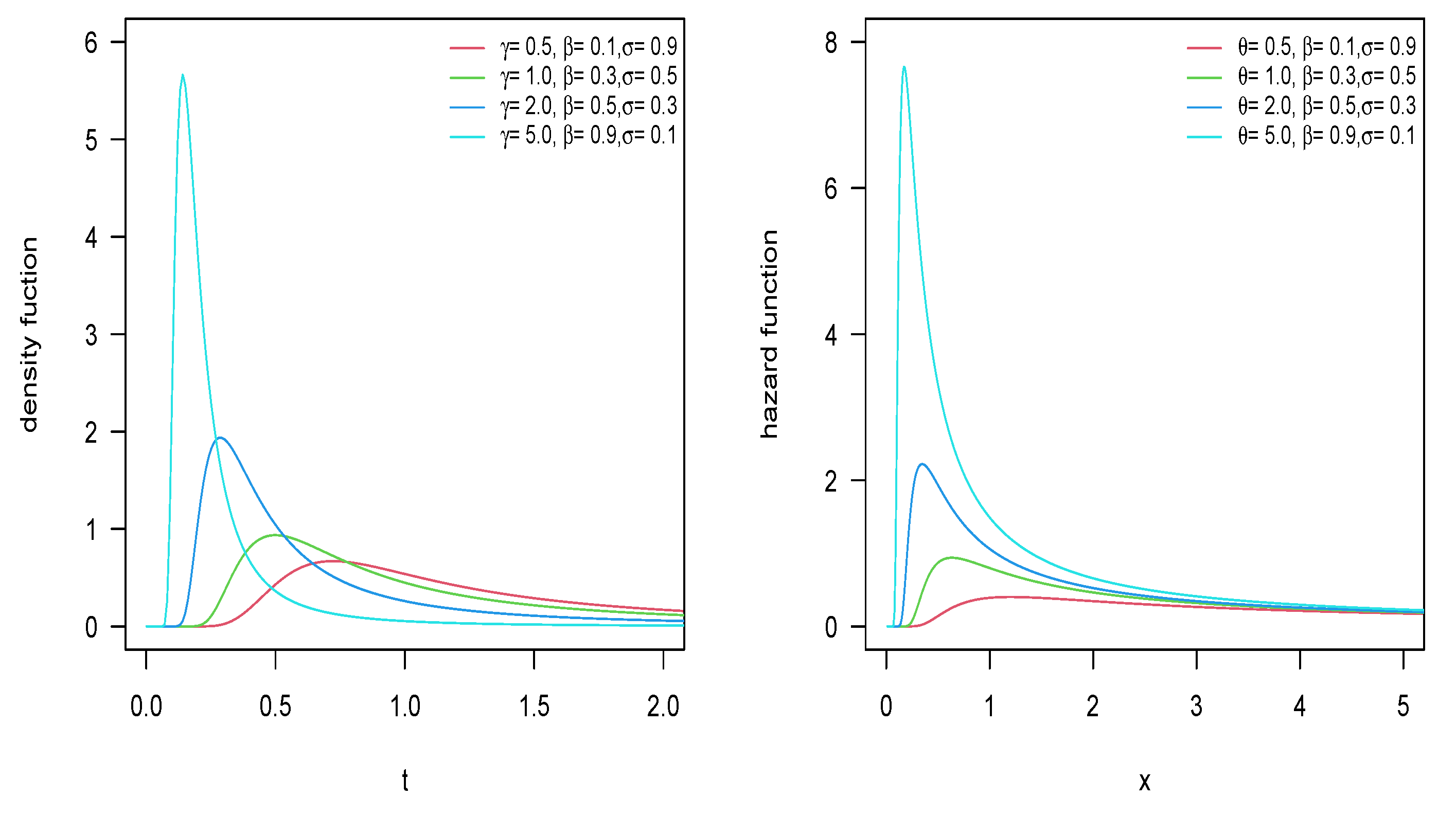
2.2. Model Properties
2.3. Shannon Entropy
2.4. Pseudo-Random Number Generator of the Model
| Algorithm 1 Simulating values of the IPM-PS model |
|
3. Parameter Estimation
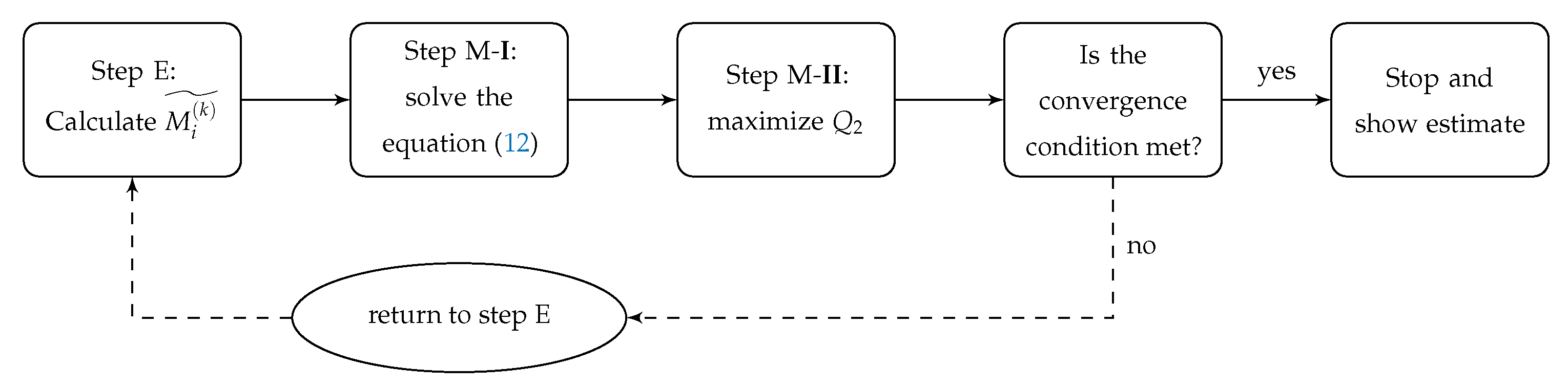
EM Algorithm
- E step: For , define and calculate:
- step M-I: is updated as the solution of the non-linear equationwhere is the sum of the elements of .
- step M-II: Given the vector , update by maximizingin relation to each of the parameters.
- If the convergence condition is reached, the algorithm stops. Otherwise, we return to step E for a new iteration.
4. Simulation Study
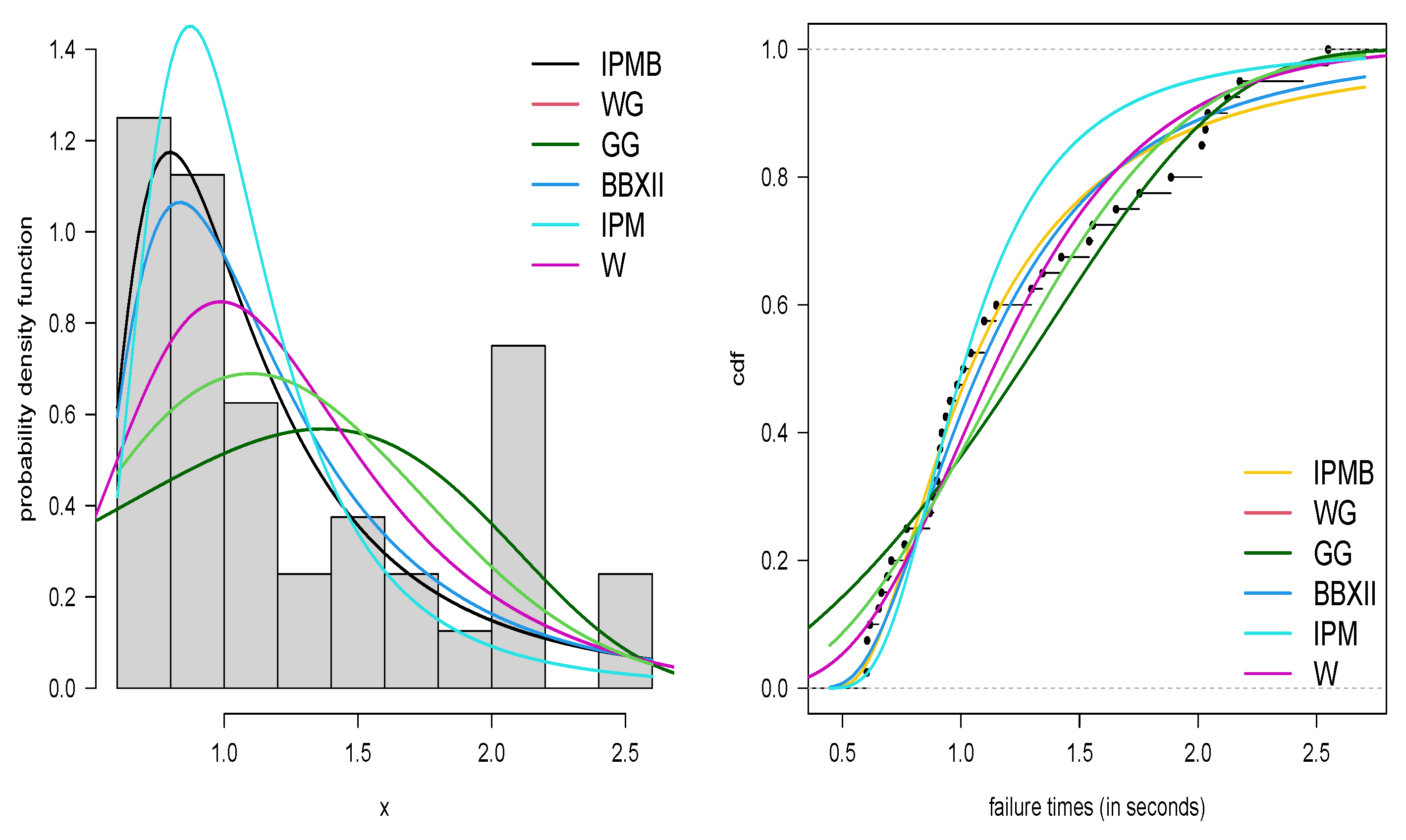
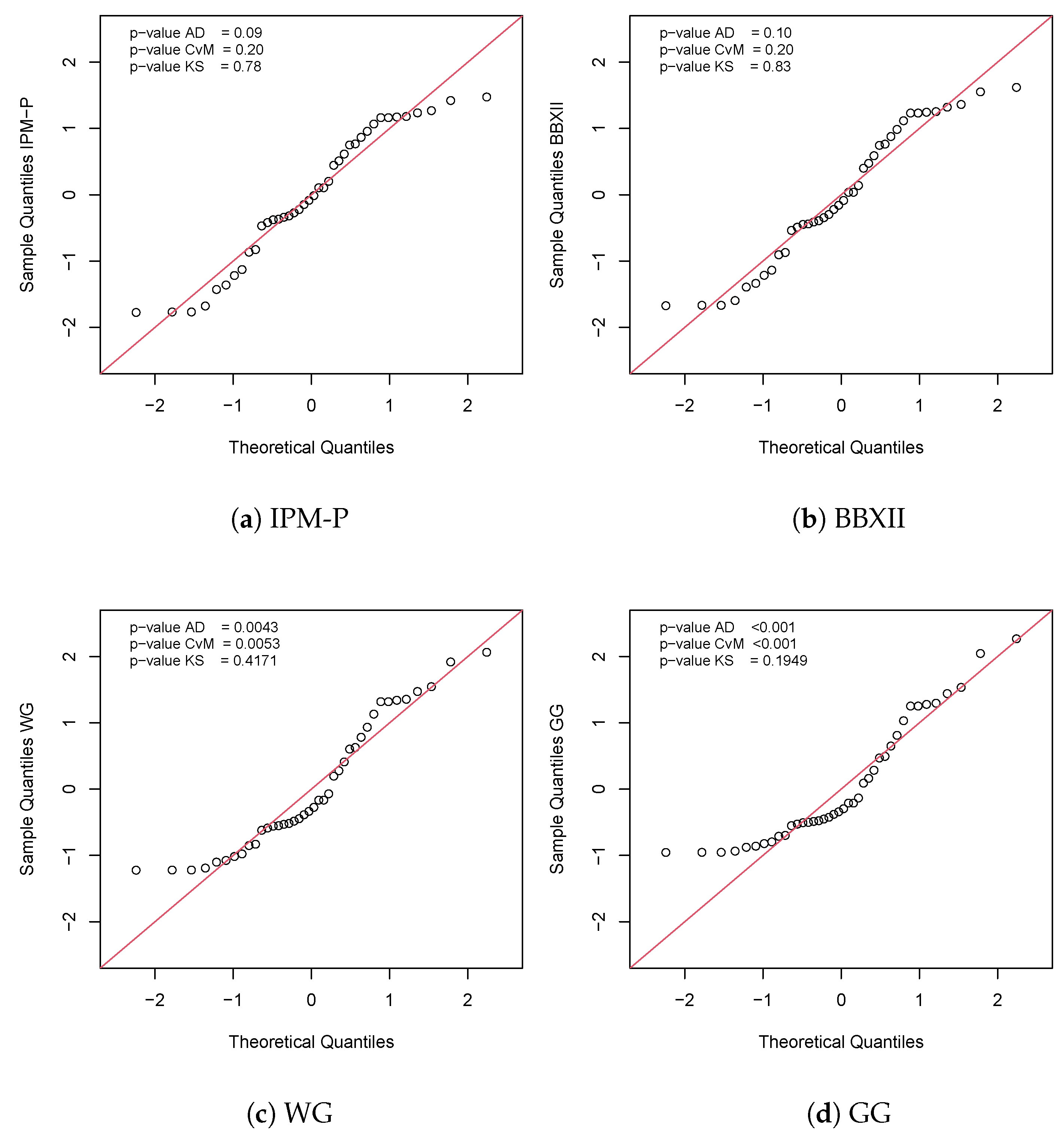
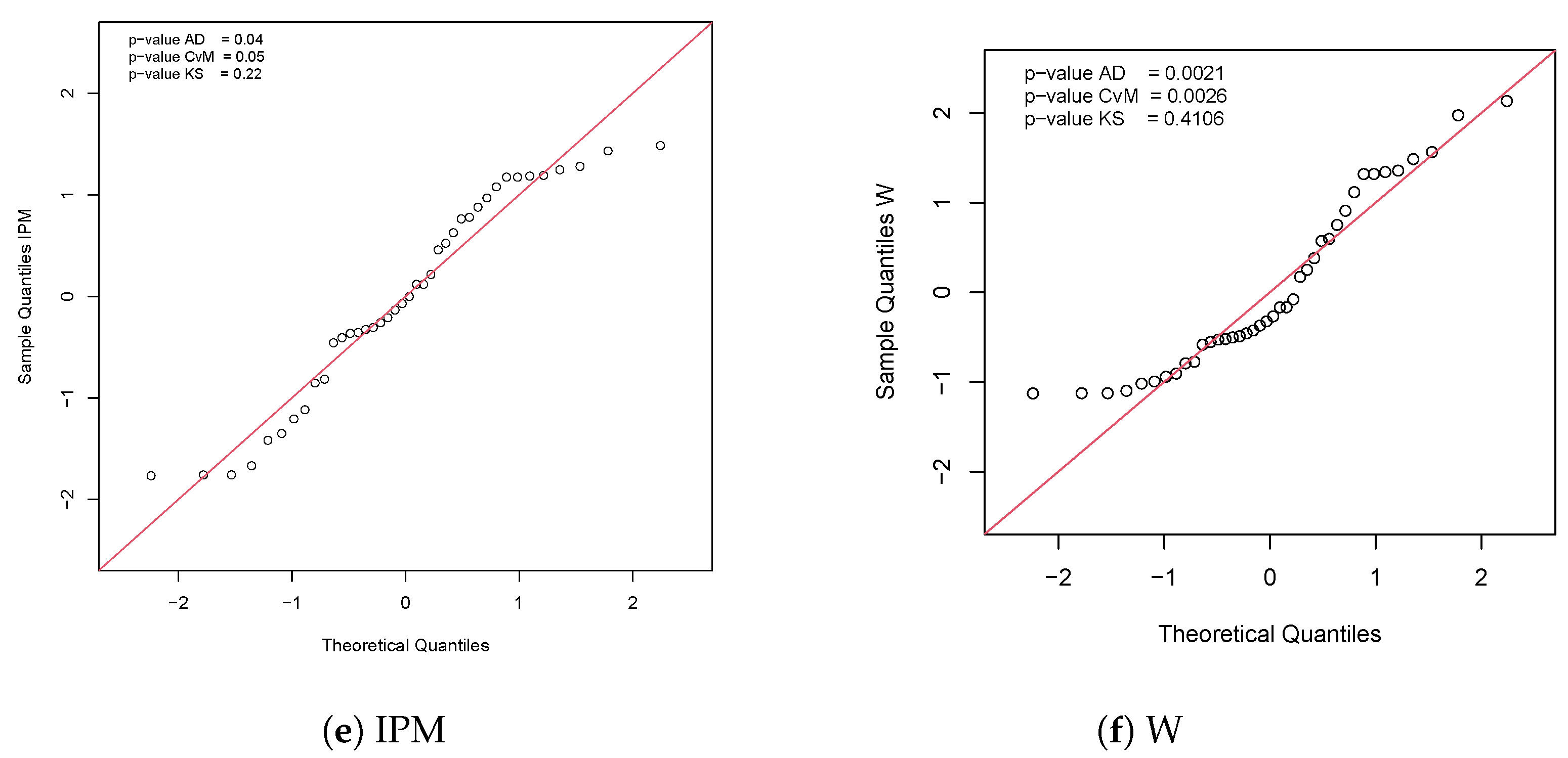
5. Applications
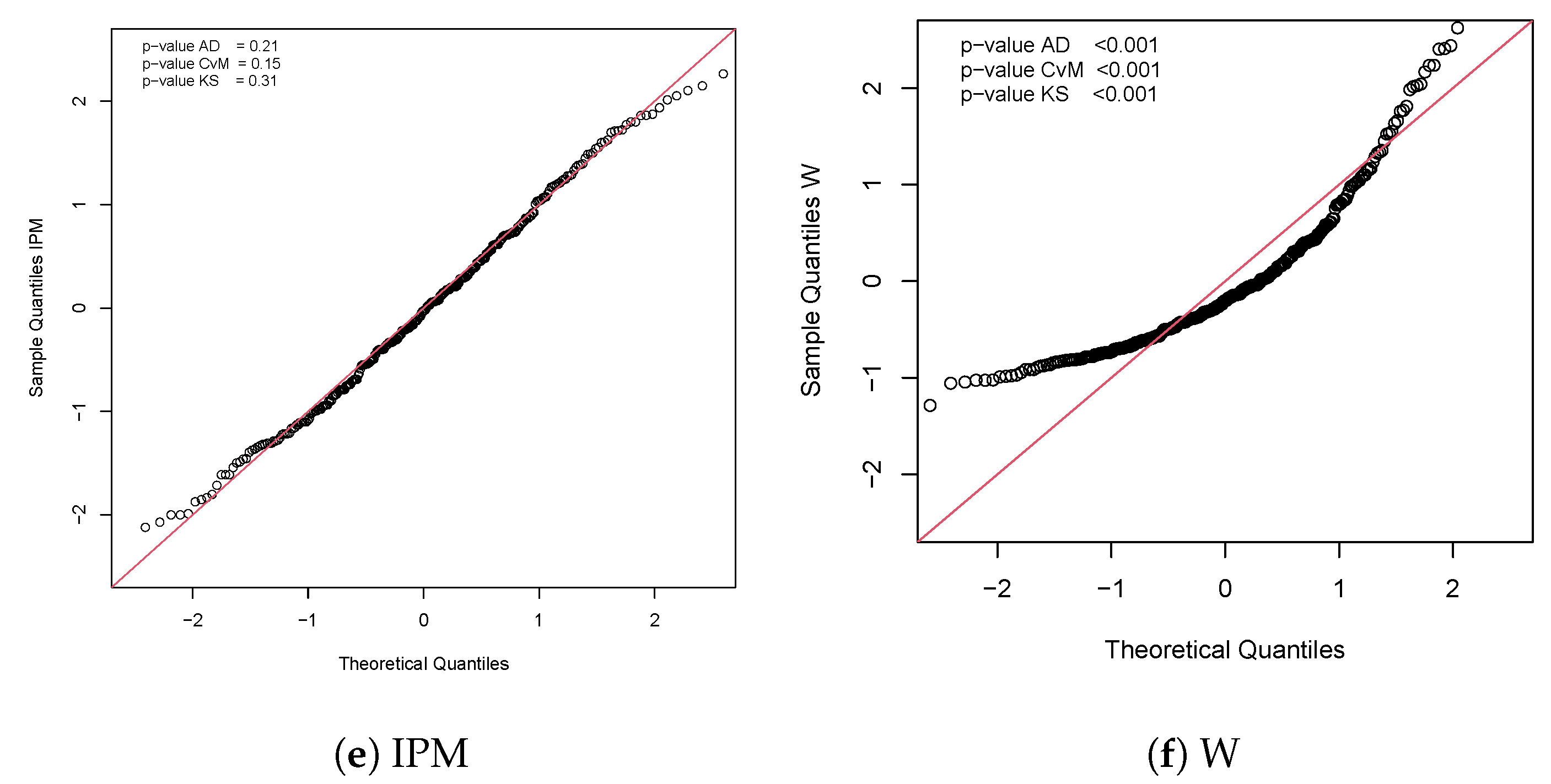
5.1. Application 1
5.2. Application 2
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
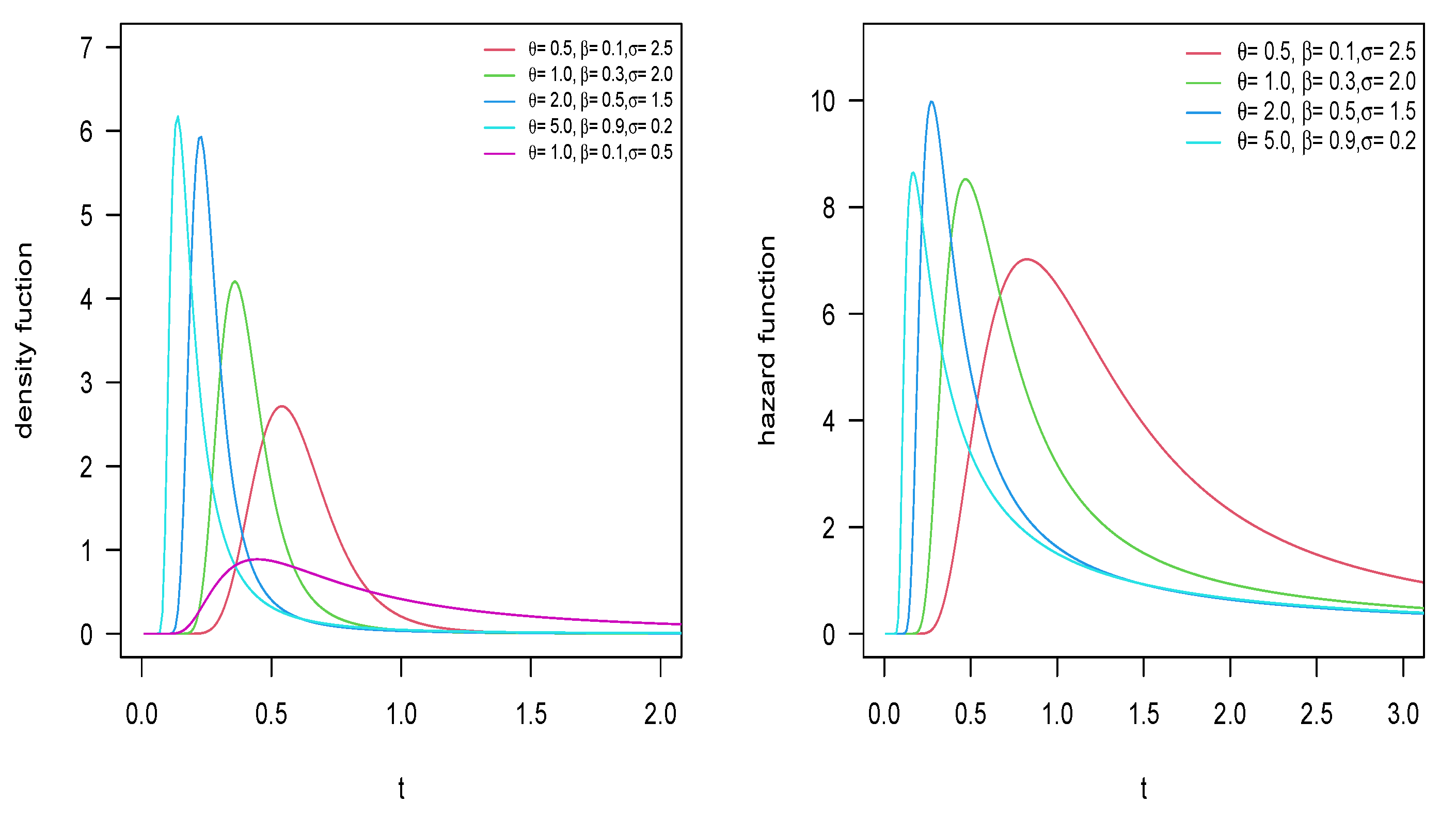
Appendix A. Additional Plots

Appendix B. Explicit form for the Integral in u(r) of r-th Moment of the IPM- PS
Appendix C. Explicit form for the Integral in Equation (9) for the Shannon Entropy
Appendix D. Inverse and Derivatives of A(·)
Appendix E. Oakes’ Method for the IMP-PS Distribution
Appendix E.1. Double Derivatives of the Function Q in Relation to the Parameters ζ
Appendix E.2. Double Derivatives of Function Q in Relation to Parameters and Expectation Mi
Appendix F. PDF of Distributions Used in Applications
References
- Mahmoudi, E.; Jafari, A.A. The compound class of linear failure rate-power series distributions: Model, properties, and applications. Commun.-Stat.-Simul. Comput. 2017, 46, 1414–1440. [Google Scholar] [CrossRef]
- Silva, R.B.; Bourguignon, M.; Dias, C.R.; Cordeiro, G.M. The compound class of extended Weibull power series distributions. Comput. Stat. Data Anal. 2013, 58, 352–367. [Google Scholar] [CrossRef]
- Jafari, A.A.; Tahmasebi, S. Gompertz-power series distributions. Commun.-Stat.-Theory Methods 2016, 45, 3761–3781. [Google Scholar] [CrossRef]
- Silva, R.B.; Cordeiro, G.M. The Burr XII power series distributions: A new compounding family. Braz. J. Probab. Stat. 2015, 29, 565–589. [Google Scholar] [CrossRef]
- Shafiei, S.; Darijani, S.; Saboori, H. Inverse Weibull power series distributions: Properties and applications. J. Stat. Comput. Simul. 2016, 86, 1069–1094. [Google Scholar] [CrossRef]
- Elbatal, I.; Zayedm, M.; Rasekhi, M. The Exponential Pareto Power Series Distribution: Theory and Applications. Pak. J. Stat. Oper. Res. 2017, 13, 603–615. [Google Scholar] [CrossRef]
- Shekari, M.; Zamani, H.; Saber, M.M. The compound class of Janardan-power series distributions: Properties and applications. J. Data Sci. 2019, 17, 259–278. [Google Scholar] [CrossRef]
- Jordanova, P.; Petrova, M.; Stehlik, M. Compound power series distribution with negative multinomial summands: Characterisation and risk process. Revstat 2020, 18, 47–69. [Google Scholar]
- Elbatal, I.; Altun, E.; Afify, A.Z.; Ozel, G. The Generalized Burr XII Power Series Distributions with Properties and Applications. Ann. Data Sci. 2019, 6, 571–597. [Google Scholar] [CrossRef]
- Rivera, P.A.; Calderín-Ojeda, E.; Gallardo, D.I.; Gómez, H.W. A Compound Class of the Inverse Gamma and Power Series Distributions. Symmetry 2021, 13, 1328. [Google Scholar] [CrossRef]
- Shakhatreh, M.K.; Dey, S.; Kumar, D. Inverse Lindley power series distributions: A new compounding family and regression model with censored data. J. Appl. Stat. 2022, 49, 3451–3476. [Google Scholar] [CrossRef]
- Hassan, A.S.; Almetwally, E.M.; Gamoura, S.C.; Metwally, A.S. Inverse Exponentiated Lomax Power Series Distribution: Model, Estimation, and Application. J. Math. 2022, 2022, 1998653. [Google Scholar] [CrossRef]
- Aldahlan, M.A.; Jamal, F.; Chesneau, C.; Elbatal, I.; Elgarhy, M. Exponentiated power generalized Weibull power series family of distributions: Properties, estimation and applications. PLoS ONE 2020, 15, e0230004. [Google Scholar] [CrossRef]
- Chesneau, C.; Agiwal, V. Statistical theory and practice of the inverse power Muth distribution. J. Comput. Math. Data Sci. 2021, 1, 100004. [Google Scholar] [CrossRef]
- Noak, A. A class of random variable with discrete distribution. Ann. Inst. Stat. Math. 1950, 21, 127–132. [Google Scholar] [CrossRef]
- Jodrá, P.; Gómez, H.W.; Jiménez-Gamero, M.D.; Alba-Fernández, M.V. The power muth distribution. Math. Model. Anal. 2017, 22, 186–201. [Google Scholar] [CrossRef]
- Muth, E.J. Reliability models with positive memory derived from the mean residual life function. Theory Appl. Reliab. 1977, 2, 401–435. [Google Scholar]
- Singh, S.V.; Elgarhy, M.; Ahmad, Z.; Sharma, V.K.; Hamedani, G.G. New Class of Probability Distributions Arising from Teissier Distribution. In Mathematical Modeling, Computational Intelligence Techniques, and Renewable Energy. Advances in Intelligent Systems and Computing; Springer: Singapore, 2021; Volume 1287. [Google Scholar]
- Abdullah, A.M.; Elgarhy, M. A new Muth generated family of distributions with applications. J. Nonlinear Sci. Appl. 2018, 11, 1171–1184. [Google Scholar]
- Almarashi, M.; Jamal, F.; Chesneau, C.; Elgarhy, M. A new truncated Muth generated family of distributions with applications. Complexity 2021, 2021, 1211526. [Google Scholar] [CrossRef]
- Georg, M. LambertW: An R package for Lambert W x F Random Variables. In R Package Version 0.6.6.; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J.R. Stat. Soc. Ser. 1977, 39, 1–22. [Google Scholar]
- Oakes, D. Direct calculation of the information matrix via the EM algorithm. J.R. Stat. Soc. 1999, 61, 479–482. [Google Scholar] [CrossRef]
- Raqab, M.Z.; Kundu, D.; Al-Awadhi, F.A. Compound zero-truncated Poisson normal distribution and its applications. Commun.-Stat.-Theory Methods 2021, 50, 3030–3050. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Technol. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Gallardo, D.I.; Romeo, J.S.; Meyer, R. A simplified estimation procedure based on the EM algorithm for the power series cure rate model. Commun. Stat.-Simul. Comput. 2017, 46, 6342–6359. [Google Scholar] [CrossRef]
- Jo, S.; Choi, T.; Park, B.; Lenk, P. bsamGP: An R Package for Bayesian Spectral Analysis Models Using Gaussian Process Priors. J. Stat. Softw. 2019, 90, 1–41. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 3 March 2023).
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 1, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Dunn, P.K.; Smyth, G.K. Randomized quantile residuals. J. Comput. Graph. Stat. 1996, 5, 236–244. [Google Scholar]
- Murthy, D.P.; Xie, M.; Jiang, R. Weibull Models; Wiley & Sons, Incorporated, John: Hoboken, NJ, USA, 2003. [Google Scholar]
- Vásquez, J.K.J.; Rodrigues, J.; Balakrishnan, N. A useful variance decomposition for destructive Waring regression cure model with an application to HIV data. Commun. Stat.-Theory Methods 2022, 51, 6978–6989. [Google Scholar] [CrossRef]
- Azimi, R.; Esmailian, M.; Gallardo, D.I.; Gómez, H.J. A New Cure Rate Model Based on Flory–Schulz Distribution: Application to the Cancer Data. Mathematics 2022, 10, 4643. [Google Scholar] [CrossRef]
- Conway, R.W.; Maxwell, W.L. A queuing model with state dependent services rates. J. Ind. Eng. 1962, 12, 132–136. [Google Scholar]
- Consul, P.C.; Famoye, F. Lagrangian Probability Distributions; Birkhäuser: Boston, MA, USA, 2006. [Google Scholar]



| Distribution | Notation | |||
|---|---|---|---|---|
| Geometric | Geo | 1 | ||
| Poisson | Po | |||
| Bell | Be | |||
| Logarithmic | Lo |
| IPM-G | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (0.1;−1) | (0.2;−1) | (0.5;−1) | (0.1;0.5) | (0.2;0.5) | (0.5;0.5) | (0.1;1) | (0.2;1) | (0.5;1) | |
| 1.4953 | 1.3291 | 0.8307 | 1.0860 | 0.9654 | 0.6034 | 0.9569 | 0.8505 | 0.5316 | |
| 3.7277 | 3.3135 | 2.0710 | 1.7405 | 1.5471 | 0.9670 | 1.0671 | 0.9485 | 0.5928 | |
| V | 1.4919 | 1.5470 | 1.3809 | 0.5611 | 0.6152 | 0.6029 | 0.1515 | 0.2251 | 0.3102 |
| IPM-L | |||||||||
| 1.5769 | 1.4891 | 1.1984 | 1.1453 | 1.0815 | 0.8705 | 1.0091 | 0.9529 | 0.7669 | |
| 3.9312 | 3.7123 | 2.9878 | 1.8355 | 1.7333 | 1.3950 | 1.1253 | 1.0627 | 0.8553 | |
| V | 1.4447 | 1.4950 | 1.5515 | 0.5238 | 0.5636 | 0.6373 | 0.1070 | 0.1546 | 0.2671 |
| IPM-P | |||||||||
| (0.1;−1) | (0.5;−1) | (2;−1) | (0.1;0.5) | (0.5;0.5) | (2;0.5) | (0.1;1) | (0.5;1) | (2;1) | |
| 1.5797 | 1.2805 | 0.5201 | 1.1474 | 0.9301 | 0.3777 | 1.0109 | 0.8194 | 0.3328 | |
| 3.9383 | 3.1924 | 1.2966 | 1.8388 | 1.4906 | 0.6054 | 1.1273 | 0.9138 | 0.3711 | |
| V | 1.4428 | 1.5527 | 1.0261 | 0.5224 | 0.6255 | 0.4627 | 0.1054 | 0.2423 | 0.2604 |
| IPM-B | |||||||||
| 1.4981 | 0.9098 | 0.0056 | 1.0881 | 0.6608 | 0.0041 | 0.9587 | 0.5822 | 0.0036 | |
| 3.7348 | 2.2681 | 0.0139 | 1.7438 | 1.0590 | 0.0065 | 1.0691 | 0.6492 | 0.0040 | |
| V | 1.4905 | 1.4404 | 0.0139 | 0.5599 | 0.6224 | 0.0065 | 0.1500 | 0.3103 | 0.0040 |
| True Value | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bias | RMSE | SE | CP | bias | RMSE | SE | CP | bias | RMSE | SE | CP | ||||
| 0.5 | 1 | 0.5 | −0.0783 | 0.2152 | 0.7088 | 0.9310 | −0.0516 | 0.1879 | 0.5608 | 0.9570 | −0.0270 | 0.1543 | 0.3481 | 0.9660 | |
| 0.1415 | 0.3005 | 0.3507 | 0.9830 | 0.0851 | 0.2266 | 0.3132 | 0.9770 | 0.0366 | 0.1552 | 0.2365 | 0.9600 | ||||
| 0.0542 | 0.1328 | 0.3841 | 0.9990 | 0.0315 | 0.0887 | 0.2806 | 0.9700 | 0.0115 | 0.0490 | 0.1764 | 0.9660 | ||||
| −0.0336 | 0.1055 | 0.5604 | 0.9990 | −0.0156 | 0.0583 | 0.4467 | 0.9870 | −0.0012 | 0.0152 | 0.2789 | 0.9700 | ||||
| 0.2 | 0.0432 | 0.2111 | 0.7731 | 0.9770 | 0.0404 | 0.1643 | 0.5337 | 0.9710 | 0.0244 | 0.1133 | 0.4813 | 0.9650 | |||
| 0.0291 | 0.2075 | 0.3240 | 0.9870 | 0.0036 | 0.1581 | 0.2447 | 0.9710 | −0.0144 | 0.1000 | 0.2726 | 0.9660 | ||||
| 0.0717 | 0.1825 | 0.3119 | 0.9800 | 0.0427 | 0.1368 | 0.2091 | 0.9770 | 0.0049 | 0.0633 | 0.1412 | 0.9660 | ||||
| −0.0824 | 0.1625 | 0.7174 | 0.9800 | −0.0530 | 0.1189 | 0.5045 | 0.9770 | −0.0118 | 0.0438 | 0.4565 | 0.9600 | ||||
| 0.1 | 0.0318 | 0.3060 | 0.7434 | 0.9910 | 0.0370 | 0.1503 | 0.5364 | 0.9820 | 0.0224 | 0.0873 | 0.3129 | 0.9740 | |||
| 0.0220 | 0.1894 | 0.3427 | 0.9900 | −0.0004 | 0.1342 | 0.1942 | 0.9820 | −0.0149 | 0.0793 | 0.1091 | 0.9690 | ||||
| 0.1113 | 0.2970 | 0.2888 | 0.9950 | 0.0495 | 0.1596 | 0.2069 | 0.9910 | 0.0049 | 0.0714 | 0.1289 | 0.9790 | ||||
| −0.1054 | 0.1927 | 0.8066 | 0.9850 | −0.0620 | 0.1356 | 0.5439 | 0.9810 | −0.0157 | 0.0545 | 0.3312 | 0.9740 | ||||
| −0.2 | −0.0930 | 0.5089 | 0.9152 | 0.9920 | −0.3430 | 0.3655 | 0.6773 | 0.8670 | −0.0577 | 0.1943 | 0.4614 | 0.9770 | |||
| −0.0131 | 0.1356 | 0.5921 | 0.9820 | −0.0122 | 0.0952 | 0.4580 | 0.9770 | −0.0102 | 0.0600 | 0.1467 | 0.9690 | ||||
| 0.1882 | 0.5432 | 0.3252 | 0.9870 | 0.6742 | 0.5457 | 0.2439 | 0.9790 | 0.0299 | 0.1385 | 0.1670 | 0.9670 | ||||
| −0.0843 | 0.2032 | 1.5664 | 0.9870 | −0.0321 | 0.1230 | 1.2458 | 0.9790 | −0.0027 | 0.0490 | 0.6344 | 0.9690 | ||||
| 2 | 0.5 | −0.0806 | 0.2093 | 0.6795 | 0.9480 | −0.0514 | 0.1836 | 0.5117 | 0.9580 | −0.0259 | 0.1457 | 0.3659 | 0.9640 | ||
| 0.1295 | 0.3017 | 0.3595 | 0.9480 | 0.0793 | 0.2278 | 0.2954 | 0.9570 | 0.0306 | 0.1502 | 0.2486 | 0.9610 | ||||
| 0.0753 | 0.3383 | 0.3635 | 0.9810 | 0.0493 | 0.2218 | 0.2676 | 0.9770 | 0.0130 | 0.1080 | 0.1768 | 0.9640 | ||||
| −0.0298 | 0.1464 | 1.0769 | 0.9710 | −0.0147 | 0.0859 | 0.8224 | 0.9680 | −0.0026 | 0.0273 | 0.5823 | 0.9610 | ||||
| 0.2 | 0.0740 | 0.2136 | 0.7317 | 0.9840 | 0.0601 | 0.1733 | 0.5319 | 0.9720 | 0.0357 | 0.1092 | 0.3357 | 0.9620 | |||
| −0.0043 | 0.2099 | 0.3093 | 0.9940 | −0.0331 | 0.1597 | 0.2420 | 0.9800 | −0.0301 | 0.0960 | 0.1545 | 0.9773 | ||||
| 0.1360 | 0.4811 | 0.2876 | 0.9990 | 0.0386 | 0.3577 | 0.2110 | 0.9840 | 0.0117 | 0.1953 | 0.1302 | 0.9730 | ||||
| −0.1161 | 0.2187 | 1.3044 | 0.9890 | −0.0635 | 0.1622 | 1.0014 | 0.9810 | −0.0307 | 0.0906 | 0.6472 | 0.9790 | ||||
| 0.1 | 0.0607 | 0.2558 | 0.7508 | 0.9820 | 0.0583 | 0.1669 | 0.5352 | 0.9750 | 0.0319 | 0.0834 | 0.3194 | 0.9610 | |||
| −0.0236 | 0.1883 | 0.2961 | 0.9880 | −0.0389 | 0.1417 | 0.1934 | 0.9850 | −0.0369 | 0.0802 | 0.1125 | 0.9770 | ||||
| 0.1271 | 0.5441 | 0.2831 | 0.9900 | 0.0454 | 0.3748 | 0.2013 | 0.9850 | −0.0184 | 0.2258 | 0.1271 | 0.9710 | ||||
| −0.1214 | 0.2400 | 1.4822 | 0.9900 | −0.0758 | 0.1800 | 1.0671 | 0.9850 | −0.0251 | 0.1043 | 0.6699 | 0.9700 | ||||
| True Value | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bias | RMSE | SE | CP | bias | RMSE | SE | CP | bias | RMSE | SE | CP | ||||
| 0.5 | 1 | 0.5 | −0.0622 | 0.2006 | 1.9905 | 0.9560 | −0.0363 | 0.1847 | 1.6212 | 0.9370 | −0.0024 | 0.1493 | 1.2423 | 0.9250 | |
| 0.0651 | 0.2493 | 0.3158 | 0.9810 | 0.0375 | 0.1969 | 0.2600 | 0.9750 | 0.0091 | 0.1452 | 0.2192 | 0.9640 | ||||
| −0.0147 | 0.1516 | 0.3144 | 0.9950 | −0.0107 | 0.1141 | 0.2390 | 0.9880 | −0.0007 | 0.0612 | 0.1604 | 0.9600 | ||||
| 0.2062 | 0.6869 | 0.3978 | 0.9970 | 0.1358 | 0.4748 | 0.3247 | 0.9860 | 0.0308 | 0.2132 | 0.2472 | 0.9790 | ||||
| 1 | 1 | 0.5 | −0.0671 | 0.2085 | 1.9345 | 0.9780 | −0.0362 | 0.1757 | 1.5427 | 0.9680 | −0.0047 | 0.1427 | 1.1113 | 0.9630 | |
| 0.1230 | 0.2947 | 0.3180 | 0.9720 | 0.0747 | 0.2279 | 0.2599 | 0.9670 | 0.0300 | 0.1518 | 0.2044 | 0.9610 | ||||
| 0.0477 | 0.1797 | 0.3475 | 0.9990 | 0.0318 | 0.1319 | 0.2552 | 0.9890 | 0.0232 | 0.0788 | 0.1712 | 0.9750 | ||||
| −0.0689 | 0.7308 | 0.3882 | 0.9860 | −0.0660 | 0.5294 | 0.3077 | 0.9800 | −0.0733 | 0.2831 | 0.2201 | 0.9700 | ||||
| 2 | 1 | 0.5 | −0.0498 | 0.2110 | 1.9715 | 0.9890 | −0.0269 | 0.1836 | 1.4665 | 0.9790 | 0.0140 | 0.1499 | 0.9608 | 0.9620 | |
| 0.2355 | 0.4180 | 0.3275 | 0.9850 | 0.1689 | 0.3203 | 0.2734 | 0.9770 | 0.0789 | 0.2077 | 0.2061 | 0.9660 | ||||
| 0.1628 | 0.2579 | 0.4444 | 0.9910 | 0.1314 | 0.2060 | 0.3156 | 0.9800 | 0.0900 | 0.1405 | 0.2010 | 0.9690 | ||||
| −0.6167 | 1.0444 | 0.3925 | 0.9870 | −0.5380 | 0.8661 | 0.2884 | 0.9700 | −0.4140 | 0.6041 | 0.1868 | 0.9680 | ||||
| 0.2 | 0.0313 | 0.2495 | 2.3864 | 0.9870 | 0.0317 | 0.1588 | 1.8656 | 0.9750 | 0.0166 | 0.0944 | 1.1976 | 0.9690 | |||
| −0.0124 | 0.1935 | 0.3168 | 0.9740 | −0.0226 | 0.1509 | 0.2235 | 0.9640 | −0.0148 | 0.0916 | 0.1374 | 0.9600 | ||||
| −0.0050 | 0.2085 | 0.2938 | 0.9920 | −0.0132 | 0.1564 | 0.2118 | 0.9840 | −0.0053 | 0.0944 | 0.1310 | 0.9710 | ||||
| 0.0839 | 0.7085 | 0.6032 | 0.9760 | 0.0707 | 0.6137 | 0.4598 | 0.9690 | 0.0243 | 0.3381 | 0.2975 | 0.9600 | ||||
| 0.1 | −0.0712 | 2.0289 | 0.5630 | 0.9980 | 0.0211 | 0.4026 | 1.8901 | 0.9860 | 0.0226 | 0.0769 | 1.2122 | 0.9750 | |||
| −0.0311 | 0.1827 | 1.5422 | 0.9890 | −0.0362 | 0.1445 | 0.2628 | 0.9630 | −0.0223 | 0.0838 | 0.1108 | 0.9600 | ||||
| 0.1051 | 2.3623 | 0.2907 | 0.9860 | −0.0180 | 0.4423 | 0.2134 | 0.9720 | −0.0124 | 0.1098 | 0.1326 | 0.9630 | ||||
| 0.1186 | 0.8074 | 2.1261 | 0.9930 | 0.1449 | 0.7578 | 0.5784 | 0.9820 | 0.0339 | 0.4028 | 0.3221 | 0.9720 | ||||
| −0.2 | −0.4583 | 9.7743 | 2.7164 | 0.9830 | −0.4739 | 12.7700 | 2.1530 | 0.9730 | −0.0805 | 0.3246 | 1.5611 | 0.9640 | |||
| −0.0713 | 0.1657 | 0.8047 | 0.9920 | −0.0574 | 0.1282 | 0.5628 | 0.9700 | −0.0297 | 0.0823 | 0.2070 | 0.9640 | ||||
| 1.9332 | 44.2624 | 0.2751 | 0.9810 | 0.6835 | 19.8681 | 0.2140 | 0.9750 | 0.0041 | 0.3105 | 0.1543 | 0.9670 | ||||
| 0.4587 | 1.1872 | 1.5392 | 0.9350 | 0.3772 | 0.9874 | 1.1873 | 0.9480 | 0.2001 | 0.6025 | 0.5607 | 0.9680 | ||||
| 2 | 0.5 | −0.0590 | 0.2046 | 1.9976 | 0.9990 | −0.0304 | 0.1798 | 1.6217 | 0.9970 | −0.0080 | 0.1471 | 1.2477 | 0.9780 | ||
| 0.0573 | 0.2482 | 0.3209 | 0.9720 | 0.0264 | 0.1917 | 0.2614 | 0.9660 | 0.0030 | 0.1434 | 0.2185 | 0.9640 | ||||
| −0.0344 | 0.3092 | 0.3113 | 0.9710 | −0.0322 | 0.2375 | 0.2369 | 0.9630 | −0.0191 | 0.1419 | 0.1599 | 0.9600 | ||||
| 0.1937 | 0.6670 | 0.7954 | 0.9920 | 0.1345 | 0.4885 | 0.6508 | 0.9910 | 0.0442 | 0.2692 | 0.4960 | 0.9960 | ||||
| 0.2 | 0.0340 | 0.2413 | 2.4225 | 0.9990 | 0.0386 | 0.1560 | 1.8048 | 0.9970 | 0.0244 | 0.1040 | 1.2031 | 0.9750 | |||
| −0.0328 | 0.1934 | 0.3199 | 0.9900 | −0.0439 | 0.1442 | 0.2199 | 0.9800 | −0.0426 | 0.0997 | 0.1404 | 0.9750 | ||||
| −0.0440 | 0.4214 | 0.2895 | 0.9760 | −0.0698 | 0.3155 | 0.2063 | 0.9660 | −0.0712 | 0.2201 | 0.1306 | 0.9600 | ||||
| 0.1083 | 0.7683 | 1.2248 | 0.9900 | 0.0881 | 0.6356 | 0.8844 | 0.9890 | 0.0750 | 0.4350 | 0.5925 | 0.9770 | ||||
| 0.1 | 0.0424 | 0.3420 | 2.5115 | 0.9950 | 0.0432 | 0.1536 | 1.8904 | 0.9840 | 0.0251 | 0.0815 | 1.2635 | 0.9760 | |||
| −0.0544 | 0.1891 | 0.3697 | 0.9890 | −0.0615 | 0.1495 | 0.1969 | 0.9780 | −0.0453 | 0.0904 | 0.1155 | 0.9620 | ||||
| −0.0891 | 0.5873 | 0.2878 | 0.9760 | −0.1124 | 0.3823 | 0.2082 | 0.9690 | −0.0837 | 0.2395 | 0.1376 | 0.9600 | ||||
| 0.1957 | 0.9359 | 1.4253 | 0.9770 | 0.1527 | 0.7494 | 0.9803 | 0.9700 | 0.0904 | 0.4559 | 0.6600 | 0.9600 | ||||
| True Value | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bias | RMSE | SE | CP | bias | RMSE | SE | CP | bias | RMSE | SE | CP | ||||
| 0.5 | 1 | 0.5 | −0.0647 | 0.2052 | 0.8458 | 0.9460 | −0.0478 | 0.1802 | 0.6633 | 0.9590 | −0.0147 | 0.1416 | 0.4704 | 0.9680 | |
| 0.1279 | 0.2899 | 0.3174 | 0.9810 | 0.0847 | 0.2194 | 0.2624 | 0.9700 | 0.0290 | 0.1470 | 0.2165 | 0.9660 | ||||
| 0.0497 | 0.1415 | 0.3509 | 0.9860 | 0.0337 | 0.1005 | 0.2645 | 0.9770 | 0.0138 | 0.0524 | 0.1724 | 0.9660 | ||||
| −0.0459 | 0.1832 | 0.4464 | 0.9800 | −0.02568 | 0.1092 | 0.3532 | 0.9700 | −0.0096 | 0.0355 | 0.2483 | 0.9660 | ||||
| 1 | 1 | 0.5 | −0.0847 | 0.2197 | 0.6442 | 0.9140 | −0.0610 | 0.1796 | 0.4419 | 0.9320 | −0.0410 | 0.1520 | 0.2637 | 0.9660 | |
| 0.3063 | 0.4903 | 0.3231 | 0.9410 | 0.1980 | 0.3386 | 0.2662 | 0.9530 | 0.1006 | 0.2180 | 0.2066 | 0.9650 | ||||
| 0.1920 | 0.2799 | 0.4858 | 0.9770 | 0.1303 | 0.1996 | 0.3501 | 0.9840 | 0.0621 | 0.1136 | 0.2256 | 0.9670 | ||||
| −0.2241 | 0.3527 | 0.4201 | 0.9980 | −0.1380 | 0.2337 | 0.3036 | 0.9720 | −0.0570 | 0.1193& | 0.1887 | 0.9670 | ||||
| 2 | 1 | 0.5 | −0.1390 | 0.2193 | 0.3709 | 0.9800 | −0.1131 | 0.2028 | 0.2551 | 0.9720 | −0.0769 | 0.1726 | 0.1665 | 0.9690 | |
| 0.4175 | 0.7326 | 0.7068 | 0.9720 | 0.2426 | 0.3786 | 0.6131 | 0.9750 | 0.1299 | 0.2173 | 0.5371 | 0.9690 | ||||
| 0.2107 | 0.3243 | 1.1496 | 0.9710 | 0.1259 | 0.1832 | 0.8568 | 0.9860 | 0.0606 | 0.0907 | 0.6019 | 0.9970 | ||||
| −0.1562 | 0.3359 | 0.4613 | 0.9520 | −0.0743 | 0.1487 | 0.3479 | 0.9600 | −0.0249 | 0.0592 | 0.2285 | 0.9670 | ||||
| 0.2 | 0.0480 | 0.2630 | 0.9211 | 0.9830 | 0.0406 | 0.1583 | 0.6999 | 0.9710 | 0.0302 | 0.1154 | 0.4400 | 0.9620 | |||
| 0.0248 | 0.2076 | 0.2906 | 0.9820 | 0.0048 | 0.1533 | 0.2014 | 0.9710 | −0.0150 | 0.1023 | 0.1310 | 0.9640 | ||||
| 0.0713 | 0.2349 | 0.3063 | 0.9820 | 0.0371 | 0.1427 | 0.2312 | 0.9710 | 0.0110 | 0.0792 | 0.1428 | 0.9690 | ||||
| −0.1069 | 0.2299 | 0.6043 | 0.9830 | −0.0648 | 0.1703 | 0.45543 | 0.9800 | −0.0273 | 0.0914 | 0.2912 | 0.9770 | ||||
| 0.1 | 0.0342 | 0.2980 | 1.0518 | 0.9850 | 0.0365 | 0.1766 | 0.7190 | 0.9830 | 0.0244 | 0.1115 | 0.4275 | 0.9790 | |||
| −0.0005 | 0.1861 | 0.3416 | 0.9920 | −0.0024 | 0.1333 | 0.1743 | 0.9830 | −0.0170 | 0.0828 | 0.0993 | 0.9770 | ||||
| 0.0662 | 0.2706 | 0.3296 | 0.9850 | 0.0390 | 0.1859 | 0.2283 | 0.9790 | 0.0079 | 0.1049 | 0.1405 | 0.9670 | ||||
| −0.0831 | 0.2456 | 0.8136 | 0.9990 | −0.0680 | 0.1914 | 0.5084 | 0.9940 | −0.0246 | 0.1092 | 0.3080 | 0.9870 | ||||
| −0.2 | −0.0708 | 0.5232 | 1.0911 | 0.9910 | −0.0421 | 0.3010 | 0.8699 | 0.9800 | −0.0405 | 0.1763 | 0.6136 | 0.9610 | |||
| −0.0469 | 0.1546 | 0.5067 | 0.9940 | −0.0306 | 0.1091 | 0.2603 | 0.9740 | −0.0168 | 0.0697 | 0.1356 | 0.9630 | ||||
| 0.0746 | 0.5990 | 0.3029 | 0.9890 | 0.0283 | 0.2960 | 0.2443 | 0.9740 | 0.0078 | 0.1507 | 0.1721 | 0.9670 | ||||
| 0.0228 | 0.3499 | 1.2728 | 0.9830 | 0.0135 | 0.2384 | 0.8195 | 0.9750 | 0.0152 | 0.1336 | 0.5331 | 0.9610 | ||||
| 2 | 0.5 | −0.0619 | 0.1945 | 0.8590 | 0.9980 | −0.0416 | 0.1753 | 0.6607 | 0.9890 | −0.0078 | 0.1412 | 0.4426 | 0.9990 | ||
| 0.1125 | 0.2791 | 0.3363 | 0.9330 | 0.0729 | 0.2173 | 0.2650 | 0.9420 | 0.0159 | 0.1457 | 0.2127 | 0.9620 | ||||
| 0.0729 | 0.3018 | 0.3538 | 0.9800 | 0.0496 | 0.2202 | 0.2627 | 0.9720 | 0.0111 | 0.1150 | 0.1710 | 0.9670 | ||||
| −0.0283 | 0.1944 | 0.9046 | 0.9700 | −0.0194 | 0.1299 | 0.7037 | 0.9890 | −0.0050 | 0.0526 | 0.4684 | 0.9620 | ||||
| 0.2 | 0.0729 | 0.2117 | 0.9636 | 0.9900 | 0.0547 | 0.1564 | 0.6760 | 0.9850 | 0.0360 | 0.1081 | 0.4496 | 0.9780 | |||
| −0.0273 | 0.1958 | 0.3055 | 0.9910 | −0.0261 | 0.1517 | 0.2120 | 0.9720 | −0.0333 | 0.0975 | 0.1393 | 0.9610 | ||||
| 0.0640 | 0.4303 | 0.3059 | 0.9920 | 0.0357 | 0.3279 | 0.2164 | 0.9830 | −0.0037 | 0.1831 | 0.1390 | 0.9680 | ||||
| −0.0937 | 0.2673 | 1.2401 | 0.9910 | −0.0715 | 0.2148 | 0.8714 | 0.9860 | −0.0324 | 0.1177 | 0.5893 | 0.9690 | ||||
| 0.1 | 0.0749 | 0.2478 | 0.9590 | 0.9990 | 0.0682 | 0.1670 | 0.6936 | 0.9880 | 0.0354 | 0.0876 | 0.4347 | 0.9720 | |||
| −0.0373 | 0.1903 | 0.3065 | 0.9910 | −0.0583 | 0.1447 | 0.1788 | 0.9840 | −0.0433 | 0.0885 | 0.1002 | 0.9730 | ||||
| 0.0770 | 0.4571 | 0.2880 | 0.9780 | −0.0244 | 0.3578 | 0.2171 | 0.9660 | −0.0335 | 0.2197 | 0.1390 | 0.9600 | ||||
| −0.1132 | 0.2756 | 1.3742 | 0.9970 | −0.0447 | 0.2279 | 0.9692 | 0.9870 | −0.0210 | 0.1420 | 0.6188 | 0.9670 | ||||
| True Value | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bias | RMSE | SE | CP | bias | RMSE | SE | CP | bias | RMSE | SE | CP | ||||
| 0.5 | 1 | 0.5 | −0.0913 | 0.2344 | 1.3674 | 0.9830 | −0.0599 | 0.1952 | 1.0293 | 0.9730 | −0.0365 | 0.1549 | 0.6736 | 0.9620 | |
| 0.1068 | 0.2685 | 0.4348 | 0.9830 | 0.0550 | 0.2051 | 0.3611 | 0.9730 | 0.0148 | 0.1424 | 0.2791 | 0.9760 | ||||
| 0.0100 | 0.1186 | 0.3590 | 0.9830 | −0.0102 | 0.0794 | 0.2659 | 0.9710 | −0.0235 | 0.0514 | 0.1677 | 0.9660 | ||||
| −0.0437 | 0.1403 | 0.6819 | 0.9730 | −0.0199 | 0.0769 | 0.5082 | 0.9710 | −0.0102 | 0.0192 | 0.3254 | 0.9620 | ||||
| 0.2 | −0.3935 | 1.6522 | 1.3146 | 0.9740 | 0.0161 | 0.1571 | 0.9409 | 0.9700 | −0.0014 | 0.0963 | 0.6257 | 0.9640 | |||
| 0.0066 | 0.1899 | 0.6875 | 0.9910 | −0.0069 | 0.1390 | 0.2749 | 0.9820 | −0.0142 | 0.0852 | 0.1846 | 0.9740 | ||||
| 0.1861 | 1.6107 | 0.2626 | 0.9910 | −0.0048 | 0.1053 | 0.1808 | 0.9720 | −0.0271 | 0.0631 | 0.1135 | 0.9640 | ||||
| −0.1176 | 0.1962 | 0.9611 | 0.9940 | −0.0758 | 0.1442 | 0.5331 | 0.9800 | −0.0293 | 0.0677 | 0.3649 | 0.9740 | ||||
| 0.1 | 0.0042 | 0.4007 | 1.2466 | 0.9850 | 0.0154 | 0.1490 | 0.8994 | 0.9760 | 0.0025 | 0.0896 | 0.5491 | 0.9690 | |||
| 0.0016 | 0.1708 | 0.4576 | 0.9930 | −0.0082 | 0.1162 | 0.2241 | 0.9810 | −0.0163 | 0.0703 | 0.1307 | 0.9750 | ||||
| 0.0608 | 0.3558 | 0.2454 | 0.9850 | 0.0043 | 0.1201 | 0.1726 | 0.9760 | −0.0269 | 0.0726 | 0.1080 | 0.9650 | ||||
| −0.1368 | 0.2118 | 0.9204 | 0.9930 | −0.0904 | 0.1640 | 0.5495 | 0.9860 | −0.0351 | 0.0812 | 0.3475 | 0.9690 | ||||
| −0.2 | −0.8713 | 1.3807 | 1.3926 | 0.9870 | −0.1653 | 0.5025 | 1.0040 | 0.9720 | −0.1012 | 0.2560 | 0.6365 | 0.9610 | |||
| −0.0079 | 0.1100 | 1.2154 | 0.9850 | −0.0110 | 0.0795 | 0.4796 | 0.9770 | −0.0106 | 0.0525 | 0.1965 | 0.9960 | ||||
| 1.6920 | 3.4927 | 0.2594 | 0.9980 | 0.1181 | 0.4368 | 0.1866 | 0.9870 | 0.0243 | 0.1559 | 0.1196 | 0.9790 | ||||
| −0.1205 | 0.2113 | 1.3655 | 0.9870 | −0.0667 | 0.1424 | 1.1179 | 0.9770 | −0.0189 | 0.0593 | 0.5751 | 0.9690 | ||||
| 2 | 0.5 | −0.0965 | 0.2355 | 1.2621 | 0.9820 | −0.0541 | 0.1903 | 0.9674 | 0.9760 | −0.0320 | 0.1521 | 0.6883 | 0.9670 | ||
| 0.1020 | 0.2691 | 0.4254 | 0.9820 | 0.0378 | 0.2007 | 0.3501 | 0.9760 | 0.0082 | 0.1424 | 0.2801 | 0.9650 | ||||
| −0.0087 | 0.2752 | 0.3522 | 0.9720 | −0.0554 | 0.2024 | 0.2537 | 0.9690 | −0.0565 | 0.1107 | 0.1619 | 0.9650 | ||||
| −0.0279 | 0.1621 | 1.3228 | 0.9820 | −0.0034 | 0.1044 | 0.9964 | 0.9760 | −0.0076 | 0.0282 | 0.6670 | 0.9680 | ||||
| 0.2 | 0.0260 | 0.2239 | 1.2350 | 0.9890 | 0.0190 | 0.1622 | 0.9383 | 0.9750 | 0.1019 | 0.6279 | 0.6200 | 0.9690 | |||
| −0.0117 | 0.1867 | 0.3544 | 0.9870 | −0.0280 | 0.1361 | 0.2810 | 0.9750 | −0.0241 | 0.0879 | 0.1840 | 0.9670 | ||||
| −0.0061 | 0.3345 | 0.2585 | 0.9900 | −0.0570 | 0.2333 | 0.1800 | 0.9800 | −0.0743 | 0.1438 | 0.1147 | 0.9720 | ||||
| −0.1002 | 0.2056 | 1.4290 | 0.9870 | −0.0636 | 0.1509 | 1.0908 | 0.9700 | −0.0263 | 0.0760 | 0.7386 | 0.9690 | ||||
| 0.1 | 0.0180 | 0.2640 | 1.1769 | 0.9880 | 0.0133 | 0.1712 | 0.8844 | 0.9790 | 0.0022 | 0.0750 | 0.5468 | 0.9680 | |||
| −0.0212 | 0.1646 | 0.3278 | 0.9800 | −0.0311 | 0.1141 | 0.2360 | 0.9750 | −0.0263 | 0.0693 | 0.1289 | 0.9680 | ||||
| 0.0163 | 0.3927 | 0.2341 | 0.9830 | −0.0587 | 0.2823 | 0.1714 | 0.9780 | −0.0799 | 0.1674 | 0.1069 | 0.9680 | ||||
| −0.1189 | 0.2260 | 1.4648 | 0.9830 | −0.0674 | 0.1733 | 1.1255 | 0.9790 | −0.0305 | 0.0991 | 0.6944 | 0.9680 | ||||
| Distribution | IPM-B | GP | WP | BBXII | IPM | W |
|---|---|---|---|---|---|---|
| −12.610 (1.5148) | 0.0037 (1.1 ) | 5.3277 (0.0043) | 15.156 (1.2348) | 0.144 (0.253) | − | |
| 6.0506 (0.6685) | 0.1198 (2.9 ) | 0.0280 (6.7 ) | 0.9763 (0.6613) | 2.484 (0.505) | 4.169 (0.1610) | |
| 0.0660 (0.0143) | 0.0997 (0.4975) | 4.2861 (0.3996) | 14.812 (0.9717) | 1.075 (0.069) | 28.565 (0.4119) | |
| 0.0016 (0.5050) | − | − | 0.8248 (0.5488) | − | − | |
| − | − | − | 7.4191 (1.4849) | − | − | |
| AIC | 1909.79 | 2174.64 | 2012.36 | 1911.41 | 1913.79 | 2063.75 |
| BIC | 1924.79 | 2185.89 | 2023.61 | 1930.16 | 1926.82 | 2071.25 |
| Distribution | IBM | 95% CI | Interval Length |
|---|---|---|---|
| IPMB | 0.1910 | (0.1836–0.1985) | 0.0149 |
| BBXII | 0.1922 | (0.1847–0.1998) | 0.0151 |
| IPM | 0.1938 | (0.1763–0.2113) | 0.0175 |
| WP | 0.2364 | (0.2264–0.2464) | 0.0199 |
| Distribution | IPM-P | GG | WG | BBXII | IPM | W |
|---|---|---|---|---|---|---|
| 0.1398 (0.2946) | 0.0728 (0.3357) | 0.0078 (6.6 ) | 7.3236 (3.5 ) | 0.019 (0.041) | − | |
| 2.4751 (0.6374) | 1.6926 (0.0125) | 2.4962 (0.1401) | 11.366 (8.4 ) | 5.893 (0.309) | 2.3451 (0.2798) | |
| 1.0698 (0.2219) | 2.2587 (0.0225) | 0.9392 (0.0032) | 0.3442 (2.2 ) | 0.044 (0.001) | 1.3937 (0.0998) | |
| 0.0459 (1.9492) | − | − | 0.0673 (6.3 ) | − | − | |
| − | − | − | 6.3903 (3.8 ) | − | − | |
| AIC | 64.68 | 72.85 | 65.62 | 65.92 | 68.68 | 66.58 |
| BIC | 71.44 | 77.92 | 71.69 | 74.36 | 76.13 | 69.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrios-Blanco, L.; Gallardo, D.I.; Gómez, H.J.; Bourguignon, M. A Compound Class of Inverse-Power Muth and Power Series Distributions. Axioms 2023, 12, 383. https://doi.org/10.3390/axioms12040383
Barrios-Blanco L, Gallardo DI, Gómez HJ, Bourguignon M. A Compound Class of Inverse-Power Muth and Power Series Distributions. Axioms. 2023; 12(4):383. https://doi.org/10.3390/axioms12040383
Chicago/Turabian StyleBarrios-Blanco, Leonardo, Diego I. Gallardo, Héctor J. Gómez, and Marcelo Bourguignon. 2023. "A Compound Class of Inverse-Power Muth and Power Series Distributions" Axioms 12, no. 4: 383. https://doi.org/10.3390/axioms12040383
APA StyleBarrios-Blanco, L., Gallardo, D. I., Gómez, H. J., & Bourguignon, M. (2023). A Compound Class of Inverse-Power Muth and Power Series Distributions. Axioms, 12(4), 383. https://doi.org/10.3390/axioms12040383








