1. Introduction
Parabolic-type equations containing advective terms are often used in modern physics and chemical kinetics models. As typical examples, some research papers can be mentioned. Namely, in [
1] the two-dimensional linear equation of this type is used for numerical simulation of the solidification process in a latent heat thermal energy storage of a hexagonal shape tube form. Most often, the purpose of the study is not one physical quantity but some combination of them. In this case, systems of equations are used for modeling. In particular, in [
2] design-based numerical study is carried out to analyze magnetohydrodynamical mixed convection heat transfer inside a water-filled semicircular cavity having cylindrical obstacles inside. A system of four equations for pressure, temperature, and velocities along the x- and y-axis directions is used here for modeling. In [
3], the system of equations of chemical kinetics is studied, proposed by Martiel and Goldbeter [
4] for production and relay of cAMP in
D. discoideum. These are reaction-diffusion equations, with the addition of an advection term due to an imposed external flow. The paper studies at what ratio of control parameters account for the production and degradation of extracellular cAMP, respectively, the boundary-induced instability occurs. In [
5], the periodic wave trains are described by means of the spatial version of the Dysthe equations for the normalized amplitude envelope and the envelope of the self-induced velocity potential. In [
6], the numerical simulations of the solution of the reaction-diffusion-advection system of equations is used to describe the thermalization effects on plug flow reactor fuel conversion. The work [
7] shows how systems of equations of the reaction-diffusion-advection type can describe the mechanisms of the occurrence of anomalously large acoustic nonlinearities in non-single-phase, defective and structurally inhomogeneous media.
It is extremely rare that it is possible to obtain the solution of such systems of equations analytically. For example, in [
8], where the solution of the form of a set of solitons for Coupled Burger System of Fractional-Order is constructed. Much more often, such systems can be solved numerically. At the same time, the capabilities of modern computers do not allow checking the reliability of the obtained numerical results for multidimensional problems, using, for example, the mesh thickening method. Verification is carried out in most cases through comparison with the available experimental results, as, for example, in [
5,
6], where the periodic wave trains are observed by utilizing surface gravity water wave packets, or are just based on experience. Analytical studies of the solution’s existence, and what is more important obtaining its mathematically justified approximation are essential to verify the numerical results. However, these studies are so complex that they cannot cover the entire set of model tasks, especially when it comes to systems. However, any mathematically sound result should be used in combination with numerical solution methods, for example, to construct efficient meshes or to select initial conditions in numerical schemes.
The stationary reaction-diffusion-advection equations occur in the modeling of processes in the atmospheric boundary layer [
9,
10]. If we are talking about stationary distribution, then it is necessary to analyze the stability of the model problem solution. There are various methods how to establish solution stability. Thus, in [
3] the linear stability analysis of the system in a moving reference frame was performed to complete the numerical study of the convectively unstable regime. The study of the stabilization to stable stationary solution gives an answer to the question of suitable initial conditions for the numerical calculations. Some aspects of stabilization problems were considered for semilinear parabolic equations in [
11,
12].
In a number of important applications cases (large sources in the case of fast reactions or strong interactions), the solutions of parabolic equations have domains with large gradients called internal transition layers. For example, these are propagating fronts that arise in different areas such as chemical and biological kinetics, population dynamics, combustion and nonlinear wave theory (see [
13,
14,
15]. Various classes of such problems are presented in [
16,
17,
18]. Note that such problems include the Burgers’ and Burgers’ type equations, that are used for modeling in gas dynamics, shallow water waves, and traffic flow and provide fundamental examples for many important topics in nonlinear PDE such as traveling waves, shock formation, similarity solutions, singular perturbation, and numerical methods for parabolic and hyperbolic Equations (see [
19,
20,
21,
22,
23] and references therein). The numerical implementation of the problems with internal transition layers requires a preliminary analysis of the existence conditions and stability [
24,
25,
26,
27,
28].
Here we present a methodology for a comprehensive study of nonlinear equations and systems, which makes it possible to obtain
a mathematically justified solution with an internal transition layer approximation;
the conditions for the existence of its stable stationary solution;
the domain of attraction of a stable stationary solution.
In this paper, this technique is worked out on the example of a scalar singularly perturbed Burgers-type equation on a segment. The question of stabilization to a stationary stable solution has not yet been considered for the problem stated. The existing results concern the solutions of the front form of singularly perturbed nonlinear parabolic equations and systems not containing advective term [
29,
30]. However, the research methodology proposed in mentioned papers is not suitable for Burgers-type equations, since it relies on the fact that the formation of a non-stationary solution with a transition layer occurs in a time that is asymptotically small compared to the stabilization time, in contrast to the problem we considered here, in which these times are comparable due to the presence of the large advective term. It should also be noted that a numerical description of the initial functions set suitable for stabilization to the stationary solution is obviously impossible. The proposed method for describing the domain of attraction of a stable solution (a set of initial functions), based on the asymptotic method of differential inequalities for singularly perturbed equations, is new and very effective. The study can be extended to the multidimensional case and the case of systems of equations, but this promising problem is very laborious. Nevertheless, even the results of the above study can already give an idea of the applicability conditions for more complex models and can be used in various studies, for example, in solving coefficient inverse problems [
31,
32,
33].
In this paper, we consider the initial-boundary-value problem for reaction-diffusion-advection equation and the question of its moving front-type solution stabilizing over an infinitely large time interval to the stationary solution with an internal layer.
The existence of a moving front solution is investigated in [
34]. The existence conditions of an asymptotically stable stationary solution are known from [
35]. To prove the stabilization theorem, in this paper we use the method of upper and lower solutions, which for this class of problems is justified in [
36,
37]. The main idea of the proof is to show that the upper and lower solutions of the initial-boundary-value problem on an asymptotically large time interval fall into the stationary solution attraction domain. The upper and lower solutions with large gradients are constructed according to the asymptotic method of differential inequalities [
16,
18,
34] as modifications of asymptotic approximations of the solutions in a small parameter. The study conducted in this work gives an answer about the non-local domain of attraction of the stationary solution. In addition, there is obtained an estimate of the stabilization time interval, which is the criterion for the numerical solution stationing.
The statement considered in the article is a generalization of problems from the nonlinear theory of waves. Some formulations of model problems using Burgers-type equations can be found in research papers [
38,
39]. The physical meaning of the various nonlinear terms included in the equations is explained in [
7].
2. Problem Statement
We consider the following initial-boundary-value problem for the reaction-diffusion-advection equation:
Here
T is any positive value,
is a small parameter;
are three times differentiable functions with partial derivatives up to the third order continuous in the set of variables;
, where
is the valid interval of variable
v, and
;
is a smooth function for which the consistency conditions hold:
If there is a stationary solution
to the problem (
1), it can be defined as a solution to a boundary value problem
with the same functions
A and
B and values
, as in the statement (
1).
We assume some propositions.
Proposition 1. Let the equation with the additional condition has a solution on the segment and with additional condition has a solution , and the inequalities hold: The existence conditions of moving front solution to problem (
1) are formulated in [
34] in the assumption that the initial function
has a front form. At each instant of time the front is localized in some vicinity of point
, to the left of this vicinity the solution is close to function
and to the right to function
In [
35], the existence conditions of Lyapunov asymptotically stable stationary solution with internal transition layer to problem (
1) are obtained. We consider the transition layer to be localized in some vicinity of point
The estimate of the local domain of attraction is obtained in [
40].
The aim of this work is to study the stationing of the solution to problem (
1) to the stationary stable solution. To do this it is necessary to require the conditions for the existence of a front-type solution to problem (
1) set in [
34] and the conditions for the existence and stability of the stable stationary solution set in [
35]. In order to formulate these conditions, we need to study the so-called associated systems for problems (
1) and (
2).
2.1. Associated Systems
For a detailed description of the solution behavior nearby the transition layer we introduce stretched variables
The differential operators of Equations (
1) and (
2) rewritten through stretched variables have the form:
We consider the so-called “associated equations” for problems (
1) and (
2)
where
x and
W are parameters,
and the admissible values
W will be specified later. We shall further consider the first of these equations as the second is obtained from it if we put
.
From the associated Equation (
4) we come to the equivalent associated system
and then to the equation
determining the trajectories on the phase plain
Each of the points
on the phase plane is a rest point of system (
5). Let us consider the phase trajectories
Due to the Proposition 1 the phase trajectory
enters the rest point
when
, and
enters the rest point
when
If at each instant of time there exists a pair of parameters
for which the equality
holds, the phase trajectories intersect and there exists the solution
to the first Equation (
4) (or to the second Equation (
4) in case
) coming out the saddle point
and entering the saddle point
Moreover the parameters
and
are related by the equality
Proposition 2. Let on the interval there exists a unique solution of the equation and besides the inequality holds.
Under Propositions 1 and 2 we have if and if .
Proposition 3. Let the Cauchy problem has a unique solution for
Proposition 4. Let the inequalities hold: if and if .
3. Study Algorithm
We will conduct our research using the method of the upper and lower solutions [
36,
37]. According to [
36] if there exist the upper (
) and lower (
) solutions of problem (
2) then there exists the solution
to problem (
2) enclosed between the upper and lower solutions:
According to [
37] from the existence of the upper (
) and lower (
) solutions of problem (
1) and from the inequality
the existence of the solution
to this problem follows for which the inequalities hold:
where
T is a positive value.
The upper and lower solutions of each of the problems (
1) and (
2) we will construct according to the asymptotic method of differential inequalities [
16] as modifications of the second-order asymptotic approximations in the small parameter of these solutions, therefore we will connote them by the subscript “2”.
According to [
40] the domain
is the local domain of attraction of stable stationary solution.
In order to prove the stabilization theorem, we will show that during an asymptotically large but finite time interval
T, the upper and lower solutions of problem (
1) will be included in the domain of stability of the stationary solution, as a result of which the limit equality will follow:
4. Asymptotic Approximation of Moving Front Solution
According to [
34] the second order asymptotic approximation
of problem (
1) is constructed separately on each of the intervals
and
For the purposes of this study, we need a third-order asymptotic approximation that we construct as the expansion at exponents of
Here the functions
(
) connote the regular part to that the solution is close away from
and
are the transition layer functions depending on the stretched variable
determined by the first expression (
3). The parameters
and
are related by the equality
We assume the expansion
where
is the same as in Proposition 3.
The functions
and
are continuously matched at a point
at each instant of time so that the equality holds:
The main regular terms of the asymptotic approximation are determined by the Proposition 1:
The functions
for
are the solutions to initial problems
with known functions
and
The 0-th order transition layer functions
for each value of parameter
are the solutions to problems
on half-line
for
and
for
.
By use of the notation
Equations (
13) take the form of the first Equation (
4). According to
Section 2.1 we come to the equations
where functions
are given by expressions (
6). The function
on each of the half-lines
and
is the solution to the corresponding Equation (
16) with the additional condition following from (
14):
.
Under Propositions 1 and 4 the standard estimates for the transition layer functions hold:
where
and
are some positive constants. The analogous estimates hold for the derivatives of functions
.
Next, for brevity, we introduce the notations
and the same notations for the derivatives of these functions.
The
i-th order transition layer functions,
for each value of parameter
are the solutions to linear problems
where
are known functions depending on further determined terms of asymptotic approximation with
in particular
Problems (
18) can be solved explicitly:
By construction, the functions
have exponential estimates like (
17) so for the functions
the similar estimates hold.
Function
is continuous due to the boundary conditions at
of problems (
13) and (
18).
The coefficients
in the expansion (
11) are determined from the following conditions for the derivatives:
Taking into account the equality
(see notations (
15), (
16) and equality (
7)) we obtain that the functions
are the solutions to linear problems
where function
is determined in (
9) and
are known functions, in particular
5. The Moving Front Upper and Lower Solutions
In [
34], the following upper and lower solutions of problem (
1) are constructed:
where
Here
and
are the points of transition layer localization, respectively, for the upper and lower solutions.
The moving front solution can have an internal transition layer at any point of the interval
that is rather far (order of
) from its endpoints. We will consider the upper solution with an internal transition layer that at each moment
is localized in the neighborhood of point
and the lower solution with internal transition layer in the neighborhood of point
, where
is the transition layer point of the stationary solution. For this we put
where
and
are the solutions to Cauchy problem from Proposition 3, respectively, with the initial condition
and the initial condition
. The functions
,
,
are the solutions to Cauchy problems similar to (
22), with
replaced, respectively, by
and
.
We introduce functions and the stretched variables We will determine the functions further.
The variable
and parameters
and
W of the functions
(see (
10)) included in (
25) are replaced by
,
,
for the upper solution and by
,
,
for the lower solution.
The functions
are the solutions to problems
where
R,
,
are positive constants, and
is notation (
12).
The explicit expressions for
are the following:
Under Proposition 1 the functions
take positive values for
.
The functions
in the upper solution are determined as the solutions to problems
on the half-line
for functions with superset “
” and on the half-line
for functions with superset “
” for each
The functions
are known and have exponential estimates like (
17).
We set the same problems to determine the low solution terms , changing by and by
The functions
and
decrease exponentially to zero and have estimates like (
17).
The function
in the expressions for
is determined as a solution to initial problem
where
is a known function that is bounded and strictly positive (see [
34]) and
. The function
is strictly positive for
The function is determined from similar problem with replaced by . This function is also strictly positive for
6. Stationary Solution Asymptotic Approximation
The asymptotic approximation
of the solution to problem (
2) is constructed in the way indicated in [
35]. That is
where
are regular part functions that are similar to ones in expressions (
10) and
are transition layer functions depending on variable
(see (
3)).
The functions
are the solutions to problems
on half-line
for
and on half-line
for
and have the exponential estimates like (
17) where
is changed by
.
Let us introduce the notation
On each half-line
and
the function
is a solution to Cauchy problem (see
Section 2.1 and Equation (
16))
where
is determined by expression (
6) with the replacement of
by
.
For brevity, we will further use notations and the same for derivatives of these functions.
The transition layer functions of the
i-th order(
) we determine as solutions to linear problems
on half-line
for
and on half-line
for
with known functions
, in particular
The explicit solutions to these problems are
For the functions
the exponential estimates like (
17) are also valid.
We represent the value
as an expansion in
exponents
where the coefficients
we determine from the condition for derivatives (
21) with
, and
replaced by
.
The coefficient
is determined in Proposition 2 and
are the solutions of equations
where
are known values, in particular
Equations (
39) are solvable due to Proposition 2.
8. Stabilization of the Solution of the Initial-Boundary Value Problem
The purpose of this paper is to prove the following theorem.
Theorem 2. For every smooth initial function of problem (1), that is consistent with boundary conditions and enclosed between the upper and lower solutions given by expressions (24), (25) the limiting equality holds:where and are the solutions to problems (1) and (2), respectively. The proof is based on the following assertion [
37].
For any smooth initial function of problem (
1) that is consistent with boundary conditions and is enclosed within the interval
There exists the solution
of problem (
1) for which the inequalities hold:
where
T is any positive value.
The proof of the Theorem 2 includes the following steps:
From these inequalities and estimates (
44) it will follow that for the mentioned
t the solution
of the parabolic problem will be located inside the local domain of attraction (
43) of the stable stationary solution.
Due to the asymptotic stability, this will infer the fulfillment of the limit equality from Theorem 2.
8.1. Step 1
Let us estimate the time interval
sufficient for the inequality
to hold for
. We introduce the function
where
,
are the coefficients, respectively, in the sum (
38) and in the first sum (
26). The function
is determined from Cauchy problem (
30) and the value
from Equation (
42). From Proposition 3 and definition of
(see (
26)) it follows that the function
is a solution to the problem
From Proposition 2 it follows that
, and
. Consequently
is asymptotically stable rest point of Equation (
47) therefore, there exists a moment
such that for
the estimate
is valid. The value
can be obtained similarly to that was done in [
41] by passing from problem (
47) to the equivalent integral equation. The result is
Thus, for large enough
the inequality
can be carried out. It follows from the same reasoning that the inequality
can also be carried out for large enough
.
Before we turn to Step 2 let us obtain some estimates that hold when .
8.2. The Estimates for Q-Functions
The functions
are the solutions to Cauchy problems
with the functions
determined by expressions (
6) where
is replaced by
by
W by
(see Equations (
16), notation (
15) and boundary condition (
14)).
The functions
are the solutions to Cauchy problems (see Equations (
34), notation (
33) and the boundary conditions at
of problems (
32))):
In order to obtain the relations between functions and , we will use the theorem on the dependence of the solution to Cauchy problem on parameters.
The parameter
has the following representation:
where
is determined by expression (
8),
As
, from Equations (
22) and (
39) with taking into account expressions (
23) and (
40) we get
. Then for
we have
.
Now using the theorem on the dependence of the Cauchy problem solution on a parameter we come to the equalities
where
are the functions of the form
with positive constants
C and
. Here the exponential estimates like (
17) for functions
were taken into account.
From the explicit expressions (
20) and (
37) for functions
and
given the expressions (
19), (
36) and the estimates
valid for
we obtain the relation
where the functions
have the form like (
49).
8.3. The Estimate for
Considering Equations (
22), (
39), and explicit expressions (
23), (
40) for
we can obtain the Cauchy problem for the function
:
For
the estimates are valid:
Taking into account Proposition 2 the solution of this problem has the estimate
.
Finally, with a large enough positive value
in expression (
46) it is fulfilling that
.
8.4. Step 2
We will prove that the right inequality in the chain (
45) holds for
for such values of
t that
. The left inequality in the chain can be proved by the same reasoning and the central one follows from the known properties of the upper and lower solutions [
37,
42,
43].
First, let us consider the difference of functions
and
on the segment
Considering the estimates (
48), (
50) along with the boundary conditions at
and
of problems (
13), (
18), (
32), and (
35)we come to equality:
Here the term
is positive (see (
6) and (
7)) and so the right-hand side is positive as
.
Further let us consider the difference of functions and on the segment
In this segment, we have the expression
The functions
and
both are the solutions to problem (
27) with difference just in the values of positive constants
and
R. Thus, we can choose these values in a way that for
the inequalities hold
.
By means of the representation
expressions (
48), (
50) and the choice of functions
and
we have the inequality
where
and
(
) are positive constants.
The rest of the proof of the inequality
is analogous to the proof of the upper and lower solutions ordering from [
44].
The right inequality (
45) on the segment
is proved similar to how it is done on the segment
Thus, both the steps of the proof of Theorem 2 are completed.
9. Examples of Solution Formation
In this section, we give two examples of equations, from the theory of wave physics, namely for shock fronts with linear and cubic absorption [
38,
39].
Example 1. We consider the following problem for Burgers’ type equation with linear addition term:
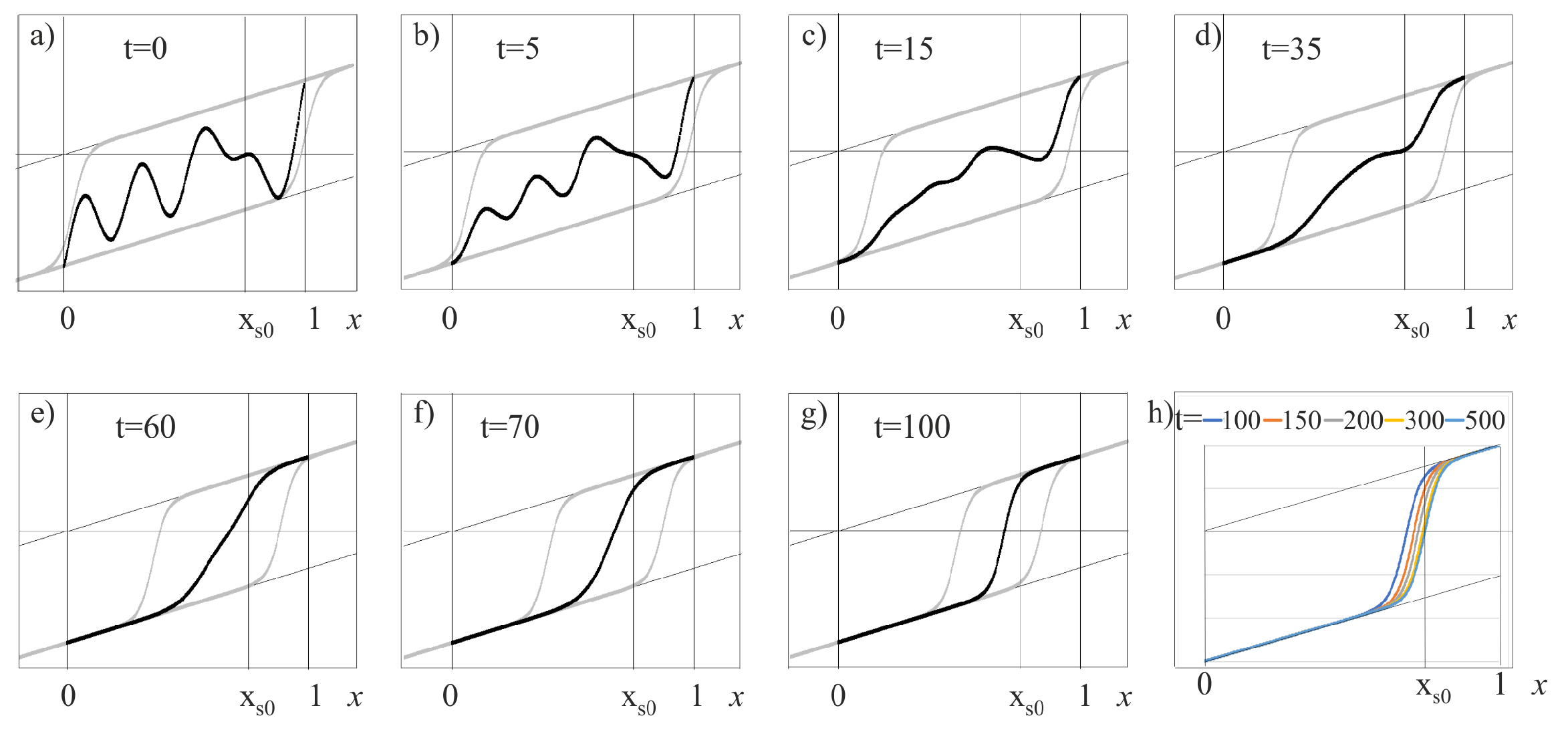
Figure 1 shows the numerical solution to problem (
51) with
at different moments of time: its transformation over time from a given initial function into a solution of the front form (black bold lines on a–g), and drawing at sufficiently large
t arbitrarily close to a stationary solution with internal transition layer nearby the point
(h). At each moment of time, the solution is enclosed between the upper and lower solutions. Solid bold gray lines on a–g connote functions
and
that are the major terms in the upper and lower solutions with
Example 2. We consider the following problem for Burgers’ type equation with cubic addition term using various initial functions The reduced equation solutions are
,
.
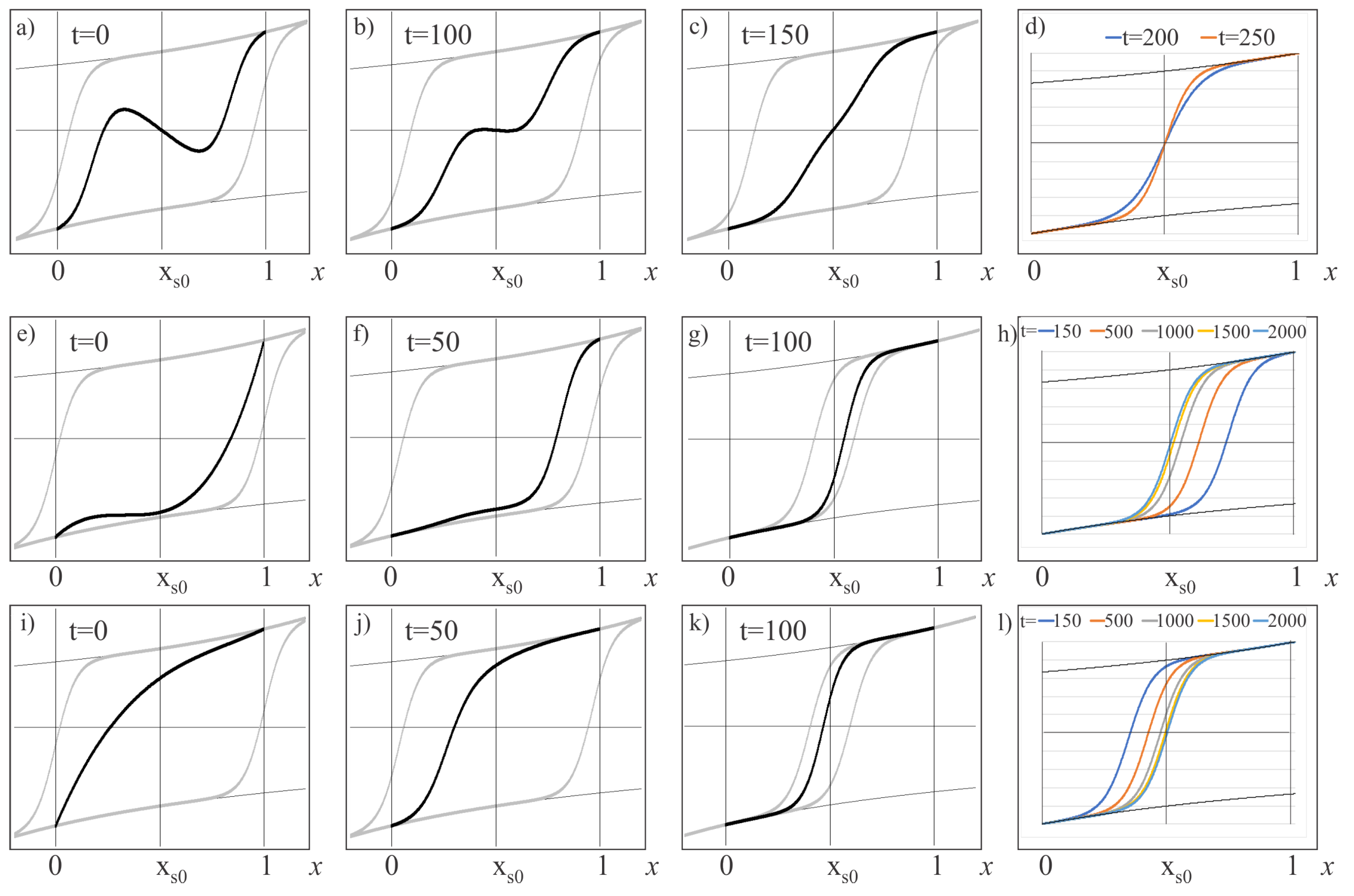
Figure 2a–d refers to the solution to problem (
52) with an initial function I); (e–h)—with initial function II) and (i–l)—with initial function III). In case ((
52) I) stabilization of the solution to a stationary one occurs without the formation of a moving front; in case ((
52) II) the moving front is formed to the right of the stationary solution localization point, then approaches it with time; in problem ((
52) III), the formed front moves to the stationary solution from the left. In each case
.
The stationary solution has an internal transition layer localized nearby the point
. Solid bold gray lines on
Figure 2a–c,e–g,i–k connote the major terms of the upper and lower solutions. The laws of motion of the upper and lower solutions are given, respectively, by functions
,
that are obtained from equation
with initial values
,
by means of the Runge–Kutta method.
For the numerical solution of the parabolic equation, the method of lines was used. A uniform mesh of nodes was introduced on the segment . According to the method of lines, the solution of the parabolic equation was reduced to the solution of a system of linear differential equations for the values of the numerical solution at the grid nodes, the latter was carried out using the one-stage Rosenbrock scheme with complex coefficient. During the numerical calculation, a time step of was used. The original code was created in a C++ compiler.
Note that the main foundation of this work is to obtain a theoretical result on the stabilization of the parabolic problem solution. Numerical experiments are given here for illustration purposes only. The result of numerical experiments fully corresponds to what was previously proven strictly mathematically, which in itself confirms the validity of numerical calculations.