Abstract
This work proposed a new hybridised network of 3-Satisfiability structures that widens the search space and improves the effectiveness of the Hopfield network by utilising fuzzy logic and a metaheuristic algorithm. The proposed method effectively overcomes the downside of the current 3-Satisfiability structure, which uses Boolean logic by creating diversity in the search space. First, we included fuzzy logic into the system to make the bipolar structure change to continuous while keeping its logic structure. Then, a Genetic Algorithm is employed to optimise the solution. Finally, we return the answer to its initial bipolar form by casting it into the framework of the hybrid function between the two procedures. The suggested network’s performance was trained and validated using Matlab 2020b. The hybrid techniques significantly obtain better results in terms of error analysis, efficiency evaluation, energy analysis, similarity index, and computational time. The outcomes validate the significance of the results, and this comes from the fact that the proposed model has a positive impact. The information and concepts will be used to develop an efficient method of information gathering for the subsequent investigation. This new development of the Hopfield network with the 3-Satisfiability logic presents a viable strategy for logic mining applications in future.
MSC:
03B52; 68T27; 68N17; 68W50
1. Introduction
Artificial intelligence (AI) technology has advanced significantly with the development of a hybrid system that combines neural networks, logic programming models, and SAT structures. The artificial neural network (ANN) is a robust analysis operating model that has previously seen extensive investigation and application by specialists and researchers due to its capacity to manage and display complex challenges. The Hopfield neural network (HNN), established by Hopfield & Tank [1], is one of the many neural networks. The HNN is a recurrent network that performs similarly to the human brain and can solve various challenging mathematical problems. A symbolised representing structure that governs the data stored in the HNN was produced by using Wan Abdullah’s (WA) approach that describes logic rules [2]. Abdullah suggested one of the earliest approaches to incorporate SAT into the HNN. The work was explained by embedding the SAT structure into the HNN by reducing the cost function to a minimum value. Abdullah offered a unique logic programming as a symbolic rule to represent the HNN to solve the issue by determining the symbol’s reduced cost function using the final Lyapunov energy function. Therefore, the method successfully surpassed the traditional learning method like Hebbian learning and can intelligently compute the relationship between the reasoning.
The work is expanded by Sathasivam when the SAT structure, specifically Horn Satisfiability (HornSAT), is utilised [3]. The proposed logic demonstrates how well the HornSAT can converge to the least amount of energy. Years later, Kasihmuddin et al. [4] pioneered the work of 2-Satisfiability (2SAT). The 2SAT structure is being implemented in the HNN as the systematic logical rule. According to the previous work, the proposed 2SAT in the HNN manages to reach a high global minima ratio in a respectable amount of time. Two literals are used in every clause of the suggested logical structure, and a disjunction joins all clauses. By contrasting the cost function and the Lyapunov energy function, this logical rule was incorporated into the HNN. Mansor et al. [5] then expanded the logical rule’s order by suggesting a systematic logical rule with a higher order. This work improves the previous work by adding three literals per clause, namely 3-Satisfiability (3SAT) in the HNN. The third-order Lyapunov energy function is evaluated with the cost function to determine the third-order synaptic weight. Despite the suggested study’s associative memory of the HNN with 3SAT expanding exponentially, it defined the global minimum ratio’s superior value. The proposed 3SAT increases the network’s storage capacity in the HNN because the neuron’s ability to produce many local minima solutions is still limited. The use of systematic SAT in ANNs was made possible in large part by this research. The rigidity of the logical composition, which added to overfitting results in the HNN, is the drawback of any kSAT. As soon as the number of neurons is elevated, the literals in a clause result in low synaptic weight values, which reduces the likelihood of finding global minimum solutions. Various options in the search space solutions are required to ensure a thorough exploration of the neurons. Thus, to overcome the downside of the structure, we offer a hybridised network of 3SAT logic that uses fuzzy logic and a metaheuristic algorithm to significantly widen the search space and improve the presentation of logic programming in the HNN.
The word fuzzy refers to things that appear not to be adequate or ambiguous [6]. Numerous-valued logic allows an idea to have some degree of reality [7]. It can simulate human experience and decision-making. Fuzzy logic has been used in numerous scientific fields, including neural networks, machine learning, artificial intelligence, and data mining [8,9,10,11]. This method can handle insufficient, inaccurate, inconsistent, or uncertain data. Since then, a broad range of research has shown the benefits of this approach, including the fact that the fuzzy sets are straightforward to use, the method does not require a sophisticated mathematical model, and the cost of computing is little [12]. Fuzzy logic builds the proper rules via a fuzzification and defuzzification process. Incorporating the fuzzy logic process with the HNN lowers the processing cost and enables the suggested scheme to accommodate more accurate neurons. As part of the defuzzifying procedure, any suboptimal neuron will be modified using the alpha-cut technique until the ideal neuron state is found. Then, we integrate the network with a metaheuristic algorithm, a Genetic Algorithm (GA). The Darwinian Theory of Survival of the Fittest is replicated by the GA, a form of natural selection. The GA was proposed by Holland [13] as a widely used optimisation technique founded on the population of metaheuristic algorithms. A population of potential solutions is improved over time as part of the implementation of the GA, which is an iterative process. The paradigm of computer intelligence known as metaheuristic algorithms is particularly effective at handling challenging optimisation problems.
Thus, the objectives of this research are listed as follows: (1) To construct a continuous search space by applying a fuzzy logic system in the training phase of 3-Satisfiability logic. (2) To create a design structure integrating a Genetic Algorithm to improve all the logical combinations of reasoning that will minimise the cost function. (3) To produce a new performance metric to evaluate the method’s efficiency in obtaining the highest clauses of satisfying assignments in the learning phase. (4) To establish a thorough assessment of the suggested hybrid network using the generated datasets that can perform significantly with the Hopfield neural network model. Our findings indicated that the suggested HNN-3SATFuzzyGA exhibits the finest performance in conditions of error analysis, efficiency evaluation, energy analysis, similarity index performance, and computational time. The layout of this article is as follows: Section 2 provides an outline structure of 3-Satisfiability. Section 3 describes the application of 3SAT into the Hopfield Neural Network. The general formulation of fuzzy logic and Genetic Algorithm is explained in Section 4 and Section 5, respectively. Section 6 discusses the execution of the suggested model of HNN-3SATFuzzyGA. Additionally, Section 7 listed the experimental and parameter sets, along with the performance evaluation metrics used. Section 8 reviewed the outcomes and discussion on the findings of HNN-3SATFuzzyGA. Section 9 concludes the paper’s results and suggestions for future research.
2. 3-Satisfiability
Satisfiability signifies a logical rule that includes several clauses with literals . The SAT problem explores whether a specific SAT formula is satisfactory when it has a value that evaluates it as accurate. Our study will focus on 3-Satisfiability, also known as 3SAT. Hence, the following describes the principles structure of a 3SAT problem: (1) a set of a clause, , is connected by AND with, where . If , the Boolean SAT will have three clauses. The value of may increase according to the number of clauses specified. (2) For each clause of the Boolean SAT, there will be literals that are connected by OR The literals are for every . Moreover, since this study focuses on 3SAT, it will consist of only three literals per clause. (3) The choice of the literal’s condition can be either negative or positive. The principal formula for 3SAT is
where signifies a set of a clause. Meanwhile, indicate the number of clauses in the third, second and first order, respectively. The value of 3 (third), 2 (second) and 1 (first) indicates the order of clauses in . Given that, the overall amount of clauses in is and the entire literals included in for all order of clauses are . Since this study focuses on 3SAT, Equation (2) below is an example that signifies the logical rule with exactly three literals per clause:
The assignments that correlate to the 3SAT can be expressed as [5]. Determining a list of assignments that will translate the entire formulation into TRUE is the main objective of the 3SAT. If the logical rule provides the actual value, the is considered fulfilled; if it provides a false value, the is not fulfilled.
3. 3-Satisfiability in the Hopfield Neural Network
The HNN is one of the subdivisions of the ANN that has a feedback mechanism where every single neuron output is sent back into the input [1]. Because of the non-symbolic nature of the HNN structure, the logical conceptualisation of 3SAT can improve its capacity for great storage. The general mathematical formula for the neuron’s activation is presented as follows:
where signifies the threshold value and indicates the weight for component to .
The 3SAT algorithm used in this study, known as HNN-3SAT, uses three neurons for each sentence. Additionally, the HNN’s synaptic weight connection is symmetrical with and there is no self-connection of between any of the neurons. The structure serves as the framework for the compelling content addressable memory (CAM), which was used to store and recover every necessary pattern from handling the optimisation problem. All the variables will be assigned to the specified cost function, to embed the . In the meantime, the following formula is used to generate the cost function for 3SAT:
where is the sum of clauses and in Equation (5) below can be shifted parallel to the corresponding state of the literal:
By assessing the inconsistencies of the 3SAT structure rule, the minimum cost function must be achieved [14]:
Note that the amount of grows in direct proportion to the number of inconsistencies in the clauses [14]. In this case, when the number of unsatisfied clauses rises, will rise as well. is the lowest amount that can be attained for the cost function. The HNN will use the local field equation during the retrieval phase to execute the iterative updating of neurons. The parameters of the synaptic weight, such as , can be decided by associating the cost function with the Lyapunov energy function of HNN using Wan Abdullah’s (WA) approach [2]. The stable condition of the neurons is represented by the minimal values from the energy function [3]. Each variant of the HNN-3SAT has a different generalised Lyapunov final energy function.
4. Fuzzy Logic
The motivation of fuzzy logic appears when there are wide-ranging ways humans use imprecise information to make judgments. Traditional Boolean logic only will not always be able to unravel a problem. Zadeh [15] proposed fuzzy logic and fuzzy set to apply vagueness and control better with human reasoning errors, while Mamdani [16] was the first to bring these ideas into the control theory. Both accomplishments make it possible to use fuzzy logic in various applications successfully.
4.1. Fuzzy Set
Zadeh [15] created the theory of a fuzzy set to represent vague concepts and handle informational uncertainty. The fuzzy set can be thought of as a smooth set, unlike the classical sets, in which the fuzzy set chooses whether to belong to or not belong to a particular set gradually or progressively instead of just sharply. Distinguishing a fuzzy set in to realise the involvement of any element , where , with a membership degree that corresponds to the range between zero and one and is a process of characterising a membership function . The membership function of is symbolised by the symbol where the ordered pair can likewise be used to describe this fuzzy set in :
in which where means a portion does not fit into a fuzzy set and means is a component of a fuzzy set. The notation of the set can be demonstrated as a discrete universe [17].
where indicates union through all . The degree of membership of in is identified as .
4.2. Fuzzy Logic System
The critical components of a fuzzy logic system (FLS) are presented in Figure 1. It includes the fuzzifier stage, which converts crisp inputs into fuzzy sets. Then, the rules-based converts fuzzy sets from the backgrounds to equivalent fuzzy sets. Lastly, the defuzzifier stage will receive a crisp assessment from the fuzzy sets.
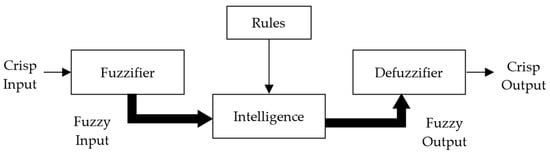
Figure 1.
The components of a fuzzy logic system (FLS).
5. The Genetic Algorithm
The GA replicates the Darwinian Theory of Survival of the Fittest, a form of natural choice commonly utilised as an optimisation technique based on the population of metaheuristic algorithms. The GA is executed by refining the population of possible solutions over time. It was first proposed by Holland [13] as a method for finding good-quality answers to the combinatorial optimisation problem. Holland adopted the natural GA processes of selection, crossover, and mutation. In line with the findings, Zamri et al. [18] used a multi-discrete GA to enhance the functionality of the weighted random k satisfiability in the HNN. It works remarkably well in various optimisation issues, mainly when attempting a global search in a discrete space. It is an iterative process that must create two definitions before the iteration may initiate. The search space is defined by (1) a genetic model of the search area and (2) a fitness function which frequently represents the goal function of the optimisation problem and calculates how suitable a candidate solution is. There are five main steps in GA: (1) initialisation, (2) fitness evaluation, (3) selection, (4) crossover and (5) mutation. The flowchart for the GA method is shown in Figure 2.
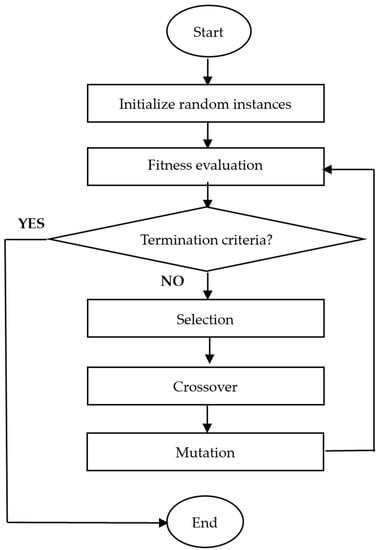
Figure 2.
Flowchart of principal steps in the GA method.
6. Fuzzy Logic System and Genetic Algorithm in 3-Satisfiability Logic Programming
The discovery of the HNN and SAT models, satisfying assignments of embedded logical structure, results in an optimal training phase (when the cost function is zero). A metaheuristic algorithm was used as the training method to carry out the kSAT minimisation objective in the HNN [14]. The optimisation operators enable the algorithm to enhance the network’s convergence towards cost function minimisation [19]. is used as the instance for the state of neurons in the training phase’s representation of the 3SAT’s potentially satisfying assignments. The drawback of the previous approach is the usage of representations. In this study, the process is to employ the neuron’s expression continuously so that every component in the exploration universe will be computed with various fitness functions. As a result, we embedded fuzzy logic in the system in the first stage. Additionally, the domain of fuzzy sets and functions is introduced when the binary (Boolean) problem is made continuous while maintaining its logical nature. A metaheuristic algorithm is employed in the second stage to obtain the best solution for the system to converge optimally. We cast it into the framework of the hybrid function between two techniques and then return (transform) the solution to the initial binary structure. This section explains how fuzzy logic incorporates the GA in 3SAT, namely the HNN-3SATFuzzyGA. The proposed technique is allocated into two stages: (1) the Fuzzy logic system’s stage and (2) the Genetic algorithm’s stage.
Firstly, the fuzzy logic control system is used in determining the output with three inputs . For example, three literals represent the input of and and the system produces as its output. The procedure is repeated for all number of clauses. Three membership functions are set up as the inputs. Meanwhile, there are two membership functions used in the output. In the first phase, each will be randomly assigned. After that, fuzzy logic will take place to evaluate the value of the first output . The first step in the fuzzy logic system is fuzzification, where each literal will be assigned to its membership function of:
in which .
Then, fuzzy rules will be applied using the first clause block, , e.g., . By enabling to accept any value in [0, 1], we will employ Zadeh’s operators, such as the logical operator AND holds the function and logical operator OR holds the function . This conversion creates the fuzzy function logically consistent with the binary function (Boolean function). This process will be repeated for a total number of clauses . Defuzzification steps will be employed to convert fuzzy values to its crips output. The alpha-cut method will modify neuron clauses through defuzzification until the proper neuron state is attained [17]. The improved alpha-cut formula has an estimation model of:
The second phase of the learning part is applying the Genetic Algorithm (GA). The initialisation of the chromosome, is obtained from the previous phase (fuzzy logic system solutions). The fitness of each chromosome, is evaluated using a fitness function:
where the conditions meet
The sum of all clauses in implies the optimum fitness of each [18]. Equation (14) denotes the objective function of GA:
The genetic information of two parents (chromosome, ) is exchanged using crossover operators to create the offspring (new chromosome, ). The parents’ genetic information is replaced according to the segments produced in the crossover stage, which selects random crossover points [20]. One mechanism that keeps genetic diversity from one population to the next is mutation. The mutation procedure entails the flipping of a single gene from another. A gene of a given chromosome is disseminated within itself by the displacement mutation operator. The location is randomly selected from the provided gene for displacement to guarantee that both the final result and a random displacement mutation are valid. Note that the GA process will be repeated until the is achieved. Algorithm 1 shows the pseudocode for FuzzyGA.
| Algorithm 1: Pseudocode for FuzzyGA |
| Begin the first stage Step 1: Initialisation Initialise the inputs, output, membership function and rule lists . Step 2: Fuzzification Assign the literal, to it membership function which . Step 3: Fuzzy rules Apply rules lists, using the first clause block, , e.g., Step 4: Defuzzification Implement the defuzzification step and estimation model. end Begin the second stage Step 1: Initialisation Initialise random populations of the instances, . Step 2: Fitness Evaluation Evaluate the fitness of the population of the instances, . Step 3: Selection Select best and save as . Step 4: Crossover Randomly select two bits, from . Generate new solutions and save them as . Step 5: Mutation Select a solution from . Mutates the solution by flipping the bits randomly and generates . if , Update . end Update . end |
7. Experimental Setup
Matlab 2020b software is used in this experimental simulation to perform the fuzzy logic and GA as a training tool in the HNN-3SAT. The HNN models in this work produced 3SAT clauses with varying degrees of difficulty using simulated datasets. The experiment will be terminated if the CPU time used to generate data surpasses 24 h. In addition, we choose HTAF due to its stability, and notably, an excellent approach to an activation function developed in the HNN. The final energy implementation requirements value is 0.001 because it effectively reduced statistical errors [3]. The effectiveness of the HNN-3SATFuzzyGA will be assessed by comparing it with another two models, the HNN-3SAT and HNN-3SATFuzzy, for accuracy and efficacy. This section evaluates the performance of each phase of the proposed model using the relevant performance measures. The training phase and testing phase are defined as the two key phases. The relevant objectives for each phase, which are stated below, determine the best solution. The training phase involves minimising Equation (4). The evaluation metrics used in this work are training error analysis and efficiency evaluation.
Meanwhile, the testing phase includes producing global minima solutions within the desired tolerance value and calibre of the returned final neuron states. The evaluation metrics involved in this phase are testing error analysis, energy analysis, similarity index and computational time. Table 1, Table 2 and Table 3 shows the list of parameters in the execution of evaluation metrics.

Table 1.
Listing of related parameters in the HNN-3SAT.

Table 2.
Listing of related parameters in the 3SATFuzzy.

Table 3.
Listing of related parameters in the 3SATFuzzyGA.
7.1. Performance Metric
Several metrics are used to analyse the performance of all the presented HNN-3SAT models. The effectiveness of each HNN-3SAT model will be evaluated using various criteria. The following are the goals for each phase:
- Training phase—The evaluation includes how well the suggested model performs in locating the most satisfied clauses in the learning phase of the 3SAT assignments. In this phase, the computation involves error analysis to verify the performances of each model. It also assesses the efficiency of the optimisation method in the training phase.
- Testing phase—The evaluation in the testing phase comprises computing the error analysis to validate the satisfied clauses. Besides that, it calculates the similarity degree to which the final neuron state differs from or resembles the benchmark states. It also verifies the robustness of the suggested model by energy analysis and computational time.
7.1.1. Training Phase Metric
This evaluation shows that the finest form of every iteration is substantial when executing an exploring procedure [21]. The error analysis metrics for each HNN-3SAT model in the training phase include RMSE, MAE, SSE and MAPE in Equations (15)–(18). The Root Mean Square Error (RMSE) reports the real difference between the anticipated amounts and the calculated value [22]. The Mean Absolute Error (MAE) is a valuable metric for evaluating the case by assessing the change in the mean gap between the determined and expected values [23]. The ideal HNN network attempt for a smaller MAE value. Since , there will be only positive values of the MAE [24]. The Sum Squared Error (SSE) is a statistical technique for calculating how much the data deviates from expected values and makes it empirically validated [25]. The SSE is extremely sensitive to minor inaccuracy. Therefore, it will increase incorrect final solutions [26]. The Mean Absolute Percentage Error (MAPE) is a modified form of the MAE in which the results are standardised to a percentage [27]. If the measured value is zero, the MAPE cannot be employed because doing so will result in a division by zero. The MAPE evaluation with the lowest value will be the most effective network [14].
where refers to the maximum fitness attained by the proposed model and is the obtained fitness value of the network and denoted the total number of iterations in the learning phase.
The two newly proposed efficiency performance metrics in Equations (19) and (20) are inspired by Djebedjian et al. [28] for calculating the efficiency of an optimisation algorithm as the computational effort required to find an optimal solution. The iteration efficiency evaluates the number of iterations the models require to compute in the fuzzy-meta learning phase.
where is the total iteration of the networks to enter the fuzzy-meta learning phase and is the total iteration of the network.
The evaluation efficiency calculates the number of successful iterations of the model in obtaining the highest clauses of satisfying assignments in the fuzzy-meta learning phase.
where is the total of satisfying solution in the fuzzy-meta learning phase in achieving the maximum clauses and is the total iteration the networks enter the fuzzy-meta learning phase.
7.1.2. Testing Phase Metric
In evaluating the error analysis for each HNN-3SAT model in the testing phase, the same metrics of RMSE, MAE, SSE and MAPE in Equations (21)–(24) are used.
where refers to the maximum optimal solution attained by the proposed model and is the obtained optimal solution value of the network and denoted the total number of iterations in the learning phase.
In order to analyse the diversification of the 3SAT produced by the suggested models, the final neuron state, can be compared with the ideal neuron state, [29]. The similarity metrics of the Jaccard Index [29] in Equation (25) and the Gower & Legendre Index [30] in Equation (26) are applied using the benchmark information in Table 4 to examine the similarity between the positive and negative of with . The following are the formulas for both similarity metrics:

Table 4.
Benchmark information in the similarity index.
Moreover, the energy analysis is calculated to test the robustness of the proposed network. The global minima ratio () and local minima ratio are evaluated during the testing phase to check the accuracy of the final neuron states retrieved by the model. and in Equations (27) and (28), respectively, are employed to thoroughly investigate the energy analysis [3]. The computational time analysis is used to determine the productivity of the network. In Equation (29), processing time generally refers to the total time it takes to finish a simulation.
where is the product of the number of combinations and trials. Meanwhile and refers to the number of global minima and local minima, respectively. Table 5 below shows the list of parameters used in the learning and testing phases.

Table 5.
List of parameters implicated in the learning and testing phases.
8. Results and Discussion
The results of three distinct methods will be discussed in this section. HNN-3SAT uses a basic random searching algorithm without any improvisation in the training phase. Meanwhile, HNN-3SATFuzzy employs fuzzy logic alone, and HNN-3SATFuzzyGA uses fuzzy logic and a Genetic algorithm in the training phase. Finding satisfying assignments that match the reduction of Equation (6) is the purpose of the training and testing phase in the HNN. This strategy uses the WA method to achieve appropriate synaptic weight regulation [31]. A simulation of the proposed model is conducted with the dynamics of different numbers of neurons to verify the prediction. This study limits the number of neurons to to determine our suggested model’s success. Additionally, we tested training error, training efficiency, testing error, energy analysis, similarity index and computational time. Results of all the three HNN-3SAT methods in the training and testing phases are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9.
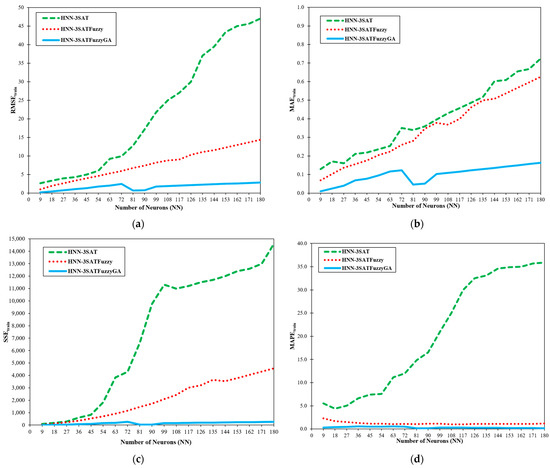
Figure 3.
The error analysis metrics in the training phase (a) RMSEtrain; (b) MAEtrain; (c) SSEtrain; (d) MAPEtrain.
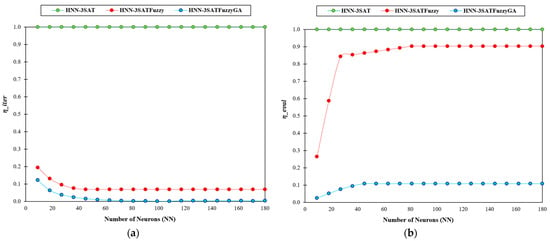
Figure 4.
The efficiency performance metrics in the training phase: (a) iteration efficiency; (b) evaluation efficiency.
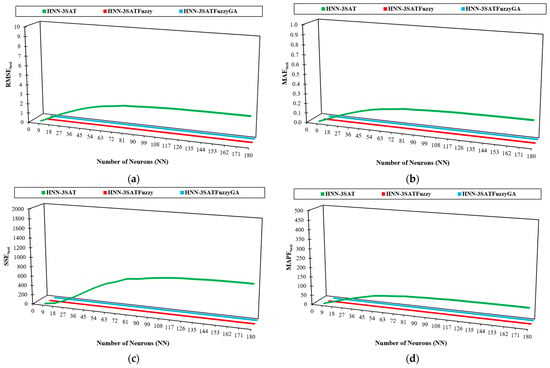
Figure 5.
The error analysis metrics in the testing phase: (a) RMSEtest; (b) MAEtest; (c) SSEtest; (d) MAPEtest.
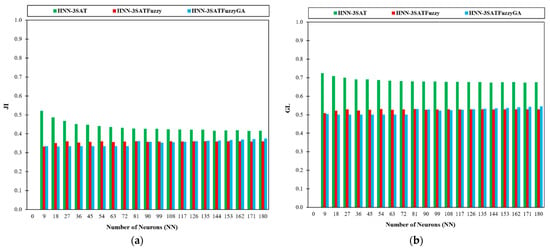
Figure 6.
The similarity metrics (a) Jaccard Index; (b) Gower and Legendre Index.
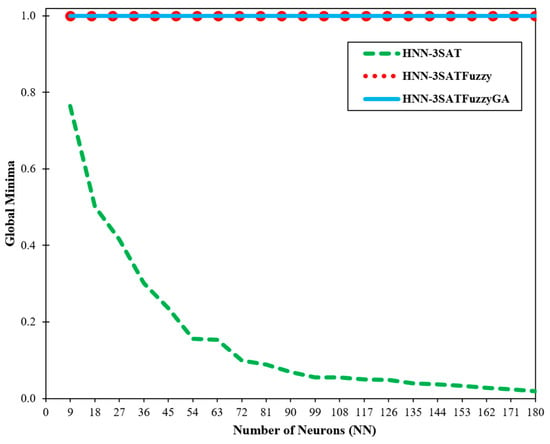
Figure 7.
Global minima ratio (zM).
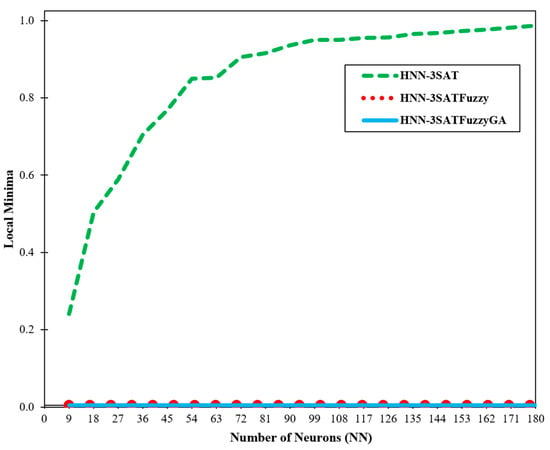
Figure 8.
Local minima ratio (yM).
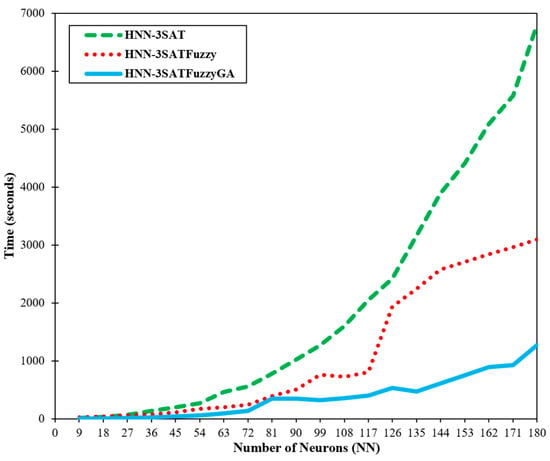
Figure 9.
Processing time.
Figure 3 displays the results of RMSEtrain, MAEtrain, SSEtrain and MAPEtrain during the training stage for the three different methods: HNN-3SAT, HNN-3SATFuzzy, and HNN-3SATFuzzyGA, respectively. According to Figure 3a,b, RMSEtrain and MAEtrain for HNN-3SATFuzzyGA outperformed those of other networks during the training phase. Despite an increase in the number of neurons (NN), the results demonstrate that the RMSEtrain and MAEtrain values for the HNN-3SATFuzzyGA network are the lowest. The HNN-3SATFuzzyGA solutions deviated from the potential solutions less. Initially, the outcomes for all networks seemed to have little difference during . However, once it reached , the results started to deviate more for RMSEtrain and MAEtrain, with performance for HNN-3SATFuzzyGA remaining low. The other two methods considerably increased toward the end of the simulations, especially HNN-3SAT. Based on RMSEtrain and MAEtrain calculations, the suggested method, HNN-3SATFuzzyGA, achieved at lower results. The leading cause of this is that fuzzy logic, and GA resolve a better solution in the training phase, enabling the achievement of in a shorter number of cycles. The reason is that the fuzzy logic system is more likely to widen the search during training using fuzzification for precise interpretations. Then, the HNN-3SATFuzzyGA utilised a systematic approach by employing the defuzzification procedure. The usage of GA also helps to optimise the solutions better. Additionally, HNN-3SATFuzzyGA could efficiently verify the proper interpretation and handle more restrictions than the other networks. In another work by Abdullahi et al. [32], a method for extracting the logical rule in the form of 3SAT to characterise the behaviour of a particular medical data set is tested. The goal is to create a reliable algorithm that can be used to extract data and insights from a set of medical records. The 3SAT method extracts logical rule-based insights from medical data sets. The technique will integrate 3SAT logic and HNN as a single data mining paradigm. Medical data sets like the Statlog Heart (ST) and Breast Cancer Coimbra (BCC) are tested and trained using the proposed method. The network has recorded good performance evaluation metrics like RMSE and MAE based on the simulation with various numbers of neurons. The results of Abdullahi et al. [32] can conclude that the HNN-3SAT models have a considerably lower sensitivity in error analysis results. According to the optimal CPU time measured with various levels of complexity, the networks can also accomplish flexibility.
Figure 3c, d demonstrates that HNN-3SATFuzzyGA has lower SSEtrain and MAPEtrain values. Since HNN-3SATFuzzyGA has a lower SSEtrain value, it has a more reliable ability to train the simulated data set. With a lower SSEtrain value for all hidden neuron counts, HNN-3SATFuzzyGA was found to have evident good-quality results. Even though the results for SSEtrain during have not deviated far from each other’s result, HNN-3SATFuzzyGA remained low until the end of the simulations compared to the other methods. Associated with HNN-3SATFuzzyGA during the final NN, the outcomes of HNN-3SAT increased drastically. The results show the MAPEtrain settings’ output for all networks. The MAPEtrain value has also provided compelling evidence of fuzzy logic and GA compatibility in 3SAT. The results for HNN-3SATFuzzyGA were significantly at a low level even after . Compared to HNN-3SATFuzzyGA, the results of HNN-3SAT converged higher, starting from . As a result, the HNN-3SATFuzzyGA approach performs noticeably better than the other two models. The effectiveness of the network is because the training phase’s operators of fuzzy logic and GA boosted the solutions’ compatibility. Compared to different networks, HNN-3SATFuzzyGA can recover a more precise final state.
Figure 4a,b shows the iteration efficiency and evaluation efficiency for the methods in the training part, respectively. A lower value of and stands to be the best result. Generally, a lower and score denotes a higher efficiency level. Based on Figure 4a, HNN-3SAT maintains the value of since it has no optimisation operator to improve the learning part. HNN-3SATFuzzyGA and HNN-3SATFuzzy have a lower value of compared to HNN-3SAT. The reason is that most of the iteration goes into the fuzzy logic and (or) GA optimisation phase. In order to search for the best maximum fitness, the training must go through the operator to locate the best solution. Meanwhile, in Figure 4b, show the results for the highest successful iterations in obtaining the highest clauses of satisfying assignments in the fuzzy-meta learning phase. HNN-3SAT remains at at all levels since it does not have an optimiser. In the meantime, HNN-3SATFuzzyGA obtained the lowest score since it can achieve the highest successful iterations to obtain maximum fitness. Fuzzy logic is responsible for widening the development effort to obtain an ideal state with satisfying assignments. Owing to the addition of a metaheuristic algorithm, such as GA, HNN-3SATFuzzyGA performed well with the help of operators like crossover and mutation. The crossover is a subclass of global search operators that maximises the search for potential solutions. In this instance, chromosomal crossover (possible satisfying assignments) leads to almost ideal states that might support 3SAT. The mutation operator is vital in locating the best solution for a particular area of the search space. Meanwhile, HNN-3SAT has no capability for exploration and exploitation since it uses a random search technique by the “trial and error” mechanism.
Figure 5 display the results of RMSEtest, MAEtest, SSEtest and MAPEtest in the testing error analyses. Examining the HNN-3SAT behaviour based on error analysis concerning global or local minima solutions is the significance of testing error analysis. The WA approach will construct the synaptic weight after completing the HNN-3SAT clause satisfaction (minimisation of the cost function). Figure 5a,b shows that the testing error for RMSEtest and MAEtest in HNN-3SAT is the highest, indicating that the model cannot induce global minima solutions. The model is overfitted to the test sets due to the unsatisfied clauses. Therefore, we need to add an optimiser such as fuzzy logic to widen the search space and GA optimise the solutions better. Based on RMSEtest and MAEtest calculations, the HNN-3SAT attains at higher results. The two methods, with an optimiser, maintain the error at a lower level. Additionally, in Figure 5c,d, we consider SSEtest and MAPEtest as two performance indicators in the testing phase when evaluating the error analysis. Notably, an increased likelihood of optimal solutions will be attributed to lower SSEtest and MAPEtest values. Lower SSEtest and MAPEtest scores denote a higher accuracy (fitness) level. The SSEtest and MAPEtest values for the HNN-3SAT model rise noticeably when the number of neurons increases. As a result, the HNN-3SAT model with greater SSEtest and MAPEtest values cannot optimise the required fitness value during the testing phase. After , the values for SSEtest and MAPEtest for the HNN-3SAT model begin to rise. The event occurred due to the HNN-3SAT trial-and-error approach, which resulted in a less ideal testing phase.
Next, we used the similarity index to analyse the similarity and dissimilarity of the generated final neuron states in Figure 6a,b. This indexing is used for divergence investigations. It is particular to binary variables [33]. According to Equations (25) and (26), we searched for the Jaccard Index (JI) and the Gower-Legendre Index (GLI) in the similarity index analysis. A comparison of the JI and GLI values obtained by several HNN-3SAT models is shown in Figure 6a, b. The JI and GLI calculate how the computed states resemble the baseline state. Examining the value of the JI in Figure 6a is best done with lower JI and GLI values. In our investigation, the HNN-3SATFuzzyGA model recorded lower JI values for lower NN between . Based on Figure 6a,b, HNN-3SAT has the highest overall similarity index values. In HNN-3SATFuzzy and HNN-3SATFuzzyGA, there is fuzzy logic or (and) GA optimisation in the training phase, resulting in a non-redundant neuron state that achieves the global minima energy due to diversification of the search space. As a result, the final neuron state differs significantly from the benchmark state, causing it to have a lower value. However, HNN-3SAT produces a similar neuron state corresponding to the global minima energy because of the limitation of neuron choice for the variable. That interprets the higher value of the JI and GLI in Figure 6a,b, respectively. Gao et al. [34] used a higher-order logical structure that can exploit the random property of the first, second, and third-order clauses. Alternative parameter settings, including varying clause orderings, ratios between positive and negative literals, relaxation and different numbers of learning trials, were used to assess the logic in the HNN. The similarity index measures formulation is used since the similarity index measurements aim to analyse neuron variation caused by the random 3SAT. The simulation indicated that the random logic was adaptable and offered various solutions. According to Karim et al. [29], the experimental results showed that random 3SAT may be implemented in the HNN and that each logical combination had unique properties. In the entire solution space, random 3SAT can offer neuron possibilities. Third-order clauses were added to the random 3SAT to boost the possible variability in the reasoning learning and retrieval stages. The simulations were used to determine the best value for each parameter to get the best outcomes. Therefore, the model’s flexible architecture can be combined with fuzzy logic and the GA to offer an alternate viewpoint on potential random dynamics for applying practical bioinformatics issues.
Figure 7 and Figure 8 show the global and local minima ratio detected by the other two networks for different numbers of neurons. A correlation between the global and local minima values and the type of energy gained in the program’s final section was found by Sathasivam [3]. The outcomes in the system have arguably reached global minima energy, except HNN-3SAT, given that the suggested hybrid network’s global minima ratio is approaching a value of 1. 3SATFuzzyGA certainly can offer more precise and accurate states when compared to the HNN. The outcome is due to how effectively the fuzzy logic algorithm and GA searches. The HNN-3SATFuzzyGA solution attained the best global minimum energy of value 1. The obtained results are from utilising the HNN-3SAT network with the fuzzy logic technique and the genetic algorithm. The fuzzy logic lessens computation load by fuzzifying and defuzzifying the state of the neurons to distinguish the right states. The suggested method can accept additional neurons. Additionally, unfulfilled neuron clauses are improved by utilising the alpha-cut process in the defuzzification stage until the proper neuron state is found. This property makes it possible for defuzzification and fuzzification algorithms to converge successfully to global minima compared to the other network. With the aid of the GA, the optimisation process is enhanced. When the number of neurons rises, the HNN-3SAT network gets stuck in a suboptimal state. It has been demonstrated that the fuzzy logic method makes the network less complex. From the results, HNN-3SATFuzzy and HNN-3SATFuzzyGA global minimum converged to ideal results with satisfactory outcomes. Calculating the time is crucial for assessing our proposed method’s efficacy. The robustness of our techniques can be roughly inferred from the effectiveness of the entire computation process. The computing time, also known as the CPU period, is the time it took for our system to complete all the calculations for our inquiry [3]. The computation technique involves training and producing our framework’s most pleasing sentences. Figure 9 shows the total computation time for the network to complete the simulations. The likelihood of the same neuron being implicated in other phrases increased as the number of neurons grew [3]. Furthermore, Figure 9 demonstrates unequivocally how superior HNN-3SATFuzzyGA is to other networks. The HNN-3SATFuzzyGA network improved more quickly than the other network after the number of clauses grew. The time taken by all techniques for more minor clauses is not significantly different. The CPU time was quicker when the fuzzy logic technique and the GA were applied, showing how effectively the methods worked.
In another application by Mansor et al. [35], the HNN can be used to optimise the pattern satisfiability (pattern SAT) problem when combined with 3SAT. The goal is to examine the pattern formed by the algorithms’ accuracy and CPU time. Based on global pattern-SAT and running time, the specific HNN-3SAT performance of the 3SAT method in performing pattern-SAT is discussed by Mansor et al. [35]. The outcomes of the simulation clearly show how well HNN-3SAT performs pattern-SAT. This work was done by applying logic programming in the HNN to prove the pattern satisfiability using 3SAT. The network in pattern-SAT works excellently as measured by the number of correctly recalled patterns and CPU time. As confirmed theoretically and experimentally, the network increased the probability of recovering more accurate patterns as the complexity increased. The excellent agreement between the global pattern and CPU time obtained supports the performance analysis. In another work by Mansor et al. [36], a very large-scale integration (VLSI) circuit design model also can be used with the HNN as a circuit verification tool to implement the satisfiability problem. In order to detect potential errors earlier than with human circuit design, a VLSI circuit based on the HNN is built. The method’s effectiveness was assessed based on runtime, circuit accuracy, and overall VLSI configuration. The early error detection in our circuit has led to the observation that the VLSI circuits in the HNN-3SAT circuit generated by the suggested design are superior to the conventional circuit. The model increases the accuracy of the VLSI circuit as the number of transistors rises. The result of Mansor et al. [36] achieved excellent outcomes for the global configuration, correctness, and runtime, showing that it can also be implemented with fuzzy logic and the GA.
9. Conclusions
The central insight of this study provides an efficient approach to creating a continuous search space that considers the optimal training phase (when the cost function is zero). The proposed model, HNN-3SATFuzzyGA, displays exciting behaviour when the network is hybridised between fuzzy logic and the GA. The application of fuzzy logic design in the first phase of the training phase demonstrates that the optimisation process is more effective at diversifying the neuron state in a bigger search space. The second contribution is designing a hybridised network between the fuzzy logic system with the GA as the second phase in the training phase, namely HNN-3SATFuzzyGA, to determine the global solutions. The effectiveness of the suggested model was then effectively contrasted with other methods. The GA performs well since it requires a few iterations to maximise the global solutions. The execution of evaluation metrics discussed in this article proves that the findings of the suggested model, HNN-3SATFuzzyGA, are excellent compared to the HNN-3SAT and HNN-3SATFuzzy. The robustness of HNN-3SATFuzzyGA architecture offers insight into potential dynamics for usage in real-world issues. The proposed HNN-3SATFuzzyGA can be included in logic mining to extract the best logical rule for real datasets problems. The sturdy architecture of HNN-3SATFuzzyGA offers a solid foundation for use in real-life settings. For instance, the proposed HNN-3SATFuzzyGA in logic mining can extract the optimum logical rule for categorising the death occurrence based on comorbidity cases linked to COVID-19 disease. Other bioinformatics applications can also be implemented in logic mining to obtain the optimum logical rule for classifying the attributes, such as identifying the characteristic of a patient with Alzheimer’s disease, recognising an early sign of a heart disease patient and many more attributes. The HNN-3SATFuzzyGA can lead to a large-scale design with classification and forecasting capabilities. Additionally, for future work, fuzzy logic integrated with metaheuristic algorithms can be applied in solving other types of logical rules, such as Random 3-Satisfiability (RAN-3SAT) and Maximum 3-Satisfiability (MAX-3SAT).
Author Contributions
Analysis and writing—original draft preparation, F.L.A.; validation and supervision, S.S.; funding acquisition, M.K.M.A.; writing—review and editing, N.R.; resources, C.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ministry of Higher Education Malaysia (MOHE) through the Fundamental Research Grant Scheme (FRGS), FRGS/1/2022/STG06/USM/02/11 and Universiti Sains Malaysia.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hopfield, J.J.; Tank, D.W. “Neural” Computation of Decisions in Optimization Problems. Biol. Cybern. 1985, 52, 141–152. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, W.A.T.W. Logic Programming on a Neural Network. Int. J. Intell. Syst. 1992, 7, 513–519. [Google Scholar] [CrossRef]
- Sathasivam, S. Upgrading Logic Programming in Hopfield Network. Sains Malays. 2010, 39, 115–118. [Google Scholar]
- Kasihmuddin, M.S.M.; Mansor, M.A.; Sathasivam, S. Robust Artificial Bee Colony in the Hopfield Network for 2-Satisfiability Problem. Pertanika J. Sci. Technol. 2017, 25, 453–468. [Google Scholar]
- Mansor, M.A.; Kasihmuddin, M.S.M.; Sathasivam, S. Artificial Immune System Paradigm in the Hopfield Network for 3-Satisfiability Problem. Pertanika J. Sci. Technol. 2017, 25, 1173–1188. [Google Scholar]
- Agrawal, H.; Talwariya, A.; Gill, A.; Singh, A.; Alyami, H.; Alosaimi, W.; Ortega-Mansilla, A. A Fuzzy-Genetic-Based Integration of Renewable Energy Sources and E-Vehicles. Energies 2022, 15, 3300. [Google Scholar] [CrossRef]
- Nasir, M.; Sadollah, A.; Grzegorzewski, P.; Yoon, J.H.; Geem, Z.W. Harmony Search Algorithm and Fuzzy Logic Theory: An Extensive Review from Theory to Applications. Mathematics 2021, 9, 2665. [Google Scholar] [CrossRef]
- El Midaoui, M.; Qbadou, M.; Mansouri, K. A Fuzzy-Based Prediction Approach for Blood Delivery Using Machine Learning and Genetic Algorithm. Int. J. Electr. Comput. Eng. 2022, 12, 1056. [Google Scholar] [CrossRef]
- de Campos Souza, P.V. Fuzzy Neural Networks and Neuro-Fuzzy Networks: A Review the Main Techniques and Applications Used in the Literature. Appl. Soft Comput. 2020, 92, 106275. [Google Scholar] [CrossRef]
- Nordin, N.S.; Ismail, M.A.; Sutikno, T.; Kasim, S.; Hassan, R.; Zakaria, Z.; Mohamad, M.S. A Comparative Analysis of Metaheuristic Algorithms in Fuzzy Modelling for Phishing Attack Detection. Indones. J. Electr. Eng. Comput. Sci. 2021, 23, 1146. [Google Scholar] [CrossRef]
- Scaranti, G.F.; Carvalho, L.F.; Barbon, S.; Proenca, M.L. Artificial Immune Systems and Fuzzy Logic to Detect Flooding Attacks in Software-Defined Networks. IEEE Access 2020, 8, 100172–100184. [Google Scholar] [CrossRef]
- Torres-Salinas, H.; Rodríguez-Reséndiz, J.; Cruz-Miguel, E.E.; Ángeles-Hurtado, L.A. Fuzzy Logic and Genetic-Based Algorithm for a Servo Control System. Micromachines 2022, 13, 586. [Google Scholar] [CrossRef] [PubMed]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Sathasivam, S.; Mamat, M.; Kasihmuddin, M.S.M.; Mansor, M.A. Metaheuristics Approach for Maximum k Satisfiability in Restricted Neural Symbolic Integration. Pertanika J. Sci. Technol. 2020, 28, 545–564. [Google Scholar]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Mamdani, E.H. Application of Fuzzy Algorithms for Control of Simple Dynamic Plant. Proc. Inst. Electr. Eng. 1974, 121, 1585–1588. [Google Scholar] [CrossRef]
- Pourabdollah, A.; Mendel, J.M.; John, R.I. Alpha-cut representation used for defuzzification in rule-based systems. Fuzzy Sets Syst. 2020, 399, 110–132. [Google Scholar] [CrossRef]
- Zamri, N.E.; Azhar, S.A.; Sidik, S.S.M.; Mansor, M.A.; Kasihmuddin, M.S.M.; Pakruddin, S.P.A.; Pauzi, N.A.; Nawi, S.N.M. Multi-discrete genetic algorithm in Hopfield neural network with weighted random k satisfiability. Neural Comput. Appl. 2022, 34, 19283–19311. [Google Scholar] [CrossRef]
- Kaveh, M.; Kaveh, M.; Mesgari, M.S.; Paland, R.S. Multiple Criteria Decision-Making for Hospital Location-Allocation Based on Improved Genetic Algorithm. Appl. Geomat. 2020, 12, 291–306. [Google Scholar] [CrossRef]
- Zhang, W.; He, H.; Zhang, S. A novel multi-stage hybrid model with enhanced multi-population niche genetic algorithm: An application in credit scoring. Expert Syst. Appl. 2019, 121, 221–232. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A Review on Genetic Algorithm: Past, Present, and Future. Multimed Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Khan, B.; Naseem, R.; Muhammad, F.; Abbas, G.; Kim, S. An Empirical Evaluation of Machine Learning Techniques for Chronic Kidney Disease Prophecy. IEEE Access 2020, 8, 55012–55022. [Google Scholar] [CrossRef]
- Ofori-Ntow, E.J.; Ziggah, Y.Y.; Rodrigues, M.J.; Relvas, S. A hybrid chaotic-based discrete wavelet transform and Aquila optimisation tuned-artificial neural network approach for wind speed prediction. Results Eng. 2022, 14, 100399. [Google Scholar] [CrossRef]
- Guo, Y.; Kasihmuddin, M.S.M.; Gao, Y.; Mansor, M.A.; Wahab, H.A.; Zamri, N.E.; Chen, J. YRAN2SAT: A Novel Flexible Random Satisfiability Logical Rule in Discrete Hopfield Neural Network. Adv. Eng. Softw. 2022, 171, 103169. [Google Scholar] [CrossRef]
- Bilal, M.; Masud, S.; Athar, S. FPGA Design for Statistics-Inspired Approximate Sum-of-Squared-Error Computation in Multimedia Applications. IEEE Trans. Circuits Syst. II Express Briefs 2012, 59, 506–510. [Google Scholar] [CrossRef]
- Qin, F.; Liu, P.; Niu, H.; Song, H.; Yousefi, N. Parameter estimation of PEMFC based on Improved Fluid Search Optimization Algorithm. Energy Rep. 2020, 6, 1224–1232. [Google Scholar] [CrossRef]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean Absolute Percentage Error for Regression Models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]
- Djebedjian, B.; Abdel-Gawad, H.A.A.; Ezzeldin, R.M. Global Performance of Metaheuristic Optimization Tools for Water Distribution Networks. Ain Shams Eng. J. 2021, 12, 223–239. [Google Scholar] [CrossRef]
- Karim, S.A.; Zamri, N.E.; Alway, A.; Kasihmuddin, M.S.M.; Ismail, A.I.M.; Mansor, M.A.; Hassan, N.F.A. Random satisfiability: A higher-order logical approach in discrete hopfield neural network. IEEE Access 2021, 9, 50831–50845. [Google Scholar] [CrossRef]
- de Santis, E.; Martino, A.; Rizzi, A. On component-wise dissimilarity measures and metric properties in pattern recognition. PeerJ Comput. Sci. 2022, 8, e1106. [Google Scholar] [CrossRef]
- Bazuhair, M.M.; Mohd Jamaludin, S.Z.; Zamri, N.E.; Mohd Kasihmuddin, M.S.; Mansor, M.A.; Alway, A.; Karim, S.A. Novel Hopfield Neural Network Model with Election Algorithm for Random 3 Satisfiability. Processes 2021, 9, 1292. [Google Scholar] [CrossRef]
- Abdullahi, S.; Mansor, M.A.; Sathasivam, S.; Kasihmuddin, M.S.M.; Zamri, N.E. 3-satisfiability reverse analysis method with Hopfield neural network for medical data set. In AIP Conference Proceedings 2266; American Institute of Physics: College Park, MD, USA, 2020. [Google Scholar]
- Meyer, A.d.S.; Garcia, A.A.F.; de Souza, A.P.; de Souza, C.L., Jr. Comparison of Similarity Coefficients Used for Cluster Analysis with Dominant Markers in Maize. Genet. Mol. Biol. 2004, 27, 83–91. [Google Scholar] [CrossRef]
- Gao, Y.; Guo, Y.; Romli, N.A.; Kasihmuddin, M.S.M.; Chen, W.; Mansor, M.A.; Chen, J. GRAN3SAT: Creating Flexible Higher-Order Logic Satisfiability in the Discrete Hopfield Neural Network. Mathematics 2022, 11, 1899. [Google Scholar] [CrossRef]
- Mansor, M.A.; Kasihmuddin, M.S.M.; Sathasivam, S. Enhanced Hopfield Network for Pattern Satisfiability Optimization. Int. J. Intell. Syst. Appl. 2016, 11, 27–33. [Google Scholar] [CrossRef]
- Mansor, M.A.; Kasihmuddin, M.S.M.; Sathasivam, S. VLSI Circuit Configuration Using Satisfiability Logic in Hopfield Network. Int. J. Intell. Syst. Appl. 2016, 9, 22–29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).