An h-Adaptive Poly-Sinc-Based Local Discontinuous Galerkin Method for Elliptic Partial Differential Equations
Abstract
1. Introduction
2. Approximation Spaces
2.1. Univariate Approximation Spaces
2.2. Bivariate Approximation Spaces
- For all ;
- For all ;
- There exists such that the following apply:
- -
- For all ;
- -
- for all .
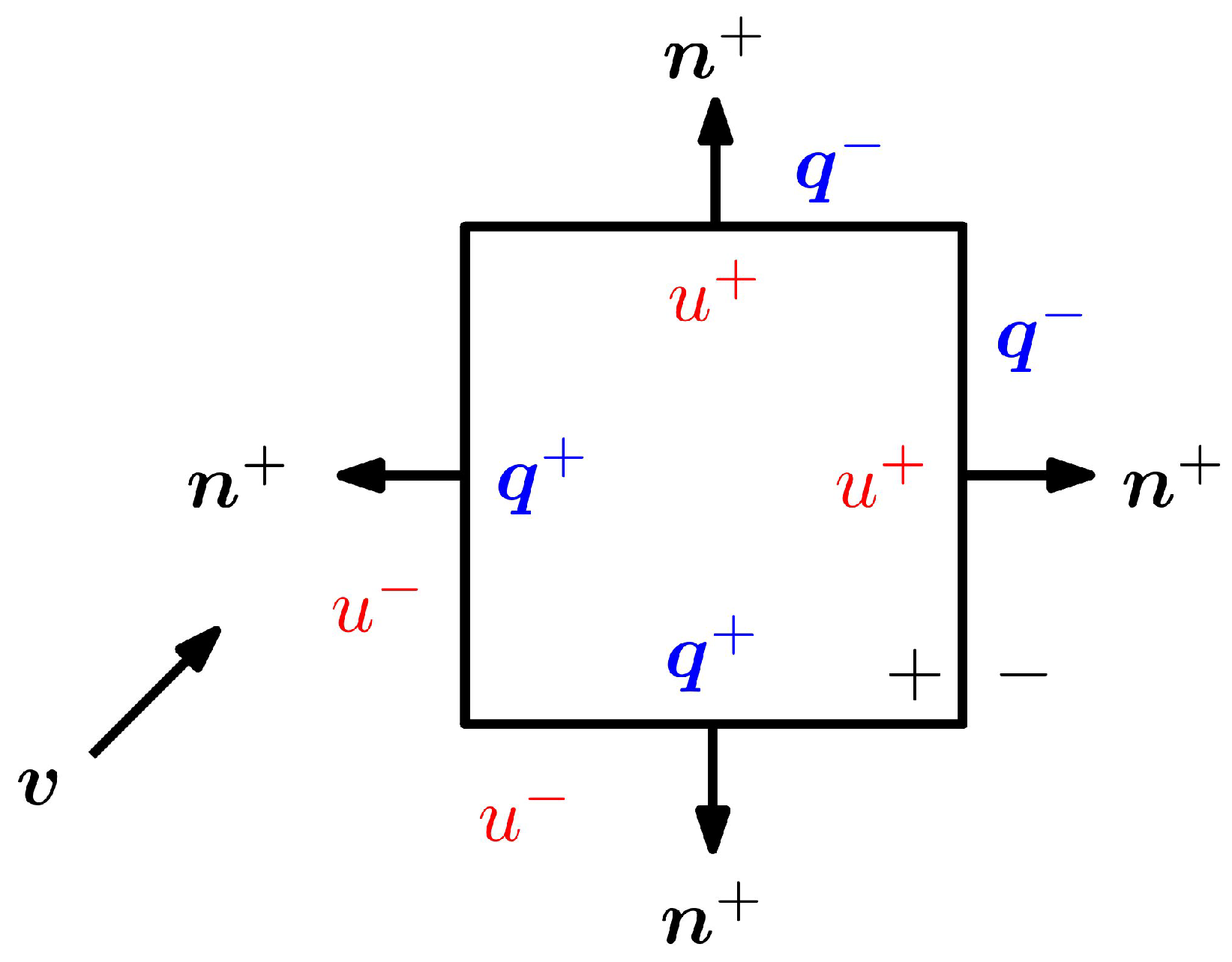
3. A Brief Overview of the Local Discontinuous Galerkin Method
4. Adaptive Poly-Sinc-Based LDG Algorithm
4.1. Local Error
4.2. Algorithm Description
| Algorithm 1: Adaptive Poly-Sinc-based LDG algorithm. |
 |
4.3. Error Analysis
4.4. Convergence Analysis of the Adaptive Algorithm
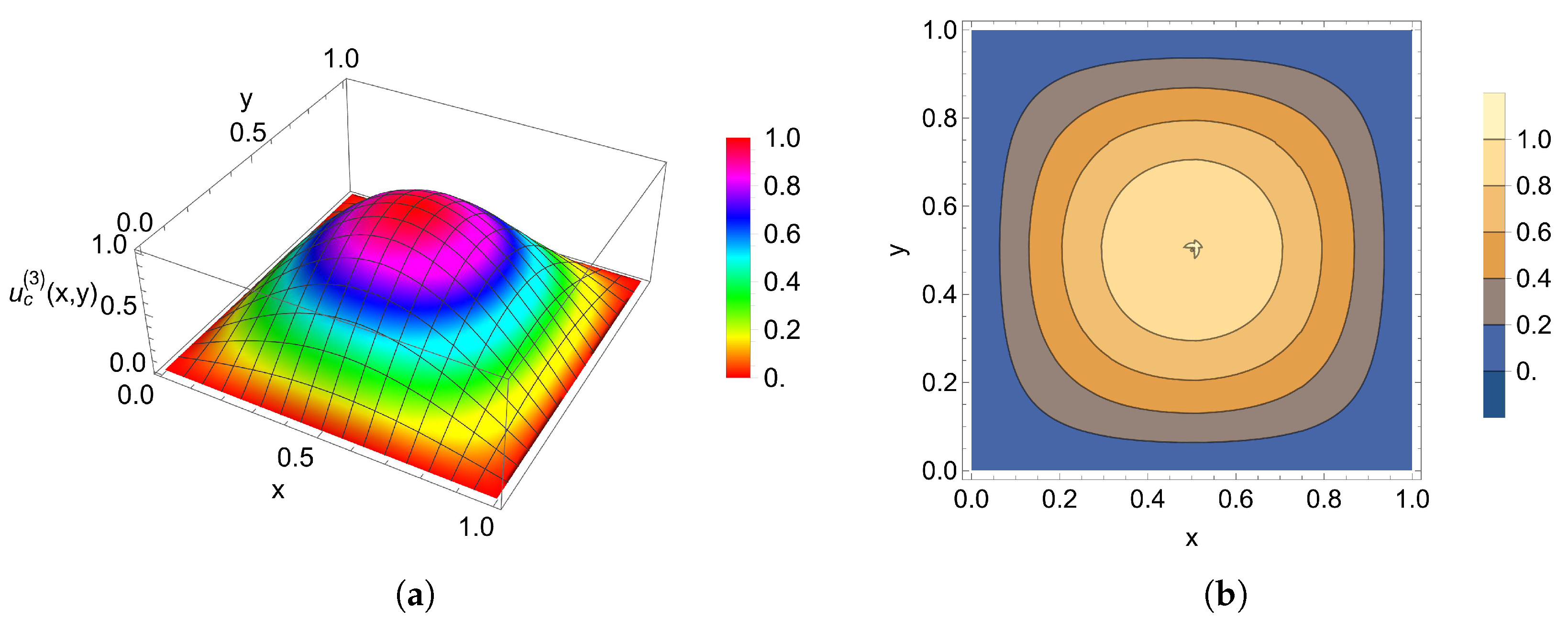
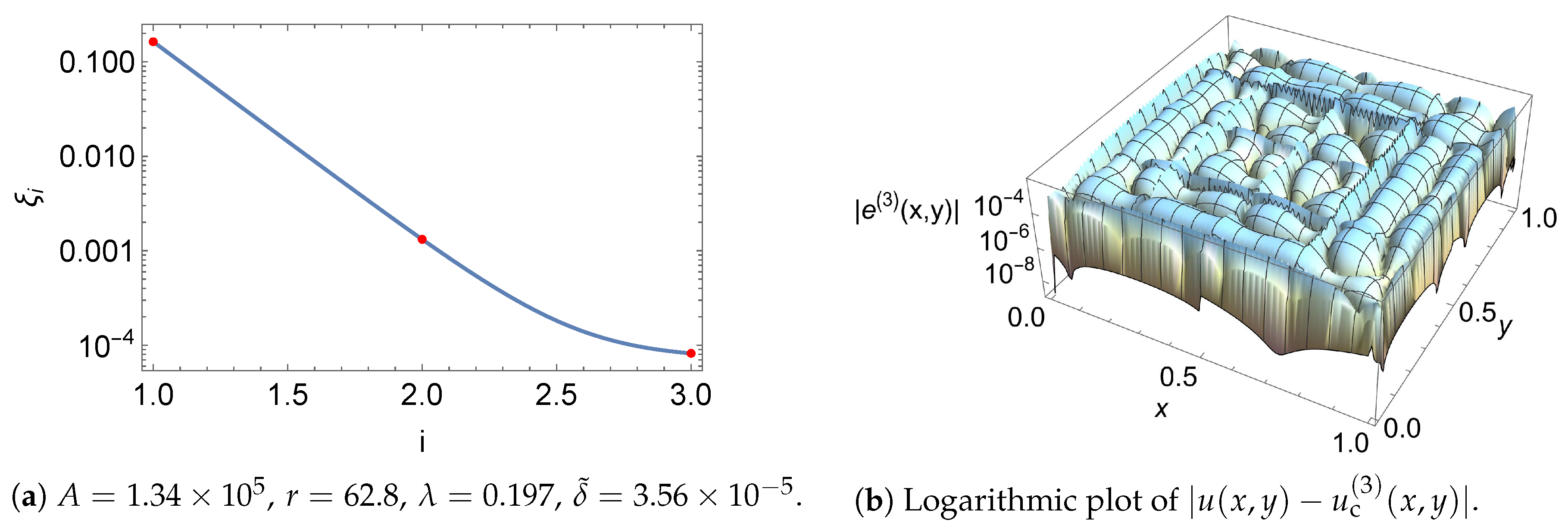
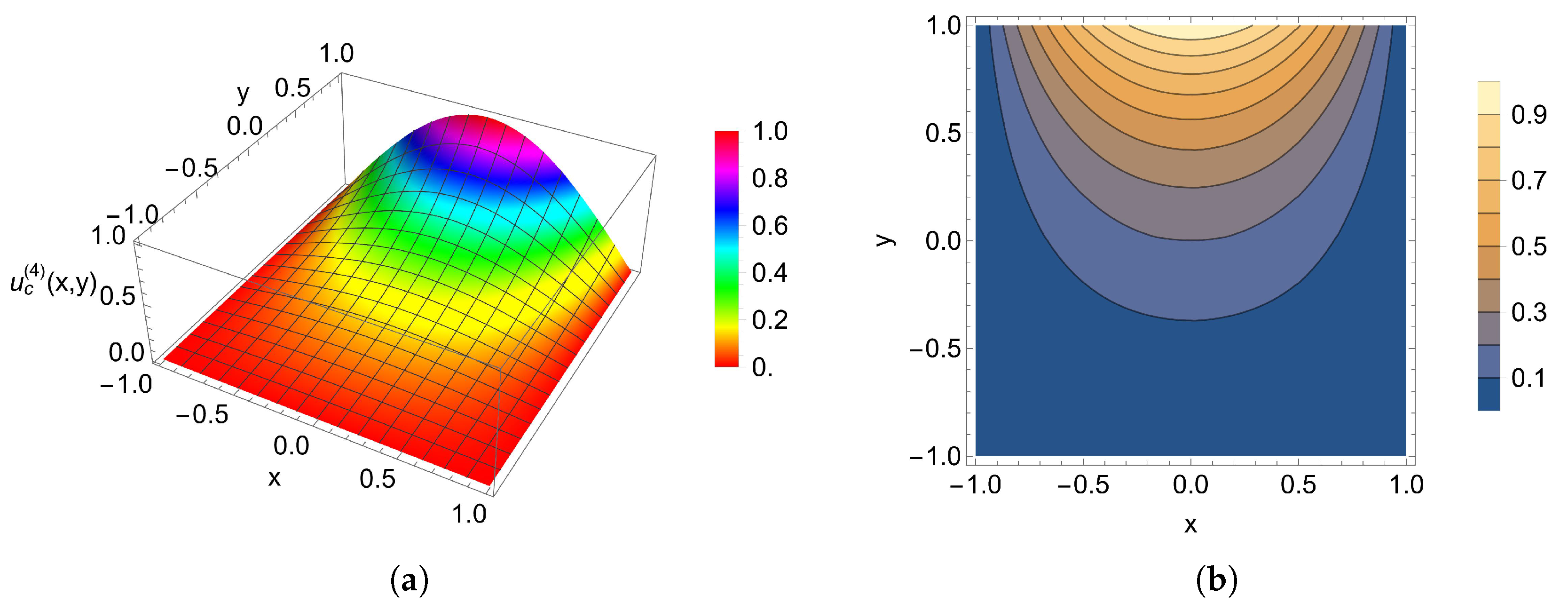
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reed, W.H.; Hill, T. Triangular Mesh Methods for the Neutron Transport Equation; Technical Report; Los Alamos Scientific Lab.: Los Alamos, NM, USA, 1973. [Google Scholar]
- Cockburn, B.; Karniadakis, G.E.; Shu, C.W. The Development of Discontinuous Galerkin Methods. In Discontinuous Galerkin Methods; Springer: Berlin/Heidelberg, Germany, 2000; pp. 3–50. [Google Scholar] [CrossRef]
- Cockburn, B.; Kanschat, G.; Perugia, I.; Schötzau, D. Superconvergence of the Local Discontinuous Galerkin Method for Elliptic Problems on Cartesian Grids. SIAM J. Numer. Anal. 2001, 39, 264–285. [Google Scholar] [CrossRef]
- Cockburn, B. Discontinuous Galerkin methods. ZAMM-J. Appl. Math. Mech. Angew. Math. Mech. Appl. Math. Mech. 2003, 83, 731–754. [Google Scholar] [CrossRef]
- Dolejší, V.; Feistauer, M. Discontinuous Galerkin Method: Analysis and Applications to Compressible Flow; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Stenger, F. Polynomial function and derivative approximation of Sinc data. J. Complex 2009, 25, 292–302. [Google Scholar] [CrossRef]
- Stenger, F.; Youssef, M.; Niebsch, J. Improved approximation via use of transformations. In Multiscale Signal Analysis and Modeling; Springer: New York, NY, USA, 2013; pp. 25–49. [Google Scholar] [CrossRef]
- Stenger, F.; El-Sharkawy, H.A.M.; Baumann, G. The Lebesgue constant for Sinc approximations. In New Perspectives on Approximation and Sampling Theory: Festschrift in Honor of Paul Butzer’s 85th Birthday; Springer International Publishing: Cham, Switzerland, 2014; pp. 319–335. [Google Scholar] [CrossRef]
- Youssef, M.; El-Sharkawy, H.A.; Baumann, G. Lebesgue constant using Sinc points. Adv. Numer. Anal. 2016, 2016. [Google Scholar] [CrossRef]
- Lybeck, N.J.; Bowers, K.L. Domain decomposition via the Sinc-Galerkin method for second order differential equations. In Domain Decomposition Methods in Scientific and Engineering Computing, Proceedings of the 7th International Conference on Domain Decomposition, Pennsylvania, PA, USA, 27–30 October 1993; American Mathematical Society: Providence, RI, USA, 1994; pp. 271–276. [Google Scholar]
- Lybeck, N.J.; Bowers, K.L. Domain decomposition in conjunction with sinc methods for Poisson’s equation. Numer. Methods Partial. Differ. Equ. 1996, 12, 461–487. [Google Scholar] [CrossRef]
- Burda, P.; Novotný, J.; Šístek, J. Precise FEM solution of a corner singularity using an adjusted mesh. Int. J. Numer. Methods Fluids 2005, 47, 1285–1292. [Google Scholar] [CrossRef]
- Youssef, M.; Baumann, G. On bivariate Poly-Sinc collocation applied to patching domain decomposition. Appl. Math. Sci. 2017, 11, 209–226. [Google Scholar] [CrossRef]
- Frei, W. How to Identify and Resolve Singularities in the Model When Meshing. 2013. Available online: https://www.comsol.com/blogs/how-identify-resolve-singularities-model-meshing/ (accessed on 28 January 2023).
- Sönnerlind, H. Singularities in Finite Element Models: Dealing with Red Spots. 2015. Available online: https://www.comsol.com/blogs/singularities-in-finite-element-models-dealing-with-red-spots/ (accessed on 28 January 2023).
- Baumann, G.; Stenger, F. Fractional calculus and Sinc methods. Fract. Calc. Appl. Anal. 2011, 14, 568–622. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C.W. The local discontinuous Galerkin method for time-dependent convection-diffusion systems. SIAM J. Numer. Anal. 1998, 35, 2440–2463. [Google Scholar] [CrossRef]
- Castillo, P.; Cockburn, B.; Perugia, I.; Schötzau, D. An A Priori Error Analysis of the Local Discontinuous Galerkin Method for Elliptic Problems. SIAM J. Numer. Anal. 2000, 38, 1676–1706. [Google Scholar] [CrossRef]
- Cockburn, B.; Kanschat, G.; Schötzau, D. The local discontinuous Galerkin method for linearized incompressible fluid flow: A review. Comput. Fluids 2005, 34, 491–506. [Google Scholar] [CrossRef]
- Yan, J.; Shu, C.W. Local discontinuous Galerkin methods for partial differential equations with higher order derivatives. J. Sci. Comput. 2002, 17, 27–47. [Google Scholar] [CrossRef]
- Castillo, P. A review of the Local Discontinuous Galerkin (LDG) method applied to elliptic problems. Appl. Numer. Math. 2006, 56, 1307–1313. [Google Scholar] [CrossRef]
- Baccouch, M. Optimal superconvergence and asymptotically exact a posteriori error estimator for the local discontinuous Galerkin method for linear elliptic problems on Cartesian grids. Appl. Numer. Math. 2021, 162, 201–224. [Google Scholar] [CrossRef]
- Cangiani, A.; Georgoulis, E.H.; Sabawi, Y.A. Adaptive discontinuous Galerkin methods for elliptic interface problems. Math. Comp. 2018, 87, 2675–2707. [Google Scholar] [CrossRef]
- Kompenhans, M.; Rubio, G.; Ferrer, E.; Valero, E. Adaptation strategies for high order discontinuous Galerkin methods based on Tau-estimation. J. Comput. Phys. 2016, 306, 216–236. [Google Scholar] [CrossRef]
- Kane, B.; Klöfkorn, R.; Dedner, A. Adaptive Discontinuous Galerkin Methods for Flow in Porous Media. In Proceedings of the Numerical Mathematics and Advanced Applications ENUMATH 2017, Voss, Norway, 25–29 September 2017; Radu, F.A., Kumar, K., Berre, I., Nordbotten, J.M., Pop, I.S., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 367–378. [Google Scholar] [CrossRef]
- Wang, F.; Ling, M.; Han, W.; Jing, F. Adaptive discontinuous Galerkin methods for solving an incompressible Stokes flow problem with slip boundary condition of frictional type. J. Comput. Appl. Math. 2020, 371, 112700. [Google Scholar] [CrossRef]
- Noventa, G.; Massa, F.; Rebay, S.; Bassi, F.; Ghidoni, A. Robustness and efficiency of an implicit time-adaptive discontinuous Galerkin solver for unsteady flows. Comput. Fluids 2020, 204, 104529. [Google Scholar] [CrossRef]
- Bassi, F.; Colombo, A.; Crivellini, A.; Fidkowski, K.J.; Franciolini, M.; Ghidoni, A.; Noventa, G. Entropy-Adjoint p-Adaptive Discontinuous Galerkin Method for the Under-Resolved Simulation of Turbulent Flows. AIAA J. 2020, 58, 3963–3977. [Google Scholar] [CrossRef]
- Bonev, B.; Hesthaven, J.S.; Giraldo, F.X.; Kopera, M.A. Discontinuous Galerkin scheme for the spherical shallow water equations with applications to tsunami modeling and prediction. J. Comput. Phys. 2018, 362, 425–448. [Google Scholar] [CrossRef]
- Beisiegel, N.; Vater, S.; Behrens, J.; Dias, F. An adaptive discontinuous Galerkin method for the simulation of hurricane storm surge. Ocean. Dyn. 2020, 70, 641–666. [Google Scholar] [CrossRef]
- Faghih-Naini, S.; Aizinger, V. p-adaptive discontinuous Galerkin method for the shallow water equations with a parameter-free error indicator. GEM-Int. J. Geomath. 2022, 13, 18. [Google Scholar] [CrossRef]
- Khalil, O.A.; Baumann, G. Discontinuous Galerkin methods using poly-sinc approximation. Math. Comput. Simul. 2021, 179, 96–110. [Google Scholar] [CrossRef]
- Khalil, O.A.; Baumann, G. Convergence rate estimation of poly-Sinc-based discontinuous Galerkin methods. Appl. Numer. Math. 2021, 165, 527–552. [Google Scholar] [CrossRef]
- Khalil, O.; El-Sharkawy, H.; Youssef, M.; Baumann, G. Adaptive piecewise Poly-Sinc methods for ordinary differential equations. Algorithms 2022, 15, 320. [Google Scholar] [CrossRef]
- Khalil, O.A.; El-Sharkawy, H.A.; Youssef, M.; Baumann, G. Adaptive piecewise Poly-Sinc methods for function approximation. Appl. Numer. Math. 2023, 186, 1–18. [Google Scholar] [CrossRef]
- Geary, R.C. The ratio of the mean deviation to the standard deviation as a test of normality. Biometrika 1935, 27, 310–332. [Google Scholar] [CrossRef]
- Stenger, F. Numerical Methods Based on Sinc and Analytic Functions; Springer Series in Computational Mathematics; Springer Science & Business Media: New York, NY, USA, 1993; Volume 20. [Google Scholar] [CrossRef]
- Stenger, F. Handbook of Sinc Numerical Methods; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar] [CrossRef]
- Youssef, M.; El-Sharkawy, H.A.; Baumann, G. Multivariate Lagrange interpolation at Sinc points: Error estimation and Lebesgue constant. J. Math. Res. 2016, 8, 4. [Google Scholar] [CrossRef]
- Baumann, G.; Stenger, F. Sinc-approximations of fractional operators: A computing approach. Mathematics 2015, 3, 444–480. [Google Scholar] [CrossRef]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis; Springer: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Youssef, M.; Baumann, G. Collocation method to solve elliptic equations, Bivariate Poly-Sinc approximation. J. Progress. Res. Math. 2016, 7, 1079–1091. [Google Scholar]
- Youssef, M. Poly-Sinc Approximation Methods. Ph.D. Thesis, German University in Cairo, Cairo, Egypt, 2017. [Google Scholar]
- Rivière, B. Discontinuous Galerkin Methods for Solving Elliptic and Parabolic Equations: Theory and Implementation; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Adjerid, S.; Chaabane, N. An improved superconvergence error estimate for the LDG method. Appl. Numer. Math. 2015, 98, 122–136. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Haasdonk, B.; Ohlberger, M. Reduced basis method for finite volume approximations of parametrized linear evolution equations. M2AN Math. Model. Numer. Anal. 2008, 42, 277–302. [Google Scholar] [CrossRef]
- Grepl, M.A. Model order reduction of parametrized nonlinear reaction–diffusion systems. Comput. Chem. Eng. 2012, 43, 33–44. [Google Scholar] [CrossRef]
- Sleeman, M.K.; Yano, M. Goal-oriented model reduction for parametrized time-dependent nonlinear partial differential equations. Comput. Methods Appl. Mech. Eng. 2022, 388, 114206. [Google Scholar] [CrossRef]
- Nochetto, R.H.; Siebert, K.G.; Veeser, A. Theory of adaptive finite element methods: An introduction. In Proceedings of the Multiscale, Nonlinear and Adaptive Approximation; DeVore, R., Kunoth, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 409–542. [Google Scholar] [CrossRef]
- Walpole, R.E.; Myers, R.H.; Myers, S.L.; Ye, K. Probability and Statistics for Engineers and Scientists, 9th ed.; Pearson Education, Inc.: Boston, MA, USA, 2012. [Google Scholar]
- Carey, G.F.; Humphrey, D.L. Finite element mesh refinement algorithm using element residuals. In Proceedings of the Codes for Boundary-Value Problems in Ordinary Differential Equations; Childs, B., Scott, M., Daniel, J.W., Denman, E., Nelson, P., Eds.; Springer: Berlin/Heidelberg, Germany, 1979; pp. 243–249. [Google Scholar] [CrossRef]
- Carey, G.F. Adaptive refinement and nonlinear fluid problems. Comput. Methods Appl. Mech. Eng. 1979, 17–18, 541–560. [Google Scholar] [CrossRef]
- Carey, G.F.; Humphrey, D.L. Mesh refinement and iterative solution methods for finite element computations. Int. J. Numer. Methods Eng. 1981, 17, 1717–1734. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 10th printing ed.; Dover Publications, Inc.: New York, NY, USA, 1972. [Google Scholar]
- Youssef, M.; Pulch, R. Poly-Sinc solution of stochastic elliptic differential equations. J. Sci. Comput. 2021, 87, 82. [Google Scholar] [CrossRef]
- Rudin, W. Functional Analysis; McGraw-Hill, Inc.: New York, NY, USA, 1973. [Google Scholar]
- Bartle, R.G.; Sherbert, D.R. Introduction to Real Analysis, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Wolfram Research, Inc. Mathematica; Version 13.0; Wolfram Research, Inc.: Champaign, IL, USA, 2021. [Google Scholar]
- Arndt, D.; Bangerth, W.; Feder, M.; Fehling, M.; Gassmöller, R.; Heister, T.; Heltai, L.; Kronbichler, M.; Maier, M.; Munch, P.; et al. Reference Documentation for deal.II Version 9.4.1: The Step-12 Tutorial Program. 2023. Available online: https://www.dealii.org/current/doxygen/deal.II/step_12.html (accessed on 19 January 2023).
- Dell’Accio, F.; Di Tommaso, F.; Nouisser, O.; Siar, N. Solving Poisson equation with Dirichlet conditions through multinode Shepard operators. Comput. Math. Appl. 2021, 98, 254–260. [Google Scholar] [CrossRef]
- Lybeck, N.J. Sinc Domain Decomposition Methods for Elliptic Problems. Ph.D. Thesis, Montana State University, Bozeman, Montana, 1994. [Google Scholar]
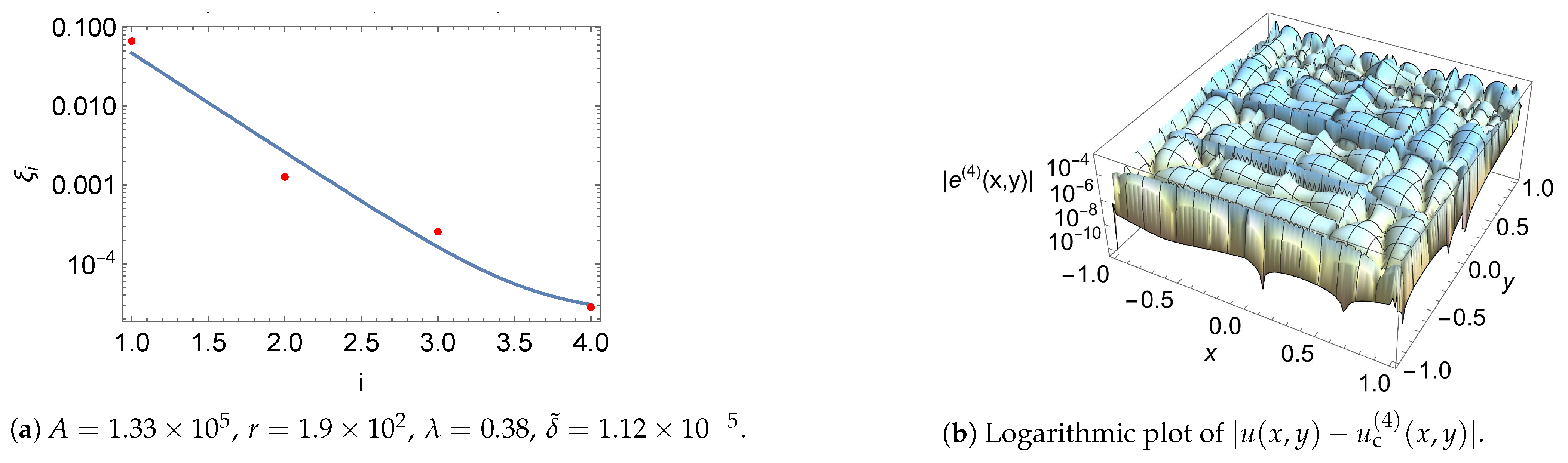
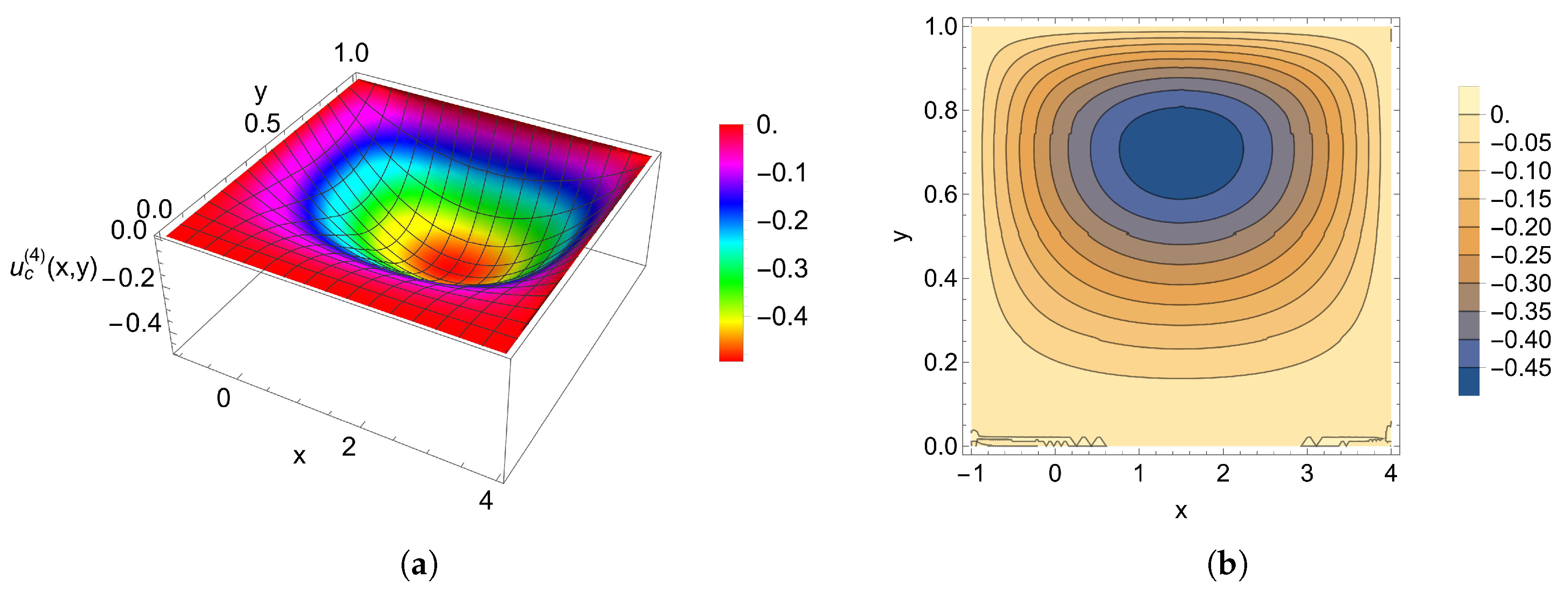
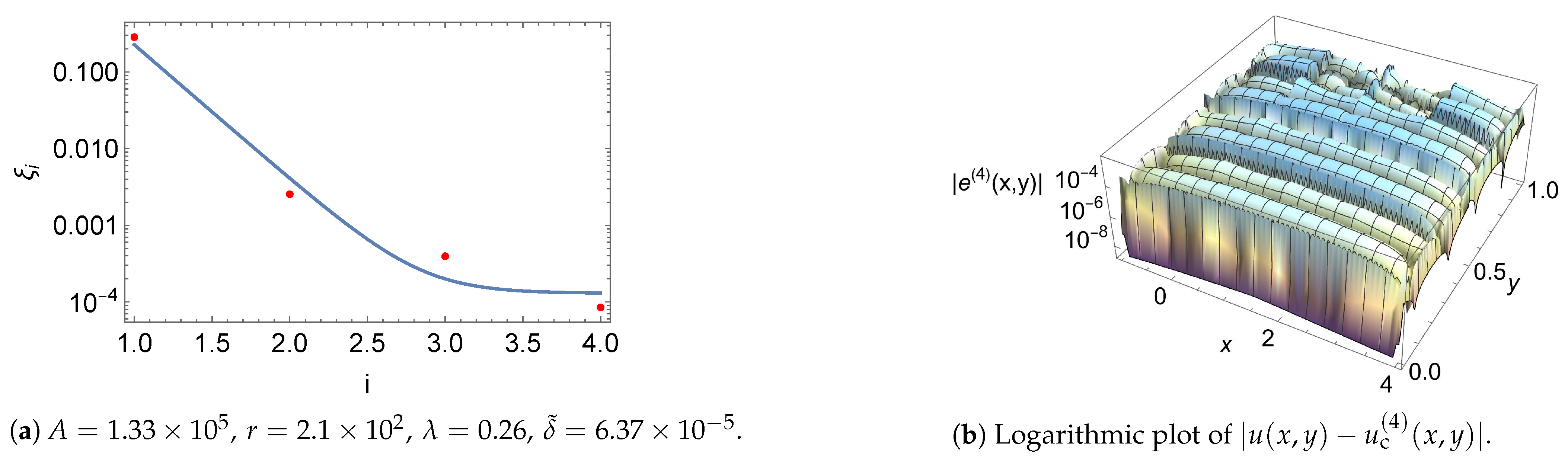
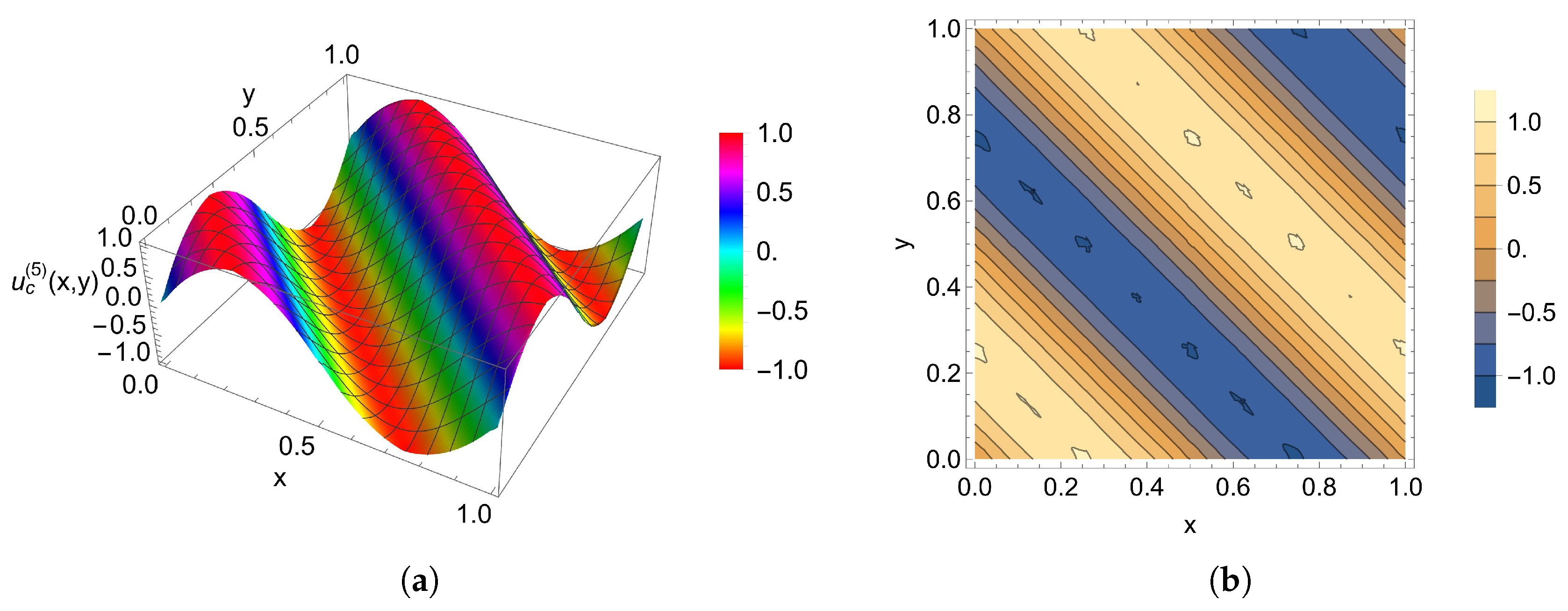
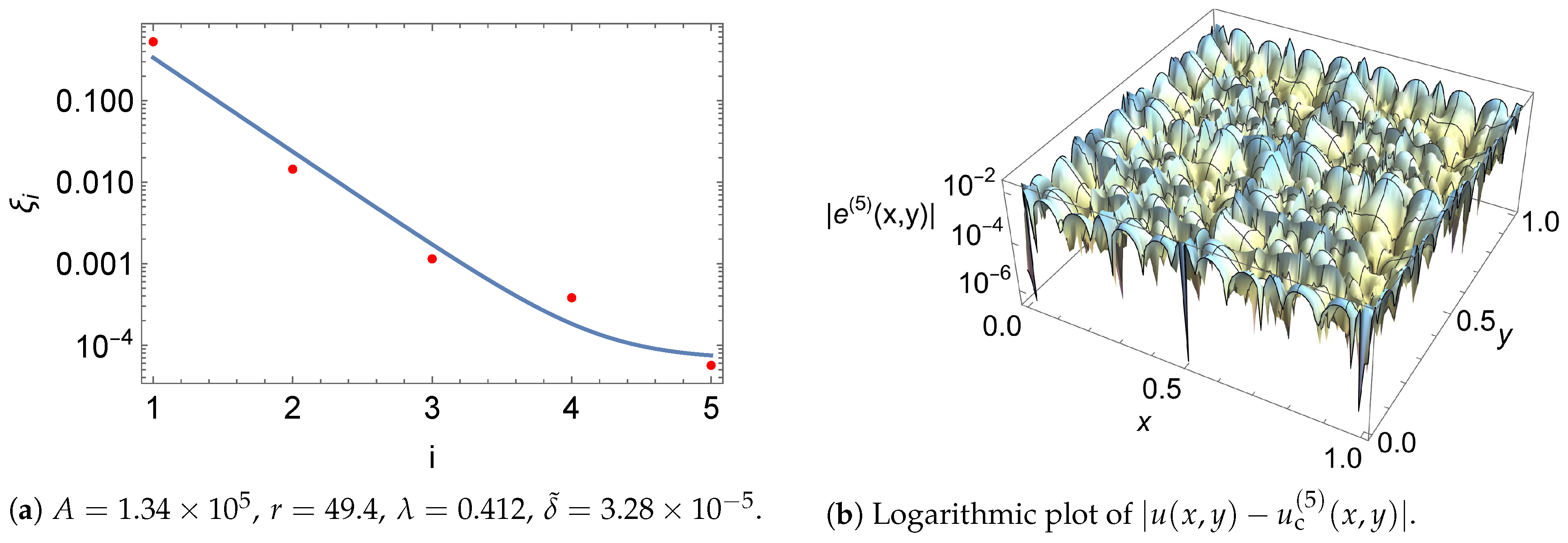
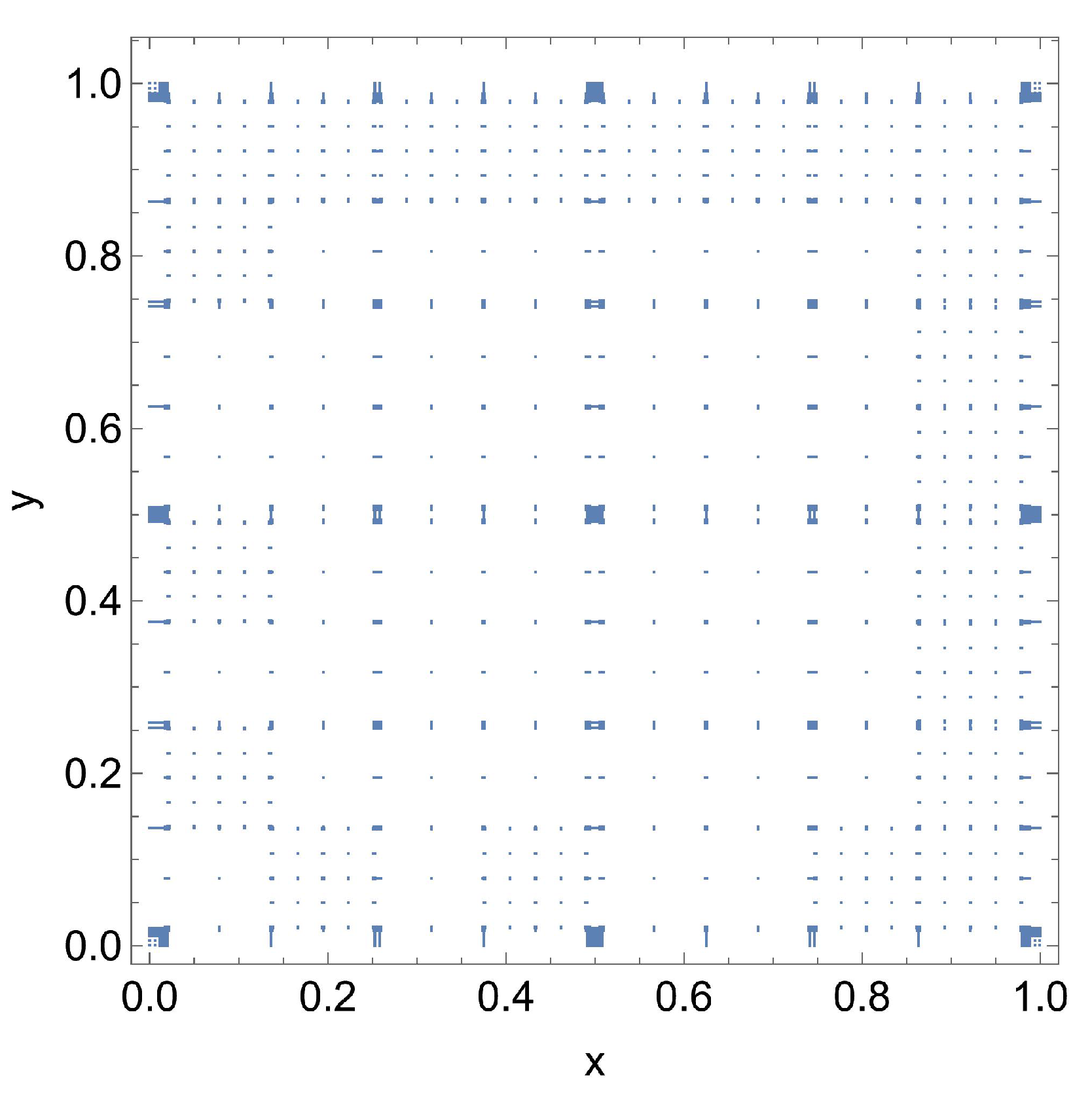
| i | |
|---|---|
| 2 | |
| 3 |
| i | |
|---|---|
| 2 | |
| 3 | |
| 4 |
| i | |
|---|---|
| 2 | |
| 3 | |
| 4 |
| i | |
|---|---|
| 2 | |
| 3 | |
| 4 | |
| 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalil, O.A.; Baumann, G. An h-Adaptive Poly-Sinc-Based Local Discontinuous Galerkin Method for Elliptic Partial Differential Equations. Axioms 2023, 12, 227. https://doi.org/10.3390/axioms12030227
Khalil OA, Baumann G. An h-Adaptive Poly-Sinc-Based Local Discontinuous Galerkin Method for Elliptic Partial Differential Equations. Axioms. 2023; 12(3):227. https://doi.org/10.3390/axioms12030227
Chicago/Turabian StyleKhalil, Omar A., and Gerd Baumann. 2023. "An h-Adaptive Poly-Sinc-Based Local Discontinuous Galerkin Method for Elliptic Partial Differential Equations" Axioms 12, no. 3: 227. https://doi.org/10.3390/axioms12030227
APA StyleKhalil, O. A., & Baumann, G. (2023). An h-Adaptive Poly-Sinc-Based Local Discontinuous Galerkin Method for Elliptic Partial Differential Equations. Axioms, 12(3), 227. https://doi.org/10.3390/axioms12030227






