On the Estimation of the Binary Response Model

Abstract

The binary logistic regression model (LRM) is practical in situations when the response variable (RV) is dichotomous. The maximum likelihood estimator (MLE) is generally considered to estimate the LRM parameters. However, in the presence of multicollinearity (MC), the MLE is not the correct choice due to its inflated standard deviation (SD) and standard errors (SE) of the estimates. To combat MC, commonly used biased estimators, i.e., the Ridge estimators (RE) and Liu estimators (LEs), are preferred. However, most of the time, the traditional LE attains a negative value for its Liu parameter (LP), which is considered to be a major drawback. Therefore, to overcome this issue, we proposed a new adjusted LE for the binary LRM. Owing to numerical evaluation purposes, Monte Carlo simulation (MCS) study is performed under different conditions where bias and mean squared error are the performance criteria. Findings showed the superiority of our proposed estimator in comparison with the other estimation methods due to the existence of high but imperfect multicollinearity, which clearly means that it is consistent when the regressors are multicollinear. Furthermore, the findings demonstrated that whenever there is MC, the MLE is not the best choice. Finally, a real application is being considered to be evidence for the advantage of the intended estimator. The MCS and the application findings pointed out that the considered adjusted LE for the binary logistic regression model is a more efficient estimation method whenever the regressors are highly multicollinear.

1. Introduction

The binary LRM (BLRM) is a common RM, and it is preferred in situations where the RV is dichotomous or binary. Forecasting a dichotomous RV is vital in epidemiology and medicine [1,2]. For example, a set of risk factors such as cholesterol and blood pressure effect on the possibility of undergoing a heart attack. The method of MLE is commonly employed to estimate the binary LRM [2,3]. In the case of MC, the variance becomes inflated, and the standard errors become high, and consequently, the t-statistic and F-ratios become insignificant [3,4,5]. To overcome the issue of MC, different biased techniques are available in the writings. One of them constructing on ridge regression (RR), see [6], for the linear RM. The logistic RR was first introduced in [7] via the results of [6]. For the same purpose three biased estimators are considered [3]. Lee and Silvapulle [8] introduced the two ridge parameters for the logistic RR estimator (LRRE). As in the LRRE, the ridge parameter plays a very important role. After these studies, many researchers focused on the collection of the ridge parameter in the LRRE [9,10,11,12,13,14]. Liu [15] discussed some limitations of the RRE and proposed another alternative estimator called the LE for handling the issue of multicollinearity in a better way. The LE for the BLRM was adapted and called the logistic LE (LLE), [16]. The theoretical and numerical properties of the LLE and its comparison with the MLE and LRRE have been discussed.

In the LLE, the LP (d) plays a main character in the estimation of the LLE and should lie between 0 and 1, i.e., $0<d<1.$ Sometimes, the Liu parameter produces negative and zero values that affect the efficiency of the LLE [17]. Several authors introduced various types of Liu estimators in the BLRM to improve the efficiency of the LE [18,19,20,21,22]. These modified Liu estimators also often produced zero values for the Liu parameter. To overcome the limitations of the available LEs, Lukman et al. [23] introduced the modified one-parameter LE for the linear RM.

In this article, we propose a new adjusted LLE (ALLE) for the BLRM. Its theoretical properties are investigated. Furthermore, the properties of the new estimator are assessed via a theoretical comparison and compared with other estimation methods. The matrix mean squared error (MMSE) and the scalar mean squared error (MSE) are used as the performance evaluation criteria. To investigate the new estimator a MCS study has been performed. The forthcoming sections are organized as follows: Section 2 presents the construction of the proposed estimator for the BLRM with a theoretical comparison. A MCS study is presented in Section 3. Section 4 is devoted to analyzing prostate cancer data. Section 5 ends with some conclusions.

2. Statistical Method

Following [7,24,25], the BLRM is defined as

$$y_i={\delta }_i+{\epsilon }_i, i=1,\dots ,n,$$

where ${\epsilon }_i$ has zero mean and variance ${\omega }_i={\delta }_i\left(1-{\delta }_i\right)$ with expectation ${\delta }_i$ of $y_i$ and are independent for each $i$. Considering, the ith value of RV to be distributed as Bernoulli $Be\left({\delta }_i\right)$, with

$${\delta }_i=\frac{exp\left(x_i^t\xi \right)}{1+exp\left(x_i^t\xi \right)}, i=1,\dots ,n,$$

(1)

where $\delta ={\left({\delta }_i\right)}_{i=1,2,\dots ,n}$, and $X={\left(x_i\right)}_{i=1,2,\dots ,n}{}^t$ is the $n\times p$ data matrix with $x_i={\left(1,x_{1i},\dots ,x_{pi}\right)}^t$; and $\xi ={\left({\xi }_j\right)}_{j=0,1,\dots p}{}^t$ is considered to be the $\left(p+1\right)$ vector of regression coefficients. The regression coefficients vector $\xi$ is usually estimated via the MLE method. The logarithm of the likelihood function for Equation (1) is computed as

$$H={\sum }_{i=1}^n{y}_{i}log\left({\delta }_i\right)+\left(1-y_i\right)log\left(1-{\delta }_i\right).$$

(2)

Let ${\widehat{\delta }}^T={\left({\widehat{\delta }}_i^T\right)}_{i=1,2,\dots ,n}$ be the estimates of $\delta$ at the T^th step, using ${\widehat{\xi }}^T$ and ${\widehat{V}}^T=diag\left({\widehat{\delta }}_i^T\left(1-{\widehat{\delta }}_i^T\right)\right).$ The following iterative algorithm is well define [26],

$${\widehat{\xi }}^{T+1}={\widehat{\xi }}^T+{\left(X^t\widehat{V}X\right)}^{-1}{X}^T{\widehat{V}}^T\left(y-{\widehat{\delta }}^T\right),$$

(3)

The Equation (3) can be written as

$${\widehat{\xi }}_{MLE}={\left(\mathsf{{\rm Y}}\right)}^{-1}{X}^t\widehat{V}\widehat{z},$$

(4)

with $\mathsf{{\rm Y}}=X^t\widehat{V}X$ and $\widehat{z}={\left(z_{\mathrm{i}}\right)}_{i=1,2,\dots ,n}$ where ${\eta }_i=x_i^t\xi$, while $z_i={\eta }_i+\left(y_i-{\delta }_i\right)\left(\partial {\eta }_i/\partial {\delta }_i\right)$. ${\widehat{\xi }}_{MLE}$ has asymptotic normal distribution as ${\widehat{\xi }}_{MLE}~N\left(\beta ,{\left(\mathsf{{\rm Y}}\right)}^{-1}\right)$ [8].

Let $\mathbb{Q}$ be the orthogonal matrix that has the eigenvectors of $\mathsf{{\rm Y}}$ as columns. Then the covariance and MMSE of the ${\widehat{\xi }}_{MLE}$ are

$$Cov\left({\widehat{\xi }}_{MLE}\right)={\mathsf{{\rm Y}}}^{-1} \mathrm{and} MMSE\left({\widehat{\xi }}_{MLE}\right)=\mathbb{Q}{\mathsf{\Gamma }}^{-1}{\mathbb{Q}}^t.$$

(5)

The scalar MSE of the ${\widehat{\xi }}_{MLE}$ is

$$MSE\left({\widehat{\xi }}_{MLE}\right)=E{\left({\widehat{\xi }}_{MLE}-\xi \right)}^t\left({\widehat{\xi }}_{MLE}-\xi \right)=tr\left(\mathbb{Q}{\mathsf{\Gamma }}^{-1}{\mathbb{Q}}^t\right)={\sum }_{j=1}^r\frac{1}{{\mu }_j},$$

(6)

where $\mathsf{\Gamma }=diag\left({\mu }_1, {\mu }_2,\dots ,{\mu }_r\right)$.

In the case of high correlated regressors, the matrix $\mathsf{{\rm Y}}$ becomes ill-conditioned, which causes the problem of multicollinearity. The LRRE is defined by Schaefer et al. [7] as a simple extension of Hoerl and Kennard [6] to treat multicollinearity effects as

$${\widehat{\xi }}_{LRRE}=R_k{\widehat{\xi }}_{MLE},$$

(7)

where $R_k={\left(\mathsf{{\rm Y}}+k{I}_r\right)}^{-1}\left(\mathsf{{\rm Y}}\right)$ with the ridge parameter k $(k>0)$ and identity matrix $I_r$. The bias vector (BV), covariance matrix (CM) and MMSE of (7) are

$$Bias\left({\widehat{\xi }}_{LRRE}\right)=-k\mathbb{Q}{\mathsf{\Gamma }}_k^{-1}\xi ,$$

(8)

$$Cov\left({\widehat{\xi }}_{LRRE}\right)=\mathbb{Q}{\mathsf{\Gamma }}_k^{-1}{\mathsf{\Gamma }\mathsf{\Gamma }}_k^{-1}{\mathbb{Q}}^t$$

(9)

and

$$\begin{gathered} MMSE\left({\widehat{\xi }}_{LRRE}\right)=R_k{\left(\mathsf{{\rm Y}}\right)}^{-1}{R}_k^t+Bias\left({\widehat{\xi }}_{LRRE}\right)Bias{\left({\widehat{\xi }}_{LRRE}\right)}^t \\ =\mathbb{Q}{\mathsf{\Gamma }}_k^{-1}{\mathsf{\Gamma }\mathsf{\Gamma }}_k^{-1}{\mathbb{Q}}^t+k^2\mathbb{Q}{\mathsf{\Gamma }}_k^{-1}\xi {\xi }^t{\mathsf{\Gamma }}_k^{-1}{\mathbb{Q}}^t, \end{gathered}$$

(10)

where ${\mathsf{\Gamma }}_k=diag\left({\mu }_1+k, {\mu }_2+k, \dots ,{\mu }_r+k\right)$. From (10) by applying the $tr \left(.\right)$ operator, we obtain the scalar MSE of the LRRE as

$$MSE\left({\widehat{\xi }}_{LRRE}\right)=tr \left\{MMSE\left({\widehat{\xi }}_{LRRE}\right)\right\}={\sum }_{j=1}^r\frac{{\mu }_j}{{\left({\mu }_j+k\right)}^2}+k^2{\sum }_{j=1}^r\frac{{\tau }_j^2}{{\left({\mu }_j+k\right)}^2},$$

(11)

where $\tau ={\mathbb{Q}}^t\xi$ and k (k > 0) is the Hoerl and Kennard [6] ridge parameter. Optimizing the Equation (11) with respect to k yields

$$k=\frac{1}{{\sum }_{j=1}^r{\widehat{\tau }}_j^2}.$$

(12)

Another estimator that treats the multicollinearity better than the LRRE was given by Liu [25] and Mansson et al. [11] for the BRLM that is named as the LLE and is defined by

$${\widehat{\xi }}_{LLE}=F_d{\widehat{\xi }}_{MLE},$$

(13)

where $F_d={\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\left(\mathsf{{\rm Y}}+d{I}_r\right)$, and $d\left(0\le d<1\right)$ is the LP. The BV and CM of (13) are given respectively by

$$Bias\left({\widehat{\xi }}_{LLE}\right)=\mathbb{Q}\left(d-1\right){\mathsf{\Gamma }}_I^{-1}\xi .$$

(14)

$$Cov\left({\widehat{\xi }}_{LLE}\right)=\mathbb{Q}{\mathsf{\Gamma }}_I^{-1}{\mathsf{\Gamma }}_d{\mathsf{\Gamma }}^{-1}{\mathsf{\Gamma }}_d{\mathsf{\Gamma }}_I^{-1}{\mathbb{Q}}^t.$$

(15)

By using (14) and (15), the MMSE is defined as

$$\begin{array}{c}MMSE\left({\widehat{\xi }}_{LLE}\right)=F_d{\mathsf{{\rm Y}}}^{-1}{F}_d^t+Bias\left({\widehat{\xi }}_{LLE}\right)Bias{\left({\widehat{\xi }}_{LLE}\right)}^t\hfill \\ =\mathbb{Q}{\mathsf{\Gamma }}_I^{-1}{\mathsf{\Gamma }}_d{\mathsf{\Gamma }}^{-1}{\mathsf{\Gamma }}_d{\mathsf{\Gamma }}_I^{-1}{\mathbb{Q}}^t+{\left(d-1\right)}^2\mathbb{Q}{\mathsf{\Gamma }}_I^{-1}\xi {\xi }^t{\mathsf{\Gamma }}_I^{-1}{\mathbb{Q}}^t,\hfill \end{array}$$

(16)

where ${\mathsf{\Gamma }}_I=diag\left({\mu }_1+1, {\mu }_2+1, \dots ,{\mu }_r+1\right)$, and ${\mathsf{\Gamma }}_d=diag\left({\mu }_1+d, {\mu }_2+d, \dots ,{\mu }_r+d\right)$. The scalar MSE of the LLE is given by

$$MSE\left({\widehat{\xi }}_{LLE}\right)=tr\left\{MMSE\left({\widehat{\xi }}_{LLE}\right)\right\}={\sum }_{j=1}^r\frac{{\left({\mu }_j+d\right)}^2}{{\mu }_j{\left({\mu }_j+1\right)}^2}+{\left(d-1\right)}^2{\sum }_{j=1}^r\frac{{\tau }_j^2}{{\left({\mu }_j+1\right)}^2},$$

(17)

where d is the LP. Optimizing the Equation (17) with respect to d yields $d={\sum }_{j=1}^r\left({\tau }_j^2-1\right)/\left({\tau }_j^2+1/{\mu }_j\right)$. For $d=1$, we obtain ${\widehat{\xi }}_{LLE}={\widehat{\xi }}_{MLE}$.

2.1. The Proposed Estimator

In the LLE, most of the time, the value of d is negative, which affects the BLRM estimation under multicollinearity. This estimator has been proposed for the Poisson RM [27]. Therefore, following [27], we define the adjusted logistic Liu estimator (ALLE), which is given as

$${\widehat{\xi }}_{ALLE}=A_d {\widehat{\xi }}_{MLE},$$

(18)

where $A_d={\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\left(\mathsf{{\rm Y}}-d_0{I}_r\right),$ and $0<d_0<1$ is the Liu parameter for the ALLE. The new estimator gives a genuine refinement in the efficacy of the BLRM coefficients. The BV, CM, MSE matrix and scalar MSE of the ALLE are given in Equations (19)–(22), respectively.

$$Bias\left({\widehat{\xi }}_{ALLE}\right)=-\left(d_0-1\right){\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\xi .$$

(19)

$$Cov\left({\widehat{\xi }}_{ALLE}\right)={\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\left(\mathsf{{\rm Y}}-d_0{I}_r\right) {\left(\mathsf{{\rm Y}}\right)}^{-1}\left(\mathsf{{\rm Y}}-d_0{I}_r\right){\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}.$$

(20)

$$\begin{array}{c}MMSE\left({\widehat{\xi }}_{ALLE}\right)=Cov\left({\widehat{\xi }}_{ALLE}\right)+Bias\left({\widehat{\xi }}_{ALLE}\right)Bias{\left({\widehat{\xi }}_{ALLE}\right)}^t\\ ={\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\left(\mathsf{{\rm Y}}-d_0{I}_r\right) {\left(\mathsf{{\rm Y}}\right)}^{-1}\left(\mathsf{{\rm Y}}-d_0{I}_r\right){\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}+{\left(d_0-1\right)}^2{\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\beta {\beta }^t{\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}.\end{array}$$

(21)

$$MSE\left({\widehat{\xi }}_{ALLE}\right)=tr\left\{MMSE\left({\widehat{\xi }}_{ALLE}\right)\right\}={\sum }_{j=1}^r\frac{{\left({\mu }_j-d_0\right)}^2}{{\mu }_j{\left({\mu }_j+1\right)}^2}+{\left(d_0-1\right)}^2{\sum }_{j=1}^r\frac{{\tau }_j^2}{{\left({\mu }_j+1\right)}^2}.$$

(22)

2.2. Theoretical Comparison

Proposition 2.1.

Let M > 0, i.e., M is a positive definite (p,d) matrix. Then$M-\tau {\tau }^t\ge 0$if and only if${\tau }^t{M}^{-1}\tau \le 1$for some vector $\tau$ [28].

Proposition 2.2.

Let${\widehat{\theta }}_1=B_{1}y$and${\widehat{\theta }}_2=B_{2}y$be estimators of $\theta$. Suppose that $D=Cov({\widehat{\theta }}_1)-Cov\left({\widehat{\theta }}_2\right)>0$, where $Cov({\widehat{\theta }}_1)$ and $Cov\left({\widehat{\theta }}_2\right)$ represents the CM of${\widehat{\theta }}_1$and ${\widehat{\theta }}_2$, respectively. Then,$MMSE\left({\widehat{\theta }}_1\right)-MMSE\left({\widehat{\theta }}_2\right)>0$if and only if$c_2^t{\left(D+c_2{c}_2^t\right)}^{-1}{c}_2<1,$where$c_2$is the bias whereas$MMSE\left({\widehat{\theta }}_j\right)=Cov\left({\widehat{\theta }}_j\right)+c_j{c}_j^t,$where$c_j$is the BV of${\widehat{\theta }}_j$[3].

Theorem 2.1.

For the BLRM, if $0<d_0<1$, then${\widehat{\xi }}_{ALLE}$is better than ${\widehat{\xi }}_{MLE}$; that is,${\Delta }_1=MMSE\left({\widehat{\xi }}_{MLE}\right)-MMSE\left({\widehat{\xi }}_{ALLE}\right)>0$if and only if $b_{ALLE}^t{\left[\left({\mathsf{{\rm Y}}}^{-1}-{\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\left(\mathsf{{\rm Y}}-d_0{I}_r\right){\mathsf{{\rm Y}}}^{-1}\left(\mathsf{{\rm Y}}-d_0{I}_r\right){\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\right)\right]}^{-1}{b}_{ALLE}<1$, where$b_{ALLE}=-\left(d_0-1\right){\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\xi$.

Proof: 

See Appendix A.  □

Theorem 2.2.

Under the BLRM, if$k>0$and$0<d_0<1$, then${\widehat{\xi }}_{ALLE}$is better than${\widehat{\xi }}_{LRRE}$; that is,${\Delta }_2=MMSE\left({\widehat{\xi }}_{LRRE}\right)-MMSE\left({\widehat{\xi }}_{ALLE}\right)>0$if and only if$b_{ALLE}^t\left[\left(\begin{array}{c}{\left(\mathsf{{\rm Y}}+k{I}_r\right)}^{-1}\mathsf{{\rm Y}}{\left(\mathsf{{\rm Y}}+k{I}_r\right)}^{-1}-{\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\left(\mathsf{{\rm Y}}-d_0{I}_r\right)\\ {\mathsf{{\rm Y}}}^{-1}\left(\mathsf{{\rm Y}}-d_0{I}_r\right){\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\end{array}\right)\right]b_{ALLE}<1,$where$b_{ALLE}=-\left(d_0-1\right){\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\xi$.

Proof: 

See Appendix A.  □

Theorem 2.3.

Under the BLRM, if$0\le d<1$and$0<d_0<1$, then${\widehat{\xi }}_{ALLE}$is better than${\widehat{\xi }}_{LLE}$; that is,${\Delta }_3=MMSE\left({\widehat{\xi }}_{LLE}\right)-MMSE\left({\widehat{\xi }}_{ALLE}\right)>0$if and only if$b_{ALLE}^t\left[\left(\begin{array}{c}{\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\left(\mathsf{{\rm Y}}+d{I}_r\right) {\left(\mathsf{{\rm Y}}\right)}^{-1}\left(\mathsf{{\rm Y}}+d{I}_r\right){\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\\ -{\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\\ \left(\mathsf{{\rm Y}}-d_0{I}_r\right){\mathsf{{\rm Y}}}^{-1}\left(\mathsf{{\rm Y}}-d_0{I}_r\right){\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\end{array}\right)\right]b_{ALLE}<1$, where$b_{ALLE}=-\left(d_0-1\right){\left(\mathsf{{\rm Y}}+I_r\right)}^{-1}\xi$.

Proof: 

See Appendix A.  □

2.3. Parameter Estimation

In the literature different methods are employed to optimize the biasing parameters; see [17,20,29,30]. Computing the critical points of the Equation (22) with respect to $d_0$, we obtain the jth term as

$$d_0^j=\frac{{\mu }_j\left(1+{\tau }_j^2\right)}{1+{\tau }_j^2{\mu }_j}.$$

(23)

In (23), replacing ${\widehat{\mu }}_j$ and ${\widehat{\tau }}_j$ by their unbiased estimators, we obtain

$${\widehat{d}}_0^j=\frac{{\widehat{\mu }}_j\left(1+{\widehat{\tau }}_j^2\right)}{1+{\widehat{\tau }}_j^2{\widehat{\mu }}_j}.$$

(24)

For practical considerations, we consider the minimum value of (24) as

$${\widehat{d}}_0^{min}=min\left(\frac{{\widehat{\mu }}_j\left(1+{\widehat{\tau }}_j^2\right)}{1+{\widehat{\tau }}_j^2{\widehat{\mu }}_j}\right).$$

(25)

3. Simulation

3.1. Design

Here the simulation study is designed, and general layout is given. The comparison criteria is the simulated MSE of the estimators, i.e., MLE, LRRE, LLE and ALLE, when the regressors are multicollinear. Considering $z_{ij}$ to be the independent standard normal pseudo-random numbers and following [2,14,23], the EVs with various levels of correlation can be generated via the following expression:

$$x_{ij}={\left(1-{\rho }^2\right)}^{1/2}{z}_{ij}+\rho z_{i\left(j+1\right)}, i=1, \dots , n;j=1, \dots , r ,$$

(26)

where $\rho$ is select so as ${\rho }^2$ be the correlation between any two explanatories. For simulation, we select four different values of $\rho$: 0.80; 0.90; 0.95; 0.99. Four different sample size are considered $n: 50; 100; 200$; 400. Moreover, we also consider different number of EVs $p:3;6;12$, and $\beta$ is selected to be the eigenvector of the matrix $\mathcal{F}$ corresponding to the largest eigenvalue [14].

The Bernoulli distribution $Be\left({\delta }_i\right)$ is used to generate observations, where ${\delta }_i=\frac{exp\left(x_i^t\beta \right)}{1+exp\left(x_i^t\beta \right)}, i=1,\dots ,n$ such that the data matrix $\mathrm{X}={(x_i^t)}_{i=1,2,\dots ,n}$. The experiment is repeated 1000 times by generating $z_{ij}$. The bias and MSE values of the estimators are computed via the equation:

$$Bias \left(\widehat{\beta }\right)={\sum }_{i=1}^R\frac{\left({\widehat{\xi }}_i-\xi \right)}{R};MSE\left(\widehat{\beta }\right)=\frac{{\sum }_{i=1}^R{\left({\widehat{\xi }}_i-\xi \right)}^t\left({\widehat{\xi }}_i-\xi \right)}{R}.$$

(27)

where $\left({\widehat{\xi }}_i-\xi \right)$ is the deviation between the parameter and its estimate for each $i$ of the BLRM estimators and R is the number replications. The R Language is used for computations.

3.2. Discussion

The estimated biases and MSEs of the BLRM estimators for changed controlled conditions are summarized in Table 1, Table 2 and Table 3 for p = 3, 6 and 12, respectively. The simulated results in Table 1, Table 2 and Table 3 clearly demonstrated that the constructed ALLE surpassed the other estimators in terms of minimum bias and MSE. In all cases, the performance of the MLE is the worst since the estimated MSE is larger as compared to the other estimators. Based on the findings of the simulation, it can be seen that there is a direct relationship between the scalar MSEs and various levels of multicollinearity. As we change the multicollinearity level from mild to severe, the estimated MSEs increase for a given sample size and number of explanatory variables (EV). However, it is clearly observed that the proposed ALLE for the BLRM is a unique estimation method due to its minimum bias as well as minimum estimated MSEs. We also provide a graphical representation for the readers to see a clear image of the constructed and other considered estimators. Figure 1a–d demonstrates the effect of collinearity on the performance of the under-studied estimators with different sizes. Figure 1 clearly shows that the proposed ALLE performed the best for all the levels of multicollinearity. In addition, when the results are compared with respect to the sample size, then it can be noticed that the estimated MSE values of all the estimators decrease as n increases. For more details, see Figure 2a–d. When the results are interpreted with regard to the number of EVs, then it is observed from Table 1, Table 2 and Table 3 that the estimated MSEs increase by increasing the value of p. Based on the results, ALLE is the most suitable and consistent option whenever the RV is binary, and the EVs are correlated due to its minimum bias and estimated MSEs. Undoubtedly, other biased estimators also attain a lower MSE in contrast to the MLE, but the variation in the proposed ALLE is quite lower than the other estimators for all evaluated states.

Table 1. Bias and MSE values of the estimators for p = 3.

		Bias			MSE
n	$\mathit{\rho }$	LRRE	LLU	ALLE	MLE	LRRE	LLU	ALLE
50	0.80	−0.1164	−0.0706	−0.0181	297.24	158.62	109.11	22.15
	0.90	0.1104	0.0454	−0.0059	495.09	255.09	187.01	40.57
	0.95	−0.0601	−0.0047	−0.0572	970.93	498.44	393.88	95.04
	0.99	0.2172	0.1165	−0.0585	4195.40	1971.66	1634.97	431.22
100	0.80	0.2245	0.1493	−0.0182	141.16	76.78	50.44	9.45
	0.90	0.1207	0.0485	−0.0047	224.26	115.77	80.56	16.53
	0.95	0.1288	0.0948	−0.0192	410.35	202.71	151.40	32.77
	0.99	−0.0330	−0.0106	−0.0178	1858.28	873.64	698.43	166.81
200	0.80	0.0348	0.0297	−0.0201	65.68	35.79	23.81	5.17
	0.90	0.1545	0.0914	−0.0048	105.27	54.22	38.29	9.97
	0.95	0.1235	0.0583	0.0107	194.05	95.79	72.44	19.80
	0.99	0.2043	0.0872	0.0328	925.09	423.63	348.39	118.45
400	0.80	0.0584	0.0394	0.0067	30.47	16.65	10.46	2.32
	0.90	0.2181	0.1382	0.0566	52.09	27.34	17.83	4.48
	0.95	0.1036	0.0689	0.0183	91.95	47.21	30.58	7.20
	0.99	0.0694	0.0341	0.0212	435.24	213.83	142.51	37.29

Table 2. Bias and MSE values of the estimators for p = 6.

		Bias			MSE
n	$\mathit{\rho }$	LRRE	LLU	ALLE	MLE	LRRE	LLU	ALLE
50	0.80	0.2889	0.1538	−0.0200	983.86	547.58	350.62	21.41
	0.90	0.0248	0.0232	−0.0343	1820.37	982.09	656.32	44.56
	0.95	0.2548	0.1422	0.0029	3505.32	1879.78	1249.99	67.30
	0.99	0.4358	0.2714	−0.0154	17,361.14	9256.68	6295.43	407.18
100	0.80	0.1648	0.1086	−0.0137	349.73	200.38	114.25	6.74
	0.90	0.1927	0.0948	0.0303	617.50	339.62	195.78	12.17
	0.95	0.2478	0.1529	0.0361	1224.53	666.51	392.01	24.99
	0.99	0.0427	0.0111	0.0100	5899.93	3172.73	1845.47	120.22
200	0.80	0.2858	0.2014	0.0484	152.74	89.51	48.15	3.12
	0.90	0.3155	0.1970	0.0865	273.10	155.04	84.30	4.79
	0.95	0.3309	0.2162	0.0968	516.23	285.45	156.09	8.09
	0.99	0.2304	0.1557	0.0749	2529.83	1393.39	756.02	37.58
400	0.80	0.1762	0.1265	0.0719	73.58	43.07	22.74	2.16
	0.90	0.1934	0.1410	0.0957	135.46	76.29	40.17	3.36
	0.95	0.2236	0.1625	0.1109	252.20	139.15	72.36	5.01
	0.99	0.2450	0.1807	0.1292	1203.21	652.75	330.89	18.81

Table 3. Bias and MSE values of the estimators for p = 12.

		Bias			MSE
n	$\mathit{\rho }$	LRRE	LLU	ALLE	MLE	LRRE	LLU	ALLE
50	0.80	0.6909	0.5045	−0.0052	3448.20	1847.27	1398.01	17.48
	0.90	0.5428	0.3454	0.0074	1,049,972.88	3275.03	2453.74	29.13
	0.95	0.6166	0.4575	0.0142	884,816.47	6229.80	4808.46	63.91
	0.99	0.4064	0.2876	−0.0199	2,162,403.68	30,159.23	23,554.65	590.93
100	0.80	0.4906	0.3261	0.0717	818.31	495.73	265.91	3.52
	0.90	0.2566	0.1681	0.0480	1447.22	861.72	454.04	5.08
	0.95	0.3170	0.2055	0.0675	2849.43	1697.90	906.36	8.21
	0.99	0.0922	0.0587	0.0131	13,816.37	8172.86	4350.73	30.44
200	0.80	0.2717	0.1904	0.1051	322.54	200.00	94.28	3.01
	0.90	0.1694	0.1185	0.0773	586.96	357.99	169.71	3.78
	0.95	0.3037	0.2306	0.1461	1144.84	698.86	330.32	4.79
	0.99	0.2496	0.1941	0.1276	5603.54	3422.06	1606.92	16.26
400	0.80	0.3649	0.2926	0.2101	143.93	91.70	41.90	2.77
	0.90	0.2928	0.2394	0.1839	257.25	160.64	71.30	2.82
	0.95	0.2859	0.2350	0.1873	498.05	309.52	136.67	3.23
	0.99	0.2874	0.2443	0.1925	2399.74	1479.83	647.96	6.25

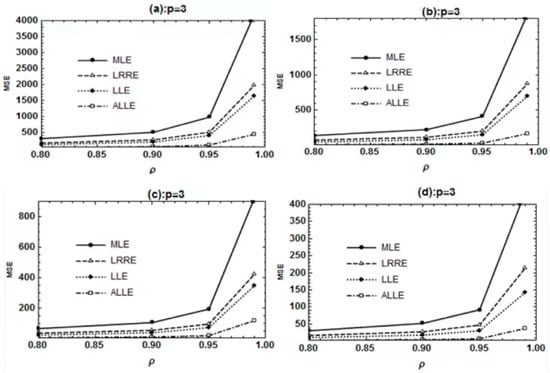
Figure 1. The BLRM estimators in relation to multicollinearity: (a). $n=50$, (b). $n=100$, (c). $n=200$, (d). $n=400$.

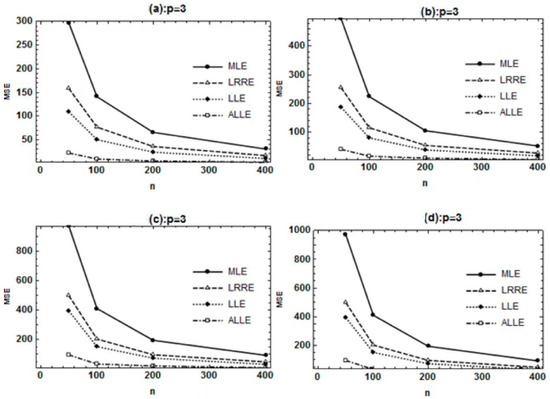
Figure 2. The BLRM estimators for various $n$: (a). $\rho =0.80$, (b). $\rho =0.90$, (c). $\rho =0.95$, (d). $\rho =0.99$.

4. Application

Here, a real application is considered to discuss the performance of the constructed estimator. For this purpose, prostate cancer data have been considered, which were taken from Kutner et al. [31]. However, the RV $y$ is the seminal vesicle invasion, i.e., presence or absence of seminal vesicle invasion: the binary RV is 1 if yes; 0 otherwise. The descriptions of seven regressors are given in Table 4.

Table 4. Explanation of the respected regressors.

N	Regressor Call	Explanation
1	PSA level	Serum prostate- specific antigen level (mg/mL).
2	Cancer volume (CV)	Estimate of prostate cancer volume (cc).
3	Weight	Prostate weight (gm)
4	Age	Age of patients (years)
5	Benign prostatic hyperplasia (BPH)	Amount of benign prostatic hyperplasia (cm2)
6	Capsular penetration (CP)	Degree of capsular penetration (cm)
7	Gleason score (GS)	Pathologically determined grade of disease using total score of two patterns (summed scores were either 6, 7, or 8 with higher scores indicating more prognosis).

Source: Adapted in part from: Hastie, T. J.; R. J. Tibshirani; and J. Friedman. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, New York; Springer. Verlag, 2001.

The eigenvalues of $\mathcal{F}$ matrix are found to be: ${\mu }_1=\mathrm{40,669.86}$, ${\mu }_2=1960.62$, ${\mu }_3=1868.34$, ${\mu }_4=176.214$, ${\mu }_5=45.520$, ${\mu }_6=18.943$ and ${\mu }_7=27.4104$. The multicollinearity of the regressors is assessed via a condition index (CI). The CI is evaluated by the eigenvalues of the $X^t\widehat{V}X$ matrix without an intercept term, while the eigenvalues of the $\mathcal{F}$ matrix include the intercept term. We observed that the $CI=\sqrt{{\mu }_{max}/{\mu }_{min}}=121.97>30$. This confirms that there is a multicollinearity issue among the regressors. Moreover, we also compute the correlations among the regressors, and the results are displayed in Figure 3. It declares the moderate correlation among CV and PSA. level, CP and PSA. level and CV and CP.

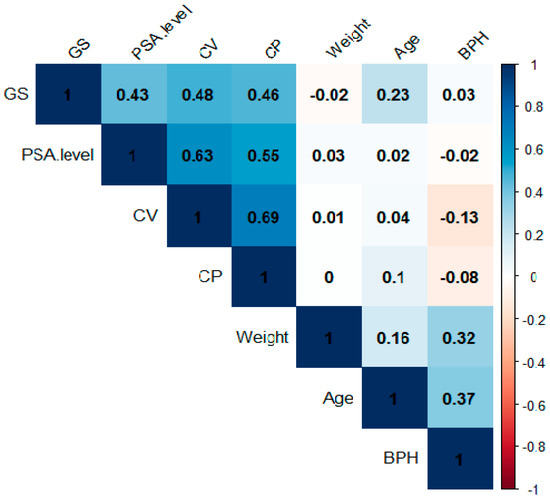
Figure 3. Correlation matrix among the seven regressors of a prostate cancer data.

The estimated coefficients (EC) and the MSE values are presented in Table 5. The EC of the MLE, LRRE, LLE and ALLE are obtained from (4), (7), (14) and (19), respectively. However, the scalar MSE values of the MLE, LRRE, LLE and ALLE are calculated using equations (6), (12), (18) and (23), respectively. The LRRE involves a shrinkage ridge parameter $\left(k\right)$, which is found to be 0.077. Whereas the Liu parameter $\left(d\right)$ for the LLE was found to be 0.5689. However, the shrinkage parameter $d_0$ of the proposed ALLE was found to be 0.0693. Table 5 reveals that ALLE decreases the EC and MSE value in a better way in comparison with the competitive estimators. It is also noticed that the MLE attains the largest MSE, which clearly indicates that it is the most sensitive estimator when there exists a multicollinearity among the regressors. In addition, the proposed ALLE is the most consistent option in the case of multicollinearity. Further, it can be noticed that the performance of LRRE is comparatively better than that of LLE and MLE. Further, it is also observed that the ALLE’s performance is better as compared to the other biased estimators as well as the MLE. Therefore, it is recommended to use the ALLE estimator when one considers the BLRM with correlated regressors because of its consistent and robust behavior against multicollinearity.

Table 5. Regression estimates and MSEs of the logistics regression estimators for the prostate cancer data.

	MLE	LRRE	LLE	ALLE
(Intercept)	−10.1574	−2.3825	−5.8266	0.4431
x1	0.1189	0.1090	0.1134	0.0985
x2	−0.1345	−0.1146	−0.1234	−0.0915
x3	0.0001	0.0002	0.0001	−0.0001
x4	0.0973	0.0220	0.0553	−0.0169
x5	−0.2281	−0.2185	−0.2228	−0.2021
x6	0.6487	0.6513	0.6501	0.5976
x7	−0.0673	−0.4491	−0.2799	−0.4555
MSE	45.6873	4.0569	15.9075	2.2935

Note: The best value is in bold font.

5. Concluding Remarks

We constructed a new adjusted logistic LE (ALLE) for the binary LRM (BLRM) to handle the multicollinearity issue. The MLE method is not a good choice due to its inflated variance and standard error whenever the regressors are multicollinear. The efficacy of the constructed estimator is judged via a MCS under various controlled conditions. The investigation has been performed for different values of correlation, sample sizes and the number of EVs. Findings showed that the ALLE’s performance is better compared to competitive ones and the MLE. Further, the MSE values of the MLE, LRRE, LLE and ALLE increase as the multicollinearity level increases. This phenomenon is particularly sharp for small sample sizes and whenever the correlation is high. However, this increase is quite smaller for the proposed ALLE. The superiority of the proposed estimator over others is also proved via a real application. The findings from both simulation and application clearly support our constructed estimator, which is a good and robust estimation method whenever there exists an imperfect but high multicollinearity among the regressors. As a result, we strongly advise practitioners to use the new estimator when estimating the unknown BLRM regression coefficients in the presence of multicollinearity.