Mathematical Model of Cyber Risks Management Based on the Expansion of Piecewise Continuous Analytical Approximation Functions of Cyber Attacks in the Fourier Series

Abstract

The comprehensive system of information security of an enterprise includes both tactical aspects of information and strategic priorities, reflecting the information policy and information strategy of the enterprise. Ensuring a given level of cybersecurity requires the identification of threat actors, their purpose, intentions of attacks on the IT infrastructure, and weak points of the enterprise’s information security. To achieve these goals, enterprises need new information security solutions. In this work, a mathematical model of the process of cyber risk management in the enterprise, which is based on the distribution of piecewise continuous analytical approximating functions of cyber attacks in the Fourier series, is obtained. A constant continuous monitoring and conduction of cyber regulatory control of the enterprise on time makes it possible to effectively ensure the cybersecurity of the enterprise in real time—predicting the emergence of cyber threats to some extent—which, in turn, determines the management of cyber risks arising in the field of information security of the enterprise. Such a Fourier series expansion of the piecewise continuous analytical approximating function of the intensity of cyber attacks on damage to standard software, obtained by approximating empirical–statistical slices of the intensity of cyber attacks on damage to standard software for each time period by analytical functions, opens up new mathematical possibilities of transition to systems of regulatory control of cyber threats of the enterprise from discrete to continuous automated process for such types of control.

1. Introduction

With the appearance of new IT technologies, the intensity of new cyber attacks on enterprise IT systems is increasing. It is also worth noting that traditional cybersecurity activities cannot fully prevent or contain these attacks due to the increasing speed and frequency of cyber attacks. The enterprise’s comprehensive information security system includes both tactical aspects of information protection (express audit of the enterprise’s information threats) and strategic priorities reflected in the enterprise’s information policy and information strategy. Ensuring a given level of cybersecurity requires the identification of threat actors, their purpose, intentions of attacks on the IT infrastructure, and weak points of the enterprise’s information security. To achieve these goals, enterprises need new information security solutions that not only meet the realities of today but also have significant development potential, taking into account current trends in the field of information security in general. At the same time, the issues of researching the intensity of cyber attacks, and their prediction and forecasting, are insufficiently researched in the scientific literature, which is related to the complexity of predicting cyber attacks as well as the availability of modern relevant methods for their forecasting.

The fight against the growing intensity of cyber threats requires the creation of a multifaceted information security strategy of the enterprise, which, in particular, includes the prediction of cyber attacks. In their scientific works, scientists Palash Goyal, Ashok Deb, and Nazgol Tavabi described computer programming methods based on neural networks and autoregressive time series models (AR, ARMA, ARIMA, ARIMAX) that use external signals from publicly available web sources to forecast cyber attacks. However, such models usually require a significant amount of data to implement computer programming in order to establish an accurate estimate of the model parameters. Most research efforts have focused on using network traffic to build predictive models. These studies are presented in the works of scientists such as E. Pontes, A. E. Guelfi, S. T. Kofuji, and A. A. Silva. Other researchers such as E. Gandotra, D. Bansal, and S. Sofat built cyber predictions using statistical modeling and algorithmic modeling. R. Douc, E. Moulines, and D. Stoffer were engaged in the use of ARCH and GARCH models, which are extensions of the classical autoregression model.

However, developing an accurate model of the dynamic behavior of time series is a difficult and important task. Therefore, there is a need for further research and development of a scientific and methodological apparatus for determining the relationship between the level of cyber risk and the frequency of audits, which makes it possible to ensure effective automation of enterprise cybersecurity processes. The general task of ensuring information security conditions the study of vulnerabilities of the IT infrastructure of the enterprise and relevant models of cyber attack prevention. In this regard, it is necessary to conduct a study of the relevant vulnerabilities and problems of all groups of cyber attacks on the enterprise.

As a result of the spread of freelance relations, as a modern type of business relation of an enterprise, there is a need to process and analyze statistical data of cyber attacks in the field of activity of an IT enterprise that involves a freelance resource. These studies should be designed to use temporal correlations between the number of cyber attacks over a period of time in order to predict the future intensity of cyber incidents, which will allow the creation of an effective forecasting system. Therefore, predicting the number of cyber attacks for a set rational time period is necessary to determine the effective frequency of the audit.

2. Literature Analysis

Fourier series are widely used in research in various fields of activity. Thus, particularly in [1,2,3], the speed of approximation of differentiable functions by generalized methods of summation of Fourier series was investigated. In [4,5], the conditions of convergence of Fourier transformations were investigated. Applied aspects of approximate properties of Fourier series were considered in [6,7,8], while the properties and application of isometric classes of functions based on their Fourier series were studied in [9,10].

In modern technical literature, the scientific problems of enterprise information security related, in particular, to the improvement of attack graphs for monitoring cybersecurity, handling of inaccuracies, cycle processing, display of incidents, and automatic selection of protective measures were investigated in the works of O.A. Lapteva [11,12,13,14], E.M. Galakhova [15], O.V. Kapustyan [16], S.P. Yevseiev, [17], and A.P. Musienko [18], respectively. The stability of the information system, in terms of functioning with the conditions of external and internal destabilizing factors, was studied in [19]. External and internal destabilizing factors include mean failures, failures of system modules, mechanical damage, thermal effects, and errors of service personnel. Ref. [20] investigated how, on the basis of the functional dependence of the probability of missing failures on a certain probability value, at different values of the probability of second-order control error, it is possible to determine the recommended interval of issuing the result, which will ensure, at a given intensity of readiness control, an acceptable probability of missing a failure. It was illustrated how, with a given intensity of issuing the result, it is possible to determine such an intensity of readiness control at which the probability of failure will not exceed the maximum permissible value. It was shown that it is possible to talk about a weak dependence of the probability of omission on the control error of the second kind, which means that the achievement of the specified reliability of the control is ensured on the basis of the intensity of the readiness control and depends less on the reliability of individual elementary checks. For the case when, in the intervals between the moments when the result is issued, the system checks the readiness of the modules randomly, the methodology for calculating the probability of failure was described. In [21], based on the use of a hierarchical concept of the organization of means of ensuring the functional stability of the company’s information system, two algorithms were developed that form a two-level system for diagnosing hidden failures. Diagnosis begins with the execution of the first algorithm, the advantages of which compared with known algorithms are that it requires less system redundancy, only two rounds of message exchange between nodes of the information system, and provides diagnosis of the information system of the subtribe when almost half of its nodes fail. In the case of an ambiguous solution to the diagnosis problem, the algorithm generates a signal about its failure and the diagnosis of the information system continues according to the second algorithm, which uses the duration of the phases as a criterion.

In [22,23,24], for evolutionary nonlinear problems with control parameters, the problems of approximate minimax estimation and making optimal decisions were considered. The authors investigated the problems of the behavior of evolutionary systems, when the system is under the influence of impulse forces of an instantaneous nature. This is important, because even in the case of linear systems, the presence of impulse action makes the behavior of the system significantly nonlinear, and the control of solutions of such systems is extremely difficult. At the same time, cyber attacks have a similar nature when they try to destabilize the system through the influence of external forces. Prediction of the number of possible cyber attacks, statistical and analytical assessments of cyber attacks, timely identification, development of an action plan and preventive measures to eliminate identical cyber attacks, implementation of a control system, and the introduction of modernized approaches to regulatory control of cyber attacks in the enterprise were carried out in [25,26].

The purpose of this work is to develop a mathematical model of cyber risks management of the enterprise, which makes it possible to move the system of regulatory control of cyber threats of the enterprise from a discrete to a continuous automated process of regulatory control.

3. Main Part

Let us consider a mathematical model of the process of managing cyber risks of the enterprise, which makes it possible to move the system of regulatory control of cyber threats of the enterprise from a discrete to a continuous automated process of regulatory control. This model differs from the existing ones, based mainly on the statistical analysis of time series, in that piecewise continuous analytical approximating functions of cyber attacks are decomposed into a Fourier series.

The research interest of this model is to determine the recommended frequency for the cyber risk management process in the enterprise. The model focuses on the following key stages of research:

• Retrospective statistical analysis of cyber risk identification time series.

  1.1.

  Determination of time intervals of regulatory control and approximation of statistical sections by analytical functions (Figure 1 and Figure 2).

  1.2.

  Graphical visualization of the implemented statistical analysis of time series of cyber risk identification (Figure 1).

• Analysis of the enterprise’s existing cyber risks strategy based on the retrospective statistical analysis of cyber risk identification time series, conducted above, highlighting weaknesses of the existing strategy, possible cyber threats, identification of potential strengths, and opportunities for further modernization.
• Development of a predictive and analytical model of regulatory control.
• Introduction of modernized approaches into the existing system of regulatory control of the enterprise.

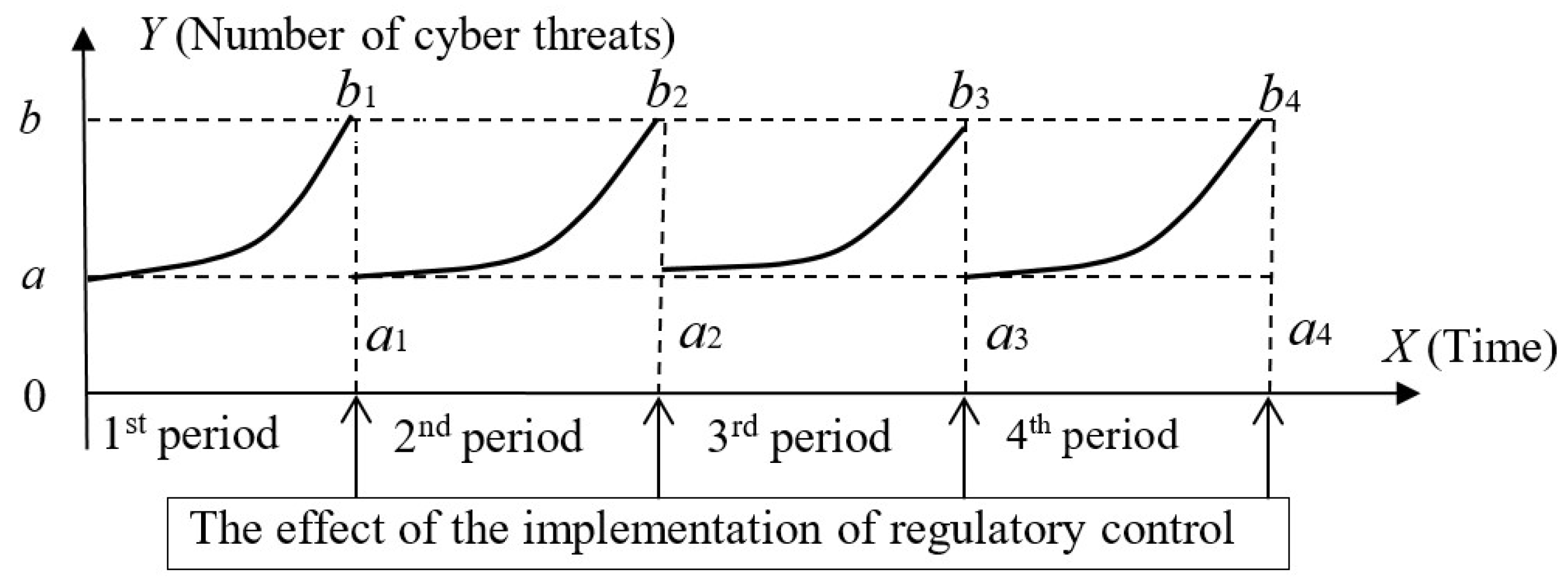
Figure 1 shows 4 time periods of regulatory control within the framework of the proposed model. The implementation of consistent activities of regulatory control ensures the minimization of cyber threats in each time period, which is illustrated in Figure 1. Figure 1 illustrates similar effects from the implementation of regulatory control and almost the same behavior in the number of cyber threats between the conducted audits.

According to part 1.1 of the abovementioned key bases of model research, an approximation of the statistical slices of cyber attacks on damage to the network infrastructure was carried out by analytical functions in the period between 4 time periods of regulatory control within the framework of the proposed model (

Table 1. Approximation of time series of cyber attacks on damage to network infrastructure by analytical functions.

Time Period	Nonlinear Equation of the Approximating Function on the Interval (0; 1)	Coefficient of Determination
1st period	$y=1.0643\times e^{0.064x}$	0.9032
2nd period	$y=1.0534\times e^{0.053x}$	0.9040
3rd period	$y=1.0626\times e^{0.065x}$	0.9012
4th period	$y=1.0596\times e^{0.059x}$	0.8933

).

Figure 2 presents a graphical interpretation of the approximation of the time series of cyber attacks on damage to the network infrastructure by analytical functions with averaged values for each time period in view of the almost identical equations of the approximating functions for different periods, which are presented in Table 1.

From Figure 2, we establish that the function is periodic with a period $T=1$ ($2l=1$, $l=1/2$); then, we expand the given function into a Fourier series on the closed interval $[0,2l]=[0,1]$. Let us write down the equation of the given function presented in Figure 2 with unknown coefficients: $y=A\times e^{Bx}$. Let us determine the estimated coordinates of the points from the bundle of nonlinear curves approximating the statistical series, which are in the confidence interval with the smallest variances in the form $y=1.0595\times e^{0.060205x}$. Note that 0.52975 is the statistical average value of the cyber threat function at its points of jump discontinuity. Thus, we have

$$y=\left\{\begin{array}{cc}1.0595\times e^{0.060205x}\hfill & k<x<k+1\hfill \\ 0.52975\hfill & x=k,k\in Z\hfill \end{array}\right.$$

(1)

For function (1), we find the coefficients of the Fourier series:

$$a_0={\int }_0^{1}1.0595\times e^{0.060205x}dx=\frac{1.0595}{0.060205}\times \left(e^{0.060205x}\right){|}_0^1=17.5982(e^{0.060205}-1)=1.09351.$$

(2)

Denoting the desired integral by I and applying the method of integration by parts twice, we obtain

$$\begin{array}{c}\hfill a_n=\frac{1}{1/2}{\int }_0^{1}1.0595e^{0.060205x}\times cos\left(\frac{\pi nx}{1/2}\right)dx=2\times 1.0595\times I=2.119\times I\\ \hfill =\left|\begin{array}{cc}{e}^{0.060205x}=U& 0.060205e^{0.060205x}dx=dU\\ cos\left(2\pi nx\right)dx=dV& V=\frac{1}{2\pi n}sin\left(2\pi nx\right)\end{array}\right|\\ \hfill =2.119\left[\left(e^{0.060205x}\times \frac{1}{2\pi n}sin\left(2\pi nx\right)\right){|}_0^1-\frac{0.060205}{2\pi n}{\int }_0^1{e}^{0.060205x}sin\left(2\pi nx\right)dx\right]\\ \hfill =\left|\begin{array}{cc}{e}^{0.060205x}=U& 0.060205e^{0.060205x}dx=dU\\ sin\left(2\pi nx\right)dx=dV& V=-\frac{1}{2\pi n}cos\left(2\pi nx\right)\end{array}\right|\\ \hfill =-2.119\times \frac{0.060205}{2\pi n}\left[-\frac{e^{0.060205x}}{2\pi n}cos\left(2\pi nx\right)\right]{|}_0^1+\frac{0.060205}{2\pi n}{\int }_0^1{e}^{0.060205x}cos\left(2\pi nx\right)dx\\ \hfill =\frac{0.127574}{2\pi n}\left(-\frac{e^{0.060205}-1}{2\pi n}+\frac{0.060205}{2\pi n}\right)\times I\end{array}$$

(3)

To find the integral I, we solve the following equation:

$$\begin{array}{c}\hfill 2.119\times I=\frac{0.127574}{2\pi n}\left(-\frac{e^{0.060205}-1}{2\pi n}+\frac{0.060205}{2\pi n}\right)\times I\Rightarrow \\ \hfill \Rightarrow I\left(2.119-\frac{0.127574}{2\pi n}\times \frac{0.060205}{2\pi n}\right)=-\frac{0.127574}{2\pi n}\times \frac{e^{0.060205}-1}{2\pi n}\end{array}$$

(4)

Thus, we have

$$I=\frac{0.127574\left(e^{0.060205}-1\right)}{0.00678-2.119{\left(2\pi n\right)}^2}.$$

(5)

Then, the coefficients $a_n$ are obtained in the form

$$\begin{array}{c}\hfill a_n=\frac{1}{1/2}{\int }_0^{1}1.{06}^{1-x}\times cos\left(\frac{\pi nx}{1/2}\right)dx=2.119\times I\\ \hfill =\frac{2.119\times 0.127574\left(e^{0.060205}-1\right)}{0.00678-2.119{\left(2\pi n\right)}^2}=\frac{0.27033\left(e^{0.060205}-1\right)}{0.00678-2.119{\left(2\pi n\right)}^2}.\end{array}$$

(6)

Similarly, we find the coefficients $b_n$:

$$\begin{array}{c}\hfill b_n=\frac{1}{1/2}{\int }_0^{1}1.0595e^{0.060205x}sin\left(\frac{\pi nx}{1/2}\right)dx=2\times 1.0595\times I=2.119\times I\\ \hfill =\left|\begin{array}{cc}{e}^{0.060205x}=U& 0.060205e^{0.060205x}dx=dU\\ sin\left(2\pi nx\right)dx=dV& V=-\frac{1}{2\pi n}cos\left(2\pi nx\right)\end{array}\right|\\ \hfill =2.119\left[\left(-e^{0.060205x}\times \frac{1}{2\pi n}sin\left(2\pi nx\right)\right){|}_0^1+\frac{0.060205}{2\pi n}{\int }_0^1{e}^{0.060205x}cos\left(2\pi nx\right)dx\right]\\ \hfill =\left|\begin{array}{cc}{e}^{0.060205x}=U& 0.060205e^{0.060205x}dx=dU\\ cos\left(2\pi nx\right)dx=dV& V=\frac{1}{2\pi n}sin\left(2\pi nx\right)\end{array}\right|\\ \hfill =2.119\left[-\left(e^{0.060205}-1\right)\times \frac{1}{2\pi n}+\frac{0.060205}{2\pi n}\left[\frac{e^{0.060205x}}{2\pi n}{sin\left(2\pi nx\right)|}_0^1-\frac{0.060205}{2\pi n}{\int }_0^1{e}^{0.060205x}sin\left(2\pi nx\right)dx\right]\right]\\ \hfill =\frac{2.119\left(1-e^{0.060205}\right)}{2\pi n}-\frac{0.0076806}{{\left(2\pi n\right)}^2}\times I\end{array}$$

(7)

To find the integral I, we solve the following equation:

$$\begin{array}{c}\hfill 2.119\times I=\frac{2.119\left(1-e^{0.060205}\right)}{2\pi n}-\frac{0.0076806}{{\left(2\pi n\right)}^2}\times I\Rightarrow \\ \hfill \Rightarrow I\left[2.119+\frac{0.0076806}{{\left(2\pi n\right)}^2}\right]=\frac{2.119\left(1-e^{0.060205}\right)}{2\pi n}.\end{array}$$

(8)

Thus, we obtain

$$I=\frac{2.119\left(1-e^{0.060205}\right)}{2\pi n\left(2.119+\frac{0.0076806}{{\left(2\pi n\right)}^2}\right)}.$$

(9)

Then, the coefficients $b_n$ will have the following form:

$$b_n=\frac{4.49020\left(1-e^{0.060205}\right)}{2\pi n\left(2.119+\frac{0.0076806}{{\left(2\pi n\right)}^2}\right)}.$$

(10)

Hence, let us write down the expansion of Function (1) in the Fourier series:

$$f\left(x\right)=1.09351+\sum _{n=1}^{\infty }\left[\frac{0.27033\left(e^{0.060205}-1\right)}{0.00678-2.119{\left(2\pi n\right)}^2}\times cos\left(2\pi nx\right)+\frac{4.49020\left(1-e^{0.060205}\right)}{2\pi n\left(2.119+\frac{0.0076806}{{\left(2\pi n\right)}^2}\right)}\times sin\left(2\pi nx\right)\right]$$

(11)

Thus, Function (11) is a continuous function that models a piecewise continuous function with points of jump irremovable discontinuities. Such a mathematical model is based on the expansion of a piecewise continuous analytical approximating function into the Fourier series, which makes it possible to move the system of regulatory control of cyber threats of the enterprise from a discrete to a continuous automated process of regulatory control.

Therefore, the approximation of statistical slices of cyber attacks on damage to the network infrastructure by analytical functions in the period between 4 time periods of regulatory control within the framework of the proposed model provides an automated approach to minimizing cyber threats in each time period.

Let us consider the mathematical possibilities of transition from a discrete to continuous automated process of cyber regulatory control of the enterprise. The modern approach to the information security of an enterprise in the sphere of action of cyber attacks is determined by the following stages: forecasting the number of possible cyber attacks; carrying out empirical–statistical and analytical evaluation of cyber attacks; identification of cyber attacks on time; development of an action plan and preventive activities to eliminate similar cyber attacks; and, most importantly, the implementation of the control system and the introduction of innovative approaches to the timely regulatory control of cyber attacks in the enterprise.

Therefore, with the growth of cyber threats, the need for express audits and their implementation on time increases the effectiveness of the enterprise’s comprehensive information security strategy.

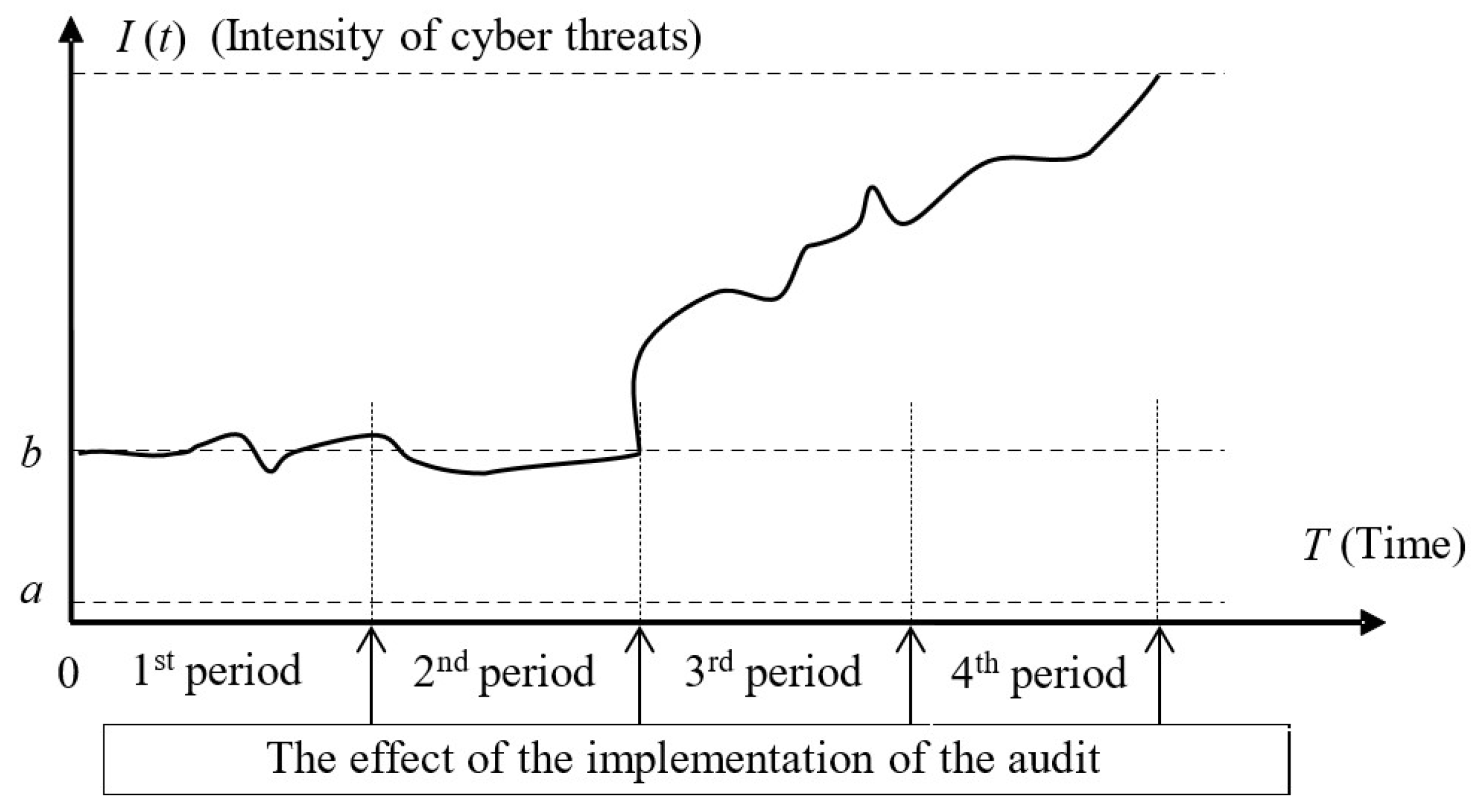
Figure 3 schematically reflects the behavior of the intensity of cyber attacks on damage to standard software for 4 time periods between conducting the scheduled regulatory control. After the scheduled regulatory control before the first time period, activities were taken that ensured the minimization of cyber threats in the first 2 time periods after the scheduled regulatory control.

Approximation of the statistical slices of cyber attacks on damage to standard software for each period by analytical functions was carried out (

Table 2. Approximation of time series of cyber attacks on damage to standard software by analytical functions.

Time Period	An Equation of the Approximating Function on the Interval (0; 1)	Coefficient of Determination
1st period	$I\left(t\right)=1.0364$	0.8731
2nd period	$I\left(t\right)=1.0453$	0.8540
3rd period	$I\left(t\right)=1.00076t$	0.8912
4th period	$I\left(t\right)=1.0237t$	0.8721

).

Based on Table 2, given the almost identical equations of approximating functions for the 1st, 2nd and 3rd, and 4th periods, respectively, it is possible to represent analytically the function of the intensity of cyber attacks on damage to standard software, combining the 1st, 2nd and 3rd, and 4th periods. Then, analytically, the function of the intensity of cyber attacks can be represented as

$$I\left(t\right)=\left\{\begin{array}{cc}1,\hfill & 0\le t<2\hfill \\ t,\hfill & 2\le t\le 4.\hfill \end{array}\right.$$

(12)

Let us expand Function (12) into a Fourier series, which will make it possible to move the regulatory control system of cyber attacks on damage of the enterprise’s standard software from a discrete to a continuous automated process of regulatory control.

Let us find the following coefficients:

$$\begin{array}{c}\hfill a_n=\frac{1}{2}{\int }_0^{4}f\left(t\right)cos\frac{\pi nt}{2}dt=\frac{1}{2}\left({\int }_0^{2}cos\frac{\pi nt}{2}dt+{\int }_2^{4}tcos\frac{\pi nt}{2}dt\right)\\ \hfill =\left|\begin{array}{cc}t=U& dt=dU\\ cos\frac{\pi nt}{2}=dV& V=\frac{2}{\pi n}sin\frac{\pi nt}{2}\end{array}\right|\\ \hfill =\frac{1}{2}\left(\frac{2}{\pi n}sin\frac{\pi nt}{2}{{|}_0^2+\left(\frac{2t}{\pi n}sin\frac{\pi nt}{2}+\frac{4}{{\pi }^2{n}^2}cos\frac{\pi nt}{2}\right)|}_2^4\right)\\ \hfill =\frac{1}{2}\times \frac{4}{{\pi }^2{n}^2}\left(cos2\pi n-cos\pi n\right)=\frac{2}{{\pi }^2{n}^2}(1-cos\pi n)=\frac{2}{{\pi }^2{n}^2}\left(1-{(-1)}^n\right);\end{array}$$

(13)

$$a_0=\frac{1}{2}{\int }_0^{4}f\left(t\right)dt=\frac{1}{2}\left({\int }_0^{2}dt+{\int }_2^{4}tdt\right)=\frac{1}{2}\left(2+\frac{t^2}{2}{\mid }_2^4\right)=\frac{1}{2}(2+6)=4;$$

(14)

$$\begin{array}{c}\hfill b_n=\frac{1}{2}{\int }_0^{4}f\left(t\right)sin\frac{\pi nt}{2}dt=\frac{1}{2}\left({\int }_0^{2}sin\frac{\pi nt}{2}dt+{\int }_2^{4}tsin\frac{\pi nt}{2}dt\right)\\ \hfill =\left|\begin{array}{cc}t=U& dt=dU\\ sin\frac{\pi nt}{2}=dV& V=-\frac{2}{\pi n}cos\frac{\pi nt}{2}\end{array}\right|\\ \hfill =\frac{1}{2}\left(-\frac{2}{\pi n}cos\frac{\pi nt}{2}{{|}_0^2+\left(-\frac{2t}{\pi n}cos\frac{\pi nt}{2}+\frac{4}{{\pi }^2{n}^2}sin\frac{\pi nt}{2}\right)|}_2^4\right)\\ \hfill =-\frac{1}{2}\times \frac{2}{\pi n}\left(cos\frac{\pi nt}{2}{{|}_0^2+tcos\frac{\pi nt}{2}|}_2^4\right)=-\frac{1}{\pi n}\left(cos\pi n-1+4cos2\pi n-2cos\pi n\right)\\ \hfill =-\frac{1}{\pi n}\left(3-cos\pi n\right)=\frac{1}{\pi n}\left({(-1)}^n-3\right).\end{array}$$

(15)

The desired expansion looks like

$$I\left(t\right)=2+\sum _{n=1}^{\infty }\left[\frac{2}{{\pi }^2{n}^2}\left(1-{(-1)}^n\right)cos\frac{\pi nt}{2}+\frac{1}{\pi n}\left({(-1)}^n-3\right)sin\frac{\pi nt}{2}\right].$$

(16)

For all $t\in (0;2)$, we have in the open interval $(0;2)$ the sum of the series $s\left(t\right)=1$, while in the open interval $(2;4)$, we have the sum of the series $s\left(t\right)=t$. At the point of jump discontinuity $t=2$,

$$s\left(t\right)=\frac{f(2-)+f(2+)}{2}=\frac{1+2}{2}=\frac{3}{2}.$$

(17)

At points $t=0$ and $t=4$, the sum $s\left(t\right)$ is equal to

$$s\left(t\right)=\frac{f\left(0\right)+f\left(4\right)}{2}=\frac{1+4}{2}=\frac{5}{2}.$$

(18)

Consider the first nine terms of the series (16)

$$\begin{array}{c}\hfill I\left(t\right)=2+\sum _{n=1}^8\left[\frac{2}{{\pi }^2{n}^2}\left(1-{(-1)}^n\right)cos\frac{\pi nt}{2}+\frac{1}{\pi n}\left({(-1)}^n-3\right)sin\frac{\pi nt}{2}\right]\\ \hfill =2+\left(\frac{2}{{\pi }^2}\left(2\right)cos\frac{\pi t}{2}+\frac{1}{\pi }(-4)sin\frac{\pi t}{2}\right)+\left(\frac{1}{2\pi }(-2)sin\pi t\right)\\ \hfill +\left(\frac{2}{9{\pi }^2}\left(2\right)cos\frac{3\pi t}{2}+\frac{1}{3\pi }(-4)sin\frac{3\pi t}{2}\right)+\left(\frac{1}{4\pi }(-2)sin2\pi t\right)\\ \hfill +\left(\frac{2}{25{\pi }^2}\left(2\right)cos\frac{5\pi t}{2}+\frac{1}{5\pi }(-4)sin\frac{5\pi t}{2}\right)+\left(\frac{1}{6\pi }(-2)sin3\pi t\right)\\ \hfill +\left(\frac{2}{49{\pi }^2}\left(2\right)cos\frac{7\pi t}{2}+\frac{1}{7\pi }(-4)sin\frac{7\pi t}{2}\right)+\left(\frac{1}{8\pi }(-2)sin4\pi t\right).\end{array}$$

(19)

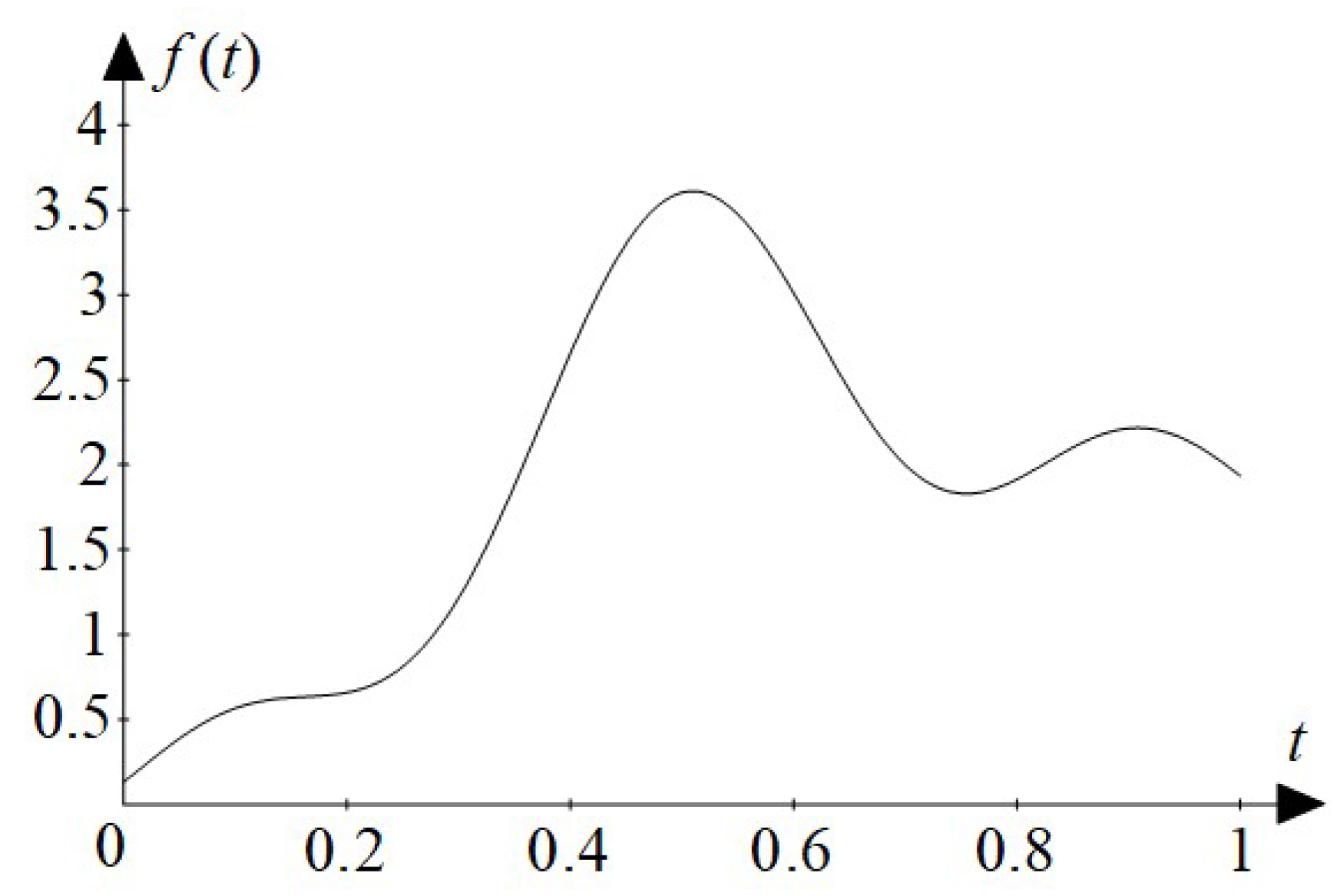
Figure 4 presents the graphs of the expansion of $I\left(t\right)$ into the Fourier series, taking into account from 3 to 8 terms in (16), respectively.

Therefore, constant continuous monitoring and timely conduction of cyber regulatory control of the enterprise makes it possible to effectively ensure the cybersecurity of the enterprise in real time—predicting the emergence of cyber threats, to some extent—which, in turn, determines the management of cyber risks arising in the field of information security of the enterprise.

Such a Fourier series expansion of the piecewise continuous analytical approximating function of the intensity of cyber attacks on damage to standard software, obtained by approximating empirical–statistical slices of the intensity of cyber attacks on damage to standard software for each time period by analytical functions, opens up new mathematical possibilities of transition to systems of regulatory control of cyber threats of the enterprise from a discrete to a continuous automated process of regulatory control.

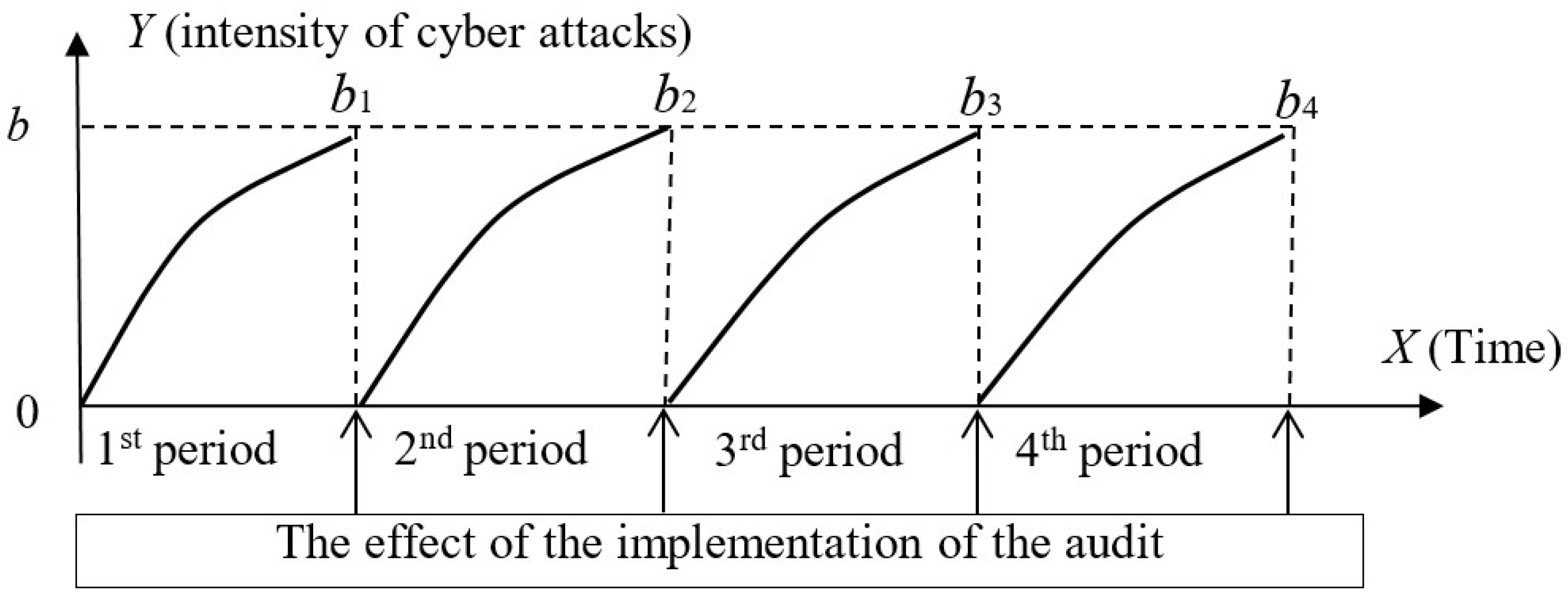
Figure 5 presents a graphical interpretation of the approximation of the time series of the intensity of cyber attacks on e-mail damage by analytical functions with averaged values for each time period.

In view of the homogeneity of the behavior of the intensity of cyber attacks in each time period, the approximation of the statistical slices of the intensity of cyber attacks on e-mail damage for each period was carried out using analytical functions (

Table 3. Approximation of time series of the intensity of cyber attacks on e-mail damage by analytical functions.

Time Period	An Equation of the Approximating Function on the Interval (0; 1)	Coefficient of Determination
1st period	$I\left(t\right)=-1.0754t^2+4.9954t$	0.7942
2nd period	$I\left(t\right)=-0.99164t^2+5.0127t$	0.8184
3rd period	$I\left(t\right)=-1.0032t^2+5.0073t$	0.8532
4th period	$I\left(t\right)=-1.0116t^2+5.0096t$	0.8258

).

Based on the data given in Table 3, it is possible to present analytically the function of the intensity of cyber attacks on e-mail damage, combining all periods in view of the standard cyclicality in each period. Then, analytically, the function of the intensity of cyber attacks can be represented as

$$I\left(t\right)=\left\{\begin{array}{cc}-t^2+5t,\hfill & 0\le t<1,\hfill \\ -{(t-1)}^2+5(t-1),\hfill & 1\le t<2,\hfill \\ -{(t-2)}^2+5(t-2),\hfill & 2\le t<3,\hfill \\ -{(t-3)}^2+5(t-3),\hfill & 3\le t\le 4.\hfill \end{array}\right.$$

(20)

Let us write the Fourier series for Function (20) only on the first interval, the graph of which is shown in Figure 6, since periodicity is performed on the other intervals. This will make it possible to move the system of regulatory control of cyber attacks on damage to standard enterprise software from a discrete to a continuous automated process of regulatory control.

Let us find the coefficients of the Fourier series for the function $f\left(t\right)=-t^2+5t$, $t\in [0;1]$.

The Fourier series expansion on the interval $(-T;T)$ has the form

$$f\left(t\right)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left(a_{n}cos\frac{\pi nt}{T}+b_{n}sin\frac{\pi nt}{T}\right),$$

(21)

$$a_0=\frac{1}{T}{\int }_{-T}^{T}f\left(t\right)dt,$$

(22)

$$a_n=\frac{1}{T}{\int }_{-T}^{T}f\left(t\right)\times cos\frac{\pi nt}{T}dt,$$

(23)

$$b_n=\frac{1}{T}{\int }_{-T}^{T}f\left(t\right)\times sin\frac{\pi nt}{T}dt.$$

(24)

In our case, $T=1$; so,

$$a_0={\int }_0^1(-t^2+5t)dt=\left(-\frac{t^3}{3}+\frac{5t^2}{2}\right){|}_0^1=\frac{13}{6}-0=\frac{13}{6},$$

(25)

$$\begin{array}{c}\hfill a_n={\int }_0^1(-t^2+5t)\times (cos\pi nt)dt\\ \hfill =\left[-t^2\frac{sin\left(\pi nt\right)}{\pi n}+5t\frac{sin\left(\pi nt\right)}{\pi n}-2t\frac{cos\left(\pi nt\right)}{{\pi }^2{n}^2}+5\frac{cos\left(\pi nt\right)}{{\pi }^2{n}^2}+2\frac{sin\left(\pi nt\right)}{{\pi }^3{n}^3}\right]{|}_0^1\\ \hfill =\left[4\frac{sin\left(\pi n\right)}{\pi n}+3\frac{cos\left(\pi n\right)}{{\pi }^2{n}^2}+2\frac{sin\left(\pi n\right)}{\pi n}-\frac{5}{{\pi }^2{n}^2}\right]=\frac{3{(-1)}^n-5}{{\pi }^2{n}^2},\end{array}$$

(26)

$$\begin{array}{c}\hfill b_n={\int }_0^1(-t^2+5t)\times sin\left(\pi nt\right)dt\\ \hfill =\left[-t^2\frac{cos\left(\pi nt\right)}{\pi n}-5t\frac{cos\left(\pi nt\right)}{\pi n}-2t\frac{sin\left(\pi nt\right)}{{\pi }^2{n}^2}+5\frac{sin\left(\pi nt\right)}{{\pi }^2{n}^2}-2\frac{cos\left(\pi nt\right)}{{\pi }^3{n}^3}\right]{|}_0^1\\ \hfill =\left[-4\frac{cos\left(\pi n\right)}{\pi n}+3\frac{sin\left(\pi n\right)}{{\pi }^2{n}^2}-2\frac{cos\left(\pi n\right)}{{\pi }^3{n}^3}-\left(-\frac{2}{{\pi }^3{n}^3}\right)\right]\\ \hfill =2\frac{-2{(-1)}^n{\pi }^2{n}^2-{(-1)}^n+1}{{\pi }^3{n}^3}.\end{array}$$

(27)

Hence, for even numbers n ($n=2k$), we have $b_n=0$, and for odd n ($n=2k-1$),

$$b_k=\frac{4{\pi }^2{(2k-1)}^2+4}{{\pi }^3{(2k-1)}^3}.$$

(28)

Thus, we have

$$f\left(t\right)=\frac{13}{12}+\sum _{k=1}^{\infty }\left[\frac{3{(-1)}^k-5}{{\pi }^2{k}^2}\times cos\left(\pi kt\right)+\frac{4{\pi }^2{(2k-1)}^2+4}{{\pi }^3{(2k-1)}^3}\times sin\left(\pi (2k-1)t\right)\right].$$

(29)

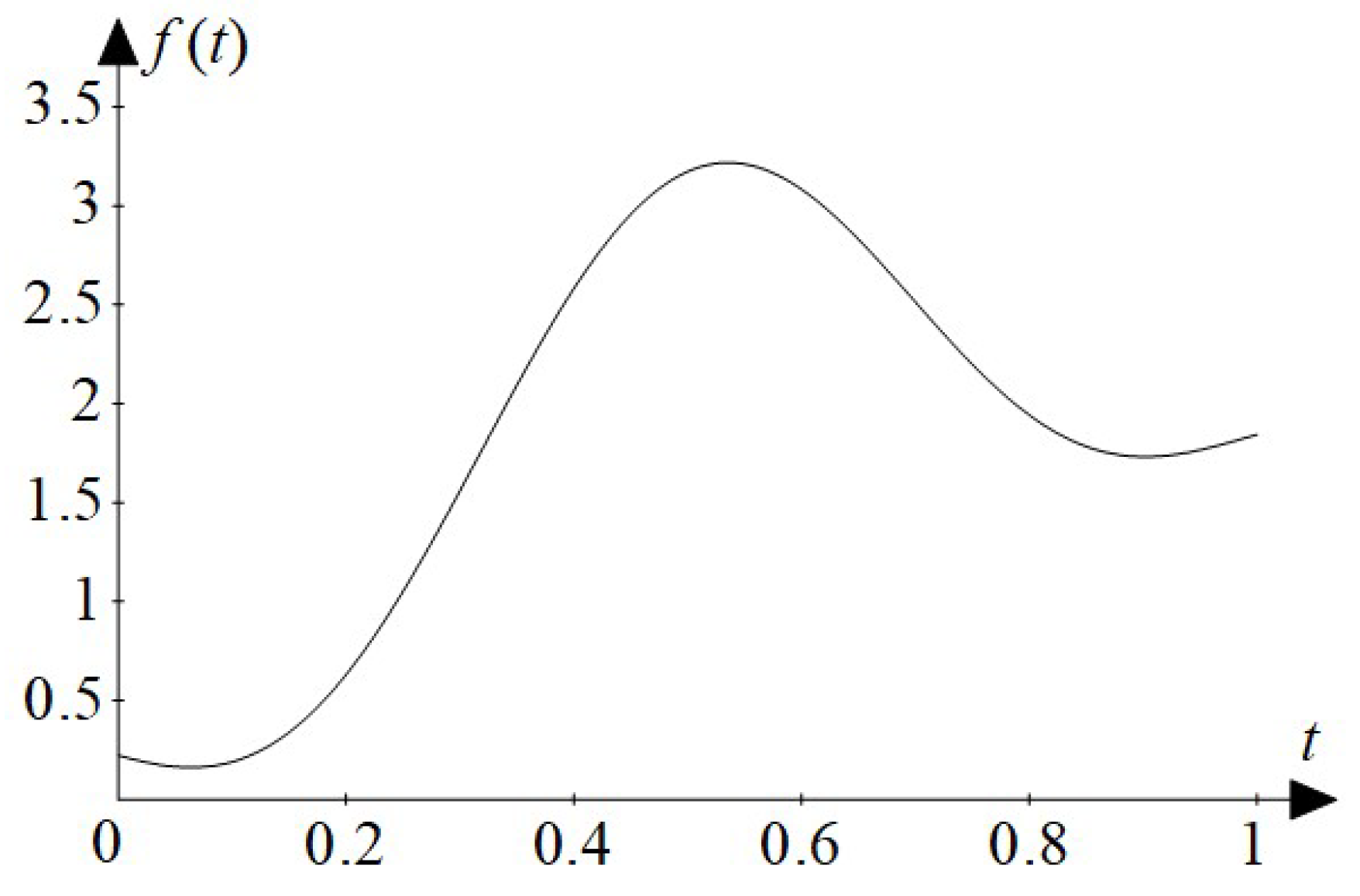
Figure 7, Figure 8 and Figure 9 present graphs of the expansion of Function (20) on the interval (0;1) into the Fourier series, taking into account 3, 5, or 7 terms of the series, respectively.

Figure 7 shows the graph of the function

$$f\left(t\right)=\frac{13}{12}-\frac{8cos\left(\pi t\right)}{{\pi }^2}+\left(4+4{\pi }^2\right)\times \frac{sin\left(\pi t\right)}{{\pi }^3},$$

(30)

which is obtained from (29) for $k=1$ on the interval $(0,1)$.

Figure 8 shows the graph of the function

$$f\left(t\right)=\frac{13}{12}-\frac{8cos\left(\pi t\right)}{{\pi }^2}+\left(4+4{\pi }^2\right)\times \frac{sin\left(\pi t\right)}{{\pi }^3}-\frac{cos\left(2\pi t\right)}{2{\pi }^2}+\left(4+36{\pi }^2\right)\times \frac{sin\left(3\pi t\right)}{27{\pi }^3},$$

(31)

which is obtained from (29) for $k=2$ on the interval $(0,1)$.

Figure 9 shows the graph of the function

$$\begin{array}{c}\hfill f\left(t\right)=\frac{13}{12}-\frac{8cos\left(\pi t\right)}{{\pi }^2}+\left(4+4{\pi }^2\right)\times \frac{sin\left(\pi t\right)}{{\pi }^3}-\frac{cos\left(2\pi t\right)}{2{\pi }^2}\\ \hfill +\left(4+36{\pi }^2\right)\times \frac{sin\left(3\pi t\right)}{27{\pi }^3}-\frac{8cos\left(3\pi t\right)}{9{\pi }^2}+\left(4+100{\pi }^2\right)\times \frac{sin\left(5\pi t\right)}{125{\pi }^3},\end{array}$$

(32)

which is obtained from (29) for $k=3$ on the interval $(0,1)$.

Therefore, with an increase in the number of terms of the Fourier series, the function will be continuous periodic in approximation to the piecewise continuous function, which enables constant continuous automated monitoring and timely conduction of cyber regulatory control of the enterprise in relation to e-mail attacks, which effectively ensures real-time cybersecurity of the enterprise.

This is due to the fact that information systems are widely implemented and used for processing, storing, and transmitting information, which, in turn, has led to the need to protect information systems, since information attacks can cause large financial and material losses. Auditing and monitoring serve to develop effective measures to ensure information security in enterprises, organizations, and institutions. With the help of an information security audit, the collection and analysis of information is carried out with regard to the information system being checked. It is conducted for the purpose of quantitative as well as qualitative assessment of the level of protection of the information system against possible attacks by intruders. The audit itself can provide an objective assessment of the security of any type of enterprise or institution, as well as prevent the realization of potential threats. The release of the company’s products at the international level is not possible without the implementation of international and industry standards, such as ISO/IEC 27001:2013 “Information security management systems. Requirements”, ITU-T X-1051 “Information security management systems. Requirements for telecommunications”, as well as ISO/IEC 27035:2011 “Information technology. Security techniques. Information security incident management”.

One of the most common types of audit is an active audit. It consists in studying the state of security of the information system from the point of view of an attacker (or an attacker with high IT skills). Active audits can be conditionally divided into two types—external and internal. Also, during an active audit, a study of system performance and stability, or stress test, is carried out. It is aimed at determining the critical load points at which the system, due to a denial-of-service attack or increased load, ceases to respond adequately to legitimate (defined by the security policy) user requests. The stress test will allow to identify “bottlenecks” in the process of formation and transmission of information and to determine the conditions under which normal operation of the system is impossible. Such testing involves simulating denial-of-service attacks as user requests to the system and conducting a general analysis of its performance. The result of an active audit is information about all vulnerabilities, degrees of their criticality and elimination methods, and information about publicly available information (information available to any potential violator) of the customer’s network. Based on the results of an active audit, recommendations are provided for the modernization of the network protection system, which make it possible to eliminate dangerous vulnerabilities and, thus, increase the level of protection of the company’s information system against the actions of an intruder with minimal costs for information security. It should be noted that the information security management system (ISMS) is a part of the overall management system, which is based on the assessment of business risks in order to create, implement, operate, constantly monitor, analyze, maintain, and improve the protection of information.

4. Conclusions

Constant continuous monitoring and regulatory control of enterprise’s cyber threats provides management with key real-time information about the enterprise’s cybersecurity efficiency, allowing not only to better understand problems when they occur but also to predict their occurrence, which improves the ability to manage risks and opportunities.

Note that the enterprise’s comprehensive information security system should include both tactical aspects of information protection and strategic priorities, which are reflected in the information policy and information strategy of the enterprise.