The Probabilistic Dual Hesitant Fuzzy Multi-Attribute Decision-Making Method Based on Cumulative Prospect Theory and Its Application

Abstract

Addressing the complex issue of multi-attribute decision-making within a probabilistic dual hesitant fuzzy context, where attribute weights are unknown, a novel decision-making method based on cumulative prospect theory is proposed, named the probabilistic dual hesitant fuzzy multi-attribute decision-making method based on cumulative prospect theory. Firstly, a decision matrix is formulated, representing probabilistic dual hesitant fuzzy information. Secondly, according to the decision maker’s authentic preference and non-membership information sensitivity, a comprehensive score function suitable for probabilistic dual hesitant fuzzy elements is proposed. The attribute weights are then determined using the entropy method. Next, the value function and decision weight function from the cumulative prospect theory are employed to compute the cumulative prospect value attributed to each available scheme. In addition, a cumulative prospect matrix is constructed, enabling the establishment of scheme rankings based on the comprehensive cumulative prospect value. Finally, the analysis of specific cases and a comparative assessment of methods pertaining to the selection of emergency response schemes collectively demonstrate the rationality and efficacy of the decision-making method presented in this study.

1. Introduction

As science and technology continue to advance, the complexity of social issues and decision-making contexts confronting humanity is escalating. With much uncertain information, processing information more effectively and completing necessary decisions has become increasingly important. In light of the escalating intricacy of decision-making challenges, multi-attribute decision-making (MADM) has evolved into a pivotal research area within contemporary decision theory and decision science. Its wide-ranging applications span engineering, logistics, medicine, and various domains. Ever since Zadeh introduced the theory of fuzzy sets (FSs) [1], it has evolved into a common way to deal with problems in the real world that are fuzzy and uncertain. Later, Atanassov defined intuitionistic fuzzy sets (IFSs) [2], which consider that the combined values of the membership and the non-membership degree cannot be more than 1. Considering that decision-makers (DMs) may hesitate about the membership value during the decision-making process, Torra proposed hesitant fuzzy sets (HFSs) [3]. HFSs, along with their expansion, provide DMs with an effective means to articulate uncertain decision-making information. Globally, many research endeavors in recent years have focused on hesitant fuzzy sets, broadening their scope to include forms such as dual hesitant fuzzy sets (DHFSs) [4], hesitant triangular fuzzy sets (HTFSs) [5], and probabilistic hesitant fuzzy sets (PHFSs) [6], among others [7]. Building on the principles of both DHFSs and PHFSs, literature [8] presents the concept of probabilistic dual hesitant fuzzy sets (PDHFSs). PDHFSs have the capability to capture decision-related insights from both membership and non-membership viewpoints while also encompassing associated probability information. In comparison to HFSs, PHFSs, and DHFSs, PDHFSs offer a more precise representation of DMs hesitations and psychological preferences, thus mitigating the insufficiency of evaluation information during the decision-making process. The gradual emergence of PDHFSs and extended applications has garnered increasing attention from scholars [9,10,11].

Currently, most PDHF multi-attribute decision-making methodologies operate on the assumption of complete rationality, adhering to the principles of classical expected utility theory. However, risky MADM problems are often encountered in real life, such as emergency scheme assessment [12], evaluation of venture capital projects [13], location planning [14], and other issues. In the face of these problems, decision makers’ rational behavior is typically limited, and they do not continuously pursue the maximum utility in their decision-making behavior, instead opting for the scheme that best suits their wishes. Therefore, Kahneman and Tversky successively proposed Prospect Theory (PT) [15] and Cumulative Prospect Theory (CPT) [16] for decision analysis under uncertain and risky conditions. Among them, PT supersedes the traditional method’s expected value with the value function (VF) and probability weight, challenging the conventional “infinite rationality” assumption of decision-makers. In contrast, CPT employs cumulative probability over singular probabilities in calculating probability weights, and this compensates for PT shortcomings regarding the violation of random dominance. CPT is more in line with DMs bounded rational decision-making behavior in uncertain environments. Some scholars have successfully applied the CPT to decision analysis, solving problems such as supplier selection and credit risk assessment [17,18].

Most of the MADM methods for CPT in the existing research are based on the evaluation information as intuitionistic fuzzy numbers, hesitant fuzzy language, or probabilistic fuzzy language. There are few types of research on extending CPT to the PDHF environment for MADM, and the practical applications are limited. Consequently, prompted by the insights derived from the preceding analysis, this study introduces a new methodology named the probabilistic dual hesitant fuzzy multi-attribute decision-making method based on cumulative prospect theory, herein termed “the CPT-based PDHF decision-making method”. Firstly, the DMs evaluative information is translated into the PDHFSs. Secondly, by considering the genuine preferences of DMs and their responsiveness to non-membership information, a comprehensive score function tailored to PDHFEs is devised to address the quantification of decision information. Next, the attribute weights are computed using the entropy method. Then, the CPT is harnessed within the PDHF environment to ascertain the Value Function (VF) and Decision Weight Function (DWF) for each scheme across diverse risk states. These calculations contribute to the creation of a comprehensive cumulative prospect decision matrix. Additionally, the schemes are subjected to a sorting process based on the magnitude of the comprehensive cumulative prospect value, which ultimately determines the final decision outcome. Ultimately, the soundness and practicability of “the CPT-based PDHF decision-making method” are substantiated through case analyses and comparisons with alternative approaches.

This study’s core structure unfolds as follows: Section 2 encompasses essential concepts and pertinent calculation formulas, including the PDHFSs, scoring functions of PDHFEs, and CPT. Section 3 introduces “the CPT-based PDHF decision-making method." Section 4 primarily encompasses the analysis of case studies about the selection of emergency response schemes alongside a comparative examination of diverse decision-making methods. Section 5 serves as the concluding segment of this study.

2. Related Concepts

2.1. Probabilistic Dual Hesitant Fuzzy Sets (PDHFSs)

Definition 1. 

Let $X$ be the domain of discourse; then $PDHF=\{⟨x,\tilde{h}(x),\tilde{g}(x)⟩|x\in X\}$ is called a probabilistic dual hesitant fuzzy set (PDHFS) on $X$. Among them, $\tilde{h}(x)=h(x)|p(x)$ and $\tilde{g}(x)=g(x)|q(x)$ represent the membership degree, non-membership degree, and the corresponding probability distribution information respectively. $h(x)|p(x)=({\gamma }_1|p_1,{\gamma }_2|p_2,\dots ,{\gamma }_{\#\tilde{h}(x)}|p_{\#\tilde{h}(x)})$, $g(x)|q(x)=({\eta }_1|q_1,{\eta }_2|q_2,\dots ,{\eta }_{\#\tilde{g}(x)}|q_{\#\tilde{g}(x)})$, $\#\tilde{h}(x)$ and $\#\tilde{g}(x)$ represent the number of corresponding elements in the membership degree and non-membership degree respectively, and satisfy ${\displaystyle \sum _{i=1}^{\#\tilde{h}(x)}{p}_i<1}$, ${\displaystyle \sum _{j=1}^{\#\tilde{g}(x)}{q}_j<1}$, ${\gamma }_i\ge 0$, ${\eta }_i\ge 0$, ${\gamma }^{*}+{\eta }^{*}\le 1$. ${\gamma }^{*}$ and ${\eta }^{*}$ represent the maximum value of membership degree and non-membership degree respectively, where $i=1,2,\dots ,\#\tilde{h}(x)$, $j=1,2,\dots ,\#\tilde{g}(x)$ [19].

Definition 2. 

For a probabilistic dual hesitant fuzzy element (PDHFE) $pdhf=⟨\tilde{h}(x),\tilde{g}(x)⟩$, abbreviated as $pdhf=⟨\tilde{h},\tilde{g}⟩=⟨h|p,g|q⟩$, its complement $p{d}^c$ is expressed as:

$$pdh{f}^c=\{\begin{array}{l}⟨\tilde{g},\tilde{h}⟩=⟨g|q,h|p⟩\begin{array}{cc},& \tilde{h}\ne \varnothing ,\tilde{g}\ne \varnothing \end{array}\\ ⟨\tilde{h},\varnothing ⟩=⟨1-h|p,⟩\begin{array}{cc},& \tilde{h}\ne \varnothing ,\tilde{g}\ne \varnothing \end{array}\\ ⟨\varnothing ,\tilde{g}⟩=⟨,1-g|q⟩\begin{array}{cc},& \tilde{h}\ne \varnothing ,\tilde{g}\ne \varnothing \end{array}\end{array}$$

(1)

Assuming two PDHFEs are $pdh{f}_1=⟨{\tilde{h}}_1,{\tilde{g}}_1⟩=⟨{\tilde{h}}_1|p_1,{\tilde{g}}_1|q_1⟩$ and $pdh{f}_2=⟨{\tilde{h}}_2,{\tilde{g}}_2⟩=⟨{\tilde{h}}_2|p_2,{\tilde{g}}_2|q_2⟩$ respectively, the operation law is defined as follows:

$$pdh{f}_1\oplus pdh{f}_2={\displaystyle \underset{{\gamma }_1\in h_1,{\gamma }_2\in h_2,{\eta }_1\in g_1,{\eta }_2\in g_2}{\overset{n}{\cup }}⟨\begin{array}{l}({\gamma }_1+{\gamma }_2-{\gamma }_1{\gamma }_2)|p_1{p}_2,\\ ({\eta }_1{\eta }_2)|q_1{q}_2\end{array}⟩}$$

(2)

$$pdh{f}_1\otimes pdh{f}_2={\displaystyle \underset{{\gamma }_1\in h_1,{\gamma }_2\in h_2,{\eta }_1\in g_1,{\eta }_2\in g_2}{\overset{}{\cup }}⟨\begin{array}{l}({\gamma }_1{\gamma }_2)|p_1{p}_2,\\ ({\eta }_1+{\eta }_2-{\eta }_1{\eta }_2)|q_1{q}_2\end{array}⟩}$$

(3)

$$\lambda pdh{f}_1={\displaystyle \underset{{\gamma }_1\in h_1,{\eta }_1\in g_1}{\overset{}{\cup }}⟨1-{(1-{\gamma }_1)}^{\lambda }|p_1,{\eta }_1{}^{\lambda }|q_1⟩}$$

(4)

$$pdh{f}_1{}^{\lambda }={\displaystyle \underset{{\gamma }_1\in h_1,{\eta }_1\in g_1}{\overset{}{\cup }}⟨{\gamma }_1{}^{\lambda }|p_1,1-{(1-{\eta }_1)}^{\lambda }|q_1⟩}$$

(5)

Among them, $\lambda$ is a constant and $\lambda \ge 0$ [19].

2.2. Score Function of Probabilistic Dual Hesitant Fuzzy Elements

2.2.1. The Original Score Function of Probabilistic Dual-Hesitant Fuzzy Elements

Definition 3. 

Let $pdhf=⟨\tilde{h},\tilde{g}⟩=⟨h|p,g|q⟩$ be any PDHFE, then its original score function $Score(pdhf)$ is:

$$Score(pdhf)={\displaystyle \sum _{i=1}^{\#\tilde{h}}{\gamma }_i\cdot p_i-}{\displaystyle \sum _{i=1}^{\#\tilde{g}}{\eta }_j\cdot q_j}$$

(6)

Its degree of deviation $\sigma (pdhf)$ is:

$$\sigma (pdhf)={\left[{\displaystyle \sum _{i=1}^{\#\tilde{h}}{({\gamma }_i-Score(pdhf))}^2\cdot p_i-}{\displaystyle \sum _{i=1}^{\#\tilde{g}}{({\eta }_j-Score(pdhf))}^2\cdot q_j}\right]}^{\frac{1}{2}}$$

(7)

The magnitude of the initial score function $Score(pdhf)$ in Equation (6) directly correlates with the quality of the associated PDHFE. The relationship depicted in Equation (7) reveals that the degree of deviation, denoted as $\sigma (pdhf)$, signifies the overall separation between the PDHFEs and the original score function. A smaller value of $\sigma (pdhf)$, signifies a better PDHFE, as demonstrated in prior research [20].

Definition 4. 

Consider two arbitrary PDHFEs denoted as $pdh{f}_1$ and $pdh{f}_2$. These original score functions and deviation degrees are $Score(pdh{f}_1)$, $Score(pdh{f}_2)$, $\sigma (pdh{f}_1)$ and $\sigma (pdh{f}_2)$ respectively. Then, the classic comparison method of two arbitrary PDHFEs is as follows:

(1) 

If $Score(pdh{f}_1)>Score(pdh{f}_2)$, then $pdh{f}_1$ is deemed superior to $pdh{f}_2$, and this relation is denoted as $pdh{f}_1>pdh{f}_2$.

(2) 

If $Score(pdh{f}_1)<Score(pdh{f}_2)$, then $pdh{f}_1<pdh{f}_2$.

(3) 

If $Score(pdh{f}_1)=Score(pdh{f}_2)$, then:

(1) 

If $\sigma (pdh{f}_1)<\sigma (pdh{f}_2)$, then denoted as $pdh{f}_1>pdh{f}_2$.

(2) 

If $\sigma (pdh{f}_1)=\sigma (pdh{f}_2)$, $pdh{f}_1$ and $pdh{f}_2$ are considered indistinguishable, and this equivalence is denoted as $pdh{f}_1~pdh{f}_2$.

2.2.2. Comprehensive Score Function of Probabilistic Dual Hesitant Fuzzy Elements

In practical decision-making scenarios, the presence of negative evaluation information tends to exert a more pronounced influence on the outcomes of the decision-making process [21]. Combined with PT, this study considers that DMs are more sensitive to non-membership and proposes a comprehensive score function for PDHFEs. In addition, DMs have a certain tendency toward evaluation values. When the decision maker gives an evaluation value of $\{0.8,0.9\}$ 1, the decision maker prefers a value with an evaluation value of 1. On the contrary, if the evaluation value is $\{0.1,0.2\}$ 0, the decision maker prefers the evaluation value to 0. This study will utilize the genuine preferences inferred through the orness measure method to elucidate the propensity of DMs to appraise data [22]. In the PDHFEs, if the probability information is not considered, membership and non-membership degree are two hesitant fuzzy elements (HFEs). The authentic preference value is based on HFEs, and the authentic preference degree and authentic preference value of HFEs are shown in Definitions 5 and 6, respectively.

Definition 5. 

Suppose $h$ is the HFE, its standardized form is shown in Formula (8).

$$\widehat{h}=\{{\widehat{\gamma }}_i={\gamma }_i/{\displaystyle \sum _{i=1}^{\#h}{\gamma }_i}|{\gamma }_i\in h\}$$

(8)

Among them, $\widehat{h}$ means that all values of hesitant fuzzy elements are standardized, ${\gamma }_i$ means the $i-th$ value in $h$, and $\#h$ means the number of all values in $h$. The representation of authentic preference degree based on $\widehat{h}$ is shown in Formula (9).

$$rpd(\widehat{h})=(\begin{array}{c}{\displaystyle \sum _{i=1}^{\#\widehat{h}}\left(\frac{\#\widehat{h}-i}{\#\widehat{h}-1}\right)},\overline{h}<0.5\\ 1-{\displaystyle \sum _{i=1}^{\#\widehat{h}}\left(\frac{\#\widehat{h}-i}{\#\widehat{h}-1}\right)},\overline{h}>0.5\\ 0.5,\overline{h}=0.5\end{array}$$

(9)

where $\overline{h}$ is the average of $h$.

Definition 6. 

Assuming that $h$ is the HFE, the expression of its authentic preference value is shown in Formula (10) [23].

$$rpv(h)=2h\cdot rpd(\widehat{h})$$

(10)

The authentic preference value adeptly mirrors DMs genuine evaluation tendencies when providing assessment information. Considering that DMs are more sensitive to non-membership, this study assigns a parameter $\vartheta$ to the non-membership part of the comprehensive score function of PDHFEs, indicating the sensitivity of DMs. The comprehensive score function of PDHFEs is shown in Definition 7.

Definition 7. 

Suppose a PDHFE is $pdhf=⟨\tilde{h},\tilde{g}⟩=⟨h|p,g|q⟩$, then its comprehensive score function expression is shown in Formula (11).

$$Score*(pdhf)=\left(rpv(h)-\sqrt{{\displaystyle \sum _{i=1}^{\#\tilde{h}}{p}_i{\left({\displaystyle \sum _{i=1}^{\#\tilde{h}}{\gamma }_i{p}_i}\right)}^2}}\right)-\vartheta \left(rpv(g)-\sqrt{{\displaystyle \sum _{i=1}^{\#\tilde{g}}{q}_i{\left({\displaystyle \sum _{i=1}^{\#\tilde{g}}{\eta }_i{q}_i}\right)}^2}}\right)$$

(11)

Among them, $rpv(h)$ and $rpv(g)$ denote the authentic preference value without taking into account the probability information. ${\gamma }_i\in h$ and $p_i\in p$ represent the membership value and probability. ${\eta }_i\in g$ and $q_i\in q$ represent the non-membership value and probability. $\#\tilde{h}(x)$ and $\#\tilde{g}(x)$ represent the count of elements in the degree of membership and non-membership. The parameter $\vartheta$ captures the decision-maker’s sensitivity towards the degree of non-membership, and $\vartheta >1$. In practical decision-making scenarios, it is imperative to account for the specific decision-maker’s sensitivity to negative information and assign values to the parameters. For computational convenience, we set $\vartheta =0.15$ in this instance.

Definition 8. 

Suppose $pdh{f}_1$ and $pdh{f}_2$ are two arbitrary PDHFEs. Compare the two PDHFEs $p{d}_1$ and $p{d}_2$ based on the comprehensive score function. The method is as follows:

(1) 

If $Score*(pdh{f}_1)>Score*(pdh{f}_2)$, then $pdh{f}_1$ is deemed superior to $pdh{f}_2$, and this relation is denoted as $p{d}_1>p{d}_2$.

(2) 

If $Score*(pdh{f}_1)=Score*(pdh{f}_2)$, $pdh{f}_1$ and $pdh{f}_2$ are considered indistinguishable, and this equivalence is denoted as $pdh{f}_1~pdh{f}_2$.

2.3. Cumulative Prospect Theory (CPT)

The Cumulative Prospect Theory (CPT), introduced by Kahneman and Tversky, stands as a pivotal theory in behavioral decision-making [16]. CPT calculates loss and gain separately, uses cumulative probability instead of single probability to calculate probability weight, explains the phenomenon of random dominance, and makes decision-making results more scientific [24]. The calculation of cumulative prospect value mainly includes two parts: the value function (VF) and the decision weight function (DWF), as shown in Formula (12).

$$V(x)={\displaystyle \sum _{t=1}^l{\pi }^{+}({\rho }_t)v(x)+}{\displaystyle \sum _{t=1}^l{\pi }^{-}({\rho }_t)v(x)}$$

(12)

Among them, the specific form of the VF $v(x)$ is shown in Formula (13), and the shape of the VF is like an S shape, as depicted in Figure 1.

$$v(x)=\{\begin{array}{c}{(x-b)}^{\alpha },x\ge b\\ -\tau {(b-x)}^{\beta },x\prec b\end{array}$$

(13)

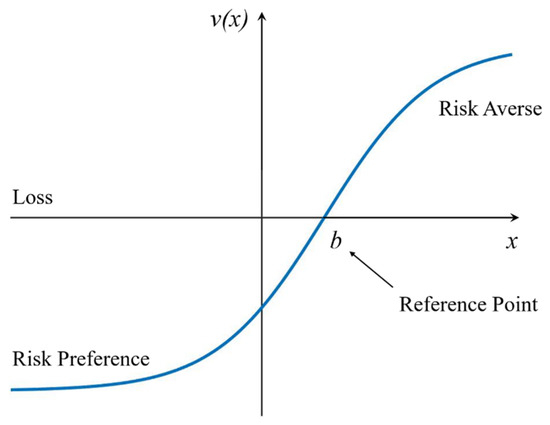
Figure 1. Value function.

Herein, $b$ serves as the reference point, with $x\ge b$ indicating a state of gain and $x\prec b$ denoting a state of loss. $\alpha$ and $\beta$ symbolize the decision maker’s risk attitude coefficients when confronted with gains and losses, respectively. The bigger $\alpha$ and $\beta$ are, the steeper the utility curve of the income area is, and the more adventurous the decision-maker is, and $\alpha >0$,$\beta <1$. $\tau$ is the avoidance coefficient, and the higher value of $\tau$ indicates that the decision maker exhibits greater sensitivity to losses, $\tau >1$.

The DWF as a non-linear, monotonically increasing function with respect to objective probability. It embodies the decision-maker’s psychological tendency to “overestimate events with low probabilities and underestimate those with high probabilities”. ${\pi }_{(t)}^{+}$ is the decision weight when faced with gains, and ${\pi }_{(t)}^{-}$ is the decision weight when faced with losses. The specific forms are shown in Formulas (14) and (15), $\rho$ is the probability of an event occurring.

$${\pi }_{(t)}^{+}={\omega }^{+}({\displaystyle \sum _{k=t}^l{\rho }_k})-{\omega }^{+}({\displaystyle \sum _{k=t+1}^l{\rho }_k})$$

(14)

$${\pi }_{(t)}^{-}={\omega }^{-}({\displaystyle \sum _{k=1}^t{\rho }_k})-{\omega }^{-}({\displaystyle \sum _{k=1}^{t-1}{\rho }_k})$$

(15)

Among them,

$${\omega }^{+}(\rho )=\frac{{\rho }_j^{\sigma }}{{[{\rho }_j^{\sigma }+{(1-{\rho }_j)}^{\sigma }]}^{1/\sigma }}$$

(16)

$${\omega }^{-}(\rho )=\frac{{\rho }_j^{\epsilon }}{{[{\rho }_j^{\epsilon }+{(1-{\rho }_j)}^{\epsilon }]}^{1/\epsilon }}$$

(17)

Herein, $\delta$ represents the risk-return attitude coefficient, while $\epsilon$ denotes the risk-loss attitude coefficient, and $\delta >0$, $\epsilon <1$.

3. The Probabilistic Dual Hesitant Fuzzy Multi-Attribute Decision-Making Method Based on Cumulative Prospect Theory

To advance future research, the multi-attribute decision-making (MADM) challenge within the probabilistic dual hesitant fuzzy (PDHF) environment is tackled using the cumulative prospect theory (CPT). This study employs the subsequent mathematical symbols to delineate its conceptual, let $Z=(A,C,E,\theta ,\rho ,w,\lambda )$ represent a MADM system with probabilistic dual hesitant fuzzy information (PDHFI) in actual decision-making. Let $A=\{A_i,i=1,2,\dots ,m\}$ be the set of alternatives in decision-making. $C={\{\mathrm{C}}_j,j=1,2,\dots ,n\text{}}$ is the attribute set. There are $t$ DMs $E=\{E_k,k=1,2,\dots ,t\}$ participating in the evaluation. The set of risk states is $\theta =\{{\theta }_{\xi },\xi =1,2,\dots ,\varsigma \}$. Let the probability of occurrence of the $\xi -th$ risk state ${\theta }_{\xi }$ be ${\rho }_{\xi }$, and ${\rho }_{\xi }$ satisfies $0<{\rho }_{\xi }\le 1$, ${\displaystyle \sum _{\xi =1}^{\zeta }{\rho }_{\xi }=1}$. $pdh{f}_{ij}^{(k,\xi )}$ represents the evaluation value of the $k-th$ expert on the attribute $C_j$ of the scheme $A_i$ in the ${\theta }_{\xi }$ risk state, where $pdh{f}_{ij}{}^{(k,\xi )}=<{\tilde{h}}_{ij}{(x)}^{(k,\xi )},{\tilde{g}}_{ij}{(x)}^{(k,\xi )}>$ is the PDHF number. $w_j=\left\{w_1,w_2,\dots ,w_n\right\}$ represents the weight vector for each attribute, with conditions $0\le w_j\le 1$ and ${\displaystyle \sum _{j=1}^n{w}_j=1}$. ${\lambda }_k=\left\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_t\right\}$ represents the objective weight vector associated with each decision maker across each attribute, where $0\le {\lambda }_k\le 1$ and ${\displaystyle \sum _{k=1}^t{\lambda }_k=1}$. The procedural sequence of “the CPT-based PDHF decision-making method” is as follows, while Figure 2 illustrates the decision-making process through a flowchart.

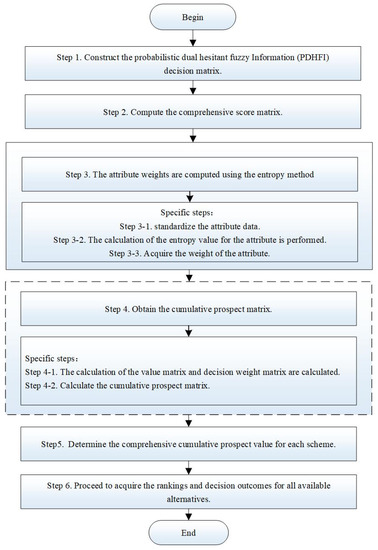
Figure 2. The procedural sequence of “the CPT-based PDHF decision-making method”.

Step 1. Construct the PDHFI decision matrix.

In the context of different risk states ${\theta }_{\xi }$, all DMs are invited to evaluate the attribute ${\mathrm{C}}_j$ of each alternative $A_i$, and obtain the evaluation information on the PDHF form. The PDHFEs are represented by $PDHF=⟨h_l(x)|p_l,g_f(x)|q_f⟩$, where $l=1,2,\dots \#\tilde{h}(x)$,$f=1,2,\dots ,\#\tilde{g}(x)$. Construct the PDHFI decision matrix as $PDH{F}^{(k,\xi )}={(pdh{f}_{ij}^{(k,\xi )})}_{m\times n}$, where $i=1,2,\dots ,m$$j=1,2,\dots ,n$.

Step 2. Compute the comprehensive score matrix.

Based on the PDHFI decision matrix, the formula (11) is used to solve the comprehensive score matrix $Scor{e}^{*\xi k}={(s_{ij})}_{m\times n}^{\xi k}$ for each attribute of DMs, $k=1,2,\dots ,t$. According to the importance of each expert, the weight of the experts is set to ${\lambda }_k$, and the final comprehensive score matrix after considering the weight of the experts is $Scor{e}^{*\xi }={(s_{ij})}_{m\times n}^{\xi }$, ${(s_{ij})}^{\xi }$ is shown in Formula (18).

$${(s_{ij})}^{\xi }={\displaystyle \sum _{k=1}^t{(s_{ij})}^{\xi k}\cdot {\lambda }_k}={(s_{ij})}^{\xi 1}\cdot {\lambda }_1+{(s_{ij})}^{\xi 2}\cdot {\lambda }_2+\dots +{(s_{ij})}^{\xi t}\cdot {\lambda }_t$$

(18)

Step 3. The attribute weights are computed using the entropy method [25].

The procedure for implementing the entropy method consists of the following steps:

Step 3-1. Set up an index data matrix $X$, and use the power coefficient method to standardize the attribute data of $X$. The standardized matrix is $Y$.

$$Y_{ij}=\frac{x_{ij}-x_{\min (j)}}{x_{\max (j)}-x_{\min (j)}}\kappa +(1-\kappa )$$

(19)

Among them, $x_{\max (j)}=\max (x_{1j},x_{2j},\cdots ,x_{nj})$, $x_{\min (j)}=\min (x_{1j},x_{2j},\cdots ,x_{nj})$, the efficacy coefficient $\kappa \in (0,1)$. The magnitude of the efficacy coefficient is a determining factor in the extent of the efficacy range, with a commonly seen value of $\kappa =0.9$.

Step 3-2. The calculation of the entropy value for the attribute is performed. Given the assumption that the entropy value of the $j-th$ attribute is represented as $e_j$, $e_j$ can be formulated as follows:

$$e_j=\frac{1}{(\ln m){\displaystyle \sum _{i=1}^m{Y}_{ij}}}\left[\begin{array}{l}(\ln {\displaystyle \sum _{i=1}^m{Y}_{ij}}){\displaystyle \sum _{i=1}^m{Y}_{ij}}\\ -{\displaystyle \sum _{i=1}^m{Y}_{ij}\ln Y_{ij}}\end{array}\right]$$

(20)

Step 3-3. Acquire the weight of the attribute. Given the assumption that the weight of the $j-th$ attribute is denoted as $w_j$, the formula for calculating the weight is as follows:

$$w_j=\frac{1-e_j}{{\displaystyle \sum _{j=1}^n(1-e_j)}}$$

(21)

Step 4. Obtain the cumulative prospect matrix.

Step 4-1. The calculation of the value matrix $v{(s_{ij}^{\xi })}_{m\times n}$ and decision weight matrix $\pi {(p_{\xi })}_{m\times n}$ in various risk states is based on the mean value ${\overline{s}}_j^{\xi }$ of the score function for each attribute, using the VF (value function) and DWF (decision weight function) methodologies. The calculation formula is shown in Formulas (22) and (23).

$$v(s_{ij}^{\xi })=\{\begin{array}{c}{(s_{ij}^{\xi }-{\overline{s}}_j^{\xi })}^{\alpha },s_{ij}^{\xi }\ge {\overline{s}}_j^{\xi }\\ -\theta {({\overline{s}}_j^{\xi }-s_{ij}^{\xi })}^{\beta },s_{ij}^{\xi }<{\overline{s}}_j^{\xi }\end{array}$$

(22)

$$\pi ({\rho }_{\xi })=\{\begin{array}{c}\begin{array}{cc}{\omega }^{+}({\displaystyle \sum _{{\xi }^{*}=\xi }^{\varsigma }{\rho }_{{\xi }^{*}})-{\omega }^{+}({\displaystyle \sum _{{\xi }^{*}=\xi +1}^{\varsigma }{\rho }_{{\xi }^{*}}),}}& s_{ij}^{\xi }\ge {\overline{s}}_j^{\xi }\end{array}\\ \begin{array}{cc}{\omega }^{-}({\displaystyle \sum _{{\xi }^{*}=1}^{\xi }{\rho }_{{\xi }^{*}})-{\omega }^{-}({\displaystyle \sum _{{\xi }^{*}=1}^{\xi -1}{\rho }_{{\xi }^{*}}),}}& s_{ij}^{\xi }<{\overline{s}}_j^{\xi }\end{array}\end{array}$$

(23)

Among them, ${\omega }^{+}({\rho }_{{\xi }^{*}})=\frac{{\rho }_{{\xi }^{*}}^{\sigma }}{{[{\rho }_{{\xi }^{*}}^{\sigma }+{(1-{\rho }_{{\xi }^{*}})}^{\sigma }]}^{1/\sigma }}$, ${\omega }^{-}({\rho }_{{\xi }^{*}})=\frac{{\rho }_{{\xi }^{*}}^{\epsilon }}{{[{\rho }_{{\xi }^{*}}^{\epsilon }+{(1-{\rho }_{{\xi }^{*}})}^{\epsilon }]}^{1/\epsilon }}$, ${\overline{s}}_j^{\xi }={\displaystyle {\sum }_{i=1}^m{s}_{ij}^{\xi }}/m$.

Step 4-2. Utilizing formula (24), compute the cumulative prospect matrix $V_{ij}$.

$$V_{ij}={(v_{ij})}_{m\times n}={\displaystyle \sum _{\xi =1}^{\zeta }\pi ({\rho }_{\xi })}(s_{ij}^{\xi })$$

(24)

Step 5. Determine the comprehensive cumulative prospect value $v_i$ for each scheme.

$$v_i=\begin{array}{cc}{\displaystyle \sum _{j=1}^n{\omega }_j\cdot v_{ij},}& i=1,2,\dots ,m\end{array}$$

(25)

Step 6. Proceed to acquire the rankings and decision outcomes for all available alternatives.

A higher comprehensive cumulative prospect value indicates a more favorable associated scheme [26]. The final decision result is obtained by sorting each scheme’s comprehensive cumulative prospect value.

4. Case Study and Methods Comparison

4.1. Case Study

In the pursuit of mitigating both human casualties and property losses stemming from significant urban crises, the municipal emergency management department introduces a set of four distinct emergency response schemes, denoted as $\{A_1,A_2,A_3,A_4\}$. The evaluation of these schemes encompasses four key attributes, denoted as $\{C_1,C_2,C_3,C_4\}$: command proficiency, rescue capability, response efficacy, and predictive accuracy [27]. In selecting and implementing the emergency response scheme, there are three possible risk states $\{{\theta }_1,{\theta }_2,{\theta }_3\}$, and the probability corresponding to the risk state is $\{0.35,0.40,0.25\}$ after expert evaluation. Three experienced emergency management experts are invited as DMs in this case, denoted as $\{E_1,E_2,E_3\}$. These DMs utilize the PDHFI format to assess each emergency response scheme and, as a result, arrive at the final decision regarding the chosen emergency response scheme. The procedural sequence and outcomes of the decision-making process are outlined as follows:

Step 1. Under different risk states, each DM $E_k$ conducts PDHF evaluation on the four emergency response schemes $A_i$ according to the four attributes ${\mathrm{C}}_j$, and the evaluation values constitute the PDHFI decision matrix. The PDHF decision matrices of all DMs under the three risk states are shown in Table 1, Table 2 and Table 3.

Table 1. The decision matrix of the 1st risk state.

DM	Scheme	Attribute
		C1	C2	C3	C4
E1	A1	{0.2|0.2, 0.3|0.1, 0.4|0.7}, {0.6|0.2, 0.7|0.3, 0.8|0.5}	{0.3|0.4, 0.4|0.2, 0.5|0.4}, {0.5|0.1, 0.6|0.4, 0.7|0.4}	{0.8|0.7, 0.9|0.1}, {0.1|0.3, 0.2|0.3}	{0.2|0.3, 0.3|0.3, 0.4|0.4}, {0.6|0.3, 0.7|0.2, 0.8|0.5}
	A2	{0.7|0.6, 0.8|0.1, 0.9|0.3}, {0.1|0.3, 0.2|0.1, 0.3|0.6}	{0.6|0.7, 0.7|0.2, 0.8|0.1}, {0.2|0.4, 0.3|0.2, 0.4|0.4}	{0.2|0.4, 0.3|0.1, 0.4|0.5}, {0.6|0.2, 0.7|0.3, 0.8|0.5}	{0.1|0.2, 0.2|0.3, 0.3|0.5}, {0.7|0.1, 0.8|0.4, 0.9|0.5}
	A3	{0.6|0.2, 0.7|0.2, 0.8|0.6}, {0.2|0.1, 0.3|0.2, 0.4|0.7}	{0.3|0.2, 0.4|0.2, 0.5|0.6}, {0.5|0.2, 0.6|0.3, 0.7|0.5}	{0.1|0.4, 0.2|0.2, 0.3|0.4}, {0.7|0.4, 0.8|0.3, 0.9|0.3}	{0.7|0.1, 0.8|0.3, 0.9|0.6}, {0.1|0.2, 0.2|0.2, 0.3|0.6}
	A4	{0.3|0.2, 0.4|0.1, 0.5|0.7}, {0.5|0.3, 0.6|0.1, 0.7|0.6}	{0.6|0.3, 0.7|0.2, 0.8|0.5}, {0.2|0.1, 0.3|0.7, 0.4|0.2}	{0.8|0.3, 0.9|0.1, 0|0}, {0|0, 0.1|0.3, 0.2|0.2}	{0.2|0.2, 0.3|0.3, 0.4|0.5}, {0.6|0.1, 0.7|0.2, 0.8|0.7}
E2	A1	{0.1|0.1, 0.2|0.2, 0.4|0.7}, {0.6|0.3, 0.7|0.2, 0.8|0.5}	{0.4|0.4, 0.5|0.4, 0.6|0.2}, {0.7|0.4, 0.8|0.2}	{0.2|0.3, 0.3|0.1, 0.4|0.6}, {0.6|0.2, 0.7|0.3, 0.8|0.5}	{0.1|0.2, 0.2|0.3, 0.3|0.5}, {0.7|0.1, 0.8|0.4, 0.9|0.5}
	A2	{0.2|0.6, 0.3|0.1, 0.4|0.3}, {0.6|0.3, 0.7|0.3, 0.8|0.4}	{0.5|0.4, 0.6|0.2, 0.7|0.4}, {0.3|0.4, 0.4|0.2, 0.5|0.4}	{0.7|0.2, 0.8|0.1, 0.9|0.7}, {0.1|0.2, 0.2|0.3, 0.3|0.5}	{0.1|0.3, 0.2|0.3, 0.3|0.4}, {0.7|0.1, 0.8|0.4, 0.9|0.5}
	A3	{0.3|0.1, 0.4|0.1, 0.5|0.8}, {0.6|0.1, 0.7|0.6}	{0.4|0.3, 0.5|0.2, 0.6|0.5}, {0.4|0.4, 0.5|0.2, 0.6|0.4}	{0.2|0.4, 0.3|0.1, 0.4|0.5}, {0.6|0.2, 0.7|0.3, 0.8|0.5}	{0.1|0.2, 0.2|0.3, 0.3|0.5}, {0.7|0.1, 0.8|0.4, 0.9|0.5}
	A4	{0.4|0.2, 0.5|0.1, 0.6|0.7}, {0.8|0.3, 0.9|0.2}	{0.2|0.2, 0.3|0.2, 0.4|0.6}, {0.6|0.4, 0.7|0.2, 0.8|0.4}	{0.3|0.3, 0.4|0.1, 0.5|0.6}, {0.6|0.3, 0.7|0.5}	{0.1|0.2, 0.2|0.3, 0.3|0.5}, {0.7|0.1, 0.8|0.4, 0.9|0.5}
E3	A1	{0.3|0.4, 0.4|0.1}, {0.5|0.1, 0.6|0.1, 0.7|0.8}	{0.2|0.3, 0.3|0.2, 0.4|0.5}, {0.65|0.3, 0.75|0.2, 0.85|0.5}	{0.1|0.2, 0.2|0.1, 0.3|0.7}, {0.75|0.2, 0.85|0.3}	{0.4|0.1, 0.5|0.3, 0.6|0.6}, {0.7|0.2, 0.8|0.4}
	A2	{0.2|0.1, 0.3|0.1, 0.4|0.8}, {0.6|0.3, 0.7|0.1, 0.8|0.6}	{0.3|0.3, 0.4|0.2}, {0.5|0.4, 0.6|0.2, 0.7|0.4}	{0.4|0.4, 0.5|0.1, 0.6|0.5}, {0.7|0.2, 0.9|0.3}	{0.3|0.2, 0.4|0.3, 0.5|0.5}, {0.6|0.4, 0.7|0.5}
	A3	{0.3|0.1, 0.4|0.1, 0.5|0.8}, {0.6|0.1, 0.7|0.6}	{0.1|0.3, 0.2|0.2, 0.3|0.5}, {0.7|0.4, 0.8|0.2, 0.9|0.4}	{0.2|0.4, 0.3|0.1, 0.4|0.5}, {0.6|0.2, 0.7|0.3, 0.8|0.5}	{0.3|0.2, 0.4|0.3, 0.5|0.5}, {0.6|0.4, 0.7|0.5}
	A4	{0.7|0.1, 0.8|0.1, 0.9|0.8}, {0.1|0.3, 0.2|0.1, 0.3|0.6}	{0.4|0.3, 0.5|0.2, 0.6|0.5}, {0.8|0.4, 0.9|0.2}	{0.3|0.4, 0.4|0.1}, {0.5|0.2, 0.6|0.3, 0.7|0.5}	{0.2|0.2, 0.3|0.3, 0.4|0.5}, {0.6|0.1, 0.7|0.4, 0.8|0.5}

Table 2. The decision matrix of the 2nd risk state.

DM	Scheme	Attribute
		C1	C2	C3	C4
E1	A1	{0.2|0.4, 0.3|0.1, 0.4|0.5}, {0.6|0.1, 0.7|0.1, 0.8|0.8}	{0.6|0.2, 0.7|0.2, 0.8|0.6}, {0.25|0.3, 0.35|0.2, 0.45|0.5}	{0.5|0.1, 0.6|0.1, 0.7|0.8}, {0.35|0.2}	{0.3|0.2, 0.4|0.3, 0.5|0.5}, {0.55|0.2, 0.65|0.4, 0.75|0.4}
	A2	{0.6|0.1, 0.7|0.1, 0.8|0.8}, {0.2|0.1, 0.3|0.1, 0.4|0.8}	{0.1|0.2, 0.2|0.2, 0.3|0.6}, {0.75|0.3, 0.85|0.2}	{0.5|0.4, 0.6|0.1, 0.7|0.5}, {0.3|0.2, 0.4|0.3}	{0.3|0.3, 0.4|0.3, 0.5|0.4}, {0.55|0.2, 0.65|0.4, 0.75|0.4}
	A3	{0.1|0.1, 0.2|0.1, 0.3|0.8}, {0.7|0.1, 0.8|0.1, 0.9|0.8}	{0.7|0.3, 0.8|0.2, 0.9|0.5}, {0.15|0.3, 0.25|0.2, 0.35|0.5}	{0.6|0.2, 0.7|0.1, 0.8|0.7}, {0.25|0.2, 0.35|0.3, 0.45|0.5}	{0.2|0.4, 0.3|0.3, 0.4|0.3}, {0.65|0.2, 0.75|0.4, 0.85|0.4}
	A4	{0.3|0.4, 0.4|0.1}, {0.5|0.1, 0.6|0.1, 0.7|0.8}	{0.4|0.2, 0.5|0.2, 0.6|0.6}, {0.65|0.5}	{0.2|0.6, 0.3|0.1, 0.4|0.3}, {0.65|0.2, 0.75|0.3, 0.85|0.5}	{0.6|0.2, 0.7|0.3, 0.8|0.5}, {0.25|0.2, 0.35|0.4, 0.45|0.4}
E2	A1	{0.2|0.1, 0.3|0.1, 0.4|0.8}, {0.8|0.2}	{0.3|0.4, 0.4|0.2, 0.5|0.4}, {0.6|0.3, 0.7|0.2, 0.8|0.5}	{0.4|0.2, 0.5|0.1, 0.6|0.7}, {0.3|0.4}	{0.1|0.3, 0.2|0.3, 0.3|0.4}, {0.6|0.1, 0.7|0.4, 0.8|0.5}
	A2	{0.4|0.4, 0.5|0.1, 0.6|0.5}, {0.7|0.8}	{0.3|0.2, 0.4|0.2, 0.5|0.6}, {0.6|0.5}	{0.2|0.1, 0.3|0.1, 0.4|0.8}, {0.7|0.5, 0.8|0.3}	{0.2|0.3, 0.3|0.3, 0.4|0.4}, {0.6|0.2, 0.7|0.4, 0.8|0.4}
	A3	{0.3|0.3, 0.4|0.1, 0.5|0.6}, {0.6|0.8}	{0.6|0.1, 0.7|0.2, 0.8|0.7}, {0.3|0.2, 0.4|0.2, 0.5|0.6}	{0.4|0.2, 0.5|0.1, 0.6|0.7}, {0.8|0.4}	{0.8|0.4, 0.9|0.3}, {0.4|0.2, 0.5|0.4}
	A4	{0.7|0.2, 0.8|0.1, 0.9|0.7}, {0.3|0.1, 0.4|0.1, 0.5|0.8}	{0.6|0.4, 0.7|0.2, 0.8|0.4}, {0.2|0.4, 0.3|0.2}	{0.9|0.3}, {0.4|0.3, 0.5|0.3, 0.6|0.4}	{0.6|0.1, 0.7|0.3, 0.8|0.6}, {0.4|0.2, 0.5|0.4}
E3	A1	{0.5|0.1, 0.6|0.1, 0.7|0.8}, {0.2|0.1, 0.3|0.1, 0.4|0.8}	{0.4|0.2, 0.5|0.2, 0.6|0.6}, {0.8|0.2, 0.9|0.2}	{0.2|0.1, 0.3|0.1, 0.4|0.8}, {0.6|0.1}	{0.6|0.3, 0.7|0.3, 0.8|0.4}, {0.3|0.3}
	A2	{0.1|0.7, 0.2|0.1, 0.3|0.2}, {0.8|0.2, 0.9|0.1}	{0.2|0.4, 0.3|0.2, 0.4|0.4}, {0.6|0.4, 0.7|0.2, 0.8|0.4}	{0.3|0.6, 0.4|0.1, 0.5|0.3}, {0.7|0.3, 0.8|0.3, 0.9|0.4}	{0.4|0.6, 0.5|0.3}, {0.9|0.1}
	A3	{0.5|0.1, 0.6|0.1, 0.7|0.8}, {0.2|0.8, 0.3|0.1}	{0.4|0.2, 0.5|0.2, 0.6|0.6}, {0.8|0.6}	{0.3|0.3, 0.4|0.1, 0.5|0.6}, {0.9|0.6}	{0.8|0.4, 0.9|0.3}, {0.2|0.3, 0.3|0.4, 0.4|0.3}
	A4	{0.4|0.8, 0.5|0.1, 0.6|0.1}, {0.9|0.1}	{0.7|0.6, 0.8|0.2, 0.9|0.2}, {0.2|0.2, 0.3|0.4, 0.4|0.4}	{0.2|0.4, 0.3|0.1, 0.4|0.5}, {0.5|0.5, 0.6|0.3, 0.7|0.2}	{0.5|0.4, 0.6|0.3, 0.7|0.3}, {0.1|0.3, 0.2|0.4}

Table 3. Decision matrix of 3rd risk state.

DM	Scheme	Attribute
		C1	C2	C3	C4
E1	A1	{0.1|0.1,0.2|0.1,0.3|0.8}, {0.7|0.3,0.8|0.1,0.9|0.6}	{0.3|0.2,0.4|0.2,0.5|0.6}, {0.2|0.3}	{0.4|0.1,0.5|0.1,0.6|0.8}, {0.1|0.6,0.2|0.1}	{0.2|0.3,0.3|0.3,0.4|0.4}, {0.6|0.4,0.7|0.4,0.8|0.2}
	A2	{0.2|0.7,0.3|0.1,0.4|0.2}, {0.6|0.2,0.7|0.1,0.8|0.7}	{0.4|0.4,0.5|0.2,0.6|0.4}, {0.4|0.4,0.5|0.2,0.6|0.4}	{0.3|0.6,0.4|0.1,0.5|0.3}, {0.5|0.3,0.6|0.3,0.7|0.4}	{0.4|0.6,0.5|0.3}, {1|0.1,1.11.2|0.9}
	A3	{0.1|0.1,0.2|0.9}, {0.8|0.8,0.9|0.1,1|0.1}	{0.4|0.2}, {0.8|0.6}	{0.3|0.3,0.4|0.1,0.5|0.6}, {0.1|0.2,0.2|0.8}	{0.8|0.4,0.9|0.3}, {0.2|0.3,0.3|0.4,0.4|0.3}
	A4	{0.6|0.8,0.7|0.1,0.8|0.1}, {0.2|0.1,0.3|0.2,0.4|0.7}	{0.5|0.6,0.6|0.2,0.7|0.2}, {0.3|0.2,0.4|0.4}	{0.2|0.4,0.3|0.1,0.4|0.5}, {0.6|0.5,0.7|0.3,0.8|0.2}	{0.3|0.4,0.4|0.3,0.5|0.3}, {0.8|0.4,0.9|0.6}
E2	A1	{0.2|0.1,0.3|0.1,0.4|0.8}, {0.6|0.1,0.7|0.1,0.8|0.8}	{0.4|0.2,0.5|0.2,0.6|0.6}, {0.1|0.2,0.2|0.2}	{0.3|0.1,0.4|0.1,0.5|0.8}, {0.7|0.1,0.8|0.3}	{0.1|0.3,0.2|0.3,0.3|0.4}, {0.8|0.3,0.9|0.4}
	A2	{0.4|0.7,0.5|0.1,0.6|0.2}, {0.8|0.2,0.9|0.1}	{0.2|0.4,0.3|0.2,0.4|0.4}, {0.6|0.4,0.7|0.2,0.8|0.4}	{0.5|0.6,0.6|0.1,0.7|0.3}, {0.3|0.3,0.4|0.3}	{0.3|0.6,0.4|0.3}, {0.6|0.1,0.8|0.4}
	A3	{0.4|0.1,0.5|0.1,0.6|0.8}, {0.7|0.8,0.8|0.1}	{0.6|0.2,0.7|0.2,0.8|0.6}, {0.2|0.6,0.3|0.3}	{0.5|0.3,0.6|0.1,0.7|0.6}, {0.3|0.6,0.4|0.2}	{0.3|0.4,0.4|0.3}, {0.7|0.3,0.8|0.4,0.9|0.3}
	A4	{0.1|0.8,0.2|0.1,0.3|0.1}, {0.7|0.1}	{0.2|0.6,0.3|0.2,0.4|0.2}, {0.6|0.2,0.7|0.4,0.8|0.4}	{0.4|0.4,0.5|0.1,0.6|0.5}, {0.1|0.5,0.2|0.3}	{0.3|0.4,0.4|0.3,0.5|0.3}, {0.8|0.3,0.9|0.4}
E3	A1	{0.2|0.4,0.3|0.1,0.4|0.5}, {0.5|0.1,0.6|0.3,0.7|0.2}	{0.4|0.3,0.5|0.2,0.6|0.5}, {0.8|0.2,0.9|0.5}	{0.3|0.6,0.4|0.1}, {0.6|0.1,0.7|0.3,0.8|0.6}	{0.6|0.3,0.7|0.3,0.8|0.4}, {0.3|0.3,0.4|0.2,0.5|0.4}
	A2	{0.6|0.7,0.7|0.1,0.8|0.2}, {0.1|0.2,0.2|0.1}	{0.7|0.4,0.8|0.2,0.9|0.4}, {0.6|0.4,0.7|0.2,0.8|0.4}	{0.3|0.2,0.4|0.1,0.5|0.7}, {0.3|0.3,0.4|0.3,0.5|0.4}	{0.4|0.3,0.5|0.3,0.6|0.3}, {0.1|0.1,0.3|0.5}
	A3	{0.8|0.8,0.9|0.1}, {0.2|0.8,0.3|0.1}	{0.6|0.6,0.7|0.2,0.8|0.2}, {0.1|0.6,0.3|0.1,0.4|0.2}	{0.3|0.3,0.4|0.1,0.5|0.6}, {0.6|0.6,0.7|0.1}	{0.8|0.4,0.9|0.3}, {0.2|0.3,0.3|0.4,0.4|0.3}
	A4	{0.2|0.3,0.3|0.1,0.4|0.6}, {0.7|0.1,0.9|0.1}	{0.7|0.6,0.8|0.2,0.9|0.2}, {0.2|0.2,0.3|0.4,0.4|0.4}	{0.3|0.2,0.4|0.1,0.5|0.7}, {0.8|0.5,0.9|0.3}	{0.6|0.4,0.7|0.3,0.8|0.3}, {0.1|0.3,0.2|0.4,0.3|0.3}

Step 2. Compute the comprehensive score matrix.

Based on the PDHFI decision matrix, Formula (11) solves the comprehensive score function. The score matrix of each expert under the three risk states is $S^{*\xi k}={(s_{ij})}_{m\times n}^{\xi k}$$(k=1,2,\dots ,t)$, as shown in Table 4.

Table 4. The comprehensive score matrix under three risk states.

		The 1st Risk State				The 2nd Risk State				The 3rd Risk State
		C1	C2	C3	C4	C1	C2	C3	C4	C1	C2	C3	C4
E1	A1	0.1306	0.2876	0.2098	0.1295	0.1148	−0.0415	0.1318	0.3087	0.0535	0.3315	0.4331	0.4177
	A2	1.6355	1.2186	0.1079	0.0358	−0.0159	−0.0178	0.1339	0.3038	0.1310	0.3490	0.2865	0.6298
	A3	−0.0312	0.2955	0.0297	−0.2270	0.0496	−0.2547	−0.0435	0.1438	−0.4044	0.0221	0.3138	0.3140
	A4	0.2969	−0.0406	0.0438	0.1313	−0.1130	0.2595	0.1373	−0.0415	−0.0156	0.1254	0.1169	0.2713
E2	A1	−0.0392	0.2517	0.1381	0.0013	0.1409	0.3131	0.5235	−0.0036	0.1451	0.4208	0.4028	0.5135
	A2	0.1220	0.1040	−0.2409	0.0309	0.4006	0.3226	0.1360	0.1264	0.5312	0.1235	0.8348	0.4864
	A3	0.0307	0.3512	0.1169	0.0358	0.1271	0.5324	0.0636	1.2012	0.4695	−0.0288	0.1080	0.4401
	A4	0.4132	0.1329	−0.0026	0.0358	2.8330	−0.0335	1.2124	−0.0422	−0.0171	0.1307	0.4041	0.5135
E3	A1	0.2070	0.1415	−0.0174	0.5515	0.1541	0.5324	0.0996	−0.0228	0.1094	0.5099	−0.1161	0.3707
	A2	0.1490	0.0623	0.3784	0.0021	0.3512	0.2135	0.3465	0.4507	−0.0110	−0.2465	0.2718	0.4183
	A3	0.0307	0.2702	0.2969	0.0021	0.1551	0.4092	0.3248	0.3140	0.2479	−0.0115	0.3238	0.3140
	A4	−0.2225	0.4009	0.0691	0.1313	1.7474	−0.2603	0.0914	0.4165	0.3315	−0.2603	0.4065	0.4166

Assume that all experts have the same importance, that is, the weights ${\lambda }_k$ of experts are equal. Finally, the comprehensive score matrix $Scor{e}^{*\xi }$ after considering the weight of each expert is shown in Table 5.

Table 5. The comprehensive scoring matrix after considering expert weights.

	The 1st Risk State				The 2nd Risk State				The 3rd Risk State
	C1	C2	C3	C4	C1	C2	C3	C4	C1	C2	C3	C4
A1	0.0995	0.2270	0.1102	0.2274	0.1366	0.2680	0.2516	0.0941	0.1027	0.4207	0.2399	0.4340
A2	0.6355	0.4616	0.0818	0.0229	0.2453	0.1728	0.2055	0.2936	0.2170	0.0753	0.4644	0.5115
A3	0.0101	0.3057	0.1478	−0.0630	0.1106	0.2289	0.1150	0.5530	0.1043	−0.0061	0.2485	0.3561
A4	0.1625	0.1644	0.0368	0.0995	1.4891	−0.0114	0.4804	0.1109	0.0996	−0.0014	0.3092	0.4005

Step 3. The attribute weights are computed using the entropy method.

According to Formulas (19)–(21), the weight set of the attribute in this case can be calculated as $w_j=\{0.1531,0.2774,0.1219,0.4476\}$, where $j=1,2,3,4$.

Step 4. Obtain the cumulative prospect matrix.

Step 4-1. In accordance with Formulas (22) and (23), determine the value matrix $v{(s_{ij}^{\xi })}_{m\times n}$ and decision weight matrix $\pi {(P_{\xi })}_{m\times n}$ of each scheme under various risk situations, using the average value ${\overline{s}}_j^{\xi }$ of each attribute score function as the reference point. Set parameter values $\alpha =\beta =0.88$, $\theta =2.25$, $\sigma =0.61$ and $\epsilon =0.69$. Table 6 and Table 7 illustrate the outcomes of the finalized calculations.

Table 6. The value matrix under three risk states.

	$\mathit{v}({\mathit{s}}_{\mathit{i}\mathit{j}}^1)$				$\mathit{v}({\mathit{s}}_{\mathit{i}\mathit{j}}^2)$				$\mathit{v}({\mathit{s}}_{\mathit{i}\mathit{j}}^3)$
	C1	C2	C3	C4	C1	C2	C3	C4	C1	C2	C3	C4
A1	−0.3671	−0.1966	0.0264	0.1946	−0.9130	0.1358	−0.0443	−0.4702	−0.0974	0.3452	−0.2319	0.0150
A2	0.4549	0.2124	−0.0471	−0.1578	−0.6645	0.0146	−0.1826	0.0466	0.1156	−0.1521	0.1871	0.1154
A3	−0.5860	0.0263	0.0762	−0.3855	−0.9709	0.0894	−0.4191	0.3365	−0.0925	−0.3691	−0.2085	−0.2151
A4	−0.2014	−0.3617	−0.1818	0.0427	0.9945	−0.4877	0.2610	−0.4288	−0.1067	−0.3572	−0.0260	−0.0876

Table 7. The decision weight matrix under three risk states.

	$\mathit{\pi }({\mathit{P}}_1)$				$\mathit{\pi }({\mathit{P}}_2)$				$\mathit{\pi }({\mathit{P}}_3)$
	C1	C2	C3	C4	C1	C2	C3	C4	C1	C2	C3	C4
A1	0.3077	0.3077	0.2911	0.2911	0.3470	0.3263	0.3470	0.3470	0.2267	0.2174	0.2267	0.2174
A2	0.2911	0.2911	0.3077	0.3077	0.3470	0.3263	0.3470	0.3263	0.2174	0.2267	0.2174	0.2174
A3	0.3077	0.2911	0.2911	0.3077	0.3470	0.3263	0.3470	0.3263	0.2267	0.2267	0.2267	0.2267
A4	0.3077	0.3077	0.3077	0.2911	0.3263	0.3470	0.3263	0.3470	0.2267	0.2267	0.2267	0.2267

Step 4-2. According to Formula (24), the cumulative prospect matrix $V_{ij}$ can be calculated. Table 8 presents the outcomes.

Table 8. The cumulative prospect matrix.

	A1	A2	A3	A4
C1	−0.4519	0.0588	−0.0603	−0.1032
C2	−0.0731	0.0321	−0.0372	−0.0082
C3	−0.5383	−0.0468	−0.1705	−0.0576
C4	0.2383	−0.3615	0.0233	−0.1562

Step 5. Calculate the comprehensive cumulative prospect value for every single scheme.

Based on Formula (25), the comprehensive cumulative prospect value of every scheme can be calculated. The outcomes are displayed in Table 9.

Table 9. The comprehensive cumulative prospect value.

	A1	A2	A3	A4
Comprehensive cumulative prospect value	−0.0484	−0.1496	−0.0299	−0.0950

Step 6. Proceed to acquire the rankings and decision outcomes for all available alternatives.

A positive correlation exists between the magnitude of the comprehensive cumulative prospect value and the desirableness of the corresponding scheme. Therefore, the final evaluation findings are graded as $A_3>A_1>A_4>A_2$, and $A_3$ is the optimal solution.

4.2. Methods Comparison

This section presents a comparative analysis of “the CPT-based PDHF decision-making method” and the decision-making methods discussed in [28,29,30], in order to highlight the advantages of the former. In prior research, the literature [28] has introduced a probabilistic hesitant fuzzy decision-making method that utilizes cumulative prospect theory, which is applied to the decision-making problem of an offshore wind farm investment. The decision-making method introduced in [28] will be referred to as ‘Method A’ hereafter. Literature [29] introduced an approach to decision-making that combines generalized, hesitant, fuzzy TODIM with CPT. This method has been employed in the context of selecting scientific research individuals for recruitment at institutions. The method from [29] is referred to as ‘Method B’. Literature [30] presented an approach to decision-making that relies on fuzzy information, which has involved the evaluation of company candidates by aggregating the findings obtained from probabilistic dual fuzzy scores. The method described in [30] is labeled as ‘Method C’.

This section will use the above three MADM methods to solve the case of the emergency management department evaluating the emergency response scheme in Section 4.1. To ensure a comprehensive comparison of decision-making methods, it is imperative that the weights and parameter values utilized in the calculation process of the aforementioned three decision-making methods align with the calculation findings presented in Section 4.1. The calculation process and decision results of Methods A, B, and C are shown below.

4.2.1. Method A

According to the method steps in [28], the cumulative prospect matrix for every rescue scheme is computed, resulting in the determination of the comprehensive utility value and the order of the outcomes of the schemes, as presented in Table 10.

Table 10. The evaluation outcomes are based on Method A.

	A1	A2	A3	A4
Comprehensive utility value	−0.0115	−0.1093	0.0011	−0.1702
Sort results for schemes	A3 > A1 > A2 > A4

The schemes are sorted according to their comprehensive utility value. The greater the utility value, the better the scheme is judged. Therefore, based on the decision-making method in [28], the ranking result of the emergency response scheme is $A_3>A_1>A_2>A_4$, and $A_3$ is the optimal emergency response scheme.

4.2.2. Method B

According to the method steps in [29], the comprehensive score value of each emergency response scheme can be calculated. The evaluation outcomes for each scheme are presented in Table 11.

Table 11. The evaluation outcomes are based on Method B.

	A1	A2	A3	A4
Comprehensive score value	−0.0359	−0.0976	−0.0014	−0.0582
Sort results for schemes	A3 > A1 > A4 > A2

The schemes undergo a sorting procedure based on the magnitude of their comprehensive score values, where a higher comprehensive score value indicates a superior scheme. Thus, leveraging the decision-making methodology expounded in [29], the emergency response schemes are ranked as $A_3>A_1>A_4>A_2$, ultimately designating Scheme $A_3$ as the preferred course.

4.2.3. Method C

Following the procedure outlined in [30], the comprehensive score value and scheme sorting result for each emergency response scheme under three risk states can be calculated, and the results for each scheme are presented in Table 12.

Table 12. The evaluation outcomes are based on Method C.

		The 1st Risk State	The 2nd Risk State	The 3rd Risk State
Score value	A1	0.1934	0.1680	0.3559
	A2	0.2456	0.2420	0.3397
	A3	0.0761	0.3420	0.2040
	A4	0.1195	0.3330	0.2318
Sort results for schemes		A2 > A1 > A4 > A3	A3 > A4 > A2 > A1	A1 > A2 > A4 > A3

Across the three distinct risk states, the emergency response schemes undergo a sorting process predicated on the magnitude of their comprehensive score values. Notably, a higher score corresponds to a more favorable scheme. Drawing upon the decision-making method detailed in [30], the best emergency response schemes in three distinct risk states are determined as $A_2$,$A_3$ and $A_1$, respectively.

4.3. Discussion

The results of the above three decision-making methods and “the CPT-based PDHF decision-making method” are compared as shown in Table 13. Figure 3 illustrates the distribution of comprehensive utility values obtained using the four decision-making methods. The best scheme, as indicated in Table 13, is consistently identified $A_3$ by the CPT-based PDHF decision-making methods, Method A and Method B. It is established that the probability associated with the three risk states, as assessed by the DM, is denoted as $P=\{0.35,0.40,0.25\}$. The outcome derived through the implementation of Method C within the second risk state, characterized by the highest probability, indicates that $A_3$ this represents the optimal solution. Therefore, it can be shown that the decision-making results of “the CPT-based PDHF decision-making method” have certain validity and reliability.

Table 13. Comparison of decision-making results of different decision-making methods.

		The CPT-Based PDHF Decision-Making Method	Method A	Method B	Method C
					The 1st Risk State	The 2nd Risk State	The 3rd Risk State
Comprehensive utility value	A1	−0.0484	−0.0115	−0.03591	0.1934	0.1680	0.3559
	A2	−0.1496	−0.1093	−0.09757	0.2456	0.2420	0.3397
	A3	−0.0299	0.0011	−0.00142	0.0761	0.3420	0.2040
	A4	−0.0950	−0.1702	−0.05823	0.1195	0.3330	0.2318
Sort results for schemes		A3 > A1 > A4 > A2	A3 > A1 > A2 > A4	A3 > A1 > A4 > A2	A2 > A1 > A4 > A3	A3 > A4 > A2 > A1	A1 > A2 > A4 > A3
Best scheme		A3	A3	A3	A2	A3	A1

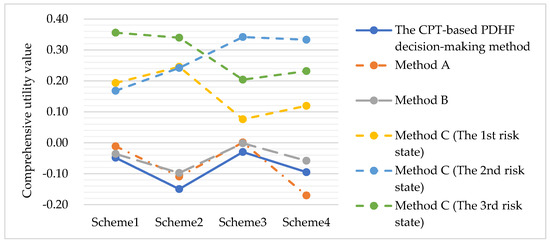
Figure 3. The distribution of the comprehensive utility value.

The distinguishing features of “the CPT-based PDHF decision-making method” alongside three other decision-making methods are displayed in Table 14. “The CPT-based PDHF decision-making method”, Method A, and Method B can consider different risk states and obtain comprehensive evaluation results. However, Method C can only obtain corresponding evaluation results under different risk states. Table 14 proposes three characteristics of the decision-making method. In addition to the decision-making method proposed in this paper that can satisfy these three characteristics simultaneously, Methods A, B, and C can only satisfy part of the characteristics. The ranking and decision-making outcomes of the final emergency response schemes exhibit only partial consistency as a result of the distinct traits and emphases of various decision-making methods. Most decision-making methods believe that $A_3$ is the best solution. However, the results of different decision-making methods are not the same. For example, the decision-making result in Method A is that $A_2$ it is better than $A_4$, which may be because Method A ignores relevant factors such as non-membership evaluation information. Although the decision-making results of Method B and ‘the CPT-based PDHF decision-making method’ are entirely consistent, Method B does not consider probability and non-membership degree evaluation information. This situation may lead to Method B in complex decision-making situations, which may cause errors in decision-making results. Method C can only draw corresponding conclusions for different risk states. Moreover, several decision-making results of Method C differ; therefore, it is challenging to provide theoretical support for complex practical decisions such as multi-risk states.

Table 14. Comparison of the characteristics of different decision-making methods.

Method	Whether to Consider the Evaluation Information of the Non-Membership Part	Whether to Comprehensively Consider the Evaluation Information of Different Risk States	Whether to Consider Probability Information
The CPT-based PDHF decision-making method	√	√	√
Method A	×	√	√
Method B	×	√	×
Method C	√	×	√

Furthermore, “the CPT-based PDHF decision-making method” presents several noteworthy advantages:

(1)

To comprehensively explain DMs evaluation information, “the CPT-based PDHF decision-making method” utilizes the PDHFS format to gather the evaluation information, given the inherent ambiguity of the decision-making information. The provided information is thorough, as it encompasses both membership and non-membership details, along with their respective probabilities. Simultaneously, this method presents an improved comprehensive scoring function to more accurately represent the genuineness and thoroughness of the assessment data.

(2)

Within the PDHF context, the “CPT-based PDHF decision-making method” introduces a method for determining cumulative prospect value, incorporates the “bounded rationality” of the DM, and delineates their constrained psychological traits. This method effectively tackles decision-making challenges in various risk scenarios and exhibits a remarkable level of precision and discriminative capability in its decision outcomes.

(3)

This study comprehensively considers the subjective and objective factors, and the attribute weight can be solved using the entropy method. Compared with existing literature that requires attribute weight information to be fully known before making a decision, “the CPT-based PDHF decision-making method” has more significant advantages.

5. Conclusions

Probabilistic dual hesitant fuzzy sets (PDHFSs) include the evaluative data pertaining to both membership and non-membership degrees, along with their associated probabilities. PDHFSs effectively capture the holistic information conveyed by decision-makers. When integrated with cumulative prospect theory (CPT), they offer significant theoretical and practical implications for decision-making research. Therefore, this study proposes “the CPT-based PDHF decision-making method." Firstly, this study constructs a probabilistic dual-hesitant fuzzy information (PDHFI) decision matrix. Secondly, according to the DMs authentic preference and non-membership information sensitivity, a comprehensive score function suitable for probabilistic dual hesitant fuzzy elements (PDHFEs) is proposed. Next, considering the subjective and objective factors comprehensively, the attribute weights are computed using the entropy method. Then, given the various risk states in decision-making dilemmas, we employ the CPT to determine the value function and the decision weight function for PDHFI. Moreover, the schemes undergo a sorting process based on their comprehensive cumulative prospect values. Following this process, the decision outcome is determined. Finally, we apply the decision-making methodology to an emergency management department’s case in selecting a response scheme, verifying the feasibility of the “CPT-based PDHF decision-making method." According to the comparative analysis and discussion with other methods, it is found that “the CPT-based PDHF decision-making method” has certain advantages, and its decision-making results are effective and reliable. The decision-making method proposed in this paper is theoretically suitable for solving different types of multi-attribute decision-making problems. It is an improvement and expansion of decision-making theory in fuzzy environments. In practical applications, decision-makers can adjust the weight and parameter values according to the actual decision-making situation, making the decision-making method more suitable for different scenarios. This method can be used for site selection of emergency resource banks, comprehensive energy project evaluation, etc. It can provide new ideas for solving problems in many fields, such as risk analysis.

In the future, we will promote the decision-making method proposed in this paper in other uncertain information environments and study new information measurement and comparison methods in probabilistic dual-hesitant fuzzy environments. In order to understand the ambiguity in the decision-making environment more comprehensively, we will consider introducing a dynamic parameter adjustment strategy to enable the model to adapt to the changing decision-making environment. In addition, we aim to improve the decision-making model’s real-time accuracy by introducing advanced machine learning and data analysis technologies to obtain and update decision parameters and weights automatically.