A Numerical Method for a Heat Conduction Model in a Double-Pane Window
Abstract
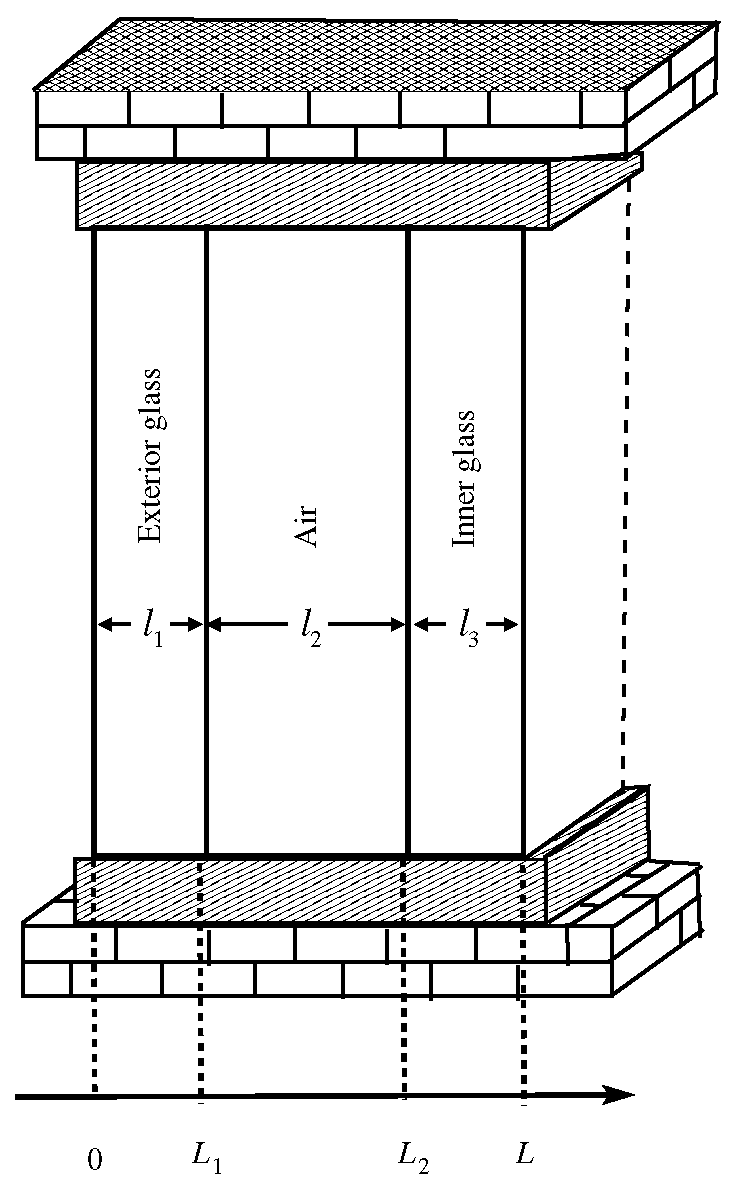
:1. Introduction
2. Change of Variable and Continuous Energy Estimation
3. Discretization of the Domain, Finite Difference Notation, and Preliminary Results
3.1. Discretization of the Domain
3.2. Finite Difference Notation
3.3. Four Useful Finite Difference Approximation Lemmas
4. Semidiscrete and Discrete Schemes for Numerical Solution of (12)–(18)
4.1. Semidiscrete Approximation of System (12)–(18)
4.1.1. Approximation of (12) on
4.1.2. Approximation of (12) on
4.1.3. Approximation of (12) on
4.1.4. Approximation of (13)
4.1.5. Semidiscrete Finite Difference Scheme to Approximate (12)–(18)
4.2. Fully Discrete Finite Difference Scheme to Approximate (12)–(18)
5. Discrete Scheme for Numerical Solution of (6)–(11)
6. Numerical Analysis: Discrete Energy, Stability, Convergence, and Order Estimates
7. A Numerical Example
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sahni, M.; Sahni, R. Applied Mathematical Modeling and Analysis in Renewable Energy, 1st ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Rashid, M.H. (Ed.) Electric Renewable Energy Systems; Elsevier: London, UK, 2015. [Google Scholar]
- Arici, M.; Karabay, H.; Kan, M. Flow and heat transfer in double, triple and quadruple pane windows. Energy Build. 2015, 86, 394–402. [Google Scholar] [CrossRef]
- Korpela, S.A.; Lee, Y.; Drummond, J.E. Heat Transfer Through a Double Pane Window. ASME J. Heat Transfer. 1982, 104, 539–544. [Google Scholar] [CrossRef]
- Han, J.; Lu, L.; Yang, H. Numerical evaluation of the mixed convective heat transfer in a double-pane window integrated with see-through a-Si PV cells with low-e coatings. Appl. Energy 2010, 87, 3431–3437. [Google Scholar] [CrossRef]
- Basok, B.I.; Davydenko, B.V.; Isaev, S.A.; Goncharuk, S.M.; Kuzhel, L.N. Numerical Modeling of Heat Transfer Through a Triple-Pane Window. J. Eng. Phys. Thermophys. 2016, 89, 1277–1283. [Google Scholar] [CrossRef]
- Aydin, O. Conjugate heat transfer analysis of double pane windows. Build. Environ. 2006, 41, 109–116. [Google Scholar] [CrossRef]
- Medved, S.; Novak, P. Heat transfer through a double pane window with an insulation screen open at the top. Energy Build. 1998, 28, 257–268. [Google Scholar] [CrossRef]
- Chow, T.-T.; Li, C.; Lin, Z. Thermal characteristics of water-flow double-pane window. Int. J. Therm. Sci. 2011, 50, 140–148. [Google Scholar] [CrossRef]
- Karabay, H.; Arıcı, M. Multiple pane window applications in various climatic regions of Turkey. Energy Build. 2012, 45, 67–71. [Google Scholar] [CrossRef]
- Rubin, M. Calculating heat transfer through windows. Int. J. Energy Res. 1982, 6, 341–349. [Google Scholar] [CrossRef]
- Aydin, O. Determination of optimum air-layer thickness in double-pane windows. Energy Build. 2000, 32, 303–308. [Google Scholar] [CrossRef]
- Arici, M.; Karabay, H. Determination of optimum thickness of double-glazed windows for the climatic regions of Turkey. Energy Build. 2010, 42, 1773–1778. [Google Scholar] [CrossRef]
- Arici, M.; Kan, M. An investigation of flow and conjugate heat transfer in multiple pane windows with respect to gap width, emissivity and gas filling. Renew. Energy 2015, 75, 249–256. [Google Scholar] [CrossRef]
- Dorfman, A.; Renner, Z. Conjugate Problems in Convective Heat Transfer: Review. Math. Probl. Eng. 2009, 2009, 927350. [Google Scholar] [CrossRef]
- Zudin, Y.B. Theory of Periodic Conjugate Heat Transfer, 2nd ed.; Springer: Berlin, Germany, 2011. [Google Scholar]
- Kazemi-Kamyab, V.; van Zuijlen, A.H.; Bijl, H. A high order time-accurate loosely-coupled solution algorithm for unsteady conjugate heat transfer problems. Comput. Methods Appl. Mech. Eng. 2013, 264, 205–217. [Google Scholar] [CrossRef]
- Ooi, E.H.; van Popov, V. An efficient hybrid BEM–RBIE method for solving conjugate heat transfer problems. Comput. Math. Appl. 2014, 66, 2489–2503. [Google Scholar] [CrossRef]
- Costa, R.; Nóbrega, J.M.; Clain, S.; Machado, G.J. Very high-order accurate polygonal mesh finite volume scheme for conjugate heat transfer problems with curved interfaces and imperfect contacts. Comput. Methods Appl. Mech. Eng. 2019, 357, 112560. [Google Scholar] [CrossRef]
- Pan, X.; Lee, C.; Choi, J.-I. Efficient monolithic projection method for time-dependent conjugate heat transfer problems. J. Comput. Phys. 2018, 369, 191–208. [Google Scholar] [CrossRef]
- Guo, S.; Feng, Y.; Tao, W.-Q. Deviation analysis of loosely coupled quasi-static method for fluid-thermal interaction in hypersonic flows. Comput. Fluids 2017, 149, 194–204. [Google Scholar] [CrossRef]
- Errera, M.-P.; Duchaine, F. Comparative study of coupling coefficients in Dirichlet-Robin procedure for fluid-structure aerothermal simulations. J. Comput. Phys. 2016, 312, 218–234. [Google Scholar] [CrossRef]
- Kazemi-Kamyab, V.; van Zuijlen, A.H.; Bijl, H. Analysis and application of high order implicit Runge-Kutta schemes for unsteady conjugate heat transfer: A strongly-coupled approach. J. Comput. Phys. 2014, 272, 471–486. [Google Scholar] [CrossRef]
- Dai, W.; Han, F.; Sun, Z. Accurate numerical method for solving dual-phase-lagging equation with temperature jump boundary condition in nano heat conduction. Int. J. Heat Mass Transf. 2013, 64, 966–975. [Google Scholar] [CrossRef]
- Tzou, D.Y. A unified approach for heat conduction from macro-to micro-scale. ASME J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro to Microscale Heat Transfer. The Lagging Behaviour, 2nd ed.; Taylor & Francis: Washington, DC, USA, 2014. [Google Scholar]
- Sun, H.; Sun, Z.Z.; Dai, W. A second-order finite difference scheme for solving the dual-phase-lagging equation in a double-layered nano-scale thin film. Numer. Methods Partial. Differ. Equ. 2017, 33, 142–173. [Google Scholar] [CrossRef]
- Ghazanfarian, J.; Abbassi, A. Effect of boundary phonon scattering on Dual-Phase-Lag model to simulate micro- and nano-scale heat conduction. Int. J. Heat And Mass Transf. 2009, 52, 3706–3711. [Google Scholar] [CrossRef]
- Sun, Z.Z. Numerical Methods for Partial Differential Equations, 2nd ed.; Science Press: Beijing, China, 2012. [Google Scholar]
- Liao, H.L.; Sun, Z.Z. Maximum norm error estimates of efficient difference schemes for second-order wave equations. J. Comput. Appl. Math. 2011, 235, 2217–2233. [Google Scholar] [CrossRef] [Green Version]

| - | - | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coronel, A.; Huancas, F.; Lozada, E.; Tello, A. A Numerical Method for a Heat Conduction Model in a Double-Pane Window. Axioms 2022, 11, 422. https://doi.org/10.3390/axioms11080422
Coronel A, Huancas F, Lozada E, Tello A. A Numerical Method for a Heat Conduction Model in a Double-Pane Window. Axioms. 2022; 11(8):422. https://doi.org/10.3390/axioms11080422
Chicago/Turabian StyleCoronel, Aníbal, Fernando Huancas, Esperanza Lozada, and Alex Tello. 2022. "A Numerical Method for a Heat Conduction Model in a Double-Pane Window" Axioms 11, no. 8: 422. https://doi.org/10.3390/axioms11080422
APA StyleCoronel, A., Huancas, F., Lozada, E., & Tello, A. (2022). A Numerical Method for a Heat Conduction Model in a Double-Pane Window. Axioms, 11(8), 422. https://doi.org/10.3390/axioms11080422







