Effect of Fuzzy Time Series on Smoothing Estimation of the INAR(1) Process
Abstract
:1. Introduction
2. Basic Definitions in Fuzzy Time Series Methods
Proposed Method
- Define the universe of discourse (set of observations which generated by the selected model in this paper) and partition it into equally lengthy intervals.
- Calculate the number of observations in each interval, and by doing so, there will be a re-division for each interval based on the number of observations contained in this interval.
- Define linguistic values represented by fuzzy set based on the redivided intervals.
- Fuzzify the actual observations.
- Identify and establish fuzzy logical relationships based on the fuzzified observations.
- Use set of rules to determine whether the trend of the forecasting goes up or down, which means we dismantle the fuzzy output into the forecasted output.
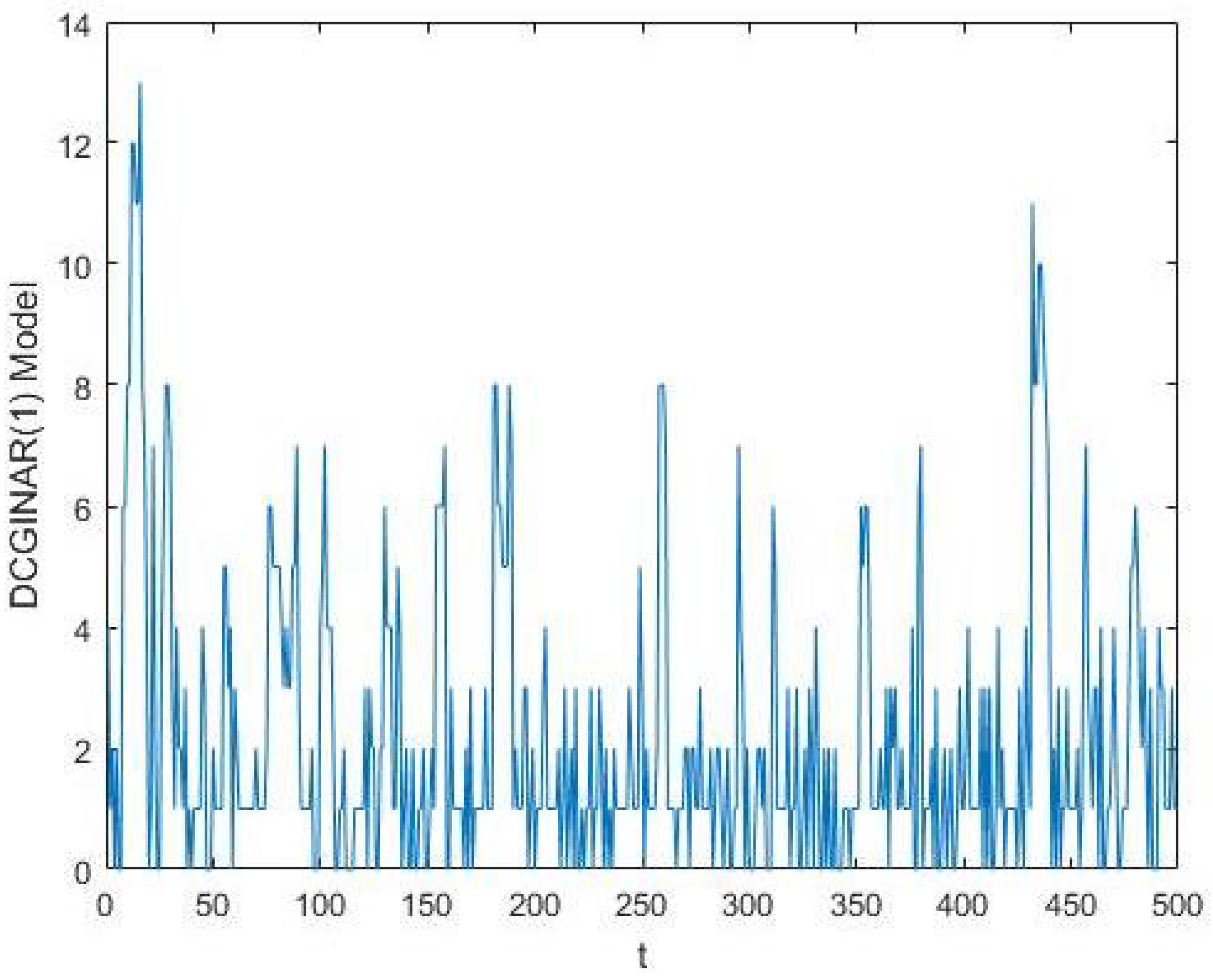
3. The Dependent Counting Geometric INAR(1) Model
3.1. Higher Order Joint Moments and Cumulants up to Order Three
3.2. Spectral and Bispectral Density Functions
4. Estimation of Spectrum and Bispectrum
- -
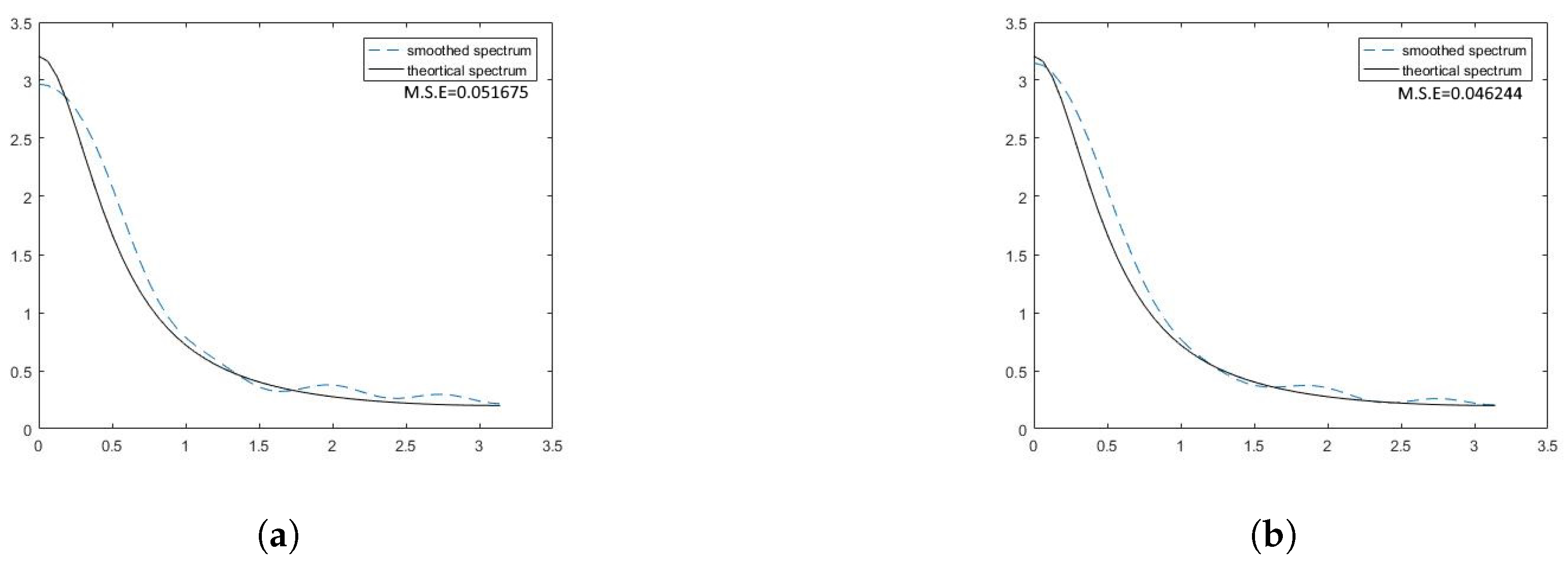
- From Figure 6, we can conclude that the forecasted observations are better than the generated observations for estimating the spectrum since the smoothed spectrum using the forecasted observations is more closer to the theoretical spectrum than the smoothed spectrum using the generated observations.
- -
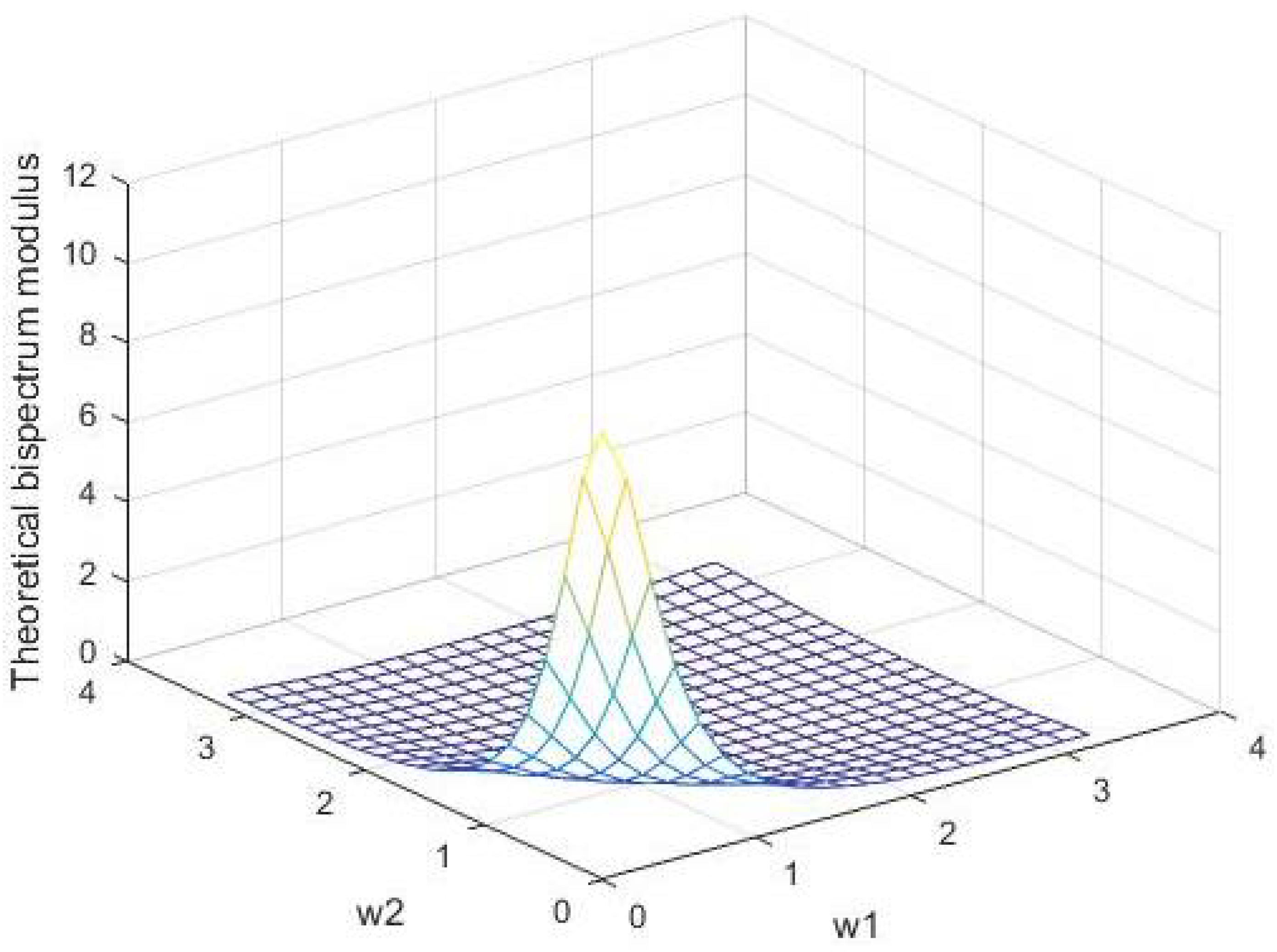
- If we compare the estimated bispectrum modulus in Figure 7 with the theoretical bispectrum modulus in Figure 4, we can conclude that the forecasted observations are better than the generated observations for estimating the bispectrum modulus. Additionally, if we compare the estimated normalized bispectrum modulus in Figure 8 with the theoretical normalized bispectrum in Figure 5, we can conclude that the forecasted observations are better than the generated observations for estimating the normalized bispectrum modulus. Using the Daniell window with the forecasted observations made the bispectrum and normalized bispectrum close to the theoretical bispectrum and normalized bispectrum.
- Depending on M.S.E which appears on each image, we find the following:
- -
- From Figure 9, we can conclude that the forecasted observations are better than the generated observations for estimating the spectrum.
- -
- If we compare the estimated bispectrum modulus in Figure 10 with the theoretical bispectrum modulus in Figure 4, we can conclude that the forecasted observations are better than the generated observations for estimating the bispectrum modulus. Additionally, if we compare the estimated normalized bispectrum modulus in Figure 11 with the theoretical normalized bispectrum in Figure 5, we can conclude that the forecasted observations are better than the generated observations for estimating the normalized bispectrum modulus.
- Depending on M.S.E, which appears on each image, we find the following:
- -
- From Figure 12, we can conclude that the forecasted observations are better than the generated observations for estimating the spectrum
- -
- If we compare the estimated bispectrum modulus in Figure 13 with the theoretical bispectrum modulus in Figure 4, we can conclude that the forecasted observations are better than the generated observations for estimating the bispectrum modulus. Additionally, if we compare the estimated normalized bispectrum modulus in Figure 14 with the theoretical normalized bispectrum in Figure 5, we can conclude that the forecasted observations are better than the generated observations for estimating the normalized bispectrum modulus.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McKenzie, E. Some simple models for discrete variate time series 1. JAWRA J. Am. Water Resour. Assoc. 1985, 21, 645–650. [Google Scholar] [CrossRef]
- Al-Osh, M.; Alzaid, A.A. First-order integer-valued autoregressive (INAR(1)) process. J. Time Ser. Anal. 1987, 8, 261–275. [Google Scholar] [CrossRef]
- Alzaid, A.; Al-Osh, M. First-order integer-valued autoregressive (INAR(1)) process: Distributional and regression properties. Stat. Neerl. 1988, 42, 53–61. [Google Scholar] [CrossRef]
- Jin-Guan, D.; Yuan, L. The integer-valued autoregressive (INAR (p)) model. J. Time Ser. Anal. 1991, 12, 129–142. [Google Scholar] [CrossRef]
- Eduarda Da Silva, M.; Oliveira, V.L. Difference equations for the higher-order moments and cumulants of the INAR(1) model. J. Time Ser. Anal. 2004, 25, 317–333. [Google Scholar] [CrossRef]
- Freeland, R.K.; McCabe, B. Asymptotic properties of CLS estimators in the Poisson AR(1) model. Stat. Probab. Lett. 2005, 73, 147–153. [Google Scholar] [CrossRef]
- Jung, R.C.; Tremayne, A. Binomial thinning models for integer time series. Stat. Model. 2006, 6, 81–96. [Google Scholar] [CrossRef]
- Weiß, C.H. The combined INAR (p) models for time series of counts. Stat. Probab. Lett. 2008, 78, 1817–1822. [Google Scholar] [CrossRef]
- Cui, Y.; Lund, R. Inference in binomial AR(1) models. Stat. Probab. Lett. 2010, 80, 1985–1990. [Google Scholar] [CrossRef]
- Bakouch, H.S.; Ristić, M.M. Zero truncated Poisson integer-valued AR(1) model. Metrika 2010, 72, 265–280. [Google Scholar] [CrossRef]
- Aly, E.E.A.; Bouzar, N. On some integer-valued autoregressive moving average models. J. Multivar. Anal. 1994, 50, 132–151. [Google Scholar] [CrossRef]
- Ristić, M.M.; Bakouch, H.S.; Nastić, A.S. A new geometric first-order integer-valued autoregressive (NGINAR(1)) process. J. Stat. Plan. Inference 2009, 139, 2218–2226. [Google Scholar] [CrossRef]
- Ristić, M.M.; Nastić, A.S.; Bakouch, H.S. Estimation in an integer-valued autoregressive process with negative binomial marginals (NBINAR(1)). Commun. Stat.-Theory Methods 2012, 41, 606–618. [Google Scholar] [CrossRef]
- Ristić, M.M.; Nastić, A.S.; Jayakumar, K.; Bakouch, H.S. A bivariate INAR(1) time series model with geometric marginals. Appl. Math. Lett. 2012, 25, 481–485. [Google Scholar] [CrossRef]
- Nastić, A.S.; Ristić, M.M. Some geometric mixed integer-valued autoregressive (INAR) models. Stat. Probab. Lett. 2012, 82, 805–811. [Google Scholar] [CrossRef]
- Nastić, A.S.; Ristić, M.M.; Bakouch, H.S. A combined geometric INAR (p) model based on negative binomial thinning. Math. Comput. Model. 2012, 55, 1665–1672. [Google Scholar] [CrossRef]
- Brännäs, K.; Hellström, J. Generalized integer-valued autoregression. Econom. Rev. 2001, 20, 425–443. [Google Scholar] [CrossRef]
- Ristić, M.M.; Nastić, A.S.; Miletić Ilić, A.V. A geometric time series model with dependent Bernoulli counting series. J. Time Ser. Anal. 2013, 34, 466–476. [Google Scholar] [CrossRef]
- Gabr, M.; El-Desouky, B.; Shiha, F.; El-Hadidy, S.M. Higher Order Moments, Spectral and Bispectral Density Functions for INAR(1). Int. J. Comput. Appl. 2018, 182, 0975–8887. [Google Scholar]
- Mohammed, H.; Teamah, A.E.M.A.; Abu-Youssef, S.; Faied, H.M. Higher Order Moments, Cumulants, Spectral and Bispectral Density Functions of the ZTPINAR(1) Process. Appl. Math. 2022, 16, 213–225. [Google Scholar]
- Jiang, P.; Yang, H.; Heng, J. A hybrid forecasting system based on fuzzy time series and multi-objective optimization for wind speed forecasting. Appl. Energy 2019, 235, 786–801. [Google Scholar] [CrossRef]
- Parfenova, V.; Bulgakova, G.; Amagaeva, Y.G.; Evdokimov, K.; Samorukov, V. Forecasting models of agricultural process based on fuzzy time series. IOP Conf. Ser. Mater. Sci. Eng. 2020, 986, 012013. [Google Scholar] [CrossRef]
- Talarposhti, F.M.; Sadaei, H.J.; Enayatifar, R.; Guimarães, F.G.; Mahmud, M.; Eslami, T. Stock market forecasting by using a hybrid model of exponential fuzzy time series. Int. J. Approx. Reason. 2016, 70, 79–98. [Google Scholar] [CrossRef]
- Möller, B.; Reuter, U. Prediction of uncertain structural responses using fuzzy time series. Comput. Struct. 2008, 86, 1123–1139. [Google Scholar] [CrossRef]
- Zhao, C.L.; Cao, X.J.; Xie, X.J.; Yuan, X.H.; Wang, B. Environmental Aspects of Drilling Operation Risks: A Probability Prediction based on Fuzzy Time Series. Ekoloji 2018, 27, 1493–1502. [Google Scholar]
- Wong, H.L.; Tu, Y.H.; Wang, C.C. Application of fuzzy time series models for forecasting the amount of Taiwan export. Expert Syst. Appl. 2010, 37, 1465–1470. [Google Scholar] [CrossRef]
- Bas, E.; Egrioglu, E.; Aladag, C.H.; Yolcu, U. Fuzzy-time-series network used to forecast linear and nonlinear time series. Appl. Intell. 2015, 43, 343–355. [Google Scholar] [CrossRef]
- Stefanakos, C. Fuzzy time series forecasting of nonstationary wind and wave data. Ocean. Eng. 2016, 121, 1–12. [Google Scholar] [CrossRef]
- El-Menshawy, M.H. On estimation of unknown parameters for nonstationary linear processes by using fuzzy time series. Pioneer J. Theor. Appl. Stat. 2017, 14, 49–60. [Google Scholar]
- Teamah, A.E.M.A.; Faied, H.M.; El-Menshawy, M.H. Effect of Fuzzy Time Series Technique on Estimators of Spectral Analysis. Recent Adv. Math. Res. Comput. Sci. 2022, 6, 29–38. [Google Scholar]
- Chen, S.M.; Hsu, C.C. A new method to forecast enrollments using fuzzy time series. Int. J. Appl. Sci. Eng. 2004, 2, 234–244. [Google Scholar]
- Song, Q.; Chissom, B.S. Fuzzy time series and its models. Fuzzy Sets Syst. 1993, 54, 269–277. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Forecasting enrollments with fuzzy time series-Part II. Fuzzy Sets Syst. 1994, 62, 1–8. [Google Scholar] [CrossRef]
- Daniell, P.J. Discussion on symposium on autocorrelation in time series. J. R. Stat. Soc. 1946, 8, 88–90. [Google Scholar]
- Rao, T.S.; Gabr, M.M. An Introduction to Bispectral Analysis and Bilinear Time Series Models; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1984; Volume 24. [Google Scholar]
- Parzen, E. Mathematical considerations in the estimation of spectra. Technometrics 1961, 3, 167–190. [Google Scholar] [CrossRef]
- Blackman, R.B.; Tukey, J.W. Particular pairs of windows. In The Measurement of Power Spectra, from the Point of View of Communications Engineering; Wiley Online Library: Hoboken, NJ, USA, 1959; pp. 98–99. [Google Scholar]











| 0.00 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 11.2352 | 9.9030 | 7.2167 | 4.8711 | 3.2912 | 2.3014 | 1.6801 | 1.2790 | 1.0108 | 0.8254 | 0.6933 | 0.5969 | 0.5252 | 0.4712 | 0.4302 | 0.3991 | 0.3759 | 0.3590 | 0.3476 | 0.3410 | 0.3388 | |
| 0.05 | 9.9030 | 7.9364 | 5.5644 | 3.7554 | 2.5791 | 1.8410 | 1.3712 | 1.0627 | 0.8530 | 0.7060 | 0.6001 | 0.5220 | 0.4636 | 0.4194 | 0.3859 | 0.3607 | 0.3421 | 0.3289 | 0.3205 | 0.3164 | 0.3164 | |
| 0.10 | 7.2167 | 5.5644 | 3.8987 | 2.6715 | 1.8703 | 1.3599 | 1.0296 | 0.8093 | 0.6577 | 0.5502 | 0.4721 | 0.4142 | 0.3708 | 0.3379 | 0.3130 | 0.2945 | 0.2811 | 0.2720 | 0.2667 | 0.2650 | 0.2667 | |
| 0.15 | 4.8711 | 3.7554 | 2.6715 | 1.8651 | 1.3289 | 0.9812 | 0.7527 | 0.5984 | 0.4911 | 0.4145 | 0.3585 | 0.3168 | 0.2855 | 0.2619 | 0.2442 | 0.2312 | 0.2220 | 0.2161 | 0.2133 | 0.2133 | 0.2161 | |
| 0.20 | 3.2912 | 2.5791 | 1.8703 | 1.3289 | 0.9612 | 0.7188 | 0.5574 | 0.4473 | 0.3701 | 0.3147 | 0.2741 | 0.2438 | 0.2211 | 0.2041 | 0.1914 | 0.1823 | 0.1761 | 0.1725 | 0.1714 | 0.1725 | 0.1761 | |
| 0.25 | 2.3014 | 1.8410 | 1.3599 | 0.9812 | 0.7188 | 0.5432 | 0.4251 | 0.3438 | 0.2866 | 0.2453 | 0.2150 | 0.1924 | 0.1755 | 0.1629 | 0.1537 | 0.1473 | 0.1432 | 0.1412 | 0.1412 | 0.1432 | 0.1473 | |
| 0.30 | 1.6801 | 1.3712 | 1.0296 | 0.7527 | 0.5574 | 0.4251 | 0.3352 | 0.2731 | 0.2291 | 0.1973 | 0.1739 | 0.1566 | 0.1437 | 0.1342 | 0.1274 | 0.1228 | 0.1201 | 0.1193 | 0.1201 | 0.1228 | 0.1274 | |
| 0.35 | 1.2790 | 1.0627 | 0.8093 | 0.5984 | 0.4473 | 0.3438 | 0.2731 | 0.2239 | 0.1890 | 0.1637 | 0.1452 | 0.1314 | 0.1213 | 0.1140 | 0.1088 | 0.1056 | 0.1040 | 0.1040 | 0.1056 | 0.1088 | 0.1140 | |
| 0.40 | 1.0108 | 0.8530 | 0.6577 | 0.4911 | 0.3701 | 0.2866 | 0.2291 | 0.1890 | 0.1604 | 0.1398 | 0.1247 | 0.1135 | 0.1054 | 0.0996 | 0.0958 | 0.0935 | 0.0928 | 0.0935 | 0.0958 | 0.0996 | 0.1054 | |
| 0.45 | 0.8254 | 0.7060 | 0.5502 | 0.4145 | 0.3147 | 0.2453 | 0.1973 | 0.1637 | 0.1398 | 0.1225 | 0.1099 | 0.1007 | 0.0940 | 0.0894 | 0.0866 | 0.0852 | 0.0852 | 0.0866 | 0.0894 | 0.0940 | 0.1007 | |
| 0.50 | 0.6933 | 0.6001 | 0.4721 | 0.3585 | 0.2741 | 0.2150 | 0.1739 | 0.1452 | 0.1247 | 0.1099 | 0.0991 | 0.0914 | 0.0859 | 0.0823 | 0.0802 | 0.0795 | 0.0802 | 0.0823 | 0.0859 | 0.0914 | 0.0991 | |
| 0.55 | 0.5969 | 0.5220 | 0.4142 | 0.3168 | 0.2438 | 0.1924 | 0.1566 | 0.1314 | 0.1135 | 0.1007 | 0.0914 | 0.0848 | 0.0802 | 0.0774 | 0.0760 | 0.0760 | 0.0774 | 0.0802 | 0.0848 | 0.0914 | 0.1007 | |
| 0.60 | 0.5252 | 0.4636 | 0.3708 | 0.2855 | 0.2211 | 0.1755 | 0.1437 | 0.1213 | 0.1054 | 0.0940 | 0.0859 | 0.0802 | 0.0765 | 0.0744 | 0.0737 | 0.0744 | 0.0765 | 0.0802 | 0.0859 | 0.0940 | 0.1054 | |
| 0.65 | 0.4712 | 0.4194 | 0.3379 | 0.2619 | 0.2041 | 0.1629 | 0.1342 | 0.1140 | 0.0996 | 0.0894 | 0.0823 | 0.0774 | 0.0744 | 0.0729 | 0.0729 | 0.0744 | 0.0774 | 0.0823 | 0.0894 | 0.0996 | 0.1140 | |
| 0.70 | 0.4302 | 0.3859 | 0.3130 | 0.2442 | 0.1914 | 0.1537 | 0.1274 | 0.1088 | 0.0958 | 0.0866 | 0.0802 | 0.0760 | 0.0737 | 0.0729 | 0.0737 | 0.0760 | 0.0802 | 0.0866 | 0.0958 | 0.1088 | 0.1274 | |
| 0.75 | 0.3991 | 0.3607 | 0.2945 | 0.2312 | 0.1823 | 0.1473 | 0.1228 | 0.1056 | 0.0935 | 0.0852 | 0.0795 | 0.0760 | 0.0744 | 0.0744 | 0.0760 | 0.0795 | 0.0852 | 0.0935 | 0.1056 | 0.1228 | 0.1473 | |
| 0.80 | 0.3759 | 0.3421 | 0.2811 | 0.2220 | 0.1761 | 0.1432 | 0.1201 | 0.1040 | 0.0928 | 0.0852 | 0.0802 | 0.0774 | 0.0765 | 0.0774 | 0.0802 | 0.0852 | 0.0928 | 0.1040 | 0.1201 | 0.1432 | 0.1761 | |
| 0.85 | 0.3590 | 0.3289 | 0.2720 | 0.2161 | 0.1725 | 0.1412 | 0.1193 | 0.1040 | 0.0935 | 0.0866 | 0.0823 | 0.0802 | 0.0802 | 0.0823 | 0.0866 | 0.0935 | 0.1040 | 0.1193 | 0.1412 | 0.1725 | 0.2161 | |
| 0.90 | 0.3476 | 0.3205 | 0.2667 | 0.2133 | 0.1714 | 0.1412 | 0.1201 | 0.1056 | 0.0958 | 0.0894 | 0.0859 | 0.0848 | 0.0859 | 0.0894 | 0.0958 | 0.1056 | 0.1201 | 0.1412 | 0.1714 | 0.2133 | 0.2667 | |
| 0.95 | 0.3410 | 0.3164 | 0.2650 | 0.2133 | 0.1725 | 0.1432 | 0.1228 | 0.1088 | 0.0996 | 0.0940 | 0.0914 | 0.0914 | 0.0940 | 0.0996 | 0.1088 | 0.1228 | 0.1432 | 0.1725 | 0.2133 | 0.2650 | 0.3164 | |
| 0.3388 | 0.3164 | 0.2667 | 0.2161 | 0.1761 | 0.1473 | 0.1274 | 0.1140 | 0.1054 | 0.1007 | 0.0991 | 0.1007 | 0.1054 | 0.1140 | 0.1274 | 0.1473 | 0.1761 | 0.2161 | 0.2667 | 0.3164 | 0.3388 |
| 0.00 | 1.9548 | 1.8822 | 1.7166 | 1.5404 | 1.3929 | 1.2800 | 1.1961 | 1.1338 | 1.0873 | 1.0522 | 1.0254 | 1.0046 | 0.9885 | 0.9759 | 0.9661 | 0.9585 | 0.9527 | 0.9485 | 0.9456 | 0.9439 | 0.9433 | |
| 0.05 | 1.8822 | 1.7636 | 1.5950 | 1.4359 | 1.3078 | 1.2108 | 1.1385 | 1.0846 | 1.0440 | 1.0132 | 0.9895 | 0.9711 | 0.9568 | 0.9456 | 0.9368 | 0.9301 | 0.9251 | 0.9215 | 0.9192 | 0.9181 | 0.9181 | |
| 0.10 | 1.7166 | 1.5950 | 1.4463 | 1.3100 | 1.2003 | 1.1165 | 1.0534 | 1.0059 | 0.9699 | 0.9423 | 0.9209 | 0.9043 | 0.8913 | 0.8811 | 0.8733 | 0.8673 | 0.8629 | 0.8599 | 0.8581 | 0.8576 | 0.8581 | |
| 0.15 | 1.5404 | 1.4359 | 1.3100 | 1.1930 | 1.0974 | 1.0232 | 0.9668 | 0.9238 | 0.8909 | 0.8655 | 0.8458 | 0.8305 | 0.8184 | 0.8091 | 0.8019 | 0.7965 | 0.7927 | 0.7902 | 0.7890 | 0.7890 | 0.7902 | |
| 0.20 | 1.3929 | 1.3078 | 1.2003 | 1.0974 | 1.0115 | 0.9440 | 0.8920 | 0.8521 | 0.8213 | 0.7975 | 0.7790 | 0.7645 | 0.7532 | 0.7444 | 0.7378 | 0.7329 | 0.7296 | 0.7276 | 0.7270 | 0.7276 | 0.7296 | |
| 0.25 | 1.2800 | 1.2108 | 1.1165 | 1.0232 | 0.9440 | 0.8809 | 0.8319 | 0.7941 | 0.7648 | 0.7421 | 0.7243 | 0.7105 | 0.6998 | 0.6915 | 0.6853 | 0.6809 | 0.6781 | 0.6767 | 0.6767 | 0.6781 | 0.6809 | |
| 0.30 | 1.1961 | 1.1385 | 1.0534 | 0.9668 | 0.8920 | 0.8319 | 0.7849 | 0.7485 | 0.7203 | 0.6983 | 0.6812 | 0.6679 | 0.6576 | 0.6499 | 0.6442 | 0.6403 | 0.6380 | 0.6373 | 0.6380 | 0.6403 | 0.6442 | |
| 0.35 | 1.1338 | 1.0846 | 1.0059 | 0.9238 | 0.8521 | 0.7941 | 0.7485 | 0.7131 | 0.6856 | 0.6643 | 0.6477 | 0.6348 | 0.6250 | 0.6177 | 0.6125 | 0.6092 | 0.6075 | 0.6075 | 0.6092 | 0.6125 | 0.6177 | |
| 0.40 | 1.0873 | 1.0440 | 0.9699 | 0.8909 | 0.8213 | 0.7648 | 0.7203 | 0.6856 | 0.6587 | 0.6379 | 0.6217 | 0.6093 | 0.6000 | 0.5931 | 0.5885 | 0.5858 | 0.5849 | 0.5858 | 0.5885 | 0.5931 | 0.6000 | |
| 0.45 | 1.0522 | 1.0132 | 0.9423 | 0.8655 | 0.7975 | 0.7421 | 0.6983 | 0.6643 | 0.6379 | 0.6174 | 0.6017 | 0.5898 | 0.5810 | 0.5747 | 0.5707 | 0.5687 | 0.5687 | 0.5707 | 0.5747 | 0.5810 | 0.5898 | |
| 0.50 | 1.0254 | 0.9895 | 0.9209 | 0.8458 | 0.7790 | 0.7243 | 0.6812 | 0.6477 | 0.6217 | 0.6017 | 0.5865 | 0.5751 | 0.5668 | 0.5611 | 0.5579 | 0.5568 | 0.5579 | 0.5611 | 0.5668 | 0.5751 | 0.5865 | |
| 0.55 | 1.0046 | 0.9711 | 0.9043 | 0.8305 | 0.7645 | 0.7105 | 0.6679 | 0.6348 | 0.6093 | 0.5898 | 0.5751 | 0.5642 | 0.5565 | 0.5516 | 0.5492 | 0.5492 | 0.5516 | 0.5565 | 0.5642 | 0.5751 | 0.5898 | |
| 0.60 | 0.9885 | 0.9568 | 0.8913 | 0.8184 | 0.7532 | 0.6998 | 0.6576 | 0.6250 | 0.6000 | 0.5810 | 0.5668 | 0.5565 | 0.5496 | 0.5456 | 0.5443 | 0.5456 | 0.5496 | 0.5565 | 0.5668 | 0.5810 | 0.6000 | |
| 0.65 | 0.9759 | 0.9456 | 0.8811 | 0.8091 | 0.7444 | 0.6915 | 0.6499 | 0.6177 | 0.5931 | 0.5747 | 0.5611 | 0.5516 | 0.5456 | 0.5427 | 0.5427 | 0.5456 | 0.5516 | 0.5611 | 0.5747 | 0.5931 | 0.6177 | |
| 0.70 | 0.9661 | 0.9368 | 0.8733 | 0.8019 | 0.7378 | 0.6853 | 0.6442 | 0.6125 | 0.5885 | 0.5707 | 0.5579 | 0.5492 | 0.5443 | 0.5427 | 0.5443 | 0.5492 | 0.5579 | 0.5707 | 0.5885 | 0.6125 | 0.6442 | |
| 0.75 | 0.9585 | 0.9301 | 0.8673 | 0.7965 | 0.7329 | 0.6809 | 0.6403 | 0.6092 | 0.5858 | 0.5687 | 0.5568 | 0.5492 | 0.5456 | 0.5456 | 0.5492 | 0.5568 | 0.5687 | 0.5858 | 0.6092 | 0.6403 | 0.6809 | |
| 0.80 | 0.9527 | 0.9251 | 0.8629 | 0.7927 | 0.7296 | 0.6781 | 0.6380 | 0.6075 | 0.5849 | 0.5687 | 0.5579 | 0.5516 | 0.5496 | 0.5516 | 0.5579 | 0.5687 | 0.5849 | 0.6075 | 0.6380 | 0.6781 | 0.7296 | |
| 0.85 | 0.9485 | 0.9215 | 0.8599 | 0.7902 | 0.7276 | 0.6767 | 0.6373 | 0.6075 | 0.5858 | 0.5707 | 0.5611 | 0.5565 | 0.5565 | 0.5611 | 0.5707 | 0.5858 | 0.6075 | 0.6373 | 0.6767 | 0.7276 | 0.7902 | |
| 0.90 | 0.9456 | 0.9192 | 0.8581 | 0.7890 | 0.7270 | 0.6767 | 0.6380 | 0.6092 | 0.5885 | 0.5747 | 0.5668 | 0.5642 | 0.5668 | 0.5747 | 0.5885 | 0.6092 | 0.6380 | 0.6767 | 0.7270 | 0.7890 | 0.8581 | |
| 0.95 | 0.9439 | 0.9181 | 0.8576 | 0.7890 | 0.7276 | 0.6781 | 0.6403 | 0.6125 | 0.5931 | 0.5810 | 0.5751 | 0.5751 | 0.5810 | 0.5931 | 0.6125 | 0.6403 | 0.6781 | 0.7276 | 0.7890 | 0.8576 | 0.9181 | |
| 0.9433 | 0.9181 | 0.8581 | 0.7902 | 0.7296 | 0.6809 | 0.6442 | 0.6177 | 0.6000 | 0.5898 | 0.5865 | 0.5898 | 0.6000 | 0.6177 | 0.6442 | 0.6809 | 0.7296 | 0.7902 | 0.8581 | 0.9181 | 0.9433 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Morshedy, M.; El-Menshawy, M.H.; Almazah, M.M.A.; El-Sagheer, R.M.; Eliwa, M.S. Effect of Fuzzy Time Series on Smoothing Estimation of the INAR(1) Process. Axioms 2022, 11, 423. https://doi.org/10.3390/axioms11090423
El-Morshedy M, El-Menshawy MH, Almazah MMA, El-Sagheer RM, Eliwa MS. Effect of Fuzzy Time Series on Smoothing Estimation of the INAR(1) Process. Axioms. 2022; 11(9):423. https://doi.org/10.3390/axioms11090423
Chicago/Turabian StyleEl-Morshedy, Mahmoud, Mohammed H. El-Menshawy, Mohammed M. A. Almazah, Rashad M. El-Sagheer, and Mohamed S. Eliwa. 2022. "Effect of Fuzzy Time Series on Smoothing Estimation of the INAR(1) Process" Axioms 11, no. 9: 423. https://doi.org/10.3390/axioms11090423
APA StyleEl-Morshedy, M., El-Menshawy, M. H., Almazah, M. M. A., El-Sagheer, R. M., & Eliwa, M. S. (2022). Effect of Fuzzy Time Series on Smoothing Estimation of the INAR(1) Process. Axioms, 11(9), 423. https://doi.org/10.3390/axioms11090423








