The Synchronization of a Class of Time-Delayed Chaotic Systems Using Sliding Mode Control Based on a Fractional-Order Nonlinear PID Sliding Surface and Its Application in Secure Communication
Abstract
1. Introduction
- Using the NLFOPID sliding surface instead of conventional sliding surfaces.
- The existence of unknown time delays.
- The limits of uncertainty and disturbance are unknown.
2. Basic Definitions of the Fractional-Order Derivative
3. The System Descriptor Equations
4. The Sliding Mode Control Approach Based on NLFPID Controllers
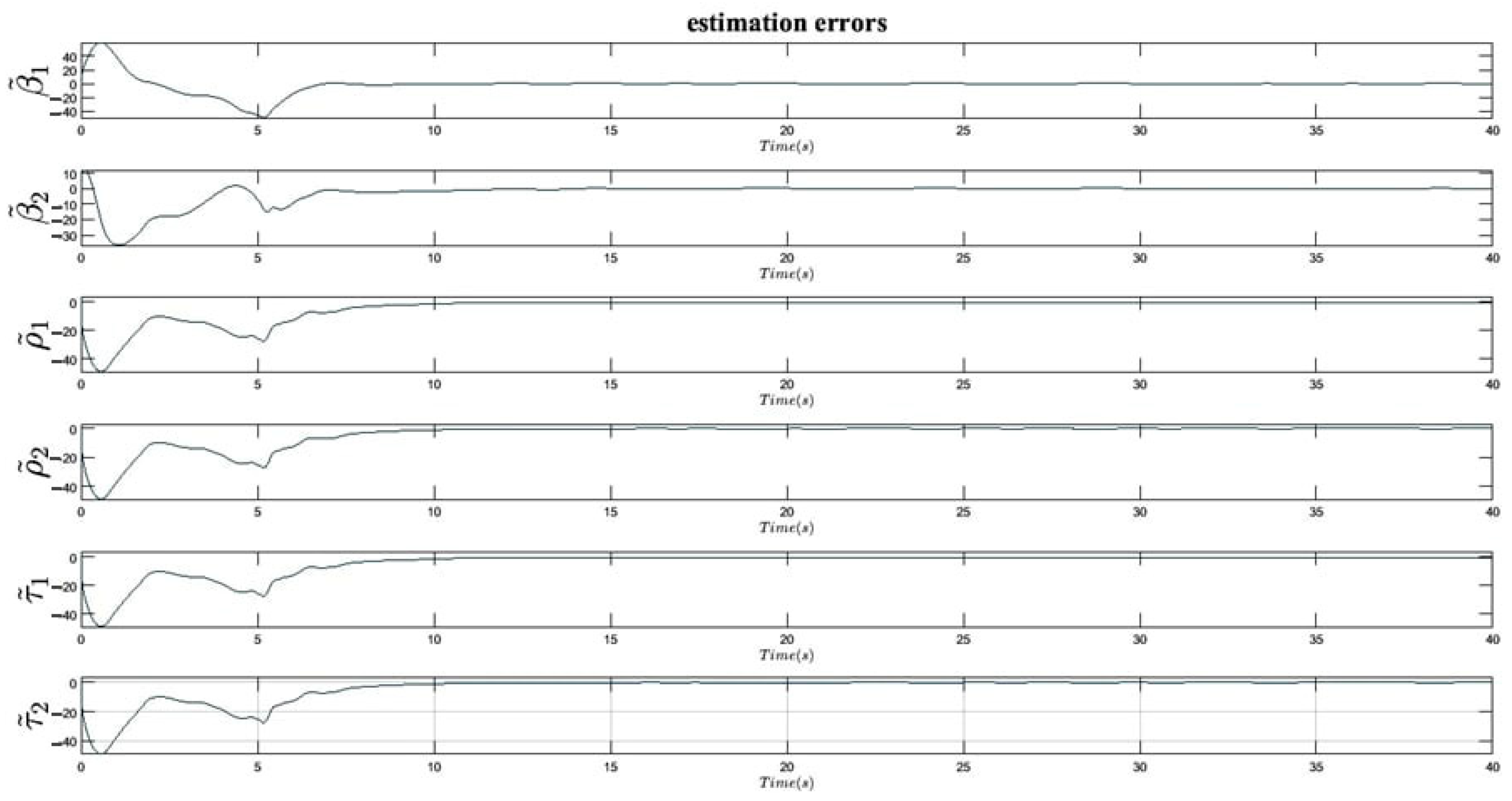
5. Stability Analysis of the Proposed Mechanism
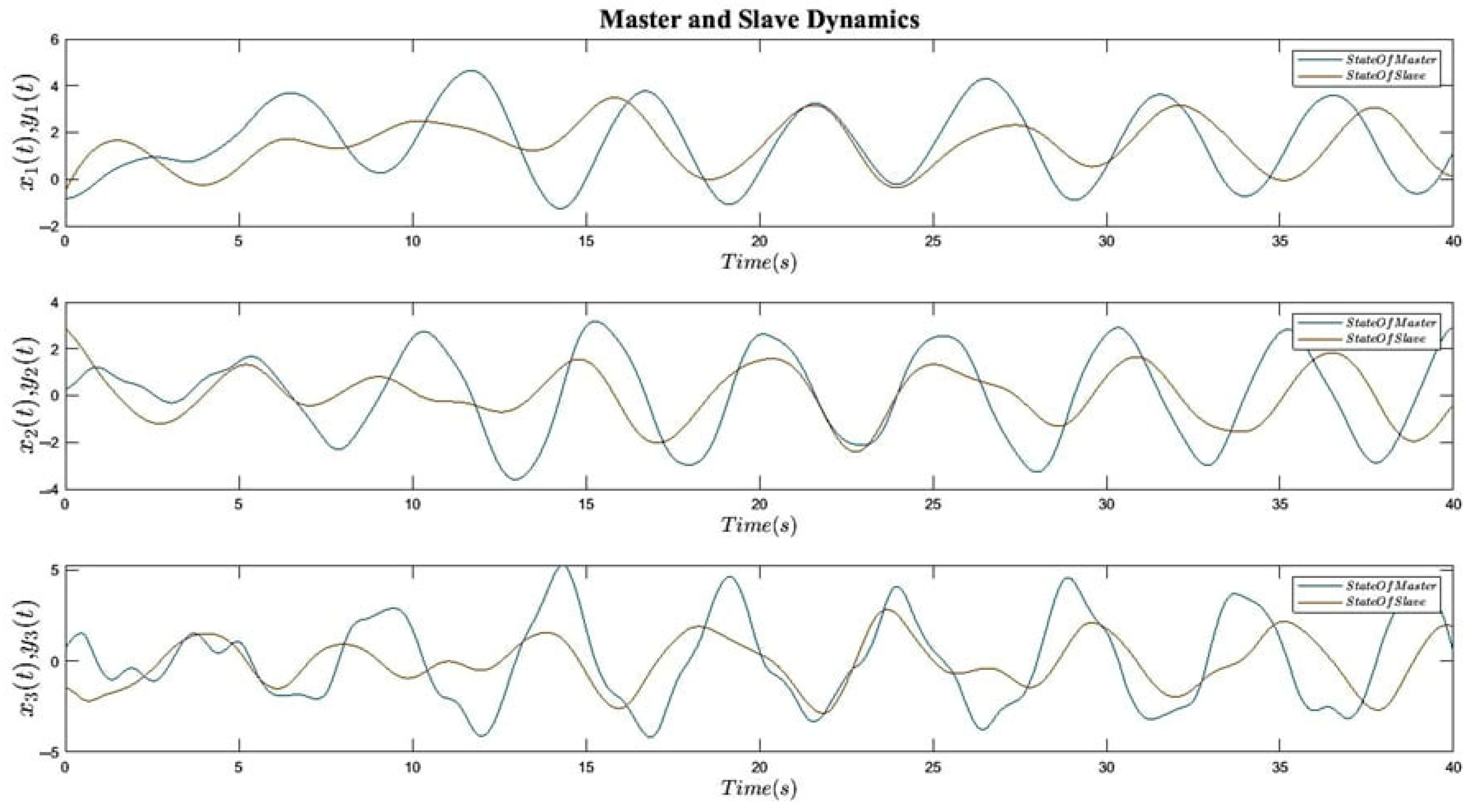
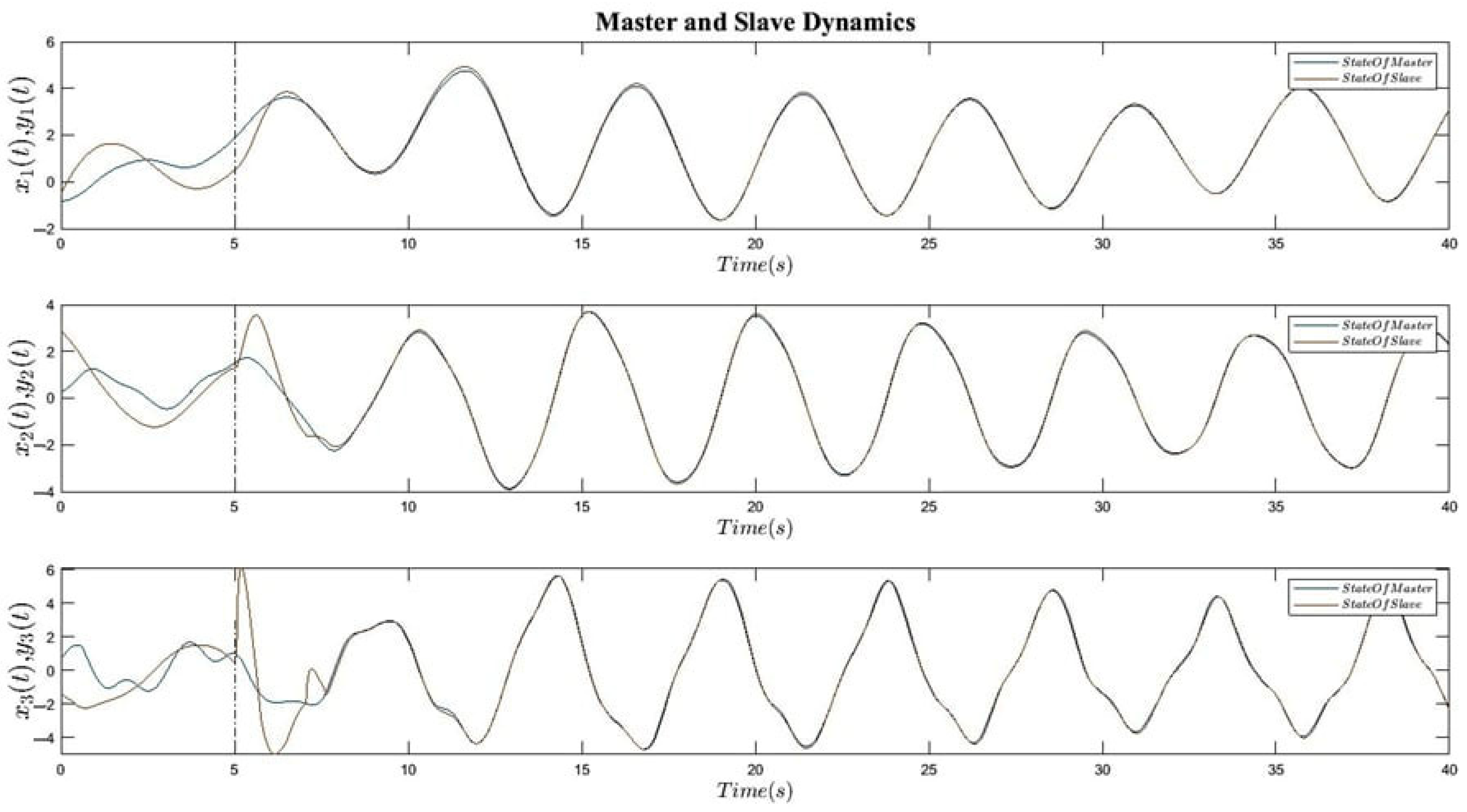
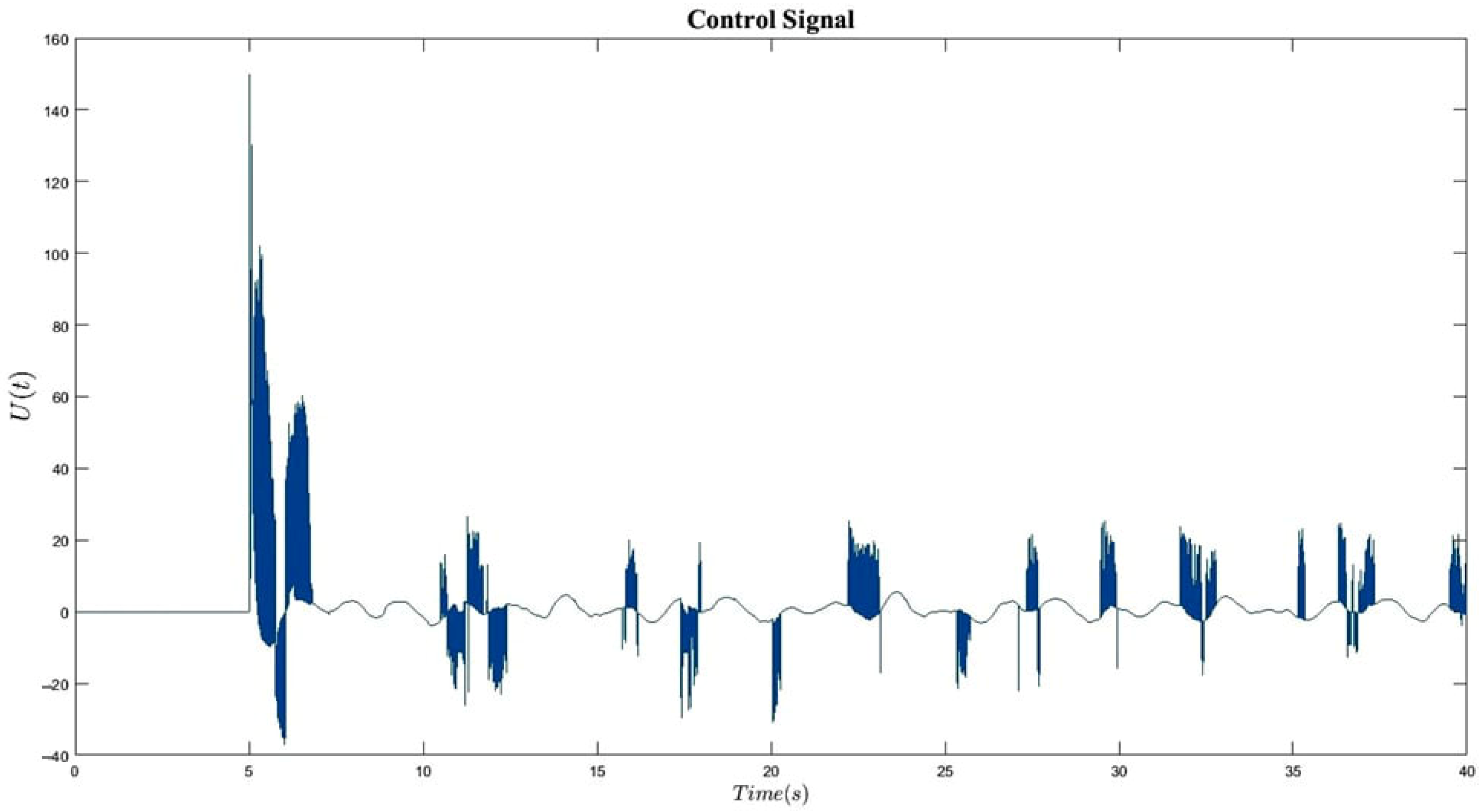
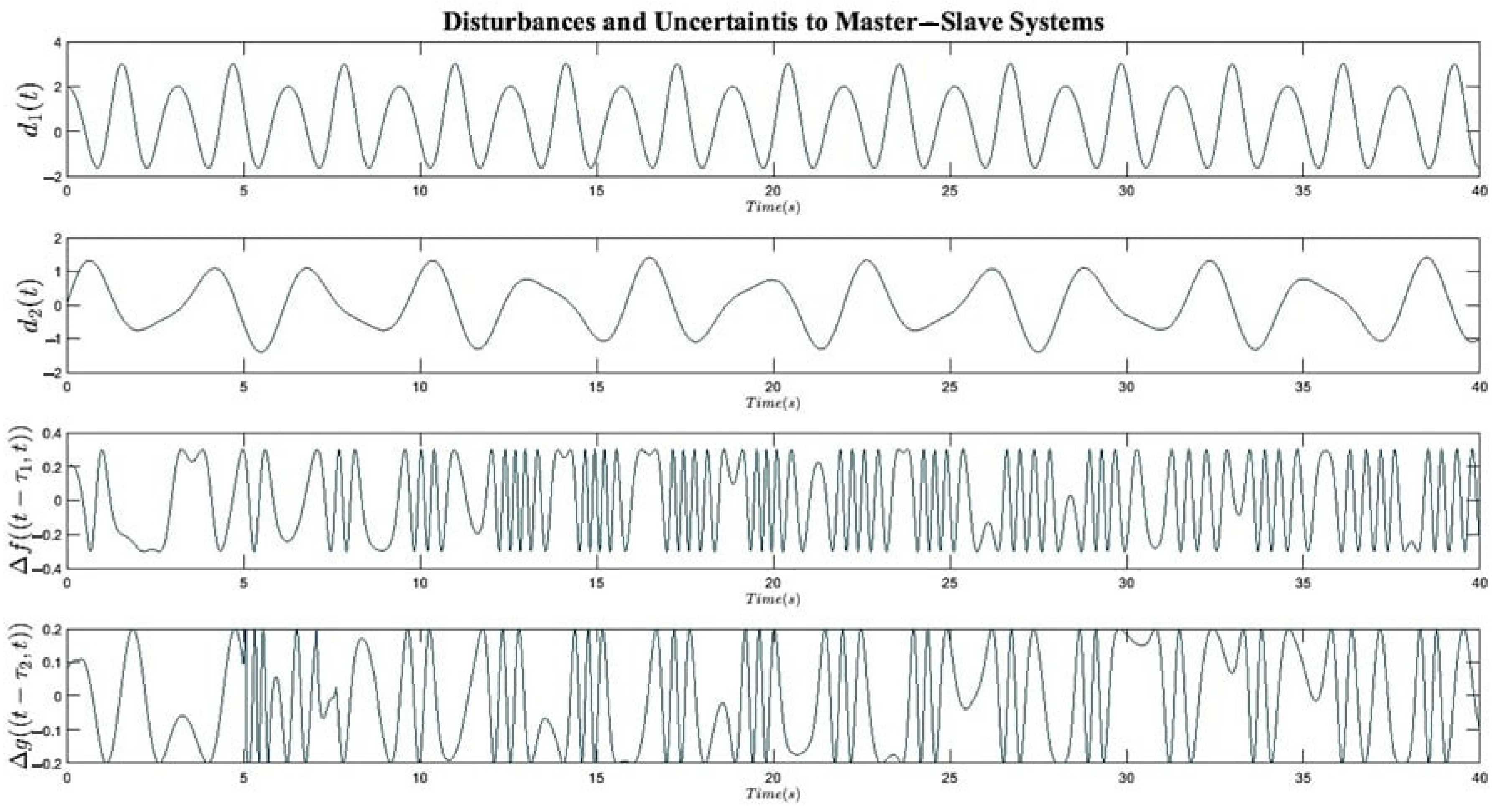
6. Simulation Results

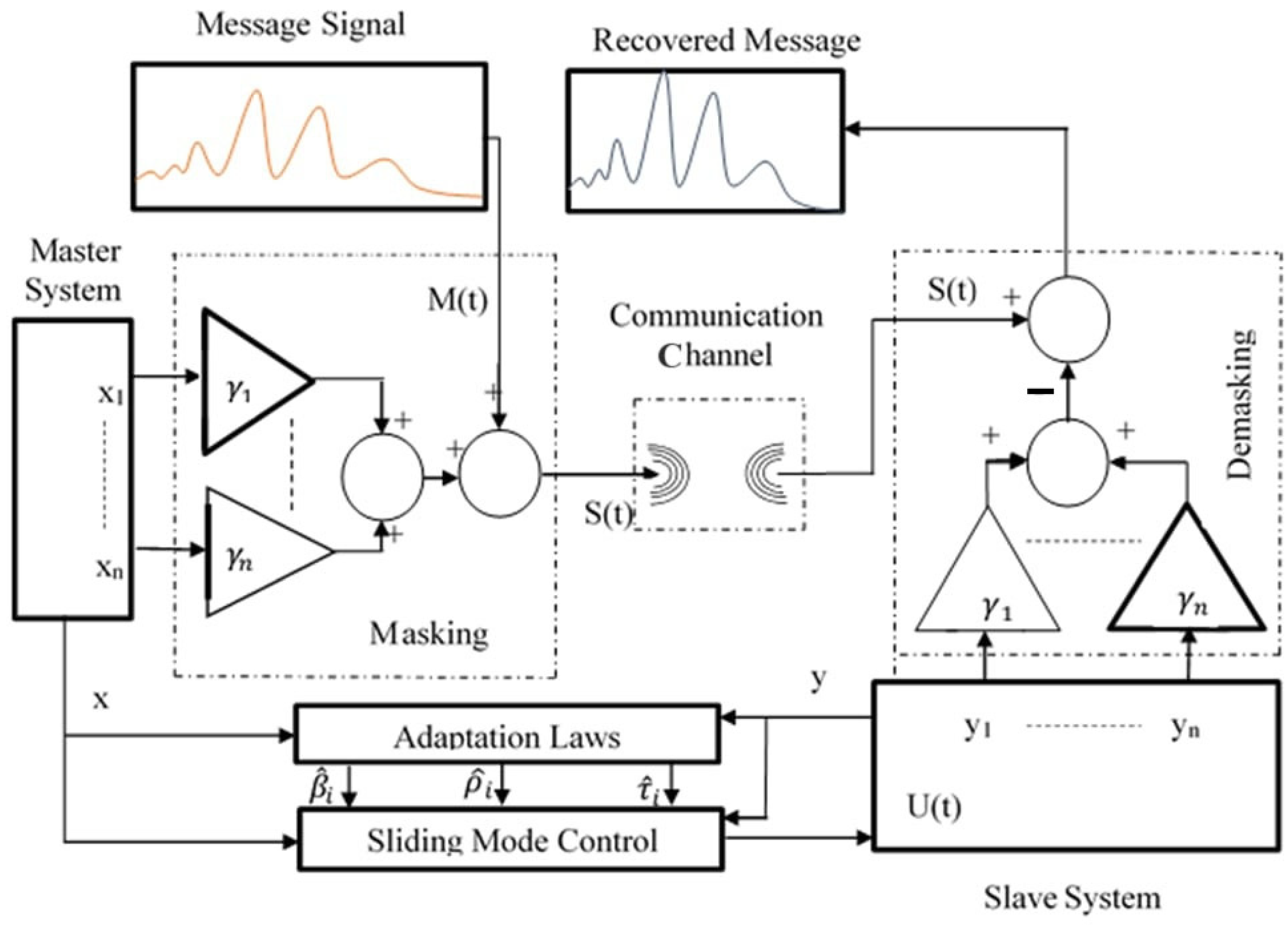
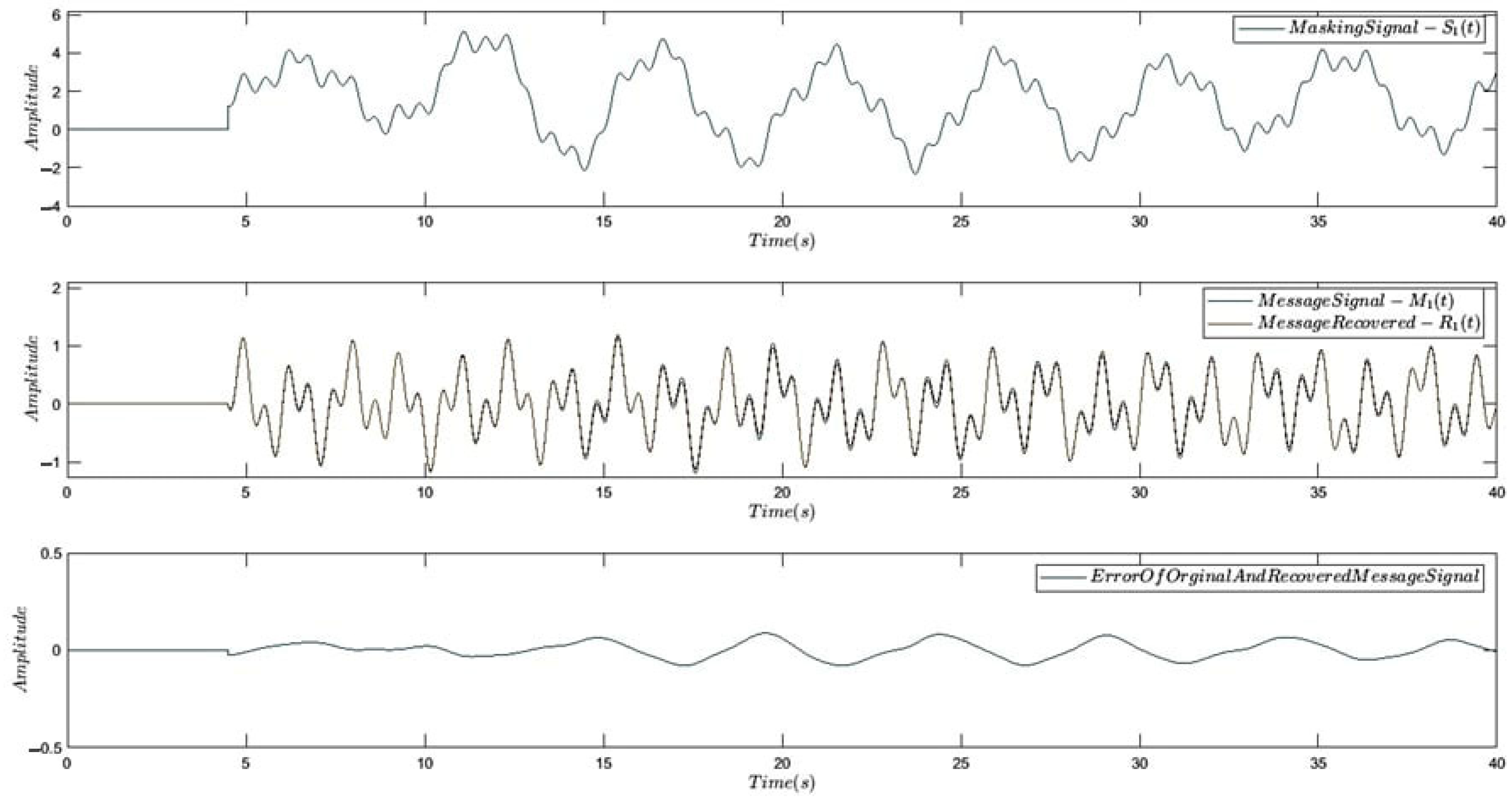
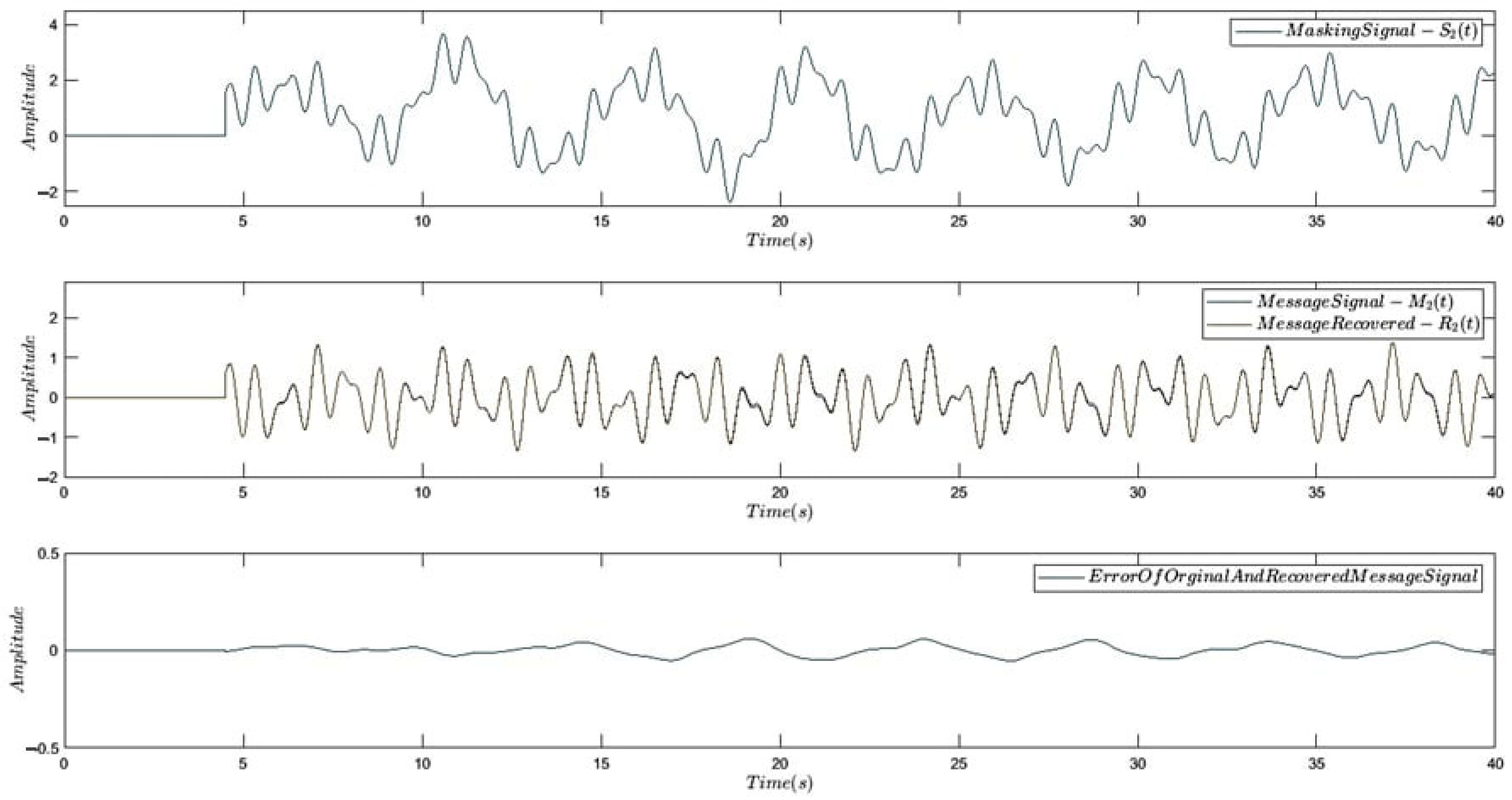
7. Application in Secure Communication
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peters, E.E. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Rössler, O.E. Chaos and chemistry. In Nonlinear Phenomena in Chemical Dynamics; Springer: Berlin/Heidelberg, Germany, 1981; pp. 79–87. [Google Scholar]
- Rapp, P.E. Chaos in the neurosciences: Cautionary tales from the frontier. Biologist 1993, 40, 89–94. [Google Scholar]
- Chen, Y.; Leung, A.Y. Bifurcation and Chaos in Engineering; Spfinge-Vereag: London, UK, 1998; pp. 169–180. [Google Scholar]
- Nijmeijer, H. Control of Chaos and Synchronization. Available online: https://www.sciencedirect.com/science/article/abs/pii/S016769119700042X?via%3Dihub (accessed on 1 December 2022).
- Pecora, L.M.; Thomas, L.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef] [PubMed]
- Maheswari, C.; Priyanka, E.; Meenakshipriya, B. Fractional order PIλDμ controller tuned by coefficient diagram method and particle swarm optimization algorithms for SO2 emission control process. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2017, 231, 587–599. [Google Scholar]
- Podlubny, I. Fractional-order systems and PI/sup/spl lambda//D/sup/spl mu//-controllers. IEEE Trans. Autom. Control. 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Rahimian, M.; Tavazoei, M. Stabilizing fractional-order PI and PD controllers: An integer-order implemented system approach. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2010, 224, 893–903. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Y. Fractional order [proportional derivative] controller for a class of fractional order systems. Automatica 2009, 45, 2446–2450. [Google Scholar] [CrossRef]
- Monje, C.A.; Calderon, A.J.; Vinagre, B.M.; Feliu, V. The fractional order lead compensator. In Proceedings of the Second IEEE International Conference on Computational Cybernetics, 2004. ICCC 2004, Vienna, Austria, 30 August–1 September 2004; pp. 347–352. [Google Scholar]
- Monje, C.A.; Vinagre, B.M.; Calderón, A.J.; Feliu, V.; Chen, Y.Q. Auto-tuning of fractional lead-lag compensators. IFAC Proc. Vol. 2005, 38, 319–324. [Google Scholar] [CrossRef]
- Oustaloup, A.; Sabatier, J.; Moreau, X. From fractal robustness to the CRONE approach. ESAIM Proc. 1998, 5, 177–192. [Google Scholar] [CrossRef]
- Yaghooti, B.; Salarieh, H. Robust adaptive fractional order proportional integral derivative controller design for uncertain fractional order nonlinear systems using sliding mode control. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2018, 232, 550–557. [Google Scholar] [CrossRef]
- Abedini, M.; Nojoumian, M.A.; Salarieh, H.; Meghdari, A. Model reference adaptive control in fractional order systems using discrete-time approximation methods. Commun. Nonlinear Sci. Numer. Simul. 2015, 25, 27–40. [Google Scholar] [CrossRef]
- Shi, B.; Yuan, J.; Dong, C. On fractional model reference adaptive control. Sci. World J. 2014, 2014, 521625. [Google Scholar] [CrossRef] [PubMed]
- Dumlu, A. Design of a fractional-order adaptive integral sliding mode controller for the trajectory tracking control of robot manipulators. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2018, 232, 1212–1229. [Google Scholar] [CrossRef]
- Binazadeh, T.; Shafiei, M. Output tracking of uncertain fractional-order nonlinear systems via a novel fractional-order sliding mode approach. Mechatronics 2013, 23, 888–892–892. [Google Scholar] [CrossRef]
- Chen, D.; Liu, Y.; Ma, X.; Zhang, R. Control of a class of fractional-order chaotic systems via sliding mode. Nonlinear Dyn. 2012, 67, 893–901. [Google Scholar] [CrossRef]
- Yahyazadeh, M.; Noei, A.R.; Ghaderi, R. Synchronization of chaotic systems with known and unknown parameters using a modified active sliding mode control. ISA Trans. 2011, 50, 262–267. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Ma, C. Modified projective synchronization of fractional-order chaotic systems via active sliding mode control. Nonlinear Dyn. 2012, 69, 511–517. [Google Scholar] [CrossRef]
- Yuan, W.; Zhou, J.; Nadal, I.; Boccaletti, S.; Wang, Z. Adaptive control of dynamical synchronization on evolving networks with noise disturbances. Phys. Rev. E 2018, 97, 022211. [Google Scholar] [CrossRef]
- Jajarmi, A.; Hajipour, M.; Baleanu, D. New aspects of the adaptive synchronization and hyperchaos suppression of a financial model. Chaos Solitons Fractals 2017, 99, 285–296. [Google Scholar]
- Cho, S.; Baek, J.; Han, S. Adaptive control using time delay control for synchronization of chaotic systems. In Proceedings of the 2016 16th International Conference on Control, Automation and Systems (ICCAS), Gyeongju, Republic of Korea, 16–19 October 2016; pp. 763–766. [Google Scholar]
- Li, W.; Liang, W.; Chang, K. Adaptive sliding mode control for synchronization of unified hyperchaotic systems. In Proceedings of the 2019 24th International Conference on Methods and Models in Automation and Robotics (MMAR), Międzyzdroje, Poland, 26–29 August 2019; pp. 93–98. [Google Scholar]
- Luo, J.; Qu, S.; Xiong, Z. Finite-time increased order chaotic synchronization using an adaptive terminal sliding mode control. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 1258–1263. [Google Scholar]
- Ghamati, M.; Balochian, S. Design of adaptive sliding mode control for synchronization Genesio–Tesi chaotic system. Chaos Solitons Fractals 2015, 75, 111–117. [Google Scholar] [CrossRef]
- Toopchi, Y.; Wang, J. Chaos control and synchronization of a hyperchaotic Zhou system by integral sliding mode control. Entropy 2014, 16, 6539–6552. [Google Scholar] [CrossRef]
- Mohadeszadeh, M.; Pariz, N. Hybrid control of synchronization of fractional order nonlinear systems. Asian J. Control. 2021, 23, 412–422. [Google Scholar] [CrossRef]
- Mirrezapour, S.Z.; Zare, A.; Hallaji, M. A new fractional sliding mode controller based on nonlinear fractional-order proportional integral derivative controller structure to synchronize fractional-order chaotic systems with uncertainty and disturbances. J. Vib. Control 2022, 28, 773–785. [Google Scholar] [CrossRef]
- Mahmoud, M.S. Disturbance observer-based robust control and its applications: 35th anniversary overview. IEEE Trans. Ind. Electron. 2019, 67, 2042–2053. [Google Scholar]
- Khan, A.; Nasreen; Jahanzaib, L.S. Synchronization on the adaptive sliding mode controller for fractional order complex chaotic systems with uncertainty and disturbances. Int. J. Dyn. Control. 2019, 7, 1419–1433. [Google Scholar] [CrossRef]
- Shirkavand, M.; Pourgholi, M. Robust fixed-time synchronization of fractional order chaotic using free chattering nonsingular adaptive fractional sliding mode controller design. Chaos Solitons Fractals 2018, 113, 135–147. [Google Scholar] [CrossRef]
- Sun, Z. Synchronization of fractional-order chaotic systems with non-identical orders, unknown parameters and disturbances via sliding mode control. Chin. J. Phys. 2018, 56, 2553–2559. [Google Scholar] [CrossRef]
- Zare, A.; Mirrezapour, S.Z.; Hallaji, M.; Shoeibi, A.; Jafari, M.; Ghassemi, N.; Alizadehsani, R.; Mosavi, A. Robust adaptive synchronization of a class of uncertain chaotic systems with unknown time-delay. Appl. Sci. 2020, 10, 8875. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation, 1st ed.; Springer Science & Business Media: London, UK, 2011. [Google Scholar]

| Root Mean Squre Error | |
|---|---|
| 0.041544 | 0.025857 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasouli, M.; Zare, A.; Hallaji, M.; Alizadehsani, R. The Synchronization of a Class of Time-Delayed Chaotic Systems Using Sliding Mode Control Based on a Fractional-Order Nonlinear PID Sliding Surface and Its Application in Secure Communication. Axioms 2022, 11, 738. https://doi.org/10.3390/axioms11120738
Rasouli M, Zare A, Hallaji M, Alizadehsani R. The Synchronization of a Class of Time-Delayed Chaotic Systems Using Sliding Mode Control Based on a Fractional-Order Nonlinear PID Sliding Surface and Its Application in Secure Communication. Axioms. 2022; 11(12):738. https://doi.org/10.3390/axioms11120738
Chicago/Turabian StyleRasouli, Mohammad, Assef Zare, Majid Hallaji, and Roohallah Alizadehsani. 2022. "The Synchronization of a Class of Time-Delayed Chaotic Systems Using Sliding Mode Control Based on a Fractional-Order Nonlinear PID Sliding Surface and Its Application in Secure Communication" Axioms 11, no. 12: 738. https://doi.org/10.3390/axioms11120738
APA StyleRasouli, M., Zare, A., Hallaji, M., & Alizadehsani, R. (2022). The Synchronization of a Class of Time-Delayed Chaotic Systems Using Sliding Mode Control Based on a Fractional-Order Nonlinear PID Sliding Surface and Its Application in Secure Communication. Axioms, 11(12), 738. https://doi.org/10.3390/axioms11120738







